Open Access Article
Open Access ArticleProbing the nature of Lewis acid sites on oxide surfaces with 31P(CH3)3 NMR: a theoretical analysis†
Farahnaz
Maleki
 and
Gianfranco
Pacchioni
and
Gianfranco
Pacchioni
 *
*
Dipartimento di Scienza dei Materiali, Università di Milano-Bicocca, via R. Cozzi 55, 20125 Milano, Italy. E-mail: gianfranco.pacchioni@unimib.it
First published on 10th August 2022
Abstract
The characterization of catalytic oxide surfaces is often done by studying the properties of adsorbed probe molecules. The 31P NMR chemical shift of adsorbed trimethylphosphine, P(CH3)3 or TMP, has been used to identify the presence of different facets in oxide nanocrystals and to study the acid–base properties of the adsorption sites. The NMR studies are often complemented by DFT calculations to provide additional information on TMP adsorption mode, bond strength, etc. So far, however, no systematic study has been undertaken in order to compare on the same footing the chemical shifts and the adsorption properties of TMP on different oxide surfaces. In this work we report the results of DFT+D (D = dispersion) calculations on the adsorption of TMP on the following oxide surfaces: anatase TiO2(101) and (001), rutile TiO2(110), tetragonal ZrO2(101), stepped ZrO2(134) and (145) surfaces, rutile SnO2(110), (101) and (100), wurtzite ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), and cubic CeO2(111) and (110). Beside the stoichiometric surfaces, also reduced oxides have been considered creating O vacancies in various sites. TMP has been adsorbed on top of variously coordinated Lewis acid cation sites, with the aim to identify, also with the support of machine learning algorithms, trends or patterns that can help to correlate the 31P chemical shift with physico-chemical properties of the oxide surfaces such as adsorption energy, Bader charges, cation–P distance, work function, etc. Some simple correlation can be found within the same oxide between the 31P chemical shift and the adsorption energy, while when the full set of data is considered the only correlation found is with the net charge on the TMP molecule, a descriptor of the acid strength of the adsorption site.
0), and cubic CeO2(111) and (110). Beside the stoichiometric surfaces, also reduced oxides have been considered creating O vacancies in various sites. TMP has been adsorbed on top of variously coordinated Lewis acid cation sites, with the aim to identify, also with the support of machine learning algorithms, trends or patterns that can help to correlate the 31P chemical shift with physico-chemical properties of the oxide surfaces such as adsorption energy, Bader charges, cation–P distance, work function, etc. Some simple correlation can be found within the same oxide between the 31P chemical shift and the adsorption energy, while when the full set of data is considered the only correlation found is with the net charge on the TMP molecule, a descriptor of the acid strength of the adsorption site.
Introduction
Nuclear magnetic resonance (NMR) is a powerful and sensitive technique that can be used to study catalytic sites and functional groups anchored on a surface.1 To this end one can directly investigate the NMR properties of the ions constituting the material, metal cations2 and oxygen anions,3,4 or use simple adsorbed molecules to probe the nature of the surface,5 in particular the acid or basic character of the adsorption sites. In this context, trimethylphosphine, P(CH3)3 or TMP, has been used to investigate oxide surfaces and characterize their acidity by studying the chemical shift of the 31P nucleus of adsorbed TMP.6 Probably one of the first studies in this field is that of Lunsford and co-workers who in 1984 studied the acidic properties of a zeolite.7 Since then, the method has been adopted for other oxides. More recently, Peng and co-workers8 have monitored the nature of various facets of anatase TiO2 (a-TiO2) nanoparticles using 31P NMR of adsorbed TMP as a surface probe. They showed that 31P NMR is capable of differentiating the facets of the titania nanoparticles. A peak at −36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ppm and a shoulder at −29
ppm and a shoulder at −29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ppm were assigned to the interaction of TMP with Ti4+ cations of the (101) and (001) facets, respectively. They also found that the TMP adsorption energy, as obtained from DFT calculations, correlates with the NMR chemical shift.8 Another oxide that has been investigated with this approach is zirconia. Isolated TMP molecules, and TMP coadsorbed with CO2, were used to study the basic properties of ZrO2 using 31P NMR.9 The 31P chemical shift of TMP adsorbed on zirconia has been discussed also in other studies, finding values in the range −28 to −50 ppm.10–13
ppm were assigned to the interaction of TMP with Ti4+ cations of the (101) and (001) facets, respectively. They also found that the TMP adsorption energy, as obtained from DFT calculations, correlates with the NMR chemical shift.8 Another oxide that has been investigated with this approach is zirconia. Isolated TMP molecules, and TMP coadsorbed with CO2, were used to study the basic properties of ZrO2 using 31P NMR.9 The 31P chemical shift of TMP adsorbed on zirconia has been discussed also in other studies, finding values in the range −28 to −50 ppm.10–13
SnO2 nanosheets and nano-shuttles were investigated using TMP probe molecules and 31P NMR to study the facet-dependent acidity.14 This work showed that the (001), (101), (110), and (100) facets can be differentiated by 31P NMR chemical shifts of adsorbed TMP. Also in this case, a linear correlation has been reported with the calculated adsorption energies of TMP on the various surfaces and the measured 31P chemical shift.14
Even ZnO plates, rods and powder samples have been investigated by means of 31P NMR of adsorbed TMP combined with DFT calculations.15 DFT was also used to study the interaction energy and the effect of oxygen vacancies on both nonpolar (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and polar (0002) surfaces of ZnO nanoparticles.15 As for other oxides, a linear relationship has been found between the adsorption energy of TMP and the calculated 31P NMR chemical shifts.
0) and polar (0002) surfaces of ZnO nanoparticles.15 As for other oxides, a linear relationship has been found between the adsorption energy of TMP and the calculated 31P NMR chemical shifts.
Finally, 31P NMR of TMP probe molecules has been used to investigate various facets of CeO2 octahedral, rod, and cube samples, as well as the concentrations of the corresponding sites.16 The dominant 31P NMR signal of adsorbed TMP is observed at −33, −47.5, and −58 ppm for octahedral, rod, and cube structures with dominant exposed (111), (110), and (100) facets, respectively. The adsorption energy of TMP on the regular CeO2(111), (110), and (100) surfaces and on the hydroxylated (111) and (100) surfaces was calculated at the DFT level and plotted against the 31P NMR chemical shifts. Notice however that these correlations are always found within the same acid center.17 The question whether similar correlations can be established for different oxides or not, so as to provide a scale of acidity of the surface from the analysis of the 31P chemical shift, remains open.
This brief summary shows the wide use of the 31P NMR technique to study oxide surfaces and the different morphologies of oxide nanostructures using adsorption of TMP probe molecules. In several of these studies the experimental results are complemented by specifically designed DFT calculations, showing a good potential of this approach to assign specific adsorption sites to a given NMR signal. However, so far, no systematic study of different oxide surfaces using the same computational approach has been reported. In the present study we compare, using the same DFT approach, the NMR chemical shifts of 31P for TMP molecules adsorbed on anatase and rutile TiO2, tetragonal ZrO2, rutile SnO2, cubic CeO2 and wurtzite ZnO. For some oxides different facets have been considered, and beside regular surfaces, in a few cases we also studied stepped surfaces with low-coordinated ions. Coverage effects on the chemical shifts have also been addressed. Finally, oxygen vacancies have been created on the surface of these oxides, and the consequences on the TMP adsorption and on the 31P NMR chemical shifts have been discussed.
Computational method
Density functional theory (DFT) calculations have been performed using the Vienna Ab Initio Simulation Package (VASP 5.4.4).18–20 For the exchange–correlation functional we used the Perdew, Burke and Ernzerhof (PBE) formulation,21 and to correct the self-interaction error, the PBE+U22,23 approach has been adopted using the following set of Hubbard U parameters: U = 3 eV for the 3d states of Ti,24U = 4.7 eV for the 3d states of Zn,25U = 4 eV for the 4d states of Zr,26U = 3.5 eV for the 4d states of Sn,27U = 4 eV for the Ce 4f states.27 Dispersion was included by means of the Grimme D3 approach.28,29 To describe the effect of the core electrons we used the projector augmented wave (PAW) method.30,31 The valence electrons explicitly considered are H (1s), C (2s, 2p), O (2s, 2p), P (3s, 3p), Ti (3s, 3p, 3d, 4s), Zn (3d, 4s), Zr (4s, 4p, 4d, 5s), Sn (4d, 5s, 5p), and Ce (5s, 6s, 5p, 4f, 5d). The energy cutoff for plane waves was set to 400 eV, and the optimizations were performed using the conjugate gradient scheme until the change in total energy between successive steps was less than 10−5 eV.We considered a-TiO2(101) surfaces with [3 × 1] and [2 × 1] supercells with 5 layers of Ti and 10 layers of O (5 TiO2 trilayers, Ti60O120 and Ti40O80 formula, respectively). Another titania facet, a-TiO2(001), was built with a [2 × 2] supercell with 6 layers of Ti and 12 layers of O (6 TiO2 trilayers, Ti24O48 formula). [3 × 2] and [2 × 1] supercells models were used for tetragonal ZrO2(101) with 5 layers of Zr and 10 layers of O (5 ZrO2 trilayers, Zr60O120 and Zr20O40 formula, respectively). The zirconia stepped surfaces, ZrO2(134) and ZrO2(145), were described as in our previous work.32 We described the SnO2(110) surface with [3 × 2] and [2 × 1] supercells with 5 layers of Sn and 10 layers of O (5 SnO2 trilayers, Sn60O120 and Sn20O40 formula, respectively). The same supercells were considered for the rutile r-TiO2(110) surface. SnO2(101) and (100) surfaces with [2 × 2] supercells with 5 and 7 layers of Sn and 10 and 14 layers of O, respectively (5 and 7 SnO2 trilayers, Sn40O80 and Sn28O56 formula, respectively) were considered. For CeO2(111) [2 × 2] and [1 × 1] supercells were used with 5 layers of Ce and 10 layers of O (5 CeO2 layers, Ce80O160 and Ce20O40 formula, respectively). The [2 × 1] and [1 × 1] supercells of CeO2(110) were built with 9 atomic layers of Ce and O (9 CeO2 layers, Ce36O72 and Ce18O36 formula, respectively). Finally, we studied two wurtzite ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) models with [3 × 2] and [2 × 2] supercells with 14 atomic layers of Zn and O (7 ZnO layers, Zn84O84 and Zn56O56 formula, respectively). In all cases the slabs were separated by more than 15 Å of vacuum.
0) models with [3 × 2] and [2 × 2] supercells with 14 atomic layers of Zn and O (7 ZnO layers, Zn84O84 and Zn56O56 formula, respectively). In all cases the slabs were separated by more than 15 Å of vacuum.
We optimized the bulk lattice parameters of each oxide using a kinetic energy cutoff of 600 eV and a 8 × 8 × 8 Monkhorst–Pack k-point grid. All atomic positions were fully optimized with convergence obtained when the ionic forces were smaller than |0.01| eV Å−1. Atomic charges have been determined using the Quantum Theory of Atoms in Molecules (QTAIM) or Bader analysis.33
The work function was computed as the energy of the vacuum level (determined applying a dipole correction to the unit cell) with respect to Fermi level (in this case the top of the valence band of the oxide).
The adsorption energies of TMP have been calculated as:
| Eads = E(TMP/MOx) − E(TMP)(g) − E(MOx) | (1) |
| Ef = E(MOx−1) + ½E(O2)(g) − E(MOx) | (2) |
Notice that at the PBE level the binding energy of the O2 molecule is overestimated, and this may reflect in some uncertainty in the computed O vacancy formation energies. However, the scope of this work is not to provide accurate values for this property but rather to assess the possibility to detect the presence of vacancies via31P NMR.
The isotropic chemical shift (δiso) is computed as δiso = σref − σcalc, where σref is the shielding value of the reference and σcalc is the chemical shielding obtained in VASP. VASP calculates the chemical “shifts” for non-metallic crystalline systems using the linear response method of Yates, Pickard, and Mauri.34,35 For 31P NMR, on the basis of experimental reports, we consider H3PO4 and (NH4)H2PO4 compounds as references since these are adopted in experimental studies. The VASP chemical shieldings for these compounds are 294 ppm and 283 ppm, respectively. With our setup the computed chemical shift for a free, gas-phase TMP molecule is of −60 ppm to be compared with an experimental value of −62 ppm, Table 1.36
| Φ | Isomer | E ads | Q | R M–P | σ calc | δ iso | δ exp | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P | M | P(CH3)3 | ||||||||||
| a Reference: H3PO4. b Reference: (NH4)H2PO4. | ||||||||||||
| Free P(CH3)3 | — | — | — | 1.20 | — | 0.00 | — | 354 | −60a | −62a | 34 | |
| a-TiO2(101) | [3 × 1] | 6.98 | 1 | −1.49 | 1.27 | 2.16 | 0.21 | 2.644 | 310 | −16a | −36a | 8 |
| [2 × 1] | 6.93 | 2 | −1.48 | 1.23 | 2.26 | 0.19 | 2.631 | 310 | −16a | |||
| 1 | −1.46 | 1.27 | 2.26 | 0.19 | 2.649 | 313 | −19a | |||||
| a-TiO2(001) | [2 × 2] | 5.93 | 2 | −1.29 | 1.20 | 2.23 | 0.15 | 2.602 | 319 | −25a | −29a | |
| 5.93 | 1 | −1.26 | 1.29 | 2.22 | 0.16 | 2.613 | 320 | −26a | ||||
| r-TiO2(110) | [3 × 2] | 6.93 | 2 | −1.76 | 1.23 | 2.25 | 0.24 | 2.659 | 298 | −4a | — | — |
| [2 × 1] | 6.89 | 2 | −1.05 | 1.21 | 2.25 | 0.17 | 2.700 | 319 | −25a | |||
| ZrO2(101) | [3 × 2] | 6.42 | 2 | −1.33 | 1.20 | 2.68 | 0.13 | 2.781 | 323 | −29a | −28 to −50a (average = −40) | 9–13 |
| 6.42 | 1 | −1.32 | 1.23 | 2.68 | 0.13 | 2.796 | 323 | −29a | ||||
| [2 × 1] | 6.48 | 2 | −1.30 | 1.25 | 2.68 | 0.10 | 2.789 | 328 | −34a | |||
| ZrO2(134) | [1 × 1] | 5.87 | 2 | −1.41 | 1.18 | 2.63 | 0.10 | 2.812 | 332 | −38a | ||
| ZrO2(145) | [1 × 1] | 6.31 | 1 | −1.43 | 1.22 | 2.65 | 0.12 | 2.809 | 333 | −39a | ||
| 6.31 | 2 | −1.44 | 1.21 | 2.63 | 0.10 | 2.799 | 332 | −38a | ||||
| SnO2(110) | [3 × 2] | 7.15 | 1 | −2.46 | 1.37 | 2.19 | 0.41 | 2.617 | 284 | −1b | −23b | 14 |
| [2 × 1] | 6.97 | 1 | −2.13 | 1.35 | 2.25 | 0.30 | 2.636 | 302 | −19b | |||
| SnO2(101) | [2 × 2] | 6.79 | 1 | −2.11 | 1.33 | 2.22 | 0.37 | 2.585 | 277 | 6b | −14b | |
| SnO2(100) | [2 × 2] | 7.69 | 1 | −1.57 | 1.31 | 2.23 | 0.27 | 2.698 | 302 | −19b | −29b | |
| CeO2(111) | [2 × 2] | 5.91 | 2 | −0.95 | 1.31 | 2.32 | 0.14 | 3.039 | 314 | −20a | −33a | 16 |
| [1 × 1] | 5.91 | 2 | −0.95 | 1.31 | 2.32 | 0.10 | 3.042 | 322 | −28a | |||
| 5.91 | 1 | −0.93 | 1.29 | 2.33 | 0.10 | 3.079 | 323 | −29a | ||||
| CeO2(110) | [2 × 1] | 4.16 | 1 | −0.85 | 1.25 | 2.30 | 0.07 | 3.148 | 340 | −46a | −47.5a | |
| [1 × 1] | 4.22 | 1 | −0.84 | 1.21 | 2.30 | 0.05 | 3.141 | 344 | −50a | |||
ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) 0) |
[3 × 2] | 5.82 | 1 | −1.68 | 1.37 | 1.07 | 0.27 | 2.339 | 335 | −41a | −43a | 15 |
| [2 × 2] | 5.87 | 1 | −1.63 | 1.33 | 1.03 | 0.24 | 2.347 | 337 | −43a | |||
| 5.87 | 2 | −1.60 | 1.37 | 1.05 | 0.24 | 2.354 | 340 | −46a | ||||
A search of correlations between some of the computed properties has been attempted using the classical approach to plot two variables. Beside this, a multiple linear regression method (MLR) has been used to fit (X1, X2, X3,…, y) with linear relationships to search for non-obvious correlations. Eqn (3) and (4) are multiple linear regression for one sample (Xn, yn) and multiple samples (X, y), respectively. In eqn (4), X is a N × (d + 1) matrix, where N is the number of data points and d is the number of parameters, so each row of X corresponds to one sample data [1, Xn1, Xn2, …, Xnd]. W is a column vector [b, W1, W2,…, Wd]T, where b is a scalar, representing the linear offset. The basic idea of multiple linear regression is to reduce the error between the fitted results yfit and the original set of values y.
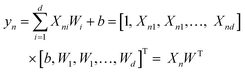 | (3) |
| y = XWT | (4) |
Results and discussion
1. TMP adsorption on stoichiometric oxide surfaces
We start the discussion from TMP adsorption on anatase and rutile TiO2, Fig. 1(a–c) and Table 1. TMP always binds preferentially with a P atom pointing towards a surface Ti4+ cation with binding energies that, at low coverage, go from −1.76 eV on r-TiO2(110) to −1.49 eV on a-TiO2(101) and −1.29 eV on a-TiO2(001). Notice that slightly different isomers can form, with very similar stabilities, Table 1. This depends on the rotation of the methyl groups with respect to the surface. At higher coverage we found a significant change in binding only for the r-TiO2(110) surface where Eads becomes −1.05 eV. In all cases the distance of the TMP molecule from the surface Ti atom is similar, around 2.6 Å, and increases slightly for higher coverages, Table 1. The computed 31P chemical shifts, referred to H3PO4, show a dependence both on the surface and on the coverage. On a-TiO2(101) at low coverage δiso is −16 ppm and it becomes −19 ppm at higher coverage. Experimentally, a chemical shift of −36 ppm has been assigned to TMP adsorbed on this surface.8 A more pronounced chemical shift, −25 ppm, is computed for the a-TiO2(001) surface, to be compared with the value of −29 ppm reported experimentally.8 On this surface virtually no change is found by increasing the coverage.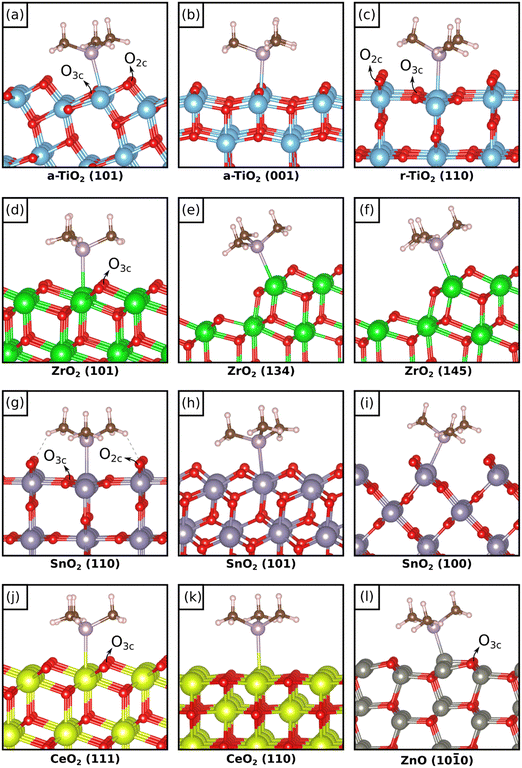 | ||
| Fig. 1 Most stable isomers of adsorbed TMP on the different oxides and facets considered in this work. | ||
If we plot the computed 31P chemical shift versus the adsorption energies we found a linear behavior with good correlation (R2 = 0.97, Fig. 2); of course, one has to consider that this correlation is obtained with only five values; furthermore, the changes in chemical shift are rather small (from −16 to −26 ppm). Nevertheless, a trend is present and shows more negative values for weaker TMP–surface interaction.
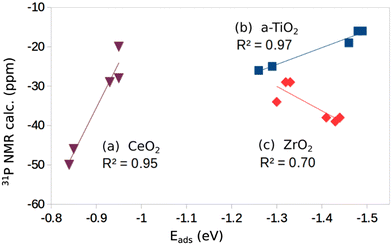 | ||
| Fig. 2 Plot of computed 31P chemical shift versus adsorption energy for individual oxide surfaces: (a) CeO2, (b) a-TiO2, (c) ZrO2. | ||
On the rutile structure, r-TiO2(110), the chemical shift shows a pronounced dependence on the coverage, and goes from −4 ppm at low coverage to −25 ppm at high coverage, Table 1. No experimental data seem to exist for this surface. When we try to add the two points computed for r-TiO2(110) to the plot of Fig. 2 the regression deteriorates and R2 becomes 0.85. This seems to indicate that a correlation between adsorption energy and chemical shift exists, but only within a given polymorph.
We move now to the zirconia surface, Fig. 1d. Here we considered the most stable (101) surface of tetragonal zirconia, t-ZrO2(101), and we studied the dependence of 31P chemical shift of adsorbed TMP on both coverage and coordination of the cation sites. To this end we considered the stepped ZrO2(134) and ZrO2(145) surfaces,37Fig. 1e, f and Table 1. On t-ZrO2(101) TMP binds to Zr7c4+ ions with Eads = −1.33 eV, a value that does not change with coverage, Table 1. On the low-coordinated Zr6c sites of the stepped surfaces the adsorption is only slightly higher, −1.41 eV or −1.44 eV. On all these systems the distance of TMP from the surface Zr ion is similar and is around 2.80 Å, Table 1. The chemical shifts of 31P go from −29 ppm on t-ZrO2(101) at low coverage, to −34 ppm by increasing the coverage. So, the density of the TMP molecules weakly affects both the adsorption energy and the chemical shift. More pronounced is the effect of coordination of the Zr ion, as the chemical shift becomes −38/−39 ppm on the two stepped zirconia surfaces. Experimentally, a range of −28 to −50 ppm has been reported for TMP on this surface,9–13 suggesting a possible role of low-coordinated sites and a relatively high coverage of TMP molecules in the measured samples.
In Fig. 2 we report the correlation between the computed 31P chemical shifts and adsorption energies (6 values). The correlation is not as good as found for the a-TiO2 system (R2 = 0.70, Fig. 2). On the other hand, also in this case a trend is found but the slope of the curve is opposite to the titania case, since here more negative values of the chemical shift correspond to more strongly bound TMP molecules, Fig. 2.
The next oxide analyzed is SnO2. Here we considered the rutile structure and the (110), (101) and (100) surfaces, Fig. 1g–i. Notice that for this oxide the reference of the chemical shifts is not the H3PO4 molecule as in other cases, but the (NH4)H2PO4 ammonium compound in order to compare our results with existing measured data14 (in order to compare with H3PO4 one has to add +11 ppm to the values of Table 1). On the r-SnO2(110) surface TMP is strongly bound with Eads = −2.46 eV, a value that decreases to −2.13 eV for higher coverage, Table 1. On the other surfaces TMP is less strongly bound and exhibits Eads = −2.11 eV on the (101) surface and −1.57 eV on the (100) facet. These values are somewhat larger than those reported by Zhang et al.14 because no dispersion was included in their study. Furthermore, their calculations refer to high coverage adsorption, and we have shown that the adsorption energy is sensitive to the coverage (see above). A great variability of the adsorption energy is found as a function of the surface structure. This is partly reflected in the Sn–P distance that shows a larger variation than in previous cases: it goes from a minimum of 2.585 Å on SnO2(101) to 2.698 Å on the (100) surface, Table 1.
The variability in adsorption energy and Sn–P distance is only partly reflected in the NMR chemical shifts. On r-SnO2(110) the 31P chemical shifts (referred to (NH4)H2PO4) is of −1 ppm at low coverage. This becomes −19 ppm at high coverage, a value close to the experimental measurement of −23 ppm.14 On the (101) and (100) surfaces, and for low coverage, the chemical shifts are 6 and −19 ppm, respectively, to be compared with experimental values of −14 and −29 ppm attributed to TMP adsorbed on these surfaces. Thus, the results show a significant dependence both on facet exposed and density of TMP molecules on the surface. In general, the agreement with the measured values is better when higher coverage of TMP is considered. Due to the small number of points, we did not attempt to correlate chemical shift and adsorption energy.
Two surfaces of CeO2 have been considered, the (111) and the (110), Fig. 1j and k, and Table 1. Of all the oxides considered, CeO2 shows the smallest binding with TMP and the longest cation–TMP distance: the binding energies, close to those reported by Tan et al.,16 go from −0.84 to −0.95 eV depending on the facet and on the coverage, while the distance goes from a minimum of 3.039 Å on CeO2(111) (low coverage) to a maximum of 3.148 Å on CeO2(110) (low coverage). These changes result in different 31P chemical shifts of TMP. On CeO2(111) we compute a value of −20 ppm at low coverage (reference H3PO4) and −29 ppm at high coverage (showing once more a dependence on the coverage). These values are in excellent agreement with a peak in the NMR spectra at −33 ppm observed experimentally.16 On the CeO2(110) surface the chemical shift is considerably larger in absolute value, −46 ppm at low coverage and −50 ppm at high coverage, again in close agreement with the experiment that shows a peak at −47.5 ppm attributed to TMP adsorbed on the (110) CeO2 surface.16 A nice correlation is found when we plot the chemical shifts for the five cases considered versus the strength of the TMP bond to CeO2 (R2 = 0.95) (Fig. 2). Here a weaker bonding corresponds to a more negative chemical shift, the same trend observed for TiO2 but opposite to what found for ZrO2.
Finally, only the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface of ZnO has been considered, Fig. 1l. Notice that the main difference in this system compared to the other oxides is the formal charge of the cation, which is +II while it is +IV in the rest of systems considered. We used two supercells that allow us to study the role of coverage. This is relatively minor on the adsorption energy, which goes from −1.68 eV to −1.60 eV going from the [3 × 2] to the [2 × 2] supercell, and modest also on the chemical shift, as this goes from −41 ppm (low coverage) to −46 ppm (high coverage). These values are in close agreement with the reported experimental shift of −43 ppm for TMP on ZnO, Table 1 (reference H3PO4).15 The adsorption energies are about 50% larger than those reported by Peng et al.15 due to the inclusion of dispersion in our work. The Zn–P distance is the shortest among the cation–P distances of all oxides considered, about 2.35 Å, Table 1. This, however, is not a factor contributing the final value of the chemical shift, as we will show below.
0) surface of ZnO has been considered, Fig. 1l. Notice that the main difference in this system compared to the other oxides is the formal charge of the cation, which is +II while it is +IV in the rest of systems considered. We used two supercells that allow us to study the role of coverage. This is relatively minor on the adsorption energy, which goes from −1.68 eV to −1.60 eV going from the [3 × 2] to the [2 × 2] supercell, and modest also on the chemical shift, as this goes from −41 ppm (low coverage) to −46 ppm (high coverage). These values are in close agreement with the reported experimental shift of −43 ppm for TMP on ZnO, Table 1 (reference H3PO4).15 The adsorption energies are about 50% larger than those reported by Peng et al.15 due to the inclusion of dispersion in our work. The Zn–P distance is the shortest among the cation–P distances of all oxides considered, about 2.35 Å, Table 1. This, however, is not a factor contributing the final value of the chemical shift, as we will show below.
2. TMP adsorption on reduced oxide surfaces
In the previous section we have discussed the adsorption of TMP on the regular, non-defective surfaces of TiO2, ZrO2, SnO2, CeO2 and ZnO. With the exception of zirconia,38 all the other oxides are classified as reducible oxides characterized by a band gap of 2–4 eV, typical of wide gap semiconductors, and by the relatively easy loss of oxygen under reactive conditions with formation of oxygen vacancies, VO.39 For these oxides, again with the exception of bulk zirconia, the presence of oxygen vacancies is rather common and often it is difficult to prepare non defective surfaces. In reducible oxides the removal of O atoms results in excess electrons that are transferred to the bottom of the conduction band. This can lead to charge localization with polaron formation.40 The most studied cases in this respect are those of TiO2−x and CeO2−x oxides where the excess of charge associated to VO centers localizes on Ti 3d or Ce 4f states. Even ZrO2, when produced in form of nanoparticles or nanofilms, increases considerably its reducibility and can lose oxygen quite easily, as recently shown both theoretically,41,42 and experimentally.43In this respect, it is interesting to study the possibility to use the 31P NMR signal of adsorbed TMP to address the effect of the presence of oxygen vacancies on the surface of the oxide. So far, the role of vacancies on the 31P chemical shift of TMP has not been studied in a systematic way. We removed an O atom from various positions of the most stable surfaces (see Fig. 1 where the Onc atoms removed are indicated) and we computed the NMR chemical shift of the TMP probe molecule adsorbed on the same cation shown in the figure, which is next neighbor or in close proximity of the defect center. Notice that it is not our aim to study the relative stability of O vacancies in these oxides (for instance in anatase TiO2 O vacancies form in the sub-surface, not on the surface), nor the level of electron localization that follows the O removal. Here we only want to see how the 31P NMR properties are depending on the presence of these defects. The analysis has been done for the larger supercells in order to avoid spurious effects due to an excessive number of O vacancies. The results, Table 2, are directly compared with those of the same system in absence of vacancies.
| E f | Isomer | E ads | q | R M–P | σ calc | δ iso | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| P | M | P(CH3)3 | ||||||||
| a-TiO2(101) | [3 × 1] | — | 1 | −1.49 | 1.27 | 2.16 | 0.21 | 2.644 | 310 | −16 |
| [3 × 1]_VO2c | 4.67 | 1 | −1.66 | 1.21 | 2.17 | 0.24 | 2.567 | 299 | −5 | |
| [3 × 1]_VO3c | 5.68 | 1 | −1.60 | 1.23 | 2.00 | 0.16 | 2.629 | 317 | −23 | |
| r-TiO2(110) | [3 × 2] | — | 2 | −1.76 | 1.23 | 2.25 | 0.24 | 2.659 | 298 | −4 |
| [3 × 2]_VO2c | 3.05 | 2 | −1.64 | 1.18 | 2.24 | 0.20 | 2.644 | 277 | 17 | |
| [3 × 2]_VO3c | 4.90 | 2 | −1.51 | 1.23 | 2.20 | 0.21 | 2.700 | 273 | 21 | |
| ZrO2(101) | [3 × 2] | — | 2 | −1.33 | 1.20 | 2.68 | 0.13 | 2.781 | 323 | −29 |
| [3 × 2]_VO | 5.97 | 2 | −1.35 | 1.16 | 2.39 | −0.02 | 2.745 | 321 | −27 | |
| SnO2(110) | [3 × 2] | — | 1 | −2.46 | 1.37 | 2.19 | 0.41 | 2.617 | 284 | 10 |
| [3 × 2]_VO2c | 2.32 | 2 | −2.11 | 1.28 | 2.24 | 0.33 | 2.605 | 304 | −10 | |
| [3 × 2]_VO3c | 3.47 | 1 | −2.23 | 1.27 | 1.97 | 0.42 | 2.631 | 273 | 21 | |
| CeO2(111) | [2 × 2] | — | 2 | −0.95 | 1.31 | 2.32 | 0.14 | 3.039 | 314 | −20 |
| [2 × 2]_VO | 2.85 | 2 | −1.08 | 1.15 | 2.30 | 0.07 | 3.131 | 333 | −41 | |
ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) 0) |
[3 × 2] | — | 1 | −1.68 | 1.37 | 1.07 | 0.27 | 2.339 | 333 | −41 |
| [3 × 2]_VO | 3.09 | 1 | −1.47 | 1.27 | 0.70 | 0.24 | 2.396 | 334 | −40 | |
On a-TiO2(101) both O2c and O3c atoms from the top layer have been removed, Fig. 1a. The vacancy formation energy, Ef = 4.67 eV, obviously indicates preferential removal of O2c with respect to O3c, Ef = 5.68 eV, Table 2. The adsorption energy of TMP to the adjacent Ti4+ site is similar to the corresponding regular surface: defective TiO2Eads = −1.66 eV (near VO2c) or −1.60 eV (near VO3c), respectively, to be compared with the regular surface Eads = −1.49 eV. The Ti–P distance is affected only for the case of VO2c, where it becomes 2.567 Å (2.644 Å on the non-defective surface). When the O2c atom is removed, the 31P signal of TMP shifts by 11 ppm, and goes from −16 ppm on the regular surface to −5 ppm on the reduced one. An opposite effect is found when the O3c atom is removed, as here the 31P chemical shift is −23 ppm, with an additional shift of −7 ppm. Notice however that VO3c centers hardly form due to the large difference in formation energy of the two defects, see Table 2.
On the rutile polymorph, r-TiO2(110), Fig. 1c, the removal of O has a lower cost than on anatase TiO2, in particular for the O2c atoms (Ef = 3.05 eV) compared to the O3c ones (Ef = 4.90 eV). When a VO2c is created, the adsorption energy of TMP to an adjacent Ti4+ site, Eads = −1.64 eV, is smaller in absolute value than on the regular surface, Eads = −1.76 eV (the effect is even larger for O3c, Table 2). No major change in the Ti–P distance is observed, Table 2. Interestingly, the 31P chemical shift goes from δiso = −4 ppm on regular r-TiO2(110) to δiso = 17 ppm on the reduced surface, r-TiO2−x(110), with a positive shift of 21 ppm, the same direction found for the anatase polymorph but more pronounced. A similar situation is found for a VO3c defect since also in this case δiso goes from −4 to +21 ppm.
Removing an O3c atom from the (101) surface of ZrO2, Fig. 1d, has a cost that, not surprisingly, is almost twice that of r-TiO2(110) (Ef = 5.97 eV, Table 2). The high band gap of zirconia results in a different electronic structure of the defect, with the excess of charge mostly localized inside the vacancy38 instead of being transferred to the low-coordinated Zr ion. This fact results in virtually no change in the properties of adsorbed TMP: Eads (−1.33 eV on the regular surface) becomes −1.35 eV, the Zr–P distance from 2.781 Å becomes 2.745 Å, and δiso from −29 ppm becomes −27 ppm. Even the charge distribution remains unchanged, Table 2. It seems that on ZrO2 the NMR signal is insensitive to the presence of O vacancies.
The SnO2(110) surface has the same structure as r-TiO2(110) but the removal of oxygen, Fig. 1g, has a much lower cost. Ef(VO2c) is in fact 2.32 eV, and also Ef(VO3c), 3.47 eV, is relatively low. When a TMP molecule is adsorbed near a vacancy the adsorption strength is reduced, −2.11 eV versus −2.46 eV on the regular surface (a similar effect is found for O3c, Table 2). Virtually no change is observed on the Sn–P distance, Table 2. On the other hand, the 31P NMR chemical shift is sensitive to the presence of the vacancy, and δiso goes from 10 ppm on stoichiometric SnO2 to −10 ppm on the reduced one, Table 2, with a shift of −20 ppm (here the shifts are given with respect to the H3PO4 molecule, as for the other systems). The effect is of similar magnitude to that computed for rutile TiO2, but of opposite sign! When the O3c atoms are removed, a hypothetical situation given the large difference in formation energy, δiso becomes 21 ppm, with a positive shift of +11 ppm due to the presence of the vacancy.
The next oxide studied is CeO2(111). Here the formation of an O3c vacancy, Fig. 1j, has a cost of 2.85 eV, comparable to that of r-TiO2 and ZnO, Table 2. The adsorption energy of TMP on the Ce ion is only moderately affected and goes from −0.95 eV on stoichiometric CeO2 to −1.08 eV on reduced CeO2, Table 2. The Ce–P distance shows an opposite behavior and becomes slightly larger (3.131 Å) for the reduced oxide where the bonding is stronger, compared to the regular surface (3.039 Å) which exhibits a weaker interaction. The presence of the VO3c center results in a significant change in the chemical shift of 31P that goes from −20 to −40 ppm. This is the same change in chemical shift observed for SnO2(110), but is associated to a reinforcement of the adsorption energy, while in SnO2 the additional shift of −20 ppm on the reduced surface is accompanied by a decrease of the TMP bond strength.
The last oxide considered is ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), where the formation of an O3c vacancy, Fig. 1l, costs 3.09 eV, Table 2. On the reduced surface TMP binds less strongly than on the regular surface, the same trend observed on r-TiO2(110) and on SnO2(110) (from −1.68 eV to −1.47 eV), but the 31P chemical shift remains unchanged, −41 ppm versus −40 ppm, the same effect found on zirconia. The practically identical chemical shift for regular and reduced ZnO surfaces is accompanied by slightly different Zn–P distances, 2.339 Å (regular) versus 2.396 Å (reduced), showing that a change of 0.06 Å in the distance does not result in a significant change in the 31P chemical shift.
0), where the formation of an O3c vacancy, Fig. 1l, costs 3.09 eV, Table 2. On the reduced surface TMP binds less strongly than on the regular surface, the same trend observed on r-TiO2(110) and on SnO2(110) (from −1.68 eV to −1.47 eV), but the 31P chemical shift remains unchanged, −41 ppm versus −40 ppm, the same effect found on zirconia. The practically identical chemical shift for regular and reduced ZnO surfaces is accompanied by slightly different Zn–P distances, 2.339 Å (regular) versus 2.396 Å (reduced), showing that a change of 0.06 Å in the distance does not result in a significant change in the 31P chemical shift.
These results clearly show that it is not straightforward to find a simple direct correlation between the 31P chemical shift and the nature of the oxide surface, stoichiometric or reduced. Despite the fact that the TMP molecule is adsorbed near the defect, the analysis of the six oxides shows a scattered behavior when an O atom is removed. On TiO2, both anatase and rutile, when the surface is reduced there is an additional positive shift in δiso of about 10–20 ppm. On SnO2 and CeO2 the adsorption of TMP on the reduced surfaces results in an additional chemical shift of about −20 ppm, opposite to the TiO2 case. Finally, for ZnO and ZrO2 there is virtually no difference in the chemical shift of TMP adsorbed on the regular or on the reduced surface. Furthermore, if we add the computed adsorption energies for the reduced oxides to the correlation curves obtained for the stoichiometric surface, Fig. 2, we observe a deterioration of R2. While disappointing, these results reflect the complexity of the origin of the 31P chemical shift in these systems.
3. Trends and correlations
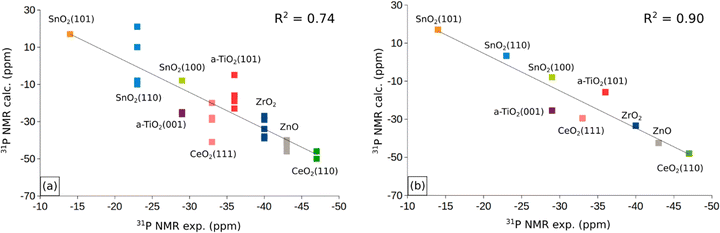
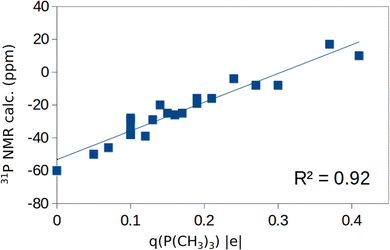
In the previous sections we have presented the raw data related to the properties of TMP molecules adsorbed on the cation sites of various oxide surfaces. A first question to address is the robustness of the computed data set. To address this point, in Fig. 3a and b we have plotted the computed versus the measured 31P NMR chemical shifts for all the systems and sites considered. In Fig. 3a we included the δiso values obtained for both the stoichiometric and reduced (defective) surfaces. Of course, the number of computed points is larger than that of the experimental data, as these cannot easily distinguish the presence of steps, defects, low-coordinated sites. Fig. 3a shows a general trend but a moderate correlation with a R2 factor of 0.74. In Fig. 3b we report the same analysis, but we averaged the computed values for each surface facet (regular or defective) and we obtain an overall good linear correlation with R2 = 0.90. The use of an average for each facet of the computed values for stoichiometric/reduced oxides is motivated by the fact that NMR spectra provide an integrated measure of oxide nanoparticles that may contain defects and irregularities. This shows that the computational approach followed reproduces the experimental trend for the various oxides, and that the computed δiso values, despite the small data set, can be used to try to find non-obvious correlations with the help of machine learning algorithms (see below).Before to attempt the use of a machine learning approach, we have plotted in Fig. S1 of the ESI† the computed 31P chemical shifts versus some of the fundamental properties reported in Tables 1 and 2: adsorption energy, Eads, charge on P atom as obtained from a Bader analysis, q(P), charge on the surface cation where the TMP molecule is adsorbed, q(M), net charge on the whole TMP molecule, q(P(CH3)3), cation–P distance, RM–P, Table 1. All computed values are included in these plots. The plot of the 31P chemical shift versus the adsorption energy, Eads, (Fig. S1a, ESI†) shows a general trend towards more positive values for stronger adsorption bonds, but with a very poor correlation (R2 = 0.41). No correlation at all exists with the charge on the P atom of TMP, Fig. S1b (ESI†), or with the charge of the metal cation, Fig. S1c (ESI†). On the contrary, some trend emerges when the Bader charge on the TMP molecule is considered, Fig. S1d (ESI†). Here all the points are along a straight line with the exception of the values associated to ZnO. Even the plot of the M–P distance versus31P chemical shift, Fig. S1e (ESI†), shows a complete absence of correlation. As we mentioned already, ZnO is characterized by a bivalent cation, at variance with the +IV nature of the Lewis acid sites in TiO2, ZrO2, SnO2, CeO2. Therefore, the same properties have plotted removing ZnO from the analysis. While there is a general improvement in the distribution of the data, Fig. S2a–d (ESI†), still no clear trend emerges, with the expect of the correlation between Bader charge on P(CH3)3 and 31P chemical shift, Fig. 4. Here a linear correlation is found, with a R2 = 0.92. One can assume that a more positive charge on TMP corresponds to a stronger acid character of the surface (larger charge donation from the probe molecule). This is associated to a more positive value of the chemical shift. In particular, the smallest q(P(CH3)3), 0.05 |e|, is found in correspondence of CeO2(110) with large negative chemical shifts, around −50 ppm. Notice that a free P(CH3)3 molecule with q(P(CH3)3) = 0 |e| has δiso = −60 ppm, Table 1. Intermediate values of q(P(CH3)3), about 0.20 |e|, are found for TiO2 and correspond to chemical shifts of the order of −20 ppm. Finally, large positive charges, q(P(CH3)3) ≈ 0.4 |e|, are found in correspondence of stoichiometric or reduced SnO2, where the 31P chemical shift is from about −10 to +20 ppm. According to this classification, the order of Lewis acid strength of the MO2 oxides considered should be SnO2 > TiO2 > ZrO2 > CeO2. When we take the 31P chemical shift as a measure of the surface acidity, then ZnO should have a behavior intermediate between that of CeO2 and ZrO2 (δiso ≈ −40 ppm).
Before concluding this section, we briefly discuss the use of machine learning algorithms to find non-obvious correlations. Of course, one could use other regressors, like the random forest, and it would be useful to increment the data set. However, using the methodology outlined in the computational section, we found two general descriptors that provide a sufficiently good correlation with some computed properties. In the first descriptor, the chemical shift δiso can be expressed as a combination of three variables, the adsorption energy of TMP, Eads, the Bader charge on TMP, q(P(CH3)3), and the charge on the surface cations, q(M), δiso = aEads + bq(P(CH3)3) + cq(M). This descriptor correlates nicely with the computed 31P NMR chemical shifts, and the regression has a R2 = 0.90, Fig. S3a (ESI†). Another descriptor is also function of three variables, the work function of the oxide Φ, defined as the position of the top of the valence band with respect to the vacuum level, and the same Bader charges that enter in the definition of φ1. The corresponding equation is therefore: δiso = aΦ + bq(P(CH3)3) + cq(M). This second descriptors also shows a linear correlation with the computed δiso values, with an R2 factor only slightly smaller than in the previous case (0.86), Fig. S3b (for the coefficients, see ESI†).
Of course, one should mention that these descriptors, while interesting, depend on quantities such as the Bader charges that can only be derived from a calculation and that are not physical observables. Therefore, it is difficult to predict the chemical shift of another system without performing a DFT calculations to obtain the Bader charges.
Conclusions
Using a DFT+D approach we have studied the adsorption properties of P(CH3)3 molecules on various oxide surfaces (a-TiO2, r-TiO2, ZrO2, SnO2, CeO2 and ZnO) with the aim to evaluate the possible use of this probe molecule combined with 31P NMR to titrate Lewis acid sites. To this end we have considered various facets, different coverages, and both stoichiometric and reduced surfaces. In general, the computed 31P chemical shifts correlate nicely with the experimental values reported in the literature (Fig. 3). However, finding a universal behavior that allows one to define a scale of acid strength based on 31P chemical shifts turns out to be not straightforward. A linear correlation exists between adsorption energy of P(CH3)3 and 31P chemical shifts only within a given oxide polymorph (Fig. 2), in agreement with what previously found. However, if one plots the 31P chemical shift versus the adsorption energy for different oxides no correlation is found (Fig. 2).When one considers a homogenous set of oxides where the cations have all the same +IV oxidation state, a-TiO2, r-TiO2, ZrO2, SnO2, and CeO2, a linear correlation is found between the 31P chemical shift and the Bader charge of the P(CH3)3 molecule (Fig. 4), showing that this is a good descriptor of the acid strength of the surface site. In fact, a larger positive charge on the probe molecule corresponds to a stronger acid site and to a more positive chemical shift. However, Bader charges are not physical observables. Furthermore, they need to be computed, limiting the predicting power of this descriptor to establish scales of acid strength. Nevertheless, based on this result one can propose the following trend in Lewis acidity of the four oxides: SnO2 > TiO2 > ZrO2 > CeO2.
The results presented show a clear dependence of the 31P chemical shift on the coverage of the adsorbed probe molecules, an aspect that is rarely discussed in the experiment. On the contrary, no clear trend or effect has been found when the oxide surface is reduced by removing O atoms and forming surface O vacancies.
Finally, the use of machine learning approaches resulted in descriptors that are functions of several variables but, one more, some of these properties are related to the nature of the adsorbed probe molecules and need to be computed before to be included in the descriptor, thus limiting the potential use to predict the behavior of other systems not considered in this work.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Italian Ministry of University and Research (MIUR) through the PRIN Project 20179337R7 and by the Australian Research Council under the Discovery Project Grant DP 200100313.References
- A. Marchetti, J. Chen, Z. Pang, S. Li, D. Ling, F. Deng and X. Kong, Adv. Mater., 2017, 29, 1605895 CrossRef PubMed
.
- H. Eckert and I. E. Wachs, J. Phys. Chem., 1989, 93, 6796–6805 CrossRef CAS
.
- F. Maleki and G. Pacchioni, J. Phys. Chem. C, 2019, 123, 21629–21638 CrossRef CAS
.
- F. Maleki and G. Pacchioni, J. Chem. Phys., 2019, 151, 224705 CrossRef PubMed
.
- E. Lima, L. C. de Ménorval, D. Tichit, M. Laspéras, P. Graffin and F. Fajula, J. Phys. Chem. B, 2003, 107, 4070–4073 CrossRef CAS
.
- A. Zheng, S. B. Liu and F. Deng, Chem. Rev., 2017, 117, 12475–12531 CrossRef CAS PubMed
.
- W. P. Rothwell, W. X. Siten and J. H. Lunsford, J. Am. Chem. Soc., 1984, 106, 2453–2455 CrossRef
.
- Y. K. Peng, Y. Hu, H. L. Chou, Y. Fu, I. F. Teixeira, L. Zhang, H. He and S. C. E. Tsang, Nat. Commun., 2017, 8, 675 CrossRef PubMed
.
- L. Zhang, B. Yue, X. Chen and H. He, J. Phys. Chem. C, 2018, 122, 24094–24102 CrossRef
.
- H. Yu, H. Fang, H. Zhang, B. Li and F. Deng, Catal. Commun., 2009, 10, 920–924 CrossRef CAS
.
- T. Riemer and H. Knozinger, J. Phys. Chem., 1996, 100, 6739–6742 CrossRef CAS
.
- J. Xu, A. Zheng, J. Yang, Y. Su, J. Wang, D. Zeng, M. Zhang, C. Ye and F. Deng, J. Phys. Chem. B, 2006, 110, 10662–10671 CrossRef CAS PubMed
.
- K. Shimizu, T. N. Venkatraman and W. Song, Appl. Catal., A, 2002, 224, 77–87 CrossRef CAS
.
- W. Zhang, Z. Lin, H. Li, F. Wanga, Y. Wena, M. Xua, Y. Wanga, X. Kea, X. Xiac, J. Chen and L. Peng, RSC Adv., 2021, 11, 25004–25009 RSC
.
- Y. K. Peng, L. Ye, J. Qu, L. Zhang, Y. Fu, I. F. Teixeira, I. J. McPherson, H. He and S. C. E. Tsang, J. Am. Chem. Soc., 2016, 138, 2225–2234 CrossRef CAS PubMed
.
- Z. Tan, G. Li, H. L. Chou, Y. Li, X. Yi, A. H. Mahadi, A. Zheng, S. C. E. Tsang and Y. K. Peng, ACS Catal., 2020, 10, 4003–4011 CrossRef CAS
.
- Y. Chu, Z. Yu, A. Zheng, H. Fang, H. Zhang, S. J. Huang, S. B. Liu and F. Deng, J. Phys. Chem. C, 2011, 115, 7660–7667 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943 CrossRef CAS PubMed
.
- S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS
.
- F. Maleki and G. Pacchioni, J. Phys.: Condens. Matter, 2021, 33, 494001 CrossRef CAS PubMed
.
- S. Tosoni and G. Pacchioni, J. Phys. Chem. C, 2020, 124, 20960–20973 CrossRef CAS
.
- F. Maleki and G. Pacchioni, ACS Catal., 2021, 11, 554–567 CrossRef CAS
.
- F. Maleki and G. Pacchioni, Surf. Sci., 2022, 718, 122009 CrossRef CAS
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS
.
- F. Maleki and G. Pacchioni, Top. Catal., 2020, 63, 1717–1730 CrossRef CAS
.
- R. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS
.
- J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef
.
- R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401 CrossRef
.
- L. Baltusis, J. S. Frye and G. E. Maciel, J. Am. Chem. Soc., 1987, 40(109), 40–46 CrossRef
.
- S. Tosoni, H.-Y. Chen and G. Pacchioni, ChemPhysChem, 2015, 16, 3642–3651 CrossRef CAS PubMed
.
- C. Gionco, M. C. Paganini, E. Giamello, R. Burgess, C. Di Valentin and G. Pacchioni, Chem. Mater., 2013, 25, 2243–2253 CrossRef CAS
.
- Z. Helali, A. Jedidi, O. A. Syzgantseva, M. Calatayud and C. Minot, Theor. Chem. Acc., 2017, 136, 1–16 Search PubMed
.
- C. Franchini, M. Reticcioli, M. Setvin and U. Diebold, Nat. Rev. Mater., 2021, 6, 560–586 Search PubMed
.
- A. Ruiz Puigdollers, S. Tosoni and G. Pacchioni, J. Phys. Chem. C, 2016, 120, 15329–15337 CrossRef CAS
.
- A. Ruiz Puigdollers and G. Pacchioni, Nanoscale, 2017, 9, 6866–6876 RSC
.
- M. A. Rahman, S. Rout, J. P. Thomas, D. McGillivray and K. T. Leung, J. Am. Chem. Soc., 2016, 138, 11896–11906 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03306b |
| This journal is © the Owner Societies 2022 |