Ellipticity controlled dissociative double ionization of ethane by strong fields

Abstract

The yields of all dissociation channels of ethane dications produced by strong field double ionization were measured. It was found that the branching ratios can be controlled by varying the ellipticity of laser pulses. The CH₃⁺ formation and H⁺ formation channels show a clear competition, producing the highest and lowest branching ratios at ellipticity of ∼0.6, respectively. With the help of theoretical calculations, such a control was attributed to the ellipticity dependent yields of different sequential ionization pathways.

---

1. Introduction

Chemical reaction control can be achieved by a variety of means. Changes in external conditions such as temperature and pressure or addition of a catalyst are typically used to achieve the desired products by suppressing the by-products or by controlling the branching ratios. Ultrafast pulsed lasers are versatile tools with controllable parameters such as wavelength, pulse duration, intensity and polarization. They can provide new insights into molecular and electron dynamics and can expand our ability to control in a precise manner.^1,2 One of the prime areas of light–matter interaction studies is photodissociation dynamics.^3–5

Hydrocarbon molecules, when subjected to a strong laser field, undergo significant and complex chemical transformation, such as multiple ionization, dissociation and bond breaking/formation leading to different fragments.⁶ Ethane, a well-studied molecule in this regard, leads to production of different fragments such as CH₃⁺, H⁺, C₂H₅⁺, C₂H₃⁺, H₃⁺, H₂⁺ and C₂H₄⁺.^7–13 In particular, formation of some of these fragments involving hydrogen migration, especially regarding the formation of H₃⁺, has been extensively studied.^9,10,14–28 As an attempt to go beyond understanding the fragmentation dynamics to achieve control, Schirmel et al. investigated the ion yield controlling in dissociative ionization of ethane by systematically varying the quadratic spectral phase and focus on the H⁺, H₃⁺ and CH₃⁺ ion yields.²⁹ In their study they found that the H₃⁺ ion yield ratio to H⁺ ion yield ratio can be controlled by means of linear chirp. On the other hand, the CH₃⁺ ion yield, which comes from two different ensembles, one from the monocation and the other from the dication, can be controlled by changing both the linear chirp and the laser pulse energy. The absence of ethane dication (C₂H₆²⁺) in the mass spectrum^30–32 has led to an investigation by Shields et al. of the potential energy surfaces of the dications in ethane with information gathered from experiment and theory.³³ Most of the previous studies concentrated on the H₃⁺ formation channel due to the role that hydrogen migration plays in the formation of this exotic species.^12,34–36 However, H₃⁺ production typically contributes less than 20% to the total yield. Less attention has been given to the major dissociation channels such as H⁺ or CH₃⁺ and how the laser ellipticity can control the branching ratios. It has been generally assumed that the dissociation happens mainly via the ground state of the dication. On the other hand, it is well known that accessing different electronic states can lead to distinct fragmentation dynamics in polyatomic molecules.^6,37–39 Here in this work, by combining photoion–photoelectron coincidence imaging using a camera-based detection system with advanced ab initio methods, we show that excited states play an important role in dissociative double ionization of ethane and that the branching ratios of major channels can be controlled by laser ellipticity.

2. Experimental methods

The experiment was carried out in a photoion–photoelectron coincidence imaging apparatus which has been described in detail previously.^40–44 Here we will only reiterate the main components. A 35 fs, 800 nm laser beam was focused by a concave mirror which is mounted on a kinematic mirror mount inside the vacuum chambers. At the focal point, it intersected the molecular beam and the estimated laser intensity was ∼2 × 10¹⁴ W cm⁻² (with a fluctuation range of 20%). A quarter waveplate was inserted in the beam to produce elliptically polarized light. Laser ellipticities of 0.05, 0.11, 0.27, 0.4, 0.59, 0.73 and 0.85 were used. Due to the large bandwidth of the laser, the highest achieved ellipticity was 0.85 in this experiment without adopting an achromatic quarter waveplate. Neat ethane gas was introduced to the chamber through a 20 μm diameter nozzle. The continuous gas beam was skimmed twice with two 1 mm diameter skimmers. The molecular beam propagation direction was perpendicular to both the laser beam and the ion/electron TOF axis. The ions and electrons produced from the dissociative ionization were then accelerated in opposite directions by the electric field and eventually impinged on two imaging detectors (each with dual microchannel plates coupled with a phosphor screen). The imaging detectors, two CMOS (Complementary Metal Oxide Semiconductor) cameras and two high-speed digitizers form two high-performing three-dimension (3D) ion/electron momentum imaging systems. Both the digitizers and the cameras were triggered by the laser beam at 1 kHz repetition rate. The imaging system detects the position of particle (x, y) using the CMOS camera and the arrival time (t) from the digitizer in coincidence to give the 3D information of each event. The position-time information (x, y, t) of each event was then converted to 3D momentum information (p_x, p_y, p_z). The electron–ion coincidence measurements were achieved by limiting the overall count rate to less than 0.2 events/laser pulse. The total data acquisition time was 70 hours.

3. Theoretical methods

Two different sets of calculations were performed to help reveal the complex dynamics involved in strong field dissociative double ionization of ethane: (1) Modeling coupled electronic/nuclear dynamics starting from specific dication states. (2) Modeling strong field sequential double ionization dynamics that produces ethane dications. These methods are described briefly below.

3.1. Modeling coupled electronic/nuclear dynamics of ethane dications

The fragmentation yield of the ground state dications into H⁺, H₂⁺, H₃⁺ and CH₃⁺ as well as the fragmentation yield resulting from the nonradiative relaxation of the D3, D4 and D6 dicationic states have been investigated using dynamical simulations with surface hopping. We used the SHARC package⁴⁵ coupled with MOLCAS⁴⁶ for the electronic structure. An ensemble of 200 trajectories was run from each initial state starting from a Wigner distribution^47–49 of the neutral ground state (D_3d geometry). The simulations were run for 2.4 ps with a step of 0.24 fs taking into account the nonadiabatic coupling using decoherence correction. The electronic structure, forces and nonadiabatic couplings were computed at the CAS(8-5)/6-31G(d) level with 7 active states in the CAS average.

3.2. Modeling strong field sequential double ionizations

For the calculation of angle dependent ionization, the first ionization of ethane was simulated with TDCIS-CAP^50–52 using the field-free Hartree–Fock (HF) ground state and singly excited configurations; the ionization of ethane cation was simulated with TDCISD-IP-CAP using singly ionized and singly excited, singly ionized configurations.⁵³ The aug-cc-pVTZ basis set was augmented with an absorbing basis consisting of three s-type orbitals with exponents of 0.0256, 0.0128, and 0.0064; three p-type orbitals with exponents of 0.0256, 0.0128 and 0.0064; four d-type orbitals with exponents of 0.0512, 0.0256, 0.0128 and 0.0064; and one f-type orbital with exponent of 0.0256 were added to each atomic center. A 7 cycle elliptically polarized 800 nm pulse with a sin² envelope was applied for a total simulation time of t_max ≈ 19 fs (with an integration timestep of 1.2 as) and with a maximum field strength of E_max = 6.88 × 10¹⁴ W cm⁻² (0.14 au).

4. Results and discussion

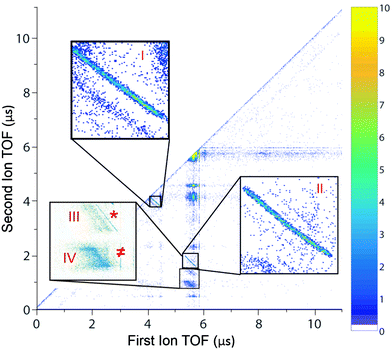
We first looked at the photoion–photoion coincidence (PIPICO) map (Fig. 1) to identify various channels with close-to-linearly polarized light (ellipticity ε = 0.05). There are two prominent two-body dissociation channels: (I) C₂H₆²⁺ → CH₃⁺ + CH₃⁺ and (II) C₂H₆²⁺ → C₂H₃⁺ + H₃⁺, in which the momentum is conserved between two charged fragments. The branching fractions are ∼35% and ∼20%, respectively. There are four other channels and among them there are two three-body dissociation channels: (III) C₂H₆²⁺ → C₂H₃⁺ + H₂⁺ + H (branching fraction 10%) and (IV) C₂H₆²⁺ → C₂H₃⁺ + H₂ + H⁺ (branching fraction 35%) in which the dissociation energy is shared among two charged fragments and one neutral fragment. The channels (*) C₂H₆²⁺ → C₂H₄⁺ + H₂⁺ and (≠) C₂H₆²⁺ → C₂H₅⁺ + H⁺ are very minor (similar with the observation by Kanya et al.^35,36) and they were included in the analysis of channels III and IV for H₂⁺ and H⁺ yield calculations, respectively. This detailed PIPICO map confirmed earlier observation of H⁺ with C₂H₃⁺ by Hagan and Eland^11,54 in the process of single photon double ionization. We note while many previous studies focused on H₃⁺ production from various hydrocarbon molecules (ethane has the highest yield of H₃⁺ among them), H₃⁺ production is still a relatively minor channel among all possible dissociation pathways.

Fig. 1 PIPICO map shows all the dissociative ionization channels of ethane dication with a laser ellipticity of 0.05. The channel assignment is as follows: (I) C₂H₆²⁺ → CH₃⁺ + CH₃⁺, (II) C₂H₆²⁺ → C₂H₃⁺ + H₃⁺, (III) C₂H₆²⁺ → C₂H₃⁺ + H₂⁺ + H, (IV) C₂H₆²⁺ → C₂H₃⁺ + H₂ + H⁺, (*) C₂H₆²⁺ → C₂H₄⁺ + H₂⁺ and (≠) C₂H₆²⁺ → C₂H₅⁺ + H⁺.

We are interested in characterizing the dication states produced through strong field double ionization. The majority of previous studies on ethane have focused on ground state ethane dication dynamics. It is true that strong field ionization strongly favors ground state production due to the exponential scaling of the rates with the ionization potentials. However, it has been well established that strong field ionization can produce excited electronic states in monocations, especially in polyatomics. How important are the excited states of ethane dications in determining the final branching ratios? To answer this question, we investigated the fragmentation yields resulting from the nonradiative relaxation of several excited states of the dication using surface hopping simulations (see Theoretical methods). The simulations of the nonradiative and fragmentation dynamics were carried out starting from the D0, D3, D4 and D6 dicationic electronic states at the equilibrium geometry of the neutral so that it corresponds to a prompt ionization of the neutral ground state in its equilibrium geometry. A set of 3 states were selected, D3, D4 and D6, because their excitation energies from D0 are close to 1 or 2 laser photons (1.5 eV). Therefore, they are the most likely states to be accessed following the strong field ionization of the dication ground state, even if they are not directly produced by strong field ionization. Final products were recorded for each trajectory and the branching ratios were tabulated with a total of 200 trajectories for each state. The results are shown in Table 1. We note a non-dissociative trajectory is defined when a molecule remains intact at the end of the simulation (2.4 ps). If allowed sufficient time, all these trajectories are likely to dissociate into one of the channels that produce C₂H₃⁺. This is because the average dissociation time of the CH₃⁺ channel is rather short (∼100 fs), which suggests CH₃⁺ dissociation is prompt. Therefore, the finite computation time range at 2.4 ps will not affect significantly the branching fraction of the CH₃⁺ dissociation channel.

Table 1 The calculated yields of different dissociation channels from different ethane dication states^a

Dication state	Energy (eV)	Lifetime (fs)	H3^+ yield (%)	H^+ yield (%)	H2^+ yield (%)	CH3^+ yield (%)	Non-dissociative (%)
a For the ground state, additional kinetic energy (KE) was added to simulate vibrationally hot states arising from internal converted excited states. This was done by sampling from a generalized Wigner distribution at a given finite temperature. The excitation energies from D0 to the excited state (at the CAS (8-5)/6-31G(d) level with 7 active states) are also reported at the equilibrium geometry of the neutral. The calculated lifetime of electronic excited states are also reported.
D6	3.03	47	13	21	6	41	19
D4	1.75	30	13	43	5	25	14
D3	1.16	21	3	59	5	18	15
D0 (4 eV mean KE)	0		9	62	0	7	22
D0 (1 eV mean KE)	0		0	81	1	7	11

---

From Table 1, we find that the CH₃⁺ channel yields correlate well with the dication states: from D0 to D6, the yield increases as the state energies increase, to a significant 41% while it is opposite with the H⁺ dissociation channel. This is not surprising because the breaking of the carbon–carbon bond requires removing electrons from the lower lying σ orbitals, which produces electronic excited states. Comparison with the experimental result of ∼35% suggests that high excited states such as D4 and D6 play an important role, as the ground state alone cannot account for the major dissociation dynamics. Even with substantial vibrational energy (4 eV) added to the ground state dication, the yield of CH₃⁺ does not increase significantly. On the other hand, both electronic and vibrational excited states can produce reasonable amount of H₃⁺ dissociation, suggesting the ground electronic dication state is not the only source for H₃⁺ production.

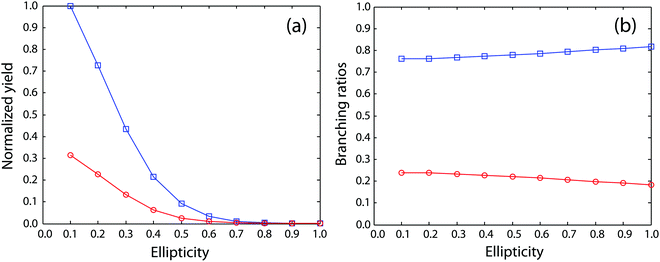
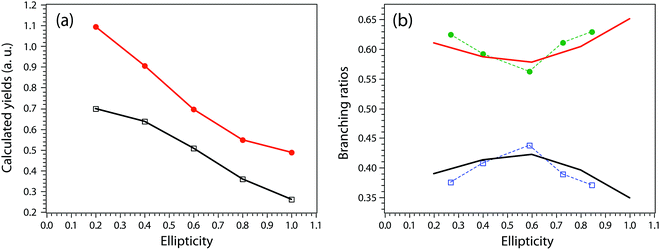
Next, we move to consider the ellipticity dependent branching ratios among different dissociation channels. Due to laser intensity and gas density fluctuation during the weeks of data acquisition, we normalized the counts of each channel with the count of ethane monocation in the same dataset (Fig. 2a) and used the normalized yield to calculate the branching ratios. The results are shown in Fig. 2b and it reveals the effect of ellipticity on the dissociative double ionization of ethane. The two major channels C₂H₆²⁺ → CH₃⁺ + CH₃⁺ and C₂H₆²⁺ → C₂H₃⁺ + H₂ + H⁺ are in competition with each other and as a result, the CH₃⁺ formation channel shows a maximum and the H⁺ formation channel a minimum at ε = 0.59, respectively. Both H₃⁺ and H₂⁺ formation channels show a similar but much smaller variation in yields with ellipticity. We note the three channels with the similar variation in branching ratios share a common fragment C₂H₃⁺, which suggests that these channels might start from same dication states. As far as we know, this is the first time that such a variation has been observed in strong field driven double ionization processes. To interpret these variations, we consider a few possibilities. The first one is electron rescattering dynamics associated with linear polarization. In this nonsequential double ionization (NSDI) process, the first ionized electron can be driven back to the ionic core and knock out a second electron. One might think that, due to the distinct electron recollision dynamics, the final state of the dication might differ significantly from those arising from sequential ionization, which is dominant at higher laser ellipticity. From the data, it seems that NSDI does play a role in the total yield of the double ionization as the normalized yield dropped significantly from ε = 0.05 to 0.1, which is a typical character of NSDI. However, the branching ratio variation is rather small. Furthermore, maximum/minimum of the branching ratios are located at ε = 0.59, at which NSDI has largely been suppressed. These considerations render the electron recollision mechanism inoperative in interpreting the branching ratio variations. The second possibility is to consider the fact that the peak electric field drops as the ellipticity increases when the pulse energy remains the same (a typical experimental implementation). Could the variation be simply due to the difference in ionization potentials of dication states that have different dissociation pathways? We carried out a simple modeling on this scenario. We calculated the ionization rates of two fictitious atoms with ionization potentials of 32 and 33 eV (simulating the ground and an excited ethane dication) at varying ellipticity using the atomic ADK ionization formulae.⁵⁵ The result is shown in Fig. 3. Very little variation was seen in the branching ratios in this case (Fig. 3b). Clearly, such a picture cannot explain the experimental observation.

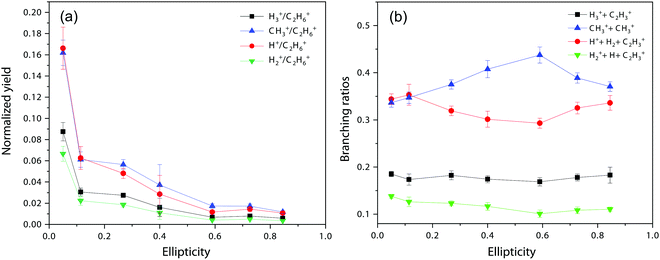Fig. 2 (a) Normalized yields of different dissociation channels. (b) Ellipticity dependent branching ratios of different dissociation channels.

Fig. 3 (a) Calculated ionization rates for two fictitious atoms with ionization potentials of 32 eV (blue) and 33 eV (red) with varying ellipticities. (b) The computed branching ratios using data from (a).

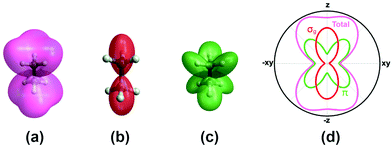
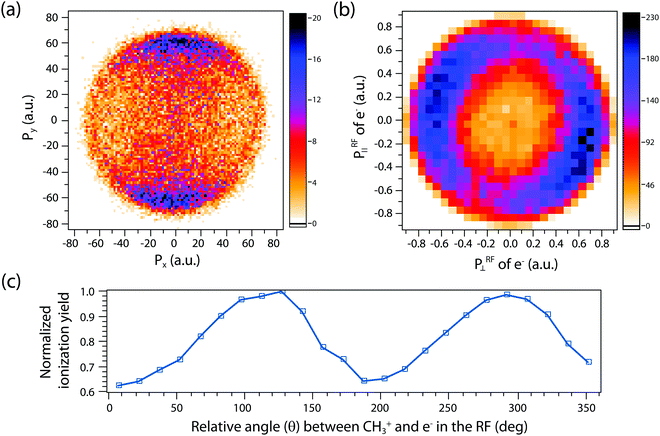
A more complete model will have to incorporate the electronic structure of ethane molecules as well as the peak electric field variation. Here, recently developed TDCIS-CAP and TDCISD-IP-CAP methods were used to model the sequential double ionization process. The neutral ethane electronic configuration is (1a_g)²(1a_2u)²(2a_1g)²(2a_2u)²(1e_u)⁴(3a_1g)²(1e_g)⁴ with a D_3d symmetry. The symmetries of HOMO−1 (3a_1g) and HOMO (1e_g) resemble those of a σ_g orbital and a π_g orbital along the carbon–carbon bond, respectively. In the following, we will adopt the σ and π naming for simplicity. We consider two different pathways via either a σ cation (the first electron was removed from the σ_g orbital) or a π cation (the first electron was removed from the π_g/π_u orbitals). We first calculated the angle dependent ionization yields of the two orbitals in neutral ethane using TDCIS-CAP method (Fig. 4) and these are used to scale the second ionization yields to give the overall double ionization yields. Then we computed the ionization yields of the two monocations at different ellipticities. To account for the relative orientation between the molecules and the laser ellipse of the elliptically polarized light, we calculated the ionization yields at 7 different alignment angles of the major axis of the laser ellipse (0 to 90 degree in a 15-degree step) in the molecular frame. The ellipticity was varied from 0.2 to 1 with a 0.2 step. Linear polarization was not considered because NSDI cannot be property modeled with a sequential model. A total of 70 calculations were performed and the overall ellipticity dependent ionization yields are shown in Fig. 5a. The ellipticity dependent branching ratios of the two monocations are plotted in Fig. 5b. It appears that this model has captured the main features of the observed branching ratio variation as the σ cation pathway matches that of CH₃⁺ production channel while the π cation pathway matches that of the sum of the three other channels with C₂H₃⁺ being the common fragment. The experimental and calculated ellipticities for the maximum/minimum in the branching ratios also match well (ε =0.6). This indicates that the observed branching variation is due to a combination of angle dependent ionization rates of different cations and the peak electric field evolution. The agreement between experiment and theory seems to further suggest that σ cation ionization produces dominantly excited states dications, while π cation ionization produces mostly ground/low-lying states. Further experimental results on recoil frame photoelectron angular distribution (RF-PAD) provides a direct evidence for the important role of σ orbital ionization played in the CH₃⁺ dissociation channel (Fig. 6). In Fig. 6a, the strong anisotropy in the CH₃⁺ momentum distribution suggests the dissociation is prompt and faster than the rotation period of ethane dications, in agreement with dynamical simulations. This validates the axial recoil approximation to allow the extraction of RF-PAD (Fig. 6b and c), which shows two peaks at 110 and 290 degrees. According to the principle of angular streaking and invoking a 90-degree vector potential rotation and a 20-degree deflection angle due to the Coulomb interaction between departing electron and ionic core, the two peaks indicate a preferred ionization direction along the molecular axis (C–C bond). A similar approach was used previously.⁵⁶ Ionization along molecular axis is a strong indication of σ orbital ionization, as shown in Fig. 4b. The prominent peaks suggest that σ orbital ionization take places at least once during the sequential ionization process. The results also reveal that excited states can be produced directly in the strong field ionization process instead of going through ionization/excitation. This is not to say that the ionization/excitation process does not take place at all. However, the RF-PAD suggests it is not the dominant process. Otherwise, we should see a suppression of ionization along the molecular axis, as predicted for π orbitals (Fig. 4c). Finally, the RF-PAD also confirms our trajectory calculation, which shows that CH₃⁺ dissociation yield correlates strongly with electronic excited dication states. The yields of various excited dication states in the TDCI ionization simulation will be addressed in a future study.

Fig. 4 (a) Calculated total ionization yield of neutral ethane. (b) and (c) The breakdown of the total yield to the MO contributions from σ_g and the doubly degenerate π_g/π_u orbitals, respectively. (d) Total angular dependence of ionization yield (pink) with respect to the polar angle about the C–C bond (z-axis). For each polar angle, the ionization yield has been averaged over the azimuthal directions in the xy plane; and the corresponding ionization contributions from the π_g/π_u orbitals (green) and σ orbitals (red).

Fig. 5 (a) The computed yield variation with laser ellipticity for sequential double ionization via a π cation (red) and a σ cation (black). (b) The branching ratio variations of the π cation ionization (red) and the σ cation ionization (black) calculated using data from (a), showing a minimum/maximum peak at ε=0.6. For comparison, the experimental branching ratios of CH₃⁺ dissociation channel (blue square) and the sum of the other three channels (green dot), are also shown for ellipticity between 0.27 and 0.85. Data for lower ellipticity at 0.05 and 0.11 were not shown because they are dominated by NSDI.

Fig. 6 (a) The (x, y) momentum distribution of CH₃⁺ dissociation in the plane perpendicular to the laser polarization plane (y, z). (b) The RF-PAD of electrons in coincidence with CH₃⁺ dissociation. The plot was obtained by having the CH₃⁺ momentum vector pointing up in the figure while rotating the coincident electron momentum vector accordingly. All momentum vectors are in the plane of polarization (y, z). The helicity of the laser was clockwise. (c) Integrated 1D RF-PAD.

It is worth pointing out that previously, in methyl iodide (CH₃I), it was found that different ionization pathways manifest in distinct angle dependent ionization yields.⁵⁶ Here we show such a pathway difference can have significant chemical consequence.

5. Conclusion

In this work, a complete characterization of the branching fractions of all dissociation pathways of strong field doubly ionized ethane was achieved and an unexpected control was demonstrated for the first time by varying the laser ellipticity. We showed that electronic excited states of the ethane dication play a far more important role than previously assumed. We attributed the branching variation with laser ellipticity to two different ionization pathways that go through the π cation and the σ cation. The different angle dependent ionization yields of the two cations lead to distinct ionization yield variations with ellipticity and thus branching ratios. Because the universality of angle dependent ionization yields, we expect a similar control to be present in many other molecular systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Research supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under Award # DE-SC0020994. FR and BM were supported by the Funds National de la Recherche Scientifique (Belgium), F.R.S.-FNRS research grant #T.0132.16. Computational resources have been provided by the Consortium des Equipements de Calcul Intensif (CECI), funded by the F. R. S.-FNRS under Grant # 2.5020.11.

References

1. R. N. Zare, Science, 1998, 279, 1875–1879.
2. N. E. Henriksen, Chem. Soc. Rev., 2002, 31, 37–42.
3. B. Sheehy and L. F. DiMauro, Annu. Rev. Phys. Chem., 1996, 47, 463–494.
4. L. J. Butler and D. M. Neumark, J. Phys. Chem., 1996, 100, 12801–12816.
5. K. Yamanouchi, Science, 2002, 295, 1659–1660.
6. S. Larimian, S. Erattupuzha, E. Lotstedt, T. Szidarovszky, R. Maurer, S. Roither, M. Schoffler, D. Kartashov, A. Baltuska, K. Yamanouchi, M. Kitzler and X. H. Xie, Phys. Rev. A, 2016, 93, 053405.
7. L. Xia, H. Z. Ren, M. Ri, J. X. Chen, Y. Hong and Q. H. Gong, Chin. Phys., 2004, 13, 1564–1568.
8. R. M. Wood, A. K. Edwards and R. L. Ezell, Radiat. Phys. Chem., 1985, 26, 635–640.
9. C. C. Tian and C. R. Vidal, J. Chem. Phys., 1998, 109, 1704–1712.
10. M. D. Burrows, S. R. Ryan, W. E. Lamb and L. C. Mcintyre, J. Chem. Phys., 1979, 71, 4931–4940.
11. D. A. Hagan and J. H. D. Eland, Org. Mass Spectrom, 1992, 27, 855–863.
12. Y. Boran, G. L. Gutsev, A. A. Kolomenskii, F. Zhu, A. Schuessler and J. Strohaber, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 035003.
13. Y. Zhang, B. H. Ren, C. L. Yang, L. Wei, B. Wang, J. Han, W. D. Yu, Y. Y. Qi, Y. M. Zou, L. Chen, E. L. Wang and B. R. Wei, Commun. Chem., 2020, 3, 160.
14. R. K. Kushawaha and B. Bapat, Chem. Phys. Lett., 2008, 463, 42–46.
15. S. De, J. Rajput, A. Roy, P. N. Ghosh and C. P. Safvan, Phys. Rev. Lett., 2006, 97, 213201.
16. S. De, A. Roy, J. Rajput, P. N. Ghosh and C. P. Safvan, Int. J. Mass Spectrom., 2008, 276, 43–48.
17. Y. Furukawa, K. Hoshina, K. Yamanouchi and H. Nakano, Chem. Phys. Lett., 2005, 414, 117–121.
18. T. Okino, Y. Furukawa, P. Liu, T. Ichikawa, R. Itakura, K. Hoshina, K. Yamanouchi and H. Nakano, Chem. Phys. Lett., 2006, 423, 220–224.
19. T. Okino, Y. Furukawa, P. Liu, T. Ichikawa, R. Itakura, K. Hoshina, K. Yamanouchi and H. Nakano, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, S515–S521.
20. K. Hoshina, H. Kawamura, M. Tsuge, M. Tamiya and M. Ishiguro, J. Chem. Phys., 2011, 134, 064324.
21. N. Ekanayake, M. Nairat, B. Kaderiya, P. Feizollah, B. Jochim, T. Severt, B. Berry, K. R. Pandiri, K. D. Carnes, S. Pathak, D. Rolles, A. Rudenko, I. Ben-Itzhak, C. A. Mancuso, B. S. Fales, J. E. Jackson, B. G. Levine and M. Dantus, Sci. Rep., 2017, 7, 4703.
22. N. Ekanayake, M. Nairat, N. P. Weingartz, M. J. Michie, B. G. Levine and M. Dantus, J. Chem. Phys., 2018, 149, 244310.
23. N. Ekanayake, T. Severt, M. Nairat, N. P. Weingartz, B. M. Farris, B. Kaderiya, P. Feizollah, B. Jochim, F. Ziaee, K. Borne, P. K. Raju, K. D. Carnes, D. Rolles, A. Rudenko, B. G. Levine, J. E. Jackson, I. Ben-Itzhak and M. Dantus, Nat. Commun., 2018, 9, 5186.
24. T. Ando, A. Shimamoto, S. Miura, A. Iwasaki, K. Nakai and K. Yamanouchi, Commun. Chem., 2018, 1, 7.
25. Y. Zhang, L. Wei, C. L. Yang, W. Yu, B. Wang, B. Yan, Y. Zou, L. Chen and B. Wei, Phys. Rev. A, 2019, 100, 052706.
26. E. Livshits, I. Luzon, K. Gope, R. Baer and D. Strasser, Commun. Chem., 2020, 3, 49.
27. N. Iwamoto, C. J. Schwartz, B. Jochim, P. K. Raju, P. Feizollah, J. L. Napierala, T. Severt, S. N. Tegegn, A. Solomon, S. Zhao, H. Lam, T. N. Wangjam, V. Kumarappan, K. D. Carnes, I. Ben-Itzhak and E. Wells, J. Chem. Phys., 2020, 152, 054302.
28. K. Hoshina, Y. Furukawa, T. Okino and K. Yamanouchi, J. Chem. Phys., 2008, 129, 104302.
29. N. Schirmel, N. Reusch, P. Horsch and K. M. Weitzel, Faraday Discuss., 2013, 163, 461–474.
30. B. E. Jones, L. E. Abbey, H. L. Chatham, A. W. Hanner, L. A. Teleshefsky, E. M. Burgess and T. F. Moran, Org. Mass Spectrom, 1982, 17, 10–18.
31. M. Rabrenovic, C. J. Proctor, T. Ast, C. G. Herbert, A. G. Brenton and J. H. Beynon, J. Phys. Chem., 1983, 87, 3305–3310.
32. T. Drewello, A. J. R. Heck and N. M. M. Nibbering, Chem. Phys. Lett., 1991, 178, 285–288.
33. G. C. Shields and T. F. Moran, Org. Mass Spectrom, 1986, 21, 479–483.
34. P. M. Kraus, M. C. Schwarzer, N. Schirmel, G. Urbasch, G. Frenking and K. M. Weitzel, J. Chem. Phys., 2011, 134, 114302.
35. R. Kanya, T. Kudou, N. Schirmel, S. Miura, K. M. Weitzel, K. Hoshina and K. Yamanouchi, J. Chem. Phys., 2012, 136, 204309.
36. R. Kanya, T. Kudou, N. Schirmel, S. Miura, K. M. Weitzel, K. Hoshina and K. Yamanouchi, Epj Web Conf., 2013, 41, 02034.
37. X. H. Xie, K. Doblhoff-Dier, S. Roither, M. S. Schoffler, D. Kartashov, H. L. Xu, T. Rathje, G. G. Paulus, A. Baltuska, S. Grafe and M. Kitzler, Phys. Rev. Lett., 2012, 109, 243001.
38. X. H. Xie, K. Doblhoff-Dier, H. Xu, S. Roither, M. S. Schffler, D. Kartashov, S. Erattupuzha, T. Rathje, G. G. Paulus, K. Yamanouchi, A. Baltuska, S. Grafe and M. Kitzler, Phys. Rev. Lett., 2014, 112, 163003.
39. A. E. Boguslavskiy, J. Mikosch, A. Gijsbertsen, M. Spanner, S. Patchkovskii, N. Gador, M. J. J. Vrakking and A. Stolow, Science, 2012, 335, 1336–1340.
40. Y. F. Lin, S. K. Lee, P. Adhikari, T. Herath, S. Lingenfelter, A. H. Winney and W. Li, Rev. Sci. Instrum., 2015, 86, 096110.
41. S. K. Lee, F. Cudry, Y. F. Lin, S. Lingenfelter, A. H. Winney, L. Fan and W. Li, Rev. Sci. Instrum., 2014, 85, 123303.
42. Q. Liao, A. H. Winney, S. K. Lee, Y. F. Lin, P. Adhikari and W. Li, Phys. Rev. A, 2017, 96, 023401.
43. S. K. Lee, Y. F. Lin, S. Lingenfelter, L. Fan, A. H. Winney and W. Li, J. Chem. Phys., 2014, 141, 221101.
44. A. H. Winney, S. K. Lee, Y. F. Lin, Q. Liao, P. Adhikari, G. Basnayake, H. B. Schlegel and W. Li, Phys. Rev. Lett., 2017, 119, 123201.
45. M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258.
46. F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541.
47. M. Hillery, R. F. O'Connell, M. O. Scully and E. P. Wigner, Phys. Rep., 1984, 106, 121–167.
48. E. J. Heller, J. Chem. Phys., 1976, 65, 1289–1298.
49. J. P. Zobel, J. J. Nogueira and L. González, Phys. Chem. Chem. Phys., 2019, 21, 13906–13915.
50. P. Krause and H. B. Schlegel, J. Phys. Chem. Lett., 2015, 6, 2140–2146.
51. P. Krause, J. A. Sonk and H. B. Schlegel, J. Chem. Phys., 2014, 140, 174113.
52. P. Krause and H. B. Schlegel, J. Chem. Phys., 2014, 141, 174104.
53. M. K. Lee, W. Li and H. B. Schlegel, J. Chem. Phys., 2020, 152, 064106.
54. J. H. D. Eland, Rapid Commun. Mass Spectrom., 1996, 10, 1560–1562.
55. M. V. Ammosov, N. B. Delone and V. P. Krainov, Sov. Phys. JETP, 1986, 91, 2008–2013.
56. A. H. Winney, G. Basnayake, D. A. Debrah, Y. F. Lin, S. K. Lee, P. Hoerner, Q. Liao, H. B. Schlegel and W. Li, J. Phys. Chem. Lett., 2018, 9, 2539–2545.

---