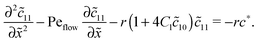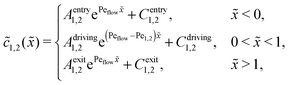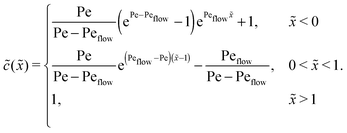The efficiency of driving chemical reactions by a physical non-equilibrium is kinetically controlled
Received
15th February 2016
, Accepted 26th April 2016
First published on 28th April 2016
Abstract
An out-of-equilibrium physical environment can drive chemical reactions into thermodynamically unfavorable regimes. Under prebiotic conditions such a coupling between physical and chemical non-equilibria may have enabled the spontaneous emergence of primitive evolutionary processes. Here, we study the coupling efficiency within a theoretical model that is inspired by recent laboratory experiments, but focuses on generic effects arising whenever reactant and product molecules have different transport coefficients in a flow-through system. In our model, the physical non-equilibrium is represented by a drift–diffusion process, which is a valid coarse-grained description for the interplay between thermophoresis and convection, as well as for many other molecular transport processes. As a simple chemical reaction, we consider a reversible dimerization process, which is coupled to the transport process by different drift velocities for monomers and dimers. Within this minimal model, the coupling efficiency between the non-equilibrium transport process and the chemical reaction can be analyzed in all parameter regimes. The analysis shows that the efficiency depends strongly on the Damköhler number, a parameter that measures the relative timescales associated with the transport and reaction kinetics. Our model and results will be useful for a better understanding of the conditions for which non-equilibrium environments can provide a significant driving force for chemical reactions in a prebiotic setting.
I. Introduction
While extant biology has sophisticated enzymes at its disposal to catalyze the molecular reactions required for metabolism, replication, and evolution,1 it is unclear which mechanisms were available on the abiotic early earth to drive and guide chemical reactions toward biochemical complexity. Much progress has been made in understanding how the basic building blocks of biomolecules, i.e. nucleotides and amino acids, may have emerged from prebiotic chemistry.2,3 However, the spontaneous assembly of these building blocks into functional biomolecules is generally considered to be highly unlikely without driving forces that help to overcome entropic and enthalpic barriers.
The underlying question is somewhat reminiscent of Levinthal’s paradox in protein folding.4 This “paradox”, which posits that a protein has too many possible conformations to find its native state by random searching, motivated much fundamental research into folding pathways and ultimately led to the concept of the “folding funnel”.5 Compared to Levinthal’s paradox, the paradox posed by the apparent spontaneous emergence of a self-replicating, evolving biomolecular system from prebiotic chemistry, seems much more daunting, since the phenomenon involves many unknowns and no analogous funnel is in direct sight.
However, a number of interesting physico-chemical coupling effects have been reported, which suggest that a type of “funnel” might be generated by the coupling of (bio)chemical reactions to physical processes involving forces, energy dissipation, or transport. For instance, membrane growth can be coupled to the formation of a transmembrane pH gradient,6 RNA replication can be coupled to vesicle growth,7 and polymerization reactions can be driven by a thermal gradient via the combined effects of thermophoresis and convection.8 Generalizing from these examples, the present study is motivated by the working hypothesis that prebiotic chemical reactions may have been guided or driven toward the spontaneous emergence of a self-replicating biomolecular system by their coupling to physical nonequilibrium processes. Schematically, this hypothesis might be represented as
where the transition from prebiotic chemistry to biochemistry is viewed as a reaction that is catalyzed by nonequilibrium physics.
By definition, out-of-equilibrium physical systems dissipate energy and generate entropy.9 A part of the dissipated energy can be used to drive a coupled chemical reaction away from its chemical equilibrium. While it is clear that there was ample physical nonequilibrium on the violent early earth, the coupling mechanisms to chemical reactions remain underexplored. For each mechanism it will be important to understand which factors determine the coupling strength, in order to predict which environments would lead to significant effects. The main purpose of the present article is to point out that the so-called Damköhler number is one such factor, and that it is relevant for any coupling mechanism involving some form of physical transport.
While there are different cases and definitions, the Damköhler number used in chemical engineering10 generally refers to a ratio
| | 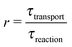 | (1) |
of a timescale
τtransport associated with a transport process and the timescale
τreaction of the chemical reaction. Here, we consider a transport process of the drift–diffusion (or diffusion–advection) type, and reversible dimerization as the chemical reaction. This minimal model, illustrated in
Fig. 1, serves as a coarse-grained description for different experimental scenarios, in which the molecular drift could be caused by an interplay of thermophoresis and convection as in
ref. 11, or by electroosmotic or other effects. The dimerization reaction is chosen not because of a particular prebiotic relevance, but because of its simplicity. In contrast to the full polymerization reaction studied in
ref. 8, the dimerization reaction permits a systematic and transparent theoretical analysis of the effects resulting from the coupling to the transport process.
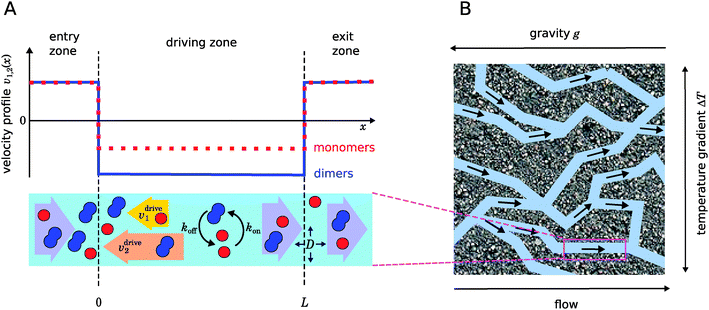 |
| | Fig. 1 Illustration of our model. (A) Schematic representation of the one-dimensional advection–diffusion–reaction model (bottom) and plot of the flow profile for monomers and dimers (top). Within the physical “driving zone”, monomers and dimers experience a different average drift velocity to the left. (B) Our model is a possible abstraction for a chemical reaction near a hydrothermal vent. The combination of a temperature gradient and gravity creates physical driving in capillaries within a porous rock. | |
The focus of our analysis is on the non-equilibrium steady state, which is reached after the coupled transport and reaction lead to stable concentration profiles. In this steady-state, the chemical balance of dimers versus monomers is substantially shifted away from its intrinsic equilibrium. The amplitude of this effect at a given strength of the physical driving is a measure of the “efficiency” of the physico-chemical coupling. We find that this efficiency depends strongly on the Damköhler number (1). Interestingly, the fold-change in efficiency that can be induced by this r-dependence increases rapidly with the physical driving strength. Due to the minimal assumptions made by our model, these findings have broad implications for the identification of possible environments and scenarios that would make the spontaneous emergence of a self-replicating, evolving biomolecular system a likely event.
II. Model
Fig. 1 illustrates our model (A) and its geochemical motivation (B). The model describes a system with a quasi-one-dimensional geometry, such as a capillary, filled with a fluid that flows at a constant flow velocity vflow, carrying along dissolved reactants. Within a finite region of the system, which we refer to as the “driving zone”, an additional force acts on the molecules, inducing a mean drift velocity relative to the fluid in the direction opposing the flow. This resembles the experimental setting of ref. 11, where a transversal temperature gradient across a section of a capillary is used to induce the drift velocity via a combination of thermophoresis and convection. A key ingredient of our model, and the experiments,8,11 is that the induced velocities are size-selective. As motivated above, our minimal model considers a reversible dimerization reaction,| | 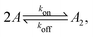 | (2) |
where monomers A dimerize at rate kon, and dimers A2 dissociate at rate koff. We denote the associated induced drift velocities with vdrive2 for dimers and vdrive1 for monomers, both of which act only within the driving zone of length L. Together with the superimposed fluid flow, we then obtain the following velocity profiles for monomers and dimers,| |  | (3) |
where we refer to the regions x < 0 and x > L as “entry zone” and “exit zone”, respectively (see also Fig. 1). If we denote the diffusion coefficients of monomers and dimers by D1 and D2, and their respective local concentrations by c1(x,t) and c2(x,t), then the combined drift–diffusion–reaction dynamics is described by the two coupled equations12| | 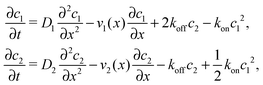 | (4) |
where the first term on the right hand side of the equations describes diffusive transport and the second term advective transport, while the third and fourth terms describe the reaction kinetics. Since the experimental diffusion coefficients of monomers and dimers will typically be very similar, and we found that small differences in the diffusion coefficients do not affect the qualitative behavior of the system, we will set D1 = D2 = D for our analysis.
As illustrated in Fig. 1B and discussed in ref. 11, drift–diffusion–reaction dynamics of the type described by eqn (4) could naturally occur within a porous rock structure near a hydrothermal vent, which releases heat from the planets core into the ocean.13 In this case, the drift velocities would arise from an interesting interplay between thermophoresis and convection,14,15 while the size-selectivity of the drift arises from a size-dependent Soret coefficient, which determines the strength of the thermophoresis effect.16 The careful experimental characterization of the thermophoresis and diffusion of RNA and DNA oligomers16 also allows us to extract rough estimates for the typical degree of size-selectivity that may be expected for nucleotide-based prebiotic reactions, see below and Appendix A.
It is useful to first clearly identify all adjustable parameters of the model and their corresponding physico-chemical interpretation. As mentioned above, we focus our analysis on the steady-state of eqn (4). Thereby, we make a tacit assumption about the physico-chemical systems to be described by our model, namely that the timescale of their relaxation into the steady-state is short compared to changes in the environment, such as fluctuations in the flow speed vflow or in the bulk concentration of the reactants. This assumption is not unplausible, given that the steady flow permits a rapid relaxation of the transport process11 (in contrast, for a purely diffusive coupling of the driving zone to the exterior bulk solution, the accumulation of the molecules inside can require a long time8). The steady-state of eqn (4) is characterized by 5 independent dimensionless numbers obtained from combinations of our system parameters. Three of these are so-called Péclet numbers, which measure the relative rate of advective transport versus diffusive transport. For the physical driving of monomers, we have
Péclet numbers always require a relevant length scale, which in this case is the length
L of the driving zone where the driving velocity
vdrive1 is nonzero. Similarly, the Péclet number for dimers is
Due to the size-selectivity of the drift, we have Pe
1 ≠ Pe
2. Both of these Péclet numbers are a function of the driving strength and will increase as the driving is intensified. However, their ratio remains constant, at a value that is specific to the type of molecules and the type of driving. In Appendix A we estimate this ratio for the thermophoretic driving of RNA or DNA, where we assume that a “monomer” in our present model corresponds to an RNA or DNA oligomer.
8 This yields 1.3 < Pe
2/Pe
1 < 2.5 for RNA, and 0.8 < Pe
2/Pe
1 < 2.3 for DNA. Finally, we have a third Péclet number associated with the flow velocity,
Together, the three Péclet numbers fully determine the steady-state of the isolated physical system,
i.e. they uniquely define the steady-state of
eqn (4) for
koff =
kon = 0, up to normalization. Similarly, there is a dimensionless number, which uniquely determines the steady-state of the isolated chemical reaction. This fourth number, which we refer to as the chemical “load”, is a measure for the total amount of reagent in the system. It is defined as the ratio of a characteristic concentration to the dissociation constant,
where
Kd = 2
koff/
kon and we choose the total monomer concentration
ĉ =
ĉ1 + 2
ĉ2 as the characteristic concentration (with
ĉ1 and
ĉ2 denoting the unperturbed monomer and dimer concentrations far away from the driving zone). The last dimensionless parameter is the Damköhler number (1), which we define as
for our model. This particular definition for the case of diffusive transport is referred to as the second Damköhler number.
17 Here, we also refer to
r as the reaction speed, since the limit (
r → ∞) corresponds to the fast reaction limit, while (
r → 0) corresponds to the slow reaction limit. Compared to the other four dimensionless numbers,
r has the unique role to characterize the coupling between the physics and the chemistry of our system. While it is obvious that
r must affect the relaxation dynamics of the coupled system into its steady-state, it is less clear what effect, if any,
r will have on the steady state. This is a central question to be addressed in ‘Results’.
For the analysis of our model, we calculated the steady-state of eqn (4) numerically. In addition, we provide several analytical results in appendices: the concentration profiles in the slow reaction limit in Appendix B, the concentration profiles in the fast reaction limit in Appendix C, and a linear response calculation valid in the regime of weak driving in Appendix D. These analytical results help us to cross-validate our numerical calculations, and to obtain the data for Fig. 5. Our main aim here is to characterize the phenomenology of the model and to extract its general implications, while the theoretical framework will be further developed elsewhere.18
III. Results
Fig. 2A shows typical steady-state concentration profiles for dimers (solid, blue) and monomers (dotted, red) spanning the entry zone, driving zone (indicated by grey shading), and exit zone; see caption for parameter values. It is apparent that the driving against the flow induces a buildup of both monomers and dimers also in the entry zone. The overall extension of the accumulation region, in which the concentrations are significantly elevated above the unperturbed bulk concentrations, is considerably larger than the length of the driving zone. As one would intuitively expect, the maximal concentrations are located at the left boundary of the driving zone.
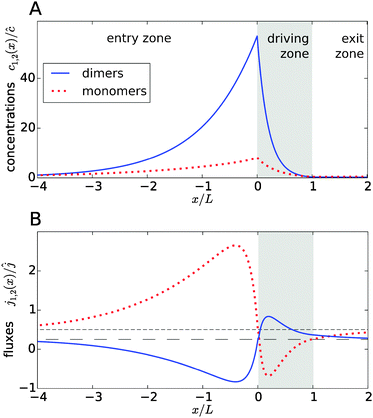 |
| | Fig. 2 Typical concentration and flux profiles. (A) Normalized concentration profiles for monomers and dimers with the Péclet numbers Pe2 = 6 for dimers, Pe1 = 4 for monomers, and Peflow = 1 for the flow (the chemical load is Cl = 1 and the Damköhler number r = 1). The driving zone is indicated by grey shading. (B) The corresponding monomer and dimer fluxes for the same set of parameters, normalized to the unperturbed flux ĉvflow of the total equilibrium concentration in the flow field. The black lines show the unperturbed flux of monomers (short dashed line) and dimers (long dashed line). The maximal accumulation occurs at the boundary between the entry zone and the driving zone (at x = 0). Due to the enhanced dimerization in the vicinity of that point, there is an excess of dimers, which relaxes by dimer fluxes pointed away from x = 0. Conversely, monomers flow preferentially towards x = 0 to feed the enhanced monomer to dimer conversion. | |
The relatively simple shape of the concentration profiles disguises a complex interplay of the diffusion–advection process with the underlying chemistry. Some of this complexity is revealed by inspecting the transport fluxes, defined as
| | 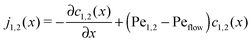 | (10) |
and plotted in
Fig. 2B. The sign of both fluxes is predominantly positive, caused by the solvent flow to the right: the black lines indicate the respective unperturbed flux of monomers,
ĉ1vflow (short-dashed), and of dimers,
ĉ2vflow (long-dashed). However, the flux profiles show that the dimer flux reverses its direction in the entry zone, while the monomer flux reverses its direction in the driving zone. Note that in the co-moving reference frame, which moves along with the fluid, the sum of monomer and dimer fluxes adds up to zero at every point, δ
j1(
x) + 2δ
j2(
x) = 0, as required by local mass conservation. In this reference frame, the direction of the fluxes changes sign exactly at the point of strongest accumulation at the left edge of the driving zone. At this point, the accumulation of monomers leads to a high production of dimers, due to the non-linearity of the dimer production rate ∼
c12(
x). The local excess of dimers relaxes through extra dimer fluxes away from the peak (blue continuous curve in
Fig. 2B), while the monomers in that area have to be replenished by monomer fluxes towards the peak (red dotted curve).
The positions of the extrema of the fluxes also mark interesting points: they correspond to the points where the chemical reaction is locally in equilibrium, i.e. dimer formation is exactly balanced by dissociation, 2koffc2 = konc12. Conversely, the chemical reaction is out of equilibrium at all other points. At all points in the exit zone, the total concentration is exactly equal to the bulk value ĉ. However, due to the physical driving, the dimer-to-monomer ratio is biased towards dimers at the interface between the driving zone and exit zone. The ratio then relaxes to the equilibrium value as the fluid moves to the right and the excess dimers dissociate.
To elucidate the physical chemistry of our model, it is useful to quantify the local dimer bias by the dimer-to-monomer ratio normalized with respect to the ratio at equilibrium,
| | 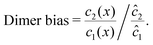 | (11) |
We can see that the increase of the local dimer bias by the physical driving is due to the combination of two effects, by writing it in the form
| | 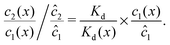 | (12) |
Here, the first term on the right hand side corresponds to the ratio of the dissociation constant to an effective local dissociation constant defined as
| | | Kd(x) = c12(x)/c2(x). | (13) |
The ratio can be considered as a measure of the local chemical imbalance: dimerization and dissociation are locally balanced if the ratio is one,
Kd/
Kd(
x) = 1, the sign of its deviation from one marks the local preferential direction of the chemical reaction, and the fold-change deviation from one indicates how far the concentrations are from chemical equilibrium. The second term on the right hand side measures the local accumulation of monomers relative to the equilibrium concentration. Taken together,
eqn (12) thus helps us to separate two contributions to the observed dimer bias according to
| Dimer bias = chemical imbalance × accumulation. |
Fig. 3 explicitly shows this separation of effects, with the dimer bias profile in Fig. 3A corresponding to the product of the accumulation in Fig. 3B and the chemical imbalance in Fig. 3C. The shape of the curves reveals a compensation effect that might be viewed as a generalization of the principle of Le Chatelier to non-equilibrium steady-states: at the point of the maximal dimer bias, i.e. the left edge of the driving zone, the chemical imbalance is shifted to the opposite direction, Kd/Kd(x) < 1, which favors monomers. Correspondingly, the peak in the monomer accumulation is more pronounced than the peak in the dimer bias, which compensates for the shifted chemical imbalance.
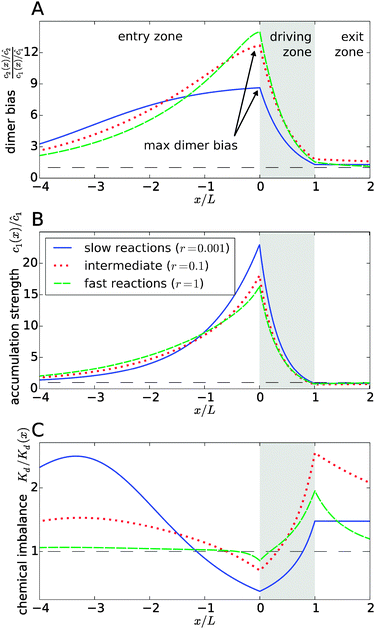 |
| | Fig. 3 Separation of the accumulation and chemical imbalance contributions to the dimer bias. (A) Profile of the dimer bias for slow, intermediate, and fast reactions (with the corresponding r-values indicated in the legend; all other parameters as in Fig. 2). (B and C) Show the corresponding profiles of the monomer accumulation strength and the chemical imbalance. The curves in (A) can be obtained as the product of the corresponding curves in (B) and (C), see main text. The arrows in (A) indicate the maximal dimer bias, which is plotted in Fig. 4. | |
In Fig. 3, all curves are shown for three different reaction speeds r (Damköhler number), representing slow, intermediate, and fast reactions. The significant difference between the curves for different r points to a strong effect of the Damköhler number on the non-equilibrium steady-state. In each case, the maximal dimer bias occurs at the point of highest accumulation. However, the amplitudes and shapes of the curves are significantly affected by r. With increasing r, the maximal dimer bias increases, while the maximal accumulation decreases, which is compensated by a shift of the chemical imbalance towards dimers.
Another effect of the Damköhler number on the steady-state is revealed by Fig. 3C. Not only the amplitude, but also the range of the chemical imbalance depends sensitively on r. For slow reactions, the effect of the physical driving reaches far into the entry and exit zones, disturbing the chemical equilibrium over long distances, due to the slow equilibration of the chemical reaction. Depending on r, the maximal chemical imbalance can either be located at the boundary between the driving zone and the exit zone or far ahead in the entry zone.
Fig. 4 shows the dependence of the maximal dimer bias, i.e. the height of the peak in Fig. 3A, on the key dimensionless parameters of the system. As one might intuitively expect, it increases monotonously as a function of the strength of physical driving, as shown in Fig. 4A, where the Péclet numbers Pe1 and Pe2 are increased at a constant ratio, Pe2 = 1.5Pe1, again for three values of r representing slow, intermediate, and fast reactions. In each case, the strength of physical driving affects the maximal dimer bias roughly exponentially, however, the chemical reaction is more sensitive to the physical driving at larger r. It is perhaps worthwhile emphasizing that any small amount of physical driving suffices to produce some accumulation, i.e. it is not required that the driving is stronger than the fluid flow, Pe1,2 > Peflow, since a “traffic jam” of solute molecules is created even when they move in the direction of the flow, but slower than the flow.
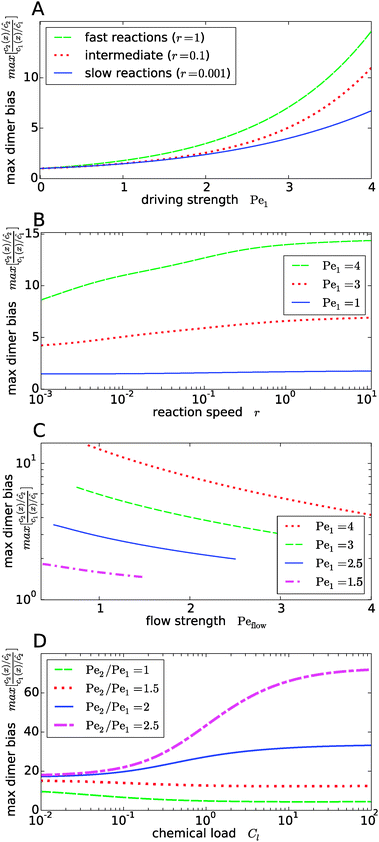 |
| | Fig. 4 Dependence of the maximal dimer bias on the system parameters. (A) Maximal dimer bias (the value at x = 0 in Fig. 3A) as a function of the driving strength (Pe1 is varied at a constant Péclet ratio of Pe2/Pe1 = 1.5); all other parameters as in Fig. 2. At stronger driving, the dimer bias becomes more sensitive to the reaction speed r (Damköhler number). (B) As in (A), but plotted as a function of r. (C) Flow-dependence of the maximal dimer bias at r = 0.1 for different driving strengths at constant Péclet ratio Pe2/Pe1 = 1.5. A stronger flow (high Peflow) washes away more solute molecules and thereby diminishes the maximal dimer bias. (D) Maximal dimer bias as a function of the chemical load Cl = ĉ/Kd at fixed reaction speed r = 0.1. The different curves correspond to different Péclet ratios obtained by varying Pe2 at constant Pe1 = 4. | |
The effect of the Damköhler number is directly plotted in Fig. 4B, for different strengths of physical driving. This plot shows that the effect of r becomes more and more significant as the driving strength is increased. For r values much larger than one, the maximal dimer bias saturates. Increasing the flow speed, Peflow, at constant driving decreases the accumulation, as shown in Fig. 4C. Essentially, the flow “washes away” the solute molecules at large Peflow. When Peflow becomes equal to Pe1, the accumulation disappears and therefore the curves end at this point. Finally, the dependence of the maximal dimer bias on the chemical load Cl is shown in Fig. 4D. For Péclet ratios that favor the accumulation of monomers, Pe2 < Pe1, an increasing chemical load reduces the maximal dimer bias. The opposite trend is obtained for higher Péclet ratios, where dimers are accumulated more efficiently than monomers. Note that the chemical load dependence only arises if the reactions are sufficiently fast (Fig. 4D shows the case of r = 0.1). In the slow reaction limit (r → 0), the accumulation of monomers and dimers decouples and the maximal dimer bias does not depend on the chemical load, as can be directly verified from the analytical expressions in Appendix B.
Our key observation from Fig. 4 is the growing sensitivity to the Damköhler number r as the strength of the physical driving is increased. This leads to the question whether the maximal fold-change that can be induced by changing r, i.e. the amplitude of the r-effect, will steadily grow with the driving strength. Also, how does the behavior depend on the Péclet ratio Pe2/Pe1? Both of these questions are addressed in Fig. 5, where the amplitude of the r-effect on the maximal dimer bias is plotted as a function of driving strength, for several different Péclet ratios. We see that the Péclet ratio determines the sign of the r-effect, with a Péclet ratio of Pe2/Pe1 ≈ 2 marking the turning point. For smaller Péclet ratios (the experimentally more relevant case), the amplitude grows monotonously with the driving strength. In contrast, for larger ratios the effect reverts such that the fast reaction limit (r → ∞) displays a weaker dimer bias than the slow reaction limit (r → 0). However, the amplitude of the reverted effect also becomes more significant with increasing driving strength.
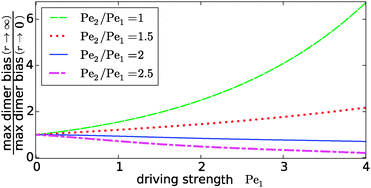 |
| | Fig. 5 Amplitude of the kinetic control of the driving efficiency. The ratio of the maximal dimer biases in the fast (r → ∞) and slow (r → 0) reaction limits indicates how much the efficiency of physical driving can be varied by changing the reaction speed. The dependence of this “amplitude” on the driving strength is qualitatively different depending on whether the Péclet ratio Pe2/Pe1 is smaller or larger than one. In either case, the effect becomes more pronounced with increased driving. The flow is kept at Peflow = 1 and the chemical load at Cl = 1. | |
The turning point Pe2/Pe1 ≈ 2 is an indirect consequence of the law of mass action. The accumulation of monomers and dimers at the left edge of the driving zone is roughly exponential in their respective Péclet number, i.e. c1,2(0) ∼ exp(Pe1,2). Therefore, since the concentration of monomers enters quadratically in the local equilibrium constant (13), the Péclet number for dimers would have to be at least twice as large in order for a local chemical equilibrium to be dominated by dimers with increasing physical driving. However, in the non-equilibrium steady-state of our system, local chemical equilibrium is only achieved in the fast reaction limit r → ∞. For finite r, the reaction at the accumulation peak at x = 0 is imbalanced towards monomers for Pe2/Pe1 < 2 and towards dimers for Pe2/Pe1 > 2. Therefore, the increase of r, which tends to restore the local chemical balance, has opposing effects depending on whether the Péclet ratio is smaller or larger than two. One has to keep in mind, however, that a change in r has a non-trivial global effect on the concentration profile. As a consequence, the curve for the boundary case Pe2/Pe1 = 2 is not completely flat.
IV. Discussion and conclusions
Our analysis revealed generic effects that occur when a chemical reaction is driven by a physical non-equilibrium process via a coupling mechanism that depends on the transport of reagents. While our minimal model serves as an explicit description only for situations where a reversible dimerization reaction is coupled to an advection–diffusion transport process, our central conclusion is far more general: in the non-equilibrium steady-state of the coupled physico-chemical system, the “driving efficiency” is kinetically controlled by the so-called Damköhler number, which measures the reaction rate relative to the transport rate. As discussed in the following, the generality of this conclusion rests on the fact that the chemical response to the physical driving is influenced both by the induced accumulation of reagents and the induced chemical imbalance. Our minimal model allowed us to cleanly separate these two contributions, see Fig. 3.
For our dimerization reaction, we quantified the chemical response by the dimer bias (11). For other reactions, the response would be quantified by a similar ratio of products to reactants. Generally, the efficiency of the physical driving is then proportional to the chemical response obtained at a given driving strength. For our model, we have seen in Fig. 4 and 5 that this efficiency depends on the Damköhler number, and that the “amplitude” of this dependence grows with the driving strength. Any physical driving mechanism that is based on a difference in transport coefficients between reactants and products will behave similarly, since the chemical response is ultimately driven by local accumulation and the law of mass action. A spatially non-homogeneous chemical conversion then counterbalances transport fluxes of reactants and products. As in our example, the steady-state of this interplay between transport and reaction will then generally be affected by the Damköhler number. However, the sign of the effect of the Damköhler number depends on system-specific transport coefficients, as we have seen in Fig. 5.
Due to the simplicity and generality of our model and analysis, it is related to a large body of previous work. The majority of the existing work that studies the interplay of reactions with transport mechanisms focuses on unbiased diffusive transport,19,20 with an emphasis on phenomena such as front propagation21,22 and aggregation.23 However, the study of chemical reactions in combination with advective transport does has a long history in the context of sedimentation problems.24–26 We believe that our present study approaches advection–diffusion–reaction models from a new angle, and hope that it will stimulate further research into the physical driving of chemical reactions.
Appendix A: size-selectivity of the Péclet numbers for RNA and DNA
The physical driving affects molecules of different sizes differently. Thus, one has to estimate how Péclet numbers depend on the size of the molecules. The effect of physical driving is independent of the external flow, which we include in our model. Hence, the realistic values of Péclet numbers can be evaluated from thermal trap accumulation experiments, where the trap has a geometry of a thin capillary and is closed on both sides.8 Without chemical reactions, the accumulation along the axis of the capillary follows an exponential law c(x) = exp(αx),8,15 where accumulation strength α is a function of the experimentally known trap width, parameters of a solvent, the temperature gradient as well as diffusion and Soret coefficients of solutes. In our model the Péclet numbers are phenomenological parameters, which correspond to α in the thermal trap experiment in ref. 8. Thus we can estimate a ratio of Péclet numbers for monomers and dimers from the corresponding ratio of accumulation strengths. The latter can be computed as a function of experimentally measured parameters from Supporting Information in ref. 8 for the gravitation-driven trap:| | 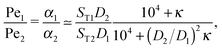 | (A1) |
where ST1 and ST2 are Soret coefficients, D1 and D2 are diffusion coefficients for monomers and dimers correspondingly and κ depends on the trap parameters (in particular, κ is proportional to the square of the width of the capillary). The ratios of Soret and diffusion coefficients can be extracted from the measurements. For RNA the values can be extrapolated from the following dependencies on the length:8
| D(n) = 643n−0.46 μm2 s−1, |
| | | ST(n) = (5.3 + 5.7n0.73) 10−3 K−1 | (A2) |
Here n refers to the number of polymerised oligomer units rather than number of bases. Hence the ratio ST(2n)/ST(n) ≈ 1.8 and D(2n) = 0.727D(n) if n is not too small. For dsDNA the corresponding dependencies are also provided in ref. 8 and 16,| | 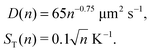 | (A3) |
From (A1) it can be seen that the ratio of Péclet numbers for monomers and dimers is then affected only by κ. In order to find the full range of possible Péclet ratios, we assume, that κ can adopt any value. Then for RNA oligomers,| | | 1.3 < PeRNA2/PeRNA1 < 2.5 | (A4) |
and for DNA oligomers,| | | 0.8 < PeDNA2/PeDNA1 < 2.3. | (A5) |
Appendix B: concentration profiles in the slow reaction limit (r → 0)
In the slow reaction limit (r → 0), the system (4) becomes completely decoupled and the equations for the steady-state concentration profiles c1(x) and c2(x) can be separately solved. We show here only the case D1 = D2 = D, but the general case can be treated in the same way. For simplicity we use the dimensionless quantities ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = x/L and
= x/L and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1,2(
1,2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = c1,2(
) = c1,2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) )/ĉ here and in the following appendices. The uncoupled solutions take the general form
)/ĉ here and in the following appendices. The uncoupled solutions take the general form
where the constants A1,2, C1,2 for the different zones must be obtained from the boundary and continuity conditions. Far away from the driving zone, i.e. for ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) → ±∞ the monomer and dimer concentrations c1 and c2 must satisfy the boundary condition
→ ±∞ the monomer and dimer concentrations c1 and c2 must satisfy the boundary condition| | ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1,2(−∞) = 1,2(−∞) = ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) 1,2 = 1,2 = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1,2(+∞), 1,2(+∞), | (B1) |
where ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) 1,2 = ĉ1,2/ĉ. Furthermore, at the boundaries of the driving zone (
1,2 = ĉ1,2/ĉ. Furthermore, at the boundaries of the driving zone (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0, 1), the concentration profiles
= 0, 1), the concentration profiles ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1,2(
1,2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) and the normalized fluxes
) and the normalized fluxes 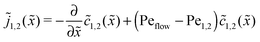 of monomers and dimers need to be continuous. This leads to
of monomers and dimers need to be continuous. This leads to| | 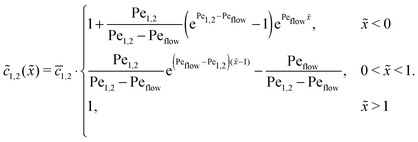 | (B2) |
Thus, the concentration profiles increase exponentially in the entry zone, drop exponentially in the driving zone, and are constant in the exit zone, fulfilling the equilibrium condition ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) 12/
12/![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) 2 = 1/Cl or, equivalently, ĉ12/ĉ2 = Kd.
2 = 1/Cl or, equivalently, ĉ12/ĉ2 = Kd.
Appendix C: concentration profiles in the fast reaction limit (r → ∞)
Next, we consider the opposite, fast reaction limit. We only treat the case of equal diffusion coefficients, D1 = D2 = D, and equal drift velocities, vdrive1 = vdrive2, for monomers and dimers in the driving zone, such that Pe1 = Pe2 = Pe. One then obtains a differential equation for the total concentration ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) =
) = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1(
1(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) + 2
) + 2![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 2(
2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) by adding twice the differential equation for dimers to the one for monomers in eqn (4). The equation for
) by adding twice the differential equation for dimers to the one for monomers in eqn (4). The equation for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) is solved as in Appendix B with the respective boundary and continuity conditions, leading to
) is solved as in Appendix B with the respective boundary and continuity conditions, leading to
In the fast reaction limit, the concentrations for monomers and dimers are locally in equilibrium,| | 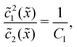 | (C1) |
at every point ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) . Since
. Since ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) =
) = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1(
1(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) + 2
) + 2![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 2(
2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), we getand the monomer concentration profile
), we getand the monomer concentration profile| | 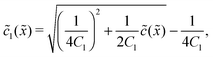 | (C3) |
while the dimer concentration profile ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 2(
2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) can be obtained from (C1).
) can be obtained from (C1).
Appendix D: linear response to weak driving
The Péclet numbers Pe1 and Pe2 represent a direct measure for the degree of physical driving of monomers and dimers, respectively. By applying perturbation theory, one can obtain the steady-state concentration profiles analytically for any reaction speed r, as long as the driving is weak, Pe1, Pe2 ≪ 1. Towards this end, we set Pe1 = δ and Pe2 = γδ, with δ ≪ 1 and a constant dimer-to-monomer driving ratio γ. Again, we limit our discussion to the case of equal diffusion coefficients D1 = D2 = D. We express the reaction–diffusion eqn (4) in terms of our dimensionless parameters and set the time derivatives to zero to obtain the equations for the steady-state,| | 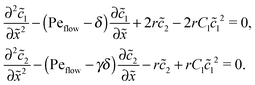 | (D1) |
For δ = 0 (no physical driving), one can combine the equations to again obtain an equation for the total concentration ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) =
) = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1(
1(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) + 2
) + 2![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 2(
2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), which contains only drift and diffusion terms. Since the distinction between the three zones becomes immaterial for δ = 0, the general solution
), which contains only drift and diffusion terms. Since the distinction between the three zones becomes immaterial for δ = 0, the general solution ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = A + BePeflowx has only two free parameters that are fixed to B = 0 and A = 1 by the boundary conditions at infinity. Hence, the unperturbed monomer and dimer concentration profiles, which we denote by
) = A + BePeflowx has only two free parameters that are fixed to B = 0 and A = 1 by the boundary conditions at infinity. Hence, the unperturbed monomer and dimer concentration profiles, which we denote by ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 10 and
10 and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 20, are spatially uniform and related by
20, are spatially uniform and related by ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 20 = Cl
20 = Cl![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 102. The expansion of the monomer and dimer profiles in δ then takes the form
102. The expansion of the monomer and dimer profiles in δ then takes the form| | 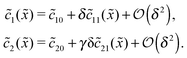 | (D2) |
Inserting this expansion into (D1) yields the equations| | 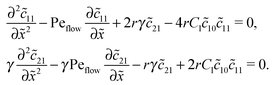 | (D3) |
for the linear response correction to the unperturbed profiles. We first consider the linear combination c* = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 11 + 2γ
11 + 2γ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 21, which satisfies the equation
21, which satisfies the equation| | 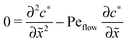 | (D4) |
with the general solution c* = AePeflow![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) + B. The constants A, B for the different zones follow from the boundary and continuity conditions stated in Appendix B. These imply that the correction terms vanish far away from the driving zone, c11(
+ B. The constants A, B for the different zones follow from the boundary and continuity conditions stated in Appendix B. These imply that the correction terms vanish far away from the driving zone, c11(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = ±∞) = 0 = c21(
= ±∞) = 0 = c21(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = ±∞), and thus c*(
= ±∞), and thus c*(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = ±∞) = 0. Using that γ
= ±∞) = 0. Using that γ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 21(
21(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = (c*(
) = (c*(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) −
) − ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 11(
11(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ))/2, one obtains an inhomogeneous linear differential equation of second order for
))/2, one obtains an inhomogeneous linear differential equation of second order for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 11(
11(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), where the inhomogeneity is proportional to c*,
), where the inhomogeneity is proportional to c*,| | 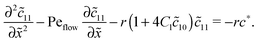 | (D5) |
This equation is straightforward to solve analytically within the entry, driving and exit zones, subjected to the corresponding boundary and continuity conditions. We used these analytical solutions, which we do not display here due to the length of the expressions, to cross-validate our numerical results.
References
-
B. Alberts, A. Johnson, J. Lewis, D. Morgan, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, Garland Science, 6th edn, 2014 Search PubMed.
- M. W. Powner, B. Gerland and J. D. Sutherland, Nature, 2009, 459, 239–242 CrossRef CAS PubMed.
- J. D. Sutherland, Angew. Chem., 2016, 55, 104–121 CrossRef CAS PubMed.
- R. Zwanzig, A. Szabo and B. Bagchi, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 2022 CrossRef.
- K. A. Dill and H. S. Chan, Nat. Struct. Biol., 1997, 4, 10 CrossRef CAS PubMed.
- I. A. Chen and J. W. Szostak, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 7965–7970 CrossRef CAS PubMed.
- I. A. Chen, R. W. Roberts and J. W. Szostak, Science, 2004, 305, 1474–1476 CrossRef CAS PubMed.
- C. B. Mast, S. Schink, U. Gerland and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8030 CrossRef CAS PubMed.
-
S. R. De Groot and P. Mazur, Non-Equilibrium Thermodynamics, Dover Publications, 1984 Search PubMed.
-
H. S. Fogler, Elements of Chemical Reaction Engineering, Pearson Education, 5th edn, 2016 Search PubMed.
- M. Kreysing, L. Keil, S. Lanzmich and D. Braun, Nat. Chem., 2015, 7, 203–208 CrossRef CAS PubMed.
-
I. R. Epstein and J. A. Pojman, An Introduction to Nonlinear Chemical Dynamics: Oscillations, Waves, Patterns and Chaos, Oxford University Press, USA, 1998 Search PubMed.
- W. F. Martin, F. L. Sousa and N. Lane, Science, 2014, 344, 1092 CrossRef CAS PubMed.
- K. Clusius and G. Dickel, Nature, 1938, 26, 546 CAS.
- P. Debye, Ann. Phys., 1939, 428, 284 CrossRef.
- S. Duhr and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19681 CrossRef PubMed.
- C. Almarcha, P. M. J. Trevelyan, P. Grosfils and A. De Wit, Phys. Rev. Lett., 2010, 104, 044501 CrossRef CAS PubMed.
-
P. Seifert, P. Hillenbrand, V. V. Palyulin and U. Gerland, in preparation.
- T. A. Waite, Phys. Rev., 1957, 107, 463 CrossRef CAS.
- C. R. Doering and D. Ben Avraham, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 38, 3035 CrossRef.
- I. R. Epstein and K. Showalter, J. Phys. Chem., 1996, 100, 13132 CrossRef CAS.
- Z. Koza, Phys. A, 2003, 330, 160 CrossRef CAS.
- P. L. Krapivsky, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 3233 CrossRef CAS.
- G. A. Gilbert, Proc. R. Soc. London, Ser., 1959, 250, 377 CrossRef CAS.
- G. G. Belford and R. L. Belford, J. Chem. Phys., 1962, 37, 1926 CrossRef CAS.
- J. R. Cann and G. Kegeles, Biochemistry, 1974, 13, 1868 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article


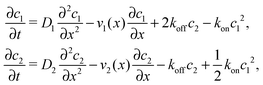
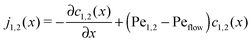
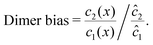
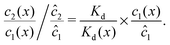


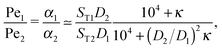
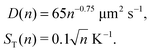
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = x/L and
= x/L and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1,2(
1,2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = c1,2(
) = c1,2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) )/ĉ here and in the following appendices. The uncoupled solutions take the general form
)/ĉ here and in the following appendices. The uncoupled solutions take the general form![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) → ±∞ the monomer and dimer concentrations c1 and c2 must satisfy the boundary condition
→ ±∞ the monomer and dimer concentrations c1 and c2 must satisfy the boundary condition![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1,2(−∞) =
1,2(−∞) = ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) 1,2 =
1,2 = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1,2(+∞),
1,2(+∞),![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) 1,2 = ĉ1,2/ĉ. Furthermore, at the boundaries of the driving zone (
1,2 = ĉ1,2/ĉ. Furthermore, at the boundaries of the driving zone (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0, 1), the concentration profiles
= 0, 1), the concentration profiles ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1,2(
1,2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) and the normalized fluxes
) and the normalized fluxes 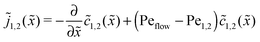 of monomers and dimers need to be continuous. This leads to
of monomers and dimers need to be continuous. This leads to
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) 12/
12/![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) 2 = 1/Cl or, equivalently, ĉ12/ĉ2 = Kd.
2 = 1/Cl or, equivalently, ĉ12/ĉ2 = Kd.
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) =
) = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1(
1(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) + 2
) + 2![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 2(
2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) by adding twice the differential equation for dimers to the one for monomers in eqn (4). The equation for
) by adding twice the differential equation for dimers to the one for monomers in eqn (4). The equation for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) is solved as in Appendix B with the respective boundary and continuity conditions, leading to
) is solved as in Appendix B with the respective boundary and continuity conditions, leading to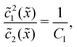
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) . Since
. Since ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) =
) = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1(
1(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) + 2
) + 2![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 2(
2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), we get
), we get![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) =
) = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1(
1(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) + 2Cl
) + 2Cl![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 12(
12(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) )
)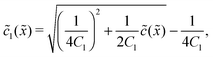
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 2(
2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) can be obtained from (C1).
) can be obtained from (C1).
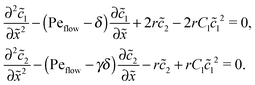
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) =
) = ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1(
1(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) + 2
) + 2![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 2(
2(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), which contains only drift and diffusion terms. Since the distinction between the three zones becomes immaterial for δ = 0, the general solution
), which contains only drift and diffusion terms. Since the distinction between the three zones becomes immaterial for δ = 0, the general solution ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = A + BePeflowx has only two free parameters that are fixed to B = 0 and A = 1 by the boundary conditions at infinity. Hence, the unperturbed monomer and dimer concentration profiles, which we denote by
) = A + BePeflowx has only two free parameters that are fixed to B = 0 and A = 1 by the boundary conditions at infinity. Hence, the unperturbed monomer and dimer concentration profiles, which we denote by ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 10 and
10 and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 20, are spatially uniform and related by
20, are spatially uniform and related by ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 20 = Cl
20 = Cl![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 102. The expansion of the monomer and dimer profiles in δ then takes the form
102. The expansion of the monomer and dimer profiles in δ then takes the form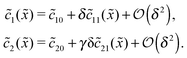
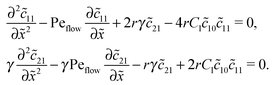
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 11 + 2γ
11 + 2γ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 21, which satisfies the equation
21, which satisfies the equation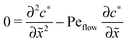
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) + B. The constants A, B for the different zones follow from the boundary and continuity conditions stated in Appendix B. These imply that the correction terms vanish far away from the driving zone, c11(
+ B. The constants A, B for the different zones follow from the boundary and continuity conditions stated in Appendix B. These imply that the correction terms vanish far away from the driving zone, c11(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = ±∞) = 0 = c21(
= ±∞) = 0 = c21(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = ±∞), and thus c*(
= ±∞), and thus c*(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = ±∞) = 0. Using that γ
= ±∞) = 0. Using that γ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 21(
21(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = (c*(
) = (c*(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) −
) − ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 11(
11(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ))/2, one obtains an inhomogeneous linear differential equation of second order for
))/2, one obtains an inhomogeneous linear differential equation of second order for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 11(
11(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), where the inhomogeneity is proportional to c*,
), where the inhomogeneity is proportional to c*,