A ‘bottom up’, ab initio computational approach to understanding fundamental photophysical processes in nitrogen containing heterocycles, DNA bases and base pairs

Abstract

The availability of non-radiative decay mechanisms by which photoexcited molecules can revert to their ground electronic state, without experiencing potentially deleterious chemical transformation, is fundamental to molecular photostability. This Perspective Article combines results of new ab initio electronic structure calculations and prior experimental data in an effort to systematise trends in the non-radiative decay following UV excitation of selected families of heterocyclic molecules. We start with the prototypical uni- and bicyclic molecules phenol and indole, and explore the structural and photophysical consequences of incorporating progressively more nitrogen atoms within the respective ring structures en route to the DNA bases thymine, cytosine, adenine and guanine. For each of the latter, we identify low energy non-radiative decay pathways via conical intersections with the ground state potential energy surface accessed by out-of-plane ring deformations. This is followed by summary descriptions and illustrations of selected rival (electron driven H atom transfer) non-radiative excited state decay processes that demand consideration once the nucleobases are merely components in larger biomolecular systems like nucleosides, and both individual and stacked base-pairs.

---

1. Introduction

Many recent experimental and theoretical studies have sought to explore the photophysics of simple heteroatom containing aromatic molecules^1–7 like phenols^8–28 and azoles^29–39 following excitation in the ultraviolet (UV) spectral region. Such systems are often termed prototypical, on the basis that a thorough understanding of their response to photoexcitation might well offer a useful guide to the photochemistry and photophysics of more complex and more biologically relevant molecules. Detailed understanding of their deactivation processes following UV excitation has thus long been seen as paramount. The first few excited states of these molecules can be partitioned in several different ways. One distinction is obvious; any given orbital promotion will support both singlet and triplet excited states. Unless stated otherwise, this Perspective focuses solely on the decay of singlet excited state molecules, since intersystem crossing to triplet states is not viewed as a significant decay process for the molecules and the (generally isolated molecule) conditions featured in this Perspective.

The nature of the orbital populated by photoexcitation is another key distinguisher. The highest occupied molecular orbital (HOMO) in the ground electronic (S₀) state of these molecules ranges between a (bonding) ring-centred π orbital or a (largely non-bonding) n orbital centred on the heteroatom, whereas the orbital populated by photoexcitation may be a (ring-centred, anti-bonding) π* orbital or a σ* orbital localised on the heteroatom – to which we return later. π* ← π transitions typically have the largest absorption cross-sections and dominate the UV absorption spectrum; the diabatic ¹ππ* states that result are often termed optically ‘bright’. π* ← n transitions are generally weaker, but much of the recent interest^1–5,7 in these molecules has centred on the (hitherto often neglected) excited states formed by σ* ← π (or σ* ← n) promotions which, for brevity, we will henceforth describe simply as ¹πσ* excited states. The ¹πσ* states generally have much smaller absorption cross-sections and, as a result, are sometimes described as optically ‘dark’.

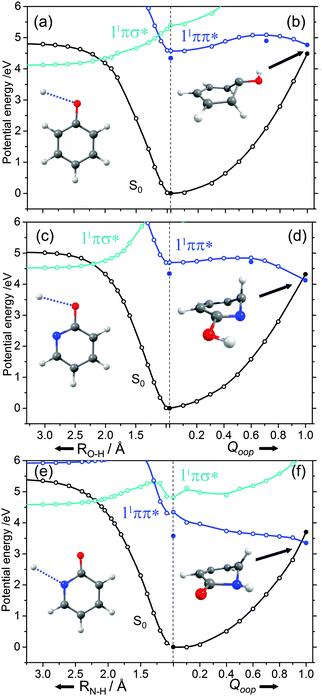
The energetic ordering of the first excited ¹πσ*, ¹nπ* and ¹ππ* states (i.e. the 1¹πσ*, 1¹nπ* and 1¹ππ* states) is molecule dependent. In the case of azoles like pyrrole^1,40 and imidazole,^41–43 the 1¹πσ* state is lowest in energy, whereas in the phenols² the 1¹ππ* state is the lowest energy excited state in the Franck–Condon (FC) region. The σ* orbital in these first row heterocycles has significant Rydberg (3s) character in the FC region, but acquires progressively more anti-bonding character upon X–H (X = N, O, etc.) bond extension. As a result, given the relative 1¹πσ* ← S₀ excitation and X–H bond dissociation energies, the potential energy surfaces (PESs) for these 1¹πσ* states are repulsive with respect to increasing R_X–H. Exciting molecules like imidazole at long UV wavelengths populates the 1¹πσ* excited state directly and results in prompt N–H bond fission. Long wavelength excitation of phenol, in contrast, populates the 1¹ππ* state which, at the diabatic level, is bound but can predissociate by coupling with the 1¹πσ* state and subsequently breaking the O–H bond on a much longer timescale.^16,19

Bond fission is just one of the several possible decay pathways available to the excited state molecules considered in this Perspective. Almost all of these pathways involve radiationless transfer from the initial state populated by photoexcitation (e.g. between different ¹ππ* and/or ¹nπ* states, from a ¹nπ* or ¹ππ* state to a ¹πσ* state, or from a ¹nπ* or ¹ππ* state to the S₀ state). As discussed below, the strength of such couplings maximises at molecular geometries where the relevant PESs become near degenerate – so called regions of conical intersection (CI).

The DNA/RNA bases illustrate this progressive increase in complexity nicely. These molecules show strong π* ← π absorptions at wavelengths ∼260 nm,^44,45 excitation of which could potentially induce photoreactions and harmful structural changes. Yet the DNA bases and base pairs display well-documented photostability.^46–53 This resistance to photodamage is attributable to ultrafast and efficient non-radiative (and non-reactive) relaxation to the S₀ state via internal conversion (IC). Femtosecond time-resolved studies of the isolated bases – in the gas phase^54–65 and in aqueous solution^66–77 – return excitation energy and environment dependent excited state lifetimes but, in all cases, these lifetimes are short; radiationless transfer to the S₀ state in the isolated bases typically occurs on a (sub)picosecond time scale. Ab initio calculations attribute such efficient excited state decay to the presence of low energy CIs between the excited (¹ππ*) and S₀ state PESs along out-of-plane deformation (ring puckering) coordinates.^78–107

Here we seek to explain, and to systematise, various of the non-radiative excited state decay processes available to related families of nitrogen containing heterocycles by pooling new results obtained using a range of ab initio electronic structure methods with existing literature data. Without question, the existing literature contains reports of more comprehensive and detailed computational studies of several of the systems covered in this Perspective, and we have sought to cite these at appropriate points in the narrative. The prime focus of the present study is the systematic analysis of the excited state photophysics of families of related molecules investigated in an (as best as possible) even handed and self-consistent manner.

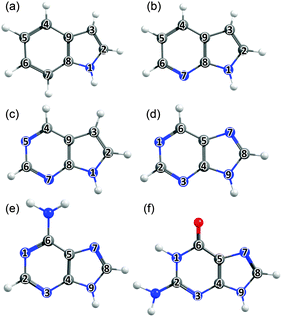
The philosophy of the study is as follows. Uracil (U), thymine (T) and cytosine (C) are pyrimidine derivatives, and hydroxypyridines and hydroxypyrimidines relate to phenol if one or more of the ring C atoms are replaced by N atoms. Adenine (A) and guanine (G) are purine derivatives. Purine itself can be viewed as the result of substituting three of the ring C atoms in indole by N atoms, and indole comprises imidazole fused with a benzene ring. This Perspective thus starts by considering trends in the excited state photophysics of the family of unicyclic molecules shown in Fig. 1, wherein C atoms in phenol are progressively replaced by N atoms, leading through selected pyridines and pyrimidines en route (after appropriate tautomerism and/or derivitization) to U, T and C. This is followed by a similar analysis of the evolving excited state photophysics of the family of bicyclic molecules shown in Fig. 2 as we step from indole through two azaindoles and purine to A and G. Both studies serve to illustrate the progressive lowering of the energies of ¹ππ*/S₀ CIs in out-of-plane deformation coordinates brought about by incorporating N atoms in the ring. The Perspective concludes by highlighting additional non-radiative decay pathways (most notably excited state H atom transfer processes) that demand consideration as the molecular size and complexity increases further – as exemplified by the ribonucleosides (Fig. 3) and the base-pairs (Fig. 4).

Fig. 1 Unicyclic molecules considered in this work: (a) phenol, (b) 2-hydroxypyridine, (c) 4-hydroxypyrimidine, (d) 2,4-dihydroxypyrimidine, (e) 2(1H)-pyridone, (f) 4(3H)-pyrimidone, (g) uracil (U), (h) thymine (T) and (i) cytosine (C), with the ring atoms numbered for future reference.

Fig. 2 Bicyclic molecules considered in this work: (a) indole, (b) 7-azaindole, (c) 5,7-azaindole, (d) 9H-purine, (e) adenine (A) and (f) guanine (G), with the ring atoms numbered for future reference.

Fig. 3 The nucleosides: (a) 5-methyluridine, (b) cytidine, (c) adenosine and (d) guanosine, with the ring atoms of the base numbered for future reference.

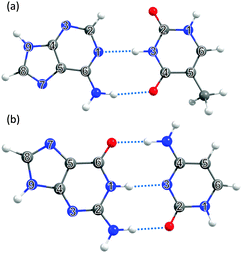Fig. 4 The DNA and RNA base pairs: (a) adenine–thymine (A–T) and (b) guanine–cytosine (G–C), with the ring atoms in the respective bases again numbered for future reference.

2. Theoretical methodology

A brief overview of the ab initio computational methods used in the present calculations is given here. Fuller details can be found in the ESI.†

2.1 Ground state tautomerism

Using the Gaussian09 computational package,¹⁰⁸ the ground state tautomers were assessed by optimising, where appropriate, the enol and keto forms along with the transition state (TS) connecting the two structures using Møller–Plesset second order perturbation theory (MP2) along with Dunning's augmented correlation consistent basis set of triple-ξ quality (AVTZ).¹⁰⁹ The minimum energy path (MEP) for tautomerism was computed at the DFT/CAM-B3LYP/AVTZ level of theory using the intrinsic reaction coordinate (IRC) algorithm embedded within Gaussian 09.

2.2 Individual bases

The geometries of the ground state minimum, all conical intersections between the S₀ and ¹ππ* PESs in the out-of-plane distortion coordinate, Q_oop, and (where appropriate) any TSs of interest were optimised using Complete Active Space-Self Consistent Field (CASSCF) methods coupled with the 6-31G(d) basis set using Gaussian09.¹¹⁰ All possible out-of-plane deformation S₀/¹ππ* CIs were initially optimised. In each case, attention then focussed on the minimum energy CI (MECI) and subsequent linear interpolations in internal coordinates (LIICs) were constructed between the S₀ minimum and this MECI. The energies along this LIIC were then calculated using Complete Active Space with second-order Perturbation Theory (CASPT2) with a cc-pVDZ (VDZ) or AVDZ basis set, using the MOLPRO v2010.1 computational package.¹¹¹ For the specific cases of phenol, 2-hydroxypyridine and 2-pyridone, unrelaxed CASPT2/AVDZ scans were also calculated along the R_X–H (X = O or N) coordinate.

2.3 Nucleosides and base pairs

The S₀ state geometries of the nucleosides were optimised using MP2/6-31G(d) whilst the S₀/¹ππ* CI geometries were optimised using CASSCF/6-31G(d). MP2/6-31G(d) and CASSCF/6-31G(d) were also used to optimise the geometries of the S₀ minimum and the S₀/¹ππ* CI, respectively, for the A–T base pair. All MP2 and CASSCF calculations were carried out using Gaussian09. In each case, potential energy profiles along the LIIC linking these optimised critical points were constructed at the CASPT2/VDZ level of theory using the MOLPRO v2010.1 computation package. Relaxed potential energy profiles along the electron-driven proton (hydrogen) transfer (EDPT) coordinate of current interest were calculated for these four nucleosides and the A–T and G–C base pairs using ADC(2)/VDZ in Turbomole v6.3¹¹² for both the S₀ and S₁ (¹nπ*(charge transfer (CT))) states. In the nucleosides, the driving coordinate of interest in each case was the terminal ribose sugar O–H bond whereas, in the base pairs, it was the individual base centred O–H or N–H bonds.

2.4 Radical-anion pairs

Calculations on the G–C and A–T radical-anion base pairs were performed in order to mimic inter-stack electron transfer. The relaxed ground state potential energy profiles of the (adenine–thymine)⁻ and (guanine–cytosine)⁻ radical-anion base pairs were computed at the TD-DFT/CAM-B3LYP/VDZ level of theory using R_N−H as the driving coordinate in Gaussian09.

3. Results and discussion

The material in this section is structured as follows: several of the target molecules can exist as both keto- and enol-tautomers, and Section 3.1 reviews how substituting C atoms in the ring by N atoms affects the relative stabilities of these tautomers in the S₀ state. The rest of the Perspective focusses on excited states. Sections 3.2 and 3.3 explore how the stabilities and non-radiative decay dynamics of the families of molecules displayed in Fig. 1 and 2 are influenced by C ↔ N atom substitution within the ring. Sections 3.4 and 3.5 then explore some of the additional non-radiative decay pathways (H atom transfer processes) that can arise in the selected nucleosides and base pairs shown in Fig. 3 and 4.

3.1 Ground state tautomerism

Table 1 compares the ground state energies of 2-hydroxypyridine, 4-hydroxypyrimidine and 2,4-dihydroxypyrimidine with those of the corresponding keto-tautomers calculated at several different levels of theory. The respective stabilities listed in Table 1 are all referenced to the more stable tautomer.

Table 1 Relative stabilities (ΔE, in cm⁻¹) of the enol (E)–keto (K) tautomers of 2-hydroxypyridine/2-pyridone, 4-hydroxypyrimidine/4-pyrimidone and 2,4-dihydroxypyrimidine/uracil in their respective S₀ states, calculated at many levels of theory and quoted relative to that of the more stable tautomer (indicated in parentheses), along with relevant experimental data (where available)

Level of theory	2-Hydroxypyridine/2-pyridone	4-Hydroxypyrimidine/4-pyrimidone	2,4-Dihydroxypyrimidine/uracil
	ΔE/cm^−1 (1a–1b)	ΔE/cm^−1 (2b–2a)	ΔE/cm^−1
			(3d–3a)	(3d–3c)	(3d–3b)
DFT/CAM-B3LYP/AVDZ	110 (E)	240 (K)	4090 (K)	4000 (K)	3830 (K)
DFT/CASSCF(10,8)/AVDZ	100 (E)	690 (K)	—	—	—
MP2/AVTZ	840 (E)	260 (E)	3370 (K)	3760 (K)	3470 (K)
DF-MP2-F12/AVTZ	800 (E)	230 (E)	3450 (K)	3780 (K)	3530 (K)
CCSD/AVTZ	420 (E)	120 (K)	3890 (K)	4050 (K)	3650 (K)
CCSD(F12*)/AVTZ	410 (E)	130 (K)	3970 (K)	4080 (K)	3710 (K)
CCSD(T)(F12*)/AVTZ	390 (E)	100 (K)	3710 (K)	3860 (K)	3550 (K)
CASPT2(12,11)/AVTZ	1130 (E)	390 (K)	—	—	—
Experiment	270 (E)^112	167 (K)^115,116	—	—	(K)^117

---

2-Hydroxypyridine/2-pyridone. As Table 1 shows, all levels of theory investigated suggest that 2-hydroxypyridine (i.e. the enol form) is the more stable tautomer [CCSD(T) ΔE_enol–keto ∼ 390 cm⁻¹] – in accord with gas phase experimental measurements.¹¹³ As Fig. 5(a) shows, the DFT/CAM-B3LYP/AVTZ calculations return a large (∼12 000 cm⁻¹) barrier to tautomerism in the isolated molecule. The greater relative stability calculated for the enol tautomer is consistent with its larger number of resonance structures over which the π electron density can be delocalised. In solution, however, the relative stabilities of the two tautomers are very sensitive to the solvent polarity; in aqueous solution, for example, the stabilisation from hydrogen bonding ensures that the keto-form is the majority tautomer.^114,115

Fig. 5 Ground state MEP along the enol/keto tautomerism IRC calculated for (a) 2-hydroxypyridine/2-pyridone, (b) 4-hydroxypyrimidine/4(3H)-pyrimidone and (c) and (d) 2,4-dihydroxypyrimidine/uracil. The red curves in (c) and (d) show the calculated MEP for the sequence 2,4-dihydroxypyrimidine (i.e. the 2,4-dienol tautomer) to the 2(3H)-enol–keto form (structure 3b) and on to the 1H,3H-diketo form, uracil (structure 3d), while the blue curves map the potential for the same 2,4-dienol to uracil rearrangement but via the intermediate 4(1H)-enol–keto tautomer (structure 3c). The energies of structures 3a–c are defined relative to the most stable structure (3d).

4-Hydroxypyrimidine/4-pyrimidone. Adding another N atom within the six-membered ring stabilises the keto tautomer to the extent that, in the isolated molecule, 4-pyrimidone is calculated (and observed^116,117) to be slightly the more stable tautomer – as shown in Table 1 and Fig. 5(b). This can be understood by recognising that, in the context of these heterocycles, the N atom is an electron donor. The C=O group in the keto form is able to accept and stabilise additional π density introduced in the 1-position, whereas an OH group in the 4-position (as in the enol form) would tend to be destabilised.

2,4-Dihydroxypyrimidine/uracil. Two independent ground state hydrogen transfer coordinates were explored for these tautomers, illustrated by the red and blue curves in Fig. 5(c) and (d). The calculations clearly show that uracil (structure 3d) is the most stable tautomer (consistent with experimental observation¹¹⁸), followed by the hemi-keto tautomers (structures 3b and 3c), with the fully enol tautomer (structure 3a) being the least stable – for the same electronic reasons as outlined above.

Cytosine, adenine and guanine. Ground state tautomerism is also possible in the other pyrimidine species shown in Fig. 1 (i.e. thymine (Fig. 1(h)) and cytosine (Fig. 1(i))) and in the various purines depicted in Fig. 2. For brevity, we restrict discussion to the DNA bases C, G and A. The distinguishing feature of these molecules (cf. those discussed above) is the amino group, which affords additional possibilities of amino–imino tautomerism and leads to a significant increase in the number of possible tautomers.

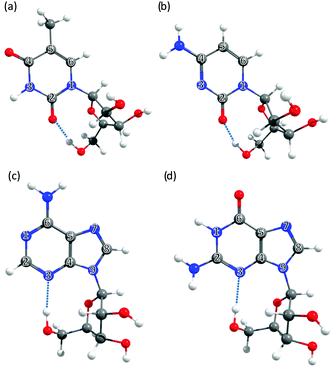
In cytosine, for example, there are fourteen possible tautomer/rotamers, five of which are shown in Fig. 6(a)–(e). The 1H-keto-amino form (Fig. 6(a)) is the preferred tautomer in the Watson–Crick (WC) base pairing. H atom migration from the N1–H group to the neighbouring O atom or to the N3 atom gives rise to three distinct tautomers – two 2-enol-amino structures (of which only the anti-rotamer is shown in Fig. 6(b)) and the 3H-keto-amino tautomer (Fig. 6(c)). The relative stabilities of the different tautomeric forms are again sensitive to the chemical environment. Microwave, resonance enhanced multiphoton ionisation (REMPI) and core level photoemission measurements reveal both the 1H-keto-amino and 2-enol-amino tautomers in jet-cooled gas phase samples.^119–122 Low temperature matrix isolation studies (in the IR and the UV) also identify both of these tautomers and conclude that the 2-enol-amino tautomer is more abundant,^123,124 whereas the 1H-keto-amino form is most stable in aqueous solution.¹²⁵ The available theoretical predictions are broadly supportive of these conclusions.^126–128 Under isolated molecule conditions, the 1H-keto-amino and 2-enol-amino tautomers are calculated to lie lowest in energy (with the former ∼500 cm⁻¹ more stable than the latter), with the two imino (Fig. 6(d) and (e)) and the 3H-keto-amino (Fig. 6(c)) tautomers consistently higher in energy. Micro-solvation with water molecules, under isolated gas-phase conditions,¹²⁷ is predicted to favour the keto-amino tautomers, particular the 1H-keto-amino structure (calculated as being ∼2040 cm⁻¹ more stable than the 3H-equivalent) and to destabilise the enol and imino tautomers.

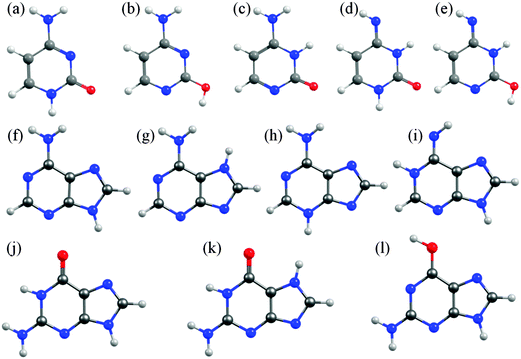Fig. 6 Selected low energy tautomeric forms for cytosine (structures (a)–(e)), adenine (structures (f)–(i)) and guanine (structures (j)–(l)).

In A, the H atom at the N9 position can migrate to any of the other nitrogen atoms within the ring, giving a total of fourteen possible tautomers/rotamers.¹²⁹ Experimental studies have identified the presence of the 9H-amino (Fig. 6(f)) and, in some cases, the 7H-amino (Fig. 6(g)) tautomers in the gas phase,^130–133 in matrix isolation conditions¹³⁴ and in polar solvent environments (e.g. water).^135–138 All of these studies concur that the canonical 9H-amino form is the dominant tautomer in all environments (as it is in DNA itself), though the 7H-amino variant gains some relative stabilisation in polar solvents by virtue of its larger dipole moment. These experimental conclusions have been reinforced by numerous ab initio studies, though most predict a significant (∼2400–3000 cm⁻¹) energy difference between the 9H- and 7H-amino tautomers.^130,139,140 The 3H-amino- and the various imino forms (e.g. the 1H,9H-imino structure shown in Fig. 6(i)) are all calculated to be considerably higher in energy.

G is functionalized with both amino and keto groups, and has the greatest number of possible tautomers.¹⁴¹ An early IR matrix isolation study showed G present as a mixture of enol and keto tautomers,¹⁴² and more recent studies have identified three different tautomers (one enol and two keto forms) in a supersonic jet.^143–146 Guided by complementary ab initio calculations, these were assigned to the 1H,7H-keto-amino (Fig. 6(k)), the 1H,9H-keto-amino (Fig. 6(j)) and the 9H-enol-amino (Fig. 6(l)) tautomers, with the latter likely present as two different rotamers. Theory^{140,145–148} also predicts that the 1H,7H-keto-amino structure is the most stable as an isolated molecule, followed by the 1H,9H-keto-amino tautomer (with reported energy separations in the range 20–250 cm⁻¹) and then the 9H-enol-amino tautomer (some 270–620 cm⁻¹ above the global minimum structure). All of the other tautomers not shown in Fig. 6 are predicted to lie at least 1000 cm⁻¹ above the global minimum. Once again, however, this energetic ordering is disturbed by solvating with water,¹⁴⁶ under which circumstances the tautomeric equilibria are predicted to shift in favour of the 3H,7H-keto-amino (now the most stable), 7H,9H-keto-amino and 3H,9H-keto-amino tautomers.

The primary aim of this Perspective is to seek trends and differences in the excited state photophysics exhibited by these molecules. Thus we choose to focus attention on the tautomeric forms adopted by the various nucleobases in the common WC or in the Hoogsteen base pairing schemes (i.e. 1H-cytosine, 9H-adenine and 1H,9H-guanine, as depicted in Fig. 1(i), 2(e) and (f)).

Nucleosides. The tautomeric equilibria in the nucleosides are assumed not to differ substantially from those found with the individual bases, apart from the obvious cases where N1 (in the pyrimidines) or N9 (in the purines) is terminated by the pentose sugar and some of the tautomeric variety associated with H migration between the various N sites in the isolated monomers is obviously precluded.

3.2 Unicyclic ring systems and the pyrimidine bases

Vertical excitation energies. Table 2 lists vertical excitation energies (VEEs) calculated for the two lowest singlet excited states of the molecules depicted in Fig. 1 (with the character of the dominant orbital promotion indicated in parentheses). Fig. 7 shows the orbital promotions involved in forming the excited states of 2-hydroxypyridine, 2-pyridone and 7-azaindole; similar figures for the other systems considered in this Perspective are shown in the ESI.† The adiabatic excitation energies (AEEs) calculated for the respective first excited states generally agree well with the available experimental values.

Table 2 Calculated vertical and (where available) adiabatic excitation energies (VEEs and AEEs) for the first three excited singlet states of the pyrimidine systems, with the dominant transition character indicated in parenthesis next to the VEE values. Available experimental values are listed also, with (A) and (V) specifying whether the measured data should be compared with the calculated AEE or VEE values. The last two columns show, respectively, the optimised energy of any TS in the PEC along the LIIC linking the (vertical) ¹ππ* state and the ¹ππ*/S₀ MECI and the energy of the ¹ππ*/S₀ MECI itself. All energies are quoted in units of eV

Molecule^ref.	ΔE(S1–S0)			ΔE(S2–S0)		ΔE(S3–S0)	ΔE(TS–S0)	ΔE(CI–S0)
	VEE	AEE	Exp.	VEE	Exp.	VEE
Enol
Phenol^9	4.57 (ππ*)	4.34	4.51 (A)	5.40 (πσ*)	—	—	4.89	4.63
2-Hydroxy-pyridine^154,155,157	4.70 (ππ*)	4.34	4.48 (A)	6.17 (nπ*)		6.79 (nσ*)	4.71	4.32
4-Hydroxy-pyrimidine	4.94 (nπ*)	4.64	—	5.18 (ππ*)	—	5.28 (nπ*)	4.55	3.81
2,4-Dihydroxy-pyrimidine	4.90 (nπ*)	4.52	—	5.02 (ππ*)	—	6.43 (πσ*)	—	3.80
Keto
2-Pyridone^156,195–197	4.34 (ππ*)	3.57	3.70 (A)	4.81 (nπ*)	—	5.15 (nσ*)	—	3.70
4-Pyrimidone	4.45 (ππ*)	—	3.85 (A)	4.92 (nπ*)	—	5.58 (nπ*)	—	3.12
Uracil^198	4.80 (nπ*)	4.17	—	5.69 (ππ*)	5.08 (V)	5.89 (πσ*)	—	3.92
Thymine^199	4.85 (nπ*)	4.17	—	5.50 (ππ*)	4.80 (V)	5.64 (πσ*)	—	4.09
Cytosine^60,119	4.58 (ππ*)	—	—	4.88 (nπ*)	3.95 (A)	5.34 (nπ*)	—	3.46

---

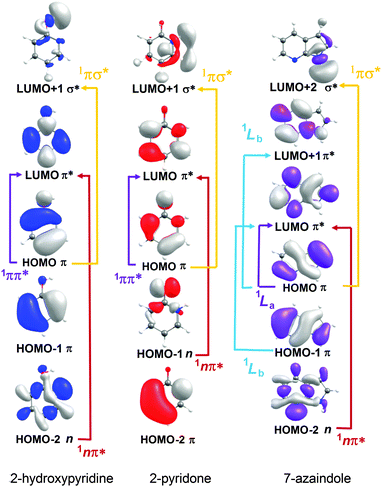Fig. 7 Dominant orbital promotions involved in forming the first few singlet excited states of 2-hydroxypyridine, 2-pyridone and 7-azaindole.

As discussed in Section 3.1, the molecules formed by introducing one (or more) N atoms into the ring can exist as enol and keto tautomers. The present calculations show the S₁ and S₂ states of 2-hydroxypyridine, 2-pyridone, 4-pyrimidone to have ¹ππ* and ¹nπ* character, respectively, in the FC region. However, this energetic ordering is reversed in the cases of 4-hydroxypyrimidine, 2,4-dihydroxypyrimidine, U and T. Fig. 7 illustrates the (expected) better spatial overlap between the orbitals involved in the π* ← π excitations cf. the π* ← n excitations.

Several trends are evident in the data collected in Table 2. Amongst the enols, the ¹ππ*-S₀ term values are similar in phenol and 2-hydroxypyridine, and larger in 4-hydroxypyrimidine and 2,4-dihydroxypyrimidine. The similar term values in phenol and 2-hydroxypyridine can be understood if the weak intramolecular H-bond between the N atom and the OH at the C2 position in the latter provides a similar stabilisation to both the π and π* orbitals. OH group(s) are π-donors. This additional electron density is preferentially localised at positions ortho- and para- to the ring-atom bearing the OH group, and can be accommodated more readily by a more electronegative N atom (cf. a C atom). The increased ¹ππ*-S₀ term values in 4-hydroxypyrimidine and 2,4-dihydroxypyrimidine (wherein the ¹ππ* state is raised above the 1¹nπ* state) are thus attributed to preferential stabilisation of the π (and destabilisation of the π*) orbital by the additional N atom. Table 2 also shows that the S₁ states of the keto tautomers (2-pyridone and 4-pyrimidone) are formed by the same orbital promotions as the corresponding enols, and that their ¹ππ*-S₀ term values are consistently smaller, despite the gradual stabilisation of the S₀ state of the keto form upon N atom inclusion (recall Table 1). This can be understood by considering the differing π donating capabilities of NH and OH groups, which will be amplified by the fact that the OH group is pendant to the ring. The in-ring N atom in the NH group is much more effective at stabilizing the electron deficiency introduced by π* ← π excitation (and thus the ¹ππ*-S₀ energy gap) in the keto tautomers.

Photodissociation vs. photostability. As noted in the Introduction, photoinduced O–H or N–H bond fission is a recognised population loss process for many small, functionalised aromatic and heteroaromatic molecules, including phenols and azoles.^1,2,7 In the case of phenol, near UV excitation to the S₁(1¹ππ*) state leads to O–H bond fission, on a nanosecond timescale. Such behaviour can be understood in terms of the potential energy cuts (PECs) shown in Fig. 8(a). The ¹ππ* state is diabatically bound with respect to stretching R_O–H, but the ¹ππ* and ¹πσ* potentials experience a CI at slightly extended bond lengths (R_O–H ∼ 1.2 Å), and O–H bond fission can occur by tunnelling under this CI.^16,17,26,27

Fig. 8 Potential energy profiles for the ground and lowest singlet excited states along, respectively, R_X–H (X = O, N) and Q_oop for phenol ((a) and (b)), 2-hydroxypyridine ((c) and (d)) and 2-pyridone ((e) and (f)). Filled points define the energies of the optimised critical structures (i.e. the S₀ and 1¹ππ* minima, the S₀/¹ππ* CI and the TS on the 1¹ππ* potential leading to the prefulvenic S₀/¹ππ* CI). The structures in each panel illustrate, respectively, the X–H bond dissociation coordinate and the optimised geometry at the prefulvenic S₀/¹ππ* CI.

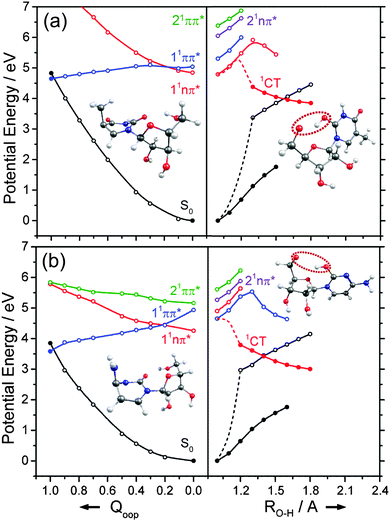
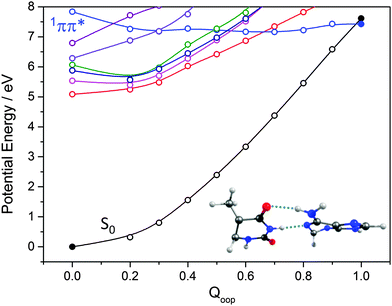
The ns lifetime of the 1¹ππ* state of phenol implies the absence of any efficient rival non-radiative decay processes. One such non-radiative decay process identified in similar photoexcited molecules is internal conversion to the ground state facilitated by a CI between the 1¹ππ* and S₀ states that can be accessed by motion along an out-of-plane ring deformation coordinate, Q_oop (via a so-called prefulvenic geometry).^14,149–152Fig. 8(b) shows the calculated geometry of this 1¹ππ*/S₀ MECI in phenol – with C1 very obviously out of the plane. As in later figures of this type, the open points show the ground (and excited) state energies calculated at a sequence of points along the LIIC connecting the optimised S₀ state geometry to that of the 1¹ππ*/S₀ MECI. The small number of filled points show the energies of the optimised critical structures (notably the minimum of the 1¹ππ* state and the energy of any TS separating this minimum excited state geometry from the MECI) calculated at the CASPT2/AVDZ level of theory. These optimised energies are also listed in Table 2. In the specific case of phenol, the key finding from these calculations is the presence of a substantial (∼0.5 eV) energy barrier in the MEP towards this prefulvenic MECI, that would be sufficient to render this pathway closed following excitation at energies not far above the origin of the 1¹ππ* state.

Fig. 8(c) and (d) show the corresponding PECs along R_O–H and the prefulvenic Q_oop coordinate for 2-hydroxypyridine. The most obvious feature of the former is the predicted elevation of the 1¹πσ* potential (or, more precisely, stabilisation of the S₀ state by the intramolecular H-bonding interaction between the OH group and the in-plane orbital on the adjacent ring N atom), which manifests itself as an increased barrier to tunnelling under the 1¹ππ*/1¹πσ* CI (cf. phenol). Indeed, if the potentials along the LIIC displayed in Fig. 8(c) are anything like quantitative, this barrier would preclude O–H bond fission as a possible decay process following excitation near the minimum of the 1¹ππ* state of 2-hydroxypyridine. As Fig. 8(d) shows, the predicted MECI along Q_oop lies at an energy below that of the 1¹ππ* minimum but, as in phenol, motion towards this prefulvenic 1¹ππ*/S₀ CI is impeded by an energy barrier (the calculated energy of the optimised TS is ∼0.37 eV above that of the 1¹ππ* state minimum (see Table 2)). Once again, therefore, theory would predict a certain photophysical stability to the 1¹ππ* state of 2-hydroxypyridine, consistent with previous theoretical studies^153,154 and experimental observations of well-resolved vibronic structure in the jet-cooled REMPI spectrum of this tautomer.^155,156 We also note that geminate recombination at the 1¹ππ*/S₀ CI could lead to branching into the S₀ state of the keto tautomer via a photoinduced dissociation-association reaction. Though entropically unfavourable under isolated gas-phase conditions, such a process would certainly merit consideration if the chromophore was suspended in a rare-gas matrix or in bulk solution.

Analogous PECs for 2-pyridone are presented in Fig. 8(e) and (f). The profiles along the X–H stretch coordinate (R_N–H in this case) show qualitative similarities with those for the 1¹ππ* and 1¹πσ* states of phenol (Fig. 8(a)) but the optimised energy of the 1¹ππ* state of 2-pyridone is well below the N–H dissociation limit, thereby excluding N–H bond fission as a possible decay channel following excitation at energies around the 1¹ππ*-S₀ origin. The predicted MECI in the prefulvenic Q_oop coordinate is below the 1¹ππ* ← S₀ vertical excitation energy, however (even after geometry optimisation, see Table 2), and the calculated PEC along the LIIC to the 1¹ππ*/S₀ CI is essentially barrierless. Such predictions also appear to be consistent with the available experimental data: the (split) origin band of the 1¹ππ*-S₀ transition of 2-pyridone shows resolved rovibronic structure and the dispersed emission spectrum following excitation to the origin level(s) reveals population of an extensive range of ground state vibrational levels.¹⁵⁷ The latter observation implies that the 1¹ππ* and S₀ states of 2-pyridone have different equilibrium geometries (as is also implied by the difference in the VEE and AEE values reported in Table 2). The reported two colour 1 + 1′ REMPI spectrum via the 1¹ππ* state, in contrast, is dominated by the origin band(s) – a finding that can most readily be explained by invoking a sharp drop in excited state lifetime upon tuning to higher energies.^154,155,158

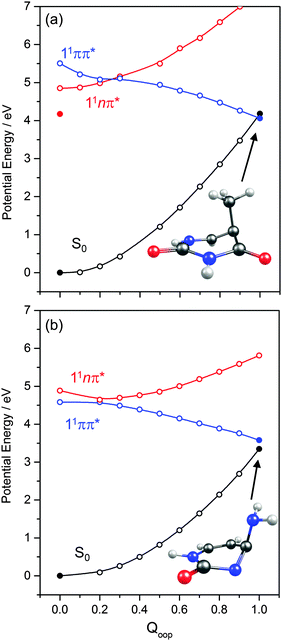
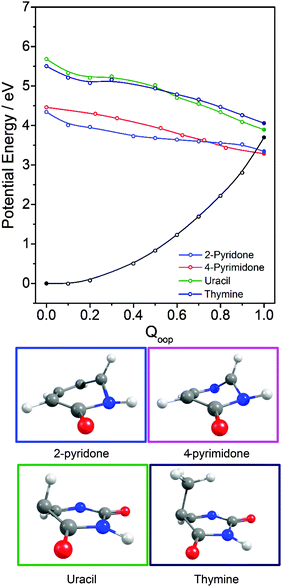
PECs along Q_oop for the ground and first three excited singlet states of (a) thymine and (b) cytosine are shown in Fig. 9. Again, these energies were calculated at the CASPT2 level for a sequence of geometries along a LIIC linking the CASSCF optimised S₀ minimum and the S₀/1¹ππ* MECI. These values are also reported in Table 2. The similarities between these PECs for T and C, and those for 2-pyridone (Fig. 8(f)), are obvious, notwithstanding the reversal in the energetic ordering of the 1¹nπ and 1¹ππ* states. In both T and C, the calculated 1¹ππ* PEC leading to the 1¹ππ*/S₀ MECI in the Q_oop coordinate is barrierless. Indeed, the predicted energy of the 1¹ππ*/S₀ MECI is even below that of the 1¹nπ origin – consistent with previous observations of ultrafast excited state decay following UV excitation of both T and C.^54,55,57,59

Fig. 9 Potential energy profiles along the out-of-plane ring deformation coordinate Q_oop for the ground and first few singlet excited states of (a) T and (b) C. Filled points represent the energies of the optimised critical structures (the S₀ and ¹nπ* state minima and the S₀/¹ππ* MECI) and the structure in each panel shows the optimised geometry of this MECI.

Notwithstanding the rich literature addressing the excited state photophysics of the DNA/RNA bases, there have been few systematic studies of the electronic and geometric reasons why such out-of-plane ring deformations are effective in promoting ultrafast excited state decay – and thus photostability – in pyrimidine derivatives like T and C, but not in simpler analogues like phenol. Yet recognising the factors that underpin this photostability could be important in guiding the development of more efficient photoprotective molecules for use in, e.g., sunscreens or artificial intraocular lenses. Thus we now summarise, and seek to rationalise, how the introduction of N atoms into the phenol ring and the addition of further OH and/or NH₂ functionalities influences the topography of the excited state PES(s) along Q_oopen route to the MECI with prefulvenic geometry.

Trends with respect to out-of-plane deformation. To aid this discussion, Fig. 10 presents an overlay of the calculated 1¹ππ* excited state PECs for phenol, 2-hydroxypyridine, 4-hydroxypyrimidine and 2,4-dihydroxypyrimidine (i.e. the enol tautomers listed in Table 2) plotted as a function of the out-of-plane deformation coordinate leading to the optimised 1¹ππ*/S₀ MECI. A similar overlay for the corresponding keto tautomers is shown in Fig. 11. The energies associated with each 1¹ππ* PEC are referenced to the minimum energy of the respective S₀ states but, for clarity and because the S₀ PECs in Q_oop are all rather similar, only one S₀ PEC (for 2-hydroxypyridine in Fig. 10, and for 2-pyridone in Fig. 11) is displayed in each panel. More detailed depictions of the ground and excited state PECs for these molecules, and side-on views illustrating the out-of-plane displacements of the ring atoms at the various S₀/1¹ππ* MECIs are provided in Fig. S1–S9 in the ESI.† The optimised energies of the various 1¹ππ*/S₀ MECIs (ΔE(CI–S₀)) and of any TS in the PEC along the LIIC linking the (vertical) 1¹ππ* state and the 1¹ππ*/S₀ MECI (ΔE(TS–S₀)) are included in Table 2.

Fig. 10 Overlaid PECs along Q_oop for the ¹ππ* states and respective ¹ππ*/S₀ MECIs for phenol, 2-hydroxypyridine, 4-hydroxypyrimidine and 2,4-dihydroxypyrimidine along with the calculated S₀ PEC for 2-hydroxypyridine. The filled points show the energies of the optimised critical structures (i.e. the S₀ state and the S₀/¹ππ* CI). The optimised geometry at each MECI is shown below.

Fig. 11 Overlaid PECs along Q_oop for the ¹ππ* states and respective ¹ππ*/S₀ MECIs for 2-pyridone, 4-pyrimidone, U and T along with the calculated S₀ PEC for 2-pyridone. The filled points show the energies of the optimised critical structures (i.e. the S₀ state and the S₀/¹ππ* CI). The optimised geometry at each MECI is shown below.

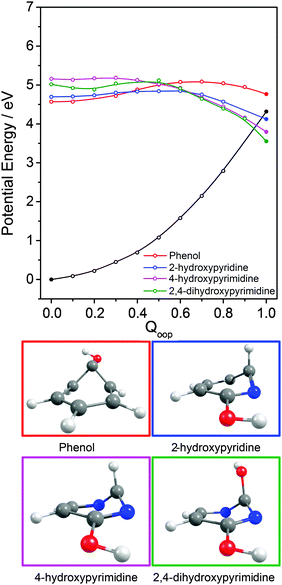
Inspecting these data, we see that the VEEs of the respective 1¹ππ* states increase across the enol series phenol → 2,4-dihydroxypyrimidine, while the energies of the 1¹ππ*/S₀ MECIs decrease. As a consequence, the barrier to accessing the 1¹ππ*/S₀ MECI decreases across the series and the gradient along Q_oop becomes progressively steeper with increasing N incorporation and ring functionalization. The VEEs of the 1¹ππ* states of the keto tautomers also increase across the series 2-pyridone → U and T.¹⁵⁹ The energies of the 1¹ππ*/S₀ MECIs increase in much the same order, but are always below the corresponding VEEs. The 1¹ππ* PECs leading to these MECIs have similar gradients in all four species, and none shows any obvious barrier. This difference in topography (cf. the enol tautomers) can plausibly be traced to differences in the extent of the π-conjugation in the enol and keto families. The sp² hybridisation of the N atom in 2-hydroxypyridine, for example, would be expected to be stronger than that in the keto analogue (2-pyridone), and thus more resistant to initial out of plane deformation – consistent with the barrier predicted in the PEC along Q_oop in the former.

Various trends revealed in these data are now considered in turn. The ground state of each of these systems is aromatic, the equilibrium geometry of the ring atoms is planar and the potential energy increases with out-of-plane ring deformation. Introducing one or more heteroatoms into the ring will weaken the rigidity, whereas adding OH groups (as in the enols) and, particularly, C=O groups (as in the keto tautomers) tends to reinforce the preference for planarity by extending the π-conjugation. π* ← π excitation destroys the aromaticity, induces some expansion of the ring, and lowers the resistance to out-of-plane ring deformation – to the extent that, in all bar phenol, the 1¹ππ* state potential is either essentially flat, or unstable, with respect to out-of-plane deformation. Under such circumstances, a CI with the S₀ PES upon distorting along Q_oop is inevitable. As Fig. 10 and Table 2 show, the energy of the 1¹ππ*/S₀ MECI in Q_oop decreases upon introducing one or more N atoms into the ring. In all cases other than phenol, the 1¹ππ*/S₀ MECI in Q_oop is calculated to lie below the VEE of the 1¹ππ* (and the 1¹nπ*) excited states. These MECIs also lie below the calculated O–H and N–H bond dissociation energies in 2-hydroxypyridine and 2-pyridone. Further, recalling Fig. 8(c) and (e), the latter excited state bond fissions are predicted to be hampered by a potential barrier (the lower part of the 1¹ππ*/1¹πσ* CI in R_X–H (X = N, O)). Thus we conclude that, at least relative to X–H bond fission, IC to the S₀ state mediated by out-of-plane distortion is likely to be the dominant decay process following long wavelength excitation of the N-containing heterocycles in Table 2. However, we also recognise that the excited state decay rate will be sensitive not just to the detailed topography of the excited state PES connecting the FC region to the 1¹ππ*/S₀ MECI in Q_oop (which may be influenced by substitution as, for example, for the cases of 5-hydroxy- and 5-aminouracil¹⁶⁰), but also to the excitation energy.

The detailed form of the out-of-plane displacement leading to the 1¹ππ*/S₀ MECI is also molecule dependent. As noted above, π* ← π excitation results in some ‘loosening’ of the ring structure and localisation of the π-bonding, with one or more ring atoms tending towards a pyramidal bonding arrangement. Among the enols, the atom exhibiting the greatest out-of-plane distortion (defined relative to the best-fit plane through the six ring atoms at the calculated geometry of the 1¹ππ*/S₀ MECI) varies between C1 in phenol, C6 in 2-hydroxypyridine and C2 in 4-hydroxypyrimidine and 2,4-dihydroxypyrimidine – as shown in Fig. 10 and Fig. S1–S4 (ESI†). The 1¹ππ*/S₀ MECI identified in phenol has a classic prefulvenic structure, with C1 (i.e. the C atom supporting the OH group) showing the greatest out-of-plane distortion, while the finding that the C2 atom in both pyrimidines shows the greatest out-of-plane distortion reflects its location between the two N atoms, which more readily adopt a local sp³ (pyramidal) coordination. The carbonyl group(s) in the keto tautomers encourage local planarity; relative to 2,4-dihydroxypyrimidine, C2 in U (and T) is less distorted out of the plane, with strain relief provided, instead, by increased puckering at C5 and C6.

The VEEs of the 1¹nπ* states of 4-hydroxypyrimidine, 2,4-dihydroxypyrimidine, U and T are all calculated to be below those of the corresponding 1¹ππ* states (see Table 2) and, as Fig. 9 showed (for the specific cases of T), the respective PESs show a CI in the Q_oop coordinate. As suggested previously,^{78–81,86,87,91,94,103} IC to the 1¹nπ* state could thus constitute another possible non-radiative decay pathway following excitation to the ‘bright’ 1¹ππ* state in these molecules. Conversely, one might also envisage instances where IC to the 1¹ππ* state (and subsequent coupling to S₀via the 1¹ππ*/S₀ MECI) could provide a non-radiative population loss route following excitation to higher vibrational levels within the 1¹nπ* manifold.

3.3 Bicyclic ring systems and the purine bases

Calculated VEEs for the first three excited singlet states of each molecule shown in Fig. 2(a)–(f) are listed in Table 3, along with the dominant character of the various excitations (in parenthesis). The excited states in each case comprise two ¹ππ* states, traditionally labelled ¹L_a and ¹L_b, and a ¹nπ* state. Apart from in the case of indole, the lowest lying ¹πσ* excited state has not been included in the present calculations, but H atom photofragment translational spectroscopy measurements following near UV photolysis of gas phase indole³³ and adenine¹⁶¹ molecules suggest that the threshold energy for N–H bond fission following radiationless transfer to the 1¹πσ* state in these molecules is ∼4.71 eV and ∼5.33 eV, respectively.

Table 3 Calculated VEEs and (where available) AEEs for the first three singlet excited states of the purine systems, with the dominant character of the transition indicated in parenthesis next to the VEE values. Available experimental values are listed also, with (A) and (V) specifying whether the measured data should be compared with the calculated AEE or VEE values. The last two columns show, respectively, the (unrelaxed) energy of any TS in the PEC along the LIIC linking the (vertical) ¹ππ* state and the ¹ππ*/S₀ MECI, and the optimised energy of the ¹ππ*/S₀ MECI. All energies are quoted in units of eV

Molecule^ref.	ΔE(S1–S0)			ΔE(S2–S0)		ΔE(S3–S0)	ΔE(TS–S0)	ΔE(CI–S0)
	VEE	AEE	Exp.	VEE	Exp.	VEE
a The relaxed S2/1^1nπ* state energy is 4.35 eV.
Indole^33,200	4.55 (ππ*)	4.44	4.37 (A)	5.07 (ππ*)	4.54 (A)	6.82 (πσ*)	5.17	5.06
7-Azaindole^201–204	4.61 (ππ*)	4.33	4.29 (A)	5.01 (ππ*)	4.32 (A)	5.20 (nπ*)	—	4.28
5,7-Azaindole	4.50 (nπ*)		—	4.97 (ππ*)	—	5.11 (ππ*)	—	3.82
Purine^205	4.70 (nπ*)	4.59	3.88 (A)	4.99 (ππ*)	—	5.68 (ππ*)	—	4.01
Adenine^160–206	4.86 (nπ*)		4.40 (A)	5.13 (ππ*)	4.48 (A)	5.28 (ππ*)	—	3.90
Guanine^207	5.25 (ππ*)	—	4.13 (A)	5.55 (nπ*)^a	—	6.53 (nπ*)	—	3.47

---

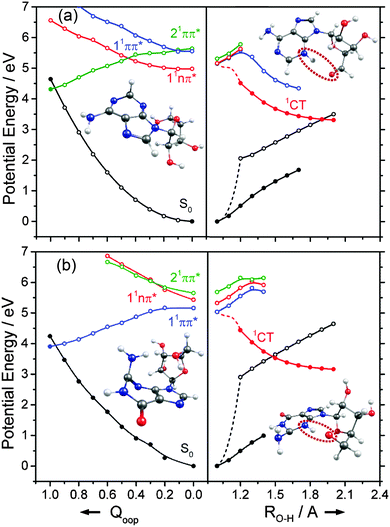
The dominant orbital promotions involved in forming these excited states in 7-azaindole were shown in Fig. 7. The ¹L_a and ¹L_b states differ in the detail of the participating π and π* orbitals. The ¹L_a ← S₀ transitions are generally pictured as π*(LUMO) ← π(HOMO) excitations and have the larger absorption cross-section.¹⁶² As in the pyrimidine systems, however, the energetic ordering of the ¹ππ* (¹L_a and ¹L_b) and ¹nπ* states is sensitive to N substitution (as Table 3 shows, the 1¹nπ* state is the S₁ state in 5,7-azaindole, purine and A) and can be modified by solvation.¹⁶³ The relative excited state energies are also sensitive functions of Q_oop, as shown for the cases of A and G in Fig. 12.

Fig. 12 Diabatic PECs along Q_oop for the ground and first three singlet excited states of (a) A and (b) G. The filled points depict the energies of optimised critical structures (i.e. the S₀, and 1¹nπ* state minimum energy geometries, and the S₀/¹ππ* MECI – the optimised geometry of which is also shown).

Viewed in terms of these diabatic PECs in Q_oop, we find that the higher energy 2¹ππ*(¹L_a) PEC correlates with the ¹ππ*/S₀ MECI in 5,7-azaindole, purine, A and G, whereas in indole and 7-azaindole it is the 1¹ππ*(¹L_b) PEC that correlates with this MECI. Fig. 13 compares calculated PECs along the LIIC linking the relevant (vertical) ¹ππ* excited state and the ¹ππ*/S₀ MECI for indole, 7-azaindole, 5,7-azaindole, purine and A. Each is referenced to a common zero of energy (the respective S₀ minimum) but again, to avoid congestion, only the S₀ PEC for indole is shown. More detailed depictions of the ground and excited state PECs for these molecules, and cross-sectional views showing the out-of-plane displacements of the ring atoms at each of the ¹ππ*/S₀ MECIs are provided in Fig. S10–S15 in the ESI.† The optimised energies of the various ¹ππ*/S₀ MECIs (ΔE(CI–S₀)) and of any TS identified in this PEC along Q_oop (ΔE(TS–S₀)) are included in Table 3.

Fig. 13 Overlaid diabatic PECs along Q_oop for the ¹ππ* state that correlates with the ¹ππ*/S₀ MECI in indole, 7-azaindole, 5,7-azaindole, purine and A. The filled points show the energies of the optimised critical structures (i.e. the S₀ state minimum and the S₀/¹ππ* MECI) and, for clarity, only the S₀ PEC calculated for indole is shown (open black points). The optimised geometry at each MECI is shown below.

Many of the trends evident in Fig. 13 are reminiscent of those discussed previously for the unicyclic systems. The ¹ππ*/S₀ MECI in indole is calculated to lie above the AEE of the 1¹ππ* state. Motion along Q_oop is thus unlikely to promote IC following photoexcitation at the 1¹ππ*(¹L_b) ← S₀ origin – consistent with the reported (∼17 ns) excited state lifetime.^164,165 As Fig. 13 shows, however, the introduction of even one N atom into the six-membered ring raises the VEE of the ¹ππ* state and lowers the energy of the ¹ππ*/S₀ MECI sufficiently that the PEC linking the FC region to the ¹ππ*/S₀ MECI in Q_oop becomes essentially barrierless. Notwithstanding that in most cases it is the diabatic 2¹ππ* PEC that links to this MECI, the available literature¹⁶⁶ supports the expectation that molecules excited to (vibrationally excited levels of) the 1¹ππ* and 1¹nπ* states will find efficient radiationless coupling pathways to this (and related) CIs with the S₀ PES.

The out-of-plane displacements required to access the various ¹ππ*/S₀ MECIs also have obvious parallels with those discussed in Section 3.2. Again, we choose to define these displacements with respect to the plane of best-fit through the (nine in this case) ring atoms. As Fig. 13 and Fig. S10–S15 (ESI†) show, the distortions are largely concentrated in the 6-membered ring. The atom showing the largest out-of-plane displacement at the ¹ππ*/S₀ MECI is again molecule dependent, but the largest distortions are always remote from the bond that fuses the two ring systems. C5 is most displaced in indole, but this switches to C6 in 7-azaindole (reflecting the energetic preference for sp³ hybridising the neighbouring N7 atom). The ¹ππ*/S₀ MECI in 5,7-azaindole is characterised by an obvious puckering around N5 and C6. Introducing an additional N atom in the 5-membered ring (as in purine, A and G) leads to a switch in the numbering convention used when describing the imidazole containing bicyclic systems – recall Fig. 2. It also allows greater relaxation of the bond common to the two rings (the C4–C5 bond in these molecules), with the result that C2 located between the N1 and N3 atoms is predicted to show the largest out-of-plane displacement at the ¹ππ*/S₀ MECI – as in the unicyclic analogues 4-hydroxypyrimidine, 2,4-dihydroxypyrimidine and 4-pyrimidone.

3.4 The ribonucleosides and deoxyribonucleosides

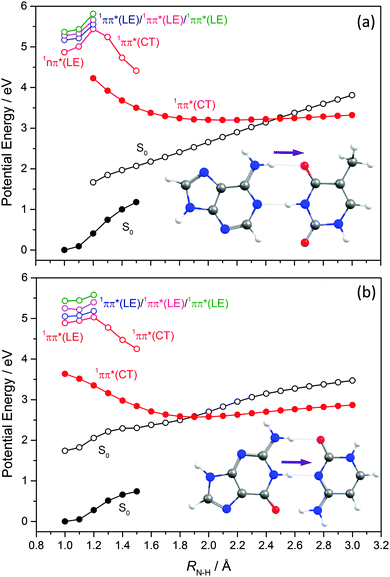
We now turn to the individual RNA base nucleosides: 5-methyluridine (uridine, thymidine), cytidine, adenosine and guanosine. The present study is limited to the oxygenated nucleosides with a ribose sugar attached to the N terminus of each base, but replacing one OH group on the ribose sugar by an H atom (as in the deoxyribonucleosides) is not expected to have any substantial effect on the excited state photophysics described in this section. The CASPT2 calculated PECs along Q_oop displayed in Fig. 14 and 15 exhibit obvious similarities with those of the precursor base. For comparative purposes, we have also scanned the Q_oop coordinate of adenosine using the ADC(2)/cc-pVDZ level of theory. The resulting PECs, shown in Fig. S34 of the ESI,† are reassuringly similar to those calculated at the CASPT2/cc-pVDZ level.

Fig. 14 Diabatic PECs for the ground and first few singlet excited states of (a) 5-methyluridine and (b) cytidine, along Q_oop (left panel) and along the EDPT coordinate (right panel) calculated at CASPT2 and ADC(2) levels of theory, respectively. Filled points in the left hand panels represent the energies of the optimised critical structures (i.e. the S₀ state minimum and the S₀/¹ππ* MECI – the optimised geometry of which is also shown) whereas the convention for using open and filled points in the right hand panels is detailed in the text.

Fig. 15 Diabatic PECs for the ground and first three singlet excited states of (a) adenosine and (b) guanosine along Q_oop (left panel) and along the EDPT coordinate (right panel) calculated at CASPT2 and ADC(2) levels of theory, respectively. Filled points in the left hand panels represent the energies of the optimised critical structures (i.e. the S₀ state minimum and the S₀/¹ππ* MECI – the optimised geometry of which is also shown). The convention for the use of open and filled points in the right hand panels is detailed in the text.

The present calculations suggest that the S₁ states of adenosine, 5-methyluridine and cytidine have predominant ¹nπ* character in the FC region, whereas that of guanosine is largely of ¹ππ* character. In each case we identify a ¹ππ*/S₀ MECI with prefulvenic geometry lying at an energy below the calculated S₁ state minimum. The calculated ¹ππ* PEC from the FC region to this MECI is in all cases barrierless. Such findings reinforce the view that the nuclear deformations required to sample this MECI are base-centred and suggest that the oxygenated ribose sugar is largely a spectator in this particular radiationless pathway. More detailed inspection reveals that the energies of the various excited states and the prefulvenic ¹ππ*/S₀ MECIs in the nucleosides are slightly destabilised relative to the corresponding quantities in the isolated base. These relative increases in excitation energy can be traced to the stabilising effects of hydrogen bonding between an O–H group of the ribose sugar and the base centred N or O atom in the ground state nucleoside.

Such H-bonding interactions are potentially important in the present context, as they can promote rival radiationless decay pathways in the DNA base residues, wherein the photoexcited state of interest develops charge-transfer (CT) character and undergoes intramolecular electron-driven proton (hydrogen) transfer (EDPT) from the terminal O–H group of the ribose to an N or O atom in the aromatic ring. In contrast to the PECs along Q_oop – which were calculated at the CASPT2 level to afford fairest comparison with the corresponding PECs for the smaller systems reported in Sections 3.1–3.3 – the PECs along the EDPT coordinate shown in the right hand panels of Fig. 14 and 15 were calculated at the ADC2 level. This is a pragmatic choice. The electronic states that promote EDPT involve orbital promotions that are sensitive to small changes in nuclear geometry. As such, a poorly chosen active space in CASSCF/CASPT2 can lead to spurious results along the charge-transfer coordinate, usually associated with important orbitals entering/leaving the active space. One way to circumvent this is to increase the active space substantially, but this leads to a large increase in computational expense. Given the available computational resources and (relatively) large size of the nucleoside molecules, the increased computational demands would have precluded detailed mechanistic study along the EDPT path with CASPT2 − especially in mapping the relaxed excited state paths.

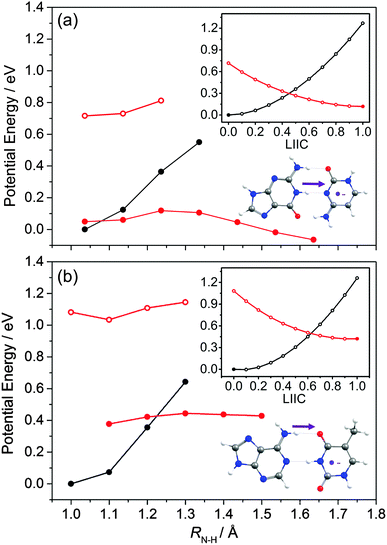
The PECs along the EDPT coordinate were derived as follows: the S₀ state was first scanned using the sugar O–H bond as the driving coordinate (henceforth identified simply as R_O–H). The filled black points in each panel depict the ‘relaxed’ S₀ state energies calculated by fixing R_O–H at selected values and allowing all other internal degrees of freedom to relax to their minimum energy configuration. The open coloured points show the various excited state energies calculated at the corresponding S₀ state geometries. A relaxed scan was then constructed for the ¹CT state (filled red points), and the corresponding S₀ state energies calculated at the relaxed S₁ geometries (shown by the open black symbols). The dashed black and red curves show the potential energy profiles for, respectively, the ground and first (adiabatic) excited states along the LIIC connecting the S₀ minimum geometry and the relaxed ¹CT structure at the shortest R_O–H distance. In all cases, the energy along the S₀ optimised reaction path rises while that of the ¹CT state declines with increasing R_O–H, with the result that the two states become degenerate at extended O–H bond lengths. The resulting ¹CT/S₀ CI is consistently calculated to lie at energies below the relevant S₁ minimum, and could thus provide an alternative radiationless route to the S₀ state following UV excitation (i.e. could provide another route to photostability).

Radiationless transfer via such a low energy ¹CT/S₀ CI was recently suggested as a possible explanation for experimental reports¹⁶⁷ that the excited state lifetime of adenosine is noticeably shorter than that of bare adenine. The calculated PECs along the O–H⋯N3 EDPT coordinate of adenosine (Fig. 15(a)) agree well with the previous calculations by Tuna et al.¹⁶⁸ These show that, following vertical excitation to the ‘bright’ ¹L_b state, there are barrierless pathways to lower energy CIs with the S₀ state in both the Q_oop and EDPT coordinates. The ¹CT/S₀ CI is calculated to lie at lower energy and, given that it is reached by intramolecular transfer of a light H atom, could very well constitute a competitive non-radiative decay pathway following UV excitation. We note the obvious analogy between such a ¹CT/S₀ CI in an EDPT coordinate and the previously discussed 1¹πσ*/S₀ CI in the R_O–H stretch coordinate in phenols. The former will generally be stabilised (and thus potentially active at lower excitation energies), however, given the presence of an acceptor O (or N) site on the aromatic ring.

The other nucleosides also show a low energy ¹CT/S₀ CI in the EDPT coordinate. The calculated PECs leading to the ¹CT/S₀ CI in guanosine, for example (right hand panel in Fig. 15(b)), have very similar profiles to those for adenosine. So, too, do the respective PECs linking the FC region to the ¹ππ*/S₀ MECI along Q_oop (left hand panel in Fig. 15(b)). The calculated PECs in the Q_oop coordinate show obvious similarities with those of the corresponding base (guanine, Fig. 12(b)). Again, the excited state and CI energies are somewhat elevated in the nucleoside – reflecting the stabilisation of the ground state by intramolecular H-bonding. As in adenosine, therefore, theory suggests that IC via the ¹CT/S₀ CI could be a competitive photoprotection pathway following UV photoexcitation of guanosine.

Analogous ¹CT/S₀ CIs have been identified in the respective EDPT coordinates for 5-methyluridine and cytidine also (Fig. 14(a) and (b)). In the specific case of 5-methyluridine, however, the present calculations return an energy barrier in the PEC linking the FC region and the ¹CT/S₀ CI, which is also calculated to lie at relatively higher energy than in the other nucleobases. For both 5-methyluridine and cytidine, the PEC along Q_oop leading to the ¹ππ*/S₀ MECI with a prefulvenic geometry is calculated to be barrierless. Based on the present limited set of calculations, it is thus tempting to suggest that: (i) EDPT will play a greater relative role in coupling photoexcited cytidine, adenosine and guanosine molecules back to their respective S₀ states; and (ii) the non-radiative decay of 5-methyluridine (uridine), and the excited state lifetimes of this nucleoside, should be largely determined by coupling at the ¹ππ*/S₀ CI in Q_oop and thus similar to that of T (U). Zgierski and Alavi reached broadly similar conclusions in prior computational studies of cytidine and bare cytosine.¹⁶⁹ However, recent time-resolved pump–probe studies of gas-phase adenosine, cytidine and 5-methyluridine return excited state lifetimes that are, in all cases, shorter than those of the corresponding isolated nucleobase.¹⁷⁰ This, the authors propose, reflects the additional excited state decay via EDPT enabled by the sugar backbone, which is not present in the isolated nucleobases.¹⁶⁹ Clearly, there is a case for further, higher level theoretical studies of the EDPT decay path in all of the nucleosides.

3.5 The DNA and RNA base pairs

EDPT has also been identified as an efficient deactivation pathway following photoexcitation of WC DNA/RNA base pairs. In the case of the WC A–T base pair,^171,172ab initio studies identified a ¹ππ* CT state arising via electronic promotion from an A-centred π orbital to a T-centred π* orbital in addition to a number of locally excited (LE) ¹nπ* and ¹ππ* states (i.e. states formed by electron promotion localised on just A or T). Excitations of the former type lead to charge separation, which is countered by excited state proton transfer.

Key PECs along this EDPT coordinate (i.e. extending one of the amine-centred N–H bonds attached to C6 in A towards the O attached to C4 in T) are shown in Fig. 16(a). Again, the filled black points show the ‘relaxed’ S₀ energies calculated by progressively extending this N–H driving coordinate and, at each R_N–H value, allowing all other internal degrees of freedom to relax to the minimum energy configuration. The open coloured points show the various excited state energies calculated at the S₀ geometries returned in this way. The filled red points define the ‘relaxed’ PEC for the ¹CT state, and the open black symbols show the corresponding S₀ state energies calculated at these relaxed S₁ geometries. As Fig. 16(a) shows, the PEC for the ¹CT state is barrierless and forms a CI with the S₀ PES at extended R_N–H. The calculated energy of this MECI is below the VEE of any of the ‘bright’ LE states. Radiationless transfer to and from this ¹CT state thus provides a route by which base pairs initially excited to a ¹ππ* LE state can return to the S₀ state and, following a ground state H atom transfer, reform the starting base pair structure – thereby constituting another possible route to photostability. Perun et al.¹⁷⁰ also calculated PECs for the corresponding ¹ππ* LE and ¹CT states for what is the most stable A–T conformer in the gas phase (characterised by H-bonds between N9–H on A and the O=C2 carbonyl group on T, and between N1–H on T and N3 on A). The PEC for the ¹CT state in this conformer, assuming R_N9–H as the driving coordinate, was found at significantly higher energies than the analogous ¹CT state in the WC A–T base pair and, crucially, not to form a CI with the S₀ PES.

Fig. 16 Potential energy profiles of (a) A–T and (b) G–C base pairs along the EDPT coordinate calculated at ADC2 level of theory. The filled black points show the ‘relaxed’ S₀ energies calculated at each R_N–H value having allowed all other internal degrees of freedom to relax to the minimum energy configuration. The open coloured points show the excited state energies calculated at these optimised S₀ geometries. The filled red points show the ‘relaxed’ PEC for the ¹CT state, while the open black points show the corresponding S₀ state energy calculated at each relaxed S₁ geometry.

Equivalent studies of the WC G–C base pair identified ¹ππ* LE states centred on both G and C and a low-lying ¹ππ* CT state formed by exciting a G-centred π electron to a C-centred π* orbital.^173–177 As Fig. 16(b) shows, the PEC for this ¹CT state calculated using R_N1–H as the driving coordinate exhibits a CI with the S₀ state. Thus, as with the WC A–T base pair, theory suggests EDPT via a ¹CT state could provide an efficient non-radiative route to the S₀ state after UV excitation of the WC G–C base pair. Again, the calculated PEC for the analogous ¹CT state in the most stable (gas phase) conformer of G–C (i.e. with H-bonds between N1–H on G and O=C2 on C, and between the C6=O on G and N1–H on C) using the R_N1–H bond in G as the driving coordinate shows no analogous CI with the S₀ PES.¹⁷⁸

Analyses of REMPI spectra of jet-cooled samples of many DNA/RNA base pair structures serve to reinforce these conclusions. The long wavelength UV absorption spectra of those structures assigned as WC conformers are broad and diffuse, whereas the corresponding spectra of all other conformers investigated to date exhibit sharp structure.^179,180 Solution phase ultrafast transient absorption studies of the WC G–C base pair confirm that the spectral breadth is attributable to the short excited state lifetime.^181,182 All such observations serve to support suggestions that the WC variants of the A–T and G–C base pairs have a special status, distinguished by the availability of uniquely efficient ¹CT state based deactivation mechanisms that minimise the opportunity for deleterious UV photoinduced chemistry. However, we also note that solution phase transient absorption studies of the WC G–C base pair (in chloroform) suggest a small yield of products arising from a double proton transfer process, wherein one of the H atoms in the amine group attached to the C4 atom in the C moiety in the ¹CT state is transferred to the O atom in the C6=O group in G.¹⁸³ The net effect of the second (reverse) H atom transfer is to return population to the S₀ state, albeit in a different tautomeric form than the starting WC base pair.

The importance of out-of-plane ring deformations in facilitating IC in N containing heterocycles has been highlighted earlier in this Article. Thus, as for the isolated bases (Fig. 9 and 11), we have used a LIIC approach to calculate PECs along the Q_oop coordinate leading to the MECI between an excited state and the S₀ state of the WC A–T base pair. As Fig. 17 shows, the potential energies of the first few singlet excited states generally increase with out-of-plane distortion. However, the PEC for one excited state in the energy range falls with increasing Q_oop and exhibits a CI with the S₀ state. Inspecting the various orbital promotions (shown in the ESI,† Fig. S33), we find that the former excited states all arise via π* ← n or π* ← π electron promotions localised on one of the chromophores, whereas the one excited state that displays a very different Q_oop dependence is the first formed by a π* ← π excitation involving orbitals that are delocalised (DE) over the entire base pair. The calculated energy of this ¹ππ*(DE)/S₀ MECI (∼7 eV) is much higher than that of the ¹ππ*/S₀ MECIs identified in the corresponding Q_oop coordinate in the isolated A or T bases. This difference can be attributed to the inter-base H-bonding interactions, which serve to restrain the out-of-plane distortion of the individual bases. This digression provides one illustration of the subtle, yet complex, consequences of non-covalent interactions on the relative efficacies of different non-radiative decay pathways: out-of-plane deformations are pivotal in promoting the non-radiative decay of the excited states of individual DNA bases yet, once non-covalently linked as a WC base pair, the dominant relaxation pathway is generally via CIs located along the EDPT coordinate.

Fig. 17 PECs along Q_oop for the ground and first few singlet excited states of the WC A–T base pair calculated at CASPT2 level of theory. Filled points define the energies of the optimised S₀ minimum and the prefulvenic ¹ππ*/S₀ MECI, the optimised geometry of which is shown at the lower right.

A thorough survey of even a subset of the many other instances where non-covalent interactions have been implicated in the non-radiative decay of stacked base pairs, and single and double stranded DNA, is outside the scope of this article. But we end by highlighting one example that serves to illustrate the potential for competition between base-pairing and base-stacking interactions. Early reports of a longer lived (∼100 ps) decay component in transient absorption studies following UV excitation of single and double-stranded oligonucleotides composed of A and T units^184,185 have since been extended and generalised to include other bases and short segments of both single and double stranded DNA.^186–193 The long lived component is now attributed to excited states arising as a result of photo-induced intrastrand electron transfer (ET), whereby a π electron from one base in a stack of nucleosides or base pairs is promoted to a π* orbital of an adjacent base in the same stack (i.e. electron hole pair creation in neighbouring stacked DNA bases). The intrastrand ET could then drive interstrand proton transfer from, or to, the base paired with, respectively, the radical anion and the radical cation formed in the ET process – yielding rare tautomers of the original base pair which then decay on a sub-nanosecond timescale. The similarities between this and the classic EDPT mechanism invoked to explain the ultrafast non-radiative decay of electronic excitation in isolated base pairs^170,172 (illustrated in Fig. 16) are self-evident. So, too, is the difference. The electron and proton implicated in these long-lived excited states originate from neighbouring bases in a stack (rather than the same base in a single base pair).

The PECs shown in Fig. 18 illustrate aspects of this behaviour. We start with a G–C base pair within a stack, and assume that the C carries a negative charge as a result of photo-induced ET from a neighbouring base (in the strand). This we model as a radical-anion G–C⁻ pair. Fig. 18(a) shows the relaxed PEC along R_N1–H (the same driving coordinate as in Fig. 16(b)) for the ground state neutral G–C base pair (solid black points), and PECs for the G–C⁻ radical-anion pair both at the relevant neutral S₀ minimum energy geometries and after allowing all other nuclear degrees of freedom to relax to the minimum energy geometry of its doublet ground (D₀) state (depicted by open and filled red points, respectively). The inset at the upper right shows the calculated neutral (S₀) and radical-anion (D₀) PECs along a LIIC linking the minimum energy geometry of the ground state neutral (at R_N1–H = 1.038 Å) and the minimum energy configuration of the radical-anion at R_N1–H = 1.238 Å. The calculated PECs show a low energy CI in the R_N1–H coordinate associated with proton transfer from the G to the C⁻. This process, which the main figure shows to be mildly exothermic, is illustrated on the structure shown at the lower right. Fig. 18(b) shows the corresponding PECs for the neutral A–T base pair and the A–T⁻ radical-anion along the same R_N–H coordinate as used in Fig. 16(a). The LIIC used in the upper insert in this case spans the range 1.0 ≤ R_N–H ≤ 1.2 Å. Though qualitatively similar to those for the G–C base pair (Fig. 18(a)), these PECs show significant differences: the energy of the neutral base pair at its equilibrium geometry is always below that of the radical-anion, and the potential energy of the relaxed D₀ PEC if anything increases with increasing R_N–H. These model calculations thus suggest no driving force for proton transfer from A to T⁻. Such contrasting propensities for proton transfer, from G to C⁻ but not from A to T⁻, accord well with the recent time-resolved vibrational spectroscopy measurements of Zhang et al.¹⁹³

Fig. 18 Calculated PECs along the N–H⋯N (N–H⋯O) proton transfer coordinate (shown by the arrow on the respective structures at the bottom right) for the neutral and radical-anion forms of the (a) G–C and (b) A–T WC base pair. The relaxed S₀ state energies are shown as black points, the open red points show the energies of the radical-anion D₀ state at the corresponding S₀ relaxed geometry, and the filled red points show the D₀ state energies after relaxing all degrees of freedom apart from the R_N–H coordinate of interest. The upper inset shows the calculated PECs along a LIIC linking the minimum energy geometries of the S₀ state (filled black point) and the D₀ state after extending R_N–H by 0.2 and 0.3 Å (filled red point) for the G–C and A–T pair, respectively.

4. Conclusions

This Perspective Article reports a systematic analysis of possible non-radiative decay mechanisms following UV photoexcitation of families of nitrogen containing heterocycles. The availability of non-radiative decay mechanisms by which photoexcited molecules can funnel back to their ground state, without experiencing potentially deleterious chemical transformation, is fundamental to molecular photostability. Photostability requires that the rate of internal conversion to the original ground state configuration far exceeds that of any competing population loss process (e.g. fluorescence, isomerisations, reaction, bond fission, etc.). To achieve such ‘ultrafast’ non-radiative decay from an excited state PES to the ground state, the molecule must be able to sample regions of conical intersection between the PESs.¹⁹⁴

The present investigation relies on use of electronic structure methods, complemented by a large body of pre-existing experimental and theoretical literature. Starting from phenol and indole, we have explored the structural and photophysical consequences of progressive incorporation of N atoms into the ring structure. Specific unicyclic systems investigated include selected hydroxypyridines, hydroxypyrimidines and the DNA bases T, U and C. Amongst the bicyclic systems, we have focussed on two azaindoles, purine, A and G. Having identified and rationalised specific photophysical trends in these families of molecular prototypes, we then extended the study to consider some of the additional richness and complexity with regard to excited state non-radiative decay that can arise via non-covalent interactions – in, for example, ribonucleosides, base pairs and stacked bases and base pairs. CIs are shown to be pervasive, but the forms of nuclear distortion required to access the CIs of lowest energy (and thus facilitate non-radiative decay) are seen to be sensitively dependent on the starting molecule, and its immediate environment. Nonetheless, as we now summarise, certain guiding trends and principles clearly emerge from the study.

Addressing first the isolated molecular prototypes, N incorporation is shown to result in a progressive relative stabilisation of the ground state keto-tautomer (cf. the enol-form), consistent with the observed dominance of keto-tautomers in the DNA/RNA nucleobases, ribonucleosides and WC base pairs. Focussing now on excited states, O–H bond fission is a common population loss process following UV photoexcitation of phenols.^9,17,19,25 However, the present work shows that incorporating even one N atom affords sufficient stabilisation of the ¹ππ* PES towards a ¹ππ*/S₀ CI in an out-of-plane deformation coordinate that IC via such prefulvenic distorted structures becomes the dominant (and efficient) decay route following UV excitation of the N-containing unicycles. Such predictions accord with the available excited state lifetime data. The simplest bicyclic system considered in this work, indole, already contains one N atom. This atom is in the 5-membered ring, however, and the lowest energy ¹ππ*/S₀ CI in the Q_oop coordinate is calculated to lie well above the S₁(¹L_b) ← S₀ origin – consistent with prior observations of fluorescence from electronically excited state indole molecules.¹⁹⁵ The present calculations show that the addition of at least one more N atom, in the 6-membered ring, is necessary in order to modify the topography of the ¹ππ* PES sufficiently that distortion along Q_oop to a CI with the S₀ PES becomes a barrierless, exothermic non-radiative decay pathway. Such trends, identified in both the unicyclic and bicyclic families, are consistent with the well-documented ultrafast excited state decay (and the photostability) of the isolated DNA(RNA) bases T(U), C, A and G.

Understanding the excited state decay dynamics of isolated nucleobases is a necessary but, as the latter part of this Perspective Article shows, not a sufficient prerequisite for unravelling the dominant non-radiative decay mechanism(s) operating when the base is a part of a larger chemical structure. In the nucleosides, for example, one or more heteroatoms in the base may experience H-bonding interactions with OH groups of the sugar backbone. From the perspective of the respective bases, such interactions are predicted to have only a minor perturbative effect on the ¹ππ* PES leading to the ¹ππ*/S₀ MECI along Q_oop. But the existence of such H-bonds can also promote new, alternative non-radiative decay pathways wherein charge-transfer character induced by the photexcitation causes an H atom to migrate from the sugar to one of the heteroatoms of the base. The present calculations hint that – particularly in the cases of adenosine, guanosine and cytidine – such an EDPT mechanism could be a competitive route for channeling excited state population back to the S₀ state via a CI in the relevant O–H⋯N coordinate.

H-bonds are central to base pair formation, and have a profound effect on the photophysics of electronically excited base pairs. Isolated base-pairs decay non-radiatively, on an ultrafast timescale. But this decay is not via¹ππ*/S₀ CIs in the Q_oop coordinate as in the individual bases; the energies of such CIs are substantially raised in the base-pairs by the interbase H-bonds that restrain the out-of-plane distortion of either component base. Rather, the minimum energy decay pathway following UV excitation involves interbase charge-transfer, and subsequent motion through a low energy CI in the EDPT coordinate associated with extending the N6–H bond in A (in the WC A–T base pair) or N1–H in G (in the WC G–C base pair). The WC structures are not the lowest energy conformers of the isolated base pairs in the gas phase. But equivalent calculations for these minimum energy conformers of A–T and G–C reveal no similar low energy ¹CT/S₀ CI in the EDPT coordinate, encouraging suggestions that the WC variants are special – by virtue of their having a particularly efficient ¹ππ* CT state based deactivation mechanism that minimises the opportunity for potentially UV induced photodamage.

This survey ends with a note of caution. Not only do studies of the isolated bases fail to reveal key aspects of the excited state photophysics displayed by the WC base pairs, but theoretical studies of the isolated base pairs also fail to account for all aspects of the photophysics exhibited by stacks of base pairs. Specifically, several recent experiments identify a longer lifetime component within the excited state decay which theory can explain by invoking a role for photoinduced intrastrand electron transfer, which drives subsequent interstrand proton transfer within a base pair – thereby returning the system to the ground state of (a variant) of the original base pair.^183–192 Given the evident influence of non-covalent interactions, it is worth reiterating that the calculations reported in this Perspective are all performed under isolated molecule conditions. Many prior absorption studies have shown that solvation affects the absorption spectra (and thus the relative energies of the excited states) of such systems. However, none of the recent time-resolved experiments or theoretical investigations suggest that solvent interactions change the following fundamental conclusion: the excited states of individual DNA/RNA bases, of the WC base pairs, and of assemblies of such base pairs, in the gas phase or in solution, all have access to a sufficiently diverse range of low energy non-radiative decay pathways to ensure rapid and efficient repopulation of the ground state, and thus photostability.

Acknowledgements

The Bristol based authors are grateful to EPSRC for the award of a Programme Grant (EP/L005913) and to colleagues Prof. Andrew Orr-Ewing and Dr Katharina Röttger for their invaluable feedback on an earlier draft of this manuscript. TNVK is grateful for the award of a TUM University Foundation Fellowship. Additional outputs that underpin data reported in this paper have been placed in the University of Bristol's research data repository and can be accessed using the following DOI: http://10.5523/bris.16bza2y6ry2iz14jsuovowv592.

References

1. A. L. Sobolewski and W. Domcke, Chem. Phys., 2000, 259, 181–191.
2. A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100.
3. M. N. R. Ashfold, B. Cronin, A. L. Devine, R. N. Dixon and M. G. D. Nix, Science, 2006, 321, 1637–1640.
4. K.-L. Han and G.-Z. He, J. Photochem. Photobiol., C, 2007, 8, 55–66.
5. M. N. R. Ashfold, G. A. King, D. Murdock, M. G. D. Nix, T. A. A. Oliver and A. G. Sage, Phys. Chem. Chem. Phys., 2010, 12, 1218–1238.
6. W. Domcke and D. R. Yarkony, Annu. Rev. Phys. Chem., 2012, 63, 325–352.
7. G. M. Roberts and V. G. Stavros, Chem. Sci., 2014, 5, 1698–1722.
8. Z. Lan, W. Domcke, V. Vallet, A. L. Sobolewski and S. Mahapatra, J. Chem. Phys., 2005, 122, 224315.
9. M. G. D. Nix, A. L. Devine, B. Cronin, R. N. Dixon and M. N. R. Ashfold, J. Chem. Phys., 2006, 125, 133318.
10. A. L. Devine, M. G. D. Nix, B. Cronin and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2007, 9, 3749–3762.
11. G. A. King, A. L. Devine, M. G. D. Nix, D. E. Kelly and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2008, 10, 6417–6429.
12. M. N. R. Ashfold, A. L. Devine, R. N. Dixon, G. A. King, M. G D. Nix and T. A. A. Oliver, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12701–12706.
13. A. Iqbal, L.-J. Pegg and V. G. Stavros, J. Phys. Chem. A, 2008, 112, 9531–9534.
14. O. P. J. Vieuxmaire, Z. Lan, A. L. Sobolewski and W. Domcke, J. Chem. Phys., 2008, 129, 224307.
15. G. A. King, T. A. A. Oliver, M. G. D. Nix and M. N. R. Ashfold, J. Phys. Chem. A, 2009, 113, 7984–7993.
16. G. A. Pino, A. N. Oldani, E. Marceca, M. Fujii, S.-I. Ishiuchi, M. Miyazaki, M. Broquier, C. Dedonder and C. Jouvet, J. Chem. Phys., 2010, 133, 124313.
17. R. N. Dixon, T. A. A. Oliver and M. N. R. Ashfold, J. Chem. Phys., 2011, 134, 194303.
18. R. A. Livingstone, J. O. F. Thompson, M. Iljina, R. J. Donaldson, B. J. Sussman, M. J. Paterson and D. Townsend, J. Chem. Phys., 2012, 137, 184304.
19. G. M. Roberts, A. S. Chatterley, J. D. Young and V. G. Stavros, J. Phys. Chem. Lett., 2012, 3, 348–352.
20. D. J. Hadden, G. M. Roberts, T. N. V. Karsili, M. N. R. Ashfold and V. G. Stavros, Phys. Chem. Chem. Phys., 2012, 14, 13415–13428.
21. S. G. Ramesh and W. Domcke, Faraday Discuss., 2013, 163, 73–94.
22. X. Xu, K. R. Yang and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 3612–3625.
23. T. N. V. Karsili, A. M. Wenge, S. J. Harris, D. Murdock, J. N. Harvey, R. N. Dixon and M. N. R. Ashfold, Chem. Sci., 2013, 4, 2434–2446.
24. S. Albert, P. Lerch, R. Prentner and M. Quack, Angew. Chem., Int. Ed., 2013, 52, 346–349.
25. T. N. V. Karsili, A. M. Wenge, B. Marchetti and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2014, 16, 588–598.
26. X. Xu, J. Zheng, K. R. Yang and D. G. Truhlar, J. Am. Chem. Soc., 2014, 136, 16378–16386.
27. K. R. Yang, X. Xu, J. Zheng and D. G. Truhlar, Chem. Sci., 2014, 5, 4661–4680.
28. S. J. Harris, T. N. V. Karsili, D. Murdock, T. A. A. Oliver, A. M. Wenge, D. K. Zaouris, M. N. R. Ashfold, J. N. Harvey, J. D. Few, S. Gowrie, G. Hancock, D. J. Hadden, G. M. Roberts, V. G. Stavros, G. Spighi, L. Poisson and B. Soep, J. Phys. Chem. A, 2015, 119, 6045–6056.
29. A. L. Sobolewski and W. Domcke, Chem. Phys. Lett., 1999, 315, 293–298.
30. B. C. Dian, A. Longarte and T. S. Zwier, J. Chem. Phys., 2003, 6, 2696–2706.
31. H. Lippert, H.-H. Ritze, I. V. Hertel and W. Radloff, Chem. Phys. Lett., 2004, 398, 526–531.
32. M.-F. Lin, C.-M. Tseng, Y. T. Lee and C.-K. Ni, J. Chem. Phys., 2005, 123, 124303.
33. M. G. D. Nix, A. L. Devine, B. Cronin and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2006, 8, 2610–2618.
34. C. Brand, J. Küpper, D. W. Pratt, W. L. Meerts, D. Krügler, J. Tatchen and M. Schmitt, Phys. Chem. Chem. Phys., 2010, 12, 4968–4979.
35. A. Iqbal and V. G. Stavros, J. Phys. Chem. A, 2010, 114, 68–72.
36. T. A. A. Oliver, G. A. King and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2011, 13, 14646–14662.
37. R. Livingstone, O. Schalk, A. E. Boguslavskiy, G. Wu, L. T. Bergendahl, A. Stolow, M. J. Paterson and D. Townsend, J. Chem. Phys., 2011, 135, 194307.
38. A. Giussani, M. Merchán, D. Roca-Sanjuán and R. Lindh, J. Chem. Theory Comput., 2011, 7, 4088–4096.
39. R. Montero, A. P. Conde, V. Ovejas, F. Castaño and A. Longarte, J. Phys. Chem. A, 2012, 116, 2698–2703.
40. B. O. Roos, P.-Å. Malmqvist, V. Molina, L. Serrano-Andrés and M. Merchán, J. Chem. Phys., 2002, 116, 7526–7536.
41. F. B. C. Machado and E. R. Davidson, J. Chem. Phys., 1992, 97, 1881–1891.
42. L. Serrano-Andrés, M. P. Fülscher, B. O. Roos and M. Merchán, J. Phys. Chem., 1996, 100, 6484–6491.
43. M. Barbatti, H. Lischka, S. Salzmann and C. M. Marian, J. Chem. Phys., 2009, 130, 034305.
44. D. Voet, W. B. Gratzer, R. A. Cox and P. Doty, Biopolymers, 1963, 1, 193–208.
45. P. R. Callis, Annu. Rev. Phys. Chem., 1983, 34, 329–357.
46. C. E. Crespo-Hernández, B. Cohen, P. M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2019.
47. B. Cohen, C. E. Crespo-Hernández, P. M. Hare and B. Kohler, in Femtochemistry and Femtobiology: Ultrafast Events in Molecular Science, ed. M. Martin and J. T. Hynes, Elsevier, 2004, pp. 463–470.
48. A. L. Sobolewski and W. Domcke, Europhys. News, 2006, 37, 20–23.
49. C. T. Middleton, K. de la Harpe, C. Su, Y. K. Law, C. E. Crespo-Hernández and B. Kohler, Annu. Rev. Phys. Chem., 2009, 60, 217–239.
50. A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2010, 12, 4897–4898.
51. T. Gustavsson, R. Improta and D. Markovitsi, J. Phys. Chem. Lett., 2010, 1, 2025–2030.
52. D. Markovitsi, T. Gustavsson and I. Vayá, J. Phys. Chem. Lett., 2010, 1, 3271–3276.
53. K. Kleinermanns, D. Nachtigallová and M. S. de Vries, Int. Rev. Phys. Chem., 2013, 32, 308–342.
54. H. Kang, K. T. Lee, B. Jung, Y. J. Ko and S. K. Kim, J. Am. Chem. Soc., 2002, 124, 12958–12959.
55. S. Ullrich, T. Schultz, M. Z. Zgierski and A. Stolow, Phys. Chem. Chem. Phys., 2004, 6, 2796–2801.
56. C. Canuel, M. Mons, F. Piuzzi, B. Tardivel, I. Dimicoli and M. Elhanine, J. Chem. Phys., 2005, 122, 074316.
57. K. Kosma, C. Schröter, E. Samoylova, I. V. Hertel and T. Schultz, J. Am. Chem. Soc., 2009, 131, 16939–16943.
58. J.-W. Ho, H.-C. Yen, W.-K. Chou, C.-N. Weng, L.-H. Cheng, H.-Q. Shi, S.-H. Lai and P.-Y. Cheng, J. Phys. Chem. A, 2011, 115, 8406–8418.
59. M. Kotur, T. C. Weinacht, C. Zhou, K. A. Kistler and S. Matsika, J. Chem. Phys., 2011, 134, 184309.
60. S. Lobsiger, M. A. Trachsel, H.-M. Frey and S. Leutwyler, J. Phys. Chem. A, 2013, 117, 6106–6115.
61. H. Kang, B. Jung and S. K. Kim, J. Chem. Phys., 2003, 118, 6717–6719.
62. S. Ullrich, T. Schultz, M. Z. Zgierski and A. Stolow, J. Am. Chem. Soc., 2004, 126, 2262–2263.
63. H. Satzger, D. Townsend, M. Z. Zgierski, S. Patchkovskii, S. Ullrich and A. Stolow, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10196–10201.
64. C. Z. Bisgaard, H. Satzger, S. Ullrich and A. Stolow, ChemPhysChem, 2009, 10, 101–110.
65. H. Kang, J. Chang, S. H. Lee, T. K. Ahn, N. J. Kim and S. K. Kim, J. Chem. Phys., 2010, 133, 154311.
66. D. N. Nikogosyan, D. Angelov, B. Soep and L. Lindqvist, Chem. Phys. Lett., 1996, 252, 322–326.
67. A. Reuther, H. Iglev, R. Laenen and A. Laubereau, Chem. Phys. Lett., 2000, 325, 360–368.
68. J.-M. L. Pecourt, J. Peon and B. Kohler, J. Am. Chem. Soc., 2000, 122, 9348–9349.
69. T. Gustavsson, A. Sharonov and D. Markovitsi, Chem. Phys. Lett., 2002, 351, 195–200.
70. T. Gustavsson, A. Sharonov, D. Onidas and D. Markovitsi, Chem. Phys. Lett., 2002, 356, 49–54.
71. A. Sharonov, T. Gustavsson, V. Carré, E. Renault and D. Markovitsi, Chem. Phys. Lett., 2003, 380, 173–180.
72. B. Cohen, P. Hare and B. Kohler, J. Am. Chem. Soc., 2003, 125, 13594–13601.
73. R. J. Malone, A. M. Miller and B. Kohler, Photochem. Photobiol., 2003, 77, 158–164.
74. T. Gustavsson, Á. Bányász, E. Lazzarotto, D. Markovitsi, G. Scalmani, M. J. Frisch, V. Barone and R. Improta, J. Am. Chem. Soc., 2006, 128, 607–619.
75. T. Gustavsson, N. Sarkar, E. Lazzarotto, D. Markovitsi and R. Improta, Chem. Phys. Lett., 2006, 429, 551–557.
76. G. M. Roberts, H. J. B. Marroux, M. P. Grubb, M. N. R. Ashfold and A. J. Orr-Ewing, J. Phys. Chem. A, 2014, 118, 11211–11225.
77. F. Buchner, A. Nakayama, S. Yamazaki, H.-H. Ritze and A. Lübcke, J. Am. Chem. Soc., 2015, 137, 2931–2938.
78. S. Matsika, J. Phys. Chem. A, 2004, 108, 7584–7590.
79. M. Z. Zgierski, S. Patchkovskii, T. Fujiwara and E. C. Lim, J. Phys. Chem. A, 2005, 109, 9384–9387.
80. S. Perun, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2006, 110, 13238–13244.
81. N. Ismail, L. Blancafort, M. Olivucci, B. Kohler and M. A. Robb, J. Am. Chem. Soc., 2002, 124, 6818–6819.
82. L. Blancafort, B. Cohen, P. M. Hare, B. Kohler and M. A. Robb, J. Phys. Chem. A, 2005, 109, 4431–4436.
83. K. A. Kistler and S. Matsika, J. Phys. Chem. A, 2007, 111, 2650–2661.
84. L. Blancafort, Photochem. Photobiol., 2007, 83, 603–610.
85. M. Merchán, R. González-Luque, T. Climent, L. Serrano-Andrés, E. Rodríguez, M. Reguero and D. Peláez, J. Phys. Chem. B, 2006, 110, 26471–26476.
86. G. Zechmann and M. Barbatti, J. Phys. Chem. A, 2008, 112, 8273–8279.
87. D. Asturiol, B. Lasorne, M. A. Robb and L. Blancafort, J. Phys. Chem. A, 2009, 113, 10211–10218.
88. S. Yamazaki, W. Domcke and A. L. Sobolewski, J. Phys. Chem. A, 2008, 112, 11965–11968.
89. Z. Lan, E. Fabiano and W. Thiel, ChemPhysChem, 2009, 10, 1225–1229.
90. K. A. Kistler and S. Matsika, Phys. Chem. Chem. Phys., 2010, 12, 5024–5031.
91. M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallova, P. Hobza and H. Lischka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21453–21458.
92. V. B. Delchev, A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2010, 12, 5007–5015.
93. M. Barbatti, J. J. Szymczak, A. J. A. Aquino, D. Nachtigallova and H. Lischka, J. Chem. Phys., 2011, 134, 014304.
94. D. Nachtigallová, A. J. A. Aquino, J. J. Szymczak, M. Barbatti, P. Hobza and H. Lischka, J. Phys. Chem. A, 2011, 115, 5247–5255.
95. C. M. Marian, J. Chem. Phys., 2005, 122, 104314.
96. S. Perun, A. L. Sobolewski and W. Domcke, J. Am. Chem. Soc., 2005, 127, 6257–6265.
97. L. Serrano-Andrés, M. Merchán and A. C. Borin, Chem. – Eur. J., 2006, 12, 6559–6571.
98. M. Barbatti and H. Lischka, J. Am. Chem. Soc., 2008, 130, 6831–6839.
99. I. Conti, M. Garavelli and G. Orlandi, J. Am. Chem. Soc., 2009, 131, 16108–16118.
100. M. Barbatti, Z. Lan, R. Crespo-Otero, J. J. Szymczak, H. Lischka and W. Thiel, J. Chem. Phys., 2012, 137, 22A503.
101. J. Petersen, M. Wohlgemuth, B. Sellner, V. Bonačić-Koutecký, H. Lischka and R. Mitrić, Phys. Chem. Chem. Phys., 2012, 14, 4687–4694.
102. B. P. Fingerhut, K. E. Dorfman and S. Mukamel, J. Phys. Chem. Lett., 2013, 4, 1933–1942.
103. C. G. Triandafillou and S. Matsika, J. Phys. Chem. A, 2013, 117, 12165–12174.
104. F. Plasser, R. Crespo-Otero, M. Pederzoli, J. Pittner, H. Lischka and M. Barbatti, J. Chem. Theory Comput., 2014, 10, 1395–1405.
105. C. M. Marian, J. Phys. Chem. A, 2007, 111, 1545–1553.
106. S. Yamazaki and W. Domcke, J. Phys. Chem. A, 2008, 112, 7090–7097.
107. L. Serrano-Andrés, M. Merchán and A. C. Borin, J. Am. Chem. Soc., 2008, 130, 2473–2484.
108. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennuchi and G. Petersson, et al., Gaussian 09, revision B.01, Gaussian Inc., Wallingford, CT, 2010.
109. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023.
110. W. J. Hehre, R. F. Stewart and J. A. Pople, J. Chem. Phys., 1969, 51, 2657–2664.
111. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., MOLPRO, version 2010.1, a package of ab initio programs, University of Cardiff, Cardiff, UK, 2010, see http://www.molpro.net.
112. Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
113. L. D. Hatherley, R. D. Brown, P. D. Godfrey, A. P. Pierlot, W. Caminati, D. Damiani, S. Melandri and L. B. Favero, J. Phys. Chem., 1993, 97, 46–51.
114. R. H. Cox and A. A. Bother-By, J. Phys. Chem., 1969, 73, 2465–2468.
115. M. Kuzuya, A. Noguchi and T. Okuda, J. Chem. Soc., Chem. Commun., 1984, 100, 435–436.
116. R. Sanchez, B. M. Giuliano, S. Melandri, L. B. Favero and W. Caminati, J. Am. Chem. Soc., 2007, 129, 6287–6290.
117. B. M. Giuliano, V. Feyer, K. C. Prince, M. Coreno, L. Evangelisti, S. Melandri and W. Caminati, J. Phys. Chem. A, 2010, 114, 12725–12730.
118. R. D. Brown, P. D. Godfrey, D. McNaughton and A. P. Pierlot, J. Am. Chem. Soc., 1988, 110, 2329–2330.
119. R. D. Brown, P. D. Godfrey, D. McNaughton and A. P. Pierlot, J. Am. Chem. Soc., 1989, 111, 2308–2310.
120. E. Nir, M. Muller, L. I. Grace and M. S. de Vries, Chem. Phys. Lett., 2002, 355, 59–64.
121. E. Nir, I. Hünig, K. Kleinermanns and M. S. de Vries, Phys. Chem. Chem. Phys., 2003, 5, 4780–4785.
122. V. Feyer, O. Plekan, R. Richter, M. Coreno, G. Vall-Ilosera, K. C. Prince, A. B. Trofimov, I. L. Zatseva, T. E. Moskovskaya, E. V. Gromov and J. Schirmer, J. Phys. Chem. A, 2009, 113, 5736–5742.
123. M. Szczesniak, K. Szczepaniak, J. S. Kwiatkowski, K. KuBulat and W. B. Person, J. Am. Chem. Soc., 1988, 110, 8319–8330.
124. G. Bazsó, G. Tarczay, G. Fogarasi and P. G. Szalay, Phys. Chem. Chem. Phys., 2011, 13, 6799–6807.
125. M. Dreyfus, O. Bensaude, G. Dodin and J. E. Dubois, J. Am. Chem. Soc., 1976, 98, 6338–6349.
126. C. Colominas, F. J. Luque and M. Orozco, J. Am. Chem. Soc., 1996, 118, 6811–6821.
127. R. Kobayashi, J. Phys. Chem., 1998, 102, 10813–10817.
128. S. A. Trygubenko, T. V. Bogdan, M. Rueda, M. Orozco, F. J. Luque, J. Sponer, P. Slavıcek and P. Hobza, Phys. Chem. Chem. Phys., 2002, 4, 4192–4203.
129. M. Hanus, M. Kabeláč, J. Rejnek, F. Ryjáček and P. Hobza, J. Phys. Chem. B, 2004, 108, 2087–2097.
130. J. Lin, C. Yu, S. Peng, I. Akiyama, K. Li, L. K. Lee and P. R. LeBreton, J. Am. Chem. Soc., 1980, 102, 4627–4631.
131. R. D. Brown, P. D. Godfrey, D. McNaughton and A. P. Pierlot, Chem. Phys. Lett., 1989, 156, 61–63.
132. C. Plützer, E. Nir, M. S. de Vries and K. Kleinermanns, Phys. Chem. Chem. Phys., 2001, 3, 5466–5469.
133. C. Plützer and K. Kleinermanns, Phys. Chem. Chem. Phys., 2002, 4, 4877–4882.
134. M. J. Nowak, L. Lapinski, J. S. Kwiatkowski and J. Leszczyński, J. Phys. Chem., 1996, 100, 3527–3534.
135. M. Dreyfus, G. Dodin, O. Bensaude and J. E. Dubois, J. Am. Chem. Soc., 1975, 97, 2369–2376.
136. M.-T. Chenon, R. J. Pugmire, D. M. Grant, R. P. Panzica and L. B. Townsend, J. Am. Chem. Soc., 1975, 97, 4636–4642.
137. N. C. Gonnella, H. Nakanishi, J. B. Holtwick, D. S. Horowitz, K. Kanamori, N. J. Leonard and J. D. Roberts, J. Am. Chem. Soc., 1983, 105, 2050–2055.
138. A. Laxer, D. T. Major, H. E. Gottlieb and B. Fischer, J. Org. Chem., 2001, 66, 5463–5481.
139. S. K. Mishra, M. K. Shukla and P. C. Mishra, Spectrochim. Acta, Part A, 2000, 56, 1355–1384.
140. L. M. Salter and G. M. Chaban, J. Phys. Chem. A, 2002, 106, 4251–4256.
141. T.-K. Ha, H.-J. Keller, R. Gunde and H.-H. Gunthard, J. Phys. Chem. A, 1999, 103, 6612–6623.
142. K. Szczepaniak and M. Szczesniak, J. Mol. Struct., 1987, 156, 29–42.
143. F. Piuzzi, M. Mons, I. Dimicoli, B. Tardivel and Q. Zhao, Chem. Phys., 2001, 270, 205–214.
144. M. Mons, I. Dimicoli, F. Piuzzi, B. Tardivel and M. Elhanine, J. Phys. Chem. A, 2002, 106, 5088–5094.
145. M. Mons, F. Piuzzi, I. Dimicoli, L. Gorb and J. Leszczynski, J. Phys. Chem. A, 2006, 110, 10921–10924.
146. K. Seefeld, R. Brause, T. Häber and K. Kleinermanns, J. Phys. Chem. A, 2007, 111, 6217–6221.
147. M. Hanus, F. Ryjáček, M. Kabelaáč, T. Kubař, T. V. Bogdan, S. A. Trygubenko and P. Hobza, J. Am. Chem. Soc., 2003, 125, 7678–7688.
148. L. Gorb, A. Kaczmarek, A. Gorb, A. J. Sadlej and J. Leszczynski, J. Phys. Chem. B, 2005, 109, 13770–13776.
149. S. Kato, J. Chem. Phys., 1988, 88, 3045–3056.
150. I. J. Palmer, I. N. Ragazos, F. Bernardi, M. Olivucci and M. A. Robb, J. Am. Chem. Soc., 1993, 115, 673–682.
151. A. L. Sobolewski, C. Woywod and W. Domcke, J. Chem. Phys., 1993, 98, 5627–5641.
152. F. Zhang, Y.-J. Ai, Y. Luo and W.-H. Fang, J. Chem. Phys., 2009, 130, 144315.
153. A. L. Sobolewski, Chem. Phys. Lett., 1993, 211, 293–299.
154. A. L. Sobolewski and L. Adamowicz, J. Phys. Chem., 1996, 100, 3933–3941.
155. H. Ozeki, M. C. R. Cockett, K. Okayama, M. Takahashi and K. Kimura, J. Phys. Chem., 1995, 99, 8608–8612.
156. D. Lee, S. J. Baek, K.-W. Choi, Y. S. Choi and S. K. Kim, Bull. Korean Chem. Soc., 2002, 23, 277–280.
157. A. Held, B. B. Champagne and D. W. Pratt, J. Chem. Phys., 1991, 95, 8732–8743.
158. M. R. Nimlos, D. F. Kelley and E. R. Bernstein, J. Phys. Chem., 1989, 93, 643–651.
159. S. Maeda, Y. Harabuchi, T. Taketsugu and K. Morokuma, J. Phys. Chem. A, 2014, 118, 12050–12058.
160. D. Nachtigallová, H. Lischka, J. J. Szymczak, M. Barbatti, P. Hobza, Z. Gengeliczki, G. Pino, M. P. Callahane and M. S. de Vries, Phys. Chem. Chem. Phys., 2010, 12, 4924–4933.
161. M. G. D. Nix, A. L. Devine, B. Cronin and M. N. R. Ashfold, J. Chem. Phys., 2007, 126, 124312.
162. A. Z. Britten and G. Lockwood, Spectrochim. Acta, Part A, 1976, 32, 1335–1338.
163. V. Ludwig, Z. M. da Costa, M. S. do Amaral, A. C. Borin, S. Canuto and L. Serrano-Andrés, Chem. Phys. Lett., 2010, 492, 164–169.
164. J. Hager and S. C. Wallace, J. Phys. Chem., 1983, 87, 2121–2127.
165. Y. Huang and M. Sulkes, Chem. Phys. Lett., 1996, 254, 242–248.
166. M. S. de Vries, Top. Curr. Chem., 2014, 355, 33–56.
167. H. Asami, K. Yagi, M. Ohba, S.-H. Urashima and H. Saigusa, Chem. Phys., 2013, 419, 84–89.
168. D. Tuna, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2014, 118, 122–127.
169. M. Z. Zgierski and S. Alavi, Chem. Phys. Lett., 2006, 426, 398–404.
170. S. De Camillis, J. Miles, G. Alexander, O. Ghafur, I. D. Williams, D. Townsend and J. B. Greenwood, Phys. Chem. Chem. Phys., 2015, 17, 23643–23650.
171. S. Perun, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2006, 110, 9031–9038.
172. J. P. Gobbo, V. Saurí, D. Roca-Sanjuán, L. Serrano-Andrés, M. Merchán and A. C. Borin, J. Phys. Chem. B, 2012, 116, 4089–4097.
173. A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2004, 6, 2763–2771.
174. P. R. Markwick and N. L. Doltsinis, J. Chem. Phys., 2007, 126, 175102.
175. G. Groenhof, L. V. Schäfer, M. Boggio-Pasqua, M. Goette, H. Grubmüller and M. A. Robb, J. Am. Chem. Soc., 2007, 129, 6812–6819.
176. V. Saurí, J. P. Gobbo, J. J. Serrano-Pérez, M. Lundberg, P. B. Coto, L. Serrano-Andrés, A. C. Borin, R. Lindh, M. Merchán and D. Roca-Sanjuán, J. Chem. Theory Comput., 2013, 9, 481–496.
177. S. Yamazaki and T. Taketsugu, Phys. Chem. Chem. Phys., 2012, 14, 8866–8877.
178. A. L. Sobolewski, W. Domcke and C. Hättig, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17903–17906.
179. E. Nir, C. Plützer, K. Kleinermanns and M. S. de Vries, Eur. Phys. J. D, 2002, 20, 317–329.
180. A. Abo-Riziq, L. Grace, E. Nir, M. Kabelac, P. Hobza and M. S. de Vries, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 20–23.
181. N. K. Schwalb and F. Temps, J. Am. Chem. Soc., 2007, 129, 9272–9273.
182. K. Röttger and F. Temps, in Ultrafast Phenomena XIX, ed. I. Yamanouchi, S. Cundiff and R. de Vivie Riedle, 2015, vol. 162, pp. 514–516.
183. K. Röttger, H. J. B. Marroux, M. P. Grubb, P. M. Coulter, H. Böhnke, A. S. Henderson, M. C. Galan, F. Temps, A. J. Orr-Ewing and G. M. Roberts, Angew. Chem., Int. Ed., 2015, 54, 14719–14722.
184. C. Crespo-Hernández, B. Cohen and B. Kohler, Nature, 2005, 436, 1141–1144.
185. W.-M. Kwok, C. Ma and D. L. Phillips, J. Am. Chem. Soc., 2006, 128, 11894–11905.
186. T. Takaya, C. Su, K. de la Harpe, C. E. Crespo-Hernández and B. Kohler, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 10285–10290.
187. K. de la Harpe and B. Kohler, J. Phys. Chem. Lett., 2011, 2, 133–138.
188. I. Vaya, T. Gustavsson, T. Douki, Y. Berlin and D. Markovitsi, J. Am. Chem. Soc., 2012, 134, 11366–11368.
189. G. W. Doorley, M. Wojdyla, G. W. Watson, M. Towrie, A. W. Parker, J. M. Kelly and S. J. Quinn, J. Phys. Chem. Lett., 2013, 4, 2739–2744.
190. C. Su, C. T. Middleton and B. Kohler, J. Phys. Chem. B, 2012, 116, 10266–10274.
191. J. Chen, A. K. Thazhathveetil, F. D. Lewis and B. Kohler, J. Am. Chem. Soc., 2013, 136, 10290–10293.
192. D. B. Bucher, A. Schlueter, T. Carell and W. Zinth, Angew. Chem., Int. Ed., 2014, 55, 11366–11369.
193. Y. Zhang, K. de la Harpe, A. A. Beckstead, R. Improta and B. Kohler, J. Am. Chem. Soc., 2015, 137, 7059–7062.
194. W. Domcke, D. R. Yarkony and H. Koppel, Conical Intersections: Theory, Computation and Experiment, vol. 17 of Advances Series in Physical Chemistry, 2011, and references therein.
195. D. M. Sammeth, S. Yan, L. H. Spangler and P. R. Callis, J. Phys. Chem., 1990, 94, 7340–7342.
196. Y. Matsuda, T. Ebata and N. Mikami, J. Chem. Phys., 1999, 110, 8397–8407.
197. Y. Matsuda, T. Ebata and N. Mikami, J. Chem. Phys., 2000, 113, 573–580.
198. L. B. Clark, G. G. Peschel and I. Tinoco, Jr., J. Phys. Chem., 1965, 69, 3615–3618.
199. H. De Voe and I. Tinoco, Jr., J. Mol. Biol., 1962, 4, 500–517.
200. B. J. Fender, D. M. Sammeth and P. R. Callis, Chem. Phys. Lett., 1995, 239, 31–37.
201. K. Fuke, H. Yoshiuchi and K. Kaya, J. Phys. Chem., 1984, 88, 5840–5844.
202. S. K. Kim and E. R. Bernstein, J. Phys. Chem., 1990, 94, 3531–3539.
203. C. Kang, J. T. Yi and D. W. Pratt, J. Chem. Phys., 2005, 123, 094306.
204. K. Sakota and H. Sekiya, J. Phys. Chem. A, 2009, 113, 2663–2665.
205. M. Schneider, T. Hain and I. Fischer, ChemPhysChem, 2009, 10, 634–636.
206. N. J. Kim, G. Jeong, Y. S. Kim, J. Sung, S. K. Kim and Y. D. Park, J. Chem. Phys., 2000, 113, 10051–10055.
207. E. Nir, C. Janzen, P. Imhof, K. Kleinermanns and M. S. de Vries, J. Chem. Phys., 2001, 115, 4604–4611.

---

Footnote

† Electronic supplementary information (ESI) available: More details regarding the computational methods used; PECs along the relevant Q_oop coordinate for all molecules displayed in Fig. 1 and 2; depictions of the active space orbitals used for the CASSCF and CASPT2 calculations; dominant orbital excitations that contribute to the first three singlet excited states of all molecules featured in Fig. 1–3 and 4(a); and PECs for the ground and first few singlet excited states of adenosine along Q_oop calculated at the ADC(2)/cc-pVDZ level of theory. See DOI: 10.1039/c6cp00165c

---