Insights into the vibration coupling effects on reorganization energy in π-isoelectronic frameworks

Abstract

A π-isoelectronic framework denotes a category of chemical compounds or molecular structures where specific elements are arranged to share an identical count of π electrons. It presents a unique and exclusive avenue for investigating the dynamics of charge carriers at the molecular level within organic semiconductors. Despite the high similarities in molecular structure, geometry, and electron distribution among π-isoelectronic frameworks, there exists a noteworthy divergence in their reorganization energy under certain conditions. This anomaly poses a challenge to established theories in organic semiconductor science, fueling a profound interest among scientists to decipher the underlying mechanisms governing reorganization energy. Our research undertakes a comparative study of the contribution of vibrational coupling to the reorganization energy within both zigzag and armchair groups of isoelectronic frameworks. It also uncovers the peculiar odd–even effect of vibrational modes on hole reorganization energy, particularly when heteroatoms are introduced. This study offers a distinct perspective on comprehending the origins of conductivity in organic semiconductors, ushering in fresh insights into the intricate interplay between vibrational modes, reorganization energy, conductivity, and the performance of organic devices. Consequently, it furnishes a comprehensive understanding of reorganization energy through the lens of vibrational coupling and provides insights into the conductivity of organic semiconductors.

---

Introduction

Organic semiconductors have gained significant attention in the past several decades,^1–4 due to their exceptional properties, such as versatile and facile tuneable structures, solution-processability, and low-cost fabrication, making them a promising alternative to inorganic semiconductors for many applications, including organic photovoltaics (OPVs),^5,6 organic light-emitting diodes (OLEDs),^7–9 organic field-effect transistors (OFETs),^10,11etc. From an industrial perspective, certain organic electronic devices, notably OLEDs, have successfully penetrated the commercial market. However, from a scientific standpoint, our understanding of the microphysics underlying carrier transport behaviour in organic semiconductor materials remains insufficient to elucidate the intricacies of the real-world performance of organic semiconductors.

With this motivation, this study aims to take a step towards a comprehensive understanding and optimize the molecular structure of materials. Conductivity stands as a paramount parameter in the realm of organic semiconductors, exerting a substantial influence on their device performance. Its intricate determination is subject to a myriad of factors, encompassing material structures, molecular packing, film morphology, and more. This study will focus on a molecular-level analysis to investigate the essential role buried within the single molecular structure, that significantly determines the carrier transport mobility – reorganization energy (λ).^12–14

The previous studies proved that the geometric relaxation could largely determine both hole reorganization energy (λ_h) and electron reorganization energy (λ_e), during the process of the carriers’ injection into or extraction from molecules.^15–17 Therefore, π-Isoelectronic frameworks with similar planar geometries and numbers of π-electrons, are expected to have comparable reorganization energies from the current frontier molecular orbital theory.^18–22 One example is anthradithiophene (ADT), which is isoelectronic with pentacene. Both molecules exhibit similar hole reorganization energy (96 vs. 97 meV).²⁰ Besides ADT, some other fused phenyl-thiophene derivatives, exhibit similar reorganization energies with their corresponding group of segments. For example, Takimiya et al. reported four classes of thienoacene-based organic semiconductors, all exhibiting similar reorganization energies with the hydrocarbon-based arenes being isoelectronic.²³

Nonetheless, there are instances where the similarity in reorganization energies among isoelectronic systems is not consistently observed, leading to a perplexing situation that defies both established theories and our understanding of molecular reorganization energy. For example, Veaceslav et al. conducted a comprehensive examination through high-resolution gas-phase photoelectron spectroscopy on isoelectronic thiophene-fused systems. It displayed large differences in their reorganization energy, providing concrete evidence that the uniformity in reorganization energies among isoelectronic systems does not always manifest as expected.¹⁸

This study aims to systematically investigate the impact from the vibrational coupling on the reorganization energy of π-isoelectronic framework, discusses and compares both the group zigzag and group Armchair, as shown in Scheme 1. The calculated results show that both groups display superior hole injection/transport properties than electrons, which is explained from the vibration coupling point of view. Besides, it is found that paired heteroatoms would induce irregular hole reorganization energy for armchair thiophene molecules. It is proposed in this study that for centrosymmetric armchair geometry molecules, the number of sulfur atoms could largely affect the vibration modes. When the sulfur atoms are paired (even), the strong coupling between them causes significant vibration components in the long-axis direction, thereby increasing the hole reorganization energy. This observation of the odd–even effect underscores the substantial potential for further scientific exploration in comprehending the structural intricacies of isoelectronic systems. Moreover, due to the electron donation property of the sulfur atom, this phenomenon does not happen in the electron transport situation. Which makes the electron reorganization energy of the thiophene molecules in the zigzag and Armchair group highly similar. Such investigations hold the potential to establish a more robust foundational understanding of semiconductor conductivity, along with its relationship to symmetry,¹⁹ conformation,²⁴ and molecular electronic structure.^10,23

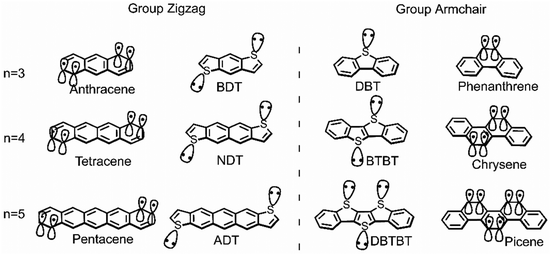Scheme 1 The chemical structure of zigzag and armchair groups of π-isoelectronic materials with increasing molecular system (n = 3, 4, 5).

Results and discussion

All the calculations were performed by the DFT programs with details in the Section S1 of the ESI.† Reorganization energies were determined using both the four-point method of adiabatic potential surface and the normal mode (NM) approach, with the results showing strong agreement between the two methods (see Fig. S1, ESI†).

Topology of molecules

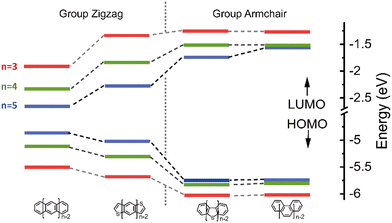
The highest occupied molecular orbital (HOMO), the lowest unoccupied molecular orbital (LUMO) and reorganization energy values for π-isoelectronic molecules of both the group zigzag and armchair are listed in Table S1 (ESI†) and visually presented in Fig. 1 and 2. There are two important information that could be read from those two figures. Firstly, for both the zigzag and armchair groups, as conjugated π systems go larger (n increases from 3 to 5), the HOMO and LUMO narrows progressively. This narrowing is primarily attributed to a greater number of electrons conjugating in the energy coupling, resulting in a more hybridized band structure. This phenomenon aligns well with previous experimental and theoretical findings.^25–29 Secondly, when comparing the group zigzag and Armchair, the molecules from the former group exhibit a smaller HOMO–LUMO bandgap than the group Armchair molecules. This trend aligns with the characteristics observed in other carbon-based materials.^30,31 Researchers have conducted extensive investigations into the impact of molecular topology on the electronic structure of carbon-based materials, particularly concerning the unique properties associated with massless Dirac fermion.³² These distinct features arise from nonbonding edge states localized in the zigzag-shaped edges and electron wave interference in the armchair-shaped ones.^33–36 Hence, it plays a pivotal role in shaping the macroscopic properties of carbon materials. The carrier transport with zigzag edges exhibits metallic characteristics, while those with armchair edges display semiconducting behaviour.³⁶ Given these clear disparities in the properties of these two groups of molecules (as shown in Fig. S2 and S3, ESI†), the upcoming sections of our discussion will analyse them separately.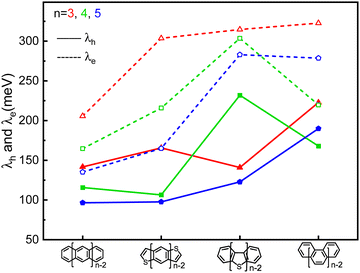

Fig. 1 The HOMO and LUMO energy of the π-isoelectronic frameworks.

Fig. 2 The comparison of the calculated hole (solid line) and electron (dash line) reorganization energy of the π-isoelectronic frameworks.

The vibration modes leading higher λ_e than λ_h

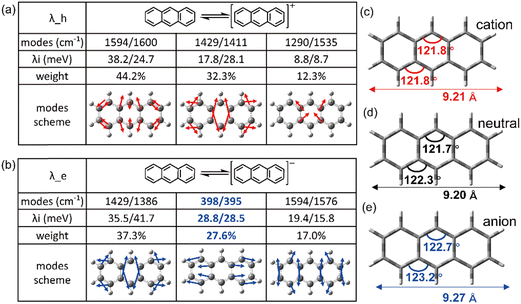
It is evident that all the molecules display a reorganization energy for holes smaller than that for electrons, as illustrated in Fig. 2 by the comparison between the solid line and the dashed line. The high hole transport mobility observed in these π-isoelectronic materials is in good agreement with experimental findings.³⁷ To look into how the vibration coupling mode impacts the molecular reorganization energy,^38,39 we have chosen to focus on Anthracene from the zigzag group and DBT from the Armchair group.

In group zigzag. Fig. 3 displays the three most significant contributed vibrational modes for both λ_h and λ_e in anthracene. For the hole situation (λ_h) in Fig. 3a, it indicates that the three in-plane scissoring vibration modes predominantly occur along the short axis, resulting in minimal geometric expansion after hole injection into a neutral molecule and exerting little stretching effect on the molecular framework. This can be observed in the changes in bond angles as the molecule transitions from its neutral state to the cation state, as shown in Fig. 3d and c. Specifically, the inter-ring bond angles vary from 121.7° to 121.8°and intra-ring bond angles range from 122.3° to 121.8°.

Fig. 3 The top three contributed vibrational modes for (a) hole and (b) electron injection into anthracene. The bond angles of aromatic rings and skeleton length for (c) cation, (d) neutral and (e) anion state of anthracene.

For the λ_e analyzation in Fig. 3b, the direction of the vibration arrows shows that the in-plane scissoring vibration display along the long axis, especially for the vibration modes 398 cm⁻¹/395 cm⁻¹, which contributes as significant as 27.6% to λ_e. The stretching effect causing the effective enlarging geometry of the molecular skeleton, along the long axis, which is much more prominent than the short axis, owing to the robust structure of the benzene ring. This could be clearly demonstrated by tracking the quantitative in the ring bond angles following electron injection. Comparing them in Fig. 3d and e, the inter-ring bond angles (from 121.7° to 122.7°) and intra-ring bond angles (from 122.3° to 123.2°) undergo significant increases after electron injection as well as the skeleton length in the long axis.

As a result, it can be concluded that the change in bond angles for both the inner and outer rings of benzene, resulting from electron injection, is significantly more pronounced compared to hole injection. This disparity results in a higher reorganization energy for electrons than for holes.

In group armchair. A similar geometric transformation occurs within group armchair, as illustrated in Fig. 4a and b. Taking DBT as an example, in the case of hole injection, the stretching modes primarily affect the short-axis direction, resulting in minimal geometric differences. On the other hand, for λ_e of DBT, the critical vibrational modes mainly lie at 1638/1613 cm⁻¹ and 1343/1338 cm⁻¹, contributing approximately around 55.7% and 11.1%, respectively. Both modes lead to the stretching of C=C bonds along the long axis, thus effectively elongating the molecular skeleton. Consequently, this results in a more pronounced structural relaxation along the long axis, leading to a greater electron reorganization energy compared to hole injection.

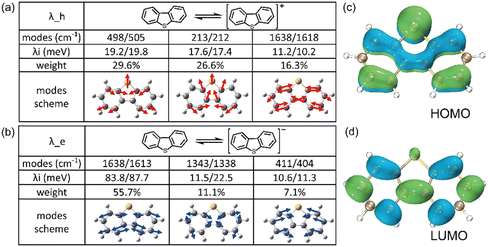Fig. 4 The composition of the top three contributed modes to (a) λ_h and (b) λ_e of DBT, respectively. The electon distribution at (c) HOMO and (d) LUMO of neutral DBT.

It is worth emphasizing that during electron injection, the position of the sulfur atom remains relatively fixed for these two vibrational modes. This behaviour can be attributed to the electron-donating property of sulfur, which is supported by the electron distribution illustrated in Fig. 4c and d. In these figures, it's evident that the probability of carrier injection into the HOMO around the sulfur atom is significantly greater than that into the LUMO.

The role of heteroatoms for the vibration coupling

λ _h in group zigzag. In contrast to previously published studies regarding the highly similar reorganization energy in isoelectronic materials,²³ the isoelectronic acenes and thienoacenes systems exhibit notable variations in their hole reorganization energy, as detailed presented in Table S1 (ESI†). As an example, when n equals 3, the hole reorganization energy (λ_h) is 141.7 eV for acene and 165.6 eV for thienoacenes.

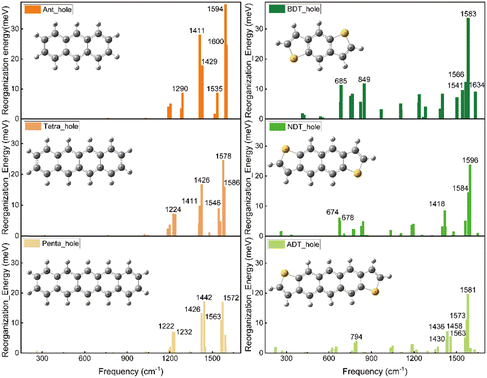
Fig. 5 illustrates the hole-vibrational coupling modes, with a focus on the top 6 weight contributions, and the corresponding frequencies are marked. When comparing the decomposed vibration modes in the acenes (left column) and thienoacene molecules (right column), it becomes evident that there are very few hole-vibration modes below 1000 cm⁻¹ in the acenes. Conversely, a notable observation is the emergence of multiple vibration modes below 1000 cm⁻¹ upon the introduction of the sulfur heteroatom. This trend is consistent across all three thienoacene molecules. It's important to highlight that we have chosen 1000 cm⁻¹ as the threshold to distinguish between high and low-frequency modes, for the sake of clarity.

Fig. 5 Molecular geometries and their corresponding hole-vibrational coupling modes, featuring the top 6 weight contributions to reorganization energy. The acenes with increasing molecular size n = 3, 4, 5, are listed in the left column. The isoelectronic thienoacene molecules are displayed in the right column. The frequency values for the primary vibrational modes are indicated.

For example, the two modes 674 and 678 cm⁻¹ contribute significantly for the hole reorganization energy of NDT. However, there is few vibrations modes in low frequency region (<1000 cm⁻¹) for tetracene. To further look into the heteroatom effect, take a specific vibration mode from the high frequency region to compare, the vibration mode at 1426 cm⁻¹ for tetracene and 1418 cm⁻¹ for NDT, respectively, as shown in Fig. S4 (ESI†). In the case of tetracene, a majority of carbon atoms participate in this vibration mode. Whereas in NDT, it is noticeable that the sulfur atom remains relatively stable in this mode. However, in the low-frequency region, specifically in the two vibration modes at 674 and 678 cm⁻¹, the sulfur atom does become involved. Therefore, when compared to acenes molecules, the introduction of the heteroatom sulfur leads to additional vibration modes in the low-frequency region. These additional modes contribute to the higher reorganization energy.

λ _h in group armchair. As reported by many researchers, the topology could largely affect the nonbonding edge state and thus the electron band structure of carbon materials. In this paper, heteroatom sulfur is included, as discussed above, the heteroatom plays a pivotal role in affecting the reorganization energy. In this part, it will focus on the heteroatom effect on the armchair shaped molecules. In contrast to zigzag thiophene molecules where the number of sulfur atoms (two) remains constant, the armchair-fused thiophene molecules exhibit an increase in the number of sulfur atoms as the molecular chain elongates.

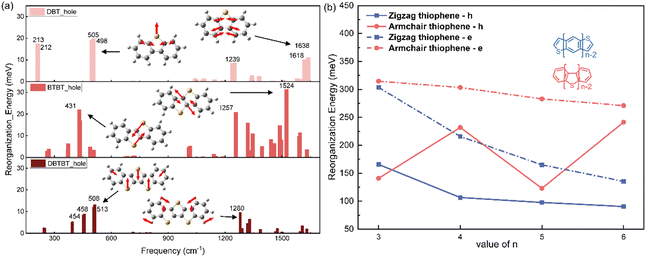
Similar with the thienoacenes in group zigzag, the phenomenon that the sulfur inducing vibration modes at the low frequency region happens as well, when it is introduced into the middle of the molecules in group Armchair. This could tell from Fig. S5 (ESI†), which shows the overall comparison of the vibration modes of all the molecules. Specifically, as shown in Fig. 6a, for the DBT, BTBT and DBTBT, the vibration modes at low frequency region (<1000 cm⁻¹) involve the sulfur atom. However, the vibration modes at high frequency region (>1000 cm⁻¹), does not involve the sulfur atom. This observation provides evidence that sulfur tends to participate in vibrations at low frequencies rather than at high frequencies, which is consistent with the behavior observed in the zigzag group. Nevertheless, the λ_h values for the Armchair group with fused thioenoacenes exhibit an oscillating trend as the chain prolongs, as shown in Fig. 6b (res solid line). To elucidate the impact of the heteroatom on λ_h in armchair thienoacenes, the decomposition of their vibration modes is presented in Fig. 6a.

Fig. 6 Analysis of normal modes in armchair thienoacenes and their corresponding hole reorganization energies as the molecular size extends is presented as follows: (a) the decomposition of hole reorganization energy with normal modes of armchair thienoacene. The frequencies of the top three modes are displayed. (b) The reorganization energy comparison of the zigzag and armchair group with heteroatom sulfur.

Notably, the vibrational modes of DBT at low frequency region (top of Fig. 6a) account for significant component of its hole reorganization energy. Both vibration modes at 505 cm⁻¹ and 213 cm⁻¹ involve the sulfur atom (shown in Fig. 6a and Fig. S6, ESI†), in which the stretching C–S bond plays a significant contribution for the reorganization energy. The C–S stretching occurs along the shorter axis direction, resulting in a relatively minor structural relaxation throughout the entire molecular framework.

When n equals 4, as depicted in Fig. 6a's normal modes decomposition, it is evident that the λ_h value for BTBT exhibits a noteworthy influence from the sulfur-vibrational modes at 431/435 cm⁻¹. The mode displays a symmetrically opposing manner along the elongated axis of the molecule. Consequently, the centrosymmetric vibrations of sulfur-related bonds within BTBT induce a substantial structural adaptation attributable to the stretching components along the molecule's long axis, resulting in a more pronounced hole reorganization energy compared to DBT. When n equals 5 (the bottom of Fig. 6a), the vibrations of three sulfur atoms occur in opposing directions along the shorter axis of the molecular framework. This situation closely resembles the scenario observed in DBT. Hence, the presence of paired sulfur atoms, which induce strong vibration modes along the long axis direction, is the primary factor contributing to the high reorganization energy of BTBT. This phenomenon is responsible for the oscillating trend observed in the hole reorganization energy for the group Armchair with heteroatom. The videos for the comparison of these vibration modes related with sulfur atom in three molecules, could be found in the ESI.†

Hence, it can be postulated that the parity of the number of thiophene rings in the armchair group significantly impacts λ_h. In cases where there is an odd number of sulfur atoms, the vibrations in which sulfur participates are primarily along the short axis direction, exerting little effect on molecular geometry relaxation during hole injection. Conversely, when the number of sulfur atoms is even, the strong interaction between paired sulfur atoms leads to a substantial vibrational component along the long-axis direction of the molecules. This, in turn, results in significant molecular geometry relaxation, ultimately leading to higher values of λ_h. This hypothesis finds support in the calculations for DB4T, which exhibit similar behaviour to BTBT, as shown in Fig. 6b.

Moreover, the odd–even heteroatom effect can be extended to other elements with similar electron-donating characteristics, such as oxygen (O). To illustrate, we have explored the introduction of fused oxygen atoms at the same fused positions of the armchair group, as depicted in Fig. S7 (ESI†). In this context, the armchair group exhibits behaviour highly analogous to the armchair thienoacenes. It shows reduced reorganization with an odd number of hetero-aromatics and higher reorganization energy with paired hetero-atoms in an armchair structural configuration. This implies that utilizing various heteroatoms within an armchair topology could modulate the reorganization energy, which is a promising strategy for the structural design of materials.

Is λ_e different from λ_h?

Both the substantial natural atomic orbital (NAO) value (39%) associated with the HOMO components and the positive natural population analysis (NPA) charge (0.38) attributed to the sulfur atom in DBT (as shown in Fig. S8, ESI†) underscore the substantial impact of the sulfur atom's electron-donating property on the hole transfer process. It leads the electron-rich region around the sulfur atom during the hole transporting process, as shown in Fig. S9 (ESI†).

Consequently, it is evident that the heteroatom has a more pronounced impact on the hole transport process compared to the electron transport process, resulting in a weaker influence on λ_e in comparison to λ_h. This distinction can be observed in Fig. 4b, where the sulfur atom does not participate in the vibration modes after electron injection. Hence, the oscillatory phenomenon induced by the heteroatom in hole reorganization energy does not apply to electron reorganization energy as the molecular chain lengthens for the armchair thiophene molecules, as demonstrated and confirmed in Fig. 6b.

Conclusion

In summary, we performed a comparative analysis of hole and electron reorganization energies within π-isoelectronic frameworks in both zigzag and armchair-configured molecules. This study seeks to elucidate the significant disparities in reorganization energy despite the strikingly similar planar geometry and conjugated electrons. Firstly, it displays there are more pronounced variations in molecular geometry following electron injection as compared to hole injection. This discrepancy arises because vibration modes exert a more substantial influence along the long axis after electron injection. Secondly, the introduction of heteroatom-sulfur significantly influences the low-frequency (<1000 cm⁻¹) vibration modes. In the case of armchair thiophenes molecules, the number of sulfur atoms plays a substantial role in shaping these vibration modes. Specifically, when sulfur atoms are paired in an even configuration, their strong coupling results in significant components along the long-axis direction, thus giving rise to the observed oscillation trend in the hole reorganization energy. However, due to the electron-donating property of sulfur, this phenomenon does not apply to electron transport scenarios. We anticipate that this study will provide a comprehensive understanding of π-isoelectronic frameworks by delving into the intricacies of vibration coupling at the single molecular level. This perspective introduces fresh insights into the complex interplay among vibrational modes, reorganization energy, conductivity, and the performance of organic devices. Consequently, it offers an effective approach to shaping and comprehending the structural characteristics of organic semiconductors.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

The manuscript was a collaborative effort involving all authors. Y. Zhu conceived the work, conducted simulations, and drafted the initial version of the manuscript. X. Xing contributed to the results discussion, extensively revised and rewrote the manuscript. C. Zhao and H. Meng participated in discussions concerning specific results. The final version of the manuscript has been approved by all authors.

Conflicts of interest

The authors declare no competing financial interest

Acknowledgements

This work was financially supported by the National Key Research and Development Program of China (2023YFB3608902), the GuangDong Basic and Applied Basic Research Foundation (2023A1515111072), the Foundation for Youth Innovative Talents in Higher Education of Guangdong Province (2023KQNCX094) and the Department of Science and Technology of Guangdong Province (2021A0505060003). We thank Clémence Corminboeuf, Maria Fumanal and Sergi Vela from Ecole Polytechnique Fédérale de Lausanne for helpful discussions.

References

1. C. W. Tang and S. A. Vanslyke, Appl. Phys. Lett., 1987, 51, 913–915.
2. R. Wu, M. Matta, B. D. Paulsen and J. Rivnay, Chem. Rev., 2022, 122, 4493–4551.
3. M. Berggren, E. D. Głowacki, D. T. Simon, E. Stavrinidou and K. Tybrandt, Chem. Rev., 2022, 122, 4826–4846.
4. C. Gu, A.-B. Jia, Y.-M. Zhang and S. X.-A. Zhang, Chem. Rev., 2022, 122, 14679–14721.
5. Y. Ou, A. Sun, H. Li, T. Wu, D. Zhang, P. Xu, R. Zhao, L. Zhu, R. Wang, B. Xu, Y. Hua and L. Ding, Mater. Chem. Front., 2021, 5, 876–884.
6. R. Duan, G. Han, L.-B. Qu and Y. Yi, Mater. Chem. Front., 2021, 5, 3903–3910.
7. H. Nie, K. Hu, Y. Cai, Q. Peng, Z. Zhao, R. Hu, J. Chen, S.-J. Su, A. Qin and B. Z. Tang, Mater. Chem. Front., 2017, 1, 1125–1129.
8. H. Wu, X. Song, B. Zhang, Z. Wang, T. Zhang, A. Qin and B. Z. Tang, Mater. Chem. Front., 2020, 4, 1706–1713.
9. Y. Li, K. Ding, H. Wu, Q. Wan, Y. Ma, Y. Huang, Z. Wang, W. Zhang, J. Hou and B. Z. Tang, Mater. Chem. Front., 2022, 6, 316–324.
10. L. Ueberricke, J. Schwarz, F. Ghalami, M. Matthiesen, F. Rominger, S. M. Elbert, J. Zaumseil, M. Elstner and M. Mastalerz, Chem. – Eur. J., 2020, 26, 12596–12605.
11. Y. Che and D. F. Perepichka, Angew. Chem., Int. Ed., 2021, 60, 1364–1373.
12. H. Oberhofer, K. Reuter and J. Blumberger, Chem. Rev., 2017, 117, 10319–10357.
13. C. He, Z. Chen, T. Wang, Z. Shen, Y. Li, J. Zhou, J. Yu, H. Fang, Y. Li, S. Li, X. Lu, W. Ma, F. Gao, Z. Xie, V. Coropceanu, H. Zhu, J.-L. Bredas, L. Zuo and H. Chen, Nat. Commun., 2022, 13, 2598.
14. Z. Zhang, Y. Zhu, Y. Wu, C. Zhao and H. Meng, Adv. Theory Simul., 2021, 4, 2100236.
15. N. E. Gruhn, D. A. da Silva Filho, T. G. Bill, M. Malagoli, V. Coropceanu, A. Kahn and J.-L. Brédas, J. Am. Chem. Soc., 2002, 124, 7918–7919.
16. N. S. Hush, Trans. Faraday Soc., 1961, 57, 557–580.
17. R. A. Marcus, J. Electroanal. Chem., 1997, 438, 251–259.
18. V. Coropceanu, O. Kwon, B. Wex, B. R. Kaafarani, N. E. Gruhn, J. C. Durivage, D. C. Neckers and J.-L. Brédas, Chem. – Eur. J., 2006, 12, 2073–2080.
19. W. Huang, W. Xie, H. Huang, H. Zhang and H. Liu, J. Phys. Chem. Lett., 2020, 11, 4548–4553.
20. K.-H. Lin and C. Corminboeuf, Phys. Chem. Chem. Phys., 2020, 22, 11881–11890.
21. N. Fedik, R. Zubatyuk, M. Kulichenko, N. Lubbers, J. S. Smith, B. Nebgen, R. Messerly, Y. W. Li, A. I. Boldyrev, K. Barros, O. Isayev and S. Tretiak, Nat. Rev. Chem., 2022, 6, 653–672.
22. D. G. Truhlar, P. C. Hiberty, S. Shaik, M. S. Gordon and D. Danovich, Angew. Chem., 2019, 58, 12332–12338.
23. K. Takimiya, S. Shinamura, I. Osaka and E. Miyazaki, Adv. Mater., 2011, 23, 4347–4370.
24. J. T. Blaskovits, K.-H. Lin, R. Fabregat, I. Swiderska, H. Wu and C. Corminboeuf, J. Phys. Chem. C, 2021, 125, 17355–17362.
25. Z. Shi, R. Yang, L. Zhang, Y. Wang, D. Liu, D. Shi, E. Wang and G. Zhang, Adv. Mater., 2011, 23, 3061–3065.
26. G. Tang, Z. Zhang, X. Deng, Z. Fan, Y. Zeng and J. Zhou, Carbon, 2014, 76, 348–356.
27. Y. Yamada, H. Tanaka, S. Kubo and S. Sato, Carbon, 2021, 185, 342–367.
28. H. Jeong, S. Park, J. Yang, H.-M. Lee, S. An, Y. Yamada and J. Kim, Carbon, 2023, 201, 829–836.
29. G. R. Hutchison, M. A. Ratner and T. J. Marks, J. Am. Chem. Soc., 2005, 127, 2339–2350.
30. J. Kim, N. Lee, Y. H. Min, S. Noh, N.-K. Kim, S. Jung, M. Joo and Y. Yamada, ACS Omega, 2018, 3, 17789–17796.
31. M. Zhang, Z. Wu, H. Jia, P. Li, L. Yang, J. Hao, J. Wang, E. Zhang, L. Meng, Z. Yan, Y. Liu, P. Du, X. Kong, S. Xiao, C. Jia and X. Guo, Sci. Adv., 2023, 9, eadg4346.
32. T. Y. Yang, Q. Wan, D. Y. Yan, Z. Zhu, Z. W. Wang, C. Peng, Y. B. Huang, R. Yu, J. Hu, Z. Q. Mao, S. Li, S. A. Yang, H. Zheng, J. F. Jia, Y. G. Shi and N. Xu, Nat. Mater., 2020, 19, 27–33.
33. T. Enoki, S. Fujii and K. Takai, Carbon, 2012, 50, 3141–3145.
34. P. Koskinen, S. Malola and H. Häkkinen, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 073401.
35. X. Jia, M. Hofmann, V. Meunier, B. G. Sumpter, J. Campos-Delgado, J. M. Romo-Herrera, H. Son, Y.-P. Hsieh, A. Reina, J. Kong, M. Terrones and M. S. Dresselhaus, Science, 2009, 323, 1701–1705.
36. Y. Yamada, M. Kawai, H. Yorimitsu, S. Otsuka, M. Takanashi and S. Sato, ACS Appl. Mater. Interfaces, 2018, 10, 40710–40739.
37. L. An, J. Feng, Y. Zhang, R. Wang, H. Liu, G.-C. Wang, F. Cheng and P. Xi, Adv. Funct. Mater., 2019, 29, 1805298.
38. T. J. H. Hele, B. Monserrat and A. M. Alvertis, J. Chem. Phys, 2021, 154, 244109.
39. P. Ghosh, A. M. Alvertis, R. Chowdhury, P. Murto, A. J. Gillett, S. Dong, A. J. Sneyd, H.-H. Cho, E. W. Evans, B. Monserrat, F. Li, C. Schnedermann, H. Bronstein, R. H. Friend and A. Rao, Nature, 2024, 629, 355–362.

---

Footnote

† Electronic supplementary information (ESI) available: Details of computational methods, figures and other supporting information are presented. See DOI: https://doi.org/10.1039/d4tc01744g

---