%V_Bur index and steric maps: from predictive catalysis to machine learning

Abstract

Steric indices are parameters used in chemistry to describe the spatial arrangement of atoms or groups of atoms in molecules. They are important in determining the reactivity, stability, and physical properties of chemical compounds. One commonly used steric index is the steric hindrance, which refers to the obstruction or hindrance of movement in a molecule caused by bulky substituents or functional groups. Steric hindrance can affect the reactivity of a molecule by altering the accessibility of its reactive sites and influencing the geometry of its transition states. Notably, the Tolman cone angle and %V_Bur are prominent among these indices. Actually, steric effects can also be described using the concept of steric bulk, which refers to the space occupied by a molecule or functional group. Steric bulk can affect the solubility, melting point, boiling point, and viscosity of a substance. Even though electronic indices are more widely used, they have certain drawbacks that might shift preferences towards others. They present a higher computational cost, and often, the weight of electronics in correlation with chemical properties, e.g. binding energies, falls short in comparison to %V_Bur. However, it is worth noting that this may be because the steric index inherently captures part of the electronic content. Overall, steric indices play an important role in understanding the behaviour of chemical compounds and can be used to predict their reactivity, stability, and physical properties. Predictive chemistry is an approach to chemical research that uses computational methods to anticipate the properties and behaviour of these compounds and reactions, facilitating the design of new compounds and reactivities. Within this domain, predictive catalysis specifically targets the prediction of the performance and behaviour of catalysts. Ultimately, the goal is to identify new catalysts with optimal properties, leading to chemical processes that are both more efficient and sustainable. In this framework, %V_Bur can be a key metric for deepening our understanding of catalysis, emphasizing predictive catalysis and sustainability. Those latter concepts are needed to direct our efforts toward identifying the optimal catalyst for any reaction, minimizing waste, and reducing experimental efforts while maximizing the efficacy of the computational methods.

---

Sílvia Escayola

Sílvia Escayola Gordils received her BSc in Chemistry (2016) and her MSc in Advanced Catalysis and Molecular Modelling (2017) from the University of Girona. She is currently a PhD student in the DiMoCat and QuantumChemDev research groups and works under the supervision of Prof Miquel Solà, Dr Albert Poater and Dr Eduard Matito, and has spent short periods in Uppsala with Prof Henrik Ottosson and in Chicago with Prof Laura Gagliardi. Her research interests include computational physical organic chemistry, aromaticity, catalysis, and theoretical material design.

Naeimeh Bahri-Laleh

Naeimeh Bahri-Laleh obtained her PhD in polymer engineering at Iran Polymer and Petrochemical Institute (IPPI) in March 2011. She was appointed as Assistant Professor at Engineering Department of IPPI in September 2012. She is currently working as a professor of polymerization engineering at the same institute. Since November 2023 she is Visiting Researcher at the Institute for Sustainability with Knotted Chiral Meta Matter (WPI-SKCM) at Hiroshima University to perform research in the field of functional materials with mechanically interlocked molecular architecture. Her research mainly focuses on the coordination and cationic polymerizations, polyolefins, functional materials and molecular modelling.

Albert Poater

Albert Poater finished the PhD in Chemistry in 2006, supervised by Prof Miquel Duran and Prof Miquel Solà, at the University of Girona. After periods in Chile with Prof Alejandro Toro-Labbé; in Montpellier with Prof Odile Eisenstein and a long postdoc in University of Salerno with Prof Luigi Cavallo, in 2010 he became an independent researcher as Ramón y Cajal in Girona, apart from Visiting Researcher at KAUST in Saudi Arabia, and at LCC-CNRS in Toulouse. In 2019 he became Serra Húnter Associate Professor at University of Girona and received the ICREA ACADÈMIA award. His expertise is in DFT calculations on the mechanism of inorganic and organometallic catalysis; and predictive catalysis mainly related on green chemistry.

---

1. Introduction

In modern times, the field of chemistry has introduced synthetic catalysts with vast potential for numerous applications. Such catalysts are key in addressing the pressing challenge of energy demands,^1,2 in particular, sustainable sources, as well as the removal of toxic gases.³ However, throughout history, natural catalysts like enzymes have been employed unknowingly by humans to produce food and beverages. While nature has had billions of years to evolve highly efficient enzymes for essential reactions,⁴ chemists have a shorter timeframe to develop efficient catalysts. In both natural and synthetic contexts,⁵ successful molecular catalysts are built by designing functional catalytic pockets,^6,7 specific regions where reactions occur. These pockets are created by arranging atoms in three-dimensional space. On the other hand, in synthetic chemistry, two primary strategies for catalyst development exist: high-throughput screening of a wide catalyst range,⁸ and informed design with iterative enhancements.^9,10 Moreover, the main challenge in catalyst design involves refining ineffective prototypes into systems meeting stringent industrial standards. Even slight changes in a catalyst's active site can significantly alter its performance. Achieving selectivity often means favouring one reaction pathway by only 1–2 kcal mol⁻¹, which is less than a hydrogen bond.¹¹ A small drop in activation energy by the same measure can greatly boost catalytic activity.

In the complex realm of transition metal complexes, choosing the most effective catalyst presents a formidable challenge, typically addressed through trial and error or intuition rather than methodical reasoning. A conventional approach to tackle this issue involves employing molecular descriptors that can systematically rearrange the catalyst space, as illustrated in Fig. 1a.¹² This methodology facilitates the virtual design of novel catalysts. The purpose of these descriptors is to establish quantitative connections between characteristics of the catalytic environment (akin to the concept of enzymatic catalysis, referring to the region surrounding the active metal centre) and its observed experimental behaviour.

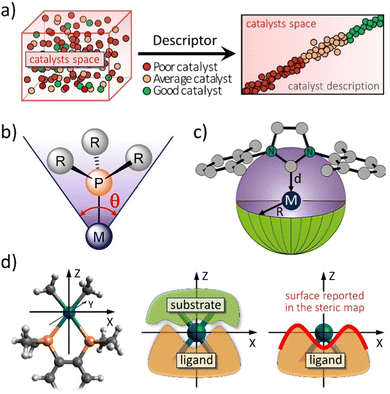Fig. 1 (a) The challenge to choose the right catalyst from molecular descriptors. Representation of (b) the Tolman cone angle, (c) the buried volume descriptor, and (d) how the steric maps are built (plane XY) from the interaction between the ligand and the substrate. Adapted with permission.¹² Copyright © 2016, American Chemical Society.

The categorization of catalyst behaviour using molecular descriptors,¹³ like steric parameters and maps or any measure related to electronics, can expedite the design of improved catalysts. Particularly, concentrating on descriptors capable of capturing the shape of catalytic pockets, those simple tools can serve as distinct identifiers for characterizing transition metal catalysts and, potentially, metalloproteins, extending their application to biocatalysis.¹⁴ In chemistry, steric indices quantify the spatial bulk of molecules or their constituent groups. They measure alterations in molecular characteristics arising from repulsive forces, typically van der Waals interactions, but also others, between different segments of a molecule. These indices are useful in predicting the reactivity, stability, and physical properties of chemical compounds. Even though there are indices also related to energetics, like molecular electrostatic potential^15,16 or repulsive energy,^17–19 the most common steric indices used in chemistry are the steric hindrance index (SHI), the van der Waals volume (VdW), and the Tolman cone angle (CA).²⁰ First, the SHI is a measure of the degree to which a functional group or atom in a molecule is blocked or obstructed by adjacent substituents. It is calculated by comparing the experimental bond angles of a molecule with the ideal bond angles for the same molecule with no steric hindrance, easy to visualize for phosphane ligands.¹⁶ Higher SHI values indicate greater steric hindrance. Second, VdW is a measure of the size of a molecule or a functional group, and it is calculated based on the van der Waals radii of its constituent atoms. A higher VdW value indicates a larger spatial bulk of the molecule. Third, the CA is a measure of the steric hindrance caused by a substituent on a metal centre in organometallic chemistry (Fig. 1b). It is defined as the angle between two lines drawn from the metal centre to the outermost atoms of the substituent. A larger CA value indicates greater steric hindrance. Overall, steric indices are important tools in chemical research, especially in the design and synthesis of new molecules with desired properties. And the aim of this review is to stress the importance of the concepts of steric index of the buried volume of Nolan, Cavallo and coworkers,²¹ %V_Bur (Fig. 1c),²² and the associated steric maps of Cavallo and coworkers (Fig. 1d),^12,14 and how they have been expanded to many applications,²³ mainly thanks to the creation of a user friendly web server. The %V_Bur parameter is a steric index that has been found to be highly correlated with the binding energy of metal catalysts.^22,24 These index was first introduced by Cavallo and coworkers in a series of papers in the early 2000s,^25,26 and has since then been used extensively in the rational design of new catalysts and materials.

The %V_Bur parameter is a measure of the volume occupied by the ligands around a metal centre, taking into account the valence electrons of the ligands that are buried in the coordination sphere of the metal. It is calculated using quantum mechanical methods, such as density functional theory (DFT), and has been found to be a good indicator of the steric hindrance experienced by the ligands around the metal centre. One of the key applications of the %V_Bur parameter has been in the de novo design of metal catalysts for a range of chemical reactions. The steric hindrance around the metal centre can have a significant impact on the selectivity and activity of the catalyst,²⁷ and so a thorough understanding of these effects is essential for guided design purposes.

A number of studies have shown a high correlation between the %V_Bur parameter and the binding energy of ligands to metal centres, a key factor in determining the reactivity of metal catalysts.²⁸ In general, those studies found that ligands with larger %V_Bur values correspond to weaker binding to the metal centre, while ligands with smaller %V_Bur values result in stronger binding. This is translated to the reactivity of the catalysts.²⁹ These findings hold significant implications for the design of new catalysts. For example, if a ligand is required to have strong binding to the metal centre, then ligands with smaller %V_Bur values may be preferred. Conversely, if a ligand is required to have weaker binding to the metal centre, then ligands with larger %V_Bur values may be more suitable. Interestingly, the metal does not influence significantly the %V_Bur parameter itself, but, merely adjusts it based on the bonded ligands, and obviously on the radius with the linking atom of the ligand under study.³⁰ This is one of the strengths of the %V_Bur parameter, since it remains consistent regardless of the computational approach used on the metal, facilitating a uniform assessment of ligand–metal binding.

The scope of %V_Bur parameter covers the whole range of reactions, including hydrogenation,^31,32 oxidation,^33–35 cross-coupling reactions,³⁶ polymerization,^29,37,38 among others.

To sum up, the %V_Bur parameter developed by Cavallo and coworkers has proven to be instrumental in the development of novel catalysts and materials. Its strong correlation with the binding energy of ligands to metal centres has allowed for the development of more efficient and selective catalysts, while its applications in materials science have led to the development of materials with specific properties. As research in this area continues to advance, it is likely that the %V_Bur parameter will gain even greater significance in the formulation of new catalysts and materials for a range of applications.

Despite the broad scope of the %V_Bur parameter and associated steric maps, as evidenced by over 2000 papers on these topics, this review focuses on their specific applications. To provide context, an overview of these applications is presented. Importantly, from the moment %V_Bur was initially developed, the aim was for it to serve not only as a descriptive tool but also as a predictive one. This predictive potential aligns with machine learning (ML) approaches, and ultimately with predictive catalysis.³⁹ The number of catalysts available is huge, creating a nearly infinite set to consider, and thus unaffordable for human analysis, i.e. how they could be used is not easy to order. Thus, integrating concepts like steric indices, ML, and predictive catalysis is essential to enhance past efforts and experience.⁴⁰

2. From catalysis to machine learning via predictive catalysis

After the pioneering work and ideas about computing machinery and intelligence of Alan Turing,⁴¹ the term machine learning was coined in 1959 by Arthur Samuel,⁴² from the American company IBM. In addition to artificial intelligence (AI), curiously he was also a pioneer in the field of computer games. Then during the 60s and 70s research was done on ML for pattern classification,⁴³ especially through the efforts of Duda and Hart.⁴⁴ In the 80s the horizons expanded towards neural networks. And currently, modern ML consists of the classification of data based on models which have been developed, and from which to make predictions for future outcomes.

In detail, ML is based on the study of computer algorithms that automatically improve (artificial intelligence) by using data and checking how previous decisions evolve.⁴⁵ Machine learning algorithms have the ability to build a model based on sample data, in order to make predictions or decisions without having explicitly programmed them.⁴⁶ It can turn out to be more effective to help the machine develop its own algorithm, rather than having human programmers specify all the needed steps.⁴⁷ These ML algorithms are used in a wide variety of situations, for example in medicine, for email filtering, or computer vision. Ultimately, they apply for many purposes and are especially useful where the development of conventional algorithms fall short or it is even unfeasible.

Machine learning has a lengthy history of applications in computational chemistry.^48,49 For example, it is used for the prediction of various chemical and biological properties. Currently, within this discipline, ML is in a state of transition, marked by its integration with big data science tools, holding the potential to substantially transform the field.⁵⁰ The minimization of the error relative to reference data allows ML algorithms to deliver predictive models mapping a set of descriptors into one or more properties of interest. These models can handle robustly sets of data that can be very large and complex and, once compiled, they allow to make accurate predictions on any computer in a fraction of a second.⁵¹ The fast execution of ML predictions allows the exploration of the large chemical space with different approaches,⁵² including the multi-objective optimization,⁵³ and inverse design.^54,55

2.1. What we can do with predictive catalysis

Predictive catalysis, understood as the prediction of the result of a catalytic reaction using efficient computational models, has the potential to revolutionize the optimization procedure of catalysed reactions in the coming years and constitutes a first step towards the use of artificial intelligence, or more specifically machine learning to synthetic chemistry.⁵⁶

Predictive catalysis proposes disruptively changing the flow chart of operations aimed at optimizing a synthetic procedure. Rather than conducting an exhaustive experimental screening of reaction conditions followed by mechanistic calculations to understand the best experimental results, this approach proposes to reverse the order. Thus, the calculations are performed in a first stage and allow predicting a limited set of key experimental parameters for the optimization of the process that in a second stage will be evaluated in the synthetic laboratory.⁵⁷ This change would enable calculations to function akin to surgical precision, directing experiments efforts exclusively toward the most promising candidates identified through computational analysis. Molecular descriptors here constitute a foundational element in predictive catalyst design, quantifying catalyst properties and facilitating the linkage between experimental behaviour and structure.^58–60

2.2. Towards big data for machine learning

The long-term goal would be to feed ML systems with reliable data. The global revolution of ML is highly beneficial for computational chemistry, and in particular catalysis, since its application will allow for uncovering hidden aspects of catalysts. Minimizing the errors of current algorithms relative to the reference data allows to deliver predictive models that map a set of descriptors to one or more properties of interest. Thus, the data obtained in the different predictive catalysis subprojects would feed databases that could be used by AI algorithms. These algorithms automatically improve their performance by using reported data and checking the evolution of prior decisions.

The expertise of our research group in predictive catalysis is well-founded. This dedicated research team has been organized to effectively address the project outlined for this ongoing review.

Predictive catalysis might appear inferior to machine learning, yet it has a huge comparative advantage, since it does not require the use of any indispensable database. Actually, it is a matter of making a minimal database based on the great reliability that it has already achieved today through DFT calculations. In addition, some projects could be defined not merely as predictive catalysis, but rather predictive chemistry, given the low impact of the catalyst. Nevertheless, the pivotal aspect remains that calculations are conducted prior to experiments, resulting in reduced experimental needs owing to predictions derived from computations. Examples of Poater's work in predictive chemistry and predictive catalysis include the development of computational tools and methods to predict the properties,⁶¹ reactivity,^62,63 and behaviour of chemical compounds and catalysts.⁶⁴ However, the range of uses and applications is much broader, including the development of ML algorithms to predict the reactivity of chemical compounds based on their molecular structure and properties,⁶⁴ while there are other examples using computational models to predict the performance of catalysts in chemical reactions,⁵⁷ including the rate and selectivity of the reaction. These predictions can be used to guide the synthesis and optimization of new catalysts, leading to more efficient and sustainable chemical processes.

2.3. Predictive catalysis examples in computational chemistry from the research group

The research team already has former examples of predictive catalysis, with or without the subsequent experimental tests. Different strategies were planned, and here we summarize some of them.

The use of web-servers to predict the reactivity, either by energy barriers in olefin metathesis;⁶⁵ or by means of sterical indices such as %V_Bur or steric maps.¹⁴ Those latter tools have attracted high interest and, actually, are the base of the use of the steric indices discussed as a main topic in this review, without which servers, probably the divulgation of those indices would be much less and not significant in the catalytic field, and simply constrained to the relatively low number of users of the Cavallo group, developer of the Fortran code.

In line with the main philosophy of predictive catalysis, some of us participated in past works, with anticipation of preliminary calculations to reduce the later experimental efforts: either screening ligands to combine with metals to test hydrogenation catalytic systems,^31,66 or unveiling the reaction mechanism of a particular process in homogeneous catalysis.⁶⁷ In detail, CO₂ fixation, through functionalization of epoxides to cyclic carbonates by NbCl₅,⁶⁸ led to test the results in a more productive heterogeneous system.⁶⁹ The reactions of SiO₂-200 instead of SiO₂-700 with the niobium precursor, according to the two different protocols, generated surface complexes presenting significant, but different, populations of close active centres (bipodal instead of monopodal). Thus, the demonstration of the dual metal catalysis was achieved, together with the support of a DFT study on model silica surfaces. The observed differences in catalytic efficiency were correlated with an unprecedented cooperative effect between two neighbouring Nb centres on the surface. On the other hand, the simple modification of the niobium-based catalyst, substituting the chloride by ethyl ligands led to null dual metal catalysis. Hence, this work demonstrates that dual metal catalysis is like a golden nugget in catalysis, and not easy to get.⁷⁰ Continuing with CO₂ fixation it was addressed which should be the most suitable nucleophilic agent to activate the epoxide, and these computational tests were then derived in the laboratory, only with the best nucleophiles.⁷¹ This solution for CO₂ fixation combined with epoxides by the catalytic role of two niobium centres was not a unique solution, but at the same time contributed to solving the hydrophenoxylation of alkynes,⁷² contemporary with Houk and coworkers,⁷³ where two gold moieties are involved.⁷⁴ In addition, the concept of dual catalysis probably was not included in other works because it failed, and instead the reaction pathway was guided by a monometallic scheme. In this sense, in some of our works this occurred,⁷⁰ and even for the abovementioned cyclization of epoxides with CO₂ failed with the niobium catalysts when the chloride ligands were substituted by alkoxide ligands. But the success of the concept of dual metal catalysis went beyond, since the dual character is not mandatorily metallic, but two organic molecules were demonstrated to cooperate towards better catalytic performance. For instance, CO₂ has been recently fixed by means of two units of ascorbic acid.⁷⁵ And in 2023 nickel(II) complexes of tripodal ligands could fixate at atmospheric CO₂ pressure, and the best catalyst was fully characterized by steric maps.⁷⁶ Another solution by means of calculations was the reduction of the kinetic cost defined by the rate determining step (rds) by means of finding out alternative catalytic systems with several examples, monitoring the substituents on the phosphine to achieve milder conditions in a palladium-catalysed benzosilole formation from aryloxyethynyl silanes and towards milder conditions by predictive catalysis via steric hindrance in the pincer–Ru-catalysed hydrogenation of thioesters.⁷⁷

On the other hand, in some cases, the proposed modifications turned out to be almost sterile, for example the modification of a pincer ligand bound to ruthenium for N₂O fixation.⁷⁸ However, those are not failures of predictive catalysis, but a finding that it is not always possible to improve the existing catalytic systems. Finally, and above all, the goal of predictive catalysis and, in fact, the final challenge is the proposal and achievement of new generations of catalysts, either with unaffordable projects including the bis-ylidene ruthenium complexes to get rid of the costly phosphine dissociation in olefin metathesis using 1st or 2nd generation Grubbs catalysts (RuCl₂(NHC or PR₃)(PR₃) = CHPh),⁷⁹ where NHC is a N-heterocyclic carbene (NHC), or the annulated C₆₀ on NHC ligands in Ru-based olefin metathesis catalysts.⁸⁰ However, other became successful, with next experimental studies, take for instance, with regard to the functionalization of carbon allotropes, Poater predicted the reactivity and regioselectivity of the Pauson–Khand reaction in armchair, zig-zag and chiral nanotubes,⁸¹ a reaction that was then carried out in the laboratory in collaboration with Prof. Fernando Langa (UCM); or in collaboration with Prof. Jean-Luc Renaud the successful reductive amination by bifunctional(cyclopentadienone)Iron–Tricarbonyl Complexes,⁸² analogous to Knölker catalysts, moving to mild conditions simply adding electronwithdrawing groups on the cyclopentadienone ring.^63,83

2.4. Hot topics in computational chemistry

Some of the hot topics in computational chemistry are the following, in which %V_Bur or/and steric maps have or could have a role: (1) Reaction mechanisms: computational methods can be used to study reaction mechanisms and predict reaction pathways, which is useful for developing new synthetic methods and understanding chemical reactivity; (2) Sustainable chemistry: computational chemistry is also being used to develop sustainable chemical processes and materials, such as renewable energy sources and biodegradable plastics; (3) Quantum computing in computational chemistry: quantum computers are expected to revolutionize computational chemistry by enabling the simulation of larger and more complex chemical systems; (4) Protein–ligand binding: computational methods are being developed to predict the binding affinity of small molecules to proteins, which has applications in drug discovery; (5) Molecular simulations of biomolecules: molecular simulations can provide insight into the behaviour of biomolecules, such as DNA, RNA, and proteins, at the atomic level; (6) Reactive molecular dynamics: reactive molecular dynamics simulations can be used to study the kinetics of chemical reactions at the atomic level; (7) Multi-scale modelling: multi-scale modelling approaches integrate computational methods at different length and time scales to simulate complex chemical systems, such as biological membranes and polymers; (8) Drug discovery and design: computational chemistry plays a critical role in drug discovery by identifying and optimizing lead compounds, predicting their pharmacological properties, and simulating their interactions with biological targets, and in addition, to identify potential drug candidates and design more effective drugs with fewer side effects; (9) Protein structure prediction: computational methods are being used to predict the structure of proteins, which is important for understanding their function and designing drugs that target specific proteins; (10) Materials discovery and design: computational methods are useful to accelerate the discovery and design of new materials with desirable properties, such as high strength, conductivity, and catalytic activity; (11) Electronic structure calculations: electronic structure calculations are used to study the electronic properties of molecules and materials, such as their energy levels and charge distribution; (12) Solvation models: solvation models are used to simulate the behaviour of molecules in solution, which is important for understanding biochemical processes and designing new materials; (13) Machine learning in computational chemistry: ML methods are being increasingly used in computational chemistry to develop more accurate models for predicting molecular properties and reactions; (14) Big data and data mining: large databases of chemical and biological data are being analysed using ML and data mining techniques to identify patterns and correlations that can be used to develop more accurate predictive models; (15) Artificial intelligence and deep learning: AI and deep learning techniques are being applied to computational chemistry to develop more efficient algorithms and models.

3. Chemical indices related to reactivity

Several indices have been developed and are used in chemistry to quantify various properties of molecules, including reactivity, stability, and physical properties. In the following sections, we will discuss some of the most important indices used in chemistry, with particular emphasis on the steric indices.

3.1. Steric indices

Very generally, the steric indices are measures of the spatial hindrance or crowding around a particular atom or group of atoms within a molecule. They may consider the size and shape of the substituent groups, the number of bonds, and the number of lone pairs of electrons surrounding the atom of interest. A higher steric index indicates more crowding and hindrance, which can affect the reactivity and physical properties of the molecule. The steric hindrance index, the van der Waals volume, and the cone angle are three commonly used steric indices. The steric hindrance index measures the degree to which a functional group or atom in a molecule is blocked or obstructed by adjacent substituents, the van der Waals volume index measures the size of a molecule or functional group, and the Tolman cone angle measures the steric hindrance caused by a substituent on a metal centre in organometallic chemistry.

3.2. Electronic indices

Indices that measure the electronic properties of molecules, which play a crucial role in determining their reactivity, stability, and physical properties. The electronegativity, electron affinity, and ionization potential are three important electronic indices. Electronegativity measures the tendency of an atom to attract electrons, electron affinity measures the energy released when an atom gains an electron, and ionization potential measures the energy required to remove an electron from an atom or molecule.

3.3. Aromaticity indices

While aromaticity is exclusive to certain molecular systems with ring structures and lacks a univocal characterization, its fundamental role is undeniable, especially given its significant influence on molecular stability, reactivity, and electronic properties. Therefore, a variety of indices exist, which can be organized into the following groups: Energetic,⁸⁴ geometric,⁸⁵ magnetic,^86–88 electronic,^89,90 and reactivity-based measures.⁹¹

3.4. Spectroscopic indices

Indices that measure the spectral properties of molecules, which are important in identifying and characterizing chemical compounds. The infrared (IR) spectrum, the ultraviolet-visible (UV-Vis) spectrum, and the nuclear magnetic resonance (NMR) spectrum are three commonly used spectroscopic indices. The IR spectrum measures the absorption of infrared radiation by molecules, the UV-Vis spectrum measures the absorption of ultraviolet and visible radiation by molecules, and the NMR spectrum measures the magnetic properties of nuclei in molecules.

3.5. Other indices

Other important indices in chemistry include thermodynamic indices, kinetic indices, and thermophysical indices. Thermodynamic indices, such as entropy and enthalpy, are measures of the energy and heat changes in chemical reactions. Kinetic indices, such as reaction rate and activation energy, are measures of the speed and mechanism of chemical reactions. Thermophysical indices, such as melting point and boiling point, are measures of the physical properties of chemical compounds.

Overall, these indices play a crucial role in chemical research and are used in a wide range of fields, from drug development to materials science and catalysis. By providing important insights into the behaviour of chemical compounds, these indices help chemists design and synthesize new molecules with specific properties and improve our understanding of the fundamental principles of chemistry. To sum up, the above indices and others are essential tools in chemistry for quantifying various properties of molecules and compounds. Next, the most used indices are discussed with a brief description:

The acid dissociation constant, commonly abbreviated as pK_a, is a measure of the strength of an acid in solution. It is defined as the negative logarithm of the acid dissociation constant (K_a), which is the equilibrium constant for the dissociation of an acid in water. A lower pK_a value indicates a stronger acid, and a higher pK_a value indicates a weaker acid. The pK_a value is an important index in determining the pH of a solution and the reactivity of acids in chemical reactions.

Basicity, also known as the basic dissociation constant (pK_b), is a measure of the strength of a base in solution. It is defined as the negative logarithm of the basic dissociation constant (K_b), which is the equilibrium constant for the dissociation of a base in water. A higher pK_b value indicates a stronger base, and a lower pK_b value indicates a weaker base. The basicity of a compound is an important index in determining its ability to accept protons in chemical reactions.

The dipole moment, is a measure of the polarity of a molecule. It is defined as the product of the charge on each atom and the distance between them. A higher dipole moment indicates a more polar molecule, which can affect its physical and chemical properties, such as solubility, reactivity, and melting point.

Electronegativity, is a measure of the ability of an atom to attract electrons towards itself in a chemical bond. It is a fundamental concept in chemistry and is used to explain various chemical phenomena, such as the polarity of molecules, the strength of chemical bonds, and the reactivity of chemical compounds. Electronegativity is measured on the Pauling scale, where higher values indicate higher electronegativity.

Magnetic aromaticity indices, being the Nucleus Independent Chemical Shift (NICS) the most extended in the general chemistry community.^86,87 NICS measures the magnetic susceptibility at specific points in the space (ghost atoms) to assess aromaticity. However, some authors have warned about the limitations of NICS and its occasional misinterpretations.^92,93 Therefore, they advocate for the importance of relying on multiple indices based on different aspects of aromaticity.

The Hammett acidity function, commonly abbreviated as H0, is a measure of the strength of an acid in organic chemistry. It is defined as the logarithm of the ratio of the equilibrium constants of two acids, one being a reference acid and the other being the acid of interest. The H0 index is an important index in determining the reactivity of organic acids in chemical reactions since 1932.⁹⁴ By extension, in 1937 it was introduced an empirical equation relying on two parameters to establish a connection between reaction rates and equilibrium constants for reactions involving aromatic compounds,⁹⁵ that since then it is a reference in catalysis.^96,97 and can also be found in combination with steric maps to combine the electronic and steric properties of the ligands.⁹⁸

Henry's law constant, is a measure of the solubility of a gas in a liquid. It is defined as the ratio of the concentration of the gas in the liquid to its partial pressure in the gas phase at equilibrium. The Henry's law constant is an important index in environmental chemistry and is used to determine the fate and transport of gases in the environment.

Hydrophobicity, is a measure of the tendency of a molecule or functional group to repel water. It is a crucial index in determining the solubility and stability of molecules in aqueous environments. Hydrophobicity is often quantified using various indices, such as the octanol–water partition coefficient (log P), which measures the partitioning of a molecule between an organic solvent and water.

The melting point, is a measure of the temperature at which a solid substance melts and becomes a liquid. It is an important physical property of compounds and can be used to identify and characterize them. The melting point is affected by various factors, such as the strength and type of intermolecular forces between molecules, the molecular weight and shape, and the presence of impurities.

Polarizability, is a measure of the ability of an atom or molecule to form a temporary dipole moment in response to an external electric field. It is an important index in determining the reactivity and stability of molecules, particularly those involved in non-covalent interactions, such as van der Waals forces. Polarizability is influenced by various factors, such as the size, shape, and electronic structure of the molecule.

The reactivity index, is a measure of the relative reactivity of a molecule towards a specific reaction or reagent. It is often used in computational chemistry and theoretical studies to predict the outcome of chemical reactions and to design new molecules with specific properties. The reactivity index is calculated from various parameters, such as the molecular orbital energies and electron densities.

Solubility, is a measure of the ability of a substance to dissolve in a solvent. It is an important index in determining the physical and chemical properties of compounds and is influenced by various factors, such as the nature of the solute and solvent, temperature, pressure, and the presence of other solutes. The solubility index is often quantified using various indices, such as the solubility product constant (K_sp) and the dissolution rate. In detail, K_sp is a measure of the solubility of a compound in water. It is defined as the equilibrium constant for the dissolution of a solid in water, thus, K_sp is an important index in determining the solubility and precipitation of compounds in solution.

Steric hindrance, is a measure of the obstruction of the movement or reaction of a molecule by the presence of other groups or atoms in its vicinity. It is an important index in determining the reactivity and stability of compounds, particularly those involved in organic reactions. Steric hindrance can be quantified using various indices as shown above and that will be in detail discussed in the next section.

The van der Waals radius, is a measure of the effective radius of an atom or molecule, which is defined as the distance between the nuclei of two atoms when they are in their most stable state. It is an important index in determining the strength of intermolecular forces and the solubility of molecules in polar solvents. van der Waals radius is influenced by various factors such as the size and shape of the atom or molecule and the nature of the intermolecular forces. VdW interactions are generally used to quantify the steric hindrance, as well.

4. Steric indices

There are several steric indices used in chemistry to measure the spatial bulk or volume of molecules or functional groups. These indices play an important role in predicting the behaviour of chemical compounds and in the design and synthesis of new molecules with specific properties. The most commonly used steric indices in chemistry are the steric hindrance index, the van der Waals volume, the cone angle and the buried volume (%V_Bur).

The steric hindrance index, is a measure of the degree to which a functional group or atom in a molecule is blocked or obstructed by adjacent substituents. Steric hindrance can affect the reactivity of a molecule by preventing or slowing down chemical reactions that involve the affected functional group or atom. The SHI is calculated by comparing the experimental bond angles of a molecule with the ideal bond angles for the same molecule with no steric hindrance. The ideal bond angles are calculated based on the size and shape of the atoms and functional groups involved in the bond. A higher SHI value indicates greater steric hindrance, and therefore, lower reactivity. This steric index is a measure of the bulkiness of a molecule. It is calculated by counting the number of atoms that are close to each other in three-dimensional space, and is used to predict the stability and reactivity of a molecule. The SHI refers to a measure of the size of a molecule in relation to the molecular size of its neighbours. This SHI is used to describe the molecular size and shape of a molecule in a system, and it is an important parameter for the design of chemical reactions and for the study of molecular interactions. However, one application of this steric index is specially in drug design, where it is used to predict the pharmacological activity of a drug and its potential for adverse side effects. By determining the steric index of a drug molecule, researchers can predict how it will interact with its target protein and with other molecules in the body. This information is crucial in designing drugs that are effective and safe for human use.

The van der Waals volume, is a measure of the size of a molecule or a functional group. It is calculated based on the van der Waals radii of its constituent atoms. The VdW index is important in determining the shape and size of molecules, and it plays a key role in the development of drugs and other compounds with specific physical and chemical properties. A higher VdW value indicates a larger spatial bulk of the molecule. The VdW index is particularly useful in predicting the solubility, stability, and bioavailability of drugs.

The Tolman cone angle, is a measure of the steric hindrance caused by a substituent on a metal centre in organometallic chemistry.^20,99 Mathematically, the CA is a measure of the shape of a molecule, calculated by determining the angle between the vector from the central atom to the centre of gravity of the molecule, and the vector from the central atom to the furthest point on the molecule. In detail, it is calculated by drawing a cone-like shape around the molecule and measuring the angle of the cone. This angle is defined as the angle between the axis of the molecule and the axis of its neighbours in a system. This angle provides information about the overall shape of the molecule and can be used to predict its reactivity and stability.

The CA index is used to predict the reactivity and selectivity of metal-catalysed reactions, as it can affect the orientation and accessibility of reactants near the metal centre. A smaller CA value indicates greater steric hindrance, and therefore, lower reactivity. The CA index is particularly useful in designing new catalysts for organic reactions, where the selectivity of the reaction is important. However, commonly, the CA is applied to assess ligands like phosphanes,¹⁰⁰ phosphites,¹⁰¹ and similar ligands. This is especially fitting due to the distinctive conical shapes of these ligands, even in cases of unsymmetrical phosphanes. The Tolman cone angle has been the favoured steric parameter for such ligands, despite some corrections and criticisms over the years,¹⁰¹ and being present book by Crabtree in the key educational in organometallics.¹⁰² This parameter has proven exceptionally valuable to the chemical community, even when expanded the concept to steric maps.¹⁰³ Although the solid angle concept then appeared, and it was a viable alternative,^104–107 it was not as intuitive and did not provide distinct advantages over the cone angle, and the bidimensional representations by Immirzi and Musco were not conclusive either,¹⁰⁸ as the cone angle radial profiles of Taverner and coworkers.¹⁰⁹ As a result, the solid angle did not gain significant traction in describing steric properties of phosphanes and related ligands.¹¹⁰

General steric descriptors, link the successful CA for phosphines with the %V_Bur of Nolan, Cavallo and coworkers. Actually, those indices are more general than the CA. In detail are proposed by Taft,¹¹¹ Charton^112,113 and Verloop.^114,115

The %V_Bur index, developed quantitatively by Cavallo and coworkers, is a steric index that quantifies the volume of a molecule in a specific region of space. This index has found numerous applications in the study of the structure and reactivity of molecules and materials. One particularly interesting application is the correlation of %V_Bur with binding energy, which has important implications for the design of new catalysts and materials. However, the most important feature of %V_Bur index is that, while the Tolman CA had been proven highly effective for assessing phosphanes, it was clear that it was not the most suitable choice for characterizing the steric attributes of the emerging category of NHC ligands,^21,116 which possess nearly C₂-symmetric structures. NHC ligands have gained significant traction as highly efficient alternatives to traditional phosphanes in the last decades. Their application often results in smoother reaction conditions and novel reactivity. This is particularly evident in areas such as iridium-catalysed hydrogenation,^117–119 palladium-catalysed C–C coupling reactions,^120–122 ruthenium-catalysed olefin metathesis,^123–129 and even unforeseen reactivity, exemplified by gold-catalysed reactions.^130,131 Moreover, the saturated NHC skeletons play a pivotal role in introducing asymmetry to the NHC ring,^124,132,133 enabling the use of chiral NHCs in asymmetric synthesis.^134–136 And then for NHC ligands the use of %V_Bur could be extended to any type of ligand, unlike the limited CA.

Other steric indices. there are several other steric indices used in chemistry, including the steric strain energy (SSE), the steric energy (SE), and the steric shielding constant (SSC). These indices are used to measure the energy of steric interactions and the degree of shielding of atoms or functional groups from chemical reactions. Then, to switch to multidimensional steric parameters, Sterimol steric parameters developed by Verloop are a set of measures used to quantify the size and shape of ligands on metal centres within coordination complexes.^137,138 These parameters involve evaluating the dimensions of specific substituents along defined directions in three-dimensional space,^139,140 providing insights into the steric interactions within a catalyst's catalytic pocket, enabling the comparison of different ligands and their effects on catalytic behaviour.¹⁴¹ Knowing that understanding steric effects in asymmetric catalysts remains largely empirical, in 2012, Sigman and coworkers revisited the past results with Charton indices.¹⁴² Prior research has shown correlations between Charton steric parameters and simple substituents in substrates and ligands, but these correlations are lacking for more complex substituents. However, the potential application of steric parameters is high for asymmetric catalysis, while those tools were commonly used in quantitative structure–activity relationships (QSAR), a technique for optimizing pharmaceutical functions. By reassessing steric/enantioselection relationships using the more advanced Sterimol parameters within a QSAR context, it is possible to establish strong correlations in processes where Charton parameters fell short. More recently, in 2019 the steric occupancy descriptors by Denmark and coworkers could lead to choose selectively chiral catalysts using machine learning and chemoinformatics.¹⁴³ By employing robust molecular descriptors that remain independent of the catalyst scaffold, a universal training set was assembled, focusing on steric and electronic characteristics. This training set served as a foundation for training ML models that can predict outcomes with high precision across a wide range of selectivity scenarios. The use of support vector machines and deep feed-forward neural networks was showcased in predicting outcomes for the chiral phosphoric acid-catalysed thiol addition to N-acylimines, highlighting the potential of this strategy to enhance catalyst selection and development. In 2021 they proposed a novel quantitative quadrant descriptor that relies on conformer-dependence to establish connections between catalyst structure and performance in enantioselective reactions.¹⁴⁴ The versatility of these descriptors is exemplified across three distinct reactions: (1) copper-catalysed enantioselective cyclopropanation of alkenes, (2) rhodium-catalysed enantioselective hydrogenation of α-substituted N-acyl-enamides, and (3) enantioselective addition of thiols to N-acyl imines. By merging the interpretive qualities of quadrant models with a quantitative approach, this research offers a steric descriptor that enables statistically meaningful correlations between the stereoselectivity and steric occupancy of catalyst quadrants. The descriptor's concise dimensionality, ability to account for conformational and stereostructural influences, and direct relevance to fundamental structural properties make it well-suited for establishing Quantitative Structure-Selectivity Relationships (QSSR) using smaller datasets from asymmetric reactions.

Overall, steric indices are crucial tools in chemical research, as they provide important insights into the behaviour of chemical compounds and help chemists design new molecules with specific properties. These indices are used in a wide range of fields, from drug development to materials science and catalysis.

5. %V_Bur index and steric maps

5.1. Definition of %V_Bur

The mathematical concept of %V_Bur is very simple. Synthetically, it is necessary to establish the central metal atom (M) that the ligand coordinates with. In cases of transition metal complexes being analysed, the metal centre's coordinates from the structure can naturally serve this purpose. However, when dealing with the ligand's standalone structure, it becomes essential to designate a presumed metal centre to which the ligand attaches through its bonding atom(s). After determining the position of the central M atom, a sphere centred on M with a radius of R is constructed. This sphere is divided by a regularly spaced 3D cubic grid with intervals of s, defining cubic voxels (v_xyz) with a volume of s³. The distance between the centre of each voxel and all atoms in the ligand is examined to see if any atom falls within the van der Waals distance from the voxel's centre. If none of the ligand's atoms are within this distance, the volume s³ of that voxel is considered as free volume (V_Free). On the other hand, if a single ligand atom is within the van der Waals distance, the volume s³ of that voxel is labelled as buried volume (V_Bur). This leads to eqn (1):

V_Sphere = Σv_xyz = V_Free + V_Bur = Σv_xyz(free) + Σv_xyz(buried) (1)

While the V_Bur value shows the portion of the coordination sphere occupied by the ligand, the more understandable %V_Bur descriptor of eqn (2) is preferred:

%V_Bur = 100·V_Bur/V_Sphere (2)

With the necessity to define the atom radii, considering that the binding energies of NHC ligands with metals had been corrected for solvent effects using the COSMO model,¹⁴⁵ the same atomic radii were first used for calculating %V_Bur values. Nonetheless, the validity of these previously used COSMO radii had been not verified quantitatively against a specific set of experimental or computational data. Additionally, a drawback of these radii is their reliance on varied atomic sizes depending on hybridization states, leading to cumbersome and potentially error-prone input management for accurate atom labelling. Despite this, the advantage of a broader range of radii that accounts for the hybridization state of atoms is evident, offering enhanced flexibility to the overall methodology. When switching to bondi radii,¹⁴⁶ and particularly scaled by 1.17 the agreement with experimental data like binding energies increased significantly. With respect to COSMO radii, for Bondi radii no requirement exists for input manipulation to designate the hybridization states of atoms; thus, structures derived from theoretical or experimental methods can be directly employed without modification.

Emphasize that ligand is used here because it is the easiest example, and also the pioneer, of using the V concept, but it is really extrapolable to any structure one can imagine, from metallic organic frameworks^147,148 to silicates,^31,149 clusters,^150,151 amino acids or enzymes,^14,152 to give some diametrically opposed examples. And take for instance, the %V_Bur index of the ligand can lead to explain how pesticides trap free metals from the soil,¹⁵³ or unveil the complexation of trichlorosalicylic acid with metals to enhance the resulting complexes as antibacterial agents.¹⁵⁴

5.2. %V_Bur on NHC ligands

The origin of %V_Bur is implicitly linked to the development of the NHC ligand, and its fundamental role in catalysis.¹⁵⁵ They are very symmetrical structures, and without them the %V_Bur would surely never have been needed, and their flexibility and asymmetry was also responsible for the evolution of the concept to steric maps, to deal with particularly asymmetric NHCs. Actually, much like or even more than phosphanes, N-heterocyclic carbene (NHC) ligands are highly flexible structures that can be easily customized,^156,157 allowing precise adjustments of both steric and electronic properties.^24,158,159 This characteristic has prompted a series of investigations aimed at accurately characterizing and categorizing various NHC ligands through experimental^160–162 and theoretical means.^25,163,164 Within this realm of research, the %V_Bur allowed to quantitatively assess the varying steric bulk among different NHC ligands, measuring the spatial occupancy occupied by the NHC ligand within the metal centre's first coordination sphere. The necessity for an index that does not treat ligands as cones, but as shape unbiased approach with the buried volume came after the work on NHC ligands by Nolan and coworkers.^21,165

At a first glance, to save computational time, the challenge would revolve to determine the appropriate NHC geometry for %V_Bur calculations, as a free organic ligand. However, the DFT-optimized geometries of uncoordinated NHC ligands led to erroneous estimates of the %V_Bur values compared to the experimental performance in reactivity in catalysis. This simple choice had drawbacks. Many instances demonstrated that structures with aromatic N-substituents on free NHC ligands tended to favour configurations where these N-substituents were coplanar with the NHC rings.²² Yet, this conformation inadequately represented NHCs in most organometallic complexes, where the aromatic N-substituents were typically orthogonal to the NHC mean planes, but mainly the reason is that when the NHC ligands are free their substituents are greatly expanded by space, which is forbidden when bonded.^22,166 But before accepting this drawback of %V_Bur, several other options were considered and discarded. Complexes like (NHC)Ni(CO)₃ were initially attractive, given their use in calculating the CA;²⁶ however, these were unsuitable due to instability with bulkier NHC ligands. Similarly, (NHC)AgCl complexes were not ideal,¹⁶⁷ as the trans-positioning of the Cl ligand led to an inadequately constrained complex. Moreover, the experimentally available (NHC)Ir(CO)₂Cl complexes were chosen as model systems to determine NHC geometries for %V_Bur calculations.¹⁶⁸ These complexes possess a square-planar coordination geometry around the Ir centre, with one Cl ligand trans to the NHC ligand, which facilitates their use to explore the steric and electronic attributes of NHC ligands.

5.3. Correlation of %V_Bur with reactivity

There is no straightforward correlation between the SI or %V_Bur and yield in chemical reactions, as the yield depends on a variety of factors such as reaction conditions, reactant concentrations, and catalysts. However, these parameters can affect the reaction rate and selectivity, which can in turn affect the yield.

In general, larger substituent groups or atoms can lead to steric hindrance, which can slow down or prevent reactions. This can result in lower yields or unwanted side reactions. On the other hand, smaller groups or atoms may increase reactivity and selectivity, leading to higher yields. However, this is not always the case, and the effect of steric hindrance can be complex and depend on the specific reaction and conditions.²² Similarly, larger %V_Bur values can lead to stronger repulsion between atoms, which can also affect reaction rates and selectivity. However, the effect of %V_Bur on yield will depend on the specific reaction and the other factors mentioned above.

There have been several studies that have investigated the correlation between steric index and %V_Bur with yield in chemical reactions. Generally, a higher steric index or %V_Bur is associated with lower reaction yield, as the bulky substituents can hinder the reaction from proceeding efficiently. However, this correlation is not always straightforward and can depend on the specific reaction conditions and substrates involved.¹² Overall, the relationship between steric index, %V_Bur, and yield in chemical reactions is complex and cannot be described by a simple correlation. It is important to consider these parameters in the context of the specific reaction and conditions being studied.

However, the correlation of %V_Bur with binding energy is more robust, and it has important implications for the design of new catalysts and materials with specific properties. The ability to predict binding energies based on steric considerations can lead to the development of more efficient and selective catalysts, as well as materials with higher adsorption capacities for carbon dioxide and other gases. As computational power and theoretical methods continue to advance, the applications of the %V_Bur index and other steric indices are likely to expand even further, leading to new discoveries and advances in various fields.

Initially, in 2003, %V_Bur values were employed to provide a qualitative understanding of trends observed in experimentally measured bond disruption enthalpies (BDEs) within a set of CpRu(NHC)Cl complexes, whose geometries were determined through DFT optimizations.²¹ The experimentally measured BDEs and DFT binding energies were qualitatively correlated with the %V_Bur values of the various NHC ligands. Depending on the nature of the metal, the metal is placed closer or farther from the linking atom of the ligand, and by extension of the whole ligand, either NHC or phosphane.^165,169 For example for metal-carbon distances ranging from 2.28 Å for nickel,²⁶ to practically 2.00 Å for ruthenium.¹⁷⁰ In 2009, apart from this parameter, with a set of DFT-optimized (NHC)Ir(CO)₂Cl complexes,²² the BE of the Ir–C bond was correlated to %V_Bur of the corresponding NHC ligand, and a new and better procedure to calculate %V_Bur, including Bond radii scaled by 1.17, sphere radius R = 3.5 Å and Ir–C distance at 2.10 Å, which parameters were not further modified since then, except for the latter. And, more importantly, from that moment, the calculation of %V_Bur through SambVca software was provided to the chemical community with open access via a web-based graphical interface accessible at the following URL: https://www.molnac.unisa.it/OMtools.php.¹⁷¹ This led to an explosion of use of this steric parameter by the world research community.

Even though, specially at the beginning, the %V_Bur was related to correlate with binding energies (BEs), since the ability to accurately predict BEs is of great importance for the design of new materials and devices with specific properties, the scope of %V_Bur expanded to many other properties and parameters. Moreover, even though electronic indices are more widely used, the reason to predominate could be under debate since: (1) they cost more to calculate computationally; (2) when multilinear regressions are performed, the weight of the electronics does not exceed 10% by weight, some of the sterics being so important that even having to include an electronic term is negligible.^172,173 However, it should be noted that this may be due to the fact that the steric index itself already includes part of the electronic content per se. Among the parameters used to include explicitly the electronic contribution of the NHC ligands in multilinear regressions, the difference of energy between the singlet ground state and the triplet,^22,116 or the energy of the frontier molecular orbitals, either the highest occupied molecular orbital (HOMO),¹⁷⁴ or the lowest unoccupied molecular orbital (LUMO),¹⁷² have been the most used. Obviously, excluding the electronic part facilitates the calculation, since only with the web server a researcher can get the results quickly, in less than a second, avoiding the need for knowledge in quantum computing. This has favoured applications in education,¹⁷⁵ in theoretical but also experimental catalysis.

One of the studies that was a total validation by %V_Bur came from the hand of Clavier and Nolan in 2010, when they correlated the BDEs of phosphanes,¹⁷⁶ surpassing even the results of the Tolman CA, almost specifically designed for this type of ligand. Fig. 2 shows how closely related are both indices for a series of phosphanes. In 2019 Jover and Cirera led to similar conclusions with an extended series of 119 phosphorous based ligands, expanding the correlations with reaction energy barriers in the Suzuki–Miyaura reaction.¹⁷⁷ Later on, still in the same type of reaction, as many other studies that used the steric maps to rationalize the reactivity in cross coupling reactions,^36,178,179 Fletcher and coworkers unveiled the catalytic cycle for the enantioselective Rh(i)-catalysed coupling of boronic acids and racemic allyl halides,¹⁸⁰ which facilitates the reactions with racemic substrates.

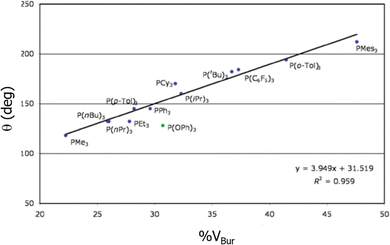Fig. 2 Correlation between the Tolman cone angle and the %V_Bur for a series of phosphanes. Reproduced with permission.¹⁷⁶ Copyright © 2010, Royal Chemical Society.

Focusing on NHC ligands, although studies were initially focused on complexes with Pd for cross-coupling reactions^181–183 and Ru,¹⁸⁴ particularly for olefin metathesis,^185,186 and also Rh¹⁸⁷ and Au,^188,189 the use was soon extended to any other imaginable metal,^24,190 take for instance Al or Ga,^191,192 and not at all important are the contributions in organocatalysis, particularly organopolymerization.^193–195 And next, to any type of ligand^153,154,196 or structure.¹⁴

5.4. Complementarities, limitations of %V_Bur

The %V_Bur parameter assesses the portion of the first coordination sphere encircling a metal centre that is taken up by the organic ligand. As %V_Bur emphasizes space occupation around the metal rather than specific attributes of a particular ligand class, it is applicable in constructing property–structure relationships for any catalyst or ligand category. For instance, this parameter has been employed to quantify ligand steric effects in high oxidation-state metal catalysis,¹⁹⁷ and, in conjunction with the Tolman cone angle, to elucidate the improvement of nickel catalysis in cross-coupling reactions through distant steric influences.¹⁹⁸ Thus, it allows combinations with other parameters.

Proposed catalyst descriptors often fall short by simplifying complex catalyst features into single numerical values. This disregard for the intricate chemical behaviour linked to the 3D shape of catalytic pockets is particularly relevant in asymmetric synthesis, where catalyst selectivity hinges on de-symmetrizing the catalytic pocket. Common descriptors like the Tolman CA or %V_Bur struggle to encompass these nuanced attributes but clash to reproduce them and cannot face the chemical behaviour tied to the 3D. As a result, researchers have sought alternative descriptors capable of representing the 3D catalyst shape. Some solutions include stereocartography, which maps areas of maximum asymmetry and have the capacity to unveil stereoselectivity of a chiral catalyst;^199,200 the accessible molecular surface, quantifying intrinsic steric properties of chelating ligands based on solvent accessible surface area;²⁰¹ and Sterimol steric parameters, a set of measures successfully portraying the size and shape of a ligand on a metal by gauging substituent dimensions along specific directions.^202,203 These methods are effective for quantifying catalytic pocket variations and establishing quantitative relationships between catalyst behaviour and structure. However, they lack the ability to provide a visual 3D representation of catalytic pocket shape.

In NHC ligands at some point some discrepancies appeared, with similar %V_Bur for two typical NHC ligands, SIMes and SIPr, when it was clear that the second should be more sterically hindered, and thus this pushed towards steric maps, and also explanations about the flexibility of the substituents on the imidazole ring.^204,205 One first approach in 2010 to solve this issue was a study by Cavallo and coworkers about the static and dynamic properties of 11 N-heterocyclic carbene (NHC) ligands within Ru complexes of the formula (NHC)Cl₂Ru=CH₂.²⁰⁶ Through dynamic trajectory analysis (see Fig. 3), it was evident that the flexibility of Ru complexes could vary significantly based on the nature of the N substituent. The N substituent opposite the Ru–ylidene bond was folded inwards to protect the vacant coordination position at the Ru centre. On the other hand, limited flexibility was observed for the N substituent situated beside the Ru–ylidene bond. For NHCs with a single ortho substituent, whether a simple Me or a bulkier i-Pr group, a preferred folding pattern was observed that bended the unsubstituted side of the ring toward the halide–Ru–halide plane.

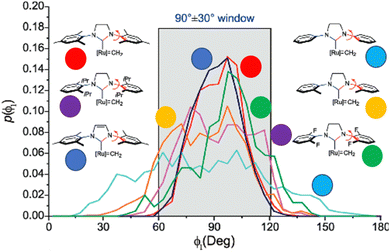Fig. 3 The φ₁ angle distribution for Ru based olefin metathesis catalysts ([Ru] represents the Ru(Cl₂)(PMe₃) unit. A value of φ₁ equal to 90° or −90° signifies configurations in which the aromatic ring of the N substituent is positioned perpendicular to the average plane of the NHC ring. Conversely, a value of φ₁ equal to 0° or 180° corresponds to configurations where the aromatic ring of the N substituent is aligned with the mean plane of the NHC ring). Reproduced by permission.²⁰⁶ Copyright © 2010, American Chemical Society.

This dynamic flexibility in terms of buried volume played a pivotal role, allowing NHCs to adjust their encumbrance around the metal to accommodate larger substrates. The phenyl N substituent can rotate almost freely, whereas rotation of the mesityl (or greater) N substituents is quite restricted (see Fig. 3). However, steric maps improved the latter analysis of the buried volume, uncovering distinct reactive pockets for NHCs with mesityl or 2,6-diisopropylphenyl N substituents. As %V_Bur can be considered to a simple number, it is sometimes not sufficient to explain the reactivity of a catalyst,²⁰⁷ or similarly to rule out on steric features that a catalyst is inefficient, for example comparing NHC-based catalysts ruthenium and iron.²⁰⁸

5.5 The evolution of %V_Bur to steric maps.

5.5.1. Steric maps. They are also known as steric field maps or electrostatic potential maps, are graphical representations of the three-dimensional distribution of electron density in a molecule. They are used to predict and visualize the interactions between atoms and molecules and to determine the reactivity of chemical compounds. Steric maps can be representations of molecular structures that highlight the three-dimensional arrangements of atoms and functional groups in a molecule.

The main advantage of using steric maps is that they provide a quick and easy way to visualize the spatial arrangements of atoms and functional groups in a molecule. This information can be used to predict potential interactions between a molecule and other biological or chemical entities, such as enzymes, receptors, or other drugs.

5.5.2. Steric maps by Cavallo. For all the arguments already mentioned above, and to be able to understand multidimensional realities, which could not be evaluated with parameters, and specifically the %V_Bur could not address, the context of %V_Bur parameter was moved to two-dimensional steric maps by Cavallo and coworkers, with the ability to understand asymmetry in the first coordination sphere around the active centre,²⁰⁹ generally the metal, by metal catalysts. On the other hand, amazingly, and importantly, as well, the notion of a catalytic pocket originated not in chemistry, but in enzymatic catalysis and has been well-established since Fischer's introduction of the lock-and-key model.²¹⁰ This concept readily extends to molecular transition-metal catalysts, where optimal catalytic activity and selectivity rely on matching shapes between the substrate and catalyst, both in enzymatic and synthetic catalysis. Nonetheless, tools for visualizing the shape of catalytic pockets in transition-metal complexes are surprisingly limited. The prevalent method involves generating a ball-and-stick or space-filling Corey–Pauling–Koltun (CPK) representation of the catalyst in a specific orientation to maximize catalytic pocket exposure.^211,212 However, these approaches face challenges in depicting distinctions between related systems, and they lack a quantitative depiction of the pocket surrounding the metal centre.

In this context, to unveil the rhodium-catalysed 1–4 addition,²¹³ in 2010 Cavallo, Dorta and coworkers introduced the concept of topographic steric maps,¹⁸⁷ which can be likened to geographical maps in the field of physicochemistry. These maps visualize the interaction surface between the catalyst and substrate(s), sculpted by the ligands within the complex. The numerical grid defining this surface allows for quantitative analysis. By setting the metal centre as a reference point akin to sea level and optimizing the complex's orientation for maximum metal exposure from above, altimetric contours provide a quantitative depiction of the catalytic pocket. Elevation from the metal centre is measured similarly to geographical features on physical maps.^12,187 A colour scheme, ranging from deep blue to dark red, can be employed to highlight regions within the catalytic pocket that can accommodate the substrate either above or below the “sea level”. In this context, elevation, depicted through isocontour lines, provides a numerical representation of the catalytic pocket's structure. Analogous to geographical maps, steric maps of the topography can be oriented towards specific hemispheres (north or south, east or west) or quadrants (such as northwest or southeast).

These concepts' evolution can be implemented by the catalysis community,¹² leveraging the downloadable source code from the SambVca web server for buried volume and steric map calculations under the GNU General Public License.¹⁷¹

One of the key applications of steric maps is in the field of drug design, where they are used to predict the potential interactions between a drug molecule and its target protein. By analysing the steric maps of both the drug and the target protein, researchers can identify areas of the molecule that may cause unwanted interactions, such as clashes with other parts of the protein or other drugs. This information can be used to modify the drug molecule to minimize these interactions and increase its efficacy.

Another important application of steric maps is in the study of protein–protein interactions, where they can be used to visualize the complex interactions between different proteins in a cellular environment. By analysing the steric maps of multiple proteins, researchers can identify potential interactions between proteins and design experiments to test these interactions.

Steric maps have also been used in the study of enzyme–substrate interactions, where they can be used to predict the interactions between an enzyme and its substrate. By analysing the steric maps of both the enzyme and the substrate, researchers can identify potential interactions between the two molecules and design experiments to test these interactions.

5.5.3. How to understand a steric map. To construct the steric map, the entire complex was positioned within a Cartesian framework. This involved placing a designated point at the origin, a second point along the z-axis, and a third point in the xz plane. These points corresponded to either an atom or the midpoint of a specific group of atoms. For instance, in Fig. 1d, the complex was aligned so that the metal centre occupied the origin, the midpoint between the two P atoms extended in the negative z-axis direction, and one of the P atoms lay in the xz-plane. Following the alignment of the complex, any atoms not relevant to the steric map calculations were removed. Subsequently, an analysis was performed on the first coordination sphere surrounding the metal. In the case of Fig. 1d, the PdMe₂ fragment was eliminated from the complex, and the analysis focused on the MeDuPhos ligand.¹⁴

In more level of detail, behind the steric steric maps, upon orienting the complex and excluding specific atoms, a sphere with a radius of R, centred at the origin, is divided into sections using a regular three-dimensional cubic mesh of spacing s.¹² This mesh defines cubic voxels (v). To ascertain whether any ligand atoms fall within the van der Waals distance of a given voxel's centre, the distance between the centre of each voxel and all the ligand atoms is calculated. If no atom is within the van der Waals distance, the voxel is marked as “free”; otherwise, it is marked as “buried”. Once all voxels within the sphere are designated as free or buried, the program scans the sphere's top (from positive z-values) to identify the z-value of the first buried voxel. This process yields a surface denoted as S(x,y) = z_B. This surface outlines the ligand's exposed area facing the incoming reactants, essentially defining the shape of the reactive pocket. Positive z_B values indicate that the ligands extend into the z > 0 hemisphere, the region where the reacting groups are situated. A visual depiction of the interaction surface between the catalyst and the substrate can be found in Fig. 1d. Lastly, the maps are straightforward two-dimensional isocontour depictions of the interaction surface S(x,y) = z_B, illustrated in Fig. 1d. By default, a sphere with a radius (R) of 3.5 Å surrounding the metal centre is utilized, and a mesh spacing of 0.1 Å is employed to survey the sphere for buried voxels. The van der Waals radii for atoms are sourced from the Cambridge Structural Database (CSD), with references provided in ref. 46. While hydrogen atoms weren't factored into the steric maps detailed in this study, the Web server database included the hydrogen radius from the Bondi set for alignment with CSD conventions.¹⁴⁶ Furthermore, radii not covered by these sources are standardized to 2.00 Å, followed by a scaling factor of 1.17, adhering to the CSD procedure. Currently, the steric maps presented herein are produced through the SambVca2.1 Web application. Since the graphical interface accommodates a maximum of 1000 atoms, the input files for generating the catalytic pocket of systems overcoming this number must be edited to exclude atoms. Take for instance, for the Amycalotopsis orientalis and the S221M/V223F/Y359A mutant of Streptomyces coelicolor, sourced from Protein Data Bank entries 2R5V and 3ZGJ respectively, were edited to exclude atoms situated more than 15 Å from the metal centre.¹² Following this adjustment, the steric maps were generated uploading the modified files.

Determining the appropriate size for the first coordination sphere prompts the question: “What Is the Optimal First Coordination Sphere Size?” In the analyses discussed earlier, a sphere encompassing the metal centre with a radius of 3.5 Å was consistently applied. However, this is particularly valid for transition metal catalysts. The chosen 3.5 Å radius holds significance as it was found optimal for correlating the DFT dimerization energy of 33 N-heterocyclic carbenes in the Wanzlick equilibrium.²² This value also demonstrated robustness in explaining a substantial amount of experimental data. Considering that typical bond distances between metals and ligands fall within the range of 2.0 to 2.5 Å, the utilization of a 3.5 Å radius to define the metal's first coordination sphere is expected to encompass the approximate van der Waals volume occupied by coordinated metal atoms. While this radius is the default choice, it is acknowledged that different studies might benefit from different values. For instance, surfaces, biological applications, bimetallic systems, where reactivity occurs between substrates connected to two distinct metal atoms, require a different protocol, and enlarge the size.

A similar outcome is observed when assessing the catalytic pocket of the metal organic framework (MOF) at radii of 3.5 Å and 6.0 Å, as shown in Fig. 4.¹⁴⁸ Despite these variations, this methodology has consistently succeeded in characterizing the overall asymmetry and contour of the catalytic pocket, regardless of the radius. However, it is important to note that for situations where bulkiness is not influenced by groups directly bound to the metal, a larger radius becomes essential to comprehensively capture the catalytic pocket's shape.

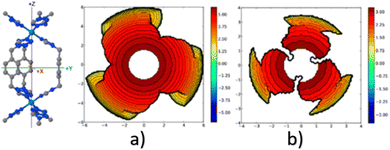Fig. 4 Steric maps (plane xy) of the cavity of a MOF of iron, with a radius (a) 3.5 Å and (b) 6.0 Å. The centre of the MOF is at the origin, and the iron atoms are on the z axis. The isocontour curves of the steric maps are given in Å. Reproduced with permission.¹⁴⁸ Copyright © 2018, American Chemical Society.

The steric maps of Cavallo and coworkers introduced SambVca 2,¹² a freely accessible web application designed to generate topographic steric maps that describe the catalytic pocket encircling a metal centre in various types of transition metal complexes. SambVca 2 features a user-friendly graphical interface, and it not only computes the buried volume steric descriptor but also serves as a full replacement for its predecessor, SambVca 1. These descriptors, the buried volume, and the topographic steric maps are designed to be adaptable across different systems, enabling the compilation of a comprehensive atlas spanning all ligand classes. They are also user friendly because the web server accepts different types of files, with format of X-ray,^214,215 or any computed structure,^33,216 even a designed structure with a building molecule package would lead to reasonable results.

In 2011, adhering to a similar approach, Houk, Montgomery, and Liu devised a method to visualize hindrance around a catalytic centre.²¹⁷ They utilized a graphical representation based on two-dimensional ligand steric contour maps, where contours indicate the distance between the ligand's van der Waals surface and the substrate. This approach was first employed to elucidate the reversal of regioselectivity in reductive couplings of alkynes and aldehydes catalysed by Ni–NHC complexes. More recently, Liu and Montgomery applied the same method to rationalize simultaneously the regio- and enantiocontrol in the same reaction when employing a novel class of highly hindered, enantiopure tailored NHC ligands.²¹⁸

Overall, steric maps are a powerful tool for predicting the steric effects on the reactivity and selectivity of chemical reactions, and they have found wide applications in various areas of chemistry, including organic synthesis, catalysis, and materials science. The method provides a quantitative measure of the steric hindrance in molecules and materials, allowing for a better understanding of their steric and electronic structure and reactivity. The applications of steric maps discussed in this article demonstrate its utility in the design of new catalysts and materials with specific steric and electronic properties, and its potential for advancing the fields of chemistry and materials science.

As computational power and theoretical methods continue to advance, the applications of steric maps are likely to expand even further, leading to new discoveries and advances in various fields. For example, in ionic liquids the steric maps have been able to understand the carbon dioxide,²¹⁹ fixation being the ionic liquids, not simple spectators, but the main protagonist. Moreover, the method may be applied to study the steric and electronic properties of new classes of materials, such as MOFs and porous organic polymers (POPs),¹⁴⁸ which have attracted significant attention due to their potential applications in gas storage, separations, and catalysis.

5.6. Beyond the limits of the steric maps

Steric maps may be combined with other theoretical methods, such as density functional theory and molecular dynamics simulations, to gain a more comprehensive understanding of the properties and reactivity of molecules and materials. This will allow for the development of more accurate and predictive models for the design of new catalysts, materials, and devices.

To sum up, the applications of steric maps developed by Cavallo and coworkers have provided significant insights into the steric and electronic structure of molecules and materials,¹² allowing for the design of new catalysts and materials with specific properties. As the method continues to advance, it has the potential to revolutionize the fields of chemistry and materials science, leading to new discoveries and advances in various areas. Despite the clear qualitative character of steric maps,^220,221 still currently to quantify, the %V_Bur index must be used to quantify,^{174,222–224} or in combination,^{31,219,225,226} preferentially because it covers both quantitative and qualitative aspects.

To demonstrate the versatility of steric maps of Cavallo and coworkers as a flexible instrument capable of offering a distinctive representation of nearly any ligand employed in homogeneous catalysis, they were utilized with a range of common ligands frequently found in organometallic chemistry. Embracing the principles akin to Tolman and Sterimol methodologies, the fundamental concept guiding the creation of topographic steric maps lies in their inherent user-friendliness, assuming a crystallographic or computationally determined structure is accessible.

In addition to providing a visual representation of the catalytic pocket, the steric maps of Cavallo and co-workers also serve as distinctive markers for transition metal complexes. This can be illustrated with a series of important chiral ligands in catalysis,²²⁷ since in the complexes where they participate they are recognized to induce enantioselectivity in several well-established reactions, such as Diels–Alder cycloadditions, Michael and Mukaiyama–Michael additions, Heck and asymmetric hydrogenations. Among them, bisoxazoline and binaphthyl ligands within C₂ symmetric complexes and a phosphinooxazoline ligand within C₁ symmetric complex. In detail, a straightforward visual examination of the ball-and-stick or CPK structures of those three complexes does not readily facilitate a comparison of these different systems. Conversely, the steric maps not only distinguished between the individual complexes but also provided an intuitive indication of how various ligands shape the catalytic pocket differently.¹² For instance, the slender bisoxazoline ligand occupies space around the equator of the catalytic pocket, with upward-facing t-butyl groups creating relatively gentle protrusions in the south-western and north-eastern quadrants. In contrast, the complex with a binaphthyl ligand forms a groove from the north-west to the south-east, akin to the former complex. The notable differences lie in the naphthyl groups of the binaphthyl ligand, which cover the bottom of the catalytic pocket in the north-western and south-eastern quadrants, along with the enhanced hindrance caused by the phenyl groups in south-western and north-eastern quadrants. The catalytic pocket of the complex with the monodentate phosphinooxazoline ligand can be seen as a combination of both the two previous complexes, resembling the western hemisphere with the bisoxazoline and the eastern hemisphere of the binaphthyl. Consequently, the %V_Bur values indicate that the complex containing the binaphthyl has a significantly larger %V_Bur than with bisoxazoline, while the monodentate falls in between in terms of %V_Bur.

And the final goal of steric maps actually is the first aim that was thought for them. In detail, steric maps should also serve as valuable tools for catalyst design by facilitating the evaluation of the impact of structural modifications. In this sense, Bertrand and collaborators synthesized cyclic (alkyl)(amino)carbenes containing a six-membered backbone (CAAC-6).²²⁸ In comparison to their counterparts with a five-membered structure (CAAC-5), these carbenes exhibit increased %V_Bur and enhanced donor and acceptor properties, as demonstrated by the observed n → π* transition extending into the visible spectrum. Their pronounced ambiphilic nature enables the carbene to insert intramolecularly into an unactivated C(sp³)–H bond. As ligands, they demonstrate superior performance over the five-membered analogues in the palladium-mediated α-arylation of ketones using aryl chlorides. However, the use of %V_Bur and steric maps was preceded by former experimental work, involving CAAC-5 Pd-complexes revealed that featuring unhindered ethyl substituents, lacked the ability to catalyse the α-arylation reaction. In contrast, complexes incorporating a bulky substituent in place of ethyl groups, displayed high reactivity with the less sterically demanding chlorobenzene. However, the latter catalysts exhibited reduced reactivity when faced with bulkier aryl chlorides like o-chlorotoluene or 2-chloro-m-xylene.²²⁹ Thus, a combination of experiments and topographic maps enhanced the race for a new generation of efficient catalysts. And Szostak and coworkers increased even more the sterical hindrance of CAAC ligands, reaching the CAAC–IPr* ligand,²³⁰ catalytically proved for Cu-catalysed hydroboration of alkynes (Fig. 5). In detail, with the %V_Bur of 49.5% and 49.4% for [Cu(IPr*–CAAC^Me)Cl] and [Cu(IPr*^MeO–CAAC^Me)Cl], respectively, represented the bulkiest CAACMe ligands, for example, comparing the first with the homologous with the IPr ligand, the %V_Bur drops to 41.9%. Anyway, the values for the CAAC–IPr* ligands are still lower than the value of 52.1% for the catalyst [Cu(IPr*)Cl].

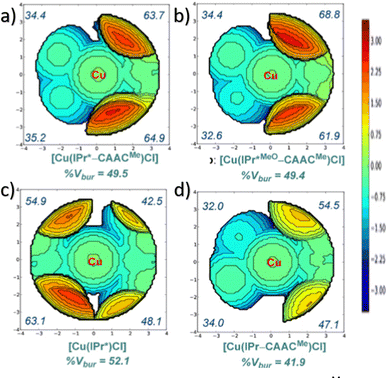Fig. 5 Steric maps of (a) [Cu(IPr*–CAAC^Me)Cl], (b) [Cu(IPr*^MeO–CAAC^Me)Cl], (c) [Cu(IPr*)Cl], and (d) [Cu(IPr-CAAC^Me)Cl] showing %V_Bur per quadrant. Adapted with permission.²³⁰ Copyright © 2022, Royal Chemical Society.

We can relate %V_Bur and steric maps to computational chemistry, but from the beginning it was created with the desire to go beyond the boundaries of computational chemistry, and reach all of chemistry, but this was not enough either, and it was reached physics and biology.

At the executive level, how would this be done? therefore facilitating its use and with any structure optimized with computational calculations these tools would be valid, but also with X-ray diffraction, and at an informative level it was intended not to have to make use of hydrogens because in this experimental technique they cannot be detected It must be said that the agreement with or not the inclusion of hydrogen atoms did not reduce precision in the correlations where they could be involved, sending the message that their weight is overestimated, and in fact, heteroatoms are the agents that mark the steric hindrance.

But if that was not enough, i.e. ignoring the hydrogen atoms, these tools would be almost as valid simply with structures created by hand using pre-parameterized bonds, from any molecule building software, protein building, or of materials.

6. Fields of practical utility of %V_Bur and steric maps

First of all, it must be said that among the applications only a minimal summary of these can be reached, since today there are already more than 2000 works that have made use of the %V_Bur concepts or steric maps, and that have cited the pioneering works by Cavallo and collaborators. And those studies that use them in combination with other indices or steric tools are particularly interesting, and validate them, or especially refute them, not only to know what the positive aspects are, but above all to visualize what their limitations are.

The concepts of steric maps and %V_Bur have uses in all the range of computational chemistry. Thus, knowing about computational chemistry is an interdisciplinary field that combines chemistry, physics, mathematics and computer science to develop and apply computational methods to study chemical systems, to distinguish what are the hot topics in computational chemistry is intriguing, and in all there is potential participation, thus let's summarize them in the following list:

6.1. Sterical hindrance of ligands

The main use of %V_Bur and steric maps is simple quantification of the steric hindrance that a particular ligand causes at the metal centre, and especially if there is asymmetry the steric maps and %V_Bur by quadrants gain weight. In summary, it is about describing how the size of a ligand affects, that is, how it is arranged in space. Most of the papers are related to NHC ligands, and in particular ligated to ruthenium,^206,231 copper,^232,233 gold,²³⁴ and palladium,^178,235 but actually, the most important actor is the ligand itself,^24,236 and the metal simply can tune a bit its flexibility. There is a tendency to think that the rule that the more sterically a ligand is, the worse is the resulting catalysis. But we could give many counterexamples that this is not the case. There are different reasons, either because it blocks a coordination of an additional ligand, because it leaves the perfect cavity in the first coordination sphere around the metal to interact with the substrates, and actually, it is common then that the most sterically protected metal centre is the most effective catalytically.^237,238

Take for instance, the IPr* (1,3-bis(2,6-diisopropylphenyl)imidazol-2-ylidene) ligand represents a sterically hindered ligand compared to the common IPr (1,3-bis(2,6-diisopropylphenyl)imidazol-2-ylidene), however Nolan, Szostak and coworkers unveiled that in most of the cases the catalytic performance is better for the first NHC ligand in cross coupling reactions,^239,240 despite the origin of IPr* in 2012 by Nolan was devoted basically only to selectivity, and steric maps unveiled that the increase of %V_Bur was not fundamental,²⁴¹ but also the asymmetry of each quadrant unveiled by the steric maps (see Fig. 6).²⁴² Through the utilization of density functional theory some scenarios were delineated in which the NHC ligand assumes an active role and instances in which it merely acts as an observer. Alternatively, its modification does not yield substantial alterations to its catalytic function or performance. Actually, the differentiation of the maps, as well as the %V_Bur is much greater for the free ligands than when they are in the complex. In fact, in the same study, maps are also provided without the ligand trans to NHC, which is dissociated by olefin metathesis catalysis. But the conclusion of this and other studies is that it is better to do the steric study of a ligand with the conformation of the complex,^14,242 since the flexibility exists.

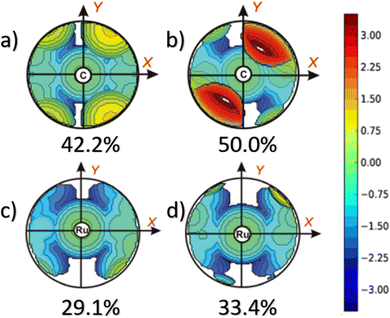Fig. 6 Steric maps and %V_Bur of the free (a) IPr and (b) IPr* NHC ligands, and in the ruthenium dichloride indenylidene complexes for (c) IPr and (d) IPr* NHC ligands. The isocontour curves of the steric maps are in Å. The xz plane is the mean plane of the NHC ring, whereas the yz plane is the plane orthogonal to the mean plane of the NHC ring, and passing through the carbene C atom of the NHC ring. The carbene C atom of the NHC ring is at the origin. Reproduced with permission.²⁴² Copyright © 2013, Royal Chemical Society.

The next IPr# by Szostak and coworkers even increased more the sterical hindrance,²⁴³ up to the limit in terms of NHC ligands. And in 2016, Michalak, Poater and coworkers in 2016 an efficient and readily scalable process involving NHC-copper(I) halide catalysis for the addition of terminal alkynes to 1,1,1-trifluoromethyl ketones,²³² in an aqueous environment for the first time. Utilizing DFT calculations, the relationship between the catalytic alkynylation yield and the sterics of N-heterocyclic carbenes (NHCs), represented by buried volume (%V_Bur), is elucidated. The findings underscore the predominant influence of steric effects on the reaction yield, the kinetic cost being lower the greater the steric hindrance of the NHC ligand. The reason is not a reduction in the relative energy of the rds but of the rate determining intermediate (rdi).⁹⁷

But after these last 2 decades with supremacy of NHC ligands in organometallic catalysis, particularly due to the strong donation of σ in combination with an adjustable steric environment, it has not meant stagnation, since recently Szostak and coworkers for example have generated thiazol- 2-ylidenes,²⁴⁴ which are competitive to NHCs. The thiazole heterocycle and enhanced π-electrophilicity are shown to result in a class of highly active carbene ligands for electrophilic cyclization reactions to form valuable oxazoline heterocycles, and this transformative process has been partly mapped sterics, which have helped to locate the structural differences between both types of ligand.

Moreover, switching to pincer based catalysis, and in particular, to the Overman rearrangement reaction with a gold catalyst, achieving precise spatial control in gold catalysis presents inherent challenges due to the linear coordination nature of Au(I) and the generally planar ligands adopted by Au(III) complexes. Klein and coworkers introduced a novel (NNN)_diiPrAu–OH complex characterized by sterically hindered properties, suggesting the potential of the (NNN) ligand framework to interact steric interactions with substrates through its strategically positioned aryl groups.²⁴⁵ To explore these steric aspects in greater depth, variations in the ortho-substituent of the aryl group in (NNN)_xAu–Cl complexes allowed to manipulate the buried volume surrounding the Cl atom, and this variation was subsequently correlated with yields achieved in an Au-catalysed Overman rearrangement. Thus, the (NNN) pincer ligand was announced as an attractive platform for efficiently designing Au(III) complexes with the potential for stereoselective catalysis. On the other hand, the NNN pincer ligand was also ligated to ruthenium by Milstein and coworkers to carry out the reforming of aqueous ethylene glycol to glycolic acid and molecular hydrogen as a green subproduct.²⁴⁶ Indeed, the planarity of pincer ligands makes them excellent candidate ligands for using steric maps and %V_Bur,²⁴⁷ to elucidate how hindered the reactivity of their metal centre will be.

Cavallo, Rueping and coworkers in 2020 introduced a regiodivergent protocol for the cleavage of C–O bonds using magnesium catalysis.²⁴⁸ Employing readily accessible magnesium catalysts, this method achieves the targeted hydroboration of diverse epoxides and oxetanes (see Fig. 7a), leading to the formation of secondary and tertiary alcohols with exceptional yields and regioselectivities. The selectivity towards 2,2-disubstituted epoxides was achieved for 13 examples, whereas the other 42 led to excellent enantiospecificity. Detailed mechanistic investigations along with DFT calculations shed light on the unanticipated regiodivergence observed in the reaction. Essentially, the steric maps of the coordinated epoxide intermediate, i.e. the rdi depicted in Fig. 7b, reveal a predictable observation: the western quadrants containing the unaltered carbon atom of the epoxide exhibit lower hindrance compared to the eastern quadrants housing the substituted carbon atom (Fig. 7c).

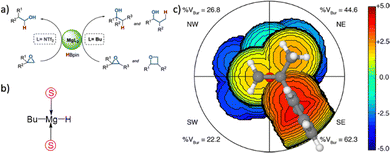Fig. 7 (a) Regiodivergent ring opening of epoxides. (b) Rate determining intermediate and (c) its steric map including the %V_Bur of the quadrants (The origin is set at the midpoint of the C–C bond within the epoxide, and the O atom of the epoxide is positioned along the Z-axis. The scale of the steric contours is included in Å). Adapted with permission.²⁴⁸ Copyright © 2020, American Chemical Society.

6.2. Selectivity in catalysis

Steric maps serve to highlight the catalyst's exposed surface facing the substrate, which can then undergo a more comprehensive analysis to uncover the physicochemical attributes of the catalytic pocket.^249–251 For instance, scrutinizing the catalytic pocket solely through its steric attributes falls short in elucidating the enantioselectivity in the asymmetric 1,4-addition of phenylboronic acid to 2-cyclohexenone, resulting in chiral 3-phenylcyclohexanone, driven by Rh-catalysts led by Dorta and coworkers.¹⁸⁷ With two catalysts exhibiting remarkable enantioselectivity, with enantiomeric excesses of 90% and 99%, the great performance of the first was anticipated, however the even higher enantioselectivity of the second was unexpected, and posed a conundrum, considering that the enantioselective induction is expected to be influenced by the small, upward-oriented S=O moieties. Investigating the catalytic pocket through its steric characteristics confirmed the marked asymmetry of the catalytic pocket of the first, exhibiting a groove aligned from northwest to southeast shaped by the upward-oriented p-tolyl groups. Computational analysis validated that the preferred transition state accommodates the reacting groups within this groove. Conversely, the steric map of the second portrays a notably flatter catalytic pocket, implying that the heightened enantioselectivity exhibited is not solely driven by steric effects. Here, expanding the assessment to the surfaces of the catalytic pockets, based on the steric maps using electrostatic potentials derived from DFT calculations, yields an alternative perspective on the two catalysts. Remarkably, the electrostatic potential map of the catalytic pocket of the best displays marked asymmetry, featuring areas of highly negative electrostatic potential near the S=O moieties. Conversely, the electrostatic potential map of the less good is more uniform. Consequently, the electrostatic map of both catalysts shares a resemblance in shape.¹⁸⁷ The favoured transition state once again positions the reacting groups within the northwest to southeast groove, which, in this instance, is influenced by the electrostatic potential on the catalytic pocket's surface. In summary, employing steric maps to visualize catalytic pockets and characterizing their surfaces with a broad property such as electrostatic potential enables the elucidation of the origins of the stereoselectivities exhibited by this pair of catalysts.

Aiming to predict and understand how different structures influence reactivity, Doyle and coworkers introduced a versatile and quantitative method for classifying reactivity differences,²⁵² known as 'reactivity cliffs,' in 11 sets of chemical reactions involving Ni and Pd catalysts. These reactions utilize monodentate phosphine ligands. The study revealed a distinct molecular descriptor, termed ‘minimum percent buried volume [%V_Bur(min)]’, which effectively separates the datasets into regions of high and low reactivity using a consistent threshold in cross-coupling catalysis. Experimental investigations on organometallic systems show that this threshold aligns with whether the metal is doubly or singly bound to ligands, and that %V_Bur(min) provides a valuable predictive insight into ligand behaviour in catalytic processes. Thus, %V_Bur can put the threshold in any catalytic reaction to predict if it will be or not feasible, and it is also a tool to discriminate between families of substrates to interact with the metal centre, either by the total number or by quadrants.²⁵³

Stereoselectivity plays an important role in some chemical reactions, particularly in polymerizations involving a semi-chiral monomer.²⁵⁴ Under these circumstances, the steric index around the active catalytic centre, where the living polymer chain is growing, dictates the stereoregularity of the final polymer.²⁵⁵ It helps to design new efficient catalysts that subsequently lead to major advances in the development of either homogeneous or heterogeneous catalysts for semi-chiral derivative polymers, such as polyolefins.

In 2023, Osuna, Bietti, Costas and coworkers used the steric maps to enhance the enantioselective hydroxylation at unactivated tertiary C–H Bonds.²⁵⁶ Here, the challenge of achieving those enantioselective C–H oxidations has been endeavoured. In detail, the hydroxylation of tertiary C–H bonds within cyclohexane structures using H₂O₂ as the oxidant combined with a manganese catalyst, exhibited a structural congruence with the substrate, much like the lock-and-key recognition mechanism observed in enzymatic active sites. Theoretical calculations in this project by molecular dynamics simulations is the right tool to understand the behaviour of those catalysts in solution and at interfaces. They revealed that the enantioselectivity observed is a consequence of the precise fitting of the substrate's scaffold into the catalytic site. This fitting was accomplished through a network of weak non-covalent interactions that are complementary in nature. This enantioselective process leads to stereoretentive C(sp3)–H hydroxylation, enabling the generation of multiple stereogenic centres within the molecule in a single step—up to four in number. These centres can be individually controlled and manipulated using conventional methods, offering a streamlined approach to access a range of chiral frameworks from a single precursor. The importance of the binding pockets is thus described by the steric maps leading to simple images that help to understand how the substrate interact, and even can be expanded to chirality.²⁵⁷

6.3. Reactivity in catalysis

Since copper-catalysed atom transfer radical polymerization (Cu-ATRP) is a widely utilized technique for controlled radical polymerization,²⁵⁸ extensive research into its mechanisms had been performed. And in 2019, the crucial transition states governing the activation and deactivation of the polymer chain during Cu-ATRP were computationally explored by Coote, Matyjaszewski, Peng and coworkers.²⁵⁹ They covered the gap to understand how ligands and initiators influence these processes. This study introduced the first computational investigation into the activation transition states of Cu-ATRP, shedding light on factors that impact activation and deactivation rates. Unusually, the bromine atom transfer between the polymer chain and the Cu catalyst occurs through a bent geometry, involving significant interactions between the polymer chain end and the catalyst's ancillary ligand. This interaction complexity dictates activation and deactivation rates, controlled by both the Cu catalyst's electronic properties and steric repulsions between the ligand and initiator. Furthermore, the flexibility of the ligand backbone was found to be pivotal in activation. Through theoretical analyses, three important descriptors were identified: catalyst's HOMO energy (E_HOMO), percent buried volume (%V_Bur), and catalyst distortion energy (ΔE_dist), capturing electronic, steric, and flexibility influences on reactivity, respectively. These descriptors were then correlated with experimental activation rate constants using multivariate linear regression, yielding a reliable predictive model for ligand effects on reactivity. Validation using various ligands demonstrates an average error of under ±2 kcal mol⁻¹ compared to experimentally derived activation energies. The same methodology was extended to predict the reactivity of different alkyl halide initiators, using descriptors of bond dissociation energy (BDE) and Cu–X halogenophilicity. Thus, the digital rendition of the steric map, represented as an array of points defining the surface in Cartesian space, holds potential as a digital steric descriptor for applications like multilinear regression analysis.^260–263 And thus, it could also be incorporated into workflows designed for high-throughput screening of novel catalysts using ML methodologies.²⁶⁴ Even though in most of cases the %V_Bur is a perfect structural tool/parameter to correlate with a series of data, experimental or computational,^265–267 it is also necessary to be honest in recognizing that it does not seem that the %V_Bur is one of the variables with the best behaviour in terms of the reproduction of the structural and/or steric part,^61,268,269 with preference for the Tolman electronic parameter (TEP),^270,271 and sometimes the bond distances²⁶⁸ and angles can be a better choice.^61,269 And particularly, in the activation of the C–O bond of the allylic alcohol, catalysed by palladium, the multiple linear regression analysis does not use as a variable either the %V_Bur or the C–O bond distance but the angle with the metal.²⁶⁹ Actually, most of the studies base the use of steric maps, independently of the catalytic reaction under study, and based on the cleft on the metal centre, where the substrate should interact, as Gramage-Doria and coworkers have developed with non-biological catalysts that mirror enzyme principles.²⁷² These catalysts typically possess adaptable molecular recognition sites for substrate binding, often following conformational selection pathways. The catalyst comprised an inflexible substrate-recognition site stemming from a zinc-porphyrin in the second coordination sphere. Thus, the catalytic pocket is the aim of steric maps,^273,274 and the lability of the ligands is also fundamental, because if it is easy to dissociate a ligand, take for instance a chloride, the sterical hindrance on the metal centre drops automatically.²⁷⁵ In 2020, Occhipinti, Jensen and coworkers unveiled the Z-selectivity in olefin metathesis of monothiolate ruthenium indenylidene catalysts.²⁷⁶ The study is very simple, it was the replacement of a pyridine ligand by a thiolate ligand (see Fig. 8a). To further investigate the steric influences of the thiolate, a comparison was made between the %V_Bur of 95.0% for its active species, after removing a pyridine ligand (see Fig. 8b), and its corresponding dichloride (without pyridine, as well). The results indicate a substantial contribution of the thiolate to the overall steric congestion, with a %V_Bur value of 86.4% for the dichloride catalyst. Interestingly, a minor portion of this difference arises from the sulphur atom itself, signifying the effect of replacing chlorine with sulphur. Upon solely considering ruthenium and the atoms directly bonded to it, the %V_Bur values were slightly larger again for the thiolate (67.7%) in comparison to the dichloride (67.0%).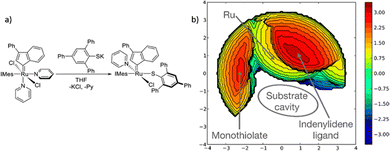

Fig. 8 (a) Synthesis of the thiolate Ru based catalyst and (b) its steric map. Adapted with permission.²⁷⁶ Copyright © 2020, American Chemical Society.

6.4. Macromolecular chemistry

One instance of catalyst design through the comparative analysis of catalytic pockets within related complexes can be observed in the advancement of chelating ligands tailored for the Pd-catalysed copolymerization of ethylene with olefins possessing a polar functional group. Presently available catalysts encounter a limitation in selectively producing high-molecular-weight linear polymers, a drawback that prompts the need for improvement. Additionally, the conventional approach of augmenting molecular weight in olefin polymerization—by inhibiting the chain termination reaction through heightened steric hindrance around the active centre of the catalytic system—cannot be readily applied.^277,278 For instance, the straightforward enhancement of steric hindrance in the substituents on the P atom of a phosphinesulfonato Pd–ligand in prototype Drent-type catalysts, aimed at the copolymerization of ethylene with higher and bulkier olefins, leads to a significant reduction in the incorporation of the co-monomer. This decrease occurs due to the proximity of this steric hindrance to the coordinated monomer, illustrating the complex considerations needed for catalyst design.

Carrow and collaborators addressed this dual challenge by formulating Pd catalysts featuring a chelating P(V)–P(III) ligand founded on a phosphonic diamide-phosphine (PDAP) motif.²⁷⁹ This PDAP framework offers distinct electronic attributes along with the capacity for controlled modulation of steric hindrance by adjusting the bulkiness of the substituents positioned distantly from the coordinated monomer. This modulation aims to maintain efficient rates of co-monomer insertion.

Initial assessment of steric hindrance in the crystallographic structures of Pd-complexes revealed that the compound, encompassing the prototype PDAP ligand featuring a diisopropyl, phosphonic diamide group, exhibited notably elevated steric hindrance in contrast to other prevalent ligands like the carboxylate-based ligand or the di-tert-butyl phosphine oxide ligand. Moreover, a visual examination of the catalytic pocket highlighted that the PDAP ligand imposed hindrance on the O-oriented side of the complex (western hemisphere), while its influence on the P-oriented side, adjacent to the coordination position available for the incoming monomer in the eastern hemisphere, remained minimal. This analysis led to the conclusion that altering the amine substituents in the PDAP ligand could serve as a viable avenue for manipulating the polymerization behaviour of the catalyst.

Subsequent evaluation of the catalytic copolymerization performance of Pd complexes harbouring an array of distinctively substituted PDAP ligands enabled the identification of complexes, which emerged as potent catalysts for the copolymerization of ethylene with polar vinyl monomers, leading to the synthesis of high-molecular-weight copolymers (with molecular weights reaching up to 105 g mol⁻¹).

On the other hand, Falivene and Cavallo in 2017 discussed the guidelines to select the right NHC for the organopolymerization of monomers with a polar group. The report is based on the DFT stability of zwitterion and spirocycle adducts of polar monomers and free NHCs. The conclusion is that apart from the sterical hindrance of the NHC, the singlet–triplet energy gap of the NHC, with particular needed energy gaps leading to zwitterionic adducts and spirocycle adducts when using large or low energy gaps, respectively. In addition, apart from explaining the current systems, the analysis of 45 NHC/monomer pairings the study led to a framework for anticipating the behaviour of novel NHC/monomer combinations, even though to date those data have not been tested experimentally, in a clear example that computational and experimental results should go together, and following this order,²⁸⁰ as suggested by predictive catalysis/chemistry,⁶⁴ and machine learning on chemistry. And still in polymerization, Talarico and coworkers in 2023 combined the steric maps and %V_Bur concepts with the energy decomposition analysis using the associated activation strain model (ASM) and this led to unveil the origins of the stereoselectivity for propene polymerization promoted by pyridylamido-type nonmetallocene systems.²⁸¹ The correlation between the precise modification of the ligand and the resulting stereoregularity in propene derived polymers was systematically elucidated. This encompassed factors such as the size of the metallacycle, the nature of the bridge within the molecule, and the substituents located at the ortho-position of the aniline fragments. Utilizing a combination of DFT calculations and %V_Bur together with steric maps, the calculated outcomes aligned with the experimental trends. Notably, it was observed that introducing substituents to the bridge or the ortho-positions of the aniline units amplified the level of stereoselectivity. Through an analysis known as the ASM–NEDA analysis, a dissection of the steric and electronic influences was achieved.²⁸² This detailed examination underscored the manner in which subtle modifications to the ligand could exert an impact on the stereoselectivity of the propene transformation process, and by extension for 1-decene oligomerization the use of steric maps could unveil the role of group IV diamine bis(phenolate) catalysts.²⁸³

Overall, it must be assessed that quantitatively the use of the concepts of steric maps is frankly focused on ligands such as NHCs,^24,65 but especially the explosion has come in the reproduction of catalytic surfaces where simple polymerization,^284,285 or hydrogenation reactions take place.^31,149

6.5. Computational studies

Quantum computing has the potential to revolutionize computational chemistry by enabling the simulation of large, complex chemical systems that are currently beyond the capabilities of classical computers. And although the %V_Bur is referred to experiments, in most cases it has been used in pure computational studies. Chen and coworkers linked the Extended Transition State-Natural Orbital for Chemical Valence-method (ETS-NOCV) with (L)W(CO)₅, where L = amines or phosphanes,²⁸ with the carbonyl stretching frequencies and %V_Bur, and resulting with the estimation of the σ-donor and π-acceptor abilities of phosphines from experimental observables. However, in other cases the uses of %V_Bur is performed by experimentalists directly,^286,287 and actually this one of the aims of the developers of those tools, to be used by any researcher.^12,14,22 Take for instance, in 2018 Neidig and coworkers used those tools to characterize the reactivity of (NHC)Fe(1,3-dioxan-2-ylethyl)₂ complexes, because of the NHC ligand, linking the major structural perturbations observed crystallographically.²⁸⁷ And luckily, the trend is to bring together the two approaches, experimental and computational, in most recent studies.²⁸⁸ When the two approaches are really complementary it is more challenging, when both cover different aspects. In 2017, Naumann, Falivene and coworkers could explain the role of N-heterocyclic olefins (NHOs) in polymerization of (meth)acrylic monomers.²⁸⁹ Experimentally, this research focused on the zwitterionic organopolymerization of four acrylic monomers, facilitated by NHOs, i.e. the neutral initiators. Imidazole-derivatives were found to efficiently polymerize the selected monomers, while other derivatives like imidazoline and benzimidazole showed different behaviour. Without additives, the polymerization reactions lead to relatively uncontrolled results, producing mostly atactic material. However, when a μ-type ligand like LiCl was introduced, acrylamide polymerization becomes significantly more efficient, resulting in highly isotactic acrylamides with substantial molecular weight. On the other hand, using computational tools like DFT, the study delved into the intricacies of zwitterionic chain growth and competing reactions such as spirocycle and enamine formation. NHOs with unsaturated backbones were better suited to support zwitterionic chain growth, with spirocycles acting as inhibitors that slow down but did not fully halt polymerization. In contrast, enamine formation acted as an irreversible termination point and was energetically preferred. By introducing specific substitutions on the exocyclic carbon of the NHO structure, certain pathways that favour controlled polymerization were identified. Notably, the research established a relationship between initiation energy barriers, buried volume (%V_Bur), and the Parr electrophilicity index.

6.6. Material and surface science

Computational chemistry together with steric maps are being used to design and optimize new materials for a wide range of applications, including energy storage, catalysis, and electronics. Steric maps have also found applications in the field of materials science, particularly in the design of new materials with specific steric and electronic properties. One of the major advantages of steric maps is that they allow for the prediction of the steric hindrance and electronic structure of complex molecules and materials, providing insights into their properties and reactivity. For instance, in a study by Shams et al., they focused on the hydrofinishing of polyalphaolefins (PAOs) through hydrogenation.³¹ The effectiveness of using halloysite clay as a support for immobilizing Pd nanoparticles in the development of efficient catalysts under mild conditions was explored, simply screening the environment of the metal centre.²⁹⁰ The research delved into the impact of halloysite's hydrophobicity on the efficiency of PAO hydrofinishing. To adjust the hydrophobicity of the Hal surface, cetrimonium bromide was employed. Experimental findings indicate that the presence of CTAB reduces the catalyst's activity and computationally by steric maps (Fig. 9), the presence of cetrimonium bromide on the first sphere of palladium reduces its capacity to allocated molecular hydrogen or even worse, the olefins. The %V_Bur jumped from 64.5 to 87.1% when the cetrimonium bromide was added. This predictive catalysis exercise is valid to save experimental efforts, in analogy with other studies.²⁹¹ On the other hand, steric maps could also scrutinize in olefin polymerization the role of the common cocatalysts in Ziegler–Natta catalysis, from a steric point of view.²⁹²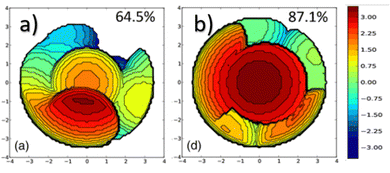

Fig. 9 %V_Bur and steric maps on the metal centre bonded to the halloysite: (a) without and (b) with cetrimonium bromide (xy plane, with the palladium placed in the centre and the z-axis the oxygen bonded to palladium, including the oxygen of the closest methoxy group in the xz plane. Curves are given in Å, with a radius of 3.5 Å).³¹ Copyright © 2022, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.

6.7. Biological applications

Topographic steric maps offer a versatile approach beyond synthetic molecular catalysts, extending their utility to biological contexts. This is evident in their application to characterize the catalytic pockets of both natural and artificially designed metalloenzymes.²⁹³ To illustrate this potential, Röthlisberger et al. examined a comparison between the catalytic pockets of the wild-type mononuclear p-hydroxymandelate synthase from Amycolatopsis orientalis and an in silico-designed triple mutant (S221M/V223F/Y359A) of a related enzyme from Streptomyces coelicolor.²⁹⁴ The wild-type enzyme catalyses the conversion of phenylpyruvate to (S)-mandelate (Fig. 10a),²⁹⁵ while the engineered mutant aims to induce opposite enantioselectivity, favouring the formation of (R)-mandelate.^295,296 The active sites of both proteins exhibit a trigonal bipyramidal Fe centre (Fig. 10b),^297,298 with coordinating residues such as His181, His261, and Glu340, along with available positions for catalysis. In the wild-type enzyme's catalytic pocket, certain residues (positions 223, 234, 261, 340, 350, and 359) constrain the space above the metal (Fig. 10c), resulting in an open subpocket in the south-western quadrant, where the aromatic ring of (S)-mandelate is positioned. Conversely, the mutant's catalytic pocket situates the aromatic ring of (R)-mandelate in the north-western quadrant. Notably, the mutant's catalytic pocket can accommodate (R)-mandelate, which would be infeasible in the wild-type pocket due to the clashing of its aromatic ring with the bulky Tyr359 residue. This comparison between the steric maps of the catalytic pockets reveals that mutations such as V223F and Y359A have distinct effects: V223F impedes the open space where (S)-mandelate's aromatic ring would be situated, while Y359A opens up space in the north-western quadrant, facilitating accommodation of (R)-mandelate's aromatic ring. Thus, by employing steric maps, the study gains insight into the structural basis of enantioselectivity alterations in metalloenzymes, underscoring the broader applicability of these maps in elucidating catalytic mechanisms in diverse contexts.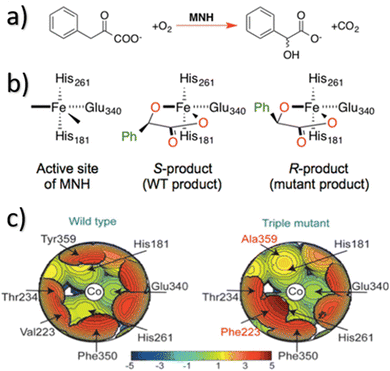

Fig. 10 (a) Scope of the reaction. (b) Catalytic active site. (c) Steric map of the catalytic active site from the crystal of the wild-type A. orientalis (left) and of S221M/V223F/Y356A muntant of S. coelicolor. Reproduced with permission.¹² Copyright © 2016, American Chemical Society.

In 2020, in one of the pioneering research works about pandemic COVID, Poater showed the effectiveness of inhibitors in blocking the COVID protease (SARS-CoV-2 M^pro), and α-ketoamide derivative substrates experimentally developed by Hilgenfeld and coworkers.²⁹⁹ Following biological characterization, DFT calculations were employed to not only elucidate the thermodynamically favourable interaction mechanism of the active inhibitor with respect to the non-active ones, but also to shed light on the kinetic aspects of this interaction.³⁰⁰ Aromaticity, a concept that has been debated and unverifiable,³⁰¹ plays a pivotal role in explaining the role of histidine (His41 of M^pro, see Fig. 11a). His41 establishes a hydrogen bond with the hydroxyl group and facilitates the proton transfer from the thiol of Cys145 at negligible energy expense, thus favouring the interaction with the inhibitor acting as a Michael acceptor. The steric hindrance around His41 is minimal, as evidenced by the steric maps (Fig. 11b), confirming it as the region with the least hindrance within the first coordination sphere of the thiol group where reactivity occurs. These maps also provide insight into the significantly poorer activity of certain inhibitors. In these cases, the presence of a cyclohexyl residue (as opposed to the cyclopropyl residue) complicates the necessary free rotation of His41. This rotation is crucial for sequential proton donation and acceptance. The expected steric clash between the pyridine ring and Gln189 is replaced by this hindered rotation. Thus, apart from the aromaticity to explain the reactivity, to unveil why the substrate with a cyclohexyl substituent does not work, steric maps were basic. Continuing with hydrogen bonds, steric maps allowed Posada-Pérez et al. also explain how the series of halides interacted with nickel but had a totally different stability due to hydrogen bonds with 3 amino groups that are located,³⁰² if possible in the same plane as the halide symmetrically. Thus, in this case, steric maps achieve an understanding not only of the first coordination sphere, but of the second, and doing so not in a biological system, but a simple inorganic complex. This is another reference of the versatility of this type of topographic steric maps.

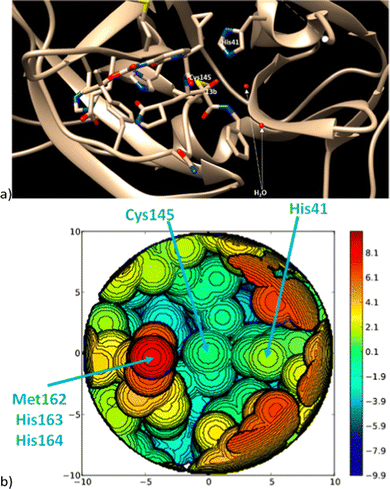Fig. 11 (a) Region around the sulphur of Cys145 of M^pro in the X-ray structure in space group C2. (b) Steric map around the sulphur of Cys145 of M^pro from the crystallographic structure (space group C2) of the protease M^pro. On the z axis, there is the sulphur atom of Cis45 and the carbon atom of the carbonyl of the substrate is at the origin, while its oxygen atom is on the xz plane (in Å). Reproduced with permission.³⁰⁰ Copyright © 2020, American Chemical Society.

In homology with the characterization of protein surfaces based on the attributes of exposed amino acids, a similar approach could be adopted for characterizing the catalytic pocket of catalysts.³⁰³ This involves assessing attributes like hydrophobic/hydrophilic nature, polar/apolar regions, aromatic patches, hydrogen bond donors and acceptors, as well as Lewis base and acid groups. Simplistically Vidal-López et al. with an initiative addressing the challenge of CO₂ emissions in the environment, sequestered CO₂ through reactions with epoxides.³⁰⁴ As commented before, this method not only captures CO₂ but also renders it functional, resulting in the formation of cyclic carbonates. This study specifically delved into the synthesis of cyclic organic carbonates catalysed by metal-salen complexes. Employing DFT calculations, the reaction was scrutinized, describing not only the structure and electronic properties of the catalysts, but by means of %V_Bur and steric maps calculations get the right understanding of the distinct catalytic pockets in monometallic first-row transition metals versus group III salen complexes. In addition, this led predictive catalysis results that emphasize the pivotal role of the bite O–Metal–O angle in the catalytic process.

An additional avenue of development involves combining the steric map source code with the ongoing advancements in computational methods for real-time molecular structure optimization.^305–308 This integration could facilitate the creation of a web-based 3D computer-aided design platform,³⁰⁹ enabling interactive modifications of initial catalyst structures.

6.8. Machine learning and artificial intelligence

Machine learning algorithms are being increasingly used in computational chemistry to develop predictive models for properties such as solubility, reactivity, and toxicity.^51,54 This section of ML and AI, discussed in Section 2, becomes not a typology of study, but an ingredient that can help any of the other applications that have the tools of steric characterization. In fact, these are part of the parameters considered by the AI. All sample applications are from the last 5 years, but not the last 2 basically. Like this, Xin, Tong and coworkers generated degradable stereoregular poly(lactic acids) exhibiting enhanced thermal and mechanical attributes over atactic polymers by means of stereoselective ring-opening polymerization catalysts.¹⁷⁴ Nonetheless, the quest for these catalysts with high stereoselectivity remains primarily empirical, their objective revolved around establishing a comprehensive framework that could merge computational insights with experimental methods to efficiently predict and optimize catalyst selection. Thus, they constructed a Bayesian optimization workflow utilizing a subset of literature data concerning stereoselective lactide ring-opening polymerization.³¹⁰ Through this algorithm, they successfully unearthed multiple novel aluminum catalysts, facilitating either isoselective or heteroselective polymerization. Computationally, it was fundamental the identification of ligand descriptors with mechanistic significance, notably including in multilinear analyses the percent buried volume (%V_Bur) and the energy of the HOMO.¹⁷⁴

In a simpler way, only with a parameter as the %V_Bur, through ML in particular Dou and coworkers in 2023 have published a study of the asymmetric catalysis of indolization by a [3 + 2] annulation.³¹¹ Using the %V_Bur steric parameter, they managed to find a linear correlation with Gibbs energy difference calculated between 2 competing diastereomeric transition states. Thus, here, %V_Bur is the way that leads to the message that the simpler the better.

7. Beyond steric maps and the concept of %V_Bur

Since the beginning of the concept of %V_Bur and steric maps, the science has continued to evolve and there are already new proposals based on it. Although steric maps already have applications in bimetallic systems and biological systems, departing from the monometallic centre scheme, Broere and coworkers developed a systematic study to quantify the steric properties of dinucleating ligands.³¹² Actually, the research adapted buried volume and G-parameter methods originally used for analysing 1,8-naphthyridine ligands and extended them for analysing dinuclear complexes. The reliability of the new methods was confirmed by comparing them to existing mononuclear approaches and dimerization energies of R(PNNP*)Cu₂H complexes. This demonstrated that the expanded approaches effectively calculate the steric characteristics of 1,8-napthyridine-based dinuclear complexes. The study also revealed that altering phosphine substituents on PNNP ligands offers a wide range of steric properties in resulting complexes. Indeed, this confirms the validity of past results with steric maps and the concept of the old %V_Bur because only in the first sphere around the metal is where the reactivity is decisive.^22,176 In fact, from 3.5 Å of radius the effect at least on the metal centre and the substrates with which it interacts could be practically omitted. Thus, the protonation state of the PNNP backbone has minimal impact on sterics, while modifying linkers between phosphines and the naphthyridine core or adjusting metal distances can influence steric congestion in the bimetallic core. Changes to the ligand backbone affect complex rigidity, influencing flexibility to adopt lower steric encumbrance geometries in the dinuclear core. This approach could potentially offer insights into modifying the reactivity of other dinuclear complexes through rational ligand design, employing easily accessible software for parameter calculation.

If we see synthetically which are the examples of the applications of these concepts included in the following, the future of those tools is gorgeous, and specially together with the unknown limits of AI:

• The analysis of molecular interactions in drug discovery, including the prediction of potential drug targets, the evaluation of drug candidates, and the design of new drugs.

• The study of molecular reactivity and stability, including the prediction of chemical reactions and the analysis of the factors that influence reaction outcomes.

• The design and synthesis of new chemical compounds, including the optimization of molecular structure to improve properties such as solubility, stability, and potency.

• The analysis of protein–ligand interactions, including the prediction of binding affinity and the identification of potential drug targets.

One potential advancement involves exploring alternative methods of characterizing the catalytic pocket's surface through various physicochemical properties beyond steric hindrance, such as electrostatic potential maps. Similarly, to characterizing protein surfaces based on exposed amino acid properties, catalyst catalytic pockets could be assessed for hydrophobic/hydrophilic, polar/apolar, and aromatic regions, hydrogen bond donors and acceptors, or Lewis base and acid groups.

Another avenue for development could entail integrating the steric map source code with computational methods aimed at real-time geometry optimization of molecular structures. This integration could pave the way for a web-based 3D computer-aided design system that enables interactive modification of initial catalyst skeletons. Actually, new webs or servers that collect several of those indices are ongoing. Take for instance, in 2023, GitHub was presented by dos Passos Gomes, Friedrich and Gensch,³¹³ gathering the calculation of the bite angle,^314,315 buried volume,²² conformer tools, dispersion descriptor, exact ligand CA,²⁰ ligand solid angle,^316–318 local force constant, pyramidalization, solvent accessible surface area, Sterimol parameters^137,138 and Extended tight-binding (XTB) electronic descriptors.^319,320

Lastly, the digital steric map, represented by an array of Cartesian points defining the surface, might be utilized as a steric descriptor within multilinear regression analysis or embedded within a workflow for high-throughput catalyst screening through machine learning techniques.

8. Conclusions and future perspectives

Overall, predictive catalysis by DFT calculations is a powerful tool for the study of catalytic reactions and provides a comprehensive understanding of the reaction mechanism, energy profile, and reactivity of catalytic systems. These concepts of %V_Bur and steric maps are tools commonly used in the design and optimization of drugs, catalysts, and materials, as well as in the prediction of the properties and behaviour of molecules in different environments.

Knowing that steric indices are a type of parameter that describes the spatial arrangement of atoms in a molecule, they can be used to quantify the degree of steric hindrance or sterically-induced strain in a molecule, which can in turn affect its reactivity and stability.

In conclusion, the Steric index, Tolman cone angle, steric maps, and %V_Bur of Nolan and Cavallo are all important parameters used in the study of molecular interactions and in the design of chemical reactions. These tools provide valuable information about the molecular size and shape, spatial orientation, and stability of molecular interactions, and they are widely used in the fields of drug design, chemical engineering, and materials science.

In conclusion, the applications of steric maps in drug design, structure prediction, reactivity prediction, synthesis design, and molecular docking make them an important tool in the field of molecular science. With their ability to visualize the distribution of electron density in a molecule and to predict the interactions between atoms and molecules, they provide valuable information for understanding and optimizing the properties of chemical compounds.

Overall, the relationship between steric index or %V_Bur and yield is complex and can depend on multiple factors. However, these parameters can be useful in predicting the reactivity and selectivity of chemical reactions and in designing more efficient catalysts.

The acceleration of catalyst engineering through computer-aided design is achievable by condensing molecular catalyst features into numerical descriptors. These descriptors establish connections between reactivity and structure. Within this framework, the introduction of topographic steric maps has been pivotal. Apart from being user friendly to obtain, these maps offer a visual representation of the catalytic pocket, the area in a catalyst where substrates bind and undergo reactions. This visualization allows for alterations by adjusting various parameters. When combined with DFT calculations, these steric maps facilitate swift exploration of catalyst structural modifications, enabling the online creation by a web server of new catalysts for the broader chemical community. Thus, this review focuses on the utilization of topographic steric maps to either rationalize the behaviour of existing catalysts, ranging from synthetic molecular entities to metalloenzymes, or to design enhanced catalysts.

Last but not least, future research in the field of %V_Bur and steric maps is likely to focus on the development of new computational tools and techniques to enhance its accuracy and predictive power. As the field of chemistry continues to evolve, those tools will undoubtedly play an important role in enabling researchers to understand and control the electronic properties and reactivity of molecules and materials, opening up new avenues for the design and synthesis of novel compounds and materials with important applications in various fields.

Author contributions

All the authors wrote and revised the manuscript.

Abbreviations

%VBur	Percentage of buried volume
AI	Artificial intelligence
CA	Cone angle
DFT	Density functional theory
ETS-NOCV	Extended Transition State-Natural Orbital for Chemical Valence
HOMO	Highest occupied molecular orbital
LUMO	Lowest unoccupied molecular orbital
ML	Machine learning
MOF	Metal organic framework
NHC	N-heterocyclic carbene
NHO	N-heterocyclic olefin
rdi	Rate determining intermediate
rds	Rate determining step
SHI	Steric hindrance index
TEP	Tolman electronic parameter
XTB	Extended tight-binding
VdW	van der Waals volume

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Spanish Ministerio de Ciencia e Innovación for project PID2021-127423NB-I00 and the Generalitat de Catalunya for project 2021SGR623. A. P. is a Serra Húnter Fellow and ICREA Academia Prize 2019. S. E. thanks Universitat de Girona and DIPC for an IFUdG2019 PhD fellowship. We are extremely thankful to Dr Montserrat Rodríguez that participated actively to a better understanding of the manuscript. The authors want to thank the insightful comments of Prof. Luigi Cavallo.

References

1. Chemistry for Tomorrow's World (Royal Society of Chemistry, 2009), https://go.nature.com/31AWVup.
2. Basic Research Needs for Catalysis Science (US Department of Energy, 2017), https://go.nature.com/2yU0iR1.
3. J. A. Luque-Urrutia, T. Ortiz-García, M. Solà and A. Poater, Inorganics, 2023, 11, 88.
4. S. Placzek, I. Schomburg, A. Chang, L. Jeske, M. Ulbrich, J. Tillack and D. Schomburg, Nucleic Acids Res., 2017, 45, D380.
5. M. Foscato and V. R. Jensen, ACS Catal., 2020, 10, 2354.
6. C. T. Porter, G. J. Bartlett and J. M. Tornton, Nucleic Acids Res., 2004, 32, D129.
7. H. Neurath, Science, 1984, 224, 350.
8. T. R. Boussie, G. M. Diamond, C. Goh, K. A. Hall, A. M. LaPointe, M. Leclerc, C. Lund, V. Murphy, J. A. W. Shoemaker, U. Tracht, H. Turner, J. Zhang, T. Uno, R. K. Rosen and J. C. Stevens, J. Am. Chem. Soc., 2003, 125, 4306.
9. A. Holzwarth, H.-W. Schmidt and W. F. Maier, Angew. Chem., Int. Ed., 1998, 37, 2644.
10. S. J. Taylor and J. P. Morken, Science, 1998, 280, 267.
11. V. Babin, C. Leforestier and F. Paesani, J. Chem. Theory Comput., 2013, 9, 5395.
12. L. Falivene, R. Credendino, A. Poater, A. Petta, L. Serra, R. Oliva, V. Scarano and L. Cavallo, Organometallics, 2016, 35, 2286.
13. R. Todeschini and V. Viviana Consonni, Handbook of Molecular Descriptors, Wiley, 2000.
14. L. Falivene, Z. Cao, A. Petta, L. Serra, A. Poater, R. Oliva, V. Scarano and L. Cavallo, Nat. Chem., 2019, 11, 872.
15. C. H. Suresh, Inorg. Chem., 2006, 45, 4982.
16. B. J. Dunne, R. B. Morris and A. G. Orpen, J. Chem. Soc., Dalton Trans., 1991, 653.
17. M. L. Caffery and T. L. Brown, Inorg. Chem., 1991, 30, 3907.
18. T. L. Brown, Inorg. Chem., 1992, 31, 1286.
19. K. J. Lee and T. L. Brown, Inorg. Chem., 1992, 31, 289.
20. C. A. Tolman, Chem. Rev., 1977, 77, 313.
21. A. C. Hillier, W. J. Sommer, B. S. Yong, J. L. Petersen, L. Cavallo and S. P. Nolan, Organometallics, 2003, 22, 4322.
22. A. Poater, B. Cosenza, A. Correa, S. Giudice, F. Ragone, V. Scarano and L. Cavallo, Eur. J. Inorg. Chem., 2009, 1759.
23. S. Díez-González and S. P. Nolan, Coord. Chem. Rev., 2007, 251, 874.
24. H. Jacobsen, A. Correa, A. Poater, C. Costabile and L. Cavallo, Coord. Chem. Rev., 2009, 253, 2784.
25. L. Cavallo, A. Correa, C. Costabile and H. Jacobsen, J. Organomet. Chem., 2005, 690, 5407.
26. R. Dorta, E. D. Stevens, N. M. Scott, C. Costabile, L. Cavallo, C. D. Hoff and S. P. Nolan, J. Am. Chem. Soc., 2005, 127, 2485.
27. Y. Zhang, C. Wang, S. Mecking and Z. Jian, Angew. Chem., Int. Ed., 2020, 59, 14296.
28. E. P. A. Couzijn, Y.-Y. Lai, A. Limacher and P. Chen, Organometallics, 2017, 36, 3205.
29. A. Poater and L. Cavallo, Dalton Trans., 2009, 8878.
30. P. M. R. Wingering, S. Hohnstein, F. Krämer, M. E. A. Dilanas, C. Ruiz-Martínez, I. Fernández and F. Breher, Chem. – Eur. J., 2023, e202301529.
31. A. Shams, S. Sadjadi, J. Duran, S. Simon, A. Poater and N. Bahri-Laleh, Appl. Organomet. Chem., 2022, 36, e6719.
32. Y. Sun, Q. Zhao, H. Wang, T. Yang, J. Wen and X. Zhang, Chem. – Eur. J., 2020, 26, 11470.
33. S. S. Harmalkar, V. R. Chari, R. K. Kunkalekar and S. N. Dhuri, New J. Chem., 2022, 47, 1852.
34. G. Y. Sánchez Delgado, D. Paschoal, M. A. L. de Oliveira and H. F. Dos Santos, J. Inorg. Biochem., 2019, 200, 110804.
35. P. Gao, J. Xu, T. Zhou, Y. Liu, E. Bisz, B. Dziuk, R. Lalancette, R. Szostak, D. Zhang and M. Szostak, Angew. Chem., Int. Ed., 2023, 62, e202218427.
36. G. M. Meconi, S. V. C. Vummaleti, J. A. Luque-Urrutia, P. Belanzoni, S. P. Nolan, H. Jacobsen, L. Cavallo, M. Solà and A. Poater, Organometallics, 2017, 36, 2088.
37. L. Falivene, L. Cavallo and G. Talarico, ACS Catal., 2015, 5, 6815.
38. M. Voccia, L. Odenwald, M. Baur, F. Lin, L. Falivene, S. Mecking and L. Caporaso, J. Am. Chem. Soc., 2022, 144, 15111.
39. M. P. Maloney, B. A. Stenfors, P. Helquist, P.-O. Norrby and O. Wiest, ACS Catal., 2023, 13(21), 14285.
40. J. C. A. Oliveira, J. Frey, S.-Q. Zhang, L.-C. Xu, X. Li, S.-W. Li, X. Hong and L. Ackermann, Trends Chem., 2022, 4, 863.
41. S. Harnad, The Annotation Game: On Turing (1950) on Computing, Machinery, and Intelligence, in The Turing Test Sourcebook: Philosophical and Methodological Issues in the Quest for the Thinking Computer, ed. R. Epstein and G. Peters, Kluwer, 2008, pp. 23–66, ISBN 9781402067082.
42. A. Samuel, IBM J. Res. Dev., 1959, 3, 210.
43. N. Nilsson, Learning Machines, McGraw Hill, 1965.
44. R. Duda and P. Hart, Pattern Recognition and Scene Analysis, Wiley Interscience, 1973.
45. R. Kohavi and F. Provost, Glossary of terms, Mach. Learn., 1998, 30, 271.
46. J. R. Koza, F. H. Bennett, D. Andre and M. A. Keane, Automated Design of Both the Topology and Sizing of Analog Electrical Circuits Using Genetic Programming, Artificial Intelligence in Design '96, Springer, Dordrecht, 1996, pp. 151–170 DOI:10.1007/978-94-009-0279-4_9.
47. E. Alpaydin, Introduction to Machine Learning, 4th edn, MIT, pp. xix, 1–3, 2020, pp. 13–18, ISBN 978-0262043793.
48. A. Tkatchenko, Nat. Commun., 2020, 11, 4125.
49. K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547.
50. D. Balcells and B. B. Skjelstad, J. Chem. Inf. Model., 2020, 60, 6135.
51. R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268.
52. J.-L. Reymond, Acc. Chem. Res., 2015, 48, 722.
53. J. P. Janet, S. Ramesh, C. Duan and H. J. Kulik, ACS Cent. Sci., 2020, 6, 513.
54. B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360.
55. J. G. Freeze, H. R. Kelly and V. S. Batista, Chem. Rev., 2019, 119, 6595.
56. P. S. Gromski, A. B. Henson, J. M. Granda and L. Cronin, Nat. Rev. Chem., 2019, 3, 119.
57. P. Friederich, G. Dos Passos Gomes, R. De Bin, A. Aspuru-Guzik and D. Balcells, Chem. Sci., 2020, 11, 4584.
58. N. Fey, A. G. Orpen and J. N. Harvey, Coord. Chem. Rev., 2009, 253, 704.
59. N. Fey, Dalton Trans., 2010, 39, 296.
60. M. Foscato, G. Occhipinti, V. Venkatraman, B. K. Alsberg and V. R. Jensen, J. Chem. Inf. Model., 2014, 54, 767.
61. M. Tomasini, J. Zhang, H. Zhao, E. Besalú, L. Falivene, L. Caporaso, M. Szostak and A. Poater, Chem. Commun., 2022, 58, 9950.
62. R. Monreal-Corona, À. Díaz-Jiménez, A. Roglans, A. Poater and A. Pla-Quintana, Adv. Synth. Catal., 2023, 365, 760.
63. N. Joly, M. Gimferrer, S. Escayola, M. Cendra, S. Coufourier, J.-F. Lohier, Q. Gaignard Gaillard, S. Gaillard, M. Solà, J.-L. Renaud and A. Poater, Organometallics, 2023, 42, 1784.
64. R. Monreal-Corona, A. Pla-Quintana and A. Poater, Trends Chem., 2023, 5, 935.
65. E. Pump, A. Poater, N. Bahri-Laleh, R. Credendino, L. Serra, V. Scarano and L. Cavallo, Catal. Today, 2021, 388–389, 394.
66. S. Karimi, N. Bahri-Laleh, S. Sadjadi, G. Pareras, M. Nekoomanesh-Haghighi and A. Poater, J. Ind. Eng. Chem., 2021, 97, 441.
67. A. Hanifpour, N. Bahri-Laleh, M. Nekoomanesh-Haghighi and A. Poater, Appl. Organomet. Chem., 2021, 35, e6227.
68. V. D’Elia, A. A. Ghani, A. Monassier, J. Sofack-Kreutzer, J. D. A. Pelletier, M. Drees, S. V. C. Vummaleti, A. Poater, L. Cavallo, M. Cokoja, J.-M. Basset and F. E. Kühn, Chem. – Eur. J., 2014, 20, 11870.
69. V. D'Elia, H. Dong, A. Rossini, C. Widdifield, S. V. C. Vummaleti, Y. Minenkov, A. Poater, E. Abou-Hamad, J. D. A. Pelletier, L. Cavallo, L. Emsley and J. M. Basset, J. Am. Chem. Soc., 2015, 137, 7728.
70. S. Arayachukiat, P. Yingcharoen, S. V. C. Vummaleti, L. Cavallo, A. Poater and V. D’Elia, Mol. Catal., 2017, 443, 280.
71. W. Natongchai, J. A. Luque-Urrutia, Ch Phyngpanyia, M. Solà, V. D’Elia, A. Poater and H. Zipse, Org. Chem. Front., 2021, 8, 249.
72. A. Gómez-Suárez, Y. Oonishi, A. R. Martin, S. V. C. Vummaleti, D. J. Nelson, D. B. Cordes, A. M. Z. Slawin, L. Cavallo, S. P. Nolan and A. Poater, Chem. – Eur. J., 2016, 22, 1125.
73. M. H. Larsen, K. N. Houk and A. S. K. Hashmi, J. Am. Chem. Soc., 2015, 137, 10668.
74. Ó. Belman, A. Brotons Rufes, M. Tomasini, L. Falivene, L. Caporaso, J. Ó. C. Jiménez-Halla and A. Poater, Catalysts, 2021, 11, 704.
75. S. Arayachukiat, C. Kongtes, A. Barthel, S. V. C. Vummaleti, A. Poater, S. Wannakao, L. Cavallo and V. D’Elia, ACS Sustainable Chem. Eng., 2017, 5, 6392.
76. S. Muthuramalingam, M. Velusamy, S. Singh Rajput, M. Alam and R. Mayilmurugan, Chem. – Asian J., 2023, 18, e202201204.
77. M. Tomasini, J. Duran, S. Simon, L. M. Azofra and A. Poater, Mol. Catal., 2021, 510, 111692.
78. S. Escayola, M. Solà and A. Poater, Inorg. Chem., 2020, 59, 9374.
79. A. Poater, R. Credendino, C. Slugovc and L. Cavallo, Dalton Trans., 2013, 42, 7271.
80. J. P. Martínez, S. V. C. Vummaleti, L. Falivene, S. P. Nolan, L. Cavallo, M. Solà and A. Poater, Chem. – Eur. J., 2016, 22, 6617.
81. J. P. Martínez, M. Vizuete, L. M. Arellano, A. Poater, F. M. Bickelhaupt, F. Langa and M. Solà, Nanoscale, 2018, 10, 15078.
82. S. Moulin, H. Dentel, A. Pagnoux-Ozherelyeva, S. Gaillard, A. Poater, L. Cavallo, J.-F. Lohier and J.-L. Renaud, Chem. – Eur. J., 2013, 19, 17881.
83. M. Gimferrer, N. Joly, S. Escayola, E. Viñas, S. Gaillard, M. Solà, J.-L. Renaud, P. Salvador and A. Poater, Organometallics, 2022, 41, 1204.
84. K. Cyrański, Chem. Rev., 2005, 105, 3773.
85. J. Kruszewski and T. M. Krygowski, Tetrahedron Lett., 1972, 13, 3839.
86. P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. V. E. Mommes, J. Am. Chem. Soc., 1996, 118, 6317.
87. A. Stanger, Eur. J. Org. Chem., 2020, 3120.
88. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500.
89. F. Feixas, E. Matito, J. Poater and M. Solà, Chem. Soc. Rev., 2015, 44, 6434.
90. D. Szczepanik, M. Andrzejak, J. Dominikowska, B. Pawetek, T. M. Krygowski, H. Szatylowicz and M. Solà, Phys. Chem. Chem. Phys., 2017, 19, 28970.
91. Z. Mucsi, B. Viskolcz and I. G. Csizmadia, J. Phys. Chem. A, 2007, 111, 1123.
92. F. Feixas, J. O. C. Jiménez-Halla, E. Matito, J. Poater and M. Solà, J. Chem. Theory Comput., 2010, 6, 1118.
93. S. Pelloni, G. Monaco, P. Lazzeretti and R. Zanasi, Phys. Chem. Chem. Phys., 2011, 13, 20666.
94. L. P. Hammett and A. J. Deyrup, J. Am. Chem. Soc., 1932, 54, 2721.
95. L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96.
96. L. Perrin, E. Clot, O. Eisenstein, J. Loch and R. H. Crabtree, Inorg. Chem., 2001, 40, 5806.
97. S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101.
98. H. Zheng, L. Pei, H. Deng, H. Gao and H. Gao, Eur. Polym. J., 2023, 184, 111773.
99. C. A. Tolman, J. Am. Chem. Soc., 1970, 92, 2956.
100. C. A. Tolman, W. C. Seidel and L. W. Gosser, J. Am. Chem. Soc., 1974, 96, 53.
101. K. A. Bunten, L. Chen, A. L. Fernandez and A. J. Poë, Coord. Chem. Rev., 2002, 233–234, 41.
102. R. H. Crabtree, The Organometallic Chemistry of the Transition Metals, Wiley, 2014.
103. A. Saurwein, T. Eisner, S. Inoue and B. Rieger, Organometallics, 2022, 41, 3679.
104. B. C. Taverner, J. Comput. Chem., 1996, 17, 1612.
105. B. C. Taverner, J. M. Smith, D. P. White and N. J. Coville, S. Afr. J. Chem., 1997, 50, 59.
106. D. White, B. C. Taverner, N. J. Coville and P. W. Wade, J. Organomet. Chem., 1995, 495, 41.
107. D. White, B. C. Taverner, P. G. L. Leach and N. J. Coville, J. Comput. Chem., 1993, 14, 1042.
108. A. Immirzi and A. Musco, Inorg. Chim. Acta, 1977, 25(C), L41.
109. J. M. Smith, B. C. Taverner and N. J. Coville, J. Organomet. Chem., 1997, 530, 131.
110. A. Fedullo, S. Antinucci, A. Immirzi and G. Monaco, J. Macromol. Sci., Phys., 2005, 44, 583.
111. C. Hansch, A. Leo and R. W. Taf, Chem. Rev., 1991, 91, 165.
112. M. Charton and B. Charton, J. Am. Chem. Soc., 1975, 97, 6472.
113. M. Charton, Chem. Tech., 1975, 5, 245.
114. A. Verloop, W. Hoogenstraaten and J. Tipker, Development and Application of New Steric Substituent Parameters in Drug Design, Academic Press, 1976, vol. 7, pp. 165–207.
115. A. Verloop, The STERIMOL approach to drug design, Marcel Dekker, 1987.
116. A. Poater, F. Ragone, S. Giudice, C. Costabile, R. Dorta, S. P. Nolan and L. Cavallo, Organometallics, 2008, 27, 2679.
117. A. C. Hillier, H. M. Lee, E. D. Stevens and S. P. Nolan, Organometallics, 2001, 20, 4246.
118. H. M. Lee, T. Jiang, E. D. Stevens and S. P. Nolan, Organometallics, 2001, 20, 1255.
119. L. D. Vázquez-Serrano, B. T. Owens and J. M. Buriak, Chem. Commun., 2002, 2518.
120. N. Marion, O. Navarro, J. Mei, E. D. Stevens, N. M. Scott and S. P. Nolan, J. Am. Chem. Soc., 2006, 128, 4101.
121. G. A. Grasa, M. S. Viciu, J. Huang, C. Zhang, M. L. Trudell and S. P. Nolan, Organometallics, 2002, 21, 2866.
122. G. A. Grasa, M. S. Viciu, J. Huang and S. P. Nolan, J. Org. Chem., 2001, 66, 7729.
123. T. Weskamp, W. C. Schattenmann, M. Spiegler and W. A. Herrmann, Angew. Chem., Int. Ed., 1998, 37, 2490.
124. M. Scholl, S. Ding, C. W. Lee and R. H. Grubbs, Org. Lett., 1999, 1, 953.
125. J. Huang, E. D. Stevens, S. P. Nolan and J. L. Peterson, J. Am. Chem. Soc., 1999, 121, 2674.
126. A. Fürstner, Angew. Chem., Int. Ed., 2000, 39, 3012.
127. T. M. Trnka and R. H. Grubbs, Acc. Chem. Res., 2001, 34, 18.
128. L. Jafarpour and S. P. Nolan, J. Organomet. Chem., 2001, 617–618, 17.
129. A. H. Hoveyda and R. R. Schrock, Chem. – Eur. J., 2001, 7, 945.
130. A. Correa, N. Marion, L. Fensterban, M. Malacria, S. P. Nolan and L. Cavallo, Angew. Chem., Int. Ed., 2008, 47, 718.
131. N. Marion, P. de Frémont, G. Lemière, E. D. Stevens, L. Fensterbank, M. Malacria and S. P. Nolan, Chem. Commun., 2006, 2048.
132. T. W. Funk, J. M. Berlin and R. H. Grubbs, J. Am. Chem. Soc., 2006, 128, 1840.
133. M. C. Perry and K. Burgess, Tetrahedron: Asymmetry, 2003, 14, 951.
134. J. J. Van Veldhuizen, S. B. Garber, J. S. Kingsbury and A. H. Hoveyda, J. Am. Chem. Soc., 2002, 124, 4954.
135. T. J. Seiders, D. W. Ward and R. H. Grubbs, Org. Lett., 2001, 3, 3225.
136. V. Nair, S. Bindu and V. Sreekumar, Angew. Chem., Int. Ed., 2004, 43, 5130.
137. A. Verloop and E. J. Ariens, Drug Design, 3, Academic Press, New York, 1976.
138. A. Verloop, The STERIMOL. Application to Drug Design, Marcel Dekker, New York, 1997.
139. Y. Wang, H. Zhou, K. Yang, C. You, L. Zhang and S. Luo, Org. Lett., 2019, 21, 407.
140. W. Draber, Z. Naturforsch., C: J. Biosci., 1996, 51, 1.
141. A. V. Brethomé, S. P. Fletcher and R. S. Paton, ACS Catal., 2019, 9, 2313.
142. K. C. Karper, E. N. Bess and M. S. Sigman, Nat. Chem., 2012, 4, 366.
143. A. F. Zahrt, J. J. Henle, B. T. Rose, Y. Wang, W. T. Darrow and S. E. Denmark, Science, 2019, 363, eaau5631.
144. A. F. Zahrt, N. I. Rinehart and S. E. Denmark, Eur. J. Org. Chem., 2021, 2343.
145. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799.
146. A. Bondi, J. Phys. Chem., 1964, 68, 441.
147. G. Pareras, D. Detiana and A. Poater, Catalysts, 2020, 10, 687.
148. J. Poater, M. Gimferrer and A. Poater, Inorg. Chem., 2018, 57, 6981.
149. N. Bahri-Laleh, S. Sadjadi, M. M. Heravi and M. Malmir, Appl. Organomet. Chem., 2018, 32, e4283.
150. Y. Li, H. K. Kim, R. D. McGillicuddy, S.-L. Zheng, K. J. Anderton, G. J. Stec, D. Cui and J. A. Mason, J. Am. Chem. Soc., 2023, 145, 9304.
151. Y.-Z. Li, R. Ganguly, K. Y. Hong, Y. Li, M. E. Tessensohn, R. Webster and W. K. Leong, Chem. Sci., 2018, 9, 8723.
152. M. Tomasini, L. Caporaso, J. Trouvé, J. Poater, R. Gramage-Doria and A. Poater, Chem. – Eur. J., 2022, 28, e202201970.
153. S. Kaur, V. Kumar, M. Chawla, L. Cavallo, A. Poater and N. Upadhyay, Front. Chem., 2017, 5, 43.
154. V. Kumar, M. Chawla, L. Cavallo, A. B. Wani, A. Manhas, S. Kaur, A. Poater, H. Chadar and N. Upadhyay, Inorg. Chim. Acta, 2018, 469, 379.
155. A. Gómez-Suárez, D. J. Nelson and S. P. Nolan, Chem. Commun., 2017, 53, 2650.
156. D. Bourissou, O. Guerret, F. P. Gabbaï and G. Bertrand, Chem. Rev., 2000, 100, 39.
157. S. Diez-Gonzalez and S. P. Nolan, Coord. Chem. Rev., 2007, 251, 874.
158. R. W. Alder, M. E. Blake, L. Chaker, J. N. Harvey, F. Paolini and J. Schutz, Angew. Chem., Int. Ed., 2004, 43, 5896.
159. D. J. Nelson and S. P. Nolan, Chem. Soc. Rev., 2013, 42, 6723.
160. F. Glorius, Top. Organomet. Chem., 2007, 21, 1.
161. C. M. Crudden and D. P. Allen, Coord. Chem. Rev., 2004, 248, 2247.
162. S. Popov and H. Plenio, Eur. J. Inorg. Chem., 2021, 3708.
163. G. Frenking, M. Solà and S. F. Vyboishchikov, J. Organomet. Chem., 2005, 690, 6178.
164. L. Moran-González, J. R.-G. Pedregal, M. Besora and F. Maseras, Eur. J. Inorg. Chem., 2022, e202100932.
165. M. S. Viciu, O. Navarro, R. F. Germaneau, R. A. Kelly III, W. Sommer, W. Sommer, N. Marion, E. D. Stevens, L. Cavallo and S. P. Nolan, Organometallics, 2004, 23, 1629.
166. A. Cervantes-Reyes, F. Rominger, M. Rudolph and A. S. K. Hashmi, Chem. – Eur. J., 2019, 25, 11745.
167. P. de Fremont, N. M. Scott, E. D. Stevens, T. Ramnial, O. C. Lightbody, C. L. B. Macdonald, J. A. C. Clyburne, C. D. Abernethy and S. P. Nolan, Organometallics, 2005, 24, 6301.
168. R. A. Kelly III, H. Clavier, S. Giudice, N. M. Scott, E. D. Stevens, J. Bordner, I. Samardjiev, C. D. Hoff, L. Cavallo and S. P. Nolan, Organometallics, 2008, 27, 202.
169. S. Fantasia, J. L. Petersen, H. Jacobsen, L. Cavallo and S. P. Nolan, Organometallics, 2007, 26, 5880.
170. X. Luan, R. Mariz, M. Gatti, C. Costabile, A. Poater, L. Cavallo, A. Linden and R. Dorta, J. Am. Chem. Soc., 2008, 130, 684.
171. GNU v.3 (Free Sofware Foundation, 2007).
172. L. Falivene and L. Cavallo, Coord. Chem. Rev., 2017, 344, 101.
173. P. V. S. Nylund, N. C. Ségaud and M. Albrecht, Organometallics, 2021, 40, 1538.
174. X. Wang, Y. Huang, X. Xie, Y. Liu, Z. Huo, M. Lin, H. Xin and R. Tong, Nat. Commun., 2023, 14, 3647.
175. A. Poater, ICERI2022 Proceedings, 2022, p. 5472.
176. H. Clavier and S. P. Nolan, Chem. Commun., 2010, 46, 841.
177. J. Jover and J. Cirera, Dalton Trans., 2019, 48, 15036.
178. T. Zhou, S. Ma, F. Nahra, A. M. C. Obled, A. Poater, L. Cavallo, C. S. J. Cazin, S. P. Nolan and M. Szostak, iScience, 2020, 23, 101377.
179. K. Mikami, Polymer, 2020, 203, 122738.
180. L. van Dijk, R. Ardkhean, M. Sidera, S. Karabiyikoglu, Ö. Sari, T. D. W. Claridge, G. C. Lloyd-Jones, R. S. Paton and S. P. Fletcher, Nat. Catal., 2021, 4, 184.
181. A. Chartoire, M. Lesieur, L. Falivene, A. M. Z. Slawin, L. Cavallo, C. S. J. Cazin and S. P. Nolan, Chem. – Eur. J., 2012, 18, 4517.
182. O. H. Winkelmann, A. Riekstins, S. P. Nolan and O. Navarro, Organometallics, 2009, 28, 5809.
183. M. C. D’Alterio, È. Casals-Cruañas, N. V. Tzouras, G. Talarico, S. P. Nolan and A. Poater, Chem. – Eur. J., 2021, 27, 13481.
184. M. Rouen, P. Queval, E. Borré, L. Falivene, A. Poater, M. Berthod, F. Hugues, L. Cavallo, O. Baslé, H. Olivier-Bourbigou and M. Mauduit, ACS Catal., 2016, 6, 7970.
185. C. A. Urbina-Blanco, X. Bantreil, H. Clavier, A. M. Z. Slawin and S. P. Nolan, Beilstein J. Org. Chem., 2010, 6, 1120.
186. E. Pump, A. Leitgeb, A. Kozłowska, A. Torvisco, L. Falivene, L. Cavallo, K. Grela and C. Slugovc, Organometallics, 2015, 34, 5383.
187. A. Poater, F. Ragone, R. Mariz, R. Dorta and L. Cavallo, Chem. – Eur. J., 2010, 16, 14348.
188. S. Gaillard, X. Bantreil, A. M. Z. Slawin and S. P. Nolan, Dalton Trans., 2009, 6967.
189. A. Gómez-Suárez, R. S. Ramón, O. Songis, A. M. Z. Slawin, C. S. J. Cazin and S. P. Nolan, Organometallics, 2011, 30, 5463.
190. N. V. Tzouras, F. Nahra, L. Falivene, L. Cavallo, M. Saab, K. Van Hecke, A. Collado, C. J. Collett, A. D. Smith, C. S. J. Cazin and S. P. Nolan, Chem. – Eur. J., 2020, 26, 4515.
191. M. M. Wu, A. M. Gill, L. Yunpeng, L. Falivene, L. Yongxin, G. Ganguly, L. Cavallo and F. García, Dalton Trans., 2015, 44, 15166.
192. M. M. Wu, A. M. Gill, L. Yunpeng, L. Yongxin, R. Ganguly, L. Falivene and F. García, Dalton Trans., 2017, 46, 854.
193. C. Schiebel, M. Voccia, L. Falivene, I. Göttker-Schnetmann, L. Caporaso and S. Mecking, Angew. Chem., Int. Ed., 2021, 60, 18472.
194. S. Naumann, K. Mundsinger, L. Cavallo and L. Falivene, Polym. Chem., 2017, 8, 5803.
195. L. Falivene and L. Cavallo, Macromolecules, 2017, 50, 1394.
196. A. Nikol, Z. Zhang, A. Chelouan, L. Falivene, L. Cavallo, A. Herrera, F. W. Heinemann, A. Escalona, S. Frieß, A. Grasruck and R. Dorta, Organometallics, 2020, 39, 1348.
197. B. S. Billow, T. J. McDaniel and A. L. Odom, Nat. Chem., 2017, 9, 837.
198. K. Wu and A. G. Doyle, Nat. Chem., 2017, 9, 779.
199. K. B. KLipkowitz, C. A. D’Hue, T. Sakamoto and J. N. Stack, J. Am. Chem. Soc., 2002, 124, 14255.
200. P. A. Champagne, Chem. Sci., 2021, 12, 15662.
201. K. Angermund, W. Baumann, E. Dinjus, R. Fornika, H. Görls, M. Kessler, C. Krüger, W. Leitner and F. Lutz, Chem. – Eur. J., 1997, 3, 755.
202. K. C. Harper and M. S. Sigman, J. Org. Chem., 2013, 78, 2813.
203. K. C. Harper, S. C. Vilardi and M. S. Sigman, J. Am. Chem. Soc., 2013, 135, 2482.
204. B. J. Dunne, R. B. Morris and A. G. Orpen, J. Chem. Soc., Dalton Trans., 1991, 653.
205. K. D. Cooney, T. R. Cundari, N. W. Hoffman, K. A. Pittard, M. D. Temple and Y. Zhao, J. Am. Chem. Soc., 2003, 125, 4318.
206. F. Ragone, A. Poater and L. Cavallo, J. Am. Chem. Soc., 2010, 132, 4249.
207. M.-C. Wu, Y.-F. Liang, T. Jurca, G. P. A. Yap, T.-F. Leung and T.-G. Ong, J. Am. Chem. Soc., 2022, 144, 12996.
208. A. Poater, S. V. C. Vummaleti, E. Pump and L. Cavallo, Dalton Trans., 2014, 43, 11216.
209. C. Duchemin, J. Kim and P. J. Chirik, JACS Au, 2023, 3, 2007.
210. E. Fischer, Ber. Dtsch. Chem. Ges., 1894, 27, 2985.
211. L. Pauling and R. B. Corey, Proc. Natl. Acad. Sci. U. S. A., 1951, 37, 272.
212. L. Pauling, R. B. Corey and H. R. Branson, Proc. Natl. Acad. Sci. U. S. A., 1951, 37, 205.
213. R. Mariz, A. Poater, M. Gatti, E. Drinkel, J. J. Bürgi, X. Luan, S. Blumentritt, A. Linden, L. Cavallo and R. Dorta, Chem. – Eur. J., 2010, 16, 14335.
214. J. J. Dunsford, D. S. Tromp, K. J. Cavell, C. J. Elsevier and B. M. Kariuki, Dalton Trans., 2013, 42, 7318.
215. F. Mazars, G. Zaragoza and L. Delaude, Inorg. Chim. Acta, 2023, 556, 121676.
216. L. Zapf, M. Riethmann, S. A. Föhrenbacher, M. Finze and U. Radius, Chem. Sci., 2023, 14, 2275.
217. P. Liu, J. Montgomery and K. N. Houk, J. Am. Chem. Soc., 2011, 133, 6956.
218. H. Wang, G. Lu, G. J. Sormunen, H. A. Malik, P. Liu and J. Montgomery, J. Am. Chem. Soc., 2017, 139, 9317.
219. A. Rajjak Shaikh, S. Posada-Pérez, A. Brotons-Rufes, J. J. Pajski, Vajiha, G. Kumar, A. Mateen, A. Poater, M. Solà, M. Chawla and L. Cavallo, J. Mol. Liq., 2022, 367, 120558.
220. I. Ritacco, M. Voccia, S. Impemba, M. F. Carmellone, S. Milione and L. Caporaso, Eur. J. Inorg. Chem., 2023, e202200588.
221. F. Vermersch, L. Oliveira, J. Hunter, M. Soleilhavoup, R. Jazzar and G. Bertrand, J. Org. Chem., 2022, 87, 3511.
222. A. Cicolella, E. Romano, V. Barone, C. De Rosa and G. Talarico, Organometallics, 2022, 41, 3872.
223. K. Bevernaege, N. Tzouras, A. Poater, L. Cavallo, S. P. Nolan, F. Nahra and J. Winne, Chem. Sci., 2023, 14, 9787.
224. L. Zapf, S. Peters, R. Bertermann, U. Radius and M. Finze, Chem. – Eur. J., 2022, 28, e202200275.
225. J. Poater, S. Escayola, A. Poater, F. Teixidor, H. Ottosson, C. Viñas and M. Solà, J. Am. Chem. Soc., 2023, 145, 22527.
226. V. Aomchad, S. Del Globo, A. Poater and V. D’Elia, Catal. Today, 2021, 375, 324.
227. T. P. Yoon and E. N. Jacobsen, Science, 2003, 299, 1691.
228. C. M. Weinstein, G. P. Junor, D. R. Tolentino, R. Jazzar, M. Melaimi and G. Bertrand, J. Am. Chem. Soc., 2018, 140, 9255.
229. M. Melaimi, R. Jazzar, M. Soleilhavoup and G. Bertrand, Angew. Chem., Int. Ed., 2017, 56, 10046.
230. W. Chu, T. Zhou, E. Bisz, B. Dziuk, R. Lalancette, R. Szostak and M. Szostak, Chem. Commun., 2022, 58, 13467.
231. L. M. Azofra, S. V. C. Vummaleti, Z. Zhang, A. Poater and L. Cavallo, Organometallics, 2020, 39, 3972.
232. P. Czerwinski, E. Molga, L. Cavallo, A. Poater and M. Michalak, Chem. – Eur. J., 2016, 22, 8089.
233. M. Dolna, M. Nowacki, O. Danylyuk, A. Brotons-Rufes, A. Poater and M. Michalak, J. Org. Chem., 2022, 87, 6115.
234. E. A. Martynova, M. Zuccarello, D. Kronenberg, M. Beliš, A. Czapik, Z. Zhang, K. Van Hecke, M. Kwit, O. Baudoin, L. Cavallo and S. P. Nolan, Dalton Trans., 2023, 52, 7558.
235. H. Clavier, A. Correa, L. Cavallo, E. C. Escudero-Adán, J. Benet-Buchholz, A. M. Z. Slawin and S. P. Nolan, Eur. J. Inorg. Chem., 2009, 1767.
236. V. Fasano, A. W. McFord, C. P. Butts, B. S. L. Collins, N. Fey, R. W. Alder and V. K. Aggarwal, Angew. Chem., Int. Ed., 2020, 59, 22403.
237. U. Prieto-Pascual, A. Martínez de Morentin, D. Choquesillo-Lazarte, A. Rodríguez-Diéguez, Z. Freixa and M. A. Huertos, Dalton Trans., 2023, 52, 9090.
238. C. P. Giarrusso, D. V. Zeil and V. L. Blair, Dalton Trans., 2023, 52, 7828.
239. G. Li, P. Lei, M. Szostak, E. Casals-Cruañas, A. Poater, L. Cavallo and S. P. Nolan, ChemCatChem, 2018, 10, 3096.
240. S. C. Shi, S. P. Nolan and M. Szostak, Acc. Chem. Res., 2018, 51, 2589.
241. S. Manzini, C. A. Urbina-Blanco, A. M. Z. Slawin and S. P. Nolan, Organometallics, 2012, 31, 6514.
242. A. Poater, L. Falivene, C. A. Urbina-Blanco, S. Manzini, S. P. Nolan and L. Cavallo, Dalton Trans., 2013, 42, 7433.
243. Q. Zhao, G. Meng, G. Li, R. Lalancette, R. Szostak and M. Szostak, Chem. Sci., 2021, 12, 10583.
244. J. Zhang, T. Li, X. Li, A. Lv, X. Li, Z. Wang, R. Wang, Y. Ma, R. Fang, R. Szostak and M. Szostak, Commun. Chem., 2022, 5, 60.
245. S. Engbers, E. A. Trifonova, K. M. van der Geest, W. J. Nauta, K. M. Hess and E. M. N. Klein, ChemCatChem, 2022, 14, e202200870.
246. Y.-Q. Zou, N. von Wolff, M. Rauch, M. Feller, Q.-Q. Zhou, A. Anaby, Y. Diskin-Posner, L. J. W. Shimon, L. Avram, Y. Ben-David and D. Milstein, Chem. – Eur. J., 2021, 27, 4715.
247. J. A. Luque-Urrutia and A. Poater, Inorg. Chem., 2017, 56, 14383.
248. M. Magre, E. Paffenholz, B. Maity, L. Cavallo and M. Rueping, J. Am. Chem. Soc., 2020, 142, 14286.
249. P. Viereck, G. Hierlmeier, P. Tosatti, T. P. Pabst, K. Puentener and P. J. Chirik, J. Am. Chem. Soc., 2022, 144, 11203.
250. G. Antinucci, B. Dereli, A. Vittoria, P. H. M. Budzelaar, R. Cipulla, G. P. Goryunov, P. S. Kulyabin, D. V. Uborsky, L. Cavallo, C. Ehm, A. Z. Voskoboynikov and V. Busico, ACS Catal., 2022, 12, 6934.
251. M. Kamitani, K. Yujiri and H. Yuge, Organometallics, 2020, 38, 3535.
252. S. H. Newman-Stonebraker, S. R. Smith, E. Borowski, E. Peters, T. Gensch, H. C. Johnson, M. S. Sigman and A. G. Doyle, Science, 2021, 374, 301.
253. N. Joly, L. Bettoni, S. Gaillard, A. Poater and J.-L. Renaud, J. Org. Chem., 2021, 86, 6813.
254. A. Shams, M. Mehdizadeh, H.-R. Teimoury, M. Emami, S. A. Mirmohammadi, S. Sadjadi, E. Bardají, A. Poater and N. Bahri-Laleh, J. Ind. Eng. Chem., 2022, 116, 359.
255. N. Bahri-Laleh, L. Falivene and L. Cavallo, Polyolefins J., 2014, 1, 139.
256. A. Palone, G. Casadevall, S. Ruiz-Barragan, A. Call, S. Osuna, M. Bietti and M. Costas, J. Am. Chem. Soc., 2023, 145, 15742.
257. G. Zuccarello, L. J. Nannini, A. Arroyo-Bondía, N. Fincias, I. Arranz, A. H. Pérez-Jimeno, M. Peeters, I. Martín-Torres, A. Sadurní, V. García-Vázquez, Y. Wang, M. S. Kirillova, M. Montesinos-Magraner, U. Caniparoli, G. D. Núñez, F. Maseras, M. Besora, I. Escofet and A. M. Echavarren, JACS Au, 2023, 3, 1742.
258. K. Matyjaszewski and N. V. Tsarevsky, J. Am. Chem. Soc., 2014, 136, 6513.
259. C. Fang, M. Fantin, X. Pan, K. De Fiebre, M. L. Coote, K. Matyjaszewski and P. Liu, J. Am. Chem. Soc., 2019, 141, 7486.
260. C. B. Santiago, J.-Y. Guo and M. S. Sigman, Chem. Sci., 2018, 9, 2398.
261. M. S. Sigman, K. C. Harper, E. N. Bess and A. Milo, Acc. Chem. Res., 2016, 49, 1292.
262. K. C. Harper and M. S. Sigman, Science, 2011, 333, 1875.
263. M. Orlandi, M. Escudero-Casao and G. Licini, J. Org. Chem., 2021, 86, 3555.
264. D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186.
265. K. Muratov and F. Gagosz, Angew. Chem., Int. Ed., 2022, 61, e202203452.
266. J. D. Pizarro, F. Molina, M. R. Fructos and P. J. Pérez, Organometallics, 2020, 39, 2553.
267. A. Cervantes-Reyes, T. Saxl, P. M. Stein, M. Rudolph, F. Rominger, A. M. Asiri and A. S. K. Hashmi, ChemSusChem, 2021, 14, 2367.
268. M. Yan, X. Kang, S. Li, X. Xu, Y. Luo, S. He and C. Chen, Organometallics, 2022, 41, 3212.
269. D. Liu, Z. Xu, X. Lu, H. Yu and Y. Fu, ACS Catal., 2022, 12, 13921.
270. A. Padunnappattu, C. Duhayon, V. César and Y. Canac, Organometallics, 2022, 41, 2868.
271. R. Wei, S. Ju and L. L. Liu, Angew. Chem., Int. Ed., 2022, 61, e202205618.
272. L. Poyac, S. Scoditi, X. Dumail, M. Granier, S. Clément, R. Gramage-Doria, C. H. Devillers and S. Richeter, Chem. Commun., 2022, 58, 13270.
273. X. Zhang, C. Yang, P. An, C. Cui, Y. Ma, Y. Ma, H. Liu, H. Wang, X. Yan, G. Li and Z. Tang, Sci Adv., 2022, 8, eadd5678.
274. S. Barman, E. A. Jaseer, N. Garcia, M. Elanany, M. Khawaji, W. Xu, S. Lin, H. Alasiri, M. N. Akhtar and R. Theravalappil, Chem. Commun., 2022, 58, 10044.
275. M. E. Greaves, T. O. Ronson, F. Maseras and D. J. Nelson, Organometallics, 2021, 40, 1997.
276. W. Smit, J. B. Ekeli, G. Occhipinti, B. Wozniak, K. W. Törnroos and V. R. Jensen, Organometallics, 2020, 39, 397.
277. L. Deng, T. K. Woo, L. Cavallo, P. M. Margl and T. Ziegler, J. Am. Chem. Soc., 1997, 119, 6177.
278. G. Talarico, V. Busico and L. Cavallo, Organometallics, 2004, 23, 5989.
279. W. Zhang, P. M. Waddell, M. A. Tiedemann, C. E. Padilla, J. Mei, L. Chen and B. P. Carrow, J. Am. Chem. Soc., 2018, 140, 8841.
280. J. E. Borowski, S. H. Newman-Stonebraker and A. G. Doyle, ACS Catal., 2023, 13, 7966.
281. O. D’Anania, C. De Rosa and G. Talarico, Molecules, 2023, 28, 3768.
282. A. Cicolella, E. Romano, V. Barone, C. De Rosa and G. Talarico, Organometallics, 2022, 41, 8872.
283. A. Hanifpour, N. Bahri-Laleh, M. Nekoomanesh-Haghighi and A. Poater, Mol. Catal., 2020, 493, 111047.
284. S. Zhang, C. Cao, W. Guo, Y. Zhang, M. Sun, W. Yang, L. He and Q. Huang, Ind. Eng. Chem. Res., 2022, 61, 17017.
285. L. T. Reilly, M. L. McGraw, F. D. Eckstrom, R. W. Clarke, K. A. Franklin, E. Rao Chokkapu, L. Cavallo, L. Falivene and E. Y.-X. Chen, J. Am. Chem. Soc., 2022, 144, 23572.
286. C. Duchemin, G. Smits and N. Cramer, Organometallics, 2019, 38, 4014.
287. S. B. Munoz, V. E. Fleischauer, W. W. Brennessel and M. L. Neidig, Organometallics, 2018, 37, 3093.
288. M. Koy, I. Elser, J. Meisner, J. W. Frey, K. Wurst, J. Kästner and M. R. Buchmeiser, Chem. – Eur. J., 2017, 23, 15484.
289. S. Naumann, K. Mundsinger, L. Cavallo and L. Falivene, Polym. Chem., 2017, 8, 5803.
290. M. Tabrizi, S. Sadjadi, G. Pareras, M. Nekoomanesh-Haghighi, N. Bahri-Laleh and A. Poater, J. Colloid Interface Sci., 2021, 581, 939.
291. S. Dehghani, S. Sadjadi, N. Bahri-Laleh, M. Nekoomanesh-Haghighi and A. Poater, Appl. Organomet. Chem., 2019, 33, e4891.
292. M. Fallah, N. Bahri-Laleh, K. Didehban and A. Poater, Appl. Organomet. Chem., 2020, 34, e5333.
293. F. Schwizer, Y. Okamoto, T. Heinisch, Y. Gu, M. M. Pellizzoni, V. Lebrun, R. Reuter, V. Köhler, J. C. Lewis and T. R. Ward, Chem. Rev., 2018, 118, 142.
294. D. Röthlisberger, O. Khersonsky, A. M. Wollacott, L. Jiang, J. DeChancie, J. Betker, J. L. Gallaher, E. A. Althoff, A. Zanghellini, O. Dym, S. Albeck, K. N. Houk, D. S. Tawfik and D. Baker, Nature, 2008, 453, 190.
295. O. W. Choroba, D. H. Williams and J. B. Spencer, J. Am. Chem. Soc., 2000, 122, 5389.
296. B. K. Hubbard, M. G. Tomas and C. T. Walsh, Chem. Biol., 2000, 7, 931.
297. S. M. Pratter, C. Konstantinovics, C. M. L. Di Giuro, E. Leitner, D. Kumar, S. P. de Visser, G. Grogan and G. D. Straganz, Angew. Chem., Int. Ed., 2013, 52, 9677.
298. J. Brownlee, P. He, G. R. Moran and D. H. Harrison, Biochemistry, 2008, 47, 2002.
299. L. Zhang, D. Lin, X. Sun, U. Curth, C. Drosten, L. Sauerhering, S. Becker, K. Rox and R. Hilgenfeld, Science, 2020, 368, 409.
300. A. Poater, J. Phys. Chem. Lett., 2020, 11, 6262.
301. M. Solà, Front. Chem. Lett., 2017, 5, 22.
302. S. Posada-Pérez, S. Escayola, J. Poater, M. Solà and A. Poater, Dalton Trans., 2022, 51, 12585.
303. S. J. Hubbard, S. F. Campbell and J. M. Tornton, J. Mol. Biol., 1991, 220, 507.
304. A. Vidal-López, S. Posada-Pérez, M. Solà, V. D. Elia and A. Poater, Green Chem. Eng., 2022, 3, 180.
305. J. Hostaš and J. Řezáč, J. Chem. Theory Comput., 2017, 13, 3575.
306. J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104.
307. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652.
308. A. H. Mühlbach, A. C. Vaucher and M. Reiher, J. Chem. Theory Comput., 2016, 12, 1228.
309. D. Wu, D. W. Rosen, L. Wang and D. Schaefer, Comput. Aided Des., 2015, 59, 1.
310. A. Bender, N. Schneider, M. Segler, W. P. Walters, O. Engkvist and T. Rodrigues, Nat. Rev. Chem., 2022, 6, 428.
311. C. Wu, Z. Chang, C. Peng, C. Bai, J. Xing and X. Dou, Chem. Sci., 2023, 14, 7980.
312. L. Killian, R. L. M. Bienenmann and D. L. J. Broere, Organometallics, 2023, 42, 27.
313. G. dos Passos Gomes, P. Friedrich and T. Gensch, https://github.com/digital-chemistry-laboratory/morfeus (accessed on 17/08/2023).
314. M. Portnoy and D. Milstein, Organometallics, 1993, 12, 1655.
315. P. W. N. M. Van Leeuwen, P. C. J. Kamer, L. A. Van der Veen and J. N. H. Reek, Chin. J. Chem., 2001, 19, 1.
316. J. Mathew, T. Thomas and C. H. Suresh, Inorg. Chem., 2007, 46, 10800.
317. G. K. Fukin, I. A. Guzei and E. V. Baranov, J. Coord. Chem., 2008, 61, 1678.
318. I. A. Guzei and M. Wendt, Dalton Trans., 2006, 3991.
319. D. Balcells and B. B. Skjelstad, J. Chem. Inf. Model., 2020, 60, 6135.
320. C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, WIREs Comput. Mol. Sci., 2021, 11, e1493.

---