Open Access Article
Open Access ArticleCOMPAS-3: a dataset of peri-condensed polybenzenoid hydrocarbons†
Alexandra
Wahab
a and
Renana
Gershoni-Poranne
 *b
*b
aThe Laboratory for Organic Chemistry, Department of Chemistry and Applied Biosciences, ETH Zurich, 8093 Zurich, Switzerland
bThe Schulich Faculty of Chemistry and the Resnick Sustainability Center for Catalysis, Technion - Israel Institute of Technology, Haifa 32000, Israel. E-mail: rporanne@technion.ac.il
First published on 14th May 2024
Abstract
We introduce the third installment of the COMPAS Project – a COMputational database of Polycyclic Aromatic Systems, focused on peri-condensed polybenzenoid hydrocarbons. In this installment, we develop two datasets containing the optimized ground-state structures and a selection of molecular properties of ∼39k and ∼9k peri-condensed polybenzenoid hydrocarbons (at the GFN2-xTB and CAM-B3LYP-D3BJ/cc-pvdz//CAM-B3LYP-D3BJ/def2-SVP levels, respectively). The manuscript details the enumeration and data generation processes and describes the information available within the datasets. An in-depth comparison between the two types of computation is performed, and it is found that the geometrical disagreement is maximal for slightly-distorted molecules. In addition, a data-driven analysis of the structure–property trends of peri-condensed PBHs is performed, highlighting the effect of the size of peri-condensed islands and linearly annulated rings on the HOMO–LUMO gap. The insights described herein are important for rational design of novel functional aromatic molecules for use in, e.g., organic electronics. The generated datasets provide a basis for additional data-driven machine- and deep-learning studies in chemistry.
Introduction
Polybenzenoid hydrocarbons (PBHs) are polycyclic aromatic systems (PASs) that contain only fused benzene rings. PBHs can be considered as cutouts from a graphene sheet and can be further divided into cata-condensed and peri-condensed PBHs (cc-PBHs and pc-PBHs, respectively; see Fig. 1). The difference lies in the way the benzene rings are fused to one another. While in cc-PBHs, any carbon atom can be shared by at most two adjacent rings, in pc-PBHs, a single carbon can be shared by up to three rings, which leads to the formation of “2D” structures. Because they contain only benzene—the prototypical aromatic system—PBHs are sometimes considered the prototypical PASs and serve as model systems for investigating chemical concepts such as aromaticity1 and reactivity.2 In addition to their importance for fundamental studies, PBHs are pervasive in both the natural and man-made environments, and play key roles in multiple areas of research, including the formation of stars,3–6 human health,7 environmental impact,8 and—more recently—as promising materials for organic electronics.9 PASs in general, and PBHs in particular, have been used for a variety of electronic and optoelectronic technologies, including field effect transistors,10–14 solar cells,15 chemical sensors,16 anode and cathode materials,17–21 and anolytes22 for redox-flow batteries.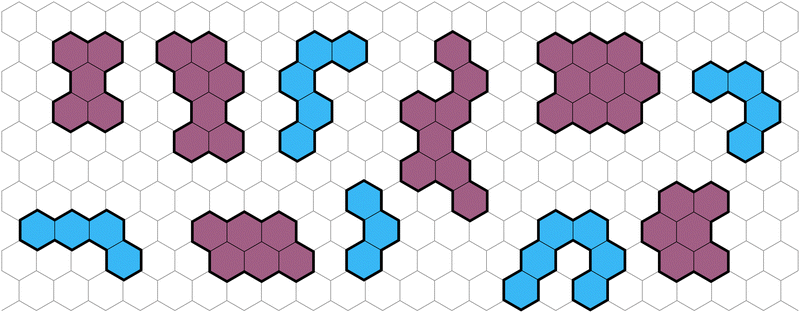 | ||
| Fig. 1 Representative examples of PBHs on a background of a hexagonal grid, cc-PBHs are colored in blue and pc-PBHs are colored in purple. | ||
Thanks to the decades of intensive computational and experimental research into PBHs, a great deal has already been discovered about them (e.g., edge effects)23–25 and several models have been developed to understand and predict their behavior (e.g., Clar's sextet theory,26–28 the Y-rule,29–31 annellation theory,32 and our own additivity approach).33,34 Nonetheless, certain aspects of their structure–property relationships remain poorly understood, which impedes rational design of improved PBH-based candidates. Recent reports on the synthesis35–38 and characterization of challenging PBHs and on computational developments39–42 aimed at further elucidation of their properties underline the ongoing interest in PBH systems and the importance of obtaining reliable and useful data for them.
Data-driven investigations, which have become increasingly accessible due to advances in computational abilities, have the potential to address these knowledge gaps, thus both deepening our chemical understanding and enabling practical molecular design. Such tools have already been applied in the chemical space of PASs, including studies focused on spectra prediction,43 performing brute-force high-throughput screenings for organic electronics,44,45 active discovery of organic semiconductors,46 and design of organic electronic materials with generative models.47 As a result, several databases have been constructed that include PASs, which focus on general chemical data,48,49 computational benchmark data,50 spectroscopic data for astrochemical studies,51–56 aromaticity,57 and organic electronic materials.58,59 However, most of these databases focus on extant molecules, or generate molecules that are biased towards certain functionalities, thus neglecting large swaths of chemical space that may contain promising new structural motifs. Furthermore, they either contain too few data (less than 1000 entries), are not consistently curated, and/or include an unsystematic mixture of PASs from different subclasses. To overcome this problem a large, systematically constructed, and well-curated database of PAS compounds is needed. To address the paucity of PAS data, our group conceptualized and initiated the first COMputational database of Polycyclic Aromatic Systems—the COMPAS Project. The COMPAS Project is designed to house several datasets, each comprising a carefully curated and methodical enumeration of the chemical space of a certain subclass of PASs, calculated at a uniform level of theory. The first installment, COMPAS-1,60 focuses on ground-state cata-condensed polybenzenoid hydrocarbons; the second installment, COMPAS-2,61 focuses on ground-state cata-condensed heterocyclic PASs. COMPAS-1 and COMPAS-2 have already been used to provide the first examples of interpretable machine and deep-learning models for PASs62,63 and to demonstrate the first generative design of PASs with targeted properties.64 Both datasets, as well as all future installments, are freely available for use, according to the FAIR65 principles of data sharing. Herein, we report on the third installment, COMPAS-3, which expands the COMPAS database to peri-condensed PBHs (pc-PBHs) in the ground state. Similarly to the previous two installments, COMPAS-3 contains two computationally-generated datasets: (1) COMPAS-3D—8844 peri-condensed PBHs comprising 1–10 rings, calculated with density functional theory (DFT) at the CAM-B3LYP-D3BJ/aug-cc-pVDZ//CAM-B3LYP-D3BJ/def2-SVP level of theory; (2) COMPAS-3x—39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482 peri-condensed PBHs comprising 1–11 rings, calculated with xTB using GFN2-xTB.
482 peri-condensed PBHs comprising 1–11 rings, calculated with xTB using GFN2-xTB.
This manuscript is divided into three main sections: (a) a description of the data generation workflow and the contents of each of the datasets; (b) a comparison between the two datasets and discussion of the differences between the two levels of computations; and (c) an analysis of the data, showcasing structure–property relationships that are revealed from the trends in the data.
Data generation workflow
The third installment of the COMPAS database focuses on peri-condensed PBHs (pc-PBHs, also known as perifusenes). The data generation workflow is depicted in Fig. 2. In the following sections, we describe in detail each step of the workflow.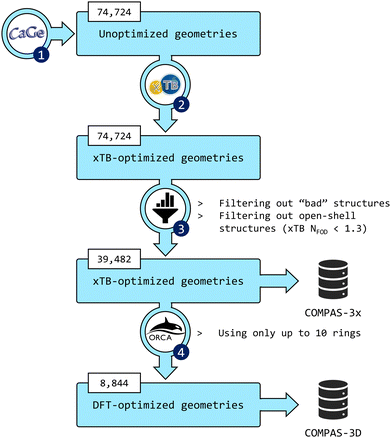 | ||
Fig. 2 Flowchart of the data-generation process. (1) CaGe66 was used to generate unoptimized geometries of pc-PBHs containing up to 11 rings. (2) xTB was used to optimize all geometries. (3) The data were filtered to remove invalid and/or unwanted molecules. The geometries and properties of the remaining molecules comprise the COMPAS-3x dataset (39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482 molecules). (4) DFT was used to further optimize the pc-PBHs containing up to 10 rings. The geometries and properties of these 8844 molecules comprise the COMPAS-3D dataset. 482 molecules). (4) DFT was used to further optimize the pc-PBHs containing up to 10 rings. The geometries and properties of these 8844 molecules comprise the COMPAS-3D dataset. | ||
Step 1. Structure enumeration
We began by enumerating the chemical space of pc-PBHs containing up to 11 rings. We emphasize that, by design, our COMPAS-3 datasets contain only closed-shell PBHs and, therefore, do not represent exhaustive enumerations (i.e., do not contain all possible pc-PBHs). We deliberately excluded all systems with (poly)radical/(poly)radicaloid character. Though such systems are undoubtedly of interest for both fundamental and practical reasons, we believe they are distinct from closed-shell molecules and should be computed and analyzed separately.We differentiate between three cases of open-shell character in the ground state (Fig. 3): (A) an odd number of hydrogens/carbons (e.g., phenalenyl radical, C13H9, is a three-ring pc-PBH with a single unpaired electron); (B) non-Kekuléan structures, i.e., PBHs for which no classical closed-shell valence structure can be drawn67,68 (e.g., triangulene, C22H12, is a non-Kekuléan six-ring pc-PBH with two unpaired electrons in the ground state); and (C) molecules that possess a closed-shell resonance structure, but have appreciable diradical character, which is a relatively common occurrence in pc-PBHs, due to their extended conjugation (e.g., zethrenes).68
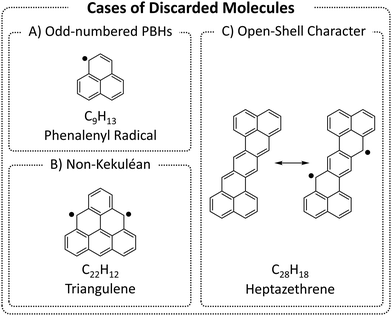 | ||
| Fig. 3 Representative examples of the three cases of (poly)radical/(poly)radicaloid molecules that were discarded from COMPAS-3. | ||
The first case can be dealt with quite easily. pc-PBHs containing the same number of rings may or may not be isomers (i.e., they may contain differing numbers of carbon and hydrogen atoms, despite having the same number of rings). Hence, in contrast to cc-PBHs, for pc-PBHs various molecular formulae exist per family (“families” are separated according to and referred to by the number of rings in the isomers). Since all formulae containing an odd number of hydrogens/carbons describe obviously radical systems, these cases were easily identified and discarded prior to structure enumeration. The remaining molecular formulae and corresponding numbers of isomers for each family are detailed in Table 1.
| No. rings | Molecular formula | Initial no. isomers (CaGe) | Final no. isomers |
|---|---|---|---|
| 4 | C16H10 | 1 | 1 |
| 5 | C20H12 | 3 | 3 |
| 6 | C22H12 | 3 | 2 |
| C24H14 | 14 | 13 | |
| 7 | C24H12 | 1 | 1 |
| C26H14 | 10 | 9 | |
| C28H16 | 67 | 58 | |
| 8 | C28H14 | 9 | 8 |
| C30H16 | 67 | 57 | |
| C32H18 | 340 | 264 | |
| 9 | C30H14 | 4 | 3 |
| C32H16 | 55 | 44 | |
| C34H18 | 398 | 308 | |
| C36H20 | 1710 | 1182 | |
| 10 | C32H14 | 1 | 1 |
| C34H16 | 42 | 32 | |
| C36H18 | 547 | 180 | |
| C38H20 | 2439 | 1594 | |
| C40H22 | 8561 | 5084 | |
| 11 | C36H16 | 26 | 17 |
| C38H18 | 333 | 216 | |
| C40H20 | 2874 | 1683 | |
| C42H22 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 598 598 |
7662 | |
| C44H24 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 621 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 060 060 |
|
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 724 724
|
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 482 482
|
We then used the chemical & abstract graph environment (CaGe) software66 to obtain the initial (unoptimized) xyz coordinates of the 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 724 structures corresponding to the chemical formulae in Table 1 (Fig. 2, step 1). We implemented subsequent filtering steps to identify and discard the non-Kekuléan structures and the molecules with open-shell character (vide infra). Table 1 details the initial (generated by CaGe) and final (following filtering) numbers of isomers predicted for each family and each chemical formula of pc-PBHs.
724 structures corresponding to the chemical formulae in Table 1 (Fig. 2, step 1). We implemented subsequent filtering steps to identify and discard the non-Kekuléan structures and the molecules with open-shell character (vide infra). Table 1 details the initial (generated by CaGe) and final (following filtering) numbers of isomers predicted for each family and each chemical formula of pc-PBHs.
Step 2. xTB optimization
The 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 724 molecules enumerated by CaGe were optimized with the GFN2-xTB method,69 xTB70 version 6.2. Harmonic vibrational frequencies were calculated after structure optimization to ensure true minima on the potential energy surface (i.e., Nimag = 0; Fig. 2, step 2). Following data filtering (vide infra), a total of 39
724 molecules enumerated by CaGe were optimized with the GFN2-xTB method,69 xTB70 version 6.2. Harmonic vibrational frequencies were calculated after structure optimization to ensure true minima on the potential energy surface (i.e., Nimag = 0; Fig. 2, step 2). Following data filtering (vide infra), a total of 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482 molecules were retained. For each of these, xTB calculations and subsequent frequencies calculations were performed to optimize the cationic and anionic forms as well. The geometries and properties of these 39
482 molecules were retained. For each of these, xTB calculations and subsequent frequencies calculations were performed to optimize the cationic and anionic forms as well. The geometries and properties of these 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482 pc-PBHs containing up to 11 rings comprise the dataset denoted as COMPAS-3x (see Table 1).
482 pc-PBHs containing up to 11 rings comprise the dataset denoted as COMPAS-3x (see Table 1).
Step 3. Data filtering
Following structure optimization with xTB, we filtered the data to remove two types of unwanted molecules: (a) those that do not have a closed-shell ground state (as discussed above) and (b) those that did not converge to valid geometries during the optimization process.The first case includes non-Kekuléan structures and molecules that have non-negligible open-shell character in the ground state, which we excluded by design. The second case includes molecules that, for technical reasons, did not cleanly converge to a PBH structure and needed to be removed to guarantee data reliability. For example, a structure containing sp3-hybridized carbons—all carbon atoms in PBHs should be sp2-hybridized. Such cases can arise when two carbon atoms, which are not supposed to share a bond, are located very closely in the starting geometry. Consequently, a spurious bond may be generated between these two carbons during the optimization process.
To identify the different types of undesired molecules, we first generated the SMILES strings of all xTB-optimized structures using the xyz2mol71 script. Molecules were discarded in any of the three following cases: (a) if a SMILES string was not generated (an indication of an invalid chemical structure); (b) if it contained any of the characters ‘@’, ‘=’, or ‘C’, (an indication of an sp3-hybridized carbon); or (c) if it contained any of the characters ‘[’,‘]’, ‘−’, or ‘+’ (an indication of radical structure, which SMILES often wrongly denotes with charge). Following this filtering step, 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820 molecules remained (i.e., 74.7% of the initial dataset). The majority of the discarded molecules (16
820 molecules remained (i.e., 74.7% of the initial dataset). The majority of the discarded molecules (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 133 out of 18
133 out of 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 904 molecules, or 85.3%) contained ‘+’ and/or ‘−’ in their SMILES string, which implies non-Kekuléan structure. Only 14.7% of the discarded molecules were removed due to problems in the optimization process.
904 molecules, or 85.3%) contained ‘+’ and/or ‘−’ in their SMILES string, which implies non-Kekuléan structure. Only 14.7% of the discarded molecules were removed due to problems in the optimization process.
Finally, we used the NFOD metric72 to remove any molecules with significant open-shell/diradical character. We note that, in a recent contribution, Lischka and coworkers demonstrated that the NFOD metric is a reliable alternative to the more demanding multi-reference calculations usually needed to determine open-shell character.73 We previously benchmarked methods for identification of diradical character and established a threshold of NFOD = 1.3 as the cutoff value (we refer the reader to the ESI of ref. 63). Thus, molecules with NFOD ≥ 1.3 were removed from the COMPAS-3 datasets, providing a final tally of 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482 molecules. It is notable that, of the initial 74
482 molecules. It is notable that, of the initial 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 724 pc-PBHs generated by CaGe, approximately 44% do not have a closed-shell ground state according to these criteria. We also highlight that other methods exist to identify open-shell character, such as the pioneering method of Lischka and coworkers from 2016.74
724 pc-PBHs generated by CaGe, approximately 44% do not have a closed-shell ground state according to these criteria. We also highlight that other methods exist to identify open-shell character, such as the pioneering method of Lischka and coworkers from 2016.74
Step 4. Further optimization with DFT
Only the molecules containing up to 10 rings were subjected to further optimization at the DFT level. The good linear correlation between xTB- and DFT-calculated properties (vide infra) demonstrates that, if desired, a linear fitting can be used to estimate DFT-level accuracy of larger molecules (see section agreement between xTB and DFT). Thus, it was deemed unnecessary to perform the more computationally expensive DFT calculations for the largest molecules.The geometries of 8844 molecules were optimized with ORCA version 5.0.375,76 using the CAM-B3LYP77–81 functional with Grimme's D382 dispersion correction with Becke Johnson damping, in combination with the def2-SVP basis set.83,84 Single-point calculations were performed on the optimized geometries using the aug-cc-pVDZ85–87 basis set (in short: CAM-B3LYP-D3BJ/aug-cc-pVDZ//CAM-B3LYP-D3BJ/def2-SVP). These methods were selected following a literature search88 and a subsequent benchmarking procedure (see Section S2 of the ESI†). The resulting DFT-optimized geometries and properties form the dataset denoted as COMPAS-3D.
Representations and properties
The list of properties provided for the molecules in the two datasets, COMPAS-3x and COMPAS-3D, is detailed in Table 2.| Properties | COMPAS-3x | COMPAS-3D |
|---|---|---|
| HOMO | ✓ | ✓ |
| LUMO | ✓ | ✓ |
| HLG | ✓ | ✓ |
| SPE (neutral) | ✓ | ✓ |
| SPE (cation) | ✓ | ✓ |
| SPE (anion) | ✓ | ✓ |
| E rel (neutral) | ✓ | ✓ |
| ZPE (neutral) | ✓ | |
| ZPE (cation) | ✓ | |
| ZPE (anion) | ✓ | |
| aIP | ✓ | ✓ |
| aEA | ✓ | ✓ |
| Disp. corr. | ✓ | ✓ |
| Dipole moment | ✓ | ✓ |
| Corrected HOMO | ✓ | |
| Corrected LUMO | ✓ | |
| Corrected HLG | ✓ | |
| Corrected aIP | ✓ | |
| Corrected aEA | ✓ | |
| N FOD | ✓ | ✓ |
| y value | ✓ |
Table 2 lists the properties contained in the COMPAS-3x and COMPAS-3D datasets. The common properties are the energies of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO), the HOMO–LUMO gap (HLG), the dispersion-corrected single point energy (SPE)—i.e., the energy of the optimized structure without zero-point corrections—for the neutral and charged species, the relative energy (Erel)—i.e., the difference in SPE between each molecule and its lowest-energy isomer—for the neutral species, the adiabatic ionization potential (aIP), the adiabatic electron affinity (aEA), the dispersion correction (disp. corr.), the dipole moment, and the NFOD. The aIP and aEA represent the SPE difference between the optimized neutral species and optimized positively and negatively charged species, respectively.
COMPAS-3x contains the zero-point energies (ZPEs) for all species (neutral and charged ±1) while COMPAS-3D does not (we did not perform frequency calculations at the DFT level). ZPE corrections have been shown to not be highly method-dependent,89 and thus can be used across methods, if desired.
For several of the properties, the xTB values were corrected to DFT-level, using the respective fitting regressions (see Fig. 6 and Table 3). These values are labeled as “Corrected” in the COMPAS-3x dataset. Additional information on the regressions is given in Section S3 of the ESI.† An in-depth comparison between the two methods is described in the following section.
| Properties | COMPAS-1 | COMPAS-3 | ||
|---|---|---|---|---|
| Slope | Intercept | Slope | Intercept | |
| HOMO | 1.618 | 9.128 | 1.556 | 8.554 |
| LUMO | 1.256 | 8.482 | 1.286 | 8.740 |
| HLG | 1.424 | 2.519 | 1.422 | 2.527 |
| aIP | 1.262 | −7.441 | 1.442 | −9.578 |
| aEA | 1.059 | 5.509 | 1.216 | 6.425 |
| E rel | 1.490 | 0.077 | 1.513 | 0.037 |
Agreement between xTB and DFT
We examined the agreement between the two chosen computation methods in two aspects: geometry and molecular properties.Geometries
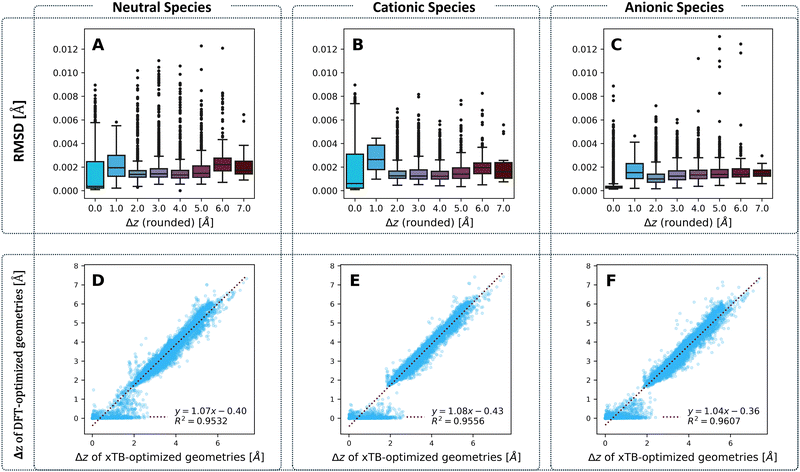
To compare the optimized geometries, we calculated the root mean square deviation (RMSD) between the geometries obtained for each molecule with the two methods, respectively. Our previous work on cc-PBHs showed that xTB and DFT do not always agree on the extent of non-planarity.60 Therefore, we examined the behavior of the RMSD in relation to molecular non-planarity, as measured by Δz (defined as the difference between the highest and lowest coordinate on the z axis after placing the molecules in the xy plane). Overall, the agreement between the methods is excellent (Fig. 4), with deviations well below 0.015 Å. We expected to observe that RMSD increases as Δz increases, however, Fig. 4A–C shows that the RMSD is relatively stable for Δz > 2.0 Å, with only a subtle increase towards the most distorted molecules. Much more surprisingly, we observed that the molecules with Δz close to 1 Å have the largest RMSD (notably, this behavior repeats itself in the RMSDs between the neutral and charged species for DFT-optimized structures, see Fig. S5 in the ESI†). In short, while xTB and DFT geometries generally agree very well, their agreement is stronger for noticeably non-planar molecules and is weakest for molecules having only a small deviation from planarity.To probe this behavior further, we plotted the Δz values from the two methods against one another (Fig. 4D–F) for the neutral, cationic, and anionic species. These plots reiterate the conclusion we reached on the basis of RMSD: the two methods have an excellent agreement on the extent of non-planarity only for molecules with Δz > 2 Å; the agreement is substantially poorer for molecules that are less distorted (i.e., more planar). Specifically, for such molecules, whereas the xTB values are spread out over the range [0,2] Å, the majority of DFT values are close to 0 Å. Meaning, DFT predicts almost completely planar geometries for these molecules while xTB predicts distortion from planarity.
This raises the question: what are the two methods treating differently, to arrive at these different geometries? One possible source of discrepancy could be the dispersion correction: our DFT calculations included Grimme's D3 dispersion correction, while xTB uses the D4 correction by default. Nonetheless, this possibility was ruled out, as the two different corrections actually show an excellent agreement, especially at smaller Δz values (see Fig. S21 in the ESI†). In principle, polycyclic aromatic systems should strive for planarity as a consequence of the sp2 hybridization of the comprising carbons. Moreover, planarity ensures better orbital overlap and therefore increased electron delocalization and aromatic stabilization. Such systems distort from planarity only when cove, fjord, and helix motifs are involved. For such motifs, the steric hindrance between hydrogens in the curved area forces the carbon scaffold out of planarity, incurring torsional strain. The fact that xTB predicts non-planar geometries suggests that it estimates this steric hindrance to be more costly than both the energetic cost of torsional strain and the stabilization gain of planarization. Conversely, the fact that DFT predicts planar geometries suggests that it either estimates the cost of torsional strain to be greater than the cost of the hydrogen–hydrogen steric hindrance, or estimates the gain of aromatic stabilization to be greater than the cost of steric hindrance. It is worth noting that previous results from our group and others have indicated that such small deviations from planarity have only a minor effect on aromatic stabilization.90,91 Thus, we believe the balance between torsional strain and steric hindrance is the more influential effect. We discuss this issue further in the section on Erel.
Molecular properties
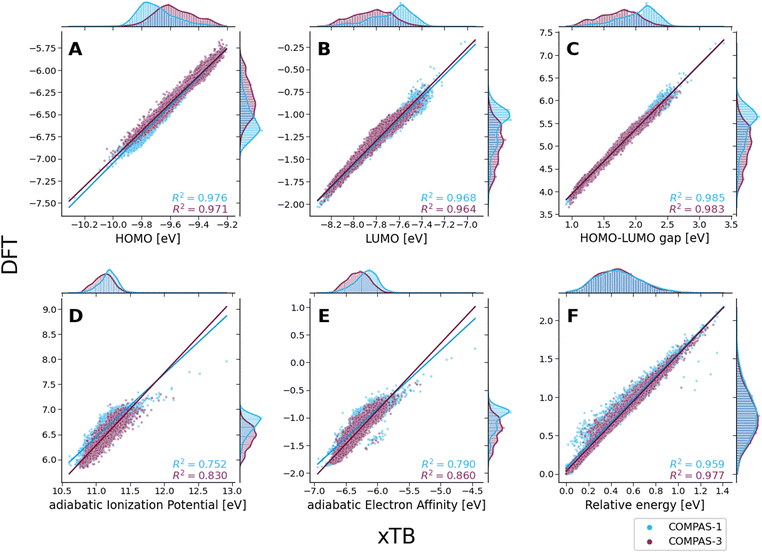
To evaluate the agreement between xTB and DFT on molecular properties, we generated violin plots of the probability distributions of the calculated properties using kernel density estimates (KDEs). Fig. 5 shows marked shifts, meaning the property values provided by the two levels of computation cover distinctly different ranges. The presence of such shifts, as well as their respective directions (i.e., higher or lower), are similar to those we observed for COMPAS-160 and were also previously noted by Bannwarth et al.69 For the HOMO, LUMO, HLG, and aEA, xTB underestimates the values by approximately 3 eV, 6 eV, 3 eV, and 5 eV, respectively. In contrast, for the aIP, xTB overestimates the values by approximately 5 eV.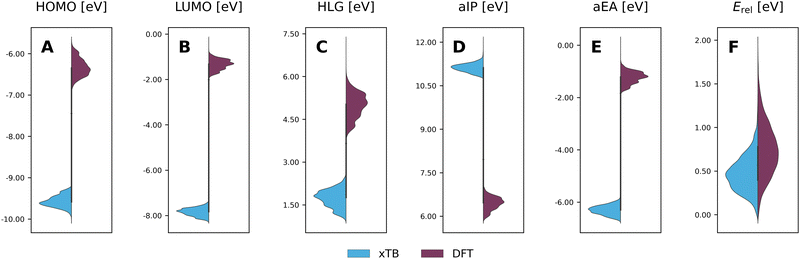 | ||
| Fig. 5 Violin plots of xTB-calculated (blue) properties vs. DFT-calculated (purple) properties: (A) HOMO; (B) LUMO; (C) HLG; (D) aIP; (E) aEA; (F) Erel. All values are reported in eV. | ||
Despite these shifts, the KDE profiles of the xTB- and DFT-calculated properties (with the exclusion of Erel, which is discussed in further detail, vide infra) are very similar, as confirmed by the good linear correlations observed between the two computational methods (Fig. 6A–E). For comparison, these plots detail the correlations for both COMPAS-1 (blue) and COMPAS-3 (purple). We note, however, that the slopes of all linear regressions are not equal to 1 (see Table 3), meaning that the difference between the methods is not simply a constant offset. We also note that the individual fitting equations for the various properties are very similar for COMPAS-1 and COMPAS-3, with the exception of the aIP and the aEA. Additionally, for the latter two properties, the pc-PBHs show better agreement with the linear fits. We believe that the pc-PBHs show slightly better agreement because they tend to be more planar than the cc-PBHs (less opportunity to form helical motifs). Nevertheless, it is clear that for most properties, one equation per property is sufficient to “correct” xTB values to DFT ones for both the COMPAS-1 and COMPAS-3 datasets, allowing inexpensive generation of additional data in the future. We refer the reader to Section S5.2 of the ESI† for further discussion on the aIP and aEA calculations, including the relationship to non-planarity and additional analysis of the outliers seen in the aEA plot.
Based on our previous RMSD analysis, we can rule out that the differences in energies stem from differences in geometries (despite the disagreement around Δz = 1 Å for a small fraction of molecules, there is an overall excellent agreement between the xTB- and DFT-optimized geometries). Nevertheless, the special case of the close-to-planar molecules discussed above already hinted at the possible source of discrepancy between the methods.
One can interpret the difference in Erel as the sum of differences in aromatic stabilization and differences in strain between any given molecule and its lowest-energy isomer. Seen in this light, we may ask if the difference in Erel arises from (a) estimation of strain (steric and torsional), (b) estimation of aromatic stabilization, or (c) both?
In this regard, we note that we deliberately chose the CAM-B3LYP functional, which has been shown not to suffer from over-delocalization errors;92,93 such errors could lead to spurious results, including exaggerated planarity and over-estimation of aromatic stabilization. Nevertheless, to try to pinpoint the source of the discrepancy, we studied the relationship between the size of the molecule and the difference in relative energy, ΔErel = Erel(DFT) − Erel(xTB). We hypothesized that if the difference stems from the way aromatic stabilization energy is estimated, then increasing the number of rings/atoms should exacerbate the problem, because of the extension of the conjugated system. In contrast, large molecules do not necessarily incur strain (in particular, torsional/helical strain) simply because they are larger; it depends on their exact geometry. Our analysis showed that the effect of the number of rings is minimal, and the effect of the number of atoms is inconsequential (see Fig. S22 in the ESI†).
We next investigated whether the issue lies with the estimation of strain, by probing the relationship between ΔErel and Δz (the deviation from planarity, which corresponds to torsional strain). Fig. 7 presents the obtained correlation, which demonstrates that an increased deviation from planarity coincides with an increase in ΔErel. To highlight that the deviation from planarity is specifically due to the existence of helical motifs, we colored the individual data points according to the largest helicene present in the molecule ([n]Helicenes—where n represents the number of rings present in the helical structure). The obvious stratification of the colored data points shows this effect clearly.
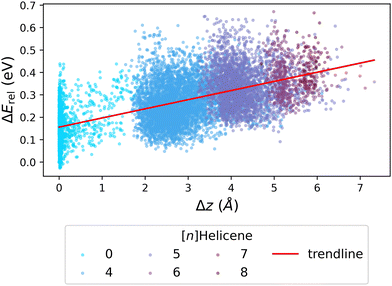 | ||
| Fig. 7 Scatter plot of ΔErelvs. Δz, colored by the longest [n]Helicene present in the molecule (0 indicates no helicene motifs). The red line shows the trendline of the data. | ||
To summarize, although we cannot affirmatively identify the source of the discrepancy in Erel between xTB and DFT, our results suggest that the issue lies in the estimation of steric hindrance versus torsional strain. This rationalization is relevant both to the Erel and to the geometry discrepancies described above for close-to-planar molecules. It is interesting to note that the two methods, xTB and DFT, have different areas of agreement when it comes to energies and geometries. Whereas the geometric differences are greatest for molecules with small deviations from planarity, the energy differences are largest for molecules that have much more pronounced non-planarity. This once again highlights that obtaining the optimized geometry for close-to-planar molecules is a subtle balance of effects.
Data analysis
In this section, we provide a data-driven chemical analysis of the COMPAS-3 datasets, including an overview of structural and property space and identification of structure–property relationships.Overview of COMPAS-3
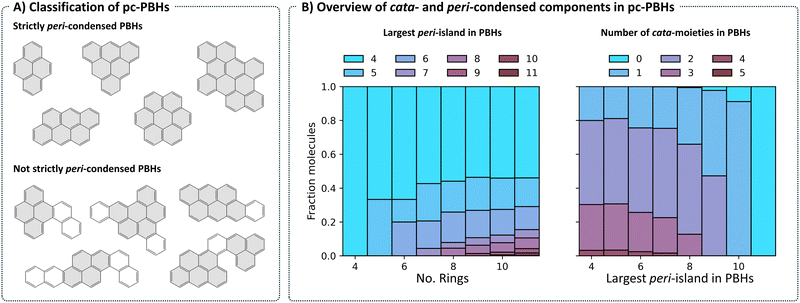
Structurally, COMPAS-3 is very similar to COMPAS-1—both contain molecules made of up to 11 benzene rings. However, as explained above, they differ in the manner of condensation. While cc-PBHs contain only cata-condensed carbons, pc-PBHs can be further divided into two categories: (a) “strictly peri-condensed”, which contain only peri-condensed carbons (also known as nanographenes); and (b) “not-strictly peri-condensed”, contain a mixture of peri-condensed and cata-condensed carbons. Given the combinatorial possibilities, there exist many more of the latter category (99%) than of the former (1%). Representative examples of molecules from each of the two categories are shown in Fig. 8A. For such molecules, we use the term peri-island to refer to the peri-condensed component(s) and the term cata-moiety to refer to their cata-condensed component(s) (colored in gray and white, respectively, in Fig. 8A).The most prevalent peri-island (53%) is the 4-ring island, i.e., pyrene, which is also the smallest Kekuléan pc-PBH. As the numbers of rings in the molecules grow, larger peri-islands can form (Fig. 8B, left). At the same time, because the total number of rings is limited, larger peri-islands also preclude the existence of multiple cata-moieties (Fig. 8B, right).
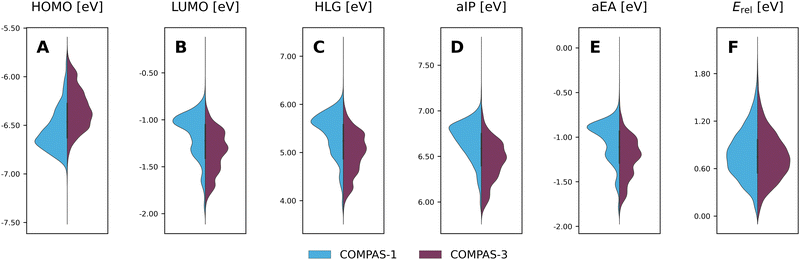
Considering the structural similarity between the COMPAS-1 and COMPAS-3 molecules, it is not surprising that the ranges of properties for the two datasets are similar, as seen in the violin plots in Fig. 9 (COMPAS-1 is shown in light blue and COMPAS-3 is shown in purple). Nevertheless, they are not identical. For example, Fig. 9A–C show that the distributions of the cc-PBHs are more heavily weighted towards lower HOMO values, higher LUMO values, and higher HLG values than the pc-PBHs. COMPAS-1 also shows broader distributions for both aIP and aEA (Fig. 9D and E), as well as a shift of the distribution peaks towards higher values in both cases. We note that, to facilitate the comparison, we recalculated the COMPAS-1D dataset at the same level as COMPAS-3D (in the original publication of COMPAS-1D we used B3LYP-D3BJ/def2-SVP;60 for comparison between the two levels of theory for COMPAS-1, see Section S4 in the ESI†).
Thus, it is apparent from these data that despite the general similarity between the cc-PBH and pc-PBH sub-classes, the inclusion of peri-condensed components does have an affect on the molecular properties. In the following sections, we investigate these effects.
Trends within the data
pc-PBHs have long held the interest of chemists and materials scientists, and have been investigated thoroughly both experimentally and computationally (vide supra). Nevertheless, to the best of our knowledge, a large-scale data-driven investigation has never before been reported. The COMPAS-3 datasets provide a unique opportunity to conduct such a study and uncover new chemical insights and structure–property relationships. In this section, we focus on COMPAS-3D, containing the DFT-calculated properties.We began by analyzing the relationship between molecular size and molecular properties. To avoid ambiguity, we opted to use the ring count as the measure of size. This means that several molecular stoichiometries are contained in the same “size” category. Also, under this classification, coronene is considered part of the 7-ring family (it contains 6 peripheral rings and 1 central ring), even though its molecular formula assigns it as a 6-ring isomer.
Fig. 10 presents boxplots of the HLG, separated and colored according to multiple different structural features.
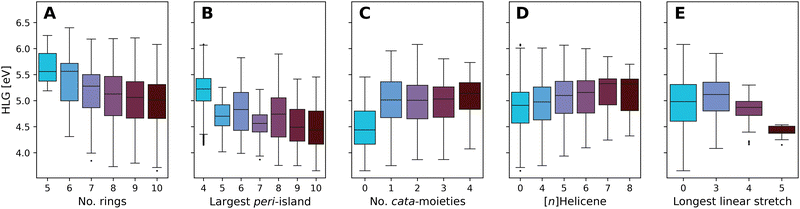 | ||
| Fig. 10 Boxplots of the DFT-calculated values of the HLG, colored by: (A) number of rings, (B) number of rings in the largest peri-island, (C) number of cata-moieties, (D) longest contained [n]Helicene, and (E) longest stretch of linearly annulated rings. Plot A presents the data from all molecules in families 5–10. Plots B–E present data from family 10 only. The number of data point within each box can be found in Tables S8–S12 in the ESI.† | ||
Fig. 10A presents the effect of size on the range of HLG values, showing a trend whereby the distribution of values shifts to smaller gaps as the molecules grow larger. The differences between consecutive families become smaller as the size increases, and for the larger families (7- to 10-ring systems) the property ranges covered are highly overlapping. This is not unexpected; it is known that extending conjugation in fused polycyclic oligomers reduces HLGs in a 1/n manner (where n is the number of double bonds).94 To ensure that subsequent analyses were not tainted by this size dependency, the remaining plots B–E show only data for family 10 (i.e., 10-ring systems).
Increasing the size of the largest peri-island (Fig. 10B) demonstrates a similar size-dependency, whereby larger islands lead to smaller HLG values. However, in contrast to the previous trend, in this case all of the molecules are of the same size, thus this effect is clearly due to the size of the island itself, not of the overall molecule. Notably, all of the groups have a large degree of overlap, with the exception of the 4-ring systems (i.e., pyrene-based pc-PBHs), which tend to have a higher range of values than the other groups.
Conversely, increasing the number of cata-moieties appears to have a minimal effect on the HLG (Fig. 10C). Among the not strictly pc-PBHs, there is barely any differentiation. However, the strictly peri-condensed molecules (i.e., number of cata-moieties = 0) have noticeably smaller gap values. In other words, adding the first cata-moiety makes a significant change, but subsequent additions do not.
To further probe the effect of different cata-moieties, we differentiated between helical and linearly annulated cata-condensed components. In Fig. 10D we examine the effect of the longest helical stretch in the molecule. As mentioned above, the longer the contained [n]Helicene, the more distorted from planarity the molecule becomes. Hence, this analysis can also be viewed as an indirect measure of non-planarity in the molecules. We observe a slight trend, whereby elongating the helicene leads to an increase in the HLG. Once again, however, there is a large degree of overlap between the groups. The effect of the longest linear stretch, which we found to be dominant in cc-PBHs60 is shown in Fig. 10E. We find that, for the pc-PBHs as well, elongating the linear stretch beyond 3 rings (i.e., a stretch of at least 4 rings) dramatically decreases the value of the HLG and substantially narrows the spread of possible HLG values. Of all features examined, this structural component also shows the best differentiation between groups, i.e., the least amount of overlap. Thus, it appears to be a dominant structural feature in pc-PBHs.
Conclusions
In this work, we introduced the third installment of the COMPAS Project, COMPAS-3, which focuses on the subclass of peri-condensed PBHs. We generated two separate datasets: (1) COMPAS-3x, and (2) COMPAS-3D. The former contains ∼39k PBHs consisting of 4–11 rings, with geometries and properties calculated with xTB (using GFN2-xTB). The latter contains ∼9k pc-PBHs consisting of 4–10 rings, with geometries and properties calculated with DFT at the CAM-B3LYP-D3BJ/aug-cc-pVDZ//CAM-B3LYP-D3BJ/def2-SVP level of theory. In addition to the generation and curation of both datasets, we compared the two computational methods and performed a structure–property analysis on the collected data.The main conclusions of our comparison between xTB and DFT are as follows: in general, the agreement between the methods is excellent for both optimized geometries and calculated properties, meaning that DFT-level accuracy can be reliably obtained from xTB calculations. However, the molecular properties, with the exception of Erel, cover vastly different ranges of values. xTB-Erel and DFT-Erel have an excellent linear correlation, but DFT-Erel is consistently greater. Furthermore, for the specific subset of close-to-planar molecules, we found that DFT flattens molecules that xTB predicts to have a deviation from planarity of approximately 1 Å. For both of these findings, our analysis suggests that the underlying cause of the discrepancy is linked to the different estimation of steric hindrance and torsional strain made by each of the methods. Specifically, DFT estimates the torsional strain to be more costly than the hydrogen–hydrogen steric hindrance; the opposite is true for xTB. We also emphasize that all of our observations are in line with what we previously showed for COMPAS-1. While this may appear trivial, it is not obvious that cata- and peri-condensed PBHs should show similar tendencies and trends, nor that the two chosen levels of theory should have similar correlations for them, given the complexity inherent in large conjugated systems
The main conclusions of our structure–property analysis are as follows: for several of structural motifs we examined, there are apparent trends for the HLG. Namely, the HLG decreases with an overall increase in molecule size, but it also decreases with an increase only in the size of the largest contained peri-island. The number of cata-moieties does not appear to have marked effect, with the exception of going from strictly peri-condensed to not strictly peri-condensed. However, the type of cata-moiety does have an effect—elongation of helical motifs shows a slight tendency to increase HLG while elongation of the longest linear stretch shows a strong tendency to decrease the HLG.
Despite these trends, the individual groups have a large extent of overlap and cannot be easily differentiated. The two exceptions are the pyrene-based pc-PBHs, which appear to have noticeably larger HLGs, and pc-PBHs containing linear stretches of four or more rings. In both of these cases, these structural motifs separate the molecules from the distributions of the rest of the data. Thus, our analysis has helped to pinpoint promising directions for further development of design principles. In the future, we plan to continue investigating these two effects, including their interplay, and how they can be used to tune the molecule properties of pc-PBHs.
To conclude, this work provides two new datasets that can assist in further data-driven investigations and inverse design of promising functional molecules. Moreover, the insights gained from our analysis deepen our understanding of these prevalent and important molecules, and can inform future rational design of PBH-based systems.
Data and software availability
The data generated in the course of this work and underpinning the analyses reported herein are openly available on Gitlab at https://gitlab.com/porannegroup/compas. The datasets are provided as .csv files. Further description of the data structure is provided on the GitLab repository.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors express their gratitude to Prof. Dr Peter Chen for his continued support, and their deep appreciation and thanks to Dr Eno Paenurk, Dr Alexandra Tsybizova, and Dr Sabyasachi Chakraborty for fruitful discussions and helpful commentary on the manuscript. The authors are grateful to the Branco Weiss Fellowship for supporting this research as part of a Society in Science grant and to the Israel Science Foundation (Grant Agreement 1745/23). R. G. P. is a Branco Weiss Fellow, a Horev Fellow, and an Alon Scholarship recipient.References
- M. Randić, Aromaticity of Polycyclic Conjugated Hydrocarbons, Chem. Rev., 2003, 103, 3449–3606, DOI:10.1021/cr9903656.
- I. Fernández, Understanding the reactivity of polycyclic aromatic hydrocarbons and related compounds, Chem. Sci., 2020, 11, 3769–3779, 10.1039/D0SC00222D.
- W. W. Youngblood and M. Blumer, Polycyclic aromatic hydrocarbons in the environment: homologous series in soils and recent marine sediments, Geochim. Cosmochim. Acta, 1975, 39, 1303–1314, DOI:10.1016/0016-7037(75)90137-4.
- A. B. Patel, S. Shaikh, K. R. Jain, C. Desai and D. Madamwar, Polycyclic Aromatic Hydrocarbons: Sources, Toxicity, and Remediation Approaches, Front. Microbiol., 2020, 11, 1–23 CrossRef PubMed.
- A. Tielens, Interstellar Polycyclic Aromatic Hydrocarbon Molecules, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337, DOI:10.1146/annurev.astro.46.060407.145211.
- E. Peeters, C. Mackie, A. Candian and A. G. G. M. Tielens, A Spectroscopic View on Cosmic PAH Emission, Acc. Chem. Res., 2021, 54, 1921–1933, DOI:10.1021/acs.accounts.0c00747.
- B. Peng, Q. Dong, F. Li, T. Wang, X. Qiu and T. Zhu, A Systematic Review of Polycyclic Aromatic Hydrocarbon Derivatives: Occurrences, Levels, Biotransformation, Exposure Biomarkers, and Toxicity, Environ. Sci. Technol., 2023, 57, 15314–15335, DOI:10.1021/acs.est.3c03170.
- H. I. Abdel-Shafy and M. S. M. Mansour, A review on polycyclic aromatic hydrocarbons: Source, environmental impact, effect on human health and remediation, Egypt. J. Pet., 2016, 25, 107–123, DOI:10.1016/j.ejpe.2015.03.011.
- J. E. Anthony, Functionalized Acenes and Heteroacenes for Organic Electronics, Chem. Rev., 2006, 106, 5028–5048, DOI:10.1021/cr050966z.
- M. Kitamura and Y. Arakawa, Pentacene-based organic field-effect transistors, J. Phys.: Condens. Matter, 2008, 20, 184011, DOI:10.1088/0953-8984/20/18/184011.
- Y. Yamashita, Organic Semiconductors for Organic Field-effect Transistors, Sci. Technol. Adv. Mater., 2009, 10, 024313, DOI:10.1088/1468-6996/10/2/024313.
- C. Wang, H. Dong, W. Hu, Y. Liu and D. Zhu, Semiconducting π-Conjugated Systems in Field-Effect Transistors: A Material Odyssey of Organic Electronics, Chem. Rev., 2012, 112, 2208–2267, DOI:10.1021/cr100380z.
- Y. Gong, X. Zhan, Q. Li and Z. Li, Progress of pyrene-based organic semiconductor in organic field effect transistors, Sci. China: Chem., 2016, 59, 1623–1631, DOI:10.1007/s11426-016-0392-7.
- M. Chen, L. Yan, Y. Zhao, I. Murtaza, H. Meng and W. Huang, Anthracene-based Semiconductors for Organic Field-effect Transistors, J. Mater. Chem. C, 2018, 6, 7416–7444, 10.1039/C8TC01865K.
- C. Aumaitre and J.-F. Morin, Polycyclic Aromatic Hydrocarbons as Potential Building Blocks for Organic Solar Cells, Chem. Rec., 2019, 19, 1142–1154, DOI:10.1002/tcr.201900016.
- S. Karuppannan and J.-C. Chambron, Supramolecular Chemical Sensors Based on Pyrene Monomer-Excimer Dual Luminescence, Chem. – Asian J., 2011, 6, 964–984, DOI:10.1002/asia.201000724.
- P. K. Ramya and C. H. Suresh, Polycyclic Aromatic Hydrocarbons as Anode Materials in Lithium-Ion Batteries: A DFT Study, J. Phys. Chem. A, 2023, 127, 2511–2522, DOI:10.1021/acs.jpca.3c00337.
- A. P. Maltsev, I. V. Chepkasov and A. R. Oganov, New promising class of anode materials for Ca-ion battery: polyaromatic hydrocarbons, Mater. Today Energy, 2024, 39, 101467, DOI:10.1016/j.mtener.2023.101467.
- S. Chang, X. Jin, Q. He, T. Liu, J. Fang, Z. Shen, Z. Li, S. Zhang, M. Dahbi, J. Alami, K. Amine, A.-D. Li, H. Zhang and J. Lu, In Situ Formation of Polycyclic Aromatic Hydrocarbons as an Artificial Hybrid Layer for Lithium Metal Anodes, Nano Lett., 2022, 22, 263–270, DOI:10.1021/acs.nanolett.1c03624.
- S. Das, P. Bhauriyal and B. Pathak, Polycyclic Aromatic Hydrocarbons as Prospective Cathodes for Aluminum Organic Batteries, J. Phys. Chem. C, 2021, 125, 49–57, DOI:10.1021/acs.jpcc.0c07853.
- D. Kong, T. Cai, H. Fan, H. Hu, X. Wang, Y. Cui, D. Wang, Y. Wang, H. Hu, M. Wu, Q. Xue, Z. Yan, X. Li, L. Zhao and W. Xing, Polycyclic Aromatic Hydrocarbons as a New Class of Promising Cathode Materials for Aluminum-Ion Batteries, Angew. Chem., Int. Ed., 2022, 61, e202114681, DOI:10.1002/anie.202114681.
- G. Wang, B. Huang, D. Liu, D. Zheng, J. Harris, J. Xue and D. Qu, Exploring polycyclic aromatic hydrocarbons as an anolyte for nonaqueous redox flow batteries, J. Mater. Chem. A, 2018, 6, 13286–13293, 10.1039/C8TA03221A.
- P. C. Mishra and A. Yadav, Polycyclic aromatic hydrocarbons as finite size models of graphene and graphene nanoribbons: Enhanced electron density edge effect, Chem. Phys., 2012, 402, 56–68, DOI:10.1016/j.chemphys.2012.04.005.
- Y. Gu, X. Wu, T. Y. Gopalakrishna, H. Phan and J. Wu, Graphene-like Molecules with Four Zigzag Edges, Angew. Chem., Int. Ed., 2018, 57, 6541–6545, DOI:10.1002/anie.201802818.
- A. Ricca, J. E. Roser, E. Peeters and C. Boersma, Polycyclic Aromatic Hydrocarbons with Armchair Edges: Potential Emitters in Class B Sources, Astrophys. J., 2019, 882, 56, DOI:10.3847/1538-4357/ab3124.
- E. Clar, K. F. Lang and H. Schulz-Kiesow, Aromatische Kohlenwasserstoffe, LXX. Mitteil. (1): Zethren (1.12; 6.7-Dibenztetracen), Chem. Ber., 1955, 88, 1520–1527, DOI:10.1002/cber.19550881008.
- E. Clar, The aromatic sextet, Wiley-Interscience, 1972 Search PubMed.
- M. Solà, Forty years of Clar’s aromatic π-sextet rule, Front. Chem., 2013, 1, 1–22, DOI:10.3389/fchem.2013.00022.
- Y. Ruiz-Morales, HOMO–LUMO Gap as an Index of Molecular Size and Structure for Polycyclic Aromatic Hydrocarbons (PAHs) and Asphaltenes: A Theoretical Study. I, J. Phys. Chem. A, 2002, 106, 11283–11308, DOI:10.1021/jp021152e.
- Y. Ruiz-Morales, The Agreement between Clar Structures and Nucleus-Independent Chemical Shift Values in Pericondensed Benzenoid Polycyclic Aromatic Hydrocarbons: An Application of the Y-Rule, J. Phys. Chem. A, 2004, 108, 10873–10896, DOI:10.1021/jp040179q.
- Y. Ruiz-Morales in Asphaltenes, Heavy Oils, and Petroleomics, ed. Mullins, O. C., Sheu, E. Y., Hammami, A. and Marshall, A. G., Springer, New York, NY, 2007, pp. 95–137 DOI:10.1007/0-387-68903-6_4.
- J. O. Oña-Ruales and Y. Ruiz-Morales, The Predictive Power of the Annellation Theory: The Case of the C32H16 Benzenoid Polycyclic Aromatic Hydrocarbons, J. Phys. Chem. A, 2014, 118, 5212–5227, DOI:10.1021/jp504257k.
- R. Gershoni-Poranne, Piecing it Together: An Additivity Scheme for Aromaticity using NICS-XY Scans, Chem. – Eur. J., 2018, 24, 4165–4172, DOI:10.1002/chem.201705407.
- P. Finkelstein and R. Gershoni-Poranne, An Additivity Scheme for Aromaticity: The Heteroatom Case, ChemPhysChem, 2019, 20, 1508–1520, DOI:10.1002/cphc.201900128.
- N. Pavliček, A. Mistry, Z. Majzik, N. Moll, G. Meyer, D. J. Fox and L. Gross, Synthesis and characterization of triangulene, Nat. Nanotechnol., 2017, 12, 308–311, DOI:10.1038/nnano.2016.305.
- S. Arikawa, A. Shimizu, D. Shiomi, K. Sato and R. Shintani, Synthesis and Isolation of a Kinetically Stabilized Crystalline Triangulene, J. Am. Chem. Soc., 2021, 143, 19599–19605, DOI:10.1021/jacs.1c10151.
- Y. Zou, X. Hou, H. Wei, J. Shao, Q. Jiang, L. Ren and J. Wu, Circumcoronenes, Angew. Chem., Int. Ed., 2023, 62, e202301041, DOI:10.1002/anie.202301041.
- Z. Ruan, J. Schramm, J. B. Bauer, T. Naumann, H. F. Bettinger, R. Tonner-Zech and J. M. Gottfried, Synthesis of Tridecacene by Multistep Single-Molecule Manipulation, J. Am. Chem. Soc., 2024, 146, 3700–3709, DOI:10.1021/jacs.3c09392.
- A. Varet, N. Prcovic, C. Terrioux, D. Hagebaum-Reignier and Y. Carissan, BenzAI: A Program to Design Benzenoids with Defined Properties Using Constraint Programming, J. Chem. Inf. Model., 2022, 62, 2811–2820, DOI:10.1021/acs.jcim.2c00353.
- J. C. Dobrowolski and S. Ostrowski, HOMA Index Establishes Similarity to a Reference Molecule, J. Chem. Inf. Model., 2023, 63, 7744–7754, DOI:10.1021/acs.jcim.3c01551.
- Y. Wang, Y. Zhou and K. Du, Enumeration, Nomenclature, and Stability Rules of Carbon Nanobelts, J. Chem. Inf. Model., 2024, 64, 1261–1276, DOI:10.1021/acs.jcim.3c02051.
- E. Masoumifeshani and T. Korona, AROFRAGA Systematic Approach for Fragmentation of Aromatic Molecules, J. Chem. Theory Comput., 2024, 20, 1078–1095, DOI:10.1021/acs.jctc.3c00875.
- P. Kovács, X. Zhu, J. Carrete, G. K. H. Madsen and Z. Wang, Machine-learning Prediction of Infrared Spectra of Interstellar Polycyclic Aromatic Hydrocarbons, Astrophys. J., 2020, 902, 100, DOI:10.3847/1538-4357/abb5b6.
- J. Hachmann, R. Olivares-Amaya, A. Jinich, A. L. Appleton, M. A. Blood-Forsythe, L. R. Seress, C. Román-Salgado, K. Trepte, S. Atahan-Evrenk, S. Er, S. Shrestha, R. Mondal, A. Sokolov, Z. Bao and A. Aspuru-Guzik, Lead candidates for high-performance organic photovoltaics from high-throughput quantum chemistry - the Harvard Clean Energy Project, Energy Environ. Sci., 2014, 7, 698–704, 10.1039/C3EE42756K.
- R. Gómez-Bombarelli, et al., Design of efficient molecular organic light-emitting diodes by a high-throughput virtual screening and experimental approach, Nat. Mater., 2016, 15, 1120–1127, DOI:10.1038/nmat4717.
- C. Kunkel, J. T. Margraf, K. Chen, H. Oberhofer and K. Reuter, Active discovery of organic semiconductors, Nat. Commun., 2021, 12, 2422, DOI:10.1038/s41467-021-22611-4.
- H. S. Kwak, Y. An, D. J. Giesen, T. F. Hughes, C. T. Brown, K. Leswing, H. Abroshan and M. D. Halls, Design of Organic Electronic Materials With a Goal-Directed Generative Model Powered by Deep Neural Networks and High-Throughput Molecular Simulations, Front. Chem., 2022, 9, 1–16 RSC.
- L. C. Sander and S. A. Wise, Polycyclic Aromatic Hydrocarbon Structure Index, 1997 Search PubMed.
- L. C. Sander and S. A. Wise, Polycyclic Aromatic Hydrocarbon Structure Index, 2020 DOI:10.6028/NIST.SP.922e2020.
- A. Karton and B. Chan, PAH335 - A diverse database of highly accurate CCSD(T) isomerization energies of 335 polycyclic aromatic hydrocarbons, Chem. Phys. Lett., 2023, 824, 140544, DOI:10.1016/j.cplett.2023.140544.
- G. Malloci, C. Joblin and G. Mulas, On-line database of the spectral properties of polycyclic aromatic hydrocarbons, Chem. Phys., 2007, 332, 353–359, DOI:10.1016/j.chemphys.2007.01.001.
- X. Tan, Towards a comprehensive electronic database of polycyclic aromatic hydrocarbons and its application in constraining the identities of possible carriers of the diffuse interstellar bands, Spectrochim. Acta, Part A, 2009, 71, 2005–2011, DOI:10.1016/j.saa.2008.07.038.
- C. W. Bauschlicher, C. Boersma, A. Ricca, A. L. Mattioda, J. Cami, E. Peeters, F. S. D. Armas, G. P. Saborido, D. M. Hudgins and L. J. Allamandola, The NASA Ames polycyclic aromatic hydrocarbon infrared spectroscopic database: the computed spectra, Astrophys. J., Suppl. Ser., 2010, 189, 341, DOI:10.1088/0067-0049/189/2/341.
- C. Boersma, C. W. Bauschlicher, A. Ricca, A. L. Mattioda, J. Cami, E. Peeters, F. S. De Armas, G. P. Saborido, D. M. Hudgins and L. J. Allamandola, The NASA Ames PAH IR spectroscopic database version 2.00: updated content, web site, and on (off) line tools, Astrophys. J., Suppl. Ser., 2014, 211, 8, DOI:10.1088/0067-0049/211/1/8.
- C. W. Bauschlicher, A. Ricca, C. Boersma and L. J. Allamandola, The NASA Ames PAH IR Spectroscopic Database: Computational Version 3.00 with Updated Content and the Introduction of Multiple Scaling Factors, Astrophys. J., Suppl. Ser., 2018, 234, 32, DOI:10.3847/1538-4365/aaa019.
- A. L. Mattioda, D. M. Hudgins, C. Boersma, C. W. Bauschlicher, A. Ricca, J. Cami, E. Peeters, F. S. De Armas, G. P. Saborido and L. J. Allamandola, The NASA Ames PAH IR Spectroscopic Database: The Laboratory Spectra, Astrophys. J., Suppl. Ser., 2020, 251, 22, DOI:10.3847/1538-4365/abc2c8.
- F. Alvarez-Ramírez and Y. Ruiz-Morales, Database of Nuclear Independent Chemical Shifts (NICS) versus NICSZZ of Polycyclic Aromatic Hydrocarbons (PAHs), J. Chem. Inf. Model., 2020, 61, 611–620, DOI:10.1021/acs.jcim.9b00909.
- J. Hachmann, R. Olivares-Amaya, S. Atahan-Evrenk, C. Amador-Bedolla, R. S. Sánchez-Carrera, A. Gold-Parker, L. Vogt, A. M. Brockway and A. Aspuru-Guzik, The Harvard Clean Energy Project: Large-Scale Computational Screening and Design of Organic Photovoltaics on the World Community Grid, J. Phys. Chem. Lett., 2011, 2, 2241–2251, DOI:10.1021/jz200866s.
- Q. Ai, V. Bhat, S. M. Ryno, K. Jarolimek, P. Sornberger, A. Smith, M. M. Haley, J. E. Anthony and C. Risko, OCELOT: An infrastructure for data-driven research to discover and design crystalline organic semiconductors, J. Chem. Phys., 2021, 154, 174705, DOI:10.1063/5.0048714.
- A. Wahab, L. Pfuderer, E. Paenurk and R. Gershoni-Poranne, The COMPAS Project: A Computational Database of Polycyclic Aromatic Systems. Phase 1: cata-Condensed Polybenzenoid Hydrocarbons, J. Chem. Inf. Model., 2022, 62, 3704–3713, DOI:10.1021/acs.jcim.2c00503.
- E. Mayo Yanes, S. Chakraborty and R. Gershoni-Poranne, COMPAS-2: a dataset of cata-condensed hetero-polycyclic aromatic systems, Sci. Data, 2024, 11, 97, DOI:10.1038/s41597-024-02927-8.
- S. Fite, A. Wahab, E. Paenurk, Z. Gross and R. Gershoni-Poranne, Text-based representations with interpretable machine learning reveal structure–property relationships of polybenzenoid hydrocarbons, J. Phys. Org. Chem., 2023, 36, e4458, DOI:10.1002/poc.4458.
- T. Weiss, A. Wahab, A. M. Bronstein and R. Gershoni-Poranne, Interpretable Deep-Learning Unveils Structure–Property Relationships in Polybenzenoid Hydrocarbons, J. Org. Chem., 2023, 88, 9645–9656, DOI:10.1021/acs.joc.2c02381.
- T. Weiss, E. Mayo Yanes, S. Chakraborty, L. Cosmo, A. M. Bronstein and R. Gershoni-Poranne, Guided diffusion for inverse molecular design, Nat. Comput. Sci., 2023, 3, 873–882, DOI:10.1038/s43588-023-00532-0.
- M. D. Wilkinson, et al., The FAIR Guiding Principles for scientific data management and stewardship, Sci. Data, 2016, 3, 160018, DOI:10.1038/sdata.2016.18.
- G. Brinkmann, O. D. Friedrichs, S. Lisken and A. Peeters, CaGe - a Virtual Environment for Studying Some Special Classes of Plane Graphs - an Update, Commun. Math. Comput. Chem., 2009, 63, 533–552 Search PubMed.
- S. J. Cyvins and I. Gutman, Topological properties of benzenoid hydrocarbons: Part XLIV. Obvious and concealed non-Kekuléan benzenoids, J. Mol. Struct.: THEOCHEM, 1987, 150, 157–169, DOI:10.1016/0166-1280(87)80035-0.
- S. Das and J. Wu, Polycyclic Hydrocarbons with an Open-Shell Ground State, Phys. Sci. Rev., 2017, 2, 20160109, DOI:10.1515/psr-2016-0109.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671, DOI:10.1021/acs.jctc.8b01176.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Extended tight-binding quantum chemistry methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493, DOI:10.1002/wcms.1493.
- J. H. Jensen “xyz2mol”. https://github.com/jensengroup/xyz2mol.
- C. A. Bauer, A. Hansen and S. Grimme, The Fractional Occupation Number Weighted Density as a Versatile Analysis Tool for Molecules with a Complicated Electronic Structure, Chem. – Eur. J., 2017, 23, 6150–6164, DOI:10.1002/chem.201604682.
- R. Nieman, J. R. Carvalho, B. Jayee, A. Hansen, A. J. Aquino, M. Kertesz and H. Lischka, Polyradical character assessment using multireference calculations and comparison with density-functional derived fractional occupation number weighted density analysis, Phys. Chem. Chem. Phys., 2023, 25, 27380–27393, 10.1039/D3CP03734G.
- A. Das, T. Müller, F. Plasser and H. Lischka, Polyradical Character of Triangular Non-Kekulé Structures, Zethrenes, p-Quinodimethane-Linked Bisphenalenyl, and the Clar Goblet in Comparison: An Extended Multireference Study, J. Phys. Chem. A, 2016, 120, 1625–1636, DOI:10.1021/acs.jpca.5b12393.
- F. Neese, The ORCA Program System, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78, DOI:10.1002/wcms.81.
- F. Neese, Software update: The ORCA program system—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606, DOI:10.1002/wcms.1606.
- A. D. Becke, Density-functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652, DOI:10.1063/1.464913.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-energy Formula Into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789, DOI:10.1103/PhysRevB.37.785.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Results Obtained with the Correlation Energy Density Functionals of Becke and Lee, Yang and Parr, Chem. Phys. Lett., 1989, 157, 200–206, DOI:10.1016/0009-2614(89)87234-3.
- R. H. Hertwig and W. Koch, On the Parameterization of the Local Correlation Functional. What is Becke-3-LYP?, Chem. Phys. Lett., 1997, 268, 345–351, DOI:10.1016/S0009-2614(97)00207-8.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57, DOI:10.1016/j.cplett.2004.06.011.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104, DOI:10.1063/1.3382344.
- E. R. Johnson and A. D. Becke, A post-Hartree-Fock Model of Intermolecular Interactions, J. Chem. Phys., 2005, 123, 024101, DOI:10.1063/1.1949201.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465, DOI:10.1002/jcc.21759.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023, DOI:10.1063/1.456153.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806, DOI:10.1063/1.462569.
- D. E. Woon and T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon, J. Chem. Phys., 1993, 98, 1358–1371, DOI:10.1063/1.464303.
- J. Liang, X. Feng, D. Hait and M. Head-Gordon, Revisiting the Performance of Time-Dependent Density Functional Theory for Electronic Excitations: Assessment of 43 Popular and Recently Developed Functionals from Rungs One to Four, J. Chem. Theory Comput., 2022, 18, 3460–3473, DOI:10.1021/acs.jctc.2c00160.
- C. W. Bauschlicher, A Comparison of the Accuracy of Different Functionals, Chem. Phys. Lett., 1995, 246, 40–44, DOI:10.1016/0009-2614(95)01089-R.
- G. Markert, E. Paenurk and R. Gershoni-Poranne, Prediction of Spin Density, Baird-Antiaromaticity, and Singlet-Triplet Energy Gap in Triplet-State Polybenzenoid Systems from Simple Structural Motifs, Chem. – Eur. J., 2021, 27, 6923–6935, DOI:10.1002/chem.202005248.
- Z. Zhou, R. K. Kawade, Z. Wei, F. Kuriakose, K. Üngör, M. Jo, M. Shatruk, R. Gershoni-Poranne, M. A. Petrukhina and I. V. Alabugin, Negative Charge as a Lens for Concentrating Antiaromaticity: Using a Pentagonal “Defect” and Helicene Strain for Cyclizations, Angew. Chem., Int. Ed., 2020, 59, 1256–1262, DOI:10.1002/anie.201911319.
- B. Komjáti, K. Urai, S. Hosztafi, J. Kökösi, B. Kováts, J. Nagy and P. Horváth, Systematic study on the TD-DFT calculated electronic circular dichroism spectra of chiral aromatic nitro compounds: A comparison of B3LYP and CAM-B3LYP, Spectrochim. Acta, Part A, 2016, 155, 95–102, DOI:10.1016/j.saa.2015.11.002.
- I. Casademont-Reig, R. Guerrero-Avilés, E. Ramos-Cordoba, M. Torrent-Sucarrat and E. Matito, How Aromatic Are Molecular Nanorings? The Case of a Six-Porphyrin Nanoring, Angew. Chem., Int. Ed., 2021, 60, 24080–24088, DOI:10.1002/anie.202108997.
- R. Gershoni-Poranne, A. P. Rahalkar and A. Stanger, The predictive power of aromaticity: quantitative correlation between aromaticity and ionization potentials and HOMO-LUMO gaps in oligomers of benzene, pyrrole, furan, and thiophene, Phys. Chem. Chem. Phys., 2018, 20, 14808–14817, 10.1039/C8CP02162G.
Footnote |
| † Electronic supplementary information (ESI) available: Details of general computational methods, templates for xTB and DFT calculations, benchmarking procedure for choosing the DFT level of theory, comparison of the COMPAS-1 dataset using the two levels of theory (this report versus the original publication), extended discussion of the outliers in the aIP and aEA plot, comparison of D3 and D4 dispersion corrections, and additional discussion of the relative energy and structure–property analyses. See DOI: https://doi.org/10.1039/d4cp01027b |
| This journal is © the Owner Societies 2024 |