Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of Y-substitution on phase composition and proton uptake of self-generated Ba(Ce,Fe)O3−δ–Ba(Fe,Ce)O3−δ composites†
Christian
Berger
 ab,
Edith
Bucher
ab,
Edith
Bucher
 b,
Rotraut
Merkle
b,
Rotraut
Merkle
 *a,
Christina
Nader
*a,
Christina
Nader
 b,
Judith
Lammer
b,
Judith
Lammer
 c,
Werner
Grogger
c,
Joachim
Maier
c,
Werner
Grogger
c,
Joachim
Maier
 a and
Werner
Sitte
*b
a and
Werner
Sitte
*b
aMax Planck Institute for Solid State Research, Heisenbergstraße 1, DE-70569 Stuttgart, Germany. E-mail: r.merkle@fkf.mpg.de; Fax: +49 711 689 1722; Tel: +49 711 689 1768
bChair of Physical Chemistry, Montanuniversitaet Leoben, Franz-Josef-Straße 18, AT-8700 Leoben, Austria. E-mail: werner.sitte@unileoben.ac.at; Fax: +43 3842 402 4802; Tel: +43 3842 402 4800
cInstitute of Electron Microscopy and Nanoanalysis (FELMI), Graz University of Technology & Graz Centre for Electron Microscopy (ZFE), Steyrergasse 17, AT-8010 Graz, Austria
First published on 15th November 2021
Abstract
Self-generated composites from the series BaCe1−(x+z)FexYzO3−δ with z = 0.2 for 0.1 ≤ x ≤ 0.6 and z = 0 for Ce![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe = 1 were obtained by one-pot synthesis. The composites consist of proton and electron conducting phases and are interesting as electrode materials for protonic ceramic fuel and electrolyser cells. X-ray diffraction with quantitative phase analysis and scanning electron microscopy with energy-dispersive X-ray spectroscopy showed that the materials consist of Fe-rich phases and a Ce-rich perovskite phase, which are present in the corresponding proportion depending on the precursor composition (Ce–Fe ratio). Substitution with Y leads to a narrowing of the miscibility gap compared to BaCe1−xFexO3−δ composites, thus favouring transformation of the composites into single cubic phases at temperatures above 1000 °C. Further, Y influences the mutual solubility of Fe3+/4+ and Ce4+ in the Ce-rich and Fe-rich phase, respectively, as shown elemental mapping via scanning transmission electron microscopy. As only a small proportion of the Y dissolves in the electrolyte-type phase, the increased proton uptake resulting from the incorporation of Y in the Ce-rich phase is limited. Strategies to overcome this limitation by substitution with ions with similar ionic radii, but different basicity, are discussed.
Fe = 1 were obtained by one-pot synthesis. The composites consist of proton and electron conducting phases and are interesting as electrode materials for protonic ceramic fuel and electrolyser cells. X-ray diffraction with quantitative phase analysis and scanning electron microscopy with energy-dispersive X-ray spectroscopy showed that the materials consist of Fe-rich phases and a Ce-rich perovskite phase, which are present in the corresponding proportion depending on the precursor composition (Ce–Fe ratio). Substitution with Y leads to a narrowing of the miscibility gap compared to BaCe1−xFexO3−δ composites, thus favouring transformation of the composites into single cubic phases at temperatures above 1000 °C. Further, Y influences the mutual solubility of Fe3+/4+ and Ce4+ in the Ce-rich and Fe-rich phase, respectively, as shown elemental mapping via scanning transmission electron microscopy. As only a small proportion of the Y dissolves in the electrolyte-type phase, the increased proton uptake resulting from the incorporation of Y in the Ce-rich phase is limited. Strategies to overcome this limitation by substitution with ions with similar ionic radii, but different basicity, are discussed.
1. Introduction
Solid oxide fuel cells (SOFCs) convert chemical energy contained in various fuels such as hydrogen, methane and other hydrocarbons, into electrical energy. The conversion takes place with high efficiency and without emission of NOx.1,2 State-of-the-art SOFCs use oxygen ionic conductors (as electrolytes) and mixed oxygen ionic–electronic conductors (as cathodes).1–3 In order to obtain sufficiently fast ionic transport, cells based on these materials require relatively high operating temperatures of 700–1000 °C, which causes materials compatibility and degradation issues. With regard to operating temperature and efficiency, protonic ceramic fuel cells (PCFCs) are an interesting alternative to SOFCs.4–6 PCFCs use proton-conducting oxides, offering the advantages of sufficiently fast ionic transport at relatively low temperatures (300–600 °C) and significantly smaller activation energies than oxygen ion conductors.7 However, as the operating temperature of the cell decreases, the electrochemical performance does as well, due to the reduced catalytic activity of the air electrode. Mixed oxygen ionic–electronic conductors, especially Co-containing perovskites such as BaCo0.7Fe0.22Y0.08O3−δ,8 Ba0.5Sr0.5Co0.8Fe0.2O3−δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 and La0.6Sr0.4Co0.2Fe0.8O3−δ,10 have been investigated as possible air electrodes in order to improve the catalytic activity at lower temperatures. However, these materials suffer from a comparably low proton uptake. An important goal therefore is to improve the proton uptake and conductivity of potential PCFC cathode materials such that the active zone for oxygen reduction is expanded beyond the gas/electrolyte/cathode triple phase boundary.11,12
9 and La0.6Sr0.4Co0.2Fe0.8O3−δ,10 have been investigated as possible air electrodes in order to improve the catalytic activity at lower temperatures. However, these materials suffer from a comparably low proton uptake. An important goal therefore is to improve the proton uptake and conductivity of potential PCFC cathode materials such that the active zone for oxygen reduction is expanded beyond the gas/electrolyte/cathode triple phase boundary.11,12
Different strategies for further optimisation of PCFC cathodes were investigated e.g. by using composites of proton-conducting and hole-conducting materials.13,14 With regard to fabrication of composite cathodes, some disadvantages are associated with conventional mixing of the two phases, such as retention of inhomogeneities and small active areas between the phases (large grain sizes).15,16 Alternatively, using one-pot self-assembly methods allows one to obtain two homogeneously distributed nanocrystalline phases with complementary functionalities during calcination.17–23 Cheng et al. used Fe substituted BaCeO3 as a model substance for their proof-of-concept study because of its good proton uptake capacity.24 BaCe0.5Fe0.5O3−δ, which was used as a precursor, decomposes into a Ce-rich (BaCe0.85Fe0.15O3−δ) and a Fe-rich (BaCe0.15Fe0.85O3−δ) thermodynamically stable phase. A membrane fabricated from the dual-phase composite thus obtained showed hydrogen permeation flux superior to a membrane obtained by conventional mixing and procession of the two single-phase compounds.24
In the present study substitution of BaCe0.5Fe0.5O3−δ with Y is investigated with the aim of increasing the oxygen vacancy concentration and the basicity of the materials, thereby enhancing the proton uptake capacity. Self-generated nanocomposites obtained from BaCe0.5Fe0.5O3−δ and BaCe1−(x+0.2)FexY0.2O3−δ (0.1 ≤ x ≤ 0.6) precursors are characterised with respect to fundamental material properties in order to gain further insights into phase composition and -distribution, as well as proton uptake capacity. Therefore, the obtained trends in proton uptake are correlated with ionic radii and basicity of various B-site substituents (Y, Yb, Sm, Gd) to suggest promising compositions for further studies.
2. Results and discussion
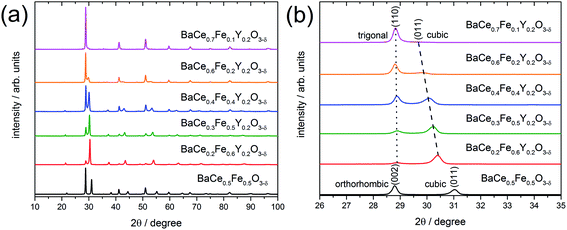
2.1 Phase analysis, lattice parameters and phase formation
X-ray powder diffraction (XRD) patterns of the composites obtained from the precursors BaCe0.5Fe0.5O3−δ and BaCe1−(x+0.2)FexY0.2O3−δ (0.1 ≤ x ≤ 0.6) calcined at 1000 °C are shown in Fig. 1a. All these samples exhibit reflections of two different perovskite phases. A quantitative analysis of the relative amounts of the two phases was performed for all investigated composites (Table S1 in the ESI†). While one of these phase is always cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (SG#221), see magnified (011) peak in Fig. 1b), the other perovskite phase belongs to the orthorhombic GdFeO3 structure (Pmcn (SG#62), magnified (002) peak in Fig. 1b) for the Y-free material. For Y-containing samples it acquires a trigonal structure (R
m (SG#221), see magnified (011) peak in Fig. 1b), the other perovskite phase belongs to the orthorhombic GdFeO3 structure (Pmcn (SG#62), magnified (002) peak in Fig. 1b) for the Y-free material. For Y-containing samples it acquires a trigonal structure (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c (SG#167), magnified (110) peak in Fig. 1b).
c (SG#167), magnified (110) peak in Fig. 1b).
In addition to the change in the space group, the positions of the reflections attributed to the cubic phase, shift towards smaller diffraction angles with decreasing Fe content (Fig. 1b). The positions of the reflections ascribed to the orthorhombic/trigonal phases are almost independent of the Ce–Fe ratio. Similar trends are observed as a function of the lattice parameters on the Fe content (Fig. 2a). According to energy-dispersive X-ray spectroscopy (EDXS) (see Chapter 2.2), the cubic phase is rich in Fe and the orthorhombic/trigonal phase is rich in Ce. Following Vegard's law,25 the lattice parameters of the cubic Fe-rich phases (Table S2†) decrease linearly with increasing Fe content of the precursor (Fig. 2a, including also BaFeO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 and BaFe0.8Y0.2O3).27 For easy comparison, for the Ce-rich phases the pseudo-cubic lattice parameters were calculated (Tables S3 and S4†). Unlike the lattice parameters of the Fe-rich phases, the lattice parameters of the Ce-rich phases show no significant dependence on the Ce content of the precursor, and closely match BaCeO3 and BaCe0.8Y0.2O3
26 and BaFe0.8Y0.2O3).27 For easy comparison, for the Ce-rich phases the pseudo-cubic lattice parameters were calculated (Tables S3 and S4†). Unlike the lattice parameters of the Fe-rich phases, the lattice parameters of the Ce-rich phases show no significant dependence on the Ce content of the precursor, and closely match BaCeO3 and BaCe0.8Y0.2O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 literature data.
28 literature data.
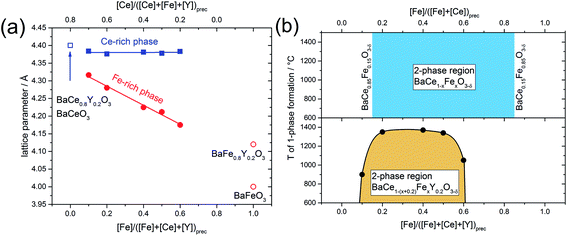 | ||
Fig. 2 (a) Lattice parameters of the cubic Fe-rich phase and pseudo-cubic lattice parameter of the trigonal Ce-rich phase as functions of the Fe and Ce content in the annealed precursor powder. The open symbols correspond to lattice parameters of BaCeO3 and BaCe0.8Y0.2O3,28 BaFeO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 and BaFe0.8Y0.2O3.27 (b) The phase diagram shows the miscibility gaps of the Y-containing samples and the Y-free samples, respectively. The mutual solubility of Ce in BaFeO3 and vice versa was determined to be 15% (BaCe0.15Fe0.85O3−δ and BaCe0.85Fe0.15O3−δ).24 26 and BaFe0.8Y0.2O3.27 (b) The phase diagram shows the miscibility gaps of the Y-containing samples and the Y-free samples, respectively. The mutual solubility of Ce in BaFeO3 and vice versa was determined to be 15% (BaCe0.15Fe0.85O3−δ and BaCe0.85Fe0.15O3−δ).24 | ||
The significant differences between the radii of the B-site ions of the ABO3 perovskite – Ce and Fe – may be considered the main driving force for the separation of the precursor into the cubic and the orthorhombic/trigonal phases. The ionic radii (Ce3+ = 1.15 Å, Ce4+ = 1.01 Å, Fe3+ = 0.785 Å, Fe4+ = 0.725 Å and Y3+ = 0.9 Å) were taken from Shannon's table of ionic radii29 under consideration of valence and coordination number (VI for all above mentioned ions).
With the help of spark plasma sintering (SPS), the precursor powders can be compacted to dense ceramic pellets at comparably low temperature. This allows us to follow the lattice parameters and phase distribution as a function of sintering temperature (Fig. S1†). Two-phase composites are obtained at lower temperatures, while for all Y-containing samples single-phase compounds are formed at elevated temperatures. The upper critical mixing temperature depends on the Ce–Fe ratio in the precursor. From these data a tentative phase diagram showing the miscibility gap of BaCe1−(x+0.2)FexY0.2O3−δ was obtained (Fig. 2b). Cheng et al. studied the Y-free precursor BaCe0.5Fe0.5O3−δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 which forms single phases with Fe-rich (below Ce-concentrations of 15%, BaCe0.15Fe0.85O3−δ) and Ce-rich compositions (below Fe concentrations of 15%, BaCe0.85Fe0.15O3−δ). The Y-free composites remain as two separate phases until the maximum sintering temperature of 1400 °C is reached (Fig. 2b and S1;† 1450 °C leads to partial melting). Therefore, it can be concluded that Y-substitution significantly decreases the upper critical mixing temperature in the Ba(Ce,Fe)O3−δ system. In the case of the Y-substituted compounds, the miscibility gap extends further to the Ce-rich (Fe-poor) side of the phase diagram than in the case of the Y-free compounds. A composite is formed from the precursor BaCe0.7Fe0.1Y0.2O3−δ (10% Fe on the B-site) at T < 900 °C, whereas the corresponding Y-free compounds with Fe concentrations below of 15% are single-phase. The addition of Y also affects the maximum applicable sintering temperature for the composites. Two-phase composites from BaCe1−(x+0.2)FexY0.2O3−δ precursors within the limits 0.2 ≤ x ≤ 0.5 may be obtained up to relatively high temperatures of T ≤ 1350 °C, Fig. 2b. For precursor compositions with either relatively low Fe content (BaCe0.7Fe0.1Y0.2O3−δ) or relatively high Fe content (BaCe0.2Fe0.6Y0.2O3−δ), two-phase composites will only be obtained up to significantly lower sintering temperatures of T ≤ 900 °C and T ≤ 1050 °C, respectively, Fig. 2b. Comparing the lattice parameters of the Fe-rich phases of composite powders (using the actual local Fe concentration from Table 1) with those of the single-phase sintered SPS pellets, a linear trend depending on Fe concentration was evident (Fig. S2†).
24 which forms single phases with Fe-rich (below Ce-concentrations of 15%, BaCe0.15Fe0.85O3−δ) and Ce-rich compositions (below Fe concentrations of 15%, BaCe0.85Fe0.15O3−δ). The Y-free composites remain as two separate phases until the maximum sintering temperature of 1400 °C is reached (Fig. 2b and S1;† 1450 °C leads to partial melting). Therefore, it can be concluded that Y-substitution significantly decreases the upper critical mixing temperature in the Ba(Ce,Fe)O3−δ system. In the case of the Y-substituted compounds, the miscibility gap extends further to the Ce-rich (Fe-poor) side of the phase diagram than in the case of the Y-free compounds. A composite is formed from the precursor BaCe0.7Fe0.1Y0.2O3−δ (10% Fe on the B-site) at T < 900 °C, whereas the corresponding Y-free compounds with Fe concentrations below of 15% are single-phase. The addition of Y also affects the maximum applicable sintering temperature for the composites. Two-phase composites from BaCe1−(x+0.2)FexY0.2O3−δ precursors within the limits 0.2 ≤ x ≤ 0.5 may be obtained up to relatively high temperatures of T ≤ 1350 °C, Fig. 2b. For precursor compositions with either relatively low Fe content (BaCe0.7Fe0.1Y0.2O3−δ) or relatively high Fe content (BaCe0.2Fe0.6Y0.2O3−δ), two-phase composites will only be obtained up to significantly lower sintering temperatures of T ≤ 900 °C and T ≤ 1050 °C, respectively, Fig. 2b. Comparing the lattice parameters of the Fe-rich phases of composite powders (using the actual local Fe concentration from Table 1) with those of the single-phase sintered SPS pellets, a linear trend depending on Fe concentration was evident (Fig. S2†).
| Precursor | ||
|---|---|---|
| Ce-rich phase | Fe-rich phase | |
| a Data for BaCe0.5Fe0.5O3−δ was taken from Cheng et al.24 | ||
| BaCe0.5Fe0.5O3−δa | Fe0.15Ce0.85 | Fe0.85Ce0.15 |
| BaCe0.2Fe0.6Y0.2O3−δ | Fe0.08± 0.01Ce0.85±0.02Y0.07±0.01 | Fe0.64±0.03Ce0.15±0.02Y0.22±0.01 |
| BaCe0.4Fe0.4Y0.2O3−δ | Fe0.10± 0.01Ce0.82±0.03Y0.09±0.02 | Fe0.53±0.01Ce0.22±0.01Y0.25±0.02 |
| BaCe0.6Fe0.2Y0.2O3−δ | Fe0.12±0.02Ce0.72±0.03Y0.16±0.01 | Fe0.39±0.03Ce0.32±0.04Y0.29±0.01 |
2.2 Microstructure and elemental distribution
Scanning electron microscopy (SEM)-EDXS were carried out on freshly polished samples to obtain the cation stoichiometry of the precursor phases (Table S5†). Additionally, the average grain sizes of the two-phase composites BaCe0.2Fe0.6Y0.2O3−δ, BaCe0.4Fe0.4Y0.2O3−δ and BaCe0.6Fe0.2Y0.2O3−δ precursors were estimated. For this purpose, a sintered pellet was broken and the fracture surface was analysed by using SEM with an in-lens secondary electron detector.The grain size distribution of self-generated composites was determined by using the image analysis software ImageJ.30 The exact determination of grain sizes over a representative sample range is difficult because the samples with low Ce content show a certain porosity (BaCe0.2Fe0.6Y0.2O3−δ and BaCe0.4Fe0.4Y0.2O3−δ) and small precipitates on the grains (BaCe0.2Fe0.6Y0.2O3−δ) (Fig. 3). The morphology of the sample with the highest Ce content differs most clearly due to the increased sintering temperature (1200 °C) compared to the Fe-rich samples (approx. 1000 °C). If one also includes the information from high-angle annular dark-field (HAADF) STEM images (Fig. 4) for BaCe0.2Fe0.6Y0.2O3−δ, a strong variation in grain size especially for the Ce rich phase (bright spots in the HAADF image) is recognized. In addition to the surface morphology images, EDXS maps of the B-site cations were recorded. These show an apparently homogeneous distribution of the cations along the image section of Fig. S3† due to the limitation in the resolution of the SEM-EDXS measurements. No individual grains could be analysed, instead a superposition of the measurement information of several grains was obtained, which is caused by the large interaction volume generated by the electron beam in SEM-EDXS.
 | ||
| Fig. 3 SEM images of BaCe0.2Fe0.6Y0.2O3−δ, BaCe0.4Fe0.4Y0.2O3−δ and BaCe0.6Fe0.2Y0.2O3−δ composite ceramics (SPS sintering, Table S6†) recorded along fracture planes with an in-lens secondary electron detector. | ||
 | ||
| Fig. 4 STEM-HAADF images with EDXS elemental maps for selected cations of composite ceramics obtained from precursors of BaCe0.2Fe0.6Y0.2O3−δ (left column), BaCe0.4Fe0.4Y0.2O3−δ (in the middle) and BaCe0.6Fe0.2Y0.2O3−δ (right column) by spark plasma sintering (conditions given in Table S6†). The bright grains in the Y maps are occasional Y-rich precipitates. | ||
Scanning transmission electron microscopy (STEM)-EDXS was carried out to determine the cation stoichiometry and distribution within the individual phases in the composites with high lateral resolution. Fig. 4 shows STEM-images images (using a HAADF detector) of two-phase composites obtained from BaCe0.2Fe0.6Y0.2O3−δ, BaCe0.4Fe0.4Y0.2O3−δ and BaCe0.6Fe0.2Y0.2O3−δ precursors and the respective cation distributions. The grain sizes of the individual phases are in the sub-micrometer range. The reduced grain growth, compared to the Y-free composite,24 is probably mainly due to the use of SPS as a sintering method (fast densification in short time at moderate temperature). In the composite formed from the BaCe0.6Fe0.2Y0.2O3−δ precursor, small amounts of the impurity phase Y2O3 are observed (bright spots in the Y-map). However, since the Y2O3 impurity phase was not detected in the XRD measurements, the fraction of this phase is rather small and therefore not significant for the investigated material properties.
The mutual solubility of Fe3+/4+ and Ce4+ ions, as well as the distribution of Y in the two phases, was investigated by STEM-EDXS (Table 1). More than 70 single spectra and 10 area scans each were measured within grains of the different phases of the composites in order to describe the cation composition statistically well (Fig. S4–S6†). Data from STEM-EDXS indicate that Y incorporation is more favourable in the Fe-rich phase than in the Ce-rich phase (as seen in Fig. S7†). The addition of Y leads to a decreased Fe and increased Ce content in the Fe-rich phase (see Fig. S8a†) compared to the Fe-rich phase of the Y-free composite. Regarding the Ce-rich phase, the Ce and Fe contents of the composites containing Y are similar (see Fig. S8b†) to those of the Y-free composite. The Ce-rich phase in the BaCe1−xFexY0.2O3−δ composites remains within the single-phase region indicated in Fig. 2b. However, for the Fe-rich phase higher Ce contents are found compared to Fig. 2b. This is probably related to the increased Y concentrations, which expand the lattice of the ferrate perovskite and thus facilitate Ce incorporation. The composition of the Fe-rich phase depends on the overall cation composition (cf. also variation of the lattice parameters in Fig. 2a), in particular for BaCe0.6Fe0.2Y0.2O3−δ rather high Y and Ce contents appear in the Fe-rich phase. In Chapter 2.3, the reasons for the element distribution between the perovskite phases are discussed.
2.3 Trends in water uptake
The water uptake of perovskites is primarily represented by the acid–base reaction (R1) (hydration reaction).27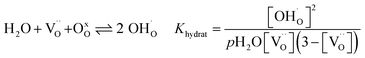 | (R1) |
Two protonic defects 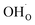 are formed by dissociative incorporation of water into an oxygen vacancy
are formed by dissociative incorporation of water into an oxygen vacancy 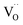 . With perovskites containing redox active transition metal ions (with mixed valence, e.g. Fe3+/4+) at the B-site, the oxygen exchange reaction (redox reaction) must also be considered ((R2)).
. With perovskites containing redox active transition metal ions (with mixed valence, e.g. Fe3+/4+) at the B-site, the oxygen exchange reaction (redox reaction) must also be considered ((R2)).
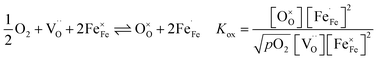 | (R2) |
In Fe-rich perovskites, the dominant electronic charge carriers under oxidising conditions (high pO2) are p-type defects (electron holes; h˙), which are transferred between the iron ions Fe×Fe (Fe3+) and 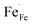 (Fe4+). The combination of oxygenation and hydration reaction ((R1) and (R2)) yields proton uptake by a redox reaction (“hydrogenation”):31–33
(Fe4+). The combination of oxygenation and hydration reaction ((R1) and (R2)) yields proton uptake by a redox reaction (“hydrogenation”):31–33
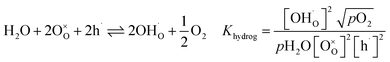 | (R3) |
From (R3) it is evident that high concentrations of protonic defects 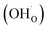 and high electron hole concentrations show opposite tendencies. High concentrations of both
and high electron hole concentrations show opposite tendencies. High concentrations of both 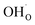 and h˙ in a single-phase material are therefore difficult to achieve. Depending on the experimental conditions, either reaction (R1) or (R2) may predominate. The hydration reaction is preferred when the sample fulfils the criterion
and h˙ in a single-phase material are therefore difficult to achieve. Depending on the experimental conditions, either reaction (R1) or (R2) may predominate. The hydration reaction is preferred when the sample fulfils the criterion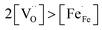 . To measure the proton uptake exclusively in the regime of predominant hydration, the samples need to be quenched to suppress the redox reaction (see Experimental chapter 3.3).27 The proton concentration was obtained from the change in sample mass after pH2O steps at constant T, under the assumption that (R1) predominates (which is ensured by the experimental conditions used). However, the distribution of the water uptake between the two phases in the composite is not easily accessible (thus no ΔH0hydrat, ΔS0hydrat can be extracted).
. To measure the proton uptake exclusively in the regime of predominant hydration, the samples need to be quenched to suppress the redox reaction (see Experimental chapter 3.3).27 The proton concentration was obtained from the change in sample mass after pH2O steps at constant T, under the assumption that (R1) predominates (which is ensured by the experimental conditions used). However, the distribution of the water uptake between the two phases in the composite is not easily accessible (thus no ΔH0hydrat, ΔS0hydrat can be extracted).
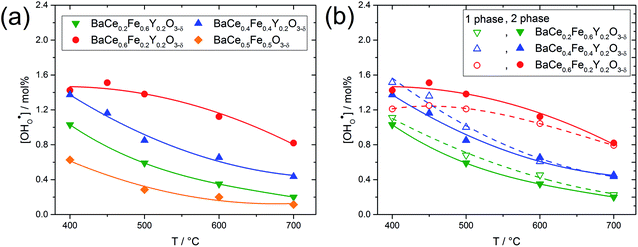
Fig. 5a shows the proton concentration of selected composites. As the temperature decreases from 700 °C to 400 °C, the proton concentration within a composite increases moderately. Two important trends can be noted: (i) the addition of Y increases the proton uptake of all composites investigated, and (ii) with increased Ce content in the composite, proton uptake increases. The reason for the decreasing slope of the proton uptake curve for BaCe0.6Fe0.2Y0.2O3−δ from 450 °C to 400 °C is not clear yet.
Fig. 5b compares the proton uptake for selected Ce–Fe ratios of the two-phase composites (closed symbols) and the corresponding single phases (obtained by sintering the composites at elevated temperatures where complete miscibility occurs). The temperatures for achieving single-phase samples can be recognized in Fig. S1.† For a given Ce–Fe ratio, the proton concentration of the two-phase composite and the single-phase material is relatively similar. This could be due to the preferential solubility of Y in the Fe-rich phases of the composites and the correspondingly lower Y concentrations in the Ce-rich phases (see Table 1). Lower Y concentrations in the Ce-rich phases reduce the concentration of oxygen vacancies as well as the basicity,27 both effects being negative for proton uptake. It has already been shown experimentally that the water uptake of electrolytes7 and mixed-conducting perovskites27 depends on the basicity of the respective materials. Recent DFT calculations support this statement and show that the proton affinity varies more strongly with material composition than with hydroxide affinity. Thus, the proton affinity dominates the trend of hydration enthalpy, and the proton affinity correlates with the basicity of the material.34
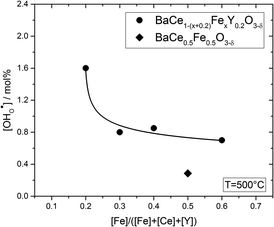
Fig. 6 shows the proton concentration as a function of Fe content at 500 °C. The increase in proton uptake is evident in comparison of the Y-containing composites (closed symbols) with the Y-free composite (open symbol). The proton concentration decreases significantly with increasing Fe content in the precursor, reaching a plateau for x ≥ 0.4 in BaCe1−(x+0.2)FexY0.2O3−δ. A possible explanation for this trend might be a reduced basicity of the material (Fe3+ is more acidic than Ce4+, see also Fig. 7). The decrease in the relative amount of the Ce-rich phase (i.e. the dominant proton-conducting phase in the composites) with increasing Fe content in the precursor could also contribute to the decrease in 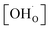 . Both effects would restrict the proton conduction in Ce-rich percolating paths in the composite. When redox active transition metals are added to the B-site of the perovskite, the proton uptake decreases. This was demonstrated e.g. for (La,Sr)(Sc,Fe)O3,35 and has also been shown for Ba(Zr0.88−xFexY0.12)O3.12 This effect is attributed to the higher covalence of Fe–O bonds (electron density is drawn from oxygen to iron and thus the basicity of the oxygen is reduced).36
. Both effects would restrict the proton conduction in Ce-rich percolating paths in the composite. When redox active transition metals are added to the B-site of the perovskite, the proton uptake decreases. This was demonstrated e.g. for (La,Sr)(Sc,Fe)O3,35 and has also been shown for Ba(Zr0.88−xFexY0.12)O3.12 This effect is attributed to the higher covalence of Fe–O bonds (electron density is drawn from oxygen to iron and thus the basicity of the oxygen is reduced).36
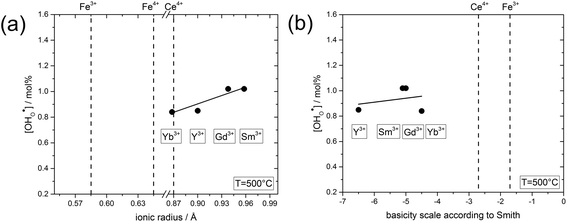 | ||
| Fig. 7 (a) Proton concentration at 500 °C of composites obtained from precursors of BaCe0.4Fe0.4B0.2O3−δ (B = Yb, Y, Gd or Sm) as a function of the ionic radius29 of B. (b) Proton concentration at 500 °C of composites obtained from precursors of BaCe0.4Fe0.4B0.2O3−δ (B = Yb, Y, Gd or Sm) as a function of the basicity39 of the binary oxides of B. | ||
In comparison with single-phase proton-conducting ferrates/cobaltates (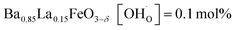 ,
, 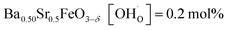 and
and 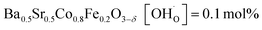 ;37 all at T = 500 °C and pH2O = 17 mbar), the proton uptake of the self-generated BaCe1−(x+0.2)FexY0.2O3−δ composites is considerably higher (0.6–1.4 mol% at T = 500 °C and pH2O = 17 mbar). A better understanding of the cation distribution within the two phases of the self-generated composites could lead to a further optimization of the proton uptake by tailored compositional variations.
;37 all at T = 500 °C and pH2O = 17 mbar), the proton uptake of the self-generated BaCe1−(x+0.2)FexY0.2O3−δ composites is considerably higher (0.6–1.4 mol% at T = 500 °C and pH2O = 17 mbar). A better understanding of the cation distribution within the two phases of the self-generated composites could lead to a further optimization of the proton uptake by tailored compositional variations.
Substitution with Y3+ increases the oxygen vacancy concentration and the basicity in both Ce- and Fe-rich phases. If Y is dissolved preferentially in the Fe-rich phase, only a small fraction of the Y will occur in the Ce-rich phase (which is the phase with the higher degree of hydration) and thus the proton uptake of the composite is only slightly improved (see Fig. 5 and 6). It is known from single-phase perovskite materials such as BaFe0.8Y0.2O3−δ and Ba0.95La0.05Fe0.8Zn0.2O3−δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 that partial substitution of Fe by oversized, redox-inactive cations such as Y3+, Zn2+ significantly increases the proton uptake of these phases. However, in absolute numbers the increase in proton uptake by Y substitution in the Fe-rich phase is only moderate, and cannot overcompensate the decrease of proton uptake by decreased Y levels in the Ce-rich phase of the present composites (the detailed variation of proton uptake in single-phase perovskite materials with Ce, Fe and Y concentrations will be published separately). Thus, in the present BaCe1−(x+0.2)FexY0.2O3−δ composites the proton uptake is less than estimated from a mixture of BaCe0.8Y0.2O2.9 and BaFe0.8Y0.2O3−δ. On the other hand, the partial dissolution of Fe in the cerate and Ce in the ferrate phase tunes both phases towards becoming triple conductors and thus has the potential to widen the active region for oxygen reduction in a composite PCFC cathode beyond the actual three phase boundary.
27 that partial substitution of Fe by oversized, redox-inactive cations such as Y3+, Zn2+ significantly increases the proton uptake of these phases. However, in absolute numbers the increase in proton uptake by Y substitution in the Fe-rich phase is only moderate, and cannot overcompensate the decrease of proton uptake by decreased Y levels in the Ce-rich phase of the present composites (the detailed variation of proton uptake in single-phase perovskite materials with Ce, Fe and Y concentrations will be published separately). Thus, in the present BaCe1−(x+0.2)FexY0.2O3−δ composites the proton uptake is less than estimated from a mixture of BaCe0.8Y0.2O2.9 and BaFe0.8Y0.2O3−δ. On the other hand, the partial dissolution of Fe in the cerate and Ce in the ferrate phase tunes both phases towards becoming triple conductors and thus has the potential to widen the active region for oxygen reduction in a composite PCFC cathode beyond the actual three phase boundary.
In the following, the influence of the ionic radius and the basicity on the proton uptake is discussed for Y and other substituents in BaCe0.4Fe0.4B0.2O3−δ composites (B = Y, Yb, Sm, Gd) (Fig. 7). The key for the proton uptake is the distribution of the acceptor between the Ce-rich and the Fe-rich phase. The mismatch in the ionic radii of Y3+ (0.9 Å) and Ce4+ (0.87 Å) can lead to strain in the Ce-rich phase, although the size effect is more severe for Y in the Fe-rich phase. Intermixing of the cations, including dissolution of part of the Y3+ in the Fe-rich phase, may be a means to reduce this strain,38 but leads to a decrease in the proton uptake. Ytterbium was explored as an alternative substituent ion for the Ba(Ce,Fe)O3−δ series to counteract strain-induced cation intermixing, since Yb3+ (0.868 Å) has almost the same ionic radius as Ce4+. However, this approach did not result in any significant increase in proton uptake, see Fig. 7a. Subsequently, two substituents with relatively large ionic radii, Gd3+ (0.94 Å) and Sm3+ (0.96 Å) were tried, but again no significant change in proton uptake was observed. Thus, it appears that the ionic radius of the substituent ion plays a subordinate role for the distribution of the acceptor, and therefore for the proton uptake of the composite. Another driving force for the formation of the self-generated composites is the balance in basicity of the two phases due to the solubility of Ce in the Fe-rich phase and vice versa and the Y distribution.39 The acceptor distribution is governed by an acid–base reaction, whereby the larger (more basic) ion experience a stronger driving force for the incorporation into the Fe-rich phase. As evident from Fig. 7b, the substituent ions studied have a relatively high basicity compared to the less basic Fe. Thus, it may be favourable for Y, Yb, Sm, Gd to dissolve in the Fe-rich phase in the sense of an acid–base reaction. Consequently, a more acidic three-valent ion, which should also have a similar ionic radius to Ce4+, may have a higher affinity to dissolving in the Ce-rich phase of Ba(Ce,Fe)O3−δ based composites, and thus improve the proton uptake. Systematic studies of the structure–property relations of composites substituted in this way will be the subject of future work.
3. Experimental
3.1 Synthesis
Nanocomposite powders were obtained for BaCe1−(x+z)FexYzO3−δ with z = 0.2 for 0.1 ≤ x ≤ 0.6 and z = 0 for Ce![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe = 1, using a sol–gel method (“one-pot” synthesis) followed by thermal treatment. Stoichiometric amounts of the corresponding metal-nitrates (Ba(NO3)2, Ce(NO3)3·6H2O, Y(NO3)2·6H2O and Fe(NO3)3·9H2O) (all from Sigma Aldrich, analytical grade quality) were mixed with distilled H2O in a stainless steel vessel. Anhydrous citric acid and EDTA (one mole each per cation) were added after the metal-nitrates were completely dissolved. Then, a 25% aqueous NH3 solution was added until pH = 8 was reached and a clear dark blue solution was obtained. The temperature was continuously increased to remove water and form a gel. Self-ignition and combustion of the dried gel occurred at approximately 500 °C. The raw ash was crushed in an agate mortar and calcined at 1000 °C for 10 h (5 K min−1 ramps for heating and cooling) in air. During this process, the precursor decomposed into a mixture of two crystalline phases, as confirmed after calcination by XRD. For all further measurements, the powders were dry ground in a zirconia ball mill and sintered in a graphite mold using a SPS uniaxial hot-press (FCT Systems GmbH, Germany). Parameters and densities from the SPS process are shown in ESI Table S6.† Long-term annealing experiments on the sintered pellets were performed to further explore the stability of the self-generated composites (see Fig. S9 in the ESI†).
Fe = 1, using a sol–gel method (“one-pot” synthesis) followed by thermal treatment. Stoichiometric amounts of the corresponding metal-nitrates (Ba(NO3)2, Ce(NO3)3·6H2O, Y(NO3)2·6H2O and Fe(NO3)3·9H2O) (all from Sigma Aldrich, analytical grade quality) were mixed with distilled H2O in a stainless steel vessel. Anhydrous citric acid and EDTA (one mole each per cation) were added after the metal-nitrates were completely dissolved. Then, a 25% aqueous NH3 solution was added until pH = 8 was reached and a clear dark blue solution was obtained. The temperature was continuously increased to remove water and form a gel. Self-ignition and combustion of the dried gel occurred at approximately 500 °C. The raw ash was crushed in an agate mortar and calcined at 1000 °C for 10 h (5 K min−1 ramps for heating and cooling) in air. During this process, the precursor decomposed into a mixture of two crystalline phases, as confirmed after calcination by XRD. For all further measurements, the powders were dry ground in a zirconia ball mill and sintered in a graphite mold using a SPS uniaxial hot-press (FCT Systems GmbH, Germany). Parameters and densities from the SPS process are shown in ESI Table S6.† Long-term annealing experiments on the sintered pellets were performed to further explore the stability of the self-generated composites (see Fig. S9 in the ESI†).
3.2 Microstructural characterisation
XRD analysis of the calcined powders was performed with a BRUKER-AXS D8 Advance ECO diffractometer using a Cu Kα radiation source (λ = 1.5406 Å) operated at 40 kV and 25 mA. The diffractogram was recorded at room temperature with a scanning rate of 0.01° s−1 with 2 s acquisition time per step. Lattice parameters of the room temperature phases were obtained from fitting the peak positions to either a cubic unit cell (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) for one phase, and an orthorhombic unit cell (space group Pmcn for the Y-free sample) or a trigonal unit cell (space group R
m) for one phase, and an orthorhombic unit cell (space group Pmcn for the Y-free sample) or a trigonal unit cell (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/i_char_0033_0304.gif) c for the Y-containing samples) for the other phase. Whole diffraction pattern profile fitting using LeBail analysis was performed by using the commercial software TOPAS.40–42
c for the Y-containing samples) for the other phase. Whole diffraction pattern profile fitting using LeBail analysis was performed by using the commercial software TOPAS.40–42
Inductively coupled plasma optical emission spectrometry (ICP-OES, SPECTRO CIROS from SPECTRO Analytical Instruments GmbH) was used to determine the average cation composition of BCFY samples. For the analyses specific sample amounts were dissolved in hydrochloric acid. The obtained cation compositions are given in Tables S7 and S8.†
Spatial cation distributions and local cation compositions were determined by EDXS in a scanning electron microscope (Zeiss Merlin) operated at 10 kV equipped with an Oxford Instruments Ultim Extreme detector. For the applied electron energy, penetration depths of 1–5 μm are expected.
Sample preparation for STEM investigations was carried out with a focused ion beam (FIB) microscope FEI NOVA 200 NanoLab. The TEM lamellae were cut out of the polished surfaces of SPS densified pellets. STEM investigations were performed with an FEI TITAN3 G2 60–300 at 300 kV accelerating voltage. The microscope is equipped with a Cs-probe corrector and a Super-X detector by FEI. STEM images were recorded with a HAADF detector. The software packages GMS 3 (Gatan) and Velox 2 (Thermo Fisher Scientific) were used to acquire HAADF images and EDXS spectrum images. STEM-EDXS measurements were performed on grains, which were not aligned along major zone axes with respect to the electron beam in order to avoid channelling effects during the measurement.43
3.3 Thermogravimetry
Thermogravimetry (STA449C Jupiter, Netzsch, Germany) was carried out with approximately 0.5–1 g of sample (sintered pellet crushed to particles) in an alumina crucible with an N2 flow of 60 ml min−1. In order to implement humid conditions the water partial pressure (pH2O) was adjusted by bubbling the gas through a thermostated water evaporator (the flow of 10 ml min−1 “protective gas” through the balance compartment of the STA449 was always kept dry). For isothermal pH2O changes, the measured buoyancy effects were negligible. In order to “freeze” the oxygen exchange reaction, the particles were quenched from 700 °C in dry N2 so that all Fe is present as Fe3+ and then cooled rapidly (20 K min−1) to the desired temperature at which the proton uptake is to be determined. An appropriate particle size is essential for the suppression of the surface controlled reaction of oxygen incorporation. The optimal particle size (here: 100–250 μm) is a compromise between reduced surface reaction (low pO2 and low T) and a reasonable time (10–100 min) for the kinetically more facile water uptake reaction to reach equilibrium (see Fig. S10†). This method avoids complications from hole-proton defect interactions and the long equilibration times at low temperatures as described in Zohourian et al.274. Summary and conclusions
Self-generated BaCe1−(x+z)FexYzO3−δ composites (z = 0.2 for 0.1 ≤ x ≤ 0.6 and z = 0 for Ce![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe = 1) were synthesized and characterized with respect to their chemical composition, phase stability and water uptake. A miscibility gap with an upper critical mixing temperature of ∼1350 °C leads to the formation of two-phase composites of all investigated precursor compositions containing Y. The composites show variable phase ratios of the cubic Fe-rich and the trigonal Ce-rich phase, with the cubic phase dominating at higher temperatures. By exposure to temperatures above the upper critical mixing temperature, single-phase perovskites are formed, with the cation stoichiometry corresponding to that of the precursor. Scanning transmission electron microscopy and scanning electron microscopy with energy-dispersive X-ray spectroscopy showed some mutual dissolution of Fe and Ce in the respective other phase, and that Y dissolves preferentially in the Fe-rich phase of the composites. The proton concentration in the Ce-rich phase of the composites is significantly lowered by the Fe incorporation. In addition, the lower degree of Y substitution in the Ce-rich phase decreases proton uptake, resulting in similar proton concentrations in single-phase and composite materials with identical overall cation composition. Knowledge of the local cation concentration of the individual phases is particularly important in the present case, since it affects properties like phase formation and water uptake. Finally, reasons for the preferred distribution of Y in the Fe-rich phase were discussed. A possible explanation is the tendency of the coexisting phases to balance their respective basicity.
Fe = 1) were synthesized and characterized with respect to their chemical composition, phase stability and water uptake. A miscibility gap with an upper critical mixing temperature of ∼1350 °C leads to the formation of two-phase composites of all investigated precursor compositions containing Y. The composites show variable phase ratios of the cubic Fe-rich and the trigonal Ce-rich phase, with the cubic phase dominating at higher temperatures. By exposure to temperatures above the upper critical mixing temperature, single-phase perovskites are formed, with the cation stoichiometry corresponding to that of the precursor. Scanning transmission electron microscopy and scanning electron microscopy with energy-dispersive X-ray spectroscopy showed some mutual dissolution of Fe and Ce in the respective other phase, and that Y dissolves preferentially in the Fe-rich phase of the composites. The proton concentration in the Ce-rich phase of the composites is significantly lowered by the Fe incorporation. In addition, the lower degree of Y substitution in the Ce-rich phase decreases proton uptake, resulting in similar proton concentrations in single-phase and composite materials with identical overall cation composition. Knowledge of the local cation concentration of the individual phases is particularly important in the present case, since it affects properties like phase formation and water uptake. Finally, reasons for the preferred distribution of Y in the Fe-rich phase were discussed. A possible explanation is the tendency of the coexisting phases to balance their respective basicity.
Author contributions
Christian Berger: conceptualization, methodology, investigation, writing – original draft, writing – review & editing, visualization. Edith Bucher: conceptualization, writing – review & editing, supervision, project administration, funding acquisition. Rotraut Merkle: conceptualization, methodology, investigation, writing – review & editing, supervision. Christina Nader: investigation, writing – review & editing. Judith Lammer: investigation, writing – review & editing, visualization. Werner Grogger: writing – review & editing. Joachim Maier: conceptualization, writing – review & editing, supervision. Werner Sitte: conceptualization, writing – review & editing, supervision.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
Financial support by the Austrian Research Promotion Agency FFG (No. 871659) and by the “Klima- und Energiefonds” within the program “Energieforschung (e!MISSION)” is gratefully acknowledged. Furthermore, the authors would like to thank Helga Hoier for XRD measurements, Annette Fuchs for SEM-EDXS measurements, Armin Sorg for SPS experiments, (all from Max Planck Institute for Solid State Research), Samir Hammoud for ICP-OES measurements (Max Planck Institute for Intelligent Systems) and Martina Dienstleder (Graz Centre for Electron Microscopy) for the FIB preparation.References
- S. C. Singhal and K. Kendall, High temperature solid oxide fuel cells: fundamentals, design and applications, Elsevier Advanced Technology, Oxford, UK, 2004 Search PubMed.
- K.-D. Kreuer, Fuel cells – Selected entries from the encyclopedia of sustainability science and technology, Springer-Verlag, New York, 1st edn, 2013 Search PubMed.
- K. Kendall and M. Kendall, High-temperature Solid Oxide Fuel Cells for the 21st Century, Academic Press, Oxford, UK, 2016 Search PubMed.
- H. Zhu and R. J. Kee, J. Electrochem. Soc., 2017, 164, F1400–F1411 CrossRef CAS.
- Y. Matsuzaki, Y. Tachikawa, T. Somekawa, T. Hatae, H. Matsumoto, S. Taniguchi and K. Sasaki, Sci. Rep., 2015, 5, 12640 CrossRef CAS.
- J. H. Shim, Nat. Energy, 2018, 3, 168–169 CrossRef CAS.
- K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359 CrossRef CAS.
- W. He, X. Wu, G. Yang, H. Shi, F. Dong and M. Ni, ACS Energy Lett., 2017, 2, 301–305 CrossRef CAS.
- D. Chen and Z. Shao, Int. J. Hydrogen Energy, 2011, 36, 6948–6956 CrossRef CAS.
- L. Nie, M. Liu, Y. Zhang and M. Liu, J. Power Sources, 2010, 195, 4704–4708 CrossRef CAS.
- M. Papac, V. Stevanović, A. Zakutayev and R. O'Hayre, Nat. Mater., 2021, 20, 301–313 CrossRef CAS.
- R. Merkle, M. F. Hoedl, G. Raimondi, R. Zohourian and J. Maier, Annu. Rev. Mater. Res., 2021, 51, 461–493 CrossRef CAS.
- L. Yang, Z. Liu, S. Wang, Y. Choi, C. Zuo and M. Liu, J. Power Sources, 2010, 195, 471–474 CrossRef CAS.
- E. Fabbri, L. Bi, D. Pergolesi and E. Traversa, Energy Environ. Sci., 2011, 4, 4984–4993 RSC.
- G. Yang, C. Su, H. Shi, Y. Zhu, Y. Song, W. Zhou and Z. Shao, Energy Fuels, 2020, 34, 15169–15194 CrossRef CAS.
- J. Druce, H. Téllez, T. Ishihara and J. A. Kilner, Faraday Discuss., 2015, 182, 271–288 RSC.
- X. Zhu, H. Wang and W. Yang, J. Membr. Sci., 2008, 309, 120–127 CrossRef CAS.
- W. Fang, F. Liang, Z. Cao, F. Steinbach and A. Feldhoff, Angew. Chem., Int. Ed., 2015, 54, 4847–4850 CrossRef CAS PubMed.
- W. Fang, F. Steinbach, Z. Cao, X. Zhu and A. Feldhoff, Angew. Chem., 2016, 128, 8790–8793 CrossRef.
- W. Fang, C. Zhang, F. Steinbach and A. Feldhoff, Angew. Chem., Int. Ed., 2017, 56, 7584–7588 CrossRef CAS PubMed.
- L. Rioja-Monllor, C. Bernuy-Lopez, M.-L. Fontaine, T. Grande and M.-A. Einarsrud, Materials, 2019, 12, 3441 CrossRef CAS PubMed.
- Y. Song, Y. Chen, W. Wang, C. Zhou, Y. Zhong, G. Yang, W. Zhou, M. Liu and Z. Shao, Joule, 2019, 3, 2842–2853 CrossRef CAS.
- Z. Zhao, J. Cui, M. Zou, S. Mu, H. Huang, Y. Meng, K. He, K. S. Brinkman and J. Tong, J. Power Sources, 2020, 450, 227609 CrossRef CAS.
- S. Cheng, Y. Wang, L. Zhuang, J. Xue, Y. Wei, A. Feldhoff, J. Caro and H. Wang, Angew. Chem., Int. Ed., 2016, 55, 10895–10898 CrossRef CAS.
- L. Vegard, Z. Phys., 1921, 5, 17–26 CrossRef CAS.
- M. Erchak, I. Fankuchen and R. Ward, J. Am. Chem. Soc., 1946, 68, 2085–2093 CrossRef CAS.
- R. Zohourian, R. Merkle, G. Raimondi and J. Maier, Adv. Funct. Mater., 2018, 28, 1801241 CrossRef.
- L. Malavasi, H. Kim and T. Proffen, J. Appl. Phys., 2009, 105, 123519 CrossRef.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671 CrossRef CAS PubMed.
- D. Poetzsch, R. Merkle and J. Maier, Adv. Funct. Mater., 2015, 25, 1542–1557 CrossRef CAS.
- D. Poetzsch, R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2014, 16, 16446–16453 RSC.
- D. Poetzsch, R. Merkle and J. Maier, Faraday Discuss., 2015, 182, 129–143 RSC.
- T. S. Bjørheim, M. F. Hoedl, R. Merkle, E. A. Kotomin and J. Maier, J. Phys. Chem. C, 2020, 124, 1277–1284 CrossRef.
- D. Han, Y. Okumura, Y. Nose and T. Uda, Solid State Ionics, 2010, 181, 1601–1606 CrossRef CAS.
- M. F. Hoedl, D. Gryaznov, R. Merkle, E. A. Kotomin and J. Maier, J. Phys. Chem. C, 2020, 124, 11780–11789 CrossRef CAS.
- R. Zohourian, PhD thesis, University of Stuttgart, 2018 Search PubMed.
- F. Baiutti, F. Chiabrera, M. Acosta, D. Diercks, D. Parfitt, J. Santiso, X. Wang, A. Cavallaro, A. Morata, H. Wang, A. Chroneos, J. MacManus-Driscoll and A. Tarancon, Nat. Commun., 2021, 12, 2660 CrossRef CAS.
- D. W. Smith, J. Chem. Educ., 1987, 64, 480 CrossRef CAS.
- Bruker AXS Topas V5, General profile and structure analysis software for powder diffraction data, User's manual, Karlsruhe, Germany, 2014 Search PubMed.
- A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218 CrossRef CAS.
- A. Le Bail, Powder Diffr., 2005, 20, 316–326 CrossRef CAS.
- D. B. Williams and C. B. Carter, Transmission Electron Microscopy – A Textbook for Materials Science, Springer, Boston, MA, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta07208k |
| This journal is © The Royal Society of Chemistry 2022 |