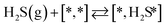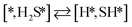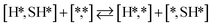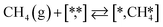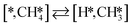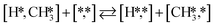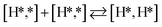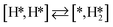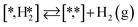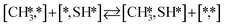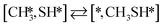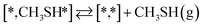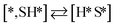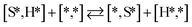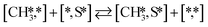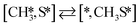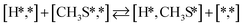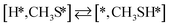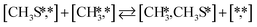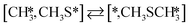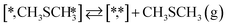First-principles microkinetic study of methane and hydrogen sulfide catalytic conversion to methanethiol/dimethyl sulfide on Mo₆S₈ clusters: activity/selectivity of different promoters

Abstract

A large fraction of the global natural gas reserves is in the form of sour gas, i.e. contains hydrogen sulfide (H₂S) and carbon dioxide (CO₂), and needs to be sweetened before utilization. The traditional amine-based separation process is energy-intensive, thereby lowering the value of the sour gas. Thus, there is a need to find alternative processes to remove, e.g., hydrogen sulfide. Mo₆S₈ clusters are promising candidates for transforming methane (CH₄) and hydrogen sulfide into methanethiol (CH₃SH) and dimethyl sulfide (CH₃SCH₃), which are high-value sulfur-containing products that can be further used in the chemical industry. Here first-principles microkinetics is used to investigate the activity and selectivity of bare and promoted (K, Ni, Cl) Mo₆S₈. The results show that methanethiol is produced via two different pathways (direct and stepwise), while dimethyl sulfide is formed via a competing pathway in the stepwise formation of methanethiol. Moreover, there is an increase in activity and a decrease in selectivity when adding an electropositive promoter (K), whereas the reverse behaviour is observed when adding an electronegative promoter (Cl). When adding Ni there is also a decrease in activity and an increase in selectivity; however, Ni is acting as an electron donor. The results provide insights and guidance as to what catalyst formulation is preferred for the removal of hydrogen sulfide in sour gas.

---

1 Introduction

Rational design of catalysts to obtain new or improved catalyst formulations with a highly selective conversion of hydrocarbon gas, such as methane (CH₄), is of utmost importance in solving seminal petroleum industry processing problems. These problems include everything from energy carrier generation (e.g., steam reforming and water gas shift on the supported Ni and CuO/ZnO/Al₂O₃ catalysts, respectively),¹ obtaining feedstock for a variety of commodity chemicals (e.g., olefin metathesis of ethylene and 2-butene to produce propylene on supported metal oxide catalysts)^2,3 and environmental remediation of refinery tail gases (e.g., H₂S oxidation on Al₂O₃ or TiO₂ in the Claus process).⁴ Yet, many fundamental aspects governing hydrocarbon catalyst conversion and selectivity are still not resolved because the underlying complex selectivity descriptors are still lacking.⁵ Of particular interest is understanding the structure–selectivity relationships in metal oxide and metal sulfide catalysts for sour natural gas catalytic conversion.⁶ Sour gas – mainly CO₂ and H₂S – molecules are invariably present in natural gas and present significant challenges for conventional oxide-based catalysts including catalyst degradation and loss of activity. The Society of Petroleum Engineers (SPE) estimates that about 40% of the world's total accessible natural gas reserves are acidic, containing large concentrations of CO₂ and H₂S, with over 10% H₂S totaling up to 350 Tcf.⁷ The concentrations of acidic gases can range up to 90% by volume and this sub-quality natural gas accounts for ∼30% of U.S. natural gas resources⁸ with the consequence that most of the gas is not utilized.⁹ A conventional approach to sweeten natural gas includes a priori removal of these gases using alkanolamines, with the two most common being monoethanolamine (MEA) and diethanolamine (DEA), via solvent recycling and adsorption/desorption processes. Typically, the energy consumed during the amine regeneration step is 3.65 MJ kg⁻¹ CO₂,^10–12 which significantly increases the cost of natural gas.

A conceptually new approach recently emerged to catalytically transform both hydrocarbon and sour gas molecules into valuable products simultaneously via reactive separation.⁶ In particular, hydrogen sulfide methane reforming¹³ has been proposed at temperatures above 1000 °C with considerable amounts of carbonyl sulfide (COS) being formed. While H₂S poisons conventional catalysts for steam reforming,¹⁴ the overall process is thermodynamically limited and a series of supported catalysts have been utilized for this reaction, including metal oxides (Pt/Al₂O₃,¹⁵ Mo,Cr/ZrO₂–SBA15 (ref. 16), Mo,Cr/ZrO₂–La₂O₃ (ref. 16) and Fe₂O₃/γ-Al₂O₃ (ref. 17)) and metal sulfides (MoS₂,Cr₂S₃ and Ce₂S₃).^18–20 The Langmuir–Hinshelwood–Hougen–Watson (LHHW) reaction mechanism on MoS₂ catalysts was proposed with the rate-determining step (RDS) being the reaction among the adsorbed species (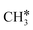, H₂S* and S*) on the catalyst surface with the participation of three catalytic sites.¹⁹ These catalysts have been used instead of thermal decomposition taking place at high (>70% for both CH₄ and H₂S) conversion above 1250 °C.²¹ In turn, CS₂ and COS have been shown to selectively react to form CH₃SH on Ni-, K-, and Co-promoted MoS₂/SiO₂, providing indirect routes of acidic gas processing to CH₃SH.^22–25 On the other hand, CH₃SH, which is isostructural with CH₃OH,²⁶ can be further converted into higher hydrocarbons. Chang and Silvestri²⁷ utilized H-ZSM-5 at 480 °C to convert CH₃SH into a mixture of hydrocarbons and H₂S with 7.0% selectivity towards C₂ and C₃ olefins with a significant amount of the carbon feed converted to dimethyl sulfide (DMS). Butter et al.²⁸ claimed overall 96.1% conversion of CH₃SH with significant amounts of CH₄ generated at 258 °C on Al-exchanged H-ZSM-5. Similarly, Mashkina et al.²⁹ identified the presence of CH₄ when CH₃SH was reacted on various acid catalysts between 350 and 400 °C, while at lower temperatures DMS was the only product observed. In general, large amounts of CH₄, DMS and coke were observed in addition to the BTX (benzene, toluene, xylene) products formed.^30–32 Insights from density functional theory (DFT) calculations have suggested less favorable free energy reactive pathways for CH₃SH as compared with CH₃OH for the same acidity catalysts due to the differences in charge transfer between the organic species and the zeolite framework.^33–35 DMS, on the other hand, was shown to yield 15.4% C₂H₄ in the product stream using WO₃/Al₂O₃, with CH₄ and C₃H₆ comprising the rest at 380 °C and 32% conversion.³⁶ Hence, obtaining partially activated CH₄ analogues, such as CH₃SH and CH₃SCH₃, to be converted to higher olefins as opposed to a complete reforming from sour gas streams is of direct interest.

In this work, we utilize DFT to investigate the activity and selectivity of bare and promoted Mo₆S₈ clusters toward methanethiol (CH₃SH) and DMS (CH₃SCH₃) using first-principles microkinetics. Earlier studies have shown that the stable and highly symmetric Mo₆S₈ cluster has many promising properties, e.g. large CO binding energy³⁷ and large dipole moment³⁸ and a number of other optical and reactive properties.^39–43 We expand our previous work⁴⁴ by adding diffusion steps in a phenomenological manner in the reaction mechanism in order to consider multiple reaction pathways and thereby selectivity. We utilize bare and K-, Cl- or Ni-promoted Mo₆S₈ clusters as a versatile and tunable H₂S-tolerant catalyst material.^{37,39,40,44,45}

2 Computational details

2.1 Electronic structure calculations

Periodic DFT calculations were performed as implemented in the VASP code.^46–49 The projector augmented wave (PAW) method of Blöchl,⁵⁰ as adapted by Kresse and Joubert,⁵¹ was used to describe the effective interaction between the valance electrons and the core. The exchange-correlation energy was described by the spin-polarized version of the PBE.⁵² The Brillouin zone was sampled using the Γ-point only. The Kohn–Sham equations have been solved self-consistently in a plane-wave basis set with a cutoff of 400 eV. The convergence criterion for the electronic self-consistency cycle, measured by the change in the total energy between successive iterations, was set to 10⁻⁶ eV. The electronic structures of the different clusters were analyzed and are shown in Fig. S10† using the crystal orbital Hamiltonian populations projected on the nearest neighbour orbitals using the LOBSTER software.^53–56

2.2 Structural optimization calculations

Transition states have been identified using the DIMER method,⁵⁷ as improved by Heyden et al.⁵⁸ The atomic positions were considered relaxed if all forces acting on the atoms were less than 0.005 eV Å⁻¹. Transition states were proven to be first-order saddle points of the potential energy surface using vibrational analysis. The intrinsic reaction coordinates (IRCs)^59,60 for the forward and backward reaction steps were identified using the damped velocity Verlet algorithm.⁶¹ The structures corresponding to potential energy minima along the IRC were further relaxed using a conjugate-gradient algorithm in order to satisfy the same optimization criterion as for transition states. Vibrational analysis was performed to ensure that the relaxed structures correspond to true potential energy minima. This procedure guarantees that reactant and product states are linked through one single transition state. Optimized structures are provided in the ESI† (Fig. S1–S3).

2.3 Microkinetic modelling

The reaction kinetics were investigated using energies and vibrational frequencies as calculated from DFT. The rate constants for the reaction between reaction intermediates were expressed using the conventional transition state theory (TST),⁶²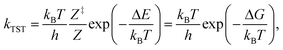where Z^‡ and Z are the internal partition functions of the transition state and initial state, respectively, ΔE is the zero-point corrected energy difference, and ΔG is the free energy difference. The free energy differences were evaluated using the Atomic Simulation Environment software package (ASE v3.15.0).^63,64

Adsorption of CH₄, H₂S, CH₃SH, H₂, and DMS was considered to be direct with rate constants expressed as

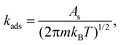where A_S is the area of the site, and the desorption is defined through the equilibriumwhere the energy of adsorption of species A (CH₄, H₂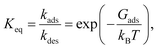S, CH₃SH, H₂, or DMS) is calculated as

E_ads = E_A* − (E_* + E_A(g)) (4)

The CH₄ : H₂S pressure ratio was kept at 1 : 12 in the kinetic calculations in order to simulate conditions necessary to avoid coke formation.¹⁶

In addition to the transition state (TS) steps and the barrierless adsorption/desorption (ads/des) steps, we also considered the diffusion steps between different clusters (diffusion) in a parametric way. From practical consideration this was done by introducing a low barrier (0.05 eV) and treating diffusion using TST.

Here we will assume a Langmuir–Hinshelwood reaction mechanism⁶² over a double site, using a double site notation [A*,B*], symbolizing adsorption on a –S–Mo– site with A adsorbed on S and B on Mo; all reaction steps are described in Table 1. We ignore the possibility of an Eley–Rideal mechanism⁶² since Eley–Rideal is usually less probable^62,65 as compared to Langmuir–Hinshelwood. In addition, we do not include a Mars–Van Krevelen mechanism⁶² since under industrial reaction conditions sulfur is in excess and the cost of creating a sulfur vacancy (Mo₆S₇) is calculated to be 2.4 eV, while the energy cost of adding one sulfur to Mo₆S₈ is 0.2 eV (here the reference state for sulfur is H₂S–H₂), which indicates that a reaction mechanism including Mo₆S₇ clusters is unlikely. The inclusion of Eley–Rideal and Mars–Van Krevelen mechanisms is a future challenge that is beyond the scope of this study.

Table 1 All reactions used in the microkinetic model using the double site notation [A*,B*], for adsorption on a –S–Mo– site with A adsorbed on S and B on Mo. The right column indicates how the reaction was treated

Reaction	Type
	Ads/des
	TS
	Diffusion
	Ads/des
	TS
	Diffusion
	Diffusion
	TS
	Ads/des
	Diffusion
	TS
	Ads/des
	TS
	Diffusion
	Diffusion
	TS
	Diffusion
	TS
	Diffusion
	TS
	Ads/des

---

Selectivity between DMS and methanethiol is defined as the ratio between the TOF of DMS and the sum of the direct and stepwise TOF of methanethiol.

The ensuing non-linear differential equations were integrated numerically using the SciPy Python package, which relies on the ODEPACK Fortran library.^66,67

3 Results and discussion

The calculated formation energies of the reactions CH₄ + H₂S → CH₃SH + H₂ and 2CH₄ + H₂S → CH₃SCH₃ + 2H₂ are −0.84 eV and −1.57 eV, respectively. This is in fair agreement with the experimental formation energies,⁶⁸ which are −0.75 eV and −1.37 eV, respectively.

The bare Mo₆S₈ cluster forms a face-capped octahedral cluster where the Mo atoms sits in octahedral positions and the S atoms occupy the face of the octahedron. The Mo–Mo and Mo–S distances are 2.62 Å and 2.44 Å, respectively. There is a charge transfer from the molybdenum atoms to the more electronegative sulfur atoms. A Bader analysis^69–72 shows a 0.7–0.8 excess of electrons per atom on the sulfur atoms, while the molybdenum atoms lose close to one whole electron per atom.

The promoters (K, Ni, and Cl) affect the structural and electronic properties of the Mo₆S₈ cluster in different ways. K adsorbs in a bridge position between two S atoms, with a bond distance of 3.00 Å, but there is no noticeable distortion in the Mo₆S₈ cluster owing to the adsorption. However, K acts as an electron donor, and via a Bader charge analysis we observe an additional charge of 0.2 and 0.1 electrons per atom to the sulfur and molybdenum atoms close to the adsorption site. Ni also adsorbs in the bridge position (bond distance of 2.15 Å) between two sulfur atoms. However, there are noticeable structural changes in the cluster; in particular, the sulfur atoms adjust so that the Ni promoter gains access to the two underlying molybdenum atoms. The Ni–Mo distances (2.43 Å and 2.60 Å) are not symmetric. However, according to the Bader charge analysis, Ni transfers 0.2 electrons almost symmetrically between the two coordinating molybdenum atoms. In marked difference with the other promoters, Cl coordinates to one molybdenum atom (bond distance 2.33 Å). There is a charge transfer to Cl (0.4 electrons) which comes from the molybdenum atom (0.2 electrons) coordinated to Cl and symmetrically from all sulfur atoms in the cluster.

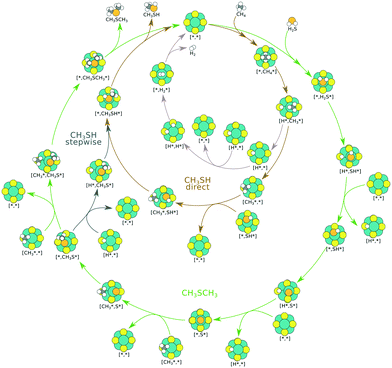
The proposed reaction mechanism of CH₄ and H₂S conversion to methanethiol and DMS is shown in Fig. 1 for the bare cluster (see Fig. S1–S3† for K-, Ni-, and Cl-promoted clusters). The reaction mechanism can be divided into three parts: (i) activation of reactants (CH₄ and H₂S), (ii) formation of methanethiol where two different pathways are considered (one direct route, SH* + 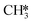, and one associative route that involves atomic S*), and finally (iii) coupling of CH₃S* and 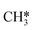to DMS. The stepwise methanethiol and DMS pathway has one common reaction intermediate, namely CH₃S* adsorbed on the Mo site. Depending on which reaction intermediate, either hydrogen or methyl, occupies the accompanying sulfur site, methanethiol or DMS will be formed. There is also a number of diffusion steps included in the reaction mechanism, which are important as this allows relevant reaction intermediates to pair up according to the dual site notation shown in Fig. 1.

Fig. 1 Proposed reaction mechanism for the conversion of CH₄ and H₂ to methanethiol and DMS. The production of methanethiol occurs along two different pathways (direct and stepwise), while the production of DMS is a competing path in the stepwise reaction. Color code: hydrogen, white; carbon, black; sulfur, yellow (Mo₆S₈) or orange (adsorbed); and molybdenum, green.

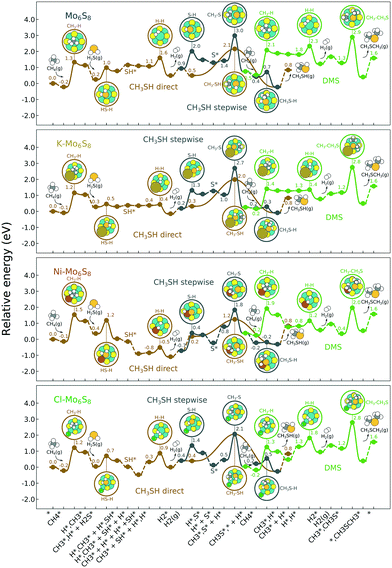
The reaction energy landscape of CH₄ and H₂S conversion to methanethiol and dimethyl sulfide is shown in Fig. 2, where all energies are referenced to the empty cluster with CH₄ and H₂S in the gas phase. The free energy landscape at 1400 K is shown in Fig. S4† and the rate constants and free energy barriers are listed in Tables S1–S4.† The activation of CH₄ on the bare and promoted Mo₆S₈ cluster occurs through a weak physisorption state with an adsorption energy of −0.21 eV, −0.09 eV, −0.13 eV and −0.21 eV on Mo₆S₈, K–Mo₆S₈, Ni–Mo₆S₈ and Cl–Mo₆S₈, respectively. From that state the C–H bond that coordinates to the cluster becomes activated and finally reaches a transition state with an energy of 1.32 eV (Mo₆S₈), 1.16 eV (K–Mo₆S₈), 1.53 eV (Ni–Mo₆S₈) and 1.22 eV (Cl–Mo₆S₈). The C–H bond distance at the transition state ranges between 1.73 Å and 1.91 Å, where the bond distance correlates with the transition state energy. The dissociative state [H*,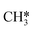] is endothermic with respect to the physisorbed state, with comparable energies (1.34 eV and 1.28 eV) for the bare and Ni–Mo₆S₈, while K–Mo₆S₈ and Cl–Mo₆S₈ are slightly less destabilized (1.13 eV and 1.15 eV).

Fig. 2 Reaction energy landscape for the conversion of CH₄ and H₂S to methanethiol and DMS. The production of methanethiol occurs along two different pathways (direct and stepwise), while the production of DMS is another path of the stepwise reaction. Energy (eV) with gas-phase H₂S and CH₄ as reference is shown for the most important steps. The insets show the transition states for all the clusters and also the adsorption site of the different promoters and intermediates. All energies are referenced to the empty cluster with CH₄ and H₂S in the gas phase. Color code: hydrogen, white; carbon, black; sulfur, yellow (Mo₆S₈) or orange (adsorbed); molybdenum, green; potassium, brown; nickel, red; and chlorine, dark green.

On the other hand, the activation of H₂S occurs through a rather strong chemisorption state with an adsorption energy of −0.88 eV, −0.76 eV, −0.78 eV and −0.89 eV on Mo₆S₈, K–Mo₆S₈, Ni–Mo₆S₈ and Cl–Mo₆S₈, respectively. The transition state involves the activation of one of the H–S bonds. K–Mo₆S₈ has the lowest barrier (0.18 eV), followed by Cl–Mo₆S₈ (0.66 eV), Mo₆S₈ (0.73 eV) and finally Ni–Mo₆S₈ (0.82 eV). The dissociation is endothermic on Mo₆S₈ and Cl–Mo₆S₈ with an energy of 0.53 eV and 0.37 eV, respectively. This is very different as compared to Ni–Mo₆S₈ where the dissociation is exothermic with an energy of −0.32 eV. On K–Mo₆S₈ the reaction is endothermic but with an energy of only 0.02 eV.

The next part involves the diffusion of hydrogen away from the sulfur part of the dual site. In the reaction energy landscape the separation of SH* and H* to two separate dual sites is shown first. Here it is clear that for the bare Mo₆S₈ this process is strongly endothermic (0.47 eV), while for the Cl- and Ni-promoted clusters this process is exothermic with −0.39 eV and −0.18 eV, respectively. On K–Mo₆S₈ the separation is slightly endothermic (0.07 eV). Similar results are found for the separation of 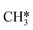and H* to two separate dual sites, where the reaction energy is 0.03 eV, −0.02 eV, −0.76 eV and −0.50 eV for Mo₆S₈, K–Mo₆S₈, Ni–Mo₆S₈ and Cl–Mo₆S₈, respectively. However, the diffusion of H* to the same dual site ([H*,H*]) displays a reverse trend where on the bare Mo₆S₈ this process is exothermic (−0.11 eV), while the same process is endothermic on K–Mo₆S₈, Ni–Mo₆S₈ and Cl–Mo₆S₈ with an energy of 0.02 eV, 0.05 eV and 0.80 eV, respectively. The two H* can associate and form 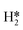on the molybdenum part of the dual site with a reaction barrier of 0.52 eV (Mo₆S₈), 0.06 eV (K–Mo₆S₈), 0.33 eV (Ni–Mo₆S₈) and 0.54 eV (Cl–Mo₆S₈). The formation of 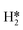is endothermic irrespective of whether the cluster is promoted or not.

The direct pathway to methanethiol involves diffusion of 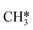and SH* to the same dual site. In the case of Mo₆S₈ this step is exothermic with −0.53 eV, and −0.01 eV on Cl–Mo₆S₈, while for the K- and Ni-promoted clusters the diffusion is endothermic, 0.13 eV and 0.90 eV on K–Mo₆S₈ and Ni–Mo₆S₈, respectively. The next step in the formation of methanethiol occurs through a transition state that involves the formation of an S–C bond. The bond distance is calculated to be 2.53 Å, 2.60 Å, 2.52 Å, 2.61 Å with an energy barrier of 1.65 eV, 1.67 eV, 1.06 eV and 1.68 eV on Mo₆S₈, K–Mo₆S₈, Ni–Mo₆S₈ and Cl–Mo₆S₈, respectively.

Besides the direct pathway there is also the possibility to further decompose SH* into elementary S*. The barrier of the transition state is 1.08 eV, 1.13 eV, 1.10 eV and 0.94 eV on Mo₆S₈, K–Mo₆S₈, Ni–Mo₆S₈ and Cl–Mo₆S₈, respectively. The S–H bond distance at the transition state ranges between 1.74 Å and 2.76 Å and the different bond distances correlate with the transition state energy. The dissociation of SH* is endothermic on all clusters. The diffusion of H* from the same dual site is endothermic, with the exception of K–Mo₆S₈ where this process is endothermic with 0.19 eV. The reverse behaviour in energy is observed for the diffusion of 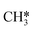to the sulfur part of the dual site occupied by S*. The reaction between S* and methyl occurs through a rather high energy barrier of 1.54 eV, 1.66 eV, 1.05 eV and 1.61 eV on Mo₆S₈, K–Mo₆S₈, Ni–Mo₆S₈ and Cl–Mo₆S₈, respectively. The S–C bond distance at the transition state ranges between 2.53 Å and 2.60 Å. The formation of CH₃S* is exothermic on all clusters. Depending on which species diffuse to the empty sulfur site, the methylthiol can react to form methanethiol (stepwise pathway) or dimethyl sulfide. In the case of diffusion of H* the reaction pathway is the same as the direct pathway but with an additional diffusion step, while in the case of diffusion of methyl the reaction can proceed to form dimethyl sulfide. In the reaction energy landscape (Fig. 2), to form dimethyl sulfide two additional steps (methane dissociation and hydrogen desorption) are necessary to keep the reaction stoichiometry. However, these are the same as described earlier. The diffusion of 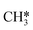to the same dual site as that of CH₃S* is exothermic, with the exception of K–Mo₆S₈ where the reaction is slightly endothermic (0.07 eV). The barrier at the transition state is high (1.60 eV, 1.57 eV, 1.61 eV and 1.62 eV on Mo₆S₈, K–Mo₆S₈, Ni–Mo₆S₈ and Cl–Mo₆S₈, respectively) and there is only a small change due to the addition of promoters. The formation is exothermic with the exception of Ni–Mo₆S₈. This is also reflected in the lower adsorption energy of dimethyl sulfide on Ni–Mo₆S₈ (−1.04 eV) as compared to the other clusters, namely −1.18 eV (Mo₆S₈), −1.08 eV (K–Mo₆S₈) and −1.18 eV (Cl–Mo₆S₈).

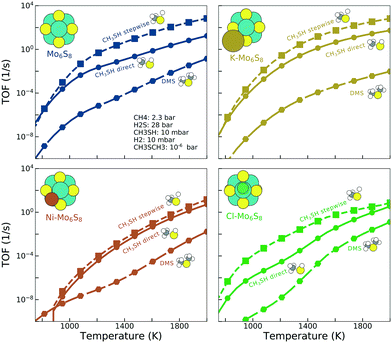
The turnover frequencies (TOFs) (Fig. 3) under industrially relevant conditions for forming methanethiol and DMS are calculated in a microkinetic model based on the reaction mechanism shown in Fig. 1 and the energy landscape shown in Fig. 2. It is clear that the formation of methanethiol occurs mainly through the stepwise mechanism. The direct pathway becomes more important at lower temperature but consequently with a rather low TOF. It is also clear that the TOF for DMS is always low as compared to the TOF for methanethiol, the exception being Ni–Mo₆S₈ at low temperatures (∼900 K). K–Mo₆S₈ displays a higher activity for methanethiol formation as compared to bare Mo₆S₈ at temperatures higher than 1200 K (see Fig. S5†); however, the production of DMS is lower over the whole temperature range. The reason behind the crossover in activity can be seen in the coverage of the active sites (Fig. S6†) where the number of free sites becomes larger on K–Mo₆S₈ as compared to that on Mo₆S₈ at 1300 K. This in turn is due to the weaker adsorption energy of S* on K–Mo₆S₈ as compared to Mo₆S₈. Ni–Mo₆S₈ and Cl–Mo₆S₈ are less active with respect to both methanethiol and DMS and also here the reason can be found in the coverage of the active site, as both clusters bind S* too strongly (Fig. S6†), which thereby poisons the active site and prevents the reaction from proceeding. It is possible that the high coverage of S* will lead to higher S-containing clusters, i.e., Mo₆S_x, x > 8; however, this remains as a challenge for future investigation.

Fig. 3 The turnover frequency as a function of temperature for the direct (dashed line and square point) and stepwise (solid line and circles) formation of methanethiol and DMS (dashed line and circles) for the bare Mo₆S₈ (blue), K–Mo₆S₈ (yellow), Ni–Mo₆S₈ (red) and Cl–Mo₆S₈ (green).

In contrast to a recent study⁴⁴ of the formation of methanethiol on bare and promoted Mo₆S₈, diffusion is included in the reaction mechanism but it is treated parametrically with an energy barrier of 0.05 eV. The sensitivity of the actual diffusion barrier is evaluated by changing the barrier to 0.005 eV and 0.5 eV. The effect on the TOF and the selectivity (see Fig. S7 and S8†) is only minor, which indicates that the exact height of the diffusion barrier is not important, although the addition of the diffusion step is crucial for the reaction mechanisms. A degree of rate control analysis (shown in Fig. S9†) confirms that the diffusion steps are crucial for the reactions to happen.

Selectivity between methanethiol and DMS is an important property when deciding the catalyst formulation. The selectivity between DMS and methanethiol, calculated as the ratio between the TOF for DMS and the TOF for methanethiol, is shown in Fig. 4. It is clear from the results that what benefit the K-promoted cluster has in activity is the reverse in selectivity. In contrast, the Ni-promoted and Cl-promoted clusters display higher selectivity as compared to the bare Mo₆S₈. There is a noticeable difference between the two promoted clusters as Ni–Mo₆S₈ is several orders of magnitude higher in selectivity at low temperature, while Cl–Mo₆S₈ surpasses the bare Mo₆S₈ in selectivity first at a temperature of 1400 K (in fact, Cl–Mo₆S₈ even surpasses Ni–Mo₆S₈ at a temperature of 1500 K). The improved selectivity is closely connected with the poisoning effect of S* (Fig. S6†).

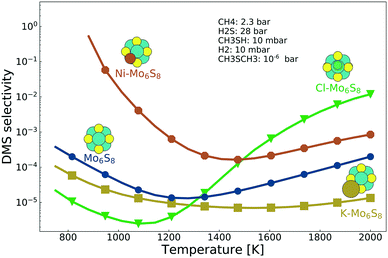Fig. 4 The selectivity between methanethiol and DMS as a function of temperature for the bare Mo₆S₈ (blue), K–Mo₆S₈ (yellow), Ni–Mo₆S₈ (red) and Cl–Mo₆S₈ (green).

4 Conclusions

The activity and selectivity of CH₄ and H₂S to methanethiol and DMS are investigated by first-principles calculations using a microkinetic model. The proposed reaction mechanism includes a dual site (sulfur and molybdenum) and phenomenological diffusion between the dual sites. The reaction landscape involves several transition states and in particular there are two different pathways to form methanethiol (direct and stepwise). The stepwise pathway is part of the pathway to form DMS, which has adsorbed sulfur as a reaction intermediate.

The promoters fall into two categories; either the activity of the main product, methanethiol, is increased (K–Mo₆S₈) or there is a loss in activity but with a gain in selectivity (Ni–Mo₆S₈ and Cl–Mo₆S₈). In the case of K and Cl, the effect is due to the electron-donor and electron-acceptor properties of the promoters. In the case of Ni the underlying reason is not as clear. Ni acts as an electron donor but still stabilizes the reaction intermediates to the extent that the dual site becomes poisoned. The results presented here highlight the balance between activity and selectivity when using promoters on Mo₆S₈ clusters and can thus guide future catalyst formulation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work by A. A. and A. H. was supported as part of the Röntgen-Ångström collaboration “Time-resolved in situ methods for design of catalytic sites within sustainable chemistry” and the Swedish Research Council. The Knut and Alice Wallenberg Foundation via the project Atomistic Design of Catalysts is also gratefully acknowledged. The microkinetic simulations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at C3SE. The work by W. T. and J. B. was supported as part of the UNCAGE-ME, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award No. DE-SC0012577. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.

References

1. V. Subramani, P. Sharma, L. Zhang and K. Liu, in Hydrogen and Syngas Production and Purification Technologies, John Wiley & Sons, Inc., 2009, pp. 14–126.
2. S. Lwin and I. E. Wachs, ACS Catal., 2014, 4, 2505–2520.
3. A. M. Rouhi, Chem. Eng. News, 2002, 80, 29.
4. M. J. Pearson, Ind. Eng. Chem. Prod. Res. Dev., 1977, 16, 154–158.
5. W. Taifan and J. Baltrusaitis, Appl. Catal., B, 2016, 198, 525–547.
6. W. Taifan and J. Baltrusaitis, Catal. Sci. Technol., 2017, 7, 2919–2929.
7. F. Lallemand, A. Rocher and N. Aimard, SPE International Oil & Gas Conference and Exhibition, Beijing, China, 2006, p. SPE 103802.
8. R. H. Hugman, E. H. Vidas and P. S. Springer, Chemical Composition of Discovered and Undiscovered Natural Gas in the Lower-48 United States. Project Summary. Final Report, 1 November 1988-31 March 1990, Technical Report PB-91-144600/XAB, Energy and Environmental Analysis, Inc., Arlington, VA (USA), 1990.
9. C. Huang and A. T-Raissi, J. Power Sources, 2007, 163, 645–652.
10. H. P. Mangalapally and H. Hasse, Energy Procedia, 2011, 4, 1–8.
11. H. P. Mangalapally, R. Notz, S. Hoch, N. Asprion, G. Sieder, H. Garcia and H. Hasse, Energy Procedia, 2009, 1, 963–970.
12. M. Lucquiaud and J. Gibbins, Chem. Eng. Res. Des., 2011, 89, 1553–1571.
13. C. Huang and A. T-Raissi, J. Power Sources, 2007, 163, 645–652.
14. P. Sadooghi and R. Rauch, Int. J. Hydrogen Energy, 2015, 40, 10418–10426.
15. S. K. Megalofonos and N. G. Papayannakos, Appl. Catal., A, 1996, 138, 39–55.
16. A. L. Martínez-Salazar, J. A. Melo-Banda, A. I. Reyes de la Torre, Y. Salazar-Cerda, M. A. Coronel-García, B. Portales Martínez, V. H. Martínez-Sifuentes, J. M. Domínguez-Esquivel and R. Silva Rodrigo, Int. J. Hydrogen Energy, 2015, 40, 17272–17283.
17. F. Galindo-Hernández, J. M. Domínguez and B. Portales, J. Power Sources, 2015, 287, 13–24.
18. F. Q. Miao and E. J. Erekson, Method for Direct Production of Carbon Disulfide and Hydrogen from Hydrocarbons and Hydrogen Sulfide Feedstock, Technical Report US Pat., A9018957, Federal Energy Technology Center, Pittsburgh, PA (US), 1998.
19. S. K. Megalofonos and N. G. Papayannakos, Appl. Catal., A, 1997, 165, 249–258.
20. S. K. Megalofonos and N. G. Papayannakos, Int. J. Hydrogen Energy, 1991, 16, 319–327.
21. Y. Li, X. Yu, Q. Guo, Z. Dai, G. Yu and F. Wang, Energy Procedia, 2017, 142, 1065–1070.
22. O. Y. Gutiérrez, L. Zhong, Y. Zhu and J. A. Lercher, ChemCatChem, 2013, 5, 3249–3259.
23. O. Y. Gutiérrez, C. Kaufmann and J. A. Lercher, ChemCatChem, 2011, 3, 1480–1490.
24. O. Y. Gutiérrez, C. Kaufmann and J. A. Lercher, ACS Catal., 2011, 1, 1595–1603.
25. O. Y. Gutiérrez, C. Kaufmann, A. Hrabar, Y. Zhu and J. A. Lercher, J. Catal., 2011, 280, 264–273.
26. J. Baltrusaitis, C. de Graaf, R. Broer and E. V. Patterson, ChemPhysChem, 2013, 14, 3960–3970.
27. C. D. Chang and A. J. Silvestri, J. Catal., 1977, 47, 249–259.
28. S. A. Butter, A. T. Jurewicz and W. W. Kaeding, Conversion of alcohols, mercaptans, sulfides, halides and/or amines, US Pat. 3894107, 1975.
29. A. V. Mashkina, V. R. Grunvald, V. I. Nasteka, B. P. Borodin, V. N. Yakovleva and L. N. Khairulina, React. Kinet. Catal. Lett., 1990, 41, 357–362.
30. V. Hulea, E. Huguet, C. Cammarano, A. Lacarriere, R. Durand, C. Leroi, R. Cadours and B. Coq, Appl. Catal., B, 2014, 144, 547–553.
31. E. Huguet, B. Coq, R. Durand, C. Leroi, R. Cadours and V. Hulea, Appl. Catal., B, 2013, 134–135, 344–348.
32. C. Cammarano, E. Huguet, R. Cadours, C. Leroi, B. Coq and V. Hulea, Appl. Catal., B, 2014, 156–157, 128–133.
33. Q.-M. Li, M. Zhang, C.-M. Wang, Y.-A. Zhu, X.-G. Zhou and Z.-K. Xie, Mol. Catal., 2018, 446, 106–114.
34. J. Baltrusaitis, T. Bučko, W. Michaels, M. Makkee and G. Mul, Appl. Catal., B, 2016, 187, 195–203.
35. M. Reina, A. Martinez, C. Cammarano, C. Leroi, V. Hulea and T. Mineva, ACS Omega, 2017, 2, 4647–4656.
36. G. A. Olah, Acc. Chem. Res., 1987, 20, 422–428.
37. X. Zheng, L. Guo, W. Li, Z. Cao, N. Liu, Q. Zhang, M. Xing, Y. Shi and J. Guo, Mol. Catal., 2017, 439, 155–162.
38. J. Zhou, J. Zhou, N. Camillone and M. G. White, Phys. Chem. Chem. Phys., 2012, 14, 8105–8110.
39. P. Liu, Y. Choi, Y. Yang and M. G. White, J. Phys. Chem. A, 2010, 114, 3888–3895.
40. C. Liu and P. Liu, ACS Catal., 2015, 5, 1004–1012.
41. M. J. Patterson, J. M. Lightstone and M. G. White, J. Phys. Chem. A, 2008, 112, 12011–12021.
42. J. M. Lightstone, M. J. Patterson and M. G. White, Chem. Phys. Lett., 2005, 413, 429–433.
43. P. Murugan, V. Kumar, Y. Kawazoe and N. Ota, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 71, 063203.
44. W. Taifan, A. A. Arvidsson, E. Nelson, A. Hellman and J. Baltrusaitis, Catal. Sci. Technol., 2017, 7, 3546–3554.
45. T. J. Paskach, G. L. Schrader and R. E. McCarley, J. Catal., 2002, 211, 285–295.
46. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
47. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
48. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
49. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118.
50. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
51. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
52. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
53. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624.
54. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
55. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567.
56. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
57. G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022.
58. A. Heyden, A. T. Bell and F. J. Keil, J. Chem. Phys., 2005, 123, 224101.
59. K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163.
60. K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.
61. H. P. Hratchian and H. B. Schlegel, J. Phys. Chem. A, 2002, 106, 165–169.
62. I. Chorkendorff and J. W. Niemantsverdriet, Concepts of Modern Catalysis and Kinetics, John Wiley & Sons, 2006.
63. S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66.
64. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
65. A. C. Luntz, in Chemical Bonding at Surfaces and Interfaces, 2008, pp. 143–255.
66. A. Hindmarsh, IMACS Transactions on Scientific Computation, 1983, vol. 1, pp. 55–64.
67. E. Hairer, G. Wanner and S. P. Nørsett, Solving Ordinary Differential Equations I, Springer Berlin Heidelberg, Berlin, Heidelberg, 1993, vol. 8.
68. NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg, MD, 20899,  DOI:10.18434/T4D303, (retrieved February 12, 2019).
69. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
70. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908.
71. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
72. M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111.

---

Footnote

† Electronic supplementary information (ESI) available: A zip file with all structures and figures of the reaction mechanism for the K-, Ni-, and Cl-promoted clusters, a free energy landscape, a comparison of the TOF for all clusters, tables with kinetic information, the steady-state coverages, the effect of the diffusion barrier on the TOF and selectivity, a degree of rate control analysis for all clusters, and the projected crystal orbital Hamiltonian populations. See DOI: 10.1039/c9cy00375d

---