A systematic study on Pt based, subnanometer-sized alloy cluster catalysts for alkane dehydrogenation: effects of intermetallic interaction

Abstract

Platinum-based bimetallic nanoparticles are analyzed by the application of density functional theory to a series of tetrahedral Pt₃X cluster models, with element X taken from the P-block, preferably group 14, or from the D-block around group 10. Almost identical cluster geometries allow a systematic investigation of electronic effects induced by different elements X. Choosing the propane-to-propene conversion as the desired dehydrogenation reaction, we provide estimates for the activity and selectivity of the various catalysts based on transition state theory. No significant Brønsted–Evans–Polanyi-relation could be found for the given reaction. A new descriptor, derived from an energy decomposition analysis, captures the effect of element X on the rate-determining step of the first hydrogen abstraction. Higher activities than obtained for pure Pt₄ clusters are predicted for Pt alloys containing Ir, Sn, Ge and Si, with Pt₃Ir showing particularly high selectivity.

---

1 Introduction

Platinum, in the form of supported nanoparticles, is one of the most suitable catalysts for the thermal dehydrogenation of light alkanes. The desired alkene products are building blocks for a wide array of commodity and specialty chemicals, or may be transformed into larger alkanes via follow-up oligomerization or metathesis reactions to serve as liquid fuel. Dehydrogenation is an attractive alternative to the traditional production of alkenes via steam cracking of petroleum-derived naphtha. Unpromoted Pt catalysts suffer from low alkene selectivity and rapid deactivation due to coking. Both undesired phenomena are mainly a consequence of alkene re-adsorption, which leads to further dehydrogenation and C–C bond breaking.^1,2 Improvements of catalyst activity, selectivity, and stability can be achieved by alloying Pt with Sn and by adding hydrogen to the alkane feed.^1,3–8 The positive effect of alloying with tin has been assumed to be a consequence of both the geometric as well as electronic modification.^9–15 The presence of evenly distributed tin atoms on the surface hinders the formation of larger active sites, which suppresses undesired C–C bond breaking eventually leading to coking and catalyst deactivation.^5,16–20 A recent experiment of our group on ethane dehydrogenation over PtSn nanoparticles (about 100 atoms, Pt/Sn ratio 3 : 1) indicated beneficial electronic effects⁸ as they were suggested by earlier theoretical work on metal surfaces.^12,13 Our own computational study on Pt₄ and Pt₃Sn tetramers predicted an improved dehydrogenation activity for the bimetallic nano cluster.²¹ The tin atom donates electron density to the active site of the catalyst, which reduces the energy barrier for the rate-determining step, the cleavage of the first C–H bond.

In this article we expand our previous work on platinum-based tetramers by a systematic quest for alternative bimetallic partner elements with similar or even better performance than the well-established Pt/Sn alloy. We compare the reaction pathways obtained from a density functional theory approach and apply ALMO-EDA (absolutely localized molecular orbital energy decomposition analysis) as well as NBO (natural bond orbital) theory to the crucial steps to gain further insights into the reaction mechanism.

2 Computational methods

We choose a representation by four atoms in a tetrahedral arrangement, which corresponds to the most stable structure among the Pt₄ isomers.^22–24 We then replace a single Pt atom by a different D-block or P-block metal and let the structure relax before propane is added to the system. Minima and intermediates occurring during the reaction with the alkane are obtained in fully unrestrained geometry optimizations. The freezing string method^25,26 is applied to obtain initial guesses for the interconnecting transition states. This procedure is followed by a final localization based on an eigenvector-following approach.²⁷ The transition states are then checked by frequency calculations proving their character as first-order saddle points on the potential energy surface. All calculations are performed with the Q-Chem program package.²⁸ We further estimate Gibbs free energies within the harmonic oscillator approach at all relevant points of the reaction pathway, including also zero point energy corrections. All translational, rotational and vibrational degrees of freedom are taken into consideration. Hindered rotations are accounted for by applying the correction suggested by Grimme, which suggests a continuous interpolation between vibrational and rotational contributions to the entropy.²⁹ A cutoff value of ω₀ = 100 cm⁻¹ was used for all calculations.

Molecular geometries are obtained from density-functional-theory (DFT) in unconstrained optimizations, using the B3LYP functional^30–33 together with the triple-zeta valence basis set of Weigend and Ahlrichs^34,35 and the effective core potentials of the Stuttgart/Köln group^36,37 for all metals. Effects of a van der Waals-correction³⁸ are tested in a series of single point B3LYP-D3 calculations for all B3LYP-converged geometries. Details of the SCF convergence, DFT grid size information and thresholds of the geometry optimizations can be found in this footnote.³⁹ Only Pt₃Ir shows a strong deviation from the tetrahedral structure at the first C–H cleavage step with a slight tendency towards a planar geometry, where one of the edges between the active site and a Pt atom becomes elongated.

We further perform a natural bond order (NBO) analysis^40,41 to investigate the relation between catalytic properties of each system and the shape of the molecular orbitals (MOs) involved. For a detailed analysis of donor–acceptor effects within the alloy clusters we apply ALMO-EDA,^42,43 an energy decomposition scheme which splits intermolecular interaction energies into frozen orbital, polarization and charge transfer contributions.

3 Results and discussion

3.1 Reaction pathways for propane dehydrogenation over Pt₄

We begin by revisiting the thermal dehydrogenation of propane over Pt₄ and extend previous investigations of its potential energy surface^21,44 by the exploration of alternative pathways. Results for electronic energies and Gibbs free energies at a rather mild reaction temperature of 400 °C are summarized in Table 1. The corresponding geometries and Gibbs free energy levels are illustrated in Fig. 1 and 2, respectively.

Table 1 Electronic and Gibbs energies for the dehydrogenation of propane over Pt₄. The corresponding geometries can be found in Fig. 1

Reaction step	Label	ΔE^a (kcal mol^−1)	ΔG^a (kcal mol^−1)
a Relative to the energy of a pure Pt4 cluster and a propane molecule at infinite distance. b These values correspond to the electronic and Gibbs free energies for the gas phase reaction C3H8 ⇌ C3H6 + H2.
Propane adsorption at C2	1a	−12.22	13.04
1st C–H cleavage (TS)	2a	−4.59	17.54
Intermediate	3a	−19.51	4.25
H migration (TS)	4a	−10.44	11.65
Intermediate	5a	−18.43	3.04
2nd C–H cleavage at C1 (TS)	6a	−16.43	6.75
Propane adsorption at C1, convex	1b	−12.68	8.26
1st C–H cleavage (TS)	2b	−5.61	16.14
Intermediate	3b	−19.56	3.87
H migration (TS)	4b	−9.32	14.09
Intermediate	5b	−18.11	3.86
2nd C–H cleavage at C2 (TS)	6b	−16.37	6.66
2nd C–H cleavage at C1 (TS)		1.49	22.11
Propane adsorption at C1, concave	1c	−12.02	9.19
1st C–H cleavage (TS)	2c	−5.31	17.05
Propane adsorption, symmetric	1d	−12.31	8.65
Intermediate	7	−26.2	−3.63
H migration (TS)	8	−22.75	−0.72
Intermediate	9	−37.88	−13.51
3rd C–H cleavage at C3 (TS)	10a	−15.73	3.49
3rd C–H cleavage at C2 (TS)	10b	−7.81	8.89
3rd C–H cleavage at C1 (TS)	10c	−8.71	10.67
Hydrogen desorption from Pt4–C3H6		−8.98	−8.69
Propene desorption from Pt4–H–H		3.27	−2.63
Hydrogen and propene desorption^b		35.76	8.86
C–C breaking in Pt4–C3H8		17.36	41.33
C–C breaking in H–Pt4–CH3–CH–CH3		20.37	41.4
C–C breaking in H–Pt4–CH3–CH2–CH2		13.53	36.1
C=C breaking in H–H–Pt4–C3H6		34.36	49.49

---

Fig. 1 Reaction pathways for the dehydrogenation of propane over Pt₄. Transition states that correspond to C–H bond breaking are emphasized by dashed circles. Three separate starting points for dehydrogenation pathways begin from three different initial adsorption geometries (1a, 1b, and 1c). A 4th adsorption geometry (1d) is a relatively exotic σ dihydrogen species. After formation of the alkene (7, 8, 9), product desorption competes with further dehydrogenation (10a, 10b, 10c) to determine selectivity.

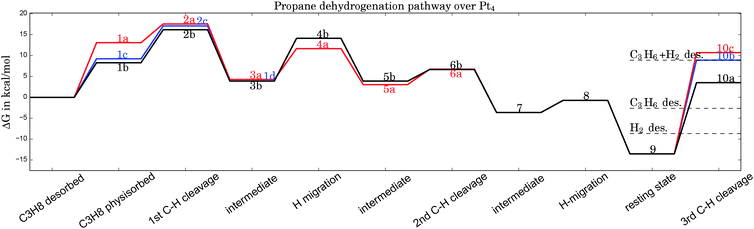Fig. 2 Gibbs free energy diagram of possible dehydrogenation pathways, calculated at 400 °C. The first hydrogen abstraction is the rate-determining step and is most likely to happen at C1, corresponding to geometry 2b in Fig. 1. Desorption energies are plotted as dashed lines.

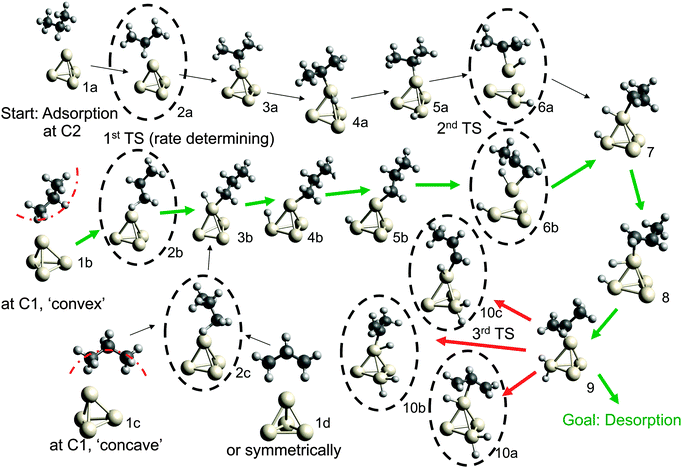
Possible adsorption scenarios involve either C2–H–Pt (see geometry 1a) or C1–H–Pt type interactions. In the latter case, three adsorption minima could be determined, where the propane is either bent towards the cluster (concave, 1c), bent off the cluster (convex, 1b), or in a highly symmetric arrangement 1d of C_2v symmetry. The strong C–H σ bonds, which are essentially nonpolar and therefore weak donors, act as ligands in the unusual high-symmetry arrangement.⁴⁵ In general, the direct observation of such σ-dihydrogen species is problematic due to the instability of the complexes formed, but could give insights into early steps of metal-mediated H–H or C–H cleavage. Recently, a relatively long-lived rhodium(I) σ-methane complex of similar geometry⁴⁶ (in solution) was characterized by NMR. We mention this finding since examples of saturated hydrocarbons within the coordination sphere of a metal center in the solid state are extremely rare.^47–49

The adsorption step is directly followed by hydrogen abstraction, leading to an intermediate where the remaining alkyl group and the H atom are attached to the same corner (3a or 3b of Fig. 1). Previous studies have focused on a reaction mechanism in which C–H bond breaking at the C2 atom (2a) is followed by hydrogen abstraction from C1 (6a).^21,44 However, two alternative pathways, where the C–H bond cleavage takes place at C1 before C2 (with the propane molecule in either the ‘convex’ 2b or ‘concave’ 2c arrangement), show slightly lower barriers for the rate-determining transition state as can be seen in Table 1. After the migration of the hydrogen atom to a different corner, the second hydrogen abstraction takes place, preferably at C2 if the first abstraction took place at C1 and vice versa. Alternative pathways, such as a repeated hydrogen abstraction from the same carbon atom or the breaking of C–C bonds are omitted from the figure due to the higher barriers involved but are listed in the table. Both pathways merge after the second hydrogen abstraction. Further H migration (7, 8) leads to the minimum energy configuration 9 with two hydrogen atoms attached to the same corner. After this step the reaction path forks to either propene desorption or further dehydrogenation via a third C–H cleavage step (10a, 10b or 10c).

From Table 1 it can be seen that at higher temperatures the desorption energy for propene decreases under the barrier for an undesired further dehydrogenation step, which explains the high selectivity towards the product alkene.²¹ This energy difference between the true barrier for a third H abstraction and the energy needed to desorb the products is an important property as it affects the selectivity. The activity of the catalyst, on the other hand, is dictated by the highest transition state along the free energy reaction pathway, corresponding to the first C–H cleavage step. The energies for this particular reaction step in all pathways (2a, 2b, 2c) differ by about 1 kcal mol⁻¹, with the option of an initial abstraction from C1 being slightly preferred. The energetic proximity of the first transition states makes it necessary to compute all three of them in the following comparison of bimetallic catalysts.

For the sake of readability, the detailed discussion of the reaction pathway after inclusion of an ad hoc van der Waals correction (B3LYP-D3) has been shifted to the ESI.† We note that this measure enhances the adsorption energies by about 5 kcal mol⁻¹ on average, but it has a negligible effect on the relative energies of the pathways shown in Fig. 2, and thus it does not affect the trends discussed in the next section.

3.2 Bimetallic variations of the tetrahedral motif: Pt₃X clusters

We broaden our analysis of the dehydrogenation reaction by the introduction of a second metal to our tetrahedral nanoparticle. A common ratio of 1 : 3 has been chosen for the bimetallic systems,^50–53 which is easily achieved by a single atom replacement. Initial guesses for the bimetallic geometries of the various Pt₃X systems are obtained from the relevant stationary points of the Pt₄ reaction pathway by replacing one of the three Pt atoms which do not directly participate in the propane adsorption. For X we choose Pt,⁴⁴ Pd,^54,55 Sn,^8,56,57 Ge,⁵⁸ Si, In,⁵⁹ Ga,⁵² Au,^60,61 Ag,^62,63 Cu,⁶⁴ Ir.^65,66 For the sake of a direct comparison we treat Pt atoms as the only active sites of the catalyst. This simplification is supported by a Mulliken charge analysis of the pure clusters, which shows a positive charge on the replacement atom in all cases.^67,68 The spin multiplicities of the different alloys vary with element X and lie between singlet and quartet for the given selection.⁶⁹ In contrast to the previous section we will focus now only on a subset of relevant geometries for the sake of readability. Furthermore, we ignore the presence of any hydrogen atoms on the catalyst from previous dehydrogenation steps.⁷⁰ This is done for two reasons. First, the amount of hydrogen on the catalyst during the reaction depends not only on the current reaction step but also on the partial pressure of hydrogen²¹ and on the interplay between the nanoparticle and its support. Both aspects are worthy of study on their own but lie beyond the scope of this article. Second, the presence of hydrogen on the catalyst introduces a bias when comparing pathways between different catalysts due to numerous hydride isomers of similar energy, and it complicates the potential energy surfaces considerably due to additional transition states and local minima that correspond to hydrogen migration. Therefore, we reduce our analysis to the following geometries: the clean catalyst, propane adsorption, propene adsorption, and the transition states describing first, second and third C–H bond cleavage, together with their corresponding precursor intermediates. Pairs of the latter, i.e. transition states and their preceding intermediates, allow an unbiased comparison of true barriers along the reaction pathway.

Fig. 3 illustrates the adsorption energies for propane onto the various catalysts. The fluctuation with catalyst type is only moderate and lies within a range of ±2.5 kcal mol⁻¹ around the average. The catalysts on the x-axis are sorted with respect to their apparent barriers for the rate-determining, first H-abstraction step at 0 Kelvin. Therefore, the x-axis can be read as a ranking of catalyst activity, starting with the best catalyst on the left end. As can be seen in Fig. 3, there is no clear correlation of activity and propane adsorption. At the high temperatures required for the endothermic reaction of propane dehydrogenation (ΔH = 20.1 kcal mol^−1 71,72), the change in Gibbs energies upon adsorption is positive. Based on DFT thermochemistry data we estimate that propane desorption becomes spontaneous at temperatures above 200 °C for most catalysts. Note that the replacement of one Pt atom by any of the suggested elements X leads to a slightly enhanced physisorption of propane at the Pt sites. In bulk alloys these small electronic electronic effects tend to be overruled by geometric and relaxation effects. A comparable DFT study of propane adsorption onto Pt(111) and Pt₃Sn(111) surfaces shows a slightly reduced physisorption for the alloy in comparison to the pure Pt surface (ΔE = 0.9 kcal mol⁻¹).⁷³

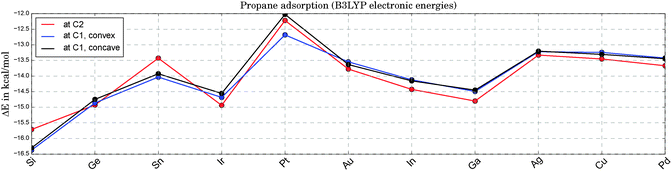Fig. 3 Electronic energies for the adsorption of propane onto Pt₃X (see 1a, 1b and 1c in Fig. 1) at zero Kelvin. Due to the weak adsorption the Gibbs free energies are all positive at experimentally relevant temperatures, indicating a negligible coverage of the catalyst with physisorbed propane.

For the sake of completeness we also tested the X sites for their adsorption qualities. In all cases, the propane adsorption on atom X is either weaker than on Pt (by 2.9 kcal mol⁻¹ on average) or an adsorption minimum could not be found (Ga, Ge, In, Sn). This agrees well with the initial finding of positive Mulliken charges at X for all Pt₃X systems under consideration.

In Fig. 4 we compare the apparent barriers for the first C–H bond cleavage. This step being the bottleneck of the overall reaction pathway, we plot ΔG, the change in Gibbs free energy, with G set to zero for propane at an infinite distance from the catalyst. We note that Ir shows a distortion from the perfect tetrahedral shape during C–H bond breakage, which introduces a slight bias in the overall comparison due to geometry effects. The distance from the active center to one Pt atom is extended by about 60%, leading to a geometry between square planar and tetrahedral.

Fig. 4 Comparison of electronic energy barriers (upper graph) and apparent Gibbs free energy barriers at 400 °C (lower graph) for the first TS states of Pt₃X (see 2a, 2b and 2c in Fig. 1). For all alloys the lowest of these options for the first C–H bond cleavage corresponds to the rate-determining step.

Energies for the second hydrogen abstraction are not discussed here but can be found in the supporting material. There is no clear trend detectable in the barrier for this step. In general, the differences between alloys are marginal.

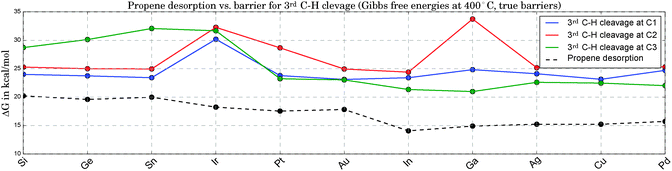
Fig. 5 compares the true barriers for the third hydrogen abstraction from C1, C2 or C3, to the desorption energy for propene. Again, we provide ΔG values at 400 °C. At this high temperature, due to the gain in entropy upon desorption, the production of propene becomes competitive with the undesired pathways of continued dehydrogenation. The latter steps eventually lead to methane and the formation of coke on the catalyst. The direct comparison of the ΔG values for propene desorption to the energetically lowest option for the third C–H bond cleavage allows an estimate to be made of the selectivity towards propene. The larger the difference between the lowest barrier and the desorption energy, the better. Propene desorption is preferred for all catalysts in this study at B3LYP level of theory,⁷⁴ but this difference shows large fluctuations. It is smallest for the three most active catalysts and larger for the least active clusters, but a clear trend is not apparent. Pt₃Ir seems to be a special case due to its comparably high barriers for the 3rd C–H cleavage, which makes it particularly interesting for future experimental investigations due to the expected higher selectivity. However, this discrepancy might also be related to the geometric distortions observed for Pt₃Ir.

Fig. 5 Comparison of ΔG values for propene desorption and for the true barrier that has to be overcome for continued C–H bond breaking at 400 °C. The difference between the lowest solid line (bond cleavage) and the dashed line (desorption) can be interpreted as a descriptor for the catalyst selectivity towards propene.

3.3 Descriptors for catalytic activity

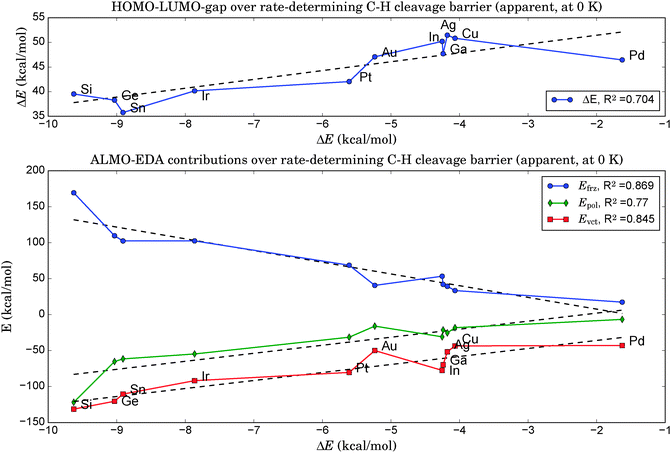
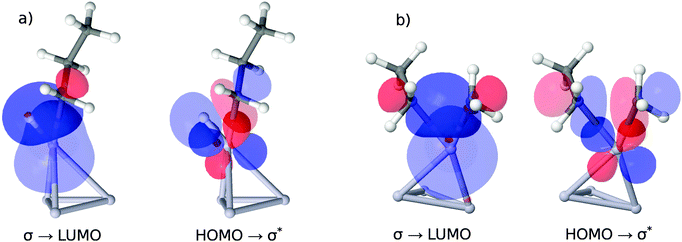
As illustrated in the upper panel of Fig. 6, a property of the clean catalyst, namely its HOMO–LUMO gap, is correlated with activity (R² = 0.71). The smaller the gap, the lower is the barrier of the rate-determining C–H cleavage step. Retrieving this information is significantly less laborious than a full evaluation of the dehydrogenation reaction for a given catalyst. It only necessitates the optimization of the pure cluster geometry as a prerequisite.

Fig. 6 Top: The difference between LUMO and HOMO energies of the clean catalyst is correlated with the barrier height of the rate-determining C–H cleavage step. Catalyst activity decreases from left to right. Bottom: The ALMO-EDA analysis shows an even stronger correlation for E_frz, the frozen energy contribution, as well as for the compensating polarization and variational charge-transfer energy contributions (E_pol and E_vct, respectively).

3.3.1 ALMO-EDA. Motivated by this finding, we performed an energy decomposition analysis on Pt₃X clusters optimized in isolation (C_3v) to gain insight into the effect of atom X (one fragment) on the electronic structure of the three platinum atoms (the other fragment) composing the rest of the structure and containing the platinum center that is the active site for the reaction. The overall multiplicity of the catalyst cluster and the multiplicity of the dopant fragment were respectively for each system as follows: Si 1,3; Ge 1,3; Sn 1,3; Ir 4,4; Pt 3,3; Au 2,2; In 2,2; Ga 2,2; Cu 2,2; Ag 2,2; Pd 3,1. The multiplicities of all Pt₃ fragments can be inferred. All clusters and fragments were uncharged, and the fragment spin states were chosen to minimize the sum of isolated fragment energies given the constraint of optimal total cluster multiplicity. The energy decomposition scheme employed was the ALMO-EDA^42,43 in which the electronic binding energy of a system of fragments is partitioned into frozen orbital interactions, E_frz, describing permanent electrostatics and Pauli repulsion from overlapping occupied orbitals, polarization, E_pol, describing intra-fragment relaxation due to the presence of other fragments, and variational charge transfer, E_vct, which includes energy lowering from the movement of charge between and delocalization of orbitals across fragments as well as the subsequent repolarization of fragments. Charge transfer contributions were not corrected for BSSE. Fig. 6b shows these EDA energy components for the interaction of the dopant atom with the other three platinum atoms in the C_3v geometry (neglecting geometric distortions) plotted against the barriers for the rate-determining C–H cleavage for each of the doped clusters listed above. All energy terms are quite large as the fragmentation employed breaks all bonds between the dopant and the three platinum atoms comprising the remainder of the cluster. One notable trend is a strongly repulsive frozen energy that decreases with decreasing catalyst activity (R² = 0.869). This unfavorable interaction stems from the large Pauli repulsion between unrelaxed, considerably overlapping, occupied orbitals on the two fragments. The repulsive interaction is partially compensated for by a sizeable, stabilizing polarization term, which likewise decreases in magnitude with decreasing activity (R² = 0.77). Because the sum of only the frozen and polarization components yields a net destabilizing interaction for all clusters considered, we conclude that charge transfer interactions such as those involved in metal–metal bond formation are responsible for the cluster structures and thus the large, repulsive frozen orbital interactions. We note that while both the charge transfer energy (R² = 0.845) and the total binding energy (R² = 0.62) are more stabilizing for more active clusters, the trend is much stronger for the charge transfer interaction. Fragment-to-fragment charge transfer analysis^43,75 of the perturbative charge transfer amplitudes, which described in some cases only half of the variational charge transfer energy lowering for these very strongly interacting systems, indicated that charge transfer both to and from the dopant was significant. These interactions affect the relative energy positions of the catalyst's highest occupied and lowest unoccupied molecular orbitals. The energetic difference between these two levels has already been shown to correlate well with cluster activity. In the next section, we apply NBO analysis to graphically demonstrate the importance of these orbitals for breaking and forming bonds in the rate-determining transition state.

3.3.2 Natural bond orbital analysis. In a second attempt to understand the link between molecular orbital energies and the cluster activity we perform a natural bond order analysis of the rate-determining step.^40,41 Canonical Kohn–Sham orbitals have an orbital energy clearly assigned to them but are usually highly delocalized. Within the NBO formalism, the converged set of orbitals (occupied and virtual) is transformed into a set of orthogonal but localized natural bond orbitals (NBOs), with the goal of associating each NBO with a bonding or lone-pair orbital of a traditional Lewis structure. This approach enables the identification of orbital interactions in crucial reaction steps. The rearrangement of electron density during the C–H cleavage is mapped onto a process of electron donation from occupied to virtual NBOs. This process and its consequence for the total energy of the system are analyzed via second order perturbation theory. We start with the definition of two fragments, the gas molecule and the clean catalyst. Note that the hydrogen atom to be removed is considered a part of the propane fragment, despite its elongated bond at the transition state geometry (lengthened by about 30%). In the NBO analysis we enforce the obvious Lewis structure for propane and obtain perturbative estimates for energy-lowering via electron donor–acceptor relations. When looking at the largest contributions stemming from interactions between the two fragments, we find the same two leading pair interactions for all catalysts of the test set.

The four orbitals involved in C–H cleavage are plotted in panel (a) of Fig. 7, given the example of Pt₄. The first interaction (left) describes a charge transfer from the σ-bond orbital of the activated C–H bond to an unoccupied, almost spherical and rather diffuse d-orbital of the nearest Pt atom. The second interaction describes an electron back-donation from an occupied d-orbital of the same Pt atom (well defined, two nodal planes) at the active site into the unoccupied anti-bonding σ* orbital of the activated C–H bond, which shows the typical extra nodal plane. Therefore, within the NBO picture, the C–H bond cleavage is described as the usual transfer of electron density from the bonding into the anti-bonding orbital, mediated via the d-orbitals of the catalyst. What links this process to a property of the clean catalyst is that the two NBOs on the catalyst fragment correspond quite closely to the HOMO and the LUMO of the cluster in the canonical orbital set, as can be deduced from a comparison of their coefficients in the basis of atomic orbitals. However, while this proves the relevance of these orbitals for C–H bond activation, it does not explain the dependence of the activity on their energy gap. A possible explanation involves the increasing flexibility (i.e. greater polarizability and greater ability to participate in CT interactions) of the electron density with decreasing HOMO–LUMO gap, commonly referred to as chemical ‘softness’. On the other hand, this argument predicts highest activities for bulk alloys with zero band gaps. We therefore suggest that an optimum catalyst combines chemical softness with a sterically suitable nodal structure of its valence orbitals which allows a precise transfer of electron density in favor of the geometric arrangement after the hydrogen abstraction.

Fig. 7 Comparison of NBO orbital interactions at the transition states for the first C–H and C–C bond cleavage, given the example of Pt₄. (a) Electron density is shifted from the σ-orbital of the activated C–H bond to an orbital which essentially corresponds to the LUMO of the clean catalyst (see text). The HOMO of the clean catalyst has good overlap with the corresponding σ*-orbital and destabilizes the activated C–H bond via back donation. (b) Same scenario for C–C breakage, but with reduced orbital overlap due to geometry constraints. The arrangement of the sp³ orbitals on the carbon atoms after bond breaking is suboptimal.

In panel (b) of Fig. 7 we apply the same NBO analysis to the situation of C–C bond breaking catalyzed by Pt₄ for a direct comparison. Again, we find the HOMO and LUMO orbital of the clean catalyst involved in a charge transfer process, indicating a similar dependence of the energetic barrier for C–C cleavage on the HOMO–LUMO gap. However, as can be derived from the energies in Table 1, this dependence is much less pronounced, and the apparent barrier heights are much higher. The higher energies are a consequence of the suboptimal arrangement of the orbitals during C–C bond breaking. A comparison of panels (a) and (b) shows that in the case of C–C breaking two directed sp³ lobes of the remaining methyl- and ethyl groups need to overlap with the d-orbital on the active metal site, while for C–H breaking only the sp³ orbital on the propyl-group has similar spatial demands. The undirected s-orbital on the H atom retains good overlap throughout the geometric rearrangement, which explains, together with the smaller angle between the lobes of the sp³ and d orbital in case (a), the lower energetic costs for H abstraction.

3.3.3 Kinetics estimates based on thermodynamics. The Brønsted–Evans–Polanyi (BEP) relation is an empirical rule that posits a linear relation between the activation energy and the reaction energy for a given elementary reaction.^76,77 Its applicability to heterogeneous catalysis on transition state metals, known for decades,⁷⁸ has recently been enhanced by quantitative approaches based on DFT calculations.^79–83 Driven by the aim to simplify computer-aided catalyst screening, linear relations were discovered between the adsorption energies of hydrogen-containing molecules and single atoms or between transition state and adsorption energies.

From a microscopic point of view, relations of the latter type indicate that the transition state must be ‘late’ in the sense of its geometry being close to that of the subsequent intermediate. Fortunately, this is true for the rate-determining step of the given reaction. Therefore, it should be possible to relate the adsorption energies of the chemisorbed products right after dissociation, here a propyl-group and a single hydrogen atom, to the barrier height for C–H bond breaking. Note that the chemisorption of the intermediates after hydrogen cleavage, not the physisorption of propane, can be a potential descriptor, since the latter is based on a different (i.e. van der Waals)-type of binding. Following ref. 84, we first assume that the chemisorption of a single H atom does not vary too strongly for the chosen catalysts. In this case, the BEP relation should also hold for just the alkyl fragment. A further simplification made by choosing a methyl group as smallest representative with the same valency leads to the relation shown in Fig. 8a. However, this graph shows a rather weak correlation (R² = 0.422), indicating that a simple mapping of kinetics onto thermodynamics is not applicable for the reaction of interest here. This is somewhat surprising, since for all catalysts tested the typical C–H bond length at the transition state lies around 1.49 Å, which suggests an almost broken bond and a close proximity to the subsequent intermediate state with the cleaved H atom chemisorbed at the same site.

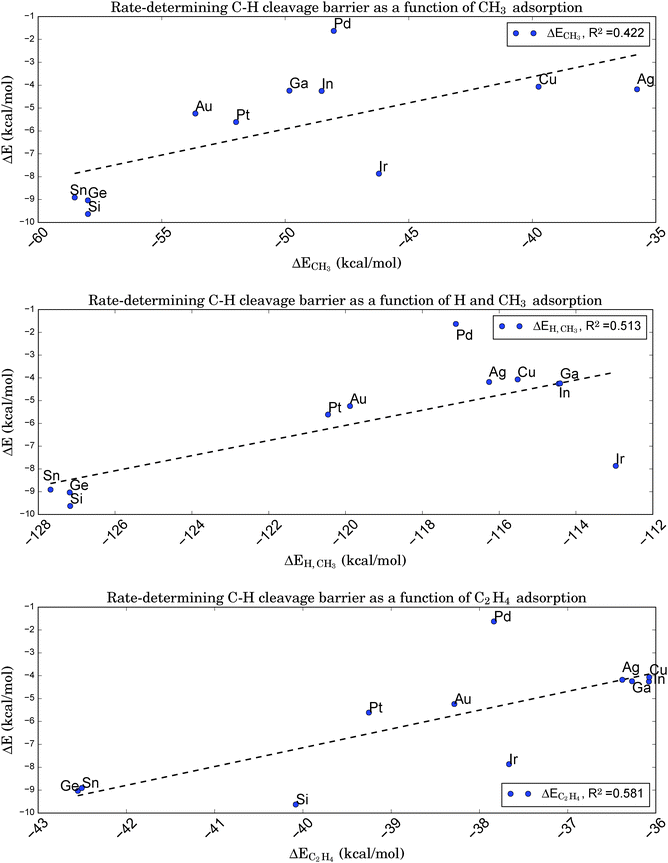Fig. 8 Brønsted–Evans–Polanyi relation between the adsorption energies of a CH₃ fragment (upper graph), a CH₃ fragment and a single H atom (middle graph), or a C₂H₄ molecule (lower graph) onto Pt₃X and the rate-determining first C–H cleavage barrier for the conversion of propane to propene. Despite the ‘late’ character of the corresponding transition state the assumed correlation to the absorption of the alkyl fragment is very weak. The correlation is slightly improved if a simultaneous adsorption of H and CH₃ at the same site is considered. Surprisingly, the adsorption of C₂H₄, the smallest alkene representative, is still better correlated, although the correlation is significantly poorer than was obtained in Fig. 6 based on electronic properties of the clean catalyst.

Adding the chemisorption energy for atomic hydrogen to the energy for methyl chemisorption and comparing this total energy to the barrier height for C–H cleavage reduces the BEP correlation even further (R² = 0.228), since variations in ΔE_H turn out to be of the same magnitude as ΔE_CH3, but are completely uncorrelated to the C–H cleavage barriers (R² = 0.014). However, a direct comparison of energies for the simultaneous adsorption of CH₃ and a single H atom at the same site shows a slightly improved correlation (R² = 0.513, see Fig. 8b) due to the inclusion of adsorbate–adsorbate interactions.

In a last attempt to derive a suitable BEP relation we compare the barrier height for C–H cleavage to the adsorption of an alkene. We pick ethene as the simplest representative of a molecule with a C–C double bond and obtain the relation shown in Fig. 8c. Interestingly, this graph shows a slightly higher correlation (R² = 0.581) than that based on CH₃ fragment energies, despite the larger ‘distance’ of the simulated geometry of alkene adsorption from the relevant transition state with respect to the reaction coordinate.

4 Conclusion

The dehydrogenation of propene over platinum-based, bimetallic nanoparticles was studied via B3LYP and B3LYP-D3 calculations on Pt₃X model systems. Crucial steps of the reaction pathway were identified in unconstrained geometry optimizations and transition state searches. Gibbs energies were obtained from frequency calculations and corrected for hindered rotations. We draw the following conclusions:

1. The physisorption of propane on bimetallic Pt₃X clusters is only weakly dependent on the replacement atom X, inducing a change of electronic energies on the order of about 2.5 kcal mol⁻¹. ΔG, the change of Gibbs energy upon propane uptake, becomes positive at higher temperatures. The average value at 400 °C lies at 8.1 kcal mol⁻¹ (4.2 kcal mol⁻¹ with D3 correction).

2. The first C–H cleavage is the rate-determining step for all catalysts of the test set, but its barrier varies significantly with element X. At 400 °C we obtain ΔG values between 12 and 21 kcal mol⁻¹ (between 8 and 16 kcal mol⁻¹ with D3 correction). Similar or slightly higher activities than calculated for Pt₄ are predicted for Pt₃Si, Pt₃Ge, Pt₃Sn and Pt₃Ir.

3. The catalytic activity is correlated with the HOMO–LUMO gap of the clean catalyst. Both orbitals participate in the activation of the C–H bond at the relevant transition state. The σ-bond of the propane molecule donates charge into a diffuse d-orbital at the active site, which corresponds to the LUMO of the clean catalyst. The HOMO of the latter donates charge into the corresponding anti bonding orbital, which stabilizes the new geometry obtained after C–H bond cleavage.

4. Smaller HOMO–LUMO gaps indicate higher activity due to the increased flexibility of the valence electron at the active site. An NBO analysis reveals that the d-orbital shape of the HOMO with its pronounced nodal features better facilitates the breaking of a C–H bond than of a C–C bond due to better overlap with the C–H anti-binding orbital.

5. A very effective and computationally cheap descriptor for the catalytic activity could be found via an energy decomposition analysis at the equilibrium geometries of the clean catalysts by treating the dopant atom X as one fragment and the remaining catalyst Pt₃ as the other. The higher the energy contributions of frozen orbital interactions, E_frz, the lower was the rate-determining step in the follow-up evaluation of the propane dehydrogenation pathways (R² = 0.87).

6. No significant Brønsted–Evans–Polanyi-relation could be found for the given reaction. The simultaneous chemisorption of atomic hydrogen and a methyl group, the smallest representative with the same valency as the corresponding reaction intermediate, on the same Pt site, is only weakly correlated (R² = 0.51) to the barrier height of the rate-determining C–H cleavage step, despite the ‘late’ character of the relevant transition state.

7. The experimentally observed high selectivity towards propene agrees well with the finding that direct C–C bond breaking, a typical, preliminary step towards coking, is less likely due to higher barriers compared to C–H bond breaking. However, transition states that lead to undesired, continued dehydrogenation of the reactant compete with the desorption of the products after the second H cleavage step. At higher temperatures, desorption becomes more likely due to the gain in entropy, explaining an overall preference towards the desired product. Pt₃Ir seems to be exceptionally selective due to the higher barriers for continued C–H abstraction, but a slight bias due to geometric effects could not be excluded in this case.

Acknowledgements

This research was supported by the XC² program funded by BP. Calculations were performed on a cluster provided by the UC Berkeley College of Chemistry through the National Science Foundation (NSF) (Grant CHE-1048789). Development of EDA methodology and application to this system was supported by a grant from the National Science Foundation (CHE-1363342). AWH thanks Dennis Salahub for helpful discussions at the CMMSE conference held in Rota, Spain.

References

1. V. Galvita, G. Siddiqi, P. Sun and A. T. Bell, J. Catal., 2010, 271, 209–219.
2. A. Virnovskaia, E. Rytter and U. Olsbye, Ind. Eng. Chem. Res., 2008, 47, 7167–7177.
3. O. A. Bariås, A. Holmen and E. A. Blekkan, J. Catal., 1996, 158, 1–12.
4. F. Delbecq and P. Sautet, J. Catal., 2003, 220, 115–126.
5. M. S. Kumar, D. Chen, A. Holmen and J. C. Walmsley, Catal. Today, 2009, 142, 17–23.
6. S. Slimane Laref, F. Delbecq and D. Loffreda, J. Catal., 2009, 265, 35–42.
7. F. Vigné, J. Haubrich, D. Loffreda, P. Sautet and F. Delbecq, J. Catal., 2010, 275, 129–139.
8. J. Wu, Z. Peng and A. T. Bell, J. Catal., 2014, 311, 161–168.
9. J. Shen, J. M. Hill, R. M. Watwe, B. E. Spiewak and J. A. Dumesic, J. Phys. Chem. B, 1999, 103, 3923–3934.
10. R. M. Watwe, R. D. Cortright, M. Mavrikakis, J. K. Norskov and J. A. Dumesic, J. Chem. Phys., 2001, 114, 4663–4668.
11. E. Janin, H. von Schenck, S. Ringler, J. Weissenrieder, T. Åkermark and M. Göthelid, J. Catal., 2003, 215, 245–253.
12. R. Alcala, J. W. Shabaker, G. W. Huber, M. A. Sanchez-Castillo and J. A. Dumesic, J. Phys. Chem. B, 2005, 109, 2074–2085.
13. J. Essen, J. Haubrich, C. Becker and K. Wandelt, Surf. Sci., 2007, 601, 3472–3480.
14. A. Virnovskaia, S. Morandi, E. Rytter, G. Ghiotti and U. Olsbye, J. Phys. Chem. C, 2007, 111, 14732–14742.
15. A. Virnovskaia, S. Jørgensen, J. Hafizovic, O. Prytz, E. Kleimenov, M. Hävecker, H. Bluhm, A. Knop-Gericke, R. Schlögl and U. Olsbye, Surf. Sci., 2007, 601, 30–43.
16. Y.-L. Tsai and B. E. Koel, J. Phys. Chem. B, 1997, 101, 2895–2906.
17. G. J. Siri, J. M. Ramallo-López, M. L. Casella, J. L. Fierro, F. G. Requejo and O. A. Ferretti, Appl. Catal., A, 2005, 278, 239–249.
18. M. P. Lobera, C. Téllez, J. Herguido and M. Menéndez, Appl. Catal., A, 2008, 349, 156–164.
19. Z. Nawaz, X. Tang, Q. Zhang, D. Wang and W. Fei, Catal. Commun., 2009, 10, 1925–1930.
20. S. Pisduangdaw, J. Panpranot, C. Methastidsook, C. Chaisuk, K. Faungnawakij, P. Praserthdam and O. Mekasuwandumrong, Appl. Catal., A, 2009, 370, 1–6.
21. A. W. Hauser, J. Gomes, M. Bajdich, M. Head-Gordon and A. T. Bell, Phys. Chem. Chem. Phys., 2013, 15, 20727–20734.
22. L. Xiao and L. Wang, J. Phys. Chem. A, 2004, 108, 8605–8614.
23. L. Xiao and L. Wang, J. Phys. Chem. B, 2007, 111, 1657–1663.
24. J. Kua and W. A. Goddard, J. Phys. Chem. B, 1998, 102, 9481–9491.
25. S. Mallikarjun Sharada, P. M. Zimmerman, A. T. Bell and M. Head-Gordon, J. Chem. Theory Comput., 2012, 8, 5166–5174.
26. A. Behn, P. M. Zimmerman, A. T. Bell and M. Head-Gordon, J. Chem. Phys., 2011, 135, 224108.
27. J. Baker, J. Comput. Chem., 1986, 7, 385–395.
28. Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. ONeill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215.
29. S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964.
30. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
31. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
32. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
33. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
34. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
35. f-functions have been removed from all basis sets for performance reasons.
36. D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141.
37. B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563–2569.
38. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
39. The SCF convergence in all optimizations is set to 10⁻⁹ Hartree, for the DFT grid size we choose 75 radial and 302 Lebedev angular points. The convergence thresholds for the maximum gradient component and for the energy difference of successive optimization steps are set to 3 × 10⁻⁵ and 4 × 10⁻⁷ Hartree, respectively.
40. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2001.
41. E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42.
42. R. Z. Khaliullin, E. A. Cobar, R. C. Lochan, A. T. Bell and M. Head-Gordon, J. Phys. Chem. A, 2007, 111, 8753–8765.
43. P. R. Horn, E. J. Sundstrom, T. A. Baker and M. Head-Gordon, J. Chem. Phys., 2013, 138, 134119.
44. S. Vajda, M. J. Pellin, J. P. Greeley, C. L. Marshall, L. A. Curtiss, G. A. Ballentine, J. W. Elam, S. Catillon-Mucherie, P. C. Redfern, F. Mehmood and P. Zapol, Nat. Mater., 2009, 8, 213–216.
45. G. J. Kubas, Metal Dihydrogen and σ-Bond Complexes, Kluwer Academic, New York, 2001.
46. W. H. Bernskoetter, C. K. Schauer, K. I. Goldberg and M. Brookhart, Science, 2009, 326, 553–556.
47. D. R. Evans, T. Drovetskaya, R. Bau, C. A. Reed and P. D. W. Boyd, J. Am. Chem. Soc., 1997, 119, 3633–3634.
48. I. Castro-Rodriguez, H. Nakai, P. Gantzel, L. N. Zakharov, A. L. Rheingold and K. Meyer, J. Am. Chem. Soc., 2003, 125, 15734–15735.
49. S. D. Pike, A. L. Thompson, A. G. Algarra, D. C. Apperley, S. A. Macgregor and A. S. Weller, Science, 2012, 337, 1648–1651.
50. V. R. Stamenkovic, B. S. Mun, M. Arenz, K. J. J. Mayrhofer, C. A. Lucas, G. Wang, P. N. Ross and N. M. Markovic, Nat. Mater., 2007, 6, 241–247.
51. N. S. Porter, H. Wu, Z. Quan and J. Fang, Acc. Chem. Res., 2013, 46, 1867–1877.
52. Y. Xu, A. C. Lausche, S. Wang, T. S. Khan, F. Abild-Pedersen, F. Studt, J. K. Nørskov and T. Bligaard, New J. Phys., 2013, 15, 125021.
53. M. Melník, P. Mikuš and C. E. Holloway, Cent. Eur. J. Chem., 2013, 11, 1902–1953.
54. Z.-F. Xu and Y. Wang, J. Phys. Chem. C, 2011, 115, 20565–20571.
55. J. Wu, L. Qi, H. You, A. Gross, J. Li and H. Yang, J. Am. Chem. Soc., 2012, 134, 11880–11883.
56. Y. Liu, D. Li, V. R. Stamenkovic, S. Soled, J. D. Henao and S. Sun, ACS Catal., 2011, 1, 1719–1723.
57. X. Wang, L. Altmann, J. Stöver, V. Zielasek, M. Bäumer, K. Al-Shamery, H. Borchert, J. Parisi and J. Kolny-Olesiak, Chem. Mater., 2013, 25, 1400–1407.
58. M. Tanabe, K. Tanaka, S. Omine and K. Osakada, Chem. Commun., 2014, 50, 6839–6842.
59. P. Sun, G. Siddiqi, W. C. Vining, M. Chi and A. T. Bell, J. Catal., 2011, 282, 165–174.
60. K.-S. Lee, H.-Y. Park, H. C. Ham, S. J. Yoo, H. J. Kim, E. Cho, A. Manthiram and J. H. Jang, J. Phys. Chem. C, 2013, 117, 9164–9170.
61. S.-Y. Lee, N. Jung, J. Cho, H.-Y. Park, J. Ryu, I. Jang, H.-J. Kim, E. Cho, Y.-H. Park, H. C. Ham, J. H. Jang and S. J. Yoo, ACS Catal., 2014, 4, 2402–2408.
62. A. D. Burrows, J. G. Jeffrey, J. C. Machell and D. P. Mingos, J. Organomet. Chem., 1991, 406, 399–408.
63. S. Bhaduri, K. Sharma, P. G. Jones and C. F. Erdbrügger, J. Organomet. Chem., 1987, 326, C46–C48.
64. B. Y. Xia, H. B. Wu, X. Wang and X. W. D. Lou, J. Am. Chem. Soc., 2012, 134, 13934–13937.
65. M. Roca-Ayats, G. García, J. Galante, M. Peña and M. Martínez-Huerta, Int. J. Hydrogen Energy, 2014, 39, 5477–5484.
66. J. Wu, S. Mallikarjun Sharada, C. Ho, A. W. Hauser, M. Head-Gordon and A. T. Bell, Appl. Catal., A, 2015, 506, 25–32.
67. We note, however, that Ir atoms on bulk PtIr surfaces are assumed to actively participate in fragmentation reactions, see ref. 68. For the sake of simplicity in the direct comparison between various bimetallic structures these optional reaction pathways are not covered in the current study.
68. Q. Qi, X. Wang, L. Chen and B. Li, Appl. Surf. Sci., 2013, 284, 784–791.
69. The following spin multiplicities are found for the ground states of the tetrahedral bimetallic Pt₃X clusters: singlet for Si, Ge and Sn, doublet for In, Ga, Al, Au, Ag and Cu, triplet for Pt and Pd, and quartet for Ir.
70. A series of preliminary calculations showed that the first transition states remain rate-determining, even if a partial hydrogen coverage of the catalysts is assumed.
71. S. Furuyama, D. M. Golden and S. W. Benson, J. Chem. Thermodyn., 1969, 1, 363–375.
72. D. A. Pittam and G. Pilcher, J. Chem. Soc., Faraday Trans. 1, 1972, 68, 2224–2229.
73. L. Nykänen and K. Honkala, J. Phys. Chem. C, 2011, 115, 9578–9586.
74. We note that the inclusion of a dispersion correction to the density functional reduces the barrier heights for continued C–H breaking relative to the energy needed for propene desorption, predicting a reduced selectivity towards the desired product (see ESI†).
75. R. Z. Khaliullin, A. T. Bell and M. Head-Gordon, J. Chem. Phys., 2008, 128, 184112.
76. J. N. Bronsted, Chem. Rev., 1928, 5, 231–338.
77. M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11–24.
78. Handbook of Heterogeneous Catalysis, ed. G. Ertl, H. Knzinger and J. Weitkamp, Wiley-VCH Verlag GmbH, Weinheim, Germany, 1997.
79. F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. Munter, P. Moses, E. Skúlason, T. Bligaard and J. Nørskov, Phys. Rev. Lett., 2007, 99, 016105.
80. V. Pallassana and M. Neurock, J. Catal., 2000, 191, 301–317.
81. J. Nørskov, J. Catal., 2002, 209, 275–278.
82. A. Michaelides, Z. P. Liu, C. J. Zhang, A. Alavi, D. A. King and P. Hu, J. Am. Chem. Soc., 2003, 125, 3704–3705.
83. L. C. Grabow, F. Studt, F. Abild-Pedersen, V. Petzold, J. Kleis, T. Bligaard and J. K. Nørskov, Angew. Chem., Int. Ed., 2011, 123, 4697–4701.
84. A. Logadottir, T. H. Rod, J. K. Nørskov, B. Hammer, S. Dahl and C. J. H. Jacobsen, J. Catal., 2001, 197, 229–231.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp00360e

‡ Current address: Graz University of Technology, Institute of Experimental Physics, Petersgasse 16, 8010 Graz, Austria.

---