 Open Access Article
Open Access ArticleCarrier transport mechanisms in polycrystalline semiconductors: from grain boundary physics to device performance
Israt Jahan
 ,
Jesus Dustin Arellano
,
Jesus Dustin Arellano
 and
Zhisheng Shi
and
Zhisheng Shi
 *
*
School of Electrical and Computer Engineering, University of Oklahoma, Norman, Ok 73019, USA. E-mail: Shi@ou.edu
First published on 19th November 2025
Abstract
Polycrystalline semiconductors are central to modern optoelectronic and energy devices, yet their performance is governed by the chemistry and electrostatics of grain boundaries (GBs). Unlike single crystals, polycrystalline systems exhibit potential barriers, trap states, and compositional inhomogeneities that critically shape carrier mobility, lifetime, and recombination. This review unifies theoretical and experimental perspectives on major transport pathways—drift–diffusion, thermionic emission, tunneling, hopping, and conduction through threading crystallites—across representative materials including Si, CdTe, CIGS, PbSe, Sb2Se3, Bi2Te3, Mg3Sb2, and halide perovskites. Particular emphasis is placed on how nanoscale probes such as Kelvin probe and conductive AFM, cathodoluminescence, and DLTS elucidate barrier heights, trap energetics, and boundary passivation effects. Chemical and structural strategies—such as halogen or alkali–fluoride treatments, dopant redistribution, anti-barrier engineering, and twin-boundary engineering—are demonstrated to transform recombination-active interfaces into conductive channels. By correlating microscopic boundary chemistry with macroscopic transport and device metrics, this review formulates general design guidelines for programmable grain architectures. The analysis establishes grain boundaries not as fixed defects but as tunable electronic interfaces, offering a roadmap for next-generation polycrystalline semiconductors optimized for high-mobility, high-stability optoelectronic and thermoelectric applications.
1 Introduction
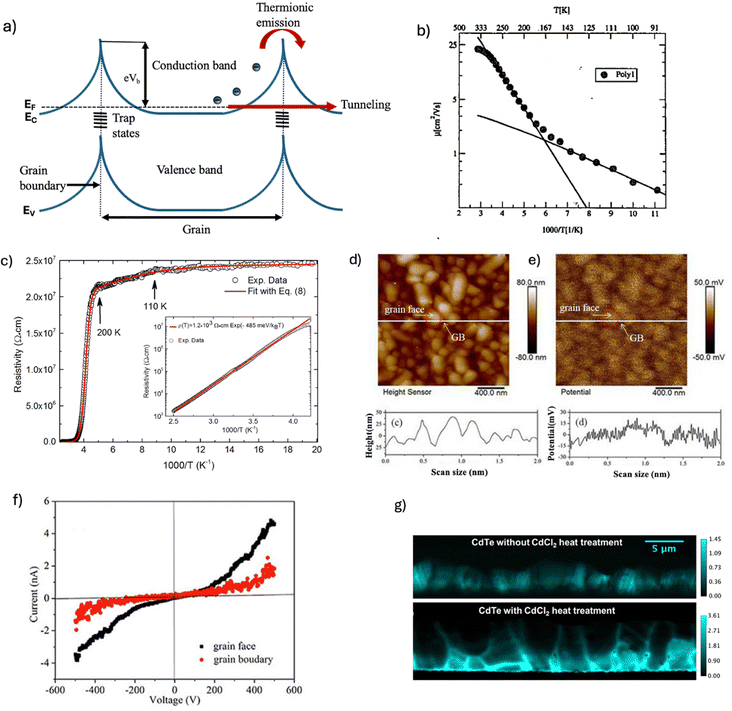
Polycrystalline semiconductors are integral to a wide range of contemporary technologies, including electronics, optoelectronics, and energy conversion systems, owing to their cost-effective fabrication methods, tunable material properties, and compatibility with large-area deposition. In contrast to single-crystalline materials, which require precise and resource-intensive growth techniques, polycrystalline thin films can be fabricated via scalable approaches such as chemical vapor deposition (CVD), molecular beam epitaxy (MBE), and solution-based processes. These fabrication routes facilitate integration over flexible or inexpensive substrates.Unlike single crystals, where the periodic and defect-minimized lattice enables smooth electronic band structures, characterized by flat conduction and valence bands that support unobstructed drift and diffusion of carriers with minimal scattering, polycrystalline materials are composed of many crystallites separated by grain boundaries (GBs). These boundaries often serve as reservoirs for electrically active defect states—frequently modelled as ionized donor- or acceptor-like traps—which can capture mobile carriers. The resultant accumulation of fixed charge at GBs induces electrostatic potential variations and leads to the formation of depletion or accumulation zones. These localized space-charge regions exhibit pronounced band bending, which in turn alters carrier transport pathways and contributes to the non-ideal electronic behaviour observed in polycrystalline films.1–3
The electrostatic band bending induced by grain boundaries (GBs) plays a pivotal role in modulating charge carrier transport. As schematically depicted in Fig. 1, energy bands in polycrystalline materials exhibit upward or downward bending near GBs, forming potential barriers that obstruct carrier motion. These barriers can reflect carriers, impose thermal repulsion, or enable quantum mechanical filtering depending on the carriers’ energy distribution and the strength of local electric fields. The extent of the barrier is often quantified using the Seto model, which correlates the barrier height to doping concentration and trap state density at the boundary interface.4 Such GB-induced potential profiles result in deviations from ideal drift–diffusion behaviour, promoting alternative transport mechanisms such as thermionic emission, field-enhanced tunneling, or hopping conduction—particularly at low temperatures or in defect-rich systems.
 | ||
| Fig. 1 Schematic band diagrams illustrating the impact of grain and twin boundaries on carrier transport. (a) Energy diagrams comparing GBs and twin boundaries (TBs): GBs act as recombination-active regions with band bending and carrier trapping, while TBs, owing to their symmetry and low defect density, provide recombination-free, conductive pathways. Adapted from Xun Xiao et al., Nat. Commun., 2020, 11, 2215. https://doi.org/10.1038/s41467-020-16075-1. Licensed under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).5 (b) Grain boundaries (GBs) can introduce hole barriers (left), electron barriers (right), impeding carrier mobility, Adapted from Nicoleta Nicoara et al., Nat. Commun., 2019, 10, 3980. Licensed under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).6 | ||
Nonetheless, through careful material and interface engineering, several polycrystalline systems have overcome these limitations and achieved state-of-the-art performance in practical devices. Polycrystalline metal halide perovskites, for instance, have rapidly emerged as leading photovoltaic materials, achieving power conversion efficiencies (PCEs) exceeding 24.8% and external quantum efficiencies (EQEs) up to 93%, rivaling those of single-crystal silicon devices.7,8 These remarkable results are attributed to long carrier diffusion lengths, benign grain boundaries, and defect-tolerant electronic structures. Polycrystalline silicon (poly-Si) remains the dominant material in commercial solar panels, balancing cost, scalability, and efficiency, with laboratory-scale devices exceeding 22% PCE.9 Likewise, cadmium selenide telluride (CST) and copper indium gallium selenide (CIGS) thin films have reached power conversion efficiencies above 22% and 23%, respectively, while offering compatibility with flexible or inexpensive substrates.10,11 In the realm of infrared and broadband photodetection, semiconductors such as lead selenide (PbSe), antimony selenide (Sb2Se3), tin sulphide (SnS), and lead sulphide (PbS) have emerged as promising candidates due to their tunable bandgaps and intrinsic tolerance to defects.12–15 These materials support long carrier lifetimes and stable performance even in the presence of high defect densities—an essential feature for mid-wave infrared (MWIR) and near-infrared sensing technologies.
Polycrystalline materials are also central to thermoelectric applications, where compounds such as bismuth telluride (Bi2Te3), lead telluride (PbTe), and half-Heusler alloys benefit from microstructural engineering strategies that selectively suppress lattice thermal conductivity while maintaining or enhancing electronic transport. This decoupling effect leads to improved thermoelectric figure of merit (ZT).16 Recently, n-type Mg3(Sb,Bi)2 has drawn considerable attention as a high-performance thermoelectric material, achieving a record peak ZT of ∼2.0 and an average ZT above 1.5 through interfacial and grain-boundary engineering.17 Furthermore, polycrystalline n-type metal oxides, including tin dioxide (SnO2) and zinc oxide (ZnO), are widely deployed in gas sensors, where carrier concentration at grain boundaries (GBs) is modulated by adsorbed gas species, yielding high chemical sensitivity.18 In thin-film transistor (TFT) applications, particularly for display backplanes and flexible electronics, polycrystalline silicon (poly-Si) remains the material of choice despite the adverse effects of grain-induced scattering. Its compatibility with established silicon processing and favourable mechanical properties ensures continued relevance in logic and active-matrix circuits.19
Among the various microstructural features in polycrystalline semiconductors, twin boundaries (TBs) stand out as a unique class of planar defects. Unlike conventional grain boundaries, TBs typically possess low defect densities and do not substantially disturb the periodic potential landscape. As a result, they rarely introduce deep-level trap states or significant band bending. In fact, TBs have been reported to facilitate directional carrier transport along specific lattice axes and may enhance overall electronic performance. In materials such as CdTe, TBs have been associated with efficient carrier collection and are increasingly regarded as electronically benign or even performance-enhancing features.2,20,21
Understanding the interplay between microstructure and charge transport is essential for advancing the performance of polycrystalline devices. This review presents an integrative analysis of charge transport mechanisms in polycrystalline semiconductors, encompassing theoretical models and experimental observations. Topics covered include major conduction mechanisms (e.g., drift–diffusion, thermionic emission, tunneling, and hopping), the roles of GBs and TBs, and the effects of structural and electrical heterogeneities. By linking microscopic defect structures to macroscopic transport behavior, this work aims to inform design strategies for high-performance polycrystalline semiconductors in photovoltaic, optoelectronic, and thermoelectric applications.
2 Fundamentals of charge carrier transport
A fundamental understanding of charge carrier transport mechanisms is pivotal for the rational design and performance enhancement of semiconductor devices. In polycrystalline semiconductors, the dominant transport phenomena are carrier drift and diffusion, which govern movement in response to applied electric fields and concentration gradients, respectively. While these mechanisms form the basis of classical semiconductor transport theory, the presence of grain boundaries (GBs) in polycrystalline systems introduces spatial inhomogeneities and electrostatic discontinuities that complicate this otherwise idealized behavior. GBs act as scattering centers and potential barriers, disrupting the continuity of carrier flow and altering the local field distribution, thereby significantly influencing both drift- and diffusion-driven transport.2.1 Drift and diffusion transport
The Charge carrier motion in semiconductors is fundamentally governed by two classical mechanisms: drift, driven by electric fields, and diffusion, arising from concentration gradients.22 When an external electric field E is applied, electrons and holes experience an electric field force that induces a net directional movement, resulting in a drift current. The average carrier velocity under the field, or drift velocity, vd, is given by:| vd = μE | (1) |
| Jdrift = qnμE | (2) |
With q representing the elementary charge and n the carrier concentration.4 In single-crystal semiconductors, mobility is typically limited by phonon scattering and ionized impurity interactions.22 However, in polycrystalline semiconductors, grain boundaries (GBs) introduce additional scattering and trapping centers that degrade carrier mobility. GBs act as electrostatic barriers, altering the local potential landscape and impeding charge flow. One of the earliest models to quantify this effect was proposed by Seto, who attributed mobility degradation to potential barriers formed at GBs due to trapped interface charges. These trapped charges induce band bending at the grain interfaces, resulting in a thermally activated transport behavior—particularly significant in low-doped polycrystalline silicon films.4 Expanding on this idea, Kim et al. developed a detailed drift–diffusion model treating GBs as amorphous regions in thermodynamic equilibrium with adjacent grains.23 Their model successfully captures both small-signal behavior and nonlinear large-signal responses in polysilicon thin films, making it broadly applicable to thin-film devices such as thin-film transistors (TFTs).
Parallel to drift, carrier motion also occurs via diffusion, a thermally induced process where particles migrate from regions of high concentration to low concentration. The diffusion current density is described by,
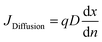 | (3) |
 | (4) |
Grain boundaries influence diffusion through two mechanisms: (1) they serve as energetic barriers hindering carrier transport, and (2) they provide fast-diffusion pathways for atomic species such as dopants and impurities.2,22 For instance, Hwang et al. showed via Auger electron spectroscopy that aluminium diffuses preferentially along GBs in polycrystalline silicon—contrasting sharply with its limited bulk diffusivity.24 This phenomenon plays a crucial role in the activation and redistribution of dopants during thermal processing steps.
To model such effects, Ling et al. proposed a diffusion-based model that incorporates GB-induced potential barriers.25 By solving the carrier continuity equation across the GB depletion region, they demonstrated how variations in grain size and barrier height influence effective diffusion currents and lateral mobility. Complementing this, Santonen et al. examined how grain size distributions affect macroscopic drift–diffusion transport.26 Their simulations revealed that broader grain size distributions reduce overall resistivity by enabling percolative pathways through low-barrier grains, effectively minimizing the number of transport-limiting junctions.
Beyond influencing carrier mobility and diffusion coefficients, GBs critically shape the local energy landscape. Electrostatic band bending at GBs results in potential barriers that carriers must overcome via thermionic emission or quantum tunneling—particularly at low temperatures or when barriers are high.27 Accurately capturing these behaviors requires incorporating position-dependent mobility, spatially varying potential profiles, and non-uniform carrier distributions into device models.
To address these complexities, multiple extensions of the Seto model have been developed,4 incorporating phenomena such as field-assisted tunneling, trap occupancy statistics, and nonlinear transport regimes. These enhancements are especially relevant for advanced polycrystalline devices, including photodetectors, TFTs, and thin-film solar cells.28 Consequently, conventional drift–diffusion frameworks must be supplemented with grain-level and statistical descriptors, including grain size, trap density, and potential inhomogeneity. A comprehensive understanding of GB-driven transport is thus indispensable for predictive modeling and performance optimization of next-generation polycrystalline electronic and optoelectronic systems.
Taken together, these studies confirm that drift–diffusion transport in polycrystalline semiconductors cannot be described by classical models alone but must explicitly account for the electrostatics and chemistry of grain boundaries. Trap-induced band bending, dopant segregation, and impurity incorporation all redefine effective mobility and diffusion pathways, shifting transport away from ideal single-crystal behavior.4,22–27 Importantly, GBs act not only as barriers but also as fast-diffusion conduits for impurities, making their chemical composition as decisive as their geometry in determining device performance. Extensions of the Seto model that incorporate field-assisted tunneling, trap statistics, and grain-size distributions demonstrate that predictive transport modeling requires grain-level descriptors rather than bulk averages.4,26,28 Thus, drift–diffusion in polycrystalline systems reflects a balance between classical band transport and boundary-limited conduction, highlighting that controlling GB chemistry, trap density, and orientation is as essential as scaling grain size for optimizing electronic and optoelectronic devices.
2.2 Scattering mechanisms
The carrier transport in polycrystalline semiconductors is influenced by various scattering mechanisms, including phonon scattering, ionized impurity scattering, and grain boundary scattering. These mechanisms collectively determine the effective carrier mobility μeff, often represented by Matthiessen's rule:
 | (5) |
Phonon scattering arises from interactions between charge carriers and lattice vibrations. In polycrystalline materials, grain boundaries introduce additional phonon scattering centers, significantly reducing thermal conductivity (Fig. 2d). For instance, studies have shown that when phonons travel across grain boundaries, the rapidly changing strain fields can induce strong phonon scattering, leading to increased interfacial thermal resistance.31 The temperature dependence of phonon-limited mobility is often expressed as: μph ∝ T−γ, where γ typically ranges from 1.5 to 2.5, depending on the material and specific phonon interactions. This relationship indicates that as temperature increases, phonon scattering becomes more significant, leading to a decrease in carrier mobility.32 Recent advancements have highlighted the role of strain fields induced by grain boundaries in enhancing phonon scattering. For example, in polycrystalline graphene, grain-boundary-induced strain fields have been identified as a decisive factor in electron scattering, affecting the material's electrical resistivity. Additionally, in materials like In2Te3, strong phonon scattering on point defects has been observed, contributing to low thermal conductivity.33–35
 | ||
| Fig. 2 Schematic illustration of scattering and energy landscape in polycrystalline semiconductors. (a) Structural complexity of grain boundaries (GBs), showing multiple phases and defect-rich regions. (b) Energy band diagram for an n-type polycrystalline material, where charged GB trap states induce band bending and depletion regions. (c) Representation of dominant scattering mechanisms, including ionized impurity scattering and grain boundary scattering. (a)–(c) are adapted from Chaoliang Hu et al., Energy Environ. Sci., 2021, 15, 1406–1422, with permission from the Royal Society of Chemistry.92 (d) Phonon scattering process affecting charge transport in polycrystalline SrTiO3−xHx. Adapted with permission from Takayoshi Katase et al., ACS Appl. Electron. Mater., 2024, 6 (10). Copyright 2024 American Chemical Society.42 | ||
Ionized impurity scattering (IIS) occurs when charge carriers interact with ionized dopants within the semiconductor (Fig. 2c). This mechanism is particularly significant in heavily doped polycrystalline films, where the Coulombic interactions between carriers and charged impurities can substantially impede carrier mobility. The mobility limited by ionized impurity scattering is inversely related to the impurity concentration and exhibits a temperature dependence that varies based on screening effects and carrier concentration.27,36 In highly doped polycrystalline semiconductors, such as aluminium-doped zinc oxide (AZO), ionized impurity scattering becomes a dominant factor affecting electron transport. Studies have shown that at high doping levels, the net charge of ionized impurities leads to Coulomb potentials, which constitute significant scattering centers for charge carriers. Furthermore, in materials like zinc tin oxide (ZTO), both ionized impurity and grain boundary scattering mechanisms have been identified as temperature-independent factors limiting electron mobility.37 Advancements in first-principles calculations have enabled more accurate predictions of carrier scattering rates due to ionized impurities. These computational methods have been applied to various semiconductors, providing insights into the impact of ionized impurity scattering on electronic transport properties.38 Recent work on n-type Mg3(Sb,Bi)2 crystallizes how the balance among ionized-impurity scattering and grain-boundary (GB) barriers determines low-temperature transport. Shuai et al.39 showed that modest Nb co-doping converts the dominant scattering from IIS to a mixed IIS + acoustic-phonon regime, thereby tripling the power factor and increasing Hall mobility from ∼19 to ∼77 cm2 V−1 s−1 through dielectric screening-driven IIS suppression. This study suggests that reducing IIS (intragrain) and lowering GB barrier resistance (intergrain) are orthogonal knobs for mobility engineering in polycrystals.
Grain boundaries in polycrystalline semiconductors serve as potential barriers to charge carriers, resulting in scattering and trapping phenomena that degrade electrical performance (Fig. 2c). The impact of grain boundary scattering on carrier mobility can be described by,
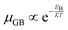 | (6) |
In summary, scattering mechanisms in polycrystalline semiconductors reflect the combined influence of lattice dynamics, impurity distribution, and grain boundary chemistry. Phonon scattering dominates at elevated temperatures, ionized impurity scattering prevails in heavily doped regimes, and grain boundary scattering governs mobility in low-doped or trap-rich systems.4,27,29–32,36–38,42 A unifying theme across these regimes is that grain boundaries act as chemically active scattering centers, where strain fields, dopant segregation, and localized defects enhance phonon and Coulombic scattering in ways that bulk models cannot capture.33–35,40,41 Importantly, evidence from organic semiconductors and oxide films shows that grain boundary engineering—through deposition control, passivation, and chemical doping—can mitigate these effects by lowering trap densities and redistributing impurities.37,40,41 These findings emphasize that scattering in polycrystalline semiconductors is not solely a structural phenomenon but a chemistry-governed process, highlighting the importance of defect chemistry and boundary treatments as decisive levers for optimizing carrier mobility.
2.3 Carrier lifetime and recombination
The Carrier lifetime—the average time a photogenerated or injected carrier remains mobile before recombination—is a pivotal parameter governing the performance of optoelectronic and photovoltaic devices. In polycrystalline semiconductors, this lifetime is significantly influenced by intrinsic material properties such as grain boundaries (GBs), dislocations, and trap states, which introduce additional non-radiative recombination pathways absent in single-crystalline counterparts. The total carrier lifetime (τeff) in polycrystalline materials is determined by the combined effects of bulk (grain interior) recombination and recombination at GBs. It is commonly expressed as:
 | (7) |
The dominant recombination mechanisms in semiconductors are: (i) radiative recombination, where electrons and holes recombine to emit photons; (ii) Auger recombination, involving a third carrier that absorbs the recombination energy; and (iii) Shockley–Read–Hall (SRH) recombination, which occurs via trap states within the bandgap. In high-quality single crystals, radiative recombination may dominate under high injection, but in polycrystalline films, SRH recombination is often the primary non-radiative pathway due to a high density of trap states near GBs.44 The SRH recombination rate is given by:
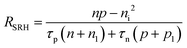 | (8) |
Grain boundaries are known to introduce defect states that trap carriers and create local band bending. This band bending separates quasi-Fermi levels, enhances recombination, and can substantially reduce effective diffusion lengths. According to Gaury and Haney, the recombination activity of GBs depends on their charge state and the type of traps present. For instance, a single donor state at the GB can dramatically suppress recombination relative to donor–acceptor continua. Experimental studies using cathodoluminescence and electron-beam-induced current (EBIC) have confirmed that GBs can either serve as recombination sinks or quasi-passive interfaces, depending on their chemical and electrical character.43,47
Carrier lifetime in polycrystalline materials is often measured using time-resolved photoluminescence (TRPL). Modern halide perovskites exhibit lifetimes exceeding 6 µs—approaching values observed in single crystals—due to intrinsic defect tolerance and high GB passivation.48 However, lifetime measurements are frequently complicated by spatial inhomogeneities caused by variation in trap density across grains and GBs. In surface-limited recombination scenarios, the lifetime can be expressed empirically as:
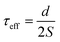 | (9) |
Collectively, these findings demonstrate that carrier lifetime in polycrystalline semiconductors is dictated not simply by bulk recombination but by the chemical nature and charge state of grain boundaries. While SRH recombination dominates in trap-rich systems such as poly-Si, CdTe, and CIGS.43–46 Halide perovskites illustrate that benign or passivated boundaries can yield lifetimes approaching those of single crystals.48 Microscopy studies further confirm that GBs may behave as either recombination sinks or quasi-passive interfaces, depending on their defect chemistry and electrostatics.43,47 This duality underscores the central role of boundary chemistry, defect passivation, and grain size control in governing τeff, with strategies such as Cl/Cu passivation in CdTe or compositional engineering in perovskites providing clear pathways to extend carrier lifetimes.46–48 Thus, lifetime engineering in polycrystalline semiconductors is less a matter of eliminating GBs and more about chemically tuning their recombination activity, establishing GB chemistry as a decisive design parameter for next-generation optoelectronic and photovoltaic devices.
3 Major conduction mechanisms
3.1 Thermionic emission across grain boundaries
 | (10) |
 | (11) |
This expression illustrates that a high density of trap states or a low carrier concentration results in an increased barrier height, thereby suppressing conduction.4,22,50 Consequently, the mobility of charge carriers in such GB-limited systems follows an Arrhenius-type temperature dependence:  . This exponential dependence has been widely observed in experiments involving temperature-dependent Hall measurements and photoconductivity studies.49,52 It reflects the thermally activated nature of carrier transport across the grain boundaries. Furthermore, the influence of grain structure becomes evident when considering the total resistance of a polycrystalline film. If a material is composed of grains of average size d, the total device resistance scales with the number of boundaries per unit length:
. This exponential dependence has been widely observed in experiments involving temperature-dependent Hall measurements and photoconductivity studies.49,52 It reflects the thermally activated nature of carrier transport across the grain boundaries. Furthermore, the influence of grain structure becomes evident when considering the total resistance of a polycrystalline film. If a material is composed of grains of average size d, the total device resistance scales with the number of boundaries per unit length:
 | (12) |
This relationship highlights key material design strategies: increasing grain size, reducing GB trap density, or enhancing carrier concentration will all serve to lower the effective resistance and improve conductivity. While Seto's model provides a foundational understanding, more recent theoretical developments have refined this picture by incorporating the effects of barrier height fluctuation, partial depletion, and image-force lowering, and non-uniform spatial distributions of trap states, which more accurately reflect the complexities of real grain boundaries in modern semiconductor materials.49,51,53
In polycrystalline CuGaSe2, Schuler et al. identified three distinct conduction regimes via Hall measurements from 80 to 350 K. Notably, the intermediate regime (150–300 K) exhibited mobility activation energies ranging between 60 and 135 meV, consistent with thermionic emission across GB barriers.27 Similarly, Cifuentes et al. reported thermionic emission as the dominant transport mechanism in Sb2Se3 thin films above 200 K, with conductivity fits yielding barrier heights of approximately 391 meV and trap densities on the order of 3.4 × 1011 cm−2.54 In ZnO-based systems, doping levels were found to govern the dominant transport mode. Kajikawa et al. observed that moderately doped Al:ZnO (∼1018 cm−3) films displayed thermionic emission-limited conduction with GB barriers between 70–120 meV.50 However, at higher doping levels exceeding 1019 cm−3, tunneling mechanisms began to dominate due to the narrowing of depletion regions.
In elemental polycrystalline semiconductors such as silicon, Lu et al. proposed a conduction model based on sequential semiconductor–grain-boundary–semiconductor (S–GB–S) barriers. Their experimental studies in thermally grown poly-Si revealed that thermionic emission dominated charge transport, with conduction scaling determined by grain size, dopant density, and GB trap states.51 Similar effects were described in polycrystalline PbS, where Slater developed a GB barrier model to explain temperature-activated photoconductivity. Activation energies up to 370 meV were found, depending on oxidation and microstructure, confirming that GB-induced potential barriers critically influence dark conductivity and its temperature dependence.55
Beyond macroscopic transport studies, direct nanoscale imaging techniques have provided microscopic confirmation of GB barriers and electrostatic potential modulation. In NiO thin films, Zhang et al. employed conductive atomic force microscopy (C-AFM) and Kelvin probe force microscopy (KPFM) to spatially map local current distribution and surface potential across grains and boundaries. Their measurements revealed nanoscale potential differences of ∼17–23 meV at GBs, and I–V curves indicative of thermionic emission behavior. These results confirmed the existence of energy barriers that modulate local carrier flow in polycrystalline NiO (Fig. 3(d–f)).56
 | ||
| Fig. 3 (a) Schematic energy band diagram illustrating that thermionic emission occurs as carriers overcome grain boundary (GB) potential barriers formed by trap states (Nt), with possible tunneling contribution under strong fields. (b) Arrhenius plot of Hall mobility in polycrystalline CuGaSe2 thin films, showing three temperature-dependent transport regimes: (I) high-temperature bulk-limited conduction, (II) intermediate-temperature thermionic emission over GB barriers (150 K–300 K), and (III) low-temperature hopping between localized states. Adapted (b) with permission from S. Schuler, “Charge carrier transport in polycrystalline CuGaSe2 thin films,” IEEE Proceedings, 2002. © 2002 IEEE.27 (c) Temperature-dependent resistivity in Sb2Se3 fitted with a thermionic emission model in region II (200 K–110 K), yielding a GB barrier height of ∼391 meV and a trap density of 3.4 × 1011 cm−2; flattening at low temperature (T < 110 K) indicates transition to hopping-assisted transport (region III). Adapted with permission from N. Cifuentes et al., J. Phys. Chem. C, 2020, 124 (14), 7677–7682. Copyright 2020 American Chemical Society.54 (d) AFM topography and (e) KPFM surface potential image of NiO film highlighting nanoscale potential dips at grain boundaries, indicating the presence of electrostatic barriers, (f) local I–V curves measured by C-AFM across grain face and grain boundary regions in NiO show suppressed current at GBs, consistent with thermionic-limited transport under moderate bias. (d)–(f) are adapted from Yidong Zhang et al., Phys. E, 2019, 111, 75–78, with permission from Elsevier.56 (g) EBIC images of CdTe before and after CdCl2 treatment reveal enhanced carrier collection along GBs post-passivation, attributed to barrier height reduction and improved thermionic emission across GBs. Adapted with permission from Chen Li et al., Phys. Rev. Lett., 2014, 112, 156103. © 2014 American Physical Society.59 | ||
Such nanoscale measurements are consistent with macroscopic device performance in halide perovskites. KPFM studies of MAPbI3 films reported by Bahrami et al. showed GB potential barriers between 20 and 43 meV, depending on humidity exposure. The presence of these electrostatic barriers limited carrier collection and exhibited thermal activation consistent with the Richardson–Schottky model of thermionic transport.57 Yun et al. further demonstrated that GBs serve as preferential paths for ion migration and recombination, supporting the idea that GBs are electrostatically active sites influencing charge separation and transport.58
The importance of GB electrostatics has also been validated using electron beam induced current (EBIC) imaging. In polycrystalline CdTe/CdS solar cells, Li et al. observed that untreated GBs appeared as dark features in EBIC maps due to poor collection efficiency. Post-CdCl2 treatment, however, these same GBs exhibited bright contrast, indicative of enhanced local collection driven by GB-induced band bending (Fig. 3g). The activation was attributed to a CdCl2-induced p-to-n type inversion at GBs that created internal fields enhancing thermionic carrier separation.59,60 These findings are consistent with first-principles calculations by Zhang et al., who showed that Cl and Cu preferentially accumulate at Te-core GBs in CdTe. Without copassivation, these boundaries host deep states near the conduction band minimum; combined Cl–Cu treatment effectively removes these levels, validating the electrostatic origin of GB barriers.61
Further insights have been gained through optoelectronic characterization techniques such as time-resolved photoluminescence (TRPL) and infrared light-beam induced current (IR-LBIC) mapping. In Cs-doped FAPbI3 thin films, Ma et al. showed that grain boundaries exhibited slightly reduced diffusion lengths (3–5 µm) and enhanced charge trapping compared to grain interiors. Despite long carrier lifetimes overall, the observed spatial heterogeneity in photoconductivity supports the presence of weak GB barriers that contribute to thermally activated transport under certain conditions.62
A clear manifestation of thermionic emission–limited charge transport has been observed in n-type Mg3Sb2-based thermoelectric materials, which display thermally activated carrier mobility below approximately 500 K. Kuo et al.63 explained this behavior using a two-phase grain/grain-boundary transport model, in which depletion layers at the grain boundaries create potential barriers of about 60 meV. Electrons must surmount these barriers to contribute to conduction, giving rise to the characteristic Arrhenius-type temperature dependence of electrical conductivity. In a complementary study, Shuai et al.39 showed that Nb co-doping effectively suppresses ionized-impurity scattering and improves dielectric screening, thereby enhancing carrier mobility once the grain-boundary barriers are partially neutralized. These studies provide modern experimental and theoretical support for the barrier-controlled transport mechanism originally proposed by Seto, confirming its continued relevance in describing charge conduction across grain boundaries in polycrystalline semiconductors.
Collectively, these findings demonstrate that thermionic emission across grain boundaries is a universal transport pathway in polycrystalline semiconductors, manifesting in diverse systems ranging from chalcogenides and oxides to halide perovskites. While activation energies and barrier heights vary widely, their magnitude is consistently governed by the density and chemistry of GB trap states as well as dopant concentration. Importantly, recent evidence shows that halogen and alkali passivation (CdCl2, Cl, Cu),59–62 dopant redistribution,50,51 and compositional tuning56–58 can lower or eliminate deep states, thereby reducing barrier heights and enabling enhanced carrier collection. This convergence of bulk transport measurements, nanoscale imaging, and first-principles calculations consolidates Seto's classical model into a broader, chemistry-aware framework, underscoring that GB barriers are not fixed structural defects but chemically tunable electrostatic interfaces that can be deliberately engineered for improved device performance.4,22,49–53,56–62
3.2 Thermionic field emission and tunneling
The classical Fowler–Nordheim (FN) equation, derived under the assumption of triangular potential barriers and zero-temperature tunneling, is widely used to describe FE:
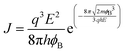 | (13) |
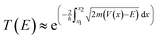 | (14) |
The transition from TE to TFE and ultimately to FE is not abrupt but governed by a characteristic electric field ET, which depends on temperature, effective mass, barrier width, and doping level. Li et al. demonstrated this transition in β-Ga2O3 Schottky diodes, identifying a universal field ET that demarcates the regime boundaries.67 Lin et al. further proposed a transport phase map that predicts the dominant conduction regime based on applied field and temperature, applicable to a wide range of semiconducting systems.68
In polycrystalline silicon, Sharma and Joshi constructed a comprehensive conduction model incorporating TE, TFE, and FE, demonstrating that resistivity and Hall mobility data could only be fitted when field-assisted tunneling components were included. Their findings highlighted the increasing dominance of TFE at low temperatures and high doping concentrations, particularly in S–GB–S (semiconductor–grain boundary–semiconductor) structures with narrow potential barriers.70
Lead chalcogenide systems such as PbSe exhibit similar behavior. Oxygen-sensitized polycrystalline PbSe films, widely used in infrared photodetectors, display nearly temperature-independent dark conductivity below 150 K—a signature of tunneling or hopping conduction through thin GB barriers.71 These findings are consistent with the formation of inversion layers and narrow depletion regions under high electric fields, reducing the need for thermal activation. Emerging material platforms, such as hybrid halide perovskites and quantum-dot-perovskite composites, also demonstrate field emission under applied bias. In these systems, strong local fields induce carrier extraction via tunneling mechanisms, as observed through ultrafast transient absorption and photocurrent measurements.72
Microscopic techniques such as conductive atomic force microscopy (C-AFM) and Kelvin probe force microscopy (KPFM) have further illuminated the localized nature of GB barriers and field-enhanced tunneling. Zhang et al. used C-AFM and KPFM to investigate NiO thin films, observing non-linear I–V characteristics and suppressed surface potential (∼17 meV) across ∼60 nm-wide depletion regions at GBs—indicative of field-enhanced conduction channels.56 In monolayer WSe2, Su et al. employed tip-enhanced KPFM and photoluminescence imaging to reveal steep potential gradients and mid-gap states at tilted GBs, consistent with band bending and charge trapping that facilitate tunneling under high local fields.73
In CVD-grown polycrystalline graphene, Park et al. applied multi-probe scanning tunneling potentiometry (STP) to show that GBs act as high-resistance junctions, exhibiting localized voltage drops and reduced transmission probabilities. Although Dirac fermion transport introduces complexities, the observed conductance suppression across disordered GBs is consistent with tunneling-like behavior.33 Finally, Chen et al. developed a spatially resolved polycrystalline cathode emission model incorporating grain orientation, local field enhancement, and barrier inhomogeneity, achieving excellent agreement with emission current maps observed experimentally via EBIC and cathodoluminescence.65
Collectively, these results establish that thermionic-field emission and tunneling are universal transport pathways in polycrystalline semiconductors once depletion widths are narrowed by high doping, field-induced band bending, or boundary defect chemistry. Across oxides, chalcogenides, hybrid perovskites, and even 2D materials, a common theme emerges: the transition from thermionic emission to field-assisted tunneling is governed less by temperature alone and more by the electrostatic and chemical environment of grain boundaries. Chemical dopant redistribution in ZnO:Al and poly-Si narrows depletion widths and enables tunnelling;36,69,70 oxygen sensitization in PbSe modifies inversion layers and depletion regions;71 and halide perovskites exhibit field-assisted extraction that is strongly dependent on GB defect passivation and local field gradients.72 Microscopy studies further confirm that barrier inhomogeneity, mid-gap states, and electrostatic dips at GBs act as tunneling hot-spots.56,73 Together, these findings refine the classical models of TE and FE into a chemistry-aware tunneling framework, underscoring that GB-mediated transport can be deliberately tuned through doping, compositional control, and targeted passivation to optimize devices ranging from transparent conductors to infrared photodetectors and thin-film photovoltaics.33,36,56,65,67–73
3.3 Hopping conduction
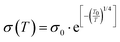 | (15) |
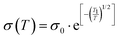 | (16) |
This stronger temperature dependence reflects enhanced localization due to repulsive interactions among hopping carriers.75
In polycrystalline Sb2Se3, Cifuentes et al. observed a transition from thermionic emission to hopping conduction with decreasing temperature: between 160–250 K, an activation energy of ∼0.111 eV suggests defect-assisted transport, while below 110 K, the system obeys VRH behavior with T0 ≈ 2.31 × 106 K (Fig. 3c).54 Similar behavior is seen in ZnSnO3 thin films, where VRH dominates below 100 K. The extracted density of states (∼1019 eV−1 cm−3) corroborates this hopping framework.77
In oxidized nanocrystalline PbTe(In), hopping conduction prevails below 150 K, attributed to enhanced carrier localization along inversion channels at oxidized grain surfaces. Impedance spectroscopy confirmed a shift in transport dynamics, highlighting the role of microstructural evolution on conduction pathways.78
In Al-doped ZnO, VRH behavior is reported for underdoped films with weakly connected grains between 100–180 K.79 Likewise, polycrystalline CdS and CuInSe2 exhibit low-temperature hopping conduction across grain boundaries, often governed by trap-controlled transport.80,81 In amorphous oxides such as IGZO, the stronger temperature dependence observed (∝ T−1/2) below 150 K confirms ES-VRH behavior, suggesting a significant Coulomb gap due to electron–electron interactions in disordered networks.82
Experimental nanoscale techniques such as KPFM and C-AFM have provided direct visualization of these hopping pathways. For example, in NiO thin films, Zhang et al. observed localized current channels aligning with GB potential minima, consistent with the formation of hopping percolation networks.56 Similarly, in AZO films, KPFM studies confirm suppressed conductivity and potential barriers aligned with grain boundaries.79
Hopping conduction dominates at temperatures below ∼150–200 K, where thermal energy is insufficient to overcome grain boundary barriers or activate band-like transport. Instead, carriers tunnel between localized states within grains or across GBs. This behavior is exacerbated in materials with small grains, high trap densities, or oxygen/vacancy-related defects.54,79,81 Collectively, these studies confirm that hopping conduction is a universal transport regime in disordered or defect-rich polycrystalline semiconductors, emerging whenever band-like or thermionic transport is suppressed by carrier localization. Across systems ranging from Sb2Se3 and CdSe to ZnO, PbTe, and IGZO, a consistent picture emerges: hopping behavior reflects the density and distribution of localized states at or near grain boundaries, which in turn are dictated by the underlying defect chemistry. Oxygen incorporation, vacancy complexes, and dopant under-saturation enhance localization and promote variable-range hopping.54,56,75–82 Microscopy evidence further corroborates that GBs act as preferential sites for hopping pathways, with potential minima forming percolation networks that constrain long-range transport.56,79 Thus, hopping conduction highlights the dual role of grain boundaries—not merely as scattering centers, but as chemically activated networks of localized states. Recognizing this chemical origin underscores that reducing trap density through boundary passivation, oxygen control, or dopant optimization remains central to suppressing hopping and restoring extended-state conduction in polycrystalline semiconductors (Table 1).
| Mechanism | Physical origin | Governing equation/model | Dominant conditions | Representative materials |
|---|---|---|---|---|
| Drift–diffusion4,22–26,28 | Carrier motion under electric field (drift) and concentration gradient (diffusion); GBs add barriers and scattering | 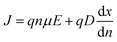 |
E < 103 V cm−1; moderate T (200–400 K); carriers not strongly depleted at GBs | Si, CIGS, TFT |
| Thermionic emission4,27,50,54–57,59,61 | Thermal excitation of carriers over GB potential barriers |  |
High T (>200 K); moderate doping (1014–1016 cm−3). Barrier heights 60–400 meV; reduced after halogen/alkali passivation | CuGaSe2, Sb2Se3, ZnO, CdTe, PbS, NiO, MAPbI3 |
| Thermionic field emission (TFE) & tunneling33,36,56,65,67–70,73 | Mixed thermal activation + tunneling through narrow GB barriers at high doping/field | 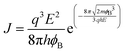 |
High doping (>1017 cm−3) thin barriers (<5 nm); temperature-independent conduction at high doping; tunneling-dominated transport | ZnO:Al, poly-Si, PbSe, NiO, perovskites, WSe2, graphene |
| Hopping conduction54,56,74–82 | Localized carriers hop between defect states at GBs or within grains | 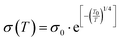 (VRH) (VRH) |
Dominant <150–200 K; Low T (<150 K); high density of localized states; disordered GBs | Sb2Se3, CdSe, ZnSnO3, PbTe, AZO, CdS, CuInSe2, IGZO, NiO |
| Threading crystallites83–85 | Columnar/elongated grains aligned with field; core–shell structures enable anisotropic conduction | Percolative current along oriented crystallites | Highly textured polycrystals; conductive threads | PbSe/CdSe core–shell, sensitized PbSe, 1D PbSe arrays |
3.4 Conduction through threading crystallites
As discussed earlier, long-range charge transport is typically hindered in polycrystalline semiconductors by potential barriers at grain boundaries, localized trap states, and disorder-induced carrier scattering. However, in materials exhibiting columnar or interconnected microcrystalline morphologies, threading crystallites—elongated grains or grain cores aligned preferentially along the field direction—can serve as high-mobility conduction pathways. These microstructures resemble the “shish–kebab” morphology known from polymer crystallization, where a central thread (shish) aligns embedded crystallites (kebabs) directionally. Analogously, in semiconductor thin films, shish–kebab-like pathways offer percolative transport channels that effectively bypass high-resistance grain boundary regions.Such arrangements have also been observed in other systems, including vertically aligned 1D PbSe microcrystals grown via wet chemical methods or MBE, where grain boundaries are absent in the growth direction but present laterally, confirming preferential anisotropy.85
The mechanism aligns with quasi-1D percolation theory and dual-path transport models where carrier mobility is not averaged over a randomly oriented grain network but is instead defined by the presence and continuity of these aligned threads. In CSJ simulations, recombination is minimized due to this structural segregation, yielding enhanced lifetime and detector responsivity that scale with crystallite core continuity and shell integrity.83 Mathematically, the recombination rate reduction in this model is expressed as:
 | (17) |
Lowering n or p due to spatial separation significantly reduces Rtotal, improving effective carrier lifetime τ, and thus signal gain.
 | ||
| Fig. 4 Conceptual and simulated representations of the charge separation and threading crystallite transport model in sensitized polycrystalline PbSe films. (a) Schematic of p-type to n-type inversion of the surface of crystallites induced by oxygen sensitization, forming a core–shell structure. (b) Idealized polycrystalline geometry used in the numerical model, where each sphere represents an individual crystallite and its corresponding grain boundary environment. (a) and (b) are adapted from B. Weng et al., Proc. SPIE, 2013, 8993, 8993–37, with permission from SPIE.85 (c) Pristine core–shell morphology showing spatial separation of electrons and holes across the PbSe/CdSe interface. (d) Optimized structure exhibiting vertically aligned (threaded) PbSe cores, enabling long-range hole transport, injection of new carriers, and recombination suppression by confining minority electrons to the shell. (c) and (d) are adapted from R. M. Mirzaei and Z. Shi, Appl. Phys. Lett., 2024, 125 (8), with the permission of AIP Publishing.84 | ||
Further, the “charge separation” model proposed by Zhao et al. simulates and explains how these threading cores form continuous carrier lanes for majority carriers, enabling transport across multiple grains without cross-type recombination.83 Their numerical simulations showed >40× enhancement in carrier lifetime and >45× increase in responsivity due to this structure. Additionally, microstructural analysis of MBE-grown or chemically grown 1D PbSe arrays confirms that shish–kebab structures form naturally on (100)-oriented facets and exhibit superior photoluminescence and I–V behavior compared to conventional polycrystalline films.85
Taken together, these studies establish that conduction through threading crystallites represents a morphology-driven transport pathway that fundamentally differs from conventional grain-boundary-limited conduction. While demonstrated most clearly in PbSe/CdSe heterostructures, the principle is general: axially aligned grains or core–shell structures create quasi-1D channels that bypass lateral grain boundary barriers and provide spatial separation of electrons and holes.83–85 This dual-lane conduction suppresses recombination and enhances mobility, explaining high responsivity and long carrier lifetimes in sensitized PbSe detectors and related films. Importantly, the formation of these threaded cores is not purely structural but is strongly influenced by chemical treatments such as oxygen or halogen sensitization, which drive inversion layers and core elongation.83,84 Thus, the shish–kebab mechanism highlights a critical interplay between microstructural anisotropy and grain boundary chemistry, underscoring that device performance can be optimized not only by reducing defect density but also by programming grain connectivity and orientation. This morphology-based conduction model broadens the design space for polycrystalline semiconductors, offering a scalable alternative to single-crystal growth for optoelectronic and detector applications.83–85
4 Factors affecting carrier transport
Carrier transport in polycrystalline semiconductors is intricately influenced by both structural and electrical heterogeneities. In contrast to single crystals, the presence of grain boundaries (GBs), microstructural defects, and spatially non-uniform dopant distributions introduces localized variations in electrostatic potential, scattering rates, and recombination dynamics. This section systematically explores the major physical, structural, and material-dependent factors that modulate charge carrier conduction in polycrystalline films.4.1 Microstructural features
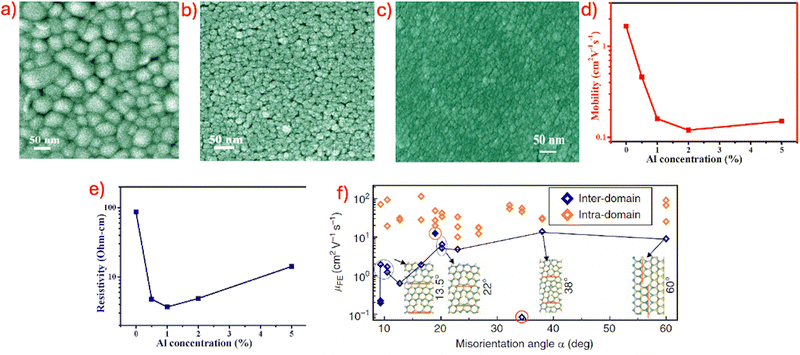 | ||
| Fig. 5 Impact of grain boundary structure and doping on carrier transport in polycrystalline semiconductors. (a)–(c) FESEM images showing grain size refinement in ZnO with increasing Al doping from 0% to 5%, resulting in denser grain boundaries. (d)–(e) Hall effect measurements reveal a monotonic decrease in mobility and an increase in resistivity with increasing Al content, attributed to enhanced grain boundary scattering. (f) Mobility variation as a function of misorientation angle α, indicating increased barrier-limited transport across high-angle grain boundaries (α > 20°), where mobility saturates below 16 cm2 V−1 s−1. Adapted (a)–(e) from B. Mahapatra and S. Sarkar, Heliyon, 2022, 8 (10), e10961, with permission from Elsevier,79 and Adapted (f) from T. H. Ly, D. J. Perello, J. Zhao, et al., Nat. Commun., 2016, 7, 10426. Licensed under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).93 | ||
The relationship between grain size and mobility is often captured through thermionic emission models, where mobility µ follows an Arrhenius-type dependence on temperature and barrier height ΦB. Larger grains reduce the number of GBs encountered per unit length, effectively minimizing the impact of such barriers on carrier transport. These findings underscore that grain size is not merely a structural parameter but a key determinant of trap density and electrostatic barrier distribution, where chemical dopants and processing conditions jointly govern the balance between refinement-induced scattering and enhanced carrier collection.10,79
High crystallinity is also essential for minimizing intra-grain scattering.95 Polycrystalline films synthesized via low-temperature methods (e.g., sol–gel or spin coating) often suffer from nanocrystallinity and poor lattice ordering, resulting in higher scattering and defect densities.96,97 Conversely, high-temperature vapor deposition methods yield larger and more ordered grains, which enhance carrier mobility.97 Thus, grain orientation and crystallinity dictate whether GBs behave as high-barrier interfaces or quasi-one-dimensional conduction pathways, emphasizing that chemical control of growth kinetics and thermal treatments is as critical as structural alignment for optimizing transport.88,95–97
Twin boundaries are a unique class of planar defects characterized by a mirror symmetry. They typically introduce minimal disruption to the lattice potential and are often electrically benign or even beneficial. In CdTe and Sb2Se3, twin boundaries have been shown to act as low-resistance pathways for carrier flow. TEM studies have confirmed that twin boundaries do not introduce significant mid-gap states, in contrast to general high-angle GBs.21,99 Taken together, these observations highlight that GB type governs carrier transport far beyond geometry, with high-angle GBs acting as recombination-active traps, while coherent twin boundaries remain chemically and electronically benign, offering low-resistance channels for transport.21,93,98,99
4.2 Electrical effects at the grain boundaries
In NiO thin films, KPFM measurements have demonstrated that GBs exhibit significant potential variations compared to grain interiors. These variations are linked to differences in work function and electronic conductivity, suggesting that GBs in NiO can act as barriers to charge transport.56 Consequently, GB band bending emerges as a chemically tunable parameter: defect passivation, doping, or compositional engineering can reshape depletion profiles and barrier heights, turning recombination-active boundaries into quasi-transparent interfaces.4,56
In CdTe thin-film solar cells, chlorine (Cl) incorporation through post-deposition CdCl2 treatment leads to the preferential segregation of Cl atoms at grain boundaries (GBs), where they play a crucial role in modifying the local defect chemistry. Using advanced characterization techniques such as scanning transmission electron microscopy (STEM), energy-dispersive X-ray spectroscopy (EDX), and nanoscale secondary ion mass spectrometry (NanoSIMS), researchers have directly observed elevated Cl concentrations at GBs compared to grain interiors. This segregation alters the electronic environment of GBs, either passivating or modifying deep-level trap states that typically act as non-radiative recombination centers. While Cl can effectively passivate some defect sites, excessive or uneven Cl accumulation may lead to the formation of complex defect clusters that introduce new trap states. These defect-mediated recombination pathways can limit the collection of photogenerated carriers before they reach the junction, thereby reducing device efficiency. Experimental findings are supported by density functional theory (DFT) simulations, which show that Cl atoms can replace Te atoms or occupy interstitial sites at GBs, leading to a reduction in deep mid-gap states and suppression of Fermi level pinning.101,102
Overall, the impact of GB traps demonstrates that recombination is governed less by structural disorder alone and more by the local defect chemistry, where targeted passivation (e.g., Cl incorporation) can transform deep recombination centers into electronically benign sites.94,100–102
4.3 Material specific factors
In SnO2:F films, conductivity initially increases with fluorine doping as carrier concentration increases. However, Hall measurements show that beyond ∼1.2 × 1020 cm−3, mobility peaks (∼42 cm2 V−1 s−1) and then declines due to enhanced ionized impurity scattering.103 These studies confirm that doping serves as a double-edged lever: while moderate levels shrink depletion widths and enhance transport, excessive doping induces Coulombic scattering, making compensation control and chemical homogeneity essential for mobility optimization.4,36,103
Collectively, these results show that passivation is not a one-size-fits-all remedy but a chemically specific intervention, where alkali fluorides, halides, hydrogen, or organic modifiers each alter trap energetics in distinct ways, reinforcing GB chemistry as the decisive factor in suppressing recombination and enhancing transport (Fig. 6(c–d)).6,48,86,87,104,105
 | ||
| Fig. 6 The influence of grain size, trap states, and passivation strategies on carrier transport in polycrystalline semiconductors. (a) and (b) Fluorescence lifetime imaging microscopy (FLIM) analysis of ∼300 perovskite grains reveal that smaller grains exhibit shorter photoluminescence (PL) lifetimes and reduced intensity, indicating increased trap-assisted non-radiative recombination at GBs. (a) and (b) are adapted from Mengjin Yang et al., Phys. Chem. Chem. Phys., 2017, 19, 5043–5050, with permission from the Royal Society of Chemistry.94 (c) Schematic illustration of how electron-rich molecular passivators mitigate defect states (e.g., halide vacancies) and suppress trap-assisted recombination by stabilizing interfacial electron clouds at the perovskite grain surfaces. Adapted from Qihuang Gong et al., Adv. Mater., 2020, 32 (39), 2005506. Licensed under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).48 (d) Post-deposition treatment (PDT) in CIGSe films enables passivating recombination-active sites and enhancing charge collection. Adapted from Nicoleta Nicoara, X. Fu, T. P. Weiss, et al., Nat. Commun., 2019, 10, 3980. Licensed under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).6 (e) Schematic illustration showing the difference in interfacial potential barriers (Eb) at a conventional grain boundary and at a metal–semiconductor interface in n-type Mg3(Sb,Bi)2. The metal inclusion reduces the barrier height and promotes carrier transmission across the interface. Adapted from Li et al., Nat. Commun., 2023, 14, 7428. Licensed under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).17 | ||
In contrast, solution-processed methods like the sol–gel technique often yield films with nanoscale grain sizes, higher porosity, and less uniform microstructure. These characteristics contribute to increased grain boundary scattering, higher trap densities, and reduced electrical conductivity. For example, sol–gel derived ZnO thin films have shown smaller grain sizes and poorer crystallinity at lower annealing temperatures, which corresponded to inferior electrical characteristics. However, controlled post-annealing at elevated temperatures can partially mitigate these issues by promoting grain coalescence and improving film densification.107
The difference in electrical performance between sol–gel and PLD-grown films is evident in studies on ZnSnO3 thin films. While direct studies on ZnSnO3 by Islam et al. could not be verified, similar investigations by Cai et al. demonstrated that Ta-doped ZnSnO3 films fabricated via sol–gel methods exhibited limited conductivity and mobility, largely attributed to the presence of voids and microstructural inhomogeneity. These films often require high-temperature processing (>500 °C) to achieve crystallization and improved transport properties.108
Together, these findings highlight the importance of selecting and optimizing the film deposition technique for applications in photovoltaics, thermoelectrics, and sensors. By engineering the grain structure and minimizing defect-mediated transport barriers, significant improvements in carrier transport can be achieved.
5 Design guidelines and outlook
5.1 Design guidelines for optimizing carrier transport
Optimizing charge transport in polycrystalline semiconductors necessitates precise control over grain boundary (GB) structures, chemical compositions, and electronic properties. As GB-mediated mechanisms, such as thermionic emission, often dominate transport behavior, the following strategies are pivotal in mitigating transport barriers and enhancing carrier mobility.In summary, optimizing charge transport in polycrystalline semiconductors requires coupling grain boundary chemistry with microstructural control. Passivation treatments, such as Cl in CdTe and perovskites,101,102 or alkali fluorides in CIGSe,6 neutralize traps and reduce recombination. Controlled doping narrows depletion widths without inducing excessive scattering, consistent with Seto's barrier model.4,109 Orientation control in Cu2O and ZnO,89,90 and benign twin boundaries in perovskites,5 and Bi2Te3,110 provide low-resistance pathways. Moreover, low-defect growth methods such as CVD or laser crystallization further enhance mobility.111,112 Finally, recent advances in n-type Mg3(Sb,Bi)2 further illustrate the principle, where grain-boundary metallization and anti-barrier interface engineering have effectively eliminated resistive barriers and yielded record thermoelectric performance.17,91 Collectively, these strategies highlight that transport is dictated less by grain size alone than by the chemical and structural state of GBs, which can be deliberately engineered for high-performance photovoltaic, thermoelectric, and optoelectronic devices (Table 2).
| Strategy | Description | Impact on carrier transport | Representative materials |
|---|---|---|---|
| Chemical passivation (Cl, Cu, alkali metals, H)6,59,61,86,87 | Incorporation of passivating agents (e.g., Cl, Cu, H) at GBs to neutralize/compensate trap states via bond formation/charge reduction | Reduces recombination, lowers barrier height, enhances mobility and lifetime | CdTe, CIGS, Si |
| GB potential barrier tuning (dopant/trap control)4,50,57 | Modulate GB electrostatics by adjusting dopant density and filled trap density | Tailors barrier height and band bending; balances conductivity vs. recombination | Perovskites |
| Grain orientation control/texturing88–90 | Promote highly oriented/columnar grains to reduce effective GB density and align internal fields. | Enhances carrier collection along preferred paths (GB-enhanced EBIC after CdCl2). | Sb2Se3, Cu2O, ZnO:Al |
| GB passivation by oxidation/secondary phase segregation6,55,84 | Controlled O2/air or halogen (Cl/I) treatments modify GB chemistry and band alignment. | Suppresses active traps, may form conductive channels | PbS/PbSe |
| Ion migration suppression57,58 | Engineer GBs (dopants/additives, passivation) to limit halide/ion transport pathways. | Enhances stability, reduces hysteresis, preserves carrier lifetimes by limiting bias-induced contact potential difference (CPD) changes at GBs. | Halide perovskites |
| Nanocrystallite/GB size optimization27,54 | Controlling grain size via annealing or deposition conditions | Balances scattering vs. barrier effects; larger grains reduce GB density | Sb2Se3, CuGaSe2 |
| Grain-boundary metallization and anti-barrier interface engineering17,91 | Introduction of metallic inclusions (Nb, Ta) and low-work-function interlayers (W, Mo) at GBs to form metal–semiconductor interfaces that reduce or invert potential barriers. | Enhances carrier mobility and electrical conductivity without degrading Seebeck coefficient | n-type Mg3(Sb,Bi)2 |
5.2 Outlook for polycrystalline semiconductors
The continued advancement of polycrystalline semiconductors in optoelectronics, thermoelectrics, and sensors hinges on the ability to design grain architectures and control local transport mechanisms. Future progress will require close integration of materials chemistry, device physics, and data-driven design strategies.Taken together, these developments underscore that future innovation will depend on treating grain boundaries not as static defects but as programmable, chemically tunable features of polycrystalline semiconductors. By integrating advanced imaging, statistical modeling, boundary engineering, and sustainable processing, the field is positioned to achieve grain architectures with optimized carrier transport. This vision sets the stage for polycrystalline semiconductors to play a central role in next-generation optoelectronic, photovoltaic, and thermoelectric technologies.
6. Conclusions
This review establishes a unified framework connecting microscopic carrier transport theory with macroscopic electrical behavior in polycrystalline semiconductors. By integrating drift–diffusion, thermionic emission, tunneling, hopping, and shish–kebab conduction models with nanoscale experimental evidence, it clarifies how grain-boundary barriers, defect states, and crystallographic orientation collectively dictate charge mobility and recombination. The analysis demonstrates that grain boundaries are not merely performance-limiting defects but tunable electronic interfaces whose chemistry and structure can be engineered for enhanced functionality. Comparative insights from chalcogenide, oxide, and perovskite systems reveal that boundary passivation, dopant redistribution, and twin-boundary control can suppress non-radiative losses while promoting selective transport. Such findings underscore the transformative potential of grain-boundary engineering as a design strategy rather than a corrective process. Future advances will depend on coupling in situ and operando characterization with multiscale modeling to capture carrier dynamics under real device operation. Integrating data-driven approaches with atomic-level imaging could enable predictive design of grain architectures with programmable transport characteristics. By reframing grain boundaries as functional building blocks, this work outlines a roadmap toward high-mobility, high-stability polycrystalline semiconductors for next-generation optoelectronic, thermoelectric, and sensing technologies.Author contributions
Israt Jahan: conceptualization, methodology, visualization, investigation, writing – original draft, writing – review and editing; Jesus Dustin Arellano: resources, writing- review, and editing; Zhisheng Shi: conceptualization, methodology, resources, supervision, writing – review and editing.Conflicts of interest
The authors declare that they have no conflict of interest.Data availability
This article is a review, and no new data were generated or analysed as part of this review. All data discussed are available in the cited literature.Acknowledgements
This work is partially supported by the United States Air Force Lab under contract no. FA2377-25-P-B008 through True Colors Infrared Imaging Inc. and AFRL DAGSI program under contract number RY4-UO-25-2-AFRL3.Notes and references
- H. F. Matare, J. Appl. Phys., 1984, 56, 2605–2631 CrossRef CAS.
- A. Kelly and K. M. Knowles, Crystallography and crystal defects, John Wiley & Sons, 2020 Search PubMed.
- K. Schulgasser, J. Appl. Phys., 1976, 47, 1880–1886 CrossRef CAS.
- J. Y. W. Seto, J. Appl. Phys., 1975, 46, 5247–5254 CrossRef CAS.
- X. Xiao, W. H. Li, Y. J. Fang, Y. Liu, Y. C. Shao, S. Yang, J. J. Zhao, X. Z. Dai, R. Zia and J. S. Huang, Nat. Commun., 2020, 11, 2215 CrossRef CAS PubMed.
- N. Nicoara, R. Manaligod, P. Jackson, D. Hariskos, W. Witte, G. Sozzi, R. Menozzi and S. Sadewasser, Nat. Commun., 2019, 10, 3980 CrossRef PubMed.
- N. J. Jeon, H. Na, E. H. Jung, T. Y. Yang, Y. G. Lee, G. Kim, H. W. Shin, S. I. Seok, J. Lee and J. Seo, Nat. Energy, 2018, 3, 682–689 CrossRef CAS.
- M. Jeong, I. W. Choi, E. M. Go, Y. Cho, M. Kim, B. Lee, S. Jeong, Y. Jo, H. W. Choi, J. Lee, J. H. Bae, S. K. Kwak, D. S. Kim and C. Yang, Science, 2020, 369, 1615–1620 CrossRef CAS PubMed.
- F. Schindler, A. Fell, R. Müller, J. Benick, A. Richter, F. Feldmann, P. Krenckel, S. Riepe, M. C. Schubert and S. W. Glunz, Sol. Energy Mater. Sol. Cells, 2018, 185, 198–204 CrossRef CAS.
- M. A. Scarpulla, B. McCandless, A. B. Phillips, Y. F. Yan, M. J. Heben, C. Wolden, G. Xiong, W. K. Metzger, D. Mao, D. Krasikov, I. Sankin, S. Grover, A. Munshi, W. Sampath, J. R. Sites, A. Bothwell, D. Albin, M. O. Reese, A. Romeo, M. Nardone, R. Klie, J. M. Walls, T. Fiducia, A. Abbas and S. M. Hayes, Sol. Energy Mater. Sol. Cells, 2023, 255, 112289 CrossRef CAS.
- J. Keller, K. Kiselman, O. Donzel-Gargand, N. M. Martin, M. Babucci, O. Lundberg, E. Wallin, L. Stolt and M. Edoff, Nat. Energy, 2024, 9, 467–478 CrossRef CAS.
- S. Ganguly, M. H. Jang, Y. H. Tan, S. S. Yoo, M. C. Gupta and A. W. Ghosh, J. Appl. Phys., 2019, 126, 143103 CrossRef.
- M. S. Mahdi, K. Ibrahim, A. Hmood, N. M. Ahmed, S. A. Azzez and F. I. Mustafa, RSC Adv., 2016, 6, 114980 RSC.
- Q. Lv, R. Li, L. Fan, Z. Huang, Z. Huan, M. Yu, H. Li, G. Liu, G. Qiao and J. Liu, Sensors, 2023, 23, 8413 CrossRef CAS PubMed.
- S. Chen, H.-B. Li, Y. Fu, G.-Q. Liu, M. Ishaq, J. Luo, J.-M. Li, B. Che, J.-T. Luo, L. Ding, T. Chen and G.-X. Liang, Nano Res., 2025, 18, 94907159 CrossRef.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- J. W. Li, Z. J. Han, J. C. Yu, H. L. Zhuang, H. H. Hu, B. Su, H. Z. Li, Y. L. Jiang, L. Chen, W. S. Liu, Q. Zheng and J. F. Li, Nat. Commun., 2023, 14, 7428 CrossRef PubMed.
- N. Yamazoe and K. Shimanoe, Sens. Actuators, B, 2008, 128, 566–573 CrossRef CAS.
- S. Lee, Y. J. Cho, B. Han, J. Lee, S. Choi, T. Kang, H. Y. Chu, J. Kwag, S. C. Kim and J. Jang, Adv. Eng. Mater., 2022, 24, 2100910 CrossRef CAS.
- H. P. Komsa and A. V. Krasheninnikov, Adv. Electron. Mater., 2017, 3, 1600468 CrossRef.
- H. Li, X. X. Liu, Y. S. Lin, B. Yang and Z. M. Du, Phys. Chem. Chem. Phys., 2015, 17, 11150–11155 RSC.
- S. M. Sze and K. K. Ng, Physics of Semiconductor Devices, Wiley, New York, NY, USA, 3 edn, 2006 Search PubMed.
- D. M. Kim, A. N. Khondker, S. S. Ahmed and R. R. Shah, IEEE Trans. Electron Devices, 1984, 31, 480–493 Search PubMed.
- J. C. M. Hwang, P. S. Ho, J. E. Lewis and D. R. Campbell, J. Appl. Phys., 1980, 51, 1576–1581 CrossRef CAS.
- C. H. Ling, Solid State Electrochem., 1984, 27, 633–638 CrossRef CAS.
- M. Santonen, A. Lahti, Z. J. Rad, M. Miettinen, M. Ebrahimzadeh, J. P. Lehtiö, E. Snellman, P. Laukkanen, M. Punkkinen, K. Kokko, K. Parkkinen and M. Eklund, IEEE Trans. Electron Devices, 2025, 72, 1184–1190 CAS.
- S. Schuler, S. Nishiwaki, J. Beckmann, N. Papathanasiou, S. Brehme, S. Siebentritt and M. Lux-Steiner, Charge carrier transport in polycrystalline CuGaSe2 thin films, 2002 Search PubMed.
- Y. Watanabe, Annu. Rev. Mater. Sci., 1985, 15, 71–98 Search PubMed.
- S. Husein, M. Stuckelberger, B. West, L. Ding, F. Dauzou, M. Morales-Masis, M. Duchamp, Z. Holman and M. I. Bertoni, J. Appl. Phys., 2018, 123, 245102 CrossRef.
- J. U. Rahman, N. V. Du, W. H. Nam, W. H. Shin, K. H. Lee, W.-S. Seo, M. H. Kim and S. Lee, Sci. Rep., 2019, 9, 8624 CrossRef PubMed.
- Q. Hao and J. Garg, ES Mater. Manuf., 2021, 14, 36–50 Search PubMed.
- S. Wang, S. Hui, K. L. Peng, T. P. Bailey, X. Y. Zhou, X. F. Tang and C. Uher, J. Mater. Chem. C, 2017, 5, 10191–10200 RSC.
- S. Park, M. A. Shehzad, M. F. Khan, G. Nazir, J. Eom, H. Noh and Y. Seo, Carbon, 2017, 112, 142–148 CrossRef CAS.
- S. E. Krasavin and V. A. Osipov, Sci. Rep., 2022, 12, 14553 CrossRef CAS PubMed.
- E. Zuñiga-Puelles, A. Özden, R. Cardoso-Gil, C. Hennig, C. Himcinschi, J. Kortus and R. Gumeniuk, J. Mater. Chem. A, 2025, 13, 9357–9371 RSC.
- N. Sommer, J. Hüpkes and U. Rau, Phys. Rev. Appl., 2016, 5, 024009 CrossRef.
- D. C. Hamilton, E. Arca, J. Pan, S. Siol, M. Young, S. Lany and A. Zakutayev, J. Appl. Phys., 2019, 126, 035701 CrossRef.
- A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Nat. Commun., 2021, 12, 2222 CrossRef CAS PubMed.
- J. Shuai, J. Mao, S. W. Song, Q. Zhu, J. F. Sun, Y. M. Wang, R. He, J. W. Zhou, G. Chen, D. J. Singh and Z. F. Ren, Energy Environ. Sci., 2017, 10, 799–807 RSC.
- Y. P. Wang, S. G. Sun, Y. A. Huang, Y. Fu, J. N. Qi, K. Tie, Z. W. Wang, F. Jiao, R. M. Si, X. S. Chen, L. Q. Li and W. P. Hu, Aggregate, 2023, 4, e379 CrossRef CAS.
- J. Quirk, M. Rothmann, W. Li, D. Abou-Ras and K. P. McKenna, Appl. Phys. Rev., 2024, 11, 011308 CAS.
- T. Katase, S. Nomoto, X. He, S. Kitani, T. Honda, H. Hiramatsu, H. Hosono and T. Kamiya, ACS Appl. Electron. Mater., 2024, 6, 7424–7429 CrossRef CAS.
- B. Gaury and P. M. Haney, Phys. Rev. Appl., 2017, 8, 054026 CrossRef PubMed.
- A. Cuevas and D. Macdonald, Sol. Energy, 2004, 76, 255–262 CrossRef CAS.
- W. K. Metzger, I. L. Repins, M. Romero, P. Dippo, M. Contreras, R. Noufi and D. Levi, Thin Solid Films, 2009, 517, 2360–2364 CrossRef CAS.
- J. Wong, J. L. Huang, S. Varlamov, M. A. Green and M. Keevers, Prog. Photovoltaics, 2012, 20, 915–922 CAS.
- T. Fuyuki, H. Kondo, T. Yamazaki, Y. Takahashi and Y. Uraoka, Appl. Phys. Lett., 2005, 86, 262108 CrossRef.
- X. Yang, Y. Fu, R. Su, Y. Zheng, Y. Zhang, W. Yang, M. Yu, P. Chen, Y. Wang, J. Wu, D. Luo, Y. Tu, L. Zhao, Q. Gong and R. Zhu, Adv. Mater., 2020, 32, 2002585 CrossRef CAS PubMed.
- Z. Gao, C. Leng, H. Zhao, X. Wei, H. Shi and Z. Xiao, Adv. Mater., 2023, 36, 2304855 CrossRef PubMed.
- Y. Kajikawa, J. Appl. Phys., 2013, 114, 043719 CrossRef.
- N. C. Lu, L. Gerzberg, C. Y. Lu and J. D. Meindl, IEEE Trans. Electron Devices, 1983, 30, 137–149 Search PubMed.
- E. L. Murphy and R. H. Good, Phys. Rev., 1956, 102, 1464–1473 CrossRef CAS.
- D. K. Schroder, Semiconductor Material and Device Characterization, Wiley, 3rd edn, 2006 Search PubMed.
- N. Cifuentes, S. Ghosh, A. Shongolova, M. R. Correia, P. M. P. Salomé, P. A. Fernandes, S. Ranjbar, S. Garud, B. Vermang, G. M. Ribeiro and J. C. González, J. Phys. Chem. C, 2020, 124, 7677–7682 CrossRef CAS.
- J. C. Slater, Phys. Rev., 1956, 103, 1631–1644 CrossRef CAS.
- Y. D. Zhang, J. X. Zuo, P. J. Li, Y. H. Gao, W. W. He and Z. Zheng, Physica E, 2019, 111, 75–78 CrossRef CAS.
- B. Bahrami, S. Mabrouk, N. Adhikari, H. Elbohy, A. Gurung, K. M. Reza, R. Pathak, A. H. Chowdhury, G. Saianand, W. J. Yue, J. T. Zai, X. F. Qian, M. Liang and Q. Q. Qiao, InfoMat, 2020, 2, 409–423 CrossRef CAS.
- J. S. Yun, J. Seidel, J. Kim, A. M. Soufiani, S. J. Huang, J. Lau, N. J. Jeon, S. I. Seok, M. A. Green and A. Ho-Baillie, Adv. Energy Mater., 2016, 6, 1600330 CrossRef.
- C. Li, Y. L. Wu, J. Poplawsky, T. J. Pennycook, N. Paudel, W. J. Yin, S. J. Haigh, M. P. Oxley, A. R. Lupini, M. Al-Jassim, S. J. Pennycook and Y. F. Yan, Phys. Rev. Lett., 2014, 112, 156103 CrossRef PubMed.
- P. R. Edwards, S. A. Galloway and K. Durose, Thin Solid Films, 2000, 372, 284–291 CrossRef CAS.
- L. X. Zhang, J. L. F. Da Silva, J. B. Li, Y. F. Yan, T. A. Gessert and S. H. Wei, Phys. Rev. Lett., 2008, 101, 155501 CrossRef PubMed.
- X. J. Ma, F. Zhang, Z. D. Chu, J. Hao, X. H. Chen, J. M. Quan, Z. Y. Huang, X. M. Wang, X. Q. Li, Y. F. Yan, K. Zhu and K. J. Lai, Nat. Commun., 2021, 12, 5009 CrossRef CAS PubMed.
- J. J. Kuo, S. D. Kang, K. Imasato, H. Tamaki, S. Ohno, T. Kanno and G. J. Snyder, Energy Environ. Sci., 2018, 11, 429–434 RSC.
- R. G. Forbes, R. Soc. Open Sci., 2019, 6, 190912 CrossRef PubMed.
- D. Z. Chen, R. Jacobs, J. Petillo, V. Vlahos, K. L. Jensen, D. Morgan and J. Booske, Phys. Rev. Appl., 2022, 18, 054010 CrossRef CAS.
- S. K. Kolekar, R. V. Godbole, V. P. Godbole and C. V. Dharmadhikari, AIP Adv., 2020, 10, 045129 CrossRef CAS.
- W. Li, K. Nomoto, D. Jena and H. G. Xing, Appl. Phys. Lett., 2020, 117, 222104 CrossRef CAS.
- C. B. Lin, J. D. Chen and Y. Y. Fu, Appl. Phys. Lett., 2024, 124, 074103 CrossRef CAS.
- V. H. Nguyen, U. Gottlieb, A. Valla, D. Muñoz, D. Bellet and D. Muñoz-Rojas, Mater. Horiz., 2018, 5, 715–726 RSC.
- K. Sharma and D. P. Joshi, J. Appl. Phys., 2009, 106, 024504 CrossRef.
- Z. Dashevsky, V. Kasiyan, G. Radovsky, E. Shufer and M. Auslender, Proc. SPIE, 2008, 7142 DOI:10.1117/12.815199.
- F. P. Garcia de Arquer, X. Gong, R. P. Sabatini, M. Liu, G. H. Kim, B. R. Sutherland, O. Voznyy, J. Xu, Y. Pang, S. Hoogland, D. Sinton and E. Sargent, Nat. Commun., 2017, 8, 14757 CrossRef CAS PubMed.
- W. Su, N. Kumar, H. Shu, O. Lancry and M. Chaigneau, J. Phys. Chem. C, 2021, 125, 26883–26891 CrossRef CAS.
- N. F. Mott, J. Non-Cryst. Solids, 1968, 1, 1–17 CrossRef CAS.
- B. I. Shklovskii and A. L. Efros, Electronic Properties of Doped Semiconductors, Springer, Berlin, Heidelberg, 1984 Search PubMed.
- D. Yu, C. J. Wang, B. L. Wehrenberg and P. Guyot-Sionnest, Phys. Rev. Lett., 2004, 92, 216802 CrossRef PubMed.
- C. C. Hsu, C. H. Chou, W. C. Jhang and P. T. Chen, Physica B, 2019, 569, 80–86 CrossRef CAS.
- A. A. Dobrovolsky, Z. M. Dashevsky, V. A. Kasiyan, L. I. Ryabova and D. R. Khokhlov, Semicond. Sci. Technol., 2009, 24, 075010 CrossRef.
- B. Mahapatra and S. Sarkar, Heliyon, 2022, 8, e10961 CrossRef CAS PubMed.
- R. Rahman and J. A. Scales, Appl. Phys. Lett., 2016, 109, 092103 CrossRef.
- C. Guillen and J. Herrero, J. Appl. Phys., 1992, 71, 5479–5484 CrossRef CAS.
- J. J. Wang, J. S. Bi, G. B. Xu and M. X. Liu, Electronics, 2024, 13, 1427 CrossRef CAS.
- L. H. Zhao, J. J. Qiu, B. B. Weng, C. Chang, Z. J. Yuan and Z. S. Shi, J. Appl. Phys., 2014, 115, 084502 CrossRef.
- M. Rastkar Mirzaei and Z. Shi, Appl. Phys. Lett., 2024, 125, 083501 CrossRef CAS.
- B. Weng, J. Qiu, L. Zhao, Z. Yuan, C. Chang and Z. Shi, SPIE Proc., 2013, 8993, 899311 CrossRef.
- G. Hahn, M. Käs and B. Herzog, Solid State Phenom., 2010, 156–158, 343–349 CAS.
- N. H. Nickel, Solid State Phenom., 2010, 156–158, 351–356 CAS.
- X. X. Wen, Z. H. Lu, X. K. Yang, C. Chen, M. A. Washington, G. C. Wang, J. Tang, Q. Zhao and T. M. Lu, ACS Appl. Mater. Interfaces, 2023, 15, 22251–22262 CrossRef CAS PubMed.
- S. Han and A. J. Flewitt, Thin Solid Films, 2020, 704, 138000 CrossRef CAS.
- M. Birkholz, B. Selle, F. Fenske and W. Fuhs, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 205414 CrossRef.
- X. Y. Li, Y. S. Du, K. Y. Yang, S. K. Li, J. Y. Zhang, L. Li, J. J. Xing, G. H. Rao, J. T. Zhao and K. Guo, Adv. Funct. Mater., 2025, e12586 CrossRef.
- C. Hu, K. Xia, C. Fu, X. Zhao and T. Zhu, Energy Environ. Sci., 2022, 15, 1406–1422 RSC.
- T. H. Ly, D. J. Perello, J. Zhao, Q. M. Deng, H. Kim, G. H. Han, S. H. Chae, H. Y. Jeong and Y. H. Lee, Nat. Commun., 2016, 7, 10426 CrossRef CAS PubMed.
- M. Yang, Y. Zeng, Z. Li, D. H. Kim, C.-S. Jiang, J. van de Lagemaat and K. Zhu, Phys. Chem. Chem. Phys., 2017, 19, 5043–5050 RSC.
- M. S. Hammer, D. Rauh, V. Lorrmann, C. Deibel and V. Dyakonov, Nanotechnology, 2008, 19, 485701 CrossRef PubMed.
- J. Sengupta, R. K. Sahoo and C. D. Mukherjee, Mater. Lett., 2012, 83, 84–87 CrossRef CAS.
- S. F. Varol, D. Sahin, M. Kompitsas and G. Çankaya, RSC Adv., 2014, 4, 13593–13600 RSC.
- H. Bishara, S. Lee, T. Brink, M. Ghidelli and G. Dehm, ACS Nano, 2021, 15, 16607–16615 CrossRef CAS PubMed.
- R. E. Williams, Q. M. Ramasse, K. P. McKenna, L. J. Phillips, P. J. Yates, O. S. Hutter, K. Durose, J. D. Major and B. G. Mendis, ACS Appl. Mater. Interfaces, 2020, 12, 21730–21738 CrossRef CAS PubMed.
- A. Broniatowski, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 5895–5905 CrossRef CAS PubMed.
- M. J. Watts, P. Hatton, R. Smith, T. Fiducia, A. Abbas, R. Greenhalgh, J. M. Walls and P. Goddard, Phys. Rev. Mater., 2021, 5, 035403 CrossRef CAS.
- J. Moseley, M. M. Al-Jassim, H. L. Guthrey, J. M. Burst, J. N. Duenow, R. K. Ahrenkiel and W. K. Metzger, J. Appl. Phys., 2016, 120, 105704 CrossRef.
- W. Zheng, Y. N. Zhang and J. Q. Tian, Chalcogenide Lett., 2017, 14, 275–281 CAS.
- W. S. Cai, Z. G. Zang and L. M. Ding, J. Semicond., 2021, 42, 030203 CrossRef CAS.
- P. Xiao, L. F. Lan, T. Dong, Z. G. Lin, W. Shi, R. H. Yao, X. H. Zhu and J. B. Peng, Appl. Phys. Lett., 2014, 104, 051607 CrossRef.
- S. Wang, V. Mirkhani, K. Yapabandara, R. Cheng, G. Hernandez, M. P. Khanal, M. S. Sultan, S. Uprety, L. Shen, S. Zou, P. Xu, C. D. Ellis, J. A. Sellers, M. C. Hamilton, G. Niu, M. H. Sk and M. Park, J. Appl. Phys., 2018, 123, 161503 CrossRef.
- J. S. Huang and C. F. Lin, J. Appl. Phys., 2008, 103, 014304 CrossRef.
- S. Q. Cai, Y. M. Li, X. Chen, Y. Y. Ma, X. J. Liu and Y. Q. He, J. Mater. Sci.: Mater. Electron., 2016, 27, 6166–6174 CrossRef CAS.
- I. T. Lu, J. J. Zhou, J. Park and M. Bernardi, Phys. Rev. Mater., 2022, 6, L010801 CrossRef CAS.
- K. C. Kim, J. Lee, B. K. Kim, W. Y. Choi, H. J. Chang, S. O. Won, B. Kwon, S. K. Kim, D. B. Hyun, H. J. Kim, H. C. Koo, J. H. Choi, D. I. Kim, J. S. Kim and S. H. Baek, Nat. Commun., 2016, 7, 12449 CrossRef CAS PubMed.
- P. Barathieu, B. Caussat, E. Scheid, D. Jaume and J. P. Couderc, J. Electrochem. Soc., 2001, 148, C149–C155 CrossRef CAS.
- Y. Do, D. Y. Jeong, S. Lee, S. Kang, S. Jang and J. Jang, Adv. Eng. Mater., 2020, 22, 1901430 CrossRef CAS.
- Y. T. Liu, J. H. Yang, B. J. Lawrie, K. P. Kelley, M. Ziatdinov, S. V. Kalinin and M. Ahmadi, ACS Nano, 2023, 17, 9647–9657 CrossRef CAS PubMed.
- Z. R. He, S. Bi and K. Asare-Yeboah, Coatings, 2025, 15, 164 CrossRef CAS.
- L. Cademartiri and K. J. M. Bishop, Nat. Mater., 2015, 14, 2–9 CrossRef CAS PubMed.
- M. I. Saidaminov, O. F. Mohammed and O. M. Bakr, ACS Energy Lett., 2017, 2, 889–896 CrossRef CAS.
- Y. F. Miao, M. Ren, Y. T. Chen, H. F. Wang, H. R. Chen, X. M. Liu, T. F. Wang and Y. X. Zhao, Nat. Sustain., 2023, 6, 1465–1473 CrossRef.
| This journal is © The Royal Society of Chemistry 2025 |



