 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Milliwatt three- and four-pulse double electron electron resonance for protein structure determination†
Markus
Teucher‡
 *,
Jason W.
Sidabras‡§
*,
Jason W.
Sidabras‡§
 * and
Alexander
Schnegg
*
* and
Alexander
Schnegg
*
EPR Research Group, Max Planck Institute for Chemical Energy Conversion, Stift-straße 34-36, Mülheim an der Ruhr, 45470, Germany. E-mail: markus.teucher@cec.mpg.de; jwsidabras@mcw.edu; alexander.schnegg@cec.mpg.de
First published on 9th May 2022
Abstract
Electron paramagnetic resonance (EPR) experiments for protein structure determination using double electron–electron resonance (DEER) spectroscopy rely on high-power microwave amplifiers (>300 W) to create the short pulse lengths needed to excite a sizable portion of the spectrum. The recently introduced self-resonant microhelix combines a high B1 conversion efficiency with an intrinsically large bandwidth (low Q-value) and a high absolute sensitivity. We report dead times in 3-pulse DEER experiments as low as 14 ± 2 ns achieved using less than 1 W of power at X-band (nominally 9.5 GHz) for experiments on a molecular ruler and a T4 lysozyme sample for concentrations down to 100 μM. These low-power experiments were performed using an active volume 120 times smaller than that of a standard pulse EPR resonator, while only a 11-fold decrease in the signal-to-noise ratio was observed. Small build sizes, as realized with the microhelix, give access to volume-limited samples, while shorter dead times allow the investigation of fast relaxing spin species. With the significantly reduced dead times, the 3-pulse DEER experiment can be revisited. Here, we show experimentally that 3-pulse DEER offers superior sensitivity over 4-pulse DEER. We assert that the microhelix paves the road for low-cost benchtop X-band pulse EPR spectrometers by eliminating the need for high-power amplifiers, accelerating the adoption of pulse EPR to a broader community.
1 Introduction
Double electron–electron resonance (DEER), also known as pulsed electron–electron double resonance (PELDOR)1,2 is a valuable tool in structural biology3 used to monitor conformational changes and interactions between biomacromolecules in different environments, regardless of overall size. It is based on measuring distances between dipolar-coupled paramagnetic centers that can be either native to the protein4,5 or artificially introduced at sites of interest via site-directed spin labeling (SDSL).6 The r−3 distance dependency of the dipolar coupling strength is used to extract precise distance information in the range from 1.5 to 8 nm and up to 16 nm7 for perdeuterated samples. Based on these characteristics, DEER can complement techniques like nuclear magnetic resonance (NMR), X-ray diffraction, and cryogenic electron microscopy (cryo-EM).DEER is a two-frequency experiment first introduced in the form of the 3-pulse sequence shown in Fig. 1(a).8,9 The working principle of this sequence is to record the intensity of a Hahn echo (observer) as a function of the temporal position of a -pulse applied at a second, so-called pump, frequency, exciting a different part of the spectrum. If the pump and observer spins are dipolar coupled, the Hahn echo intensity will be modulated by the dipolar coupling frequency,10 encoding the distance information. The observer echo intensity is subject to transverse relaxation exp(−2τdip/Tm), where Tm is the phase memory time, and the total length of the sequence (2τdip) determines the accessible distance range with τdip being the dipolar evolution time.11
The 3-pulse DEER sequence is referred to as “dead-time limited” since, at the so-called zero time (T = 0), an overlap between the pump pulse and the first observer pulse occurs. This overlap leads to a distortion of the first part of the time trace on the order of the ringdown time of the resonator, visualized in Fig. 1(a) as a shaded gray area. These first data points of the time trace are crucial for the determination of the zero time, which defines the absolute positions of the distance peaks, and for the determination of the modulation depth λ, which provides information on the number of interacting partners, of the time trace.
Due to these limitations, DEER was not widely used until the introduction of the “dead-time free” 4-pulse DEER sequence, shown in Fig. 1(b), which adds a second-pulse to the observer sequence to refocus the primary echo.12,13 Stepping the pump pulse in the time between the two observer-pulses, with the primary echo marking the zero time, allows for the collection of the full dipolar time trace.14 The drawback of the 4-pulse sequence lies in the prolongation of the pulse experiment (2τ1 + 2τdip), leading to a decreased observer signal intensity due to transverse relaxation effects.
The possibility to perform dead-time free 3-pulse DEER experiments could be highly beneficial for measurements with fast relaxing spin species, like transition metal ions5 or spins in relaxation enhancing environments such as liposomes, nanodiscs, or cells.15–17 One approach to overcome the obstacles connected with the 3-pulse DEER sequence is to improve the microwave resonator to significantly minimize the dead time. The achievable gain in sequence length is 2τ1 (see Fig. 1), which is usually in the order of 400–800 ns. Since the observer echo intensity is dependent on the phase memory time Tm of the sample, the maximum potential signal gain Sgain can be calculated as the ratio of the intensity of the transverse relaxation curves of the two experiments
 | (1) |
We report that the self-resonant microhelix at X-band (nominally 9.5 GHz), as described in Sidabras et al.,21 significantly reduces the resonator dead time while maintaining an adequate concentration sensitivity for DEER experiments. Herein, we show that despite a reduction in sample volume by a factor of 120 (85 nL with respect to 10 μL), the concentration sensitivity is only reduced by a factor of 11 due to the geometry of the microhelix. The geometry of the microhelix is well suited for pulse EPR experiments since it is providing a homogeneous microwave magnetic field (B1) profile, a large B1 conversion efficiency, a broad bandwidth, easy sample access, and an EPR signal enhancement proportional to the number of turns of the helix compared with the single-turn loops typically used as micro-resonators. Leveraging the characteristics of the microhelix, we performed a series of 3-pulse and 4-pulse DEER experiments with milliwatt incident power using a molecular ruler and a T4 lysozyme sample, removing the requirement of expensive high-power microwave amplifiers and gaining back a factor of two in concentration sensitivity for a standard protein sample. Lifting such power requirements allows to envision an affordable bench-top pulse EPR spectrometer for protein structure determination. This work seeks to highlight the current sensitivity of the microhelix for DEER spectroscopy, while exploring the use of 3-pulse DEER to enhance the sensitivity of the DEER experiment.
2 Theory
Microwave resonators are a central component of an EPR spectrometer. Resonators concentrate the magnetic component of the microwave field (B1) in the sample volume, while the electric component is spatially decoupled, minimizing microwave power losses and related heating effects. Resonators are usually characterized by the quality factor (Q-value), which can be calculated in various ways with the same result.22 A suitable definition for pulse EPR experiments is based on the relation between the operating frequency of the resonator ν0 and the bandwidth Δν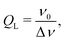 | (2) |
 ). The conversion efficiency describes how well a resonator converts the incident microwave power Pmw into a magnetic field at the sample.23
). The conversion efficiency describes how well a resonator converts the incident microwave power Pmw into a magnetic field at the sample.23
2.1 Micro-resonators
While conventional resonators have dimensions that are on the order of the resonance wavelength, micro-resonators are a class of resonators whose dimensions are orders of magnitude smaller. Accordingly, they are well-suited for small sample volumes and for EPR experiments on volume-limited samples such as microcystals21,24 or integrated in microfluidic setups.25The concentration of a microwave field to a very confined space allows for superior conversion efficiencies; however, due to the restricted volume, the concentration sensitivity is typically reduced. Consequently, micro-resonators are commonly optimized for absolute sensitivity26 and can include superconducting materials,27,28 to push towards the quantum limit.29,30
High conversion efficiencies mean that the incident power required to achieve the same B1 field strength is reduced compared with conventional resonators. The reduced power consumption permits the miniaturization of the spectrometer hardware, working towards fully integrated EPR spectrometers on silicon chips using, e.g., complementary metal oxide semiconductor (CMOS) technology.31,32 Recent advancements in this field open up completely new applications.33
To date, most micro-resonators have a planar geometry,34,35 since such geometries are easy to manufacture. However, planar micro-resonators have the inherent disadvantage of inhomogeneous B1 field distributions, making pulse spectroscopy challenging. In contrast, 3D structures, such as the recently introduced microhelix,21 can largely alleviate this problem, making it suitable for pulse EPR experiments.
2.2 Sensitivity considerations
During a pulse, the magnetization is tipped into the x/y-plane and, from the rotation component of the magnetization, an electromotive force (emf) applies a current back onto the resonator. After the pulse, the magnetization, and in turn the emf signal, decay exponentially at the rate of the transverse relaxation time constant Tm.36 The maximum voltage V0 immediately after the pulse can be expressed as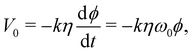 | (3) |
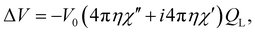 | (4) |
In case of pulse EPR experiments, this is particularly beneficial for the microhelix (see eqn (3)), since the voltage generated by the emf at the receiver, and therefore the EPR signal intensity, is increased by the number of turns k of the microhelix compared to a single-loop resonator with equivalent geometry.
2.3 Dead time and tingdown
The power incident on the receiver during a microwave pulse is orders of magnitude larger than the EPR signal. After the application of a pulse, the energy stored in the resonator requires several cycles to dissipate, which is usually referred to as resonator ringdown. Spectroscopically more relevant is the time it takes until an undistorted signal can be recorded, which depends on the strength of the signal with respect to the noise floor and is referred to as detector dead time. The duration of the dead time τd can be calculated as | (5) |
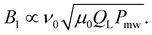 | (6) |
Conventional pulse experiments suffer from dead times on the order of 30–100 ns![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41–44 with a few exceptions where lower dead times could be achieved using purpose-built systems.45,46 This is one reason why pulse EPR experiments are based on echo detection as opposed to the direct detection of the free induction decay (FID) as in NMR experiments. Apart from these imposed limits to perform Fourier transform EPR,44 the study of fast relaxing spin signals is largely hindered due to the requirement to shorten the overall pulse sequence length.45 Again, the use of the microhelix is beneficial since the high conversion efficiency reduces the required incident power and thus the dead time. These advantages of micro-resonators were known at a very early stage.47
41–44 with a few exceptions where lower dead times could be achieved using purpose-built systems.45,46 This is one reason why pulse EPR experiments are based on echo detection as opposed to the direct detection of the free induction decay (FID) as in NMR experiments. Apart from these imposed limits to perform Fourier transform EPR,44 the study of fast relaxing spin signals is largely hindered due to the requirement to shorten the overall pulse sequence length.45 Again, the use of the microhelix is beneficial since the high conversion efficiency reduces the required incident power and thus the dead time. These advantages of micro-resonators were known at a very early stage.47
A wide variety of approaches have been developed to minimize resonator dead times in order to overcome the associated problems. In certain cases, phase cycling48 can be useful if the phase of the signal of interest can be changed with respect to the ringdown.45 Another remarkable approach is based on the use of an arbitrary waveform generator (AWG) to synthesize active cancellation pulses that destructively interfere with the resonator ringdown.49,50 Apart from experimental approaches, computational methods, such as linear prediction (LP)51 can be used to reconstruct signals backwards in time, based on the frequency content present in the recorded data, as it is common in NMR.52,53
In addition to the discussed detector dead time, another type of signal distortion arises if two pulses are placed too close to each other in time, since the Q-value of the resonator leads to a delay in the build-up and in the the dissipation of the energy stored in the resonator with respect to the applied incident power. The result is a filtering of the pulse shape in Fourier space. Especially if the pulse length is shorter than the time it takes for the stored energy in the resonator to reach maximum Umax, the pulse will be distorted in shape and amplitude. Generally, when the pulse is switched on, the pulse amplitude follows
 | (7) |
 | (8) |
This is referred to as pulse build-up and ringdown. Consequently, the ringdown of one pulse can interfere with the build-up of a second adjacent pulse if they are close enough to each other in time as it is the case between the first observer pulse and the pump pulse in the 3-pulse DEER sequence (see Fig. 1(b)). However, with the microhelix (critically coupled QL-value of 110 and over-coupled QL-value of 44; see Table S2, ESI†), this problem has largely been alleviated.
In summary, based on the given definitions, the 3-pulse DEER experiment is actually not dead time limited, since the utilized observer echo detection occurs well beyond the dead time of the resonator. The limiting factor are distortions arising from the overlap of pulse build-up and ringdown times between the first observer and the pump pulse. Nevertheless, we will use the term dead time in the context of the 3-pulse DEER experiment as it is established in literature.
3 Results and discussion
3.1 Comparison between microhelix and commercial resonator
To compare the performance between the microhelix and a commercially available split ring resonator (Bruker ER 4118X-MS-3), we performed equivalent DEER experiments (see Table S2 (ESI†) for a comparison of the resonator properties, Fig. S1 (ESI†) for the DEER setups and Table S3 (ESI†) for the experimental parameters) on a dinitroxide ruler (NO–NO ruler; see Materials and Methods) with 2.0 nm interspin distance that is soluble in aqueous solvents.54 The MS-3 resonator required an incident power of 45 W at the resonator to perform the experiment. In contrast, the microhelix required only 43 mW of incident power. This corresponds to a difference in power of three orders of magnitude, or 30 dB. The corresponding time traces presented in Fig. 2(a) are characterized by having the same homogeneous 3D background decay function and the same modulation depth at different noise levels. From the modulation depths of both time traces (λ = 0.17), we can conclude that the excitation profiles of the pump pulses in each resonator are exciting the same fraction of spins. Therefore, both resonators provide a sufficient bandwidth (see Fig. 10) and have a comparable B1 field homogeneity (see Fig. S2, ESI†). | ||
| Fig. 2 Comparison of DEER data obtained on the NO–NO ruler sample using a commercially available split ring resonator (Bruker MS-3) and the microhelix. A side by side comparison of resonator properties is given in Table S2 (ESI†). The first column shows the primary data with background fit (gray areas are excluded from data evaluation). In the second column, the form factors obtained by subtracting the fitted background function from the primary data are shown alongside the fit from the Tikhonov regularization. The third column presents the corresponding distance distributions obtained from Tikhonov regularization, and the fourth column presents the distance distribution obtained via a DEERNet analysis (generic network). The DEERNet outputs are presented to provide an unbiased analysis and error estimation. The modulation depth λ (or signal amplitude) of the time trace was determined as the average amplitude of the form factor signal after the dipolar signal is decayed. The noise N of the DEER data was calculated by taking twice the standard deviation between form factor and form factor fit after the dipolar signal is decayed. The signal-to-noise ratio (SNR) is the ratio between the modulation depth and the noise. An overview over all parameters used to acquire these data is given in Table S3 (ESI†). The accumulation time of each data set presented in this figure is 16 min. (a) Comparison of the DEER data obtained from the MS-3 resonator (green) and the microhelix (blue). (b) DEER data obtained with the microhelix using overall shorter pulses (blue) and shorter observer pulses in conjunction with a shaped pump pulse (dark gray, sech/tanh pulse with −40 to −90 MHz frequency sweep) with respect to (a). | ||
One of the most distinctive differences between the two resonators is the active volume. The sample volume of the Bruker MS-3 resonator with a 2.8 mm outer and 1.8 mm inner diameter capillary is approximately 10 l, while the microhelix can host a 0.4 mm outer and 0.3 mm inner diameter capillary, providing an active volume of 0.085 μl. The differences in size result in significantly different surface-area-to-volume ratios for the samples. The fact that this does not influence the background dimensionality of the DEER time traces recorded with the microhelix is an important finding regarding the applicability of the microhelix.
The DEER time trace recorded with the microhelix has a noise level (N = 0.022) 11 times higher than that of the MS-3 resonator (N = 0.002). Since the modulation depths λ are equivalent, an 11-times lower signal-to-noise ratio (SNR) (8 versus 90) is realized. In a simplified picture, the noise of a DEER time trace corresponds to the noise of the observer echo, where the intensity is proportional to the number of spins excited by the observer pulse sequence. The DEER signal is only reduced by a factor of 11, while the sample volume of the microhelix is 120 times smaller than that of the MS-3 resonator. This is because the echo intensity when using the microhelix is increased by the number of turns (k = 6.5), as shown in eqn (3). From these principles, we expect the concentration sensitivity of the microhelix to be a factor of 18 lower than that of the MS-3, compared with the volume ratio. Additionally, the microhelix was critically coupled (QL-value of 110), resulting in an additional square root of 2 improvement to the sensitivity,55 which leads to an estimated factor of 13 difference between the MS-3 and microhelix. Additional gains in the SNR for the microhelix are anticipated based on the high B1 conversion efficiency (3.2mT/ versus 0.4mT/
versus 0.4mT/ for the MS-3). The high B1 conversion efficiency requires the utilized 300 W high-power amplifier to be significantly attenuated (by 30 dB with respect to the MS-3; see Table S3, ESI†) for the same pulse lengths, which effectively eliminates room temperature noise from the amplifier. Ultimately, the distance distributions of both time traces are in good agreement with each other, especially taking into account the higher noise level of the time trace of the microhelix.
for the MS-3). The high B1 conversion efficiency requires the utilized 300 W high-power amplifier to be significantly attenuated (by 30 dB with respect to the MS-3; see Table S3, ESI†) for the same pulse lengths, which effectively eliminates room temperature noise from the amplifier. Ultimately, the distance distributions of both time traces are in good agreement with each other, especially taking into account the higher noise level of the time trace of the microhelix.
The SNR of the DEER time traces using the microhelix can be improved by utilizing overall shorter pump and observer pulses (32 and 48 ns Gaussian) in conjunction with over-coupling the microhelix (QL-value of 44; see Table S2, ESI†) to accommodate the larger excitation bandwidths of the pulses (see Fig. S1 and S10, ESI†). As shown in Fig. 2(b), this allows an increase in the signal from 0.17 to 0.43 with respect to the data shown in (a) while the noise level also increases from 0.022 to 0.039 due to an observer echo reduction caused by the larger excitation bandwidth of the pump pulse.56 Overall, this results in a moderate SNR increase to 11 (from 8) with respect to 90 for the MS-3 resonator. The application of a shaped sech/tanh pump pulse allows a further increase in the signal to 0.55 without significantly increasing the noise level, resulting in an SNR of 13. These experiments with shorter pulse lengths and shaped pulses could not be performed with the MS-3 resonator and the existing 300 W solid-state amplifier because the available power at the resonator was insufficient. A 1 kW TWT X-band amplifier would be required to perform these experiments. The gains shown here should also be achievable using the MS-3 resonator, noting that a TWT amplifier would introduce more noise at the receiver than the employed solid state amplifier.
3.2 3-Pulse DEER
Shown in Fig. 3(a) are 3-pulse and 4-pulse DEER time traces recorded with the microhelix using the same experimental parameters. The raw data of the 3-pulse DEER experiment are presented in Fig. S3 (ESI†). The section of the 3-pulse time trace distorted from the overlap between the pump pulse and the/2-observer pulse (see Fig. 1) was excluded from data analysis. The 3-pulse and 4-pulse DEER time traces are characterized by having the same background decay function, indicating that the influence of spin diffusion effects is negligible.18–20 | ||
| Fig. 3 Dead time correction using the DEER-Stitch method43 of 3-pulse DEER data recorded with Gaussian pulses using the NO-NO ruler sample. (a) 3-pulse and 4-pulse DEER experiments performed with the microhelix using 275 mW of power. The 3-pulse DEER raw data are shown in Fig. S3 (ESI†). (b) Stitching of the 4-pulse to the 3-pulse data using a 40 ns overlap and assuming 20 ns dead time. (c) Comparison of the stitched 3-pulse and the 4-pulse time trace via rmsd. Fig. S4 (ESI†) depicts exemplary results of different overlap/dead time combinations. (d) 3D plot showing the rmsd between the stitched 3-pulse and the 4-pulse time trace in dependence of the chosen dead time and overlap between the time traces. (e) The rmsd as a function of the overlap for a fixed dead time. (f) Average rmsd in the given overlap range (2 to 40 ns) for different dead times. The rmsd analysis shows that the dead time is (20 ± 2) ns when using a 32 ns (13.6 ns FWHM) Gaussian pump pulse alongside 48 ns (20.4 ns FWHM) Gaussian observer pulses. An overlap of 40 ns between the time traces is sufficient to have an appropriate stitching result. For the analogous evaluation of DEER data acquired using rectangular pulses, see Fig. S5 (ESI†). | ||
To experimentally revive the 3-pulse data from the remaining dead time, we used the DEER-Stitch method introduced by Lovett et al.43 The idea of this method is to measure a short 4-pulse DEER time trace alongside the desired 3-pulse time trace using the same experimental parameters. The length of the 4-pulse sequence should just be long enough to cover the dead time and to provide a region of overlap between the two signals. The 4-pulse time trace is then fitted to the 3-pulse time trace by minimizing the standard deviation of the two traces in the region of overlap. Finally, the data are “stitched” together, resulting in a dead-time free time trace. This is only practical if a reasonable SNR gain can be realized using the 3-pulse sequence over the 4-pulse sequence, and only a very short 4-pulse time trace is required to compensate for the dead time, as it is the case with the microhelix.
The stitching procedure of the data is shown in Fig. 3(b). The 3-pulse data were positioned along the time axis for a given dead time (in this case 20 ns) and the 4-pulse time trace was scaled by multiplying the trace with a constant value that minimizes the standard deviation in a defined region of overlap (shaded red area, here 40 ns). The result is presented in Fig. 3(c) in comparison with the 4-pulse data.
The previously published DEER-Stitch method requires a priori knowledge about the dead time and the length of the overlap that is required to fit the data. The latter is dependent on the dipolar frequencies present in the sample and the SNR, while the dead time can vary for a given resonator based on the utilized pulse shapes/lengths and the Q-factor. Herein, we show that all this information can be retrieved directly from the data itself if the dead time and the extension of the region of overlap were varied for a given data set. This was achieved by calculating the root-mean-square deviation (rmsd) of the stitched 3-pulse with respect to the 4-pulse reference data (see Fig. 3(c)) for different dead time and overlap parameters (see also Fig. S4, ESI†). This analysis of the DEER-Stich method can be plotted as a 3D-matrix as presented in Fig. 3(d). The aim is to find the dead time value that minimizes the rmsd, and the minimal length of the overlap that allows for a stable solution.
We found it insightful to look at 2D-projections of this 3D-matrix. Fig. 3(e) shows how the rmsd develops for a given dead time when the size of the region of overlap is increased. The rmsd values clearly stabilize within the first 10 to 20 ns, which suggests that for this particular pair of time traces an overlap of no longer than 40 ns is required to correctly stitch the data. Fig. 3(f) shows the average rmsd that is realized for each dead time when varying the length of the overlap as given in Fig. 3(e). From this, we determined the actual dead time of the measured 3-pulse DEER time trace. When using a 32 ns (13.6 ns FWHM) Gaussian pump pulse alongside 48 ns (20.4 ns FWHM) Gaussian observer pulses, the dead time is (20 ± 2) ns. (We utilized Gaussian pulses to avoid “2 + 1” artifacts in the DEER data.57)
However, shorter dead times can be accomplished using rectangular pulses, since these can be brought closer together without overlapping in the time domain. In Fig. S5 (ESI†), the same evaluation is presented for DEER experiments using rectangular pulses that match in length with the FWHM of the used Gaussian pulses (14 ns pump and 20 ns observer). Rectangular pulses allow for dead times as short as (14 ± 2) ns. The measured dead time of the over-coupled microhelix can no longer be attributed to resonator ringdown but is purely caused by the inevitable overlap of the half-pulses in the 3-pulse DEER sequence (see Fig. 1). This is entering a regime where the correction needed to reconstruct the DEER signal is marginal, which means that the overall fidelity of the DEER stitch method is increased if setups allowing for short dead times are used. For standard DEER time increments of 8 ns, the dead time of the microhelix affects as little as two data points.
In summary, the 4-pulse time trace required to compensate for the very short dead time in the 3-pulse data using the DEER-Stitch method needs to be a total of 60 ns long: 20 ns for the dead time and 40 ns for the overlap when using Gaussian pulses. For rectangular pulses, the 4-pulse time trace length should be in a similar range despite the even shorter dead time of 14 ns (see Fig. S5, ESI†). Practically, one might actually record slightly longer time traces and some data points symmetrically around the zero time to better judge if the method is performing as expected. This is a priori not required but it is a best practice and does not add too much additional acquisition time, making Deer-Stitch an overall good method to benefit from the SNR gain realized by the 3-pulse DEER experiment. The SNR and distance analysis of the stitched 3-pulse and the 4-pulse time trace are presented in Fig. 4. Both time traces are characterized by having the same signal (λ = 0.37) and the same background decay function. Correspondingly, the distance distributions are in very good agreement with each other. The noise level of the 3-pulse time trace is lower than that of the 4-pulse time trace (N = 0.004 versus 0.007), which is reflected in the SNR of the 3-pulse DEER being about a factor of 1.7 higher than that of the 4-pulse DEER (SNR = 92 versus 53).
 | ||
| Fig. 4 Comparison of stitched 3-pulse (DEERS) and 4-pulse DEER data using Gaussian pulses obtained on the NO–NO ruler sample. The first column shows the primary data with background fit (gray areas are excluded from data evaluation). In the second column, the form factors obtained by subtracting the fitted background function from the primary data are shown alongside the fit from the Tikhonov regularization. The third column presents the corresponding distance distributions obtained from Tikhonov regularization, and the fourth column presents the distance distribution obtained via a DEERNet analysis (generic network). The stitching procedure of the data is presented in Fig. 3. The 3-pulse time trace has a dead time of 20 ns, and about 40 ns are required as overlap to stitch the data reliably. The SNR of the 3-pulse time trace is a factor of 1.7 higher than the SNR of the 4-pulse time trace. | ||
It has to be noted that this improvement factor is an upper estimate since it does not include the acquisition time of the short 4-pulse DEER experiment required for the stitching. Finding a generally valid approach to include the 4-pulse DEER acquisition time in the SNR calculation is challenging since making a fair comparison requires to achieve an SNR matching between the 3-pulse and 4-pulse DEER time traces that is strongly dependent on the relaxation properties of the sample and the relative length of the time traces. Besides this point, the nuclear modulation averaging applied in 4-pulse DEER leads to a step-wise prolongation of the the 4-pulse time trace (up to 128 ns) that results in a small but hard to quantify decrease in SNR of the 4-pulse DEER time trace with respect to the 3-pulse DEER time trace.
3.3 Fast relaxation
To better assess the achievable observer signal gain when comparing 3-pulse and 4-pulse DEER, the phase memory time Tm of the NO–NO ruler sample was determined at 50, 80, and 100 K via echo decay experiments. The echo decay transients shown in Fig. S6 (ESI†) are characterized by strong deuterium ESEEM (electron spin echo envelope modulation) effects due to the utilized deuterated solvent. The determined phase memory times are 1.1, 0.9, and 0.7 μs at 50, 80, and 100 K, respectively. An overview of the theoretically achievable signal gains when performing a 3-pulse over a 4-pulse DEER experiment at different phase memory times is given in Table. S1 (ESI†).We have shown in Fig. 4 that a factor of 1.7 in SNR can be realized by performing a 3-pulse DEER instead of a 4-pulse DEER at 50 K. In Fig. 5(a), we show data of a 3-pulse and 4-pulse DEER experiment performed at 100 K using rectangular pulses. The data were stitched using the procedure introduced in the previous section. The dead time was determined to be (12 ± 2) ns and an overlap of 28 ns led to a sufficiently stable solution. The SNR analysis is shown in Fig. 5(b). As expected, the signal is the same for the two time traces (λ = 0.38). The 3-pulse time trace has a factor of 2 less noise than the 4-pulse time trace (N = 0.022 versus 0.045), which is reflected in an SNR that is 2.1 times better (SNR = 17 versus 8).
 | ||
| Fig. 5 Comparison of 4-pulse and stitched 3-pulse DEER data (DEERS) using rectangular pulses (622 mW) obtained on the NO-NO ruler sample at 100 K. (a) The time traces were stitched according to the parameters found in Fig. S5 (ESI†) (14 ns dead time). (b) The legend is the same as in Fig. 4. Due to the smaller phase memory time of the sample at 100 K, as shown in Fig. S6 (ESI†), the SNR of the 3-pulse DEER experiment is a factor of 2.1 higher than that of the 4-pulse DEER experiment using the same parameters. | ||
The experimentally achieved gains are smaller than the gains predicted using the simple exponential model of eqn (1) (see Table S1, ESI†). At 50 K with Tm = 1.1 μs, we realized a gain of 1.7 (versus 2.1) and at 100 K with Tm = 0.7 μs, we realized a gain of 2.1 (versus 3.1). This is in line with the expectations when considering the additional effects that are not included in this model as discussed above (see eqn (1)).
3.4 T4 lysozyme
To benchmark the performance of the microhelix on a protein, we used a T4 lysozyme 68R1/140R1 double mutant spin labeled with MTSSL (methanethiosulfonate spin label). The labeling efficiency is 106% (see Fig. S7, ESI†). The experimental parameters for all DEER data are presented in Tables S4 and S5 (ESI†).We performed DEER experiments on this sample at different concentrations, down to 100  μM. At 500 μM protein concentration and with 50% v/v deuterated glycerol the DEER data exhibit strong 1H -ESEEM effects, as presented in Fig. S8(a) (ESI†). In case of 4-pulse DEER, nuclear modulation averaging (d3 = 16 ns and m = 8) removed these ESEEM effects completely, while neither nuclear modulation averaging, nor phase cycling can remove these signals from the 3-pulse DEER data. This sample-dependent effect is a known drawback of non-deuterated solvents at X-band and required us to remove the first 104 ns of the 3-pulse DEER time trace (including dead time) in order to sufficiently stitch the data, as shown in Fig. S8(b) (ESI†). An evaluation of the stitched data is presented in Fig. 6. The 4-pulse and the stitched 3-pulse time traces are characterized by having different background functions but share the same modulation depth. The differences in the background functions can be attributed to spin diffusion effects18–20 arising from the use of different pulse sequences and sequence lengths, as well as a high protein concentration (please note the absence of these effects for the lower concentrated samples shown below). The noise level is considerably lower for the 3-pulse experiment, resulting in a SNR which is 2 times higher for the 3-pulse compared to the 4-pulse experiment. The extracted distances are in agreement with the MMM simulations58 performed on the protein crystal structure (PDB ID: 3LZM59).
μM. At 500 μM protein concentration and with 50% v/v deuterated glycerol the DEER data exhibit strong 1H -ESEEM effects, as presented in Fig. S8(a) (ESI†). In case of 4-pulse DEER, nuclear modulation averaging (d3 = 16 ns and m = 8) removed these ESEEM effects completely, while neither nuclear modulation averaging, nor phase cycling can remove these signals from the 3-pulse DEER data. This sample-dependent effect is a known drawback of non-deuterated solvents at X-band and required us to remove the first 104 ns of the 3-pulse DEER time trace (including dead time) in order to sufficiently stitch the data, as shown in Fig. S8(b) (ESI†). An evaluation of the stitched data is presented in Fig. 6. The 4-pulse and the stitched 3-pulse time traces are characterized by having different background functions but share the same modulation depth. The differences in the background functions can be attributed to spin diffusion effects18–20 arising from the use of different pulse sequences and sequence lengths, as well as a high protein concentration (please note the absence of these effects for the lower concentrated samples shown below). The noise level is considerably lower for the 3-pulse experiment, resulting in a SNR which is 2 times higher for the 3-pulse compared to the 4-pulse experiment. The extracted distances are in agreement with the MMM simulations58 performed on the protein crystal structure (PDB ID: 3LZM59).
 | ||
| Fig. 6 Comparison of stitched 3-pulse (DEERS) and 4-pulse DEER data obtained using rectangular pulses on the T4 lysozyme sample at 500 μM protein concentration and 50% v/v deuterated glycerol. The legend is the same as in Fig. 4. The shaded red areas in the distance distributions are a simulation of the interspin distance performed using MMM58 based on the protein crystal structure (PDB ID: 3LZM59). The 3-pulse DEER time trace is suffering from 1H -ESEEM as shown in Fig. S8(a) (ESI†), which required to remove the first 104 ns of the 3-pulse DEER time trace. The stitching of the data is shown in Fig. S8(b) (ESI†). The SNR of the 3-pulse DEER experiment is a factor of 2 higher than that of the corresponding 4-pulse DEER experiment using the same parameters. | ||
In order to realize signal gains in 3-pulse DEER, ESEEM effects are an important factor that needs to be considered before performing a successful experiment. Fig. 7(a) shows an echo decay experiment measured using the T4 lysozyme sample at 250 μM protein concentration with 33% v/v deuterated glycerol. In particular, the long period of 2H (≈ 444 ns) can strongly modulate the amplitude of the observer echo in DEER experiments depending on the length of the time trace, severely influencing the realizable signal gain. Fig. 7(b) is a magnification of (a) with vertical lines indicating the lengths of different DEER sequences. Highlighted are the sequence lengths of a 1.2 μs 3-pulse DEER time trace (2.4 μs sequence length, blue) in conjunction with the corresponding 1.2 μs 4-pulse DEER time trace (2.8 μs sequence length for τ1 = 0.2 μs, gray) and of a 1.4 μs 3-pulse DEER time trace (2.8 μs sequence length, red) with the corresponding 1.4 μs 4-pulse DEER time trace (3.2 μs sequence length for τ1 = 0.2 μs, green).
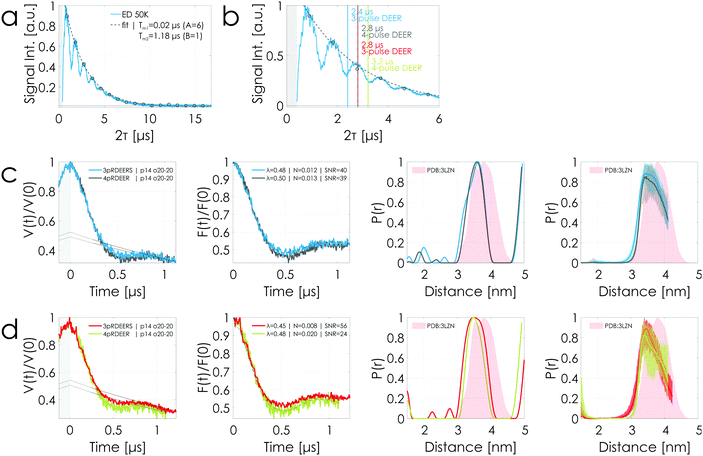 | ||
| Fig. 7 T4 lysozyme sample at 250 μM protein concentration with 33% v/v deuterated glycerol. (a) and (b) Echo decay transients (2p-ESEEM) are characterized by 1H-ESEEM (period: τ1H = 2 × 36 ns corresponding to 14 MHz) and 2H-ESEEM (period: τ2H = 444 ns corresponding to 2 MHz). (a) Data were evaluated as shown in Fig. S5 (ESI†). The phase memory time Tm was determined to be 1.2 μs. (b) is a magnification of (a) highlighting the color-coded sequence lengths (see Fig. 1) of the DEER experiments presented below. (c) and (d) Comparison of 1.2 μs and 1.4 μs stitched 3-pulse and 4-pulse DEER time traces acquired using rectangular pulses. The legend is the same as in Fig. 4. All DEER time traces were performed using the same parameters and have the same number of averages per point (see Tables S4 and S5, ESI†). 4-pulse DEER experiments were performed using nuclear modulation averaging. The stitching of the data is presented in Fig. S9 (ESI†). Color coding in accordance with the highlighted sequence lengths in (b). | ||
The corresponding DEER data are presented in Fig. 7(c) and (d) with the stitching procedure shown in Fig. S9 (ESI†). It has to be noted that all experiments were performed using the same parameters and the same averaging times (see Tables S4 and S5, ESI†). The 4-pulse DEER experiments had been performed using the above described nuclear modulation averaging for 1H -ESEEM. All DEER data are characterized by having within the error the same modulation depth but different noise levels. Based on the echo decay curve in Fig. 7 (b), the observer echo intensity of the 1.2 μs 3-pulse DEER time trace (blue), situated in a minimum of the echo decay curve, is expected to be smaller than the one of the corresponding 4-pulse DEER time trace (gray) situated at a maximum. Fig. 7(c) shows that both DEER time traces reach the same SNR. In contrast, the 1.4 μs 3-pulse DEER time trace (red), situated at a maximum of the echo decay curve, is characterized by a twofold better SNR than the 4-pulse counterpart (green) situated in a minimum (see Fig. 7(d)). In other words, the 1.4 μs 4-pulse DEER time trace placed on a minimum is characterized by a worse SNR than the shorter 1.2 μs 4-pulse DEER time trace placed on a maximum (SNR = 24 versus 39). This is within the expectation based on the longer sequence length. But, remarkably, the 1.4 μs 3-pulse DEER time trace placed on a maximum is characterized by a better SNR than the shorter 1.2 μs 3-pulse DEER time trace placed on a minimum (SNR = 56 versus 40). This clearly highlights the strong influence of ESEEM on realizable signal gains when performing 3-pulse over 4-pulse DEER experiments.
To assess the concentration sensitivity of the microhelix and to perform a true DEER-Stitch experiment, we carried out a 1.4 μs 3-pulse DEER experiment alongside a 0.5 μs 4-pulse DEER experiment using the T4 lysozyme sample at a 100 μM protein concentration with 50% v/v deuterated glycerol. The result is presented in Fig. 8. This experiment was performed using only 350 mW of power (see Table S4, ESI†) reaching a SNR of 23 after averaging the 3-pulse experiment for 8.5 h and the 4-pulse experiment for 3.7 h (see Table S6, ESI†). The evaluated distances are in good agreement with the data recorded at higher protein concentrations.
 | ||
| Fig. 8 Comparison of stitched 3-pulse (DEERS) and 4-pulse DEER data obtained using rectangular pulses on the T4 lysozyme sample at 100 μM protein concentration and 50% v/v deuterated glycerol. The legend is the same as in Fig. 4. After 8.5 h of averaging time for the 3-pulse and 3.7 h for the 4-pulse experiment a SNR of 23 was reached using just 350 mW of power. The raw data and the stitching are shown in Fig. S10 (ESI†). | ||
4 Conclusions and outlook
We have demonstrated the feasibility to perform DEER experiments using a 3D-micro-resonator, the microhelix, which has three significant advantages for pulse EPR over conventional resonators and other micro-resonators. The microhelix has (i) significantly lower power requirements (up to three orders of magnitude; see Fig. 2 and Table S3, ESI†) based on the high B1 conversion efficiency, (ii) a low Q-value that significantly reduces the filtering of the excitation allowing for adjacent pulses, (iii) a helical geometry that results in an EPR signal intensity 6.5 times higher than expected from the reduction of volume alone. The combination of the first two characteristics significantly lowers experimental dead times (down to 14 ± 2 ns; see Fig. 3 and Fig. S4, ESI†), while the second and third makes it feasible to perform DEER experiments.Only with a perfect spectrometer and a critically coupled resonator one can expect to achieve the dead times of eqn (5). With conventional resonators dead times (primarily due to the microwave reflections of an overcoupled resonator) are on the order of 5–10 times longer than τd calculated viaeqn (5).41 By requiring three orders of magnitude less power than a conventional resonator (43 mW with respect to 45 W), the self-resonant microhelix comes closer to an ideal dead time. By measuring a dead time of 14 ± 2 ns using 3-pulse DEER, and calculating a critically coupled resonator dead time with eqn (5) of 12 ns we are in a regime where the dead time is no longer dominated by the microwave resonator. The dead time of the spectrometer could not be measured directly, since the microhelix was just used as a drop-in replacement for a commercial X-band resonator without any modifications to the spectrometer configuration. However, in a modified spectrometer, FT-EPR experiments may take advantage of the reported short dead times in the future.
The DEER data in Fig. 2(a) highlight the shortcoming of micro-resonators, in particular with respect to protein samples: the low concentration sensitivity due to the small active volume. We show that the microhelix can partially compensate for this because of signal gains related to its helical geometry (see eqn (3)) and the lower noise levels due to the ultra-low power required to generate the high B1 in the sample. Overall, the feasibility of the microhelix as a reliable geometry for DEER distance measurements down to 100 μM protein concentration (see Fig. 8) is presented.
Using a standard 100 μM T4 lysozyme sample, this work shows that the microhelix has currently a concentration sensitivity that is a factor of 11 lower when compared to commercial X-band resonator, while requiring 120 times less sample volume. The concentration sensitivity could be further improved by placing a low noise amplifier (LNA) close to the resonator, resulting in a gain in echo intensity by a factor of 3 to 10, while effectively eliminating the receiver noise.60,61
We note that the experimental dead times are no longer limited by the resonator ringdown but by reflections within the spectrometer and the inevitable pulse overlaps within the pulse sequence (see Fig. 3 and Fig. S5, ESI†). The short dead time of the microhelix gives access to measurements of compounds with fast relaxing spins and allows sensitivity gains of up to 2 times to be realized through use of the 3-pulse over the 4-pulse DEER sequence (see Fig. 4–7). The nature of this sensitivity gain (see eqn (1) and Table. S1, ESI†)) could allow the microhelix to outperform conventional X-band resonators for samples containing fast-relaxing spin species like transition metal ions5 or spins in relaxation-enhancing environments.
Although scaling the self-resonant microhelix to Q-band (nominally 35 GHz) would improve the overall sensitivity compared to X-band, it would not reach the concentration sensitivity achieved with a dedicated Q-band cavity. Since the microhelix is a self-resonant structure, its geometry determines the operating frequency. A Q-band version of the microhelix would have a volume that is about 4 times smaller than at X-band. While the absolute sensitivity would be increased by a similar factor, the concentration sensitivity would be reduced by this factor. However, by envisioning a dedicated spectrometer at a frequency between X-band and Q-band, there may be a suitable concentration sensitivity maximum taking into account both the EPR signal enhancement at higher frequencies and the volume increase at lower frequencies. Commercially available Q-band resonators remain dead time limited with dead times in the order of 25 to 50 ns.
The use of costly and large specialized equipment (W-band; nominally 94 GHz) or costly high power TWT amplifiers (X-band and Q-band) limits the possibility for widespread adoption of pulse EPR spectroscopy. In contrast, the small size of the microhelix requires only a small homogeneous B0-field region that can be achieved with a compact electromagnet, combined with the ability to perform pulse EPR experiments with orders of magnitude less microwave power (eliminating the need for bulky high power amplifiers) allows us to envision an affordable bench-top pulse EPR spectrometer for obtaining structural information on proteins. Such more compact and cost-efficient spectrometer designs would make pulse EPR more accessible to a broader community.62,63
5 Materials and methods
5.1 Samples
We used as a model system the water-soluble ˙ON-(PE) 2 P-NO˙ molecular ruler, referred to as a NO-NO ruler for short. The structural formula is presented in Fig. 9(a), and the synthesis is described in Teucher et al.54 The ruler consists of two nitroxides that are held by a stiff rod-like spacer at a distance of 2.0 nm.64 A stock solution of the NO–NO ruler was prepared in D2 O using 50% v/v deuterated glycerol to ensure a glass-like freezing at a 1.4 mM final molecule concentration. | ||
| Fig. 9 (a) Structural formula of the utilized NO–NO ruler, which is characterized by a well-defined 2.0 nm interspin distance. (b) Structure of T4 lysozyme (PDB ID: 3LZM59) with one MTSSL (R1) attached at each labeling site using the software MMM.58 | ||
As a protein sample, we used T4 lysozyme spin labeled at residues 68 and 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65 with MTSSL (methanethiosulfonate spin label) in a buffer solution consisting of 50 mM MOPS (3-(N-Morpholino)propanesulfonic acid) and 25 mM NaCl at a of pH 6.8. The structure of the spin labeled protein is presented in Fig. 9(b). A continuous wave EPR spectrum of the spin labeled protein is presented in Fig. S7 (ESI†). The the spin labeling efficiency was determined to be 106%. Samples were prepared using a 1 mM stock solution of the protein in conjunction with deuterated glycerol and buffer solution to obtain the desired concentrations.
65 with MTSSL (methanethiosulfonate spin label) in a buffer solution consisting of 50 mM MOPS (3-(N-Morpholino)propanesulfonic acid) and 25 mM NaCl at a of pH 6.8. The structure of the spin labeled protein is presented in Fig. 9(b). A continuous wave EPR spectrum of the spin labeled protein is presented in Fig. S7 (ESI†). The the spin labeling efficiency was determined to be 106%. Samples were prepared using a 1 mM stock solution of the protein in conjunction with deuterated glycerol and buffer solution to obtain the desired concentrations.
In case of the MS-3 resonator, 20 l of sample was inserted into quartz tubes (2.8 mm outer diameter, 1.8 mm inner diameter) and shock frozen in liquid nitrogen (active volume approximately 10 μl). Samples for the microhelix were prepared by allowing capillary forces to take up about 0.1 μl of sample in 0.4 mm outer and 0.3 mm inner diameter (active volume approximately 0.085 μl) quartz capillaries. The samples were then inserted into the microhelix and frozen upon insertion of the probehead into the cryostat.
5.2 Instrumentation
Spin counting was performed using a MiniScope MS-5000 benchtop continuous wave EPR spectrometer from Magnettech by Freiberg Instruments (Berlin, Germany). All pulsed EPR experiments were performed using a Bruker ELEXSYS E580 X-band spectrometer equipped with a Bruker SpinJet-AWG (±400 MHz bandwidth, 1.6 GSa s−1 sampling rate, 14 bit amplitude resolution) and a 300 W solid-state amplifier from HBH Microwave (Stutensee, Germany). The use of an AWG allows for precise creation of pulse shapes at the expense of microwave power incident on the sample. To stay within the linear region of the AWG single-sideband mixer, the power from the fundamental source must be lowered. This results in a maximum power output of 75 W incident on the resonator. The self-resonant microhelix was tested as a drop-in replacement for a commercial X-band resonator and no changes to the spectrometer configuration were performed.A Bruker split ring resonator ER 4118X-MS-3 was used alongside the self-resonant microhelix of Sidabras et al.21 The MS-3 resonator has a 3 mm inner diameter at 4 mm cavity height and was used in conjunction with 2.8 mm outer and 1.8 mm inner diameter sample tubes, providing a 10 l sample volume. The microhelix consists of about 6.5 windings of a 0.125 mm silver wire coated with polytetrafluoroethylene (PTFE), creating a cylindrical cavity of 0.4 mm inner diameter and 1.2 mm effective height. The 0.4 mm outer and 0.3 mm inner diameter capillary tubes provide a 0.085 μl sample volume. Bandwidth profiles of both resonators determined via transient nutation experiments using ProDeL in Xepr are shown in Fig. 10.
 | ||
| Fig. 10 Resonator bandwidth profiles were obtained via transient nutation experiments using ProDel in Xepr. The bandwidth profiles of the MS-3 resonator (green) and the microhelix (blue) were shifted to the same center frequency and normalized for better comparability. Both resonators were in an over-coupled states when the bandwidth profiles were recorded. The microhelix provides bandwidths in the range of 112 MHz (QL = 85 using eqn (2), dotted blue line) up to 342 MHz (QL = 28, solid blue line) depending on the degree of overcoupling, which is considerably larger than the bandwidth of the fully overcoupled MS-3 resonator with approximately 85 MHz (QL = 112, solid green line). Additionally, the microhelix has already a bandwidth of 90 MHz when critically coupled.21 The vertical broken line highlights the center of the resonator dip. The two solid black lines are separated by 65 MHz and placed symmetrically around the center of the dip, illustrating the utilized DEER setup alongside the field-swept echo (FSE) spectrum of a nitroxide (gray). Additional resonator properties are given in Tab. S2. | ||
The MS-3 resonator has a conversion factor (efficiency parameter) Λ of 0.4mT/ for an over-coupled QL of about 500, while the microhelix has a Λ of 3.2mT/
for an over-coupled QL of about 500, while the microhelix has a Λ of 3.2mT/ with a critically coupled QL = 110 at 50 K. Additional resonator-specific properties are listed in Table. S2 (ESI†).
with a critically coupled QL = 110 at 50 K. Additional resonator-specific properties are listed in Table. S2 (ESI†).
5.3 DEER Setup
DEER experiments were performed using either the 3-pulse sequence (τ/2) obs − (τ1 − T) − (π)pump − (τ1) − (π) obs − (echo)8,9 or the dead-time free 4-pulse DEER sequence (τ/2)obs − (τ1) − (π)obs − (τ1 + T) − (π)pump − (τ2 − T) − (π)obs − (τ2) − (echo)12,13 shown in Fig. 1. For both experiments, we used 16-step phase cycling66 using (0) − (π) for (π/2)obs and (π)obs, and (0) − (π/2) − (π) − (3π/2) for (π)pump. The pump frequency was always placed on the spectral maximum of the nitroxide spectrum with the observer 65 MHz higher in frequency (if not stated differently). The main frequency of the spectrometer was set to the observer frequency with the AWG providing the frequency offset for the pump pulse. To ensure a uniform excitation bandwidth for all pulses in the respective observer echo sequence, π/2 and π-pulses were set to have the same length compensated by different amplitudes.All pulse lengths and amplitudes were optimized separately for each experiment via echo-detected transient nutation experiments. In the case of rectangular and Gaussian pulses, the predefined pulse shapes 0 and 1 in Xepr were used, respectively. Gaussian pulses are defined in Xepr via , where tp is the pulse length and FWHM is the full width at half maximum of the pulse. This allows rectangular and Gaussian pulses to relate to each other in the time domain.57 Shaped pulses were programmed in MATLAB R2019b (The MathWorks Inc., Natick, MA, USA) using the pulse function in EasySpin version 5.2.28.67
, where tp is the pulse length and FWHM is the full width at half maximum of the pulse. This allows rectangular and Gaussian pulses to relate to each other in the time domain.57 Shaped pulses were programmed in MATLAB R2019b (The MathWorks Inc., Natick, MA, USA) using the pulse function in EasySpin version 5.2.28.67
5.4 Data analysis
We define the SNR as the ratio between the modulation depth λ and the standard deviation of the noise. The standard deviation was calculated around zero after subtracting the form factor fit from the form factor. Just the zero-centered section was used which required omitting the first 40/80 data points of the time trace for the NO-NO ruler/T4 lysozyme sample, respectively.DEER data evaluation was performed using Tikhonov regularization68 and DEERNet deep neural network processing,69,70 both provided in DeerAnalysis 2019 (ETH Zurich, Zurich, Switzerland).71,72 We subtracted the fitted background function from the primary DEER data73 to maintain a uniform noise level over entire the time trace, which is also independent of the modulation depth. Background subtraction over division induces an artificial broadening of the distances distributions.73
DEER distance distribution simulations of the T4 lysozyme 68R1/140R1 sample were performed using MMM 2020.1 (ETH Zurich, Zurich, Switzerland).58 The illustration of the protein structure in Fig. 9(b) was created using PyMOL version 2.3.0 (Schrödinger LLC., New York, NY, USA).
All code and data is available upon request.
Author contributions
AS initiated the project and provided the facilities. MT and JWS designed the research. JWS designed and developed the microhelix. MT and JWS prepared the EPR samples and performed all experiments. MT, JWS and AS discussed the results. MT and JWS and wrote the manuscript. All authors revised the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Max Planck Society (MT, JWS, AS), the EU Horizons 2020 Marie Skłodowska Curie Fellowship (Act-EPR; no. 745702 (JWS)), and Bundesministerium für Bildung und Forschung under contract number 01186916/1 (EPRoC, Grant reference number: 03SF0565B, MT, JWS, AS). Mian Qi, Ninive Cati, and Adelheid Godt (Bielefeld University, Germany) synthesized and kindly provided the NO-NO ruler sample. Alex Garces and Michael T. Lerch (Medical College of Wisconsin, USA) kindly provided the T4 Lysozyme sample used in this work.Notes and references
- G. Jeschke, eMagRes, 2016, 1459–1476 CrossRef CAS.
- O. Schiemann, C. A. Heubach, D. Abdullin, K. Ackermann, M. Azarkh, E. G. Bagryanskaya, M. Drescher, B. Endeward, J. H. Freed and L. Galazzo, et al. , J. Am. Chem. Soc., 2021, 143, 17875–17890 CrossRef CAS PubMed.
- G. Jeschke, Emerging Top. Life Sci., 2018, 2, 9–18 CrossRef CAS PubMed.
- C. R. Timmel and J. R. Harmer, Structural Information from Spin-Labels and Intrinsic Paramagnetic Centres in the Biosciences, Springer, 2014, vol. 152, pp. 1–329 Search PubMed.
- D. Abdullin and O. Schiemann, ChemPlusChem, 2020, 85, 353–372 CrossRef PubMed.
- W. L. Hubbell, C. J. López, C. Altenbach and Z. Yang, Curr. Opin. Struct. Biol., 2013, 23, 725–733 CrossRef CAS PubMed.
- T. Schmidt, M. A. Wälti, J. L. Baber, E. J. Hustedt and G. M. Clore, Angew. Chem., 2016, 55, 15905–15909 CrossRef CAS PubMed.
- A. Milov, K. Salikhov and M. Shirov, Fiz. Tverd. Tela, 1981, 23, 975–982 CAS.
- A. Milov, A. Ponomarev and Y. D. Tsvetkov, Chem. Phys. Lett., 1984, 110, 67–72 CrossRef CAS.
- K. Salikhov, I. Khairuzhdinov and R. Zaripov, Appl. Magn. Reson., 2014, 45, 573–619 CrossRef CAS.
- G. Jeschke, Annu. Rev. Phys. Chem., 2012, 63, 419–446 CrossRef CAS PubMed.
- R. E. Martin, M. Pannier, F. Diederich, V. Gramlich, M. Hubrich and H. W. Spiess, Angew. Chem., 1998, 37, 2833–2837 CrossRef.
- M. Pannier, S. Veit, A. Godt, G. Jeschke and H. W. Spiess, J. Magn. Reson., 2000, 142, 331–340 CrossRef CAS PubMed.
- K. Salikhov and I. Khairuzhdinov, Appl. Magn. Reson., 2015, 46, 67–83 CrossRef CAS.
- R. Igarashi, T. Sakai, H. Hara, T. Tenno, T. Tanaka, H. Tochio and M. Shirakawa, J. Am. Chem. Soc., 2010, 132, 8228–8229 CrossRef CAS PubMed.
- A. Martorana, G. Bellapadrona, A. Feintuch, E. Di Gregorio, S. Aime and D. Goldfarb, J. Am. Chem. Soc., 2014, 136, 13458–13465 CrossRef CAS PubMed.
- B. Joseph, A. Sikora, E. Bordignon, G. Jeschke, D. S. Cafiso and T. F. Prisner, Angew. Chem., 2015, 127, 6294–6297 CrossRef.
- J. Soetbeer, M. Hülsmann, A. Godt, Y. Polyhach and G. Jeschke, Phys. Chem. Chem. Phys., 2018, 20, 1615–1628 RSC.
- J. Soetbeer, M. Millen, K. Zouboulis, M. Hülsmann, A. Godt, Y. Polyhach and G. Jeschke, Phys. Chem. Chem. Phys., 2021, 23, 5352–5369 RSC.
- T. Bahrenberg, S. M. Jahn, A. Feintuch, S. Stoll and D. Goldfarb, Magn. Reson., 2021, 2, 161–173 CrossRef CAS.
- J. W. Sidabras, J. Duan, M. Winkler, T. Happe, R. Hussein, A. Zouni, D. Suter, A. Schnegg, W. Lubitz and E. J. Reijerse, Sci. Adv., 2019, 5, eaay1394 CrossRef CAS PubMed.
- E. Ginzton, Microwave Measurements, McGraw-Hill, 1957 Search PubMed.
- J. S. Hyde and W. Froncisz, in Advanced EPR, ed. A. Hoff, Elsevier, Amsterdam, 1989, ch. Loop Gap Resonators, pp. 277–305 Search PubMed.
- N. Dayan, Y. Ishay, Y. Artzi, D. Cristea, E. Reijerse, P. Kuppusamy and A. Blank, Rev. Sci. Instrum., 2018, 89, 124707 CrossRef PubMed.
- N. Dayan, Y. Ishay, Y. Artzi, D. Cristea, B. Driesschaert and A. Blank, J. Magn. Reson. Open, 2020, 2, 100005 CrossRef.
- Y. Artzi, Y. Twig and A. Blank, Appl. Phys. Lett., 2015, 106, 084104 CrossRef.
- H. Malissa, D. Schuster, A. Tyryshkin, A. A. Houck and S. A. Lyon, Rev. Sci. Instrum., 2013, 84, 025116 CrossRef CAS PubMed.
- A. J. Sigillito, H. Malissa, A. M. Tyryshkin, H. Riemann, N. V. Abrosimov, P. Becker, H.-J. Pohl, M. L. Thewalt, K. M. Itoh and J. J. Morton, et al. , Appl. Phys. Lett., 2014, 104, 222407 CrossRef.
- A. Bienfait, J. Pla, Y. Kubo, M. Stern, X. Zhou, C. Lo, C. Weis, T. Schenkel, M. Thewalt and D. Vion, et al. , Nat. Nanotechnol., 2016, 11, 253 CrossRef CAS PubMed.
- V. Ranjan, S. Probst, B. Albanese, T. Schenkel, D. Vion, D. Esteve, J. Morton and P. Bertet, Appl. Phys. Lett., 2020, 116, 184002 CrossRef.
- T. Yalcin and G. Boero, Rev. Sci. Instrum., 2008, 79, 094105 CrossRef CAS PubMed.
- J. Anders, A. Angerhofer and G. Boero, J. Magn. Reson., 2012, 217, 19–26 CrossRef CAS PubMed.
- J. Anders and K. Lips, J. Magn. Reson., 2019, 306, 118–123 CrossRef CAS PubMed.
- R. Narkowicz, D. Suter and R. Stonies, J. Magn. Reson., 2005, 175, 275–284 CrossRef CAS PubMed.
- R. Narkowicz, D. Suter and I. Niemeyer, Rev. Sci. Instrum., 2008, 79, 084702 CrossRef CAS PubMed.
- D. Hoult and R. Richards, J. Magn. Reson., 2011, 213, 329–343 CrossRef CAS PubMed.
- R. Schumacher, Introduction to Magnetic Resonance: Principles and Applications, W. A. Benjamin, 1970 Search PubMed.
- G. Feher, Phys. Rev., 1959, 114, 1219–1244 CrossRef CAS.
- G. Jeschke, Einführung in die ESR-Spektroskopie, Johannes Gutenberg Universität, Mainz, 1998 Search PubMed.
- G. M. Smith, P. A.-S. Cruickshank, D. R. Bolton and D. A. Robertson, Electron Paramagnetic Resonance, The Royal Society of Chemistry, 2008, vol. 21, pp. 216–233 Search PubMed.
- P. P. Borbat, R. H. Crepeau and J. H. Freed, J. Magn. Reson., 1997, 127, 155–167 CrossRef CAS PubMed.
- W. Hofbauer, K. Earle, C. Dunnam, J. Moscicki and J. Freed, Rev. Sci. Instrum., 2004, 75, 1194–1208 CrossRef CAS.
- J. Lovett, B. W. Lovett and J. Harmer, J. Magn. Reson., 2012, 223, 98–106 CrossRef CAS PubMed.
- M. K. Bowman, H. Chen and A. G. Maryasov, eMagRes, 2017, 387–406 CAS.
- M. Bonora, S. Pornsuwan and S. Saxena, J. Phys. Chem. B, 2004, 108, 4196–4198 CrossRef CAS.
- P. A. Cruickshank, D. R. Bolton, D. A. Robertson, R. I. Hunter, R. J. Wylde and G. M. Smith, Rev. Sci. Instrum., 2009, 80, 103102 CrossRef PubMed.
- H. Mahdjour, W. Clark and K. Baberschke, Rev. Sci. Instrum., 1986, 57, 1100–1106 CrossRef CAS.
- S. Stoll and B. Kasumaj, Appl. Magn. Reson., 2008, 35, 15–32 CrossRef CAS.
- T. W. Borneman and D. G. Cory, J. Magn. Reson., 2012, 225, 120–129 CrossRef CAS PubMed.
- J. M. Franck, R. P. Barnes, T. J. Keller, T. Kaufmann and S. Han, J. Magn. Reson., 2015, 261, 199–204 CrossRef CAS PubMed.
- J. Makhoul, Proc. IEEE, 1975, 63, 561–580 Search PubMed.
- G. Zhu and A. Bax, J. Magn. Reson., 1990, 90, 405–410 CAS.
- P. Koehl, Prog. Nucl. Magn. Reson. Spectrosc., 1999, 34, 257–299 CrossRef CAS.
- M. Teucher, M. Qi, N. Cati, H. Hintz, A. Godt and E. Bordignon, Magn. Reson., 2020, 1, 285–299 CrossRef.
- G. Rinard, R. Quine, S. Eaton, G. Eaton and W. Froncisz, J. Magn. Reson., 1994, 108, 71–81 CrossRef.
- M. Yulikov, P. Lueders, M. F. Warsi, V. Chechik and G. Jeschke, Phys. Chem. Chem. Phys., 2012, 14, 10732–10746 RSC.
- M. Teucher and E. Bordignon, J. Magn. Reson., 2018, 296, 103–111 CrossRef CAS PubMed.
- G. Jeschke, Prot. Sci., 2018, 27, 76–85 CrossRef CAS PubMed.
- M. Matsumura, J. Wozniak, S. Dao-Pin and B. Matthews, J. Biol. Chem., 1989, 264, 16059–16066 CrossRef CAS PubMed.
- R. Narkowicz, H. Ogata, E. Reijerse and D. Suter, J. Magn. Reson., 2013, 237, 79–84 CrossRef CAS PubMed.
- M. Šimėnas, J. O'Sullivan, C. W. Zollitsch, O. Kennedy, M. Seif-Eddine, I. Ritsch, M. Hülsmann, M. Qi, A. Godt, M. M. Roessler, G. Jeschke and J. J. Morton, J. Magn. Reson., 2021, 322, 106876 CrossRef PubMed.
- G. Jeschke, J. Magn. Reson., 2019, 306, 36–41 CrossRef CAS PubMed.
- D. Goldfarb, J. Magn. Reson., 2019, 306, 102–108 CrossRef CAS PubMed.
- G. Jeschke, M. Sajid, M. Schulte, N. Ramezanian, A. Volkov, H. Zimmermann and A. Godt, J. Am. Chem. Soc., 2010, 132, 10107–10117 CrossRef CAS PubMed.
- C. J. López, Z. Yang, C. Altenbach and W. L. Hubbell, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E4306–E4315 Search PubMed.
- C. E. Tait and S. Stoll, Phys. Chem. Chem. Phys., 2016, 18, 18470–18485 RSC.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- Y.-W. Chiang, P. P. Borbat and J. H. Freed, J. Magn. Reson., 2005, 172, 279–295 CrossRef CAS PubMed.
- S. G. Worswick, J. A. Spencer, G. Jeschke and I. Kuprov, Sci. Adv., 2018, 4, eaat5218 CrossRef CAS PubMed.
- J. L. Amey, J. Keeley, T. Choudhury and I. Kuprov, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, 1–7 CrossRef PubMed.
- G. Jeschke, V. Chechik, P. Ionita, A. Godt, H. Zimmermann, J. Banham, C. Timmel, D. Hilger and H. Jung, Appl. Magn. Reson., 2006, 30, 473–498 CrossRef CAS.
- G. Jeschke, DeerAnalysis 2013 User Manual, 2013, pp. 1–41 Search PubMed.
- L. F. Ibáñez and G. Jeschke, Phys. Chem. Chem. Phys., 2020, 22, 1855–1868 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d1cp05508a |
| ‡ These authors contributed equally to this work. |
| § Present address: Medical College of Wisconsin, Department of Biophysics, 8701 Watertown Plank Road, Milwaukee, WI 53226. |
| This journal is © the Owner Societies 2022 |

