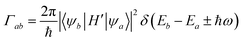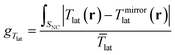Light-to-matter chirality transfer in plasmonics

Abstract

Plasmonic nanostructures are important tools in the study of chirality in the nanoscale. They are systems composed of conducting materials that support resonant excitations of the oscillatory motion of their conduction electrons. Exciting these plasmonic modes effectively localizes radiant energy in and around these nanostructures, which act as electromagnetic antennas operating in the UV-to-IR spectral range. Plasmonic systems can enhance the chiroptical activity of chiral molecules in near-field interaction with them, affording improved sensing capabilities at low analyte concentration or in samples with a low enantiomeric excess. They have also become an important platform through which to test and develop artificial materials with exceptionally large chiroptical activity, through the creation of plasmonic structures or assemblies with chiral geometries or arrangements. The fabrication of chiral plasmonic nanostructures employs a variety of techniques, the most common including the introduction of chiral asymmetry through top–down designs or introducing chiral molecules to direct the chiral growth of the structure. Recently, a different approach is being explored, which involves using chiral light as the only source of asymmetry in developing chiral plasmonic nanostructures. Chirality in this case arises from local transformations occurring on the surface or environment of the nanostructure, in a pattern that follows the local, chiral pattern of excitation induced by the impinging light. This article introduces and explores light-to-matter chirality transfer in plasmonics, contextualizes it within an introductory overview of light–matter interaction and chirality, reviews examples of this nascent technique and discusses its potential in exploiting different energy-transfer mechanisms supported by plasmonic nanostructures.

---

Eva Yazmin Santiago

Eva Yazmin Santiago is a postdoctoral researcher at CINBIO, Universidade de Vigo, Spain. Her research focuses on the theoretical and computational modeling of light–matter interactions in nanostructures and their chiroptical properties. She earned her PhD degree in 2023 from Ohio University, United States, where she studied the optical and photothermal properties of plasmonic nanomaterials. She did research on the same topic at the Universidad Nacional Autónoma de México, where she obtained her Bachelor's degree in 2017.

Muhammad Irfan

Muhammad Irfan is a PhD student at Departamento de Física Aplicada, Universidade de Vigo, Spain and doing his research work at CINBIO with Team NanoTech. His PhD work focuses on modelling excited optical states using ab initio techniques. He is working on different projects including Förster Resonance Energy Transfer (FRET), molecular chirality and photocatalytic degradation. He is also exploring the use of double-hybrid exchange–correlation functionals in modelling spin-resolves states in transition metal complexes. His research aims to enhance the understanding of electronic structures and energy transfer mechanisms, contributing to advancements in computational chemistry and materials science.

Oscar Ávalos-Ovando

Oscar Avalos-Ovando obtained his PhD in Physics at Ohio University in 2018. He is currently a post-doctoral fellow and adjunct professor at Ohio University's Physics Department. Dr Avalos-Ovando is a theoretical/computational condensed matter physicist, specialized in diverse simulations of nano-systems such as 2D materials, plasmonic structures, quantum dots, among others.

Alexander O. Govorov

Alexander O. Govorov is a Distinguished Professor of Theoretical Physics at Ohio University, United States. His research centers on the theory of optical and electronic properties of nanostructures and bio-assemblies. His theoretical predictions have motivated experiments and have been implemented in many research labs worldwide. Dr Govorov is a Fellow of the American Physical Society and the recipient of several international awards, including the Bessel Research Award (A. V. Humboldt Foundation), the Walton Visitor Award (Ireland), 2014 Jacques-Beaulieu Excellence Research Chair Award (INRS, Montreal), etc.

Miguel A. Correa-Duarte

Miguel A. Correa-Duarte received his degree in Chemistry from the University of Santiago de Compostela, Spain, in 1997, and his PhD from the University of Vigo, Spain, in 2002. He is currently the Director of the Research Center in Nanomaterials and Biomedicine (CINBIO) and a Full Professor at the University of Vigo. Additionally, he is a member of IISG and CIBERSAM. His current research interests focus on nanomaterials, particularly the synthesis and functionalization of structures such as core–shell nanohybrids, carbon nanotube-based inorganic and organic nanocomposites, and nanoreactors. These materials are developed for applications in plasmonic-based sensing and photocatalysis.

Lucas V. Besteiro

Lucas V. Besteiro is a Ramón y Cajal Research Fellow at University of Vigo, Spain. He completed his PhD at University of Santiago de Compostela, Spain, after which he held a postdoctoral position at Ohio University, USA, from 2014 to 2017, followed by a postdoctoral fellowship at University of Electronic Science and Technology of China, China, jointly appointed with Institut National de la Recherche Scientifique, Canada, until 2020. His work in computational physics touches on material science and nanophotonics, and his main research interests lie in the field of plasmonics, particularly in studying hot carriers and their role in photocatalysis.

---

1. Introduction and overview

The interaction of light with matter is at the heart of several important threads in the development of modern science and technology. These include the discovery of lasing and its myriad applications, the proliferation of characterization and sensing techniques using different parts of the electromagnetic spectrum, the development of telecommunications technology, advances towards photonic computing, or even motivating the birth of quantum mechanics through the description of blackbody radiation and the photoelectric effect. Today, a student or researcher interested in nanophotonics or nanotechnology will probably have some familiarity with the term “plasmonics” and some of the ideas behind it, as it is present today in a very large number of scientific publications across different areas. The field of plasmonics deals with phenomena and applications related to the resonant oscillations of the cloud of quasi-free electrons present in conducting materials, especially when at least one dimension of the conductor is in the nanoscale. Plasmonic nanostructures are often referred as nanoantennas, as their behaviour resemble the coupling of macroscopic antennas with long-wavelength electromagnetic radiation, but their nanoscale sizes achieve coupling with shorter-wavelength radiation, through the visible spectrum and down to ultraviolet (UV) wavelengths.^1,2 This strong, resonant interaction with light can be exploited both for their own optical properties,^3–6 inducing changes in the optical response of other systems,^7–12 or for their capability of inducing local changes in their environment.^13–16 Readers interested in some facet of this field can not only encounter excellent general reviews,^17–20 a wide expanse of work dealing with fundamental exploration and modelling of plasmonic phenomena is also available.^21–26 They can also learn about varied fabrication techniques,^27–32 and applications in sensing,^33–36 photodetection,^37–40 photoheating,^15,41–43 photochemistry,^{13,14,44–46} and other areas.^47–51 This focus article intends to offer both an entry point and brief overview to a particular research thread in plasmonics, relatively new and still developing, related to a storied aspect of the study of plasmonic nanocrystals: their capability to produce strong chiroptical signals exploiting chiral asymmetries in single nanostructures, aggregates, or structured metamaterials.^52,53

The research thread that we will explore in detail in this article develops a particular path for the creation of plasmonic nanostructures with chiral asymmetries, starting with achiral plasmonic nanostructures and becoming asymmetric through their interaction with chiral light, without involving chiral molecules. This light-to-matter chirality transfer is mediated by physical or chemical transformations initiated by light occurring around the nanostructures. A notable case of this phenomenon is the photogrowth of a material layer over the metal, following the symmetry (or lack thereof) of the combined system of plasmonic resonator and light.^54,55 Of course, it is important to realize that this is not the only method for creating chiral plasmonic systems, which can be efficiently produced with techniques such as lithography,^56,57 DNA-origami templating,^58,59 or growth controlled by chiral molecules.^60–62 Nonetheless, controlling the evolution of the nanostructures’ shape through the symmetry of the light impinging on them holds significant scientific interest on several accounts: firstly, and obviously, it represents a new path for controlling matter in the nanoscale, potentially in conditions that are not accessible to other methods; serves as a test space for improving our understanding of the local evolution of surface reactions in plasmonic photocatalysis, and in so-doing allows us to refine our models of energy-transfer mechanisms from plasmon to environment; can be developed as a passive technique to evaluate properties of the light; and can be used to refine our understanding of the light–matter interaction when working with chiral light. Related to this last point, let us underscore that, although light-to-matter chirality transfer on plasmonic nanostructures can be understood as a form of chiral photocatalysis, as it involves both concepts at its core, this process is wholly distinct from enantioselective photocatalysis. Chiral photocatalysis refers to the latter, to the control of the chirality of a molecular sample through different photocatalytic processes involving chiral light. They are thus different phenomena, they operate at different spatial scales, and involve different physical mechanisms. Yet, due to the well-known capabilities of using plasmonic resonators to influence different optical and chemical processes at the molecular scale, the possibility of achieving strongly enantioselective photocatalysis exploiting the properties of chiral and achiral plasmonics is actively pursued.^63–65 So, for the purpose of clearly distinguishing these two families of phenomena, we will provide a brief overview of light–matter interaction in the particular context of using chiral light.

This article will provide an introductory overview to light–matter interaction and chirality, building up to a discussion of light-to-matter chirality transfer. Section two will introduce chirality in matter and in light. Section three will describe fundamental ideas behind modelling the interaction of light with chiral matter, attending to the similarities and differences of modelling discrete transitions in molecules and collective oscillations in plasmonic systems. Section four will engage directly with the topic of light-to-matter chirality transfer in plasmonic systems, presenting a discussion on theoretical and experimental work in the field that is structured according to the different physical mechanisms that can induce the imprinting of chirality. Finally, section five presents brief conclusions based on the prior discussion, presenting the thoughts of the authors about the foreseeable future of this field of study.

2. Chirality

2.1. Geometry and chiral matter

Chirality is the relationship between two objects that can be transformed into each other by a mirror transformation, but not under translation and rotation. These two objects are enantiomers, with one labelled as left-handed and the other right-handed, taking advantage of our familiarity with the paradigmatic enantiomeric pair, our hands. The conditions for chirality of a system, e.g. a molecule, can be expressed using ideas from group theory, the mathematical framework used to describe the symmetries of an object or space. The symmetry of a chiral object can be described by a point group that is purely rotational, i.e. lacks reflection symmetry, inversion symmetry, and axes of improper rotations, which combine rotation around an axis with a reflection across a plane perpendicular to that axis.

Chirality is a geometrical concept with several significant implications in the natural sciences. This connection is, of course, far from surprising, as the spatial arrangement of atoms directly determines the available electronic states in a molecule or a crystal, and symmetry plays an important role in understanding the properties of matter. But chiral asymmetries play a particularly important role in biology, because life on Earth is homochiral,⁶⁶ and enantiomers of chiral molecules can have drastically different effects in living organisms. This highlights chirality as a property of interest in biological, medical, and pharmaceutical contexts,^67–71 including more specific ones such as food science.^72–74 Consequently, the study of chirality in the micro and nanoscale is strongly motivated by applications, which has motivated much research on the chiroptical properties of matter for the purpose of sensing and manipulation,^64,75,76 as well as fundamental interest in physics and optics.^77–79

Before starting the discussion of chirality in electromagnetic fields, it is useful to introduce some additional terms that are useful to group different types of material systems attending to their asymmetry. Then, to the above general description of chiral 3D geometries, we can append several additional terms used to describe systems that are not strictly chiral, but still have chiroptical activity. The first, 2D chirality, or planar chirality, describes geometries that are chiral only when confined to the reduced dimensionality of a plane, but not if we consider them as living in 3D space. This is an important category in the context of this article, as many of the systems that we will discuss in examples of light-to-matter chirality transfer are structures supported on a substrate. A 2D chiral object will provide a chiroptical signal, but its handedness will be flipped depending on whether we are illuminating it from above or below. Fig. 1a and b show examples of chiral structures in 3D and 2D, respectively. The object is first mirrored to obtain a mirror image. The image is then rotated in an attempt to perfectly match the original object. If this can be achieved, the structure is achiral; however, when we cannot superimpose the object and the mirror image, by definition, the structure is chiral.

Fig. 1 Types of chirality with example geometries. (a) Objects with intrinsic 3D chirality cannot be superimposed over their mirror images through any translation and rotation in 3D space. (b) Objects with intrinsic 2D chirality have the same property if we restrict the possible transformations to those within the plane of the object. (c) Extrinsic chirality arises when an achiral 2D object is excited by light at angle such that the combined system of object plus light is chiral in 2D. (d) Chirality induced on a plasmonic nanoparticle by closing its distance to a chiral molecule. The plot shows the CD of the whole system where δ is the gap, in nm, between the nanoparticle and molecule.

Now, it is useful to extend our vocabulary to encompass systems that, even if not geometrically chiral, can have a chiroptical response under illumination. We can then contrast systems with 3D or 2D chirality, which have intrinsic chirality, to those with extrinsic chirality, which only showcase chiral asymmetry if considered together with the impinging light. This latter category then includes systems whose chiroptical response arises from the excitation conditions, most typically when planar resonators are probed with circularly polarized light (CPL) arriving at an angle lower than 90°,^80,81 but can also occur through other mechanisms, like the interaction of single-resonator and lattice modes in planar metamaterials.^82,83 Fig. 1c shows an example of extrinsic chirality created by the direction of the incident light on a planar metamaterial.^84,85 This is due to an oblique incidence, which breaks the symmetry of the whole arrangement. However, if a line of symmetry of the geometry was contained within the plane of incidence, the combined response of the system would remain achiral. Lastly, the term of induced chirality is used when an achiral system registers a chiroptical response because it is in close electromagnetic interaction with a chiral element.⁸⁶ Within the context of plasmonics, a relevant example is the interaction of a chiral molecule with an achiral plasmonic resonator or lattice, with the latter not only enhancing the chiroptical signal of the molecule, but also inducing a chiroptical signal at its plasmonic modes.^{11,83,87–89} Fig. 1d shows the chiroptical response—circular dichroism (CD) in particular, which we describe in detail in a later section—for a chiral molecule and a plasmonic nanoparticle approaching each other. Individually, the plasmonic nanoparticle is nonchiral (CD = 0) and the chiral molecule CD is represented by the red line on the plot. However, when the gap between them is small enough, the CD increases at a wavelength corresponding to the nanoparticle plasmon resonance.

2.2. Chirality in light

The paradigmatic case of chiral light is a circularly polarized planewave. A planewave will have a specific polarization and direction. When no polarization can be determined, we say that the light is unpolarized and can be constructed by the incoherent sum of many planewaves with different polarizations. A polarized wave with a well-defined direction of propagation is typically described as having three basic types of polarization: linear, circular and elliptical. Let us describe in some more detail such cases. Light can be described as an electromagnetic wave composed, as the name suggests, of an electric and magnetic field oscillating perpendicularly to the direction of propagation. We can write each of these fields as

E = E₀e^{i(k·x−ωt)}, B = B₀e^{i(k·x−ωt)}

where E₀ and B₀ are the polarization vectors for the electric and magnetic fields, respectively, and are perpendicular to each other. Meanwhile, k and ω are the wavevector and angular frequency of the planewave, respectively. These two magnitudes are connected by the dispersion relation of the medium through which the light propagates, as ω = ck/n, where c is the speed of light in vacuum, k is the module of the planewave's wavevector, and n is the real part of the refractive index of the propagation medium. The refractive index is in general both a complex-valued and frequency-dependent magnitude, where the real part affects the propagation of light while the imaginary part accounts for the attenuation of the electromagnetic field.⁹⁰ The phase velocity of a wave is v_p = ω/k, and thus the real part of refractive index is the ratio of the speed of light in vacuum to its speed in a specific medium (n = c/v_p), giving us information on how much a monochromatic wave slows down when traveling through a material.

Let us now focus on the oscillating electric field, both for simplifying our discussion, and because the optical phenomena that we will discuss are dominated by electric, rather than magnetic, effects. Furthermore, we can choose a wave moving in the z direction to work with a more specific notation. Then, we can write the electric field of a planewave propagating along the z axis and with its electric field oscillating in the orthogonal x–y plane as

E = E₀e^i(kz−ωt), E₀ = (E_x, E_y, 0)

Importantly, each of the components of the polarization vector is a complex-valued number, so we can express them in terms of the individual amplitudes and phases, as

E_x = |E_x|e^iδ_x, E_y = |E_y|e^iδ_y

It will be more convenient, however, to discuss the polarization of the plane wave in terms of the phase difference between these two components of the polarization vector, δ = δ_y − δ_x. Then, we can identify a plane wave that is linearly polarized as one with no phase difference between the components of its polarization vector (δ = 0). Linearly polarized light (LPL) has its electric field oscillating in a fixed plane containing both the direction of propagation and the polarization vector. The electric field for linear polarization in the ê direction can be expressed as

E = E₀êe^{i(k·r−ωt)}

Particularly, a planewave moving in the z direction with an arbitrary initial phase can be written as

E = (|E_x|x̂ + |E_y|ŷ)e^i(kz−ωt)

In contrast, an elliptically polarized planewave has its electric field rotating around the direction of propagation, and our wave propagating along the z axis is written by the more general expression

E = (|E_x|x̂ + |E_y|e^iδŷ)e^i(kz−ωt)

where |E_x| and |E_y| are not equal, δ is nonzero or both. From this expression, we can single out circularly polarized light (CPL) as a particular case of elliptical polarization, in which the amplitude of the field does not change as it rotates (|E_x| = |E_y|) and the components of the polarization vector have a fixed phase difference of a quarter rotation (δ = ±π/2). The sign of their relative phase defines the wave handedness. Then, by analyzing the previous equations, we can see that a circularly polarized wave is the superposition of two perpendicular linearly polarized planewaves with the same amplitude and a phase difference of ±π/2. This is illustrated on Fig. 2a, which illustrates a frozen snapshot of a circularly polarized plane wave, in red, alongside two linearly polarized waves, in blue and green. Now, in order to define its handedness, it is important to define from which perspective we are going to evaluate the rotating field. Two options are available: either from that of the light source or from that of the object towards which the light propagates (see them also in Fig. 2a). These define two different reference systems and labelling conventions. In this text we will use the “source” convention, but both are valid and widely used in the published literature (in fact, some of the work we will reference in later sections use the other convention). Then, we can recognize that the wave in Fig. 2a is left-handed circularly polarized (LCP) because an observer at the source would see the electric field rotate counterclockwise when attending to a fixed plane orthogonal to the wave's propagation direction. For a wave moving in the z direction like the one described by the equation above for elliptical polarization, we obtain an LCP wave when |E_x| = |E_y| = E₀, and the phase difference is δ = π/2, so that

E_LCP = E₀(x̂ + iŷ)e^i(kz−ωt)

Whereas right-handed circularly polarized (RCP) light would correspond to a phase difference δ = −π/2, so that

E_RCP = E₀(x̂ − iŷ)e^i(kz−ωt)

It is worth noting that a linear planewave could also be seen as a superposition of two circularly polarized planes of opposite handedness and equal amplitude. The phase difference between them would define the polarization direction of the linearly polarized wave. In fact, treating CPL as the fundamental type of polarization, with LPL being a linear combination of circularly polarized (CP) modes with opposite handedness, is the more natural approach from the perspective of quantum mechanics: photons, being massless particles with spin s = 1, have only two available states, with their spin pointing either along or opposite to their direction of propagation.^91,92 Then, photons have a spin angular momentum (SAM) of and a helicity when propagating along the z axis, i.e. the projection of the SAM over its propagation direction, of S_z = ±ħ. The state with positive helicity corresponds to an RCP photon, while the negative helicity corresponds to an LCP photon (see Fig. 2b).^93,94

Fig. 2 (a) Schematic diagram of a CP wave and the two LP waves composing it, with time fixed. Both source and object are labelled to indicate the two distinct perspectives that give rise to the two naming conventions for the handedness of CPL. In this example, the source (object) sees a counterclockwise (clockwise) rotation in the highlighted plane as time advances, so that it corresponds to LCPL (RCPL). (b) Photons are circularly polarized. (Left) Schematic diagrams of the rotating electric field at a fixed time, labelled with the handedness of the state in the source convention. (Right) Corresponding helicity, i.e. projection of the magnetic moment (from spin) over the propagation direction, of the photons with opposite handedness. (c) Vortex beams with orbital angular momentum. Intensity and phase profiles for the primary mode of a Laguerre–Gaussian beam with l = [−2, −1, 0, 1, 2]. The top row shows the phase front for the different modes. The middle row shows the corresponding azimuthal phase profiles, and the bottom row shows the corresponding planar intensity profile. Reproduced from ref. 95.

Circularly polarized light is then the fundamental state of light and can thus be considered as the paradigmatic case of chiral light. As such, in this article we will focus on CPL for discussing the interaction of chiral light with matter. But it is important to keep in mind that the category of chiral light is not exhausted by CPL. We can obtain a more general perspective if we consider the complete angular momentum of light, composed of both orbital, L, and spin component, S, as

In this context, and as described above, CPL is light composed by photons with angular momentum solely derived from their intrinsic spin, which is parallel (or antiparallel, for its opposite handedness) to their direction of propagation. Light, however, can also carry orbital angular momentum (OAM),^94,96,97 which implies a departure from being a plane wave, with a planar phase front. A beam with OAM has a phase dependence on the azimuthal angle around the beam propagation direction, such as the helical phase front shown in Fig. 2c. A beam with an OAM of L_z = lħ, with l∈[0, ±1, ±2, …] different from zero, is a vortex beam with topological charge l. This topological charge corresponds with the number of full phase twists per wavelength described by the beam.^95,98–100 Vertex beams are varied in type and in their applications,^101,102 allowing for the chiral manipulation of matter, e.g. through inducing circular movement patterns in nanoparticles,^103,104 inducing chiral currents in plasmonic nanostructures,^105,106 or, in clear examples of light-to-matter chirality transfer, carving twisting chiral metal spikes^107–110 or photopolymerizing chiral pillars,¹¹¹ several micra in size. Optical beams with OAM are examples of the even more general category of structured light,^112–114 which extends to cover any optical field with relevant spatial inhomogeneities in some of the parameters describing it,¹¹³ and includes other examples of chiral light.^115,116 Nonetheless, and as mentioned above, CPL or SAM light remains the paradigmatic and fundamental form of chiral light. It is also arguably the simplest to produce in standard optical setups, and more straightforward to study theoretically in describing the interaction between chiral light and matter. Consequently, in the remainder of this article we will only consider CPL as the chiral light inducing asymmetry in the nanoscale. Circularly polarized light is also an important, routinely used probe for the study of the chirality of matter. Incidentally, understanding some basics ideas underlying the interaction of CPL with chiral matter is useful to set the background against which we will discuss light-to-matter chirality transfer. Then, let us preface our discussion on the interaction of chiral light with achiral matter by presenting some basic ideas regarding the interaction of chiral light with chiral matter.

3. Interaction of light with chiral matter

3.1. General aspects

From a macroscopic perspective, investigating whether matter is chiral in its microscopic composition mainly depends on exploring how a sample interacts with the polarization of light. Although the absence of chiroptical properties does not guarantee that no microscopic chiral components are present in the sample, the presence of proper chiroptical phenomena does report on the presence of some form of chirality. There are two fundamental magnitudes for quantifying the chiroptical response of matter: circular dichroism and optical rotation. Both are manifestations of the optical activity in chiral media. To define circular dichroism, we must first introduce dichroism. Dichroism refers to a sample's selectivity in its response to light with two different characteristics, such as polarization. When light travels through a dichroic material, a differing extinction coefficient for two polarized rays causes one to be absorbed more efficiently. Then, the dichroic material will have a different appearance depending on the light polarization. And just like there are different types of polarization, there are also different types of dichroism. Linear dichroism refers to the differential absorption between beams with orthogonal linear polarization, and offers information about the anisotropy of the sample. Similarly, circular dichroism (CD) is the difference of amount of light absorbed for left- and right-circularly polarized light. This differential absorption can be expressed as a difference of several magnitudes, with the absorbance of the sample being particularly straightforward to measure, measuring transmission along the path of the input beam:

CD_A = ΔA = A_LCP − A_RCP,

where A is the absorbance, or the attenuation of an incoming beam after a path of length d, A = log(I₀/I_d), and it is measured under beams of circularly polarized beams of opposite handedness. An alternative, commonly used metric is that of circular dichroism obtained as the difference of molar extinction coefficient under LCP and RCP light, Δε = ε_LCP − ε_RCP. Here, the reader should be aware of the ambiguity arising from using the same notation for molar extinction coefficient and permittivity. One should note that these magnitudes group together absorption and scattering, but these can also be addressed separately with an appropriate setup, by measuring light scattered from the path of the input beam.^117–119 A visual schematic description of circular dichroism when light traverses through a chiral medium is shown in Fig. 3a. When two incident light beams with different circular polarization and equal intensity travel through a chiral medium, the transmitted polarizations have different intensities due to the preferential interaction of the sample with one of the polarizations. When working with films or other planar systems, common in the study of chiral metamaterials,^120,121 instead of measuring absorbance one would work with absorption, also noted as A, reflectance R, or transmittance, T. These magnitudes, which are normalized by the beam intensity, are connected by the principle of conservation of energy, so that A + R + T = 1. It is worth noting that many plasmonic metamaterials are prepared over continuous metallic substrate layers, or mirror backplanes,^122,123 so that no power is transmitted and the above relationship holds simply between A and R.

Fig. 3 (a) Schematic diagram of the phenomenon of circular dichroism, showing the differing attenuation for RCP and LCP light rays traveling through a chiral medium. This differential absorption is also depicted through bars indicating the amplitude of the different CPL beams before and after they cross the material. (b) Schematic diagram of the phenomenon of optical rotation, showing how a linearly polarized plane wave has its polarization plane rotated along the direction of propagation when travelling through a chiral substance.

Measuring CD in a sample is an indication of it having some microscopic chiral component, and its particular CD spectrum provides information on its characteristics, not only through its absolute magnitude (as a measure of both chirality and interaction strength) but also through its features at different wavelengths (related to the energy of the molecular transition involved, if that is the case, or to the spatial scale of the chiral phenomenon producing it).¹²⁴

In measuring chirality through circular dichroism, it is often informative to use a normalized magnitude that removes the dependence on factors such as molecular concentration, so that the interpretation of the chiroptic spectra relates only to the chirality of the sample. The so-called g-factor,¹²⁵ g_A, or Kuhn's dissymmetry or anisotropy factor, is defined as the CD of the sample normalized by the average of the absorbance under LCPL and RCPL:

Given that the values of A are positive, it is clear that g_A can take values between −2 and +2. As a rule of thumb, we can expect small chiral molecules to have absolute values of g_A in the order of ∼10⁻²–10⁻⁵, while chiral plasmonic nanostructures can reach larger values, up to ∼10⁻¹ for colloidal structures and even ∼10⁰ for planar metamaterials.^116,126,127

The second of the characteristic optical responses of chiral matter is optical rotation, also known as circular birefringence, which is the ability to rotate the polarization plane of linearly polarized light. When CPL travels through an optically active medium, the light has a different velocity depending on its handedness. Since a linearly polarized planewave is the sum of two circularly polarized planewaves of opposite handedness, the velocity difference between LCPL and RCPL changes their relative phase difference, which in turn causes a rotation of the linearly polarized planewave. Fig. 3b shows an incident vertically linearly polarized planewave passing through a chiral medium. Once the light ray fully escapes the material, the polarization direction is rotated relative to its initial orientation. This optical rotation can be measured with an instrumented called a polarimeter and it is commonly used to obtain the relative concentration of enantiomers of chiral molecules in a sample.¹²⁸ In particular, the magnitude used to report a sample's optical rotation is the optical rotatory dispersion (ORD), or its specific rotation spectrum. The specific rotation is the angle at which optical rotation occurs at a particular wavelength, temperature and concentration of the chiral material. It is important to note that CD and ORD are not independent from each other, as they are connected through Kramers–Kronig transformations.¹²⁹ Although both can be determined experimentally, measuring and computing CD is often favoured because it can be easier to interpret.¹³⁰ In the rest of this article we will focus on discussing CD characterization. We will not discuss, however, the experimental approaches used to measure these and other (e.g. Raman optical activity or circularly polarized luminescence) chiroptical magnitudes, pointing instead to useful recent monographs on this topic.^131–134

These two magnitudes, CD and ORD, are metrics for two fundamental phenomena associated with chiral media: differential CPL absorption and differential CPL propagation velocity. Both deal with how matter responds differently to electromagnetic fields oscillating with different symmetries. We can concisely describe the behaviour of these materials by expanding the constitutive relations connecting the microscopic and macroscopic electric and magnetic fields in the medium.¹³⁵ Usually, the electric field, E, and the electric displacement field, D, are parallel to each other, and the same applies to the magnetic flux density, B, and magnetic field strength, H, but a more general account of a medium's response includes additional field couplings. Bi-isotropic media are a general category of such materials, of which chiral media is a subclass. The constitutive relations of bi-isotropic materials can be written as:

In these equations, ε is the permittivity of the medium, which is a measure of how the material responds to an electric field, and μ is its magnetic permeability, which is a measure of its response to a magnetic field. The subscript in these variables denotes their values in vacuum. Meanwhile, the dimensionless parameters χ and κ define the bi-isotropic nature of the material. The chirality parameter κ, or Pasteur parameter, defines the material's degree of handedness. It can be positive or negative, one being the mirror image of the other. In the matrix with the constitutive relations, we can see how the chirality parameter introduces a phase dependence between the electric and magnetic fields, whereas the Tellegen parameter, χ, introduces a direct coupling between the magnitudes of the electric and magnetic fields. This latter parameter is related to the magnetoelectric effect.¹³⁶ In particular, κ ≠ 0 describes a chiral medium, and χ ≠ 0 describes a non-reciprocal medium. If both chirality and Tellegen parameters are nonzero, we have the general case of bi-isotropic medium. The following table summarizes the materials resulting from differing values for κ and χ.

	Non-chiral (κ = 0)	Chiral (κ ≠ 0)
Reciprocal (χ = 0)	Simple isotropic medium	Pasteur medium
Non-reciprocal (χ ≠ 0)	Tellegen medium	General bi-isotropic medium

We will now proceed by just considering reciprocal chiral materials, so we will take the case where κ ≠ 0 and χ = 0, which is also known as Pasteur media. In that case, the constitutive relations are expressed as follows

Additionally, the refractive indices for LCP and RCP are expressed as
where the plus and minus sign represent each handedness of the CPL.⁸¹ From this relationship the effect of optical rotation is apparent, with the distinct propagation speed for CPL with opposite handedness. But it is important to remember that the refractive index is complex-valued, where the real part defines the velocity of propagation of the wave and the imaginary part relates to the amount of light that is absorbed by the medium causing the electromagnetic wave to be attenuated. Consequently, a difference in the imaginary part of the refractive index leads to a difference of the attenuation for RCP and LCP, which we already defined as circular dichroism. Therefore, the refractive index and the chirality parameter are closely connected to CD and ORD as follows

ORD ∝ Re(κ)l

CD ∝ Im(κ)l

where l is the optical path length, which is the product of the material thickness and the refractive index.

Up to this point we have described the effect of chiral matter on light propagating through it, without touching on the microscopic structure that can give rise to this behaviour. Let us now briefly discuss key points of the interaction of light with chiral molecular media, containing chiral molecules or chiral nanostructures. As stated in the introduction, the main aim of this article is to describe and discuss ways of using the asymmetry of CPL to induce the development of chirality in initially achiral nanostructures. In this context, understanding the origin of the chiral response of small molecules provides a good contrasting system to highlight the chiroptical characteristics of plasmonic structures, not to mention it being of intrinsic interest. The study of chiroptical activity is, after all, in good part driven by our interest in characterizing and manipulating the stereochemical conformation of many molecular compounds, from sweeteners to drugs.^137–140 However, one common limitation in the study of molecular chirality is their relatively small dissymmetry factors, in the order of ∼10⁻²–10⁻³, or lower.¹⁴¹ This is due in part to the size disparity between the chiral chromophores—up to a few nm—and the wavelength of the light exciting them—hundreds of nm. The creation of larger molecular aggregates with chiral structures can bridge this disparity (see Fig. 4a), with larger systems such as liquid crystals providing significant dissymmetry in their interaction with CPL.¹¹⁶ The relevant size scale at which the system is chiral also determines the spectral regions at which the dichroism is most notable, with larger chiral structures offering chiroptical activity at longer wavelengths. Yet, chiral molecular media, especially single chiral chromophores, cannot match the chiroptical dissymmetry values that are possible to reach with chiral plasmonic resonators.^53,78 A fundamental reason for this is the much larger electronic density of plasmonic materials, and the number of electrons involved in the optical interaction of the material. When a plasmonic nanostructure is excited, the impinging light is exciting a collective oscillation mode of the system, involving the quasi-free carriers in its conduction band. The resonant excitation of these modes leads to strong optical cross sections when compared with materials that absorb light through single-electron optical transitions, such as molecules or semiconductors. In Fig. 4b we can see a comparison of absorption cross sections of a dye with semiconductor quantum dots (QDs) and plasmonic nanostructures with the same volume in a semi-log scale that makes apparent the large disparity, with the metal dominating with their antenna-like response. Moreover, this panel also illustrates how plasmonic nanostructures made with a given material change their optical spectrum drastically when changing their shape, because it constrains the possible displacement of the charge and thus defines the resonant modes supported by the structure.^20,142,143 This is a momentous feature when it comes to study chirality in the nanoscale, as we will show below. In the following subsections we develop and contrast the fundamental ideas giving rise to the chiroptical response of small molecules and plasmonic nanostructures. We begin discussing small chiral molecules to contextualize the study of chiral plasmonics in several aspects. One being historical, as the chiroptical activity of molecules precedes and motivated further study in nanoscale chirality. It also serves as a contrasting reference, highlighting differences in the relevant light–matter interaction mechanisms behind both, and their resulting typical chiroptical responses. This can be of special interest when studying the chiroptical signal of molecular–plasmonic hybrids in the context of molecular characterization or even chiral photocatalysis.

Fig. 4 Molecular and plasmonic systems interact differently with light. (a) Schematic diagram of different types of chiral molecules and chiral molecular assemblies with increasing size scales. It illustrates how the spatial scale of the chiral asymmetry relates to the resulting chiroptical spectrum of the molecular system. (b) Absorption cross sections of a dye, two semiconductor QDs and two Au nanoresonators, illustrating that the optical response of plasmonic nanoparticles is stronger than semiconductor systems of equal volume, and significantly more so than single chromophores. Moreover, the optical response of plasmonic structures is very sensitive to their geometry. Panel a reproduced from ref. 116. Panel b reproduced from ref. 144.

3.2. Chiral molecules

The optical response in small systems is best described by a fully quantum mechanical framework, with the promotion of one electron from an occupied to an unoccupied electronic state. This transition is mediated by the absorption of a photon with a wavelength corresponding to the energy difference between the original and the excited electronic configuration, ΔE = hc/λ. The collection of such transitions composes the absorption spectrum of the system, while transitions from configurations of higher to lower energies compose its emission spectrum. The latter being different from the absorption due to differences in the vibrational states between ground state and excited state of the molecule.¹⁴⁵ Optical transitions must fulfil not only conservation of energy, as stated above, but also conserve angular momentum of the electron–photon system. In atomic physics this leads to the familiar selection rules on the changes in the electronic quantum numbers between initial and final states in single-electron transitions, ΔS = 0 and Δl = ±l.¹⁴⁶ Such selection rules do not strictly rule out other transitions, but rather recognize them as forbidden within the context of an electric dipole transition and thus of comparatively low strength.¹⁴⁷ Transitions with larger multipolar electric orders, and magnetic transitions can still occur, but at slower rates. Moreover, in the context of molecular spectroscopy, real transitions will not in general be purely dipolar–electric, as transitions connecting two geometrically complex molecular states will generally be described by a multipolar expansion in both electric and magnetic moments. The dominant contributions will nonetheless be those from the electric and magnetic transition dipole modes. Let us briefly describe the optical excitation of an electric dipole transition, to then extend our discussion to tackle the relevance of the magnetic dipole transition moment when studying chiral molecules.

By considering the general description of the excitation of an electric dipolar mode, we can examine factors that determine the likelihood of two different optical processes to occur, or their ratio between absorption cross sections, showing explicit ties to the symmetry of the electronic states involved and to their relative orientation with respect to the polarization of light. Both can be made apparent if we consider Fermi's golden rule, that computes the transition probability between two states, Γ_ab, under a weak time-dependent perturbation of the system. This perturbation, H′, is added to the time-independent term to write the total Hamiltonian as H + H₀ + H′. The calculation involves a volume integral that includes the spatially extended electronic wavefunctions of the initial and final states. These wavefunctions are denoted in bra-ket notation as |ψ_a〉 and |ψ_b〉. We can write the golden rule for an optical transition driven by an external oscillating field as

with the interaction term, approximated to its leading order, being
where ê is the polarization vector of the external field, A₀ is the amplitude of its vector potential, m_e is the rest mass of the electron, and p_i is the momentum operator of the i-th electron. Then, considering that we can express the electric dipolar transition between states |ψ_a〉 and |ψ_b〉 using the momentum operator as
the transition probability depends on a factor

|ê·μ_ab|²

This expression encodes the two dependences mentioned earlier: the transition moment μ_ab depends on the spatial extension and relative phase of the initial and final wavefunctions, and its projection over the polarization of the external wave determines that transition probability, being maximum when both are aligned. As mentioned above, μ_ab is only the first term of a longer multipolar expansion that characterizes the charge displacement undergone through the transition, and it is the relevant description of the transition when determining whether a linearly polarized planewave can excite it.

A general optical transition will also be characterized by a magnetic transition moment, which can be intuitively understood as arising from a current created by the electronic displacement in the transition. The magnetic dipolar transition mode can be written as¹³⁰

and characterizes how strongly the magnetic part of the electromagnetic radiation can couple with the transition. Note that this expression computes the orbital magnetic momentum and neglects the effect of electron spin, spin–orbit coupling, and other sources of magnetic hyperfine structure. This is a reasonable assumption when exploring the chirality of molecules, which arises fundamentally from the spatial asymmetry in the electron density.¹⁴⁸ In the context of molecular chirality, the existence and orientation of the magnetic transition dipole moment is key for producing an asymmetry of excitation with oppositely-polarized CPL. We will present its role while exploring a simple case of a small chiral molecule, with the goal of connecting these expressions with some geometrical intuitions.

Our example system will be propylene oxide, or methyloxirane (Fig. 5a), for which we present a collection of numerical data obtained from ab initio simulations of both of its enantiomers, in gas phase. Our results were obtained with Gaussian software, within both DFT and TDDFT formalism. We will first comment on general optical simulated results, to then discuss the origins of chirality in a selected optical transition. One first observation, looking at the molar extinction coefficient data, of R- and S-methyloxirane, can be made on the similarity of both curves, indistinguishable from each other, in Fig. 5b. This, of course, is in line with the statements made at the end of Section 3a, on the small chiroptical effects, relative to their optical response, arising in small chiral molecules. A more adequate way of evaluating the optical activity of each enantiomer is to compute the CD of this chiral molecule, and whose computational spectrum we include in Fig. 5c, where the opposite chiroptical signal for the enantiomers is apparent. The maximum g-factor, or dissymmetry factor, for these molecules is slightly under 3 × 10⁻³, at wavelengths around 160 nm. In both panels, we see the complete spectra for these molecules, which are of course composed of a variety of different discrete transitions. We will now focus on a single transition to discuss several relevant magnitudes.

Fig. 5 Numerical results for ab initio simulations of methyloxirane, or propylene oxide enantiomers. (a) Ball-stick 3D models of both enantiomers, accompanied by their Lewis structure diagrams. (b) Molar extinction coefficient of both enantiomers. Their spectra are indistinguishable at this scale. (c) Circular dichroism of both enantiomers. (d) Circular dichroism of the individual optical transition connecting the ground state with the first excited state. Inset: Electric and magnetic transition dipole moments for both enantiomers, rotated so that m_S and m_R overlap and the projection of μ_S and μ_R are clearly shown to be equal and opposite, and thus R_S = −R_R. (e) Maps of the electrostatic potential surrounding the R-methyloxirane (top) and S-methyloxirane (bottom) at both their ground state and first excited state. The maps are plotted on isosurfaces of electronic density. (f) Two isosurfaces, with positive (turquoise) and negative (purple) values, of the difference of electronic density between the first excited state and ground state for both enantiomers.

We present in Fig. 5d CD data for the first optical transition in each of the enantiomers, connecting their ground state with their first excited state. A given bright mode of a molecule can absorb CPL, but we are interested in characterizing its differential absorption rate under CPL with opposite handedness, from an understanding of the electronic states involved in the transition. For this, we introduce a magnitude known as rotational strength, R_ab, which quantifies the degree of chirality of a given transition, and on which both optical rotation and circular dichroism depend.^148,149 Conveniently, the dissymmetry factor for a given transition can be expressed as a function of its rotational strength, as

where D_ab is the total amplitude of the absorption line,

D_ab = |μ_ab|² + |m_ab|²

although the magnetic term is often neglected in this expression because dipolar–magnetic modes interact weakly with incoming light and the dipolar–electric modes dominate the spectra. Rotational strength is, in turn, defined as¹⁵⁰

R_ab = Im[μ_ab·m_ab] = |μ_ab||m_ab|cos θ

with θ being the angle between these two vectors. Being μ_ab purely real and m_ab purely imaginary, R_ab as defined above is real. It is useful to define an additional magnitude to connect the rotational strength with the chiroptical signals discussed in Section 3a, which is the optical rotation parameter, β. This is a complex function, i.e. β = β_R + iβ_I, and the ORD is proportional to β_R, while the CD is proportional to β_I. Their expressions, and relationship with the rotational strengths, can be written for ideal states without dephasing, as^130,149
Here the index in the sum runs through the possible excited states, and consequently R_0i is the rotational strength of the transition from the ground state to the i-th excited state, which occurs at frequency ω_i. From the equation above, it is clear that the rotational strength, and consequently the ORD and CD, of an optical transition depends on the relative orientations of μ_ab and m_ab. Achiral transitions are those for which these vectors are orthogonal (or either are zero), while the optical activity increases as the angle between them decreases, being maximal when they are parallel. We can derive some intuition about why this is so if we interpret, analogically with classical systems, the magnetic transition dipole m_ab as determining an axis around which the electronic charge rotates as the optical transition occurs.^149,151 Then, aligned electric and magnetic transition dipoles describe an helical, and thus chiral, movement of the electronic density along a given direction, with flipped helicity if they become antiparallel. On the contrary, when non-zero electric and magnetic transition dipoles are orthogonal, their interaction creates transition dipoles that are not chiral but have other properties that make them interesting for their study as emitters, such as near- and far-field directionality.¹⁵²

In Fig. 5d we show the CD of the first optical transition of methyloxirane, together with a representation of the transition dipole moments determining it. The notation for the vectors in the figure is simplified and refers to the transition from the ground state to the first excited state, with the subscript noting which enantiomer they correspond to. Note also that one of the pairs of vectors has been rotated to overlap m_S with m_R, so that it is apparent how the projection of μ_S and μ_R over the magnetic dipole are antiparallel, flipping the sign of the rotational strength between the enantiomers. The two states connected by the first optical transition are shown in Fig. 5e, depicting electrostatic potential maps over isosurfaces of global electronic density, for both enantiomers. Such representation allows us to see the charge displacement induced by the absorption of the photon, although this is made clearer when examining isosurfaces of the difference between the electronic density of the first excited state and the ground state, in Fig. 5f. Here it is clear how the spatial distribution of charge transfer is a complex one that is not clearly described by a dipolar or quadrupolar transition, but rather invites a helical interpretation, as qualitatively sketched above. For further reading on the topic, other chiral molecules that afford a clear geometrical interpretation of the symmetry of the optical modes are helicene molecules.^153–155

Now we will turn our attention towards fundamental aspects of light–matter interaction when working with plasmonics nanostructures. In doing so we will see clear differences on the material support of their chiroptical response, but we will also discuss it in analogy to molecular chirality and the coupled dipole model seen above.

3.3. Chiral plasmonic nanostructures

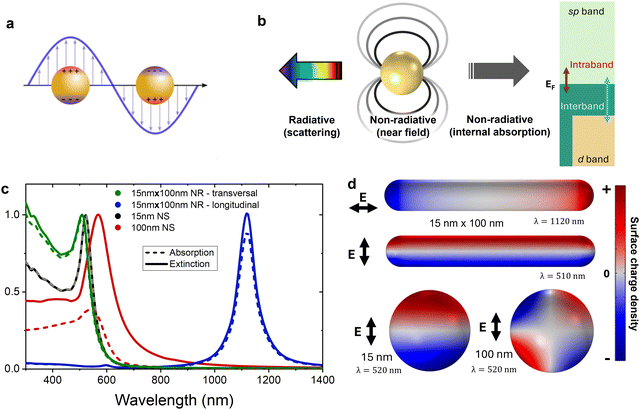
In contrast with the discrete transitions undergone by a single electron in molecular optical transitions, plasmonic excitation necessarily involves many electrons, and it is easiest to understand it in a classical picture, with the electromagnetic waves displacing the quasi-free electrons in the conduction band of a metal. In this picture, the external force induces polarization in the conductor and a corresponding internal electric force in opposition to it (see Fig. 6a). As with a classical mechanical oscillator, if the external driving force, i.e. the electromagnetic wave, matches the natural frequency of the plasmonic nanostructure, it will excite the system resonantly and drive it to a larger oscillation amplitude, i.e. charge displacement or polarization. A plasmon is the hybrid mode combining photonic and material properties arising when such resonances are excited. As with their mechanical analogues, the amplitude of these resonant oscillations would diverge to infinity if not for dissipation or dephasing mechanisms, of which Fig. 6b presents a graphical summary, classifying them by type. The energy stored in the plasmon can be lost by radiating it back to the far field or it can lose it locally,¹⁵⁶ be it through non-radiative electromagnetic interaction, or by exciting a distribution of electronic states different than that following the collective oscillation characterizing the plasmon. In the latter case, we can distinguish between the types of transitions leading to producing excited electrons (or holes) with high kinetic energies. They can be excited within the conduction band (intraband transitions), or from lower-energy bands into the conduction band (interband transitions). Interband transitions in metals are similar to the optical transitions in a semiconductor or a molecule, in that they promote a single electron to an excited state once a photon above a threshold energy is absorbed.

Fig. 6 (a) Schematic diagram of a plasmonic nanosphere being excited by an external electric field at a frequency lower than its resonance frequency. The charges follow the external field excitation and accumulate on the metal surface. (b) All the different decay processes involved in a nanoparticle after interacting with an electromagnetic field. (c) Normalized absorption and extinction cross section for different-sized nanoparticles (diameters of 15 nm and 100 nm) and a 15 nm × 100 nm nanorod (longitudinal and transversal mode). (d) The surface charge density for a 15 nm nanosphere and a 15 nm × 100 nm nanorod at their corresponding plasmon resonance.

Surface plasmon resonances (SPR), i.e. hybrid photon–electron modes propagating along a conductor–dielectric interface, are of both current and historic interest, and a more complete introduction to plasmonics should discuss their properties in some detail.^157,158 However, for the topic at hand we are most interested on the plasmonic modes supported by discrete metal nanostructures, or localized surface plasmon resonances (LSPR). As other types of plasmonic modes, LSPRs’ spectra are sensitive to the material composition of the resonator and changes in the dielectric constant of their environment. Moreover, given that the nanostructures’ surface constrains the charge displacement induced by light, their optical response is strongly dependent on their geometry.^159,160 This, of course, is the origin of the strong chiroptical response of chiral plasmonic nanostructures.

In order to discuss the spectral sensitivity of plasmonic systems to their geometry, let us briefly introduce the magnitudes through which we can characterize the optical response of single plasmonic nanostructures, i.e. their optical cross sections. Through them we describe the effective “area” that a particle interposes in the path of incoming photons. The extinction cross section of a plasmonic nanoparticle informs about the overall interaction strength of light with the nanostructrure, and is the single-particle magnitude that connects with measurements of absorbance in transmission. Then, as the transmitted intensity is that that was neither absorbed nor scattered from its original path, the extinction cross section is the sum of its absorption and scattering cross sections. These can be obtained by normalizing the power of the incoming light diverted into each of these processes by the external light's intensity, so that

These cross sections are routinely computed using analytical or numerical methods. The power absorbed by the metal can be obtained by computing the losses due to Joule photoheating, as
In the second part of this expression the currents were expressed in terms of the conductivity of the metal, which depends on the imaginary part of its relative permittivity, ε_metal. This magnitude can be obtained experimentally¹⁶¹ or through first-principles.^162,163 Importantly, this permittivity can include information that permits describing most of the non-radiative decay mechanisms shown in Fig. 6b. In general, we can write the relative permittivity of a metal as
where ε_int corresponds to the effects of interband transitions at high frequencies, and ε_Drude accounts for the response of the metal as a conductor and can be approximated as Drude-like metal with the parameters of plasma frequency, ω_p, and effective dissipation rate, γ. Additional dissipation channels, like charge injection and electron-surface scattering can also be phenomenologically described by introducing additional contributions to the effective dissipation rate.^144,164 On the other hand, the scattered power can be computed by integrating the Poynting vector of the scattering fields, S_scat, over a surface surrounding the nanostructure
Returning to the geometry-dependent response of a plasmonic nanostructure, the first general point that we can make is that its optical response depends on its size. Nanoparticles much smaller than their resonant wavelength, i.e. within the quasistatic approximation, can have their dynamic response well described by a point dipole. Also, in this regime the absorption cross section is typically dominant.¹⁶⁵ See in Fig. 6c and d for instance the cases of a small Au nanosphere (NS) and the different modes of a Au nanorod (NR), all of which satisfy this condition. Note that the AuNR remains small with respect to the resonant wavelength due to the large change in resonant wavelength when changing the aspect ratio of the resonator. This, in turn, exemplifies how the optical response depends not only on the size, but also the shape of the nanostructure. By changing the overall size and aspect ratio of Au NRs, their longitudinal resonances can be tuned into the near infrared (IR).^20,166 On the other hand, the larger 100 nm AuNS is a simple example of a particle that is large enough for its dipolar mode to be able to radiate more effectively to the far-field, therefore scattering at its resonant mode. This larger gold sphere also shows retardation effects—i.e. those arising from part of the structure experiencing the exciting light wave at different phases—that give rise to multipolar modes, such as the quadrupolar one depicted in Fig. 6d. Overall, the main point that we would like to stress here is the large sensitivity of plasmonic resonances to the geometry that supports them. Now, what if this geometry is chiral?

Let us examine the plasmonic response of a chiral nanoparticle under CPL through the example of one pitch of a gold nanohelix, as shown in the inset of Fig. 7a.¹⁶⁷ This is a nanostructure composed of a metal, Au, with an achiral crystalline structure, but with a geometry possessing a helical shape and thus chiral. The extinction cross section of this nanohelix under CPL of opposite handedness is shown in Fig. 7a, and metrics of CD_ext and g_ext are shown in Fig. 7b. For illustration purposes, these data are all obtained for only one direction of incidence of light, as indicated in the inset of Fig. 7a,d and e, where LCP and RCP are represented by the red and blue circular arrows, respectively. However, we should keep in mind that this is an intrinsically 3D chiral structure, so it also shows a chiroptical signal if we consider the orientational averaging expected from a sample in solution.¹⁶⁷ In Fig. 7a we observe two strong resonances, at 715 nm and 920 nm, although a weak resonance occurs at 630 nm under RCPL, which matches the handedness of the nanohelix. At 715 nm, it interacts more strongly with RCPL, while the opposite occurs at 920 nm. This results in a CD that, naturally, changes sign between these values (Fig. 7b). The g-factor, shown in the same panel, has a qualitatively distinct spectral profile, e.g. with a much more pronounced peak at 630 nm due to the absence of a plasmon peak for LCP, highlighting the normalized character of this metric.

Fig. 7 (a) Extinction cross section of a gold chiral helix (inset). (b) Extinction g-factor (left axis), circular dichroism (right axis). (c) Comparison of CD from the extinction obtained from the full field simulation and from the multipolar expansion of the dynamic charge distribution up to the electric quadrupolar moment. The figure also includes the curves arising only from the electric dipole (ED), magnetic dipole (MD), and electric quadrupole (EQ). (d) and (e) Current density, alongside normalized vector fields showing their direction, when excited at a wavelength of 715 nm and 920 nm for RCP and LCP. Insets in panels a and d and e show a grey arrow marking the direction of propagation of the incident light, and red and blue circular arrows indicating the direction of rotation for the electric field of LCPL and RCPL, respectively. Data in all the panels were obtained under this single illumination condition. The helix has a radius of 30.5 nm and a pitch of 70 nm, while the wire has a radius of 10.5 nm. We arbitrarily chose a right-handed helix; a left-handed helix would show opposite results.

It may be useful to reflect on the analogies and differences between the optical response of chiral molecules and chiral plasmonic nanostructure. The data used above to evaluate the polarization-dependent response of the helical structure uses an explicit, complete description of the plasmonic structure and its dynamic physical response. However, we can also describe its charge distribution using a multipolar expansion, to draw parallels with the evaluation of molecular transition dipolar modes to compute the chiroptical activity of a molecule. In doing so, we could reasonably expect that excitation of small plasmonic nanostructures will be well described by its dipolar modes, but this will not hold as the nanoparticle becomes larger, in relation to the wavelength of the incoming light. Also, nanostructures with a local chiral response can require larger multipolar moments to describe the induced asymmetric charge distribution. Let us examine this point using our example helical geometry in Fig. 7. We can compute the extinction cross section of the system from the terms of a truncated multipolar expansion of its charge distribution under illumination, as¹⁶⁸

In this expression we see the electric and magnetic dipoles, p and m, respectively, and the electric quadrupole, Q_e. The last two are computed at the reference point r₀, which we take as the origin in our example. Note also the double-dot product between the sum of Jacobian matrices of the electric field and the quadrupolar moment. Importantly, these moments are not transition moments connecting two electronic states, as it was the case discussing the molecular excitation, but expressions describing the charge and current densities, ρ and J, across the metal. They can be computed from the electromagnetic simulation results with their usual expressions:
Now, we can compare the magnitude of CD_ext as computed from the full numerical simulations with that obtained through the expression above accounting for specific moments in multipolar expansion of the dynamic response of the helix. The relevant data is presented in Fig. 7c, in which also the different contributions are distinguished. From these data it is clear that, although the electric and magnetic dipolar moments are responsible for a significant amount of the final dichroism, the contribution of the electric quadrupolar moment is patently important. We can also see, from the imperfect match between the full-field simulation and the CD_ext obtained up to the electric quadrupole, that the contribution of higher order moments is not negligible either.

We can complement this point by observing the spatial distribution of currents excited at the surface of the helix, shown in Fig. 7d and e, which inform us about the overall symmetry of the two main plasmonic modes supported by this chiral geometry. For the mode excited under 715 nm light, we can see in Fig. 7d how the plasmonic mode has two internal changes of polarity within the length of the helix. This qualitative observation matches the relatively large contribution of electric quadrupole moment to the CD at this wavelength, as seen in Fig. 7c. In contrast, the mode excited at 920 nm presents a single inversion of the current direction along its length. This smaller spatial frequency, relative to that of the mode excited at 715 nm, is expected from a resonance excited at a longer wavelength. Overall, we can see that both polarizations excite the modes with similar patterns, even though each of them couples more strongly to one of the modes, in accordance with the data in Fig. 7a. Naturally, the polarization exciting the strongest currents also suffers the largest extinction at each wavelength.

Through this analysis we have tried to create an intuitive bridge between the origin of chirality in small molecules and in plasmonic nanostructures, which are ultimately connected through their interaction with electromagnetic fields exciting them. It can be seen how in both cases the chiral signal arises from the asymmetric distribution of the charge displacement produced by the optical excitation. But this analysis also highlights important differences between both systems, such as the different typical size scales at which their chiroptical response originates and the corresponding relevance of larger multipolar moments in describing the plasmonic excitation. And, more fundamentally, they differ in the electronic nature of their respective optical excitations, because in the case of molecules we are computing optical transition dipoles that describe discrete transitions between electronic states, while in the case of plasmonic nanostructures we compute dynamic spatial charge distributions. The former is a property of the molecule, which can be preferentially excited by one polarization of CPL. The latter is a property of the combined system of nanostructure and light. Now, having used the chirality in small molecules as a scaffold to discuss and contrast with chiroptical response in plasmonic systems, we leave the molecules behind and focus on light-to-matter chirality transfer. This is a phenomenon that, incidentally, forgoes chiral molecules to seed this asymmetry into plasmonic structures, using CPL instead to induce permanent chirality in achiral plasmonic structures.

4. Light-to-matter chirality transfer

After discussing chiral light and its interaction with chiral matter, let us now explore the interaction of chiral light with achiral matter, and how light-to-matter chirality transfer can be achieved. It is important to clarify that we will focus on the development of intrinsic chiral features under CPL in fully microscopically achiral systems. We can contrast such transformation with two different scenarios. The first contrasting scenario is one having a sample with pre-existing cryptochirality, i.e. constituted of chiral constituents—either molecules or nanostructures—but displaying no chiroptical signal,¹⁶⁹ that develops optical activity upon enantioselective processes driven by light. This can occur, e.g., by selectively modifying enantiomers in a racemic mixture^170–172 or by separating the enantiomers composing it.^64,173,174 Here there is no development of microscopic intrinsic chirality. The second contrasting scenario is one in which light-induced chirality is transient. Examples include inducing rotational currents inside a metal nanoparticle,¹⁷⁵ or exert torque and initiate the rotation of plasmonic nanocrystals.¹⁷⁶ Here there is a microscopic system developing chirality in a manner that is discontinued once illumination with chiral light is interrupted. In contrast, light-to-matter chirality transfer involves exploiting mechanisms to imprint such transient microscopic chirality into developing nanostructures with intrinsic chirality.

Then, light-to-matter chirality transfer would be characterized by transforming systems fully lacking microscopic chirality into intrinsically microscopic chiral ones through changes driven by CPL, so that they develop intrinsic chirality that remains once the illumination ceases. When discussing molecular media, light-to-matter chirality transfer can correspond to the subcategory of chiral photocatalysis known as photochemical asymmetric fixation, in which chiral light will induce a transformation of an achiral compound into a chiral one.¹⁷² It can also occur by inducing the preferential conformation of chiral supramolecular aggregates from achiral building elements.^177–179 When discussing light-to-matter chirality transfer in plasmonic nanostructures, which is the focus of this article, the starting point is a fully achiral seed, that under CPL illumination changes its geometry or its immediate environment to develop permanent intrinsic chirality. In this case, the changes effected by CPL can be considered continuous, due to the comparatively large scale of the structures, rather than discrete chemical and conformational changes in molecules. Let us now explore specific details regarding the physical mechanisms capable of initiating continuous chiral transformation of plasmonic systems, as we discuss the possibilities they afford while reviewing current demonstrations of light-to-matter chirality transfer in plasmonics.

4.1. Inducing local chirality in plasmonic nanostructures

The geometry of a plasmonic system is crucial in determining its dynamic response under excitation, as it constrains the spatial displacement of the mobile carriers in the conductor. This is one of the central characteristics of the optical response of plasmonic materials, and a major point of interest for applications due to the spectral tunability that this entails. The confluence of a nanostructure's geometry with the polarization of the incoming radiation will determine which modes are excited. We have seen several examples in Fig. 6 and 7. The local dynamics of the mobile charges will then produce far-field responses that are characteristic of the combination of system composition and geometry, and the impinging radiation. Importantly, different local responses can have similar far-field signatures, and deducing the former from the latter is in general not possible without ambiguity. Consequently, we often rely on exploring the local dynamics of plasmonic systems—be it through numerical models or other techniques—to fully understand the response of a plasmonic system. A relevant example of this ambiguity in the context of this overview is that of achiral plasmonic nanoparticles being illuminated with CPL, as the far-field response will not distinguish between opposite polarization of CPL, even though they are initiating different local charge dynamics. The currents within the plasmonic nanostructures will inherit the chiral asymmetry of the external fields exciting them. See Fig. 7d and e for an illustration of this distinction in a chiral geometry, and Fig. 8a and b in an achiral geometry. The far-field metrics are identical under LCPL and RCPL, leading to the absence of CD in the far-field response that informs us that the structure is not chiral. The local response, however, inherits the chirality of the incoming CPL radiation and its excitation pattern is different under the different polarizations. In Fig. 8b we can see a map of the differential local electric field amplitude between LCPL and RCPL across a cross-sectional cut of a Au nanoprism, with the local light intensity computed as a straightforward extension of the expression for the planewave intensity shown above:
The local pattern of the local field maps under each CPL handedness is a transient 2D chiral pattern. In fact, in the case of an elongated object such as the prism shown in Fig. 8a and b one can achieve a local chiral pattern even with linearly polarized light (LPL) if its polarization is not aligned with any of the main axes of the object.^82,180 This occurs in systems whose cross-sectional shape presents a truncated rotational symmetry, belonging to the C_2v space group. Objects in space groups C_nv are left unchanged under reflections and proper and unproper rotations of 2π/n radians. It is useful to consider other objects in C_nv groups with n > 2, which also have a truncated rotational symmetry and will in general develop a chiral local response when illuminated with orthogonally incident CPL (but not with LPL). We can see in Fig. 8c schematic diagrams of such chiral responses in the local fields excited by CPL for C_nv geometries with increasing n. In particular, they illustrate the critical importance of the achiral seed having a truncated rotational symmetry, because as it becomes closer to having a continuous rotational symmetry the regions with differential response become smaller and closer together. In the limit, with n → ∞, we have a fully rotationally symmetric circle, in which no local CD response is possible.^55,79 Then, achiral plasmonic seeds with more reduced rotational symmetry will become better candidates for creating more notably chiral patterns in the local field excitation, and elongated geometries such as rectangular nanoprisms are particularly suitable seeds over which CPL can develop local chiral patterns. Other considerations that are relevant when selecting the geometry of an achiral seed are the absolute size of the nanostructure and the wavelength of the imprinting radiation, as these choices will affect the field distribution of the local chiral pattern and, consequently, the growth pattern and ultimately the chiroptical spectrum of the modified nanostructure. But for the reshaping to occur, these transient field patterns, which disappear after interrupting the illumination, must induce physical or chemical changes on and around the nanostructure's surface. Let us now turn our attention to the different mechanisms by which they can be imprinted onto the NC.

Fig. 8 Local and far-field responses when CPL excites achiral plasmonic NCs. (a) Far-field signal of a Au nanoprism of 110 × 40 × 40 nm³. The plot shows the computed far-field extinction profile of the structure in aqueous solution, also indicating its negligible CD. Inset: Schematic diagram of the Au nanoprism being illuminated by LCPL or RCPL, and an equal fraction of their power passing through. (b) Near-field differential field pattern of the same Au nanoprism under CPL with λ = 540 nm. Inset: Schematic diagram of the Au nanoprism being illuminated by LCPL or RCPL, and generating a local near-field response. (c) Schematic diagrams of local patterns of differential near-field excitation arising when achiral NCs with increasing rotational symmetry are placed under LCPL or RCPL. The different colours indicate opposite signs of ΔI_CD. Panels a and b were adapted from ref. 180. Panel c was adapted from ref. 79.

4.2. Imprinting local chirality in plasmonic nanostructures

The possibility of inscribing such local chiral field pattern becomes available if the plasmonic excitation initiates processes changing the nanostructure's shape, or immediate environment, in a manner that preserves their spatial pattern of the local charge dynamics. Then, such transformation would fix the transient chiral asymmetry in an originally achiral structure, achieving light-to-matter chirality transfer. The resulting intrinsically chiral nanostructure will then showcase far-field chiroptical response. For the nanostructure or its environment to change their local configuration, some physical or chemical change needs to occur. It is useful, in structuring the discussion, to contemplate the different physical mechanisms that can affect the nanostructure's environment under light excitation, and in what conditions they can contribute to preserving the local asymmetry of the hybrid light–matter system. Discussing specific mechanisms would suggest different types of candidate experimental scenarios capable of realizing light-to-matter chirality transfer. We will consider three different families of mechanisms, which are those allowing the local deposition of energy from the plasmonic mode (see Fig. 9a) and underlying the phenomenon of plasmonic photocatalysis. The first consists in driving optical processes in the environment of the resonator through the strongly enhanced electric fields generated around it. Fig. 9b shows an excited field around an achiral rectangular prism, with a local chiral patter resulting of being under CPL. The second family of mechanisms consists in injecting excited charge carriers from the metal into its environment, which then can contribute to advancing redox reactions. Fig. 9c shows a schematic diagram of the different populations of excited carriers in the metal, and how some can leave it to occupy external states, while Fig. 9d depicts a family of possible redox reactions, triggered by such charge carrier injection, capable of reshaping the metal structure. The last energy-transfer mechanism consists in increasing the local temperatures through photoheating. Fig. 9d depicts notable stages on the excitation and relaxation cycle of a plasmonic structure under pulsed light, illustrating a strategy to induce photothermal catalysis without significantly increasing the macroscopic temperature of the sample. Such pulsed techniques could also be suitable to provide transient inhomogeneous temperature patterns. We will now discuss them separately in some detail, while reviewing published results that are relevant in the context of light-to-matter chirality transfer.

Fig. 9 Energy transfer mechanisms in plasmonic photocatalysis, in the context of light-to-matter chirality transfer. (a) Schematic diagram illustrating an excited plasmonic nanostructure and its local environment. The chart indicates the main categories of mechanisms leading to the transfer of energy from the plasmonic mode into the environment. The three non-radiative processes can deposit energy locally. (b) Cross-sectional map showing the enhancement light intensity around a rectangular prism illuminated with CPL. (c) Schematic diagram depicting intraband hot electron excitation and injection from the plasmonic metal to its environment. The electrons need sufficient energy to traverse an interfacial potential barrier or reach empty molecular orbitals. A similar diagram could be shown for hole injection. A typical energy distribution of excited carriers in a plasmonic NC (red curve) is overlaid onto the states of the metal. The high-energy electrons and holes excited through intraband (depicted) and interband (not depicted) transitions can induce redox reactions at the metal's surface. (d) Diagram depicting the general mechanism of ion aggregation, one of other possible redox reactions that can lead to NC growth. (e) Schematic diagram of the steps involved in a photocatalyst prepared to drive a reaction thermically, under pulsed illumination. Panel b was adapted from ref. 180. Panels c and d were adapted from ref. 55. Panel d was adapted from ref. 181.

4.2.1. Local fields promoting optical transitions. One of the most prominent features of plasmonic systems is the enhanced near field surrounding the excited nanoparticle. These intense local fields are responsible for the plasmonic enhancement of different optical effects, such as molecular fluorescence,¹⁸² or surface-enhanced Raman scattering (SERS),¹⁸³ but they also play a role in photochemistry, as they can enhance the rate of optical absorption in semiconductor catalysts¹⁸⁴ or directly in nearby reactants,¹⁴ or even manipulate the distribution of the sample through mass transfer.¹⁸⁵ One very interesting feature of these fields, in the context of chirality transfer, is that they closely track the charge displacement in the metal, which in turn follows the symmetry of the light's polarization. Consequently, environmental transformations driven by the near field of plasmonic nanostructures under continuous wave illumination can retain the local chiral pattern created by the confluence of the structure's geometry and the polarization of light.^79,180 Then, choosing an adequate material that can undergo physical or chemical transformations in a manner that is sensitive to the local pattern of field intensity, and also change its optical properties in the process, can inscribe a chiral shape upon the achiral plasmonic structure, so that the resulting chiral system can be detected through optical methods operating in the far-field, i.e. measuring CD or ORD.

There already exists exciting, published work exploring the use of different polymers to inscribe in the environment features of enhanced local fields of plasmonic nanostructures. In fact, some of them were even presented as techniques to visualize the spatial features of these fields.¹⁶ We can highlight several categories of approaches that have proven fruitful in this task and hold additional promise for being exploited in light-to-matter chirality transfer using plasmonics. The first uses polymers such as polymethyl methacrylate (PMMA) chains containing azo dyes that photoisomerize, with the azo dyes facilitating the motion of the monomers along the direction of polarization of light (see Fig. 10a).¹⁸⁶ Being the photon absorption proportional to the local field intensity, the migration of these monomers creates physical patterns that can be then measured with techniques such as AFM, providing results such as those shown in Fig. 10a. Now, having an achiral plasmonic system irradiated under CPL, the chiral spatial pattern of local field intensity can also induce a migration that follows with the same asymmetry, as demonstrated by Horrer et al., using gold disk trimers.¹⁸⁷ In Fig. 10b we can find contrasted AFM maps and numerical simulations of these trimers under light with different polarizations, which show that the resulting height patterns of the polymer do follow the near fields created by the plasmonic response, and create a chiral pattern under CPL.

Fig. 10 (a) Atomic force microscopy (AFM) images of a silver bowtie dimer after spin coating of polymer, before (top) and after (bottom) irradiation with light polarized orthogonally to the dimer major axis. (b) Gold trimer after polymer deposition and illumination with differently polarized light beams (polarization noted by the black symbols in top row). The top row shows AFM images, while the bottom row shows near field maps obtained from numerical simulations. Scale bars are 300 nm. (c) Scanning electron microscopy (SEM) images (left) of gold metasurface after driving 2-photon polymerization with light polarized along the horizontal (top) and vertical (bottom) axes, accompanied by maps of quadratic near field enhancement, |E(r)|²/E₀², from numerical simulations (right). Scale bars without label are 200 nm. (d) Standing plasmon mode in a silver nanowire 2 μm long, showing a SEM image (left) excited by light polarized along its length after driving 2-photon polymerization around it, and with a map of normalized electric field from numerical simulations (right). (e) Au nanotriangles excited with different orientations relative to linearly polarized light. The SEM images show the nanotriangles and the hydrogel coalesced at their hot spots, while the accompanying panels show in field enhancement maps, |E(r)|/E₀, from numerical simulations. Panel a was adapted from ref. 16 and 186. Panel b was adapted from ref. 187. Panel c was adapted from ref. 188. Panel d was adapted from ref. 189. Panel e was adapted from ref. 190.

Another technique employs epoxy photoresists capable of undergoing two-photon polymerization (2pp) that creates a rigid structure where the photon density is sufficiently large, thus favoring such process within the regions with strong plasmonic near fields.^188,189,191 This can be seen as a particular approach to focusing a laser within the broader field of 2pp applications to additive manufacturing.¹⁹² After rinsing the photoresist, the polymerized structures remain and can be measured through AFM and other microscopy techniques. Fig. 10c includes an example of this process, with SEM images showing polymer mapping of the electromagnetic hot spots in a plasmonic metasurface, alongside numerical simulations of the local electric field,¹⁸⁸ while Fig. 10d illustrates the same principle by mapping a multipolar longitudinal excitation mode in a long silver nanowire.¹⁸⁹ Multiphoton plasmonic lithography can also be performed by inducing the photochemical cross-linking of proteins to create hydrogels. Fig. 10e illustrates results by using this technique on single gold nanotriangles, coalescing these hydrogels at different tips of the triangle depending on the linear polarization of the laser, which in turn excites different plasmonic modes that develop different near-field patterns with distinct electromagnetic hot spots.¹⁹⁰ Recent results by Morozov et al. also explore this technique in mapping the local field distribution of dipolar modes excited in lattices of plasmonic nanostructures.¹⁹³ Altogether, these techniques have shown not only the capability of structuring matter around the plasmonic nanostructures in a manner that reflects the local field patterns, but have also demonstrated that they can capture small variations in such patterns under different polarizations, including CPL.

4.2.2. Electron/hole transfer. The first stage of the optical excitation of a plasmonic nanostructure, in a classical perspective, is the initiation of the conduction electron movement inside the metal, which oscillates with the frequency of the incoming light. This collective oscillation is, then, composed of electrons close to the Fermi energy of the metal. The diagram in Fig. 9c labels these as Drude-like electrons, bringing to mind the image of free electrons moving between the ionic lattice of the metal as a consequence of the external electric field. This intuitive phenomenological description of the excited carriers does not describe well, however, other phenomena that are relevant in this context, such as the excitation of high-energy electrons inside the metal.¹⁹⁴ In contrast with the low-energy, Drude-like electrons moving in the collective oscillation, these can have up to the total energy of the photon exciting the nanostructure. These high-energy intraband electron (and holes) can be excited due to mechanisms that allow non-vertical transitions in the band diagram of the metal, i.e. processes through which the electron gains more momentum than what is available in the photon, such as electron scattering with crystal phonons or with the nanostructure's surface.^195,196 Surface-mediated full-photon absorption can be understood in terms of the confinement of the electronic wavefunction inside the metal. The metal-environment interface interrupts the periodicity of the metal ions and consequently of the electronic density of the metal extending over them. This is a boundary on which the plasmonic mode loses coherence, leading to its energy exciting single-electron states with up to the total energy of the photon exciting the nanostructure.^197–199 Through this mechanism, light in the visible and IR regions exciting a plasmonic resonance can excite electron (holes) that can contribute to redox reactions around the metal, be it by leaving the metal after their excitation^144,200 or by directly promoting a transfer between electronic states of metal and environment.²⁰¹ Exciting with light of shorter wavelengths (e.g. under ∼540 nm, or above ∼2.3 eV, in Au) can also excite interband transitions, that specifically create high-energy holes when exciting close to the threshold energy, and can also contribute to driving redox reactions.^200,202 The range of surface reactions to which these charge carriers can contribute to includes processes that can modify the shape of the metal nanoparticle itself, be it through growth or dissolution,²⁰³ or directing the growth of materials surrounding it.^54,204 Importantly, these reactions can be triggered in an inhomogeneous way that follows the excitation pattern of the plasmon. There are two key properties of high-energy plasmonic charge carriers causing this. First, these so-called “hot” carriers will be preferentially excited at places where the electric field is strongest. From this, we know that the overall excitation pattern of hot carriers is similar to that of the enhanced field of particular plasmonic modes. Second, the lifetime of these hot carriers is very short, and shorter the more kinetic energy they have.¹⁹⁵ In the general context of photocatalysis, this is an unfortunate factor that limits the achievable internal quantum yield of, e.g. solar-to-chemical energy conversion. In this particular context, however, it implies that the hot carriers will in general not travel far from their excitation point before sharing their kinetic energy through electron–electron scattering, so that their contribution to surface reaction will be most prominent near their excitation point. Consequently, charge injection can be considered as a localized phenomenon that also broadly follows the excitation pattern of the plasmonic resonance. As the latter will have a reduced, chiral symmetry under CPL excitation, this mechanism is a good candidate for light-to-matter chirality transfer through plasmonic photocatalysis. As such, most of the published examples of this phenomenon exploit charge transfer to drive redox transformations. In summarizing these results, we can classify them in two categories, depending on whether they develop chiral nanostructures exploiting intrinsic 2D or 3D chiral excitation patterns. Fig. 11 and 12 illustrate examples of each case. For planar growth, or growth exploiting intrinsic 2D chiral excitation patterns, the relative orientation of the nanoparticles and the impinging CPL beam is fixed, whereas when considering colloidal growth the relative particle-beam orientation changes as the particles move and rotate in solution. To understand the implications of this difference, it is illustrative to compare Fig. 11a and 12a, which show surface maps of the local circular dichroism on the excitation rates of intraband hot carriers in achiral cubes, obtained through numerical simulations, in both configurations.⁵⁵ The main differences between them are the distinct excitation patterns, with intrinsic 2D and 3D chirality, respectively, and the absolute magnitude of the dichroism in these excitation patterns; for which we see a difference in three orders of magnitude. This patently points out the comparative simplicity of working with supported resonators when pursuing light-to-matter chirality transfer. Experimental examples of this planar approach have permitted to see the creation of consistently chiral Au nanostructures starting from achiral Au nanocubes (Fig. 11b).²⁰⁵ In this figure we can see how their single-particle chiroptical response did not differ much after inducing photogrowth with different wavelengths. This is so due to their relatively small size and aspect ratio equal to one, so they do not support plasmonic modes with markedly different geometrical patterns. Cubes also are, due to their four-fold rotational symmetry, comparatively challenging geometries to use as seeds for chiral growth.^55,180 It is not surprising, then, than the demonstration of the light-to-matter chirality transfer phenomenon was first demonstrated using elongated Au nanoprisms, with an aspect ratio above unity and thus reduced to two-fold rotational symmetry. In a seminal publication,⁵⁴ Saito et al., demonstrated the deposition and growth of PbO₂ on a clear chiral pattern over Au nanoprisms illuminated under CPL. The SEM images in Fig. 11c also illustrate how they obtained Au@PbO₂ hybrids with opposite handedness when using CPL with opposite polarization. Recently, experiments by Prof. Dionne's group have shown similar results exploring PbO₂ growth over Au bipyramidal structures, demonstrating control over the position along the metal structure where the dielectric grows by changing the plasmonic excitation pattern via illuminating with different wavelengths (see Fig. 11d).²⁰⁴ Work in Prof. Tatsuma's group has explored this phenomenon in plasmonic metasurfaces,²⁰⁶ which are, incidentally, paradigmatic 2D plasmonic materials and thus natural candidates to explore light-to-matter chirality transfer in the plane. Fig. 11e shows a SEM image of the initial, achiral Ag metamaterial, together with the asymmetry factor obtained after driving metal photogrowth with CPL beams of opposite handedness. Lastly, recent results by Prof. Biteen, Prof. Kotov and others have shown the directed photoreduction of silver nanoparticles into substrate-supported helicoids with handedness controlled by impinging CPL, achieving clean, symmetric CD responses under opposite polarizations (see Fig. 11f).²⁰⁷

Fig. 11 (a) Schematic diagram of the planar illumination condition for a Au nanocube, with the nanoparticle being illuminated from a fixed direction, and map of the differential rate of intraband hot carrier excitation under both polarizations of CPL. (b) Wavelength-dependent plasmon-induced chiral growth of AuNCs, including SEM images of a 100 nm-sized AuNC seed and equivalent nanoparticles after growth under RCP illumination at 565 nm and 640 nm, with the single-particle scattering CD spectra of these three NC. (c) SEM images, of Au nanoprisms with PbO₂ grown following chiral patterns under broadband CPL light of opposite handedness. The insets show 3D diagrams of the resulting metal-dielectric chiral hybrids. (d) SEM images of Au bipyramids with PbO₂ grown following chiral patterns under CPL with wavelengths of 488 nm (left) and 660 nm (right), resulting from illumination with opposite CPL polarization. Insets show 3D diagrams of the chiral hybrids. (e) Dissymmetry factor of the Ag metasurface (SEM image in right) after illumination with CPL with opposite polarizations in the 600 nm to 700 nm wavelength band. (f) SEM images of the nanohelicoids grown under LCPL (Δ) and RCPL (Λ), together with their CD spectra contrasted with that of pillars grown under LPL. Panel a was reproduced from ref. 55. Panel b was adapted from ref. 205. Panel c was adapted from ref. 54. Panel d was adapted from ref. 204. Panel e was adapted from ref. 206. Panel f was adapted from ref. 207.

Fig. 12 (a) Schematic diagram of the model for continuous CPL illumination of a colloidal Au nanocube, with the effective response being an average of six different directions for the propagation of light, and map of the differential rate of intraband hot carrier excitation under both polarizations of CPL. (b) Scheme of transformation of achiral nanobars into chiral ones in a colloidal suspension, driving galvanic replacement reaction CPL illumination of colloidal Au@Ag nanoprisms, alongside 3D models of the resulting geometries (obtained with TEM tomography), TEM images of the chiral bimetallic structures, and dissymmetry factor of the sample after illumination with CPL at 660 nm. (c) Geometrical analysis of the tomographic reconstruction of one of the resulting chiral structures (in blue), together with its mirror image (in red). Four transversal cross-sections of the geometries are shown. Quantitative measures of the geometric chirality of the nanostructure and its cross-sections are also shown. (d) Photodeposition of Ag over Au nanorods under 630 nm light. (i) Absorbance of the samples after 12 h of CPL illumination; (ii) STEM images of the chiral bimetallic samples, with energy-dispersive X-ray spectroscopy maps identifying elemental spatial distribution; (iii) CD spectra of the samples. Panel a was reproduced from ref. 55. Panels b and c were adapted from ref. 208. Panel d was reproduced from ref. 209.

Driving chiral photogrowth in solution is a more challenging proposition, because the reaction times (which can be minutes or even many hours)^208,209 entail that the relative orientation between the nanostructure and the beam will change significantly during the full growth process. Computational models such as those producing the data in Fig. 12a can account for this variance by calculating the effective response as an average of illumination conditions that model a system spending the same amount of time in all orientations. In this case, although the excitation pattern remains chiral—as long as the nanoparticle does not offer a spherical cross-section to the beam—,^55,79,210 its dichroic amplitude is greatly diminished in relation with the planar case (see Fig. 11a), in which the nanostructure is static with respect to the CPL beam. There have been, nonetheless, at least three demonstrations of light-to-matter chirality transfer on colloidal plasmonic nanostructures to date. Kim et al. explored the synthesis of chiral aggregates of achiral Au spherical NPs directed by CPL illumination.²¹¹ This example sidesteps the limitations that we described above regarding the geometry of the achiral seed by exploiting interparticle interactions, so that the multi-particle aggregate breaks the rotational symmetry and can lead to their blending into chiral superstructures. Ghalawat et al. demonstrated the development of chiral plasmonic nanostructures in both planar and colloidal setups through CPL-directed galvanic replacement reaction over Au@Ag nanoprisms (Fig. 12b and c).²⁰⁸ The geometry of the nanostructures after CPL irradiation while deposited on a substrate acquires a patently chiral shape similar to those described in the previous paragraph. However, although their transformations under CPL while in solution do not present such obviously clear geometric chirality, they also showcase clear and consistent chiroptical properties (Fig. 12b), and detailed geometrical analysis of their shapes, as obtained from electron microscopy tomography, clearly reveal their chirality. Saito et al. worked with Au nanostructures with different geometries, namely spheres, triangular plates and rods, and drove photochemical Ag growth over them using CPL light.²⁰⁹ They achieved clear, significant chiroptical effects for the Ag photogrowth over Au nanorods, especially when exciting them at a wavelength closer to their longitudinal plasmon modes (see Fig. 12d). These articles are remarkable demonstrations that the local chiral excitation of the plasmonic nanostructures is robust enough to be imprinted in the noisy context of room temperature colloidal suspensions, and pave the way for future work in light-to-matter chirality transfer in this medium.

4.2.3. Photoheating. Lastly, plasmonic excitation will inexorably dissipate a significant fraction of the energy absorbed from light in the form of heat, also sharing it with its environment. Fig. 13a indicates typical timescales for the different stages of energy degradation, i.e. from more to less ordered states, in a gold nanoparticle after being excited by a short pulse.²¹² Of course, under continuous illumination, all these processes would be concurrent, but contemplating the case of pulsed excitation is useful to understand the different typical timescales of these processes, and is relevant for our discussion on light-to-matter chirality transfer. This linear succession of events starts with an external pulse exciting a plasmonic mode in a metal nanostructure, and this collective electron oscillation entails the transfer of radiant energy into electronic degrees of freedom. This energy will then be shared across electrons and with the atomic lattice supporting the electronic states, raising the temperature of the metal. At this point the metal can also exchange energy with its environment through phonon–phonon coupling, transferring heat around the plasmonic system and raising the temperature of surrounding materials, so that it can drive phase changes^213,214 or chemical transformations.¹⁸¹ Thus, plasmonic photoheating can also trigger physicochemical changes around the nanoparticle, in a manner that changes with its shape or optical response, so it could also generate chiral asymmetries under CP illumination through this mechanism.

Fig. 13 (a) Schematic diagram depicting significant stages and approximate timescales involved in the transfer of energy from the highly ordered collective oscillation of electrons in a plasmon, to single-particle states, to then the lattice and finally dissipating when heating the local environment. (b) Computational results showing timescales for two types of surface inhomogeneity on the lattice temperature of a gold nanoprism: chiral asymmetry and temperature inhomogeneity, as defined in the text. The inset shows the normalized surface temperature after being illuminated with a RCPL pulse at 682 nm, at the time of maximum g_T,lattice, at t ∼ 1 ps. (c) (i)–(v) Schematic diagram of the transient optical response, indicating in different shades of red the excited state of local electronic states, and labelling the different stages with notable phenomena and their properties. (Right) Computational data showing the transient values of the electronic temperature, T_e, after pumping with CPL. (Top) Plot indicating T_e at both extremes of the structure, as well as their difference. (Bottom) Surface maps of T_e for the resonator at four selected times, with symbol legend shared with the data in the top panel. Panel a was reproduced from ref. 212. Panel c was reproduced from ref. 215.

There are different ways in which metal photoheating can create systems with chiroptical activity. Let us explicitly contrast them with the kind of temperature-driven chiral photogrowth that we aim to discuss in this article. First, one can exploit plasmonic photoheating to create macroscopic chiroptical activity from a sample composed of a racemic mixture of plasmonic chiral nanoparticles or assemblies, by selectively destroying one enantiomer¹⁷⁰ or facilitating handedness switching in chiral assemblies.²¹⁶ Such an approach mimics what can be achieved by enantioselective photodegradation in a racemic mixture of chiral molecules,¹⁷² thus creating macroscopic chirality only if the sample already has chiral structures at the nanoscale. Another alternative is using pulsed vortex beams, as mentioned in Section 2b, to carve twisting pillars from metal substrates.^107–110 This approach does not exploit chiral temperature gradients on the surface of the metal structures, as resulting from asymmetric plasmonic excitation, but rather depends on directing the mass transport dynamics of the overheated metal in a chiral pattern.

For a temperature-directed process that develops chirality in achiral plasmonic structures, following the chiral excitation pattern created from impinging CPL, it is necessary that the metal surface showcases asymmetric distributions of surface temperature. This immediately presents a difficulty, due to the large thermal diffusivities of typical plasmonic materials like noble metals. Thermal diffusivity is a composite magnitude of the thermal conductivity, k, density, ρ, and heat capacity, c_p, of a material, as in D_T = k/ρc_p, which characterizes how fast heat is transferred within the material.^217,218 So, a plasmonic nanostructure sees a rapid homogenization of the temperature across the metal through internal heat diffusion, in shorter timescales than those characterizing heat exchange with the environment. Then, under continuous wave illumination, plasmonic nanoparticles offer no distinct temperature gradients across their surface.¹⁸⁰

On the other hand, working with pulsed laser offers distinct possibilities when working with plasmonic nanoparticles as photoheaters. Each laser pulse can concentrate a large amount of energy, such that we can even enter regimes in which a plasmonic nanostructure is destroyed when excited by it.²¹⁹ At different power regimes we can use trains of short laser pulses as, e.g. an energy efficient way of raising the temperature in a photocatalytic setup, avoiding heating a whole macroscopic sample.¹⁸¹ However, such strategies take advantage of the asymmetry between thermal conductivity of the metal and its environment, thus creating significant temperature gradients at their interfaces, but not necessarily introducing local gradients along the metal surface, where lattice temperature inhomogeneities will remain short-lived. For diffusivities around α ∼ 150 nm² ps⁻¹, representative of e.g. gold and silver, we can estimate typical temperature homogenization times in the order of tens of ps for structure with cross-sectional areas around 10³–10⁴ nm². Chiral asymmetries will disappear at even shorter timescales. To illustrate this, in Fig. 13b we present computational results for a gold nanoprism, with dimensions of 60 × 70 × 200 nm, photoexcited with a 100 fs LCP pulse. Its surface temperature was computed assuming a 1T model, i.e. assuming a direct energy transfer from plasmon to lattice temperature through Joule effect. This can be then considered an overestimate of realistically expected temperature inhomogeneities, as in the more realistic 2T model the energy in the electronic degrees of freedom also diffuses while coupling with the lattice.²¹⁰ In this panel the magnitudes measuring chiral asymmetry and general temperature inhomogeneity are derived from the lattice temperature, T_lat. The latter is computed as an integral across the NC surface, S_NC, having the average surface temperature as the reference, as

while the chiral asymmetry is computed as the aggregate local dissymmetry using a distribution mirrored along the short axis of the NC
and where the average lattice temperature is simply computed using the surface area of the NC as
Then, data in Fig. 13b shows that for the numerical model the inhomogeneity in the lattice surface temperature persists for over 10 ps, consistent with the above estimation, while the more subtle chiral asymmetry decays within a single ps. Working with pulsed illumination on larger plasmonic nanostructures can lead to more pronounced and longer-lasting temperature gradients on the metal surface, but taking advantage of phototemperature inhomogeneities for chiral development will remain a competition against the rapid thermalization in the metal. This will be clearer if we estimate the local behaviour in anisotropic plasmonic resonators using a coupled 2T temperature model. With it one models the excitation of the conducting electrons with an effective electronic temperature, T_e, coupled with the lattice temperature, T_lat. In this case, the energy stored in T_e will diffuse as it couples with the lattice and raises T_lat,^210,220 which leads to a lower asymmetry in this latter magnitude. As such, Fig. 13c, reproduced from recent work exploring such transient chiral modes in achiral plasmonic resonators,²¹⁵ shows the evolution from asymmetric to homogeneous T_e in an achiral plasmonic resonator excited under CPL, which would be in turn responsible for any asymmetries in the lattice temperature. Another limiting factor can be metal reshaping,²²¹ which would tend to smooth out fine and sharp features in the metal if the temperature is too large. Together with fast thermal diffusion, this challenge can perhaps point towards the use of relatively large plasmonic achiral seeds, even protected from deformation with thin external coatings.²²² If any chiral temperature pattern on the thermal surface gradients are retained on its outer layer, it could drive spatially-differentiated chemical or physical accretion processes. Regardless of these challenges, or perhaps because of them, exploiting thermal asymmetries produced on plasmonic nanostructures remains an interesting scenario, that can be further explored through the excitation large anisotropic plasmonic geometries with ultra-short CPL pulses.^42,181,223

5. Summary and outlook

Chirality is a geometrical idea with important implications in the machinery of life. It is a subtle concept with large, concrete implications at the human scale. Understanding microscopic chirality is necessary to advance our understanding of nanoscience and nanotechnology in many applications, but most critically in biology and medicine. In this article we have discussed basic principles of light–matter interaction when dealing with chiral matter, to contextualize current ongoing research on light-to-matter chirality transfer using circularly polarized light to imprint chiral asymmetries on achiral plasmonic nanoantennas. This phenomenon also depends on subtle mechanisms that direct changes at the nanoscale, even at the single-particle level, to produce macroscopic chiroptical activity. We have discussed not only the possible mechanistic routes through which this can be achieved, but also difficulties and limitations to these. As such, experimental setups exploring light-to-matter chirality transfer are also valuable scenarios to explore fundamental mechanisms in plasmon-assisted photocatalysis, through which we can create spatial patterns in energy-transfer around the metal with sub-particle resolution using only the polarization of light.

The overview presented here focuses squarely on the use of plasmonic nanostructures for light-to-matter chirality transfer because, due to the strong and malleable collective electronic response as well as their typical sizes, they are particularly well-suited for locally instantiating chiral patterns when excited by light in (and near) the visible spectrum. The pioneering experimental examples in this line of research, cited above, exploit these properties. But the overall phenomenon is susceptible of being explored in different systems with appropriately scaled electromagnetic responses, such as dielectric metamaterials inducing photocatalysis by exciting smaller, embedded materials in mesoscale spatial patterns originated by their collective modes,^224–228 or even molecular aggregates with collective behaviour.^229–232 Light-to-matter chirality transfer is an inherently multiscale phenomenon that stands to benefit from, and also enrich, research in light–matter interaction using systems with collective electronic behaviour. Moreover, clarifying different aspects of how such collective behaviour can direct chemical processes over distinct spatial patterns also stands to produce insights in how to exploit such inhomogeneities to advance research in enantioselective photocatalysis using plasmonic nanoantennas in hybrid-material photocatalysts in multiscale strategies.

Author contributions

LVB conceived the manuscript. AOG, MACD, LVB acquired funds. EYS, MI, and OAO performed numerical simulations. EYS and LVB wrote the original draft. All authors contributed to reviewing and editing the manuscript.

Data availability

Data and codes used to create new figures for this article, related to the following items, are available at DOI: https://doi.org/10.5281/zenodo.14748371. Fig. 5: Gaussian 16 inputs and selected ouputs. Fig. 6c and d: COMSOL Multiphysics models. Fig. 7: COMSOL Multiphysics models. Fig. 13b: COMSOL Multiphysics model.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the projects PID2020-118282RA-I00, PID2023-146766NB-I00, PID2020-113704RB-I00, PID2023-147495OB-I00, TED2021-130038A-I00, TED2021-132101B-I00, and RYC2021-033818-I, funded by MCIN/AEI/10.13039/501100011033 and European Union “NextGenerationEU”/PRTR; ED431F 2024/21, ED481A/2023-087, ED431C 2022/24, and ED431G 2023/06: Centro Singular de Investigación de Galicia accreditation 2023-2027 funded by Xunta de Galicia; HORIZON-EIC-2022-PATHFINDERCHALLENGES-01-06 (no. 101115149), and HORIZON-HLTH-2022-DISEASE-06-TWO-STAGE (no. 101080889) funded by the European Union Horizon 2020 Research and Innovation Program. A. O. G. acknowledges generous support from the United States-Israel Binational Science Foundation (BSF), grant #2018050. Publication in Open Access was supported by Universidade de Vigo and CISUG.

References

1. V. Giannini, A. I. Fernández-Domínguez, S. C. Heck and S. A. Maier, Chem. Rev., 2011, 111, 3888–3912.
2. J. Aizpurua and R. Hillenbrand, in Plasmonics, ed. S. Enoch and N. Bonod, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, vol. 167, pp. 151–176.
3. S. Daqiqeh Rezaei, Z. Dong, J. You En Chan, J. Trisno, R. J. H. Ng, Q. Ruan, C.-W. Qiu, N. A. Mortensen and J. K. W. Yang, ACS Photonics, 2021, 8, 18–33.
4. P. Cencillo-Abad, D. Franklin, P. Mastranzo-Ortega, J. Sanchez-Mondragon and D. Chanda, Sci. Adv., 2023, 9, eadf7207.
5. M. K. Chen, Y. Wu, L. Feng, Q. Fan, M. Lu, T. Xu and D. P. Tsai, Adv. Opt. Mater., 2021, 9, 2001414.
6. F. Liu, D. Wang, H. Zhu, X. Zhang, T. Liu, S. Sun, X. Zhang, Q. He and L. Zhou, Laser Photonics Rev., 2023, 17, 2201001.
7. X. Wang, S.-C. Huang, S. Hu, S. Yan and B. Ren, Nat. Rev. Phys., 2020, 2, 253–271.
8. J. Mosquera, Y. Zhao, H. Jang, N. Xie, C. Xu, N. A. Kotov and L. M. Liz-Marzán, Adv. Funct. Mater., 2020, 30, 1902082.
9. P. Anger, P. Bharadwaj and L. Novotny, Phys. Rev. Lett., 2006, 96, 113002.
10. W. Park, D. Lu and S. Ahn, Chem. Soc. Rev., 2015, 44, 2940–2962.
11. L. M. Kneer, E.-M. Roller, L. V. Besteiro, R. Schreiber, A. O. Govorov and T. Liedl, ACS Nano, 2018, 12, 9110–9115.
12. T. Zhao, D. Meng, Z. Hu, W. Sun, Y. Ji, J. Han, X. Jin, X. Wu and P. Duan, Nat. Commun., 2023, 14, 81.
13. V. Jain, R. K. Kashyap and P. P. Pillai, Adv. Opt. Mater., 2022, 10, 2200463.
14. U. Aslam, V. G. Rao, S. Chavez and S. Linic, Nat. Catal., 2018, 1, 656–665.
15. W. Wang, X. Yan, J. Geng, N. Zhao, L. Liu, T. Vogel, Q. Guo, L. Ge, B. Luo and Y. Zhao, ACS Nano, 2021, 15, 16376–16394.
16. X. Zhou, O. Soppera, J. Plain, S. Jradi, X. Wei Sun, H. Volkan Demir, X. Yang, C. Deeb, S. K. Gray, G. P. Wiederrecht and R. Bachelot, J. Opt., 2014, 16, 114002.
17. W. A. Murray and W. L. Barnes, Adv. Mater., 2007, 19, 3771–3782.
18. P. R. West, S. Ishii, G. V. Naik, N. K. Emani, V. M. Shalaev and A. Boltasseva, Laser Photonics Rev., 2010, 4, 795–808.
19. L. Wang, M. Hasanzadeh Kafshgari and M. Meunier, Adv. Funct. Mater., 2020, 30, 2005400.
20. J. Zheng, X. Cheng, H. Zhang, X. Bai, R. Ai, L. Shao and J. Wang, Chem. Rev., 2021, 121, 13342–13453.
21. M. Urbieta, M. Barbry, Y. Zhang, P. Koval, D. Sánchez-Portal, N. Zabala and J. Aizpurua, ACS Nano, 2018, 12, 585–595.
22. L. Jiang, T. Yin, A. M. Dubrovkin, Z. Dong, Y. Chen, W. Chen, J. K. W. Yang and Z. Shen, Light: Sci. Appl., 2019, 8, 21.
23. Y. Wu, G. Li and J. P. Camden, Chem. Rev., 2018, 118, 2994–3031.
24. B. Wang, P. Yu, W. Wang, X. Zhang, H. Kuo, H. Xu and Z. M. Wang, Adv. Opt. Mater., 2021, 9, 2001520.
25. K. B. Crozier, ACS Photonics, 2024, 11, 321–333.
26. J. L. Montaño-Priede, M. Zapata-Herrera, R. Esteban, N. Zabala and J. Aizpurua, Nanophotonics, 2024, 13, 4771–4794.
27. X. Lu, M. Rycenga, S. E. Skrabalak, B. Wiley and Y. Xia, Annu. Rev. Phys. Chem., 2009, 60, 167–192.
28. A. Biswas, I. S. Bayer, A. S. Biris, T. Wang, E. Dervishi and F. Faupel, Adv. Colloid Interface Sci., 2012, 170, 2–27.
29. A. Yadav, B. Gerislioglu, A. Ahmadivand, A. Kaushik, G. J. Cheng, Z. Ouyang, Q. Wang, V. S. Yadav, Y. K. Mishra, Y. Wu, Y. Liu and S. RamaKrishna, Nano Today, 2021, 37, 101072.
30. K. Yang, X. Yao, B. Liu and B. Ren, Adv. Mater., 2021, 33, 2007988.
31. N. Sarfraz and I. Khan, Chem. – Asian J., 2021, 16, 720–742.
32. B. Wen, J. Yang, C. Hu, J. Cai and J. Zhou, Adv. Mater. Interfaces, 2024, 11, 2300856.
33. J. N. Anker, W. P. Hall, O. Lyandres, N. C. Shah, J. Zhao and R. P. Van Duyne, Nat. Mater., 2008, 7, 442–453.
34. P. Wang, M. E. Nasir, A. V. Krasavin, W. Dickson, Y. Jiang and A. V. Zayats, Acc. Chem. Res., 2019, 52, 3018–3028.
35. R. M. Kim, J. H. Han, S. M. Lee, H. Kim, Y.-C. Lim, H.-E. Lee, H.-Y. Ahn, Y. H. Lee, I. H. Ha and K. T. Nam, J. Chem. Phys., 2024, 160, 061001.
36. A. Stefancu, J. Aizpurua, I. Alessandri, I. Bald, J. J. Baumberg, L. V. Besteiro, P. Christopher, M. Correa-Duarte, B. De Nijs, A. Demetriadou, R. R. Frontiera, T. Fukushima, N. J. Halas, P. K. Jain, Z. H. Kim, D. Kurouski, H. Lange, J.-F. Li, L. M. Liz-Marzán, I. T. Lucas, A. J. Meixner, K. Murakoshi, P. Nordlander, W. J. Peveler, R. Quesada-Cabrera, E. Ringe, G. C. Schatz, S. Schlücker, Z. D. Schultz, E. X. Tan, Z.-Q. Tian, L. Wang, B. M. Weckhuysen, W. Xie, X. Y. Ling, J. Zhang, Z. Zhao, R.-Y. Zhou and E. Cortés, ACS Nano, 2024, 18, 29337–29379.
37. A. Dorodnyy, Y. Salamin, P. Ma, J. Vukajlovic Plestina, N. Lassaline, D. Mikulik, P. Romero-Gomez, A. Fontcuberta, I. Morral and J. Leuthold, IEEE J. Sel. Top. Quantum Electron., 2018, 24, 1–13.
38. J. Huang and L. Luo, Adv. Opt. Mater., 2018, 6, 1701282.
39. W. Li, Z. J. Coppens, L. V. Besteiro, W. Wang, A. O. Govorov and J. Valentine, Nat. Commun., 2015, 6, 8379.
40. P. Berini, Laser Photonics Rev., 2014, 8, 197–220.
41. R. Rodríguez-Oliveros and J. A. Sánchez-Gil, Opt. Express, 2012, 20, 621.
42. G. Baffou and H. Rigneault, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035415.
43. H. H. Richardson, M. T. Carlson, P. J. Tandler, P. Hernandez and A. O. Govorov, Nano Lett., 2009, 9, 1139–1146.
44. P. H. C. Camargo and E. Cortés, Plasmonic Catalysis: From Fundamentals to Applications, Wiley, 1st edn, 2021.
45. M. Dhiman, J. Mater. Chem. A, 2020, 8, 10074–10095.
46. C. Brissaud, L. V. Besteiro, J.-Y. Piquemal and M. Comesaña-Hermo, Solar RRL, 2023, 2300195.
47. S. I. Azzam, A. V. Kildishev, R.-M. Ma, C.-Z. Ning, R. Oulton, V. M. Shalaev, M. I. Stockman, J.-L. Xu and X. Zhang, Light: Sci. Appl., 2020, 9, 90.
48. J.-S. Lin, X.-D. Tian, G. Li, F.-L. Zhang, Y. Wang and J.-F. Li, Chem. Soc. Rev., 2022, 51, 9445–9468.
49. Z. He, C. Y. Zhang, Y. Lei, G. Song and Y. Yao, Mater. Today, 2023, 62, 168–189.
50. B. J. Shastri, A. N. Tait, T. Ferreira De Lima, W. H. P. Pernice, H. Bhaskaran, C. D. Wright and P. R. Prucnal, Nat. Photonics, 2021, 15, 102–114.
51. C. Lian, C. Vagionas, T. Alexoudi, N. Pleros, N. Youngblood and C. Ríos, Nanophotonics, 2022, 11, 3823–3854.
52. M. Hentschel, M. Schäferling, X. Duan, H. Giessen and N. Liu, Sci. Adv., 2017, 3, e1602735.
53. M. J. Urban, C. Shen, X.-T. Kong, C. Zhu, A. O. Govorov, Q. Wang, M. Hentschel and N. Liu, Annu. Rev. Phys. Chem., 2019, 70, 275–299.
54. K. Saito and T. Tatsuma, Nano Lett., 2018, 18, 3209–3212.
55. L. V. Besteiro, A. Movsesyan, O. Ávalos-Ovando, S. Lee, E. Cortés, M. A. Correa-Duarte, Z. M. Wang and A. O. Govorov, Nano Lett., 2021, 21, 10315–10324.
56. L. Shao and J. Zheng, Appl. Mater. Today, 2019, 15, 6–17.
57. E. S. A. Goerlitzer, A. S. Puri, J. J. Moses, L. V. Poulikakos and N. Vogel, Adv. Opt. Mater., 2021, 9, 2100378.
58. C. Zhou, X. Duan and N. Liu, Acc. Chem. Res., 2017, 50, 2906–2914.
59. K. Martens, F. Binkowski, L. Nguyen, L. Hu, A. O. Govorov, S. Burger and T. Liedl, Nat. Commun., 2021, 12, 2025.
60. A. Ben-Moshe, S. G. Wolf, M. B. Sadan, L. Houben, Z. Fan, A. O. Govorov and G. Markovich, Nat. Commun., 2014, 5, 4302.
61. H.-E. Lee, H.-Y. Ahn, J. Mun, Y. Y. Lee, M. Kim, N. H. Cho, K. Chang, W. S. Kim, J. Rho and K. T. Nam, Nature, 2018, 556, 360–365.
62. B. Ni, M. Mychinko, S. Gómez-Graña, J. Morales-Vidal, M. Obelleiro-Liz, W. Heyvaert, D. Vila-Liarte, X. Zhuo, W. Albrecht, G. Zheng, G. González-Rubio, J. M. Taboada, F. Obelleiro, N. López, J. Pérez-Juste, I. Pastoriza-Santos, H. Cölfen, S. Bals and L. M. Liz-Marzán, Adv. Mater., 2023, 35, 2208299.
63. X. Wei, J. Liu, G.-J. Xia, J. Deng, P. Sun, J. J. Chruma, W. Wu, C. Yang, Y.-G. Wang and Z. Huang, Nat. Chem., 2020, 12, 551–559.
64. M. L. Solomon, A. A. E. Saleh, L. V. Poulikakos, J. M. Abendroth, L. F. Tadesse and J. A. Dionne, Acc. Chem. Res., 2020, 53, 588–598.
65. P. Bainova, J.-P. Joly, M. Urbanova, D. Votkina, M. Erzina, B. Vokata, A. Trelin, P. Fitl, G. Audran, N. Vanthuyne, J. Vinklarek, V. Svorcik, P. Postnikov, S. R. A. Marque and O. Lyutakov, ACS Catal., 2023, 13, 12859–12867.
66. L. D. Barron, in Strategies of Life Detection, ed. O. Botta, J. L. Bada, J. Gomez-Elvira, E. Javaux, F. Selsis and R. Summons, Springer US, Boston, MA, 2008, vol. 25, pp. 187–201.
67. J. P. Riehl, Mirror-image asymmetry: an introduction to the origin and consequences of chirality, Wiley, Hoboken, NJ, 2010.
68. H. Alkadi and R. Jbeily, Infect. Disord.:Drug Targets, 2018, 18, 88–95.
69. D. W. Green, J. Lee, E. Kim, D. Lee and H. Jung, Adv. Mater. Interfaces, 2016, 3, 1500411.
70. X. Zhao, S.-Q. Zang and X. Chen, Chem. Soc. Rev., 2020, 49, 2481–2503.
71. K. Dong, C. Xu, J. Ren and X. Qu, Angew. Chem., 2022, 134, e202208757.
72. G. G. Birch and R. S. Shallenberger, Crit. Rev. Food Sci. Nutr., 1976, 8, 57–95.
73. G. D’Orazio, C. Fanali, M. Asensio-Ramos and S. Fanali, TrAC, Trends Anal. Chem., 2017, 96, 151–171.
74. N. Dubovski, Y. Ben Shoshan-Galeczki, E. Malach and M. Y. Niv, Food Chem., 2022, 373, 131393.
75. S. Yoo and Q.-H. Park, Nanophotonics, 2019, 8, 249–261.
76. L. A. Warning, A. R. Miandashti, L. A. McCarthy, Q. Zhang, C. F. Landes and S. Link, ACS Nano, 2021, 15, 15538–15566.
77. F. Xie, M. Ren, W. Wu, D. Yu, W. Cai and J. Xu, Phys. Rev. Lett., 2020, 125, 237401.
78. Z. Wang, F. Cheng, T. Winsor and Y. Liu, Nanotechnology, 2016, 27, 412001.
79. H. Okamoto, J. Mater. Chem. C, 2019, 7, 14771–14787.
80. E. Plum, V. A. Fedotov and N. I. Zheludev, J. Opt. A: Pure Appl. Opt., 2009, 11, 074009.
81. J. Mun, M. Kim, Y. Yang, T. Badloe, J. Ni, Y. Chen, C.-W. Qiu and J. Rho, Light: Sci. Appl., 2020, 9, 139.
82. A. Movsesyan, L. V. Besteiro, X. Kong, Z. Wang and A. O. Govorov, Adv. Opt. Mater., 2021, 10, 2101943.
83. E. S. A. Goerlitzer, M. Zapata-Herrera, E. Ponomareva, D. Feller, A. Garcia-Etxarri, M. Karg, J. Aizpurua and N. Vogel, ACS Photonics, 2023, 10, 1821–1831.
84. R. Singh, E. Plum, W. Zhang and N. I. Zheludev, Opt. Express, 2010, 18, 13425–13430.
85. S. A. Mousavi, E. Plum, J. Shi and N. I. Zheludev, Sci. Rep., 2015, 5, 8977.
86. S. Allenmark, Chirality, 2003, 15, 409–422.
87. A. O. Govorov, J. Phys. Chem. C, 2011, 115, 7914–7923.
88. N. A. Abdulrahman, Z. Fan, T. Tonooka, S. M. Kelly, N. Gadegaard, E. Hendry, A. O. Govorov and M. Kadodwala, Nano Lett., 2012, 12, 977–983.
89. C. Wang, D. Lu, L. Sun and Q. Zhang, Chin. J. Chem., 2024, 42, 903–919.
90. D. J. Griffiths, Introduction to Electrodynamics, Pearson Education, 2014.
91. R. Shankar, Principles of quantum mechanics, Plenum Press, New York London, 2nd edn, 1994.
92. S. Weinberg, The quantum theory of fields. 1: Foundations, Cambridge Univ. Press, Cambridge, Paperback ed., 10. print., 2014.
93. J. W. Simmons and M. J. Guttmann, States, waves, and photons: a modern introduction to light, Addison-Wesley Pub. Co., Reading, Mass., 1970.
94. A. T. O’Neil, I. MacVicar, L. Allen and M. J. Padgett, Phys. Rev. Lett., 2002, 88, 053601.
95. A. Lininger, G. Palermo, A. Guglielmelli, G. Nicoletta, M. Goel, M. Hinczewski and G. Strangi, Adv. Mater., 2023, 35, 2107325.
96. M. J. Padgett, Opt. Express, 2017, 25, 11265.
97. A. Forbes, L. Mkhumbuza and L. Feng, Nat. Rev. Phys., 2024, 6, 352–364.
98. Y. Shen, X. Wang, Z. Xie, C. Min, X. Fu, Q. Liu, M. Gong and X. Yuan, Light: Sci. Appl., 2019, 8, 90.
99. J. Chen, C. Wan and Q. Zhan, Adv. Photonics, 2021, 3, 064001.
100. Y. Chen, W. Du, Q. Zhang, O. Ávalos-Ovando, J. Wu, Q.-H. Xu, N. Liu, H. Okamoto, A. O. Govorov, Q. Xiong and C.-W. Qiu, Nat. Rev. Phys., 2021, 4, 113–124.
101. G. F. Quinteiro Rosen, P. I. Tamborenea and T. Kuhn, Rev. Mod. Phys., 2022, 94, 035003.
102. A. Porfirev, S. Khonina and A. Kuchmizhak, Prog. Quantum Electron., 2023, 88, 100459.
103. M. Padgett and R. Bowman, Nat. Photonics, 2011, 5, 343–348.
104. Y. Yang, Y.-X. Ren, M. Chen, Y. Arita and C. Rosales-Guzmán, Adv. Photonics, 2021, 3, 034001.
105. T. Arikawa, T. Hiraoka, S. Morimoto, F. Blanchard, S. Tani, T. Tanaka, K. Sakai, H. Kitajima, K. Sasaki and K. Tanaka, Sci. Adv., 2020, 6, eaay1977.
106. D.-J. Yang and J.-C. Liu, Nanoscale, 2023, 15, 11860–11866.
107. K. Toyoda, K. Miyamoto, N. Aoki, R. Morita and T. Omatsu, Nano Lett., 2012, 12, 3645–3649.
108. K. Toyoda, F. Takahashi, S. Takizawa, Y. Tokizane, K. Miyamoto, R. Morita and T. Omatsu, Phys. Rev. Lett., 2013, 110, 143603.
109. S. Syubaev, A. Zhizhchenko, A. Kuchmizhak, A. Porfirev, E. Pustovalov, O. Vitrik, Yu Kulchin, S. Khonina and S. Kudryashov, Opt. Express, 2017, 25, 10214.
110. T. Omatsu, K. Miyamoto, K. Toyoda, R. Morita, Y. Arita and K. Dholakia, Adv. Opt. Mater., 2019, 7, 1801672.
111. J. Ni, C. Wang, C. Zhang, Y. Hu, L. Yang, Z. Lao, B. Xu, J. Li, D. Wu and J. Chu, Light: Sci. Appl., 2017, 6, e17011.
112. H. Rubinsztein-Dunlop, A. Forbes, M. V. Berry, M. R. Dennis, D. L. Andrews, M. Mansuripur, C. Denz, C. Alpmann, P. Banzer, T. Bauer, E. Karimi, L. Marrucci, M. Padgett, M. Ritsch-Marte, N. M. Litchinitser, N. P. Bigelow, C. Rosales-Guzmán, A. Belmonte, J. P. Torres, T. W. Neely, M. Baker, R. Gordon, A. B. Stilgoe, J. Romero, A. G. White, R. Fickler, A. E. Willner, G. Xie, B. McMorran and A. M. Weiner, J. Opt., 2017, 19, 013001.
113. O. V. Angelsky, A. Y. Bekshaev, S. G. Hanson, C. Y. Zenkova, I. I. Mokhun and Z. Jun, Front. Phys., 2020, 8, 114.
114. A. Forbes, M. De Oliveira and M. R. Dennis, Nat. Photonics, 2021, 15, 253–262.
115. D. Ayuso, O. Neufeld, A. F. Ordonez, P. Decleva, G. Lerner, O. Cohen, M. Ivanov and O. Smirnova, Nat. Photonics, 2019, 13, 866–871.
116. J. L. Greenfield, J. Wade, J. R. Brandt, X. Shi, T. J. Penfold and M. J. Fuchter, Chem. Sci., 2021, 12, 8589–8602.
117. L.-Y. Wang, K. W. Smith, S. Dominguez-Medina, N. Moody, J. M. Olson, H. Zhang, W.-S. Chang, N. Kotov and S. Link, ACS Photonics, 2015, 2, 1602–1610.
118. Y. Hwang, B. Hopkins, D. Wang, A. Mitchell, T. J. Davis, J. Lin and X. Yuan, Laser Photonics Rev., 2017, 11, 1700216.
119. S. Zhou, J. Bian, P. Chen, M. Xie, J. Chao, W. Hu, Y. Lu and W. Zhang, Light: Sci. Appl., 2022, 11, 64.
120. Z. Han, F. Wang, J. Sun, X. Wang and Z. Tang, Adv. Mater., 2023, 35, 2206141.
121. Q.-M. Deng, X. Li, M.-X. Hu, F.-J. Li, X. Li and Z.-L. Deng, npj Nanophotonics, 2024, 1, 20.
122. E. Plum and N. I. Zheludev, Appl. Phys. Lett., 2015, 106, 221901.
123. P. Yu, L. V. Besteiro, Y. Huang, J. Wu, L. Fu, H. H. Tan, C. Jagadish, G. P. Wiederrecht, A. O. Govorov and Z. Wang, Adv. Opt. Mater., 2019, 7, 1800995.
124. B. Ranjbar and P. Gill, Chem. Biol. Drug Des., 2009, 74, 101–120.
125. W. Kuhn, Trans. Faraday Soc., 1930, 26, 293–308.
126. S. W. Im, H. Ahn, R. M. Kim, N. H. Cho, H. Kim, Y. Lim, H. Lee and K. T. Nam, Adv. Mater., 2020, 32, 1905758.
127. A. Wu, Y. Y. Tanaka and T. Shimura, APL Photonics, 2021, 6, 126104.
128. L. Kvittingen and B. J. Sjursnes, J. Chem. Educ., 2020, 97, 2196–2202.
129. P. L. Polavarapu, J. Phys. Chem. A, 2005, 109, 7013–7023.
130. Comprehensive chiroptical spectroscopy, ed. N. Berova, Wiley, Hoboken, NJ, 2012.
131. J. Kwon, K. H. Park, W. J. Choi, N. A. Kotov and J. Yeom, Acc. Chem. Res., 2023, 56, 1359–1372.
132. Y. Sang, J. Han, T. Zhao, P. Duan and M. Liu, Adv. Mater., 2020, 32, 1900110.
133. E. Er, T. H. Chow, L. M. Liz-Marzán and N. A. Kotov, ACS Nano, 2024, 18, 12589–12597.
134. X. Zhang, L. Zhang, J. Zhu, T. Qin, H. Huang, B. Xiang, H. Liu and Q. Xiong, Nanoscale, 2025, 17, 4175–4194.
135. A. H. Sihvola and I. V. Lindell, Microwave Opt. Technol. Lett., 1991, 4, 295–297.
136. M. Fiebig, J. Phys. D: Appl. Phys., 2005, 38, R123–R152.
137. P. A. Temussi, Trends Biochem. Sci., 2009, 34, 296–302.
138. G. Alvarez-Rivera, M. Bueno, D. Ballesteros-Vivas and A. Cifuentes, TrAC, Trends Anal. Chem., 2020, 123, 115761.
139. L. A. Nguyen, H. He and P.-H. Chuong, Int. J. Biomed. Sci., 2006, 2, 85–100.
140. A. Calcaterra and I. D’Acquarica, J. Pharm. Biomed. Anal., 2018, 147, 323–340.
141. M. Wakabayashi, S. Yokojima, T. Fukaminato, K. Shiino, M. Irie and S. Nakamura, J. Phys. Chem. A, 2014, 118, 5046–5057.
142. L. V. Besteiro, K. Gungor, H. V. Demir and A. O. Govorov, J. Phys. Chem. C, 2017, 121, 2987–2997.
143. N. J. Ray, J. H. Yoo, J. T. McKeown, S. Elhadj, S. H. Baxamusa, M. A. Johnson, H. T. Nguyen, W. A. Steele, J. M. Chesser, M. J. Matthews and E. Feigenbaum, ACS Appl. Nano Mater., 2019, 2, 4395–4401.
144. L. Chang, L. V. Besteiro, J. Sun, E. Y. Santiago, S. K. Gray, Z. Wang and A. O. Govorov, ACS Energy Lett., 2019, 4, 2552–2568.
145. G. M. Barrow, Introduction to molecular spectroscopy, Hassell Street Press, 2021.
146. J. M. Hollas, Basic atomic and molecular spectroscopy, Royal Society of Chemistry, Cambridge, UK, 2002.
147. P. R. Bunker and P. Jensen, Molecular symmetry and spectroscopy, NRC Research Press, Ottawa, 2nd edn, 2006.
148. J. A. Schellman, Chem. Rev., 1975, 75, 323–331.
149. Circular dichroism: principles and applications, ed. N. Berova, K. Nakanishi and R. W. Woody, Wiley-VCH, New York Weinheim, 2nd edn, 2000.
150. L. Rosenfeld, Z. Med. Phys., 1929, 52, 161–174.
151. A. Rodger and B. Nordén, Circular dichroism and linear dichroism, Oxford University Press, Oxford, 1997.
152. M. F. Picardi, A. V. Zayats and F. J. Rodríguez-Fortuño, Phys. Rev. Lett., 2018, 120, 117402.
153. H. Tanaka, M. Ikenosako, Y. Kato, M. Fujiki, Y. Inoue and T. Mori, Commun. Chem., 2018, 1, 38.
154. T. Mori, Chem. Rev., 2021, 121, 2373–2412.
155. R. G. Uceda, C. M. Cruz, S. Míguez-Lago, L. Á. De Cienfuegos, G. Longhi, D. A. Pelta, P. Novoa, A. J. Mota, J. M. Cuerva and D. Miguel, Angew. Chem., Int. Ed., 2024, 63, e202316696.
156. W.-S. Chang, B. Willingham, L. S. Slaughter, S. Dominguez-Medina, P. Swanglap and S. Link, Acc. Chem. Res., 2012, 45, 1936–1945.
157. S. A. Maier, Plasmonics: fundamentals and applications, Springer, New York, 2007.
158. Plasmonics, ed. S. Enoch and N. Bonod, Springer, New York, 2012.
159. C. Noguez, J. Phys. Chem. C, 2007, 111, 3806–3819.
160. K. L. Kelly, E. Coronado, L. L. Zhao and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 668–677.
161. R. L. Olmon, B. Slovick, T. W. Johnson, D. Shelton, S.-H. Oh, G. D. Boreman and M. B. Raschke, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 235147.
162. A. Marini, R. Del Sole and G. Onida, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 115101.
163. I.-B. Lin, T. W.-H. Sheu and J.-H. Li, Opt. Express, 2014, 22, 30725.
164. S. A. Lee and S. Link, Acc. Chem. Res., 2021, 54, 1950–1960.
165. M. Pelton and G. W. Bryant, Introduction to metal-nanoparticle plasmonics, Wiley, Science Wise Publishing, Hoboken, New Jersey, 2013.
166. J. Pérez-Juste, I. Pastoriza-Santos, L. M. Liz-Marzán and P. Mulvaney, Coord. Chem. Rev., 2005, 249, 1870–1901.
167. L. K. Khorashad, L. V. Besteiro, M. A. Correa-Duarte, S. Burger, Z. M. Wang and A. O. Govorov, J. Am. Chem. Soc., 2020, 142, 4193–4205.
168. G. Zhu, H. Wei, Z. Sun, J. Liu, X. Wei, Y. Liang, W. Peng and Y. Fang, New J. Phys., 2023, 25, 103044.
169. K. Mislow and P. Bickart, Isr. J. Chem., 1976, 15, 1–6.
170. O. Ávalos-Ovando, L. V. Besteiro, A. Movsesyan, G. Markovich, T. Liedl, K. Martens, Z. Wang, M. A. Correa-Duarte and A. O. Govorov, Nano Lett., 2021, 21, 7298–7308.
171. L. K. Khorashad, L. V. Besteiro, M. A. Correa-Duarte, S. Burger, Z. M. Wang and A. O. Govorov, J. Am. Chem. Soc., 2020, 142, 4193–4205.
172. Y. Inoue, Chem. Rev., 1992, 92, 741–770.
173. A. Canaguier-Durand, J. A. Hutchison, C. Genet and T. W. Ebbesen, New J. Phys., 2013, 15, 123037.
174. C. Genet, ACS Photonics, 2022, 9, 319–332.
175. N. Ichiji, T. Ishida, I. Morichika, D. Oue, T. Tatsuma and S. Ashihara, Nanophotonics, 2024, 13, 4751–4760.
176. Y. E. Lee, K. H. Fung, D. Jin and N. X. Fang, Nanophotonics, 2014, 3, 343–350.
177. Z. Zhang, T. Harada, A. Pietropaolo, Y. Wang, Y. Wang, X. Hu, X. He, H. Chen, Z. Song, M. Bando and T. Nakano, Chem. Commun., 2021, 57, 1794–1797.
178. J. S. Kang, S. Kang, J.-M. Suh, S. M. Park, D. K. Yoon, M. H. Lim, W. Y. Kim and M. Seo, J. Am. Chem. Soc., 2022, 144, 2657–2666.
179. C. He and Y. Li, Chin. Chem. Lett., 2023, 34, 108077.
180. A. Movsesyan, A. Muravitskaya, L. V. Besteiro, E. Y. Santiago, O. Ávalos-Ovando, M. A. Correa-Duarte, Z. Wang, G. Markovich and A. O. Govorov, Adv. Opt. Mater., 2023, 11, 2300013.
181. A. Baldi and S. H. C. Askes, ACS Catal., 2023, 13, 3419–3432.
182. F. Tam, G. P. Goodrich, B. R. Johnson and N. J. Halas, Nano Lett., 2007, 7, 496–501.
183. J. Langer, D. Jimenez De Aberasturi, J. Aizpurua, R. A. Alvarez-Puebla, B. Auguié, J. J. Baumberg, G. C. Bazan, S. E. J. Bell, A. Boisen, A. G. Brolo, J. Choo, D. Cialla-May, V. Deckert, L. Fabris, K. Faulds, F. J. García De Abajo, R. Goodacre, D. Graham, A. J. Haes, C. L. Haynes, C. Huck, T. Itoh, M. Käll, J. Kneipp, N. A. Kotov, H. Kuang, E. C. Le Ru, H. K. Lee, J.-F. Li, X. Y. Ling, S. A. Maier, T. Mayerhöfer, M. Moskovits, K. Murakoshi, J.-M. Nam, S. Nie, Y. Ozaki, I. Pastoriza-Santos, J. Perez-Juste, J. Popp, A. Pucci, S. Reich, B. Ren, G. C. Schatz, T. Shegai, S. Schlücker, L.-L. Tay, K. G. Thomas, Z.-Q. Tian, R. P. Van Duyne, T. Vo-Dinh, Y. Wang, K. A. Willets, C. Xu, H. Xu, Y. Xu, Y. S. Yamamoto, B. Zhao and L. M. Liz-Marzán, ACS Nano, 2020, 14, 28–117.
184. T. Torimoto, H. Horibe, T. Kameyama, K. Okazaki, S. Ikeda, M. Matsumura, A. Ishikawa and H. Ishihara, J. Phys. Chem. Lett., 2011, 2, 2057–2062.
185. T. Shoji and Y. Tsuboi, J. Phys. Chem. Lett., 2014, 5, 2957–2967.
186. C. Hubert, R. Bachelot, J. Plain, S. Kostcheev, G. Lerondel, M. Juan, P. Royer, S. Zou, G. C. Schatz, G. P. Wiederrecht and S. K. Gray, J. Phys. Chem. C, 2008, 112, 4111–4116.
187. A. Horrer, Y. Zhang, D. Gérard, J. Béal, M. Kociak, J. Plain and R. Bachelot, Nano Lett., 2020, 20, 509–516.
188. T. Geldhauser, S. Ikegaya, A. Kolloch, N. Murazawa, K. Ueno, J. Boneberg, P. Leiderer, E. Scheer and H. Misawa, Plasmonics, 2011, 6, 207–212.
189. C. Gruber, A. Hirzer, V. Schmidt, A. Trügler, U. Hohenester, H. Ditlbacher, A. Hohenau and J. R. Krenn, Appl. Phys. Lett., 2015, 106, 081101.
190. B. B. Rajeeva, D. S. Hernandez, M. Wang, E. Perillo, L. Lin, L. Scarabelli, B. Pingali, L. M. Liz-Marzán, A. K. Dunn, J. B. Shear and Y. Zheng, Adv. Sci., 2015, 2, 1500232.
191. K. Ueno, S. Juodkazis, T. Shibuya, Y. Yokota, V. Mizeikis, K. Sasaki and H. Misawa, J. Am. Chem. Soc., 2008, 130, 6928–6929.
192. H. Wang, W. Zhang, D. Ladika, H. Yu, D. Gailevičius, H. Wang, C. Pan, P. N. S. Nair, Y. Ke, T. Mori, J. Y. E. Chan, Q. Ruan, M. Farsari, M. Malinauskas, S. Juodkazis, M. Gu and J. K. W. Yang, Adv. Funct. Mater., 2023, 33, 2214211.
193. Y. M. Morozov, N. Gisbert Quilis, S. Fossati, L. De Laporte, C. Gusenbauer, A. Weber, J. L. Toca-Herrera, F. Wiesner, U. Jonas and J. Dostalek, J. Phys. Chem. C, 2024, 128, 18641–18650.
194. G. V. Hartland, L. V. Besteiro, P. Johns and A. O. Govorov, ACS Energy Lett., 2017, 2, 1641–1653.
195. L. V. Besteiro, X.-T. Kong, Z. Wang, G. Hartland and A. O. Govorov, ACS Photonics, 2017, 4, 2759–2781.
196. A. M. Brown, R. Sundararaman, P. Narang, W. A. Goddard and H. A. Atwater, ACS Nano, 2016, 10, 957–966.
197. X. Li, D. Xiao and Z. Zhang, New J. Phys., 2013, 15, 023011.
198. T. V. Shahbazyan, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 235431.
199. L. V. Besteiro, X.-T. Kong, Z. M. Wang and A. O. Govorov, in Plasmonic Catalysis: From Fundamentals to Applications, ed. E. Cortés and P. H. C. Camargo, Wiley, 1st edn, 2021.
200. P. Christopher and M. Moskovits, Annu. Rev. Phys. Chem., 2017, 68, 379–398.
201. P. V. Kumar, T. P. Rossi, D. Marti-Dafcik, D. Reichmuth, M. Kuisma, P. Erhart, M. J. Puska and D. J. Norris, ACS Nano, 2019, 13, 3188–3195.
202. P. Lyu, R. Espinoza and S. C. Nguyen, J. Phys. Chem. C, 2023, 127, 15685–15698.
203. S. Bhanushali, S. Mahasivam, R. Ramanathan, M. Singh, E. L. Harrop Mayes, B. J. Murdoch, V. Bansal and M. Sastry, ACS Nano, 2020, 14, 11100–11109.
204. T. Qiao, P. Bordoloi, T. Miyashita, J. A. Dionne and M. L. Tang, Nano Lett., 2024, 24, 2611–2618.
205. S. Lee, C. Fan, A. Movsesyan, J. Bürger, F. J. Wendisch, L. De S. Menezes, S. A. Maier, H. Ren, T. Liedl, L. V. Besteiro, A. O. Govorov and E. Cortés, Angew. Chem., Int. Ed., 2024, e202319920.
206. T. Ishida, A. Isawa, S. Kuroki, Y. Kameoka and T. Tatsuma, Appl. Phys. Lett., 2023, 123, 061111.
207. J.-Y. Kim, C. McGlothin, M. Cha, Z. J. Pfaffenberger, E. S. Turali Emre, W. Choi, S. Kim, J. S. Biteen and N. A. Kotov, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2312082121.
208. M. Ghalawat, D. Feferman, L. V. Besteiro, W. He, A. Movsesyan, A. Muravitskaya, J. Valdez, A. Moores, Z. Wang, D. Ma, A. O. Govorov and G. Markovich, ACS Nano, 2024, 18, 28279–28291.
209. K. Saito, Y. Nemoto and Y. Ishikawa, Nano Lett., 2024, 24, 12840–12848.
210. O. Ávalos-Ovando, V. A. Bahamondes Lorca, L. V. Besteiro, A. Movsesyan, Z. Wang, G. Markovich and A. O. Govorov, Appl. Phys. Rev., 2023, 10, 031412.
211. J.-Y. Kim, J. Yeom, G. Zhao, H. Calcaterra, J. Munn, P. Zhang and N. Kotov, J. Am. Chem. Soc., 2019, 141, 11739–11744.
212. L. V. Besteiro, P. Yu, Z. Wang, A. W. Holleitner, G. V. Hartland, G. P. Wiederrecht and A. O. Govorov, Nano Today, 2019, 27, 120–145.
213. O. Neumann, A. S. Urban, J. Day, S. Lal, P. Nordlander and N. J. Halas, ACS Nano, 2013, 7, 42–49.
214. M. S. Zielinski, J.-W. Choi, T. La Grange, M. Modestino, S. M. H. Hashemi, Y. Pu, S. Birkhold, J. A. Hubbell and D. Psaltis, Nano Lett., 2016, 16, 2159–2167.
215. A. S. Kim, A. Goswami, M. Taghinejad and W. Cai, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2318713121.
216. J. Song, C.-Y. Ji, X. Ma, J. Li, W. Zhao and R.-Y. Wang, J. Phys. Chem. Lett., 2024, 15, 975–982.
217. F. P. Incropera, D. P. DeWitt, T. L. Bergman and A. S. Lavine, ed., Foundations to heat transfer, Wiley, Singapore, 6. ed., internat. student version, 2013.
218. A. N. Salazar, Eur. J. Phys., 2003, 24, 351–358.
219. S. Hashimoto, D. Werner and T. Uwada, J. Photochem. Photobiol., C, 2012, 13, 28–54.
220. A. Schirato, M. Maiuri, A. Toma, S. Fugattini, R. Proietti Zaccaria, P. Laporta, P. Nordlander, G. Cerullo, A. Alabastri and G. Della Valle, Nat. Photonics, 2020, 14, 723–727.
221. A. B. Taylor, A. M. Siddiquee and J. W. M. Chon, ACS Nano, 2014, 8, 12071–12079.
222. G. Albrecht, S. Kaiser, H. Giessen and M. Hentschel, Nano Lett., 2017, 17, 6402–6408.
223. C. D. Stanciu, F. Hansteen, A. V. Kimel, A. Kirilyuk, A. Tsukamoto, A. Itoh and Th Rasing, Phys. Rev. Lett., 2007, 99, 047601.
224. A. Capretti, A. Lesage and T. Gregorkiewicz, ACS Photonics, 2017, 4, 2187–2196.
225. W. Wang and L. Qi, Adv. Funct. Mater., 2019, 29, 1807275.
226. J. Peng, J. Hou, T. Tang, J. Li and Z. Chen, Phys. Status Solidi B, 2022, 259, 2200114.
227. T. J. Cui, S. Zhang, A. Alù, M. Wegener, S. J. Pendry, J. Luo, Y. Lai, Z. Wang, X. Lin, H. Chen, P. Chen, R.-X. Wu, Y. Yin, P. Zhao, H. Chen, Y. Li, Z. Zhou, N. Engheta, V. Asadchy, C. Simovski, S. Tretyakov, B. Yang, S. D. Campbell, Y. Hao, D. H. Werner, S. Sun, L. Zhou, S. Xu, H.-B. Sun, Z. Zhou, Z. Li, G. Zheng, X. Chen, T. Li, S. Zhu, J. Zhou, J. Zhao, Z. Liu, Y. Zhang, Q. Zhang, M. Gu, S. Xiao, Y. Liu, X. Zhang, Y. Tang, G. Li, T. Zentgraf, K. Koshelev, Y. Kivshar, X. Li, T. Badloe, L. Huang, J. Rho, S. Wang, D. P. Tsai, A. Y. Bykov, A. V. Krasavin, A. V. Zayats, C. McDonnell, T. Ellenbogen, X. Luo, M. Pu, F. J. Garcia-Vidal, L. Liu, Z. Li, W. Tang, H. F. Ma, J. Zhang, Y. Luo, X. Zhang, H. C. Zhang, P. H. He, L. P. Zhang, X. Wan, H. Wu, S. Liu, W. X. Jiang, X. G. Zhang, C.-W. Qiu, Q. Ma, C. Liu, L. Li, J. Han, L. Li, M. Cotrufo, C. Caloz, Z.-L. Deck-Léger, A. Bahrami, O. Céspedes, E. Galiffi, P. A. Huidobro, Q. Cheng, J. Y. Dai, J. C. Ke, L. Zhang, V. Galdi and M. Di Renzo, J. Phys. Photonics, 2024, 6, 032502.
228. L. Yuan, Y. Zhao, A. Toma, V. Aglieri, B. Gerislioglu, Y. Yuan, M. Lou, A. Ogundare, A. Alabastri, P. Nordlander and N. J. Halas, Nano Lett., 2024, 24, 172–179.
229. S. K. Saikin, A. Eisfeld, S. Valleau and A. Aspuru-Guzik, Nanophotonics, 2013, 2, 21–38.
230. Q. Li and Z. Li, Adv. Sci., 2017, 4, 1600484.
231. M. Guerrini, A. Calzolari, D. Varsano and S. Corni, J. Chem. Theory Comput., 2019, 15, 3197–3203.
232. S. Ma, S. Du, G. Pan, S. Dai, B. Xu and W. Tian, Aggregate, 2021, 2, e96.

---