The elasticity of MOFs under mechanical pressure

Abstract

Nowadays, there is fast growing interest for characterization of mechanical behaviors of different classes of MOFs materials under moderate and high applied pressures to search for the stable one to resist different mechanical constraints in both processing and complex applications. This review article presents the performance and properties of rigid and flexible Metal–Organic Frameworks (MOFs) under mechanical pressure without or with different pressure-transmitting media. With the current reports, we could find a wide range of the bulk moduli of MOFs, which are mainly lower than the traditional pores material zeolite. Among all the MOF materials discussed in this article, the HKUST-1 (Cu-BTC) has the highest bulk modulus. In addition, we discussed the possibilities of MOFs in the applications as mechanical energy absorption/storage materials.

---

Ke Yang

Ke Yang received his Ph.D. degree from the Institute Charles Gerhardt Montpellier, Université de Montpellier in 2014. He joined the faculty of Institute of New Energy, China University of Petroleum (Beijing) in 2015 as a lecturer. His research interest focuses on the MOFs materials synthesis, physical properties and application on energy storage and gas adsorption.

Guanglin Zhou

Guanglin Zhou received his Ph.D. degree from the College of Chemical Engineering, China University of Petroleum (Beijing) in 2009 with Jinsen Gao. He is an Associate Professor in Institute of New Energy, China University of Petroleum (Beijing). His research interest focuses on the technology of petro chemical and coal chemical, the industrial application of catalyst and adsorber.

Quan Xu

Quan Xu received his Ph.D. degree from the Department of Materials Science and Engineering, University of North Texas in 2013. He is an Associate Professor in Institute of New Energy, China University of Petroleum (Beijing). His research interest focuses on the development of membrane catalysis technology, bioinspired materials, nanomaterials for environmental applications and bio-devices.

---

Introduction

As a very important series of pores crystal materials, metal organic frameworks (MOFs) have a high diversity with a controllable pore size, shape, topology and chemical environment via the selection of different metal centres and organic linkers. As MOFs have the combined properties of polymers and inorganic materials, they are very different with the traditional polymers and inorganic pores materials such as zeolite. The new structure design and synthesis, properties and applications are a very interesting research field in recent decades. To fully achieve their utilization functionalities in the different fields, such as gas storage/separation, catalysis, sensors, electronic devices and many others, in addition to high chemical and thermal stabilities, MOFs must be also stable enough to resist to different mechanical constraints in both processing (also called shaping) and various practical applications. There is currently rapidly growing interest in characterizing the mechanical behaviours of this class of materials under different conditions, which have been discussed in theory by Cheetham et al.¹ In recent years, more results have been reported, especially the research of our team and co-workers in flexible MOFs as MIL-53 (MIL stands for Materials of the Institute Lavoisier) and MIL-47, which was pulled from the rigid to flexible field.² Indeed, the mechanical constraint can be loaded on the MOFs in terms of tension, compression, shear, bending, torsion, impact or any combinations of the above, depending on the explored applications and the nature/magnitude of the loads. The properties of the MOFs were intensively explored under low mechanical loads within the elastic limit wherein deformation is usually relatively small and reversible. In this content, a series of experimental techniques, including high-pressure X-ray diffraction and neutron diffraction, were employed sometimes in tandem with quantum, as well as force field-based molecular simulations to determine the corresponding elastic properties of MOFs. In this study, we mainly discuss the bulk modulus (K), the inverse of compressibility, corresponding to a measure of the mechanical resilience of the MOF framework against volumetric changes under uniform hydrostatic pressure.

In the typical industrial processing and applications explored so far by the collaborators of the group (gas/vapour adsorption-separation), the MOFs undergo many cycles of pressurization/compression under hydrostatic conditions and indeed the K elastic property is the most relevant mechanical property of the host framework to be characterized. In this study, we provide a global overview of the literature dealing with this elastic property. The other mechanical properties, such as the hardness, a measure of the framework resilience towards permanent plastic deformation, the yield strength and the fracture toughness, are much more scarcely explored to date in the fields of MOFs¹ and thus they are not detailed further.

Above the estimation of these elastic properties, the structural behaviour for a series of both rigid and flexible MOFs was characterized intensively by mercury porosimetry, X-ray and neutron diffraction experiments under moderate and high applied pressures. These different characterization techniques focus on the loss of crystallinity, framework collapse and even the amorphization of a series of MOFs under hydrostatic compression using specific cells, including the Diamond Anvil Cell (DAC). Finally, the promising future of some MOFs for mechanical energy absorption-related applications are discussed and proposed.

Structural behavior of MOFs under applied pressures

1. Rigid MOFs

Cu-BTC (BTC for benzene-1,3,5-tricarboxylate) is one of the first rigid MOFs investigated by high pressure X-ray diffraction. Chapman et al.³ first revealed that Cu-BTC showed linear framework compression up to ∼2 GPa in the absence or presence of Fluorinert as pressure-transmitting media, which is assumed to not enter the pores. The relatively small unit cell variation of ∼6% was evidenced and this phenomenon was fully reversible, even though some changes in the sample morphology were observed depending on the rate of pressure release. This experimental observation was further confirmed by molecular dynamics simulations based on a flexible force field to represent the MOF framework^4,5 emanating from two different groups.

Moggach et al.⁶ further conducted high pressure single crystal measurements on MOF-5 in the presence of diethylformamide (DEF), which is supposed to enter the pores. They reported Density Functional Theory (DFT) calculations for the empty solid as it was the only way to probe the mechanical properties of this solid in the absence of guest molecules, the size of its pore being very large to avoid the inclusion of the pressure-transmitting media they currently used. They predicted a gradual decrease in the unit cell volume up to 14% at 3.2 GPa, this compressibility being mediated through the Zn–O bonds. Above this critical pressure, this solid was shown to be amorphous.

High-pressure X-ray powder diffraction measurements were also performed by Chapman et al.⁷ on the ZIF-8 (ZIF for Zeolitic Imidazolate Framework) solid under an applied pressure of up to 1 GPa without a fluid (non-hydrostatic) or with the non-penetrating inert fluid, Fluorinert, to focus only on the intrinsic high-pressure behavior of this MOF. As illustrated in Fig. 1, they reported that the framework compresses rapidly with a unit cell variation of 5% over 0.3 GPa, while for a pressure above 0.34 GPa, an irreversible structural transition occurs corresponding to the amorphization of the structure, which retains some structural order.

Fig. 1 Relative change in the lattice parameters of ZIF-8 up to 0.34 GPa before amorphization occurs as evidenced by the high pressure diffraction data recorded under hydrostatic and non-hydrostatic compression (λ = 0.60511 Å) (adapted from ref. 7).

The Zn(Im)₂ phase and its LiB(Im)₄ boron imidazolate frameworks analogues with alternate Zn cations being replaced by Li and B, respectively, were also explored by high pressure single crystal diffraction.⁸ This was the first study to report that the Zn-phase undergoes a phase transition in the range of 0.54–0.84 GPa, corresponding to a relative volume change of 9% while the tetragonal symmetry is maintained.⁸ The LiB(Im)₄ was established to be more mechanically resilient with a similar phase transition occurring at higher pressures (1.69 GPa) with a smaller unit cell volume change (∼6%). These data were further discussed in light of the complementary results issued from nano-indentation measurements and DFT calculations.

High-pressure single crystal experiments reported recently by Moggach et al.⁹ also evidenced an amorphization of scandium terephthalate Sc₂BDC₃ (BDC for 1,4-benzene dicarboxylate) in the presence of the non-penetrating Fluorinert at the same range of applied pressures (0.4 GPa), which was this time fully reversible once the applied pressure was released.

Another MOF labelled as ZAG-4 (ZAG stands for zinc alkyl gate), which is comprised of Zn–O–P–O 8-membered rings fused through zinc into a 1-D chain was also recently investigated as a single crystal using a 4 : 1 methanol/ethanol mixture as the transmitting medium.¹⁰ This material showed a gradual decrease in its unit cell volume up to 10 GPa, corresponding to a relative change of 27% without a loss of crystallinity. This transformation was shown to be fully reversible, the quality of the single crystal being intact after a release of the pressure.

2. Flexible MOFs

The first study on the very well-known breathing MIL-53(Cr) was reported in 2010 by the Madirel group in Marseille. Beurroies et al.¹¹ evidenced by mercury porosimetry experiments, an apparent volume of intruded Hg at about 55 MPa that does not correspond to any porosity of this solid (Fig. 2). Such a signature was assigned to a structural transition involving a unit cell volume change of ∼38%, which was not confirmed by further analysis.

Fig. 2 Cumulative volume of intruded mercury in a two cycles intrusion–extrusion as a function of the applied pressure obtained for the MIL-53(Cr) sample (adapted from ref. 11).

A computational approach based on molecular dynamics simulations using a flexible force field for the framework was further performed by the group and provided the first theoretical confirmation that this experimental findings can be assigned to a sudden contraction of the structure under an applied external pressure of about 50 MPa (Fig. 3), corresponding to a structural transition between a large pore and a closed pore forms, which involves a unit cell volume change (32%) of similar magnitude than the one obtained by porosimetry measurements.^11,12 This structural switching was predicted to be fully reversible consistent again with the experimental results. In addition, the incorporation of CO₂ within the pores was shown to induce an additional internal stress on the framework that leads to (i) a significant decrease in the external pressure required to induce the structural switching of the MIL-53(Cr) and (ii) an irreversible structural transformation, as depicted in Fig. 3.¹²

Fig. 3 Evolution of the simulated unit cell volume for MIL-53(Cr) as a function of the external applied pressure at 300 K (bare form: empty circle symbols; loaded with 1 CO₂/u.c.: solid square symbols) (reproduced from ref. 12 with permission from The Royal Society of Chemistry).

In complement to this, the MIL-47(V) solid, which has been shown to behave as rigid in the presence of guest molecules,^13–16 was later explored under applied pressure using a combination of mercury porosimetry, Raman spectroscopy, high pressure X-ray diffraction, and molecular dynamics simulations. Herein, one should notice that silicone oil was used as a pressure-transmitting medium because its kinetic diameter largely exceeds the window size of MIL-47(V), which ensures that it does penetrate the pores. This joint experimental/computational effort was able for the first time in this class of solids to unambiguously assign the apparent volume of intruded Hg occurring at ∼125 MPa to a reversible structural transition between a large pore and closed pore versions (Fig. 4).²

Fig. 4 X-ray diffraction patterns of the MIL-47(V) as a function of the applied pressure. Compression of (a) 0.1 MPa, (b) 51.1 MPa, (c) 90.1 MPa, (d) 147.1 MPa, (e) 178.1 MPa, (f) 340.1 MPa and decompression of (g) 3.1 MPa. The asterisks correspond to the Bragg peaks characteristic of the close pore form of the solid (λ = 0.709622 Å) (reproduced from ref. 2 with permission from The Royal Society of Chemistry).

A very recent high-pressure X-ray powder diffraction report on the aluminium version of MIL-53 (ref. 17) in the presence of mineral oil as non-penetrating media confirmed the presence of a structural transition from a large pore to a closed pore form but unexpectedly, as shown in Fig. 5. (i) This phase transition occurs with a gradual decrease in the unit cell volume, which drastically deviates with the sudden transition evidenced for MIL-53(Cr)/MIL-47(V). (ii) The volume of the closed pore form is only attained at about 6 GPa vs. 0.3 GPa for MIL-53(Cr)/MIL-47(V). The amino-functionalized MIL-53(Al) also showed a similar profile of the pressure dependence of the unit cell volume. Such behavior can only be possible if we assume that the mineral oil enters the pore of the MIL-53(Al)–NH₂ structure because this solid is known to exist only in a closed pore form when its pores are empty. The authors further demonstrated that both materials maintain their crystallinity up to high applied pressure (6 and 11 GPa for the pristine and the functionalized solids, respectively).

Fig. 5 Evolution of the unit cell volume and cell parameters for MIL-53(Al) as a function of the external applied pressure at ambient temperature (reproduced from ref. 17 with permission from The Royal Society of Chemistry).

Another contribution to this family of MIL-53 solids comes from Gascon et al.,¹⁸ who reported the results of high pressure X-ray powder diffraction of the very closed pores of MIL-53(In) functionalized with amino functional groups (similar structure than the non-modified MIL-53(Fe)) using mineral oil as the non-penetrating media. Fig. 6 clearly shows that the crystallinity of this solid is only slightly affected at a high pressure ∼23 GPa and that the compression of the framework is fully reversible at pressures of up to 15 GPa.

Fig. 6 X-ray diffraction patterns of the MIL-53(In)–NH₂ as a function of the applied pressure. The planes correspond to the main reflections as depicted in green (λ = 0.709622 Å) (reproduced from ref. 18 with permission from The Royal Society of Chemistry).

3. Impact of the presence of guest molecules

Studies related to the guest dependent pressure behaviour of these solids are still scarce. They focused mainly on (i) rigid or semi-flexible MOF frameworks (MOF-5, Cu-BTC, and ZIF-8), and (ii) a limited set of guest molecules (alcohol/water, diethylformamide, I₂) used experimentally as pressure transmitting fluids that penetrate the pores. Furthermore, the mechanical properties of these guest-loaded MOFs were primarily characterized in the high pressure domain (>1 GPa).

Chapman et al.^1,3 revealed for instance by high pressure X-ray diffraction measurements that the incorporation of a mixture of methanol–ethanol–water (MEW) and isopropyl alcohol (IPA) into the pores of Cu-BTC induces a unit cell variation profile, which differs from the one obtained with the non-penetrating Fluorinert liquid. The existence of a transition between two distinct regions of near linear compressibility was then observed (see Fig. 7) and it could be attributed to a structural change from a pore filling to a pore emptying states, the value of the transition pressure was higher when the larger isopropyl alcohol molecule is considered. A detailed structural analysis was later provided by Graham et al.¹⁹ using high pressure X-ray diffraction experiments performed on single crystals.

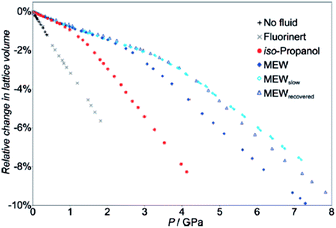Fig. 7 Relative change in the lattice parameters of Cu-BTC compressed in the presence of MEW and isopropyl alcohol (IPA) as a function of the pressure, showing two linear regions of compression (adapted from ref. 3).

Moggach et al.⁶ further evidenced by means of high pressure single crystal measurements that diethylformamide adsorbed in MOF-5 tends to stabilize the framework by significantly decreasing the magnitude of the unit cell volume change when the pressure increases and also shifting the onset of amorphization at higher pressures (see Fig. 8).⁶

Fig. 8 Relative change in lattice parameters for MOF-5 compressed in the absence (empty squares: DFT calculations) and in the presence of DEF (filled squares: experiments) as a function of the pressure (adapted from ref. 6).

High-pressure X-ray diffraction experiments using single crystals were performed by Moggach et al.²⁰ on ZIF-8 using methanol and ethanol as the hydrostatic medium, which penetrate into the pores under an applied pressure. They found a structural transition in the range of 0.90–1.47 GPa between two phases (I and II) characterized by the same cubic symmetry (space group I43m), but with different twists of the imidazolate ligands to slightly increase the accessible pore volume, as illustrated in Fig. 9. This transition involves a local rearrangement of the structure, which involves only a tiny change in the unit cell volume (∼1.5%). This guest-assisted structural transition, also called “gate closing/opening”, increases the size and shape of the narrow channels that connect the pores, leading to an overall increase in pore volume. This structural transformation was shown to be fully reversible once the applied pressure was released. It was also reported that the incorporation of pentane/isopentane instead of methanol/ethanol within the pores of ZIF-8 does not lead to any phase transition under an applied pressure, which emphasizes that this structural modification is really driven by the nature of the penetrating media. Compared to the empty case, which shows an amorphization at low pressure, (0.34 GPa), one observes that the inclusion of guest molecules allow ZIF-8 to be much more mechanical stable up to high pressures.

Fig. 9 Comparison of the structures of ZIF-8 at ambient pressure (phase I) and at 1.47 GPa (phase II) showing the change in orientation of the imidazolate linkers (adapted from ref. 20).

In complement to this contribution, Cheetham et al.²¹ explored by high-pressure single crystal and powder diffraction the mechanical behaviour of ZIF-4. They reported reversible amorphization of this structure, which occurs at different applied pressures depending on the nature and size of the pressure transmitting fluid. In some cases, the solid undergoes a structural transition from its initial form (orthorhombic symmetry) to the ZIF-4(I) phase (monoclinic symmetry), corresponding to a unit cell volume change of ∼15%.

Moggach et al.⁹ further showed that while the empty scandium terephthalate Sc₂BDC₃ structure shows reversible amorphization at 0.4 GPa, the crystallinity of the same solid containing methanol in its pores is retained up to 3 GPa (Fig. 10). This increase in mechanical stability was explained by the well-ordered arrangement of methanol within the pores predicted by Monte Carlo simulations, which tend to reinforce the resilience of the pore wall.

Fig. 10 Change in the unit cell volume for Sc₂BDC₃ compressed in the absence (red squares) and in the presence of methanol (blue lozenges) as a function of the pressure (adapted from ref. 9).

Finally, in the case of the highly flexible solid MIL-53(Al)–NH₂, Gascon et al.¹⁷ reported that the use of ethanol instead of mineral oil as pressure-transmitting media drastically changes the pressure dependence profile for the unit cell volume, as illustrated in Fig. 11. In the case of ethanol, the structural transition between the large pore and the close pore form is not observed anymore (rather a continuous decrease). This was assigned to the formation of densely packed ethanol in the pores, which would prevent the structural transition.¹⁷

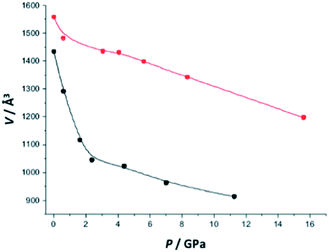Fig. 11 Change in the unit cell volume for MIL-53(Al)–NH₂ compressed in the presence of mineral oil (black circles) and of ethanol (red circles) as a function of the pressure (reproduced from ref. 17 with permission from The Royal Society of Chemistry).

Elastic properties of MOFs in hydrostatic conditions

As mentioned in the introduction, one of the most convenient parameters to characterize the mechanical properties of MOFs under uniform hydrostatic pressure is the bulk modulus, K. The values reported to date in the literature for the different MOFs introduced above were obtained by (i) using a 2^nd/3^rd order Birch–Murnaghan equation of states^22,23 to fit the pressure dependence of the unit cell volume or (ii) calculating the product of the initial volume of the MOF structure by the derivative of the pressure over the volume. These two approaches were also applied when force-field based molecular dynamics simulations were undertaken. In complement to this, density functional theory calculations were intensively employed to predict the bulk modulus of additional MOFs, including the series of IRMOFs, DUTs and UiO-66(Zr)s. These calculations also employ the Birch–Murnaghan equation of states to fit the total energy of the structure vs. the strain corresponding to the application of a uniform hydrostatic pressure. Table 1 summarizes the experimental and theoretical values obtained for the MOFs in the absence of guest molecules within their pores. Only a few results were collected experimentally. The K values are distributed widely depending on the topology, the density, the connectivity and the rigid/flexible nature of the MOF frameworks. It can also be observed that the rigid frameworks are obviously more resilient to deformation and indeed a higher value of K (lower compressibility) is obtained, which makes these materials more attractive for further industrial applications. Apart from the direct correlation between a high value of bulk modulus and a low density of the material, the resulting K values for MOFs are generally lower than those reported for the other well-known family of porous solids, the zeolites (30–70 GPa (ref. 1)), which are usually characterized by their higher framework densities.

Table 1 List of the bulk moduli determined for a series of MOFs without any guest molecules within their pores (all the experimental values are reported at ambient temperature, Density Functional Theory (DFT) calculations correspond to data at 0 K while force field based Molecular Dynamics (MD) is also reported at ambient temperature)

Materials	Framework dynamics	Bulk modulus (GPa)	Method	Reference
MOF-5	Rigid	∼17.0	DFT	24
	Rigid	∼18.2	DFT	25
	Rigid	∼18.5	DFT	26
	Rigid	∼17.0	DFT	27
	Rigid	∼20.0	Force field energy minimization	28
	Rigid	∼4.0	MD	28
	Rigid	∼14.4	Force field energy minimization	29
	Rigid	∼15.34	DFT	30
	Rigid	∼16.66	MD	31
IRMOF-8	Rigid	∼11.28	MD	31
IRMOF-14	Rigid	∼10.05	MD	31
MOF-C22	Rigid	∼6.88	MD	31
MOF-C30	Rigid	∼4.11	MD	31
MOF-177	Rigid	∼10.10	DFT	30
DUT-6	Rigid	∼10.73	DFT	30
MOF-14 (interpenetrated)	Rigid	∼14.8	DFT	32
MOF-14 (single net)	Rigid	∼5.5	DFT	32
DUT-34	Rigid	∼9.1	DFT	32
DUT-23	Rigid	∼13.2	DFT	32
HKUST-1 (Cu-BTC)	Rigid	∼30.7	Experiment (no fluid)	3
	Rigid	∼29.5	Experiment (Fluorinert)	3
	Rigid	∼25	DFT	5
	Rigid	∼35.2	MD	4
	Rigid	∼24.53	DFT	33
UIO-66	Rigid	∼41.01	DFT	33
		∼15	Experiment (silicon oil AP100)	Our work
Hf-UiO-66	Rigid	∼39.49	DFT	33
Ti-UiO-66	Rigid	∼42.07	DFT	33
UiO-67	Rigid	∼17.15	DFT	33
UiO-68	Rigid	∼14.40	DFT	33
ZIF-4-1	Rigid	∼15.2	Experiment (Daphne oil 7474)	21
ZIF-4	Rigid	∼7.78	Experiment (Daphne oil 7474)	21
Zn(Im)2	Rigid	∼14	Experiment (anhydrous 2-propanol)	34
LiB(Im)4	Rigid	∼16.6	Experiment (anhydrous 2-propanol)	8
ZIF-8	Rigid	∼6.5	Experiment (Fluorinert)	7
	Rigid	∼9.23	DFT	35
	Flexible	∼7.75	Experiment (no fluid)	35
NH2-MIL-53(In)	Flexible	∼10.09	Experiment (mineral oil)	18
MIL-53(Cr) (large-pore form)	Flexible	∼1.8	MD	12

---

To clarify the analysis of the data, we also report the K values for some MOFs in Table 2, which contain guest molecules or solvent used as pressure-transmitting fluid inside their pores. As already emphasized above, the usual trend is an improvement of the mechanical resilience of the MOF framework in the presence of a guest, which leads to higher K values. Interestingly, one can observe that some values of K become even higher than those reported for denser zeolites, which make these considered solids with optimal features for further industrial applications.

Table 2 List of the bulk moduli (K) determined for a series of MOFs in the presence of guest molecules within their pores (the experiments and the molecular dynamics were carried out at ambient temperature)

Material	Guest molecules	Bulk modulus (GPa)	Method	Reference
NH2-MIL-53(Al) (large-pore form, 0 to 2 GPa)	Mineral oil	∼7.4	Experiment	17
NH2-MIL-53(Al) (large-pore form, 2 to 11 GPa)	Mineral oil	∼71	Experiment	17
NH2-MIL-53(Al) (large-pore form, 2 to 11 GPa)	Ethanol	∼85	Experiment	17
MIL-53(Cr) (large-pore form)	CO2	∼0.75 (300 K)	MD	12
HKUST-1 (Cu-BTC)	Isopropyl alcohol	∼117.6, ∼25.9	Experiment	3
	Methanol–ethanol–water	∼116.0, ∼33.6	Experiment	3
	Methanol–ethanol–water (slow)	∼114.5, ∼41.9	Experiment	3
	Methanol–ethanol–water (recovered)	∼134.4, ∼32.5	Experiment	3
ZAG-4	Methanol, ethanol	∼11.7	Experiment	10
ZIF-4-I	Methanol : ethanol	∼16.45	Experiment	21
MOF-5	Diethyl formamide (DEF)	22.3–242.5	Experiment	6

---

We could note that for the same MOFs, the K values obtained from the experimental and theoretical calculations could be different, especially for the UIO-66; we trust our experimental data is more acceptable. Therefore, without considering the effects of the guest molecules within their pores, the HKUST-1 (Cu-BTC) has the largest bulk modulus among all the results reported in this study. In addition, with the values in Tables 1 and 2, we could conclude that the introduction of the guest molecules within their pores could increase the bulk modulus; the guest molecules share some of the pressure, making the materials more elastic. The differences in bulk modulus between the different MOFs should be related to the topology structure, the metal centre, the organic linker, the functionalization group, the chemical environment, but how they affect and which is the main effect still needs more targeted and stricter experiments. In our following study, we will discuss how the different metal centres and functionalization affect the mechanical behaviour of MOFs.

Outlook of application: promising MOFs for mechanical energy absorption/storage

The highly flexible structural behavior of MIL-53(Cr) under mechanical stimuli led the group in Madirel (Université Aix-Marseille) to propose the use of such materials to store the energy in play during the transition between the large pore and the closed pore forms discussed above.¹¹ This mechanical way to store the energy is complementary to the strategy previously envisaged with the intrusion–extrusion of water at high pressures in hydrophobic solids, including mesoporous silica³⁶ and zeosil³⁷ (hydrophobic zeolites), and even more recently, MOFs with ZIF-8, which showed shock-absorber behavior at about 27 MPa with a stored energy of 13 J g⁻¹.³⁸ Very recently, Patarin et al. reported that ZIF-8 upon high pressure intrusion–extrusion of aqueous KCl, LiCl, and NaCl solutions of variable concentration can even show higher stored energy, sometimes slightly exceeding 20 J g⁻¹.³⁹

The energy storage capacity of MIL-53(Cr) was estimated using the following relationship, which corresponds to the work: W = P × ΔV, where P corresponds to the transition pressure and ΔV the unit cell volume between the large pore and the closed pore forms. The resulting value of 12 J g⁻¹ was similar to the best performance reported to date for some of the hydrophobic materials, including silica, silicalite and zeosil (∼4–12 J g⁻¹)^37,38,40,41 and also for ZIF-8 (13 J g⁻¹).^38,42

Indeed, MOFs were already in the good range of performance and because of their extraordinary number of possible structures and chemical compositions, there was at that time serious hope of obtaining even better performance. This was later confirmed by the exploration of MIL-47(V)² in the group that showed a similar volume change between the large pore and the closed pore forms, while the transition pressure was much higher (125 MPa vs. 55 MPa), leading to an even higher absorbed mechanical energy (33 J g⁻¹). In both MIL-53(Cr) and MIL-47(V) cases, the structural transformation was shown to be reversible and associated with relatively large hysteresis, which makes these materials potentially attractive for energy absorption applications in the form of nano-dampers.

With our research results, it could be indeed pointed out that MOF structures do not collapse, even under very high pressures up to 5 GPa, which emphasizes the stability of this material upon mechanical pressure, an indispensable prerequisite for further applications. This observation highlights the interest of selecting this family of MOFs compared to other relatively flexible MOFs such as some ZIFs that show an irreversible amorphization even at moderate pressure as discussed above.²⁰ Moreover, the long term stability of silicalite and hydrophobic samples in water is limited,^43,44 whereas the applications we mention herein for MOFs are expected to be realized in inert fluids.

The general reports are mainly purely force on the physical characteristics such as the unit cell dimensions. However, little study was involved to discuss the effects of the chemical composition or chemical environment on the elasticity of the MOFs materials. In fact, in our study, we investigated the impact of different metal centres and functionalization on the mechanical behaviour of MOFs. The results show that modifications of the chemical composition could obviously change the pressure domain of the stability and compressibility; these will be reported minutely in the next study. The studies of the effect of the chemical composition or chemical environment on the elasticity will complete our knowledge on the physical properties of the MOFs materials and this information also needs to be considered in the design of MOFs for further applications.

These preliminary results pave the way towards either the tuning of existing MOFs or the design of novel ones able to maximize the energy storage capacity, which can be achieved by combining large unit cell variations and high transition pressures. In addition to the interest of MOFs in terms of nano-springs/dampers, the challenge is to also imagine a way to develop a system with an irreversible structural transition to absorb the mechanical energy during compression without any further release.

Acknowledgements

We acknowledge the National Nature Science Foundation of China (No. 51505501) for their support.

Notes and references

1. J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059–1080.
2. P. G. Yot, Q. Ma, J. Haines, Q. Yang, A. Ghoufi, T. Devic, C. Serre, V. Dmitriev, G. Ferey, C. Zhong and G. Maurin, Chem. Sci., 2012, 3, 1100–1104.
3. K. W. Chapman, G. J. Halder and P. J. Chupas, J. Am. Chem. Soc., 2008, 130, 10524–10526.
4. L. Zhao, Q. Yang, Q. Ma, C. Zhong, J. Mi and D. Liu, J. Mol. Model., 2011, 17, 227–234.
5. M. Tafipolsky, S. Amirjalayer and R. Schmid, J. Phys. Chem. C, 2010, 114, 14402–14409.
6. A. J. Graham, D. R. Allan, A. Muszkiewicz, C. A. Morrison and S. A. Moggach, Angew. Chem., Int. Ed., 2011, 50, 11138–11141.
7. K. W. Chapman, G. J. Halder and P. J. Chupas, J. Am. Chem. Soc., 2009, 131, 17546–17547.
8. T. D. Bennett, J. C. Tan, S. A. Moggach, R. Galvelis, C. Mellot-Draznieks, B. A. Reisner, A. Thirumurugan, D. R. Allan and A. K. Cheetham, Chemistry, 2010, 16, 10684–10690.
9. A. J. Graham, A.-M. Banu, T. Düren, A. Greenaway, S. C. McKellar, J. P. S. Mowat, K. Ward, P. A. Wright and S. A. Moggach, J. Am. Chem. Soc., 2014, 136(24), 8606–8613.
10. K. J. Gagnon, C. M. Beavers and A. Clearfield, J. Am. Chem. Soc., 2013, 135, 1252–1255.
11. I. Beurroies, M. Boulhout, P. L. Llewellyn, B. Kuchta, G. Ferey, C. Serre and R. Denoyel, Angew. Chem., Int. Ed., 2010, 49, 7526–7529.
12. Q. Ma, Q. Yang, A. Ghoufi, G. Ferey, C. Zhong and G. Maurin, Dalton Trans., 2012, 41, 3915–3919.
13. I. Deroche, S. Rives, T. Trung, Q. Yang, A. Ghoufi, N. A. Ramsahye, P. Trens, F. Fajula, T. Devic, C. Serre, G. Ferey, H. Jobic and G. Maurin, J. Phys. Chem. C, 2011, 115, 13868–13876.
14. S. Rives, H. Jobic, F. Ragon, T. Devic, C. Serre, G. Férey, J. Ollivier and G. Maurin, Microporous Mesoporous Mater., 2012, 164, 259–265.
15. S. Rives, H. Jobic, D. I. Kolokolov, A. A. Gabrienko, A. G. Stepanov, Y. Ke, B. Frick, T. Devic, G. Ferey and G. Maurin, J. Phys. Chem. C, 2013, 117, 6293–6302.
16. F. Salles, H. Jobic, T. Devic, P. L. Llewellyn, C. Serre, G. Férey and G. Maurin, ACS Nano, 2009, 4, 143–152.
17. P. Serra-Crespo, A. Dikhtiarenko, E. Stavitski, J. Juan-Alcaniz, F. Kapteijn, F.-X. Coudert and J. Gascon, CrystEngComm, 2015, 17, 276–280.
18. P. Serra-Crespo, E. Stavitski, F. Kapteijn and J. Gascon, RSC Adv., 2012, 2, 5051–5053.
19. A. J. Graham, J. C. Tan, D. R. Allan and S. A. Moggach, Chem. Commun., 2012, 48, 1535–1537.
20. S. A. Moggach, T. D. Bennett and A. K. Cheetham, Angew. Chem., Int. Ed., 2009, 48, 7087–7089.
21. T. D. Bennett, P. Simoncic, S. A. Moggach, F. Gozzo, P. Macchi, D. A. Keen, J. C. Tan and A. K. Cheetham, Chem. Commun., 2011, 47, 7983–7985.
22. F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247.
23. F. Birch, Phys. Rev., 1947, 71, 809–824.
24. M. Mattesini, J. M. Soler and F. Ynduráin, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094111.
25. W. Zhou and T. Yildirim, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 109–0121.
26. A. Samanta, T. Furuta and J. Li, J. Chem. Phys., 2006, 125, 084714.
27. D. Bahr, J. Reid, W. Mook, C. Bauer, R. Stumpf, A. Skulan, N. Moody, B. Simmons, M. Shindel and M. Allendorf, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 184106.
28. J. A. Greathouse and M. D. Allendorf, J. Phys. Chem. C, 2008, 112, 5795–5802.
29. M. Tafipolsky and R. Schmid, J. Phys. Chem. B, 2009, 113, 1341–1352.
30. B. Lukose, B. Supronowicz, P. St. Petkov, J. Frenzel, A. B. Kuc, G. Seifert, G. N. Vayssilov and T. Heine, Phys. Status Solidi B, 2012, 249, 335–342.
31. S. S. Han and W. A. Goddard, J. Phys. Chem. C, 2007, 111, 15185–15191.
32. N. Klein, I. Senkovska, I. A. Baburin, R. Gruenker, U. Stoeck, M. Schlichtenmayer, B. Streppel, U. Mueller, S. Leoni, M. Hirscher and S. Kaskel, Chem.–Eur. J., 2011, 17, 13007–13016.
33. H. Wu, T. Yildirim and W. Zhou, J. Phys. Chem. Lett., 2013, 4, 925–930.
34. E. C. Spencer, R. J. Angel, N. L. Ross, B. E. Hanson and J. A. K. Howard, J. Am. Chem. Soc., 2009, 131, 4022–4026.
35. J.-C. Tan, B. Civalleri, C.-C. Lin, L. Valenzano, R. Galvelis, P.-F. Chen, T. D. Bennett, C. Mellot-Draznieks, C. M. Zicovich-Wilson and A. K. Cheetham, Phys. Rev. Lett., 2012, 108, 095502.
36. B. Lefevre, A. Saugey, J. L. Barrat, L. Bocquet, E. Charlaix, P. F. Gobin and G. Vigier, Colloids Surf., A, 2004, 241, 265–272.
37. V. Eroshenko, R.-C. Regis, M. Soulard and J. Patarin, J. Am. Chem. Soc., 2001, 123, 8129–8130.
38. L. Tzanis, M. Trzpit, M. Soulard and J. Patarin, J. Phys. Chem. C, 2012, 116, 20389–20395.
39. G. Ortiz, H. Nouali, C. Marichal, G. Chaplais and J. Patarin, J. Phys. Chem. C, 2014, 118, 7321–7328.
40. B. Lefevre, A. Saugey, J. L. Barrat, L. Bocquet, E. Charlaix, P. F. Gobin and G. Vigier, J. Chem. Phys., 2004, 120, 4927–4938.
41. N. Gokulakrishnan, J. Parmentier, M. Trzpit, L. Vonna, J. L. Paillaud and M. Soulard, J. Nanosci. Nanotechnol., 2013, 13, 2847–2852.
42. G. Ortiz, H. Nouali, C. Marichal, G. Chaplais and J. Patarin, Phys. Chem. Chem. Phys., 2013, 15, 4888–4891.
43. R. Denoyel, P. Llewellyn, I. Beurroies, J. Rouquerol, F. Rouquerol and L. Luciani, Part. Part. Syst. Charact., 2004, 21, 128–137.
44. T. Karbowiak, C. Paulin, A. Ballandras, G. Weber and J.-P. Bellat, J. Am. Chem. Soc., 2009, 131, 9898–9899.

---