Phase stability and charge compensation in disordered rock salt compounds based on nickel and titanium

Abstract

Disordered rock salt compounds (DRX) are increasingly investigated as an alternative to established layered oxides, due to the significant compositional flexibility allowing the use of cheap elements, as well as the demonstrated high specific discharge capacities. In this work we investigate DRXs based on Ni as the main redox active element and Ti as a charge compensator and structure stabilizer, according to composition Li_2yTi_yNi_2−3yO₂ (0.50 ≤ y ≤ 0.67). We prepare such materials by solid state synthesis and carefully investigate their stability as single phases by combining theoretical calculations based on density functional theory and in situ X-ray diffraction, elucidating the role of entropy in the synthesis process. By a combination of SEM, ICP-AES and X-ray and neutron diffraction we reveal that the above-mentioned formula indicating a solid solution is only appropriate at high temperatures. When increasing the Li content and lowering the temperature, a secondary Li₂TiO₃-like phase emerges. The electrochemical performances showed a low capacity in the first cycle, which appears to be kinetically limited as it strongly increases at 50 °C. A strong voltage hysteresis is nonetheless present regardless of the temperature and is the main bottleneck limiting energy efficiently in these compounds. By combined operando X-ray diffraction and X-ray absorption near edge structure (XANES) spectroscopy, we demonstrate such hysteresis can be observed both structurally in the unit cell parameters as well as electronically at the Ni K-edge, hence in the Ni oxidation state. Our study confirms the peculiar, coupled behaviour of Ni and O redox in this class of materials, which needs to be overcome if new improved compositions are to be designed. We therefore provide a clear structural analysis of the synthesis and electrochemical behaviour of the Li_2yTi_yNi_2−3yO₂ family of compounds, identifying the main bottlenecks towards their improvement.

---

Matteo Bianchini

Matteo Bianchini studied physics engineering at Politecnico di Milano and obtained his PhD in Solid State Chemistry in 2015 with Prof. Masquelier, Dr Croguennec and Dr Suard in a collaboration between LRCS, ICMCB and ILL. He was later a postdoctoral researcher in the group of Prof. Ceder at LBNL, where he worked on the design, synthesis, and characterization of new materials for next generation Na- and K-ion batteries. He then became a postdoctoral researcher at BELLA-KIT (Prof. Janek), where he investigated Ni-rich cathode materials for Li-ion batteries, prior to joining BASF as a lab team leader to co-supervise the BELLA lab. In 2021 Matteo obtained the chair of Inorganic Active Materials for Electrochemical Energy Storage at the University of Bayreuth, where he has built his group to continue investigating and developing electrode materials and solid electrolytes for the next generation of batteries.

---

Introduction

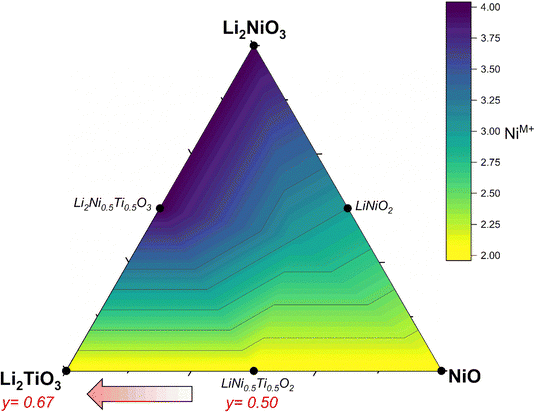
The successful commercialization of Li-ion batteries as electrochemical energy storage solutions with high energy density made a wide range of applications possible, including portable electronic devices, power tools and electric vehicles.¹ In the past decade, many efforts have been made to develop high energy density cathode active materials (CAMs), which are nevertheless still considered as one of the main bottlenecks for further improvements.² Commercial lithium transition metal oxides are compounds with formula Li(TM)O₂ (with TM being a mixture of Mn/Al, Co and Ni) that crystallize in a layered crystal structure.^3,4 Despite their success, layered CAMs have a practical gravimetric capacity in the range of 160–230 mA h g⁻¹, that is insufficient for some applications (for example for achieving extended driving ranges at affordable price in electric vehicles), along with safety issues that increase with increasing achievable reversible capacity and that have not been overcome yet.² To address these drawbacks, the extensive exploration of new materials brought attention to Li-rich cation disordered rock salt (DRX) materials,^5,6 due to the larger capacities achievable (even over 300 mA h g⁻¹)^2,7 often relying on the oxygen redox contribution beyond the one from the transition metals alone.^8–10 In terms of stoichiometry, DRX materials can also be written as Li_1+x(TM)_1−xO₂, yet now Li and TM occupy statistically the same crystallographic site. Concerning Li diffusion, the hopping mechanism is the same between layered and rock salt structures: lithium ions jump through a tetrahedral site between two octahedral sites (o–t–o diffusion pathway).¹¹ The Li⁺ in this tetrahedral site represents an activated state for lithium diffusion and the energy of this state will affect the lithium mobility in the crystal. The energy migration barrier is strongly dependent on the electrostatic repulsion between the Li⁺ and the element face-sharing the tetrahedron, and consequently increases when there are one or several TMs close to the activated Li⁺. In layered oxides, the tetrahedron is always face-sharing with one TM from the layer above/below, yet Li diffusion is still possible within the Li layers. On the other hand, when no face-sharing TM are present, Li migration proceeds through 0-TM channels leading to an enhanced hopping rate, especially if compared to the 1-TM or 2-TM channels with a high migration barrier, thus inactive for Li diffusion in the structure. Therefore, the Li excess (x > 0) in the composition is key to the formation of a percolating network of 0-TM channels (it was shown that it should be x > 0.1 to allow percolation).⁸ Moreover, in contrast to layered oxides, where a large amount of lithium removal affects the structure and consequently lithium transport due to strong electrostatic interactions between Li⁺,O²⁻ and TM⁺ along the c unit cell parameter,^12,13 in DRX compounds the more homogeneous cation distribution generates less structural changes and potentially less deterioration during cycling.¹⁴ Finally, one of the common degradation mechanisms of layered materials is their reduction at the surface, making them transform into a disordered rock salt phase; such a mechanism is hence expected to play a minor role in DRX materials.^4,15 Despite the above-mentioned benefits of DRX materials such as the oxygen activity along cycling, volume stability and high specific capacity, there are still drawbacks that need to be overcome. These are in particular the slow kinetics often reported (but not always),¹⁶ the low average voltage and large voltage hysteresis, as well as the voltage decay associated with the anionic reactions.¹⁷

In terms of design criteria, the DRX formula can further be expanded as Li_1+x(M′M′′)_1−xO₂, where M′ represents a redox active species and M′′ is a redox inactive element ideally with a d⁰ electronic configuration, which has been reported to be often essential to promote the disorder and stabilize the crystal structure.¹⁸ Most DRX compositions reported use Ni or Mn as redox-active species, while common d⁰ elements are Ti, Nb, Mo and few others. So far, Mn-based DRX proved superior in terms of observed capacities,¹⁹ yet Ni is also promising due to its 2 e⁻ redox capability, high potential expected for Ni^2+/4+ vs. Li⁺/Li, and the large know-how developed in the field of Ni-rich layered CAMs, especially concerning their synthesis at scale. In this work, we investigate DRX compounds with a target composition Li_2yTi_yNi_2−3yO₂ (0.50 ≤ y ≤ 0.67) where the Ni redox activity Ni²⁺ → Ni^3+/4+ is exploited and Ti⁴⁺ is used as charge compensator. Ti being lighter and cheaper than most other d⁰ elements,²⁰ it may be expected to partially offset the higher cost of Ni with respect to Mn. Fig. 1 illustrates a Gibbs triangle in the chemical space comprising NiO–Li₂NiO₃–Li₂TiO₃. Here, Ni in the reported compounds is the only element which formally changes oxidation state from 2+ (NiO) to 4+ (Li₂NiO₃). Along the NiO–Li₂NiO₃ tie line, we find the important cathode material LiNiO₂ (LNO), which is a prototypical Ni-rich layered oxide.⁴ Under sufficiently oxidizing conditions, one can over-lithiate LNO to reach Li₂NiO₃. While this compound should be redox-inactive based on the Ni valence state, it has been shown to possess significant capacity, mostly attributed to O redox activity, which however fades quickly.²¹ Therefore, in our aim to design a DRX CAM exploiting mostly Ni redox, we target the lower portion of the Gibbs triangle where Ni is divalent. From LiNiO₂, it is possible to substitute Ti for Ni according to LiNi_1−zTi_zO₂. This substitution (doping) has been already heavily investigated and will not be discussed further, as overall it decreases the available capacity significantly.^22,23 On the other hand, we target the region at the bottom of Fig. 1 between LiNi_0.5Ti_0.5O₂ and Li₂TiO₃. We start for y = 0.5 at LiNi_0.5Ti_0.5O₂, which is a stoichiometric compound (Li/TM = 1) and has been reported to possess a disordered rock salt structure.^24–27 Since this compound is not Li-rich, it possesses few 0-TM channels and therefore no percolation pathways for Li, hence it displays very low specific capacity.²⁷ On the other hand, in the direction followed by the materials we investigate (marked with a red arrow in Fig. 1) the compounds become Li-rich with increasing y, while Ni maintains his 2+ oxidation state throughout the series. The compounds have been labelled as LNTO50, LNTO55, LNTO60 as function of the y value (where the number represents the amount of Ti and half the amount of Li), whereas LTO67 corresponds to Li_1.33Ti_0.67O₂ (or Li₂TiO₃). The same compositional region was studied very recently by Li et al.,²⁸ whom however indicated it as a two phase region with xLi₂TiO₃·(1 − x)LiTi_0.5Ni_0.5O₂ composition. Their findings highlight the activation of the anionic redox mechanism through a ligand-to-metal charge transfer process. However, it is at present unclear whether these materials are indeed a biphasic mixture, or rather single phase. Hence, we undertook our study to verify the single vs. 2-phase behavior of such samples, and to further highlight the structural, electrochemical and charge transfer behavior of these materials.

Fig. 1 Gibbs triangle (pseudo phase diagram) in the system Li₂TiO₃–Li₂NiO₃–NiO. The red arrow depicts the compositions of the materials Li_2yTi_yNi_2−3yO₂ under investigation. The color scale indicates the expected nominal Ni oxidation state.

Experimental section

Materials synthesis

All the materials were synthesized by solid-state reaction preceded by a mixing of the precursors in a Spex ball mill for 1.50 h using zirconia jars. The used precursors are nickel(II) hydroxide (61% Ni, Alfa Aesar), titanium(IV) oxide (nanopowder, Sigma-Aldrich ≥ 99.5%) and lithium carbonate (1% excess, Thermo Scientific 99.998%). The mixture was pelletized and calcined in air at three different annealing temperatures (700 °C, 800 °C and 900 °C) for 10 h in an alumina crucible with a heating rate of 7 °C min⁻¹ and cooling rate of 5 °C min⁻¹.

Computational details

The optimization of the structural models for Li_2yTi_yNi_2−3yO₂ (y = 0.5; 0.6; 0.67) were performed by using the Vienna Ab initio Simulation Package (VASP)^29–31 within the projector augmented-wave approach³² employing the Perdew–Burke–Ernzerhof (PBE)³³ with the r²SCAN functional.³⁴ Correlation effects of the 3d-Ni orbitals (corresponding parameter U_Ni = 2.1 eV)³⁵ as well as long-range dispersion with Grimme's D4 correction³⁶ were taken into account. For the calculations of the total energy a plane-wave energy cut-off of 600 eV and 4 × 4 × 4 gamma centered k-point grid were used.

The initial structural models are based on cubic Li_0.98Ni_1.02O₂ (S.G. Fm3̄m, a = 4.1708(5) Ų¹) and layered Li_0.98Ni_1.02O₂ (R3̄m, a = 2.87758(3) Å, c = 14.1980(1) Å⁵). For each composition (y = 0.5; 0.6; 0.67) the occupancies of the metal cations Li, Ni and Ti were adjusted accordingly. In the cubic system (y = 0.5: Li₄Ni₂Ti₂O₈; y = 0.6: Li₄NiTi₃O₈) the 2 × 2 × 2 supercell was chosen as starting point (P1, a = b = c = 5.857 Å, α = β = γ = 60°). With y = 0.67 (Li₈Ti₄O₁₂), a 2 × 2 × 3 supercell was employed (P1, a = b = 5.862 Å, c = 8.794 Å, α = β = γ = 60°). For all the possible configurations generated by Supercell the total energy was calculated using VASP. The final structure with the most stable configuration was then used for comparison with the hexagonal one. For the layered structure type (y = 0.5: Li₄Ni₂Ti₂O₈; y = 0.6: Li₄NiTi₃O₈) the starting point was a 2 × 2 × 1 supercell (P1, a = b = 10.042 Å, c = 5.021 Å, α = β = γ = 33.29°), whereas for y = 0.67: Li₂TiO₃ a 2 × 2 × 2 supercell was chosen (P1, a = b = 10.042 Å, c = 5.021 Å, α = β = γ = 33.29). Again, the total energy of all possible configurations given by supercell was calculated and the most stable one was selected for comparison with the cubic phase. For Li₂TiO₃ (y = 0.67), which is layered but with a honeycomb ordering resulting in a monoclinic unit cell, only one cell was calculated, since there is no partial occupancy of Li or Ti (optimized cell: P1, a = 5.071 Å, b = 8.796 Å, c = 9.706 Å, α = γ = 90°, β = 100.16°³⁷).

Material characterization methods

Powder X-ray diffraction (XRD) patterns were collected using a Stoe StadiP diffractometer with a Mythen2K detector in Debye–Scherrer geometry in 2θ angular range of 5–50° equipped with a monochromatic Mo-Kα₁ radiation (wavelength λ = 0.70932 Å). The acquisition was performed on powder packed in a 0.5 mm diameter borosilicate glass capillary. Neutron powder diffraction (NPD) was carried out on the D2B neutron diffractometer at the Institut Laue-Langevin (ILL). Powder samples were put into cylindrical vanadium cans and measured in transmission geometry at λ = 1.59485(3) Å (https://doi.org/10.5291/ILL-DATA.5-23-77), where the λ value was opportunely refined using FullProf software.³⁸ For both XRD and NPD, structural refinements of the rock salt crystalline models were performed against the collected data and the error bars reported as 3σ accordingly to the value obtained from the FullProf software. In situ temperature resolved XRD was performed by using the Stoe ST2K furnace mounted on the Stoe StadiP diffractometer. Patterns were recorded in the 2θ range of 5–35° at a temperature between 30 °C and 900 °C. The temperature is hold at each temperature every 10° for 10 minutes, during which the acquisition is carried out. A sapphire capillary with two open ends was filled with the powder and the XRD data were collected in air as function of temperature. Quartz wool was placed on each side of the powder sample to prevent his movement during the experiment. The furnace undergoes a rocking movement during acquisition to improve powder averaging.

The morphological features of the samples sputtered with platinum were observed using a LEO-1530 electron microscope in secondary electron detector mode and a magnification of 75 000×. Particle size distribution was estimated using the ImageJ software.

ICP-AES

The metal elements were determined by ICP-AES (Inductively Coupled Plasma – Atomic Emission Spectroscopy with a spectrometer iCap 6500 from Thermo Instruments). About 2–3 mg of the samples was dissolved in 1 mL of hydrochloric acid, hydrofluoric acid and nitric acid at 180 °C for 12 hours. All samples were dissolved three times. The digestions were diluted, and analysis of the elements was accomplished with different calibration solutions and an internal standard. 4 wavelengths of each element were used for calculation/analysis.

Electrochemical measurements

Cathodes were prepared by slurry casting on Al foil. The slurry was obtained by dispersing 80 wt% active material, 10 wt% Super C65 carbon black (Timcal) and 10 wt% Solef polyvinylidene fluoride (PVDF) binder in N-methyl-2-pyrrolidone. The slurry was dried overnight and the as-obtained tapes were cut into round electrodes using a steel punch. For the electrochemical testing, coin half-cells consisting of cathode, porous glass fiber (Whatman, GF/D grade), Li metal anode (Albemarle Germany GmbH) and 90 μL LP30 electrolyte (1 M LiPF₆ in 1 : 1 EC/DMC) were assembled inside an Ar-filled glovebox. The loading of the electrodes was ≈3 mg cm⁻². The electrochemical behavior of every compound was tested in the voltage range between 1.5 and 4.8 V versus Li⁺/Li at C/10 (1C corresponding to a current density of 200 mA g⁻¹). The tests were performed at room temperature (25 °C controlled in a binder chamber) and at 50 °C under the same experimental conditions. Operando XRD and X-ray absorption near-edge structure (XANES) spectra at the Ni K-edge were collected semi-simultaneously on the same coin cell in transmission mode at the beamline NOTOS of the ALBA Synchrotron in Barcelona. The half-cell was charged and discharged for 1 cycle at C/15 (1C corresponding to a current density of 149 mA g⁻¹) while XRD patterns and XANES patterns were alternately acquired (0.5 s for XRD in the 7 to 50° angular range, 11 min for XANES in the energy range from 8200 eV to 8700 eV).

Results

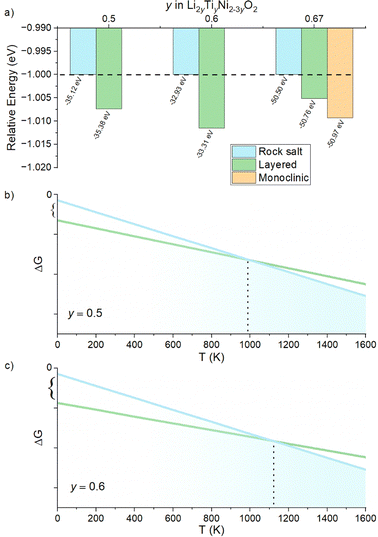
We begin our study with a computational investigation to evaluate the likelihood of obtaining rock salt structures; in other word to quantify at a given composition the phase stability of a rock salt structure versus a layered one, which is also likely for the materials in this phase diagram. Two different structural models (NaCl-type and layered-type) for Li_2yTi_yNi_2−3yO₂ were investigated by DFT on supercells generated by the software Supercell.³⁹ All details on the supercells used can be found in the Experimental section. For Li₂TiO₃ (y = 0.67), which is layered but with a honeycomb ordering resulting in a monoclinic unit cell, the energy of the ordered monoclinic cell was also calculated. The results of our calculations are summarized in Fig. 2a.

Fig. 2 (a) Relative energies of the Li_2yTi_yNi_2−3yO₂ system given per formula unit, as computed with VASP. The layered phase shows the lowest energy and thus highest stability compared to the NaCl type. (b and c) Schematic representation of the Gibbs free energy vs. temperature plotted for different Li contents (y = 0.5 in (b), y = 0.6 in (c)). In both cases a transition T might be reached where the RS overcome to the LS in stability.

The computed relative energies of each phase were calculated at 0 K to understand whether the layered structure (LS) or rock salt structure (RS) was more stable as a function of the different Li content in the ground state. The results displayed in Fig. 2a show that the LS exhibits lower energy values than the RS, which for this reason would be energetically less stable. Therefore, one may expect the synthesis of our target compounds as a single RS phase to be challenging, and that phase separation may be preferable. On the other hand, the difference in energy between rock salt and ground state layered phase is small (0.26 eV, 0.38 eV and 0.47 eV for y = 0.5, 0.6 and 0.67, respectively), growing slightly with increasing y. One should then notice that in the reported calculations there is no entropic component. In fact, a different case could be expected when the configurational entropy contribution for the two different phases is included. In particular, the configurational entropy corresponds to all the distinct ways in which the lattice sites can be occupied at a specific composition.⁴⁰ In the disordered RS phase, the cations are randomly distributed in the same site, while in the layered phase, they are ordered. Therefore, there is no configurational entropy for a “perfect” layered structure, while one may expect a large configurational entropy for a rock salt phase. In light of these considerations, since the energetic difference at 0 K between the phases is small, we expect that by sufficiently increasing the temperature, the Gibbs free energy of the rock salt phase will drop to more negative values as compared to the layered one (Fig. 2b). When y > 0.5, as shown in Fig. 2c, this transition temperature might rise due to the higher initial enthalpic difference to overcome, but it would occur nonetheless. Working under the above-mentioned assumptions, we predict to observe a pure rock salt phase above a certain synthesis temperature, and that the exact value would increase with increasing y.

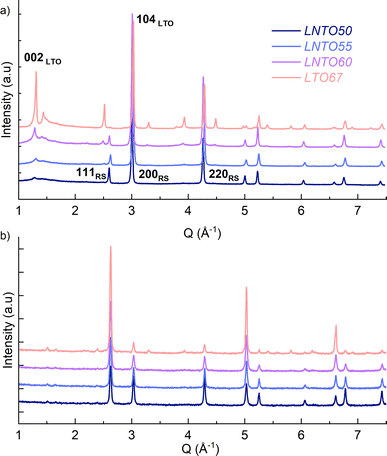
The samples were then synthesized by solid state synthesis at 700, 800 and 900 °C as described in the Experimental section, and further investigated by X-ray and neutron diffraction, as gathered in Fig. 3.

Fig. 3 X-ray diffraction (a) and neutron diffraction (b) patterns of the samples annealed at 700 °C. The 2θ angle is converted to the scattering vector Q to compare the two experiments despite the different wavelength (XRD: λ = 0.70932 Å, NPD: λ = 1.59485(3) Å).

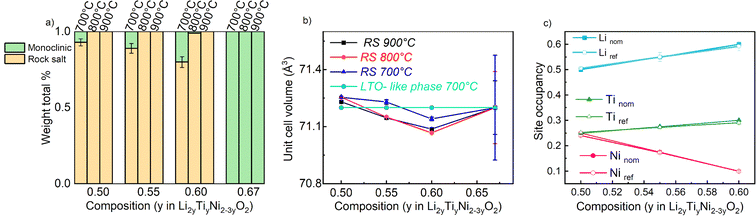
The samples synthetized at 900 °C and 800 °C (Fig. S1 and S2†) exhibit characteristic diffraction peaks of a rock salt-type structure with Fm3̄m space group. The end member Li₂TiO₃ crystallizes into a monoclinic structure with C2/c space group⁴¹ regardless of the temperature used. For this end-member, one may notice the low 002/104 peak intensity ratio: this can be used to indicate a high degree of Li/Ti mixing.⁴² However, because of the significant impact of other structural defects such as stacking faults, the exact Li/Ti distribution is not investigated further. By decreasing the temperature to 700 °C (Fig. 3), the samples y = 0.5, 0.55 and 0.6 still appear as rock salt, yet a secondary phase starts to emerge associated to a Li₂TiO₃-like phase, observed for all the synthetized samples at this temperature but with a clearly increasing trend for increasing Li content. Namely, the second phase grows upon Li and Ti addition as evidenced from the evolution of the 002_LTO peak in the XRD pattern in Fig. 3. All diffraction data were analysed by Rietveld refinement assuming a single rock salt phase at 800 °C and 900 °C, while using two-phase fitting for the samples annealed at 700 °C. As shown in Fig. 4a, with this method we are able to estimate the phase fractions and unit cell parameters of the different phases observed. Here, the results clearly show how by decreasing the temperature and increasing the y content, the monoclinic phase amount consequently grows, conforming to our DFT-based predictions. As can be seen in Fig. 3, the superstructure peaks related to the C2/c phase are barely present in the NPD data, even for pure Li₂TiO₃, while they are clear in the XRD data around 1.3 Å⁻¹. This may seem surprising, but it stems from the structure factors for NPD being all essentially zero below Q = 2.5 Å⁻¹. For this reason, and due to the higher precision on the wavelength obtainable with X-rays, the phase fractions reported in Fig. 4a and the unit cell volumes reported in Fig. 4b are obtained from refinement of the XRD data alone.

Fig. 4 Evolution of the phase content from Rietveld refinement in the Li_2yTi_yNi_2−3yO₂ system. A pure rock salt phase is detected for the samples annealed at 900 °C and 800 °C, while a Li₂TiO₃-like phase appears and grows with increasing y at 700 °C. (b) Unit cell volume of the cubic phases. The value obtained for the Li₂TiO₃-like phase is divided by 6 to account for the larger Z in this structure. (c) Evolution of the site occupancy factors for the samples at 700 °C. Value in (a) and (b) are from refinement of XRD data, while those in (c) from combined refinement of XRD and NPD data.

In Fig. 4b we gather the unit cell volumes obtained via Rietveld refinement. The behaviour of the samples annealed at 900 °C and 800 °C revealed a decreasing trend as function of increasing y that can be ascribed to a single solid solution behavior. However, as expected from the average ionic radius of the cations (barely changing from 0.704 to 0.708 across the materials' series), only a very slight trend is observed. Instead, for the samples synthesized at 700 °C, fitted with a 2-phase model (refining only the structural parameters of the rock salt phase and maintaining constant those found from the refinement of the as-prepared Li₂TiO₃ phase), a fully linear trend was not detected.

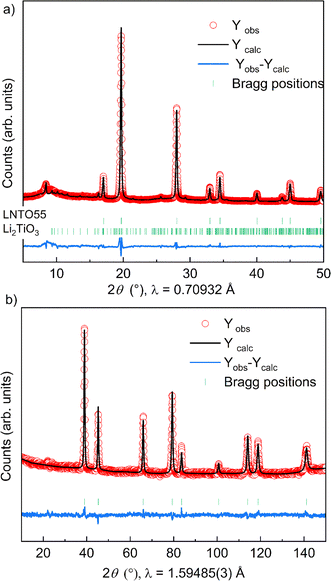
The fact that we observe an increasing amount of Li₂TiO₃-like phase with increasing y raises the question: what is the composition of the actual rock salt phase we observe? To answer this question, we firstly verified the nominal composition of the synthetised materials using ICP-AES measurements performed for all the samples synthetized at 700 °C. The different cationic ratio (Li/Ti, Li/Ni, Ni/Ti) are reported in Table S1.† The resulting data reveal that, while the Li/Ti ratio was in good agreement with the theoretical value, the Li/Ni and Ni/Ti ratio slightly differed from the expected ones, pointing towards a slight Ni-deficiency in the samples. We then used our X-ray and neutron diffraction data to carry out a combined refinement against a unique (rock salt) structural model. Since three atoms occupy the 4a Wyckoff site, we chose the following constraints for the refinement: (i) the cations fully occupy the site (Li + Ni + Ti = 1) and (ii) given that the Li/Ti ratio was found as expected by ICP, the Li content fixed to two times the Ti content (Li–2Ti = 0). Having three unknown atoms contents on a site and two constraints, we proceed to the refinement. It should be mentioned that in this case, the added sensitivity of neutrons to light elements (Li, O) and to Debye–Waller factors makes a combined refinement a better choice to determine the cations distribution in the rock salt-type phase. The site occupancies are reported in Fig. 4c, as obtained by combined Rietveld refinement for the samples at 700 °C. Tables 1 and 2 gather the structural results from the combined refinement. The combined refinement of XRD and NPD for an exemplary sample, LNTO55 made at 700 °C, is also displayed in Fig. 5. The structural parameters of the compounds annealed at 900 °C and 800 °C are instead shown in Table S2.†

Table 1 Exemplary structural parameters obtained from Rietveld refinement of combined XRD and NPD of the sample Li_1.1Ni_0.35Ti_0.55O₂ (LNTO55) synthesized at 700 °C

Li1.1Ni0.35Ti0.55O2
S.G.: Fm3̄m, Z = 4		χ^2: 1.42
a, b, c = 4.14382(24) Å	XRD		NPD
Vol = 71.154(6) Å^3	RBragg: 2.16%		RBragg: 6.80%
	Rwp: 4.81%		Rwp: 16.3%

---

Atoms	Wyckoff site	Atomic positions			Biso	Occupancy
		x	y	z
O	4b	0.5	0.5	0.5	1.15(12)	1.00000
Ti	4a	0.0	0.0	0.0	0.83(9)	0.269(6)
Ni	4a	0.0	0.0	0.0	0.83(9)	0.169(3)
Li	4a	0.0	0.0	0.0	0.83(9)	0.547(18)
Constraints: Li + Ni + Ti = 1; Li-2Ti = 0

---

Table 2 Structural parameters from combined XRD and NPD for the samples LNTO50, LNTO55 and LNTO60 synthesized at 700 °C

Sample	Method	Unit cell parameters (Å)	Unit cell volume (Å^3)	Biso (Å^2)	Site occupancy
LNTO50 700 °C	XRD	4.1457(2)	71.254(6)	—	—
	NPD	4.1458(1)	71.256(3)	—	—
	Combined	4.1451(2)	71.220(6)	Li, Ni, Ti: 1.06(6); O: 1.20(6)	Li: 0.505(3)
					Ni: 0.240(3)
					Ti: 0.252(3)
LNTO55 700 °C	XRD	4.1451(4)	71.22(1)	—	—
	NPD	4.1442(2)	71.172(62)	—	—
	Combined	4.1438(2)	71.154(6)	Li, Ni, Ti: 0.83(9); O: 1.2(1)	Li: 0.55(2)
					Ni: 0.169(3)
					Ti: 0.269(6)
LNTO60 700 °C	XRD	4.1430(3)	71.115(9)	—	—
	NPD	4.1432(2)	71.123(6)	—	—
	Combined	4.1423(3)	71.074(9)	Li, Ni, Ti: 1.05(9); O: 1.4(1)	Li: 0.60(2)
					Ni: 0.097(3)
					Ti: 0.293(9)

---

Fig. 5 Combined Rietveld refinement of XRD (a) and NPD (b) patterns for the exemplary sample LNTO55 synthesized at 700 °C. Due to the very weak peak intensities, the secondary Li₂TiO₃-like phase is only included in the XRD refinement.

From this analysis, as can be clearly seen in Fig. 4c, we can state that the refined values in general do not exhibit a discrepancy from the nominal ones, i.e. the synthesized rock salt-type phases, despite a Li₂TiO₃-like impurity, have composition very close to the desired one. Nonetheless, it is worth mentioning that we cannot determine the composition of the Li₂TiO₃-like side phase, hence STEM/EDX might be the ideal method to further verify in the future the elemental composition of both phases.

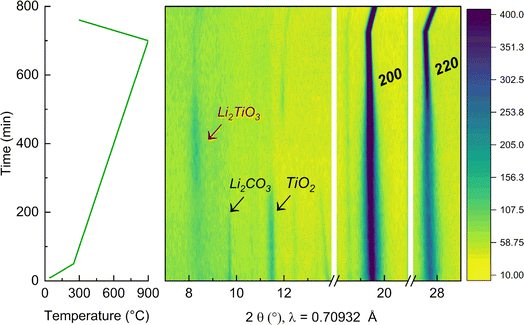
To further elucidate the reason for the presence of a secondary Li₂TiO₃-like phase at low temperature, in situ XRD during synthesis of the y = 0.50 sample was performed, as reported in Fig. 6. The experiment was carried out in the temperature range between 25 °C and 900 °C (where the cubic phase can be synthesized phase-pure). First, the mixture of the precursors was pre-annealed at 350 °C to dehydrate Ni(OH)₂ into NiO⁴³ and avoid the occurrence of an exothermic reaction from the release of water. NiO presents a cubic structure with space group Fm3̄m⁴⁴ and the presence of the Bragg peaks associated to this phase are already visible at the beginning of the experiment. At this initial stage, the additional detected reflections were indexed to the precursors Li₂CO₃ and TiO₂. Upon annealing, these reflections start vanishing at 350 °C and 400 °C, respectively. More interestingly, when the temperature is raised to 600 °C, a clear new peak is detectable at low angles (around 2θ = 8.30°), which can be indexed to an intermediate Li₂TiO₃ phase that quickly forms during synthesis. This is in agreement with our DFT calculations, showing that at low T a layered-type phase would be preferred. Furthermore, it clearly shows the importance of intermediate compounds during solid state synthesis, which template and ultimately affect which final phases can be accessed and at which temperature.⁴⁵ Again in agreement with our expectations, as the temperature increases beyond 700 °C and entropic effects start to dominate, the Li₂TiO₃-like phase disappears and a pure rock salt phase forms. Finally, the peaks 200 and 220 of the cubic crystal structure become much more pronounced as the compound further crystallizes, exhibiting a stronger intensity that persist to the final temperature at 900 °C and further during the cooling step. By decreasing the temperature, the reflections of the rock salt phase remain strong and shift to higher angles indicating a contraction of the lattice parameters.

Fig. 6 In situ XRD during the synthesis of the sample LNTO50 starting from NiO, Li₂CO₃ and TiO₂ as precursors. On the left the temperature evolution over time is shown. The central panels contain contour plots showing the Bragg peaks evolution during the synthesis from 25 °C to 900 °C. The color scale bar appears on the right.

Finally, to complete our structural investigation, scanning electron microscopy (SEM) data of the samples annealed at 700 °C were collected to analyse their morphology. The acquired images show that the primary particle sizes of the as prepared compounds are highly agglomerated into secondary particles. Roughly, the sample with y = 0.50 have average primary particles of less than 80 nm, that increases with Li and Ti content as shown in Fig. S3.† However, such primary particles are agglomerated to clusters of several hundreds of nm.

Electrochemical behavior and charge compensation

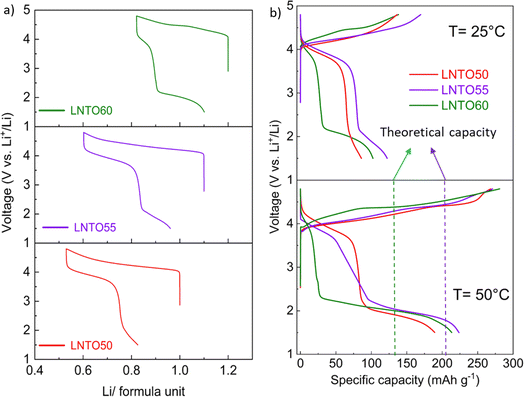
Galvanostatic charge/discharge tests were carried out for the pristine materials annealed at 700 °C to determine their electrochemical behaviour. Fig. 7 gathers the first cycle voltage profiles of LNTO50, LNTO55 and LNTO60 within the voltage range 1.5–4.8 V at C/10 and room temperature. LTO was not tested due to the expected limited capacity due to the low electrical conductivity.⁴⁶ In Fig. 7a, the voltage profile versus Li/formula unit is provided. All the curves revealed large hysteresis and rather low specific discharge capacity. For LNTO50 (LiNi_0.50Ti_0.50O₂) the capacity was expected to be limited²⁵ based on previous reports.²⁷ However, one could expect an improvement with increasing y, assuming a contribution from O redox is also possible. In the LNTO55 sample, approximately 0.6 Li are extracted per formula unit (122.1 mA h g⁻¹), higher if compared to LNTO50 and LNTO60 materials (86 mA h g⁻¹ and 102.2 mA h g⁻¹ respectively). This proves the Li excess is beneficial to Li percolation, yet the obtained capacities are lower than the theoretical capacity expected by Ni redox contribution, hence it is unclear if O is also contributing to the charge compensation. The overall performance of the Li-rich electrodes shows limited performance as compared to the results shown by Li et al.,²⁸ most likely because of the different synthesis process (in their case a sol–gel process yields smaller and less agglomerated crystallites). Nonetheless, the shape of our curves (with their large voltage hysteresis) is closely related to the ones that Li et al. reported, suggesting the O redox contribution is present. To overcome possible kinetic limitations, we further examined the electrochemical behavior of the electrodes at 50 °C, leaving the other parameters unchanged. The reversible capacity tested in this condition is greatly improved as shown in Fig. 7b. Again, the sample LNTO55 delivers the highest discharge capacity with about 223.7 mA h g⁻¹, followed by LNTO60 (213.4 mA h g⁻¹) and finally LNTO50 (189.3 mA h g⁻¹) although the voltage hysteresis still appears very large. From these results we can conclude that (i) clear kinetic limitations are present in the studied materials, and (ii) a capacity larger than the theoretical one based on Ni redox can be observed for both LNTO55 and LNTO60 compounds (g_theo = 216.9 mA h g⁻¹ and 132.7 mA h g⁻¹, respectively), implying a clear contribution of oxygen to the charge compensation process.

Fig. 7 Galvanostatic cycling of LNTO50, LNTO55 and LNTO60 samples synthesized at 700 °C tested in Li half cells. (a) Voltage profiles versus lithium amount in the voltage range 1.5–4.8 V at 25 °C and C/10 current rate. (b) Comparison of voltage profiles vs. specific capacity measured at 25 °C and 50 °C (same rate and voltage window as in (a)). The theoretical capacity based on the redox activity of Ni alone is indicated with dashed lines for LNTO55 (violet) and LNTO60 (green).

To better understand the charge compensation mechanism at the structural and electronic level, a semi-simultaneous operando XRD and XANES study was conducted during the first electrochemical cycle. Fig. 8a displays the XRD data, giving us insight on the material's structural evolution, while Fig. 8b exhibits the XANES spectra at the Ni K edge, informing us on the Ni redox behavior. We chose to study the LNTO55 sample, which showed the best electrochemical performances. The operando XRD results (Fig. 8a) didn't show noticeable phase changes in the crystal structure during both charge and discharge, indicating that a single rock salt phase is well preserved along the first cycle as shown by the evolution of the 200 and 220 reflections. To further investigate the structural parameters, we performed a Le Bail fit of the acquired patterns, whose results are displayed in Fig. 8c and d. When charging to 4.36 V, the unit cell parameters revealed a shift towards higher angular values, consistent with a unit cell shrinkage due to oxidation of Ni (Ni³⁺ being smaller than Ni²⁺). Notably, from around 4.36 V to 4.8 V, the unit cell parameter variation becomes less pronounced, suggesting the structural evolution is also less pronounced at higher voltage.⁴⁷ During discharge to 2.0 V the cell parameters shift back to lower angles, consistent with a unit cell expansion, attributed to the elongated Ni–O bond distance, then followed by a steep variation at the end of discharge at 1.5 V. It is interesting to notice here the change in structural parameters, i.e. after one cycle the unit cell parameter is larger than in the pristine state, pointing to a somewhat irreversible behavior. The lattice evolution as a function of the composition is shown in Fig. 8d, where a strong structural hysteresis is observed and a bimodal linear trend is observed in different voltage regions, presumably coinciding with the regions where nickel and oxygen are redox active. To corroborate the structural observation, with XANES at the Ni K-edge we observed directly the Ni oxidation state. These data are displayed in Fig. 8e and reveal a similar bimodal linear behavior as in the XRD data, namely there is a linear trend with two different slopes in different regions of the charge/discharge (linear fits are provided in Fig. S4 and S5†). The evaluation of Ni oxidation state was performed by determining the position of the white line for each spectrum. In Fig. 8e, the standard spectra of LiNiO₂ and NiO are also added for a qualitative comparison. During charge, a noticeable edge shift to higher energy was observed from the pristine state of 3.0 V to a charged state at 4.8 V, indicating Ni oxidation from 2+ to 3+ and even beyond.⁴⁸ On the other hand, during discharge the edge undergoes a shift back towards lower energy values when Ni is reduced to 2+ valence state, demonstrating a good reversibility of the Ni redox process. Fig. 8d summarizes the observed change in cell parameters in charge and discharge states showing a similarity with the Ni K-edge evolution (Fig. 8g). As already mentioned in the introduction, the findings of Li et al.²⁸ helped us to rationalize the peculiar behavior detected pointing out an explanation by the unusual Ni and O redox mechanism observed. A kinetically activated Ni^3+/4+ intermediate state is formed in charge and it triggers the activation of the oxygen oxidation, observed at the top of charge, reflected by the barely noticeable variation in cell parameters and K-edge energy. In discharge, contrary to expectations, the Ni^3+/4+ is reduced before the oxygen (as evidenced by the severe edge shift) due to his high instability which leads to an inversion of cationic and anionic redox during discharge.

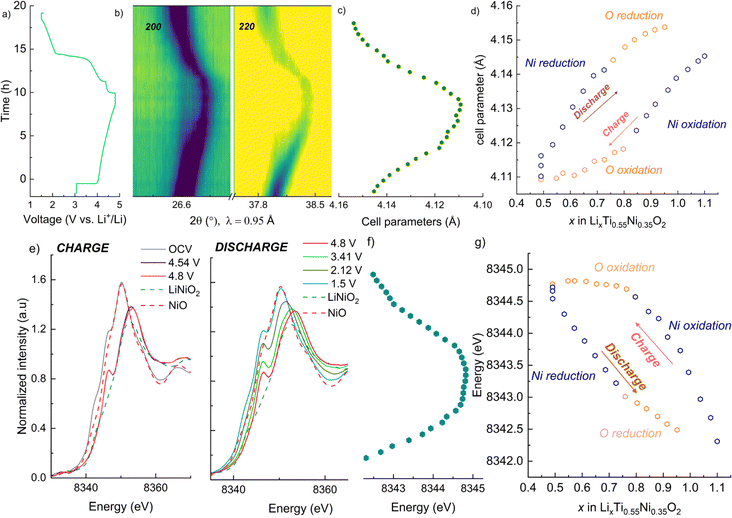Fig. 8 Semi-simultaneous operando synchrotron XRD and XANES of the sample LNTO55 during the initial cycle, with charge to 4.8 V and discharge to 1.5 V. (a) Voltage vs. time during the operando XRD/XANES experiment. (b) Contour plot showing the evolution of the 200 and 220 rock salt reflections, (c) consequent cell parameters evolution in charge and discharge, obtained from Le Bail fit. (d) Unit cell parameters vs. Li content. (e) Ni K-edge spectra collected during the initial cycle during charge (left) and discharge (right). (f) Observed change in the K-edge energy, obtained tracking the white line position. (g) Evolution of the K-edge energy vs. Li content. In (d) and (g), the choices of the points belonging to the O and Ni regions is given by the highest R² observed in the linear fit (Fig. S4 and S5†).

Discussion

In our investigation we have shown for the first time how in these series of materials the composition, the temperature and consequently the configurational entropy played a strong role in reaching a pure disordered rock salt structure, to the disadvantage of the layered Li₂TiO₃-like phase encountered at lower synthesis temperature. Therefore whether one writes these compounds as a solid solution or as a biphasic mixture also strongly depends on the synthesis route. Unfortunately, high temperature does not only lead to single phase rock salt materials, but also to crystallites growth. Here we show that already at 700 °C the samples display kinetic limitations, therefore it is unlikely that using high synthesis temperature could be of any use to improve electrochemical performances.

Our study also further demonstrated that the variation of the compositions from a stoichiometric lithium amount to a lithium rich one is necessary to create Li percolation pathways and enhance the electrochemical performances. Nonetheless, even when the synthesis temperature is kept low to avoid crystallites growth, Li-rich samples are made and the cycling temperature is raised to 50 °C, one can obtain high specific capacity but cannot avoid the huge voltage hysteresis. This is terribly detrimental to the energy density of the cathode material as the average voltage is more than 1 V lower in discharge than in charge, determining an extremely poor energetic efficiency. Our simultaneous operando XRD and XANES results clearly confirmed the results of Li et al., showing that this behavior is intrinsic to the coupled Ni–O charge compensation in these materials and likely hard to avoid. Nonetheless, strategies to change the kinetics of Ni–O charge transfer, by doping or other means, should be the primary objective to reduce the voltage hysteresis in this class of compounds.

More in general, Ni redox in DRX revealed high polarization that may be ascribed to the unfavourable Li diffusion kinetics, but also to significant voltage and structural hysteresis.^8,49 The detected voltage hysteresis is associated with anionic redox, which in this case mostly takes place asymmetrically between charge and discharge.¹⁷ Interestingly, Ji et al. observed similar features during cycling when Nb⁵⁺ is used as d⁰ element. In fact, the first-charge voltage showed a clear plateau at ∼4.3 V attributed to the anionic redox contribution where accordingly to their XANES results, Ni oxidation barely is responsible to the observed capacity, suggesting sluggish oxygen oxidation as a charge compensation mechanism.⁵⁰ It's worth mentioning that although Li enrichment in the structure and the formation of the Li–O–Li configuration are considered to be the necessary condition to activate anionic redox, Fukuma et al.⁵¹ pointed out that the structural disorder and the formation of a linear Ni–O–Ni configuration can also contribute to the anionic redox.

On the other hand, other studies revealed that when Ru⁵⁺ is exploited as charge compensation element, significantly lower hysteresis is observed, and the anionic redox chemistry of O²⁻/O⁻ redox is identified at high potential after Ni oxidation, leading to a resulting capacity which rely in both cathodic and anionic redox processes separately but reversibly.⁵² Therefore the choice of charge-compensating element, and its electronic structure (Ru⁵⁺ being not a d⁰ element), as well as the possibly induced short range-order in the materials, are all key elements to be considered for the future design of DRXs that are based on Ni redox but are not plagued by significant voltage hysteresis.

Conclusions

In conclusion, we investigated a family of Li–Ni–Ti–O rock salt compounds with Li_2yTi_yNi_2−3yO₂ as target composition. We evidenced a two-phase system (disordered rock salt and a small amount of Li₂TiO₃-like phase) rather than a solid solution unless the temperature is higher than 700 °C. Increasing the Li and Ti content increases the amount of Li₂TiO₃-like secondary phase. Our findings helped rationalize how the effect of the temperature and composition can play a key role in achieving a pure cubic crystal structure, thanks to DFT computations combined with monitoring the structural evolution during synthesis by in situ XRD. The results showed the reflection of the Li₂TiO₃-like phase forming first, as expected from a more energetically favoured phase, and its gradual disappearance by further increasing the temperature promoting the formation of the rock salt structure due to its larger configurational entropy. The compounds, whom we have verified to have the expected stoichiometry, have been tested electrochemically and exhibit large voltage hysteresis and low specific capacity at room temperature, which can however be enhanced by increasing the temperature, pointing to clear kinetic limitations of the reaction in this material. The simultaneous operando XRD and XANES study conducted on the Li_1.1Ni_0.35Ti_0.55O₂ sample highlights how the rock salt phase is maintained stable along the first cycle. We also tracked the behaviour of the cell parameters and Ni K-edge position, which confirmed that the O redox mechanism plays a role in the charge compensation and evidenced the clear presence of a structural hysteresis as well, on top of the poor Li diffusion kinetics. At the moment, such hysteresis given by the peculiarity of the electronic distribution in the oxidized Ni–O bond, and the ensuing voltage one, are the main bottleneck to the exploitation of these materials. To change this behavior, a vast chemical space of high-energy cathodes can be opened up by cation-doping, exploiting a mix of redox TM and by substituting Ti⁴⁺ with other high-valent non-redox-active ions (which could be d¹⁰ or d⁰, or even d³).⁵³ On the other hand, fluorine substitution can be also performed by partially replacing O²⁻ ions with F⁻ ions allowing to decrease the total anionic charge and expand the compositional space, as already extensively demonstrated.¹⁶ This strategy can also improve the electrochemical performance by maximizing the TM redox amount.⁵⁴

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The use of the D2B diffractometer at ILL under beamtime 5-23-775 is gratefully acknowledged. The synchrotron X-ray diffraction and XANES experiments were made possible through the support of beam station BL16-NOTOS at the ALBA Synchrotron (proposal no. 2022097072). Computational resources funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – INST [91/242-1] FUGG are acknowledged. Use of the KeyLab Electron and Optical Microscopy at the Bayerisches Polymerinstitut is gratefully acknowledged.

References

1. M. S. Whittingham, Ultimate Limits to Intercalation Reactions for Lithium Batteries, Chem. Rev., 2014, 114(23), 11414–11443,  DOI:10.1021/cr5003003.
2. D. Chen, J. Ahn and G. Chen, An Overview of Cation-Disordered Lithium-Excess Rocksalt Cathodes, ACS Energy Lett., 2021, 1358–1376,  DOI:10.1021/acsenergylett.1c00203.
3. B. L. Ellis, K. T. Lee and L. F. Nazar, Positive Electrode Materials for Li-Ion and Li-Batteries, Chem. Mater., 2010, 22(3), 691–714,  DOI:10.1021/cm902696j.
4. M. Bianchini, M. Roca-Ayats, P. Hartmann, T. Brezesinski and J. Janek, There and Back Again—The Journey of LiNiO₂ as a Cathode Active Material, Angew. Chem., Int. Ed., 2019, 58(31), 10434–10458,  DOI:10.1002/anie.201812472.
5. M. Bianchini, F. Fauth, P. Hartmann, T. Brezesinski and J. Janek, An In Situ Structural Study on the Synthesis and Decomposition of LiNiO₂, J. Mater. Chem. A, 2020, 8(4), 1808–1820,  10.1039/c9ta12073d.
6. R. J. Clément, Z. Lun and G. Ceder, Cation-Disordered Rocksalt Transition Metal Oxides and Oxyfluorides for High Energy Lithium-Ion Cathodes, Energy Environ. Sci., 2020, 13(2), 345–373,  10.1039/C9EE02803J.
7. R. Wang, X. Li, L. Liu, J. Lee, D.-H. Seo, S.-H. Bo, A. Urban and G. Ceder, A Disordered Rock-Salt Li-Excess Cathode Material with High Capacity and Substantial Oxygen Redox Activity: Li_1.25Nb_0.25Mn_0.5O₂, Electrochem. Commun., 2015, 60, 70–73,  DOI:10.1016/j.elecom.2015.08.003.
8. Y. Fan, W. Zhang, Y. Zhao, Z. Guo and Q. Cai, Fundamental Understanding and Practical Challenges of Lithium-Rich Oxide Cathode Materials: Layered and Disordered-Rocksalt Structure, Energy Storage Mater., 2021, 40, 51–71,  DOI:10.1016/j.ensm.2021.05.005.
9. A. M. Abakumov, S. S. Fedotov, E. V. Antipov and J.-M. Tarascon, Solid State Chemistry for Developing Better Metal-Ion Batteries, Nat. Commun., 2020, 11(1), 4976,  DOI:10.1038/s41467-020-18736-7.
10. M. Li, T. Liu, X. Bi, Z. Chen, K. Amine, C. Zhong and J. Lu, Cationic and Anionic Redox in Lithium-Ion Based Batteries, Chem. Soc. Rev., 2020, 49(6), 1688–1705,  10.1039/C8CS00426A.
11. A. Urban, J. Lee and G. Ceder, The Configurational Space of Rocksalt-Type Oxides for High-Capacity Lithium Battery Electrodes, Adv. Energy Mater., 2014, 4(13), 1400478,  DOI:10.1002/aenm.201400478.
12. K. Kang and G. Ceder, Factors That Affect Li Mobility in Layered Lithium Transition Metal Oxides, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(9), 094105,  DOI:10.1103/PhysRevB.74.094105.
13. G. G. Amatucci, J. M. Tarascon and L. C. Klein, CoO₂, The End Member of the Li_xCoO₂ Solid Solution, J. Electrochem. Soc., 1996, 143(3), 1114–1123,  DOI:10.1149/1.1836594.
14. J. Lee, A. Urban, X. Li, D. Su, G. Hautier and G. Ceder, Unlocking the Potential of Cation-Disordered Oxides for Rechargeable Lithium Batteries, Science, 2014, 343(6170), 519–522,  DOI:10.1126/science.1246432.
15. J. Zheng, P. Xu, M. Gu, J. Xiao, N. D. Browning, P. Yan, C. Wang and J.-G. Zhang, Structural and Chemical Evolution of Li- and Mn-Rich Layered Cathode Material, Chem. Mater., 2015, 27(4), 1381–1390,  DOI:10.1021/cm5045978.
16. Z. Lun, B. Ouyang, D.-H. Kwon, Y. Ha, E. E. Foley, T.-Y. Huang, Z. Cai, H. Kim, M. Balasubramanian, Y. Sun, J. Huang, Y. Tian, H. Kim, B. D. McCloskey, W. Yang, R. J. Clément, H. Ji and G. Ceder, Cation-Disordered Rocksalt-Type High-Entropy Cathodes for Li-Ion Batteries, Nat. Mater., 2021, 20(2), 214–221,  DOI:10.1038/s41563-020-00816-0.
17. G. Assat, D. Foix, C. Delacourt, A. Iadecola, R. Dedryvère and J.-M. Tarascon, Fundamental Interplay between Anionic/Cationic Redox Governing the Kinetics and Thermodynamics of Lithium-Rich Cathodes, Nat. Commun., 2017, 8(1), 2219,  DOI:10.1038/s41467-017-02291-9.
18. A. Urban, A. Abdellahi, S. Dacek, N. Artrith and G. Ceder, Electronic-Structure Origin of Cation Disorder in Transition-Metal Oxides, Phys. Rev. Lett., 2017, 119(17), 176402,  DOI:10.1103/PhysRevLett.119.176402.
19. J. Lee, D. A. Kitchaev, D.-H. Kwon, C.-W. Lee, J. K. Papp, Y.-S. Liu, Z. Lun, R. J. Clément, T. Shi, B. D. McCloskey, J. Guo, M. Balasubramanian and G. Ceder, Reversible Mn2+/Mn4+ Double Redox in Lithium-Excess Cathode Materials, Nature, 2018, 556(7700), 185–190,  DOI:10.1038/s41586-018-0015-4.
20. R. G. Reddy, P. S. Shinde and A. Liu, Review—The Emerging Technologies for Producing Low-Cost Titanium, J. Electrochem. Soc., 2021, 168(4), 042502,  DOI:10.1149/1945-7111/abe50d.
21. M. Bianchini, A. Schiele, S. Schweidler, S. Sicolo, F. Fauth, E. Suard, S. Indris, A. Mazilkin, P. Nagel, S. Schuppler, M. Merz, P. Hartmann, T. Brezesinski and J. Janek, From LiNiO₂ to Li₂NiO₃: Synthesis, Structures and Electrochemical Mechanisms in Li-Rich Nickel Oxides, Chem. Mater., 2020, 32(21), 9211–9227,  DOI:10.1021/acs.chemmater.0c02880.
22. K. Kang, D. Carlier, J. Reed, E. M. Arroyo, G. Ceder, L. Croguennec and C. Delmas, Synthesis and Electrochemical Properties of Layered Li_0.9Ni_0.45Ti_0.55O₂, Chem. Mater., 2003, 15(23), 4503–4507,  DOI:10.1021/cm034455+.
23. L. Croguennec, E. Suard, P. Willmann and C. Delmas, Structural and Electrochemical Characterization of the LiNi₁−_yTi_yO₂ Electrode Materials Obtained by Direct Solid-State Reactions, Chem. Mater., 2002, 14(5), 2149–2157,  DOI:10.1021/cm011265v.
24. S. Zheng, D. Liu, L. Tao, X. Fan, K. Liu, G. Liang, A. Dou, M. Su, Y. Liu and D. Chu, Electrochemistry and Redox Characterization of Rock-Salt-Type Lithium Metal Oxides Li1+z/3Ni1/2-z/2Ti1/2+z/6O2 for Li-Ion Batteries, J. Alloys Compd., 2019, 773, 1–10,  DOI:10.1016/j.jallcom.2018.09.261.
25. S. Prabaharan, Li₂NiTiO₄? A New Positive Electrode for Lithium Batteries: Soft-Chemistry Synthesis and Electrochemical Characterization, Solid State Ionics, 2004, 172(1–4), 39–45,  DOI:10.1016/j.ssi.2004.01.036.
26. L. Sebastian and J. Gopalakrishnan, Li₂MTiO₄ (M = Mn, Fe, Co, Ni): New Cation-Disordered Rocksalt Oxides Exhibiting Oxidative Deintercalation of Lithium. Synthesis of an Ordered Li₂NiTiO₄, J. Solid State Chem., 2003, 172(1), 171–177,  DOI:10.1016/S0022-4596(03)00010-0.
27. L. Zhang, H. Noguchi, D. Li, T. Muta, X. Wang, M. Yoshio and I. Taniguchi, Synthesis and Electrochemistry of Cubic Rocksalt Li–Ni–Ti–O Compounds in the Phase Diagram of LiNiO₂–LiTiO₂–Li[Li_1/3Ti_2/3]O₂, J. Power Sources, 2008, 185(1), 534–541,  DOI:10.1016/j.jpowsour.2008.06.054.
28. B. Li, K. Kumar, I. Roy, A. V. Morozov, O. V. Emelyanova, L. Zhang, T. Koç, S. Belin, J. Cabana, R. Dedryvère, A. M. Abakumov and J.-M. Tarascon, Capturing Dynamic Ligand-to-Metal Charge Transfer with a Long-Lived Cationic Intermediate for Anionic Redox, Nat. Mater., 2022, 21(10), 1165–1174,  DOI:10.1038/s41563-022-01278-2.
29. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186,  DOI:10.1103/PhysRevB.54.11169.
30. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186,  DOI:10.1103/PhysRevB.54.11169.
31. G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561,  DOI:10.1103/PhysRevB.47.558.
32. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775,  DOI:10.1103/PhysRevB.59.1758.
33. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
34. J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, Accurate and Numerically Efficient R2SCAN Meta-Generalized Gradient Approximation, J. Phys. Chem. Lett., 2020, 11(19), 8208–8215,  DOI:10.1021/acs.jpclett.0c02405.
35. O. Y. Long, G. Sai Gautam and E. A. Carter, Evaluating Optimal U for 3d Transition-Metal Oxides within the SCAN+ U Framework, Phys. Rev. Mater., 2020, 4(4), 045401,  DOI:10.1103/PhysRevMaterials.4.045401.
36. E. Caldeweyher, C. Bannwarth and S. Grimme, Extension of the D3 Dispersion Coefficient Model, J. Chem. Phys., 2017, 147(3), 034112,  DOI:10.1063/1.4993215.
37. K. Mukai, M. Yashima, K. Hibino and T. Terai, Experimental Visualization of Interstitialcy Diffusion of Li Ion in β-Li₂TiO₃, ACS Appl. Energy Mater., 2019, 2(8), 5481–5489,  DOI:10.1021/acsaem.9b00639.
38. H. M. Rietveld, A Profile Refinement Method for Nuclear and Magnetic Structures, J. Appl. Crystallogr., 1969, 2(2), 65–71,  DOI:10.1107/S0021889869006558.
39. K. Okhotnikov, T. Charpentier and S. Cadars, Supercell Program: A Combinatorial Structure-Generation Approach for the Local-Level Modeling of Atomic Substitutions and Partial Occupancies in Crystals, J. Cheminf., 2016, 8, 17,  DOI:10.1186/s13321-016-0129-3.
40. C. Sutton and S. V. Levchenko, First-Principles Atomistic Thermodynamics and Configurational Entropy, Front. Chem., 2020, 8, 757,  DOI:10.3389/fchem.2020.00757.
41. K. Kataoka, Y. Takahashi, N. Kijima, H. Nagai, J. Akimoto, Y. Idemoto and K. Ohshima, Crystal Growth and Structure Refinement of Monoclinic Li₂TiO₃, Mater. Res. Bull., 2009, 44(1), 168–172,  DOI:10.1016/j.materresbull.2008.03.015.
42. A. Watanabe, T. Matsunaga, A. Abulikemu, K. Shimoda, K. Yamamoto, T. Uchiyama and Y. Uchimoto, Structural Analysis of Imperfect Li₂TiO₃ Crystals, J. Alloys Compd., 2020, 819, 153037,  DOI:10.1016/j.jallcom.2019.153037.
43. A. Pokle, D. Weber, M. Bianchini, J. Janek and K. Volz, Probing the Ni(OH) ₂ Precursor for LiNiO₂ at the Atomic Scale: Insights into the Origin of Structural Defect in a Layered Cathode Active Material, Small, 2023, 19(4), 2205508,  DOI:10.1002/smll.202205508.
44. F. Ascencio, A. Bobadilla and R. Escudero, Study of NiO Nanoparticles, Structural and Magnetic Characteristics, Appl. Phys. A, 2019, 125(4), 279,  DOI:10.1007/s00339-019-2579-8.
45. M. Bianchini, J. Wang, R. J. Clément, B. Ouyang, P. Xiao, D. Kitchaev, T. Shi, Y. Zhang, Y. Wang, H. Kim, M. Zhang, J. Bai, F. Wang, W. Sun and G. Ceder, The Interplay between Thermodynamics and Kinetics in the Solid-State Synthesis of Layered Oxides, Nat. Mater., 2020, 19(10), 1088–1095,  DOI:10.1038/s41563-020-0688-6.
46. Ģ. Vītiņš, G. Ķizāne, A. Lūsis and J. Tīliks, Electrical Conductivity Studies in the System Li₂TiO₃-Li_1.33Ti_1.67O₄, J. Solid State Electrochem., 2002, 6(5), 311–319,  DOI:10.1007/s100080100239.
47. S. Muhammad, H. Kim, Y. Kim, D. Kim, J. H. Song, J. Yoon, J.-H. Park, S.-J. Ahn, S.-H. Kang, M. M. Thackeray and W.-S. Yoon, Evidence of Reversible Oxygen Participation in Anomalously High Capacity Li- and Mn-Rich Cathodes for Li-Ion Batteries, Nano Energy, 2016, 21, 172–184,  DOI:10.1016/j.nanoen.2015.12.027.
48. S. Ho Chang, S.-G. Kang, S.-W. Song, J.-B. Yoon and J.-H. Choy, Crystal Structure and Spectroscopic Properties of Li_xNi_1−yTi_yO₂ and Their Electrochemical Behavior, Solid State Ionics, 1996, 86–88, 171–175,  DOI:10.1016/0167-2738(96)00117-8.
49. N. Yabuuchi, M. Takeuchi, M. Nakayama, H. Shiiba, M. Ogawa, K. Nakayama, T. Ohta, D. Endo, T. Ozaki, T. Inamasu, K. Sato and S. Komaba, High-Capacity Electrode Materials for Rechargeable Lithium Batteries: Li₃NbO₄-Based System with Cation-Disordered Rocksalt Structure, Proc. Natl. Acad. Sci. U.S.A., 2015, 112(25), 7650–7655,  DOI:10.1073/pnas.1504901112.
50. H. Ji, D. A. Kitchaev, Z. Lun, H. Kim, E. Foley, D.-H. Kwon, Y. Tian, M. Balasubramanian, M. Bianchini, Z. Cai, R. J. Clément, J. C. Kim and G. Ceder, Computational Investigation and Experimental Realization of Disordered High-Capacity Li-Ion Cathodes Based on Ni Redox, Chem. Mater., 2019, 31(7), 2431–2442,  DOI:10.1021/acs.chemmater.8b05096.
51. R. Fukuma, M. Harada, W. Zhao, M. Sawamura, Y. Noda, M. Nakayama, M. Goto, D. Kan, Y. Shimakawa, M. Yonemura, N. Ikeda, R. Watanuki, H. L. Andersen, A. M. D'Angelo, N. Sharma, J. Park, H. R. Byon, S. Fukuyama, Z. Han, H. Fukumitsu, M. Schulz-Dobrick, K. Yamanaka, H. Yamagishi, T. Ohta and N. Yabuuchi, Unexpectedly Large Contribution of Oxygen to Charge Compensation Triggered by Structural Disordering: Detailed Experimental and Theoretical Study on a Li₃NbO₄–NiO Binary System, ACS Cent. Sci., 2022, 8(6), 775–794,  DOI:10.1021/acscentsci.2c00238.
52. X. Li, Y. Qiao, S. Guo, K. Jiang, M. Ishida and H. Zhou, A New Type of Li-Rich Rock-Salt Oxide Li₂Ni_1/3Ru_2/3O₃ with Reversible Anionic Redox Chemistry, Adv. Mater., 2019, 31(11), 1807825,  DOI:10.1002/adma.201807825.
53. H. Ji, A. Urban, D. A. Kitchaev, D.-H. Kwon, N. Artrith, C. Ophus, W. Huang, Z. Cai, T. Shi, J. C. Kim, H. Kim and G. Ceder, Hidden Structural and Chemical Order Controls Lithium Transport in Cation-Disordered Oxides for Rechargeable Batteries, Nat. Commun., 2019, 10(1), 592,  DOI:10.1038/s41467-019-08490-w.
54. D. Chen, J. Ahn, E. Self, J. Nanda and G. Chen, Understanding Cation-Disordered Rocksalt Oxyfluoride Cathodes, J. Mater. Chem. A, 2021, 9(12), 7826–7837,  10.1039/D0TA12179G.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta02265c

‡ Current address: Inst. Mat. Wissensch., Chem. Mat. Synth., Heisenbergstr. 3, D-70569 Stuttgart, Germany.

---