Efficient first principles based modeling via machine learning: from simple representations to high entropy materials†
Kangming
Li
 *a,
Kamal
Choudhary
*a,
Kamal
Choudhary
 b,
Brian
DeCost
b,
Brian
DeCost
 b,
Michael
Greenwood
c and
Jason
Hattrick-Simpers
b,
Michael
Greenwood
c and
Jason
Hattrick-Simpers
 *adef
*adef
aDepartment of Materials Science and Engineering, University of Toronto, 27 King's College Cir, Toronto, ON, Canada. E-mail: kangming.li@utoronto.ca; jason.hattrick.simpers@utoronto.ca
bMaterial Measurement Laboratory, National Institute of Standards and Technology, 100 Bureau Dr, Gaithersburg, MD, USA
cCanmet MATERIALS, Natural Resources Canada, 183 Longwood Road south, Hamilton, ON, Canada
dAcceleration Consortium, University of Toronto, 80 St George St, Toronto, ON M5S 3H6, Canada
eVector Institute for Artificial Intelligence, 661 University Ave, Toronto, ON, Canada
fSchwartz Reisman Institute for Technology and Society, 101 College St, Toronto, ON, Canada
First published on 17th April 2024
Abstract
High-entropy materials (HEMs) have recently emerged as a significant category of materials, offering highly tunable properties. However, the scarcity of HEM data in existing density functional theory (DFT) databases, primarily due to computational expense, hinders the development of effective modeling strategies for computational materials discovery. In this study, we introduce an open DFT dataset of alloys and employ machine learning (ML) methods to investigate the material representations needed for HEM modeling. Utilizing high-throughput DFT calculations, we generate a comprehensive dataset of 84k structures, encompassing both ordered and disordered alloys across a spectrum of up to seven components and the entire concentration range. We apply descriptor-based models and graph neural networks to assess how material information is captured across diverse chemical-structural representations. We first evaluate the in-distribution performance of ML models to confirm their predictive accuracy. Subsequently, we demonstrate the capability of ML models to generalize between ordered and disordered structures, between low-order and high-order alloy systems, and between equimolar and non-equimolar compositions. Our findings suggest that ML models can generalize from cost-effective calculations of simpler systems to more complex scenarios. Additionally, we discuss the influence of dataset size and reveal that the information loss associated with the use of unrelaxed structures could significantly degrade the generalization performance. Overall, this research sheds light on several critical aspects of HEM modeling and offers insights for data-driven atomistic modeling of HEMs.
I. Introduction
The quest for novel materials is pivotal in advancing technology and addressing global challenges. High-entropy materials (HEMs), characterized by their multiple principal elements and high chemical disorder, have emerged as an important material class. Their remarkable properties have attracted significant attention, leading to applications in diverse areas such as catalysis, batteries, and hydrogen storage.1–6The vast design space of HEMs offers immense opportunities but also poses substantial challenges in material discovery. Data-driven approaches, particularly machine learning (ML), have been increasingly employed to explore this space.7–10 While numerous studies have focused on developing ML models using experimental data, these datasets are relatively small, typically ranging from hundreds to thousands of data points, and cover only a limited portion of the potential design space.11–13
High-throughput density functional theory (DFT) calculations have become a key method for generating extensive materials data. Recent efforts have led to the curation of several large DFT datasets encompassing millions of materials.14–18 However, these datasets lack representations for HEMs due to the prohibitive computational cost to simulate chemical disorder.19 The computational expense of DFT methods typically scales with 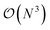 , where N is the system size. While ordered phases can be represented by small primitive cells, disordered phases require theoretically infinite primitive cell due to the aperiodic atomic arrangement. Structures with over thousands of atoms randomly distributed on the lattice may be considered sufficiently representative of HEMs, but this approach is computationally intensive and rarely used. The standard approach is the use of special quasirandom structures (SQSs) to approximate the correlation function of disordered phases, allowing the simulation of disordered materials with down to tens of atoms. Yet, the computational cost of SQSs is still significantly higher than that for ordered structures.20–23
, where N is the system size. While ordered phases can be represented by small primitive cells, disordered phases require theoretically infinite primitive cell due to the aperiodic atomic arrangement. Structures with over thousands of atoms randomly distributed on the lattice may be considered sufficiently representative of HEMs, but this approach is computationally intensive and rarely used. The standard approach is the use of special quasirandom structures (SQSs) to approximate the correlation function of disordered phases, allowing the simulation of disordered materials with down to tens of atoms. Yet, the computational cost of SQSs is still significantly higher than that for ordered structures.20–23
The inclusion of SQSs in the next phase of high-throughput DFT databases development has been proposed.24 However, the prioritization of specific SQS data types and their implications remain unresolved questions. Most existing studies have focused on equimolar compositions,25–30 while non-equimolar compositions, which could offer superior material performance, are largely underexplored.31 ML models trained on equimolar data have been applied to non-equimolar compositions without further DFT validation.32,33 The generalization performance of these ML models may be severely degraded,34,35 due to the highly biased sampling of local chemical environments in a single equimolar material. In addition, it is unclear whether data of binary compounds are sufficient to extrapolate to HEMs with five or more elements,26 or if the use of multi-element SQSs is necessary for systematic accuracy improvement. Furthermore, there is an accuracy-efficiency trade-off regarding the size of SQSs. A larger SQS can better approximate the disordered phase but requires substantially more compute. The suitable SQS size for the HEM modeling is closely related to the composition range and number of elements under consideration. Deviating from equimolar concentration or increasing the number of alloying elements would require larger SQSs to mimic the statistics of a random structure.30,31 It is therefore important to discuss the choices of the SQS parameters such as composition, number of elements, and system size in the HEM modeling.
Traditionally, ordered structures and SQS data are often exclusively used in the HEM modeling.25–33 One reason is that these methods are specifically designed to use only either ordered structures or SQSs and thus are inflexible in terms of the choice of structure sets. In contrast, many ML methods provide general representations of crystal structures independent of chemical order, which offer greater flexibility and potentially higher accuracy and efficiency.36–42 However, there is a lack of ML studies that treat ordered structures and SQSs on equal footing.
In this work, we focus on formation energy as it is crucial for thermodynamic stability assessment. The DFT-experimental deviation of formation energy is estimated to be 0.05 to 0.25 eV per atom,43–46 comparable to the experimental variability of 0.08 eV per atom.46 While formation energy prediction has been a main target for ML studies (more commonly on DFT47–49 than on experimental data49,50), it is largely limited to ordered structures due to the lack of SQS data.47–49
To address these gaps, we perform high-throughput DFT calculations to curate a large dataset for HEMs. Our SQS-containing dataset includes approximately 84k alloys with 2 to 7 components, spanning a wide range of system sizes, chemical orders, and compositions. We examine the effects of various factors on the predictive accuracy of descriptor-based ML models and graph neural networks. Particularly, we focus on their out-of-distribution generalization capabilities, i.e., the ability to generalize to structures with different characteristics (such as more complex structures) than the training data. We first assess the predictive capabilities of ML models based on in-distribution performance. Then, we evaluate their out-of-distribution generalization capabilities, including comparisons between ordered structures and SQSs, low-order and high-order systems, and equimolar and non-equimolar compositions. Additionally, we discuss the impact of training data size and quantify information loss associated with using unrelaxed structures.
II. Computational details
A. DFT calculations
DFT calculations were conducted using the Vienna Ab initio Simulation Package (VASP) code.51–53 We used the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation for the exchange–correlation functional54 and a plane-wave basis cutoff of 520 eV. We adopted the Methfessel–Paxton broadening scheme with a smearing width of 0.1 eV.55 The electronic convergence cutoff was set to 10−5 eV per atom. Structures were fully relaxed to an energy convergence criterion of 10−4 eV per atom. For k-point sampling, grids with a density exceeding 1000 k-points per reciprocal atom were utilized following the Monkhorst–Pack scheme.56 All calculations were spin-polarized. The Pymatgen package was used for input file generation and data analysis.41 Body-centered cubic (bcc) and face-centered cubic (fcc) structures were generated using the Alloy Theoretic Automated Toolkit:57 ordered structures (2 to 8 atoms) through structure enumeration, and disordered structures (27, 64, or 125 atoms) using the SQS approach.21 Formation energies were calculated relative to the most stable unary phases of the constituent elements.B. ML modeling
Here we consider XGBoost (XGB),58 random forest (RF),59,60 and the Atomistic LIne Graph Neural Network (ALIGNN).61 XGB and RF are tree ensembles that use compositional and structural descriptors extracted from atomic structures based on the Voronoi tessellation featurization scheme39 implemented in the Matminer package.40 We use a descriptor set that consists of 145 compositional features62 related to stoichiometry, element properties, valence orbital shells, and ionic properties, and 128 structural features39 including statistics of coordination numbers, chemical ordering, local difference of element properties, and variance in the bond lengths and atomic volumes. ALIGNN is a graph neural network that explicitly encodes bond angle information.61 These models are representative of the state-of-the-art performance of descriptor-based models and graph neural networks based on their performance in various prediction tasks in the JARVIS learderboard.63We used the following hyperparameters for XGB, RF and ALIGNN models. These hyperparameters have been used in our previous work showing consistently good model performance across various materials datasets,35,63 and they were also found to be suitable for our dataset based on the hyperparameter grid search (ESI†). For the RF model, we disabled bootstrapping, used 100 estimators, 30% of the features for the best splitting, and default settings (scikit-learn version 1.3.0 (ref. 60)) for other hyperparameters. For the XGB model, we used a forest with 6 parallel trees, 500 boosting rounds, a learning rate of 0.4, an L1 and L2 regularization strength of 0.01 and 0.1 respectively, the histogram tree grow method, a subsample ratio of columns to 0.5 when constructing each tree, and a subsample ratio of columns to 0.7 for each level. For the ALIGNN model, we used 2 ALIGNN layers, 2 GCN layers, a batch size of 32, and layer normalization, while keeping other hyperparameters the same as in the original ALIGNN implementation.61 We trained the ALIGNN model for 50 epochs as we found additional training provided negligible performance improvement. We used the OneCycle learning rate scheduler,64 with 30% of the training budget allocated to linear warmup and 70% to cosine annealing.
The ML models were trained with either relaxed structures or unrelaxed structures as input structures, and the formation energies of the relaxed structures as the prediction target. While the relaxed structures were obtained from DFT structural relaxations and can have local and global lattice distortions, the unrelaxed structures have an ideal bcc or fcc lattice with each atom sitting exactly on the lattice site. In addition, the lattice parameters of unrelaxed structures were set to be the same for ML training. Therefore, ML models trained with unrelaxed structures only learn from the atomic configuration in a way similar to on-lattice models.29,65–67
III. Results
A. DFT formation energy dataset
Our DFT dataset encompasses bcc and fcc structures composed of Cr, Mn, Fe, Co, Ni, Cu, Al, and Si. The 3d transition-metal elements are chosen because they are the main components of Cantor alloys, one of the most important family of HEMs, with the bcc and fcc phases being the most relevant disordered phases. Al and Si are included due to their potential in enhancing corrosion resistance and developing durable materials for clean energy infrastructure.68 The dataset covers all possible 2- to 7-component alloy systems formed by these eight elements. For each alloy system, the dataset covers ordered structures and SQSs over the entire concentration range. The concentration step is 1/n for ordered structures with n (2 ≤ n ≤ 8) atoms, and is equal to 11.1%, 12.5%, and 8% for SQSs with 27, 64, and 125 atoms, respectively. Table 1 gives an overview of the numbers of alloy systems and structures. More details on the dataset can be found in the ESI.†| No. components | 2 | 3 | 4 | 5 | 6 | 7 | Total |
|---|---|---|---|---|---|---|---|
| Alloy systems | 28 | 56 | 70 | 56 | 28 | 8 | 246 |
| Ordered | 4975 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 098 098 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 494 494 |
6157 | 3132 | 3719 | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 575 575 |
| SQS | 715 | 3302 | 3542 | 4718 | 1183 | 762 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222 222 |
| Ordered + SQS | 5690 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 036 036 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875 875 |
4315 | 4481 | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
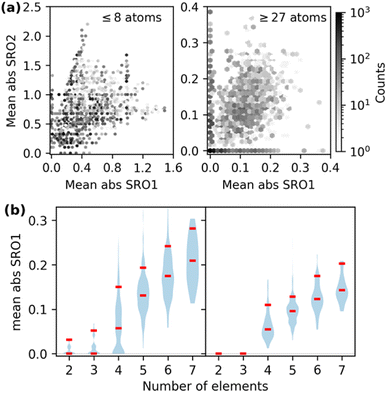
The combination of ordered structures and SQSs can enable diverse sampling of chemical order, which is quantified by the Warren–Cowley short-range order (SRO) parameter for a pair of species i and j:69
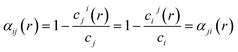 | (1) |
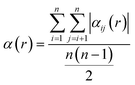 | (2) |
In Fig. 1(a), we show the distribution of overall chemical ordering for the first two shells. Ordered structures span a wide range of the SRO space but are poorly represented in the region with low SRO that is characteristic of the chemical disorder of HEMs. The low SRO portion of our dataset predominantly consists of SQS data.
Some of the generated SQSs in Fig. 1(a) have non-zero SRO ranging between 0.1 and 0.3. Although SQSs with non-zero SRO are beneficial for modeling SRO effects in HEMs, it is worth emphasizing that the original intent of the SQS method was to minimize SRO to enable unbiased studies of chemically disordered systems. The significant SRO in this SQS dataset reflects the challenges in fully capturing chemical disorder within the SQS framework. As depicted in Fig. 1(b), the minimal SRO parameters increases with the number of elements for a given system size. For a specific system size and element count (e.g., 27-atom SQSs with two elements), higher SRO is associated with SQSs deviating further from equimolar concentration. This is because increasing the number of components reduces the number of atoms per element (deviating from concentrated compositions has a similar effect on the minority elements), hence making it difficult to arrange atoms to create diverse local environments in an SQS. Although using 64-atom SQSs can reduce the average SRO of binary and ternary structures to 0, further reducing the SRO in structures with more components or stronger non-equimolar deviation would require even larger system sizes. This highlights the computational challenge of directly simulating complex HEMs within the DFT-SQS framework, especially considering the 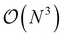 scaling of DFT costs.
scaling of DFT costs.
B. Generalization performance with relaxed structures
ML models can be used as surrogates of DFT calculations to efficiently screen the vast HEM space. To demonstrate their predictive ability, we train and evaluate the model performance with a random 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 train–test split of the whole dataset. We used mean absolute error (MAE) and normalized error (MAE normalized by the mean absolute deviation, MAD, of test data) as performance metrics. MAD quantifies the statistical fluctuation of the test data and can be seen as the MAE of a baseline model that always predicts the mean of the test data. A model with a normalized error below 0.2 is often considered a good predictive model.61,70,71 The RF and XGB models achieve an MAE of 0.016 eV per atom and 0.014 eV per atom, respectively, and a normalized error of 0.147 and 0.128, respectively, demonstrating the good predictive ability of the tree-based models. Compared to the tree-based models, the ALIGNN model achieves an even lower MAE of 0.007 eV per atom, or a normalized error of 0.064. The better ALIGNN performance is attributed to the use of deep graph neural networks for automated feature extraction and the explicit incorporation of bond angle information, consistent with the superior performance of graph neural networks over shallow ML methods seen in benchmark studies.61,71
2 train–test split of the whole dataset. We used mean absolute error (MAE) and normalized error (MAE normalized by the mean absolute deviation, MAD, of test data) as performance metrics. MAD quantifies the statistical fluctuation of the test data and can be seen as the MAE of a baseline model that always predicts the mean of the test data. A model with a normalized error below 0.2 is often considered a good predictive model.61,70,71 The RF and XGB models achieve an MAE of 0.016 eV per atom and 0.014 eV per atom, respectively, and a normalized error of 0.147 and 0.128, respectively, demonstrating the good predictive ability of the tree-based models. Compared to the tree-based models, the ALIGNN model achieves an even lower MAE of 0.007 eV per atom, or a normalized error of 0.064. The better ALIGNN performance is attributed to the use of deep graph neural networks for automated feature extraction and the explicit incorporation of bond angle information, consistent with the superior performance of graph neural networks over shallow ML methods seen in benchmark studies.61,71
The training and test sets created via random splitting are expected to follow the same statistical distribution, and the examined performance is referred to as the in-distribution performance. In practical applications, however, ML models often encounter new data that do not necessarily follow the same distribution as the training data. It is therefore crucial to evaluate whether trained ML models can generalize beyond their original data distribution. Such an assessment not only provides an estimation of the extended applicability domain of the models but also sheds light on the types of data that should be prioritized in future DFT calculations for improved predictions.
Here we evaluate the out-of-distribution performance by training on a specific group of structures and evaluating on the rest of structures. The grouping criteria considered here are based on the system size, the number of elements, and the composition. Given that most literature DFT data comprise small-sized structures with few elements and/or equimolar composition, we focused on whether models trained on these simpler materials could generalize to more complex ones.
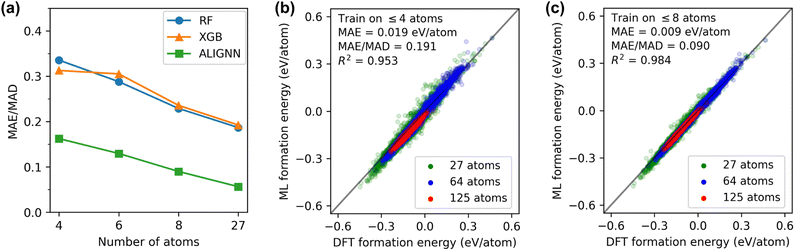
We first assessed the models' ability to generalize predictions from small to large structures. Fig. 2(a) presents normalized errors for models trained on structures with ≤N atoms and tested on structures with >N atoms. Remarkably, the ALIGNN model trained on structures with ≤4 atoms exhibited good performance 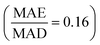 on structures with >4 atoms. This is notable considering the limited chemical orders and compositions in the training set compared to the diverse chemical space of the 5- to 125-atom structures in the test set. Including larger structures in the training set systematically improved ALIGNN performance, reducing its normalized error on large SQSs to 0.05 when trained on structures with ≤27 atoms. RF and XGB models also benefited from including larger structures, though their normalized errors remained significantly higher than that of the ALIGNN model.
on structures with >4 atoms. This is notable considering the limited chemical orders and compositions in the training set compared to the diverse chemical space of the 5- to 125-atom structures in the test set. Including larger structures in the training set systematically improved ALIGNN performance, reducing its normalized error on large SQSs to 0.05 when trained on structures with ≤27 atoms. RF and XGB models also benefited from including larger structures, though their normalized errors remained significantly higher than that of the ALIGNN model.
Fig. 2(b) shows the distribution of ALIGNN prediction errors on SQSs. The ALIGNN model trained on structures with ≤4 atoms achieves a MAE of 0.019 eV per atom on SQSs and the performance is consistently good for SQSs of different sizes. The ALIGNN performance on SQSs can be further improved with a 53% decrease in the MAE when ordered structures with up to 8 atoms are added into the training set, as shown in Fig. 2(c). This good generalization performance suggests that existing large DFT databases containing mainly ordered structures could be a good starting point for HEM modeling.
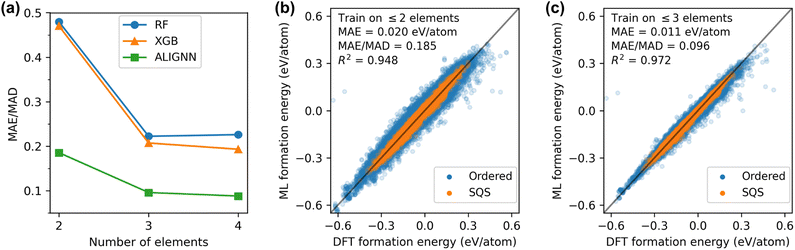
Next, we examine the generalization performance from low-order to high-order systems. This is motivated by the availability of lower-order systems in current DFT datasets and the difficulty to rely on DFT to explore the vast high-order materials space. As shown in Fig. 3(a), the ALIGNN model trained on binary alloys can generalize reasonably well to alloys with three or more components, with a normalized error below 0.2 which is much lower than those obtained with the RF and XGB models. Additionally including ternary alloys into the training data can significantly improve the model performance than training only binary structures. However, this enhancement in accuracy reaches a plateau when structures with four or more components are included in the training dataset, indicating diminishing returns in accuracy boost from expanding the complexity of the training structures. Fig. 3(b) and (c) show the parity plots for the ALIGNN predictions on structures with more than 2 components and more than 3 components, respectively. In both cases, the prediction errors tend to be larger for ordered structures than for SQSs, which may be related to the fact that ordered structures can present very distinct and diverse chemical order compared to SQSs (Fig. 1). These results suggest that SQSs may be an easier target than ordered structures for ML models in terms of achieving good accuracy, in contrast to the fact that SQSs are traditionally considered as more complex representations and also computationally heavier for DFT calculations.
It is worth noting that the good generalization from low-order to high-order systems is not surprising. Indeed, from a physical perspective, low-order systems are expected to contain sufficient information of many-body interactions to describe high-order systems. For instance, it is common practice in the Calphad community to develop multicomponent databases based on the thermodynamic assessment of binary and ternary systems.72,73 Therefore, contrary to the recent claim that this is an emergent out-of-distribution generalization enabled by advanced neural network architectures,74 we argue that this capability to generalize from low-order to high-order systems should be common to various ML models, including the traditional tree ensembles shown here.
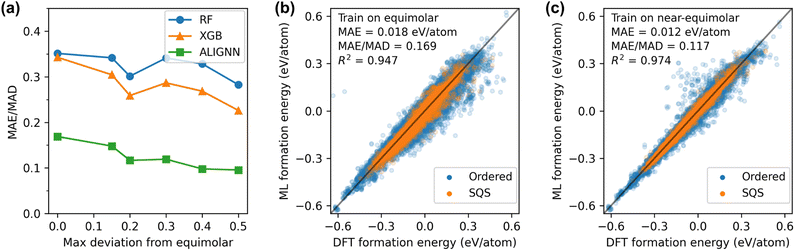
The third type of the out-of-distribution performance is based on alloy compositions. Studies focusing on HEMs have predominantly concentrated on equimolar compositions,25–30 leaving a comparative dearth of data on non-equimolar compositions. Here we explore the extent to which models trained on equimolar alloys could extend their predictive capabilities to non-equimolar counterparts. Additionally, we systematically discern the impact of varying the concentration range covered in the training data. To this end, we quantify the deviation from the equimolar composition by max Δc, defined as the maximum concentration fraction difference between any two elements in a structure. Setting a maximum value for max Δc is equivalent to setting the concentration range. For instance, with max Δc ≤ 0.2 (20%), the atomic fractions of all elements would fall within the 10% range from the equimolar composition.
We evaluate the model performance by training on all structures with max Δc below a given threshold value and testing on remaining structures. The results for the threshold value of 0 are shown in Fig. 4(a) and (b). The ALIGNN model trained on only equimolar alloys achieves a good performance with a normalized error of 0.169 for non-equimolar alloys. It is worth noting that the number of equimolar structures (7.7k data) only accounts for 9% of the whole dataset. Moreover, only 2% of the equimolar data structures SQSs while the rest of the training data are ordered structures. Despite the constrained quantity and compositional range of the training data, the ALIGNN model exhibits a robust capability to generalize to non-equimolar alloys, in particular for SQSs. Expanding the training set to include near-equimolar structures are found to improve the model performance. As demonstrated in Fig. 4(c), setting the threshold to 0.2, wherein the training dataset represents 40% of the entire dataset, resulted in a normalized error of 0.117, or a 30% reduction in error compared to the equimolar case. However, further incrementing the threshold value beyond 0.2 yielded marginal improvements in performance, suggesting a saturation point in the efficacy of expanding the concentration range within the training data.
C. Effects of data size and use of unrelaxed structures on model performance
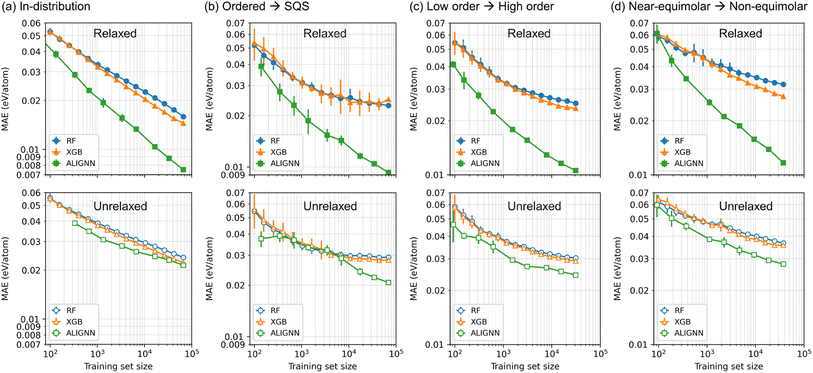
Fig. 5 reveals the effects of training set size on the model performance. In both in-distribution and out-of-distribution generalization tasks, the ALIGNN model exhibits superior performance across both small-data and large-data regimes when trained on relaxed structures. Notably, ALIGNN demonstrates a more favorable performance-versus-data scaling compared to the tree ensembles, with its performance advantage amplifying alongside the augmentation of the training set size. A compelling example of this is depicted in Fig. 5(b), where ALIGNN models trained on merely about 600 ordered structures reach the same MAE on SQSs as tree ensembles trained on a dataset over 100× larger (69.6k ordered structures). This contrasts with the performance saturation of tree ensembles observed beyond 7k ordered structures, while ALIGNN's MAE persistently decreases with an increased number of training data.When trained on the unrelaxed structures, all the ML models show the degraded performance compared to the ones obtained with the relaxed structures. The ALIGNN model, in particular, undergoes the most pronounced degradation, with its performance advantage narrowing to a margin only slightly better than that of the tree ensembles. In addition, the performance-versus-data scaling of the ALIGNN model also becomes similar to that of the tree ensembles.
The performance degradation here is likely due to the information loss in the training data: when trained on unrelaxed structures, ML models are confined to leveraging solely on-lattice configurational information for energy mapping, thereby losing access to information such as local structural distortions and variations in cell shape and volume. Therefore, in scenarios where only unrelaxed structures are accessible, tree ensembles might already capture the majority of the learnable information from the training data. Consequently, graph neural networks like ALIGNN may not necessarily yield substantial performance enhancements over descriptor-based models in these settings. This underscores that the distinct advantage of graph neural networks is considerably diminished without the availability of relaxed structures for training. Conversely, the results achieved with relaxed structures underscore the significant amount of learnable information embedded in structural relaxation and the enhanced capability of graph neural networks to effectively utilize this information when available. This highlights the critical role of structural details in model training and the potential of advanced neural network models to extract deeper insights from complex structural data in materials science.
D. Comparison between models across generalization tasks
The previous sections are focused on the generalizations from ordered to disordered structures, from low-order to high-order alloys, and from equimolar compositions to non-equimolar compositions. Equally pertinent, however, is the exploration of these generalizations in reverse: from disordered to ordered structures, from high-order to low-order alloys, and from non-equimolar to equimolar compositions. Such reverse generalizations are particularly relevant in a top-down modeling approach, where one might e.g. start with data on complex high-order HEMs and aim to extrapolate to simpler, lower-order systems.Table 2 shows a comparison of the model performance for the in-distribution and six out-of-distribution tasks. When trained on relaxed structures, ALIGNN consistently outperforms the tree ensembles across all generalization tasks, achieving up to a 60% reduction in MAE. However, this performance disparity between ALIGNN and the tree-based models becomes less pronounced when training is based on unrelaxed structures.
| Structure | Model | ID | Ordered → SQS | SQS → ordered | Low → high | High → low | Equi → non-equi | Non-equi → equi |
|---|---|---|---|---|---|---|---|---|
| Relaxed | RF | 0.016 | 0.023 | 0.040 | 0.025 | 0.038 | 0.037 | 0.029 |
| XGB | 0.014 | 0.025 | 0.038 | 0.023 | 0.036 | 0.036 | 0.025 | |
| ALIGNN | 0.007 | 0.009 | 0.025 | 0.011 | 0.013 | 0.018 | 0.010 | |
| Unrelaxed | RF | 0.024 | 0.029 | 0.043 | 0.030 | 0.043 | 0.043 | 0.036 |
| XGB | 0.022 | 0.028 | 0.042 | 0.029 | 0.041 | 0.041 | 0.032 | |
| ALIGNN | 0.021 | 0.021 | 0.043 | 0.024 | 0.030 | 0.032 | 0.026 | |
| MAD | 0.109 | 0.101 | 0.104 | 0.111 | 0.097 | 0.106 | 0.130 | |
| Training set size | 67k | 70k | 14k | 6k | 78k | 8k | 76k | |
Compared to the generalization from ordered to disordered structures, the generalization from disordered to ordered structures is more difficult, evidenced by up to a 180% increase in MAE. The better generalization in the former case could be largely due to the data diversity for ordered structures (Fig. 1(a)), rather than the larger training set size of ordered structures, considering that the performance scaling with data size is relatively modest (as shown in Fig. 5(b)).
Compared to the generalization from equimolar to non-equimolar structures, the generalization from non-equimolar to equimolar is easier with a lower MAE. This outcome aligns with expectations, given the significantly larger dataset and the greater diversity found in non-equimolar compositions.
Compared to the generalization from low-order to high-order alloys, the generalization from high-order to low-order alloys is more difficult. However, this cannot be simply explained by the dataset size nor the data diversity. Indeed, the number of high-order structures is more than an order of magnitude larger than that of low-order structures. Furthermore, structures with four or more elements are expected to provide more diverse sampling of chemical environments than binary and ternary structures. Instead, this difficulty might be explained from a physics perspective. When building physics-based model Hamiltonians, a common practice is to use a bottom-up approach, where one first fits the two-body interaction parameters with low-order systems, and gradually adds more model parameters by including higher-order interactions for more complex systems.67 This is often considered to be physically more reasonable than just performing a single fit for all the model parameters once. The latter can be prone to overfitting by inappropriately attributing more contribution to the higher-order interactions, whereas the bottom-up approach provides a way to add regularization to higher-order interactions. In a similar spirit, the ML models trained on low-order structures can learn well low-order interactions and thus generalize to high-order systems even without knowing high-order interactions. By contrast, training only on high-order systems means the models need to decode simultaneously the low-order and high-order interactions from high-order structures, which could make the learning more difficult and would require more data than the bottom-up approach.
IV. Discussion
The out-of-distribution generalization results can provide insights for future DFT dataset construction. For instance, we demonstrate that ordered structures contain sufficient information for ML models to generalize well to SQSs, highlighting the usefulness of the existing DFT databases as a good starting point for HEM modeling. Furthermore, we reveal that continuously adding more complex representation would not be an efficient strategy to systematically improve the generalization performance. For example, further including quaternary systems into the binary and ternary training data only improves marginally model accuracy. These results call for the design of effective sampling strategies that take into account both the usefulness and the cost of a data point. Namely, one should weigh between an extensive but indirect sampling with many inexpensive calculations of ordered structures and a direct but expensive sampling of a few SQSs. There is a similar trade-off between an extensive sampling of many low-order systems and a direct sampling of a few high-order systems.We also reveal that the unavailability of DFT-relaxed structures cause significant performance degradation. This degradation is attributed to the loss of learnable information related to lattice distortion in the unrelaxed data rather than the intrinsic limitation of ML models. With unrelaxed structures, graph neural networks do not have a significant performance advantage over tree ensembles, which may be explained by the reduced amount of learnable information being a limiting factor. One possible solution is to develop ML interatomic potentials by training on the relaxation trajectory data and then use the trained ML interatomic potentials to relax the structures. However, this would incur higher training cost and also additional compute cost to perform additional simulations for relaxations. On the other hand, ML models trained on unrelaxed structures can be seen as on-lattice models,29,65–67 which are widely used for thermodynamic and kinetic modeling thanks to their high efficiency with respect to off-lattice models or interatomic potentials. Therefore, from the cost-effective perspective, one interesting line of research may be to develop descriptor-based on-lattice models, since their accuracy is similar to neural networks, to study thermodynamics such as chemical order and phase diagram for HEMs.
V. Conclusion
In summary, we create a DFT dataset of formation energies for 84k alloys with up to 7 components and a diverse range of concentrations and chemical orders. We find a good in-distribution performance of ML models on the dataset, with a best MAE of 0.007 eV per atom. Furthermore, we systematically investigate the generalizability of ML models between different types of structures, revealing that models trained on simpler alloy systems can generalize well to more complex ones. In addition, we analyze the effects of dataset size, and highlight the performance degradation due to the unavailability of relaxed structures. We believe these results, with our publicly available datasets and ML models, can provide valuable insights for the first principles based modeling of HEMs.Data availability
The curated DFT dataset, including structures, energies, and various attributes (atomic magnetic moment and charge etc.) is publicly available on Zenodo at https://doi.org/10.5281/zenodo.10854500.Code availability
The code used for ML training and analysis is publicly available on GitHub at https://github.com/mathsphy/high-entropy-alloys-dataset-ML.Author contributions
K. L. conceived the project, performed the DFT calculations, dataset curation, ML training and analysis, and drafted the manuscript. J. H.-S. supervised the project. K. L., K. C., B. D., M. G., and J. H.-S. discussed the results. All authors reviewed and edited the manuscript, and contributed to the manuscript preparation.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research was undertaken thanks in part to funding provided to the University of Toronto's Acceleration Consortium from the Canada First Research Excellence Fund (Grant number: CFREF-2022-00042). The computations were made on the resources provided by the Calcul Quebec, Westgrid, and Compute Ontario consortia in the Digital Research Alliance of Canada (alliancecan.ca), and the Acceleration Consortium (acceleration.utoronto.ca) at the University of Toronto. We acknowledge partial funding provided by Natural Resources Canada's Office of Energy Research and Development (OERD). Certain commercial products or company names are identified here to describe our study adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the products or names identified are necessarily the best available for the purpose.References
- J.-W. Yeh and S.-J. Lin, Breakthrough applications of high-entropy materials, J. Mater. Res., 2018, 33, 3129 CrossRef CAS
.
- D. B. Miracle and O. N. Senkov, A critical review of high entropy alloys and related concepts, Acta Mater., 2017, 122, 448 CrossRef CAS
.
- E. P. George, D. Raabe and R. O. Ritchie, High-entropy alloys, Nat. Rev. Mater., 2019, 4, 515 CrossRef CAS
.
- Y. Ma, Y. Ma, Q. Wang, S. Schweidler, M. Botros, T. Fu, H. Hahn, T. Brezesinski and B. Breitung, High-entropy energy materials: challenges and new opportunities, Energy Environ. Sci., 2021, 14, 2883 RSC
.
- A. Amiri and R. Shahbazian-Yassar, Recent progress of high-entropy materials for energy storage and conversion, J. Mater. Chem. A, 2021, 9, 782 RSC
.
- Y. Sun and S. Dai, High-entropy materials for catalysis: A new frontier, Sci. Adv., 2021, 7, eabg1600 CrossRef CAS PubMed
.
- J. Rickman, G. Balasubramanian, C. Marvel, H. Chan and M.-T. Burton, Machine learning strategies for high-entropy alloys, J. Appl. Phys., 2020, 128, 221101 CrossRef CAS
.
- L. Qiao, Y. Liu and J. Zhu, A focused review on machine learning aided high-throughput methods in high entropy alloy, J. Alloys Compd., 2021, 877, 160295 CrossRef CAS
.
- Z. W. Chen, L. Chen, Z. Gariepy, X. Yao and C. V. Singh, High-throughput and machine-learning accelerated design of high entropy alloy catalysts, Trends Chem., 2022, 4, 577 CrossRef CAS
.
- R. Li, L. Xie, W. Y. Wang, P. K. Liaw and Y. Zhang, High-throughput calculations for high-entropy alloys: a brief review, Front. Mater., 2020, 7, 290 CrossRef
.
- W. Huang, P. Martin and H. L. Zhuang, Machine-learning phase prediction of high-entropy alloys, Acta Mater., 2019, 169, 225 CrossRef CAS
.
- K. Kaufmann and K. S. Vecchio, Searching for high entropy alloys: a machine learning approach, Acta Mater., 2020, 198, 178 CrossRef CAS
.
- Q. Zhou, F. Xu, C. Gao, D. Zhang, X. Shi, M.-F. Yuen and D. Zuo, Machine learning-assisted mechanical property prediction and descriptor-property correlation analysis of high-entropy ceramics, Ceram. Int., 2023, 49, 5760 CrossRef CAS
.
- S. Curtarolo, W. Setyawan, G. L. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang and O. Levy,
et al., Aflow: an automatic framework for high-throughput materials discovery, Comput. Mater. Sci., 2012, 58, 218 CrossRef CAS
.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder,
et al., Commentary: the materials project: a materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef
.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, Materials design and discovery with high-throughput density functional theory: the open quantum materials database (OQMD), JOM, 2013, 65, 1501 CrossRef CAS
.
- K. Choudhary, K. F. Garrity, A. C. Reid, B. DeCost, A. J. Biacchi, A. R. Hight Walker, Z. Trautt, J. Hattrick-Simpers, A. G. Kusne and A. Centrone,
et al., The joint automated repository for various integrated simulations (jarvis) for data-driven materials design, npj Comput. Mater., 2020, 6, 173 CrossRef
.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, Open Catalyst 2020 (OC20) Dataset and Community Challenges, ACS Catal., 2021, 11, 6059 CrossRef CAS
, 2010.09990..
- Y. Ikeda, B. Grabowski and F. Körmann, Ab initio phase stabilities and mechanical properties of multicomponent alloys: a comprehensive review for high entropy alloys and compositionally complex alloys, Mater. Charact., 2019, 147, 464 CrossRef CAS
.
- A. Zunger, S.-H. Wei, L. Ferreira and J. E. Bernard, Special quasirandom structures, Phys. Rev. Lett., 1990, 65, 353 CrossRef CAS PubMed
.
- A. Van de Walle, P. Tiwary, M. De Jong, D. Olmsted, M. Asta, A. Dick, D. Shin, Y. Wang, L.-Q. Chen and Z.-K. Liu, Efficient stochastic generation of special quasirandom structures, Calphad, 2013, 42, 13 CrossRef CAS
.
- J. Yang, P. Manganaris and A. Mannodi-Kanakkithodi, A high-throughput computational dataset of halide perovskite alloys, Digital Discovery, 2023, 2, 856 RSC
.
- K. Li and C.-C. Fu, Ground-state properties and lattice-vibration effects of disordered fe-ni systems for phase stability predictions, Phys. Rev. Mater., 2020, 4, 023606 CrossRef CAS
.
- J. Shen, S. D. Griesemer, A. Gopakumar, B. Baldassarri, J. E. Saal, M. Aykol, V. I. Hegde and C. Wolverton, Reflections on one million compounds in the open quantum materials database (oqmd), J. Phys.: Mater., 2022, 5, 031001 Search PubMed
.
- G. B. Bokas, W. Chen, A. Hilhorst, P. J. Jacques, S. Gorsse and G. Hautier, Unveiling the thermodynamic driving forces for high entropy alloys formation through big data ab initio analysis, Scr. Mater., 2021, 202, 114000 CrossRef CAS
.
- W. Chen, A. Hilhorst, G. Bokas, S. Gorsse, P. J. Jacques and G. Hautier, A map of single-phase high-entropy alloys, Nat. Commun., 2023, 14, 2856 CrossRef CAS
.
- P. Sarker, T. Harrington, C. Toher, C. Oses, M. Samiee, J.-P. Maria, D. W. Brenner, K. S. Vecchio and S. Curtarolo, High-entropy high-hardness metal carbides discovered by entropy descriptors, Nat. Commun., 2018, 9, 4980 CrossRef
.
- K. Kaufmann, D. Maryanovsky, W. M. Mellor, C. Zhu, A. S. Rosengarten, T. J. Harrington, C. Oses, C. Toher, S. Curtarolo and K. S. Vecchio, Discovery of high-entropy ceramics via machine learning, npj Comput. Mater., 2020, 6, 42 CrossRef
.
- Y. Lederer, C. Toher, K. S. Vecchio and S. Curtarolo, The search for high entropy alloys: a high-throughput ab-initio approach, Acta Mater., 2018, 159, 364 CrossRef CAS
.
- C. Jiang and B. P. Uberuaga, Efficient ab initio modeling of random multicomponent alloys, Phys. Rev. Lett., 2016, 116, 105501 CrossRef PubMed
.
- V. Sorkin, Z. Yu, S. Chen, T. L. Tan, Z. Aitken and Y. Zhang, A first-principles-based high fidelity, high throughput approach for the design of high entropy alloys, Sci. Rep., 2022, 12, 11894 CrossRef CAS PubMed
.
- G. Vazquez, P. Singh, D. Sauceda, R. Couperthwaite, N. Britt, K. Youssef, D. D. Johnson and R. Arróyave, Efficient machine-learning model for fast assessment of elastic properties of high-entropy alloys, Acta Mater., 2022, 232, 117924 CrossRef CAS
.
- J. Zhang, B. Xu, Y. Xiong, S. Ma, Z. Wang, Z. Wu and S. Zhao, Design high-entropy carbide ceramics from machine learning, npj Comput. Mater., 2022, 8, 5 CrossRef
.
- K. Li, B. DeCost, K. Choudhary, M. Greenwood and J. Hattrick-Simpers, A critical examination of robustness and generalizability of machine learning prediction of materials properties, npj Comput. Mater., 2023, 9, 55 CrossRef
.
- K. Li, D. Persaud, K. Choudhary, B. DeCost, M. Greenwood and J. Hattrick-Simpers, Exploiting redundancy in large materials datasets for efficient machine learning with less data, Nat. Commun., 2023, 14, 7283 CrossRef CAS PubMed
.
- K. T. Schütt, H. Glawe, F. Brockherde, A. Sanna, K.-R. Müller and E. K. Gross, How to represent crystal structures for machine learning: Towards fast prediction of electronic properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205118 CrossRef
.
- F. Faber, A. Lindmaa, O. A. Von Lilienfeld and R. Armiento, Crystal structure representations for machine learning models of formation energies, Int. J. Quantum Chem., 2015, 115, 1094 CrossRef CAS
.
- O. Isayev, C. Oses, C. Toher, E. Gossett, S. Curtarolo and A. Tropsha, Universal fragment descriptors for predicting properties of inorganic crystals, Nat. Commun., 2017, 8, 15679 CrossRef CAS PubMed
.
- L. Ward, R. Liu, A. Krishna, V. I. Hegde, A. Agrawal, A. Choudhary and C. Wolverton, Including crystal structure attributes in machine learning models of formation energies via voronoi tessellations, Phys. Rev. B, 2017, 96, 024104 CrossRef
.
- L. Ward, A. Dunn, A. Faghaninia, N. E. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom and M. Dylla,
et al., Matminer: An open source toolkit for materials data mining, Comput. Mater. Sci., 2018, 152, 60 CrossRef
.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python materials genomics (pymatgen): a robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314 CrossRef CAS
.
- K. Choudhary, B. DeCost, C. Chen, A. Jain, F. Tavazza, R. Cohn, C. W. Park, A. Choudhary, A. Agrawal and S. J. Billinge,
et al., Recent advances and applications of deep learning methods in materials science, npj Comput. Mater., 2022, 8, 59 CrossRef
.
- R. S. Kingsbury, A. S. Rosen, A. S. Gupta, J. M. Munro, S. P. Ong, A. Jain, S. Dwaraknath, M. K. Horton and K. A. Persson, A flexible and scalable scheme for mixing computed formation energies from different levels of theory, npj Comput. Mater., 2022, 8, 195 CrossRef
.
- V. Stevanović, S. Lany, X. Zhang and A. Zunger, Correcting density functional theory for accurate predictions of compound enthalpies of formation: Fitted elemental-phase reference energies, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115104 CrossRef
.
- C. J. Bartel, A. W. Weimer, S. Lany, C. B. Musgrave and A. M. Holder, The role of decomposition reactions in assessing first-principles predictions of solid stability, npj Comput. Mater., 2019, 5, 4 CrossRef
.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, The open quantum materials database (oqmd): assessing the accuracy of dft formation energies, npj Comput. Mater., 2015, 1, 1 Search PubMed
.
- C. J. Bartel, Review of computational approaches to predict the thermodynamic stability of inorganic solids, J. Mater. Sci., 2022, 57, 10475 CrossRef CAS
.
- S. D. Griesemer, Y. Xia and C. Wolverton, Accelerating the prediction of stable materials with machine learning, Nat. Comput. Sci., 2023, 3, 934 CrossRef PubMed
.
- S. Gong, S. Wang, T. Xie, W. H. Chae, R. Liu, Y. Shao-Horn and J. C. Grossman, Calibrating dft formation enthalpy calculations by multifidelity machine learning, JACS Au, 2022, 2, 1964 CrossRef CAS
.
- Y. Mao, H. Yang, Y. Sheng, J. Wang, R. Ouyang, C. Ye, J. Yang and W. Zhang, Prediction and classification of formation energies of binary compounds by machine learning: an approach without crystal structure information, ACS Omega, 2021, 6, 14533 CrossRef CAS
.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS
.
- M. Methfessel and A. T. Paxton, High-precision sampling for Brillouin-zone integration in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616 CrossRef CAS
.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef
.
- A. Van De Walle, M. Asta and G. Ceder, The alloy theoretic automated toolkit: A user guide, Calphad, 2002, 26, 539 CrossRef CAS
.
-
T. Chen and C. Guestrin, XGBoost, in Proc. 22nd ACM SIGKDD Int. Conf. Knowl. Discov. Data Min., ACM, New York, NY, USA, 2016, pp. 785–794 Search PubMed
.
- L. Breiman, Random forests, Mach. Learn., 2001, 45, 5 CrossRef
.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825 Search PubMed
.
- K. Choudhary and B. DeCost, Atomistic line graph neural network for improved materials property predictions, npj Comput. Mater., 2021, 7, 185 CrossRef
.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, A general-purpose machine learning framework for predicting properties of inorganic materials, npj Comput. Mater., 2016, 2, 1 CrossRef
, 1606.09551..
- K. Choudhary, D. Wines, K. Li, K. F. Garrity, V. Gupta, A. H. Romero, J. T. Krogel, K. Saritas, A. Fuhr, P. Ganesh, et al., Large scale benchmark of materials design methods, arXiv, 2023, preprint, arXiv:2306.11688, DOI:10.48550/arXiv.2306.11688.
- L. N. Smith and N. Topin, Super-convergence: Very fast training of neural networks using large learning rates, Artificial intelligence and machine learning for multi-domain operations applications, SPIE, 2019, vol. 11006, pp. 369–386 Search PubMed.
- J. M. Sanchez, F. Ducastelle and D. Gratias, Generalized cluster description of multicomponent systems, Phys. A, 1984, 128, 334 CrossRef
.
- Y. Wang, K. Li, F. Soisson and C. S. Becquart, Combining dft and calphad for the development of on-lattice interaction models: The case of fe-ni system, Phys. Rev. Mater., 2020, 4, 113801 CrossRef CAS
.
- K. Li, C.-C. Fu, M. Nastar, F. Soisson and M. Y. Lavrentiev, Magnetochemical effects on phase stability and vacancy formation in fcc fe-ni alloys, Phys. Rev. B, 2022, 106, 024106 CrossRef CAS
.
- J. Hattrick-Simpers, K. Li, M. Greenwood, R. Black, J. Witt, M. Kozdras, X. Pang and O. Ozcan, Designing durable, sustainable, high-performance materials for clean energy infrastructure, Cell Rep. Phys. Sci., 2023, 4, 101200 CrossRef CAS
.
- J. M. Cowley, An Approximate Theory of Order in Alloys, Phys. Rev., 1950, 77, 669 CrossRef CAS
.
- S. Gong, K. Yan, T. Xie, Y. Shao-Horn, R. Gomez-Bombarelli, S. Ji and J. C. Grossman, Examining graph neural networks for crystal structures: limitations and opportunities for capturing periodicity, Sci. Adv., 2023, 9(45), eadi3245 CrossRef PubMed
.
- A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, Benchmarking materials property prediction methods: the Matbench test set and Automatminer reference algorithm, npj Comput. Mater., 2020, 6, 1 CrossRef
.
-
C. Zhang and M. C. Gao, Calphad modeling of high-entropy alloys, High-Entropy Alloys: Fundamentals and Applications, 2016, p. 399 Search PubMed
.
- H.-L. Chen, H. Mao and Q. Chen, Database development and calphad calculations for high entropy alloys: challenges, strategies, and tips, Mater. Chem. Phys., 2018, 210, 279 CrossRef CAS
.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Scaling deep learning for materials discovery, Nature, 2023, 1, 80 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta00982g |
| This journal is © The Royal Society of Chemistry 2024 |