Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Impact of Ni(II) coordinatively unsaturated sites and coordinated water molecules on SO2 adsorption by a MOF with octanuclear metal clusters†
Juan L.
Obeso‡
 ab,
Karuppasamy
Gopalsamy‡
c,
Mohammad
Wahiduzzaman‡
c,
Eva
Martínez-Ahumada
b,
Dong
Fan
c,
Hugo A.
Lara-García
ab,
Karuppasamy
Gopalsamy‡
c,
Mohammad
Wahiduzzaman‡
c,
Eva
Martínez-Ahumada
b,
Dong
Fan
c,
Hugo A.
Lara-García
 d,
Francisco J.
Carmona
e,
Guillaume
Maurin
d,
Francisco J.
Carmona
e,
Guillaume
Maurin
 *c,
Ilich A.
Ibarra
*c,
Ilich A.
Ibarra
 *bf and
Jorge A. R.
Navarro
*bf and
Jorge A. R.
Navarro
 *e
*e
aInstituto Politécnico Nacional, Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada, LNAgua, Legaria 694, Col. Irrigación, Miguel Hidalgo, 11500, CDMX, Mexico
bLaboratorio de Fisicoquímica y Reactividad de Superficies (LaFReS), Instituto de Investigaciones en Materiales, Universidad Nacional Autónoma de México, Circuito Exterior s/n, CU, Coyoacán, 04510, Ciudad de México, Mexico. E-mail: argel@unam.mx
cICGM, Univ. Montpellier, CNRS, ENSCM, Montpellier, 34293, France. E-mail: guillaume.Maurin1@umontpellier.fr
dInstituto de Física, Universidad Nacional Autónoma de México, Circuito Exterior s/n, CU, Coyoacán, 04510, Ciudad de México, Mexico
eDepartamento de Química Inorgánica, Universidad de Granada, Av. Fuentenueva S/N, Granada, 18071 Spain. E-mail: jarn@ugr.es
fOn Sabbatical as “Catedra Dr Douglas Hugh Everett” at Departamento de Química, Universidad Autónoma Metropolitana-Iztapalapa, San Rafael Atlixco 186, Col. Leyes de Reforma 1ra Seccion, Iztapalapa, C.P. 09310, Ciudad de México, Mexico
First published on 7th March 2024
Abstract
A Ni-based pyrazolate MOF (NiBDP) is studied for SO2 adsorption under static conditions, demonstrating a high SO2 uptake of 8.48 mmol g−1 at 298 K and 1 bar while maintaining a high chemical stability. The influence of Ni(II) coordinatively unsaturated metal sites and coordinated water on the SO2 adsorption performance of this MOF is investigated by using a combination of experimental techniques, including FTIR and in situ DRIFTS measurements, along with Density Functional Theory calculations. The pore-filling of the SO2 adsorbates within the material, at the molecular level, is further unravelled through grand Canonical Monte Carlo simulations employing a newly DFT-derived accurate set of force field parameters.
Introduction
The standard families of porous materials, e.g., activated carbons, zeolites, and mesoporous silica, have been extensively studied for the adsorption of small molecules within their porous cavities for diverse applications.1,2 More recently, metal–organic frameworks (MOFs), constructed by metal-containing nodes and organic linkers,3 which can propagate in one to three dimensions, have been shown to represent a milestone in the capture of greenhouse (CH4 and CO2)4–11 and toxic gases (NH3, NOx and SO2).12,13 The diversity of metal ions and organic ligands that can be used for the construction of MOFs facilitates their architecture design and, hence, the modulation of chemical features in the pore walls (e.g., functionalization) and of pore dimension/shape to optimize the interactions with a given guest molecule.14 Therefore, a selection of MOFs has emerged as promising candidates in the field of material science for the adsorption of toxic and corrosive gases.15 Typically, SO2 has gained a lot of interest since it is the main precursor of acid rain, and the hazardous effects of SO2 on the environment and on human health are a huge concern. Thus, SO2 capture by MOFs has been investigated since 2008, when Yaghi et al.,16 reported the SO2 adsorption by several MOFs with diverse chemical and structural features. After two decades of worldwide efforts, certain chemical characteristics have been recognized to render MOF materials not only resistant to SO2 exposure but also with attractive capture performance.17–19 These included the use of (i) high valent-metal ions, such as Zr4+, Al3+, In3+, and Sc3+ with carboxylate ligands; (ii) robust metal clusters with strong metal–ligand bonds, for example, the use of pyrazolate or imidazolate ligands and late transition M2+ ions; and (iii) the inclusion of coordinately unsaturated metal sites (CUS) or functional groups (X–H), capable of interacting with SO2 by coordination bonds,20 hydrogen bonds,21 and other supramolecular interactions.22Nickel(II)-based MOFs are a priori attractive sorbents owing to the good abundance of this metal and their usually high thermal and chemical stabilities. Moreover, from a chemical point of view, Ni-based compounds are known to exhibit interesting properties such as electrocatalytic capabilities,23 magnetic properties,24 energy storage,25 and detection.26 Although some M2+-based MOFs are considered unstable to SO2 adsorption, the combination of polyazolate ligands and divalent metals increases the MOF structural stability over alkaline or acidic environments.27 MOFs formed by strong Ni2+–N(azolate) bonds provide greater chemical and thermal stability compared to their carboxylate analogues. According to Pearson's hard–soft acid–base principle, a highly chemically stable MOF material can be constructed using azolate ligands with low-valent transition metals. The pKa value for the deprotonation of N–H bonds shows high structure robustness.28 These characteristics make attractive the study of Ni2+ pyrazolate-based MOFs for the adsorption of corrosive gases.29
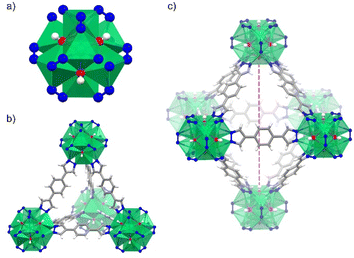
Herein, we investigate a Ni(II)-based MOF, [Ni8(OH)4(H2O)2(BDP)6] termed NiBDP (H2BDP = 1,4-bis(pyrazol-4-yl)benzene), for SO2 capture. This material is based on octanuclear Ni(II) hydroxo clusters [Ni8(OH)4(H2O)2], linked by BDP to form [Ni8(OH)4(H2O)2(BDP)6] cluster (Fig. 1a). NiBDP material, along with an isoreticular series of MOFs, has been studied earlier for dynamic breakthrough SO2 adsorption.30 Results showed an SO2 uptake of 2.02 mmol g−1 at 303 K, and cycling experiments revealed a reversible physisorption process.
Although this Ni(II)-based MOF was previously investigated under SO2 (dynamic breakthrough), we decided to explore its SO2 adsorption capacities under static condition at room temperature and 1 bar, in order to gain a comprehensive understanding on the SO2 adsorption mechanism. Also, neither experimental exploration in thermodynamic conditions nor a complete understanding of the microscopic mechanism in play have been reported so far in the literature. Thus, we have embarked on the task of coupling advanced experimental and theoretical approaches to revisit the SO2 adsorption performance of NiBDP in static mode and gain a full picture of the adsorption mechanism at the molecular level. A special attention has been also paid to assess computationally the impact of coordinated water on the SO2 adsorption isotherms by considering different NiBDP-nH2O structures (where n = 0, 1, 2, correspond to distinct structure models possessing 100%, 50%, and zero CUS sites per metal node) that mimic scenarios of full, partial or non-evacuation of the CUS sites during the experimental activation of the sample.
Experimental
Synthesis of NiBDP
NiBDP was synthesized according to the reported procedure.31 In a typical synthesis, 63.1 mg (0.3 mmol) of 4,4′-benzene-1,4-diylbis(1H-pyrazole) (H2BDP) were dissolved in 16 mL of DMF, and 99.2 mg (0.4 mmol) of Ni(AcO)2·4H2O were dissolved in 4 mL of H2O. The two limpid solutions were mixed and refluxed for 6 h under stirring. The light green solid obtained was filtered and washed with EtOH and Et2O, yielding 89 mg (66%). IR (KBr) 3433(br), 1655(vs.), 1574(s), 1390(m), 1358(m), 1250(s), 1182(w), 1124(w), 1057(s), 958(s), 845(m), 658(w), 540(w), 505(w) cm−1.Characterization methods
Detailed information on the instrumental techniques is available in the ESI: Section S1.†SO2 sorption measurements
SO2 adsorption–desorption isotherms were measured in a Dynamic Gravimetric Gas/Vapour Sorption Analyser, DVS vacuum (Surface Measurement Systems Ltd) with a static method. The samples were activated at 423 K under vacuum (1 × 10−6 bar) for 5 hours. SO2 adsorption isotherm was carried out at 298 K up to 1 bar.DFT geometry optimization
Periodic DFT calculations were conducted to optimize the atomic position and cell volume of both the empty NiBDP-nH2O structures (where n = 0, 1, 2, correspond to different structure models possessing 100%, 50%, and zero CUS sites per metal node) and the associated guest-loaded structures with SO2 adsorbed onto them using Vienna Ab initio Simulation Package (VASP).32 The core and valence electrons of the interacting elements were treated with projector-augmented-wave (PAW) potentials and plane-wave basis sets.33 The general gradient approximation (GGA) to the exchange–correlation functional according to Perdew–Burke–Ernzerhof (PBE)34 was used along with a combination of Grimme's empirical dispersion correction with Becke–Johnson damping (DFT-D3/BJ).35 To account for the electronic correlation of d electrons on-site, Hubbard U correction was considered for Ni(II) atoms, with the benchmark U value of 6.4 eV previously validated on different properties of Ni(II) oxide systems as well as Ni(II) MOFs.36–38Γ point meshes for sampling the Brillouin zone were used along a plane-wave kinetic energy cutoff of 520 eV. The energy and ionic force convergence criteria were set to 1 × 10−6 eV and 0.02 eV Å−1, respectively. Consequently, the atomic partial charges of the MOF atoms of the DFT-optimized empty MOF structures were derived by employing the density-derived electrostatic and chemical (DDEC) charge partitioning scheme as implemented in the chargemol program.39,40 These atomic partial charges are provided in Table S1 in the ESI.† The textural properties of NiBDP-nH2O (n = 0, 1, 2) MOFs, including pore volume (PV), surface area (SA), largest cavity diameter (LCD) and pore limiting diameter (PLD), were calculated by using Zeo++ software (see details for the calculations in the ESI†),41 and tabulated in Table S2.†Force field parameterization
The consideration of generic force field for MOF frameworks combined with force field models for the guest molecules is known to dramatically fail to describe specific interactions between coordinative unsaturated MOFs with any guest molecules.42–46 Therefore, such MOF- CUS sites/guest molecule interactions require a specific FF parameterization based on first-principle quantum calculations. To do so, a 100% CUS containing model of the NiBDP MOF (i.e., NiBDP-0H2O) was first considered and an approaching path consisting of 10 different configurations associated to different SO2–Ni CUS (NiBDP-0H2O) separating distances were constructed while maintaining the same orientation as DFT-optimized minimum energy structure (Fig. S9†). Subsequently, single point energy calculations were performed to deduce the corresponding interaction energies for a SO2 molecule within the NiBDP-0H2O pore using the energy expression: Eint = ENiBDP-0H2O+SO2 − (ENiBDP-0H2O + ESO2), where, ENiBDP-0H2O+SO2 corresponds to the single point energies of the SO2 loaded NiBDP-0H2O adsorption configurations along the interacting path, while ENiBDP-0H2O and ESO2 correspond to the energy associated to an empty NiBDP-0H2O MOF and an isolated SO2 molecule, respectively. The resulting interaction energy curve was then fitted to an analytical function combining van der Waals (vdW) and coulombic terms. Here, non-bonded interactions between SO2 and NiBDP-0H2O MOF atoms other than Ni(II) sites were modeled with standard Lennard-Jones (LJ) 12-6 potential while a Morse potential was employed to describe the interactions between SO2 and Ni(II) atoms. The LJ parameters (ε and σ) for the MOF atoms were adopted from the universal force field (UFF),47 whereas the SO2 molecule was represented by the three-site LJ charged model reported by Ketko et al.,48 (Tables S3–S5†). LJ cross-terms were then calculated using the Lorentz–Berthelot combination rules. The Ewald summation technique49 was employed to compute the long-range coulombic contributions, in which, the atomic partial charges of the MOF are determined using the DDEC charge partitioning scheme as mentioned above, while the charges for SO2 are obtained from the potential model of Ketko et al.48 Finally, the Morse potential parameters, D, α, and r0 associated with the Ni(II)–O(SO2)– and Ni(II)–S(SO2) specific interactions were determined using the General Utility Lattice Program (GULP)50 by minimizing the energy differences with respect to the DFT counterpart. The corresponding fitting curve and the parameters are available in the ESI.†Monte Carlo simulations
The SO2 adsorption isotherms for all three NiBDP-nH2O (n = 0, 1, 2) structures were calculated through the GCMC simulations implementing the force field discussed above using the Complex Adsorption and Diffusion Simulation Suite (CADSS) of the program.42 Nonetheless, for the NiBDP-2H2O structure, the SO2 adsorption isotherm was computed by using generic UFF parameters for all framework atoms, as the system does not contains any CUS sites. We employed a simulation box comprising eight-unit cells (2 × 2 × 2) of the MOFs. The atomic positions of the MOFs' skeletons were held fixed during the adsorption, and Monte Carlo trial moves for the guest molecules. The host–guest nonbonded interactions were computed in real space using a cutoff of 12.0 Å. The long-range electrostatic interactions were calculated using the Ewald summation technique49 with an accuracy of 1 × 10−6. For each pressure point, 1 × 107 and 2 × 107 Monte Carlo steps including insertion/deletion, translation and rotational moves, were considered for equilibration and production, respectively. The Peng–Robinson equation of state was used to determine the gas-phase fugacity for SO2 molecules.51 The overall adsorption isotherms were obtained by running GCMC simulations for different fugacities ranging from 10−4 to 1 bar. Additionally, the enthalpy of SO2 adsorption at infinite dilution was computed employing Widom's test particle insertion method.52Results and discussion
Characterization of NiBDP
NiBDP MOF was synthesized according to the reported procedure.31 This structure crystallizes in the face cubic centered (fcu) topology with the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. Each Ni(II) ion is bonded to three N atoms from different organic linkers, and three of the six μ4-O observed in the octanuclear cluster (Fig. 1a). It is important to note that two of the six oxygen atoms belong to coordinated water molecules rather than hydroxo ligands.53 The structure contains two types of cages: an octahedral cage (diameter of ∼16 Å) connecting to eight tetrahedral cages (diameter of ∼9 Å) accessible via triangular windows (diameter of ∼6 Å), (Fig. 1b, c and S1†). In the octahedral cage, the OH groups point toward the centre of the pore, which can favor interactions with SO2 in addition to the Ni(II) sites, as it was demonstrated for other materials, such as the MFM-300 family.54 The crystalline structure was confirmed by PXRD (Fig. S2†). Based on N2 sorption measurements at 77 K (Fig. S3†), the activated NiBDP shows a BET surface area of 1220 m2 g−1, which is lower than the previously reported (1730 m2 g−1).55 The corresponding theoretically calculated surface areas of NiBDP_0H2O and NiBDP_2H2O are 2650 m2 g−1 and 2480 m2 g−1, respectively, suggesting that the CUS sites of the investigated sample are not fully evacuated. In addition, elemental analysis (EA) of NiBDP (Ni8(OH)4(H2O)2(BDP)6](H2O)2(DMF)10) was conducted. Anal. calc. for NiBDP (2589.90 g mol−1) C, 47.3; H, 5.06; N, 18.4; Ni, 18.1, found C, 46.7; H, 5.10; N, 18.2; Ni, 18.8. Nickel content was determined on the basis of TGA (Fig. S4†). Also, electronic spectra (Fig. S5†) characterization is indicative of the presence of the characteristic d–d transition bands of Ni(II) in a poorly distorted Oh environment (3T2g(F) ← 3A2g(F), 10
m space group. Each Ni(II) ion is bonded to three N atoms from different organic linkers, and three of the six μ4-O observed in the octanuclear cluster (Fig. 1a). It is important to note that two of the six oxygen atoms belong to coordinated water molecules rather than hydroxo ligands.53 The structure contains two types of cages: an octahedral cage (diameter of ∼16 Å) connecting to eight tetrahedral cages (diameter of ∼9 Å) accessible via triangular windows (diameter of ∼6 Å), (Fig. 1b, c and S1†). In the octahedral cage, the OH groups point toward the centre of the pore, which can favor interactions with SO2 in addition to the Ni(II) sites, as it was demonstrated for other materials, such as the MFM-300 family.54 The crystalline structure was confirmed by PXRD (Fig. S2†). Based on N2 sorption measurements at 77 K (Fig. S3†), the activated NiBDP shows a BET surface area of 1220 m2 g−1, which is lower than the previously reported (1730 m2 g−1).55 The corresponding theoretically calculated surface areas of NiBDP_0H2O and NiBDP_2H2O are 2650 m2 g−1 and 2480 m2 g−1, respectively, suggesting that the CUS sites of the investigated sample are not fully evacuated. In addition, elemental analysis (EA) of NiBDP (Ni8(OH)4(H2O)2(BDP)6](H2O)2(DMF)10) was conducted. Anal. calc. for NiBDP (2589.90 g mol−1) C, 47.3; H, 5.06; N, 18.4; Ni, 18.1, found C, 46.7; H, 5.10; N, 18.2; Ni, 18.8. Nickel content was determined on the basis of TGA (Fig. S4†). Also, electronic spectra (Fig. S5†) characterization is indicative of the presence of the characteristic d–d transition bands of Ni(II) in a poorly distorted Oh environment (3T2g(F) ← 3A2g(F), 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 cm−1; 3T1g(F) ← 3A2g(F), 15
350 cm−1; 3T1g(F) ← 3A2g(F), 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870 cm−1; 3T1g(P) ← 3A2g(F), 25
870 cm−1; 3T1g(P) ← 3A2g(F), 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1).
800 cm−1).
SO2 sorption in NiBDP
Previously, the SO2 capture in NiBDP was reported using breakthrough experiments for an N2/SO2 mixture. However, under these conditions, a relatively low SO2 concentration (PSO2 = 0.025 bar) was considered. NiBDP showed a total uptake of 2.02 mmol g−1 at 303 K. The SO2 affinity was attributed to the Lewis acid–base interactions with crystal defects.30 However, equilibrium adsorption–desorption isotherms are more appropriate to gain deep insights into the adsorption capacity, adsorption mechanism and to understand the adsorption behavior of certain gases within a porous material.56 Thus, the SO2 adsorption–desorption isotherms were investigated for NiBDP. The corresponding SO2 sorption isotherm is shown in Fig. 2. A steep profile is observed in the adsorption isotherm from 0 to 0.025 bar. At this stage, SO2 adsorption reaches a value of 1.85 mmol g−1 and remains almost constant up to 0.45 bar (1.89 mmol g−1). This SO2 uptake is similar to that reported so far for other MOFs like MFM-133 (1.2 mmol g−1),57 MFM-422 (1.8 mmol g−1),57 SIFSIX-3-Zn (1.89 mmol g−1),58 and ELM-12 (1.95 mmol g−1)59 at 0.1 bar implying that NiBDP can be used as an alternative SO2 adsorbent at low gas pressures. Interestingly, a sharp jump in the SO2 adsorption capacity from 1.89 mmol g−1 up to 7.22 mmol g−1 is observed at 0.45 bar, which ultimately reaches a total SO2 uptake of 8.48 mmol g−1 at 1 bar. The latter value is comparable to a variety of MOF materials such as UiO-66-Cu,57 MFM-300(In)60 and MIL-53(Al)-TDC61 with a reported SO2 uptake of 8.2 mmol g−1, 8.28 mmol g−1, and 8.9 mmol g−1, respectively, under similar working conditions (1 bar and 298 K). Considering the experimental BET surface area of NiBDP (1220 m2 g−1), the SO2 uptake of 8.48 mmol g−1 aligns well with other microporous MOFs with similar surface area, for instance, UiO-66, possessing the same fcu topology and a BET surface area of 1221 m2 g−1, can adsorb 8.6 mmol g−1 of SO2 at 298 K and 1 bar.57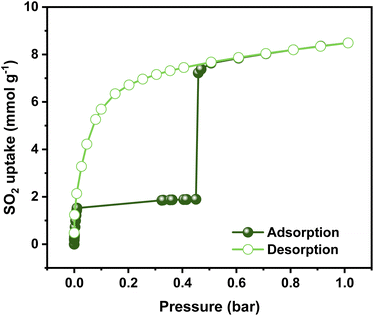 | ||
| Fig. 2 Experimental SO2 adsorption–desorption isotherm of an activated NiBDP sample (filled green circles = adsorption; open green circles = desorption) at 298 K up to 1 bar. | ||
Interestingly, the adsorption isotherm profile is unusual for a well-defined microporous MOF. In the low-pressure region, a rapid adsorption profile is defined, which can be related to a high interaction between the Ni2+ CUS sites and the SO2 molecule, which can be postulated as a possible main adsorption site for NiBDP and gives rise to adsorbate seeding in the pore structure.61 Then, a subsequent almost horizontal plateau is observed, which can be associated with the presence of weaker interaction sites such as water molecules and hydroxide groups coordinated to the Ni2+ sites. Later, the sudden step at 0.45 bar followed by a linear adsorption (SO2 saturation up to 1 bar) should be related to an adsorbate clustering, giving rise to pore filling. The observed seeding and clustering adsorption behavior can be related to the water adsorption mechanism unraveled for the MOF-303 system.62
Finally, the retention of NiBDP crystallinity after SO2 adsorption was corroborated by PXRD analysis (Fig. S2†), demonstrating that the inclusion of polyazolate-containing ligands and borderline soft acid Ni2+ in MOFs improves their structural stability against corrosive gases.63
Furthermore, the isosteric enthalpy of adsorption (ΔH) for SO2 adsorption was calculated at low coverage using the virial method (Fig. S6†).64 The calculated value at low SO2 loading (<0.03 bar) is −41.2 kJ mol−1, which is in good agreement with the value reported in earlier (−40.1 kJ mol−1).30 This relatively high value can be associated with moderately strong SO2 interaction with NiBDP. Typically, a MOF material with CUS sites usually shows a high ΔH value (−80/−90 kJ mol−1) due to the strong coordination between the metal and the SO2 molecule.26 The lower value obtained here can be related to a decrease in the availability of Ni2+ CUS sites due to the presence of coordinated water.
FTIR and DRIFTS analysis in NiBDP
FTIR experiments were carried out on a NiBDP sample before and after exposure to SO2 gas and moisture traces to confirm the stability (Fig. S7†). The FTIR spectra of NiBDP show the characteristic bands for a pyrazolate MOF material. The bands related to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C
O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C are associated with the peaks at 1649 and 1574 cm−1, respectively.65 The bands at 1410 and 1385 cm−1 are related to C
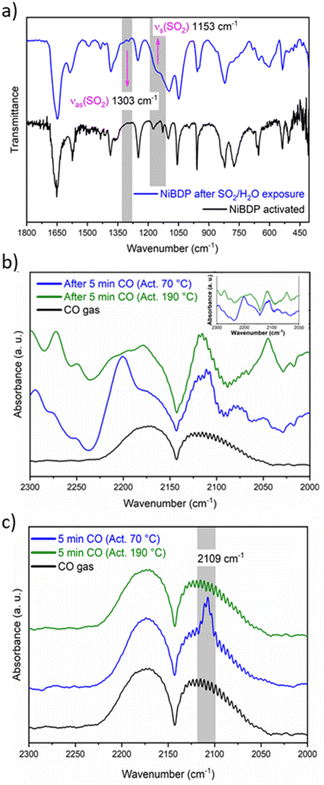
C are associated with the peaks at 1649 and 1574 cm−1, respectively.65 The bands at 1410 and 1385 cm−1 are related to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N. The bands at 1240 and 510 cm−1 are assigned to N–N bonds in the organic linker and the coordination bonds between Ni and N, respectively.66 Also, after SO2 adsorption show different bands from the region 1800–450 cm−1 (Fig. 3a). Two principal SO2 bands at 1153 cm−1 and 1303 cm−1 are observed, that are related to asymmetric and symmetric stretching modes of SO2 molecules within the pores. This type of interaction agrees with SO2 physisorption on Ni(BDC)(TED)0.5 with bands at 1144 and 1326 cm−1.67 Finally, the formation of hydrolyzed species of SO2 (i.e., SO32− or HSO32−) due to the presence of water is discarded due to the lack of characteristic IR bands for these ions.
N. The bands at 1240 and 510 cm−1 are assigned to N–N bonds in the organic linker and the coordination bonds between Ni and N, respectively.66 Also, after SO2 adsorption show different bands from the region 1800–450 cm−1 (Fig. 3a). Two principal SO2 bands at 1153 cm−1 and 1303 cm−1 are observed, that are related to asymmetric and symmetric stretching modes of SO2 molecules within the pores. This type of interaction agrees with SO2 physisorption on Ni(BDC)(TED)0.5 with bands at 1144 and 1326 cm−1.67 Finally, the formation of hydrolyzed species of SO2 (i.e., SO32− or HSO32−) due to the presence of water is discarded due to the lack of characteristic IR bands for these ions.
In addition, in situ DRIFTS measurements were conducted using CO as a probe molecule. This technique is a powerful tool to characterise acid/base sites for different porous materials, including MOFs.68 Even though the chemical nature of CO is different to SO2, this study is useful to gain insight into the possible adsorption sites for the guest molecules, as previously reported69 in particular to make the distinction between the interactions with Ni2+ CUS sites or the coordinated water molecules. Herein, the CO adsorption was studied by DRIFTS in situ analysis at 298 K after sample activation at two different temperatures, 70 and 190 °C under a He atmosphere.
The IR spectra of the activated sample are shown in Fig. S8.† When the sample was activated at 70 °C, broadband was observed between 3450 and 3200 cm−1. On the other hand, when the sample was activated at 190 °C, this band partially decreased in intensity. This band is associated with water molecules that are not fully desorbed from the Ni2+ centers. Fig. 3b shows the spectra after 5 min of a continuous CO flux. The CO gas spectrum is composed of two asymmetric peaks centered at 2173 and 2113 cm−1. When the CO is absorbed by the MOF, these two peaks are also observed, but the shape changes. The principal difference between the samples activated at 70 °C and 190 °C seems to be a peak depicted at 2200 cm−1. However, compared to the blank spectra (Fig. 3b, inset), it is observed that this peak belongs to the sample.
To analyze the difference in CO adsorption between the two activation methods, a subtraction of the spectra before and after the admittance of CO was carried out. Fig. 3c shows the subtracted spectra. It is evident that a peak appears at 2109 cm−1 when the sample is activated at 70 °C. This peak was already assigned to the adsorption of CO over metallic Ni.70 Therefore, the DRIFT analysis confirms that both Ni2+ CUS sites and coordinated water can interact with the guest molecules in activated NiBDP sample.
SO2 adsorption simulations
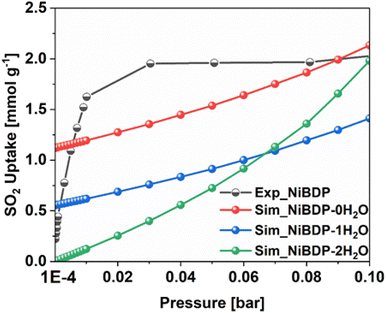
To further gain insights into the effect of Ni2+ CUS sites and coordinated water molecules in the SO2 adsorption, the adsorption of SO2 in NiBDP with and without evacuated Ni(II) CUS sites were systematically studied through GCMC simulations to fully understand the resulting adsorption behavior. As a starting point, we computed the SO2 single component adsorption isotherm for NiBDP-2H2O MOF at 298 K, covering a pressure range from 1 × 10−4 to 1 bar, and by using the generic UFF potential parameters as the system does not contain CUS sites. As illustrated in Fig. 4, our GCMC simulations result in an SO2 uptake of 15.2 mmol g−1 for this NiBDP-2H2O structure at 1 bar, which exceeds the experimentally determined maximum uptake of 8.48 mmol g−1. This deviation is expected due to the difference in the experimental BET surface area (1220 m2 g−1) and theoretical N2 surface area (NiBDP_0H2O and NiBDP_2H2O of 2650 m2 g−1 and 2484 m2 g−1, respectively).This discrepancy further underscores the ambiguity about the proper activation of CUS-containing MOFs, where the number of weakly coordinated water molecules removed from the framework and the creation of CUS sites can vary significantly, influenced by specific experimental conditions and activation procedures. CUS sites are considered the most attractive and predominant adsorption sites for all types of approaching guest molecules, especially under very low-pressure conditions. To further assess the influence of CUS sites present within the NiBDP framework on its SO2 uptake performance, we further considered two model systems, namely NiBDP-1H2O (with 50% CUS sites, i.e., one H2O per metal node) and NiBDP-0H2O (with 100% CUS sites, no H2O on the metal nodes). In the literature, it has been widely debated that generic force fields such as UFF47 and DREIDING71 are not capable of accurately predicting the strong host–guest interactions in MOFs containing CUS sites.
Therefore, in the current study, we derived a specific set of Morse type potential parameters through periodic DFT calculations to accurately assess the strength of the pair-wise SO2–Ni(II) CUS sites interactions using the 100% CUS containing NiBDP-0H2O model (see parametrization details in the experimental section). Notably, DFT determined minimum energy geometry of SO2 adsorption configuration in NiBDP-0H2O framework reveals that an SO2 molecule interacts with four Ni(II) open metal sites through an oxygen atom, with characteristic separation distances ranging from 2.27 to 2.49 Å (Fig. S10†), accompanied by a DFT-derived binding energy of −118.6 kJ mol−1. As also depicted in Fig. S10,† the second oxygen atom of the SO2 molecule was found to be oriented toward the nitrogen atom of the MOF framework, maintaining a separation distance of 2.93 Å.
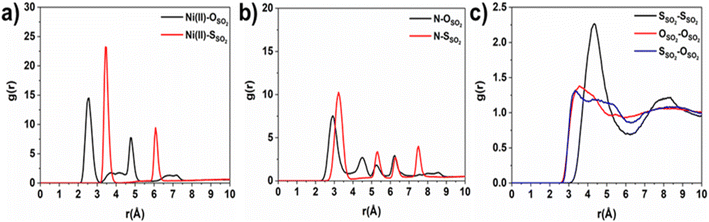
Consequently, GCMC simulations performed utilizing our newly DFT-derived SO2/Ni(II) force fields effectively reproduce the characteristic SO2–Ni(II) interacting distances (see Fig. 5a) observed in the DFT equilibrium geometry as demonstrated in the corresponding radial distribution function (RDF) plots calculated under low-pressure conditions (Fig. 6a, S11 and S12†). The steep simulated uptake of SO2 in NiBDP-0H2O at the very initial stage of adsorption (Fig. 4) corresponds to the initial binding of each Ni(II) site by 1SO2 molecule as illustrated in Fig. 5a with a characteristic interacting Ni–O(SO2) distance of 2.5 Å (as shown by the RDF plotted in Fig. 6a). Fig. 6b evidence an additional interaction between the second oxygen of SO2 with framework nitrogen atoms (Fig. S10†), the corresponding calculated RDFs between N–O(SO2) and N–S(SO2) showing peaks at 2.9 Å and 3.2 Å, respectively. This dual-site adsorption mode is probably the origin of the overestimation of the experimental adsorption uptake in the very low domain of pressure.
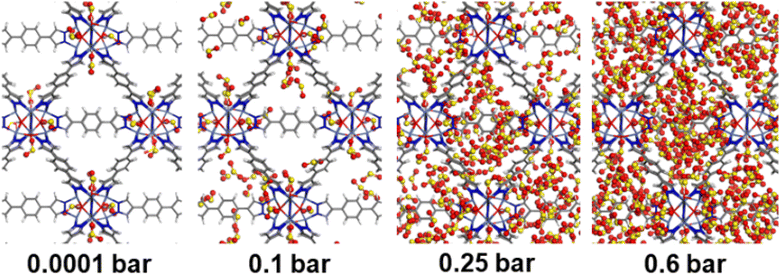
Second, Fig. 5 illustrates that at a moderate pressure range, SO2 molecules predominantly populate the region in the vicinity of the organic ligands, giving rise to an adsorbate clustering effect. Finally, at higher pressures, SO2 molecules further cluster giving rise to the filling of the entire pore volume of the NiBDP structure. This behavior justifies the unusual step shape of the SO2 isotherm. The overall adsorption behavior of NiBDP-1H2O and NiBDP-2H2O is illustrated in Fig. S13 and S14,† respectively. Fig. 6c displays the RDF for SO2/SO2 interaction in NiBDP-0H2O at 298 K. The first characteristic peak was observed at 3.3 Å between S(SO2)–O(SO2), and the second characteristic peak was observed between O(SO2)–O(SO2) at 3.6 Å. These contacts are followed by S(SO2)–S(SO2) at 4.4 Å. RDF analysis of SO2–SO2 interactions pointed out that SO2 molecules are distributed well around the NiBDP-0H2O pore volume.
Furthermore, the enthalpy of adsorption calculated at very low coverage SO2 adsorption is found to be −113.0 kJ mol−1 in excellent agreement with the DFT calculated binding energy. These attributes provide a clear indication of achieving an accurate adsorption isotherm at low pressure using this newly derived force field. Indeed, as shown in Fig. 4, the GCMC calculations effectively reproduce the shape of the experimental SO2 adsorption isotherm at low pressure (1 × 10−4 bar). NiBDP-2H2O shows a distinct SO2 adsorption isotherm profile at low pressure associated with a simulated adsorption enthalpy of −45 kJ. mol−1, more in line with the experimental data that suggests that the activated sample still contains a large concentration of coordinated water. As expected, NiBDP-1H2O is in-between.
A deeper analysis of these simulated isotherms at very low-pressure regions (1 × 10−4 to 0.1 bar) unravels the SO2 adsorption mechanism in all NiBDP-nH2O (n = 0, 1, 2) systems. However, depending on the availability of CUS sites in NiBDP frameworks, the amount of SO2 uptake varies, with NiBDP-2H2O, NiBDP-1H2O and NiBDP-0H2O showing 0.00 mmol g−1, 0.55 mmol g−1 and 1.12 mmol g−1 at 1 × 10−4 bar, respectively. This highlights that the presence of CUS sites in the NiBDP framework enhances SO2 uptake at a very low-pressure domain. Nevertheless, for all three NiBDP MOFs, our GCMC-predicted SO2 isotherms exceed the experimental results above 0.2 bar, which may be attributed to differences in the experimentally and theoretically calculated BET surface area (see above).
Conclusions
In summary, a Ni(II)-based pyrazolate MOF, NiBDP, has been investigated for SO2 adsorption under static conditions. This material exhibits exceptional chemical stability and a maximum SO2 adsorption capacity of 8.48 mmol g−1 at 298 K and 1 bar and an unusual step isotherm. Molecular simulations reveal that the SO2 uptake of this material strongly depends on the concentration of Ni CUS sites and the presence of coordinated water molecules with stepwise seeding and clustering of adsorbate molecules. FTIR and in situ DRIFTS experiments corroborated the presence of coordinated water molecules and the availability of Ni(II) CUS sites in the structure simultaneously. A microscopic picture of the SO2 adsorption mechanism has thus been gained in line with the unusual adsorption isotherm profile exhibited by this material. Thereby, the study highlights the relevance of robust Ni-pyrazolate MOF materials for high SO2 stability.Conflicts of interest
There are no conflicts to declare.Acknowledgements
I. A. I. thanks PAPIIT UNAM (IN201123), México, for financial support. J. L. O. thanks CONAHCYT for the PhD fellowship (1003953). We thank U. Winnberg (Euro Health) for scientific discussions and G. Ibarra-Winnberg for scientific encouragement. The authors are grateful to Spanish MCIN/AEI/10.13039/501100011033 (Projects PID2020-113608RB-I00; TED2021-129886B-C41).References
- M. Sai Bhargava Reddy, D. Ponnamma, K. K. Sadasivuni, B. Kumar and A. M. Abdullah, RSC Adv., 2021, 11, 12658–12681 RSC.
- S. He, J. Yang, S. Liu, X. Wang, X. Che, M. Wang and J. Qiu, Chem. Eng. J., 2023, 454, 140202 CrossRef CAS.
- H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276–279 CrossRef CAS.
- X. Zheng, H. Zhang, L.-M. Yang and E. Ganz, Cryst. Growth Des., 2021, 21, 2474–2480 CrossRef CAS.
- H. Zhang, X. Zheng, L.-M. Yang and E. Ganz, Inorg. Chem., 2021, 60, 2656–2662 CrossRef CAS PubMed.
- H. Zhang, L.-M. Yang, H. Pan and E. Ganz, Phys. Chem. Chem. Phys., 2020, 22, 24614–24623 RSC.
- H. Zhang, L.-M. Yang and E. Ganz, Langmuir, 2020, 36, 14104–14112 CrossRef CAS PubMed.
- H. Zhang, C. Shang, L.-M. Yang and E. Ganz, Inorg. Chem., 2020, 59, 16665–16671 CrossRef CAS PubMed.
- H. Zhang, L.-M. Yang, H. Pan and E. Ganz, Cryst. Growth Des., 2020, 20, 6337–6345 CrossRef CAS.
- H. Zhang, L.-M. Yang and E. Ganz, ACS Sustain. Chem. Eng., 2020, 8, 14616–14626 CrossRef CAS.
- H. Zhang, L.-M. Yang and E. Ganz, ACS Appl. Mater. Interfaces, 2020, 12, 18533–18540 CrossRef CAS PubMed.
- T. Islamoglu, Z. Chen, M. C. Wasson, C. T. Buru, K. O. Kirlikovali, U. Afrin, M. R. Mian and O. K. Farha, Chem. Rev., 2020, 120, 8130–8160 CrossRef CAS PubMed.
- V. B. López-Cervantes, J. L. Obeso, A. Yañez-Aulestia, A. Islas-Jácome, C. Leyva, E. González-Zamora, E. Sánchez-González and I. A. Ibarra, Chem. Commun., 2023, 59, 10343–10359 RSC.
- S. He, J. Yang, S. Liu, X. Wang and J. Qiu, Adv. Funct. Mater., 2023, 2314133 CrossRef.
- M. Woellner, S. Hausdorf, N. Klein, P. Mueller, M. W. Smith and S. Kaskel, Adv. Mater., 2018, 30, 1704679 CrossRef PubMed.
- D. Britt, D. Tranchemontagne and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 11623–11627 CrossRef CAS PubMed.
- N. S. Bobbitt, M. L. Mendonca, A. J. Howarth, T. Islamoglu, J. T. Hupp, O. K. Farha and R. Q. Snurr, Chem. Soc. Rev., 2017, 46, 3357–3385 RSC.
- E. Martínez-Ahumada, M. L. Díaz-Ramírez, M. de J. Velásquez-Hernández, V. Jancik and I. A. Ibarra, Chem. Sci., 2021, 12, 6772–6799 RSC.
- A. J. Rieth, A. M. Wright and M. Dincă, Nat. Rev. Mater., 2019, 4, 708–725 CrossRef CAS.
- K. Tan, S. Zuluaga, H. Wang, P. Canepa, K. Soliman, J. Cure, J. Li, T. Thonhauser and Y. J. Chabal, Chem. Mater., 2017, 29, 4227–4235 CrossRef CAS.
- K. Tan, S. Zuluaga, Q. Gong, Y. Gao, N. Nijem, J. Li, T. Thonhauser and Y. J. Chabal, Chem. Mater., 2015, 27, 2203–2217 CrossRef CAS.
- R. Colorado-Peralta, J. María Rivera-Villanueva, J. Manuel Mora-Hernández, D. Morales-Morales and L. Ángel Alfonso-Herrera, Polyhedron, 2022, 224, 115995 CrossRef CAS.
- C. Bao, Q. Niu, Z.-A. Chen, X. Cao, H. Wang and W. Lu, RSC Adv., 2019, 9, 29474–29481 RSC.
- M. Kurmoo, H. Kumagai, M. Akita-Tanaka, K. Inoue and S. Takagi, Inorg. Chem., 2006, 45, 1627–1637 CrossRef CAS PubMed.
- S. Zheng, X. Li, B. Yan, Q. Hu, Y. Xu, X. Xiao, H. Xue and H. Pang, Adv. Energy Mater., 2017, 7, 1602733 CrossRef.
- V. B. López-Cervantes, D. W. Kim, J. L. Obeso, E. Martínez-Ahumada, Y. A. Amador-Sánchez, E. Sánchez-González, C. Leyva, C. S. Hong, I. A. Ibarra and D. Solis-Ibarra, Nanoscale, 2023, 15, 12471–12475 RSC.
- C. Pettinari, A. Tăbăcaru and S. Galli, Coord. Chem. Rev., 2016, 307, 1–31 CrossRef CAS.
- T. He, Z. Huang, S. Yuan, X.-L. Lv, X.-J. Kong, X. Zou, H.-C. Zhou and J.-R. Li, J. Am. Chem. Soc., 2020, 142, 13491–13499 CrossRef CAS PubMed.
- A. J. Rieth and M. Dincă, J. Am. Chem. Soc., 2018, 140, 3461–3466 CrossRef CAS PubMed.
- L. M. Rodríguez-Albelo, E. López-Maya, S. Hamad, A. R. Ruiz-Salvador, S. Calero and J. A. R. Navarro, Nat. Commun., 2017, 8, 14457 CrossRef PubMed.
- N. M. Padial, E. Quartapelle Procopio, C. Montoro, E. López, J. E. Oltra, V. Colombo, A. Maspero, N. Masciocchi, S. Galli, I. Senkovska, S. Kaskel, E. Barea and J. A. R. Navarro, Angew. Chem., Int. Ed., 2013, 52, 8290–8294 CrossRef CAS PubMed.
- J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. S. Palakkal and R. S. Pillai, J. Phys. Chem. C, 2020, 124, 16975–16989 CrossRef CAS.
- M. R. Tchalala, P. M. Bhatt, K. N. Chappanda, S. R. Tavares, K. Adil, Y. Belmabkhout, A. Shkurenko, A. Cadiau, N. Heymans, G. De Weireld, G. Maurin, K. N. Salama and M. Eddaoudi, Nat. Commun., 2019, 10, 1328 CrossRef CAS.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
- T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2010, 6, 2455–2468 CrossRef CAS PubMed.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- K. Gopalsamy, M. Wahiduzzaman, A. Daouli, M. Badawi and G. Maurin, ACS Appl. Nano Mater., 2022, 5, 15123–15132 CrossRef CAS.
- E. Haldoupis, J. Borycz, H. Shi, K. D. Vogiatzis, P. Bai, W. L. Queen, L. Gagliardi and J. I. Siepmann, J. Phys. Chem. C, 2015, 119, 16058–16071 CrossRef CAS.
- J. A. Gee and D. S. Sholl, J. Phys. Chem. C, 2015, 119, 16920–16926 CrossRef CAS.
- H. Fang, H. Demir, P. Kamakoti and D. S. Sholl, J. Mater. Chem. A, 2014, 2, 274–291 RSC.
- E. Martínez-Ahumada, D. won Kim, M. Wahiduzzaman, P. Carmona-Monroy, A. López-Olvera, D. R. Williams, V. Martis, H. A. Lara-García, S. López-Morales, D. Solis-Ibarra, G. Maurin, I. A. Ibarra and C. S. Hong, J. Mater. Chem. A, 2022, 10, 18636–18643 RSC.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- M. H. Ketko, G. Kamath and J. J. Potoff, J. Phys. Chem. B, 2011, 115, 4949–4954 CrossRef CAS.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- D.-Y. Peng and D. B. Robinson, Ind. Eng. Chem. Fundam., 1976, 15, 59–64 CrossRef CAS.
- B. Widom, J. Chem. Phys., 1963, 39, 2808–2812 CrossRef CAS.
- N. Masciocchi, S. Galli, V. Colombo, A. Maspero, G. Palmisano, B. Seyyedi, C. Lamberti and S. Bordiga, J. Am. Chem. Soc., 2010, 132, 7902–7904 CrossRef CAS PubMed.
- S. Yang, J. Sun, A. J. Ramirez-Cuesta, S. K. Callear, W. I. F. David, D. P. Anderson, R. Newby, A. J. Blake, J. E. Parker, C. C. Tang and M. Schröder, Nat. Chem., 2012, 4, 887–894 CrossRef CAS PubMed.
- E. López-Maya, C. Montoro, V. Colombo, E. Barea and J. A. R. Navarro, Adv. Funct. Mater., 2014, 24, 6130–6135 CrossRef.
- K. V. Kumar, S. Gadipelli, B. Wood, K. A. Ramisetty, A. A. Stewart, C. A. Howard, D. J. L. Brett and F. Rodriguez-Reinoso, J. Mater. Chem. A, 2019, 7, 10104–10137 RSC.
- J. Li, G. L. Smith, Y. Chen, Y. Ma, M. Kippax-Jones, M. Fan, W. Lu, M. D. Frogley, G. Cinque, S. J. Day, S. P. Thompson, Y. Cheng, L. L. Daemen, A. J. Ramirez-Cuesta, M. Schröder and S. Yang, Angew. Chem., Int. Ed., 2022, 61, e202207259 CrossRef CAS PubMed.
- X. Cui, Q. Yang, L. Yang, R. Krishna, Z. Zhang, Z. Bao, H. Wu, Q. Ren, W. Zhou, B. Chen and H. Xing, Adv. Mater., 2017, 29, 1606929 CrossRef PubMed.
- Y. Zhang, P. Zhang, W. Yu, J. Zhang, J. Huang, J. Wang, M. Xu, Q. Deng, Z. Zeng and S. Deng, ACS Appl. Mater. Interfaces, 2019, 11, 10680–10688 CrossRef CAS PubMed.
- M. Savage, Y. Cheng, T. L. Easun, J. E. Eyley, S. P. Argent, M. R. Warren, W. Lewis, C. Murray, C. C. Tang, M. D. Frogley, G. Cinque, J. Sun, S. Rudić, R. T. Murden, M. J. Benham, A. N. Fitch, A. J. Blake, A. J. Ramirez-Cuesta, S. Yang and M. Schröder, Adv. Mater., 2016, 28, 8705–8711 CrossRef CAS PubMed.
- A. López-Olvera, J. A. Zárate, E. Martínez-Ahumada, D. Fan, M. L. Díaz-Ramírez, P. A. Sáenz-Cavazos, V. Martis, D. R. Williams, E. Sánchez-González, G. Maurin and I. A. Ibarra, ACS Appl. Mater. Interfaces, 2021, 13, 39363–39370 CrossRef PubMed.
- N. Hanikel, X. Pei, S. Chheda, H. Lyu, W. Jeong, J. Sauer, L. Gagliardi and O. M. Yaghi, Science, 2021, 374, 454–459 CrossRef CAS PubMed.
- V. Colombo, S. Galli, H. J. Choi, G. D. Han, A. Maspero, G. Palmisano, N. Masciocchi and J. R. Long, Chem. Sci., 2011, 2, 1311 RSC.
- A. Nuhnen and C. Janiak, Dalton Trans., 2020, 49, 10295–10307 RSC.
- F. Salles, G. Maurin, C. Serre, P. L. Llewellyn, C. Knöfel, H. J. Choi, Y. Filinchuk, L. Oliviero, A. Vimont, J. R. Long and G. Férey, J. Am. Chem. Soc., 2010, 132, 13782–13788 CrossRef CAS PubMed.
- K. I. Hadjiivanov, D. A. Panayotov, M. Y. Mihaylov, E. Z. Ivanova, K. K. Chakarova, S. M. Andonova and N. L. Drenchev, Chem. Rev., 2021, 121, 1286–1424 CrossRef CAS PubMed.
- K. Tan, P. Canepa, Q. Gong, J. Liu, D. H. Johnson, A. Dyevoich, P. K. Thallapally, T. Thonhauser, J. Li and Y. J. Chabal, Chem. Mater., 2013, 25, 4653–4662 CrossRef CAS.
- V. Bon, E. Brunner, A. Pöppl and S. Kaskel, Adv. Funct. Mater., 2020, 30, 1907847 CrossRef CAS.
- E. Martínez-Ahumada, M. L. Díaz-Ramírez, H. A. Lara-García, D. R. Williams, V. Martis, V. Jancik, E. Lima and I. A. Ibarra, J. Mater. Chem. A, 2020, 8, 11515–11520 RSC.
- C. C. Zhang, J. Shi, S. Hartlaub, J. P. Palamara, I. Petrovic and B. Yilmaz, Catal. Commun., 2021, 150, 106273 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Instrumental techniques and characterization. See DOI: https://doi.org/10.1039/d3ta07582f |
| ‡ These authors contributed equally to this manuscript. |
| This journal is © The Royal Society of Chemistry 2024 |