Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
13Ccarbene nuclear magnetic resonance chemical shift analysis confirms CeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) C double bonding in cerium(IV)–diphosphonioalkylidene complexes†
C double bonding in cerium(IV)–diphosphonioalkylidene complexes†
Cameron F.
Baker
 a,
John A.
Seed
a,
John A.
Seed
 a,
Ralph W.
Adams
a,
Ralph W.
Adams
 a,
Daniel
Lee
a,
Daniel
Lee
 *b and
Stephen T.
Liddle
*b and
Stephen T.
Liddle
 *a
*a
aDepartment of Chemistry, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: daniel.lee@manchester.ac.uk; steve.liddle@manchester.ac.uk
bDepartment of Chemical Engineering, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK
First published on 6th December 2023
Abstract
Diphosphonioalkylidene dianions have emerged as highly effective ligands for lanthanide and actinide ions, and the resulting formal metal–carbon double bonds have challenged and developed conventional thinking about f-element bond multiplicity and covalency. However, f-element–diphosphonioalkylidene complexes can be represented by several resonance forms that render their metal–carbon double bond status unclear. Here, we report an experimentally-validated 13C Nuclear Magnetic Resonance computational assessment of two cerium(IV)–diphosphonioalkylidene complexes, [Ce(BIPMTMS)(ODipp)2] (1, BIPMTMS = {C(PPh2NSiMe3)2}2−; Dipp = 2,6-diisopropylphenyl) and [Ce(BIPMTMS)2] (2). Decomposing the experimental alkylidene chemical shifts into their corresponding calculated shielding (σ) tensor components verifies that these complexes exhibit Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds. Strong magnetic coupling of Ce
C double bonds. Strong magnetic coupling of Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ/π* and π/σ* orbitals produces strongly deshielded σ11 values, a characteristic hallmark of alkylidenes, and the largest 13C chemical shift tensor spans of any alkylidene complex to date (1, 801 ppm; 2, 810 ppm). In contrast, the phosphonium-substituent shielding contributions are much smaller than the Ce
C σ/π* and π/σ* orbitals produces strongly deshielded σ11 values, a characteristic hallmark of alkylidenes, and the largest 13C chemical shift tensor spans of any alkylidene complex to date (1, 801 ppm; 2, 810 ppm). In contrast, the phosphonium-substituent shielding contributions are much smaller than the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ- and π-bond components. This study confirms significant Ce 4f-orbital contributions to the Ce
C σ- and π-bond components. This study confirms significant Ce 4f-orbital contributions to the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonding, provides further support for a previously proposed inverse-trans-influence in 2, and reveals variance in the 4f spin–orbit contributions that relate to the alkylidene hybridisation. This work thus confirms the metal–carbon double bond credentials of f-element–diphosphonioalkylidenes, providing quantified benchmarks for understanding diphosphonioalkylidene bonding generally.
C bonding, provides further support for a previously proposed inverse-trans-influence in 2, and reveals variance in the 4f spin–orbit contributions that relate to the alkylidene hybridisation. This work thus confirms the metal–carbon double bond credentials of f-element–diphosphonioalkylidenes, providing quantified benchmarks for understanding diphosphonioalkylidene bonding generally.
Introduction
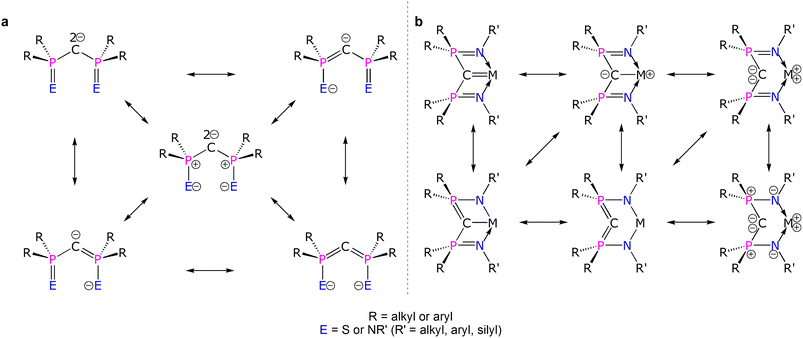
Diphosphonioalkylidene (methanediide) ligands, {(R2PE)2C2−} (R = alkyl or aryl; E = S or NR’; R' = silyl, aryl, alkyl), have proven to be popular carbene ligands for metals across the Periodic Table, and in particular they have been effective in developing formal M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (M = lanthanide and actinide) double bond interactions that have challenged and developed conventional thinking on f-element multiple bonding and covalency.1–10 The E = NR′ variant, the Bis(IminoPhosphorano)Methanediide (BIPM) class, has proven to be very versatile, supporting formal M
C (M = lanthanide and actinide) double bond interactions that have challenged and developed conventional thinking on f-element multiple bonding and covalency.1–10 The E = NR′ variant, the Bis(IminoPhosphorano)Methanediide (BIPM) class, has proven to be very versatile, supporting formal M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds over M oxidation states +3 to +6, novel bonding motifs, reactivity, and magnetism, and even transuranium derivatives.11–25 However, the polarised nature of electropositive metal bonding and the various resonance forms that can be drawn for these methanediides (Fig. 1a)4 raises fundamental questions over how best to pictorially represent BIPM bonding to metals and then what those representations actually mean (Fig. 1b).26 This is because any M
C double bonds over M oxidation states +3 to +6, novel bonding motifs, reactivity, and magnetism, and even transuranium derivatives.11–25 However, the polarised nature of electropositive metal bonding and the various resonance forms that can be drawn for these methanediides (Fig. 1a)4 raises fundamental questions over how best to pictorially represent BIPM bonding to metals and then what those representations actually mean (Fig. 1b).26 This is because any M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR2 linkage features a C-atom that is supported to various extents by tensioned M and R stabilising contributions; the phosphonium-substituents can in principle stabilise the C-centres of M
CR2 linkage features a C-atom that is supported to various extents by tensioned M and R stabilising contributions; the phosphonium-substituents can in principle stabilise the C-centres of M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CBIPM complexes, that is take on ylide P
CBIPM complexes, that is take on ylide P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond character, thus diminishing the extent of M
C double bond character, thus diminishing the extent of M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond character. Consequently, the extent of M
C double bond character. Consequently, the extent of M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond character of diphosphonioalkylidene complexes has remained open to qualitative interpretation.27–30 Thus, quantification to provide a more rigorous descriptive framework is required.
C double bond character of diphosphonioalkylidene complexes has remained open to qualitative interpretation.27–30 Thus, quantification to provide a more rigorous descriptive framework is required.
In recent years, 13C NMR spectroscopic studies of transition metal alkylidenes have delivered a comprehensive understanding of M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR2 double bonds.31–35 In particular, the isotropic chemical shift (δiso) is intimately dependent on the shielding (σ) tensors, and a signature feature of alkylidene complexes which has emerged is that the σ11 tensor component, which is in the M
CR2 double bonds.31–35 In particular, the isotropic chemical shift (δiso) is intimately dependent on the shielding (σ) tensors, and a signature feature of alkylidene complexes which has emerged is that the σ11 tensor component, which is in the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR2 plane and orthogonal to the M
CR2 plane and orthogonal to the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ- and π-bond principal axes, is substantially deshielded due to strong magnetic coupling of the M
C σ- and π-bond principal axes, is substantially deshielded due to strong magnetic coupling of the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ/π* and π/σ* orbitals.31 When considering applying that approach to diamagnetic lanthanide- and actinide-BIPM complexes, where data are available they exhibit a wide range of 13C NMR Ccarbene chemical shifts4,7,8,10 implying a varied range of bonding scenarios where the more deshielded the Ccarbeneδiso value is the more multiple bond character it will likely have to the metal, if not disproportionately shifted by spin orbit effects. However, in contrast to transition metal alkylidenes31–36 a detailed dissection of the shielding tensors beyond calculated δiso values has remained largely untested for f-element–BIPM complexes.30,37,38
C σ/π* and π/σ* orbitals.31 When considering applying that approach to diamagnetic lanthanide- and actinide-BIPM complexes, where data are available they exhibit a wide range of 13C NMR Ccarbene chemical shifts4,7,8,10 implying a varied range of bonding scenarios where the more deshielded the Ccarbeneδiso value is the more multiple bond character it will likely have to the metal, if not disproportionately shifted by spin orbit effects. However, in contrast to transition metal alkylidenes31–36 a detailed dissection of the shielding tensors beyond calculated δiso values has remained largely untested for f-element–BIPM complexes.30,37,38
In recent years NMR spectroscopy has emerged as a powerful tool for quantifying f-element chemical bonding when the individual contributions to the shielding tensors are analysed in detail,39 because the chemical shifts of a wide range of nuclei have proven to be very sensitive to the nature of their interactions with f-block ions.30,37,38,40–62 Recently some of us,56,58,62 and others,53,54 demonstrated that 15N, 29Si, and 31P NMR spectroscopies combined with computational analysis of chemical shielding tensor properties provides powerful probes of f-element–ligand covalency, so our attention turned to examining BIPM–f-element complexes using 13C NMR spectroscopy. We focus on two cerium(IV)-carbene complexes [Ce(BIPMTMS)(ODipp)2] (1, BIPMTMS = {C(PPh2NSiMe3)2}2−; Dipp = 2,6-diisopropylphenyl)15,18 and [Ce(BIPMTMS)2] (2) (Fig. 2).19 Using 13C–31P 2D solution NMR spectroscopy the 13C δiso of the carbene centres in 1 and 2 were previously determined to be 324.6 (JPC = 149 Hz) and 343.5 (JPC = 170 Hz) ppm, respectively. These downfield δiso values are unusually highly deshielded and well into the usual range (200–400 ppm) of alkylidenes,36 and a range of spectroscopic, magnetic, and computational methods consistently describe 1 and 2 as having no appreciable temperature independent paramagnetism (TIP) and being closed-shell singlet (i.e. not multi-reference) formulations.18,19 These two complexes therefore represent ideal benchmarks from which to quantify the nature of the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CBIPM bonds and so inform the debate that surrounds the multiple bonding aspect of BIPM complexes generally.
CBIPM bonds and so inform the debate that surrounds the multiple bonding aspect of BIPM complexes generally.
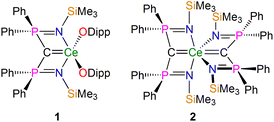 | ||
| Fig. 2 Cerium-carbene complexes 1 and 2. These complexes are the two subject molecules of this study. Dipp = diisopropylphenyl. | ||
Here, we report an assessment of the shielding tensors that underpin the δiso values for 1 and 2. This work confirms that Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond interactions are indeed present in 1 and 2, revealing dominant σ11 data that are the hallmark of alkylidenes, and the largest tensor spans of any metal-alkylidene complex. The data quantifies the relative extent of Ce
C double bond interactions are indeed present in 1 and 2, revealing dominant σ11 data that are the hallmark of alkylidenes, and the largest tensor spans of any metal-alkylidene complex. The data quantifies the relative extent of Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ- and π-bond stabilisation with respect to the smaller phosphonium-substituent contributions, provides further support for the previously proposed inverse-trans-influence (ITI) in 2, and reveals variance in the spin–orbit-induced spin-polarisation of the Ccarbene that can be related to the σ- and π-components and their variable levels of 2s vs. 2p character. Overall, this work confirms the M
C σ- and π-bond stabilisation with respect to the smaller phosphonium-substituent contributions, provides further support for the previously proposed inverse-trans-influence (ITI) in 2, and reveals variance in the spin–orbit-induced spin-polarisation of the Ccarbene that can be related to the σ- and π-components and their variable levels of 2s vs. 2p character. Overall, this work confirms the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond credentials of these diphosphonioalkylidene complexes and provides quantified benchmarks for diphosphonioalkylidene bonding more generally.
C double bond credentials of these diphosphonioalkylidene complexes and provides quantified benchmarks for diphosphonioalkylidene bonding more generally.
Results
Solid-state NMR spectroscopy of 1 and 2
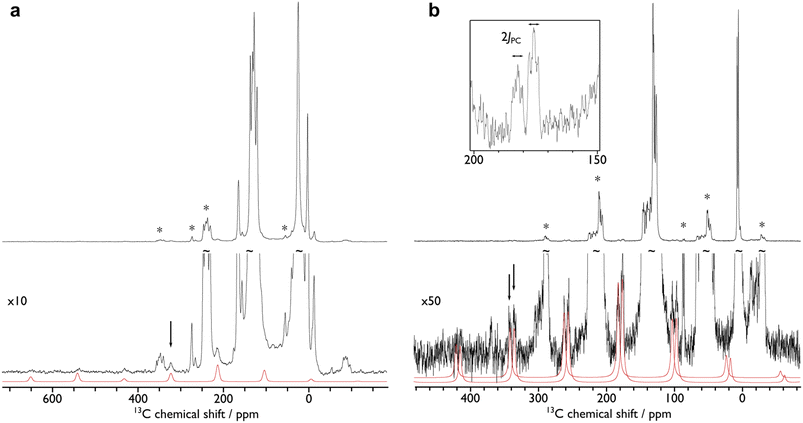
In order to confirm the solution δiso values for 1 and 2 and provide experimental benchmarking for the computational analysis of 1 and 2, solid-state {1H-}13C CPMAS NMR spectra were recorded permitting fitting of the chemical shift anisotropy (CSA) parameters (Fig. 3). The solid-state 13C δiso of the carbene centre in 1 is 322.5 ppm, and for 2 two values of 334.5 and 341.5 ppm were determined, consistent with the two different Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C distances found in the solid-state structure of 2 (Ce
C distances found in the solid-state structure of 2 (Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C = 2.385(2) and 2.399(3) Å);19 both sets of solid-state δiso values are in excellent agreement with the solution δiso values (vide supra). Moreover, the solid-state JPC of 2 (170 ± 20 Hz) could be extracted, owing to the high crystallinity and corresponding small 13C linewidths of the sample, and is consistent with the solution JPC value (vide supra). Fitting of the CSA parameters (Fig. 3) produced δ11, δ22, δ33, span (Ω), and skew (κ) values of 815.9, 136.7, 14.9, 801 ppm, and −0.70 for 1 and 816.5/823.5, 180.6/187.6, 6.4/13.4, 810/810 ppm, and −0.57/−0.57 for the two carbene centres in 2. For 1 and 2 the spans of the chemical shift tensor Ω values of approximately 801 and 810/810 ppm are the largest to date for any metal-alkylidene.31–35 The κ values are consistent with the presence of M
C = 2.385(2) and 2.399(3) Å);19 both sets of solid-state δiso values are in excellent agreement with the solution δiso values (vide supra). Moreover, the solid-state JPC of 2 (170 ± 20 Hz) could be extracted, owing to the high crystallinity and corresponding small 13C linewidths of the sample, and is consistent with the solution JPC value (vide supra). Fitting of the CSA parameters (Fig. 3) produced δ11, δ22, δ33, span (Ω), and skew (κ) values of 815.9, 136.7, 14.9, 801 ppm, and −0.70 for 1 and 816.5/823.5, 180.6/187.6, 6.4/13.4, 810/810 ppm, and −0.57/−0.57 for the two carbene centres in 2. For 1 and 2 the spans of the chemical shift tensor Ω values of approximately 801 and 810/810 ppm are the largest to date for any metal-alkylidene.31–35 The κ values are consistent with the presence of M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds, with 2 being close to the ideal of 0.5 and the deviation for 1 being accounted for by the slight pyramidalisation of the carbene in that complex. The extremely large deshielding of δ11 for these M
C double bonds, with 2 being close to the ideal of 0.5 and the deviation for 1 being accounted for by the slight pyramidalisation of the carbene in that complex. The extremely large deshielding of δ11 for these M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C carbenes suggests strong magnetic coupling between occupied and vacant orbitals, in particular
C carbenes suggests strong magnetic coupling between occupied and vacant orbitals, in particular 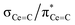 and
and 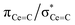 .
.
Computational benchmarking of the 13Ccarbene NMR spectroscopic properties of 1 and 2
The computational assessment began by taking the solid-state crystallographic coordinates of 1 and 2 and geometry optimising the H-atom positions whilst constraining the heavy atom positions at the BP86 TZ2P all-electron ZORA relativistic level (Tables S1 and S2†). Using the resultant atom coordinates scalar relativistic (SR) and spin–orbit relativistic (SOR) single point energy calculations for 1 and 2 were conducted using a range of functionals (BP86, PBE0-HF25 (default HF setting in ADF), PBE-HF40, B3LYP-HF20 (default HF setting in ADF), B3LYP-HF30, B3LYP-HF35, and B3LYP-HF40) and in turn those data were used to compute the SR and SOR 13Ccarbeneδiso values in a benzene solvent continuum (Tables S3 and S4†). For 1 the best agreement was found using the B3LYP-HF20 functional, where the computed SR 13Ccarbeneδiso value of 298.4 ppm shifts to 324.9 ppm in the SOR calculation. Both 13Ccarbeneδiso values for 2 were computed, but since the variance for pairs of values was ≤0.4 ppm we present average data; the B3LYP-HF30 functional gave the best agreement, with the computed SR 13Ccarbeneδiso value of 258.9 ppm shifting to 341.8 ppm in the SOR calculation. These values are in excellent agreement with the solution and solid-state δiso data for 1 and 2, and the use of slightly different functionals (10% difference in HF mixing) was considered acceptable.63 From these calculations we extracted the δ11, δ22, δ33, Ω, and κ values for 1 and 2; the calculated values are 834.2, 132.5, 7.9, 842.1 ppm and −0.69 for 1 and 836.6, 190.7, −1.9, 838.5, and −0.54 (av.) for 2, which fit well with the experimental MAS NMR data.Molecular orbital and natural bond orbital benchmarking of 1 and 2
Having established that the B3LYP-HF20 and -HF30 functionals satisfactorily reproduce the experimental 13Ccarbeneδiso and CSA values of 1 and 2, respectively, their electronic structures were reanalysed at those levels of theory. In both cases the Molecular Orbital (MO) manifolds for 1 and 2 are qualitatively quite similar to the previously published BP86 data,15,18,19 revealing Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ- and π-bonding combinations. The Nalewajski-Mrozek Ce
C σ- and π-bonding combinations. The Nalewajski-Mrozek Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond orders for 1 and 2 are computed to be 1.10 and 1.16, respectively, consistent with a two-fold bonding interaction where each component has a sub-one bond order, i.e. each component is polarised. These B3LYP values are very similar to the BP86 values of 1.10 for both 1 and 2. However, there is much greater mixing of orbital coefficients across the B3LYP frontier MOs of 1 and 2 compared to the corresponding BP86 calculations, a situation also encountered when comparing BP86 and B3LYP data in the aforementioned terminal uranium(VI)-nitride 15N NMR spectroscopic study.58
C bond orders for 1 and 2 are computed to be 1.10 and 1.16, respectively, consistent with a two-fold bonding interaction where each component has a sub-one bond order, i.e. each component is polarised. These B3LYP values are very similar to the BP86 values of 1.10 for both 1 and 2. However, there is much greater mixing of orbital coefficients across the B3LYP frontier MOs of 1 and 2 compared to the corresponding BP86 calculations, a situation also encountered when comparing BP86 and B3LYP data in the aforementioned terminal uranium(VI)-nitride 15N NMR spectroscopic study.58
In order to provide a chemically localised and hence more instructive model than the delocalised MO description, the Natural Bond Orbitals (NBOs) of 1 and 2 were examined using the B3LYP-HF20 and -HF30 functionals, respectively. In both cases NBO identifies clear-cut σ- and π-bonding interactions constituting Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonding interactions (Fig. 4 and 5). For 1, the Ce
C double bonding interactions (Fig. 4 and 5). For 1, the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ-bond is found to be 13% Ce (6s/6p/5d/4f: 1/0/32/67%) and 87% Ccarbene (2s/2p: 15/85%) character. The Ce
C σ-bond is found to be 13% Ce (6s/6p/5d/4f: 1/0/32/67%) and 87% Ccarbene (2s/2p: 15/85%) character. The Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π-bond in 1 is similarly polarised being composed of 11% Ce (6s/6p/5d/4f: 1/1/31/67%) and 89% Ccarbene (2s/2p: 2/98%). For 2, the Ce
C π-bond in 1 is similarly polarised being composed of 11% Ce (6s/6p/5d/4f: 1/1/31/67%) and 89% Ccarbene (2s/2p: 2/98%). For 2, the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ-bond is 15% Ce (6s/6p/5d/4f: 3/0/47/50%) and 85% Ccarbene (2s/2p: 11/89%) but the π-bonds are more polarised at 7% Ce (6s/6p/5fd/4f: 0/0/53/47%) and 93% Ccarbene (2s/2p: 0/100%) character. We note in passing that these NBO data are in good agreement with the previously reported BP86-NBO data (see Tables S5 and S6† for BP86–B3LYP comparisons).15,18,19 Given that these calculations satisfactorily reproduce the experimentally determined δiso spectroscopic data, they: (i) quantify significant contributions of 5d- and 4f-orbital bonding character for Ce; (ii) acknowledging that the bonding is polarised, support the Ce
C σ-bond is 15% Ce (6s/6p/5d/4f: 3/0/47/50%) and 85% Ccarbene (2s/2p: 11/89%) but the π-bonds are more polarised at 7% Ce (6s/6p/5fd/4f: 0/0/53/47%) and 93% Ccarbene (2s/2p: 0/100%) character. We note in passing that these NBO data are in good agreement with the previously reported BP86-NBO data (see Tables S5 and S6† for BP86–B3LYP comparisons).15,18,19 Given that these calculations satisfactorily reproduce the experimentally determined δiso spectroscopic data, they: (i) quantify significant contributions of 5d- and 4f-orbital bonding character for Ce; (ii) acknowledging that the bonding is polarised, support the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonding interaction description.
C double bonding interaction description.
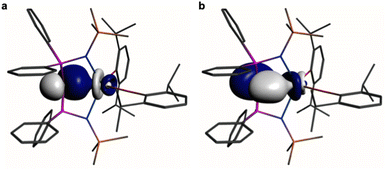 | ||
Fig. 4 Natural Bond Orbitals (NBOs) of 1 at the B3LYPHF20 level. (a) The Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ-NBO. (b) The Ce C σ-NBO. (b) The Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π-NBO. Hydrogen atoms are omitted for clarity. C π-NBO. Hydrogen atoms are omitted for clarity. | ||
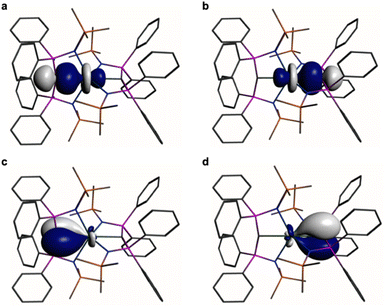 | ||
Fig. 5 Natural Bond Orbitals (NBOs) of 2 at the B3LYPHF30 level. (a and b) The two Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ-NBOs. (c and d) The two Ce C σ-NBOs. (c and d) The two Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π-NBOs. Hydrogen atoms are omitted for clarity. C π-NBOs. Hydrogen atoms are omitted for clarity. | ||
Computational chemical shielding analysis of 1 and 2
In order to contextualise the following discussion, it is useful to relate the δiso to its isotropic shielding (σiso) and in turn σiso to its constituent diamagnetic (σd), paramagnetic (σp) and spin–orbit (σso) shielding components. The δiso is derived from the σiso of the NMR nucleus being considered when adjusted for the σiso and δiso of the NMR nucleus standard reference (here the 13C nucleus of CH4 at δiso −4.3 ppm).Ramsey's formalism, eqn (1), relates NMR interactions to a quantum-mechanical perspective by decomposing magnetic shielding contributions into σd and σp components. These parameters are dependent on electron orbital angular momenta,64–66 and whilst this does not directly translate to the MO approach of hybrid DFT (B3LYP), it provides a framework with which to rationalise NMR magnetic shielding calculations when σso contributions are included,67eqn (2).
| σiso = σd + σp | (1) |
| σiso = σd + σp + σso | (2) |
The 13Ccarbeneσd values for 1 and 2 are 268.6 and 258.9 ppm, respectively. As expected, there is relatively little variation for these values, since σd derives principally from tightly-bound core electron densities that respond little to valence-level perturbations.67 The ∼10 ppm variance within the 13Ccarbeneδiso values of >320 ppm can be considered to be minor and thus negligible to the discussion.
Turning to the 13Ccarbeneσso data, the values for 1 and 2 are −23.6 and −79.7 ppm, respectively, which is consistent with σso contributions in other CeIV–C complexes,55 but in passing a σso of close to −80 ppm is indicative of significant 4f-orbital character in the bonding, which is notable given the usual ‘core-like’ description of 4f-orbitals. This likely reflects the strong Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ-bonding in 2, see below. These are clearly not insignificant contributions to the 13Ccarbeneσiso values of 1 and 2, but given the observed 13Ccarbeneδiso values of >320 ppm, which would be >280 ppm in the absence of spin–orbit effects it is clear that whilst the σso data should not be ignored they can be considered to be secondary to the primary determinant of the 13Ccarbeneδiso values, which is the σp values.
C σ-bonding in 2, see below. These are clearly not insignificant contributions to the 13Ccarbeneσiso values of 1 and 2, but given the observed 13Ccarbeneδiso values of >320 ppm, which would be >280 ppm in the absence of spin–orbit effects it is clear that whilst the σso data should not be ignored they can be considered to be secondary to the primary determinant of the 13Ccarbeneδiso values, which is the σp values.
The σp term can be presented in reduced form as:
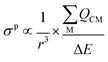 | (3) |
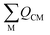 is the sum of the charge density and bond order matrix elements over the relevant atoms (M), and ΔE is the energy separation between the ground and excited states in question.39,46,64–66
is the sum of the charge density and bond order matrix elements over the relevant atoms (M), and ΔE is the energy separation between the ground and excited states in question.39,46,64–66
The σp term is inversely proportional to the energy gap between the occupied and virtual orbitals that become magnetically coupled in the presence of an externally applied magnetic field, so smaller ΔE gaps produce larger σp values. However, examination of the HOMO–LUMO gaps of 1 and 2 shows that they are unremarkable (2.846–4.218 eV in B3LYP calculations) and so a disproportionate effect on σp from ΔE can be discounted.
Field-induced magnetic mixing of the ground state with low-lying, thermally inaccessible, paramagnetic states in 1 and 2, that is TIP, has been previously found to be negligible18,19 and multi-reference calculations on 1 and 2 showed little multi-reference character.18,19 This suggests that any TIP effects on the σp term will be modest,52,58 and thus the 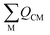 term will, like the ΔE term, not introduce a disproportionate effect on σp.
term will, like the ΔE term, not introduce a disproportionate effect on σp.
Turning to the remaining r3 term, σp is inversely proportional to r3. This is because as a nucleus (M) withdraws charge from the NMR nucleus (C) the C valence orbitals contract due to the increased electron deficiency at C. Thus, the 1/r3 term becomes larger (i.e. the NMR nucleus is more deshielded) resulting in a larger σp term. Put another way, the larger the bond order of, so more covalent, the bond involving the NMR nucleus the larger σp becomes.46 In this context, recalling the δiso values of 1 and 2, the σp values of −382.1 and −333.1 ppm are large, and hence significant, and consistent with the presence of Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond interactions.
C double bond interactions.
Molecular orbital shielding analysis
The external field-induced magnetic coupling of occupied and virtual orbitals must be symmetry-allowed, since the angular momentum operators belong to the same irreducible representations as the rotational operators. The contributions to deshielding can be distributed over many components because the MOs are often delocalised, and so are difficult to fully identify. Furthermore, as mentioned above, the B3LYP MO manifold contains ‘split’ Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ- and π-bonding combinations across different MOs. However, noting the above framework and using the ADF NMR analysis package enables identification and recombination of the principal components that contribute to the σp term of 1 and 2.
C σ- and π-bonding combinations across different MOs. However, noting the above framework and using the ADF NMR analysis package enables identification and recombination of the principal components that contribute to the σp term of 1 and 2.
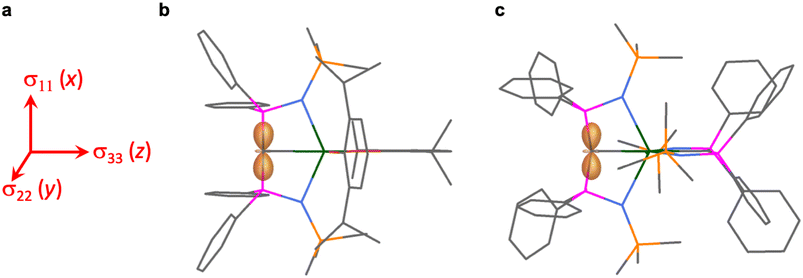
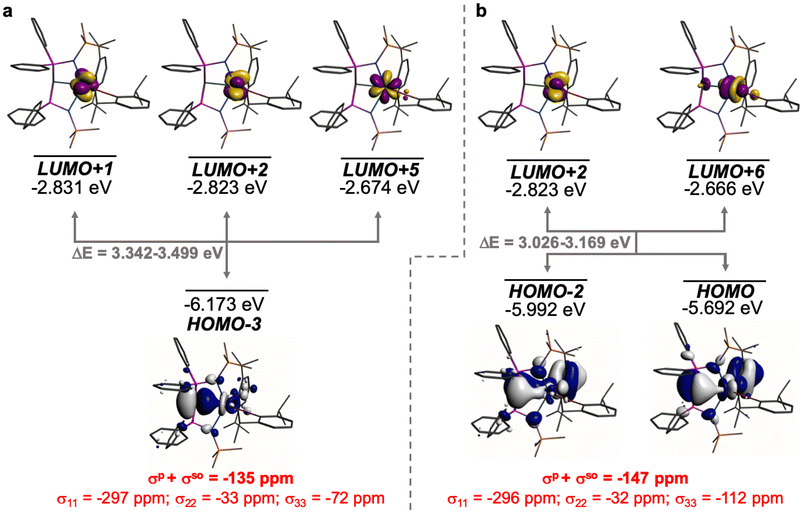
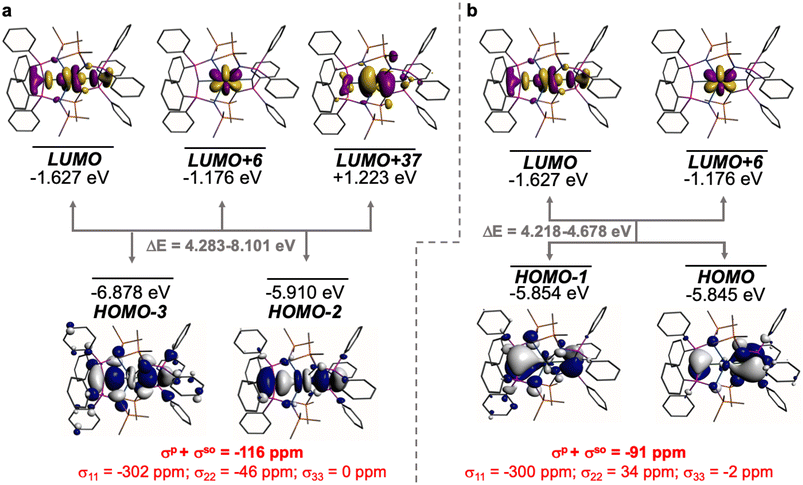
The shielding effects can be understood in terms of the rotated orbital model,31,68–71 which considers the action of the angular momentum operator on magnetically coupled occupied and virtual orbitals, which can be visualised as a 90° rotation of an idealised occupied C p-orbital to mix with an orthogonal vacant orbital. This has been comprehensively described elsewhere for alkylidenes,31 but of pertinence to the results here in brief the computed orientations of the 13C σ11, σ22, and σ33 shielding tensor principal components of 1 and 2 are shown in Fig. 6, where it can be seen that they align closely to the principal axes (x, y, and z). Thus, magnetic coupling of the σ and π* and π and σ* orbitals will correspond to rotation about the x axis resulting in σ11 deshielding along the x axis. The results of the MO analysis are presented in Fig. 7 and 8. For 1 and 2, for a given BIPMTMS ligand the occupied Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ-bond mixes with unoccupied Ce
C σ-bond mixes with unoccupied Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π*- and 4f-orbitals and the Ce
C π*- and 4f-orbitals and the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π-bond mixes with unoccupied Ce
C π-bond mixes with unoccupied Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ*- and f-orbitals. In all cases, the dominant individual σ contribution to the σiso is σ11, which is deshielded due to strong σ/π* and π/σ* magnetic couplings that are orthogonal to the σ11 direction (x axis), and this is a signature feature of alkylidene complexes. Thus, for both 1 and 2 the principal magnetic coupling of orbitals that is responsible for the shielding tensors at the carbene centres derives from orbitals associated with the Ce
C σ*- and f-orbitals. In all cases, the dominant individual σ contribution to the σiso is σ11, which is deshielded due to strong σ/π* and π/σ* magnetic couplings that are orthogonal to the σ11 direction (x axis), and this is a signature feature of alkylidene complexes. Thus, for both 1 and 2 the principal magnetic coupling of orbitals that is responsible for the shielding tensors at the carbene centres derives from orbitals associated with the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C linkage as found analogously in transition metal alkylidenes.31–35
C linkage as found analogously in transition metal alkylidenes.31–35
Natural localised molecular orbital shielding analysis
Whilst the MO analysis above provides a qualitatively instructive framework to probe the field-induced magnetic coupling of occupied and virtual orbitals, the analysis is incomplete due to the delocalised nature of MOs. In order to derive a more complete picture the shielding data in terms of the Natural Localised Molecular Orbitals (NLMOs) were analysed,72,73Table 1. The NLMOs for 1 and 2 are in each case very similar to the respective NBO data (see Tables S7 and S8† for NBO-NLMO comparisons). Compared to B3LYP, the BP86 data tend to return larger 4f-orbital contributions at the expense of 5d-orbital contributions for Ce. However, the C 2s/2p% and total M/C% values vary little, so since NLMOs are effectively NBOs that have been allowed to expand to include other small orbital coefficients to ensure the orbital occupancy is 100%, the B3LYP NLMO analysis is directly representative of the B3LYP NBO bonding description above.| Compound | SR | SOR | Δ so | % NBO | Occ. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NLMOa | Lb | NLc | L + NL | Lb | NLc | L + NL | Lb | NLc | L + NL | |||
| a B3LYP calculations (HF = 20%, 1; 30% 2), all shielding parameters are in ppm. b Lewis contribution of the NLMO. c Non-Lewis contribution of the NLMO. d Defined as σ(SOR) − σ(SR) to isolate the SO component. e Essentially isotropic so only the average values provided. f Minor component so only average values provided. g Multiple NLMOs, but % NBOs all >85%. h Multiple NLMOs, but all occupancies >1.71 electrons per NLMO. i Data given for one carbene only since the data for both are identical. | ||||||||||||
| 1 | ||||||||||||
σ-Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
σ iso | −135 | 4 | −131 | −186 | 3 | −183 | −51 | −1 | −52 | 89 | 1.78 |
| σ 11 | −432 | 20 | −412 | −495 | 18 | −477 | −63 | −2 | −65 | |||
| σ 22 | 3 | −11 | −8 | −76 | −13 | −89 | −79 | −2 | −81 | |||
| σ 33 | 25 | 3 | 28 | 13 | 3 | 16 | −12 | 0 | −12 | |||
π-Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
σ iso | −123 | 15 | −108 | −121 | 16 | −105 | 2 | 1 | 3 | 85 | 1.70 |
| σ 11 | −405 | 35 | −370 | −400 | 32 | −368 | 5 | −3 | 2 | |||
| σ 22 | −5 | 4 | −1 | 2 | 9 | 11 | 7 | 5 | 12 | |||
| σ 33 | 42 | 8 | 50 | 35 | 7 | 42 | −7 | −1 | −8 | |||
| 2 × C–P | σ iso | −57 | −5 | −62 | −40 | −5 | −45 | 17 | 0 | 17 | 98 | 1.96 |
| σ 11 | −9 | 2 | −7 | 14 | 1 | 15 | 23 | −1 | 22 | |||
| σ 22 | −88 | −12 | −100 | −60 | −12 | −72 | 28 | 0 | 28 | |||
| σ 33 | −75 | −5 | −80 | −73 | −5 | −78 | 2 | 0 | 2 | |||
| 1score-Ce | σ iso | 200 | 0 | 200 | 204 | 0 | 204 | 4 | 0 | 4 | 100 | 2.00 |
| Σ other | σ iso | −9 | 7 | −2 | −4 | 5 | 1 | 5 | −2 | 3 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| 2 | ||||||||||||
σ-Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
σ iso | −101 | −11 | −112 | −227 | −5 | −232 | −126 | 6 | −120 | 89 | 1.79 |
| σ 11 | −386 | −4 | −390 | −563 | 4 | −559 | −177 | 8 | −169 | |||
| σ 22 | 71 | −30 | 41 | −126 | −20 | −146 | −197 | 10 | −45 | |||
| σ 33 | 13 | 1 | 14 | 7 | 1 | 8 | −6 | 0 | −6 | |||
π-Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
σ iso | −100 | 13 | −87 | −101 | 13 | −88 | −1 | 0 | −1 | 85 | 1.71 |
| σ 11 | −394 | 35 | −359 | −390 | 35 | −355 | 4 | 0 | 4 | |||
| σ 22 | 13 | 0 | 13 | 7 | 0 | 7 | −6 | 0 | −6 | |||
| σ 33 | 82 | 5 | 87 | 81 | 5 | 86 | −1 | 0 | −1 | |||
| 2 × C–P | σ iso | −65 | −10 | −75 | −24 | −12 | −36 | 41 | −2 | 39 | 98 | 1.96 |
| σ 11 | 4 | −2 | 2 | 54 | −4 | 50 | 50 | −2 | 48 | |||
| σ 22 | −100 | −23 | −123 | −27 | −26 | −53 | 73 | −3 | 70 | |||
| σ 33 | −99 | −5 | −104 | −99 | −5 | −104 | 0 | 0 | 0 | |||
| 1score-Ce | σ iso | 201 | 0 | 201 | 207 | 0 | 207 | 6 | 0 | 6 | 100 | 2.00 |
| Σ other | σ iso | −11 | 10 | −1 | 2 | −1 | 1 | 13 | −11 | 2 | ||
Inspection of the data in Table 1 reveals that the principal shielding contributions to the δiso values of 1 and 2 are dominated by the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ- and π-bond components supplemented by smaller C–P bond contributions. These contributions are in essence counter-balanced only by the σd contribution from the 1s core Ccarbene orbital since various Lewis and Non-Lewis contributions from the Ce ions and other minor contributions tend to cancel out. Thus, like any other M
C σ- and π-bond components supplemented by smaller C–P bond contributions. These contributions are in essence counter-balanced only by the σd contribution from the 1s core Ccarbene orbital since various Lewis and Non-Lewis contributions from the Ce ions and other minor contributions tend to cancel out. Thus, like any other M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR2 bond, the Ccarbene centres in 1 and 2 exhibit δiso values that reflect stabilisation of the Ccarbene by the metal- and R-substituents (where here R = the phosphonium groups).
CR2 bond, the Ccarbene centres in 1 and 2 exhibit δiso values that reflect stabilisation of the Ccarbene by the metal- and R-substituents (where here R = the phosphonium groups).
Focussing on the SOR-NLMO-NMR aspects of Table 1, the data clearly show a dominance of the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds in total (1: −288 ppm; 2, −320 ppm) over the total two C–P bonds (1: −45 ppm; 2, −36 ppm) to the shielding. Thus, for 1 and 2 the M (here Ce) is performing the dominant stabilising role with the C–P constituting a much smaller stabilising role.
C bonds in total (1: −288 ppm; 2, −320 ppm) over the total two C–P bonds (1: −45 ppm; 2, −36 ppm) to the shielding. Thus, for 1 and 2 the M (here Ce) is performing the dominant stabilising role with the C–P constituting a much smaller stabilising role.
Where the split of σ- vs. π-bonding of the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds in 1 and 2 are concerned, in both cases the former component dominates over the latter, being ∼2
C bonds in 1 and 2 are concerned, in both cases the former component dominates over the latter, being ∼2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and ∼3
1 and ∼3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. This confirms that the σ-components are strongest, but it is also the case that for 1 and 2 in each case the π-components are over twice that of the two C–P bonds combined. The Ce
1, respectively. This confirms that the σ-components are strongest, but it is also the case that for 1 and 2 in each case the π-components are over twice that of the two C–P bonds combined. The Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π-bonds are thus clearly far from being negligible, and weaker π-bonds compared to σ-bonds would anyway be anticipated from basic σ- and π-orbital overlap efficiency arguments. The presence of Ce
C π-bonds are thus clearly far from being negligible, and weaker π-bonds compared to σ-bonds would anyway be anticipated from basic σ- and π-orbital overlap efficiency arguments. The presence of Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π-bonds from this analysis is also consistent with the QTAIM data that consistently present non-zero ellipticity parameters consistent with the presence of double bonds rather than the zero ellipticity parameters that are associated with single and triple bonds.
C π-bonds from this analysis is also consistent with the QTAIM data that consistently present non-zero ellipticity parameters consistent with the presence of double bonds rather than the zero ellipticity parameters that are associated with single and triple bonds.
Whilst the NLMO analysis does not report which virtual orbitals the NLMO orbitals are magnetically coupled to, the MO analysis provides the necessary framework to rationalise the NLMO shielding data. In particular, echoing the MO analysis the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ- and π-bonds all exhibit large deshielded σ11 values, that are consistently the largest components of the breakdown of σiso, resulting from σ/π* and π/σ* magnetic coupling that can be visualised as rotation of the relevant C p-orbitals about the x axis. Interestingly, for both complexes the C–P bonds show not insignificant deshielded σ22 and σ33 values, reflecting magnetic coupling that can be visualised as rotation of the C p-orbital aligned along the P–C–P bond (x axis) into the σ* (z axis, rotation about the y axis) and π* (y axis, rotation about the z axis), respectively. These contributions are facilitated by the T-shaped nature of the Ce
C σ- and π-bonds all exhibit large deshielded σ11 values, that are consistently the largest components of the breakdown of σiso, resulting from σ/π* and π/σ* magnetic coupling that can be visualised as rotation of the relevant C p-orbitals about the x axis. Interestingly, for both complexes the C–P bonds show not insignificant deshielded σ22 and σ33 values, reflecting magnetic coupling that can be visualised as rotation of the C p-orbital aligned along the P–C–P bond (x axis) into the σ* (z axis, rotation about the y axis) and π* (y axis, rotation about the z axis), respectively. These contributions are facilitated by the T-shaped nature of the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CP2 linkages in 1 and 2,31 but are still far smaller than the main Ce
CP2 linkages in 1 and 2,31 but are still far smaller than the main Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ- and π-bond contributions to the shielding.
C σ- and π-bond contributions to the shielding.
The NLMO analysis also reveals another interesting feature, which is that the σ-component is larger for 2 than for 1 even though in 2 there are two mutually trans-carbene donors; these strong σ-donors would ordinarily be anticipated to result in mutually weaker, not stronger, trans bonding. Thus, the shielding and bond order data presented here further support the presence of an ITI, which had previously been proposed for 2 on the basis of structural data and 5p-orbital in- and out-of-core calculations.19 This situation for 2 is accompanied by the π-bonding component still being present, but weaker than the π-bonding component in 1, which is in-line with the flexible nature of the bonding of these carbenes. This also likely reflects the dominance of the σ-bonding leaving the Ce ion with a diminished requirement for additional π-bonding compared to the situation in 1.
Since increased stabilisation is another way of articulating stronger bonding in covalent interactions, then given the relationship between shielding and σp and the NBO (and NLMO) bonding descriptions, these data support the presence of Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonding interactions in 1 and 2.
C double bonding interactions in 1 and 2.
The data in Table 1 also permits an analysis of the spin–orbit contributions by subtraction of the SR-NLMO values from the SOR-NLMO data. Notably, for 1 and 2 the dominant spin–orbit contributions are mediated by the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ-bonds rather than the π-bonds. This can be rationalised by recalling that the 4f-orbitals will likely mediate the majority of the spin–orbit contributions from the Ce ion, and that transfer of spin–orbit-induced spin-polarisation to the NMR-nucleus (Ccarbene) will be via the C 2s orbital (Fermi contact). The NBO (and NLMO) data consistently show significant 4f contributions to the Ce-bonding, but variable 2s C-character. The Ce
C σ-bonds rather than the π-bonds. This can be rationalised by recalling that the 4f-orbitals will likely mediate the majority of the spin–orbit contributions from the Ce ion, and that transfer of spin–orbit-induced spin-polarisation to the NMR-nucleus (Ccarbene) will be via the C 2s orbital (Fermi contact). The NBO (and NLMO) data consistently show significant 4f contributions to the Ce-bonding, but variable 2s C-character. The Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ-bonds consistently show ∼11–15% C 2s character, which is evidently sufficient to mediate the spin-polarisation by Fermi contact, whereas the Ce
C σ-bonds consistently show ∼11–15% C 2s character, which is evidently sufficient to mediate the spin-polarisation by Fermi contact, whereas the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π-bonds exhibit ≥98% 2p character and thus they have little 2s character to mediate spin–orbit contributions. Notably, the NLMO spin–orbit contribution for 2 is large, as it was for the σso value from the shielding analysis, for the Ce
C π-bonds exhibit ≥98% 2p character and thus they have little 2s character to mediate spin–orbit contributions. Notably, the NLMO spin–orbit contribution for 2 is large, as it was for the σso value from the shielding analysis, for the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ-bond. This further supports the presence of significant 4f-orbital character in the Ce
C σ-bond. This further supports the presence of significant 4f-orbital character in the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, even though 4f-orbitals are normally regarded as being ‘core-like’, which is also consistent with the presence of ITI bonding in 2.
C bond, even though 4f-orbitals are normally regarded as being ‘core-like’, which is also consistent with the presence of ITI bonding in 2.
Discussion
This study was prompted by the fact that diphosphonioalkylidenes have proven to be a highly effective ligand class for developing the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond chemistry of the lanthanides and early actinides, but the nature of these formal M
C double bond chemistry of the lanthanides and early actinides, but the nature of these formal M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interactions has been an open question due to the number of resonance forms that can be used to depict them. By undertaking computational analysis of experimental 13C NMR spectroscopic data of the two cerium(IV)–diphosphonioalkylidene complexes 1 and 2 the shielding values that underpin the experimentally observed δiso data have been computationally decomposed in detail, thus bringing quantitative benchmarks to a hitherto qualitatively descriptive framework.
C interactions has been an open question due to the number of resonance forms that can be used to depict them. By undertaking computational analysis of experimental 13C NMR spectroscopic data of the two cerium(IV)–diphosphonioalkylidene complexes 1 and 2 the shielding values that underpin the experimentally observed δiso data have been computationally decomposed in detail, thus bringing quantitative benchmarks to a hitherto qualitatively descriptive framework.
Having identified DFT functionals that reproduce the 13Ccarbeneδiso values to within 2 ppm, there can be confidence in the resulting computational benchmarking descriptions. It is interesting to note that whilst the BP86 functional does not reproduce the δiso values as well as B3LYP functionals, the MO, bond order, NBO, and NLMO analysis from either functional for 1 and 2 are, like-for-like, very similar. So whilst BP86 does not fare as well as B3LYP in the fine detail of reproducing shielding tensors, which are exceedingly sensitive to the computed wavefunction and spin–orbit effects, any differences recede with the arguably coarser orbital and bond order metrics. The tentative implication is that BP86 is adequate for ‘generic’ orbital and bond order analysis, but a hybrid functional really is needed for ‘specific’ sensitive spectroscopic parameters, a situation that was also found in modelling a terminal uranium(VI)-nitride.58
The consistent picture that emerges from the computational analysis is that the highly deshielded experimentally observed 13Ccarbeneδiso values are predominantly due to large, negative σp values, which in themselves directly reflect strong Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C multiple bonds and external field-induced magnetic coupling of occupied and vacant orbitals associated with that linkage. Indeed, complexes 1 and 2 exhibit the largest 13C chemical shift tensor spans of any metal-alkylidene to date.31–35 The NLMO-NMR analysis reveals a dominance of Ce
C multiple bonds and external field-induced magnetic coupling of occupied and vacant orbitals associated with that linkage. Indeed, complexes 1 and 2 exhibit the largest 13C chemical shift tensor spans of any metal-alkylidene to date.31–35 The NLMO-NMR analysis reveals a dominance of Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ- over π-bond contributions, but these combined are far greater than the contributions from the phosphonium-substituents. The Ce
C σ- over π-bond contributions, but these combined are far greater than the contributions from the phosphonium-substituents. The Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π-bonds, perhaps the most debatable component of the bonding, are hence shown to be far more substantial than the two phosphonium-substituents combined, which together reaffirms the notion that the Ce
C π-bonds, perhaps the most debatable component of the bonding, are hence shown to be far more substantial than the two phosphonium-substituents combined, which together reaffirms the notion that the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond is principally stabilised by the Ce ion, with the two phosphonium-substituents providing much weaker stabilisation. These data are all consistent with prior QTAIM data, whose ellipticity parameters were consistent only with the presence of Ce
C bond is principally stabilised by the Ce ion, with the two phosphonium-substituents providing much weaker stabilisation. These data are all consistent with prior QTAIM data, whose ellipticity parameters were consistent only with the presence of Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds in 1 and 2. Indeed, the consistent picture that emerges from the MO and NLMO analysis is the dominance of the strongly deshielded σ11 component, which is a signature of alkylidenes.31
C double bonds in 1 and 2. Indeed, the consistent picture that emerges from the MO and NLMO analysis is the dominance of the strongly deshielded σ11 component, which is a signature of alkylidenes.31
The NLMO analysis also clearly shows that the two Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ-bonds in 2 are evidently strong, which given they are mutually trans is notable and provides further support for the prior suggestion of the presence of an ITI in 2.19 The NLMO analysis also shows variable transmittance of spin–orbit-coupling, which can be related to the hybridisation of the alkylidene centres, i.e. greater 2s character facilitates greater σso. That there are substantial spin–orbit contributions that likely originate from the Ce 4f-orbitals, which are usually described as ‘core-like’ and hence interacting little with ligand frontier orbitals, is notable and in-line with the overall description of 1 and 2 as exhibiting significant Ce
C σ-bonds in 2 are evidently strong, which given they are mutually trans is notable and provides further support for the prior suggestion of the presence of an ITI in 2.19 The NLMO analysis also shows variable transmittance of spin–orbit-coupling, which can be related to the hybridisation of the alkylidene centres, i.e. greater 2s character facilitates greater σso. That there are substantial spin–orbit contributions that likely originate from the Ce 4f-orbitals, which are usually described as ‘core-like’ and hence interacting little with ligand frontier orbitals, is notable and in-line with the overall description of 1 and 2 as exhibiting significant Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds. Lastly, the clearly larger spin–orbit contributions for 2 compared to 1 reflects the strong Ce
C double bonds. Lastly, the clearly larger spin–orbit contributions for 2 compared to 1 reflects the strong Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C σ-bonding, which again emphasises the presence of an ITI in this tetravalent complex.
C σ-bonding, which again emphasises the presence of an ITI in this tetravalent complex.
Conclusions
To conclude, assessing the shielding tensors that underpin the δiso values for 1 and 2 has enabled a detailed investigation of the nature of the Ce–BIPM interactions in these complexes, including confirming the Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond character, revealing a record 13C chemical shift tensor span, signature deshielded σ11 components, and providing further support for the presence of an ITI in 2. The known 13Ccarbene chemical shift range for f-element–diphosphonioalkyidene complexes spans over 300 ppm,1–10 and so clearly there is a wide variance of bonding situations, from highly ionic at low, shielded δiso values all the way to substantial covalent M
C double bond character, revealing a record 13C chemical shift tensor span, signature deshielded σ11 components, and providing further support for the presence of an ITI in 2. The known 13Ccarbene chemical shift range for f-element–diphosphonioalkyidene complexes spans over 300 ppm,1–10 and so clearly there is a wide variance of bonding situations, from highly ionic at low, shielded δiso values all the way to substantial covalent M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds at high, deshielded δiso values. This work confirms the M
C double bonds at high, deshielded δiso values. This work confirms the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond credentials of f-element–diphosphonioalkylidene complexes, suggesting that mid-/high-valent uranium congeners also do indeed possess significant U
C double bond credentials of f-element–diphosphonioalkylidene complexes, suggesting that mid-/high-valent uranium congeners also do indeed possess significant U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds,38 thus providing benchmarks towards the upper end of M
C double bonds,38 thus providing benchmarks towards the upper end of M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonding character that will help provide an overall quantified framework for understanding diphosphonioalkylidene bonding generally.
C double bonding character that will help provide an overall quantified framework for understanding diphosphonioalkylidene bonding generally.
Methods
Magic angle spinning (MAS) NMR spectra were recorded on a Bruker 9.4 T (400 MHz 1H Larmor frequency) AVANCE III spectrometer equipped with a 4 mm HFX MAS probe that was used in 1H/19F/13C triple resonance mode. Experiments were acquired at ambient temperature using a MAS frequency of 8 or 11 kHz. 1H- and 13C-pulses of 100 kHz and 50 kHz were used, respectively, and spectra were recorded after {1H}13C cross-polarisation (CP, 4 ms for 1 and 2 ms for 2) and an echo sequence that used a free-evolution delay of 1 rotor period either side of the π-pulse. For CP, a 70–100% ramp was used for 1H to match 50 kHz 13C spin-locking. The 1H T1 was 0.14 s for 1 and 3.5 s for 2. Recycle delays of 1.0 and 4.6 s were used for 1 and 2, respectively and the {1H-}13C CPMAS NMR spectra were recorded for 88 and 65 hours, respectively. The 13C chemical shifts were referenced to TMS using an external reference sample. Spectral simulations were performed in the solid line-shape analysis (SOLA) module v2.2.4 in Bruker TopSpin v4.0.9. Samples were packed into 4 mm o.d. zirconia rotors in a glove box and sealed with a Kel-F rotor cap. Care must be taken with air sensitive compounds to minimise sample decomposition during measurements.Restricted calculations were performed using the Amsterdam Density Functional (ADF) suite version 2017 with standard convergence criteria.74,75 Geometry optimisations were performed using coordinates derived from the respective crystal structures as the starting points. The H-atom positions were optimised, but the non-H-atom positions were constrained as a block. The DFT geometry optimisations employed Slater type orbital (STO) TZ2P polarisation all-electron basis sets (from the Dirac and ZORA/TZ2P database of the ADF suite). Scalar relativistic approaches (spin–orbit neglected) were used within the ZORA Hamiltonian76–78 for the inclusion of relativistic effects and the local density approximation (LDA) with the correlation potential due to Vosko et al. was used in all of the calculations.79 Generalised gradient approximation corrections were performed using the functionals of Becke and Perdew.80,81
Scalar and spin–orbit relativistic (ZORA-TZ2P-all-electron) single point energy calculations were then run on the geometry optimised coordinates. The conductor-like screening model (COSMO) was used to simulate benzene solvent effects. The functionals screened included BP86, PBE0-HF25, PBE0-HF40, B3LYP-HF20, B3LYP-HF30, B3LYP-HF35, and B3LYP-HF40, with B3LYP-HF20 and B3LYP-HF30 giving the closest agreement of computed NMR properties compared to experiment for 1 and 2, respectively. Nalewajski-Mrozek values were computed within the ADF program. NBO and NLMO analyses were carried out on the respective B3LYP data using NBO6.82 These calculations used the Hartree–Fock RI scheme to suspend the dependency key and overcome numerical issues. The MOs and NBOs were visualised using ADFView.
NMR shielding calculations were carried out using the NMR program within ADF.72,73,83–87 Calculated nuclear shieldings were converted to chemical shifts by subtraction from the calculated nuclear shielding of CH4 calculated at the same SR or SOR functional level in each case (HF20 SR/SOR = 191.3/192.1; HF30 SR/SOR = 191.4/192.2). MO contributions to the nuclear shieldings were calculated at the scalar and spin–orbit levels, the former with the FAKESO key. Scalar and spin–orbit NLMO calculations of the computed nuclear shieldings were carried out using NBO6 and ADF. These calculations used the Hartree–Fock RI scheme to suspend the dependency key and avoid numerical issues. Shielding tensors were visualised using TensorView.88
Data availability
All data are available within this article, the ESI (Tables S1–S8†), or from S. T. L. on reasonable request.Author contributions
C. F. B. and J. A. S. prepared and purified the compounds and assisted in acquiring and analysing the solid-state NMR data. D. L. acquired and analysed the solid-state NMR data. R. W. A., D. L., and S. T. L. supervised and directed the research. S. T. L. conceived the central idea, conducted the DFT calculations, analysed the data, and wrote the manuscript with input from all the authors.Conflicts of interest
The author declares no competing interests.Acknowledgements
Funding and support from the UK Engineering and Physical Sciences Research Council (grants EP/W029057/1, EP/M027015/1, EP/F030517/1, EP/V007580/1, EP/K039547/1), European Research Council (grants 239621 and 612724), and The University of Manchester including computational resources and associated support services from the Computational Shared Facility are gratefully acknowledged. The Alexander von Humboldt Foundation is thanked for a Friedrich Wilhelm Bessel Research Award to S. T. L. David Bonham is acknowledged and thanked for assistance in acquiring the solid-state NMR spectra.Notes and references
- N. D. Jones and R. G. Cavell, J. Organomet. Chem., 2005, 690, 5485–5496 CrossRef CAS.
- T. Cantat, N. Mézailles, A. Auffrant and P. Le Floch, Dalton Trans., 2008, 1957–1972 RSC.
- T. W. Hayton, Dalton Trans., 2010, 39, 1145–1158 RSC.
- S. T. Liddle, D. P. Mills and A. J. Wooles, Chem. Soc. Rev., 2011, 40, 2164–2176 RSC.
- M. Ephritikhine, C. R. Chim., 2013, 16, 391–405 CrossRef CAS.
- T. W. Hayton, Chem. Commun., 2013, 49, 2956–2973 RSC.
- V. H. Gessner, J. Becker and K.-S. Feichtner, Eur. J. Inorg. Chem., 2015, 1841–1859 CrossRef CAS.
- M. Gregson, A. J. Wooles, O. J. Cooper and S. T. Liddle, Comments Inorg. Chem., 2015, 35, 262–294 CrossRef CAS.
- S. T. Liddle, Angew. Chem., Int. Ed., 2015, 54, 8604–8641 CrossRef CAS PubMed.
- M. Fustier-Boutignon, N. Nebra and N. Mézailles, Chem. Rev., 2019, 119, 8555–8700 CrossRef CAS PubMed.
- D. P. Mills, L. Soutar, W. Lewis, A. J. Blake and S. T. Liddle, J. Am. Chem. Soc., 2010, 132, 14379–14381 CrossRef CAS.
- O. J. Cooper, D. P. Mills, J. McMaster, F. Moro, E. S. Davies, W. Lewis, A. J. Blake and S. T. Liddle, Angew. Chem., Int. Ed., 2011, 50, 2383–2386 CrossRef CAS.
- D. P. Mills, F. Moro, J. McMaster, J. van Slageren, W. Lewis, A. J. Blake and S. T. Liddle, Nat. Chem., 2011, 3, 454–460 CrossRef CAS PubMed.
- D. P. Mills, O. J. Cooper, F. Tuna, E. J. L. McInnes, E. S. Davies, J. McMaster, F. Moro, W. Lewis, A. J. Blake and S. T. Liddle, J. Am. Chem. Soc., 2012, 134, 10047–10054 CrossRef CAS PubMed.
- M. Gregson, E. Lu, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Angew. Chem., Int. Ed., 2013, 52, 13016–13019 CrossRef CAS PubMed.
- E. Lu, O. J. Cooper, J. McMaster, F. Tuna, E. J. L. McInnes, W. Lewis, A. J. Blake and S. T. Liddle, Angew. Chem., Int. Ed., 2014, 53, 6696–6700 CrossRef CAS.
- M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, Chem. Sci., 2016, 7, 155–165 RSC.
- M. Gregson, E. Lu, F. Tuna, E. J. L. McInnes, C. Hennig, A. C. Scheinost, J. McMaster, W. Lewis, A. J. Blake, A. Kerridge and S. T. Liddle, Chem. Sci., 2016, 7, 3286–3297 RSC.
- M. Gregson, E. Lu, D. P. Mills, F. Tuna, E. J. L. McInnes, C. Hennig, A. C. Scheinost, J. McMaster, W. Lewis, A. J. Blake, A. Kerridge and S. T. Liddle, Nat. Commun., 2017, 8, 14137 CrossRef CAS PubMed.
- E. Lu, J. T. Boronski, M. Gregson, A. J. Wooles and S. T. Liddle, Angew. Chem., Int. Ed., 2018, 57, 5506–5511 CrossRef CAS PubMed.
- E. Lu, A. J. Wooles, M. Gregson, P. J. Cobb and S. T. Liddle, Angew. Chem., Int. Ed., 2018, 57, 6587–6591 CrossRef CAS PubMed.
- A. J. Wooles, D. P. Mills, F. Tuna, E. J. L. McInnes, G. T. W. Law, A. J. Fuller, F. Kremer, M. Ridgway, W. Lewis, L. Gagliardi, B. Vlaisavljevich and S. T. Liddle, Nat. Commun., 2018, 9, 2097 CrossRef PubMed.
- E. Lu, S. Sajjad, V. E. J. Berryman, A. J. Wooles, N. Kaltsoyannis and S. T. Liddle, Nat. Commun., 2019, 10, 634 CrossRef CAS PubMed.
- E. Lu, B. E. Atkinson, A. J. Wooles, J. T. Boronski, L. R. Doyle, F. Tuna, J. D. Cryer, P. J. Cobb, I. J. Vitorica-Yrezabal, G. F. S. Whitehead, N. Kaltsoyannis and S. T. Liddle, Nat. Chem., 2019, 11, 806–811 CrossRef CAS PubMed.
- C. A. P. Goodwin, A. J. Wooles, J. Murillo, E. Lu, J. T. Boronski, B. L. Scott, A. J. Gaunt and S. T. Liddle, J. Am. Chem. Soc., 2022, 144, 9764–9774 CrossRef CAS PubMed.
- A. T. Normand, E. D. S. Carrizo, C. Magnoux, E. Lobato, H. Cattey, P. Richard, S. Brandès, C. H. Devillers, A. Romieu, P. Le Gendre and P. Fleurat-Lessard, Chem. Sci., 2021, 12, 253–269 RSC.
- S. T. Liddle, J. McMaster, J. C. Green and P. L. Arnold, Chem. Commun., 2008, 1747–1749 RSC.
- L. A. Solola, A. V. Zabula, W. L. Dorfner, B. C. Manor, P. J. Carroll and E. J. Schelter, J. Am. Chem. Soc., 2016, 138, 6928–6931 CrossRef CAS.
- D. S. Levine, T. D. Tilley and R. A. Andersen, Organometallics, 2017, 36, 80–88 CrossRef CAS.
- P. Rungthanaphatsophon, P. Huang and J. R. Walensky, Organometallics, 2018, 37, 1884–1891 CrossRef CAS.
- S. Halbert, C. Copéret, C. Raynaud and O. Eisenstein, J. Am. Chem. Soc., 2016, 138, 2261–2272 CrossRef CAS.
- K. Yamamoto, C. P. Gordon, W.-C. Liao, C. Copéret, C. Raynaud and O. Eisenstein, Angew. Chem., Int. Ed., 2017, 56, 10127–10131 CrossRef CAS.
- C. P. Gordon, K. Yamamoto, K. Searles, S. Shirase, R. A. Andersen, O. Eisenstein and C. Copéret, Chem. Sci., 2018, 9, 1912–1918 RSC.
- C. P. Gordon, D. B. Culver, M. P. Conley, O. Eisenstein, R. A. Andersen and C. Copéret, J. Am. Chem. Soc., 2019, 141, 648–656 CrossRef CAS.
- C. P. Gordon, C. Raynaud, R. A. Andersen, C. Copéret and O. Eisenstein, Acc. Chem. Res., 2019, 52, 2278–2289 CrossRef CAS PubMed.
- V. H. Gessner, F. Meier, D. Uhrich and M. Kaupp, Chem.–Eur. J., 2013, 19, 16729–16739 CrossRef CAS PubMed.
- D. E. Smiles, G. Wu, P. Hrobárik and T. W. Hayton, Organometallics, 2017, 36, 4519–4524 CrossRef CAS.
- A. H. Greif, P. Hrobárik, J. Autschbach and M. Kaupp, Phys. Chem. Chem. Phys., 2016, 18, 30462–30474 RSC.
- J. Vĺcha, J. Novotný, S. Komorovsky, M. Straka, M. Kaupp and R. Marek, Chem. Rev., 2020, 120, 7065–7103 CrossRef PubMed.
- S. P. Gabuda, L. G. Falaleeva and Y. V. Gagarinskii, Phys. Status Solidi B, 1969, 33, 435–438 CrossRef CAS.
- H. Cho, W. A. De Jong and C. Z. Soderquist, J. Chem. Phys., 2010, 132, 084501 CrossRef PubMed.
- P. Hrobárik, V. Hrobáriková, A. H. Greif and M. Kaupp, Angew. Chem., Int. Ed., 2012, 51, 10884–10888 CrossRef PubMed.
- L. A. Seaman, P. Hrobárik, M. F. Schettini, S. Fortier, M. Kaupp and T. W. Hayton, Angew. Chem., Int. Ed., 2013, 52, 3259–3263 CrossRef CAS PubMed.
- L. Martel, N. Magnani, J.-F. Vigier, J. Boshoven, C. Selfslag, I. Farnan, J.-C. Griveau, J. Somers and T. Fanghänel, Inorg. Chem., 2014, 53, 6928–6933 CrossRef CAS PubMed.
- L. Martel, J.-F. Vigier, D. Prieur, S. Nourry, A. Guiot, K. Dardenne, J. Boshoven and J. Somers, J. Phys. Chem. C, 2014, 118, 27640–27647 CrossRef CAS.
- D. E. Smiles, G. Wu, P. Hrobárik and T. W. Hayton, J. Am. Chem. Soc., 2016, 138, 814–825 CrossRef CAS PubMed.
- C. Capan, R. J. Dempsey, S. Sinkov, B. K. McNamara and H. Cho, Phys. Rev. B, 2016, 93, 224409 CrossRef.
- A. M. Mounce, H. Yasuoka, G. Koutroulakis, J. A. Lee, H. Cho, F. Gendron, E. Zurek, B. L. Scott, J. A. Trujillo, A. K. Slemmons, J. N. Cross, J. D. Thompson, S. A. Kozimor, E. D. Bauer, J. Autschbach and D. L. Clark, Inorg. Chem., 2016, 55, 8371–8380 CrossRef CAS PubMed.
- L. Martel, E. Capelli, M. Body, M. Klipfel, O. Benes, L. Maksoud, P. E. Raison, E. Suard, L. Visscher, C. Bessada, C. Legein, T. Carpentier and A. Kovács, Inorg. Chem., 2018, 57, 15350–15360 CrossRef CAS PubMed.
- L. Martel, A. Hen, Y. Tokunaga, F. Kinnart, N. Magnani, E. Colineau, J.-C. Griveau and R. Caciuffo, Phys. Rev. B, 2018, 98, 014410 CrossRef CAS.
- M. A. Devore, C. A. Klug, M. R. Kriz, L. E. Roy and M. S. Wellons, J. Phys. Chem. A, 2018, 122, 6873–6878 CrossRef CAS PubMed.
- K. C. Mullane, P. Hrobárik, T. Cheisson, B. C. Manor, P. J. Carroll and E. J. Schelter, Inorg. Chem., 2019, 58, 4152–4163 CrossRef CAS.
- S. L. Staun, D. C. Sergentu, G. Wu, J. Autschbach and T. W. Hayton, Chem. Sci., 2019, 10, 6431–6436 RSC.
- D.-C. Sergentu, G. T. Kent, S. L. Staun, X. Yu, H. Cho, J. Autschbach and T. W. Hayton, Inorg. Chem., 2020, 59, 10138–10145 CrossRef CAS.
- G. B. Panetti, D.-C. Sergentu, M. R. Gau, P. J. Carroll, J. Autschbach, P. J. Walsh and E. J. Schelter, Nat. Commun., 2021, 12, 1713 CrossRef CAS.
- B. L. L. Réant, V. E. J. Berryman, A. R. Basford, L. E. Nodaraki, A. J. Wooles, F. Tuna, N. Kaltsoyannis, D. P. Mills and S. T. Liddle, J. Am. Chem. Soc., 2021, 143, 9813–9824 CrossRef PubMed.
- O. Ordoñez, X. Yu, G. Wu, J. Autschbach and T. W. Hayton, Inorg. Chem., 2021, 60, 12436–12444 CrossRef PubMed.
- J. Du, J. A. Seed, V. E. J. Berryman, N. Kaltsoyannis, R. W. Adams, D. Lee and S. T. Liddle, Nat. Commun., 2021, 12, 5649 CrossRef CAS PubMed.
- G. T. Kent, X. Yu, G. Wu, J. Autschbach and T. W. Hayton, Chem. Sci., 2021, 12, 14383–14388 RSC.
- G. T. Kent, X. Yu, C. Pauly, G. Wu, J. Autschbach and T. W. Hayton, Inorg. Chem., 2021, 60, 15413–15420 CrossRef CAS PubMed.
- G. T. Kent, X. Yu, G. Wu, J. Autschbach and T. W. Hayton, Chem. Commun., 2022, 58, 6805–6808 RSC.
- J. Du, J. Hurd, J. A. Seed, G. Balázs, M. Scheer, R. W. Adams, D. Lee and S. T. Liddle, J. Am. Chem. Soc., 2023, 145, 21766–21784 CrossRef CAS PubMed.
- ADF Manual, Release 2017, p. 57 Search PubMed.
- N. F. Ramsey, Phys. Rev., 1950, 78, 699–703 CrossRef CAS.
- N. F. Ramsey, Phys. Rev., 1951, 83, 540–541 CrossRef CAS.
- N. F. Ramsey, Phys. Rev., 1952, 86, 243–246 CrossRef CAS.
- C. M. Widdifield and R. W. Schurko, Concepts Magn. Reson., Part A, 2009, 34, 91–123 CrossRef.
- K. Sutter and J. Autschbach, J. Am. Chem. Soc., 2012, 134, 13374–13385 CrossRef CAS PubMed.
- P.-A. Payard, L. A. Perego, L. Grimaud and I. Ciofini, Organometallics, 2020, 39, 3121–3130 CrossRef CAS.
- C. Raynaud, E. Norbert-Agaisse, B. R. James and O. Eisenstein, Inorg. Chem., 2020, 59, 17038–17048 CrossRef CAS PubMed.
- W. J. Transue, Y. Dai, M.-L. Y. Riu, G. Wu and C. C. Cummins, Inorg. Chem., 2021, 60, 9254–9258 CrossRef CAS PubMed.
- J. Autschbach, J. Chem. Phys., 2008, 128, 164112 CrossRef PubMed.
- J. Autschbach and S. Zheng, Magn. Reson. Chem., 2008, 46, S45–S55 CrossRef PubMed.
- C. Fonseca Guerra, J. G. Snijders, G. Te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. Van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- E. Van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- E. Van Lenthe, A. E. Ehlers and E. J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 2134 CrossRef CAS.
- G. Schreckenbach and T. Ziegler, J. Phys. Chem., 1995, 99, 606–611 CrossRef CAS.
- J. Autschbach and E. Zurek, J. Phys. Chem. A, 2003, 107, 4967–4972 CrossRef CAS.
- M. Krykunov, T. Ziegler and E. Van Lenthe, Int. J. Quantum Chem., 2009, 109, 1676–1683 CrossRef CAS.
- S. K. Wolff, T. Ziegler, E. Van Lenthe and E. J. Baerends, J. Chem. Phys., 1999, 110, 7689–7698 CrossRef CAS.
- J. Autschbach, Mol. Phys., 2013, 111, 2544–2554 CrossRef CAS.
- R. P. Young, C. R. Lewis, C. Yang, L. Wang, J. K. Harper and L. J. Mueller, TensorView: A Software Tool for Displaying NMR Tensors, Magn. Reson. Chem., 2019, 57, 211–223 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details. See DOI: https://doi.org/10.1039/d3sc04449a |
| This journal is © The Royal Society of Chemistry 2024 |