Biomimetic growth in polymer gels

Abstract

By modeling gels growing in confined environments, we uncover a biomimetic feedback mechanism between the evolving gel and confining walls that enables significant control over the properties of the grown gel. Our new model describes the monomer adsorption, polymerization and cross-linking involved in forming new networks and the resultant morphology and mechanical behavior of the grown gel. Confined between two hard walls, a thin, flat “parent” gel undergoes buckling; removal of the walls returns the gel to the flat structure. Polymerization and cross-linking in the confined parent generates the next stage of growth, forming a random copolymer network (RCN). When the walls are removed, the RCN remains in the buckled state, simultaneously “locking in” these patterns and increasing the Young's modulus by two orders of magnitude. Confinement of thicker gels between harder or softer 3D walls leads to controllable mechanical heterogeneities, where the Young's modulus between specific domains can differ by three orders of magnitude. These systems effectively replicate the feedback between mechanics and morphology in biological growth, where mechanical forces guide the structure formation throughout stages of growth. The findings provide new guidelines for shaping “growing materials” and introducing new approaches to matching form and function in synthetic systems.

---

Anna C. Balazs

I joined the Editorial Board in 2015 and even in those early days, you could feel that this journal was going to be something special. The RSC team and editors did a great job in getting it off the ground and letting the community know that this was a home for showcasing new discoveries in materials science. Given the caliber of papers being published in Materials Horizons, I think that the journal will continue to be the go-to resource for reading about cutting edge findings. I look forward to the continued success of the journal in the next decade.

---

New concepts

Morphogenesis refers to the coupling of the progressive growth and structure formation that commonly occurs when soft biomaterials are confined by harder surfaces. Translating this behavior into the synthetic realm would enable fabrication of biomimetic materials whose forms can be dynamically fashioned for optimal functionality. We develop a new model for the progressive growth of gels localized between various walls to determine how confining surfaces control the shape and mechanical properties of the grown materials. The model describes a “parent” gel swollen by monomers, and the subsequent polymerization, cross-linking and inter-chain exchange involved in growing a random copolymer network. The studies reveal that these growing gels replicate the feedback between mechanics and morphology in biological growth, where mechanical forces guide the structure formation, which introduces new mechanical forces that act on subsequent growth. We demonstrate how physical patterning of growing gels can produce Young's moduli that are order of magnitude greater than the parent network. Our findings provide guidelines for tailoring the shape and mechanical properties of “growing” materials, and introduce new approaches to matching form and function in synthetic systems.

I. Introduction

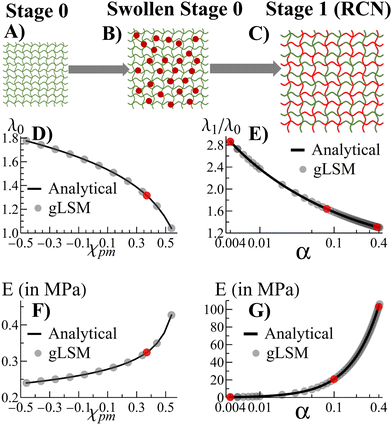
Morphogenesis refers to the coupling of structure formation and progressive growth in biological matter. Due to the crowded environments presented in the biological realm, the growth of soft biomaterials commonly occurs in the presence of confining boundaries formed by neighboring matter (e.g., the extracellular matrix, vascular channels, muscle, and bone). Due to the latter boundaries, structures grow under local mechanical stresses, which continue to guide the structural evolution of the biomaterial. The dynamic link between growth and mechanical forces leads to an inherent coupling between form and function in biology, with the emerging forms being sculpted over time to meet the ultimate functionality. This beneficial coupling is not commonly seen in the development of synthetic materials, which typically cannot undergo self-sustained, continuous growth. Recently, however, researchers developed biomimetic polymer gels that can continue to absorb monomers and cross-linkers from fluidic surroundings to form additional mass and propagate the growth of the network.^1–4 Also, there has been work on formation of 3D shapes of gels due to confinement.^5,6 Here, we develop a computational approach to simulate the progressive growth of these gels (Fig. 1) and investigate how neighboring surfaces control the developing shapes and enhance the utility of the grown material. These systems are seen to replicate the feedback between mechanics and morphology in biological growth, where mechanical forces guide the structure formation, which templates further growth and introduces new mechanical forces that guide subsequent growth. The findings provide new guidelines for shaping “growing materials” and thus introducing new approaches to matching form and function in synthetic systems.

Fig. 1 Schematic of the (A) as-prepared primary polymer network (in green) (B) Stage 0 primary network swollen in a liquid containing monomers and crosslinkers (red disks). The absorbed secondary monomers undergo polymerization, cross-linking, and inter-chain exchange with the primary network (not shown) to form a Stage 1 random copolymer network (RCN). (C) Schematics of the swollen Stage 1 RCN in the same monomer solution as in Stage 0. The green and red lines depict the primary and secondary polymer chains respectively. (D) The equilibrium degree of swelling λ₀ and (F) Young's modulus E of the Stage 0 primary gel as a function of the polymer-monomer interaction parameter χ_pm. (E) The relative degree of swelling λ₁/λ₀ and (G) Young's modulus E for Stage 1 of growth of the RCN as a function of the cross-linker fraction α at χ_pm= 0.33. In (D)–(G), the lines represent the steady state numerical solution obtained using Mathematica™ and the symbols denote the numerical solutions obtained using the gLSM simulation. The model parameters are provided in the main text. For the remainder of the paper, gLSM simulations were conducted using one of the parameter values indicated by the red symbols.

We previously developed an analytical model³ to investigate the growth of gels from an initial polymer network (“parent”). The model revealed how growth can be tailored to create samples of specified size and mechanical properties. We now translate the analytical model into a lattice-based computational technique, which we refer to as the “gel lattice spring model” (gLSM).^7–10Via the gLSM, we explicitly simulate the adsorption, polymerization and cross-linking of monomers, and the formation of new networks in the “parent” gel. We can vary the properties of individual elements in the gel to introduce levels of structural heterogeneity not readily achievable in analytical models. Consequently, we can probe and visualize gel growth in the presence of confining boundaries that mimic constrained environments affecting development within living systems.

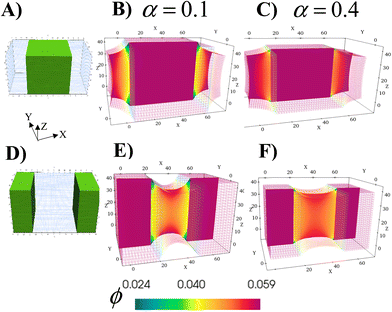
Fig. 1A–C depict the scheme for gel growth described in our analytical model³ for unconstrained growth. In Stage 0, the primary (parent) gel is placed into a liquid composed of monomer and cross-linkers. This “monomer solution” can diffuse into the gel and cause it to swell (Fig. 1B). As the last step of Stage 0, this swollen gel equilibrates to reach its final size.

Stage 1 starts with the polymerization of the monomers adsorbed at the end of Stage 0. This polymerization leads to the formation of the secondary chains, which then cross-link to form a distinct, new network within the primary gel. At this point, the secondary chains can undergo exchange reactions with the primary gel to form a random copolymer network (RCN). Note that during the latter crosslinking process, we calculate the amount of sol (a mixture of disconnected, small gel-like pieces and uncross-linked chains) and remove them from our final RCN (Fig. 1C).

In the last step of Stage 1, the RCN is placed in a bath that is identical to the initial monomer solution as in Fig. 1B. The RCN gel swells as monomeric units from the solution are incorporated into the network. This swollen gel now forms the medium for Stage 2 and so on.

Alternatively, we also carried out an analytical model that forms a different network, namely, the interpenetrating polymer network (IPN).³ Using our analytical model,³ we found that chains in the primary network within the swollen IPN (Stage 1) are relatively stretched. This stretching is entropically unfavorable and hinders uptake of monomer and cross-linker during further stages of growth. In contrast, the chain-exchange reactions between the primary (green) and secondary (red) networks (Fig. 1) relieve the tension from chain stretching. In addition, the exchange reaction leads to the formation of a considerable quantity of sol and hence, the RCN remains soft. As a result, the RCN provides the distinct advantage that the gel network can grow multiple times.³ Consequently, we focus on the RCNs in the following studies.

Using our computational gLSM,^7–10 we examine gel growth at hard surfaces, and within a soft matrix. These situations mimic the constraints in biological environments and the confining walls in manmade devices. Consequently, the findings can provide insight into the feedback between local mechanical stresses and the evolving structure in biological morphogenesis, and yield guidelines for adapting morphogenesis to fabricate materials where form is dynamically fashioned for optimal functionality.

It is important to note that schemes other than the ones cited above have led to successful gel growth.^11–16 For example, researchers embedded photo-active iniferter groups into the parent gel. With the application of light, the iniferters draw on monomers and cross-linkers from the surrounding solution to initiate a photo-controlled radical polymerization (photo-CRP) and thereby grow a “child” within the parent network.¹¹ Researchers also harnessed structurally tailored and engineered macromolecular (STEM) gels as a foundation for synthesizing growing gels.^12–14 The system is comprised of a primary cross-linked “scaffold” containing latent active sites (inimers), which are used to initiate the polymerization and incorporation of the secondary chains in the initial scaffold. The STEM gel properties and functionality can be modified through these secondary chains (or the controlled attachment of organic molecules, proteins, or nanoparticles), which differentiate the grown gel from the initial scaffolds.

Below, we detail the governing equations in the gLSM and validate the model by comparison with results obtained from the analytical theory.

II. Methodology

In these simulations, a gel is represented by a set of hexahedral elements so that their vertices form a lattice, and the lattice nodes move due to elastic and osmotic forces from the adjacent elements. To model the process of gel growth in successive stages, we utilize our theoretical methodology that was formulated in ref. 3 Below, we describe the theoretical model, and then describe the incorporation of the theoretical framework into the gel lattice spring model (gLSM) for computer simulations. The primary network is characterized by the cross-link density, c₀, and the polymer volume fraction in the un-deformed state, ϕ₀. The un-deformed primary network is then swollen by immersing in a bath containing the secondary monomer and cross-linker. The degree of swelling of the primary un-deformed gel in the monomer solution (before polymerization and cross-linking) at equilibrium is denoted λ₀. Note, λ₀ = (V₀/V_ini)^1/3, where V₀ is the volume of swollen primary gel and V_ini is the volume of the as-prepared (un-deformed) primary gel. This degree of swelling characterizes the growth of the Stage 0 gel. The number fraction of cross-linkers in the imbibed secondary monomers is given by α. When equilibrated, the size of the swollen primary gel is fixed, and the absorbed monomeric units undergo a reversible chain-growth polymerization reaction, and the resulting polymer chains exhibit the Flory molecular weight distribution (MWD).¹⁷ The polymer chains further undergo simultaneous cross-linking and inter-chain exchange with the primary polymer network to form Stage 1 random copolymer network (RCN). After removal of the sol fraction, the sample is swollen in the same monomer solution as before, and the stage of growth is considered to be complete. The degree of swelling given by λ₁ = (V₁/V_ini)^1/3, where V₁ is the gel sample volume after the first stage of growth, characterizes growth of the gel during Stage 1.

For the primary polymer network, the equilibrium degree of swelling in the secondary monomer solution is determined by the balance of elastic and osmotic forces. The total elastic stress of the equilibrated sample, σ_tot, is balanced by the Flory–Huggins osmotic pressure due to the monomers, π_FH(ϕ):

σ_tot = π_FH(ϕ) (1)

To calculate the elastic stress in the gel, σ_tot in eqn (1), we use the neo-Hookean model,^18–20 which describes the elastic stress in a polymer network as a function of deformation. For the primary network, the elastic stress is given by σ_tot = σ_el(c₀, λ) = c₀λ⁻³ (λ² − 1/2). Here, the degree of swelling λ characterizes the deformation of a swollen gel. The elastic stress σ_el depends on the cross-link density c₀ of the polymer network. The expression for σ_el can also be formulated^7–9 in terms of the volume fraction ϕ = ϕ₀λ⁻³.

The Flory–Huggins osmotic pressure is given by

π_FH(ϕ) = −[ϕ + ln(1 − ϕ) + χ_pmϕ²] (2)

Here, ϕ is the volume fraction of the monomers in the primary polymer network. The osmotic pressure in eqn (2) depends on the Flory–Huggins parameter χ_pm, which describes interactions between the primary and the secondary monomeric units. Note that the monomer solution is comprised solely of the secondary monomers, without any other solvent. As described above, the absorbed monomers then undergo chain-growth polymerization reaction, and the resulting polymer chains exhibit the Flory molecular weight distribution (MWD). Then, the primary network and the newly formed polymer chains undergo inter-chain exchange and cross-linking to form the Stage 1 random copolymer network (RCN). The calculations related to polymerization and cross-linking are based on our previous study³ and given in detail in the ESI.†

Below, we briefly discuss the change in the stress balance calculations for the growth of RCN networks. In the process of simultaneous cross-linking and inter-chain exchange, the network exchange leads to the formation of a single network of cross-linked random copolymers consisting of the primary and secondary monomeric units. As a result, there is only one contribution to the elastic stress σ_tot characterized by the single cross-link density c^(RCN)₁. The sol fraction, S^(RCN)₁, removed from the network also contains the primary and secondary monomeric units. The calculations of c^(RCN)₁ and S^(RCN)₁ are discussed in the ESI.†

After the first stage of growth, the size of the Stage 1 RCN gel is determined by the following equation for the force balance

σ_el(c^(RCN)₁, λ/λ₀) = π_FH[ϕ⁽¹⁾(λ), ψ⁽¹⁾(λ)] (3)

Here, ϕ⁽¹⁾(λ) = (1 − S^(RCN)₁)ϕ₀λ⁻³ is the volume fraction of the primary monomeric units after removal of the sol fraction, and ψ⁽¹⁾(λ) = (1 − S^(RCN)₁)(1 − ϕ₀λ₀⁻³)(λ₀/λ)³ is the volume fraction of the secondary monomers incorporated into the Stage 1 RCN. As described above, λ₀ is the degree of swelling of the primary network. The osmotic pressure in eqn (3) depends on the volume fraction of both primary and secondary monomeric units:

π_FH(ϕ, ψ) = −[ϕ + ψ + ln(1 − ϕ − ψ) + χ_pmϕ²] (4)

The RCN is in the un-deformed state after each stage of growth due to the inter-chain exchange. The amount of primary monomers in the RCN decreases from stage to stage because of the removal of the sol fraction.

The incorporation of the above theory into the computational gLSM approach is described in the ESI.† Using the results of the gLSM, we plot the growth of the initial parent network (in Fig. 1D) and the equilibrium Young's modulus (Fig. 1F). The latter values depend on the Flory–Huggins parameter χ_pm, which describes interactions between the primary and secondary monomers. The value of χ_pm affects the amount of secondary units that are adsorbed. Using the value of χ_pm = 0.33, we characterize how the degree of swelling (Fig. 1E) and the equilibrium Young's modulus (Fig. 1G) for Stage 1 RCN changes as a function of the cross-linker fraction, α. Note that the gLSM results reproduces the analytical results obtained from the above eqn (1)–(4).

III. Results and discussion

The number of hexahedral elements along the directions X, Y, Z are given by L_X, L_Y, and L_Z, respectively. To validate our computational approach, we compare results obtained from the theory and gLSM simulations with a sample size of L_X × L_Y × L_Z (where L_X = L_Y = L_Z = 3) for the degree of swelling of the RCN at Stages 0 and 1. In Fig. 1C and D the solid black circles representing results from the gLSM simulations lie on top of the line obtained from the analytical calculations. The plots show that the gLSM results are in quantitative agreement with results from the analytical model.

The parameters used in the gLSM simulations representing the gel properties of the Stage 0 gel are taken from^3,9ϕ₀ = 0.139 and c₀ = 1.3 × 10⁻³. The spatial discretization of the undeformed (initial) sample is chosen as uniform along the X, Y, Z directions, and is given by dX = dY = dZ = 1, the time step of the simulations is chosen to be⁹ dt = 0.001, and the dimensionless kinetic coefficient was set at Λ₀ = 1000. For the polymerization and cross-linking of the Stage 1 gel, we use the rate of polymerization to depolymerization to be γ₊/γ₋ = 5 × 10⁶. Three distinct values of the fraction of cross-linker were used for different simulation scenarios: α = 0.004, 0.1, 0.4. We explicitly state the value of α where the simulation results are described. The results are presented in dimensionless simulation units. The units of modulus (stress) in physical units is given by σ₀ = k_BT/v_s = 135.33 MPa where k_B is the Boltzmann's constant, T is chosen to be 20 °C and v_s = 0.018 is the molar volume of water. The unit of length and time is chosen such that^9,21D = l₀²/t₀ = 2 × 10⁻⁵ cm² s⁻¹, which gives l₀ = 40 μm and t₀ = 1 s.

The simulations proceed through the following steps. The Stage 0 sample is prepared by swelling the parent gel in a bath containing a monomer solution. The gLSM equations for Stage 0 are used to model the dynamic swelling of the sample until it reaches the final equilibrium state. The volume fraction of absorbed monomers, ψ, at this swollen, equilibrated state are then utilized to build the Stage 1 RCN network by polymerizing and cross-linking the ψ monomers (see equations in Sections S1 and S2 in the ESI†). Equations described in Section S3 (ESI†) is then used to simulate the behavior of the Stage 1 RCN network after the chain-exchange and removal of the sol fraction have occurred. Note that the gel equations are not evolved during this process of polymerization and cross-linking.

Once the Stage 1 RCN is formed, we utilize the equations mentioned in Section S3 in the ESI† to model the dynamical evolution of the Stage 1 gel until it reaches final equilibrium configuration. Specifically, the nodes are evolved using eqn (S3.6) (ESI†) while the forces are calculated using (see eqn (S3.19) and (S3.22), ESI†) and the mobility is evaluated using (see eqn (S3.23), ESI†). When only a fraction of the gel elements in Stage 0 undergo polymerization and cross-linking, the elements contributing to the Stage 1 RCN gel are evolved with the relative deformation tensors and the RCN related dynamical equations, while the elements without the RCN are evolved with the equations of the Stage 0 gel.

In modeling confined samples, we utilized the Morse potential to represent the repulsion between the hard walls and freely swelling gel nodes. Specifically, we utilized the calculation of node-to-node forces as given in ref. 22. The parameters used for the Morse potential are provided in the ESI.†

Below, we use this computational approach to compare the systems’ behavior when gels of different sizes and shapes grow in the absence or presence of bordering walls. In particular, we determine the effects of confinement on systems of increasing complexity: thin, square samples; rectangular layers; mechanically patterned thin gels; and thicker gels bounded by hard or soft walls. As we show below for thin gels, growth to Stage 1 can trap the formation of non-equilibrium structures, even when shape-defining walls are removed. Analogous to biological morphogenesis,^15,23–29 the stresses are seen to play a vital role in directing the process of growth.

A. Confinement between hard surfaces: Stage 0 for a square gel layer

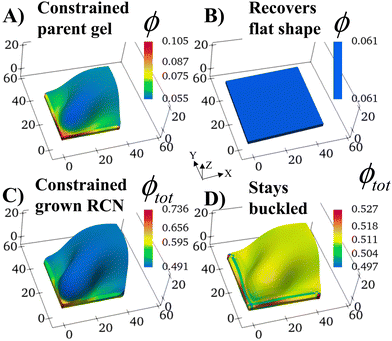
We consider a square flat gel in the as-prepared un-deformed state with the degree of swelling λ_ini = 1. The sample size is 35 × 35 × 2 elements in X, Y, Z directions, respectively. At Stage 0 in the absence of confinement, the swollen primary gel also is a square flat layer with the degree of swelling λ₀ = 1.3187 as the solvent is uniformly distributed in the sample.

The shape of the Stage 0 gel changes drastically if before swelling, we introduce two hard walls at the faces X = 0 and Y = 0 of the as-prepared primary gel. We require gel nodes on these surfaces to remain fixed in space, and thereby prohibiting their motion. In the course of swelling, these two immobile gel surfaces cause a spatially non-uniform distribution of solvent. The degree of swelling close to the constrained surfaces is less than that at the free boundaries, which are in contact with the solvent, and hence, the gel loses its initial square shape.

The constrained surfaces generate an uneven distribution of stress within the swelling gel. As a result, the parent gel morphs into a buckled structure (Fig. 2A) to diminish stress in the material. Such buckling has been predicted and observed when swollen polymer gels are confined by a hard surface^30–36 or purposefully planned through site-specific swelling.³⁷ The colors in the plot indicate the local volume fraction of polymer ϕ, which is an effective measure of stress in the sample (high stress at high values of ϕ). The polymer volume fraction (and stress) is highest at the bound edges since the gel anchored at the wall is constrained from expanding. The center of the sample shows the lowest ϕ, as seen in Fig. 2A.

Fig. 2 Shape changes due to gel swelling in square shaped gels of size 35 × 35 × 2 due to confining boundaries at the left and bottom surfaces. (A) The swollen “buckled” configuration of the Stage 0 gel. Upon release of the boundary constraints, the Stage 0 gel goes from the buckled (A) to the flat (B) configuration. (C) The final swollen configuration of the grown Stage 1 RCN gel at α = 0.4 where growth of Stage 1 was done starting with the buckled configuration (A) of the Stage 0 gel. Upon release of boundary constraints, the Stage 1 RCN does not relax back to a flat state but stays buckled (D). The color bars represent the volume fraction ϕ of the primary gel in (A) and (B), and the total volume fraction ϕ_tot of the Stage 1 RCN gel in (C) and (D).

The structural evolution of the confined parent gel goes through an intermediate, kinetically unstable state where any small perturbation pushes the system into the buckled structure (Fig. S2, ESI†). If the confining walls are now removed from the Stage 0 morphed sample, the primary gel eventually returns to a relaxed flat state, which has a lower free energy than the buckled structure (Fig. 2B).

If now unconstrained growth occurs on a free, flat parent, the resulting Stage 1 layer would also assume a flat geometry, i.e., the growth occurs without a shape change (Fig. S3, ESI†). The flat layers can still be altered by changing the cross-link density in the sample. An increase in the cross-link density leads to a decrease in the degree of swelling and in the mesh size within the gel (Fig. S3, ESI†).

B. Confinement between hard surfaces: Stage 1

With the walls remaining fixed in place, we initiate Stage 1 growth by polymerizing and cross-linking the species that diffused into the parent gel during its swelling and buckling. The fraction of cross-linker was chosen to be α = 0.4. After the chain-exchange and removal of the sol fraction, the Stage 1 RCN sample (Fig. 2C) effectively replicates the form of the confined parent network. When the walls are removed at this stage, however, the gel does not relax back to a flat configuration but remains in the buckled state (Fig. 2D). The growth fixes an energetically unfavorable, deformed shape into a stable configuration. The shape of the flat parent gel can be refashioned into other geometries with the introduction of different siding (e.g., walls on three or all four sides). While the free parent gel is mutable in this manner, the progeny is not.

The distortion induced in the confined parent gel is more pronounced in the progeny, as indicated by Fig. 3A. The maximum height in the diagonal cross-section for the Stage 1 (confined or released) is 1.45 times greater than the height for the parent. Thus, the shape of the confined parent gel templates and amplifies the morphology of subsequent growth. In a manner of speaking, the system encompasses “memory” since the buckled shape in Stage 0 under confinement is stored in the system and recalled to regulate the next stage of development during gel growth.

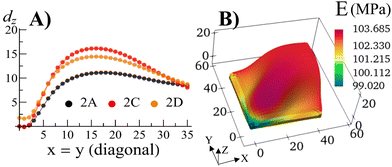Fig. 3 (A) The displacement d_z in the vertical direction of the middle layer of the gel elements with respect to a flat reference state where the mid-layer has the value of Z = 1.0 for the Stage 0 gel, and Z = 1.3187 for the Stage 1 gel as a function of the index of the diagonal gel nodes. (B) The Young's modulus E of the Stage 1 gel after release of constraints for the sample shown in Fig. 2D.

For the relaxed Stage 1 RCN grown under confinement, the distribution of solvent in the sample (Fig. 2D) affects the variation in local mechanical properties, i.e., the Young's modulus shown in Fig. 3B (see ESI† Fig. S4).

C. Growth in rectangular samples

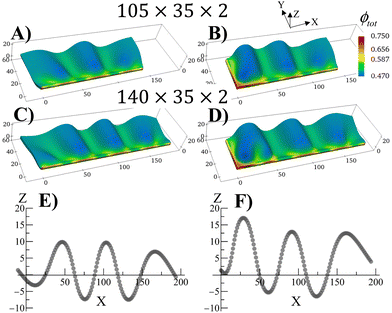
The swollen pinned square gel displays just one prominent buckle, which is stabilized during the growth process (Fig. 2). It is known that long strips of gel that are attached to a hard surface can exhibit a periodic buckling pattern when swollen.^30,33,34,38 The same mechanism that produced the buckling instability in Fig. 2 can be used to modulate the shape of grown RCN gels by varying aspect ratio of the primary gel and boundary constraints. To demonstrate the latter behavior, we consider rectangular primary gel samples, which are three or four times longer than the square gel in Fig. 2. During Stage 0, the samples swell in the monomer solution with no boundary constraints. After polymerization, cross linking and chain-exchange, the boundary constraints are applied, and the sample containing the grown RCN are put back into the monomer solution to complete Stage 1 of growth. The fraction of cross-linker was chosen to α = 0.1.

Fig. 4 shows Stage 1 grown rectangular RCN samples, where the primary parent gels are three (Fig. 4A and C) and four (Fig. 4B and D) times longer than that for the square gel in Fig. 2. The samples presented in Fig. 4 are still attached to the confining walls. For the cases shown in Fig. 4A and B, the primary gels were attached to a hard surface along the long axis at Y = 0. Fig. 4A and B show that the Stage 1 grown RCN gels exhibit distinct buckles, with the longer sample in Fig. 4B displaying three such waves. As seen in other example of confined swollen gels,^30,31 the buckling pattern has a characteristic wave length as evident from Fig. 4E,³⁰ which shows the Z coordinate of nodes along the top, unconstrained edge of the sample in Fig. 4B.

Fig. 4 Buckling due to confinement during swelling in rectangular shaped Stage 1 RCN gels at α = 0.4 when grown from freely swollen flat Stage 0 primary gels. (A) and (D) shows the swollen buckled configuration of the grown Stage 1 RCN gel. The gel sizes are 105 × 35 × 2 in (A) and (B), and 140 × 35 × 2 in (C) and (D). The bottom surfaces of the Stage 1 gels were fixed to a wall in (A) and (C) whereas the both left and bottom surfaces were fixed to walls in (B) and (D). The color bars represent the total volume fraction ϕ_tot of the Stage 1 RCN gels in (A)–(D). (E) and (F) The displacement d_z in the vertical direction of the mid-layer of the gel elements with respect to a flat reference state where the mid-layer has the value of Z = 1.3187 for the Stage 1 gel as a function of the index of the gel nodes along the X-direction and for the edge nodes in the Y-direction.

The introduction of additional confining wall at X = 0 leads to a slightly different bucking patterns in Stage 1 grown RCN gels as shown in Fig. 4C and D. At lengths further away from the additional confining surface, however, the influence of this wall is diminished, and the system again exhibits regular periodicity as seen in Fig. 4E.

The RCNs in Fig. 4 are grown from a flat layer at Stage 0, and the constraints are only introduced in the Stage 1 system. If the constraints are subsequently removed, the grown RCN will relax back to the flat shape, effectively recalling the shape of the parent (see Movie S1, ESI†). Conversely, if the parent gel is attached to a hard surface and buckles during Stage 0, then the grown RCN retains the periodically buckled pattern when the constraints are released (see Movie S2, ESI†). Again, the grown RCN shows “memory” effects as the system replicates the before-growth structure of the parent.

D. Structural patterning during Stage 1 growth

Just as the pinning of walls affects the mechanical behavior (see Fig. 2), the sample can be structurally patterned to tailor the buckling patterns.³⁷ Thus, the structural patterning and concomitant growth can be harnessed to create materials with specified morphology and properties. In living systems, morphological patterns are generally formed in conjunction with the growth process, i.e., patterning and growth occur simultaneously. One form of structural patterning involves spatial variations between hard and soft tissue. In the cases described below, the fraction of cross-linkers α in Stage 1 RCN is set higher in one region than the other and the entire sample experiences Stage 1 growth. In this way, structural patterning and growth of the gel are occurring simultaneously. Thus, the gels described here, capture the scenario when growth and development evolve in a dynamically changing landscape, where the stiff region affects the morphology of the soft domains, which in turn influence the shape of the hard region. The findings can reveal how the two biomimetic processes (growth and morphological evolution) can be dynamically interconnected to tailor the design of synthetic structural materials.

To facilitate comparisons with the examples in Section III.B, we focus on square-shaped gels that are bound by two hard walls. Specifically, we assume that the parent gels swell freely during Stage 0 so the RCN gels are formed in flat samples. Then, the sample faces along X = 0 and Y = 0 are fixed to hard surfaces, and the RCN gels swell to complete Stage 1 of growth.

After Stage 0, the secondary monomers are distributed uniformly throughout the parent network. We assume, however, that during cross-linking of the secondary polymers at Stage 1, one half of a sample encompasses four times the amount of cross-linker than the rest of the sample. Experimentally, this form of patterning could be achieved through photo-induced polymerization and cross-linking, where one half of the sample is irradiated for a longer period than the other.^1,2,4

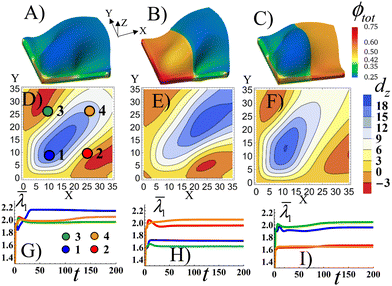
As a point of reference, Fig. 5A shows the Stage 1 RCN gel with a uniform distribution of the secondary cross-links for α = 0.1 that is bound by the X = 0 and Y = 0 walls. The colors indicate the spatial distribution of the total volume fraction of polymer in gel the ϕ_tot. Similar to Fig. 2C, the confinement introduces bucking along diagonal of the sample. The bucking pattern is symmetric, as evident in Fig. 5D which shows the nodal displacements in the Z direction, d_z, in the middle plane of the gel sample. Fig. 5D also shows that the gel is buckled upward along the diagonal (blue corresponds to positive d_z), whereas the areas in the upper left and lower right corners are buckled downward (red corresponds to negative d_z). To characterize the elastic strain in different parts of the sample, in Fig. 5G we plot the average strain [small lambda, Greek, macron]₁ (see the ESI†) as a function of time t in the four quadrants of the sample, as marked by circles in Fig. 5D. The highest strain is observed in quadrant 1, which experiences the effects of both walls (see blue line in Fig. 5G). The plots also indicate that buckling occurs directly after the initial swelling of the RCN gel during Stage 1 of growth, as indicated by the peaks in the curves just after t = 0 (Fig. 5G).

Fig. 5 Buckling due to patterning and confinement bound by the X = 0 and Y = 0 walls during swelling in square shaped Stage 1 RCN gels of size 35 × 35 × 2 when grown from freely swollen flat Stage 0 primary gels. In (A), the gel has uniform distribution of the secondary cross-links at α = 0.1. In (B), the left half of gel has α = 0.4, while the right half has α = 0.1. In (C), the left half of gel has α = 0.1, and the right half has α = 0.4. The colors indicate the spatial distribution of the total volume fraction of polymer in gel the ϕ_tot. (D)–(F) The heat-map of the displacement d_z along the vertical direction of the mid-layer of the gel elements with respect to a flat reference state where the mid-layer has the value of Z = 1.3187 for the Stage 1 gel as a function of the index of the gel nodes along the X and Y direction. In (G)–(I), the average strain [small lambda, Greek, macron]₁ is shown as a function of time for the central gel elements of the quadrants labeled by 1, 2, 3, 4.

In Fig. 5B, the left half of the Stage 1 RCN gel encompasses four times more secondary cross-links, α = 0.4, than the right half, α = 0.1 As a result, the left half is stiffer and less swollen than the right one. The buckling pattern becomes asymmetric relative to the central diagonal of the sample (Fig. 5E). The out-of-plane displacements d_z of the stiffer part are lower in the bottom left corner, which is most perturbed by the confining walls, than those in Fig. 5D. The highest displacements, both positive and negative, are now shifted to the right, (relative to Fig. 5) and are localized in the softer part of the sample (Fig. 5E). Correspondingly, the average strain [small lambda, Greek, macron]₁ is greater in the softer quadrants (2 and 4) than stiffer ones (1 and 3) as seen in Fig. 5H.

When the softer and stiffer parts in Stage1 RCN are switched in position (Fig. 5C), the qualitative behavior is quite similar to that observed in Fig. 5B. Namely, the soft part exhibits higher out-of-plane displacements (Fig. 5F) and greater average strains (Fig. 5I) than the stiffer part of the sample. Now, however, the peak in the buckle height is shifted to quadrant 1 (as opposed to being in quadrant 4 in Fig. 5B).

Relative to the structure in Fig. 5A, the patterned, mechanically stiffer regions in Fig. 5B and C effectively “iron out” the wrinkles in those areas, and the wrinkles are shifted to the softer domains of the gel. Notably, forming layers that encompass both well-defined corrugations and flat domains is useful in a range of applications,³⁹ but is difficult to achieve. For example, this form of patterning might require two separate rolling devices (as in the case of thin metallic sheets), one roller to form the flat surface and another to introduce the corrugations.⁴⁰ These simulation results indicate a means of controllably “growing” analogous patterned, heterogeneous surfaces.

When the gel systems in Fig. 5 are detached from the hard walls, the parent gel for the case in Fig. 5A relaxes to the flat shape, while the parent gels for the cases shown in Fig. 5B and C reflect the patterning introduced at Stage 0 and assume a double roll shape⁴¹ (see ESI,† Fig. S5) Additionally, we show the final equilibrium shapes obtained for different boundary constraints – the swelling of the flat grown RCN gel when three sides of the gel are constrained by walls, and when all four sides are constrained (see ESI,† Fig. S6).

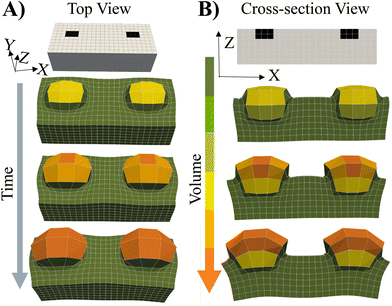
E. Growth of blocks in layered structures

The ability to grow micro- to macroscopic gels that bridge separated surfaces or encase distinct regions addresses a number of technological challenges, from healing damaged devices, to creating a new connection between individual units or providing a protective coating for exposed surfaces. The schematics in Fig. 6A and D illustrate the two different cases considered here; green marks the regions in the parent gel where growth of the RCN gel takes place. As before, the parent gel is swollen in monomer solution (Stage 0). Stage 1 growth is initiated by selective polymerization and cross-linking in the specified areas (a process that can be experimentally achieved by using a photomask with the appropriate shape) and the subsequent chain-exchange.

Fig. 6 The schematics in (A) and (D) show the two different patterns for gel growth. The green regions mark the regions in the parent gel where Stage 1 growth takes place. The hollow mesh region shown in blue denotes the region of the parent gel that do not participate in Stage 1 growth. In (B) and (E), the sample cross-sections are shown for the resulting Stage 1 gels with softer RCN at α = 0.1. In (C) and (F), the sample cross-sections are shown for the resulting gels with stiffer RCN at α = 0.4. The color bar indicates the local volume fraction of polymer in the Stage 0 gel, with red marking the highest and blue indicating the lowest. The total volume fraction ϕ_tot for the regions where Stage 1 growth takes place is 0.281 for (B) and (E) and 0.512 for (C) and (F).

The formed RCN gel can be softer or stiffer depending on the fraction of cross-linkers α in the solution. To complete Stage 1, the entire gel sample is placed in the initial solution to swell the material to equilibrium. Fig. 6B and E show cross-sections of the resulting samples with softer RCN at α = 0.1; Fig. 6C and F correspond to Stage 1 samples with stiffer RCN at α = 0.4. The color bar indicates the local volume fraction of polymer, with red marking the highest and blue indicating the lowest. As seen from the figures, the total volume fraction of polymer in the stiffer grown RCNs is much higher that than in the softer primary gel, specifically,ϕ_tot = 0.281 for α = 0.1 and ϕ_tot = 0.512 for α = 0.4.

Notably, the relative location of the growing material is a determining factor in the final morphology of the system (Fig. 6). Whether the growing material at the edges is soft or hard, the central grown area resembles a solid brick, whereas the outer primary gels appear “pinched” as these regions respond to stresses imposed by the grown inner domains. For the parameter values used for these simulations, the Young's modulus of the grown RCN-containing layers is approximately three orders of magnitude higher than Young's modulus of the primary gel matrix. Specifically, Young's modulus of the matrix is 0.33 MPa, whereas the maximum value of Young's modulus of the grown softer gel is 20.8 MPa and that for the grown stiffer RCN gel is 103.1 MPa.

Given the bio-mimetic nature of our approach, the simulations provide guidelines for growing materials with a cartilage-like or even a bone-like mechanical properties within soft “tissue” of a polymer gel. More generally, these studies reveal how the relative growth of the softer or harder domains affects the morphology of neighboring layers. Moreover, the non-growing and growing parts can be viewed as having different growth rates, with the rate in the “non-growing” region being significantly slower than the rapid rate in the growing part. Thus, the simulations can also be used to expose morphological changes in neighboring areas that have substantially different rates of growth.

F. Growth of an inclusion

To cover the range of potential mechanical heterogeneities in the grown materials, we simulated the system's behavior when the spatially localized “seeds” are embedded near the top of a flat, free-standing, swollen gel.⁴ In this context, the word “seeds” refers to localized, embedded regions that selectively undergo grown. The initial placement of the seeds in a parent gel is indicated by the black squares in Fig. 7. This particular case allows us to investigate growth of a soft material embedded in a soft, deformable network.

Fig. 7 (A) Top and (B) Side views of the Stage 1 RCN gel with the patterned growth. The Stage 0 primary gel swells uniformly to a brick-like shape (not shown). The regions marked by the black squares undergo growth at α = 0.004. The time evolution of swelling of the gel sample shows that the patterned regions swell and protrude out from the gel surface. The color bar shows the volume of the gel elements with the minimum and maximum of 2.09 and 51, respectively, i.e., an increase in volume of about 25 times.

The cross-link density in the parents (Stage 0) and embedded seeds are initially set to the same value, c₀. The entire sample (Stage 0) is immersed in solution and swollen by the uptake of monomer and cross-linkers. Stage 1 growth occurs solely within the seeds where the fraction of crosslinks is α = 0.004.

As seen in Fig. 7, the subsequent increase in the polymer concentration and volume in the seed region causes the newly formed network to protrude from the surface (above the black squares). The color bar indicates that the new layer bulges not only upward, but also outward, maximizing the volume available for growth and counteracting the restrictive forces from the bounding, non-growing domain (in green). The less cross-linked parent layer is also deformed by the localized expansion of the seeds. These findings and structural features show qualitative agreement with experiments^1,2,4 where photomasks were used to selectively irradiate only the seed regions, localizing the optically catalyzed polymerization, cross-linking and resultant growth solely to these illuminated regions. Additionally for comparison, we show the swelling of an uniformly cross-linked primary Stage 0 gel prepared in the shape of the grown RCN 1 gel (see ESI† Fig. S7).

IV. Conclusions

These studies were inspired by the growth of biological tissue, which typically evolves in the presence of neighboring walls due to the spatial crowding characteristic of the local environment. To probe the effect of confining walls on the growth and structural evolution of biomimetic materials, we developed a computational approach to model the growth of polymer gels in the absence and presence of such neighboring surfaces. The initial parent gel was immersed and swollen in a liquid monomer, thereby forming Stage 0 growth. We showed that confinement plays a critical role on the Stage 0 sample and subsequent growth of the random copolymer network (RCN) from this parent. In particular, if the RCN is grown on a flat Stage 0 surface, and then confined by walls, this RCN will buckle due to the competition between the constraining forces from the wall and the elastic and osmotic forces in a swelling network. If the confining walls are removed, the RCN returns to the initial flat structure of the Stage 0 parent.

If the Stage 0 is confined, it undergoes buckling due the competition of the latter forces. When Stage 1 growth occurs in this deformed body of parent gel, the underlying layer effectively templates the subsequent growth of the RCN. If the walls are removed at this stage, the RCN remains buckled. If, however, the RCN grows on a flat parent and is subsequently confined, the resulting buckling disappears when the walls are removed at this stage. In essence, the RCN exhibits a “memory” effect; removal of the walls from the grown RCN returns the morphology of initial structure of the Stage 0 parent. In both cases, the Young's modulus of the RCN could be two orders of magnitude greater than that for the parent depending on the amount of cross-linker in the monomer bath.

When a thicker gel was grown between 3D walls, the Young's modulus of the grown RCN was three orders of magnitude greater than that for the parent material under elevated content of cross-linker in the bath. In the two cases considered here, the growing portion (shown in green in Fig. 6A and D) displayed a higher crosslink density than the non-growing material since cross-linking monomers were absorbed from the solution in the formation of the RCN. The high stress imposed by the more cross-linked harder gel causes the bounding, softer network to be “pinched” at the interfaces. If the growth occurs in the central block, then the ends become pinched and if the growth occurs at the outer pillars, the central domain becomes pinched. Hence, the location of the growing domain dictates the morphology of the entire slab. These results also show that selective localization of the growth provides a means to generate well-controlled structural heterogeneity in one sample. This mode of fabricating mechanically patterned, three-dimensional networks can potentially be more effective than binding together mechanically different components to form heterogeneous structures.

The scenario involving growth from a parent embedded within a soft gel also highlights useful design rules. Namely, localizing or arranging the growing seeds into appropriate patterns can permit new forms of additive manufacturing, where 3D printing can be augmented by purposeful designs that grow into the desired structures.

In the context of self-healing materials, the results suggest approaches for creating coatings that fill existing fissures. Additionally, if the container housing the materials system is sufficiently large to accommodate growth above, below and at the sides of the non-growing domains, then growth of the RCN provides protective coating to hinder further damage.

Overall, the finding provide bio-inspired guidelines for simultaneously fashioning the form and mechanics of synthetic materials. Much as the coupled control over mechanical and spatial variation is beneficial for biological functionality, such purposefully designed heterogeneous materials can exhibit new useful materials’ properties.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

ACB gratefully acknowledges support from DOE grant number DE-SC0005247 to support the work of S. B. and from DOE grant number DE-FG02-02ER45998 to support V. V. Y. This research was supported in part by the University of Pittsburgh Center for Research Computing through the resources provided. Specifically, this work used the H2P cluster, which is supported by NSF award number OAC-2117681.

References

1. X. Zhou, Y. Zheng, H. Zhang, L. Yang, Y. Cui, B. P. Krishnan, S. Dong, M. Aizenberg, X. Xiong, Y. Hu, J. Aizenberg and J. Cui, Nat. Commun., 2023, 14, 3302.
2. X. Xiong, S. Wang, L. Xue, H. Wang and J. Cui, ACS Appl. Mater. Interfaces, 2022, 14, 8473–8481.
3. R. Chatterjee, S. Biswas, V. V. Yashin, M. Aizenberg, J. Aizenberg and A. C. Balazs, Soft Matter, 2021, 17, 7177–7187.
4. L. Xue, X. Xiong, B. P. Krishnan, F. Puza, S. Wang, Y. Zheng and J. Cui, Nat. Commun., 2020, 11, 963.
5. R. Takahashi, H. Miyazako, A. Tanaka, Y. Ueno and M. Yamaguchi, Lab Chip, 2021, 21, 1307–1317.
6. C. Y. Li, D. Jiao, X. P. Hao, W. Hong, Q. Zheng and Z. L. Wu, Adv. Mater., 2023, 35, 2211802.
7. V. V. Yashin and A. C. Balazs, Science, 2006, 314, 798–801.
8. V. V. Yashin and A. C. Balazs, J. Chem. Phys., 2007, 126, 124707.
9. O. Kuksenok, V. V. Yashin and A. C. Balazs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041406.
10. S. Biswas, V. V. Yashin and A. C. Balazs, Soft Matter, 2018, 14, 3361–3371.
11. M. Chen, Y. Gu, A. Singh, M. Zhong, A. M. Jordan, S. Biswas, L. T. J. Korley, A. C. Balazs and J. A. Johnson, ACS Cent. Sci., 2017, 3, 124–134.
12. J. Cuthbert, T. Zhang, S. Biswas, M. Olszewski, S. Shanmugam, T. Fu, E. Gottlieb, T. Kowalewski, A. C. Balazs and K. Matyjaszewski, Macromolecules, 2018, 51, 9184–9191.
13. A. Beziau, A. Fortney, L. Fu, C. Nishiura, H. Wang, J. Cuthbert, E. Gottlieb, A. C. Balazs, T. Kowalewski and K. Matyjaszewski, Polymer, 2017, 126, 224–230.
14. J. Cuthbert, A. Beziau, E. Gottlieb, L. Fu, R. Yuan, A. C. Balazs, T. Kowalewski and K. Matyjaszewski, Macromolecules, 2018, 51, 3808–3817.
15. Q. Mu, K. Cui, Z. J. Wang, T. Matsuda, W. Cui, H. Kato, S. Namiki, T. Yamazaki, M. Frauenlob, T. Nonoyama, M. Tsuda, S. Tanaka, T. Nakajima and J. P. Gong, Nat. Commun., 2022, 13, 6213.
16. T. Matsuda, R. Kawakami, R. Namba, T. Nakajima and J. P. Gong, Science, 2019, 363, 504–508.
17. P. J. Flory, Principles of polymer chemistry, Cornell University Press, Ithaca, 1st edn, 1953.
18. T. L. Hill, An introduction to statistical thermodynamics, Dover, New York, 1986.
19. A. Onuki, Adv. Polym. Sci., 1993, 109, 63–121.
20. A. D. Drozdov, Finite Elasticity and Viscoelasticity, World Scientific, Singapore, 1996.
21. T. Zhang, V. V. Yashin and A. C. Balazs, Soft Matter, 2018, 14, 1822–1832.
22. P. Wriggers, Computational contact mechanics, Springer-Verlag Berlin Heidelberg, Netherlands, 2nd edn, 2006.
23. A. Trushko, I. Di Meglio, A. Merzouki, C. Blanch-Mercader, S. Abuhattum, J. Guck, K. Alessandri, P. Nassoy, K. Kruse, B. Chopard and A. Roux, Dev. Cell, 2020, 54, 655–668.
24. W.-H. Xie, B. Li, Y. P. Cao and X. Q. Feng, J. Mech. Behav. Biomed. Mater., 2014, 29, 594–601.
25. A. E. Shyer, T. Tallinen, N. L. Nerurkar, Z. Wei, E. S. Gil, D. L. Kaplan, C. J. Tabin and L. Mahadevan, Science, 2013, 342, 212–218.
26. T. Savin, N. A. Kurpios, A. E. Shyer, P. Florescu, H. Liang, L. Mahadevan and C. J. Tabin, Nature, 2011, 476, 57–62.
27. J. Yan, C. Fei, S. Mao, A. Moreau, N. S. Wingreen, A. Košmrlj, H. A. Stone and B. L. Bassler, eLife, 2019, 8, e43920.
28. H. Liang and L. Mahadevan, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 22049–22054.
29. B. Schamberger, R. Ziege, K. Anselme, M. Ben Amar, M. Bykowski, A. P. G. Castro, A. Cipitria, R. A. Coles, R. Dimova, M. Eder, S. Ehrig, L. M. Escudero, M. E. Evans, P. R. Fernandes, P. Fratzl, L. Geris, N. Gierlinger, E. Hannezo, A. Iglič, J. J. K. Kirkensgaard, P. Kollmannsberger, Ł. Kowalewska, N. A. Kurniawan, I. Papantoniou, L. Pieuchot, T. H. V. Pires, L. D. Renner, A. O. Sageman-Furnas, G. E. Schröder-Turk, A. Sengupta, V. R. Sharma, A. Tagua, C. Tomba, X. Trepat, S. L. Waters, E. F. Yeo, A. Roschger, C. M. Bidan and J. W. C. Dunlop, Adv. Mater., 2023, 35, 2206110.
30. T. Mora and A. Boudaoud, Eur. Phys. J. E, 2006, 20, 119–124.
31. A. G. Fletcher, M. Osterfield, R. E. Baker and S. Y. Shvartsman, Biophys. J., 2014, 106, 2291–2304.
32. H. Zhang and Y. Hu, J. Mech. Phys. Solids, 2023, 172, 105155.
33. S. J. DuPont Jr., R. S. Cates, P. G. Stroot and R. Toomey, Soft Matter, 2010, 6, 3876.
34. B. Li, Y. P. Cao, X. Q. Feng and H. Gao, Soft Matter, 2012, 8, 5728.
35. Q. Wang, Y. Yin, H. Xie, J. Liu, W. Yang, P. Chen and Q. Zhang, Soft Matter, 2011, 7, 2888–2894.
36. D. Vella, Nat. Rev. Phys., 2019, 1, 425–436.
37. Z. J. Wang, W. Hong, Z. L. Wu and Q. Zheng, Angew. Chem., Int. Ed., 2017, 56, 15974–15978.
38. J. Zhang, X. Zhao, Z. Suo and H. Jiang, J. Appl. Phys., 2009, 105, 93522.
39. T. Li, K. Hu, X. Ma, W. Zhang, J. Yin and X. Jiang, Adv. Mater., 2020, 32, 1906712.
40. T. Wang, Y. Wang, L. Bian and Q. Huang, Mater. Sci. Eng., A, 2019, 765, 138318.
41. O. Oshri, S. Biswas and A. C. Balazs, Phys. Rev. E, 2019, 99, 033003.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00983a

---