Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the impact of ammonium ion substitutions on heterogeneous ice nucleation†
Katarina E.
Blow
 *a,
Thomas F.
Whale
*a,
Thomas F.
Whale
 b,
David
Quigley
b,
David
Quigley
 a and
Gabriele C.
Sosso
a and
Gabriele C.
Sosso
 b
b
aDepartment of Physics, University of Warwick, Gibbet Hill Road, Coventry CV4 7AL, UK. E-mail: k.blow@warwick.ac.uk
bDepartment of Chemistry, University of Warwick, Gibbet Hill Road, Coventry CV4 7AL, UK. E-mail: g.sosso@warwick.ac.uk
First published on 24th July 2023
Abstract
Understanding the mechanisms underpinning heterogeneous ice nucleation in the presence of ionic inclusions is important for fields such as cryopreservation and for improved models of climate and weather prediction. Feldspar and ammonium are both present in significant quantities in the atmosphere, and experimental evidence has shown that feldspar can nucleate ice from ammonium-containing solutions at temperatures warmer than water alone. In recent work, Whale hypothesised that this increase in nucleation temperature is due to an increase in configurational entropy when an ammonium ion is included in the ice hydrogen bond network (T. F. Whale, J. Chem. Phys., 2022, 156, 144503). In this work, we investigate the impact of the inclusion of an ammonium ion on the hydrogen bond network by direct enumeration of the number of structures found using Rick's algorithm. We also determine the energy of these systems and thus compare the effects of enthalpy and entropy to test Whale's hypothesis. We find that the inclusion of an ammonium ion increases the total number of configurations under conditions consistent with a realistic surface charge. We also find that the enthalpic contribution is dominant in determining the location of the ammonium ion within the structure, although we note that this neglects other practicalities of ice nucleation.
1 Introduction
The freezing of liquid water into ice is a widespread occurrence which plays an important role in many processes, including cryopreservation1,2 and the water cycle.3 In the atmosphere, heterogeneous nucleation of clouds by ice nucleating particles (INPs) allows for ice formation under conditions where nucleation would otherwise not be possible. These INPs can lead to large increases of ice nuclei concentrations at relatively high temperatures.4 The presence of these ice particles can lead to changes in the properties of clouds such as precipitation likelihood,3 albedo, and lifetime. Therefore a greater understanding of the behaviour of ice nucleation by INPs could help form better models for climate and weather prediction.5,6 The effect of impurities within the aqueous phase as a result of aqueous aerosols is also important.7 Of particular interest as an INP is feldspar,8 which recent experimental work has shown displays unexpected increases in nucleation temperatures when in the presence of the ammonium ion (NH4+)9–11 a common component of atmospheric aerosols and solutes in cloud droplets.12As can be seen in Fig. 1, at intermediate concentrations of NH4Cl, there is an increase in the heterogeneous nucleation temperature of water when in the presence of feldspar. This is not evident when the ammonium ion is replaced by a sodium ion, or when feldspar is replaced with pollen washing water (PWW), indicating that this increase is the result of some interaction between ammonium and feldspar. Various other ice nucleants, such as silver iodide, kaolinite and montmorillonite, are also known to nucleate ice at warmer temperatures in dilute ammonium solutions than in pure water.9,13 In ref. 9, Whale argues that the increase in nucleation temperature upon inclusion of an ammonium ion is the result of an increase in the configurational entropy of the ice phase.
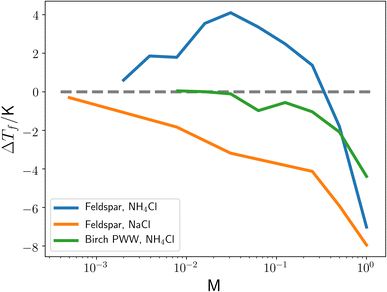 | ||
| Fig. 1 The change in the highest temperature where a droplet was observed to become completely frozen, ΔTf, as a function of the molarity of NH4Cl and NaCl solvents. Feldspar corresponds to a solution also containing 0.05 weight% BCS376 feldspar, PWW corresponds to pollen washing water from Betula pendula, with PWW and feldspar solutions having different Tf in the presence of only water (i.e. 0 M). The dashed grey line is a reference for ΔTf = 0. This figure is adapted from ref. 9. | ||
Water molecules within ice form a random hydrogen bond network subject to the Bernal–Fowler ice rules.14 The permutations of these bonds give rise to a configurational entropy. Enumeration of these permutations was first attempted by Pauling.15 The Pauling entropy is now known to be a slight underestimate, and further studies have expanded and improved upon this prediction,16–21 with a theoretical investigation of the effect of ordering on heterogeneous ice nucleation being performed by Fletcher.22 Simulations have also been used to investigate the configurational entropy of ice. Most of these rely on either enhanced sampling techniques or thermodynamic integration, giving good agreement with both experimental and theoretical values of the entropy.23–27
To the best of our knowledge, the current computational literature surrounding ice/ammonium/feldspar interaction is limited, and generally focused on the dynamics of the surface interactions. Kumar et al. found evidence for the adsorption of ammonium onto feldspar surfaces, although with different strengths depending on the geometry of the exposed plane. It was found that for certain planes the ammonium had a preferential orientation with respect to the surface, but this did not translate into templating the ice structure.28
In this work, we have investigated the changes in enthalpy and configurational entropy upon the insertion of an ammonium ion into ice, by a direct enumeration of the number of states. While this approach has limitations in terms of scaling and the accuracy of the entropy, it allows a more direct comparison of ice structures and enthalpies than other techniques, and readily extends to partially-periodic structures such as the ice slabs studied here.
2 Methodology
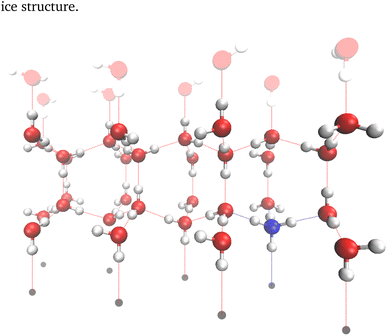
Ice consists of stacked, puckered rings of water molecules. In this work, these stack along the z direction and the Bernal–Fowler ice rules14 are always obeyed. Henceforth, the puckered ring structures will be referred to as ice bilayers, and consist of two ice layers within which the oxygen atoms reside at the same z value. Each of the 2N molecules in the bilayer must have one inter-bilayer and three intra-bilayer connections to other molecules. These connections are hydrogen bonds between the oxygens of two water molecules, consisting of a hydrogen bond donor (the water molecule with a hydrogen along the direction of the bond), and a hydrogen bond acceptor (the other water molecule). There must therefore be 3N hydrogens associated with the intra-bilayer connections. The insertion of an ammonium ion does not distort the ice lattice as it is isostructural with water,29–31 and does not change the number of intra-bilayer hydrogens needed for a valid ice structure.A sample configuration of the ice cell considered in these simulations is presented in Fig. 2 and was created using the visual molecular dynamics (VMD) software.32 This cell consists of 32 molecules arranged into two bilayers of 16 molecules, along with a “ghost layer” of fictitious atoms (paler water molecules) and a “base” of grey circles – the role of these will be explored in greater detail below. This unit cell is sufficiently small to tractably enumerate all permutations of the hydrogen bonding network.
2.1 Entropy
The configurational entropy of ice was calculated by generating structures33 which obeyed the Bernal–Fowler ice rules14 and then determining the number of unique configurations found. The number of truly unique structures, W, is related to the entropy of the system, S, through Boltzmann's equation of entropyS = kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W W | (1) |
PBCs were omitted in the z direction for two reasons. Firstly, the inclusion of an ion into a block of ice will necessarily lead to an unbalanced number of connections, which must be balanced by either inclusion of ions of the opposite valence, or the creation of defects within the hydrogen bond lattice. As we wish to investigate the inclusion of single ions and do not allow defect creation, the use of full PBCs is impossible. Additionally, we investigate the effect of the charge of the nucleating surface on the entropy. When computing the entropy, this was approximated by enforcing a designated number of “connections” to a fictional nucleating surface, henceforth referred to as the “base”, 3 Å below the oxygens with the lowest z value. A connection is here defined as an oxygen in the layer closest to the base (referred to as the contact layer) donating a hydrogen bond to the base. It should be noted that a structure with e.g. two connections to the base will always donate two and only two hydrogen bonds to the base, although the origin of these donated bonds is not fixed. Fig. 2 shows a structure with six of eight possible connections to base (represented by grey circles) as coloured lines. Also present is an upper ghost layer, which consists of fictitious atoms to allow for the propagation of a hydrogen bond reordering across the top of the ice layer during the application of Rick's algorithm33 – no restrictions are made on connections to this ghost layer.
As stated, a fixed number of connections to the base is meant to approximately model the effect of a charged feldspar surface on the available permutations of the ice network. As the number of connections increases from half the total number of connections, there is a greater propensity for the base to attract the positively charged hydrogens of the water molecule – equivalent to an increase in the negative charge on the base, which would also make it more likely for the positively charged ammonium ion to reside nearer the base. This treatment implicitly assumes that only one macrostate (defined by ammonium location and number of connections to the base) is accessible, and all configurations within this macrostate are approximately energetically equivalent and therefore contribute equally to the entropy (i.e. all microstates are equally accessible at the temperature of interest). We note that this may not be entirely accurate, but is a good first approximation. This assumption will be investigated in more detail in Section 3.2.
2.2 Structure generation
Initial configurations of ice XI were generated using the GenIce package,35 and were then modified so that all inter-bilayer bonds consisted of hydrogen bond donation in the −z direction, consistent with a strongly negatively charged base. For scenarios where the number of connections did not equal the number of molecules in the contact layer, the molecules to disconnect from the base were chosen at random. Where relevant, the positions of ions and their valency were specified. After this procedure, any molecules which did not accept and donate the appropriate number of hydrogen bonds were identified and corrected similarly to step one of ref. 35. In this procedure, a list of molecules without the appropriate number of bonds was created. The molecule corresponding to the first element of this list then had an incorrect bond inverted (i.e. if a water molecule donated three hydrogen bonds, one of these was chosen at random to become an accepted hydrogen bond), ensuring that this did not violate the number of connections to the base or the hydrogen bonds donated by an ammonium. If either of the molecules connected by the flipped bond did not have the correct number of accepted and donated hydrogen bonds after this procedure, they were reintroduced to the back of the list, and the procedure was iterated until the structure was valid. As this procedure introduces a degree of randomness into the starting configurations, the initial configurations so generated had a degree of uniqueness. This uniqueness was only lacking when this procedure was unnecessary, for pure ice with all molecules in the contact layer connected to the base. Although there is the same degree of ordering in the z direction (albeit in the opposite direction) when there are no molecules connected to the base,22 the stochastic nature of rectifying an incorrect number of accepted/donated hydrogen bonds still ensured a random distribution of bonds within each bilayer.These configurations were then read in to generate a directed graph, with each vertex corresponding to the position of the central atom of a molecule, with four directed edges per vertex. The number of incoming edges (here analogous to accepted hydrogen bonds) and outgoing edges (here analogous to donated hydrogen bonds) was determined by the valency of the molecule. Water has two incoming and two outgoing vertices, obeying the Bernal–Fowler ice rules,14 whereas ammonium has four outgoing edges. For the contact and top layers of the structures, which contain undercoordinated molecules/vertices, “ghost layers” of vertices not representing real molecules were introduced (grey circles and pale atoms in Fig. 2).
From these initial graphs, further structures were generated in accordance with Rick's algorithm.33 In Rick's algorithm, a starting vertex and edge are selected. This forms the start of a path moving between vertices along edges of the same sense – i.e. if the starting edge, e0, is incoming to the starting vertex, N0, then edge ei is incoming to Ni and vice versa. At each new vertex, a random selection of the next edge is made and the path is continued. If no appropriate edge is found, e.g. if the path leads to a vertex with no incoming edges, representing an ammonium ion, then the path is terminated and a new starting vertex and edge are generated. The ghost layer is present to facilitate the creation of loops across the top of the slab – if the edge connects to a ghost layer, then the next vertex on the path is a vertex connected to the ghost later with the opposite sense of edge (incoming/outgoing). This is analogous to a section of path which ends in an edge of the right sense coming from the ghost layer. When the path forms a complete loop back to a vertex it has previously visited, then all of the edges along that loop are flipped, such that incoming edges become outgoing edges and vice versa. Any edges in the path before the start of the loop are ignored. This ensures that the new structures are generated, but the number of incoming and outgoing edges of each vertex is never changed. A schematic of this procedure is presented in ESI Fig. S1.†33 Representation of the hydrogen bond used a string to store the sense of edges between vertices. It was deemed that each unique string corresponded to a different hydrogen bond configuration, although this did not and could not account for any symmetries present in the atomic system.
Due to computational constraints, enumeration was deemed to be converged once 250 iterations occurred without finding a new structure (see ESI Fig. S2† for results of different stopping criteria). Three independent configurations were produced and run for all relevant investigations, allowing for the identification of a “run” (i.e. the output of our implementation of Rick's algorithm33) which had a significantly lower number of structures than expected. It is worth noting that at the number of structures considered here, small differences in the observed number of structures make a negligible difference to the observed entropy. Although Rick's algorithm is sufficient to generate all possible configurations of hydrogen bonds on the ice lattice,17 it cannot account for the creation of Bjerrum defects, which may happen in a realistic system. This could possibly be investigated in future work by the inclusion of OH− and/or H3O+ ions into the initial lattice.
We enumerated the number of structures from a starting configuration of both ice XI and ice Ih (as output by GenIce,35 using the Python package NetworkX36 to compute a mapping) and found that the number of generated configurations were very similar. Small differences between the found number of structures is expected due to termination of the algorithm.
Using our implementation of Rick's algorithm,33 a cell containing 32 water molecules (consisting of 4 layers) with 8 fixed connections to the base was found to have 2401 unique configurations. Using eqn (1), this gives the entropy of a completely connected ice structure of this size as 1.07 × 10−22 J K−1. In comparison, the Lipscomb entropy of a mole of polar ice is 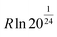 , which would give the entropy of the same system as 5.51 × 10−23 J K−1.16 At close to a factor of two, this is a significant difference. Although the Lipscomb value may not be entirely correct, a large deviation demonstrates that the uniqueness condition imposed on found structures in this work is likely to be insufficient, which is not unexpected. However, we expect the overestimate to be less severe in structures containing an ammonium ion due to the decrease in the possible number of symmetry operations.
, which would give the entropy of the same system as 5.51 × 10−23 J K−1.16 At close to a factor of two, this is a significant difference. Although the Lipscomb value may not be entirely correct, a large deviation demonstrates that the uniqueness condition imposed on found structures in this work is likely to be insufficient, which is not unexpected. However, we expect the overestimate to be less severe in structures containing an ammonium ion due to the decrease in the possible number of symmetry operations.
As we are interested in the differences in configurational entropy between ammonium-containing and pure ice, inaccuracies in the method of counting structures should not significantly influence the observed entropy difference, if the uniqueness criterion is applied consistently.
2.3 Energy calculation
A random sample of structures were then input to GROMACS (2023.1)37 for energy evaluation with the CHARMM36 (July 2022)38 and TIP4P/Ice39 force-fields with a Coulomb cutoff of 12 Å and long-range smooth particle-mesh Ewald electrostatics with a grid spacing of 1 Å and an interpolation order of 4.40 A van der Waals cutoff was applied with a smooth switching of the force to 0 between 10 Å and 12 Å. PBCs were applied in all 3 directions, with the expansion of the z vector from a length of ≈8.5 Å to 255 Å to incorporate a significant vacuum gap. The 32 molecule unit cell was also explicitly replicated 4 times in the y direction and 3 times in the longer x direction to satisfy the minimum image criterion used by GROMACS. All computed energies have been divided by 12 to present the energy of the original cell. This procedure was validated by comparison to a density functional theory calculation, and the results are presented in ESI Fig. S3.† Energies are presented in units of kBT, of the entire 32 molecule simulation box, for temperature T in Kelvin and for Boltzmann's constant kB. This allows for a more direct comparison to both the thermal energy available to the system, and the entropy. Here, the temperature is taken as 262 K, which, according to ref. 9, corresponds to the maximum temperature for ice nucleation on feldspar in the presence of ammonium.GROMACS input files used GenIce ice XI physical water oxygen positions,35 with the angle mismatch between the TIP4P/Ice39 H–O–H angle and the O–O–O hydrogen bond angle being offset between both oxygens (no such offset was necessary for ammonium). Configurations were then minimised with a maximum force tolerance of 100 kJ mol−1 nm−1 with an energy step size of 0.01 kJ mol−1 for a maximum of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps using the steepest descent algorithm. The length of all hydrogen bonds were constrained during minimisation through the application of the LINCS algorithm.41 Initial configurations which proved to be mechanically unstable upon energy minimisation were excluded from the analysis. This occurred for a sufficiently small number of samples that excluding the same fraction from the total population of generated structures does not significantly alter the entropy estimate. A lower force tolerance led to mechanical instability in a significant number of cases. A comparison of different force tolerances is shown in ESI Fig. S4.† A random “set” of 1000 approximately evenly-spread configurations was used for most energy calculations due to the large number of possible structures (for the effect of number of structures per set on the spread of energies, see ESI Fig. S5†).
000 steps using the steepest descent algorithm. The length of all hydrogen bonds were constrained during minimisation through the application of the LINCS algorithm.41 Initial configurations which proved to be mechanically unstable upon energy minimisation were excluded from the analysis. This occurred for a sufficiently small number of samples that excluding the same fraction from the total population of generated structures does not significantly alter the entropy estimate. A lower force tolerance led to mechanical instability in a significant number of cases. A comparison of different force tolerances is shown in ESI Fig. S4.† A random “set” of 1000 approximately evenly-spread configurations was used for most energy calculations due to the large number of possible structures (for the effect of number of structures per set on the spread of energies, see ESI Fig. S5†).
To model the energetic effect of the implicit surface charge of the base, a charged wall was simulated by the addition of charged atoms 3 Å under contact layer oxygen/nitrogen positions. These atoms had a Lennard-Jones σ = ε = 0 and were restrained to their original positions.
When considering the effect of having an ammonium ion within the ice structure on the energy, we completely neglect any entropic contribution. In addition, we investigate the assumption that a reasonable surface charge can have the effect of constraining the stable state of a system to a single fixed number of connections to the base.
3 Results
3.1 Entropy
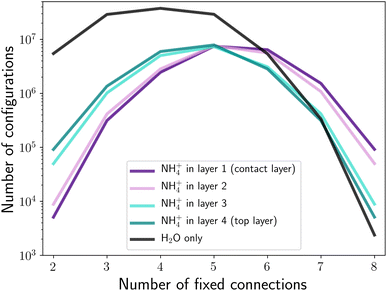
Fig. 3 shows the number of structures generated, as a function of NH4+ position and number of connections to the base. The x-axis is not fully symmetric, starting at two fixed connections rather than zero fixed connections, as, regardless of where the ammonium is placed, there are no defect-free configurations containing an ammonium with fewer than two fixed connections to the base. This is explained in more detail later on.We expect the substitution of NH4+ for H2O to introduce changes to the hydrogen bond network, and this will therefore affect the total number of permutations. A water molecule accepts two hydrogen bonds, and donates two hydrogen bonds.14 In contrast, ammonium donates four hydrogen bonds and does not accept any.
At the maximum of eight fixed connections, the inclusion of an ammonium at any position in the cell increases the number of possible configurations. For pure ice, forcing all molecules in the contact layer to be connected to the base means that, in order to satisfy the correct number of connections, all remaining hydrogen bonds must be donated within the bilayer. If there are two extra hydrogen bonds to donate (arising from the inclusion of NH4+), then these can be accepted by the bilayer above. It can be seen in Fig. 3 that the location of the ammonium can lead to significant differences in the number of extra configurations available. This is especially true for inclusion in different bilayers (i.e. layers 1 and 2 compared to layers 3 and 4), but also applies for the different intra-bilayer positions (due to the PBCs, the only applicable difference between bilayer positions is the direction of the inter-bilayer bond). The large difference in number of structures between bilayers is due to the propagation of the effects of NH4+, as discussed by Whale.9 When the NH4+ is placed in the contact layer, b0, there are an additional two hydrogen bonds which can be donated to other bilayers (all intra-bilayer hydrogen bonds must be satisfied). As every molecule in the contact layer is constrained to donate a hydrogen bond to the base, this means that two hydrogen bonds can be donated to the bilayer above, b1. Again, there are now two additional hydrogen bonds in this bilayer which are accepted by the bilayer above, b2, thus propagating to the top of the structure. This is equally true when ammonium is placed in any bilayer, bi. Although the bilayers below have been constrained such that all of the −z inter-bilayer bonds involve hydrogen bond donation, the addition of new bonds means that two hydrogen bonds can be donated to the bi+1 bilayer, and the existence of these donated hydrogen bonds will also propagate up. As there is no hydrogen bond acceptance in the −z direction, there can be no downwards propagation, leading to a number of configurations heavily stratified by the bilayer in which the NH4+ resides (see Fig. 4).
The entropy contribution of ammonium, as discussed by Whale, does not account for intra-bilayer differences. This is due a simplification made in the consideration of the donation of two extra hydrogen bonds – Whale assumes that these bonds can be anywhere within the bilayer.9 In reality, although the donation of the extra bonds will affect the rest of the bilayer, the extra bonds themselves must be present at the location of the ammonium. Placing an ammonium in the contact layer replaces a water molecule which donates one inter-bilayer bond (towards the base) and one intra-bilayer bond, with an ammonium donating one inter-bilayer bond and three intra-bilayer bonds. These extra intra-bilayer bonds will then lead to the donation of two inter-bilayer bonds, pointing up towards the next bilayer. Importantly, these bonds can be donated by any appropriate atom in the bilayer – although not all choices are equally likely, as will be discussed further below. In comparison, if the ammonium instead replaces a water molecule in layer 2, then two donated intra-bilayer bonds are replaced by three donated intra-bilayer bonds and one donated inter-bilayer bond. Again, the additional intra-bilayer bond leads to an extra donated bond to the bilayer above from any appropriate atom. The net effect of including the ammonium within the bilayer is the same, two additional donated bonds to the bilayer above. However, when placed in the contact layer, both of these donated inter-bilayer bonds can originate from any appropriate atom within the bilayer. When placed in layer 2, only one of these donated bonds can originate from anywhere, the other is fixed to the location of the NH4+, leading to a decrease in the number of possible configurations compared to the contact layer.
As a result of neglecting the location of the extra donated bonds, the entropy increase suggested by Whale is an overestimate. This is expected, as the equation given is presented simply as a brief validation of the hypothesis.9 Although our estimate of the entropy increase is also likely to not be entirely accurate (due to the small unit cell and the lack of consideration of symmetries in the ice lattice), we can provide a more detailed analysis of the actual entropy increase.
As can be seen in Fig. 3, for eight connections to the base the inclusion of an ammonium ion increases the entropy of the structure relative to pure ice. As the number of connections decreases, the location of the ammonium becomes more important in determining if its inclusion leads to an entropic gain. At seven fixed connections, there is no entropic benefit to including the ammonium in the very top layer, although it is still favourable at any other location; and at six connections the entropic gain is only present for an ammonium in the contact layer. At low numbers of connections to the base (which is analogous, but not exactly equivalent, to having more connections to the ghost layer) the opposite trend holds – the further the ammonium is from the contact layer, the larger the number of structures, although it is still lower than the number of pure ice structures. At five connections to the base, the number of ammonium-containing structures is approximately equal regardless of position. This is due to the crossover between it being entropically favourable to be near the base and to being near the ghost layer.
Considering all possible ammonium-containing structures (i.e. all possible ammonium locations and number of connections to the base), the addition of ammonium reduces the possible number of configurations found in this work. Although the number of structures found, especially for pure ice, is likely to be an overestimate as a result of not considering symmetry-related structures, the differences are significant. However, the number of connections attempts to link the computed entropy to the surface charge, which will also influence the location of the ammonium. For a positive charge (low number of connections), the most structures are found when the ammonium is in the top layer, which also minimises the coulombic repulsion between NH4+ and the positive base. For the case of a negative charge (high number of connections), the most favourable location is in the contact layer, consistent with a coulombic attraction between the positively charged ion and the negatively charged base. As feldspar is negatively charged,11 we assume that we are limited to only considering structures with a high fraction of connections to the base (an assumption which will be somewhat investigated in Section 3.2). When considering only this regime, the inclusion of ammonium increases the entropy of ice.
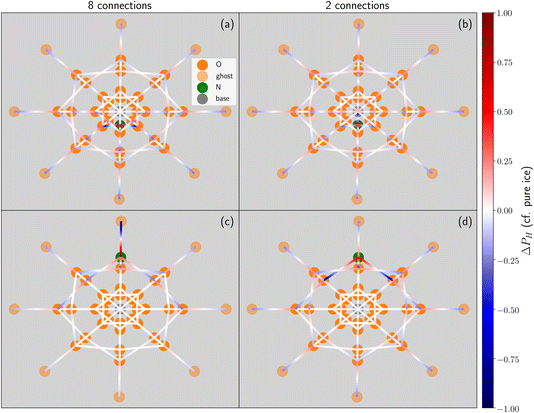
We show the difference in hydrogen positions upon the inclusion of an ammonium in Fig. 4. These “spiderweb plots” describe the hydrogen bonds between water molecules, wherein the ice cell (see Fig. 2) has been projected onto a two dimensional representation. The darker orange circles represent the oxygen atoms of each water molecule and the green circle represents the nitrogen of the ammonium atom. Each concentric ring of circles represents one of the four ice layers. The fictitious base and the ghost layer are represented by the single central grey circle and the outermost ring of pale orange circles, respectively. The average probability, PH, for a hydrogen to be located at a given position was calculated for both all configurations found for this specific ice cell, and separately for all configurations of the equivalent pure ice structure. The hydrogen bonds are represented by lines, the colour of which corresponds to the difference in PH (ΔPH) between the pure ice structure and the ammonium-containing ice. The color map indicates a greater (red) or lesser (blue) propensity for a hydrogen bond to be located at a specific position within a given ice cell compared to the average, pure ice structure. The darker the colour, the more the ammonium has changed the hydrogen bond network at a given position. Note that for positions where the probability of finding a hydrogen is never allowed in either the pure ice or ammonium structures (e.g. from the base when all connections are fixed) the ΔPH is 0, and on these plots are indistinguishable from bonds which are unchanged by the inclusion of an ammonium.
Fig. 4 gives these spiderweb plots for two locations of the ammonium (contact layer and top layer) for both of the extremes of connections to the base, eight and two. It should be noted by comparison of panels (a) and (d) that, using the colours of the edges as a guide to the eye, there is less propagation of new structures downwards from an ammonium in the top layer with two connections to the base, than there is upwards propagation for an ammonium in the contact layer with eight connections to the base. This is reflected in the slightly decreased number of structures when there are two connections to the base and the ammonium is in the top layer, when compared to ammonium in the contact layer and eight fixed connections. This is an artefact of forcing the number of connections to the base. As the number of connections to the base cannot be changed by the inclusion of an ammonium, the additional donated inter-bilayer bonds must propagate upwards (which is why configurations with one fixed connection are not allowed even when the ammonium is in the top layer). Additionally, when ammonium is in the top layer, there are no configurations of the basal bilayer which are available to ammonium-containing structures but not to the pure ice structure. The small deviations visible in panel (d) are due to configurations which are more common as a result of the changes in the layer above (i.e. they correspond to allowed states matching more likely realisations of the hydrogen bond network in the bilayers above). It can be seen that the scenario depicted in panel (b) is characterised by a more pronounced difference in terms of the total hydrogen bond network, despite the lower number of structures.
Fig. 4(a) also shows that not every location of a donated inter-bilayer bond is equally likely. Instead, they are more likely to originate from water molecules next to the ammonium ion. This is because the adjacent water molecule must accept a hydrogen bond from the ammonium ion, but must also donate two hydrogen bonds. Far away from the ammonium, where only the addition of two donated hydrogen bonds matter, a water molecule has to donate two hydrogen bonds between three intra-bilayer bonds and one inter-bilayer bond. Considering a simplistic treatment where only the Bernal–Fowler ice rules14 matter, the probability of this water molecule donating to an inter-bilayer bond is 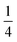 . If instead we consider a water adjacent to the ammonium, again subject to this simplistic treatment, then the probability of donating to an inter-bilayer bond is
. If instead we consider a water adjacent to the ammonium, again subject to this simplistic treatment, then the probability of donating to an inter-bilayer bond is 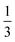 , as it must accept a hydrogen bond from the ammonium. Therefore, there is an increased probability for donated inter-bilayer bonds to originate from water molecules connected to the ammonium. This difference in probability propagates outwards, although the magnitude dissipates with increasing distance from the ammonium. Considering the inter-bilayer bonds from the water atoms in layer two located exactly along the horizontal middle of panel (a), it can be seen that the probability is lower than for the waters immediately adjacent to the ammonium, but higher than for the water furthest away from the ammonium location (in this representation, immediately opposite). That most disruption to the hydrogen bond network occurs near the ammonium is visible for all panels. Although this effect will become less pronounced further from the ammonium site, the size of the unit cells considered here is not sufficient to calculate the rate of this decay. This makes it difficult to give an analytic estimate of the true entropy difference of including an ammonium as no part of the structure retains a bulk-like character.
, as it must accept a hydrogen bond from the ammonium. Therefore, there is an increased probability for donated inter-bilayer bonds to originate from water molecules connected to the ammonium. This difference in probability propagates outwards, although the magnitude dissipates with increasing distance from the ammonium. Considering the inter-bilayer bonds from the water atoms in layer two located exactly along the horizontal middle of panel (a), it can be seen that the probability is lower than for the waters immediately adjacent to the ammonium, but higher than for the water furthest away from the ammonium location (in this representation, immediately opposite). That most disruption to the hydrogen bond network occurs near the ammonium is visible for all panels. Although this effect will become less pronounced further from the ammonium site, the size of the unit cells considered here is not sufficient to calculate the rate of this decay. This makes it difficult to give an analytic estimate of the true entropy difference of including an ammonium as no part of the structure retains a bulk-like character.
3.2 Energy
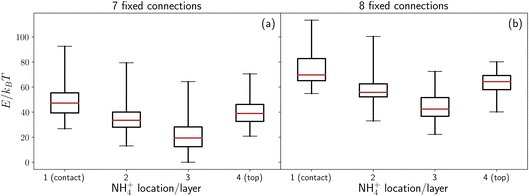
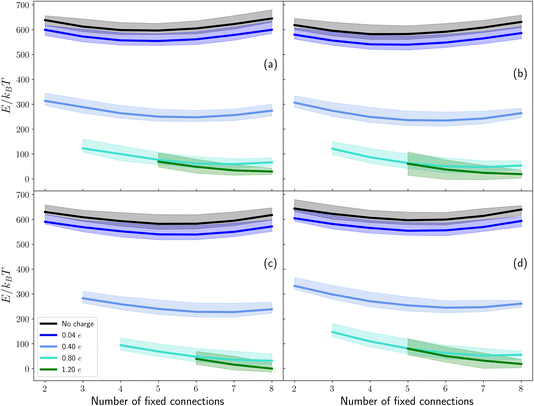
In the previous section we implicitly considered the effect of charge by enforcing a fixed number of connections between the ice contact layer and the base. We now investigate if this is a reasonable approximation by explicitly considering the energy of a set of sample configurations, first in the absence of any electric field due to surface charge, and then by modelling the surface as a collection of charged points.Our analysis shows that in order for the ammonium ion to increase the entropy of the ice slabs considered here, the number of connections to the base must be high. The energies of sets of ammonium-containing ice with seven (panel (a)) and eight (panel (b)) connections to the base is presented in Fig. 5. These energies do not include any contribution of charge, other than that implicit to the rationale of using connections. It can be seen that the sets in panel (a) have a lower energy than the sets presented in panel (b). This is due to the lower total dipole when there are only seven fixed connections to the base, compared to eight. This indicates that a lower number of connections to the base leads to more stable structures in the absence of an electric field/surface charge. The lack of symmetry about the NH4+ location indicates that this is not an artefact of electrostatics. Although the small extent of the system in the z direction may not provide a complete picture of the behaviour of a more realistic cell, interesting trends can be observed and some extrapolations can be made.
As the ammonium is placed further up the structures, the overall dipole moment of the structure decreases. This agrees well with the energy trend for the first three layers – as the average dipole moment of the set decreases, so does the median energy of the set. However, when ammonium is placed in the top layer (where the dipole is minimal), the energy of the set increases again. One possible reason for this is a large energy penalty to having an undercoordinated NH4+. When the ammonium ion is in the contact layer, both rotations of water connections and rotations of the ammonium are observed. Rotation of an ammonium – and the associated removal of its connection to the base – led to a significant reduction in the energy of the system, although the rotation of a water connection did not lead to an energy decrease of the same magnitude. This may provide evidence for a significant energy penalty for an undercoordinated ammonium in the system as evaluated by GROMACS.
In Fig. 5, any energetic penalty which may occur as a result of considering only a large fraction of connections is unbalanced – i.e. there is no explicit charge contribution which may balance the increased dipole due to the large fraction of bonds pointing in the −z direction. Both the increase in energy of a set with the number of fixed connections and the rotation of the hydrogen bond network indicate that a negative surface charge is needed to stabilise configurations with all connections fixed to the base (conversely, a positive surface charge would be needed to stabilise configurations with no connections to the base).
The effects of varying negative surface charge are presented in Fig. 6. For no charge, it can be seen that the energy of a set is lowest approximately in the middle of the range of fixed connections. This is due to this set having a low average dipole moment. As the number of fixed connections moves away from the middle, the median energy of the set increases due to the increased dipole. From comparison with ESI Fig. S6,† it can be seen that the full energy variation of the set includes configurations with an energy more than three standard deviations away from the median. This may, but does not necessarily, indicate that we have applied insufficiently stringent criteria to determine mechanically unstable structures. Regardless of origin, these structures comprise a small fraction of the total analysed structures, and we therefore do not expect them to significantly influence the validity of our conclusions.
As the negative charge on the base increases, the median energies of all sets decreases (although this is influenced by the balancing effect of a negative basal charge on the positively charged ammonium).40 Fewer structures with eight fixed connections to the base are mechanically unstable, indicating the expected attraction between slightly positively charged hydrogens and the negatively charged base, thus stabilising structures with a large fraction of connections. As expected, structures with a low fraction of connections are destabilised. At the largest charge presented here, eight fixed connections to the base is not only stabilised, but becomes the most energetically favourable set (for the same ammonium position). Even at a charge of 1.20e across the base, the lowest energy position for the ammonium ion with seven or eight connections to the base is determined to be the penultimate layer (other than a handful of configurations in layer two with energies more than three standard deviations from the mean; for a comparison of sets with seven and eight connections for this surface charge, see ESI Fig. S6†). We would like to note that a surface charge of 2e was also investigated, but led to a spread of an order of magnitude in energy for sets determined to be mechanically stable, and this has therefore not been analysed.
A surface charge of 1.20e across the footprint of the ice (corresponding to 0.15e on each of the eight fictitious grey basal atoms presented in Fig. 2) is a realistic and relatively modest surface charge. In both ammonium-containing ice and pure ice (see ESI Fig. S7†) increasing the surface charge stabilises a larger number of connections to the base. This lends weight to Whale's hypothesis.9 However, due to electrostatic effects, a comparison between the energies of the ammonium-ice and pure ice systems cannot be made.40
It should also be noted that the positively charged ammonium ion is likely to be attracted to the negatively charged feldspar and hence be present at or near the surface when an ice nucleus forms. No explicit thermodynamic comparison to pure ice can be made without calculating the free energy change of moving an ammonium ion from solution into the ice nucleus, however experiments do demonstrate that ammonium is implicated in the ice formation, be this due to thermodynamics or kinetic trapping.
3.3 Interplay between entropic and enthalpic effects
We have shown that for a large fraction of connections to the base (here, seven or eight) the entropy of ammonium-containing ice is greater than that of pure ice, with an ammonium in the contact layer leading to the largest increase in configurational entropy. We have also shown that a large number of connections can be stabilised by a reasonable surface charge applied across the base, with the most energetically favourable position for the ammonium in the penultimate layer.The most stable position for the ammonium will be a combination of the competing effects of enthalpy and entropy. Although energy and enthalpy are not equivalent, there is a systematic shift relating to the pressure and volume of the system. As all structures considered here were generated from the same original ice structures, we expect this shift to be negligibly different between the systems considered here. As we are only interested in differences in enthalpy, we here consider enthalpy and energy to be equivalent.
For eight fixed connections to the base at a surface charge of 1.20e, the difference in median enthalpy between the sets for ammonium in layers 1 and 3 is approximately 30 kBT. In contrast, the difference in entropy is approximately 2.3 kBT, indicating that enthalpy is dominant. This is also true for seven fixed connections, where the difference in enthalpy is again approximately an order of magnitude above the difference in entropy. It is worth noting that here we only consider the entropy and enthalpy of a single number of connections to the base, and retain the assumption of all configurations with the same number of connections to the base being equal.
4 Discussion and conclusions
Although the results presented in Section 3.3 show that the most favourable position of the ammonium is in the penultimate layer, this may not necessarily be the case in reality. Not only have we presented evidence that there may be a significant energy penalty for an undercoordinated ammonium, but we note that in a realistic system the positive ammonium may be attracted to the negatively charged feldspar and the ice may grow around this. The kinetics of the system, which we cannot take into account here, will likely play a significant role in determining where the ammonium is located within the ice phase. We also note that none of the studies of ammonium/feldspar interactions cited here provide evidence that the ammonium is not rejected into solution when ice forms.We also acknowledge the presence of several simplifications in our enthalpy calculations which may affect our results. Firstly, we cannot compare the energy of a set of pure ice configurations to that of a set of ammonium-containing ice configurations. A potential avenue for comparison, which is also more representative of the experimental setup, would be the inclusion of some solution (containing an extra ammonium for pure ice) in the simulation box in addition to the ice. Secondly, we assume that the only interaction between the base and the ice is due to coulombic effects. Molecular dynamics simulations performed by Cox et al. show that the interaction between water molecules and a surface can influence the nucleation rates in complex ways.42 This is compounded by the potential for complex interactions between ammonium and feldspar, such as cation substitution10,11,28 and attachment.11,43 We also represent the charged base as being comprised of distinct points of charge under the connections of the contact layer atoms, whereas a more reasonable model might consist of a more uniform charge density, or as distinct points of different charges representing different ions present at the feldspar surface. In addition, we take the energy of a structure to be the minimised energy, instead of computing a finite temperature average. This assumes that all minima are of approximately the same shape in the free energy landscape, such that the finite temperature contributions to the energy are so similar for each configuration that they can be neglected when considering enthalpy differences.
There are several limitations in our determination of the entropy of the systems studied here. Due to computational constraints, we are limited to investigating a small unit cell with PBCs – although the cell cannot reasonably be made larger, investigating the effects of these PBCs may be of interest. We also lack any filtering of symmetry-related structures in our enumeration, which may be important in computing entropy differences if inclusion of NH4+ at different layers breaks differing numbers of symmetries. In addition, we cannot use Rick's algorithm to investigate the effect of creating defects in the system,33 although future work could focus on the impact of including hydroxide or hydronium ions (although this leads to difficulties with charge within a relatively small unit cell). We also note that Whale's hypothesis implies that a negatively charged ion with few connections should stabilise nucleation on a positively charged surface,9 which could also be explored in more detail.
Although the focus of this work has been on feldspar/ammonium interactions, it is not only within clouds where heterogeneous nucleation of water in the presence of solutes is important. Within e.g. the growing field of cryopreservation it is vitally important to control freezing under physiological solute conditions, and achieving this goal is often aided by nucleants.1,2 We cannot draw a direct comparison to these fields, but we highlight the influence of configurational entropy on nucleation temperatures.
In agreement with Whale's hypothesis, we have found that when ice is mostly connected to a base, the inclusion of an ammonium increases the configurational entropy.9 We compute a “best guess” of a reasonable entropy change in the presence of ammonium on feldspar as the increase in the entropy for the inclusion of an ammonium ion in the contact layer, allowing seven and eight connections to the base. The number of structures for only seven and eight connections are included (despite lower numbers of connections to the base also being possible) as an attempt to account for the true range of accessible structures – the degree of energy variation within a set at a fixed number of connections is not negligible on the scale of variation between sets at different numbers of connections. We note that exploring this energetic equivalence may be a promising avenue for future work. This procedure gives a value of about 0.72 J K−1 mol−1. This is very close to the value Whale found was needed to account for the experimentally observed increase in freezing temperature, 0.62 J K−1 mol−1.9 We have also found that the necessary high numbers of connections to the base can be stabilised by a reasonable negative surface charge, again in agreement with Whale's hypothesis.9 Finally, we find that the enthalpic contribution is more dominant in the overall change in free energy than the entropic contribution. All three of these elements – entropy, enthalpy and charge – are important considerations when discussing the heterogeneous nucleation of ice from an ammonium-containing solution on feldspar.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Gareth Tribello for providing a sample implementation of Rick's algorithm. The authors would like to acknowledge the use of the computational facilities provided by the University of Warwick Scientific Computing Research Technology Platform. Most calculations were performed using the Sulis Tier 2 HPC platform hosted by the Scientific Computing Research Technology Platform at the University of Warwick. We are grateful for the use of the very high memory nodes, which were necessary for this work. Sulis is funded by EPSRC Grant EP/T022108/1 and the HPC Midlands+ consortium. Data associated with this manuscript can be accessed viahttps://wrap.warwick.ac.uk/179657. We would also like to acknowledge the EPSRC Centre for Doctoral Training in Modeling of Heterogeneous Systems (EPSRC Grant No. EP/S022848/1). DQ is funded by EPSRC Program Grant No. EP/R018820/1.Notes and references
- A. Baskaran, M. Kaari, G. Venugopal, R. Manikkam, J. Joseph and P. V. Bhaskar, Int. J. Biol. Macromol., 2021, 189, 292–305 CrossRef CAS.
- G. J. Morris and E. Acton, Cryobiology, 2013, 66, 85–92 CrossRef.
- J. Mülmenstädt, O. Sourdeval, J. Delanoë and J. Quaas, Geophys. Res. Lett., 2015, 42, 6502–6509 CrossRef.
- G. Lloyd, T. Choularton, K. Bower, J. Crosier, M. Gallagher, M. Flynn, J. Dorsey, D. Liu, J. W. Taylor, O. Schlenczek, J. Fugal, S. Borrmann, R. Cotton, P. Field and A. Blyth, Atmos. Chem. Phys., 2020, 20, 3895–3904 CrossRef CAS.
- T. Storelvmo, Annu. Rev. Earth Planet. Sci., 2017, 45, 199–222 CrossRef CAS.
- U. Lohmann and J. Feichter, Atmos. Chem. Phys., 2005, 5, 715–737 CrossRef CAS.
- D. J. Cziczo, K. D. Froyd, C. Hoose, E. J. Jensen, M. Diao, M. A. Zondlo, J. B. Smith, C. H. Twohy and D. M. Murphy, Science, 2013, 340, 1320–1324 CrossRef CAS.
- J. D. Atkinson, B. J. Murray, M. T. Woodhouse, T. F. Whale, K. J. Baustian, K. S. Carslaw, S. Dobbie, D. O'Sullivan and T. L. Malkin, Nature, 2013, 498, 355–358 CrossRef CAS.
- T. F. Whale, J. Chem. Phys., 2022, 156, 144503 CrossRef CAS PubMed.
- T. F. Whale, M. A. Holden, T. W. Wilson, D. O'Sullivan and B. J. Murray, Chem. Sci., 2018, 9, 4142–4151 RSC.
- A. Kumar, C. Marcolli, B. Luo and T. Peter, Atmos. Chem. Phys., 2018, 18, 7057–7079 CrossRef CAS.
- J. M. Lightstone, T. B. Onasch, D. Imre and S. Oatis, J. Phys. Chem. A, 2000, 104, 9337–9346 CrossRef CAS.
- S. E. Worthy, A. Kumar, Y. Xi, J. Yun, J. Chen, C. Xu, V. E. Irish, P. Amato and A. K. Bertram, Atmos. Chem. Phys., 2021, 21, 14631–14648 CrossRef CAS.
- J. D. Bernal and R. H. Fowler, J. Chem. Phys., 1933, 1, 515–548 CrossRef CAS.
- L. Pauling, J. Am. Chem. Soc., 1935, 57, 2680–2684 CrossRef CAS.
- W. N. Lipscomb, J. Chem. Phys., 1954, 22, 344 CrossRef CAS.
- J. F. Nagle, J. Math. Phys., 1966, 7, 1484–1491 CrossRef CAS.
- E. H. Lieb, Phys. Rev., 1967, 162, 162 CrossRef CAS.
- E. H. Lieb, Phys. Rev. Lett., 1967, 18, 692 CrossRef CAS.
- M. V. Kirov, Phys. A: Stat., 2013, 392, 680–688 CrossRef CAS.
- R. Howe and R. W. Whitworth, J. Chem. Phys., 1987, 86, 6443–6445 CrossRef CAS.
- N. H. Fletcher, J. Chem. Phys., 1959, 30, 1476–1482 CrossRef CAS.
- J.-L. Kuo, J. V. Coe, S. J. Singer, Y. B. Band and L. Ojamäe, J. Chem. Phys., 2001, 114, 2527–2540 CrossRef CAS.
- T. Hayashi, C. Muguruma and Y. Okamoto, J. Chem. Phys., 2021, 154, 044503 CrossRef CAS.
- B. A. Berg, C. Muguruma and Y. Okamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 092202 CrossRef.
- M. V. Ferreyra and S. A. Grigera, Phys. Rev. E, 2018, 98, 042146 CrossRef CAS.
- C. P. Herrero and R. Ramírez, Chem. Phys. Lett., 2013, 568, 70–74 CrossRef.
- A. Kumar, A. K. Bertram and G. N. Patey, ACS Earth Space Chem., 2021, 5, 2169–2183 CrossRef CAS.
- L. J. Conway, K. Brown, J. S. Loveday and A. Hermann, J. Chem. Phys., 2021, 154, 204501 CrossRef CAS PubMed.
- C. G. Salzmann, Z. Sharif, C. L. Bull, S. T. Bramwell, A. Rosu-Finsen and N. P. Funnell, J. Phys. Chem. C, 2019, 123, 16486–16492 CrossRef CAS.
- R. Brill and S. Zaromb, Nature, 1954, 173, 316–317 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS.
- S. W. Rick and A. Haymet, J. Chem. Phys., 2003, 118, 9291–9296 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford university press, 2017 Search PubMed.
- M. Matsumoto, T. Yagasaki and H. Tanaka, J. Comput. Chem., 2017, 39, 61–64 CrossRef.
- A. A. Hagberg, D. A. Schult and P. J. Swart, Proceedings of the 7th Python in Science Conference, Pasadena, CA USA, 2008, pp. 11–15 Search PubMed.
- S. Páll, A. Zhmurov, P. Bauer, M. Abraham, M. Lundborg, A. Gray, B. Hess and E. Lindahl, J. Chem. Phys., 2020, 153, 134110 CrossRef.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes and I. Vorobyov, et al. , J. Comput. Chem., 2010, 31, 671–690 CrossRef CAS.
- J. L. F. Abascal, E. Sanz, R. García Fernández and C. Vega, J. Chem. Phys., 2005, 122, 234511 CrossRef CAS PubMed.
- J. S. Hub, B. L. de Groot, H. Grubmüller and G. Groenhof, J. Chem. Theory Comput., 2014, 10, 381–390 CrossRef CAS PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- S. J. Cox, S. M. Kathmann, B. Slater and A. Michaelides, J. Chem. Phys., 2015, 142, 184704 CrossRef PubMed.
- J. D. Russell, Trans. Faraday Soc., 1965, 61, 2284–2294 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3fd00097d |
| This journal is © The Royal Society of Chemistry 2024 |