Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cation disorder dominates the defect chemistry of high-voltage LiMn1.5Ni0.5O4 (LMNO) spinel cathodes†
Jiayi
Cen
 ab,
Bonan
Zhu
ab,
Bonan
Zhu
 ab,
Seán R.
Kavanagh
ab,
Seán R.
Kavanagh
 ac,
Alexander G.
Squires
ac,
Alexander G.
Squires
 ab and
David O.
Scanlon
ab and
David O.
Scanlon
 *ab
*ab
aDepartment of Chemistry and Thomas Young Centre, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: d.scanlon@ucl.ac.uk
bThe Faraday Institution, Quad One, Harwell Science and Innovation Campus, Didcot OX11 0RA, UK
cDepartment of Materials and Thomas Young Centre, Imperial College London, Exhibition Road, London SW7 2AZ, UK
First published on 12th April 2023
Abstract
High-voltage spinel LiMn1.5Ni0.5O4 (LMNO) can exist in a Mn/Ni ordered P4332 or disordered Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m arrangement with a majority of literature studies reporting improved electrochemical performance for the disordered phase. Through modifying synthesis conditions, the Mn/Ni ordering can be tuned, however oxygen and Mn3+ stoichiometries are also affected, making it difficult to decouple these responses and optimise performance. Here, we investigate all intrinsic defects in P4332 LMNO under various growth conditions, using density functional theory (DFT) calculations. We find that the majority of defects are deep and associated with small polarons (Mn3+, Mn2+ and Ni3+) formation. The tendency for cation disorder can be explained by the low formation energy of the antisite defects and their stoichiometric complexes. The intrinsic Fermi level of LMNO varies from moderately n-type under oxygen-poor conditions to weakly p-type under oxygen-rich conditions. Our work explains experimental observations (e.g. the Mn/Ni disorder) and provides guidelines for defect-controlled synthesis.
m arrangement with a majority of literature studies reporting improved electrochemical performance for the disordered phase. Through modifying synthesis conditions, the Mn/Ni ordering can be tuned, however oxygen and Mn3+ stoichiometries are also affected, making it difficult to decouple these responses and optimise performance. Here, we investigate all intrinsic defects in P4332 LMNO under various growth conditions, using density functional theory (DFT) calculations. We find that the majority of defects are deep and associated with small polarons (Mn3+, Mn2+ and Ni3+) formation. The tendency for cation disorder can be explained by the low formation energy of the antisite defects and their stoichiometric complexes. The intrinsic Fermi level of LMNO varies from moderately n-type under oxygen-poor conditions to weakly p-type under oxygen-rich conditions. Our work explains experimental observations (e.g. the Mn/Ni disorder) and provides guidelines for defect-controlled synthesis.
Introduction
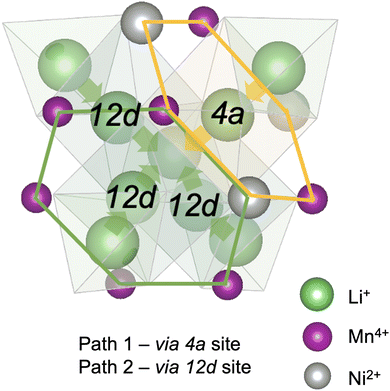
High-voltage spinel LiMn1.5Ni0.5O4 (LMNO) is a promising cobalt-free cathode material which can deliver high energy density (650 W h kg−1) due to its high operating voltage ∼4.7 V (vs. Li+/Li) arising from the Ni2+/Ni4+ couple.1 As an important derivative of the extensively studied LiMn2O4 mixed-valence spinel (LMO), LMNO has structural and chemical similarities with LMO.2–4 In both structures Li+ occupy tetrahedral (Td) sites, and the transition metals (TM) occupy octahedral (Oh) sites of the cubic close-packed oxygen arrays. In addition, they have 3D diffusion channels where Li+ migrate through “gate sites”: six-member cation rings perpendicular to the diffusion path.5 LMNO, however, has improved energy density and cycling stability compared to LMO partly due to a reduced prevalence of Mn3+ in LMNO. Mn3+ gives rise to pronounced Jahn–Teller (JT) distortion and Mn dissolution via disproportionation reactions (2Mn3+ → Mn2+ + Mn4+) leading to structural instability.2,6–8Depending on synthesis conditions, LMNO can show site disorder in the octahedral TM cation sites (see Fig. 1).9 A lower synthesis/anneal temperature (∼700 °C) leads to the formation of the ordered (P4332) phase, where Ni and Mn are located at 4b and 12d Wyckoff sites.10–12 In the ideal P4332 LMNO, all Mn species present as redox-inactive Mn4+. The Ni2+/Ni4+ couple gives rise to a distinctive voltage at ∼4.7 V.4 Higher synthesis temperatures (>700 °C) promote the formation of the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m LMNO with Mn and Ni disordered across the 16d sites. High temperature synthesis may also drive oxygen vacancy formation, which is expected to be compensated by the reduction of Mn4+ to Mn3+, leading to an off-stoichiometric composition (LiMn1.5Ni0.5 O4−δ) with the formation of rock-salt phase (e.g. LixNi1−xO) impurities.11,13 Mn3+ is redox active and the Mn3+/Mn4+ redox reaction introduces an additional plateau at ∼4 V on the voltage profile.4 The disordered phase generally exhibits better cycling stability and rate capability than the ordered phase, however the connection between disorder and performance has remained unclear, with increasing attention placed on understanding the role of cation disorder.14–22
m LMNO with Mn and Ni disordered across the 16d sites. High temperature synthesis may also drive oxygen vacancy formation, which is expected to be compensated by the reduction of Mn4+ to Mn3+, leading to an off-stoichiometric composition (LiMn1.5Ni0.5 O4−δ) with the formation of rock-salt phase (e.g. LixNi1−xO) impurities.11,13 Mn3+ is redox active and the Mn3+/Mn4+ redox reaction introduces an additional plateau at ∼4 V on the voltage profile.4 The disordered phase generally exhibits better cycling stability and rate capability than the ordered phase, however the connection between disorder and performance has remained unclear, with increasing attention placed on understanding the role of cation disorder.14–22
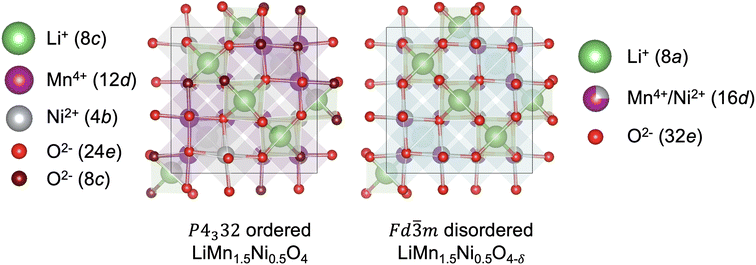 | ||
Fig. 1 Representative structures (with Wyckoff positions) of the P4332 ordered and Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m disordered LMNO. m disordered LMNO. | ||
While some studies found that Mn/Ni disorder increases with oxygen vacancy and Mn3+ formation, others have suggested that the “disordered” phase from different studies is likely to be samples with partial cation disordering, a varying degree of oxygen content and impurity phases.13,19,20,23–25 Regardless, the correlation between cation disorder and oxygen content has made it difficult to distinguish the key driving factor for improved performance, illustrating the need to decouple these effects and study their impacts independently.
Density functional theory (DFT) is a key tool for studying the defect chemistry of functional materials.26,27 Previous defect studies17,24,28–30 have focused on understanding the effects of specific defects on the P4332 and Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m LMNO with various Mn/Ni orderings using a 56-atom supercell. The insights obtained at a microscopic level, such as the Madelung potentials and electronic structures, revealed the likely impacts of oxygen vacancies, which can then be used to explain electrochemical behaviours (e.g. voltage changes and ionic conduction) and to propose optimisation strategies. The high formation energies of TM Frenkel defects explain the sluggish TM ordering transition kinetics. Although they have provided useful insights on defect formation and cation disorder, these studies have various deficiencies: (i) ignoring the effect of atomic chemical potentials on the defect formation energies; (ii) neglecting to address the spurious long-range Coulomb interactions between charged defects inherent within the supercell approach; (iii) calculating defect properties within a small supercell corresponding to unrealistically large defect concentrations.31,32
m LMNO with various Mn/Ni orderings using a 56-atom supercell. The insights obtained at a microscopic level, such as the Madelung potentials and electronic structures, revealed the likely impacts of oxygen vacancies, which can then be used to explain electrochemical behaviours (e.g. voltage changes and ionic conduction) and to propose optimisation strategies. The high formation energies of TM Frenkel defects explain the sluggish TM ordering transition kinetics. Although they have provided useful insights on defect formation and cation disorder, these studies have various deficiencies: (i) ignoring the effect of atomic chemical potentials on the defect formation energies; (ii) neglecting to address the spurious long-range Coulomb interactions between charged defects inherent within the supercell approach; (iii) calculating defect properties within a small supercell corresponding to unrealistically large defect concentrations.31,32
In this paper, we present a comprehensive study of the energetics and behaviour of intrinsic defects in P4332 LMNO. We first systematically study the magnetic ordering in bulk LMNO, before computing bulk properties and all stable competing phases in the Li–Mn–Ni–O chemical space to determine the phase stability region. We then calculate all intrinsic defects in all possible charge states, using Bader charges, charge densities and Madelung site potential analysis to characterise charge compensation mechanisms and identify small polaron formation. We also investigate a range of likely defect complexes and the migration of lithium defects. Finally, we discuss the effect of synthesis conditions on defect chemistry and how this can explain experimental observations and guide defect-controlled synthesis.
Methodology
Computational details
Calculations were performed using spin-polarised plane-wave DFT as implemented in the Vienna ab initio Simulation Package33–35 (VASP) code (version 5.4.4). PAW pseudopotentials36,37 (version PBE_5.4) of Li_sv, Mn_pv, Ni_pv and O were used to model the core electrons. Calculations were performed with the GGA(PBEsol) + U method38,39 where U values for d-orbitals of Mn and Ni were set to 3.9 and 6.0 eV, respectively, based on previous literature studies.40,41 The initial structure of P4332 LMNO obtained from Materials Project42 contains 56 atoms in a primitive cell with 8 formula units of LiMn1.5Ni0.5O4. The structure was optimised using a plane-wave cutoff of 550 eV and a Γ-centered Monkhorst–Pack43k-point sampling of 3 × 3 × 3 (kpoint-spacing of 0.2528 Å−1) following convergence tests with respect to energy cutoff and k-points. Tolerances of 10−5 eV and 10−2 eV Å−1 were applied to electronic and ionic convergence respectively for bulk and defect calculations.Pymatgen (version 2020.12.31)44,45 was used to investigate the magnetic ordering of the bulk structure. Additional calculations were performed using the HSE06 hybrid functional46 on the ferrimagnetic (FiM) ground state47 LMNO structure (Mn ↑ Ni ↓) to compare with the PBEsol + U results. A denser Γ-centered 4 × 4 × 4 k-point mesh was used to produce the electronic density of states (DOS) and band structure (path from Bradley and Cracknell48).49
Defect calculations were conducted using the PBEsol + U functional on a cubic 2 × 2 × 2 (448-atom) supercell with Γ-only k-point grid. Performing calculations using hybrid functional would be practically infeasible with our chosen supercell size due to the exorbitant computational cost. More details about our choice of density functional for this study can be found on page S1 and S2 of the ESI document.† The ferrimagnetic spin configuration was initialised for all defects with fixed-volume relaxations.50 The force tolerance was raised to 2 × 10−2 eV Å−1 for interstitial defects. Defect calculations set up and analysis were facilitated by DOPED.51,52 A lean version of the ShakeNBreak53 approach was used to aid the location of the ground-state defect structures.54,55 With access to the ground state and many metastable defect structures, defect configuration landscape can be explored. This is important for magnetic materials, whereby the magnetic moment of defect structure forms an additional dimension of potential energy surface. Defects with incorrect polaronic localisation upon relaxations were found to exist as higher-energy metastable structures (typically 0.2–3 eV above the ground state). Displacement distributions with standard deviations of 0.02 Å and 0.05 Å were tested on individual defect structures and the lowest energy relaxed structures were taken for further analysis. Climbing-image nudged elastic band (cNEB) method was used to calculate point defect migration barriers.56,57 All crystal structure diagrams were prepared using VESTA.58
Defect analysis
The formation energy of a defect X in a charge state q with respect to the host lattice is calculated using26,50,59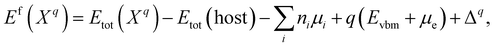 | (1) |
The chemical potential stability limits of LMNO are defined by the equality
| μLi + 1.5μMn + 0.5μNi + 4μO = ΔHf (LiMn1.5Ni0.5O4), | (2) |
| μNi + μO ≤ ΔHf (NiO) | (3) |
In a solid, defects typically occur in multiple charge states with positive/negative charge states involving removal/addition of electrons. The actual position of Fermi level (μe) is determined by minimising the system energy under self-consistent charge neutrality condition using py-sc-fermi:50,78,79
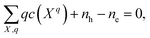 | (4) |
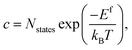 | (5) |
Madelung potentials can suggest where ions in a structure are situated in the energy landscape and the likelihood of redox.81 They are the electrostatic energies by approximating ions as point charges and can be expressed by a sum of pair-wise interactions: 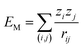 , where zi and zj are the formal charges on ion i and j respectively and rij is the interionic distance. Cations have negative potentials and anions have positive potentials.82 A higher potential corresponds to a greater attraction to negative charge (and thus electron polaron formation), and a lower potential to positive charge (thus hole polaron formation).
, where zi and zj are the formal charges on ion i and j respectively and rij is the interionic distance. Cations have negative potentials and anions have positive potentials.82 A higher potential corresponds to a greater attraction to negative charge (and thus electron polaron formation), and a lower potential to positive charge (thus hole polaron formation).
Defect complex calculations involved constructing supercells with two point defects at a range of pair distances (e.g. nearest and farthest). We performed defect complex analysis on the lowest energy configurations, which are those with the smallest pair distance. A generalised equation R1 + R2 ⇌ P was used to represent their formation, where R1 and R2 are reactants (isolated defects) and P is the product (complex). The enthalpy change for the forward reaction
| ΔH = Ef(P) − Ef(R1) − Ef(R2), | (6) |
The equilibrium concentration of complexes can be approximated according to the mass-action law50,83 using
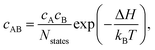 | (7) |
The Gibbs free energy change ΔG for complex formation can be calculated following:
| ΔG = ΔH − TΔS. | (8) |
S = kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W = kB W = kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(NstatesCcX), ln(NstatesCcX), | (9) |
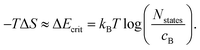 | (10) |
Results and discussion
Bulk properties
| Theory/Exp | PBEsol + U | HSE06 | Exp |
|---|---|---|---|
| Lattice constant [Å] | 8.17 | 8.15 | 8.166(3) |
| (Ni–O) × 6 [Å] | 2.05 | 2.06 | 2.068(2) |
| (Mn–O) × 2 [Å] | 1.88 | 1.87 | 1.870(4) |
| (Mn–O) × 2 [Å] | 1.91 | 1.90 | 1.914(1) |
| (Mn–O) × 2 [Å] | 1.94 | 1.93 | 1.932(4) |
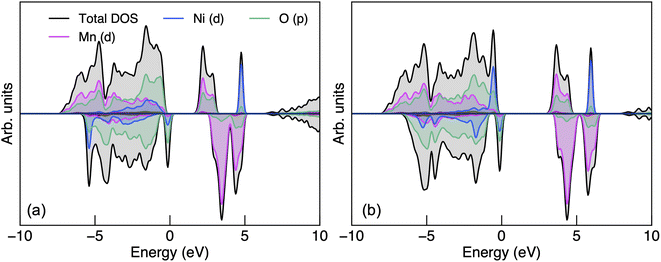 | ||
| Fig. 2 The electronic density of states of P4332 LiMn1.5Ni0.5O4 obtained from (a) PBEsol + U and (b) HSE06 calculations. | ||
| Theory | PBEsol + U | HSE06 | ||
|---|---|---|---|---|
| Spin channel | VBM spin ↓ | CBM spin ↑ | VBM spin ↓ | CBM spin ↑ |
| O | 71% | 24% | 61% | 21% |
| Ni | 24% | 0% | 34% | 0% |
| Mn | 4% | 70% | 4% | 72% |
The CBM has a greater proportion of Mn 3d states than O 2p states with both functionals. The presence of oxygen character at the CBM suggests polar covalent Mn–O bonding with hybridised states. Since Mn and Ni dominate the CBM and VBM respectively, charge localisation would occur on Mn (for electron polarons) and Ni (for hole polarons). The Mn 3d states in the spin-up channel at the CBM also suggest that Mn would adopt a high-spin configuration when an additional electron is populated to form Mn3+ (d4). Liu et al.89 suggested that the 2p unoccupied states from O is related to the O2 release phenomena under thermal treatment, the formation of the rock-salt impurity phases LixNi1−xO and high-temperature phase Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m LiMn1.5Ni0.5 O4−δ where Mn3+ is also redox-active. Ryoo et al.90 related the bonding characteristics of Mn–O and Ni–O, both hybridised with a similar degree of covalency, to the propensity for cation disordering in LMNO at elevated temperatures. In contrast, cation ordering is strongly preserved in P4332 LiGe1.5Ni0.5O4 despite Ge4+ having the same ionic radius to Mn4+, even at a very high temperature (e.g. 950 °C), due to the contrasting bonding motifs of Ge–O (ionic) and Mn–O (polar covalent).90
m LiMn1.5Ni0.5 O4−δ where Mn3+ is also redox-active. Ryoo et al.90 related the bonding characteristics of Mn–O and Ni–O, both hybridised with a similar degree of covalency, to the propensity for cation disordering in LMNO at elevated temperatures. In contrast, cation ordering is strongly preserved in P4332 LiGe1.5Ni0.5O4 despite Ge4+ having the same ionic radius to Mn4+, even at a very high temperature (e.g. 950 °C), due to the contrasting bonding motifs of Ge–O (ionic) and Mn–O (polar covalent).90
Fig. S2† shows the electronic band structure and both functionals show weak band dispersion, reflecting strong electron–electron correlations. LMNO is calculated to be a wide-gap semiconductor, with an indirect band gap of 1.76 and 3.17 eV determined using PBEsol + U and HSE06 functionals, respectively. The hybrid approach, in theory, should give a more reliable prediction of fundamental band gap compared to PBEsol + U, in which the magnitude of the band gap is influenced by the choice of U values.91 There is limited experimental data on the fundamental band gap to compare with the current study, though an optical gap between 1.2–1.3 eV has been reported experimentally.92,93 The large difference between the fundamental and optical band gaps is likely due to the strong excitonic effects in flat d-band wide gap materials.94,95
Phase stability
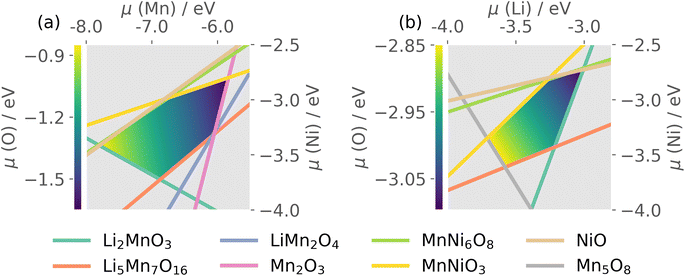
Thermodynamic stability of LMNO was determined by computing formation energies of all stable competing phases in the Li–Mn–Ni–O phase diagram, where Li2Ni2O3 was obtained using structure prediction.96 Formation energies of all stable competing phases are summarised in Tables S4 and S5.†The host material is thermodynamically stable and there are 20 intersection points bounding the stability region in the chemical potential space. Each intersection point corresponds to a facet in the phase diagram where the corresponding phases are in equilibria with the host (see Table S6†). O-rich (μO = 0 eV) oxidizing conditions are usually Mn- and Ni-poor, and favour p-type (acceptor) defect formation. O-poor, Mn- and Ni-rich reducing conditions favour n-type behaviour, which can occur under higher temperature and/or reduced oxygen partial pressure and/or under the presence of oxygen-reducing agents (e.g. LiH).97
The quaternary phase space of LMNO yields a 4D stability region, thus to allow visualisation on a 2D plot, we show in Fig. 3 the stability region where μLi and μMn were set to the average values over all atomic chemical potentials intersection points. LMNO is stable across a small μNi range, a moderate μLi range and a larger μMn range. The size of the stability field reflects the ease of synthesizing the target product experimentally and determines the range of variation in defect formation energy over all possible growth conditions. Thus, there is a greater sensitivity of defect concentrations to Mn-related than Ni-related growth environments. The ease of nickel oxide impurity phase formation upon synthesizing LMNO is reflected by the small μNi window.12,62
Defect structure and energetics
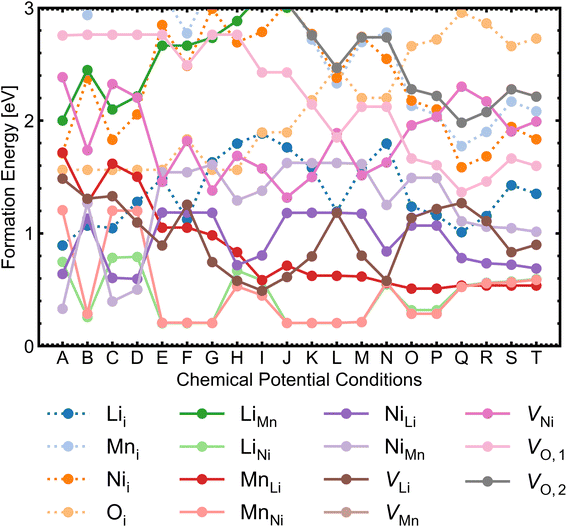
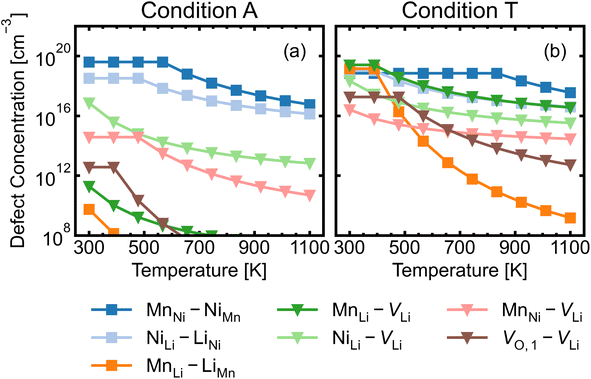
We investigated a range of intrinsic point defects in all possible charge states. This includes all vacancies (VLi, VTM and VO), antisites (LiTM, TMLi and TMTM) and interstitials (Lii, TMi and Oi); ‘TM’ refers to a transition metal species (Mn or Ni) and vacancies on symmetry inequivalent oxygens in the 24e and 8c sites are denoted by VO,1 and VO,2 respectively. For interstitials, we tested six symmetry inequivalent interstitial positions and their corresponding Wyckoff positions are specified in Table S7.† In addition, the potential formation of peroxide species from oxygen interstitials was tested by placing Oi at distances ∼1.4 Å from Ohost and relaxing the defect geometry from this structure.98 We also considered a range defect complexes including the antisite-pair defects (LiMn–MnLi, LiNi–NiLi and MnNi–NiMn), vacancy-pair (Schottky) defects (e.g. VO–VLi, MnNi–VLi) and a lithium Frenkel-pair (Li+i–V−Li), due to the low formation energies (and thus high concentrations) of the constituent point defects.To illustrate the complex nature of defect chemistry of LMNO, in Fig. 4 we have plotted the formation energies of all intrinsic defects in their lowest energy charge states at the self-consistent Fermi levels over the 20 chemical potential conditions from O-rich to O-poor (increasing self-consistent Fermi levels). With the inverse–exponential relationship between defect concentration and formation energy (eqn (5)), the large variation in formation energies across different chemical potentials indicates a strong sensitivity of defect concentrations to growth conditions in LMNO. Transitioning from O-rich to O-poor (A → T), the formation energies of several n-type defects (e.g. oxygen vacancies) decrease sharply (by ≥0.5 eV). Therefore, the formation of these defects are highly sensitive to the oxygen and/or temperature environments. Formation energies of MnNi and LiNi defects remain be the lowest in each chemical potential condition, thus the disordering in LMNO is greatly driven by those defects. This may also explain typical LMNO samples are not perfectly stoichiometric on the cation sites and are often slightly Ni-deficient LiNi0.5−xMn1.5+xO4 (x < 0.1).99
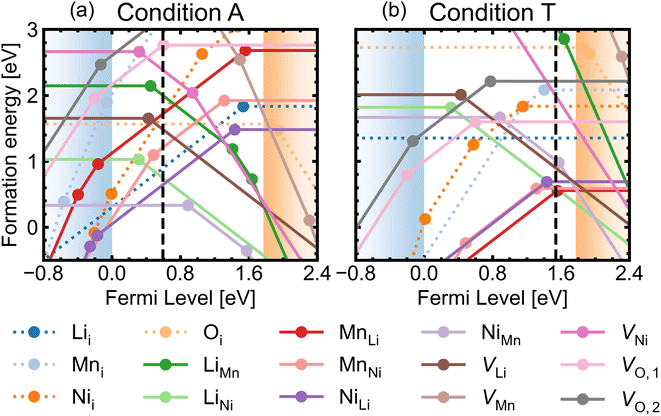
Fig. 5 shows the defect transition levels under two contrasting conditions A (O-rich; p-type) and T (O-poor; n-type). The gradient of each line corresponds to defects' charge states. The Fermi level where the formation energy of a defect X in two charge states q1/q2 becomes equal is termed as the thermodynamic transition level ε(q1/q2) where Xq1 and Xq2 are in thermodynamic equilibrium, and is represented by a filled circle.
Below we discuss the lowest-formation-energy (highest concentration) defects at the self-consistent Fermi level, and their likely influences on material properties.
Antisite behaviour is found to depend on the change in local coordination environment for the TM involved (e.g. Oh → Oh, Oh → Td). For MnNi and NiMn with no change in coordination (Oh → Oh) at the defect site, fully ionised charge states (+2 and −2 respectively) give Mn4+ and Ni2+ species (see Table 3), while other charge states correspond to the addition of localised electrons/holes to the d orbitals of Mn/Ni, as confirmed by Bader charge density and the site-projected magnetisation analysis.100,101 For example, the magnetisation on the Ni0Mn defect site is 0.1 μB, suggesting no unpaired electrons and corresponds to Ni4+ (d6) low-spin configuration. The local geometry near Ni4+ is slightly distorted with Ni4+–O ranging between 1.85–1.88 Å which is shorter than that of Ni2+–O = 2.06 Å (see Table 1). Similarly, the Mn0Ni defect site corresponds to Mn2+ (d5) high-spin of −4.5 μB. The sign change in the magnetisation reflects a spin flip relative to Mn in the bulk and this is related to the complex orbital interactions exchanging the spin information.
| Defect | Magnetisation [μB] | Bader chargea | Species | Average TM–O bond lengthsb [Å] |
|---|---|---|---|---|
| a Bader charge in bulk LMNO (Wyckoff sites): Li+ (8c): 0.89; Mn4+ (12d): 1.81; Ni2+ (4b): 1.21; O12− (24e): −1.06; O22− (8c): −1.05. b Average TM–O bond length in bulk LMNO: Mn4+–O: 1.91 Å; Ni2+–O: 2.05 Å. | ||||
| Mn2+Ni | 3.1 | 1.84 | Mn4+ (d3) | 1.92 |
| Mn+Ni | −3.7 | 1.70 | Mn3+ (d4) | 2.02 |
| Mn0Ni | −4.5 | 1.46 | Mn2+ (d5) | 2.13 |
| Ni2−Mn | 1.7 | 1.22 | Ni2+ (d8) | 2.04 |
| Ni−Mn | −0.9 | 1.32 | Ni3+ (d7) | 1.95 |
| Ni0Mn | 0.1 | 1.39 | Ni4+ (d6) | 1.87 |
| Mn3+Li | 4.4 | 1.50 | Mn2+ (d5) | 1.99 |
| Mn2+Li | 4.4 | 1.52 | Mn2+ (d5) | 1.98 |
| Mn+Li | 4.4 | 1.51 | Mn2+ (d5) | 1.98 |
| Mn0Li | 4.4 | 1.51 | Mn2+ (d5) | 1.98 |
| Ni3+Li | −1.8 | 1.30 | Ni2+ (d8) | 1.94 |
| Ni2+Li | −1.8 | 1.29 | Ni2+ (d8) | 1.94 |
| Ni+Li | −1.8 | 1.29 | Ni2+ (d8) | 1.94 |
| Ni0Li | −1.7 | 1.27 | Ni2+ (d8) | 1.93 |
Moorhead-Rosenberg et al.102 suggested the spin on Mn3+ and Mn2+ should be parallel to that of Ni2+ due to the oxygen-mediated super-exchange interaction. This coincides with the spin-flip phenomena shown in Table 3. However, a spin flip is not observed on all defects and there is no clear trend whether a certain spin orientation is preferred. Magnetic interactions are influenced by the point defects and each defect has a complex potential energy surface, meaning that different defect structures and magnetic states may be found, depending on the initial structures, their magnetisation values and the choice of electronic minimisation algorithm. In each case, different degrees of structural perturbation (rattling) and magnetisation initialisations were tested, to aid the location of the true ground state defect.53–55 One spin flip usually gives less than 0.1 eV difference in energy. However, multiple spin flips can lead to a large energy change (e.g. ∼1 eV) and give erroneous results. All calculations have been checked and rerun to ensure there are no multiple spin flips on the TM cations.
For MnLi and NiLi defects with a change in coordination (Oh → Td) at the defect site, we observe a strong preference of Mn and Ni species to adopt the lowest stable positive oxidation states (a closer charge to Li+) for these element (i.e. Mn2+ and Ni2+) (see Table 3). Ni coordinating to O in a Td crystal field would favour a high-spin configuration as the size of ligand field splitting is reduced (ΔTd = 4/9ΔOh), where ΔTd and ΔOh are the Td and Oh crystal field splitting energy respectively.103 The average bond lengths of Td Mn2+–O is 1.98 Å, which is longer than the standard Oh Mn4+–O bond lengths between 1.87–1.94 Å (see Table 1). The energetic penalties for Ni to adopt Ni4+ (d6), Ni3+ (d7) and Ni2+ (d8) in a Td field are 2.13 ΔOh, 1.26 ΔOh and 0.84 ΔOh, respectively, while for Mn in Mn4+ (d3), Mn3+ (d4) and Mn2+ (d5), they are 0.84 ΔOh, 0.42 ΔOh and 0 ΔOh respectively. Configurations with the lowest energetic penalties (i.e. Ni2+ and Mn2+) are favoured on the Li+ site. In addition, the ionic radius of Mn2+ in a four-coordination environment is 0.66 Å, which is closer to that of Li+ (0.59 Å), compared to Mn4+ (0.39 Å).104 Literature studies2,7,21,105 suggest the formation of Mn2+ as a consequence of Mn3+ disproportionation reactions. Mn2+ are detrimental to performance as they easily dissolve in electrolytes leading to capacity fading.23 Additionally, our results may also explain the fact that Mn only exist in the reduced Mn2+ states upon migration from the Oh to the Td sites during the structural transition upon heating highly delithiated LMNO.106
LiTM defects involve changing the coordination of Li (Td → Oh). We found that fully ionised Li−Ni is always the most stable charge state across all synthesis conditions at their self-consistent Fermi levels. In addition, the formation energies of Li−Ni are lower than LiMn, indicating that Li+ would preferentially form on the Ni sites over the Mn sites. Similar observations were found on Li-doped LMNO, where Li+ sat in the 4b positions.21 This inevitably replaces some Ni2+, leading to reduced capacity.
Among vacancy defects, VO and VLi have much lower formation energies (thus exist in higher concentrations) than VMn and VNi under all conditions (see Fig. 4). Therefore, oxygen and lithium vacancies are discussed here. For lithium vacancies, while V−Li (removing a Li+ ion) generates little disturbance to the system, V0Li (removing a Li atom) reveals the delithiation mechanism.16,86 A localised hole is observed on the Ni in proximity to the defect site, with a magnetisation of −0.9 μB which is nearly half of the original value (−1.7 μB) for Ni2+. This suggests that Ni2+ (d8) is oxidised to Ni3+ (d7) low-spin configuration, with the Bader charge of 1.33 compared to 1.21 for bulk Ni2+ in agreement with the reduction in Ni–O bond lengths from 2.05 Å to 1.86–2.05 Å. The Ni–O bonds become more covalent and exhibit a JT distortion associated with d7 low-spin. Madelung potential analysis on the unrelaxed V0Li structure confirmed that the nearest Ni to the vacant lithium site is oxidised to Ni3+.107 The average Madelung site potential on Ni is −24.55 V, whereas the Ni3+ site has the most negative potential, with −27.38 V.
Oxygen vacancies are found to be non-negative U type (stable in the 0 and +1 charge states, likely aided by polaronic stabilisation of excess electrons), adopting the neutral state under most growth conditions.108VO,1 are lower in energy than VO,2 at each charge state (Fig. 5). This can be explained from their local coordination as mentioned previously, with VO,1 configuration having less unfavourable electrostatic repulsion between the cations than that of VO,2, reflected in the average Madelung potentials of 26.31 V (O1) and 29.37 V (O2). In the neutral state (V0O,1 and V0O,2), there are two five-coordinated Mn3+ which acquire the electrons donated from VO, with magnetisation values between 3.6–3.7 μB compared to ∼ 3.0 for the remaining Mn4+ species. Mn3+ have Bader charges ∼1.6 which are lower than that of Mn4+, with 1.83. In the +1 charge state, V+O,1 has a localised electron on one of the five-coordinated Mn, whereas V+O,2 has the additional electron delocalised over three five-coordinated Mn, confirmed by hybrid DFT calculations in a 56-atom supercell.
Overall, antisites and vacancies in LMNO are deep defects, generating localised states (that are distant from VBM and CBM) with small polarons on Mn sites for electrons and Ni for holes. The materials is dominated by ionic compensation rather than electronic compensation. The dopability of LMNO can be assessed by the size of the doping energy window, determined by the lowest energy compensating acceptor/donor defect at the CBM/VBM for n/p-type dopability.109 The lowest energy donor and acceptor is antisite Ni+Li and Li−Ni, giving a dopability window of 0.05 eV (for p-type, O-rich) and 0.36 eV (for n-type, O-poor). Thus LMNO is potentially n-type dopable and not p-type dopable. This behaviour is driven by the antisite defects in LMNO rather than oxygen vacancies in other n-type oxides.110,111
For Lii, a configuration with a Li–Li dumbbell split between neighbouring 12d sites is around 0.07 eV lower than a lone Li+i on the 12d site (see Fig. S3†). The preference for Li–Li dumbbell configuration was reported for the parent spinel compound LMO.86 The Madelung potentials for Li+ in the Td 8c crystal site are around −9.54 V, whereas those in the interstitial 4a and 12d are −6.84 V and −6.40 V respectively. Neutral Li0i gives an electron polaron on a neighbouring Mn (giving Mn3+) beside the Li–Li dumbbell.
For TMi, the charge compensation mechanism for non-fully-ionised states is the same as for other n-type defects where Mn4+ in the proximity to the defect site get reduced. Having tested a range of charge states, we found Mn3+ and Mn2+ but no Mn4+ species in Mni defect supercells, whereas all Ni species always exist as Ni2+ in Nii defect supercells. When q = 2, interstitial Mn and Ni exist in +2 oxidation states. Adding more electrons in the systems (q = 1, 0) led to the formation of more Mn3+. Interstitial Ni2+ prefers to be in the 12d sites, identical to the preference for Lii. Interstitial Mn2+, on the other hand, prefers to be in the 4a sites (∼0.05–0.15 eV lower in energy). This could be partly due to a size effect. The 4a sites have larger octahedral volume than the 12d sites (Table S8†).112,113 The ionic radii for Li+, Ni2+ and Mn2+ in octahedral coordination are 0.76 Å, 0.69 Å and 0.83 Å, respectively.104,113 Ions with smaller ionic radii (i.e. Li+ and Ni2+) would have a smaller volume mismatch with the smaller 12d octahedral volume, while bigger Mn2+ need sites with larger volume. Similar to the structural features observed in Lii, Li–Ni and Mn–Li split-interstitial configurations are also seen for Nii and Mni. This configuration reduces cation–cation repulsion and lattice strain, facilitated by highly mobile Li+ which can easily migrate from Td to Oh sites.114 Finally, the exchange type reaction Nii → Lii + NiLi is found to spontaneously occur, again reflecting the high mobility of Li+.83
All Oi relaxed into dumbbell configurations with O–O distance within 1.4 Å.115 In addition, they are stable in the charge neutral state over all Fermi levels, with high-lying O–O anti-bonding states. They are also known as peroxide species (Oper) and are seen in many more n-type oxides (e.g. SnO2 and BaSnO3).54,110,116 We identified two distinct Oi peroxide configurations with different TM environments: surrounded by 3Mn4+ and a Ni2+ (ground state) and surrounded by 2Mn4+ and 2Ni2+ (0.8 eV higher in energy).
Among all interstitial defects, Lii is always lower in energy than Mni and Nii, indicating that they are more likely to form in high concentration. The energetic ordering of Nii and Mni can vary depending on the chemical potential conditions. The formation energy of Oi can become lower than that of Lii in O-rich synthesis conditions. Overall, Lii, Mni and Nii are deep donors and Oi are ultra-deep acceptors with only neutral states stable across the band gap (see Fig. 5).
Defect complexes
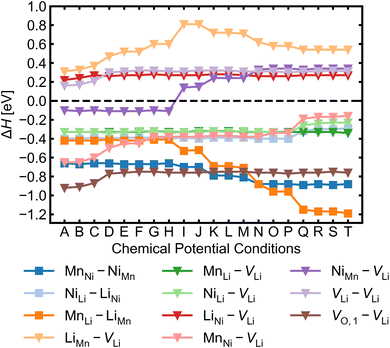
Given the low formation energies and thus high concentrations of cation antisites, lithium and oxygen vacancies, we further investigate the association of point defects, including three stoichiometric (antisite-pairs), and eight non-stoichiometric (vacancy-related) complexes. Since the formation energy on the oxygen vacancy in 24e sites (O1) is always lower and O1 has higher multiplicity than O2 (in the 8c sites), we only conduct detailed analysis on the association of VLi with VO,1.Fig. 6 shows defect complex association energies ΔH calculated following eqn (6) over 20 chemical potential limits at their self-consistent Fermi levels. ΔH for a given complex can vary with chemical potentials, even for stoichiometric complexes, due to the indirect effect on the charge-balanced Fermi level. A negative ΔH indicates an exothermic enthalpy change upon defect association. The majority of complexes have negative ΔH, and they feature point defects coulombically attracted to each other. The few complexes that feature defects of the same charge (i.e. both p-type defects) are coulombically opposed to each other, and hence have positive ΔH (e.g. LiNi–VLi). Using ΔH alone to evaluate complex formation, however, neglects a key factor – the temperature dependent entropic cost of defect association. The actual formation of a defect complex and its concentration are influenced by a range of factors, including temperature, concentrations of the constituent defects and ΔH.50,83 We considered the entropic effects in this study by approximating the entropic term using eqn (10), where lower defect concentrations and higher temperatures correspond to larger entropic costs for association into defect complexes. Correspondingly, Fig. 7 shows how ΔG increases with temperature, suggesting complex formation is sensitive to kinetic behaviour during synthesis and quenching. ΔG are generally more negative in the n-type condition than p-type, suggesting that there is a stronger driving force towards complex association even at high temperature in O-poor conditions.
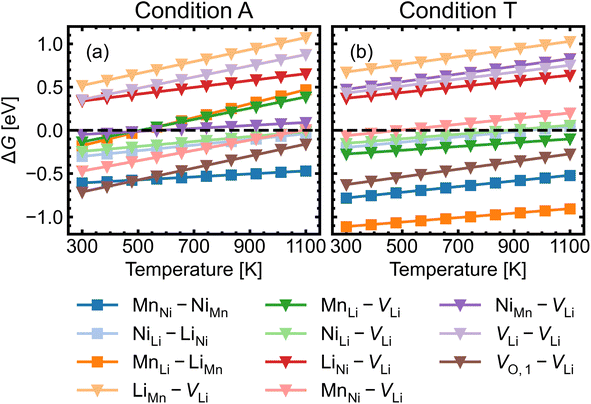 | ||
| Fig. 7 Gibbs free energy change ΔG for complex formation as a function of temperature under (a) the most intrinsically p-type O-rich condition A and (b) n-type O-poor condition T, using eqn (10). Stoichiometric complexes are denoted by squares and non-stoichiometric complexes are denoted by triangles. A negative ΔG suggests complex association is likely, provided the constituent point defects are sufficiently mobile. | ||
Fig. 8 shows the approximated temperature-dependent entropic cost (calculated using eqn (10)) for defect complexes with negative ΔG. A high degree of association is achieved when the complex association energy magnitude |ΔH| is greater than ΔEcrit, showing that one cannot use ΔH alone to evaluate complex formation. For example, under the intrinsically p-type environment (Fig. 8a), the MnLi–LiMn association energy |ΔH| = 0.4 eV is only sufficient to achieve a high degree of association at 500 K but not at 900 K. Increased entropic cost of complex formation is observed for defects with lower concentration (see Fig. 9). The stoichiometric complexes have identical density of the available microstates (Nstates = 4.40 × 1022 cm−3), the differences in the calculated complex concentrations therefore arise from the concentrations of their constituent point defects. For instance, under condition T (Fig. 9b), [MnLi–LiMn] is lower than [NiLi–LiNi] at the majority of temperature range despite that they have similar ΔEcrit and that ΔH for MnLi–LiMn is highly negative (see Fig. 6). Although complex formation is more favourable at lower temperature, this requires isolated point defects to “find” each other. Point defects with high mobility – such as lithium vacancies and interstitials– and/or those that with high concentration are likely to achieve this criterion.
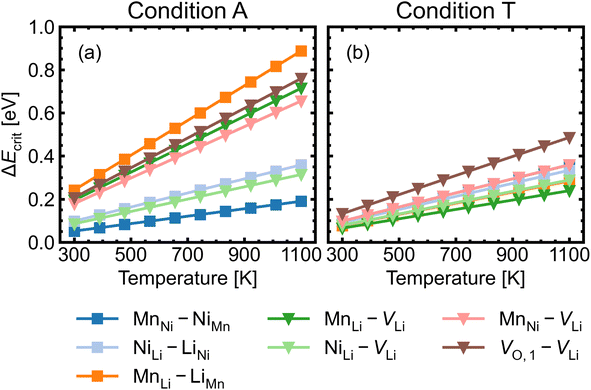 | ||
| Fig. 8 Critical association energy ΔEcrit (approximate entropic cost of complex formation; eqn (10)) as a function of temperature under (a) the most intrinsically p-type O-rich condition A and (b) n-type O-poor condition T. Stoichiometric complexes are denoted by squares and non-stoichiometric complexes are denoted by triangles. | ||
 | ||
| Fig. 9 Defect complex concentration as a function of temperature under (a) the most intrinsically p-type O-rich condition A and (b) n-type O-poor condition T, using eqn (7). Constituent point defect concentrations are fixed to the calculated concentrations at the anneal temperature (T = 973 K), following the typical frozen-defect approximation. Stoichiometric complexes are denoted by squares and non-stoichiometric complexes are denoted by triangles. Defect complex concentrations are capped at the concentration of the major constituent defect. | ||
MnNi–NiMn has the highest concentration for maximum (>99%) complex formation (i.e. saturation concentration), reflecting the strong proclivity to MnNi–NiMn cation disorder in LMNO. Complexes (e.g. MnLi–LiMn) with much lower predicted concentration contribute much less to the disorder. Since defect complex concentrations are higher in condition T than condition A, a greater range of disorder is induced by complex formation under O-poor conditions. In addition, there is a variable temperature-dependent entropic cost with complex formation, with higher defect concentrations corresponding to lower entropic costs of complex association. For example, VO,1–VLi concentration is strongly dependent on temperature, whereas it is not the case for NiLi–VLi. High synthesis/anneal temperatures will yield high point defect concentrations (eqn (7)), which then increasingly favour complex formation as the material cools to room temperature, but with the ability to equilibrate by migrating and forming complexes also decreasing with temperature. Thus the final defect distribution in the material is predicted to be sensitively dependent on the thermal history (i.e. synthesis, annealing and cooling procedures), as witnessed experimentally.117
The association of lithium vacancies with other defects can affect lithium diffusion. If VLi preferentially associates with a specific point defect, the additional species may function as a “trap” for diffusing lithium. Previous literature studies29,118 have specifically discussed the VO,1–VLi complex, with Li+ diffusion more difficult in disordered LMNO, as lithium vacancies preferentially form near oxygen vacancies – which have formation energies ∼1 eV lower in the disordered material. Our calculations indeed find strongly favourable complex binding energies for VO,1–VLi, as well as the moderate binding for MnLi–VLi and MnNi–VLi (Fig. 7). Thus O-rich conditions (e.g. Condition A) are expected to minimise the number of lithium traps (X–VLi complexes), but also yield decreased lithium vacancy concentrations, exhibiting opposing effects on the overall diffusion rate. Therefore, Li+ mobility is affected by competing interactions between other point defects with strong attraction to lithium vacancies, and is highly sensitive to the synthesis environment.
Defect migration
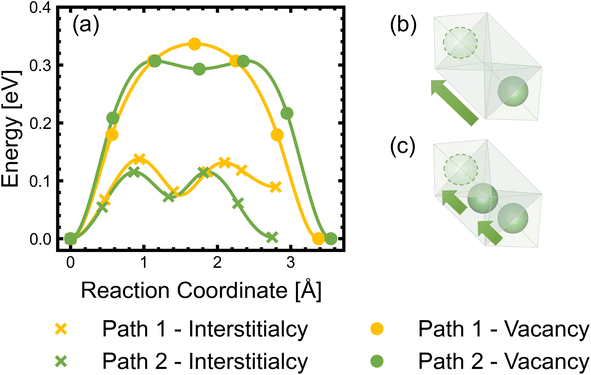
Diffusion of Li+ is a fundamental process that occurs during charge/discharge of a cathode. In a spinel framework like LMNO, Li+ migration occurs from a Td site to another Td site via an empty Oh (gate) site. There are two different gate sites (4a and 12d) in P4332 LMNO and thus two distinct migration paths for Li+ (see Fig. 10). Li diffusivity calculations have been used to explain the rate capabilities of LMNO. Most theoretical studies112,118,119 have considered the diffusion of Li+via the vacancy mechanism, which involves hopping of a single Li+ from one site to another (V−Li hopping in the opposite direction). Our calculated Li+ migration barriers via the vacancy mechanism (Fig. 11) are similar to previous studies.118,119 The activation energies for Li+ to migrate through 4a (path 1) and 12d (path 2) gate sites are 0.34 eV and 0.30 eV, respectively. This is consistent with our findings that Li interstitials preferentially sit on the 12d sites.We also considered Li+i migration via an interstitialcy mechanism, which has not been previously studied in LMNO. This involves concerted migration of three Li+: two ions of the Li–Li dumbbell and one ion that is next to the dumbbell. The path 1 end image is higher in energy, where one of the Li+ in the Li–Li dumbbell sits on a 4a site. The path 2 end image is an equivalent configuration to the initial image where both Li+ in Li–Li dumbbell sit on 12d sites. The activation energies to migrate through path 1 and path 2 are 0.14 eV and 0.12 eV, respectively. Again, migrating via 4a sites is less favourable. Nevertheless, the activation energies for Li+ to migrate via the interstitialcy mechanism are much lower than that via the vacancy mechanism. This suggests that the dominant diffusion mechanism may change during charge and discharge. Since the interstitialcy mechanism involves concerted migration of multiple Li+via the Li–Li dumbbell configuration, this migration is only possible when the concentration of Li+ is sufficiently high and it has also been shown that migration barriers can vary with Li concentration due to effects on Ni valence and thus electrostatic interactions between Li and Ni.112,120
Finally, we show that the Li+ interstitialcy migration makes the Li-Frenkel pair (Li+i–V−Li) unstable to spontaneous recombination at short pair distances. To investigate this, a Li vacancy was placed with a Li interstitial over each of the six standard positions over a range of pair distances for each calculation. From the cNEB calculations, we determine a critical spontaneous recombination distance of ∼4.6 Å, which is larger than the minimum separation (3.45 Å) between Li in their Td sites.
Self-consistent Fermi levels
While most discussions around defect chemistry are focused on two distinct O-rich (p-type)/O-poor (n-type) growth conditions, we would like to highlight that defect chemistry can be different in other intermediate growth conditions. Fig. 12 shows the calculated self-consistent Fermi level in all growth conditions. Since the ideal synthesis/anneal temperature for the ordered phase is at 700 °C, 973 K is used as the input temperature to determine the self-consistent Fermi levels.1,12,20,21 The chemical potential conditions A → T are arranged with increasing self-consistent Fermi level. To understand the defect behaviour at room/operating temperature, self-consistent Fermi levels were also calculated with constant non-lithium defect concentrations upon cooling (i.e. “frozen in”). While the kinetic barriers of non-lithium defects can be assumed to be large, the same assumption can not be applied to lithium defects (Lii and VLi) as the facile movement of Li+ is one of the desirable features for a cathode.121 In addition, it has been suggested that some lithium vacancy–interstitial pairs would recombine (i.e. the reverse reaction of Frenkel pair formation) at lower temperatures.122,123 Two variations of the “frozen” approach were applied. The former approach only allowed VLi and Lii concentrations to vary, whereas the latter also allowed LiMn and LiNi concentrations to change.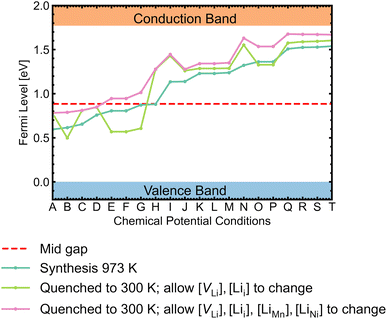 | ||
| Fig. 12 Self-consistent Fermi levels determined under all chemical potential conditions. The atomic chemical potential values can be found in Table S6.† Two variant approaches assuming certain defects are “frozen in” during synthesis were adopted to simulate defect behaviours at room temperature (300 K). | ||
The majority of conditions have Fermi levels ± 0.5 eV from the mid gap. Under the most O-poor conditions, the Fermi level is ≤0.24 eV away from the CBM. Therefore, the material is a weak semiconductor, and can be made more n-type than p-type. The intrinsic defects are not likely to generate significant quantities of free charge carriers that contribute to conductivity and electronic conduction would be mainly governed by the hopping of small polarons.86 This type of transport behaviour gives weaker electronic conduction compared to those via band-like carriers and shows a strong sensitivity to temperature due to their thermally activated hopping processes. Ni3+/Mn3+ are the dominant charge compensating ions under all conditions. In addition, Mn2+ formation is frequently observed for n-type defects, suggesting a strong driving force for Mn3+ to undergo disproportionation reactions.
The formation of oxygen vacancies and Mn3+ is a dominant feature when LMNO is synthesized at a more O-poor (n-type) condition. The electrochemical performance of LMNO synthesized under those conditions can be improved due to the increase in cation disorder and the proportion of Mn3+.12 While Mn3+ species is redox active which improves the electronic conductivity, it is subject to JT distortion and promotes Mn dissolution. Therefore, [Mn3+] should be controlled to achieve optimum performance. Ni-rich rock salt impurity phases are also likely to form under n-type conditions. This is not desirable as it leads to a decrease in capacity. Fig. S5† shows that oxygen vacancies remain at a low concentration (≪1%) in different growth environments when the spinel remains in the P4332 arrangement. Therefore, the cation ordered LMNO is not prone to be oxygen deficient and this is in line with previous studies.28,29,99 Despite the low concentration of oxygen vacancies, the fact that they exist over a range of magnitudes suggests that they can be controlled independently with regards to the cation ordering. In fact, they are highly dependent on the oxygen environment and Fermi level.
Since antisite defects are generally low energy over all chemical potential conditions, we propose that (local) cation ordering can be perturbed under many different synthesis conditions. This supports previous experimental studies13,20,21 where local Mn/Ni ordering has been perturbed without significant concentrations of oxygen vacancies and/or Mn3+. Theoretically, O-rich (p-type) conditions have a higher tendency towards Ni3+ formation. For samples which undergo a series of heat treatment processes, a more p-type condition could oxidise the pre-formed Mn3+ back to Mn4+, reducing the total number of redox active centers and leading to reduced capacity. Synthesis techniques that can take the advantage of the inherent defect chemistry of the material are more likely to achieve the fine tuning of electrochemical performance with target features. For example, Lee et al.21 utilised the preference for LiNi antisite formation (on the 4b sites) to block the Mn/Ni ordering transition pathways during the annealing process of the Li-doped LMNO samples. Their Li-doped LMNO “Mn3+-free” samples annealed at 700 °C exhibited increased Mn/Ni disordering and showed enhanced cycling stability. In this case, the undesirable effects from Mn3+ had been suppressed, as the Mn3+ generated during the first (900 °C) treatment were re-oxidised to Mn4+ when annealed at 700 °C. Unfortunately, the high concentration of LiNi defects leads to a reduced capacity. The defect chemistry of LMNO therefore plays a crucial role in affecting the electrochemical performance. To design LMNO with optimum electrochemical performance, it is important to account for defect behaviour and effectively utilise it when developing synthesis methods.
Conclusions
The bulk properties of P4332 LMNO and its intrinsic defect chemistry have been investigated using DFT. To correctly capture the magnetic properties and ground state electronic structure, we demonstrated the importance of a systematic evaluation of the magnetic ordering in the open-shell TM system. Analysis of the electronic structures indicated a high degree of hybridisation of Ni–O and Mn–O states in LMNO. The thermodynamic stability of LMNO is more sensitive to Ni chemical potentials, while there is a greater flexibility to vary the Li and Mn chemical potentials, leading to different defect properties.The intrinsic defect chemistry suggests LMNO a weak semiconductor and can be made more n-type. The formation of deep defects and small polarons indicated electronic conduction proceeds via the polaron hopping mechanism. The low formation energies for antisite defects explain the tendency towards cation disordering. There exist several defect pair complexes with strong association energies and they are sensitive to the experimental conditions and thermal history of the material. The investigation of Li defects migration revealed that Li+ can migrate via a much lower energy concerted multi-ion interstitialcy mechanism than the previously proposed vacancy mechanism. However, this is achieved via low energy Li–Li dumbbell configuration and requires sufficiently mobile Li+. The Li+ mobility is influenced by the interactions with point defects.
A comprehensive analysis of the defect chemistry over all growth conditions shows a tendency toward O-poor (n-type) conditions where Mn3+ formation is encouraged. This may explain why many experimental studies find it challenging to study solely the effect of Mn/Ni ordering on the electrochemical performance. Despite the material being a weak semiconductor, the strong dependency of defect concentrations on the Fermi level indicates that out-of-equilibrium synthesis methods and aliovalent doping can, to certain extent, change the defect landscape to fine tune the level of Ni-deficiency and Mn3+ content. Our work demonstrates that a deep understanding of the defect chemistry can help to establish connections between conflicting experimental findings. This work also provides a basis for understanding the charge compensation mechanisms of extrinsic defects. Finally, the success of a complete defect survey on LMNO suggests that this approach can be extended to understand the chemistries of other complex battery materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Faraday Institution grant number FIRG017 and used the Michael supercomputer (FIRG030). S. R. K. acknowledges the EPSRC Centre for Doctoral Training in the Advanced Characterisation of Materials (CDT-ACM) (EP/S023259/1) for funding a PhD studentship. Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by the UK Engineering and Physical Sciences Research Council (EPSRC; EP/L000202, EP/R029431, EP/T022213), this work used ARCHER2 UK National Supercomputing Services. We are also grateful to the UK Materials and Molecular Modelling Hub (MMM Hub), which is partially funded by the EPSRC (EP/P020194/1, EP/T022213/1), for computational resources on the Thomas, Young supercomputers, and to UCL for access to the Myriad (Myriad@UCL) and Kathleen (Kathleen@UCL) supercomputers.References
- G. Liang, V. K. Peterson, K. W. See, Z. Guo and W. K. Pang, Developing High-Voltage Spinel LiNi0.5Mn 1.5O4 Cathodes for High-Energy-Density Lithium-Ion Batteries: Current Achievements and Future Prospects, J. Mater. Chem. A, 2020, 8, 15373–15398 RSC.
- Y. Huang, Y. Dong, S. Li, J. Lee, C. Wang, Z. Zhu, W. Xue, Y. Li and J. Li, Lithium Manganese Spinel Cathodes for Lithium-Ion Batteries, Adv. Energy Mater., 2020, 2000997 Search PubMed.
- M. M. Thackeray and K. Amine, LiMn2O4 Spinel and Substituted Cathodes, Nat. Energy, 2021, 6, 566 CrossRef CAS.
- Q. Zhong, A. Bonakdarpour, M. Zhang, Y. Gao and J. R. Dahn, Synthesis and Electrochemistry of LiNixMn2-xO4, J. Electrochem. Soc., 1997, 144, 205–213 CrossRef CAS.
- W. Xiao, C. Xin, S. Li, J. Jie, Y. Gu, J. Zheng and F. Pan, Insight into Fast Li Diffusion in Li-excess Spinel Lithium Manganese Oxide, J. Mater. Chem. A, 2018, 6, 9893–9898 RSC.
- Z. Wan, Y. Xu, G. Sun, D. Xu and X. Luo, Conflicting Role of Inversion of the LiMn2O4 Spinel on Lithium-Ion Battery Capacity from First-Principles Calculations, J. Phys. Chem. C, 2022, 126, 7374–7382 CrossRef CAS.
- G. Zhou, X. Sun, Q.-H. Li, X. Wang, J.-N. Zhang, W. Yang, X. Yu, R. Xiao and H. Li, Mn Ion Dissolution Mechanism for Lithium-Ion Battery with LiMn2O4 Cathode: In Situ Ultraviolet-Visible Spectroscopy and Ab Initio Molecular Dynamics Simulations, J. Phys. Chem. Lett., 2020, 11, 3051–3057 CrossRef CAS PubMed.
- T. Liu, et al., Correlation between Manganese Dissolution and Dynamic Phase Stability in Spinel-Based Lithium-Ion Battery, Nat. Commun., 2019, 10, 4721 CrossRef PubMed.
- J.-H. Kim, S.-T. Myung, C. S. Yoon, S. G. Kang and Y.-K. Sun, Comparative Study of LiNi0.5Mn1.5O4−δ and LiNi0.5Mn1.5O4 Cathodes Having Two Crystallographic Structures: Fd
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and P4332, Chem. Mater., 2004, 16, 906–914 CrossRef CAS.
m and P4332, Chem. Mater., 2004, 16, 906–914 CrossRef CAS. - G. Liu, J. Zhang, X. Zhang, Y. Du, K. Zhang, G. Li, H. Yu, C. Li, Z. Li, Q. Sun and L. Wen, Study on Oxygen Deficiency in Spinel LiNi0.5Mn1.5O4 and Its Fe and Cr-doped Compounds, J. Alloys Compd., 2017, 725, 580–586 CrossRef CAS.
- M. Kunduraci and G. G. Amatucci, Synthesis and Characterization of Nanostructured 4.7 V LixMn1.5Ni0.5 O4 Spinels for High-Power Lithium-Ion Batteries, J. Electrochem. Soc., 2006, 153, A1345 CrossRef CAS.
- K. Lee, G. J. Yang and Y. Kim, Improvement of the Electrochemical Properties of LiNi0.5Mn1.5O4 by Controlling the Heating Atmosphere during Synthesis, Ceram. Int., 2017, 43, 15510–15518 CrossRef CAS.
- B. Aktekin, M. Valvo, R. I. Smith, M. H. Sørby, F. Lodi Marzano, W. Zipprich, D. Brandell, K. Edström and W. R. Brant, Cation Ordering and Oxygen Release in LiNi0.5−xMn1.5+xO4−y (LNMO): In Situ Neutron Diffraction and Performance in Li Ion Full Cells, ACS Appl. Energy Mater., 2019, 2, 3323–3335 CrossRef CAS.
- H. Duncan, B. Hai, M. Leskes, C. P. Grey and G. Chen, Relationships between Mn3+ Content, Structural Ordering, Phase Transformation, and Kinetic Properties in LiNixMn2−xO4 Cathode Materials, Chem. Mater., 2014, 26, 5374–5382 CrossRef CAS.
- J. Yoon, D. Kim, J. H. Um, M. Jeong, W. Oh and W.-S. Yoon, Effect of Local Structural Changes on Rate Capability of LiNi0.5Mn1.5O4−δ Cathode Material for Lithium Ion Batteries, J. Alloys Compd., 2016, 686, 593–600 CrossRef CAS.
- F. A. Vásquez, N. C. Rosero-Navarro, A. Miura, R. Jalem, Y. Goto, M. Nagao, Y. Tateyama, K. Tadanaga and J. A. Calderón, Kinetic Control of the Li0.9Mn1.6Ni 0.4O4 Spinel Structure with Enhanced Electrochemical Performance, ACS Appl. Mater. Interfaces, 2021, 13, 14056–14067 CrossRef PubMed.
- H. Ryoo, H. B. Bae, Y.-M. Kim, J.-G. Kim, S. Lee and S.-Y. Chung, Frenkel-Defect-Mediated Chemical Ordering Transition in a Li-Mn-Ni Spinel Oxide, Angew. Chem., 2015, 54, 7963–7967 CrossRef CAS PubMed.
- D. Liu, W. Zhu, J. Trottier, C. Gagnon, F. Barray, A. Guerfi, A. Mauger, H. Groult, C. M. Julien, J. B. Goodenough and K. Zaghib, Spinel Materials for High-Voltage Cathodes in Li-ion Batteries, RSC Adv., 2014, 4, 154–167 RSC.
- J. Liu, A. Huq, Z. Moorhead-Rosenberg, A. Manthiram and K. Page, Nanoscale Ni/Mn Ordering in the High Voltage Spinel Cathode LiNi0.5Mn1.5O4, Chem. Mater., 2016, 28, 6817–6821 CrossRef CAS.
- M. Casas-Cabanas, C. Kim, J. Rodríguez-Carvajal and J. Cabana, Atomic Defects during Ordering Transitions in LiNi0.5Mn1.5O4 and Their Relationship with Electrochemical Properties, J. Mater. Chem. A, 2016, 4, 8255–8262 RSC.
- J. Lee, N. Dupre, M. Avdeev and B. Kang, Understanding the Cation Ordering Transition in High-Voltage Spinel LiNi0.5Mn1.5O4 by Doping Li Instead of Ni, Sci. Rep., 2017, 7, 6728 CrossRef PubMed.
- J. Cabana, M. Casas-Cabanas, F. O. Omenya, N. A. Chernova, D. Zeng, M. S. Whittingham and C. P. Grey, Composition-Structure Relationships in the Li-Ion Battery Electrode Material LiNi0.5Mn1.5O4, Chem. Mater., 2012, 24, 2952–2964 CrossRef CAS PubMed.
- A. B. Haruna, P. Mwonga, D. Barrett, C. B. Rodella, R. P. Forbes, A. Venter, Z. Sentsho, P. J. Fletcher, F. Marken and K. I. Ozoemena, Defect-Engineered β-MnO2−δ Precursors Control the Structure–Property Relationships in High-Voltage Spinel LiMn1.5Ni0.5O4−δ, ACS Omega, 2021, 6, 25562–25573 CrossRef CAS PubMed.
- J. Xiao, X. Chen, P. V. Sushko, M. L. Sushko, L. Kovarik, J. Feng, Z. Deng, J. Zheng, G. L. Graff, Z. Nie, D. Choi, J. Liu, J.-G. Zhang and M. S. Whittingham, High-Performance LiNi0.5Mn1.5O4 Spinel Controlled by Mn3+ Concentration and Site Disorder, Adv. Mater., 2012, 24, 2109–2116 CrossRef CAS PubMed.
- D. W. Shin, C. A. Bridges, A. Huq, M. P. Paranthaman and A. Manthiram, Role of Cation Ordering and Surface Segregation in High-Voltage Spinel LiMn1.5Ni0.5−xMxO4 (M = Cr, Fe, and Ga) Cathodes for Lithium-Ion Batteries, Chem. Mater., 2012, 24, 3720–3731 CrossRef CAS.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, First-Principles Calculations for Point Defects in Solids, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- D. O. Scanlon, J. Buckeridge, C. R. A. Catlow and G. W. Watson, Understanding Doping Anomalies in Degenerate P-Type Semiconductor LaCuOSe, J. Mater. Chem. C, 2014, 2, 3429–3438 RSC.
- H. Shiiba, N. Zettsu, M. Nakayama, S. Oishi and K. Teshima, Defect Formation Energy in Spinel LiNi0.5Mn1.5O4−δ Using Ab Initio DFT Calculations, J. Phys. Chem. C, 2015, 119, 9117–9124 CrossRef CAS.
- P. V. Sushko, K. M. Rosso, J.-G. Zhang, J. Liu and M. L. Sushko, Oxygen Vacancies and Ordering of D-Levels Control Voltage Suppression in Oxide Cathodes: The Case of Spinel LiNi0.5Mn1.5O4−δ, Adv. Funct. Mater., 2013, 23, 5530–5535 CrossRef CAS.
- Y. Chen, Y. Sun and X. Huang, Origin of the Ni/Mn Ordering in High-Voltage Spinel LiNi0.5Mn1.5O4: The Role of Oxygen Vacancies and Cation Doping, Comput. Mater. Sci., 2016, 115, 109–116 CrossRef CAS.
- S. Kim, S. N. Hood, J.-S. Park, L. D. Whalley and A. Walsh, Quick-Start Guide for First-Principles Modelling of Point Defects in Crystalline Materials, J. Phys.: Energy, 2020, 2, 036001 CAS.
- C. Freysoldt, J. Neugebauer and C. G. Van de Walle, Electrostatic Interactions between Charged Defects in Supercells, Phys. Status Solidi B, 2011, 248, 1067–1076 CrossRef CAS.
- G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- G. Hautier, S. P. Ong, A. Jain, C. J. Moore and G. Ceder, Accuracy of Density Functional Theory in Predicting Formation Energies of Ternary Oxides from Binary Oxides and Its Implication on Phase Stability, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155208 CrossRef.
- T. Mueller, G. Hautier, A. Jain and G. Ceder, Evaluation of Tavorite-Structured Cathode Materials for Lithium-Ion Batteries Using High-Throughput Computing, Chem. Mater., 2011, 23, 3854–3862 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation, APL Mater., 2013, 1, 011002 CrossRef.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-zone Integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (Pymatgen): A Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- A. Jain, G. Hautier, C. J. Moore, S. Ping Ong, C. C. Fischer, T. Mueller, K. A. Persson and G. Ceder, A High-Throughput Infrastructure for Density Functional Theory Calculations, Comput. Mater. Sci., 2011, 50, 2295–2310 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- N. Biškup, J. L. Martínez, M. E. Arroyo y de Dompablo, P. Díaz-Carrasco and J. Morales, Relation between the Magnetic Properties and the Crystal and Electronic Structures of Manganese Spinels LiNi0.5Mn1.5O4 and LiCu0.5Mn1.5O4−δ (0 < δ < 0.125), J. Appl. Phys., 2006, 100, 093908 CrossRef.
- C. J. Bradley and A. P. Cracknell, The Mathematical Theory of Symmetry in Solids : Representation Theory for Point Groups and Space Groups, Oxford Classic Texts in the Physical Sciences, Oxford University Press, Oxford, 2010 Search PubMed.
- A. M. Ganose, A. J. Jackson and D. O. Scanlon, Sumo: Command-line Tools for Plotting and Analysis of Periodic *ab Initio* Calculations, J. Open Source Softw., 2018, 3, 717 CrossRef.
- C. G. Van de Walle and J. Neugebauer, First-Principles Calculations for Defects and Impurities: Applications to III-nitrides, J. Appl. Phys., 2004, 95, 3851–3879 CrossRef CAS.
- S. Kavanagh, Defect Oriented Python Environment Distribution, https://github.com/SMTG-UCL/doped Search PubMed.
- D. Broberg, B. Medasani, N. E. Zimmermann, G. Yu, A. Canning, M. Haranczyk, M. Asta and G. Hautier, PyCDT: A Python Toolkit for Modeling Point Defects in Semiconductors and Insulators, Comput. Phys. Commun., 2018, 226, 165–179 CrossRef CAS.
- I. Mosquera-Lois, S. R. Kavanagh, A. Walsh and D. O. Scanlon, ShakeNBreak: Navigating the Defect Configurational Landscape, J. Open Source Softw., 2022, 7, 4817 CrossRef.
- I. Mosquera-Lois, S. R. Kavanagh, A. Walsh and D. O. Scanlon, Identifying the Ground State Structures of Point Defects in Solids, npj Comput. Mater., 2023, 9, 25 CrossRef CAS.
- I. Mosquera-Lois and S. R. Kavanagh, In Search of Hidden Defects, Matter, 2021, 4, 2602–2605 CrossRef.
- G. Henkelman and H. Jónsson, Improved Tangent Estimate in the Nudged Elastic Band Method for Finding Minimum Energy Paths and Saddle Points, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- K. Momma and F. Izumi, VESTA: A Three-Dimensional Visualization System for Electronic and Structural Analysis, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- K. Hoang and M. D. Johannes, Defect Physics in Complex Energy Materials, J. Phys.: Condens. Matter, 2018, 30, 293001 CrossRef PubMed.
- C. Freysoldt, J. Neugebauer and C. G. Van de Walle, Fully Ab Initio Finite-Size Corrections for Charged-Defect Supercell Calculations, Phys. Rev. Lett., 2009, 102, 016402 CrossRef PubMed.
- R. A. Lunt, A. J. Jackson and A. Walsh, Dielectric Response of Fe2O3 Crystals and Thin Films, Chem. Phys. Lett., 2013, 586, 67–69 CrossRef CAS.
- X. Xu, S. Deng, H. Wang, J. Liu and H. Yan, Research Progress in Improving the Cycling Stability of High-Voltage LiNi0.5Mn1.5O4 Cathode in Lithium-Ion Battery, Nano-Micro Lett., 2017, 9, 22 CrossRef PubMed.
- J. Buckeridge, D. Scanlon, A. Walsh and C. Catlow, Automated Procedure to Determine the Thermodynamic Stability of a Material and the Range of Chemical Potentials Necessary for Its Formation Relative to Competing Phases and Compounds, Comput. Phys. Commun., 2014, 185, 330–338 CrossRef CAS.
- J. Buckeridge, Chemical Potential Limits Analysis Program, https://github.com/jbuckeridge/cplap Search PubMed.
- A. Jain, G. Hautier, S. Ong, C. Moore, C. Fischer, K. Persson and G. Ceder, Formation Enthalpies by Mixing GGA and GGA + U Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045115 CrossRef.
- S. P. Ong, L. Wang, B. Kang and G. Ceder, Li-Fe-P-O2 Phase Diagram from First Principles Calculations, Chem. Mater., 2008, 20, 1798–1807 CrossRef CAS.
- V. Massarotti, D. Capsoni, M. Bini, G. Chiodelli, C. Azzoni, M. Mozzati and A. Paleari, Electric and Magnetic Properties of LiMn2O4- and Li2MnO3-Type Oxides, J. Solid State Chem., 1997, 131, 94–100 CrossRef CAS.
- W.-W. Liu, D. Wang, Z. Wang, J. Deng, W.-M. Lau and Y. Zhang, Influence of Magnetic Ordering and Jahn–Teller Distortion on the Lithiation Process of LiMn2O4, Phys. Chem. Chem. Phys., 2017, 19, 6481–6486 RSC.
- Z. Yao, S. Kim, J. He, V. I. Hegde and C. Wolverton, Interplay of Cation and Anion Redox in Li4Mn2O5 Cathode Material and Prediction of Improved Li4(Mn,M)2O5 Electrodes for Li-ion Batteries, Sci. Adv., 2018, 4, eaao6754 CrossRef PubMed.
- Z. H. Wang, D. Y. Geng, W. J. Hu, W. J. Ren and Z. D. Zhang, Magnetic Properties and Exchange Bias in Mn2O3/Mn3 O4 Nanoclusters, J. Appl. Phys., 2009, 105, 07AV315 CrossRef.
- B. A. Frandsen and S. J. L. Billinge, Magnetic Structure Determination from the Magnetic Pair Distribution Function (mPDF): Ground State of MnO, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 325–334 CrossRef CAS PubMed.
- S. v. Ivanova, E. Zhecheva, D. Nihtianova and R. Stoyanova, Nano-Domain Structure of Li4Mn5O12 Spinel, J. Mater. Sci., 2011, 46, 7098–7105 CrossRef CAS.
- I. Davidson, J. Greedan, U. Von Sacken, C. Michal and W. McKinnon, Short Range and Long Range Magnetic Order in 1T-Li2NiO2, J. Solid State Chem., 1993, 105, 410–416 CrossRef CAS.
- K. Kang, C.-H. Chen, B. J. Hwang and G. Ceder, Synthesis, Electrochemical Properties, and Phase Stability of Li2NiO2 with the Immm Structure, Chem. Mater., 2004, 16, 2685–2690 CrossRef CAS.
- V. Bianchi, D. Caurant, N. Baffier, C. Belhomme, E. Chappel, G. Chouteau, S. Bach, J. Pereira-Ramos, A. Sulpice and P. Wilmann, Synthesis, Structural Characterization and Magnetic Properties of Quasistoichiometric LiNiO2, Solid State Ionics, 2001, 140, 1–17 CrossRef CAS.
- A. Kuwabara, C. A. J. Fisher, Y. H. Ikuhara, H. Moriwake, H. Oki and Y. Ikuhara, The Influence of Charge Ordering on the Phase Stability of Spinel LiNi2O4, RSC Adv., 2012, 2, 12940–12948 RSC.
- K. Hoang and M. Johannes, Tailoring Native Defects in LiFePO4: Insights from First-Principles Calculations, Chem. Mater., 2011, 23, 3003–3013 CrossRef CAS.
- A. Squires, D. Scanlon and B. Morgan, Py-Sc-Fermi: Self-Consistent Fermi Energies and Defect Concentrations from Electronic Structure Calculations, J. Open Source Softw., 2023, 8, 4962 CrossRef.
- J. Buckeridge, Equilibrium Point Defect and Charge Carrier Concentrations in a Material Determined through Calculation of the Self-Consistent Fermi Energy, Comput. Phys. Commun., 2019, 244, 329–342 CrossRef CAS.
- C. Kittel and H. Kroemer, Thermal Physics, American Association of Physics Teachers, 1998 Search PubMed.
- D. W. Davies, B. J. Morgan, D. O. Scanlon and A. Walsh, Low-Cost Descriptors of Electrostatic and Electronic Contributions to Anion Redox Activity in Batteries, IOP SciNotes, 2020, 1, 024805 CrossRef.
- D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave, I. P. Parkin, G. W. Watson, T. W. Keal, P. Sherwood, A. Walsh and A. A. Sokol, Band Alignment of Rutile and Anatase TiO2, Nat. Mater., 2013, 12, 798–801 CrossRef CAS PubMed.
- D. Krasikov and I. Sankin, Defect Interactions and the Role of Complexes in the CdTe Solar Cell Absorber, J. Mater. Chem. A, 2017, 5, 3503–3513 RSC.
- M. K. Horton, J. H. Montoya, M. Liu and K. A. Persson, High-Throughput Prediction of the Ground-State Collinear Magnetic Order of Inorganic Materials Using Density Functional Theory, npj Comput. Mater., 2019, 5, 64 CrossRef.
- A. Chakraborty, S. Kunnikuruvan, S. Kumar, B. Markovsky, D. Aurbach, M. Dixit and D. T. Major, Layered Cathode Materials for Lithium-Ion Batteries: Review of Computational Studies on LiNi1−x−yCoxMnyO2 and LiNi1−x−yCoxAlyO2, Chem. Mater., 2020, 32, 915–952 CrossRef CAS.
- K. Hoang, Understanding the Electronic and Ionic Conduction and Lithium Over-Stoichiometry in LiMn2O4 Spinel, J. Mater. Chem. A, 2014, 2, 18271–18280 RSC.
- W. H. Kan, S. Kuppan, L. Cheng, M. Doeff, J. Nanda, A. Huq and G. Chen, Crystal Chemistry and Electrochemistry of LixMn1.5Ni0. 5O4 Solid Solution Cathode Materials, Chem. Mater., 2017, 29, 6818–6828 CrossRef CAS.
- B. Aktekin, F. Massel, M. Ahmadi, M. Valvo, M. Hahlin, W. Zipprich, F. Marzano, L. Duda, R. Younesi, K. Edström and D. Brandell, How Mn/Ni Ordering Controls Electrochemical Performance in High-Voltage Spinel LiNi0.44Mn1.56O4 with Fixed Oxygen Content, ACS Appl. Energy Mater., 2020, 3, 6001–6013 CrossRef CAS.
- H. Liu, J. Zhou, L. Zhang, Z. Hu, C. Kuo, J. Li, Y. Wang, L. H. Tjeng, T.-W. Pi, A. Tanaka, L. Song, J.-Q. Wang and S. Zhang, Insight into the Role of Metal–Oxygen Bond and O 2p Hole in High-Voltage Cathode LiNixMn2−xO4, J. Phys. Chem. C, 2017, 121, 16079–16087 CrossRef CAS.
- H. Ryoo, S.-G. Lee, J.-G. Kim and S.-Y. Chung, Effect of Chemical Bonding Characteristics on Ordering Structure in Li Spinel Oxides, Adv. Funct. Mater., 2019, 29, 1805972 CrossRef.
- J. A. Santana, J. Kim, P. R. C. Kent and F. A. Reboredo, Successes and Failures of Hubbard-corrected Density Functional Theory: The Case of Mg Doped LiCoO2, J. Chem. Phys., 2014, 141, 164706 CrossRef PubMed.
- M. M. S. Sanad, H. A. Abdellatif, E. M. Elnaggar, G. M. El-Kady and M. M. Rashad, Understanding Structural, Optical, Magnetic and Electrical Performances of Fe- or Co-substituted Spinel LiMn1.5Ni0.5O4 Cathode Materials, Appl. Phys. A, 2019, 125, 139 CrossRef.
- M. Raja, S. Mahanty and R. Basu, Influence of S and Ni Co-Doping on Structure, Band Gap and Electrochemical Properties of Lithium Manganese Oxide Synthesized by Soft Chemical Method, J. Power Sources, 2009, 192, 618–626 CrossRef CAS.
- S. K. Radha, W. R. L. Lambrecht, B. Cunningham, M. Grüning, D. Pashov and M. van Schilfgaarde, Optical Response and Band Structure of LiCoO2 Including Electron-Hole Interaction Effects, Phys. Rev. B, 2021, 104, 115120 CrossRef CAS.
- S. R. Kavanagh, C. N. Savory, S. M. Liga, G. Konstantatos, A. Walsh and D. O. Scanlon, Frenkel Excitons in Vacancy-Ordered Titanium Halide Perovskites (Cs2TiX6), J. Phys. Chem. Lett., 2022, 13, 10965–10975 CrossRef CAS PubMed.
- J. Cen, B. Zhu and D. Scanlon, Exploring Battery Cathode Materials in the Li-Ni-O Phase Diagrams Using Structure Prediction, 2022, DOI:10.26434/chemrxiv-2022-gdmdh-v2.
- K. Hoang, Defect Physics, Delithiation Mechanism, and Electronic and Ionic Conduction in Layered Lithium Manganese Oxide Cathode Materials, Phys. Rev. Appl., 2015, 3, 024013 CrossRef CAS.
- M. Burbano, D. O. Scanlon and G. W. Watson, Sources of Conductivity and Doping Limits in CdO from Hybrid Density Functional Theory, J. Am. Chem. Soc., 2011, 133, 15065–15072 CrossRef CAS PubMed.
- P. Stüble, V. Mereacre, H. Geßwein and J. R. Binder, On the Composition of LiNi0.5Mn1.5O4 Cathode Active Materials, Adv. Energy Mater., 2023, 2203778 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, A Grid-Based Bader Analysis Algorithm without Lattice Bias, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A Fast and Robust Algorithm for Bader Decomposition of Charge Density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- Z. Moorhead-Rosenberg, K. R. Chemelewski, J. B. Goodenough and A. Manthiram, Magnetic Measurements as a Viable Tool to Assess the Relative Degrees of Cation Ordering and Mn3+ Content in Doped LiMn1.5Ni0.5O4 Spinel Cathodes, J. Mater. Chem. A, 2013, 1, 10745–10752 RSC.
- C. E. Housecroft, Inorganic Chemistry, Pearson, Harlow, England, 5th edn, 2018 Search PubMed.
- R. D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., Sect. A: Found. Adv., 1976, 32, 751–767 CrossRef.
- Y. Han, Y.-S. Jiang, Y. Xia, L. Deng, L.-F. Que, F.-D. Yu and Z.-B. Wang, Suppressed Phase Separation in Spinel LiNi0.5Mn1.5O4 Cathode via Interstitial Sites Modulation, Nano Energy, 2022, 91, 106636 CrossRef CAS.
- E. Hu, S.-M. Bak, Y. Liu, J. Liu, X. Yu, Y.-N. Zhou, J. Zhou, P. Khalifah, K. Ariyoshi, K.-W. Nam and X.-Q. Yang, Utilizing Environmental Friendly Iron as a Substitution Element in Spinel Structured Cathode Materials for Safer High Energy Lithium-Ion Batteries, Adv. Energy Mater., 2016, 6, 1501662 CrossRef.
- A. Y. Toukmaji and J. A. Board, Ewald Summation Techniques in Perspective: A Survey, Comput. Phys. Commun., 1996, 95, 73–92 CrossRef CAS.
- J. Coutinho, V. P. Markevich and A. R. Peaker, Characterisation of Negative-U Defects in Semiconductors, J. Phys.: Condens. Matter, 2020, 32, 323001 CrossRef CAS PubMed.
- J. Qu, V. Stevanović, E. Ertekin and P. Gorai, Doping by Design: Finding New n-Type Dopable ABX4 Zintl Phases for Thermoelectrics, J. Mater. Chem. A, 2020, 8, 25306–25315 RSC.
- D. O. Scanlon, Defect Engineering of BaSnO3 for High-Performance Transparent Conducting Oxide Applications, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 161201 CrossRef.
- J. Buckeridge, C. R. A. Catlow, M. R. Farrow, A. J. Logsdail, D. O. Scanlon, T. W. Keal, P. Sherwood, S. M. Woodley, A. A. Sokol and A. Walsh, Deep vs. Shallow Nature of Oxygen Vacancies and Consequent N-Type Carrier Concentrations in Transparent Conducting Oxides, Phys. Rev. Mater., 2018, 2, 054604 CrossRef CAS.
- X. Ma, B. Kang and G. Ceder, High Rate Micron-Sized Ordered LiNi0.5Mn1.5O4, J. Electrochem. Soc., 2010, 157, A925 CrossRef CAS.
- B. Xu and S. Meng, Factors Affecting Li Mobility in Spinel LiMn2O4—A First-Principles Study by GGA and GGA+U Methods, J. Power Sources, 2010, 195, 4971–4976 CrossRef CAS.
- S. R. Kavanagh, D. O. Scanlon, A. Walsh and C. Freysoldt, Impact of Metastable Defect Structures on Carrier Recombination in Solar Cells, Faraday Discuss., 2022, 239, 339–356 RSC.
- A. A. Sokol, S. A. French, S. T. Bromley, C. R. A. Catlow, H. J. J. van Dam and P. Sherwood, Point Defects in ZnO, Faraday Discuss., 2007, 134, 267–282 RSC.
- D. O. Scanlon and G. W. Watson, On the Possibility of P-Type SnO2, J. Mater. Chem., 2012, 22, 25236–25245 RSC.
- G. Liu, Y. Li and B. Wang, Importance of Cooling Speed on Rapid Synthesis of LiNi0.5Mn1.5O4 by a Solution Combustion Synthesis Method, Int. J. Electrochem. Sci., 2015, 10, 3124–3135 CAS.
- J. H. Kim, J.-W. Jung, S.-H. Cho, I.-D. Kim, Y. C. Park, D.-H. Seo and H.-S. Kim, Investigation of Ordering on Oxygen-Deficient LiNi0.5Mn1.5O4 −δ Thin Films for Boosting Electrochemical Performance in All-Solid-State Thin-Film Batteries, Small, 2022, 18, 2201134 CrossRef CAS PubMed.
- H. Shiiba, N. Zettsu, S. Kida, D.-w. Kim and K. Teshima, Impact of Trace Extrinsic Defect Formation on the Local Symmetry Transition in Spinel LiNi0.5Mn1.5O4−δ Systems and Their Electrochemical Characteristics, J. Mater. Chem. A, 2018, 6, 22749–22757 RSC.
- X. He, Y. Zhu and Y. Mo, Origin of Fast Ion Diffusion in Super-Ionic Conductors, Nat. Commun., 2017, 8, 15893 CrossRef CAS PubMed.
- K. Sasaki and J. Maier, Low-Temperature Defect Chemistry of Oxides. I. General Aspects and Numerical Calculations, J. Appl. Phys., 1999, 86, 5422–5433 CrossRef CAS.
- A. G. Squires, D. O. Scanlon and B. J. Morgan, Native Defects and Their Doping Response in the Lithium Solid Electrolyte Li7La3Zr2O12, Chem. Mater., 2020, 32, 1876–1886 CrossRef CAS.
- A. Squires, J. M. Dean and B. J. Morgan, Aliovalent Doping Response and Impact on Ionic Conductivity in the Antiperovskite Solid Electrolyte Li3OCl, 2021, DOI:10.33774/chemrxiv-2021-zvwhh-v2.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta00532a |
| This journal is © The Royal Society of Chemistry 2023 |