Open Access Article
Open Access ArticleControlling primary chain dispersity in network polymers: elucidating the effect of dispersity on degradation†
Takanori
Shimizu
ac,
Richard
Whitfield
 *a,
Glen R.
Jones
a,
Ibrahim O.
Raji
b,
Dominik
Konkolewicz
*a,
Glen R.
Jones
a,
Ibrahim O.
Raji
b,
Dominik
Konkolewicz
 b,
Nghia P.
Truong
b,
Nghia P.
Truong
 a and
Athina
Anastasaki
a and
Athina
Anastasaki
 *a
*a
aLaboratory of Polymeric Materials, Department of Materials, ETH Zurich, Vladimir Prelog Weg 5, 8093 Zurich, Switzerland. E-mail: richard.whitfield@mat.ethz.ch; Athina.Anastasaki@mat.ethz.ch
bDepartment of Chemistry and Biochemistry, Miami University, 651 E High St, Oxford, OH 45056, USA
cScience & Innovation Center, Mitsubishi Chemical Corporation, 1000 Kamoshida-cho, Aoba-ku, Yokohama-shi, Kanagawa 227-8502, Japan
First published on 9th November 2023
Abstract
Although dispersity has been demonstrated to be instrumental in determining many polymer properties, current synthetic strategies predominantly focus on tailoring the dispersity of linear polymers. In contrast, controlling the primary chain dispersity in network polymers is much more challenging, in part due to the complex nature of the reactions, which has limited the exploration of properties and applications. Here, a one-step method to prepare networks with precisely tuned primary chain dispersity is presented. By using an acid-switchable chain transfer agent and a degradable crosslinker in PET-RAFT polymerization, the in situ crosslinking of the propagating polymer chains was achieved in a quantitative manner. The incorporation of a degradable crosslinker, not only enables the accurate quantification of the various primary chain dispersities, post-synthesis, but also allows the investigation and comparison of their respective degradation profiles. Notably, the highest dispersity networks resulted in a 40% increase in degradation time when compared to their lower dispersity analogues, demonstrating that primary chain dispersity has a substantial impact on the network degradation rate. Our experimental findings were further supported by simulations, which emphasized the importance of higher molecular weight polymer chains, found within the high dispersity materials, in extending the lifetime of the network. This methodology presents a new and promising avenue to precisely tune primary chain dispersity within networks and demonstrates that polymer dispersity is an important parameter to consider when designing degradable materials.
Introduction
Control over polymer molar mass distributions (MMDs) has recently received considerable attention, with the development of numerous successful methods that allow for polymers with specific dispersities to be synthesized while targeting precise molecular weights and maintaining high end-group functionality.1–9 Historically, blending methods were commonplace,10 where a desired molar mass distribution could be obtained by mixing a number of polymers of different molecular weights, but more recently a number of one-pot strategies have been developed. Fors and coworkers pioneered a method where the molar mass distribution could be precisely controlled by gradually adding initiator into various controlled polymerizations.11–16 In addition, flow chemistry has been combined with mathematical models to allow specific molar mass distributions to be designed and prepared.17–26 Finally, a range of chemical methods have been developed which allow polymerization equilibria to be directly manipulated and the dispersity to be systematically tuned. For example, Chiu and coworkers utilized the photo-isomerism of initiators in cationic polymerization to vary dispersity.27 In the area of controlled radical polymerization, both our group and the Matyzjasewski group illustrated that by lowering the catalyst concentration in atom transfer radical polymerization (ATRP), the dispersity of the resulting polymers could be incrementally increased.28–32 In addition, it has been demonstrated that dispersity control was possible by adding a comonomer in organocatalyzed living radical polymerization (O-LRP)33 and that by mixing chain transfer agents (CTAs) in reversible addition–fragmentation chain transfer (RAFT) polymerization, dispersity could be tuned while maintaining high end-group fidelity.34–36 Most recently, our group expanded dispersity control to multiblock copolymers using a switchable CTA in thermal RAFT and by simply adding acid or base alongside each monomer, a low, intermediate or high dispersity block could be obtained.37,38The motivation behind these recent achievements was to elucidate the effect of dispersity on a number of different polymer properties. As such, various mechanical, thermal, rheological and self-assembly effects have been reported.11,20,39,40 For instance, the Fors group elegantly demonstrated that variations in the molar mass distribution influenced chain stiffness, yield and tensile strengths, toughness and hysteresis energy.41,42 In addition, the same group illustrated the role of dispersity in tuning the domain spacing of self-assembled block copolymer thin films,43 and most recently, the Junkers group revealed that the dispersity of the core-forming polymer block has a significant effect on polymer self-assembly.44 Very interestingly, by using higher dispersity core-forming blocks, lower dispersity nanoparticles could be prepared. In addition, dispersity has been shown to play a significant role in determining polymer brush behaviour, with effects on the interfacial and mechanical properties of brush-grafted nanoparticles demonstrated.45–52
Despite these impressive advances in dispersity control, the vast majority of current reports focus almost exclusively on linear polymers, while the development of methods to control primary chain dispersity within polymer networks and any potential effect on their properties remains far less explored.53–55 This is because controlling dispersity in polymer networks presents several challenges. For example, blending and feeding/flow methods may be incompatible in tuning dispersity in networks, unless multistep procedures are utilized.53,56 Chemical methods also face the challenge of maintaining control as the system becomes highly viscous and then heterogeneous after gelation.57 In particular, deactivation in ATRP and degenerative chain transfer in RAFT are essential in maintaining control, but these are both potentially compromised at high viscosities, thus creating the potential for additional termination.58 As such, the synthesize of networks with tuneable primary chain dispersity in a single step would be a significant development. However, to the best of our knowledge, there are only limited examples where dispersity-controlled networks have been prepared on variation of the catalyst concentration in ATRP.59,60 Matyjaszewski and coworkers demonstrated that decreasing copper concentration in activator regenerated by electron transfer (ARGET) ATRP resulted in a higher primary chain dispersity and an earlier gel point.60 However, the primary chain dispersity of the resulting networks was not measured. Most recently, Kopec and coworkers reported the primary chain dispersity of networks by using dispersity values obtained from analogous linear polymerization reaction conditions.59 There is therefore an ongoing challenge in terms of both the synthesis and characterization of these materials, so any influence of primary chain dispersity on many properties has yet to be ascertained. This includes the effect on degradability, which is arguably one of the most useful and important properties that can be incorporated into networks, with precise tuning of network degradation essential for numerous applications including drug delivery, tissue engineering, wound healing, pollution control, agriculture (water and nutrient retention in soil) and personal care (cosmetics and skin care).61–67
In this work, we sought to develop a high-yielding synthetic methodology to prepare primary dispersity-controlled network polymers, with full incorporation of starting monomer, crosslinker and polymer chains. By utilising a degradable crosslinker within these materials, we were able to directly characterize the various primary chain dispersity materials and then accurately study the effect on their degradation rate (Scheme 1). We demonstrate that dispersity has a significant effect on the rate of degradation, with higher dispersity polymers degrading more slowly than their lower dispersity analogues. Finally, we perform simulations to further understand and verify this difference.
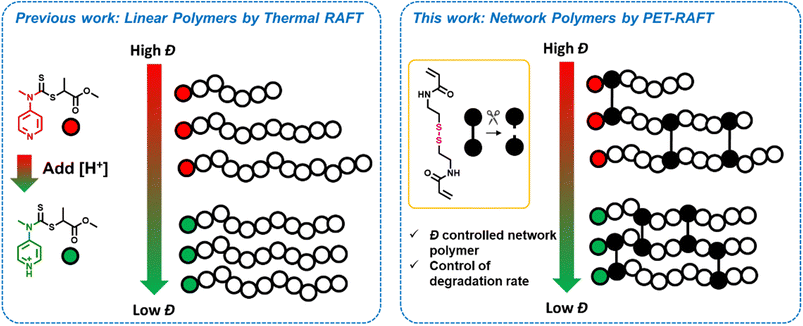 | ||
| Scheme 1 Previous approaches to tune dispersity using a switchable RAFT agent and our current approach to time the primary chain dispersity within gels to investigate their degradation. | ||
Results and discussion
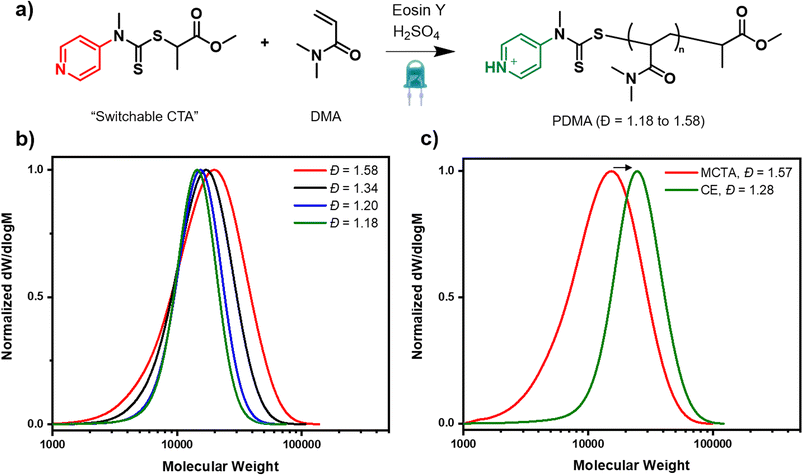
In search for an ideal system to tune dispersity in network polymers, there were three essential criteria that it was necessary to fulfil. First, excellent control over these complex syntheses must be achieved so as to allow uniform networks to be prepared. Second, quantitative conversions should be obtained in order to enable the complete incorporation of all the starting materials (i.e. monomer and crosslinker). Last, but not least, a simple handle to systematically vary the dispersity must be established while high livingness is ensured. We selected photoinduced electron/energy transfer reversible addition–fragmentation chain transfer polymerization (PET-RAFT) polymerization as this has previously been shown to afford lower amounts of termination and higher uniformity networks upon in situ crosslinking of the propagating polymer chains.58,68 Inspired by seminal work on thermal RAFT polymerization, we envisaged that the addition of various amounts of acid in the presence of the switchable CTA would enable the desired control over dispersity.37 However, given that the switchable CTA has not previously been employed to tune dispersity in PET-RAFT and the effect of the acid on the photocatalyst activity was unclear, the first objective was to develop suitable reaction conditions for a model linear polymerization system. Dimethylacrylamide (DMA) was selected as the model monomer, methyl 2-[methyl(4-pyridinyl)carbamothioylthio]propionate as the pH switchable CTA and eosin Y (EY) as the photocatalyst (Fig. 1a).37,69–71 All polymerizations were performed in a mixture of water and DMF under blue light irradiation, and first the amount of EY was varied in the absence of acid (0.005, 0.02 and 0.04 equivalents with respect to the CTA). It is expected that without acid, the CTA is in its “low activity” (low chain transfer constant state), and as such high dispersity polymers should be prepared. Indeed, after 4 hours of polymerization, broad, yet monomodal molar mass distributions were obtained. In all cases, with high final dispersity values (Đ = 1.58–1.69, Fig. 1b, S1 and Table S1†). Even though 0.04 equivalents had previously been reported as optimal for a trithiocarbonate CTA,72 for the switchable CTA, lower equivalents of EY (0.005 and 0.02 equivalents) were necessary to ensure near-quantitative conversions (∼95%) and an excellent agreement between theoretical and obtained molecular weights (Table S1,† entries 2 and 3). Full incorporation of the CTA on the polymer chains was evidenced by UV detector analysis from size exclusion chromatography (SEC) and the high livingness achieved under these polymerization conditions was further confirmed by performing a successful chain extension experiment (Fig. 1c, s2 and Table S2†). It is also worth highlighting that precisely obtaining the targeted molecular weight, even at high monomer conversion is not usually the case for many previously developed dispersity-controlled methodologies where a huge deviation from the theoretical values is typically observed when targeting high dispersity polymers.28,30,31 As this work aims to subsequently apply the optimized conditions to the synthesis of network polymers, it is necessary to be able to attain comparable molecular weights regardless of the targeted primary chain dispersity as networks with comparable compositions are the ultimate goal.Satisfied that we could obtain high-dispersity polymers, our attention turned to the synthesis of low and intermediate dispersity materials. In the presence of 3 equivalents of sulfuric acid (w.r.t CTA), the CTA is expected to be fully protonated and thus acts as a high-activity CTA. When the polymerization was conducted utilising 0.005, 0.02, 0.04 equivalents of EY (Table S3,† entries 2, 5 & 9), a clearly slower rate was observed in all cases, with just 17%, 11% and 14% of conversion achieved, respectively, in 4 hours. However, after longer reaction times, near quantitative conversions (99%) could be obtained for the lowest photocatalyst concentration (0.005 equiv.), alongside a dispersity value as low as 1.18 (Table S3, entry 3 and Fig. S3†). There was also very good agreement between theoretical and experimental molecular weights. In contrast, at higher photocatalyst concentrations (0.02 and 0.04), just 60% and 22% of conversion were achieved after 24 hours. The slower rates were attributed to the lower activity of the EY in the presence of acid and this was verified by UV-vis spectroscopy, where a lower absorption of the EY was observed in the presence of acid (Fig. S4†). As such, all subsequent experiments were conducted using 0.005 as our optimal photocatalyst concentration, as this consistently yields near-quantitative conversions while targeting both high and low dispersity materials. To obtain polymers of intermediate dispersity, the CTA was then partially protonated (0.5 and 1 equiv. of acid, Table S4†). In summary, we have demonstrated that PET RAFT polymerization is compatible with the switchable CTA and by carefully tuning the amount of acid, systematic dispersity control could be successfully achieved (Đ = 1.18–1.58, Table S4†).
Next, we wanted to investigate whether our established conditions could be applied to the preparation of dispersity-controlled network polymers by in situ crosslinking our propagating polymer chains. Our first aim was to determine the optimal amount of model crosslinker required for efficient crosslinking. Polymerizations with our previously optimized conditions and bis-acrylamide crosslinker ([DMA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [BisA]
[BisA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA]
[CTA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [EY] = 120
[EY] = 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X
X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
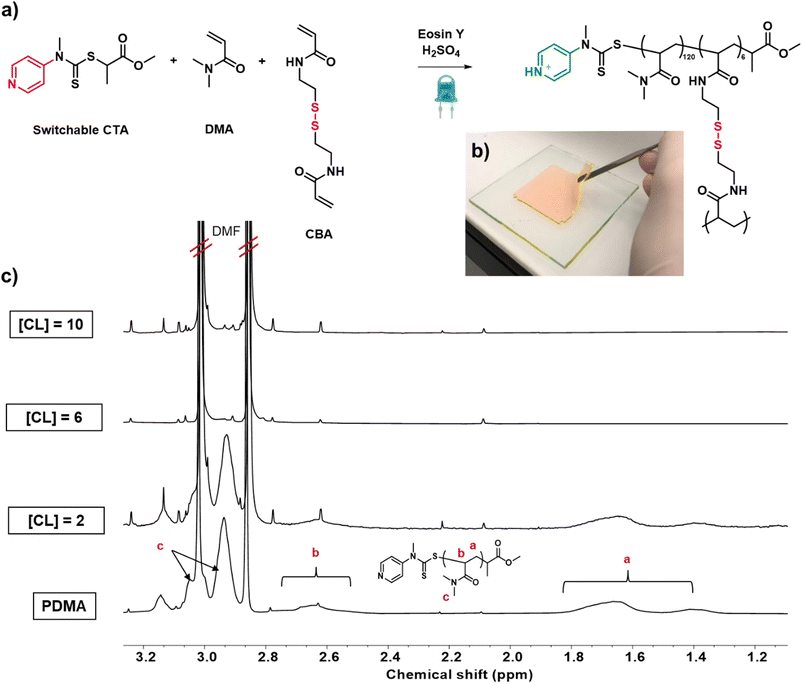
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005) were conducted in a double glass plated mould (8 × 8 × 0.3 cm) sealed with silicone rubber under a nitrogen atmosphere. Key to the success of this experiment, was to not only incorporate all starting monomer and crosslinker in the network, i.e. to obtain quantitative polymerization conversions, but also to utilize enough crosslinker so as to incorporate all the polymer chains within the network, resulting in materials with comparable compositions. The first target was to prepare networks with high primary chain dispersity. We envisaged that this would be the most challenging material to synthesize as the widest range of primary chain lengths would need to be incorporated within the network. When 2 equivalents of crosslinker ([CL] = 2 w.r.t. the CTA) were employed, an insoluble network was obtained. On extraction with water and subsequent 1H nuclear magnetic resonance (NMR) measurement, no unreacted monomer or crosslinker were observed, demonstrating that we had successfully achieved full monomer conversion (Fig. S5†). However, a significant amount of polymer was visible suggesting incomplete incorporation of the polymer chains within the material (Fig. 2c, [CL] = 2). This was attributed to the fact that many propagating chains were not able to react with the small amount of crosslinker and become part of the network. The experiment was then repeated in the presence of higher amounts of crosslinker (6 and 10 equivalents). Notably, after extraction, in addition to the absence of monomer and crosslinker, no polymer was also observed (Fig. 2c and S5,† [CL] = 6, 10). This demonstrated that full incorporation of the starting materials could be successfully achieved in a single step and it was possible to obtain a quantitative yield from our synthesis, even when targeting the highest dispersity network.
0.005) were conducted in a double glass plated mould (8 × 8 × 0.3 cm) sealed with silicone rubber under a nitrogen atmosphere. Key to the success of this experiment, was to not only incorporate all starting monomer and crosslinker in the network, i.e. to obtain quantitative polymerization conversions, but also to utilize enough crosslinker so as to incorporate all the polymer chains within the network, resulting in materials with comparable compositions. The first target was to prepare networks with high primary chain dispersity. We envisaged that this would be the most challenging material to synthesize as the widest range of primary chain lengths would need to be incorporated within the network. When 2 equivalents of crosslinker ([CL] = 2 w.r.t. the CTA) were employed, an insoluble network was obtained. On extraction with water and subsequent 1H nuclear magnetic resonance (NMR) measurement, no unreacted monomer or crosslinker were observed, demonstrating that we had successfully achieved full monomer conversion (Fig. S5†). However, a significant amount of polymer was visible suggesting incomplete incorporation of the polymer chains within the material (Fig. 2c, [CL] = 2). This was attributed to the fact that many propagating chains were not able to react with the small amount of crosslinker and become part of the network. The experiment was then repeated in the presence of higher amounts of crosslinker (6 and 10 equivalents). Notably, after extraction, in addition to the absence of monomer and crosslinker, no polymer was also observed (Fig. 2c and S5,† [CL] = 6, 10). This demonstrated that full incorporation of the starting materials could be successfully achieved in a single step and it was possible to obtain a quantitative yield from our synthesis, even when targeting the highest dispersity network.
We subsequently sought to incorporate a degradable crosslinker within our networks and to vary the primary chain dispersity within our materials. This, for the first time, would allow us to accurately understand how well controlled our synthesis was, by directly characterising the primary chain dispersity within our obtained networks. The disulfide crosslinker, N,N-cystaminebisacrylamide, (CBA) was selected and synthesised, as it is unreactive during polymerization, but cleavable on the addition of a reducing agent (Scheme S1 and Fig. S6†).58 Under our previously established conditions [DMA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CBA]
[CBA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA]
[CTA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [EY] = 120
[EY] = 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
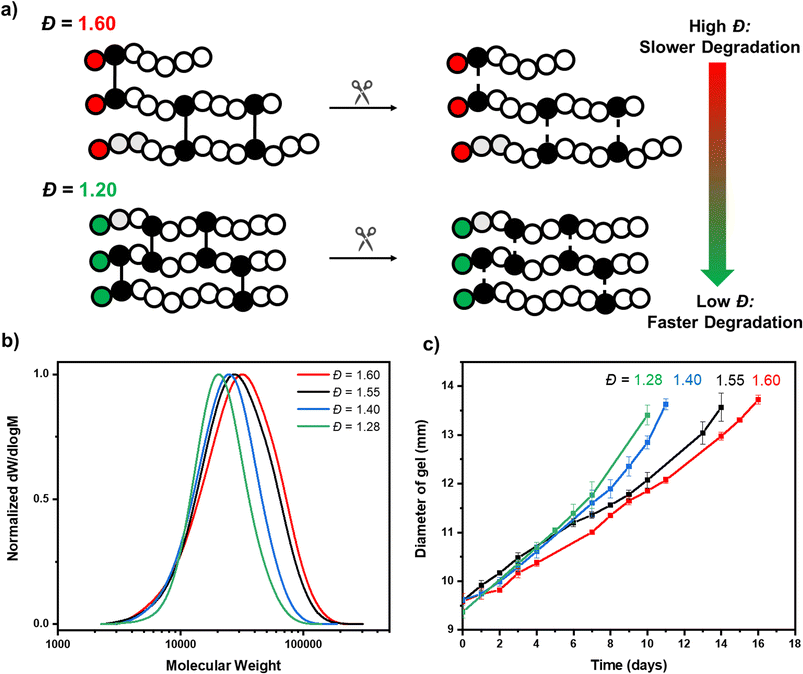
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005, a crosslinked polymer was targeted in the absence of acid with the aim of obtaining a material with the highest possible primary chain dispersity (Fig. 2a and S7†). The reaction was performed for 24 hours and a network was successfully obtained (Fig. 2b). In line with our model network, after extraction with water, no unreacted monomer or free polymer chains were observed, again successfully demonstrating full starting material incorporation and that changing the crosslinker from non-degradable to degradable had no adverse effect on the polymerization efficiency (Fig. S8†). Pleasingly, the resulting network was colorless, suggesting all EY had been effectively removed. (Fig. S9†). To characterize the primary chain dispersity of this network, it was necessary to cleave the disulfide bonds and analyze the molar mass distribution of the resulting linear polymer chains. Dithiothreitol (DTT) was selected as the reducing agent, (in combination with trimethylamine) and the cleavage experiment was performed at 60 °C in dimethylacetamide (Scheme S2† and Fig. 3a).58,73 The disulfide bonds were broken and after full dissolution of the network (24 hours), SEC of the resulting solutions was measured. As anticipated, the cleaved material had a high dispersity value of 1.60 (Table 1, entry 1 and Fig. 3b). This demonstrates that the use of the switchable CTA in PET-RAFT polymerization could be successful for the controlled preparation of high primary chain dispersity polymer networks. Importantly, this synthesis was high-yielding and only a single step was necessary.
0.005, a crosslinked polymer was targeted in the absence of acid with the aim of obtaining a material with the highest possible primary chain dispersity (Fig. 2a and S7†). The reaction was performed for 24 hours and a network was successfully obtained (Fig. 2b). In line with our model network, after extraction with water, no unreacted monomer or free polymer chains were observed, again successfully demonstrating full starting material incorporation and that changing the crosslinker from non-degradable to degradable had no adverse effect on the polymerization efficiency (Fig. S8†). Pleasingly, the resulting network was colorless, suggesting all EY had been effectively removed. (Fig. S9†). To characterize the primary chain dispersity of this network, it was necessary to cleave the disulfide bonds and analyze the molar mass distribution of the resulting linear polymer chains. Dithiothreitol (DTT) was selected as the reducing agent, (in combination with trimethylamine) and the cleavage experiment was performed at 60 °C in dimethylacetamide (Scheme S2† and Fig. 3a).58,73 The disulfide bonds were broken and after full dissolution of the network (24 hours), SEC of the resulting solutions was measured. As anticipated, the cleaved material had a high dispersity value of 1.60 (Table 1, entry 1 and Fig. 3b). This demonstrates that the use of the switchable CTA in PET-RAFT polymerization could be successful for the controlled preparation of high primary chain dispersity polymer networks. Importantly, this synthesis was high-yielding and only a single step was necessary.
| Entry | [H2SO4] | EWCa (%) | SRb | M n (SEC) | M w (SEC) | M P (SEC) | Đ |
|---|---|---|---|---|---|---|---|
| a Equilibrium water content (EWC). b Swelling Ratio (SR) were calculated based on the ratio of swollen and dried gel weight. c Cleavage was performed with DTT in dimethylacetamide. | |||||||
| 1 | 0 | 87.2 | 6.8 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
1.60 |
| 2 | 0.25 | 86.9 | 6.6 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1.55 |
| 3 | 0.5 | 89.4 | 8.4 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
1.40 |
| 4 | 0.3 | 88.5 | 7.7 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
1.28 |
Our next aim was to obtain networks with various lower primary chain dispersities, so we conducted three further syntheses with various acid concentrations (0.25, 0.5 and 3 equivalents w.r.t. CTA). In all cases, all monomer, crosslinker and polymer were quantitatively incorporated and after extraction, all acid and dye were successfully removed (Fig. S10†). On cleavage of the crosslinker with DTT, monomodal molar mass distributions were observed and the primary chain dispersity was measured to be 1.55, 1.40 and 1.28, respectively (Table 1, entries 2–4). This demonstrated the overall effectiveness of the acid-switchable CTA in tuning the dispersity within network polymers (Fig. 3b). These reactions were simple to perform, carried out in one-pot and required just a change in the acid concentration to obtain the various materials. There was a deviation between the theoretical and experimentally obtained molecular weights after cleavage of the networks and a slightly higher dispersity value was observed for the lowest dispersity material, when compared to the analogous linear polymer synthesis (e.g. 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400, Đ = 1.28 vs. 12
400, Đ = 1.28 vs. 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 Da, Đ = 1.20, Table 1 and Fig. S11†). We attribute this difference to the closer proximity of the propagating polymer chains within the network, which could result in a higher probability of termination through intramolecular combination reactions and also the reduced efficiency of deactivation by chain transfer due to the highly viscous nature of the synthesis.59,74 This is evidenced by a small amount of high molecular weight shouldering in the molar mass distributions of the various cleaved polymer networks (Fig. 3b) and demonstrates that analogous linear and network polymer syntheses do not yield identical materials. To ensure our gels were comparable, we analysed their equilibrium water contents, by immersing each of the networks in excess water for 24 hours. They were then weighed before and after freeze-drying. For all of our various primary chain dispersity networks, the solvent adsorption capacity was comparable (87–89%), indicating that each material had comparable crosslink densities and compositions (Table 1, column 3). The swelling ratios of the gels were also obtained to determine the uniformity of the crosslinked network materials. As shown in Table 1 column 4, the networks have excellent swelling ratios (6.8–8.4) which suggests good network homogeneity, even though a slight increase in swelling ratio with decreasing primary chain dispersity was observed.
500 Da, Đ = 1.20, Table 1 and Fig. S11†). We attribute this difference to the closer proximity of the propagating polymer chains within the network, which could result in a higher probability of termination through intramolecular combination reactions and also the reduced efficiency of deactivation by chain transfer due to the highly viscous nature of the synthesis.59,74 This is evidenced by a small amount of high molecular weight shouldering in the molar mass distributions of the various cleaved polymer networks (Fig. 3b) and demonstrates that analogous linear and network polymer syntheses do not yield identical materials. To ensure our gels were comparable, we analysed their equilibrium water contents, by immersing each of the networks in excess water for 24 hours. They were then weighed before and after freeze-drying. For all of our various primary chain dispersity networks, the solvent adsorption capacity was comparable (87–89%), indicating that each material had comparable crosslink densities and compositions (Table 1, column 3). The swelling ratios of the gels were also obtained to determine the uniformity of the crosslinked network materials. As shown in Table 1 column 4, the networks have excellent swelling ratios (6.8–8.4) which suggests good network homogeneity, even though a slight increase in swelling ratio with decreasing primary chain dispersity was observed.
We, therefore, proceeded to measure the degradability of our various primary chain dispersity networks, by performing experiments in glutathione solution at room temperature.75,76 We first took 9.5 mm discs of our highest primary chain dispersity (Đ = 1.60) network and performed degradation experiments in triplicate. Over time, degradation of the crosslinker occurred, as evidenced by a gradual increase in the diameter of the discs. The average size was 11 mm after 7 days, 12 mm after 12 days and 13 mm after 15 days (Table S5† and Fig. 3c). This swelling was due to the random degradation of crosslinkers increasing the distance between the remaining intact crosslinkers. This resulted in the network structure becoming less rigid and consequently it swells better. By day 17, a sufficient amount of crosslinker had been degraded for the network to reach its gel–sol transition point where it fully dissolved. The degradation experiment was then repeated with the various primary chain dispersity networks that we had previously prepared (Đ = 1.55, 1.40, 1.28). Notably, a distinct trend in degradation rate was observed depending on the initial primary chain dispersity. It was observed that the lower the dispersity of the network, the faster the rate of diameter increase and the earlier the time point of full dissolution. The network with primary chain dispersity of 1.55 fully dissolved on day 15, whereas the 1.40 and 1.28 dispersity networks required only 12 and 11 days, respectively (Tables S6–S8†). This illustrates that by carefully tuning the primary chain dispersity, the rate of degradation was directly affected. In terms of degradation time, there was a significant difference between our highest and lowest dispersity values of almost 40% (17 vs. 11 days, Fig. 3c). All experiments were performed in triplicate and the degradation was shown to be accurately reproducible with error bars illustrated in Fig. 3c. It should be highlighted that there were some small deviations in the molecular weight of the chains within our various primary chain dispersity networks (Mn = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500–22
500–22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 Da), so additional control experiments were performed. A range of different primary molecular weight networks were synthesized, while keeping the dispersity constant (either Đ = 1.28 or Đ = 1.40, Tables S9, S10 and Fig. S8†) and on degradation with glutathione, no molecular weight trend was observed (Tables S11–S15 and Fig. S12–S13†). Overall, it was concluded that primary chain dispersity significantly impacts degradation and this is a parameter that should be considered when designing degradable polymeric networks. In addition, our method provides a facile route to obtain such dispersity-controlled materials, creating many opportunities in applications where controlled degradation is required.
900 Da), so additional control experiments were performed. A range of different primary molecular weight networks were synthesized, while keeping the dispersity constant (either Đ = 1.28 or Đ = 1.40, Tables S9, S10 and Fig. S8†) and on degradation with glutathione, no molecular weight trend was observed (Tables S11–S15 and Fig. S12–S13†). Overall, it was concluded that primary chain dispersity significantly impacts degradation and this is a parameter that should be considered when designing degradable polymeric networks. In addition, our method provides a facile route to obtain such dispersity-controlled materials, creating many opportunities in applications where controlled degradation is required.
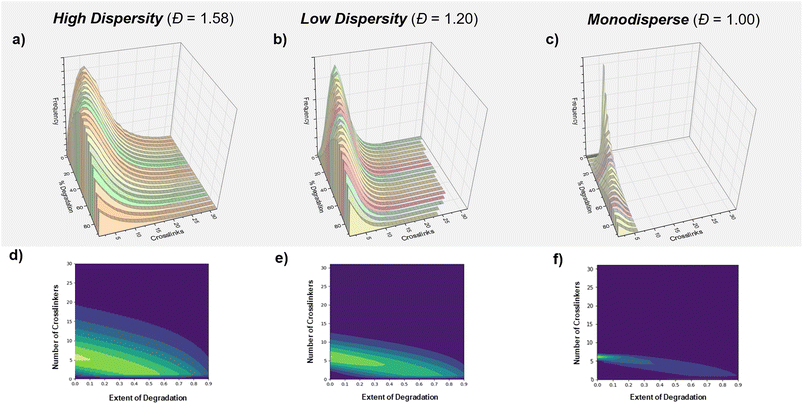
Finally, we were interested in further investigating and understanding the origin of this dispersity effect. We hypothesized that there could be two possible causes; (i) a positional effect based on the distribution of the crosslinkers within our various primary chain dispersity materials and/or (ii) an effect from different rates of glutathione diffusion. Simulations were therefore performed to understand the effect of the crosslinker distribution by converting the molar mass distributions of the highest and lowest primary chain dispersity materials to distributions of crosslinker (Fig. 4a–c and S14†). It was observed from this data that even though both materials had the same average number of crosslinkers per chain, the high dispersity sample had a significantly larger maximum number of crosslinkers per chain (60 vs. 30) and also many more chains with just 1 or 2 crosslinkers. The degradation of these materials (∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 polymer chains in total) was next simulated using a simple Python program, where crosslinkers were randomly selected and broken one by one, before a snapshot of the distribution was taken at increments of 5% degradation (or 50
000 polymer chains in total) was next simulated using a simple Python program, where crosslinkers were randomly selected and broken one by one, before a snapshot of the distribution was taken at increments of 5% degradation (or 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bonds, Fig. 4d and e). Throughout the simulation, there was a consistent theme with the high dispersity network containing more chains with larger numbers of crosslinkers, but also larger numbers of chains that had fully dissociated from the material. For example, at 80% degradation, the high dispersity material contained ∼80
000 bonds, Fig. 4d and e). Throughout the simulation, there was a consistent theme with the high dispersity network containing more chains with larger numbers of crosslinkers, but also larger numbers of chains that had fully dissociated from the material. For example, at 80% degradation, the high dispersity material contained ∼80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chains that had six or more crosslinks (31%) and ∼30
000 chains that had six or more crosslinks (31%) and ∼30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chains (12%) with ten or more crosslinkers compared to ∼55
000 chains (12%) with ten or more crosslinkers compared to ∼55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (14%) with more than 6 crosslinkers and ∼8000 chains (2%) with more than 10 crosslinkers in the low dispersity sample. In addition, when evaluating how many chains no longer had a single crosslink and had therefore dissociated from the network, ∼75% percent of the original chains had fully dissociated from the high primary chain dispersity network compared to ∼63% for the low dispersity material (Tables S16 and S17†). Coupled with the experimental data, we propose that the higher molecular weight chains are essential in extending the degradation time of the network. For example, when comparing chains with 6 and 60 crosslinkers, those with 60 crosslinkers required a much higher percentage of total degradation to be achieved so to fully dissociate from the network. The role of chains containing just 1 or 2 crosslinkers is much more limited, as these simply cleave from the network at low degradation percentages, while the remainder of the network remains intact. By lowering the primary chain dispersity, materials have fewer chains with a high number of crosslinkers, so the gel–sol point is therefore reached at a lower degradation percentage and the lifetime of the material is shortened. Indeed, the trend can be exemplified through the simulated degradation of a monodisperse sample (Table S19† and Fig. 4f). A larger number of chains are bound to the network for much longer, but this material has an even earlier gel–sol transition point and once a certain lower threshold of degradation has been reached, this material will fully dissolve. Altogether, this simulation indicates that the distribution of crosslinks based on the primary chain dispersity plays a significant role in determining the various rates of degradation. The effect of the distribution is likely to be enhanced further, due to the earlier gel point observed when higher primary chain dispersity networks are targeted, resulting in the longer polymer chains having an even greater number of crosslinkers than expected.77–79 In addition, a further effect due to diffusion cannot be ruled out.
000 (14%) with more than 6 crosslinkers and ∼8000 chains (2%) with more than 10 crosslinkers in the low dispersity sample. In addition, when evaluating how many chains no longer had a single crosslink and had therefore dissociated from the network, ∼75% percent of the original chains had fully dissociated from the high primary chain dispersity network compared to ∼63% for the low dispersity material (Tables S16 and S17†). Coupled with the experimental data, we propose that the higher molecular weight chains are essential in extending the degradation time of the network. For example, when comparing chains with 6 and 60 crosslinkers, those with 60 crosslinkers required a much higher percentage of total degradation to be achieved so to fully dissociate from the network. The role of chains containing just 1 or 2 crosslinkers is much more limited, as these simply cleave from the network at low degradation percentages, while the remainder of the network remains intact. By lowering the primary chain dispersity, materials have fewer chains with a high number of crosslinkers, so the gel–sol point is therefore reached at a lower degradation percentage and the lifetime of the material is shortened. Indeed, the trend can be exemplified through the simulated degradation of a monodisperse sample (Table S19† and Fig. 4f). A larger number of chains are bound to the network for much longer, but this material has an even earlier gel–sol transition point and once a certain lower threshold of degradation has been reached, this material will fully dissolve. Altogether, this simulation indicates that the distribution of crosslinks based on the primary chain dispersity plays a significant role in determining the various rates of degradation. The effect of the distribution is likely to be enhanced further, due to the earlier gel point observed when higher primary chain dispersity networks are targeted, resulting in the longer polymer chains having an even greater number of crosslinkers than expected.77–79 In addition, a further effect due to diffusion cannot be ruled out.
Conclusions
We have established a one-pot method to tune the primary chain dispersity in polymer networks and demonstrated a significant effect of primary chain dispersity on gel degradation. PET-RAFT polymerization was performed with a degradable crosslinker, a switchable CTA and various amounts of acid, which allowed the dispersity to be precisely tuned, while incorporating all monomer, crosslinker and polymer chains within the materials. On crosslinker degradation, the precise primary chain dispersity values were obtained and correlated to the degradation profiles. The key observation was that the higher the primary chain dispersity of the network, the slower the degradation. This was supported by simulations, which emphasized the importance of the higher molecular weight chains in the higher dispersity materials, in preserving the network until a higher extent of degradation had been reached. This work creates many new research opportunities in applications where precise tuning of network degradation is necessary.Data availability
Additional experimental details and data are provided in the ESI.† This includes SEC, UV-vis and 1H NMR data, alongside photographs of the experimental set-up and raw data from the simulations.Author contributions
T. S. methodology, investigation: polymer synthesis and degradation, validation, visualization, writing – reviewing and editing. R. W. conceptualization, project administration, supervision, methodology, visualization, writing – original draft. G. R. J. investigation: simulations, writing – reviewing and editing. I. R. investigation: ANOVA and swelling ratio calculations, conceptualization, writing – reviewing and editing. D. K. conceptualization, writing – reviewing and editing. N. P. T. conceptualization, writing – reviewing and editing. A. A. conceptualization, project administration, supervision, funding acquisition, writing – reviewing and editing.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
A. A. gratefully acknowledges ETH Zurich (Switzerland) and the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (DEPO: Grant no. 949219) for financial support. T. S. acknowledges Mitsubishi Chemical Corporation for generous support. N. P. T. acknowledges the award of a DECRA Fellowship from the ARC (DE180100076).References
- D. T. Gentekos, R. J. Sifri and B. P. Fors, Nat. Rev. Mater., 2019, 1–14 Search PubMed.
- R. Whitfield, N. P. Truong, D. Messmer, K. Parkatzidis, M. Rolland and A. Anastasaki, Chem. Sci., 2019, 10, 8724–8734 RSC.
- T. Junkers, Macromol. Chem. Phys., 2020, 221, 2000234 CrossRef CAS.
- M. R. Martinez and K. Matyjaszewski, CCS Chem., 2022, 4, 2176–2211 CrossRef CAS.
- R. Whitfield, N. Truong and A. Anastasaki, Angew. Chem., Int. Ed., 2021, 60, 19383–19388 CrossRef CAS PubMed.
- M. Nardi, E. Blasco and C. Barner-Kowollik, J. Am. Chem. Soc., 2022, 144, 1094–1098 CrossRef CAS PubMed.
- M. Chen, J. Li, K. Ma, G. Jin, X. Pan, Z. Zhang and J. Zhu, Angew. Chem., 2021, 133, 19857–19861 CrossRef.
- H. S. Wang, K. Parkatzidis, S. Harrisson, N. P. Truong and A. Anastasaki, Chem. Sci., 2021, 12, 14376–14382 RSC.
- K. Parkatzidis, M. Rolland, N. T. Phuoc and A. Anastasaki, Polym. Chem., 2021, 12, 5583–5588 RSC.
- T. Takamatsu, S. Shioya and Y. Okada, Ind. Eng. Chem. Res., 1988, 27, 93–99 CrossRef CAS.
- V. Kottisch, D. T. Gentekos and B. P. Fors, ACS Macro Lett., 2016, 5, 796–800 CrossRef CAS PubMed.
- D. T. Gentekos, L. N. Dupuis and B. P. Fors, J. Am. Chem. Soc., 2016, 138, 1848–1851 CrossRef CAS PubMed.
- M. Nadgorny, D. T. Gentekos, Z. Xiao, S. P. Singleton, B. P. Fors and L. A. Connal, Macromol. Rapid Commun., 2017, 38, 1700352 CrossRef PubMed.
- R. J. Sifri, O. Padilla-Vélez, G. W. Coates and B. P. Fors, J. Am. Chem. Soc., 2019, 142, 1443–1448 CrossRef PubMed.
- S. Domanskyi, D. T. Gentekos, V. Privman and B. P. Fors, Polym. Chem., 2020, 11, 326–336 RSC.
- S. Rosenbloom, R. Sifri and B. Fors, Polym. Chem., 2021, 12, 4910–4915 RSC.
- N. Corrigan, A. Almasri, W. Taillades, J. Xu and C. Boyer, Macromolecules, 2017, 50, 8438–8448 CrossRef CAS.
- N. Corrigan, R. Manahan, Z. T. Lew, J. Yeow, J. Xu and C. Boyer, Macromolecules, 2018, 51, 4553–4563 CrossRef CAS.
- K. Liu, N. Corrigan, A. Postma, G. Moad and C. Boyer, Macromolecules, 2020, 53, 8867–8882 CrossRef CAS.
- S. Xu, F. J. Trujillo, J. Xu, C. Boyer and N. Corrigan, Macromol. Rapid Commun., 2021, 42, 2100212 CrossRef CAS PubMed.
- M. Rubens and T. Junkers, Polym. Chem., 2019, 10, 6315–6323 RSC.
- M. Rubens and T. Junkers, Polym. Chem., 2019, 10, 5721–5725 RSC.
- T. Junkers and J. H. Vrijsen, Eur. Polym. J., 2020, 134, 109834 CrossRef CAS.
- N. Corrigan and C. Boyer, Macromolecules, 2022, 55, 8960–8969 CrossRef CAS.
- M. H. Reis, T. P. Varner and F. A. Leibfarth, Macromolecules, 2019, 52, 3551–3557 CrossRef CAS.
- D. J. Walsh, D. A. Schinski, R. A. Schneider and D. Guironnet, Nat. Commun., 2020, 11, 1–9 CrossRef PubMed.
- D. Liu, A. D. Sponza, D. Yang and M. Chiu, Angew. Chem., 2019, 58, 16210–16216 CrossRef CAS PubMed.
- R. Whitfield, K. Parkatzidis, M. Rolland, N. P. Truong and A. Anastasaki, Angew. Chem., Int. Ed., 2019, 58, 13323–13328 CrossRef CAS PubMed.
- Z. Wang, J. Yan, T. Liu, Q. Wei, S. Li, M. Olszewski, J. Wu, J. Sobieski, M. Fantin and M. R. Bockstaller, ACS Macro Lett., 2019, 8, 859–864 CrossRef CAS PubMed.
- T. Shimizu, N. P. Truong, R. Whitfield and A. Anastasaki, ACS Polym. Au, 2021, 1, 187–195 CrossRef CAS PubMed.
- M. Rolland, N. P. Truong, R. Whitfield and A. Anastasaki, ACS Macro Lett., 2020, 9, 459–463 CrossRef CAS PubMed.
- M. Rolland, V. Lohmann, R. Whitfield, N. P. Truong and A. Anastasaki, J. Polym. Sci., 2021, 59, 2502–2509 CrossRef CAS.
- X. Liu, C. G. Wang and A. Goto, Angew. Chem., 2019, 131, 5654–5659 CrossRef.
- R. Whitfield, K. Parkatzidis, N. P. Truong, T. Junkers and A. Anastasaki, Chem, 2020, 6, 1340–1352 CAS.
- K. Parkatzidis, N. P. Truong, M. N. Antonopoulou, R. Whitfield, D. Konkolewicz and A. Anastasaki, Polym. Chem., 2020, 11, 4968–4972 RSC.
- T. Nwoko, N. D. A. Watuthanthrige, B. Parnitzke, K. Yehl and D. Konkolewicz, Polym. Chem., 2021, 12, 6761–6770 RSC.
- M.-N. Antonopoulou, R. Whitfield, N. P. Truong, D. Wyers, S. Harrisson, T. Junkers and A. Anastasaki, Nat. Chem., 2022, 14, 304–312 CrossRef CAS PubMed.
- M.-N. Antonopoulou, R. Whitfield, N. P. Truong and A. Anastasaki, Eur. Polym. J., 2022, 174, 111326 CrossRef CAS.
- S. I. Rosenbloom, J. H. Hsu and B. P. Fors, J. Polym. Sci., 2022, 60, 1291–1299 CrossRef CAS.
- O. Terreau, L. Luo and A. Eisenberg, Langmuir, 2003, 19, 5601–5607 CrossRef CAS.
- S. I. Rosenbloom and B. P. Fors, Macromolecules, 2020, 53, 7479–7486 CrossRef CAS.
- S. I. Rosenbloom, D. T. Gentekos, M. N. Silberstein and B. P. Fors, Chem. Sci., 2020, 11, 1361–1367 RSC.
- D. T. Gentekos, J. Jia, E. S. Tirado, K. P. Barteau, D.-M. Smilgies, R. A. DiStasio Jr and B. P. Fors, J. Am. Chem. Soc., 2018, 140, 4639–4648 CrossRef CAS PubMed.
- A.-L. Buckinx, M. Rubens, N. R. Cameron, C. Bakkali-Hassani, A. Sokolova and T. Junkers, Polym. Chem., 2022, 13, 3444–3450 RSC.
- Z. Wang, J. Yan, T. Liu, Q. Wei, S. Li, M. Olszewski, J. Wu, J. Sobieski, M. Fantin, M. R. Bockstaller and K. Matyjaszewski, ACS Macro Lett., 2019, 8, 859–864 CrossRef CAS PubMed.
- R. Yin, Z. Wang, M. R. Bockstaller and K. Matyjaszewski, Polym. Chem., 2021, 12, 6071–6082 RSC.
- M. Romio, B. Grob, L. Trachsel, A. Mattarei, G. Morgese, S. N. Ramakrishna, F. Niccolai, E. Guazzelli, C. Paradisi and E. Martinelli, J. Am. Chem. Soc., 2021, 143, 19067–19077 CrossRef CAS PubMed.
- V. Yadav, N. Hashmi, W. Ding, T.-H. Li, M. K. Mahanthappa, J. C. Conrad and M. L. Robertson, Polym. Chem., 2018, 9, 4332–4342 RSC.
- T.-H. Li, V. Yadav, J. C. Conrad and M. L. Robertson, ACS Macro Lett., 2021, 10, 518–524 CrossRef CAS PubMed.
- C.-G. Wang, A. M. L. Chong and A. Goto, ACS Macro Lett., 2021, 10, 584–590 CrossRef CAS PubMed.
- J. C. Conrad and M. L. Robertson, JACS Au, 2023, 3, 333–343 CrossRef CAS PubMed.
- F. M. Benedetti, Y.-C. M. Wu, S. Lin, Y. He, E. Flear, K. R. Storme, C. Liu, Y. Zhao, T. M. Swager and Z. P. Smith, JACS Au, 2022, 2, 1610–1615 CrossRef CAS PubMed.
- D. Merckle and A. C. Weems, Polym. Chem., 2023, 14, 3587–3599 RSC.
- N. D. A. Watuthanthrige, P. Chakma and D. Konkolewicz, Trends Chem., 2021, 3, 231–247 CrossRef.
- I. O. Raji, O. J. Dodo, N. K. Saha, M. Eisenhart, K. M. Miller, R. Whitfield, A. Anastasaki and D. Konkolewicz, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-6ngm1.
- J. J. Lessard, K. A. Stewart and B. S. Sumerlin, Macromolecules, 2022, 55, 10052–10061 CrossRef CAS.
- C. W. A. Bainbridge, A. Wangsadijaya, N. Broderick and J. Jin, Polym. Chem., 2022, 13, 1484–1494 RSC.
- J. Cuthbert, S. V. Wanasinghe, K. Matyjaszewski and D. Konkolewicz, Macromolecules, 2021, 54, 8331–8340 CrossRef CAS.
- F. Dawson, H. Jafari, V. Rimkevicius and M. Kopeć, Macromolecules, 2023, 56, 2009–2016 CrossRef CAS PubMed.
- W. Li, H. Gao and K. Matyjaszewski, Macromolecules, 2009, 42, 927–932 CrossRef CAS.
- A. D. Metcalfe and M. W. Ferguson, J. R. Soc., Interface, 2007, 4, 413–437 CrossRef CAS PubMed.
- K. A. Davis and K. S. Anseth, Crit. Rev. Ther. Drug Carrier Syst., 2002, 19, 385–423 CrossRef CAS PubMed.
- K. S. Anseth, A. T. Metters, S. J. Bryant, P. J. Martens, J. H. Elisseeff and C. N. Bowman, J. Controlled Release, 2002, 78, 199–209 CrossRef CAS PubMed.
- M. Grosjean, L. Gangolphe and B. Nottelet, Adv. Funct. Mater., 2023, 33, 2205315 CrossRef CAS.
- G. X. Wang, D. Huang, J. H. Ji, C. Völker and F. R. Wurm, Advanced Science, 2021, 8, 2001121 CrossRef CAS PubMed.
- J. W. DuBose, C. Cutshall and A. T. Metters, J. Biomed. Mater. Res., Part A, 2005, 74, 104–116 CrossRef PubMed.
- N. De Alwis Watuthanthrige, D. Dunn, M. Dolan, J. L. Sparks, Z. Ye, M. B. Zanjani and D. Konkolewicz, ACS Appl. Polym. Mater., 2022, 4, 1475–1486 CrossRef CAS.
- S. V. Wanasinghe, M. Sun, K. Yehl, J. Cuthbert, K. Matyjaszewski and D. Konkolewicz, ACS Macro Lett., 2022, 11, 1156–1161 CrossRef CAS PubMed.
- G. Opiyo and J. Jin, Eur. Polym. J., 2021, 159, 110713 CrossRef CAS.
- J. Xu, S. Shanmugam, H. T. Duong and C. Boyer, Polym. Chem., 2015, 6, 5615–5624 RSC.
- Y. Xiu, V. A. Bobrin, N. Corrigan, Y. Yao, J. Zhang and C. Boyer, J. Polym. Sci., 2023 DOI:10.1002/pol.20230634.
- A. Bagheri, C. W. A. Bainbridge, K. E. Engel, G. G. Qiao, J. Xu, C. Boyer and J. Jin, ACS Appl. Polym. Mater., 2020, 2, 782–790 CrossRef CAS.
- W. Konigsberg, in Methods in enzymology, Elsevier, 1972, vol. 25, pp. 185–188 Search PubMed.
- K. Matyjaszewski and T. P. Davis, Handbook of radical polymerization, John Wiley & Sons, Hoboken, 2002 Search PubMed.
- D. J. Phillips and M. I. Gibson, Biomacromolecules, 2012, 13, 3200–3208 CrossRef CAS PubMed.
- J. F. Quinn, M. R. Whittaker and T. P. Davis, Polym. Chem., 2017, 8, 97–126 RSC.
- P. J. Flory, J. Am. Chem. Soc., 1947, 69, 30–35 CrossRef CAS.
- W. H. Stockmayer, J. Chem. Phys., 1943, 11, 45–55 CrossRef CAS.
- W. H. Stockmayer, J. Chem. Phys., 1944, 12, 125–131 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc05203f |
| This journal is © The Royal Society of Chemistry 2023 |