Open Access Article
Open Access ArticleFrom random to rational: improving enzyme design through electric fields, second coordination sphere interactions, and conformational dynamics
Shobhit S.
Chaturvedi
 a,
Daniel
Bím
a,
Daniel
Bím
 a,
Christo Z.
Christov
a,
Christo Z.
Christov
 b and
Anastassia N.
Alexandrova
b and
Anastassia N.
Alexandrova
 *a
*a
aDepartment of Chemistry and Biochemistry, University of California, Los Angeles, California 90095, USA. E-mail: ana@chem.ucla.edu
bDepartment of Chemistry, Michigan Technological University, Houghton, Michigan 49931, USA
First published on 13th September 2023
Abstract
Enzymes are versatile and efficient biological catalysts that drive numerous cellular processes, motivating the development of enzyme design approaches to tailor catalysts for diverse applications. In this perspective, we investigate the unique properties of natural, evolved, and designed enzymes, recognizing their strengths and shortcomings. We highlight the challenges and limitations of current enzyme design protocols, with a particular focus on their limited consideration of long-range electrostatic and dynamic effects. We then delve deeper into the impact of the protein environment on enzyme catalysis and explore the roles of preorganized electric fields, second coordination sphere interactions, and protein dynamics for enzyme function. Furthermore, we present several case studies illustrating successful enzyme-design efforts incorporating enzyme strategies mentioned above to achieve improved catalytic properties. Finally, we envision the future of enzyme design research, spotlighting the challenges yet to be overcome and the synergy of intrinsic electric fields, second coordination sphere interactions, and conformational dynamics to push the state-of-the-art boundaries.
1. Natural, evolved, and designed enzymes: can we spot the differences?
Enzymes are versatile and efficient biological catalysts crucial in virtually all cellular processes. Their remarkable ability to facilitate chemical reactions with high specificity, selectivity, and efficiency has driven the development of various enzyme design approaches with the aim of creating tailor-made catalysts for diverse applications.1–4 Enzymes can be categorized by their developmental approach into three broad types: natural, evolved (i.e., improved upon an initial activity), and designed (repurposed from existing enzymes or designed de novo), each with unique catalytic properties (Fig. 1).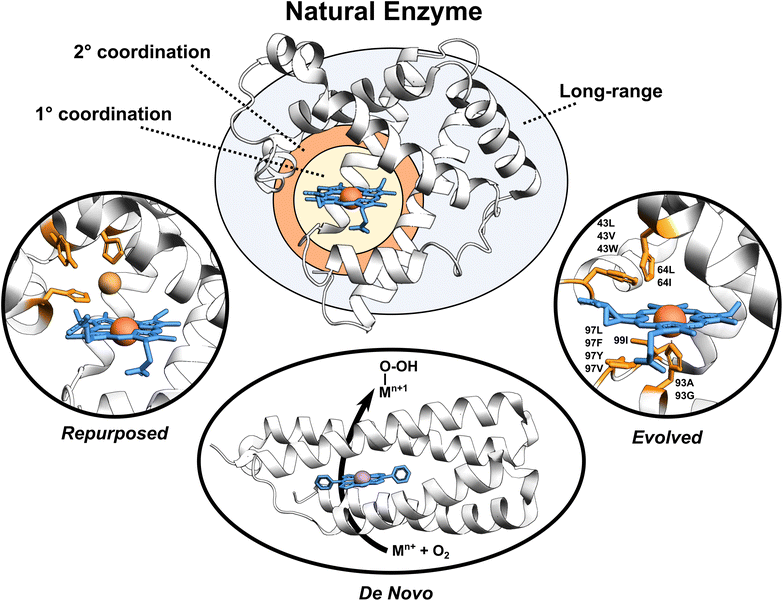 | ||
| Fig. 1 Broadly classified enzyme types. Enzyme active site, first coordination sphere, second coordination sphere, and long-range regions are highlighted. Tailored proteins showed in the figure are loosely motivated from (i) engineered copper binding site in sperm whale myoglobin mimicking the CuB-heme center,5 (ii) de novo designed porphyrin-binding protein,6 and (iii) evolved myoglobin containing an Ir(Me) site to catalyze the functionalization of C–H bonds.7 | ||
Natural enzymes have evolved over millions of years to achieve remarkable catalytic performance utilizing an array of mechanisms, including substrate positioning and transition state (TS) stabilization,8,9e.g., through the first- but also the second-coordination-sphere (SCS) effects,10 longer-range electrostatic preorganization,11 and conformational dynamics.12–14 These strategies work in concert to enable enzymes to overcome activation energy barriers and perform efficient catalysis. Despite the impressive performance of natural enzymes, these catalysts are typically optimized for specific substrates and chemical reactions, limiting their applications.15
Evolved enzymes, modified in laboratory, enhances a specific activity of an existing enzyme through directed evolution.16 This iterative process involves creating diverse enzyme variants through random mutagenesis, followed by selecting those variants with desired traits. The selected variants then serve as the starting point for the next round of mutagenesis and selection. Over several rounds, this technique mimics the principles of natural evolution, gradually refining enzyme properties toward the desired goal. Directed evolution is particularly useful when the underlying molecular mechanisms are not fully understood, as it allows enzymes to be optimized based on their observed behaviors rather than through rational design. Evolved enzymes can perform chemical reactions that are new to nature, including binding of non-native cofactors and catalyzing chemical reactions using non-native substrates.17–20 Examples of such modified enzymes include redesigning of myoglobin, to enable stereoselective cyclopropanation21 and carbene transfer reactivity,22 repurposing of native hydroxylases PolL and LdoA for transforming azidated substrates into nitrile products through oxidative conversion,23 and adapting the ethylene-forming enzyme to utilize non-native ligands and catalyze olefin aziridination as well as nitrene C–H insertion reactions.24 Mechanistic analyses of evolved enzymes indicate that catalysis is improved during evolution through several strategies; mainly altering the substrate positioning and the active site, but also through enzyme dynamics, conformational tinkering, or introducing new catalytically important interactions.25 Despite the success of these laboratory techniques, the starting protein scaffold limits the intrinsic properties of the evolved enzymes. Furthermore, observations indicate that ∼60–70% of mutations are deleterious, ∼30–40% are neutral, and less than 5% confer functional improvements,25 making the process rather random with not optimally utilizing time and resources.
Designed enzymes are rationally repurposed from existing enzymes or constructed de novo to perform new functions. These enzymes offer an opportunity to create a more chemically versatile catalysts. A straightforward strategy for enzyme design is repurposing the native enzymes for different functions. This might include an insertion of the non-native (metallo-)cofactor into a naturally occurring protein, combining the features of both the cofactor and the protein scaffold. An engineered copper binding site in the cytochrome c peroxidase (CcP)26 or sperm whale myoglobin (Mb) by Lu et al.,27 mimicking the CuB-heme center in terminal oxidases, represents an example of such endeavors. A desired strategy, however, is to assemble the complete functional enzymes de novo. De novo enzyme design involves the creation of entirely new enzymes with desired functions that do not exist in nature. This cutting-edge approach starts from scratch, beginning with a set of amino acid sequences and computationally designing their three-dimensional structures to achieve specific catalytic activities. Recently, a completely de novo designed C45 protein has been demonstrated to perform a stereoselective transfer of carbenes to olefins, heterocycles, aldehydes, and amines.28 Additional examples include the hydrolysis of ferric enterobactin by de novo Syn-F4 enzyme29 and catalysis of Kemp elimination by a computationally designed KE07 enzyme.30 This method provides an excellent opportunity for greater chemical versatility than natural enzymes, but falls short in terms of performance.31
2. Challenges and limitations of current enzyme design protocols
In the quest to design enzymes with tailored properties and functions, researchers have developed various protocols for enzyme design.32–34 Although computational enzyme design has become a widespread technique in enzyme engineering, it faces several challenges when designing de novo enzymes solo, i.e. without a help of directed evolution.31,35–37 Predominantly, standard enzyme design strategies have centered around optimizing the protein to stabilize the TS of the target reaction.30,38,39 However, these methods often fail to achieve the sub-angstrom precision necessary to manipulate the subtle SCS interactions,31 which differentiate between TS and reactant states, or indirectly affect the first coordination sphere (FCS) by restraining its dynamics in a reactive conformation. Moreover, these traditional approaches often overlook the integrated nature of enzymes, which work as unified entities to proficiently catalyze targeted reactions. As such, they typically do not optimize the protein scaffold for the desired reaction. The limitations of current computational strategies also arise from an insufficient consideration of the factors contributing to natural enzymes' catalytic efficiencies. Therefore, factors such as protein dynamics, protein conformations, correlated motions, and the long-range effects of enzyme electrostatic preorganization via internally generated electric fields are often inadequately considered or entirely neglected. Additionally, accurately accounting for complex protein dynamics and pinpointing the subtle effects of amino acid substitutions on enzyme activity remain significant challenges in computational enzyme design.35,40 As a result, despite its considerable potential, computationally designed enzymes have yet to achieve catalytic efficiencies on par with those of natural enzymes.Current enzyme design protocols often circumvent these limitations by integrating computational design with experimental methods such as directed evolution.41–44 In this setup, computational methods are frequently used as a first step to engineer inactive proteins for a target reaction. Computational protocols focus on modifying the active sites of inactive proteins and fabricating a foundational scaffold, capable of demonstrating a degree of initial activity. As these scaffolds undergo directed evolution, they evolve to exhibit efficiency and specificity approaching natural enzymes. By refining active sites for improved binding in the enzyme-bound TS and introducing advantageous mutations that promote the conversion of non-catalytic sub-conformational states into catalytic states for superior preorganization, directed evolution can improve enzyme performance.41,45 This strategy succeeded in numerous enzymatic transformations, such as Kemp elimination, retro-aldol reactions, and Morita–Baylis–Hillman reactions.43,46,47 Nevertheless, to enhance the efficacy of computational enzyme design protocols, it is imperative that all factors contributing to the development of efficient enzymes through directed evolution would be incorporated into computational design methodologies.
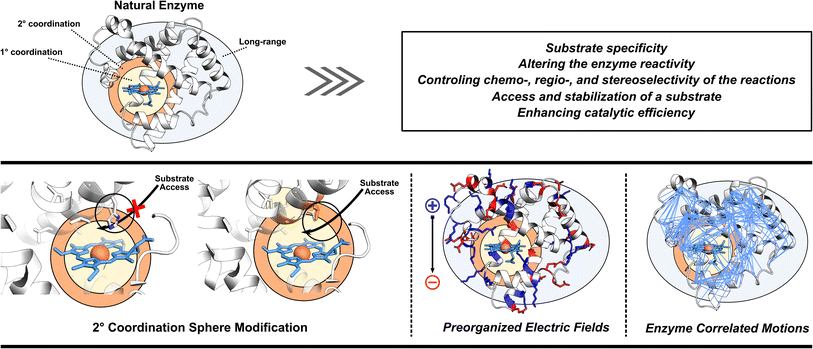
3. Missing pieces in enzyme designs
As already eluded to, the enzymatic active site is not the sole contributor to enzyme's function (Fig. 2). Enzymes also utilize adjacent regions, such as SCS, and employ long-range effects. Moreover, dynamic correlations are present between different protein regions and the active site, influencing enzyme activity.48 Thus, when optimizing or designing enzymes, it is essential to consider both the active site and further regions and investigate these additional catalytic strategies. By incorporating elements of electrostatic preorganization and catalytically significant dynamic motions into the design process, a more comprehensive and effective enzyme design can be achieved. Below we highlight specific cases where enzymes utilize their electric fields, SCS interactions, and protein dynamics to improve catalysis. These strategies are then discussed from the perspective of enzyme design in Section 4.3.1 Optimization of enzyme electric fields
Enzymes utilize large protein scaffolds surrounding the active site to facilitate catalysis. One function of these protein scaffolds is to protect the active site from undesirable side reactions. Another role involves imposing specific electric fields on their active sites.11,49–52 Within the concept of electrostatic preorganization, each amino acid's partial charges in the three-dimensional structure of protein generate a preorganized electric field that preferentially stabilizes the TS of the enzyme-catalyzed reaction over the reactants. This hypothesis has been experimentally validated using vibrational Stark effect spectroscopy.50 In the pioneering work on ketosteroid isomerase (KSI) the Stark effect spectroscopy found an exceptionally strong inherent electric field experienced by the carbon-oxygen double bond (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) of the bound steroid substrate, which increases the catalytic turnover of the reaction by favoring the charge rearrangement in KSI's rate-determining step.53 In the molecular systems, the experiments using scanning tunneling microscopy have also indicated that external oriented electric fields can enhance the catalysis of Diels–Alder reaction,54,55 homolytic O–O bond cleavage,56 Ullmann-type coupling reaction,57 and coupling of aryl iodides with a nickel(0) complex.58 These results combined indicate that an oriented electric field can be used as a tool to manipulate the reactivities of chemical reactions and offer new possibilities in enzyme design.
O) of the bound steroid substrate, which increases the catalytic turnover of the reaction by favoring the charge rearrangement in KSI's rate-determining step.53 In the molecular systems, the experiments using scanning tunneling microscopy have also indicated that external oriented electric fields can enhance the catalysis of Diels–Alder reaction,54,55 homolytic O–O bond cleavage,56 Ullmann-type coupling reaction,57 and coupling of aryl iodides with a nickel(0) complex.58 These results combined indicate that an oriented electric field can be used as a tool to manipulate the reactivities of chemical reactions and offer new possibilities in enzyme design.
Following the experiments of Boxer et al.,53 KSI enzyme served for many years as the prominent scaffold for benchmarking computational methods to capture the internal electric fields exerted on the KSI active site, and for understanding how the accurate modeling can assist in improving the fields for enhanced catalysis in KSI or designed enzymes. Importantly, computational studies utilizing hybrid quantum mechanics/molecular mechanics (QM/MM) and molecular dynamics (MD) simulations with polarizable force fields were able to compute electric fields in the active site in agreement with experimental results.59–61 Furthermore, computational analysis of the KSI enzyme by Alexandrova and co-workers also suggests that the global quantum mechanics (QM) electron density at the active site is sensitive to minor alterations in the external electric field and analysis of the charge density can thus serve as a sensitive and rigorous probe of electrostatic preorganization.62 At last, Welborn and Head-Gordon demonstrated that conformational dynamics also contribute to the reactivity at different stages of the catalytic cycle, including the catalytic step and product release, through significant fluctuations of electric fields in the KSI active site.63 This also demonstrates the importance of studying the long-range effects discussed in this perspective, and also their cooperative influence on the enzymes' reactivity, as well as their role in enzyme design.
Moreover, the electric fields can impact the electronic properties of the active site, such as altering the spin state order, electronic configuration, and rate of chemical reactions.64 To illustrate this, several computational studies have been directed to understand the impact of local electric fields on the reactivity of heme and non-heme iron proteins. The QM/MM calculations with an external electric field performed on the P450CAM protein indicated that changes in the electric field along the axis perpendicular to the heme cofactor (i.e., oriented along the reactive Fe(IV)-oxido unit) could change the ground state (GS) of the resting enzyme from a doublet to a quartet or sextet spin state depending on the magnitude of the electric field.65 Furthermore, the sign and magnitude of the external electric fields oriented along the same axis have been evidenced to alter the location of the unpaired radical site in Cpd I intermediates in ascorbate peroxidase and cytochrome c peroxidase enzymes.66 The electron paramagnetic resonance and electron nuclear double resonance experiments demonstrated that these two peroxidases exhibit a different electronic structure with the singly occupied nonbonding a1u/a2u orbital on the porphyrin ring (in ascorbate peroxidase) or on the adjacent Trp residue (in cytochrome c peroxidase).67,68 Computations suggested the radical character on the Trp was due to the presence of a single point charge at a distance of 8.7 Å from the Trp and a similar change in the electronic structure could be imparted or removed by applying an external electric field along the Fe–O bond.66 A prime example of electric fields affecting the reaction rate is observed in KSI, where a linear correlation has been observed experimentally (with the assistance of MD simulations) between the magnitude of the electric field experienced by the active site and the free energy of the reaction.53 Similarly, the QM/MM calculations of a non-heme 2-oxoglutarate (2OG)-dependent histone lysine demethylase KDM4E revealed that the energy barrier associated with the C–H hydrogen atom abstraction could be substantially lowered by applying a positive external electric field parallel to the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, thus enhancing the reaction kinetics.69 A positive external electric field here refers to an externally applied electric field that has a direction aligned with the direction of the flow of electrons.
O bond, thus enhancing the reaction kinetics.69 A positive external electric field here refers to an externally applied electric field that has a direction aligned with the direction of the flow of electrons.
Beyond their inherent influence on enzyme kinetics, electric fields also present an intriguing opportunity for targeted manipulation to control reaction selectivity.64 By adjusting electric fields, enzymes can be guided toward specific reaction pathways. For example, the local electric fields in ∼200 natural heme-iron oxygenases active sites were examined by Bím and Alexandrova in ref. 70. They have shown that the fields in these enzymes are not random and are preferentially oriented along the Fe–O axis of the supposed Cpd I intermediate. The orientation of the field showed an influence on the reactivity and selectivity of the Cpd I by modifying the oxyl-radical character of the Fe(IV)-oxido group. The authors have furthermore linked the magnitude and sign of the field with various protein functions; the largest positive local electric fields parallel to the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond were observed in the Cys-ligated heme-iron oxygenases, consistent with their highest reactivity in oxidation reactions. Fields of intermediate magnitudes were observed in the His-ligated heme-iron proteins, which are additionally oriented either in the positive or in the negative direction with respect to the Fe
O bond were observed in the Cys-ligated heme-iron oxygenases, consistent with their highest reactivity in oxidation reactions. Fields of intermediate magnitudes were observed in the His-ligated heme-iron proteins, which are additionally oriented either in the positive or in the negative direction with respect to the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, suggesting the higher tunability of the thermodynamic properties. In view of the peroxidases' subclass of His-ligated heme-iron proteins, successful correlation was observed between local electric fields in the active sites and the experimentally determined Cpd I reduction potentials. Finally, the lowest magnitude of the field with no preference for the orientation was observed in the Tyr-ligated heme-iron catalases. The lower magnitude is again consistent with their lower reactivity as compared to cytochromes P450. Another computational study on a non-heme 2OG dependent ethylene forming enzyme showed that the enzyme utilizes different intrinsic electric fields in the two L-Arg binding conformations, which are associated with distinct reactivity preferences.71 Importantly, the study also demonstrated that changes in the electric field of the enzyme could switch between the substrate L-Arg hydroxylation and ethylene forming reactivity of the enzyme. Finally, a study on the Fe(II)/2OG-dependent Ten-Eleven-Translocation-2 (TET2) enzyme demonstrated that clinical mutations related to cancers can influence the electric field along the reaction coordinate of the hydrogen atom transfer (HAT) reaction leading to a higher activation barrier and some mutations can even alter the orbital mechanism for the rate-limiting HAT reaction.72 These examples effectively illustrate the remarkable ability of enzymes to employ intrinsic fields in guiding and promoting the desired reactivity, showcasing the potential of leveraging this understanding for improved enzyme design.
O bond, suggesting the higher tunability of the thermodynamic properties. In view of the peroxidases' subclass of His-ligated heme-iron proteins, successful correlation was observed between local electric fields in the active sites and the experimentally determined Cpd I reduction potentials. Finally, the lowest magnitude of the field with no preference for the orientation was observed in the Tyr-ligated heme-iron catalases. The lower magnitude is again consistent with their lower reactivity as compared to cytochromes P450. Another computational study on a non-heme 2OG dependent ethylene forming enzyme showed that the enzyme utilizes different intrinsic electric fields in the two L-Arg binding conformations, which are associated with distinct reactivity preferences.71 Importantly, the study also demonstrated that changes in the electric field of the enzyme could switch between the substrate L-Arg hydroxylation and ethylene forming reactivity of the enzyme. Finally, a study on the Fe(II)/2OG-dependent Ten-Eleven-Translocation-2 (TET2) enzyme demonstrated that clinical mutations related to cancers can influence the electric field along the reaction coordinate of the hydrogen atom transfer (HAT) reaction leading to a higher activation barrier and some mutations can even alter the orbital mechanism for the rate-limiting HAT reaction.72 These examples effectively illustrate the remarkable ability of enzymes to employ intrinsic fields in guiding and promoting the desired reactivity, showcasing the potential of leveraging this understanding for improved enzyme design.
3.2 Utilization of second coordination sphere interactions
The FCS residues, which directly coordinate the metal are not the only decisive contributors to metalloenzymes reactivity. In fact, FCS residues are often undifferentiated in a similar group of enzymes, providing the catalytic power for their reactivity, but they are unable to control the diverse regio- or chemoselectivity. For example, heme enzymes feature a heme moiety coordinated to the iron with four equatorial Fe–N bonds, an axial ligand (such as Cys, Tyr, or His) connecting the iron to the protein, and a variable distal ligand that interacts with the substrate.73 Similarly, many non-heme iron enzymes have an active site featuring a 2His-1Asp/Glu amino acid arrangement coordinated with iron along with cosubstrates/substrate coordination.74 Since these enzymes feature the equivalent active site coordination and geometry to catalyze various reactions, differences in chemical reactivity and substrate selectivity are primarily achieved through additional effects – in this case, mainly SCS interactions.10 In the context of metalloenzymes, the SCS pertains to the area encompassing the residues that have direct interactions with the metal's FCS. On the other hand, for enzymes lacking a metal center, this region could be described as encompassing the enzyme residues that directly engage with the residues constituting the enzyme's active site.Various mechanisms for how the SCS interactions can influence enzyme catalysis can be adopted,10,75–77 such as SCS interactions near the FCS can determine whether an enzyme is highly substrate-selective, preferentially catalyzes a specific stereochemical reaction, or accepts a broad spectrum of substrates for catalysis. The heme-iron enzyme, P450CAM, which is a cytochrome P450 isozyme, utilizes hydrophobic interactions from SCS residues Ile88, Leu252, Leu255, Ile403, and Val404 to selectively hydroxylate camphor at the C5 position with a preferred regio- and stereoselectivity.78 Similarly, a non-heme iron 2OG-dependent oxygenase prolyl-4-hydroxylase does not catalyze hydroxylation of proline residues at thermodynamically much weaker C–H bonds at C3 and C5 positions, but performs a regio- and stereospecific hydroxylation at the C4 position. Computational results indicate that this is because a Tyr140 residue in the SCS holds the substrate and ferryl oxidant in a specific orientation through a network of hydrogen bonding and π-stacking interactions.79 In contrast, P450 isozymes P4502D6 and P4503A4 have oriented SCS residues such that they have large substrate binding pockets that can bind substrates of varying shapes and sizes.
Interactions of the SCS residues with the substrate/cosubstrate can also dictate their binding orientation and, therefore, the class of the reactions and the order in which they are performed by the enzyme. For example, QM calculations on models of non-heme iron lysine demethylase in the absence of the SCS residues indicated that ferryl could abstract a hydrogen atom from a dimethylated lysine substrate either from a methyl or an ‘NH’ group, and the hydroxylation mechanism can thus proceed either through a formation of a hydroxymethylaminium or an iminium intermediate.80 However, results from MD simulations of ferryl and subsequent QM/MM reaction mechanism calculations on PHF8, a non-heme iron 2OG-dependent histone lysine demethylase from class 7, indicated that the nearby SCS Ile191 locks the substrate in a conformation that makes a hydrogen atom abstraction from N–H unfeasible (Fig. 3).81 The SCS residues in PHF8 thus control the reaction path invoked by the enzyme. Similarly, a non-heme iron deoxygenase EgtB enzyme, with its 3-His residues, coordinates with the substrates γ-glutamyl Cys and N-α-trimethyl His to catalyze the C–S bond formation between them. QM cluster calculations on EgtB revealed that the O–S bond is formed before the C–S bond during the catalytic process.82 However, the QM/MM calculations with full protein residues showed that a proton-coupled electron transfer involving a conserved Tyr377 residue leads to an initial C–S bond formation and almost barrierless sulfoxidation.83 In another example, QM/MM calculations on a non-heme iron 2OG-dependent ethylene forming enzyme indicated an alternative binding mode of the cosubstrate 2OG with iron, which leads to an unusual decomposition of 2OG to ethylene plus three molecules of CO2/bicarbonate.84–86 The unusual binding mode of 2OG is supported by a salt–bridge interaction by SCS Arg171 with the carboxylate moiety of 2OG and mutation of Arg171 which is shown to affect the catalysis of the enzyme.84,85
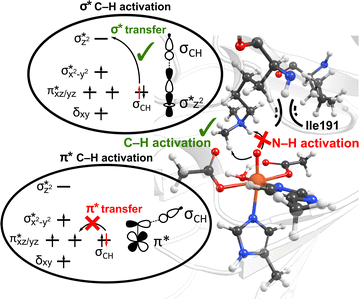 | ||
| Fig. 3 The SCS residue Ile191 in PHF8 enzyme orients the dimethylated lysine substrate in a conformation that facilitates C–H activation rather than hydrogen atom abstraction from N–H group. Additionally, the substrate positioning using Ile191 residue contributes to the preferential C–H activation via the end-on σ* hydrogen atom transfer pathway as opposed to the side-on π* approach.81 | ||
Interestingly, perturbations in the SCS have also been shown to affect the ordering of the energetically close-lying electronic states in the heme and non-heme enzymes. The hybrid QM/MM calculations on PHF8 have indicated that the substitutions in the SCS sphere and even long-range interacting residues in remote areas of the protein can affect the orbital mechanism of electron transfer during the HAT rate-limiting reaction step.75 Earlier QM/MM calculations on WT PHF8 indicated that the native enzyme preferentially transfers the electron in hydrogen atom transfer through a σ* electron transfer pathway which involves the transfer of an alpha electron from the substrate bonding orbital to the Fe dz2 orbital.81 The preferential σ* electron transfer pathway in WT PHF8 is attributed to the strict orientation of the substrate maintained due to interactions with the SCS residues, including Ile191 (Fig. 3). Upon variation of Ile191 to Ala, the QM/MM calculations indicated the modified enzyme could transfer the electron in hydrogen atom transfer through a π* electron transfer pathway.75 Additionally, the enhancement of the cross-coupling reaction of methacrylamide with 4-methoxystyrene was achieved using the artificial Rh(III) metalloenzyme via tuning the SCS. Using the combination of mutagenesis and quantum mechanics/discrete molecular dynamics (QM/DMD) calculations, the authors identified three key residues that contribute to reactivity through electronic communication to the metal site via the SCS residues' hydrogen-bonding interactions.87 At last, a study applying a combination of QM/MM and MD methods on two Fe(II)/2OG-dependent histone demethylases from class 6 (KDM6A and KDM6B) is another example of the modulating effect of the SCS on the enzyme reactivity.88 The Energy Decomposition Analysis89,90 found that in KDM6A the Trp369 residue is involved in the TS stabilization of the HAT reaction, whereas in KDM6B, the Asp291 residue is involved. Differences in hydrogen bonding of the Fe-chelating Glu252 in KDM6B with the SCS contribute to the lower energy barriers in KDM6B vs. KDM6A.88
3.3 Enhancement of important enzyme motions
The dynamic nature of enzymes allows them to undergo conformational changes, which are critical for substrate/cosubstrate diffusion and binding, catalysis, product release, or facilitating the transfer of chemical groups, electrons, or protons during catalysis, as such enabling proteins to perform diverse biological functions with remarkable precision and efficiency.91,92 The investigation of long-range collective correlated motions in enzymes has garnered significant interest both from a fundamental scientific perspective and as potential tools for enzyme regulation.93–98 Conformational changes are often facilitated by the protein's inherent flexibility and responsiveness to different stages of enzyme catalyzed reaction cycles. For instance, in KSI, the conformational dynamics of residues distant from the active site induce significant fluctuations in the electric field, contributing to the catalytic step and the release of the product.63Building on this concept, it is worth noting that certain proteins exhibit an exceptional ability to alter their conformations in response to allosteric requirements. As an example, cytochrome P450CAM exhibits a dynamic behavior characterized by multiple conformations with low structural fluctuations in the absence of substrate binding.99 However, upon binding a substrate, the enzyme undergoes a conformational selection process, prioritizing a specific conformation that is optimal for catalysis. Furthermore, P450CAM leverages motion on the hundreds of picosecond timescales to differentially process each of its substrates. This ability to modulate its conformation and dynamics in response to substrate binding highlights the enzyme's adaptability and fine-tuned control over its catalytic activity. A computational analysis of PHF8, a non-heme 2OG dependent lysine demethylase, reveals that when PHF8 is required to hydroxylate the histone substrate as part of its catalytic process, the enzyme employs motions of distant alpha helices to induce compression of the active site.81 This conformational change facilitates tighter binding between the substrate and the enzyme, thereby enhancing the efficiency of the hydroxylation reaction.
Nature has also ingeniously shaped enzymes to harness the power of molecular vibrations. These can range from rapid localized motions near the active site to large-scale correlated movements throughout the enzyme structure and may play a pivotal role in enhancing catalytic activity. The importance of long-range correlated motions could be again demonstrated through studies on PHF8. Although the Phe279 residue in PHF8 is distant from the enzyme's Fe center, its mutation to Ser entirely eliminates the enzyme's activity.100,101 Computational analysis of protein motion revealed that the Phe279 residue is involved in a network of correlated motion connected to the Fe reaction center.81 Alterations in this correlated network substantially increase the activation barriers of the rate-limiting HAT reaction catalyzed by PHF8.75 In KDM6 an anti-correlated motion of the Zn-binding domain with the active site is a key factor distinguishing class 6 KDM enzymes from classes 4 and 7.88 A study on a Fe(II)/2OG dependent DNA modifying enzyme TET2 demonstrates that a correlated motion between the main structural elements in TET2, the glycine–serine linker, and the Cys-rich N-terminal subdomain, plays a vital role in the positioning of the DNA substrate in the WT TET2, and is affected by diseases-related mutations in the enzyme.72 In another example on thermophilic alcohol dehydrogenase, rate measurements revealed that at lower temperatures (below 30 °C), the enzyme structure becomes more rigid, resulting in an increased activation energy.102 A computational model incorporating the reaction coordinates for the rate-determining step, enzymatic environment, and a specific strongly coupled active complex mode can accurately replicate the observed experimental trends.103 Analysis of the computational model suggested protein's particular internal motion acts as the rate-promoting vibration (Fig. 4).
 | ||
| Fig. 4 The vibrational motion in the human heart lactate dehydrogenase (LDH) promotes the reversible interconversion of lactate to pyruvate with nicotinamide adenine dinucleotide (NAD) as a cofactor. The productive protein motion is oriented along the hydride donor/acceptor axis, enhancing the rate of hydride transfer.104 | ||
Protein conformational dynamics is also shown to be essential in regulating the entry of substrate/cosubstrate into the active site, as well as for the subsequent release of the product upon reaction completion. To give an example, in the catalytic cycle of Escherichia coli dihydrofolate reductase (ecDHFR), the enzyme uses several low-energy excited state conformations to facilitate the exchange of substrate and cofactor.105 Mutated versions of ecDHFR that eliminate these protein motions without altering its structural and electrostatic preorganization, significantly impede the hydride transfer process.106,107 Similarly, the substitution of the flexible loop 1 in ribonuclease A (RNase A) results in the absence of NMR-detected millisecond motions in several flexible residues, in contrast to the WT enzyme. This loss of critical enzyme dynamics is found to have a substantial impact on the catalytic cycle, as evidenced by a 10-fold reduction in the product release rate constant.108 Collectively, these studies underscore the diverse ways in which proteins leverage dynamics to ultimately carry out effective catalysis.
As exemplified on a few proteins that were discussed throughout more than one category in Section 3 (e.g., PHF8, KSI, P450cam), it is important to note that the highlighted factors can exhibit interdependencies. For example, altering protein conformation can affect the local electric field within the active site. The SCS structure is indirectly influenced by the entire protein structure and dynamics, as well as the action in the active site itself. Dynamics of the protein, and especially SCS amino acids will cause dynamic fluctuations of the electric field in the active site, which in turn can either promote or inhibit catalysis. Thus, segregating the factors that impact enzymatic catalysis may appear somewhat artificial, but it can also be helpful in terms of tuning individual effects in enzyme design through rationalizable and physically meaningful means. Also, the discussed principles have mostly focused on metalloenzymes, their applicability to non-metal enzymes requires careful consideration due to potential variations in reaction mechanisms and catalytic strategies.
4. Relevance in enzyme design
In this section, we delve into the practical applications of enzyme design, showcasing how electric field, SCS interactions and protein dynamics can be harnessed to enhance enzyme performance. Building on the successful examples from recent studies, we illustrate the potential of these strategies to create more efficient designed enzymes.4.1 Case study 1: electric field optimization
The de novo Kemp eliminase enzyme KE15, designed using the standard Rosetta protocol, featured an active site centered around the catalytic base Asp48, and the Tyr126 π-stacking residue for the substrate orientation, and was integrated into a TIM barrel scaffold. Experiments revealed that the designed enzyme has a kcat = 0.007 s−1 and KM = 270 μM (kcat/KM of 27 M−1 s−1).30 In an effort to boost the efficiency of KE15, Vaissier et al. developed a computational screening approach.109 This involved short MD simulations with the polarizable AMOEBA force field to identify potentially advantageous mutations, aimed specifically at augmenting the electric field of the enzyme (Fig. 5, top). The authors' aim was to pinpoint potential mutations that could stabilize the TS through more effective electric fields at the bonds undergoing chemical transformation. The calculations assessing the electric field contributions of each residue within the KE15 sequence revealed that Asp130—located at the bottom of the TIM barrel and far from the substrate—contributed the most significant negative electric field (E = –7.29 MV cm−1) when projected onto the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond of the substrate. The authors reasoned that if a negatively charged Asp is causing destabilization of the TS, substituting it with a neutral amino acid such as Asn or a positively charged one such as Lys could potentially enhance its stabilization. This hypothesis was confirmed through both computations and experiments, leading to Asp130Lys variant of the enzyme with an experimentally measured kcat/KM value of 59 M−1 s−1. The majority of this improvement originated from a 4- to 5-fold increase in kcat.
N bond of the substrate. The authors reasoned that if a negatively charged Asp is causing destabilization of the TS, substituting it with a neutral amino acid such as Asn or a positively charged one such as Lys could potentially enhance its stabilization. This hypothesis was confirmed through both computations and experiments, leading to Asp130Lys variant of the enzyme with an experimentally measured kcat/KM value of 59 M−1 s−1. The majority of this improvement originated from a 4- to 5-fold increase in kcat.
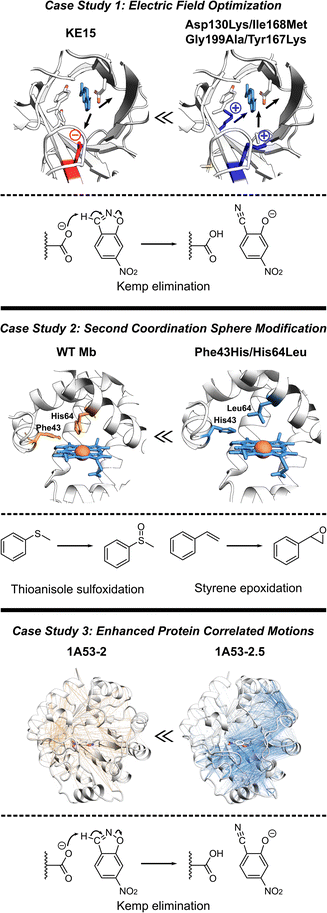 | ||
| Fig. 5 Various strategies for enhancing proteins performance discussed in this section. (Top) The optimization of internal electric fields of KE15 allowed for a 43-fold improvement of kcat for Kemp elimination reaction.109 (Middle) Protein engineering of the wild-type myoglobin afforded an improved peroxidase activity in double mutant Phe43His/His64Leu due to relocation of a distal His. The double mutant can oxidize various organic substrates and hydrogen peroxide.110 (Bottom) The computationally designed Kemp eliminase 1A53-2 was further improved by directed evolution. The evolved variant 1A53-2.5 demonstrated a 104-fold increase in kcat/kM due to enhanced correlated network and reduced fluctuations in the TS, responsible for TS stabilization.111 | ||
Observing that the individual residue projections of electric fields onto the substrate bonds of the Asp130Lys mutant enzyme did not yield considerable negative contributions, the authors confined their further exploration to identify locations for mutations closer to the active site, where the greatest electrostatic effects are expected. Subsequent computations exposed that Ile168, despite being a neutral active site residue, still contains partially charged atoms that negatively influence the electric field at the TS. However, its impact was relatively small, with values of E = –1.67 and –2.97 MV cm−1 on the bonds crucial for catalysis. Experimentally, the Ile168Met variant demonstrated enhanced activity, but the improvement was primarily reflected in KM, indicating a refinement in substrate binding rather than catalytic efficiency. Consistent with these findings, computational analyses suggested that this mutation decreases the size of the active site, thereby reducing the distance between the oxygen atom of the base and the hydrogen atom of the substrate. Additional examination also demonstrated a positive link between the strength of the electric field on the bonds critical to catalysis and the proximity of substrate binding. Consequently, a tighter substrate binding was attempted through Gly199Ala mutation, diminishing the gap between the substrate and the base and providing a significant surge in the electric field on the bonds critical for catalysis. However, at such short distances, electric fields are arguably only one (classical) part of interaction, rest being part of the QM wave function. In experiments, the Gly199Ala mutation demonstrated enhanced performance, with a notable rise in kcat and only a minimal increment in KM. In the final phase of mutagenesis, a new active-site residue, Tyr167, was identified. It was characterized by a negative contribution to the electric field (E = –3.04 MV cm−1), and hence, was replaced with Lys. Experimental results indicated that the combination of these four mutations (Asp130Lys, Ile168Met, Gly199Ala, Tyr167Lys) led to the most efficient performance to date. It resulted in a 43-fold improvement in kcat compared to the KE15 design and an overall efficiency of 403 M−1 s−1. Overall, the case study emphasizes the effectiveness of electric field optimization as a potent strategy for boosting catalytic efficiency in enzyme designs.
4.2 Case study 2: showcasing effective second coordination sphere engagement
Recent studies have established Myoglobin (Mb) as an exemplary case, demonstrating how alterations to the SCS residues can serve for engineering catalysis of non-native reactions (Fig. 5, middle).112 For instance, WT Mb demonstrates significantly lower peroxidase activity compared to native peroxidases, specifically, 2.7 M−1 s−1versus 130 M−1 s−1.113 Despite both peroxidases and Mb having a His residue in the distal pocket (His64 in Mb and His52 in cytochrome c peroxidase, CcP), the distal His in Mb is positioned closer to the Fe compared to that in CcP.114,115 By relocating the distal His residue in Mb through a double mutation (Phe43His/His64Leu), the Watanabe group managed to engineer a version of Mb whose catalytic rates for sulfoxidation and epoxidation were on par with those of native CcP.110 Similarly, merging the SCS features of chloroperoxidase (distal Glu) and DHP (distal Tyr), Yin et al. generated a Phe43Tyr/His64Asp Mb mutant, which led to a 1000-fold improvement in catalytic efficiency when compared to the native DHP from A. ornate.116Adjusting the steric bulk around the active site of Mb allowed for its redesign for a variety of reactions. The expansion of the distal cavity through a Val68Ala mutation, combined with enhanced substrate access to heme via a His64Val mutation, enabled the modified Mb to efficiently catalyze the cyclopropanation of styrene with ethyl diazoacetate, exhibiting high selectivity.21 This His64Val/Val68Ala Mb variant also displayed promising reactivity for C–H functionalization of indole at the C3 position117 and showed activity toward carbene N–H insertion with arylamine substrates, although the yield for N-methyl aniline remained relatively low.118 Enhancing the active site volume above the heme iron site through Lys29Ala mutation improved this reactivity.118 These findings highlight successful instances where SCS residues can be altered in a protein scaffold to adapt the enzyme for non-native catalysis on novel substrates. In summary, these investigations underscore the potential of manipulating the SCS environment as a means to fine-tune enzyme design.
4.3 Case study 3: illustrating enhanced protein motion
In another study, the computationally designed Kemp eliminase 1A53-2 was subjected to directed evolution.119 This process resulted in a 104-fold increase in its kcat/KM, achieved by introducing six mutations during the optimization of first-shell residues. The evolved variant, known as 1A53-2.5, demonstrated an improved shape complementarity with a TS analog. In addition, this evolved variant displayed a negative heat capacity, a phenomenon hypothesized to be a thermodynamic reflection of the structural modifications that took place during its evolution. Bunzel et al. performed MD simulations to probe the emergence of this thermodynamic effect.111 The authors conducted 5 μs of MD simulations for both the designed and evolved variants. These simulations were conducted with the variants in complex with the substrate either in the GS or the TS. The comparison of MD simulations revealed substantially different dynamical responses between the GS and TS. Particularly, the energy distribution of 1A53-2.5 was considerably more constricted in the TS compared to the GS. This analysis suggested that the appearance of a negative heat capacity in measurements signifies a reduction in energy fluctuations in the TS ensemble compared to those in the GS complex. Additionally, atomistic analysis of the MD simulations revealed that the process of evolution made several important modifications in the protein structure. These include the introduction of space-filling mutations such as Ala157Tyr and Leu184Phe, leading to improved packing of the active site, the expulsion of water from the active site upon loop closure, and more importantly a shift in the open–closed equilibrium towards the closed state.To delve deeper into the factors contributing to a less flexible TS ensemble, the authors explored alterations in dynamically correlated movements (Fig. 5, bottom). These movements establish a connection between the local active site and the broader protein scaffold in both the GS and TS ensembles. In the closed state, favored by the evolved variant 1A53-2.5, correlated motion is much more intense in the TS ensemble than in the GS ensemble. The increase in correlated motion in the TS ensemble correlates with the tightening of the TS ensemble and a negative activation heat capacity. Shortest path maps were then used to analyze the path through which these correlated motions were communicating to other parts of the protein scaffold. Only two mutations introduced during evolution are directly involved in this network. Gln211Gly increases flexibility and potentially tunes the dynamic response of the scaffold, whereas Leu184Phe enhances packing by connecting neighboring solvent-exposed loops. The analysis thus indicated that evolution introduced a dynamical network that centers on the substrate and spans the protein. This case study, therefore, illustrates the potential of harnessing increased correlated protein motion as a critical design factor. This strategy helps lock the enzyme into a conformation conducive to catalysis, thereby improving overall enzymatic performance.
5. Future prospects
The horizon of enzyme design brims with potential, but to fully harness the efficiency and productivity of these strategies, the trajectory necessitates further advancements in methodologies that seamlessly integrate the principles of electric fields and scaffold dynamics. While strides have been made, the journey ahead involves unraveling the precise amino acid mutations required to imbue enzymes with desired electric fields. Questions linger: which amino acids to modify, and to what extent, to impart the desired electric field? Solving this intricate puzzle can ultimately guide the precision engineering of enzymes to harbor tailored electrostatic landscapes. Similarly, the realm of enzyme dynamics unveils another frontier, demanding methods that adeptly incorporate catalytically advantageous enzyme motions, into the designed structures. Moving forward, enzyme design strategies must effectively embrace enzyme motion, tapping into its latent potential for enhanced catalysis while maintaining the delicate balance between flexibility and stability.In the pursuit of more effective enzyme design, the integration of intrinsic electric fields, SCS interactions, and conformational dynamics with other computational approaches, such as machine learning, offers a promising avenue for exploration. Machine learning algorithms can help identify patterns and relationships within large datasets, potentially uncovering new design strategies that were previously overlooked. For example, machine learning was combined with directed evolution to learn information from unimproved sequences, and this information has been used to expedite evolution and intelligently expand the number of properties for optimization.120 Recent advancements such as ProteinMPNN, based on deep learning, have successfully revived challenging protein designs that had previously faced setbacks when created using Rosetta or Alphafold.121–123 Deep learning methods have also improved energy-based protein binder design by assessing the compatibility of the designed enzyme with the target monomer structure.124 Furthermore, these techniques have been employed to generate starting scaffolds in the design of efficient luciferase enzymes from scratch.125 Combination of these powerful tools can assist researchers in developing a more holistic approach to enzyme design, ultimately informed by the SCS interactions, electric field properties, and the conformational dynamics of the enzyme itself.
To further enhance the accuracy and efficiency of enzyme design protocols, a synergistic approach that integrates both computational and experimental techniques is essential. Complementary experimental methods, such as X-ray crystallography, cryo-electron microscopy, nuclear magnetic resonance spectroscopy, EPR, magnetic circular dichroism, and X-ray absorption spectroscopy, can provide accurate structural and dynamics data to validate computational models.126 Such validated computational tools can explore structures and properties that can hardly be explored experimentally, thus guiding and informing experimental design. By working in tandem, these approaches can help researchers to gain a deeper understanding of enzyme mechanisms and streamline the design process. Such collaborative strategy promises to push the boundaries of enzyme design, paving the way for the development of novel biocatalysts with unprecedented capabilities.
Author contributions
All authors developed ideas that resulted in this manuscript, S. S. C. and D. B. wrote the manuscript, all authors edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the NSF-CHE grant 2203366 and NIH-NIGMS grant R01GM134047 to A. N. A. C. Z. C. acknowledges NIH-NIGMS grant 1R15GM139118 and NSF-CHE grant 2203630.References
- R. Wolfenden and M. J. Snider, The Depth of Chemical Time and the Power of Enzymes as Catalysts, Acc. Chem. Res., 2001, 34(12), 938–945, DOI:10.1021/ar000058i.
- E. M. J. Gillam and F. P. Guengerich, Exploiting the Versatility of Human Cytochrome P450 Enzymes: The Promise of Blue Roses From Biotechnology, IUBMB Life, 2001, 52(6), 271–277, DOI:10.1080/152165401317291110.
- N. P. Dunham and F. H. Arnold, Nature's Machinery, Repurposed: Expanding the Repertoire of Iron-Dependent Oxygenases, ACS Catal., 2020, 10(20), 12239–12255, DOI:10.1021/acscatal.0c03606.
- R. M. Bullock, J. G. Chen, L. Gagliardi, P. J. Chirik, O. K. Farha, C. H. Hendon, C. W. Jones, J. A. Keith, J. Klosin, S. D. Minteer, R. H. Morris, A. T. Radosevich, T. B. Rauchfuss, N. A. Strotman, A. Vojvodic, T. R. Ward, J. Y. Yang and Y. Surendranath, Using Nature's Blueprint to Expand Catalysis with Earth-Abundant Metals, Science, 2020, 369(6505), eabc3183, DOI:10.1126/science.abc3183.
- K. D. Miner, A. Mukherjee, Y.-G. Gao, E. L. Null, I. D. Petrik, X. Zhao, N. Yeung, H. Robinson and Y. Lu, A Designed Functional Metalloenzyme That Reduces O2 to H2O with Over One Thousand Turnovers, Angew. Chem., Int. Ed., 2012, 51(23), 5589–5592, DOI:10.1002/anie.201201981.
- S. I. Mann, A. Nayak, G. T. Gassner, M. J. Therien and W. F. DeGrado, De Novo Design, Solution Characterization, and Crystallographic Structure of an Abiological Mn–Porphyrin-Binding Protein Capable of Stabilizing a Mn(V) Species, J. Am. Chem. Soc., 2021, 143(1), 252–259, DOI:10.1021/jacs.0c10136.
- H. M. Key, P. Dydio, D. S. Clark and J. F. Hartwig, Abiological Catalysis by Artificial Haem Proteins Containing Noble Metals in Place of Iron, Nature, 2016, 534(7608), 534–537, DOI:10.1038/nature17968.
- J. Kraut, How Do Enzymes Work?, Science, 1988, 242(4878), 533–540, DOI:10.1126/science.3051385.
- M. Garcia-Viloca, J. Gao, M. Karplus and D. G. Truhlar, How Enzymes Work: Analysis by Modern Rate Theory and Computer Simulations, Science, 2004, 303(5655), 186–195, DOI:10.1126/science.1088172.
- S. P. de Visser, Second-Coordination Sphere Effects on Selectivity and Specificity of Heme and Nonheme Iron Enzymes, Chem.–Eur. J., 2020, 26(24), 5308–5327, DOI:10.1002/chem.201905119.
- A. Warshel, Electrostatic Origin of the Catalytic Power of Enzymes and the Role of Preorganized Active Sites, J. Biol. Chem., 1998, 273(42), 27035–27038, DOI:10.1074/jbc.273.42.27035.
- J. M. Yon, D. Perahia and C. Ghélis, Conformational Dynamics and Enzyme Activity, Biochimie, 1998, 80(1), 33–42, DOI:10.1016/S0300-9084(98)80054-0.
- V. C. Nashine, S. Hammes-Schiffer and S. J. Benkovic, Coupled Motions in Enzyme Catalysis, Curr. Opin. Chem. Biol., 2010, 14(5), 644–651, DOI:10.1016/j.cbpa.2010.07.020.
- E. Z. Eisenmesser, O. Millet, W. Labeikovsky, D. M. Korzhnev, M. Wolf-Watz, D. A. Bosco, J. J. Skalicky, L. E. Kay and D. Kern, Intrinsic Dynamics of an Enzyme Underlies Catalysis, Nature, 2005, 438(7064), 117–121, DOI:10.1038/nature04105.
- M. T. Reetz, What Are the Limitations of Enzymes in Synthetic Organic Chemistry?, Chem. Rec., 2016, 16(6), 2449–2459, DOI:10.1002/tcr.201600040.
- F. H. Arnold, Design by Directed Evolution, Acc. Chem. Res., 1998, 31(3), 125–131, DOI:10.1021/ar960017f.
- P. A. Romero and F. H. Arnold, Exploring Protein Fitness Landscapes by Directed Evolution, Nat. Rev. Mol. Cell Biol., 2009, 10(12), 866–876, DOI:10.1038/nrm2805.
- F. H. Arnold, Directed Evolution: Bringing New Chemistry to Life, Angew. Chem., Int. Ed., 2018, 57(16), 4143–4148, DOI:10.1002/anie.201708408.
- F. Nastri, D. D'Alonzo, L. Leone, G. Zambrano, V. Pavone and A. Lombardi, Engineering Metalloprotein Functions in Designed and Native Scaffolds, Trends Biochem. Sci., 2019, 44(12), 1022–1040, DOI:10.1016/j.tibs.2019.06.006.
- D. C. Miller, S. V. Athavale and F. H. Arnold, Combining Chemistry and Protein Engineering for New-to-Nature Biocatalysis, Nat. Synth., 2022, 1(1), 18–23, DOI:10.1038/s44160-021-00008-x.
- M. Bordeaux, V. Tyagi and R. Fasan, Highly Diastereoselective and Enantioselective Olefin Cyclopropanation Using Engineered Myoglobin-Based Catalysts, Angew. Chem., Int. Ed., 2015, 54(6), 1744–1748, DOI:10.1002/anie.201409928.
- M. Pott, M. Tinzl, T. Hayashi, Y. Ota, D. Dunkelmann, P. R. E. Mittl and D. Hilvert, Noncanonical Heme Ligands Steer Carbene Transfer Reactivity in an Artificial Metalloenzyme, Angew. Chem., Int. Ed., 2021, 60(27), 15063–15068, DOI:10.1002/anie.202103437.
- M. Davidson, M. McNamee, R. Fan, Y. Guo and W. Chang, Repurposing Nonheme Iron Hydroxylases To Enable Catalytic Nitrile Installation through an Azido Group Assistance, J. Am. Chem. Soc., 2019, 141(8), 3419–3423, DOI:10.1021/jacs.8b13906.
- N. W. Goldberg, A. M. Knight, R. K. Zhang and F. H. Arnold, Nitrene Transfer Catalyzed by a Non-Heme Iron Enzyme and Enhanced by Non-Native Small-Molecule Ligands, J. Am. Chem. Soc., 2019, 141(50), 19585–19588, DOI:10.1021/jacs.9b11608.
- G. Yang, C. M. Miton and N. Tokuriki, A Mechanistic View of Enzyme Evolution, Protein Sci., 2020, 29(8), 1724–1747, DOI:10.1002/pro.3901.
- J. A. Sigman, B. C. Kwok, A. Gengenbach and Y. Lu, Design and Creation of a Cu(II)-Binding Site in Cytochrome c Peroxidase That Mimics the Cu B -Heme Center in Terminal Oxidases, J. Am. Chem. Soc., 1999, 121(38), 8949–8950, DOI:10.1021/ja991195h.
- J. A. Sigman, B. C. Kwok and Y. Lu, From Myoglobin to Heme-Copper Oxidase: Design and Engineering of a Cu B Center into Sperm Whale Myoglobin, J. Am. Chem. Soc., 2000, 122(34), 8192–8196, DOI:10.1021/ja0015343.
- R. Stenner, J. W. Steventon, A. Seddon and J. L. R. Anderson, A de Novo Peroxidase Is Also a Promiscuous yet Stereoselective Carbene Transferase, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(3), 1419–1428, DOI:10.1073/pnas.1915054117.
- A. E. Donnelly, G. S. Murphy, K. M. Digianantonio and M. H. Hecht, A de Novo Enzyme Catalyzes a Life-Sustaining Reaction in Escherichia Coli, Nat. Chem. Biol., 2018, 14(3), 253–255, DOI:10.1038/nchembio.2550.
- D. Röthlisberger, O. Khersonsky, A. M. Wollacott, L. Jiang, J. DeChancie, J. Betker, J. L. Gallaher, E. A. Althoff, A. Zanghellini, O. Dym, S. Albeck, K. N. Houk, D. S. Tawfik and D. Baker, Kemp Elimination Catalysts by Computational Enzyme Design, Nature, 2008, 453(7192), 190–195, DOI:10.1038/nature06879.
- D. Baker, An Exciting but Challenging Road Ahead for Computational Enzyme Design, Protein Sci., 2010, 19(10), 1817–1819, DOI:10.1002/pro.481.
- A. Leaver-Fay; M. Tyka; S. M. Lewis; O. F. Lange; J. Thompson; R. Jacak; K. W. Kaufman; P. D. Renfrew; C. A. Smith; W. Sheffler; I. W. Davis; S. Cooper; A. Treuille; D. J. Mandell; F. Richter; Y.-E. A. Ban; S. J. Fleishman; J. E. Corn; D. E. Kim; S. Lyskov; M. Berrondo; S. Mentzer; Z. Popović; J. J. Havranek; J. Karanicolas; R. Das; J. Meiler; T. Kortemme; J. J. Gray; B. Kuhlman; D. Baker and P. BradleyRosetta3, in Methods in Enzymology, Elsevier, 2011, vol. 487, pp. 545–574, DOI:10.1016/B978-0-12-381270-4.00019-6.
- T. L. Coates, N. Young, A. J. Jarrett, C. J. Morris, J. D. Moody and D. D. Corte, Current Computational Methods for Enzyme Design, Mod. Phys. Lett. B, 2021, 35(9), 2150155, DOI:10.1142/S0217984921501554.
- G. Kiss, N. Çelebi-Ölçüm, R. Moretti, D. Baker and K. N. Houk, Computational Enzyme Design, Angew. Chem., Int. Ed., 2013, 52(22), 5700–5725, DOI:10.1002/anie.201204077.
- S. Osuna, The Challenge of Predicting Distal Active Site Mutations in Computational Enzyme Design, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11(3), e1502, DOI:10.1002/wcms.1502.
- S. L. Lovelock, R. Crawshaw, S. Basler, C. Levy, D. Baker, D. Hilvert and A. P. Green, The Road to Fully Programmable Protein Catalysis, Nature, 2022, 606(7912), 49–58, DOI:10.1038/s41586-022-04456-z.
- P.-S. Huang, S. E. Boyken and D. Baker, The Coming of Age of de Novo Protein Design, Nature, 2016, 537(7620), 320–327, DOI:10.1038/nature19946.
- K. Świderek, I. Tuñón, V. Moliner and J. Bertran, Computational Strategies for the Design of New Enzymatic Functions, Arch. Biochem. Biophys., 2015, 582, 68–79, DOI:10.1016/j.abb.2015.03.013.
- I. V. Korendovych and W. F. DeGrado, Catalytic Efficiency of Designed Catalytic Proteins, Curr. Opin. Struct. Biol., 2014, 27, 113–121, DOI:10.1016/j.sbi.2014.06.006.
- D. Bím, M. Navrátil, O. Gutten, J. Konvalinka, Z. Kutil, M. Culka, V. Navrátil, A. N. Alexandrova, C. Bařinka and L. Rulíšek, Predicting Effects of Site-Directed Mutagenesis on Enzyme Kinetics by QM/MM and QM Calculations: A Case of Glutamate Carboxypeptidase II, J. Phys. Chem. B, 2022, 126(1), 132–143, DOI:10.1021/acs.jpcb.1c09240.
- H. A. Bunzel, J. L. R. Anderson and A. J. Mulholland, Designing Better Enzymes: Insights from Directed Evolution, Curr. Opin. Struct. Biol., 2021, 67, 212–218, DOI:10.1016/j.sbi.2020.12.015.
- B. D. P. Mariz, S. Carvalho, I. L. Batalha and A. S. Pina, Artificial Enzymes Bringing Together Computational Design and Directed Evolution, Org. Biomol. Chem., 2021, 19(9), 1915–1925, 10.1039/D0OB02143A.
- A. Broom, R. V. Rakotoharisoa, M. C. Thompson, N. Zarifi, E. Nguyen, N. Mukhametzhanov, L. Liu, J. S. Fraser and R. A. Chica, Ensemble-Based Enzyme Design Can Recapitulate the Effects of Laboratory Directed Evolution in Silico, Nat. Commun., 2020, 11(1), 4808, DOI:10.1038/s41467-020-18619-x.
- T. R. Ward, Artificial Enzymes Made to Order: Combination of Computational Design and Directed Evolution, Angew. Chem., Int. Ed., 2008, 47(41), 7802–7803, DOI:10.1002/anie.200802865.
- E. C. Campbell, G. J. Correy, P. D. Mabbitt, A. M. Buckle, N. Tokuriki and C. J. Jackson, Laboratory Evolution of Protein Conformational Dynamics, Curr. Opin. Struct. Biol., 2018, 50, 49–57, DOI:10.1016/j.sbi.2017.09.005.
- L. Giger, S. Caner, R. Obexer, P. Kast, D. Baker, N. Ban and D. Hilvert, Evolution of a Designed Retro-Aldolase Leads to Complete Active Site Remodeling, Nat. Chem. Biol., 2013, 9(8), 494–498, DOI:10.1038/nchembio.1276.
- R. Crawshaw, A. E. Crossley, L. Johannissen, A. J. Burke, S. Hay, C. Levy, D. Baker, S. L. Lovelock and A. P. Green, Engineering an Efficient and Enantioselective Enzyme for the Morita–Baylis–Hillman Reaction, Nat. Chem., 2022, 14(3), 313–320, DOI:10.1038/s41557-021-00833-9.
- M. Corbella, G. P. Pinto and S. C. L. Kamerlin, Loop Dynamics and the Evolution of Enzyme Activity, Nat. Rev. Chem, 2023, 1–12, DOI:10.1038/s41570-023-00495-w.
- A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. Liu and M. H. M. Olsson, Electrostatic Basis for Enzyme Catalysis, Chem. Rev., 2006, 106(8), 3210–3235, DOI:10.1021/cr0503106.
- S. D. Fried and S. G. Boxer, Electric Fields and Enzyme Catalysis, 2017 Search PubMed.
- M. R. Hennefarth and A. N. Alexandrova, Advances in Optimizing Enzyme Electrostatic Preorganization, Curr. Opin. Struct. Biol., 2022, 72, 1–8, DOI:10.1016/j.sbi.2021.06.006.
- N. G. Léonard, R. Dhaoui, T. Chantarojsiri and J. Y. Yang, Electric Fields in Catalysis: From Enzymes to Molecular Catalysts, ACS Catal., 2021, 11(17), 10923–10932, DOI:10.1021/acscatal.1c02084.
- S. D. Fried, S. Bagchi and S. G. Boxer, Extreme Electric Fields Power Catalysis in the Active Site of Ketosteroid Isomerase, Science, 2014, 346(6216), 1510–1514, DOI:10.1126/science.1259802.
- R. Meir, H. Chen, W. Lai and S. Shaik, Oriented Electric Fields Accelerate Diels–Alder Reactions and Control the Endo/Exo Selectivity, ChemPhysChem, 2010, 11(1), 301–310, DOI:10.1002/cphc.200900848.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Electrostatic Catalysis of a Diels–Alder Reaction, Nature, 2016, 531(7592), 88–91, DOI:10.1038/nature16989.
- B. Zhang, C. Schaack, C. R. Prindle, E. A. Vo, M. Aziz, M. L. Steigerwald, T. C. Berkelbach, C. Nuckolls and L. Venkataraman, Electric Fields Drive Bond Homolysis, Chem. Sci., 2023, 14(7), 1769–1774, 10.1039/D2SC06411A.
- I. B. Stone, R. L. Starr, N. Hoffmann, X. Wang, A. M. Evans, C. Nuckolls, T. H. Lambert, M. L. Steigerwald, T. C. Berkelbach, X. Roy and L. Venkataraman, Interfacial Electric Fields Catalyze Ullmann Coupling Reactions on Gold Surfaces, Chem. Sci., 2022, 13(36), 10798–10805, 10.1039/D2SC03780G.
- N. M. Orchanian, S. Guizzo, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Electric-Field-Induced Coupling of Aryl Iodides with a Nickel(0) Complex, Chem. Commun., 2022, 58(90), 12556–12559, 10.1039/D2CC03671A.
- J. P. Layfield and S. Hammes-Schiffer, Calculation of Vibrational Shifts of Nitrile Probes in the Active Site of Ketosteroid Isomerase upon Ligand Binding, J. Am. Chem. Soc., 2013, 135(2), 717–725, DOI:10.1021/ja3084384.
- X. Wang and X. He, An Ab Initio QM/MM Study of the Electrostatic Contribution to Catalysis in the Active Site of Ketosteroid Isomerase, Molecules, 2018, 23(10), 2410, DOI:10.3390/molecules23102410.
- S. D. Fried, L.-P. Wang, S. G. Boxer, P. Ren and V. S. Pande, Calculations of the Electric Fields in Liquid Solutions, J. Phys. Chem. B, 2013, 117(50), 16236–16248, DOI:10.1021/jp410720y.
- J. Fuller, T. R. Wilson, M. E. Eberhart and A. N. Alexandrova, Charge Density in Enzyme Active Site as a Descriptor of Electrostatic Preorganization, J. Chem. Inf. Model., 2019, 59(5), 2367–2373, DOI:10.1021/acs.jcim.8b00958.
- V. V. Welborn and T. Head-Gordon, Fluctuations of Electric Fields in the Active Site of the Enzyme Ketosteroid Isomerase, J. Am. Chem. Soc., 2019, 141(32), 12487–12492, DOI:10.1021/jacs.9b05323.
- Effects of Electric Fields on Structure and Reactivity: New Horizons in Chemistry, Theoretical and Computational Chemistry, ed. S. S. Shaik and T. Stuyver, Royal Society of Chemistry, Cambridge, 2021 Search PubMed.
- W. Lai, H. Chen, K.-B. Cho and S. Shaik, External Electric Field Can Control the Catalytic Cycle of Cytochrome P450cam: A QM/MM Study, J. Phys. Chem. Lett., 2010, 1(14), 2082–2087, DOI:10.1021/jz100695n.
- S. P. de Visser, What Affects the Quartet−Doublet Energy Splitting in Peroxidase Enzymes?, J. Phys. Chem. A, 2005, 109(48), 11050–11057, DOI:10.1021/jp053873u.
- M. Sivaraja, D. B. Goodin, M. Smith and B. M. Hoffman, Identification by ENDOR of Trp191 as the Free-Radical Site in Cytochrome c Peroxidase Compound ES, Science, 1989, 245(4919), 738–740, DOI:10.1126/science.2549632.
- J. E. Huyett, P. E. Doan, R. Gurbiel, A. L. P. Houseman, M. Sivaraja, D. B. Goodin and B. M. Hoffman, Compound ES of Cytochrome c Peroxidase Contains a Trp.Pi.-Cation Radical: Characterization by Continuous Wave and Pulsed Q-Band External Nuclear Double Resonance Spectroscopy, J. Am. Chem. Soc., 1995, 117(35), 9033–9041, DOI:10.1021/ja00140a021.
- R. Ramanan, S. O. Waheed, C. J. Schofield and C. Z. Christov, What Is the Catalytic Mechanism of Enzymatic Histone N-Methyl Arginine Demethylation and Can It Be Influenced by an External Electric Field?, Chem.–Eur. J., 2021, 27(46), 11827–11836, DOI:10.1002/chem.202101174.
- D. Bím and A. N. Alexandrova, Local Electric Fields As a Natural Switch of Heme-Iron Protein Reactivity, ACS Catal., 2021, 11(11), 6534–6546, DOI:10.1021/acscatal.1c00687.
- S. S. Chaturvedi, S. B. Jaber Sathik Rifayee, R. Ramanan, J. A. Rankin, J. Hu, R. P. Hausinger and C. Z. Christov, Can an External Electric Field Switch between Ethylene Formation and l -Arginine Hydroxylation in the Ethylene Forming Enzyme?, Phys. Chem. Chem. Phys., 2023, 25(19), 13772–13783, 10.1039/D3CP01899G.
- S. O. Waheed, S. S. Chaturvedi, T. G. Karabencheva-Christova and C. Z. Christov, Catalytic Mechanism of Human Ten-Eleven Translocation-2 (TET2) Enzyme: Effects of Conformational Changes, Electric Field, and Mutations, ACS Catal., 2021, 11(7), 3877–3890, DOI:10.1021/acscatal.0c05034.
- T. L. Poulos, Heme Enzyme Structure and Function, Chem. Rev., 2014, 114(7), 3919–3962, DOI:10.1021/cr400415k.
- 2-Oxoglutarate-Dependent Oxygenases, ed. C. Schofield and R. Hausinger, Metallobiology, Royal Society of Chemistry, Cambridge, 2015, 10.1039/9781782621959.
- S. S. Chaturvedi, S. B. Jaber Sathik Rifayee, S. O. Waheed, J. Wildey, C. Warner, C. J. Schofield, T. G. Karabencheva-Christova and C. Z. Christov, Can Second Coordination Sphere and Long-Range Interactions Modulate Hydrogen Atom Transfer in a Non-Heme Fe(II)-Dependent Histone Demethylase?, JACS Au, 2022, 2(9), 2169–2186, DOI:10.1021/jacsau.2c00345.
- S. Bhunia, A. Ghatak and A. Dey, Second Sphere Effects on Oxygen Reduction and Peroxide Activation by Mononuclear Iron Porphyrins and Related Systems, Chem. Rev., 2022, 122(14), 12370–12426, DOI:10.1021/acs.chemrev.1c01021.
- K. M. Light, J. A. Hangasky, M. J. Knapp and E. I. Solomon, Spectroscopic Studies of the Mononuclear Non-Heme Fe II Enzyme FIH: Second-Sphere Contributions to Reactivity, J. Am. Chem. Soc., 2013, 135(26), 9665–9674, DOI:10.1021/ja312571m.
- K. E. Slessor, J. E. Stok, S. Chow and J. J. De Voss, Significance of Protein–Substrate Hydrogen Bonding for the Selectivity of P450-Catalysed Oxidations, Chem.–Eur. J., 2019, 25(16), 4149–4155, DOI:10.1002/chem.201805705.
- A. Timmins, M. Saint-André and S. P. de Visser, Understanding How Prolyl-4-Hydroxylase Structure Steers a Ferryl Oxidant toward Scission of a Strong C–H Bond, J. Am. Chem. Soc., 2017, 139(29), 9855–9866, DOI:10.1021/jacs.7b02839.
- N. Alberro, M. Torrent-Sucarrat, I. Arrastia, A. Arrieta and F. P. Cossío, Two-State Reactivity of Histone Demethylases Containing Jumonji-C Active Sites: Different Mechanisms for Different Methylation Degrees, Chem.–Eur. J., 2017, 23(1), 137–148, DOI:10.1002/chem.201604219.
- S. S. Chaturvedi, R. Ramanan, N. Lehnert, C. J. Schofield, T. G. Karabencheva-Christova and C. Z. Christov, Catalysis by the Non-Heme Iron(II) Histone Demethylase PHF8 Involves Iron Center Rearrangement and Conformational Modulation of Substrate Orientation, ACS Catal., 2020, 10(2), 1195–1209, DOI:10.1021/acscatal.9b04907.
- W.-J. Wei, P. E. M. Siegbahn and R.-Z. Liao, Theoretical Study of the Mechanism of the Nonheme Iron Enzyme EgtB, Inorg. Chem., 2017, 56(6), 3589–3599, DOI:10.1021/acs.inorgchem.6b03177.
- A. S. Faponle, F. P. Seebeck and S. P. de Visser, Sulfoxide Synthase versus Cysteine Dioxygenase Reactivity in a Nonheme Iron Enzyme, J. Am. Chem. Soc., 2017, 139(27), 9259–9270, DOI:10.1021/jacs.7b04251.
- S. S. Chaturvedi, R. Ramanan, J. Hu, R. P. Hausinger and C. Z. Christov, Atomic and Electronic Structure Determinants Distinguish between Ethylene Formation and l -Arginine Hydroxylation Reaction Mechanisms in the Ethylene-Forming Enzyme, ACS Catal., 2021, 11(3), 1578–1592, DOI:10.1021/acscatal.0c03349.
- S. Martinez, M. Fellner, C. Q. Herr, A. Ritchie, J. Hu and R. P. Hausinger, Structures and Mechanisms of the Non-Heme Fe(II)- and 2-Oxoglutarate-Dependent Ethylene-Forming Enzyme: Substrate Binding Creates a Twist, J. Am. Chem. Soc., 2017, 139(34), 11980–11988, DOI:10.1021/jacs.7b06186.
- Z. Zhang, T. J. Smart, H. Choi, F. Hardy, C. T. Lohans, M. I. Abboud, M. S. W. Richardson, R. S. Paton, M. A. McDonough and C. J. Schofield, Structural and Stereoelectronic Insights into Oxygenase-Catalyzed Formation of Ethylene from 2-Oxoglutarate, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(18), 4667–4672, DOI:10.1073/pnas.1617760114.
- I. S. Hassan, J. T. Fuller, V. N. Dippon, A. N. Ta, M. W. Danneman, B. R. McNaughton, A. N. Alexandrova and T. Rovis, Tuning Through-Space Interactions via the Secondary Coordination Sphere of an Artificial Metalloenzyme Leads to Enhanced Rh(iii)-Catalysis, Chem. Sci., 2022, 13(32), 9220–9224, 10.1039/D2SC03674F.
- S. B. Jaber Sathik Rifayee, S. S. Chaturvedi, C. Warner, J. Wildey, W. White, M. Thompson, C. J. Schofield and C. Christov, Catalysis by KDM6 Histone Demethylases – A Synergy between the Non-Heme Iron(II) Center, Second Coordination Sphere, and Long-Range Interactions, Chem.–Eur. J., 2023, e202301305, DOI:10.1002/chem.202301305.
- S. E. Graham, F. Syeda and G. A. Cisneros, Computational Prediction of Residues Involved in Fidelity Checking for DNA Synthesis in DNA Polymerase I, Biochemistry, 2012, 51(12), 2569–2578, DOI:10.1021/bi201856m.
- G. A. Cisneros, L. Perera, R. M. Schaaper, L. C. Pedersen, R. E. London, L. G. Pedersen and T. A. Darden, Reaction Mechanism of the ε Subunit of E. Coli DNA Polymerase III: Insights into Active Site Metal Coordination and Catalytically Significant Residues, J. Am. Chem. Soc., 2009, 131(4), 1550–1556, DOI:10.1021/ja8082818.
- M. Karplus, J. A. McCammon and W. L. Peticolas, The Internal Dynamics of Globular Protein, Crit. Rev. Biochem., 1981, 9(4), 293–349, DOI:10.3109/10409238109105437.
- P. K. Agarwal, D. N. Bernard, K. Bafna and N. Doucet, Enzyme Dynamics: Looking Beyond a Single Structure, ChemCatChem, 2020, 12(19), 4704–4720, DOI:10.1002/cctc.202000665.
- H. Berendsen, Collective Protein Dynamics in Relation to Function, Curr. Opin. Struct. Biol., 2000, 10(2), 165–169, DOI:10.1016/S0959-440X(00)00061-0.
- R. B. Fenwick, L. Orellana, S. Esteban-Martín, M. Orozco and X. Salvatella, Correlated Motions Are a Fundamental Property of β-Sheets, Nat. Commun., 2014, 5(1), 4070, DOI:10.1038/ncomms5070.
- D. Xu, S. P. Meisburger and N. Ando, Correlated Motions in Structural Biology, Biochemistry, 2021, 60(30), 2331–2340, DOI:10.1021/acs.biochem.1c00420.
- A. Tousignant and J. N. Pelletier, Protein Motions Promote Catalysis, Chem. Biol., 2004, 11(8), 1037–1042, DOI:10.1016/j.chembiol.2004.06.007.
- L. Y. P. Luk, E. J. Loveridge and R. K. Allemann, Protein Motions and Dynamic Effects in Enzyme Catalysis, Phys. Chem. Chem. Phys., 2015, 17(46), 30817–30827, 10.1039/C5CP00794A.
- P. Hanoian, C. T. Liu, S. Hammes-Schiffer and S. Benkovic, Perspectives on Electrostatics and Conformational Motions in Enzyme Catalysis, Acc. Chem. Res., 2015, 48(2), 482–489, DOI:10.1021/ar500390e.
- M. C. Thielges, J. K. Chung and M. D. Fayer, Protein Dynamics in Cytochrome P450 Molecular Recognition and Substrate Specificity Using 2D IR Vibrational Echo Spectroscopy, J. Am. Chem. Soc., 2011, 133(11), 3995–4004, DOI:10.1021/ja109168h.
- F. Abidi, M. Miano, J. Murray and C. Schwartz, A Novel Mutation in the PHF8 Gene Is Associated with X-Linked Mental Retardation with Cleft Lip/Cleft Palate, Clin. Genet., 2007, 72(1), 19–22, DOI:10.1111/j.1399-0004.2007.00817.x.
- C. Loenarz, W. Ge, M. L. Coleman, N. R. Rose, C. D. O. Cooper, R. J. Klose, P. J. Ratcliffe and C. J. Schofield, PHF8, a Gene Associated with Cleft Lip/Palate and Mental Retardation, Encodes for an Nε-Dimethyl Lysine Demethylase, Hum. Mol. Genet., 2010, 19(2), 217–222, DOI:10.1093/hmg/ddp480.
- A. Kohen, R. Cannio, S. Bartolucci and J. P. Klinman, Enzyme Dynamics and Hydrogen Tunnelling in a Thermophilic Alcohol Dehydrogenase, Nature, 1999, 399(6735), 496–499, DOI:10.1038/20981.
- D. Antoniou and S. D. Schwartz, Internal Enzyme Motions as a Source of Catalytic Activity: Rate-Promoting Vibrations and Hydrogen Tunneling, J. Phys. Chem. B, 2001, 105(23), 5553–5558, DOI:10.1021/jp004547b.
- S. D. Schwartz, Protein Dynamics and Enzymatic Catalysis, J. Phys. Chem. B, 2023, 127(12), 2649–2660, DOI:10.1021/acs.jpcb.3c00477.
- D. D. Boehr, D. McElheny, H. J. Dyson and P. E. Wright, The Dynamic Energy Landscape of Dihydrofolate Reductase Catalysis, Science, 2006, 313(5793), 1638–1642, DOI:10.1126/science.1130258.
- G. Bhabha, J. Lee, D. C. Ekiert, J. Gam, I. A. Wilson, H. J. Dyson, S. J. Benkovic and P. E. Wright, A Dynamic Knockout Reveals That Conformational Fluctuations Influence the Chemical Step of Enzyme Catalysis, Science, 2011, 332(6026), 234–238, DOI:10.1126/science.1198542.
- J. B. Watney, P. K. Agarwal and S. Hammes-Schiffer, Effect of Mutation on Enzyme Motion in Dihydrofolate Reductase, J. Am. Chem. Soc., 2003, 125(13), 3745–3750, DOI:10.1021/ja028487u.
- N. Doucet, E. D. Watt and J. P. Loria, The Flexibility of a Distant Loop Modulates Active Site Motion and Product Release in Ribonuclease A, Biochemistry, 2009, 48(30), 7160–7168, DOI:10.1021/bi900830g.
- V. Vaissier, S. C. Sharma, K. Schaettle, T. Zhang and T. Head-Gordon, Computational Optimization of Electric Fields for Improving Catalysis of a Designed Kemp Eliminase, ACS Catal., 2018, 8(1), 219–227, DOI:10.1021/acscatal.7b03151.
- T. Matsui, S. Ozaki and Y. Watanabe, On the Formation and Reactivity of Compound I of the His-64 Myoglobin Mutants, J. Biol. Chem., 1997, 272(52), 32735–32738, DOI:10.1074/jbc.272.52.32735.
- H. A. Bunzel, J. L. R. Anderson, D. Hilvert, V. L. Arcus, M. W. van der Kamp and A. J. Mulholland, Evolution of Dynamical Networks Enhances Catalysis in a Designer Enzyme, Nat. Chem., 2021, 13(10), 1017–1022, DOI:10.1038/s41557-021-00763-6.
- C. Van Stappen, Y. Deng, Y. Liu, H. Heidari, J.-X. Wang, Y. Zhou, A. P. Ledray and Y. Lu, Designing Artificial Metalloenzymes by Tuning of the Environment beyond the Primary Coordination Sphere, Chem. Rev., 2022, 122(14), 11974–12045, DOI:10.1021/acs.chemrev.2c00106.
- T. Yonetani and H. Schleyer, Studies on Cytochrome c Peroxidase, J. Biol. Chem., 1967, 242(8), 1974–1979, DOI:10.1016/S0021-9258(18)96096-5.
- Y. Isogai, H. Imamura, S. Nakae, T. Sumi, K. Takahashi, T. Nakagawa, A. Tsuneshige and T. Shirai, Tracing Whale Myoglobin Evolution by Resurrecting Ancient Proteins, Sci. Rep., 2018, 8(1), 16883, DOI:10.1038/s41598-018-34984-6.
- B. C. Finzel, T. L. Poulos and J. Kraut, Crystal Structure of Yeast Cytochrome c Peroxidase Refined at 1.7-A Resolution, J. Biol. Chem., 1984, 259(21), 13027–13036, DOI:10.1016/S0021-9258(18)90651-4.
- L. Yin, H. Yuan, C. Liu, B. He, S.-Q. Gao, G.-B. Wen, X. Tan and Y.-W. Lin, A Rationally Designed Myoglobin Exhibits a Catalytic Dehalogenation Efficiency More than 1000-Fold That of a Native Dehaloperoxidase, ACS Catal., 2018, 8(10), 9619–9624, DOI:10.1021/acscatal.8b02979.
- D. A. Vargas, A. Tinoco, V. Tyagi and R. Fasan, Myoglobin-Catalyzed C−H Functionalization of Unprotected Indoles, Angew. Chem., Int. Ed., 2018, 57(31), 9911–9915, DOI:10.1002/anie.201804779.
- G. Sreenilayam and R. Fasan, Myoglobin-Catalyzed Intermolecular Carbene N–H Insertion with Arylamine Substrates, Chem. Commun., 2015, 51(8), 1532–1534, 10.1039/C4CC08753D.
- H. A. Bunzel, H. Kries, L. Marchetti, C. Zeymer, P. R. E. Mittl, A. J. Mulholland and D. Hilvert, Emergence of a Negative Activation Heat Capacity during Evolution of a Designed Enzyme, J. Am. Chem. Soc., 2019, 141(30), 11745–11748, DOI:10.1021/jacs.9b02731.
- K. K. Yang, Z. Wu and F. H. Arnold, Machine-Learning-Guided Directed Evolution for Protein Engineering, Nat. Methods, 2019, 16(8), 687–694, DOI:10.1038/s41592-019-0496-6.
- J. Dauparas, I. Anishchenko, N. Bennett, H. Bai, R. J. Ragotte, L. F. Milles, B. I. M. Wicky, A. Courbet, R. J. De Haas, N. Bethel, P. J. Y. Leung, T. F. Huddy, S. Pellock, D. Tischer, F. Chan, B. Koepnick, H. Nguyen, A. Kang, B. Sankaran, A. K. Bera, N. P. King and D. Baker, Robust Deep Learning–Based Protein Sequence Design Using ProteinMPNN, Science, 2022, 378(6615), 49–56, DOI:10.1126/science.add2187.
- M. Baek, F. DiMaio, I. Anishchenko, J. Dauparas, S. Ovchinnikov, G. R. Lee, J. Wang, Q. Cong, L. N. Kinch, R. D. Schaeffer, C. Millán, H. Park, C. Adams, C. R. Glassman, A. DeGiovanni, J. H. Pereira, A. V. Rodrigues, A. A. Van Dijk, A. C. Ebrecht, D. J. Opperman, T. Sagmeister, C. Buhlheller, T. Pavkov-Keller, M. K. Rathinaswamy, U. Dalwadi, C. K. Yip, J. E. Burke, K. C. Garcia, N. V. Grishin, P. D. Adams, R. J. Read and D. Baker, Accurate Prediction of Protein Structures and Interactions Using a Three-Track Neural Network, Science, 2021, 373(6557), 871–876, DOI:10.1126/science.abj8754.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Highly Accurate Protein Structure Prediction with AlphaFold, Nature, 2021, 596(7873), 583–589, DOI:10.1038/s41586-021-03819-2.
- N. R. Bennett, B. Coventry, I. Goreshnik, B. Huang, A. Allen, D. Vafeados, Y. P. Peng, J. Dauparas, M. Baek, L. Stewart, F. DiMaio, S. De Munck, S. N. Savvides and D. Baker, Improving de Novo Protein Binder Design with Deep Learning, Nat. Commun., 2023, 14(1), 2625, DOI:10.1038/s41467-023-38328-5.
- A. H.-W. Yeh, C. Norn, Y. Kipnis, D. Tischer, S. J. Pellock, D. Evans, P. Ma, G. R. Lee, J. Z. Zhang, I. Anishchenko, B. Coventry, L. Cao, J. Dauparas, S. Halabiya, M. DeWitt, L. Carter, K. N. Houk and D. Baker, De Novo Design of Luciferases Using Deep Learning, Nature, 2023, 614(7949), 774–780, DOI:10.1038/s41586-023-05696-3.
- E. I. Solomon; C. B. Bell, Inorganic and Bioinorganic Spectroscopy, in Physical Inorganic Chemistry, ed. A. Bakac, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2010, pp. 1–37, DOI:10.1002/9780470602539.ch1.
| This journal is © The Royal Society of Chemistry 2023 |