Moving dynamics of a nanorobot with three DNA legs on nanopore-based tracks†
Li-Zhen
Sun
 * and
Yao-Jun
Ying
* and
Yao-Jun
Ying
Department of Applied Physics, Zhejiang University of Technology, Hangzhou 310023, China. E-mail: sunlizhen@zjut.edu.cn
First published on 15th September 2023
Abstract
DNA nanorobots have garnered increasing attention in recent years due to their unique advantages of modularity and algorithm simplicity. To accomplish specific tasks in complex environments, various walking strategies are required for the DNA legs of the nanorobot. In this paper, we employ computational simulations to investigate a well-designed DNA-legged nanorobot moving along a nanopore-based track on a planar membrane. The nanorobot consists of a large nanoparticle as the robot core and three single-stranded DNAs (ssDNAs) as the robot legs. The nanopores linearly embedded in the membrane serve as the toeholds for the robot legs. A charge gradient along the pore distribution mainly powers the activation of the nanorobot. The nanorobot can move in two modes: a walking mode, where the robot legs sequentially enter the nanopores, and a jumping mode, where the robot legs may skip a nanopore to reach the next one. Moreover, we observe that the moving dynamics of the nanorobot on the nanopore-based tracks depends on pore–pore distance, pore charge gradient, external voltage, and leg length.
1. Introduction
In living organisms, the operations of many cellular functions, such as organelle transport and synthesis, rely significantly on the dynamics of biomolecular motors.1,2 Typical examples include kinesin, dynein, and myosin that can transport various cellular cargoes along cytoskeletal tracks.3,4 Inspired by the natural motors, many artificial biomolecular nanodevices have been synthesized to accomplish specific tasks in the nano-/micro-world.5,6 The DNA molecule is one of the most important building blocks for constructing these nanodevices due to its easily programmable sequence and well-defined base pairing rule.7–9 Various DNA-based nanostructures, such as DNA switches,10,11 DNA tweezers,12,13 DNA rotors,14,15 DNA carriers,16,17 and DNA walkers,18,19 have been designed and shown promising potentials in applications, including biosensing,20–22 diagnostics,23–27 and therapeutics.28–30To achieve complex nanomechanical tasks, it is often necessary to combine the functions of multiple types of the DNA nanomachines. A novel example is the DNA nanorobot,6 which integrates the DNA carrier and walker functions to transport cargoes (such as nanoparticles31 and DNA fragments32) from a donor location to a receiver location. A recently reported cargo-sorting DNA nanorobot,33 which consists of three single-stranded DNA (ssDNA) domains (building blocks), can use one ssDNA domain like a hand to load two types of molecular cargoes at arbitrary locations, and then use the other two ssDNA domains like feet to walk randomly on a track, until the cargoes are successfully unloaded at specified destinations.
The design of different walking tracks is advancing in parallel with the development of the DNA nanorobot, expanding the range of applications for these nanomachines in various environments.34 Currently, walking tracks can be classified into one-dimensional (1D) tracks, such as carbon nanotube31,35 and double-stranded DNA backbone36; two-dimensional (2D) tracks, such as DNA paper origami33,37 and inorganic surface;38,39 and three-dimensional (3D) tracks, such as nanoparticle surface40–42 and cell membrane43. Based on these tracks, one of the most widespread mechanisms used to move the DNA-legged nanorobot is the strand displacement approach.44,45 In this approach, one walking step of the nanorobot starts by unzipping the old duplex between a DNA foot of the nanorobot and a foothold (a DNA/RNA strand complementary to foot domain) on the track and ends by forming a new duplex between the released foot and another foothold.46,47 The strand displacement reactions can be controlled by additional molecular ligands,48 metal ions,49 pH values,50 and other factors,51–54 allowing for the manipulation of the nanorobot movements. Whereas, unintended displacement interactions between robot feet and track footholds will reduce the moving efficiency of the nanorobots.55,56 Moreover, the nanorobot-track systems will be contaminated by the additional molecules, which can limit the functions of the DNA-legged nanorobots.45 Therefore, new moving strategies beyond the strand displacement approach are desirable.
Nanopores have shown promising potential in controlling the dynamics of nanomachines.57 In fact, the nanopores are initially developed for sensing biomolecules such as nucleic acids.58–62 Nanopore-based sensing is a label-free, single-molecule, high-throughput analysis technology that relies on the current signal produced by the translocation of nucleic acids through a nanopore.63 To improve resolution of the current signal, the translocation dynamics of the nucleic acids should be manipulated.64 Utilizing a multiple-nanopore platform is an effective approach65,66 that provides opposite driving forces for a nucleic acid. This “tug-of-war” effect can lead to a more prolonged retention of the nucleic acid inside the nanopores, resulting in a clearer and longer current signal output.67,68 The rapid development in nanopore fabrication technologies69,70 has made it possible to independently adjust the sizes71,72 and surface charges73,74 of the nanopores. Therefore, the moving direction and speed of the trapped nucleic acid can be manipulated by the multiple-pore device.75
Due to their ability to control the movements of the nucleic acids, the multiple-nanopore systems can be used to manipulate the walking of the DNA-legged nanorobots. In a proof-of-principle research,76 a nanoparticle–DNA assembled nanorobot with four ssDNA legs is powered to move by four nanopores placed in the corners of a square on a planar membrane. Each robot leg is captured by a corresponding nanopore, and the fuel to move the nanorobot is generated by the nanopores with distinct charges. It has also been demonstrated that this nanorobot can walk on the nanopore-based track by adjusting the direction and magnitude of the external voltage across the nanopores.77 In the non-autonomous walking process, the external voltage is artificially changed to control the movement of the DNA legs, leading them to leave the old toeholds (nanopores) for new ones. Based on the chemical reaction-free driving mechanism, the multiple-nanopore device provides the DNA-legged nanorobots with a clear and stable working environment, facilitating the accomplishment of their complicated tasks. However, it is still challenging to realize the autonomous walking of the nanorobot along the nanopore-based track.
In this article, we theoretically design a nanorobot with three ssDNA legs that can autonomously move along the nanopore-based tracks by using computational simulations. Specifically, when two ssDNA legs of the nanorobot are trapped in the nanopores, the third leg can enter another nanopore to generate an additional force for the nanorobot, which drags the lagging leg to leave its original nanopore for a new one. We observe two moving modes of the nanorobot on the nanopore-based track, a stepwise walking mode, in which the legs enter the nanopores one by one, and a jumping mode, in which the legs skip a nanopore to directly find the next one. Additionally, we study the moving dynamics of the nanorobot under various influencing factors, such as the distances between pores, pore charge gradients, and external voltages, ssDNA leg lengths.
2. Simulation model and methods
2.1. Coarse-grained model in simulation
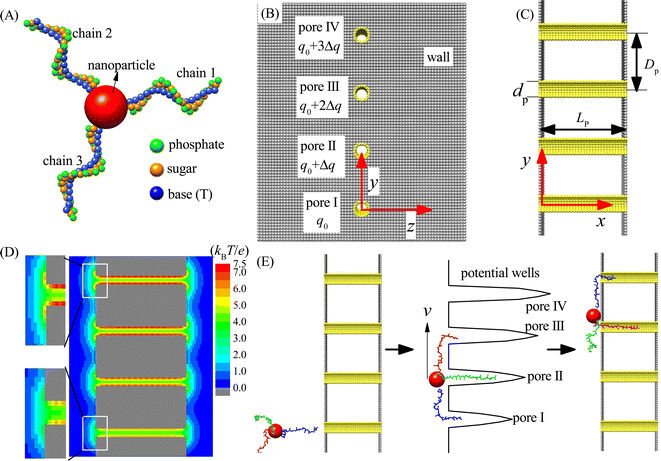
In this paper, we study the moving dynamics of the nanorobot with DNA legs on the nanopore-based track by using computational simulations. The simulation model is composed of two main components: the nanorobot with three legs (see Fig. 1A) and the membrane with four nanopores (see Fig. 1B and C).As shown in Fig. 1A, the nanorobot consists of a nanoparticle (as the robot core) and three ssDNA chains (as the robot legs). The nanoparticle is represented as a large spherical bead NP (red). The ssDNA legs are three polythymines, each having the same number of nucleotides (nts). In experimental settings, the ssDNA legs can be attached to the nanoparticle covered by thiol group or streptavidin, and the number of legs can be controlled through atomic force microscope by removing the redundant legs.77,78 In order to improve efficiency of the simulation, we use our recently developed coarse-grained (CG) model to describe the ssDNA chains.79,80 The CG model employs three bead types, namely P (green), S (orange), and B (blue), which correspond to the atomic groups phosphate, sugar, and base thymine, respectively, within each nucleotide. The mass of each bead is equal to the total mass of its corresponding atomic group, and the bead radius is determined by considering the hydration effects.81 In addition, we adopt a CG effective charge model for the nanorobot in the single salt NaCl solution, with only bead P carrying an effective negative charge −Qe, where Q ≈ 0.615 is the Manning constant,82,83 and other beads (B, S, and NP) being neutral. The parameters of the nanorobot model can be found in Table S1 of the ESI.† Here we should note that although the nanorobot legs are only considered as the polythymines, the simulation results are still qualitatively applicable to other types of ssDNA legs, such as polyadenines and polyguanines, since they have the similar environment-dependent conformations84,85 and nanopore-based translocation dynamics.86,87
As shown in Fig. 1B and C, an infinitely large membrane is placed at the y–z plane to divide the entire simulation box into two chambers of the same size. The membrane is composed of two planar walls. Four nanopores (I–IV) embedded into the membrane distribute in a line along the y-direction with a pore–pore distance Dp within the range of [48 Å, 96 Å]. The walls and nanopores are constructed using wall beads (gray) and pore beads (yellow) of the same radius (also see ESI Table S1†). The nanopores serve as the toeholds for the robot legs. To ensure that each nanopore accommodates only one robot leg and prevents the nanoparticle from passing through, we set the nanopore diameter to dp = 12 Å. Moreover, the nanopore length is fixed as Lp = 90 Å to allow that most nucleotides of one ssDNA chain can be hold by a nanopore. Despite significant advancements in nanopore fabrication technologies due to their growing applications,88,89 producing tiny pores with small distances (≤96 Å) remains challenging. Nevertheless, recent utilization of electron beam shrinking technology has allowed the fabrication of a nanopore array with a given pore–pore distance.90 Furthermore, existing techniques, such as controlled breakdown,91 electrochemical reactions,92 and laser etching,93 can adjust the nanopores to ssDNA-compatible sizes. As a result, the realization of experimental multi-pore devices in the near future is plausible. Our proof-in-principle study can provide valuable insights for the future development of chemical reaction-free nanorobot movement.
The simulation box has dimensions of 300 Å, 540 Å, and 300 Å along the x, y, and z directions, respectively, with periodic boundary conditions applied to avoid the boundary effect. The entry center of pore I is defined as the coordinate origin of the three-dimensional (3D) box, i.e., (x, y, z) = (0, 0, 0). To activate the moving of the nanorobot without the chemical reactions, a gradient of free energy along the nanopore-based track is required. In this paper, we use a pore charge gradient to generate the free energy difference for the robot legs in the nanopores. Each pore bead of the pore I carries a fixed positive charge q0 = 0.25e, and the bead charges from pore II to pore IV increase by Δq to 3Δq accordingly (see Fig. 1B). Fig. 1D shows the 2D electrostatic potential distribution at the x–y plane under the charge gradient of Δq = 0.25e. As a result, a gradient of potential wells is created due to the different ssDNA–pore attractions, which thus can power the nanorobot to move from pore I to pore IV, as shown in Fig. 1E.
2.2. The model-matched CG potentials
In our CG model, four types of the virtual bonds are used to connect the neighbouring beads of the nanorobot. For each ssDNA chain, there are three virtual bonds P–S, S–P, and S–B. Moreover, the terminal nucleotide at 3′ end of each ssDNA chain is anchored at the bead NP via the virtual bond S–NP. The model-matched potential energy for the nanorobot is given by:| UCG = Ulj + Ub + Ua + Ud + Ue. | (1) |
The above CG potentials include volume excluded interaction (Ulj), virtual bond interaction (Ub), bond–bond angle potential (Ua), dihedral potential (Ud), and bead P–bead P electrostatic interaction (Ue).
The detailed descriptions of the five potential terms in eqn (1) and the potential parameters are described in the ESI.† In brief, the volume excluded interaction Ulj between two non-bonded beads, including the nanorobot beads and membrane beads, is described using a “12-6” Lennard-Jones potential; the three virtual bond-involved interactions Ub, Ua, and Ud account for chain connectivity and angular rotation of the ssDNA legs; the electrostatic interaction Ue is described by the Manning Counterion Condensation theory81 that implicitly treats the ion effects. Especially, the energy parameters of the bond-involved interactions are derived from the Boltzmann inversion80 of the corresponding structural probability distributions, which can be statistically obtained from the experimentally measured ssDNA structures. The simulation results of the current CG model for the ssDNA structures have been validated against the experiment results.79,80
2.3. Langevin dynamics simulation
In the simulations, the beads of the nanorobot (NP, P, B, and S) are movable, while the wall and pore beads are immobile. The dynamics of a nanorobot bead i is determined by Langevin equation: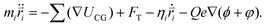 | (2) |
Here mi and  are the mass and position vector of the bead i, respectively. UCG expressed in eqn (1) is the interactions between the bead i and other beads (including other nanorobot beads, wall beads, and pore beads). The random force FT is Gaussian white noise with zero mean. The viscous force
are the mass and position vector of the bead i, respectively. UCG expressed in eqn (1) is the interactions between the bead i and other beads (including other nanorobot beads, wall beads, and pore beads). The random force FT is Gaussian white noise with zero mean. The viscous force 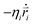 is mainly determined by the velocity
is mainly determined by the velocity 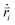 of the bead i and the viscosity coefficient ηi is proportional to the bead radius according to the Stokes’ formula. For simplicity, the viscosity coefficient ηP of the bead P is set as the unit in our simulations.
of the bead i and the viscosity coefficient ηi is proportional to the bead radius according to the Stokes’ formula. For simplicity, the viscosity coefficient ηP of the bead P is set as the unit in our simulations.
The last term in eqn (2) denotes the electric field force experienced by the charged beads in the nanorobot, which are induced by the external voltage and the pore charges. The electric field within the simulation box is influenced by the DNA charges when the nanorobot moves around. However, accounting for the effects of DNA charges on the electric field requires extremely significant computational resources, making it impractical for this study. Therefore, we assume that the electric field is independent of the DNA charges. Additionally, we do not consider the mobilities of the cations (Na+) and anions (Cl−) under the external voltage.83 Consequently, the electroosmotic flow across the nanopore is neglected, which indicates that the ion distributions only depends on the pore charges. Therefore, the external voltage-induced electric potential ϕ and pore charge-induced electric potential φ can be calculated separately. ϕ is determined by Laplace equation:94
| ∇2ϕ = 0. | (3) |
The boundary conditions of the above equation are that ϕ = 0 and ΔV beyond a distance of 60 Å away from the left wall and right wall of the membrane, respectively. In addition, the pore charge-induced φ can be calculated from the Nonlinear Poisson–Boltzmann equation:95,96
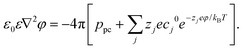 | (4) |
Here ε0 is the dielectric constant of a vacuum and ε (= 78.5 at room temperature) is the relevant dielectric constant of the solvent. ppc denotes the density of the pore charges. The subscript j represents the ion species (Na+ and Cl−) and Zj is the ionic valency. cj0 (= 0.1 mol L−1 for both Na+ and Cl−) denotes the bulk concentration of the ion species j. kB and T are the Boltzmann constant and temperature. Both ϕ and φ are solved on the cubic lattice with the lattice size 2 Å.
In our simulations, the length and energy units are set as σ0 = 1 Å and u0 = 1kBT at the room temperature (T = 25 °C). The mass unit m0 is considered as the mass of bead P (mP = 95 Da). Accordingly, the units of time and voltage are 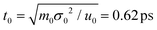 and V0 = 25.8 mV. The modified velocity-Verlet algorithm97 is employed to solve the Langevin equation with a time step Δt = 0.001t0.
and V0 = 25.8 mV. The modified velocity-Verlet algorithm97 is employed to solve the Langevin equation with a time step Δt = 0.001t0.
3. Results and discussion
We will study the moving dynamics of the nanorobot by varying the pore–pore distance Dp, the charge gradient Δq, the external voltage ΔV (applied along x-direction), and the leg length N (the number of nucleotides). All data presented in this study are averaged from 100 samples, unless otherwise mentioned.3.1. Successful probability of the nanorobot landing on the nanopore-based tracks
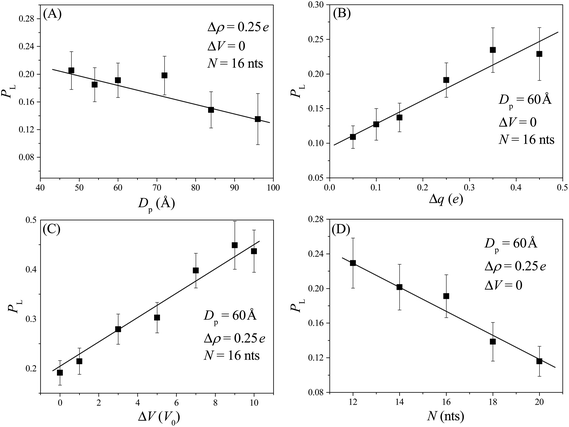
At the beginning of each simulation sample, we first equilibrate the conformation of the nanorobot for a sufficient long time (= 107Δt) and then place the nanorobot near the membrane surface with one leg near the entry of the pore I (see Fig. 1E). Afterwards, the nanorobot is left to move freely. Because of the entropic barrier at the pore entry, the nanorobot may fail to land on the nanopore-based track and diffuse away from the membrane surface. If the distance between the nanorobot and the membrane surface is greater than 20 Å, we will reposition the nanorobot to its original location and restart this sample. The successful landing probability is defined as PL = 1/(1 + nfail) with nfail as the number of failed attempts for the nanorobot landing on the nanopore-based track.Although the nanorobot is initially placed near the pore I, the neighbouring nanopore (pore II) is also involved in the landing process. If a robot leg has already entered the pore I, a longer pore–pore distance will result in a longer duration for the nanorobot to find the next pore. During the period, the leg already in the pore I may retreat back and the nanorobot can diffuse away. Therefore, we can observe that the successful landing probability PL decreases with an increase in the pore–pore distance Dp, as shown in Fig. 2A. On the other hand, if the neighbouring nanopore can provide a strong attraction for the robot legs, the nanorobot will be more likely to land on the nanopore-based track. As a result, a larger pore charge gradient Δq can lead to an increase in PL, as shown in Fig. 2B. In addition, as the external voltage applied along the x direction can effectively reduce the free energy barrier of the nanopores, we can find that PL increases with ΔV, as shown in Fig. 2C. We also explore the leg length N-dependent landing probability, as illustrated in Fig. 2D. Since the possible number of conformations for a free ssDNA chain increases with the chain length, longer ssDNA legs entering the nanopore will experience a higher entropic barrier at the pore entry due to the loss of more possible conformations. Consequently, an increase in leg length N leads to a decrease in the landing probability.
After several unsuccessful landing attempts, the nanorobot eventually lands and successfully moves along the nanopore track, taking step-by-step movements similar to the strand displacement-based movement. Here, a step is defined as the distance traveled by the nanorobot from finding a pore to finding the next one. Therefore, the entire moving process, from pore I to pore IV, can be divided into three steps: step I–II (from pore I to pore II), step II–III (from pore II to pore III), and step III–IV (from pore III to pore IV). Since the nanorobot is initially placed near the pore I, the step I–II is incomplete. Therefore, our investigation of the moving dynamics of the nanorobot focuses on the main moving process, i.e., the steps II–III and III–IV.
3.2. Two moving modes of the nanorobot
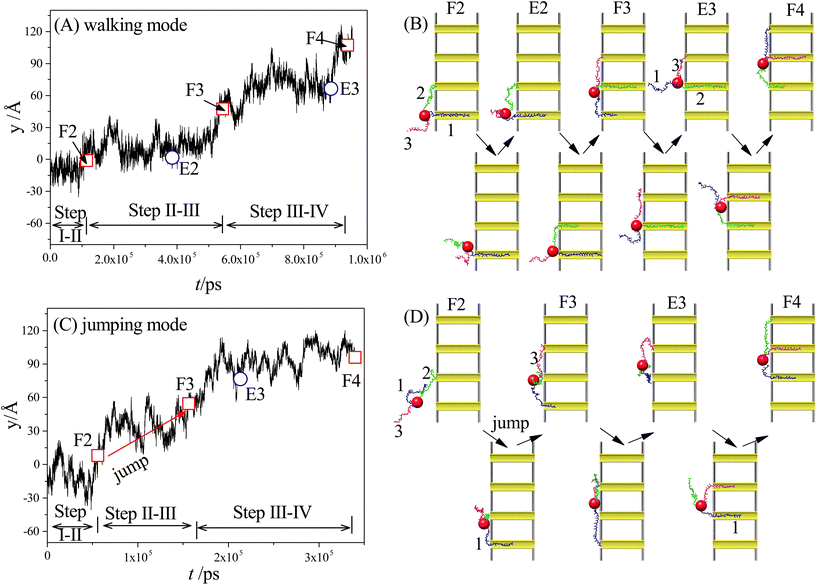
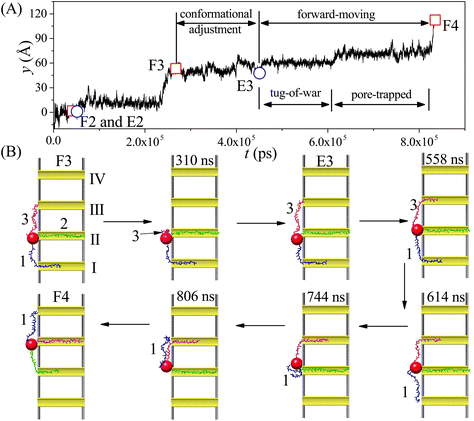
Our simulation results reveal two main moving modes of the nanorobot: the walking mode (see Fig. 3A and B) and the jumping mode (see Fig. 3C and D). Fig. 3A shows a time-evolutional trace in the y-direction for the nanoparticle (robot core) in the walking mode. The nanoparticle moves towards the pore IV with forward–backward motions, which are strongly dependent on the states of the robot legs. During the main moving process (the steps II–III and III–IV), five special states are observed (see Fig. 3B). The first state, F2, occurs when leg2 (green) finds the pore II for the first time, while leg1 (blue) is already inside the pore I and leg3 (magenta) is diffusing outside. After the state F2, the leg2 may undergo several failed attempts to enter the pore II,98 requiring necessary conformational adjustment (see the mid-state after state F2). The subsequent state E2 occurs when the head nucleotide of the leg2 successfully enters the pore II without retreating back. Due to the attraction of the pore II, most nucleotides of the leg2 quickly enter the pore (see the mid-state after the state E2), dragging the nanoparticle to approach the pore II. Meanwhile, the leg3, which is still outside the nanopores, seeks its corresponding toehold. The state F3 describes the moment when the leg3 finds the pore III for the first time, which ends the step II–III and triggers the step III–IV. In the new moving step, the states E3 (that the leg3 successfully enters the pore III) and the state F4 (that the leg1 finds the pore IV) occur in order, similar to the states E2 and F3.By analyzing the time-evolutional trace and special states in the walking mode, we can find that the nanoparticle remains in close proximity to the pore entries during the conformational adjustment periods from the F-states to the E-states. However, the nanorobot is able to move forward along the nanopore-based track during the named forward-moving period between the E-states and the F-states.
Fig. 3C displaces the trajectory of the nanoparticle during a moving event in the jumping mode. In this selected event, a notable phenomenon observed in Fig. 3D is that leg1 leaves pore I when the state F2 occurs. The moving process of the nanorobot before reaching the state F2 is depicted in ESI Fig. S1.† After the state F2, the leg1 still has a chance to re-enter the pore I (observed in the mid-state after the state F2). However, during this time, the leg3 directly finds the pore III before the leg2 can successfully enter the pore II (as shown in the state F3), giving rise to the absence of the state E2 in the step II–III. Subsequently, the states E3 and F4 occur sequentially, completing the step III–IV. It is noteworthy that the jumping behavior also can be observed in the step III–IV of other jumping events, as depicted in ESI Fig. S2.†
To achieve the autonomous moving (in the walking and jumping modes) of the nanorobot, it is essential to pull the lagging leg (e.g. leg1 in state F3) out of its original nanopore. For a two-legged nanorobot, even if the leading leg inside the next nanopore can win the “tug-of-war”, it can still be challenging to drag the lagging leg to leave its toehold. Therefore, a third leg is necessary to provide additional assistance in dragging the lagging leg. However, compared to the jumping mode, the walking mode might be more desirable as the robot core can dock with every nanopore for a while to accomplish its tasks such as drug releasing. In the following sections, we will further investigate the manipulation method of the nanorobot moving dynamics by varying the pore–pore distance Dp, the charge gradient Δq, the external voltage ΔV, and the leg length N.
3.3. Effects of the pore–pore distance Dp
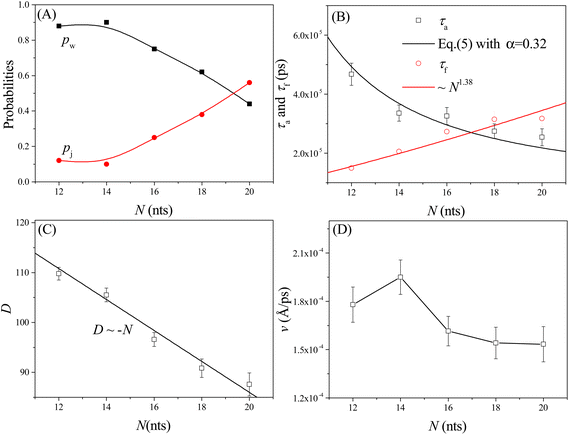
As shown in Fig. 4A, the probabilities of the walking (pw) and jumping (pj) modes are highly dependent on the pore–pore distance Dp. Here the charge gradient Δq = 0.25e, the external voltage ΔV = 0, and the leg length N = 16 nts. At short Dp (= 48 Å), almost all moving events select the jumping mode, as the 16 nts-long ssDNA chains are more likely to skip the neighboring nanopore and find a farther one. As Dp increases, the nanorobot moves in the walking mode more easily, leading to an increase in pw. When Dp ≥ 70 Å, more than 95% of the moving events choose the walking mode. Moreover, we also find that the total moving time from the state F2 to the state F4 in the walking mode tw is longer than that in the jumping mode tj (see Fig. 4B). This is because the nanorobot in the walking mode needs to spend time on adjusting its conformation to enter the nanopores one by one, whereas in the jumping mode, this duration is saved in one of the moving steps.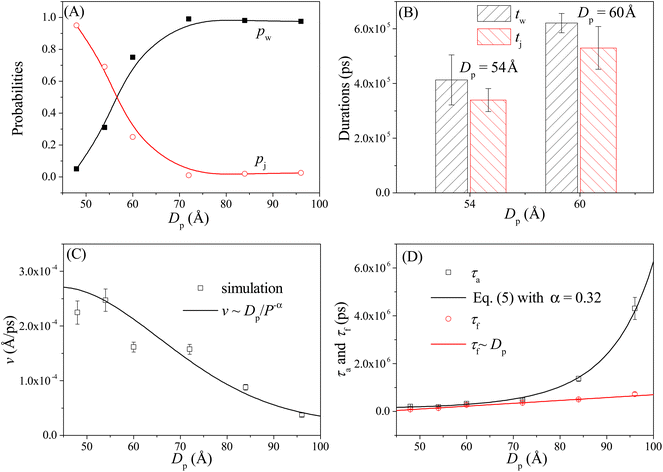 | ||
| Fig. 4 (A) The pore–pore distance Dp-dependent probabilities of the walking mode pw (solid black squares) and the jumping mode pj (open red cycles). The lines serve as visual guide. (B) The moving times for the nanorobot in the walking mode tw and jumping mode tj, respectively, at Dp = 54 Å and 60 Å. (C) The velocity v of the nanorobot moving on the nanopore-based track under various pore–pore distances. The open squares represent velocity calculated from the simulation results and the line represents the fitted relationship v ∼ Dp/P−α with P as probability distribution (see eqn (5)) of the end-to-end distance for a robot leg. (D) The Dp-dependent conformational adjustment duration τa and forward-moving duration τf. The scatters are from the simulation results. The black and red lines are fitted from the relationships of τa ∼ P−α in eqn (5) with α = 0.32 and τf ∼ Dp, respectively. The simulations are performed under the conditions of Δq = 0.25e, ΔV = 0, and N = 16 nts. | ||
In addition to the probabilities of the moving modes, the velocity v of the nanorobot moving on the nanopore-based track is also an important parameter for investigating its moving dynamics.39 The nanorobot velocity is averaged from all moving events, including both the walking and jumping modes, as v = D/t with D as the moving distance of the nanorobot and t as the total moving time from the state F2 to the state F4. We find that the nanorobot moves more slowly on the nanopore-based track as the pore–pore distance increases (see Fig. 4C), primarily due to the longer moving time t. The entire moving time t can be further divided into the conformational adjustment duration τa, which contains the time intervals between the F-states and the E-states (state E2–state F3 and state E3–state F4), and the forward-moving duration τf, which includes the time intervals between the E-states and the F-states (state F2–state E2 and state F3–state E3), i.e., t = τa + τf. Notably, the entire duration of a jumping step, during which the nanorobot skips the conformational adjustment period to directly find the next nanopore (e.g. from state F2 to state F3 in Fig. 3D or from state F3 to state F4 in Fig. S2†), is added to the forward-moving duration in the jumping modes.
The simulation results of the Dp-dependent τa (black squares) and τf (red cycles) are presented in Fig. 4D. We find that τa increases more rapidly than τf as the pore–pore distance increases, indicating that the nanorobot will spend a majority of the moving time on adjusting its conformation at long pore–pore distance. During the forward-moving periods, the nanoparticle moves from pore II to pore III and then to pore IV, causing τf to be proportional to the pore–pore distance, as τf ∼ Dp (the red line). Conversely, the conformational adjustment duration τa should be dependent on the probability distribution P of end-to-end distance Ree for a single ssDNA chain. For the leading robot leg in the F-states (e.g. the leg2 in the state F2 or the leg3 in the state F3), its one end is tethered at the nanoparticle, which is docking at a nanopore entry, while the other end is at the next pore entry, resulting in Ree ≈ Dp − Rn (the nanoparticle radius) for the leading leg at the moment. The higher probability of the leading leg finding the nanopore at the distance (Dp − Rn), The shorter time interval between two failed pore-entering attempts will be, leading to the shorter τa. Moreover, at the ion condition (0.1 mol L−1 NaCl solution) employed in this article, the polythymine can be treated as a flexible self-avoiding polymer chain.85 The relationship of P versus Ree thus can be described as P ∼ 4πRee2exp(−3Ree2/2Nb2), which is obtained from the polymer database.99 Due to the dependence of τa on P, the conformational adjustment duration τa (see the black line in Fig. 4D) is empirically expressed as:
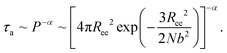 | (5) |
Here Ree = Dp − Rn. In addition, N (= 16nts) and b (= 7 Å (ref. 88)) represent the nucleotide number and the distance between two neighbouring nucleotides. We obtain α = 0.32 by fitting eqn (5) to our simulation results. According to the analyses of the Dp-dependent τa and τf in Fig. 4D, the moving time t of the nanorobot is mainly determined by the conformational adjustment duration τa, especially at long Dp. Furthermore, the moving distance D of the nanorobot is basically determined by the pore–pore distance Dp. As a result, we find that the velocity of the nanorobot follows the relationship of v ∼ Dp/P−α (see the line in Fig. 4C).
We will also explore the impact of the charge gradient, external voltage, and leg length on the moving dynamics of the nanorobot. For this purpose, selecting an appropriate pore–pore distance is crucially important, which will be based on two criteria. Firstly, the pore–pore distance should result in relatively high probabilities of both walking and jumping events, enabling us to study the variation of the moving modes under different conditions. Secondly, the pore–pore distance should be relatively large to avoid the coupling effects of two neighboring charged pores. As a result, we choose the pore–pore distance of Dp = 60 Å for our further investigations.
3.4. Effects of the charge gradient Δq
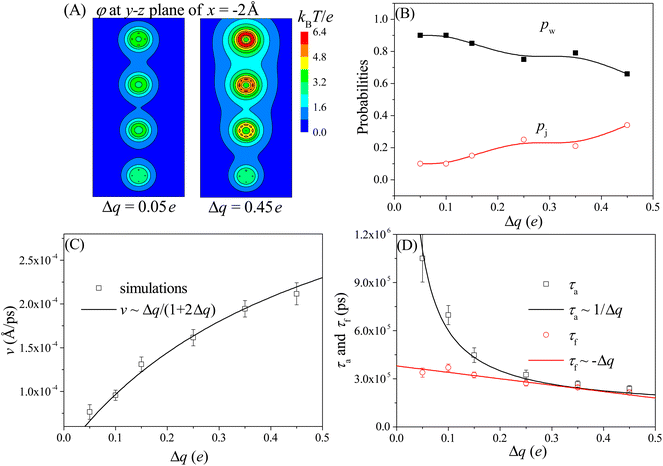
Here we study the effect of the charge gradient Δq on the moving dynamics of the nanorobot, while keeping the pore–pore distance, external voltage, and leg length at Dp = 60 Å, ΔV = 0, and N = 16 nts, respectively. Unlike the pore–pore distance, which alters the step size of the nanorobot, the charge gradient Δq modulates the moving dynamics by changing the electrostatic free energies of the robot legs inside the nanopores. In Fig. 5A, we presents the 2D electrostatic potentials φ (see eqn (4)), which are generated by the nanopore charges, at the y–z plane of x = −2 Å. Compared to the small charge gradient of Δq = 0.05e (the left panel), a large charge gradient of Δq = 0.45e (the right panel) will generate a more significant difference between the potential wells in the nanopores, impacting on not only the moving mode but also the moving velocity.Fig. 5B shows the probabilities of the walking mode pw and the jumping mode pj with various charge gradients. When a robot leg, such as the leg2 in the state F2 shown in Fig. 3B, adjusts its conformations to try to enter the nearest neighboring nanopore (pore II), the next nearest neighboring nanopore (pore III) can provide an attraction for the robot legs. If this attraction is weak at small charge gradient, most moving events still will choose the walking mode. However, As Δq increases, the attraction from the next nearest neighboring nanopore becomes stronger, leading the jumping behavior to occur more easily. Therefore, more jumping events can be observed at large charge gradient.
Meanwhile, we find that the moving velocity v of the nanorobot increases with the charge gradient Δq, as shown in Fig. 5C. Although the moving distance is nearly unchanged due to the fixed pore–pore distance, the strong nanopore-chain attraction can reduce both the conformational adjustment duration τa and the forward-moving duration τf. At large Δq, every ssDNA chain can easily enter the corresponding nanopore due to the strong nanopore–ssDNA chain attraction,100 resulting in the decrease of τa. In addition, the large Δq between nanopores provides a strong effective drag force for the nanorobot, leading the nanoparticle to move quickly from one nanopore to the next one, thereby reducing τf. However, as presented in Fig. 5D, the decrease trends of τa (black squares) and τf (red cycles) with respect to Δq are different. Specifically, It is found that the conformational adjustment duration τa is nearly inversely proportional to Δq, as τa ∼ 1/Δq, while the forward-moving duration τf shows a linear reduction of τf ∼ −Δq. From the different decrease trends of τa and τf, we can find that τa is dominant in the total moving time of the nanorobot. Therefore, based on the relationship between τa and Δq, the velocity of the nanorobot can be described by the empirical relationship v ∼ Δq/(1 + 2Δq) by fitting our simulation results, as presented in Fig. 5C.
3.5. Effects of the external voltage ΔV
The moving properties of the nanorobot presented above are obtained under the conditions without the external voltage. However, in many nanopore-device-based applications,58–61 an external voltage (across the nanopores) is required to create a steady electric field within the nanopores. Therefore, we further study the effect of the external voltage on the moving dynamics of the nanorobot. The left panel of Fig. 6A shows the 2D voltage-induced electric potential ϕ (see eqn (3)) at the x–y plane of z = 0 Å. In addition to the electrostatic potential φ generated by the pore charges, the total potential (ϕ + φ) is more complicated (see the right panel in Fig. 6A). The simulations are performed with the external voltage varying in the range of ΔV = 0–10V0, where V0 = 25.8 mV is used as the voltage unit in our CG model. The pore–pore distance, charge gradient, and leg length are fixed as Dp = 60 Å, Δq = 0.25e, and N = 16 nts, respectively.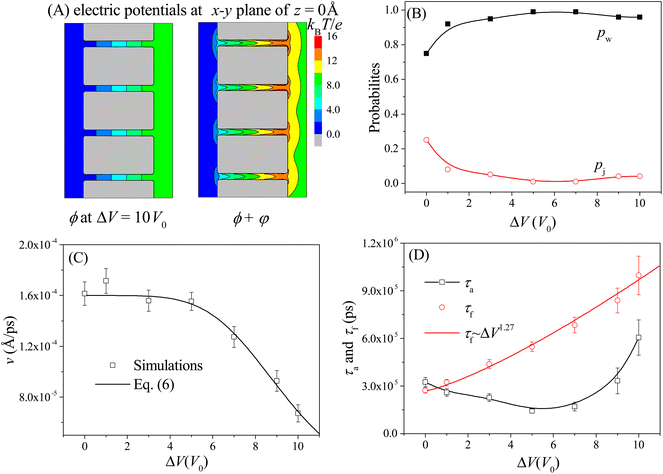 | ||
| Fig. 6 (A) The 2D electric potential ϕ induced solely by the external voltage ΔV = 10V0 (left panel) and the total electric potential ϕ + φ caused by the combination of the external voltage and nanopore charges (right panel) at the x–y plane of z = 0 Å. (B) The ΔV-dependent probabilities of the walking mode pw (solid black squares) and the jumping mode pj (open red cycles). The lines are provided as a visual guide. (C) The moving velocity v of the nanorobot as a function of the external voltage. The simulation results are represented by the scattered points and the empirical relationship in eqn (6) is shown by the line with the best-fitted parameters a = 0.106 and β = 4.93. (D) The ΔV-dependent conformational adjustment period τa and forward-moving period τf. Here Dp = 60 Å, Δq = 0.25e, and N = 16 nts. | ||
Due to the uniform size of the nanopores, the external voltage produces the same electric fields inside the nanopores, as shown in Fig. 6A, thereby deepening the free energy wells at each pore entry. As a result, during the nanorobot adjusting the conformations, the robot legs find it increasingly challenging to skip the nearest neighboring nanopore since the deep free energy well at the pore entry can trap the legs more effectively. Consequently, the probability of the walking mode pw increases with the external voltage as shown in Fig. 6B. When ΔV > 5V0, more than 90% of the moving events choose the walking mode.
Moreover, we find that as ΔV increases, the moving velocity of the nanorobot v remains nearly constant at small ΔV, and then decreases rapidly at large ΔV, as depicted in Fig. 6C. This change behavior in v is induced by the combined effects of the conformational adjustment duration τa and forward-moving duration τf, as shown in Fig. 6D. With the increase of ΔV, τf increases in a power relationship as τf ∼ ΔV1.27, while τa exhibits a non-monotonic behavior. At small ΔV, the opposite trends of τf and τaversus ΔV balance each other, leading to a nearly constant velocity of the nanorobot. However, at large ΔV, both τf and τa increase with ΔV, resulting in the decrease of velocity of the nanorobot. Combined with the empirical relationships of v with Dp and Δq shown in Fig. 4C and 5C, here we use a phenomenological function to describe the velocity for the nanorobot with the fixed leg length:
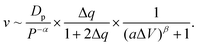 | (6) |
Here P is the distribution probability of the end-to-end distance for a robot leg expressed in eqn (5). The parameters a = 0.106 and β = 4.93 are fitted from our simulation results at Dp = 60 Å and Δq = 0.25e.
In order to investigate the moving dynamics of the nanorobot at large external voltage in detail, we present the time-evolutional trace of the nanoparticle in Fig. 7A at ΔV = 10V0. During the conformational adjustment period (from F3 to E3 in Fig. 7B), if ΔV is large, the robot leg (e.g. leg3) may be attracted back to the nanopore entry where the nanoparticle is located, and be trapped there for some time (as seen in the snapshot at 310 ns). However, this phenomenon cannot be observed at small ΔV. Therefore, we can find that the conformational adjustment duration τa decreases at small ΔV and then increase at large ΔV in Fig. 6D.
After the leg3 enters the pore III successfully (the state E3), the leg1 (already inside the pore I) and the leg3 engage in a “tug-of-war” (as seen in the snapshot at 558 ns), which can last hundreds of nanoseconds.68 The leg1 eventually loses competition (as seen in the snapshot at 614 ns) because of the free energy difference; however, it still cannot approach the pore IV smoothly. The leg1 can be trapped at the entries of the pores II and III due to the deep potential wells induced by the large ΔV (as seen in the snapshots at 744 ns and 806 ns), while the nanoparticle still lingers around the entry of the pore II, as shown in Fig. 7A. The effects of the “tug-of-war” and pore-trapped processes are more pronounced at large voltages, leading to the fast increase of the forward-moving duration τf presented in Fig. 6D. In fact, at extremely large external voltage beyond the voltage regime used in this paper, all three legs of the nanorobot will be always trapped inside the corresponding nanopores, leading to the failed moving event. Therefore, the change in the external voltage can be used to turn the moving case of the nanorobot on or off.
3.6. Effects of the leg length N
We also study the effects of the leg length N on the moving dynamics of the nanorobot. The ssDNA leg lengths of the nanorobot vary from N = 12 nts to 20 nts under the conditions of Dp = 60 Å, Δq = 0.25e, and ΔV = 0. While maintaining a fixed pore–pore distance, the nanorobot with three longer legs is more likely to skip the neighbouring nanopore to find a farther one. Therefore, the probability of walking mode pw decreases with the increase in N, as shown in Fig. 8A.However, the impact of leg length on the moving velocity v [= D/(τa + τf)] of the nanorobot is relatively complicated due to the sensitivity of the conformational adjustment duration τa, forward-moving duration τf, and the moving distance of the nanorobot D to changes in leg length (see Fig. 8B and C). On one hand, as mentioned above, the conformational adjustment duration τa depends on the occurrence probability P of the leading leg locating the next nanopore, as described in eqn (5). This probability is mainly determined by both the pore–pore distance Dp and the leg length N. However, the effects of Dp and N on the conformational adjustment duration τa are different. A larger Dp can reduce the probability of the nanorobot finding the next pore, resulting in an extended τa (see Fig. 4D). Conversely, a longer N can facilitate the nanorobot in locating the next nanopore, leading to a shorter τa (see Fig. 8B). We find that the relationship between τa and N can still be described by eqn (5) with the parameter α = 0.32 (see the black line in Fig. 8B). On the other hand, during the forward-moving process, the leading leg drags the nanoparticle to approach a nanopore by completely entering this nanopore. Therefore, the forward-moving duration τf increases with a scaling relationship as τf ∼ N1.38, which agrees with the simulation results of our previous study on the translocation of a ssDNA chain through a nanopore.79 Moreover, the moving distance D of the nanorobot from the state F2 to the state F4 (see Fig. 3B and D) linearly decreases with the leg length N, as shown in Fig. 8C.
The varied trends observed in the leg length N-dependent conformational adjustment duration τa, forward-moving duration τf, and moving distance D result in a non-monotonic pattern in moving velocity v of the nanorobot, as depicted in Fig. 8D. Specifically, in comparison to the nanorobot with 12 nt-long legs, the one with 14 nt-long legs can more easily locate the next nanopore due to its longer legs. Therefore, within a moving step, the 14 nt-long legs can facilitate the nanorobot in completing the conformational adjustment stage and thus enable it to enter the forward-moving stage more quickly. Fig. 8B reveals that the conformational adjustment duration τa for N = 14 nt is significantly shorter than that for N = 12 nt. While both an increase in τf and a decrease in D (see Fig. 8C) contribute to the reduction of the moving velocity, the drastic decrease in τa at short leg lengths takes precedence over the effects of τf and D, leading to the moving velocity v at N = 14 nt being faster than that at N = 12 nt. However, as N increases further, the decline in τa becomes more gradual. Consequently, the dominant factors influencing moving velocity shift to the forward-moving duration τf and moving distance D. Specifically, as τf increases and D decreases, these two factors collaboratively result in a reduction in v for N > 14 nt. It is essential to note that in our simulations, the moving of nanorobot only includes two complete steps (II–III and III–IV) from pore II to pore IV. For nanorobot with longer legs (>20 nts), it might not find the pore IV when lingering near the pore III. Therefore, more systematic analyses of the dependence of the moving velocity on the leg length require longer nanopore-based tracks, which will be considered in our future study.
4. Conclusions
In this proof-of-principle study, we use a CG model to investigate the moving dynamics of a well-designed nanorobot with three DNA legs on the nanopore-based track. The nanorobot is composed of a large nanoparticle and three ssDNA chains. The nanopores embedded into the membrane distribute in a line and their different charges produce a gradient of the nanopore-leg attractions for the nanorobot. The autonomous walking of the nanorobot is made possible by its three-leg design. As two legs are trapped inside the corresponding nanopores, the remaining one attempts to enter a farther nanopore, generating an effective drag force that help the lagging leg to leave its nanopore.The nanorobot can move autonomously on the nanopore-based track by using two main modes: walking and jumping. The former mode allows the nanorobot to dock with each nanopore to perform its tasks, while the latter mode involves the nanorobot skipping a nanopore to move directly to the next one. The study explores the effects of the pore–pore distance Dp, the charge gradient of the nanopores Δq, the external voltage ΔV, and leg length N, on the moving dynamics of the nanorobot. It finds that longer Dp, smaller Δq, larger ΔV, and shorter N can help the nanorobot to prefer the walking mode. Moreover, the moving velocity of the nanorobot also can be controlled by varying the conditions.
However, we should note that the current simulation model has several limitations. First, the robot core used in this study is smaller and lighter than those used in experiments, such as gold nanoparticle,19,39 CdS nanocrystal,31 and streptavidin protein,101 which may affect the quantitative results of the simulations. Whereas, as the CG model accurately reflects the key properties of the nanorobot, especially for the ssDNA chains, the simulation results are still qualitatively reliable. Second, the nanopore-based track is designed to be one-dimensional (1D) on the planar membrane, while in reality, the fabrication technologies usually produce the two-dimensional (2D) nanopores.69,70 On the 2D nanopore-based tracks, the nanorobot will have more complicated moving behaviors.77 Third, the charge gradient along the nanopore distribution is the only power source considered in this study. A large charge difference, such as Δq = 0.45e, may limit the fabrication of the nanopores and extension the track due to the high charge density of the last nanopore (≈0.23 e Å−2). Moreover, even if the nanopores with high charge density can be realized, it will attract a great amount of ions to screen the ssDNA–pore attractions. Therefore, the nanorobot cannot move along the nanopore-based track for a long distance. Our tests presented in the ESI (see the details in ESI section S4†) show that the nanorobot will be trapped when the charge density of a nanopore is greater than 0.36 e Å−2. Our future simulation studies will consider other power-generating approaches that can be easily employed in applications and can help the nanorobot move longer distance, such as the gradients of the pH value,102 ion concentration,103–105 and temperature.106,107
Author contributions
Li-Zhen Sun designed and performed simulation model; Yao-Jun Ying collected and analyzed simulation data; both authors participated in manuscript writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study is supported by the National Natural Science Foundation of China under grant no. 11704333.References
- M. Schliwa and G. Woehlke, Molecular motors, Nature, 2003, 422, 759–765 CrossRef CAS PubMed.
- M. G. L. van den Heuvel and C. Dekker, Motor proteins at work for nanotechnology, Science, 2007, 317, 333–336 CrossRef CAS PubMed.
- R. D. Vale, T. S. Reese and M. P. Sheetz, Identification of a novel force-generating protein, kinesin, involved in microtubule-based motility, Cell, 1985, 42, 39–50 CrossRef CAS PubMed.
- A. Furuta, M. Amino, M. Yoshio, K. Oiwa, H. Kojima and K. Furuta, Creating biomolecular motors based on dynein and actin-binding proteins, Nat. Nanotechnol., 2017, 12, 233–237 CrossRef CAS PubMed.
- S. Ornes, Inner Workings: medical microrobots have potential in surgery, therapy, imaging, and diagnostics, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12356–12358 CrossRef CAS PubMed.
- S. Zhao, D. Sun, J. Zhang, H. Lu, Y. Wang, R. Xiong and K. T. V. Grattan, Actuation and biomedical development of micro-/nanorobots - A review, Mater. Today Nano, 2022, 18, 100223 CrossRef CAS.
- N. C. Seeman, DNA in a material world, Nature, 2003, 421, 427–431 CrossRef PubMed.
- Y. Dong, C. Yao, Y. Zhu, L. Yang, D. Luo and D. Yang, DNA functional materials assembled from branched DNA: design, synthesis, and applications, Chem. Rev., 2020, 120, 9420–9481 CrossRef CAS PubMed.
- E. Del Grosso, E. Franco, L. J. Prins and F. Ricci, Dissipative DNA nanotechnology, Nat. Chem., 2022, 14, 600–613 CrossRef CAS PubMed.
- M. Rossetti, R. Ippodrino, B. Marini, G. Palleschi and A. Porchetta, Antibody-mediated small molecule detection using programmable DNA-switches, Anal. Chem., 2018, 90, 8196–8201 CrossRef CAS PubMed.
- Y. J. Zhou, Y. H. Wan, C. P. Nie, J. Zhang, T. T. Chen and X. Chu, Molecular switching of a self-assembled 3D DNA nanomachine for spatiotemporal pH mapping in living cells, Anal. Chem., 2019, 91, 10366–10370 CrossRef CAS PubMed.
- B. Yurke, A. J. Turberfield, A. P. Mills, F. C. Simmel and J. L. Neumann, A DNA-fueled molecular machine made of DNA, Nature, 2000, 406, 605–608 CrossRef CAS PubMed.
- B. Lertanantawong, A. Krissanaprasit, T. Chaibun, K. V. Gothelf and W. Surareungchai, Multiplexed DNA detection with DNA tweezers in a one-pot reaction, Mater. Sci. Energy Technol., 2019, 2, 503–508 Search PubMed.
- P. Kosuri, B. D. Altheimer, M. Dai, P. Yin and X. Zhuang, Rotation tracking of genome-processing enzymes using DNA origami rotors, Nature, 2019, 572, 136–140 CrossRef CAS PubMed.
- Y. Ahmadi, A. L. Nord, A. J. Wilson, C. Hütter, F. Schroeder, M. Beeby and I. Barišić, The brownian and flow-driven rotational dynamics of a multicomponent DNA origami-based rotor, Small, 2020, 16, e2001855 CrossRef PubMed.
- P. Zhang, C. Wang, J. Zhao, A. Xiao, Q. Shen, L. Li, J. Li, J. Zhang, Q. Min, J. Chen, H. Y. Chen and J. J. Zhu, Near infrared-guided smart nanocarriers for microRNA-controlled release of doxorubicin/siRNA with intracellular ATP as fuel, ACS Nano, 2016, 10, 3637–3647 CrossRef CAS PubMed.
- E. Kopperger, J. List, S. Madhira, F. Rothfischer, D. C. Lamb and F. C. Simmel, A self-assembled nanoscale robotic arm controlled by electric fields, Science, 2018, 359, 296–301 CrossRef CAS PubMed.
- M. Oishi and K. Saito, Simple single-legged DNA walkers at diffusion-limited nanointerfaces of gold nanoparticles driven by a DNA circuit mechanism, ACS Nano, 2020, 14, 3477–3489 CrossRef CAS PubMed.
- H. Fan, Y. He, Q. Shu, X. Wang, H. Cui, Y. Hu, G. Wei, H. Dong, J. Zhang and N. Hong, Three-dimensional self-powered DNA walking machine based on catalyzed hairpin assembly energy transfer strategy, Anal. Biochem., 2022, 639, 114529 CrossRef CAS PubMed.
- Z. F. Gao, Y. Ling, L. Lu, N. Y. Chen, H. Q. Luo and N. B. Li, Detection of single-nucleotide polymorphisms using an ON-OFF switching of regenerated biosensor based on a locked nucleic acid-integrated and toehold-mediated strand displacement reaction, Anal. Chem., 2014, 86, 2543–2548 CrossRef CAS PubMed.
- W. L. Song, Q. Zhang and W. B. Sun, Ultrasensitive detection of nucleic acids by template enhanced hybridization followed by rolling circle amplification and catalytic hairpin assembly, Chem. Commun., 2015, 51, 2392–2395 RSC.
- P. Peng, L. Shi, H. Wang and T. Li, A DNA nanoswitch-controlled reversible nanosensor, Nucleic Acids Res., 2017, 45, 541–546 CrossRef CAS PubMed.
- B. Li, A. D. Ellington and X. Chen, Rational, modular adaptation of enzyme-free DNA circuits to multiple detection methods, Nucleic Acids Res., 2011, 39, e110 CrossRef CAS PubMed.
- C. Jung and A. D. Ellington, Diagnostic applications of nucleic acid circuits, Acc. Chem. Res., 2014, 47, 1825–1835 CrossRef CAS PubMed.
- K. Pardee, S. Slomovic, P. Q. Nguyen, J. W. Lee, N. Donghia, D. Burrill, T. Ferrante, F. R. McSorley, Y. Furuta, A. Vernet, M. Lewandowski, C. N. Boddy, N. S. Joshi and J. J. Collins, Portable, on-demand biomolecular manufacturing, Cell, 2016, 167, 248–259 CrossRef CAS PubMed.
- A. A. Green, J. Kim, D. Ma, P. A. Silver, J. J. Collins and P. Yin, Complex cellular logic computation using ribocomputing devices, Nature, 2017, 548, 117–121 CrossRef CAS PubMed.
- R. Lopez, R. Wang and G. Seelig, A molecular multi-gene classifier for disease diagnostics, Nat. Chem., 2018, 10, 746–754 CrossRef CAS PubMed.
- S. M. Douglas, I. Bachelet and G. M. Church, A logic-gated nanorobot for targeted transport of molecular payloads, Science, 2012, 335, 831–834 CrossRef CAS PubMed.
- M. You, L. Peng, N. Shao, L. Zhang, L. Qiu, C. Cui and W. Tan, DNA “nano-claw”: logic-based autonomous cancer targeting and therapy, J. Am. Chem. Soc., 2014, 136, 1256–1259 CrossRef CAS PubMed.
- Y. J. Chen, B. Groves, R. A. Muscat and G. Seelig, DNA nanotechnology from the test tube to the cell, Nat. Nanotechnol., 2015, 10, 748–760 CrossRef CAS PubMed.
- T. G. Cha, J. Pan, H. Chen, J. Salgado, X. Li, C. Mao and J. H. Choi, A synthetic DNA motor that transports nanoparticles along carbon nanotubes., Nat. Nanotechnol., 2014, 9, 39–43 CrossRef CAS PubMed.
- Y. Chang, Z. Wu, Q. Sun, Y. Zhuo, Y. Chai and R. Yuan, Simply constructed and highly efficient classified cargo-discharge DNA robot: a DNA walking nanomachine platform for ultrasensitive multiplexed sensing, Anal. Chem., 2019, 91, 8123–8128 CrossRef CAS PubMed.
- A. J. Thubagere, W. Li, R. F. Johnson, Z. Chen, S. Doroudi, Y. L. Lee, G. Izatt, S. Wittman, N. Srinivas, D. Woods, E. Winfree and L. Qian, A Cargo-Sorting DNA Robot, Science, 2017, 357, eaan6558 CrossRef PubMed.
- Z. Wang, R. Hou and I. Y. Loh, Track-walking molecular motors: a new generation beyond bridge-burning designs, Nanoscale, 2019, 11, 9240–9263 RSC.
- J. Pan, T. G. Cha, H. Chen, F. Li and J. H. Choi, DNA walkers as transport vehicles of nanoparticles along a carbon nanotube track, Methods Mol. Biol., 2017, 1500, 269–280 CrossRef CAS PubMed.
- M. Liu, J. Cheng, S. R. Tee, S. Sreelatha, I. Y. Loh and Z. Wang, Biomimetic autonomous enzymatic nanowalker of high fuel efficiency, ACS Nano, 2016, 10, 5882–5890 CrossRef CAS PubMed.
- M. Liber, T. E. Tomov, R. Tsukanov, Y. Berger and E. Nir, A bipedal DNA motor that travels back and forth between two DNA origami tiles, Small, 2015, 11, 568–575 CrossRef CAS PubMed.
- K. Yehl, A. Mugler, S. Vivek, Y. Liu, Y. Zhang, M. Fan, E. R. Weaks and K. Salaita, High-speed DNA-based rolling motors powered by RNase H, Nat. Nanotechnol., 2016, 11, 184–190 CrossRef CAS PubMed.
- A. Bazrafshan, M. E. Kyriazi, B. A. Holt, W. Deng, S. Piranej, H. Su, Y. Hu, A. H. El-Sagheer, T. Brown, G. A. Kwong, A. G. Kanaras and K. Salaita, DNA gold nanoparticle motors demonstrate processive motion with bursts of speed up to 50 nm per second, ACS Nano, 2021, 15, 8427–8438 CrossRef CAS PubMed.
- Y. Li, G. A. Wang, S. D. Mason, X. Yang, Z. Yu, Y. Tang and F. Li, Simulation-guided engineering of an enzyme-powered three dimensional DNA nanomachine for discriminating single nucleotide variants, Chem. Sci., 2018, 9, 6434–6439 RSC.
- X. J. Yang, M. R. Cui, X. L. Li, H. Y. Chen and J. J. Xu, A self-powered 3D DNA walker with programmability and signal-amplification for illuminating microRNA in living cells, Chem. Commun., 2020, 56, 2135–2138 RSC.
- J. Fang, C. Yuan, J. J. Li, J. L. Li, T. Yang, Y. Guo, D. Wang, J. Xue, W. Fu and G. Xie, An enzyme-powered, three-dimensional lame DNA walker, Biosens. Bioelectron., 2021, 177, 112981 CrossRef CAS PubMed.
- H. Li, J. Gao, L. Cao, X. Xie, J. Fan, H. Wang, H. H. Wang and Z. Nie, A DNA molecular robot that autonomously walks on the cell membrane to drive cell motility, Angew. Chem., Int. Ed., 2021, 60, 26087–26095 CrossRef CAS PubMed.
- F. C. Simmel, B. Yurke and H. R. Singh, Principles and applications of nucleic acid strand displacement reactions, Chem. Rev., 2019, 119, 6326–6369 CrossRef CAS PubMed.
- J. Valero and M. Škugor, Mechanisms, methods of tracking and applications of DNA walkers: a review, ChemPhysChem, 2020, 21, 1971–1988 CrossRef CAS PubMed.
- N. C. Seeman, An overview of structural DNA nanotechnology, Mol. Biotechnol., 2007, 37, 246–257 CrossRef CAS PubMed.
- Y. Krishnan and F. C. Simmel, Nucleic acid based molecular devices, Angew. Chem., Int. Ed., 2011, 50, 3124–3156 CrossRef CAS PubMed.
- C. Jung, P. B. Allen and A. D. Ellington, A stochastic DNA walker that traverses a microparticle surface, Nat. Nanotechnol., 2016, 11, 157–163 CrossRef CAS PubMed.
- T. G. Cha, J. Pan, H. Chen, H. N. Robinson, X. Li, C. Mao and J. H. Choi, Design principles of DNA enzyme-based walkers: translocation kinetics and photoregulation, J. Am. Chem. Soc., 2015, 137, 9429–9437 CrossRef CAS PubMed.
- D. Yao, S. Bhadra, E. Xiong, H. Liang, A. D. Ellington and C. Jung, Dynamic programming of a DNA walker controlled by protons, ACS Nano, 2020, 14, 4007–4013 CrossRef CAS PubMed.
- Y. H. Chiang, S. L. Tsai, S. R. Tee, O. L. Nair, I. Y. Loh, M. H. Liu and Z. S. Wang, Inchworm bipedal nanowalker, Nanoscale, 2018, 10, 9199–9211 RSC.
- V. A. Turek, R. Chikkaraddy, S. Cormier, B. Stockham, T. Ding, U. F. Keyser and J. J. Baumberg, Thermo-responsive actuation of a DNA origami flexor, Adv. Funct. Mater., 2018, 28, 1706410 CrossRef.
- J. Ryssy, A. K. Natarajan, J. H. Wang, A. J. Lehtonen, M. K. Nguyen, R. Klajn and A. Kuzyk, Light-responsive dynamic DNA origami-based plasmonic assemblies, Angew. Chem., Int. Ed., 2021, 60, 5859–5863 CrossRef CAS PubMed.
- S. Qi, Y. Sun, X. Dong, I. M. Khan, Y. Lv, Y. Zhang, N. Duan, S. Wu and Z. Wang, Bispecific aptamer-initiated 3D DNA nanomotor biosensor powered by DNAzyme and entropy-driven circuit for sensitive and specificity detection of lysozyme, Nano Res., 2023, 16, 1286–1295 CrossRef CAS.
- N. Srinivas, J. Parkin, G. Seelig, E. Winfree and D. Soloveichik, Enzyme-free nucleic acid dynamical systems, Science, 2017, 358, eaal2052 CrossRef PubMed.
- B. Wang, C. Thachuk, A. D. Ellington, E. Winfree and D. Soloveichik, Effective design principles for leakless strand displacement systems, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E12182–E12191 CrossRef CAS PubMed.
- X. Shi, A. K. Pumm, J. Isensee, W. Zhao, D. Verschueren, A. Martin-Gonzalez, R. Golestanian, H. Dietz and C. Dekker, Sustained unidirectional rotation of a self-organized DNA rotor on a nanopore, Nat. Phys., 2022, 18, 1105–1111 Search PubMed.
- C. Dekker, Solid-State Nanopores, Nat. Nanotechnol., 2007, 2, 209–215 CrossRef CAS PubMed.
- B. M. Venkatesan and R. Bashir, Nanopore sensors for nucleic acid analysis, Nat. Nanotechnol., 2011, 6, 615–624 CrossRef CAS PubMed.
- M. Muthukumar, C. Plesa and C. Dekker, Single-molecule sensing with nanopores, Phys. Today, 2015, 68, 40–46 CrossRef CAS.
- D. Deamer, M. Akeson and D. Branton, Three decades of nanopore sequencing, Nat. Biotechnol., 2016, 34, 518–524 CrossRef CAS PubMed.
- Y. L. Ying, Z. L. Hu, S. Zhang, Y. Qing, A. Fragasso, G. Maglia, A. Meller, H. Bayley, C. Dekker and Y. T. Long, Nanopore-based technologies beyond DNA sequencing, Nat. Nanotechnol., 2022, 17, 1136–1146 CrossRef CAS PubMed.
- J. J. Kasianowicz, E. Brandin, D. Branton and D. W. Deamer, Characterization of individual polynucleotide molecules using a membrane channel, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13770–13773 CrossRef CAS PubMed.
- B. Luan, G. Stolovitzky and G. Martyna, Slowing and controlling the translocation of DNA in a solid-state nanopore, Nanoscale, 2012, 4, 1068–1077 RSC.
- X. Liu, M. Mihovilovic Skanata and D. Stein, Entropic cages for trapping DNA near a nanopore, Nat. Commun., 2015, 6, 6222 CrossRef CAS PubMed.
- Y. Zhang, X. Liu, Y. Zhao, J. K. Yu, W. Reisner and W. B. Dunbar, Single molecule DNA resensing using a two-pore device, Small, 2018, 14, 1801890 CrossRef PubMed.
- P. Cadinu, B. Paulose Nadappuram, D. J. Lee, J. Y. Y. Sze, G. Campolo, Y. Zhang, A. Shevchuk, S. Ladame, T. Albrecht, Y. Korchev, A. P. Ivanov and J. B. Edel, Single molecule trapping and sensing using dual nanopores separated by a zeptoliter nanobridge, Nano Lett., 2017, 17, 6376–6384 CrossRef CAS PubMed.
- P. Cadinu, G. Campolo, S. Pud, W. Yang, J. B. Edel, C. Dekker and A. P. Ivanov, Double barrel nanopores as a new tool for controlling single-molecule transport, Nano Lett., 2018, 18, 2738–2745 CrossRef CAS PubMed.
- J. Choi, C. C. Lee and S. Park, Scalable fabrication of sub-10 nm polymer nanopores for DNA analysis, Microsyst. Nanoeng., 2019, 5, 12 CrossRef PubMed.
- J. D. Spitzberg, A. Zrehen, X. F. van Kooten and A. Meller, Plasmonic-nanopore biosensors for superior single-molecule detection, Adv. Mater., 2019, 31, e1900422 CrossRef PubMed.
- S. M. Iqbal, D. Akin and R. Bashir, Solid-state nanopore channels with DNA selectivity, Nat. Nanotechnol., 2007, 2, 243–248 CrossRef CAS PubMed.
- A. Uddin, S. Yemenicioglu, C. H. Chen, E. Corigliano, K. Milaninia and L. Theogarajan, Integration of solid-state nanopores in a 0.5 μm CMOS foundry process, Nanotechnology, 2013, 24, 155501 CrossRef CAS PubMed.
- R. Ren, Y. Zhang, B. P. Nadappuram, B. Akpinar, D. Klenerman, A. P. Ivanov, J. B. Edel and Y. Korchev, Nanopore extended field-effect transistor for selective single-molecule biosensing, Nat. Commun., 2017, 8, 586 CrossRef PubMed.
- Y. Goto, K. Matsui, I. Yanagi and K. Takeda, Silicon nitride nanopore created by dielectric breakdown with a divalent cation: deceleration of translocation speed and identification of single nucleotides, Nanoscale, 2019, 11, 14426–14433 RSC.
- S. Pud, S. H. Chao, M. Belkin, D. Verschueren, T. Huijben, C. van Engelenburg, C. Dekker and A. Aksimentiev, Mechanical trapping of DNA in a double-nanopore system, Nano Lett., 2016, 16, 8021–8028 CrossRef CAS PubMed.
- W. Si, M. Yu, G. Wu, C. Chen, J. Sha, Y. Zhang and Y. Chen, A nanoparticle-DNA assembled nanorobot powered by charge-tunable quad-nanopore system, ACS Nano, 2020, 14, 15349–15360 CrossRef CAS PubMed.
- W. Si, Z. Zhu, G. Wu, Y. Zhang, Y. Chen and J. Sha, Encoding manipulation of DNA-nanoparticle assembled nanorobot using independently charged array nanopores, Small Methods, 2022, 6, e2200318 CrossRef PubMed.
- E. Henderson, Imaging and nanodissection of individual supercoiled plasmids by atomic force microscopy, Nucleic Acids Res., 1992, 20, 445–447 CrossRef CAS PubMed.
- L. Z. Sun, J. L. Qian, P. Cai, H. X. Hu, X. Xu and M. B. Luo, Mg2+ effects on the single-stranded DNA conformations and nanopore translocation dynamics, Polymer, 2022, 250, 124895 CrossRef CAS.
- L. Z. Sun, J. L. Qian, P. Cai and X. Xu, Mutual effects between single-stranded DNA conformation and Na+-Mg2+ ion competition in mixed salt solutions, Phys. Chem. Chem. Phys., 2022, 24, 20867–20881 RSC.
- D. Chakraborty, N. Hori and D. Thirumalai, Sequence-dependent three interaction site model for single- and double-stranded DNA, J. Chem. Theory Comput., 2018, 14, 3763–3779 CrossRef CAS PubMed.
- G. S. Manning, The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides, Q. Rev. Biophys., 1978, 11, 179–246 CrossRef CAS PubMed.
- N. A. Denesyuk and D. Thirumalai, Coarse-grained model for predicting RNA folding thermodynamics, J. Phys. Chem. B, 2013, 117, 4901–4911 CrossRef CAS PubMed.
- H. Chen, S. P. Meisburger, S. A. Pabit, J. L. Sutton, W. W. Webb and L. Pollack, Ionic strength-dependent persistence lengths of single-stranded RNA and DNA, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 799–804 CrossRef CAS PubMed.
- A. Y. L. Sim, J. Lipfert, D. Herschlag and S. Doniach, Salt dependence of the radius of gyration and flexibility of single-stranded DNA in solution probed by small-angle x-ray scattering, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 021901 CrossRef PubMed.
- A. Meller and D. Branton, Single molecule measurements of DNA transport through a nanopore, Electrophoresis, 2002, 23, 2583–2591 CrossRef CAS PubMed.
- D. W. Deamer and D. Branton, Characterization of nucleic acids by nanopore analysis, Acc. Chem. Res., 2002, 35, 817–825 CrossRef CAS PubMed.
- J. P. Fried, J. L. Swett, B. P. Nadappuram, J. A. Mol, J. B. Edel, A. P. Ivanov and J. R. Yates, In situ solid-state nanopore fabrication, Chem. Soc. Rev., 2021, 50, 4974–4992 RSC.
- J. Xu, X. Jiang and N. Yang, Carbon nanopores for DNA sequencing: a review on nanopore materials, Chem. Commun., 2023, 59, 4838–4851 RSC.
- Z. Yuan, X. Lei and C. Wang, Controllable fabrication of solid state nanopores array by electron beam shrinking, Int. J. Mach. Tools Manuf., 2020, 159, 103623 CrossRef.
- H. Kwok, K. Briggs and V. Tabard-Cossa, Nanopore fabrication by controlled dielectric breakdown, PLoS One, 2014, 9, e92880 CrossRef PubMed.
- J. Feng, K. Liu, M. Graf, M. Lihter, R. D. Bulushev, D. Dumcenco, D. T. Alexander, D. Krasnozhon, T. Vuletic, A. Kis and A. Radenovic, Electrochemical reaction in single layer MoS2: nanopores opened atom by atom, Nano Lett., 2015, 15, 3431–3438 CrossRef CAS PubMed.
- T. Gilboa, A. Zrehen, A. Girsault and A. Meller, Optically-Monitored Nanopore Fabrication Using a Focused Laser Beam, Sci. Rep., 2018, 8, 9765 CrossRef PubMed.
- L. Z. Sun, W. P. Cao, C. H. Wang and X. Xu, The translocation dynamics of the polymer through a conical pore: non-stuck, weak-stuck, and strong-stuck modes, J. Chem. Phys., 2021, 154, 054903 CrossRef CAS PubMed.
- H. Zhou, Macromolecular electrostatic energy within the nonlinear Poisson-Boltzmann equation, J. Chem. Phys., 1994, 100, 3152–3162 CrossRef CAS.
- N. A. Baker, Improving implicit solvent simulations: A Poisson-Centric view, Curr. Opin. Struct. Biol., 2005, 15, 137–143 CrossRef CAS PubMed.
- F. Wu, Y. Fu, X. Yang, L. Z. Sun and M. B. Luo, Driven translocation of semiflexible polyelectrolyte through a nanopore, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 912–921 CrossRef CAS.
- M. Muthukumar, Polymer translocation through a hole, J. Chem. Phys., 1999, 111, 10371–10374 CrossRef CAS.
- https://polymerdatabase.com/polymer%20physics/Excluded%20Volume.html .
- L. Z. Sun, W. P. Cao and M. B. Luo, Free energy landscape for the translocation of polymer through an interacting pore, J. Chem. Phys., 2009, 131, 194904 CrossRef PubMed.
- S. C. Liu, Y. L. Ying, W. H. Li, Y. J. Wan and Y. T. Long, Snapshotting the transient conformations and tracing the multiple pathways of single peptide folding using a solid-state nanopore, Chem. Sci., 2021, 12, 3282–3289 RSC.
- C. T. A. Wong and M. Muthukumar, Polymer translocation through α-hemolysin pore with tunable polymer-pore electrostatic interaction, J. Chem. Phys., 2010, 133, 045101 CrossRef PubMed.
- M. M. Hatlo, D. Panja and R. van Roij, Translocation of DNA molecules through nanopores with salt gradients: the role of osmotic flow, Phys. Rev. Lett., 2011, 107, 068101 CrossRef PubMed.
- Y. He, M. Tsutsui, C. Fan, M. Taniguchi and T. Kawai, Gate manipulation of DNA capture into nanopores, ACS Nano, 2011, 5, 8391–8397 CrossRef CAS PubMed.
- T. Vu, J. Borgesi, J. Soyring, M. D'Alia, S. L. Davidson and J. Shim, Employing LiCl salt gradient in the wild-type alpha-hemolysin nanopore to slow down DNA translocation and detect methylated cytosine, Nanoscale, 2019, 11, 10536–10545 RSC.
- Y. He, M. Tsutsui, R. H. Scheicher, F. Bai, M. Taniguchi and T. Kawai, Thermophoretic manipulation of DNA translocation through nanopores, ACS Nano, 2013, 7, 538–546 CrossRef CAS PubMed.
- M. Belkin and A. Aksimentiev, Molecular dynamics simulation of DNA capture and transport in heated nanopores, ACS Appl. Mater. Interfaces, 2016, 8, 12599–12608 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed descriptions for the force-field of our CG model (section S1); snapshots before state F2 for the selected jumping event (section S2); another type of jumping mode (section S3); nanorobot moving on the nanopores with high charge densities (section S4); parameters of the CG model for the nanorobot (Table S1); energy parameters of the energy potentials (Table S2); simulation data shown in Fig. 4–6 and 8 (Tables S3–S6). See DOI: https://doi.org/10.1039/d3nr03747a |
| This journal is © The Royal Society of Chemistry 2023 |