 Open Access Article
Open Access ArticleAtomistic modeling of the mechanical properties: the rise of machine learning interatomic potentials
Bohayra
Mortazavi
 *ab,
Xiaoying
Zhuang
*ac,
Timon
Rabczuk
d and
Alexander V.
Shapeev
*e
*ab,
Xiaoying
Zhuang
*ac,
Timon
Rabczuk
d and
Alexander V.
Shapeev
*e
aChair of Computational Science and Simulation Technology, Department of Mathematics and Physics, Leibniz Universität Hannover, Appelstraße 11, 30167 Hannover, Germany. E-mail: bohayra.mortazavi@gmail.com; zhuang@iop.uni-hannover.de
bCluster of Excellence PhoenixD (Photonics, Optics, And Engineering–Innovation Across Disciplines), Gottfried Wilhelm Leibniz Universität Hannover, Hannover, Germany
cCollege of Civil Engineering, Department of Geotechnical Engineering, Tongji University, 1239 Siping Road, Shanghai, China
dInstitute of Structural Mechanics, Bauhaus-Universität Weimar, Marienstr. 15, 99423 Weimar, Germany
eSkolkovo Institute of Science and Technology, Skolkovo Innovation Center, Bolshoy Bulvar 30, Moscow, 143026, Russia. E-mail: a.shapeev@skoltech.ru
First published on 4th April 2023
Abstract
Since the birth of the concept of machine learning interatomic potentials (MLIPs) in 2007, a growing interest has been developed in the replacement of empirical interatomic potentials (EIPs) with MLIPs, in order to conduct more accurate and reliable molecular dynamics calculations. As an exciting novel progress, in the last couple of years the applications of MLIPs have been extended towards the analysis of mechanical and failure responses, providing novel opportunities not heretofore efficiently achievable, neither by EIPs nor by density functional theory (DFT) calculations. In this minireview, we first briefly discuss the basic concepts of MLIPs and outline popular strategies for developing a MLIP. Next, by considering several examples of recent studies, the robustness of MLIPs in the analysis of the mechanical properties will be highlighted, and their advantages over EIP and DFT methods will be emphasized. MLIPs furthermore offer astonishing capabilities to combine the robustness of the DFT method with continuum mechanics, enabling the first-principles multiscale modeling of mechanical properties of nanostructures at the continuum level. Last but not least, the common challenges of MLIP-based molecular dynamics simulations of mechanical properties are outlined and suggestions for future investigations are proposed.
1. Introduction
Mechanical properties of materials, such as the elastic modulus, ultimate tensile strength, and maximum elongation, are key parameters in the engineering design of structures and devices. As such, in order to avoid failure of loaded components, mechanical characteristics of every building block must be carefully analyzed. Modern product design largely relies on continuum mechanics models in which materials properties are critical inputs to the models, and can directly influence the accuracy and reliability of modeling. For bulk materials, different experimental tests have been standardized to obtain various mechanical properties. For nanomaterials and nanostructures, an accurate examination of mechanical properties is, however, drastically more complex, time consuming and expensive. Because of small dimensions on the nanoscale, diverse, and in some cases unknown sources of uncertainties can affect the accuracy, reliability and reproducibility of the experimental measurements of mechanical properties. Irrespective of the aforementioned issues, it is well-known that the temperature, loading rate and existing defects may also substantially affect the mechanical and failure responses. Therefore, for the safe and efficient application of nanomaterials in various nanodevices, the development of robust and accurate theoretical methods for an elaborated examination of mechanical properties is required.Density functional theory (DFT) calculations are prominent for their excellent accuracy, flexibility and reproducibility of results. However, because of their excessive computational costs they are not efficient for studying large systems and in particular at finite temperatures. As such, even for the case of graphene,1–3 a two-dimensional (2D) form of carbon atoms, to the best of our knowledge, the mechanical properties at room temperature have not been reported by the DFT method. As a prominent member of quantum mechanics methods, DFT solves the full electronic structure of a system and hence evaluates the interactions of electrons and nuclei and subsequently provides atomic forces. For the majority of problems in mechanics and thermodynamics, one only needs forces and energies, and accordingly the data related to the electronic structure can be discarded. On the other hand, atomic forces and stresses can be also evaluated using the empirical interatomic potentials (EIPs), which is one of the most computationally efficient approaches, and can be employed to study the mechanical properties of systems with millions of atoms at elevated temperatures. When considering the simple case of graphene, as discussed in our earlier investigation,4 the molecular dynamics simulations on the basis of Tersoff,5 AIREBO,6 ReaxFF,7 and optimized Tersoff8 original parameter sets either considerably overestimate the tensile strength value and/or predict non-physical stress–strain curves.
It is, therefore, desirable to have an approach that combines the best features of DFT and classical EIPs for the analysis of mechanical properties of nanomaterials. In recent years, machine learning methods have been successfully employed to accelerate the evaluation of various materials properties.9–13 One of the most prominent accomplishments of machine learning methods in materials science is undoubtedly related to machine learning interatomic potentials (MLIPs), introduced originally by Behler and Parrinello14 in 2007. MLIPs belong to the nonparametric family of interatomic potentials, with the goal of providing DFT-level accuracy and flexibility with the computational efficiency of EIPs. The main difference between MLIPs and EIPs is the capability of the former to reach a higher level of accuracy, with a systematic increase of the number of potential function parameters. For the exploration of nanomaterials’ mechanical properties, MLIPs also show outstanding capabilities. MLIPs are commonly trained using DFT-based datasets, and their performance with respect to flexibility and accuracy15 is close to that of the DFT method, but with substantially accelerated computational time due to bypassing the expensive and also unnecessary electronic structure calculations. MLIPs nowadays can be directly employed to conduct molecular dynamics simulations over highly computationally efficient massively parallel processors and graphics processing units, using various packages, such as LAMMPS,16 TorchMD,17 GPUMD18 and MLatom.17
After the great accomplishments of MLIPs in the acceleration of materials design19,20 and evaluation of various physical properties,21–25 recently their application has been extended towards the analysis of mechanical and failure responses of nanomaterials,4,26 outperforming both DFT and EIP counterparts. In the previous review papers, the successful employment of MLIPs in the analysis of diverse properties of molecular systems27–33 and evaluation of thermal conductivity of crystalline structures13,34 have been highlighted. Nonetheless, with respect to the examination of mechanical and failure properties, to the best of our knowledge there exists currently no literature review that highlights the accuracy, advantages, shortcomings and challenges of MLIPs in comparison with the conventional counterparts. The objective of the current minireview is to address the aforementioned points, and also provide useful prospects for future studies, in order to facilitate efficient and accurate MLIP-based exploration of mechanical properties. To achieve this goal, we first briefly discuss the basic concepts of MLIPs and outline popular strategies for developing a MLIP for the analysis of mechanical properties in Section 2. In Section 3, with the support of several recent studies, robustness of MLIPs in the analysis of mechanical properties will be highlighted and shortcomings of EIP and DFT conventional counterparts will be emphasized. Section 4 elaborates the main challenges of MLIP-based molecular dynamics simulations of mechanical properties and provides suggestions for further investigations. Finally, in Section 5 the concluding remarks regarding the application of MLIPs in the examination of mechanical and failure properties will be presented.
2. Training a MLIP for the analysis of mechanical properties
As mentioned, MLIPs are nonparametric interatomic potentials and similar to other machine learning methods, they rely mostly on the quantum-mechanical data for training and testing. A typical MLIP consists of two basic elements: “descriptors”, and “regression model”, which itself is a function of descriptors (refer to ref. 17 and 28 for elaborated details). The atomic environment is captured by descriptors, which describe the nearsightedness of the MLIP within a predefined cutoff distance depending on the interaction types, for the sake of accuracy and computational efficiency as well. Behler–Parrinello14 and bispectrum coefficients35 are examples of the descriptors used in MLIPs.36 MLIPs generally include large sets of descriptors, in order to ensure a reliable description of reasonable atomic environments. The regression model is the second basic element of a MLIP, which can be based on linear/polynomial regression, kernel methods, or artificial neural networks.14,30 For the modeling of atomistic systems, numerous MLIPs have been developed and well-tested on a number of materials science problems. Among them are neural network potentials (NNPs),14 Gaussian approximation potentials (GAPs),37 moment tensor potentials (MTPs),10,38 spectral neighbor analysis potentials (SNAPs),35 deep tensor neural networks,39 Gaussian moment neural network potentials (GM-NNPs)40 and most recently neuroevolution-potentials (NEPs).41 In the present work, the theoretical backgrounds of the aforementioned MLIPs are not discussed and as such an interested reader should refer to the original works. MLIPs follow the same procedure as other machine learning methods, which means that with the incorporation of sufficiently large data, the precise understanding of the underlying physics becomes less critical. As such, after deciding on the MLIP functional form, the corresponding parameters are required to be optimized/fitted over ab initio datasets. Similarly to other machine-learning methods, the accuracy and stability can be afterward tested, and if required the model hyperparameters and/or the training data can be modified, and this process can be repeated until the desired MLIP is developed.In comparison with EIPs, MLIPs show strong dependency on the quality and diversity of DFT-based datasets used for training, meaning that the configurations or atomic environments that evolve during a simulation should be compatible with those occurring during the training process. For example, while a Tersoff EIP parameterized using the phonon dispersion of graphene42 could be employed to study the thermal and mechanical properties of highly defective graphene,43 a MLIP trained over DFT-based data of pristine graphene most probably cannot keep defective systems stable. After defining the functional form of a MLIP, the next step is to design and implement an appropriate training process. Ab initio molecular dynamics (AIMD) simulations are presently the most popular approach for preparing the required datasets for training a MLIP. AIMD simulations offer the possibility of adjusting the temperature of the system, and consequently enable automatic generation of diverse reasonable atomic environments. High temperatures during AIMD calculations are useful to capture atomic environments with larger deformations and structural instability and failures, whereas low temperature calculations can improve sampling close to the ground state. For the analysis of mechanical and failure properties, it is critical that the dynamic atomic environments corresponding to the failure initiation and progress occur during the preparation of training datasets. For this purpose, AIMD calculations should be conducted not only using the stress-free samples under high temperatures, but also over strained samples, in order to simulate the failure process by increasing the temperature.4,26,44 The size of the considered structures in the AIMD simulations is another aspect of the dataset preparation. Larger structures can be undoubtedly advantageous in capturing more diverse atomic environments, which nonetheless affect the computational efficiency. As a general rule for periodic systems, as those of popular plane-wave-based DFT calculations, the size of the training configurations in every direction should be at least twice the cutoff distance of the MLIP. Another aspect is that the configurations prepared using the AIMD simulations are correlated for close time steps, and consecutive configurations do not describe new useful atomic environments, and as such the incorporation of complete AIMD data may not only be computationally inefficient, but may also lead to overfitting issues. To efficiently avoid this issue, AIMD configurations should be subsampled for the training of MLIPs. After preparing the datasets with sufficiently large configurations to capture the possible atomic environments, the MLIP parameters are optimized, with a goal to precisely reproduce the DFT results for the energy, forces, and stresses of the training configurations. On this basis, the details of DFT calculations, MLIPs’ hyperparameters and fitting process can affect the accuracy and transferability of the developed interatomic potential. This reveals that the results by a MLIP may change, depending on the training process, and therefore it is beneficial to look for optimal setups.
In order to develop MLIPs for the analysis of mechanical properties, finding an efficient and universal training procedure is the foremost challenging issue. As discussed earlier, the training dataset has to be rich enough to capture all possible atomic environments, occurring during the molecular dynamics simulations. If the atomic environments can be directly constructed for a given problem, it becomes possible to passively develop a MLIP and conveniently employ it for the desired calculations. Since the training of a MLIP includes computational cost, such a passive training strategy omits the need for the potential retraining, and can thus improve the computational efficiency and facilitate the modeling process as well. On the other hand, if the complete atomic environment cannot be produced prior to the molecular dynamics simulations, one needs to employ active learning (also sometimes referred to as learning on the fly). In the aforementioned approaches, first a MLIP can be developed using the known configurations, and then molecular dynamics simulations can be conducted using the available MLIP to find unexplored atomic environments. With the aid of DFT calculations, energy, forces, and stresses of new configurations can be obtained, and incorporated into the original training data, and a new MLIP can be retrained. The active learning process is then continued and repeated until a stable MLIP is trained, which has been elaborately discussed in previous studies.20,45,46
In order to practically elaborate on the possible strategies for the training of a MLIP for the analysis of mechanical properties, we consider the simulation of nanoindentation of bulk materials. The on-the-fly learning of MTPs for the simulation of complex nanoindentation of bulk covalent materials has been recently successfully accomplished by Podryabinkin et al.,46 which is schematically shown in Fig. 1. One technical complexity worth noting is that the unexplored atomic environments occur within the vicinity of the nanoindenter tip, which is a small portion of a large model (as illustrated in Fig. 1a). It is thus critical that only regions with the highest extrapolation grades45 are identified and used in the additional DFT calculations, most essentially because of lack of new useful atomic environments in the rest of the model, but also due to the unaffordable cost of DFT calculations for large systems. Although active learning offers a robust opportunity to develop stable MLIPs, because of the fact that several steps of DFT calculations and MLIPs’ retraining are required, the overall computational cost is substantially higher than that of the passive fitting. For the investigation of mechanical properties under the nanoindentation, around the nanoindenter tip one expects the formation of highly disordered or amorphous configurations, whereas the crystal structure in the far regions is deformed only slightly. Therefore, one possibility is to include crystalline and various amorphous lattices in the original training datasets and conduct AIMD simulations with variable temperatures and under different initial strains, to artificially simulate structural transitions and failures. The complete AIMD trajectories could be subsampled in order to efficiently train a preliminary MLIP. The accuracy of the aforementioned MLIP can be then examined over the complete AIMD dataset, and configurations with the worst extrapolation grades45 could be identified and incorporated to the original subsampled dataset. A stable MLIP with an improved accuracy and stability can then be refitted using the second training dataset. This two-step passive training approach has recently been successfully applied in several studies for predicting the uniaxial stress–strain and failure responses of 2D materials4,44,47–50 and amorphous systems51 and showed outstanding accuracy as compared with DFT results. The two-step passive training approach can substantially facilitate the development of MLIPs, but the stability is not guaranteed and thus the necessity of on-the-fly or active learning cannot be completely omitted.
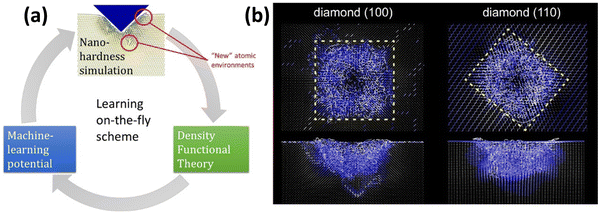 | ||
| Fig. 1 Learning on-the-fly on atomic environments for the simulation of nanoindentation of covalent bulk materials (reprinted from ref. 46, copyright 2022, American Chemical Society). | ||
3. Case studies of applications of MLIPs
In this section, we consider several examples of graphene and other 2D covalent nanomembranes, in order to not only highlight the robustness of MLIPs, but also elaborate on the bottlenecks of the popular DFT and EIP methods in the examination of mechanical and failure responses. Although the presented examples are related to 2D materials, but similar to the conventional EIP and DFT methods, from the theoretical point of view the dimensionality of the systems (1D, 2D or 3D) is not expected to affect the practicality of the MLIPs. In fact, 2D materials due to their freedom for large out-of-plane deflections are among the most complicated systems for stable molecular dynamics calculations.We first consider graphene, which shows an extremely symmetrical atomic lattice with short-range covalent interactions. As illustrated in Fig. 2, on the basis of uniaxial tensile simulations, with the original Tersoff,5 ReaxFF,7 AIREBO6 and optimized Tersoff8 EIPs and employing the original cutoff distances, the ultimate tensile strengths of the single-layer graphene at room temperature were predicted to be 200,52,53 125–138,54 150–25055,56 and 158 GPa,43 respectively, which are generally higher than the value of 130 ± 10 GPa as measured experimentally by Lee et al.57 The aforementioned EIPs also predict unexpected strain hardening at strain levels close to the ultimate strength point. Although the model with a ReaxFF7 more closely reproduces the tensile strength value of graphene, it yields very irregular and nonphysical stress–strain curves.54 It is worth noting that the unusual strain hardening and overestimation of graphene's tensile strength could be removed by the trial and error adjustment of the cutoff distance function of AIREBO and Tersoff EIPs43,56 (see Fig. 2c and d). On the other hand, uniaxial tensile simulations conducted at 1 K, on the basis of a two-step passively fitted MTP model, could very closely reproduce the direction dependent stress–strain curves of the graphene as compared with DFT results (see Fig. 2e and f).4 The results shown in Fig. 2 clearly reveal the advantages of MLIPs in the analysis of graphene's mechanical properties, in which a passively fitted MTP4 could substantially outperform the widely employed/trusted empirical interatomic potentials. It is also useful to consider the DFT results for graphene (shown in Fig. 2b, e and f), in order to understand their main bottlenecks. Graphene is characterized as a brittle material,58–60 which means that at the ultimate tensile strength point, this nanosheet suddenly cracks and fails completely. By decreasing the loading temperature, and consequently suppressing of the atomic vibrations, even ductile materials’ failure behavior approaches the brittle-like mechanism. When considering the DFT results, which correspond to the uniaxial loading at the ground state or zero temperature, the stress values after passing the ultimate tensile strength points show generally smooth patterns, which clearly contradict the expected basic behavior of brittle materials. In other words, while with DFT the failure mechanism of graphene cannot be characterized correctly, the MTP model could precisely reproduce the expected brittle failure behavior. The other critical shortcoming of the DFT method is that the analysis of mechanical properties is computationally feasible only close to the ground state and by neglecting the temperature effects. It is well-known that the atomic vibrations at finite temperatures can significantly affect the stress–strain and failure responses. At higher temperatures, the symmetry of structures decreases, and therefore larger models should be considered in order to predict realistic mechanical behavior. For the case of graphene at room temperature, with the molecular dynamics method it is necessary to include systems with several thousands of atoms and conduct the simulations for several millions of time steps to account for the stochastic nature of the failure.4 It is thus conspicuous that the realistic analysis of mechanical properties at finite temperatures is computationally infeasible to be conducted by the DFT method. To summarize, the first example of graphene could clearly confirm that a two-step passively fitted MLIP4 could undoubtedly outperform the popular EIP and DFT methods with respect to accuracy and capturing the temperature and failure mechanism, respectively.
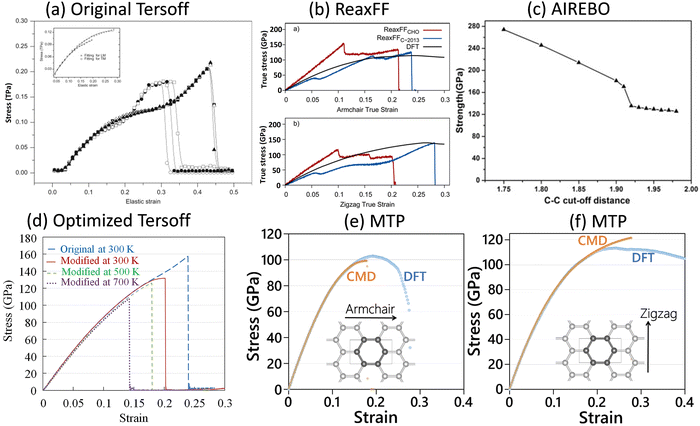 | ||
| Fig. 2 The tensile strength and elongation of the graphene monolayer predicted by (a) original Tersoff5 (reprinted from ref. 53, copyright 2010, Elsevier), (b) ReaxFF7 (reprinted from ref. 54, copyright 2015, American Chemical Society), (c) AIREBO6 (reprinted from ref. 56, copyright 2014, Elsevier), and (d) optimized Tersoff8 (reprinted from ref. 43, copyright 2016, Elsevier) EIPs, with those by (e and f) DFT (at 0 K) and MTP-based (at 1 K) models (reprinted from ref. 4, copyright 2021, John Wiley & Sons). | ||
In order to further highlight the advantages of MLIPs in comparison with EIPs in the analysis of mechanical properties, we consider the three recently experimentally synthesized 2D lattices of biphenylene,61 quasi-hexagonal-phase C60 fullerene (qHPC60)62 and BC2N,63 which are illustrated in Fig. 3. From the atomic structures, it is conspicuous that both of biphenylene (see Fig. 3a) and qHPC60 (see Fig. 3d) full-carbon monolayers are anisotropic systems, with different bonding architectures along the two perpendicular in-plane directions. MLIP-based results close to the ground states by the MTP for biphenylene64 (see Fig. 3b) and NEP for qHPC6026 (see Fig. 3e) not only clearly confirm the anisotropic mechanical characters, but more importantly very precisely reproduce the DFT results. On the other hand, using the ReaxFF65 EIP-based models, the ultimate tensile strengths of the biphenylene66 and qHPC6067 monolayers are found to be close for both the considered loading directions, which clearly contradicts the expected anisotropic behavior. Moreover, the EIP-based results at 300 K are not consistent with those by the DFT method. The underestimation of DFT results for the ultimate tensile strengths of the biphenylene66 monolayer can be attributed to the temperature effects, whereas for the qHPC6067 system the tensile strength values at 300 K are almost twice higher than those predicted by the DFT at the ground state, which reveals considerable overestimations of the tensile strength. As it is clear, the results based on the ReaxFF EIPs may overestimate or underestimate the DFT-based predictions for similar types of systems, which can obviously misguide the evaluation of mechanical properties. It is noticeable that by using a thickness of 8.78 Å26 for the qHPC60 monolayer, the ultimate tensile strengths of this system by a two-step passively fitted MTP68 (see Fig. 3f) show a discrepancy of around 15% at the maximum with those predicted by the NEP,26 which can be explained by the fact that the van der Waals (vdW) dispersion correction69 was not employed in the latter MLIP-based study. It is also noticeable that the DFT results26 in accordance with those by MLIPs26,68 clearly reveal the brittle failure mechanism for the qHPC60 monolayer. Interestingly, according to a latest experimental study,70 the room temperature thermal conductivity of the qHPC60 was measured to be around 2.7 W m−1 K−1,70 which is in excellent agreement with the value of 2.9 W m−1 K−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 68 predicted by the MTP along the x direction. On the other hand, for the x direction of the qHPC60 monolayer, the NEP-based model predicted a thermal conductivity of around 100 W m−1 K−1,71 which is almost two orders of magnitude higher than that measured experimentally.70 The molecular dynamics simulations on the basis of the polymer consistent force-field (PCFF)72 also overestimate the thermal conductivity by an order of magnitude.70 It is thus observable that the MTP models could accurately evaluate the both mechanical and thermal properties of the qHPC60 monolayer, however it is noticeable that it fails to clearly reproduce the nonlinear elasticity as those by NEP and DFT. It is once again worth mentioning that for the biphenylene64 system, the DFT results similarly to the case of graphene could not accurately predict the expected brittle failure behavior.
68 predicted by the MTP along the x direction. On the other hand, for the x direction of the qHPC60 monolayer, the NEP-based model predicted a thermal conductivity of around 100 W m−1 K−1,71 which is almost two orders of magnitude higher than that measured experimentally.70 The molecular dynamics simulations on the basis of the polymer consistent force-field (PCFF)72 also overestimate the thermal conductivity by an order of magnitude.70 It is thus observable that the MTP models could accurately evaluate the both mechanical and thermal properties of the qHPC60 monolayer, however it is noticeable that it fails to clearly reproduce the nonlinear elasticity as those by NEP and DFT. It is once again worth mentioning that for the biphenylene64 system, the DFT results similarly to the case of graphene could not accurately predict the expected brittle failure behavior.
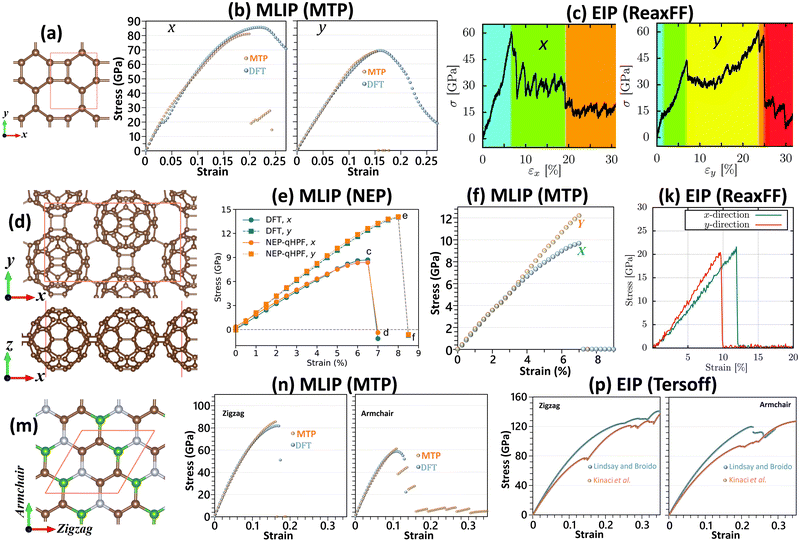 | ||
| Fig. 3 (a) Atomic structure of the fully planar biphenylene monolayer and the predicted stress–strain curves along the x and y directions by (b) MTP (reprinted from ref. 64, copyright 2022, Elsevier) and (c) ReaxFF (reprinted from ref. 66, copyright 2022, Royal Society of Chemistry). (d) Top and side views for the atomic structure of the qHPC60 monolayer and the predicted stress–strain curves along the x and y directions by (e) NEP (reprinted from ref. 26, copyright 2023, Elsevier), (f) MTP (reproduced from ref. 68 using a thickness of 8.78 Å as that of ref. 26) and (k) ReaxFF (reprinted from ref. 67, copyright 2022, Elsevier). (m) Atomic structure of the flat BC2N monolayer and the predicted stress–strain curves along the armchair and zigzag directions by (n) MTP and (p) two different Tersoff potentials (reprinted from ref. 49, copyright 2022, Elsevier). | ||
We next shift our attention to the case of BC2N63 monolayer, which is a ternary composition. As shown in Fig. 3n, close to the ground state the MTP-based models once again accurately reproduce the directional uniaxial stress–strain curves and failure behavior of the BC2N monolayer by DFT,49 confirming the robustness of MTP also for multi-elemental systems. By conducting exactly identical molecular dynamics simulations at 1 K49 along with employing two different Tersoff potentials by Kinaci et al.73 and Lindsay and Broido,74 the predicted stress–strain curves (see Fig. 3p) are found to considerably overestimate the DFT results. It has been also confirmed in another recent study for the BCN nanosheets75 that the EIP-based molecular dynamics simulations may not only predict inaccurate values for the thermal conduction and mechanical properties, but they may also misrepresent the physical behaviour, similarly to the aforementioned examples of predicting isotropic tensile strengths for clearly anisotropic systems. On the other hand, as discussed earlier and also in several recent studies for densely packed 2D lattices,4,49,64,75 the DFT method fails in accurately reproducing the failure mechanism, even in the ground-state. At finite temperatures the required calculations for the analysis of mechanical properties are exceedingly expensive and hence beyond the capability of the DFT method to be reliably examined. The presented examples clearly reveal the robustness of MLIP-based models in the analysis of mechanical properties and confirm that they can efficiently resolve the bottlenecks of popular EIP and DFT methods.
For the highly symmetrical structures, as those of graphene, biphenylene and BC2N lattices, the DFT method can provide a highly accurate and computationally efficient solution for determining the mechanical properties at the ground state. It is worth noting that vacuum in the typical plane-wave DFT method also increases computational costs. As such, for low-symmetrical and highly porous structures, as those of conductive frameworks, the DFT calculations of uniaxial tensile simulations at the ground state also start to become exceedingly expensive and complex for the implementation. For low-symmetrical systems, if MLIPs could accurately reproduce the mechanical and failure properties, then they may outperform DFT calculations, even in their “comfort zone” at the ground state. In Fig. 4, the predicted uniaxial stress–strain curves of the conductive framework of C5N nanosheets are compared using the MTP at 1 K and DFT methods.47 In the aforementioned example, two different MTPs were trained over AIMD datasets with and without the DFT-D369 vdW dispersion correction. The results shown in Fig. 4 confirm that while both two-step passively trained MTPs could accurately reproduce the tensile strengths of the C5N nanosheet, with taking the vdW dispersion correction into account the general agreement for the stress–strain curve is considerably closer to those by DFT.47 The results shown in Fig. 4c also confirm that the two-step passively fitted MTP could precisely reproduce the failure mechanism by the DFT method. The proposed modeling strategy in ref. 47 was also employed to study the mechanical properties of five different C6N7-based nanoporous conductive nanosheets,44 which are shown in Fig. 4d. The presented comparisons with DFT results44 confirm the outstanding accuracy of the two-step passively fitted MTPs in reproducing the direction-dependent mechanical and failure responses of low-symmetrical, multi-elemental and nanoporous systems.
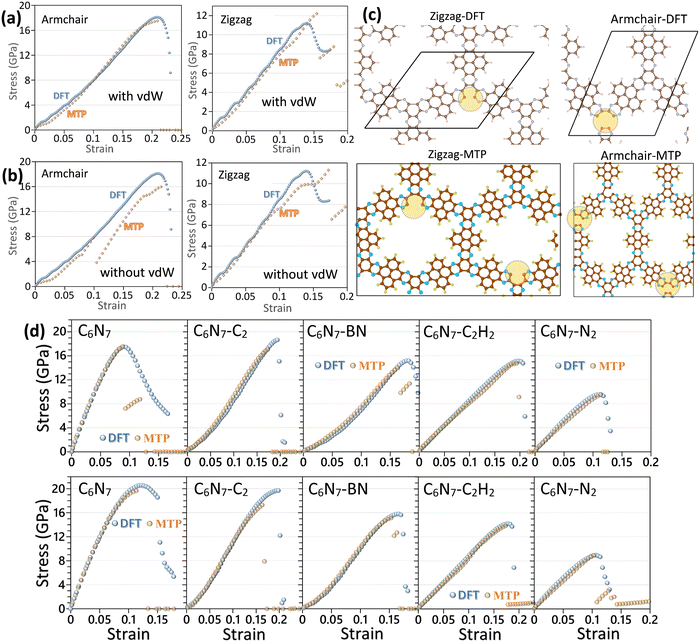 | ||
| Fig. 4 Uniaxial stress–strain curves of the C5N monolayer predicted by the DFT and MTP-based models (at 1 K), (a) with and (b) without inclusion of vdW dispersion correction in the AIMD dataset preparation. (c) Failure behaviors for the MTP and DFT models along two different loading directions (reprinted from ref. 47, copyright 2022, Royal Society of Chemistry). (d) Comparison of the uniaxial stress–strain curves of five different C6N7-based nanoporous conductive 2D frameworks along two different loading directions predicted by DFT and MTP-based models (reprinted from ref. 44, copyright 2022, Elsevier). | ||
3.1 Multiscale modeling
In the above review, the advantages of MLIPs over the EIP-based and DFT-based approaches to the calculation of mechanical properties have been emphasized. MLIPs are commonly trained using the computationally affordable DFT datasets, and they exhibit close accuracy and also take advantage of the inherent flexibility of the DFT method to investigate novel compositions. In recent studies,4,76 another novel opportunity of MLIPs has been highlighted, which is related to the first-principles multiscale modeling of mechanical and thermal properties. It has been confirmed that MLIPs passively fitted to AIMD datasets can enable first-principles multiscale modeling, in which DFT level of accuracy can be hierarchically bridged to explore the properties of macroscopic systems. Herein the basic concept of first-principles multiscale modeling of mechanical properties4 will be discussed, which is similar to that of the thermal transport.76 The aforementioned concept was practically implemented to study the mechanical properties of experimentally realized coplanar graphene/borophene heterostructures,77 for which the EIPs are unable to keep structures stable at finite temperatures.4 The first-principles multiscale modeling of mechanical and thermal conduction properties comprises four major steps,4,76 which are schematically shown in Fig. 5. In the first step, AIMD simulations were carried out over stress-free and strained atomic configurations under varying temperatures to prepare required datasets for representing the atomic environment. Next, MLIPs were developed using the two-step passive training approach explained earlier. To obtain the mechanical properties of pristine and heterostructure phases at room temperature, MLIP-based classical molecular dynamics calculations were conducted. In the final step, on the basis of data provided by MLIP-based molecular dynamics simulations, the mechanical/failure responses of macroscopic heterostructures were examined using the continuum finite element method. From the practical point of view, MLIPs can enable the modeling of nanostructures at the macroscopic level, with minimal prior physical knowledge, DFT level of accuracy and affordable computational costs. To achieve the aforementioned goals, the EIPs generally have the stability and accuracy concerns, and DFT-based calculations are not computationally feasible.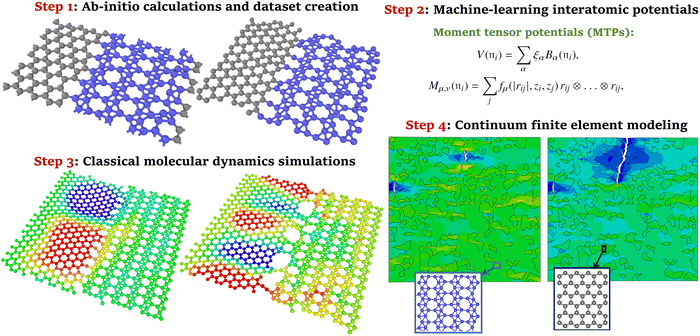 | ||
| Fig. 5 Main steps to conduct the first-principles multiscale modeling of mechanical properties (reprinted from ref. 4, copyright 2021, John Wiley & Sons). | ||
4. Challenges in the application of MLIPs
Despite the outstanding capabilities of MLIPs for the analysis of mechanical properties, similarly to other numerical approaches they are not perfect, and it is thus necessary to understand their current shortcomings and explore possibilities to enhance their performance. In the following, we will briefly present our view on the current challenges in the practical employment of MLIPs for the examination of mechanical and failure responses using the standard molecular dynamics simulations.4.1 The choice of potential
Although the accuracy of popular MLIPs is expected to be very close to that of the DFT-based training datasets, still it is not well stablished which type of MLIPs, and with which combination of hyperparameters, cutoff distances, and training strategies can yield more accurate and computationally efficient results for the modeling of mechanical properties. It is nonetheless a basic fact that two different MTPs or GAPs developed with different hypermeters, or trained over dissimilar training datasets are expected to yield close, but also different predictions. The evolution of dynamic atomic environments during the mechanical loading may moreover cause MLIPs to extrapolate or face stability issues. Because of the complex potential functions of MLIPs, one of the efficient ways to address the aforementioned challenge is to conduct comparative studies with fixed datasets, and train various types of MLIPs with different hyperparameters, and consequently directly compare the results close to the ground state with those obtained by DFT. In the next step, the thermal stability of MLIPs has to be checked at finite temperatures, taking into account that their main advantage over DFT stems from their ability to study systems with thermally vibrating atoms. For the ultimate goal of developing automated platforms for materials design, it is also highly beneficial to devise universal training strategies, as those previously proposed for MTPs.4,23,444.2 Type of interactions
In numerous recent studies, MLIPs have been already successfully employed to study the mechanical and failure properties of covalent systems. Nonetheless, the accuracy and robustness of MLIPs for other systems with metallic, ionic or magnetic interactions have not been elaborately examined. It is worth noting that using the exactly same type of MTPs, trained over identically prepared AIMD datasets, the ultimate tensile strengths of metallic χ3 borophene and covalent graphene monolayers show maximum discrepancies of around 18% and 7% with those obtained by DFT, respectively.4 Long-range interactions, such as vdW or electrostatic interactions, may also affect the mechanical properties, particularly for molecular-based systems as those of polymers. Due to substantially higher computational costs of MLIPs than EIPs, increasing the cutoff distance not only imposes higher computational costs, but may also affect the accuracy of describing the critical short-range interactions. One promising possibility is to simultaneously consider short-range interactions via a standard MLIP and capture long-range counterparts with standard EIPs, like Lennard-Jones, or Buckingham potentials, as it has been most recently successfully accomplished for the 2D vdW heterostructures.78 Nonetheless, as discussed for the cases of the C5N47 and C6N7-based44 nanosheets (see Fig. 4), short-range MLIPs trained over vdW dispersion corrected AIMD datasets could capture the effects of non-bonding interactions and more precisely reproduce the mechanical properties predicted by DFT.44,47,79 It is worth reminding that since MLIPs’ real-world accuracy is directly correlated to the DFT-based training data, different exchange–correlation functionals combined with ultra-soft pseudopotentials or projector augmented wave potentials may also affect their accuracy.80,81 In order to study the mechanical properties of crystalline solids, Perdew−Burke−Ernzerhof,82 Perdew–Burke–Ernzerhof revised for solids83 and revised Perdew–Burke–Ernzerhof84 are currently among popular choices. Depending on the type of interactions, it is required to carefully decide on the appropriate exchange–correlation functional and corresponding cutoff energy, and if needed incorporate additional setups related to the magnetic states, Hubbard-correction of materials with strong electronic Coulomb interactions85–87 or vdW dispersion correction. The aforementioned details may affect the accuracy and stability of trained MLIPs, and it is thus not guaranteed that a MLIP can exhibit similar performances for different types of training data.4.3 Transferability
As previously discussed, MLIPs can work accurately within the atomic environments fed into them during the training. On this basis, a MLIP trained over defect-free AIMD configurations will likely be unstable or unreliable for studying defective samples. As such, an MTP trained for the pristine graphene is not transferable/stable to study amorphous43 or polycrystalline88 graphene or biphenylene systems, whereas a Tersoff EIP is completely stable to study their thermo-mechanical properties.43,88 A more transferable MLIP not only requires a more complex and computationally demanding training procedure, and a larger set of parameters, but may also yield a suppressed accuracy for a given structure. For studying a particular system, taking into account that the main advantage of MLIPs when compared with EIPs is related to their superior accuracies, one convenient solution is to specifically train a MLIP. For example, recently the mechanical and failure properties of various graphene-like BC2N49 and graphyne60 nanosheets have been studied using MTPs, in which despite similar atomic interactions and the possibility of training transferable MTPs for the considered systems, separate MTPs were trained in order to maximize the accuracy for every lattice. Another open question is that if a MLIP is trained to simulate the complete stress–strain curve and failure initiation for a given structure, is it able to reproduce the elastic constants as precisely as a MLIP trained over unstrained AIMD configurations or not? In other words, while a more transferable MLIP is trained to account for the failure initiation and progress, its ability to precisely describe the small deformations correlated to elastic constants can be affected.4.4 Strain rate
Because of the required time step of the order of 10−15 s, modeling of the mechanical properties on experimental timescales is one of the main bottlenecks of the conventional molecular dynamics simulations. With the EIPs and current computational modalities, it is strictly difficult if not possible to study the mechanical properties for timescales longer than microseconds or strain rates smaller than 106 s−1. Because of the higher computational costs of MLIPs than EIPs, the strain rate dilemma becomes more pronounced. Once again, the type of interactions may affect the strain rate dependency of the predicted mechanical properties. As an example, it has been proven that the mechanical properties of χ3 borophene with metallic interactions exhibit more significant dependency on the strain rate than the covalently bonded graphene.4 Interestingly, for the graphene and borophene nanosheets4 and other lattices,26,49 it has been numerously reported that the stress–strain relations coincide for different uniaxial loading strain rates, and only the ultimate tensile strength and corresponding strain generally decrease for slower strain rates. This observation can be very useful to report the strain-rate independent mechanical properties by conducting a curve fitting26 or static loading at fixed strains.49 Adopting the NVT thermostat to artificially remove the excessive heat stemming from ultrafast loading, or applying the quasi-static loading,4 can certainly diminish the significance of strain rate but does not guarantee reaching the converged predictions. In order to more precisely evaluate the strain rate effect on the MLIP-based predicted mechanical properties, the employment of metadynamics89 approaches as those of autonomous basin climbing90 or self-learning metabasin escape90 algorithms is thus highly beneficial.5. Concluding remarks
This minireview highlights the superiority of MLIPs compared to EIPs for the analysis of mechanical and failure responses by employing the conventional molecular dynamics simulations. We briefly discussed the basic concepts of MLIPs and outlined popular strategies for developing a MLIP for the analysis of mechanical properties. Based on several recent studies, we show the robustness of MLIP-based models in the analysis of mechanical and failure responses, and moreover confirm their unique capabilities to efficiently resolve the shortcomings of both EIP and DFT methods. It is also discussed that MLIPs offer extraordinary capabilities to conduct first-principles multiscale modeling, bridging the quantum mechanics simulations to the continuum scale modeling. On this basis, by constructing efficient coupling with continuum mechanics solvers and optimization algorithms, the MLIPs can enable developing fully automated platforms, to design, optimize and explore complex mechanical and failure responses of materials and structures at the continuum level with DFT level of accuracy. The current challenges of MLIP-based molecular dynamics simulations of mechanical properties are also summarized. We are hopeful that the presented data and discussions facilitate the development of accurate and computationally robust molecular dynamics models for the analysis of failure and mechanical properties of novel materials and structures.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
B. M. and X. Z. appreciate the funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy within the Cluster of Excellence PhoenixD (EXC 2122, Project ID 390833453). B. M. is moreover thankful to Dr Chernenko for the support of this study. A. V. S. is supported by the Russian Science Foundation (Grant No. 18-13-00479, https://rscf.ru/project/18-13-00479/).References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric field effect in atomically thin carbon films, Science, 2004, 306, 666–669, DOI:10.1126/science.1102896.
- A. K. Geim and K. S. Novoselov, The rise of graphene, Nat. Mater., 2007, 6, 183–191, DOI:10.1038/nmat1849.
- A. H. Castro Neto, N. M. R. Peres, K. S. Novoselov, A. K. Geim and F. Guinea, The electronic properties of graphene, Rev. Mod. Phys., 2009, 81, 109–162, DOI:10.1103/RevModPhys.81.109.
- B. Mortazavi, M. Silani, E. V. Podryabinkin, T. Rabczuk, X. Zhuang and A. V. Shapeev, First-Principles Multiscale Modeling of Mechanical Properties in Graphene/Borophene Heterostructures Empowered by Machine–Learning Interatomic Potentials, Adv. Mater., 2021, 33, 2102807, DOI:10.1002/adma.202102807.
- J. Tersoff, Modeling solid-state chemistry: interatomic potentials for multicomponent systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 5566–5568, DOI:10.1103/PhysRevB.39.5566.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, A reactive potential for hydrocarbons with intermolecular interactions, J. Chem. Phys., 2000, 112, 6472–6486, DOI:10.1063/1.481208.
- S. G. Srinivasan, A. C. T. van Duin and P. Ganesh, Development of a ReaxFF Potential for Carbon Condensed Phases and Its Application to the Thermal Fragmentation of a Large Fullerene, J. Phys. Chem. A, 2015, 119, 571–580, DOI:10.1021/jp510274e.
- L. Lindsay and D. A. Broido, Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205441, DOI:10.1103/PhysRevB.81.205441.
- Y. Ouyang, C. Yu, G. Yan and J. Chen, Machine learning approach for the prediction and optimization of thermal transport properties, Front. Phys., 2021, 16, 1–16 Search PubMed.
- A. S. Ivan Novikov and K. Gubaev, Evgeny Podryabinkin, The MLIP package: Moment Tensor Potentials with MPI and Active Learning, Mach. Learn. Sci. Technol., 2021, 2, 025002 CrossRef.
- R. Hu, S. Iwamoto, L. Feng, S. Ju, S. Hu, M. Ohnishi, N. Nagai, K. Hirakawa and J. Shiomi, Machine–learning-optimized aperiodic superlattice minimizes coherent phonon heat conduction, Phys. Rev. X, 2020, 10, 21050 CAS.
- P. Chakraborty, Y. Liu, T. Ma, X. Guo, L. Cao, R. Hu and Y. Wang, Quenching thermal transport in aperiodic superlattices: a molecular dynamics and machine learning study, ACS Appl. Mater. Interfaces, 2020, 12, 8795–8804 CrossRef CAS PubMed.
- S. Arabha, Z. S. Aghbolagh, K. Ghorbani, M. Hatam-Lee and A. Rajabpour, Recent advances in lattice thermal conductivity calculation using machine–learning interatomic potentials, J. Appl. Phys., 2021, 130, 210903, DOI:10.1063/5.0069443.
- J. Behler and M. Parrinello, Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces, Phys. Rev. Lett., 2007, 98, 146401, DOI:10.1103/PhysRevLett.98.146401.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson, M. A. Wood and S. P. Ong, Performance and Cost Assessment of Machine Learning Interatomic Potentials, J. Phys. Chem. A, 2020, 124, 731–745, DOI:10.1021/acs.jpca.9b08723.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19, DOI:10.1006/jcph.1995.1039.
- M. Pinheiro, F. Ge, N. Ferré, P. O. Dral and M. Barbatti, Choosing the right molecular machine learning potential, Chem. Sci., 2021, 12, 14396–14413, 10.1039/D1SC03564A.
- Z. Fan, Y. Wang, P. Ying, K. Song, J. Wang, Y. Wang, Z. Zeng, K. Xu, E. Lindgren, J. M. Rahm, A. J. Gabourie, J. Liu, H. Dong, J. Wu, Y. Chen, Z. Zhong, J. Sun, P. Erhart, Y. Su and T. Ala-Nissila, GPUMD: a package for constructing accurate machine-learned potentials and performing highly efficient atomistic simulations, J. Chem. Phys., 2022, 157, 114801, DOI:10.1063/5.0106617.
- K. Gubaev, E. V. Podryabinkin, G. L. W. Hart and A. V. Shapeev, Accelerating high-throughput searches for new alloys with active learning of interatomic potentials, Comput. Mater. Sci., 2019, 156, 148–156, DOI:10.1016/j.commatsci.2018.09.031.
- E. V. Podryabinkin, E. V. Tikhonov, A. V. Shapeev and A. R. Oganov, Accelerating crystal structure prediction by machine–learning interatomic potentials with active learning, Phys. Rev. B, 2019, 99, 064114, DOI:10.1103/PhysRevB.99.064114.
- B. Mortazavi, E. V. Podryabinkin, I. S. Novikov, T. Rabczuk, X. Zhuang and A. V. Shapeev, Accelerating first-principles estimation of thermal conductivity by machine–learning interatomic potentials: a MTP/ShengBTE solution, Comput. Phys. Commun., 2021, 258, 107583, DOI:10.1016/j.cpc.2020.107583.
- Z. Liu, X. Yang, B. Zhang and W. Li, High Thermal Conductivity of Wurtzite Boron Arsenide Predicted by Including Four-Phonon Scattering with Machine Learning Potential, ACS Appl. Mater. Interfaces, 2021, 13(45), 53409–53415, DOI:10.1021/acsami.1c11595.
- B. Mortazavi, I. S. Novikov, E. V. Podryabinkin, S. Roche, T. Rabczuk, A. V. Shapeev and X. Zhuang, Exploring phononic properties of two-dimensional materials using machine learning interatomic potentials, Appl. Mater. Today, 2020, 20, 100685, DOI:10.1016/j.apmt.2020.100685.
- B. Mortazavi, E. V. Podryabinkin, S. Roche, T. Rabczuk, X. Zhuang and A. V. Shapeev, Machine–learning interatomic potentials enable first-principles multiscale modeling of lattice thermal conductivity in graphene/borophene heterostructures, Mater. Horiz., 2020, 7, 2359–2367, 10.1039/D0MH00787K.
- B. Mortazavi, A. Rajabpour, X. Zhuang, T. Rabczuk and A. V. Shapeev, Exploring thermal expansion of carbon-based nanosheets by machine–learning interatomic potentials, Carbon, 2022, 186, 501–508, DOI:10.1016/j.carbon.2021.10.059.
- P. Ying, H. Dong, T. Liang, Z. Fan, Z. Zhong and J. Zhang, Atomistic insights into the mechanical anisotropy and fragility of monolayer fullerene networks using quantum mechanical calculations and machine–learning molecular dynamics simulations, Ext. Mech. Lett., 2023, 58, 101929, DOI:10.1016/j.eml.2022.101929.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Combining Machine Learning and Computational Chemistry for Predictive Insights Into Chemical Systems, Chem. Rev., 2021, 121, 9816–9872, DOI:10.1021/acs.chemrev.1c00107.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Machine Learning Force Fields, Chem. Rev., 2021, 121, 10142–10186, DOI:10.1021/acs.chemrev.0c01111.
- J. Behler, Representing potential energy surfaces by high-dimensional neural network potentials, J. Phys.: Condens. Matter, 2014, 26, 183001 CrossRef CAS PubMed.
- J. Behler, Constructing high-dimensional neural network potentials: a tutorial review, Int. J. Quantum Chem., 2015, 115, 1032–1050, DOI:10.1002/qua.24890.
- J. Behler, Perspective: machine learning potentials for atomistic simulations, J. Chem. Phys., 2016, 145, 170901, DOI:10.1063/1.4966192.
- J. Behler, Neural network potential-energy surfaces in chemistry: a tool for large-scale simulations, Phys. Chem. Chem. Phys., 2011, 13, 17930–17955, 10.1039/C1CP21668F.
- M. Gastegger, J. Behler and P. Marquetand, Machine learning molecular dynamics for the simulation of infrared spectra, Chem. Sci., 2017, 8, 6924–6935, 10.1039/C7SC02267K.
- Y. Luo, M. Li, H. Yuan, H. Liu and Y. Fang, Predicting lattice thermal conductivity via machine learning: a mini review, npj Comput. Mater., 2023, 9, 4, DOI:10.1038/s41524-023-00964-2.
- A. P. Thompson, L. P. Swiler, C. R. Trott, S. M. Foiles and G. J. Tucker, Spectral neighbor analysis method for automated generation of quantum-accurate interatomic potentials, J. Comput. Phys., 2015, 285, 316–330 CrossRef CAS.
- H. Yanxon, D. Zagaceta, B. C. Wood and Q. Zhu, Neural network potential from bispectrum components: a case study on crystalline silicon, J. Chem. Phys., 2020, 153, 54118, DOI:10.1063/5.0014677.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- A. V. Shapeev, Moment tensor potentials: a class of systematically improvable interatomic potentials, Multiscale Model. Simul., 2016, 14, 1153–1173, DOI:10.1137/15M1054183.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Quantum-chemical insights from deep tensor neural networks, Nat. Commun., 2017, 8, 13890, DOI:10.1038/ncomms13890.
- V. Zaverkin and J. Kästner, Gaussian Moments as Physically Inspired Molecular Descriptors for Accurate and Scalable Machine Learning Potentials, J. Chem. Theory Comput., 2020, 16, 5410–5421, DOI:10.1021/acs.jctc.0c00347.
- Z. Fan, Z. Zeng, C. Zhang, Y. Wang, K. Song, H. Dong, Y. Chen and T. Ala-Nissila, Neuroevolution machine learning potentials: combining high accuracy and low cost in atomistic simulations and application to heat transport, Phys. Rev. B, 2021, 104, 104309 CrossRef CAS.
- B. Lindsay, Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205441 CrossRef.
- B. Mortazavi, Z. Fan, L. F. C. Pereira, A. Harju and T. Rabczuk, Amorphized graphene: a stiff material with low thermal conductivity, Carbon, 2016, 103, 318–326, DOI:10.1016/j.carbon.2016.03.007.
- B. Mortazavi, F. Shojaei, A. V. Shapeev and X. Zhuang, A combined first-principles and machine–learning investigation on the stability, electronic, optical, and mechanical properties of novel C6N7-based nanoporous carbon nitrides, Carbon, 2022, 194, 230–239, DOI:10.1016/j.carbon.2022.03.068.
- E. V. Podryabinkin and A. V. Shapeev, Active learning of linearly parametrized interatomic potentials, Comput. Mater. Sci., 2017, 140, 171–180, DOI:10.1016/j.commatsci.2017.08.031.
- E. V. Podryabinkin, A. G. Kvashnin, M. Asgarpour, I. I. Maslenikov, D. A. Ovsyannikov, P. B. Sorokin, M. Y. Popov and A. V. Shapeev, Nanohardness from First Principles with Active Learning on Atomic Environments, J. Chem. Theory Comput., 2022, 18, 1109–1121, DOI:10.1021/acs.jctc.1c00783.
- B. Mortazavi, M. Shahrokhi, F. Shojaei, T. Rabczuk, X. Zhuang and A. V. Shapeev, A first-principles and machine–learning investigation on the electronic, photocatalytic, mechanical and heat conduction properties of nanoporous C5N monolayers, Nanoscale, 2022, 14, 4324–4333, 10.1039/D1NR06449E.
- B. Mortazavi, Ultrahigh thermal conductivity and strength in direct-gap semiconducting graphene-like BC6N: a first-principles and classical investigation, Carbon, 2021, 182, 373–383, DOI:10.1016/j.carbon.2021.06.038.
- B. Mortazavi, I. S. Novikov and A. V. Shapeev, A machine–learning-based investigation on the mechanical/failure response and thermal conductivity of semiconducting BC2N monolayers, Carbon, 2022, 188, 431–441, DOI:10.1016/j.carbon.2021.12.039.
- S. Arabha and A. Rajabpour, Thermo-mechanical properties of nitrogenated holey graphene (C2N): a comparison of machine–learning-based and classical interatomic potentials, Int. J. Heat Mass Transf., 2021, 178, 121589, DOI:10.1016/j.ijheatmasstransfer.2021.121589 (accessed June 2, 2021).
- O. Kaya, L. Colombo, A. Antidormi, M. Lanza and S. Roche, Revealing the improved stability of amorphous boron-nitride upon carbon doping, Nanoscale Horiz., 2023, 8, 361–367, 10.1039/D2NH00520D.
- B. Mortazavi, Y. Rémond, S. Ahzi and V. Toniazzo, Thickness and chirality effects on tensile behavior of few-layer graphene by molecular dynamics simulations, Comput. Mater. Sci., 2012, 53, 298–302, DOI:10.1016/j.commatsci.2011.08.018.
- Z. Ni, H. Bu, M. Zou, H. Yi, K. Bi and Y. Chen, Anisotropic mechanical properties of graphene sheets from molecular dynamics, Phys. B: Condens. Matter, 2010, 405, 1301–1306, DOI:10.1016/j.physb.2009.11.071.
- B. D. Jensen, K. E. Wise and G. M. Odegard, Simulation of the Elastic and Ultimate Tensile Properties of Diamond, Graphene, Carbon Nanotubes, and Amorphous Carbon Using a Revised ReaxFF Parametrization, J. Phys. Chem. A, 2015, 119, 9710–9721, DOI:10.1021/acs.jpca.5b05889.
- X. Yang, S. Wu, J. Xu, B. Cao and A. C. To, Spurious heat conduction behavior of finite-size graphene nanoribbon under extreme uniaxial strain caused by the AIREBO potential, Phys. E, 2018, 96, 46–53, DOI:10.1016/j.physe.2017.10.006.
- L. He, S. Guo, J. Lei, Z. Sha and Z. Liu, The effect of Stone–Thrower–Wales defects on mechanical properties of graphene sheets – A molecular dynamics study, Carbon, 2014, 75, 124–132, DOI:10.1016/j.carbon.2014.03.044.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene, Science, 2008, 321, 385–388, DOI:10.1126/science.1157996.
- P. Zhang, L. Ma, F. Fan, Z. Zeng, C. Peng, P. E. Loya, Z. Liu, Y. Gong, J. Zhang, X. Zhang, P. M. Ajayan, T. Zhu and J. Lou, Fracture toughness of graphene, Nat. Commun., 2014, 5, 3782, DOI:10.1038/ncomms4782.
- H. Yin, H. J. Qi, F. Fan, T. Zhu, B. Wang and Y. Wei, Griffith Criterion for Brittle Fracture in Graphene, Nano Lett., 2015, 15, 1918–1924, DOI:10.1021/nl5047686.
- Z. Zhang, X. Zhang, Y. Wang, Y. Wang, Y. Zhang, C. Xu, Z. Zou, Z. Wu, Y. Xia, P. Zhao and H. T. Wang, Crack Propagation and Fracture Toughness of Graphene Probed by Raman Spectroscopy, ACS Nano, 2019, 13, 10327–10332, DOI:10.1021/acsnano.9b03999.
- F. Qitang, Y. Linghao, K. Ondřej, D. Stavrina, C. Mengyi, K. Ulrich, L. Peter and G. J. Michael, Biphenylene network: a nonbenzenoid carbon allotrope, Science, 2021, 372, 852–856, DOI:10.1126/science.abg4509.
- L. Hou, X. Cui, B. Guan, S. Wang, R. Li, Y. Liu, D. Zhu and J. Zheng, Synthesis of a monolayer fullerene network, Nature, 2022, 606, 507–510, DOI:10.1038/s41586-022-04771-5.
- T. H. Seo, W. Lee, K. S. Lee, J. Y. Hwang, D. I. Son, S. Ahn, H. Cho and M. J. Kim, Dominant formation of h-BC2N in h-BxCyNz films: CVD synthesis and characterization, Carbon, 2021, 182, 791–798, DOI:10.1016/j.carbon.2021.06.080.
- B. Mortazavi and A. V. Shapeev, Anisotropic mechanical response, high negative thermal expansion, and outstanding dynamical stability of biphenylene monolayer revealed by machine–learning interatomic potentials, FlatChem, 2022, 32, 100347, DOI:10.1016/j.flatc.2022.100347.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, The ReaxFF reactive force-field: development, applications and future directions, npj Comput. Mater., 2016, 2, 15011, DOI:10.1038/npjcompumats.2015.11.
- M. L. Pereira, W. F. da Cunha, R. T. de Sousa, G. D. Amvame Nze, D. S. Galvão and L. A. Ribeiro, On the mechanical properties and fracture patterns of the nonbenzenoid carbon allotrope (biphenylene network): a reactive molecular dynamics study, Nanoscale, 2022, 14, 3200–3211, 10.1039/D1NR07959J.
- L. A. Ribeiro, M. L. Pereira, W. F. Giozza, R. M. Tromer and D. S. Galvão, Thermal stability and fracture patterns of a recently synthesized monolayer fullerene network: a reactive molecular dynamics study, Chem. Phys. Lett., 2022, 807, 140075, DOI:10.1016/j.cplett.2022.140075.
- B. Mortazavi and X. Zhuang, Low and Anisotropic Tensile Strength and Thermal Conductivity in the Single-Layer Fullerene Network Predicted by Machine–Learning Interatomic Potentials, Coatings, 2022, 12(8), 1171, DOI:10.3390/coatings12081171.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104, DOI:10.1063/1.3382344.
- E. Meirzadeh, A. M. Evans, M. Rezaee, M. Milich, C. J. Dionne, T. P. Darlington, S. T. Bao, A. K. Bartholomew, T. Handa, D. J. Rizzo, R. A. Wiscons, M. Reza, A. Zangiabadi, N. Fardian-Melamed, A. C. Crowther, P. J. Schuck, D. N. Basov, X. Zhu, A. Giri, P. E. Hopkins, P. Kim, M. L. Steigerwald, J. Yang, C. Nuckolls and X. Roy, A few-layer covalent network of fullerenes, Nature, 2023, 613, 71–76, DOI:10.1038/s41586-022-05401-w.
- H. Dong, C. Cao, P. Ying, Z. Fan, P. Qian and Y. Su, Anisotropic and high thermal conductivity in monolayer quasi-hexagonal fullerene: a comparative study against bulk phase fullerene, Int. J. Heat Mass Transf., 2023, 206, 123943, DOI:10.1016/j.ijheatmasstransfer.2023.123943.
- H. Sun, Compass: an ab initio force-field optimized for condensed-phase applications – Overview with details on alkane and benzene compounds, J. Phys. Chem. B, 1998, 102(38), 7338–7364, DOI:10.1021/jp980939v.
- A. KInacI, J. B. Haskins, C. Sevik and T. ÇaǧIn, Thermal conductivity of BN-C nanostructures, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115410, DOI:10.1103/PhysRevB.86.115410.
- L. Lindsay and D. A. Broido, Enhanced thermal conductivity and isotope effect in single-layer hexagonal boron nitride, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 155421, DOI:10.1103/PhysRevB.84.155421.
- B. Mortazavi, F. Shojaei, M. Yagmurcukardes, A. V. Shapeev and X. Zhuang, Anisotropic and outstanding mechanical, thermal conduction, optical, and piezoelectric responses in a novel semiconducting BCN monolayer confirmed by first-principles and machine learning, Carbon, 2022, 200, 500–509, DOI:10.1016/j.carbon.2022.08.077.
- B. Mortazavi, E. V. Podryabinkin, S. Roche, T. Rabczuk, X. Zhuang and A. V. Shapeev, Machine–learning interatomic potentials enable first-principles multiscale modeling of lattice thermal conductivity in graphene/borophene heterostructures, Mater. Horiz., 2020, 7, 2359–2367, 10.1039/D0MH00787K.
- X. Liu and M. C. Hersam, Borophene-graphene heterostructures, Sci. Adv., 2019, 5, eaax6444, DOI:10.1126/sciadv.aax6444.
- I. Novikov, B. Grabowski, F. Körmann and A. Shapeev, Magnetic Moment Tensor Potentials for collinear spin-polarized materials reproduce different magnetic states of bcc Fe, npj Comput. Mater., 2022, 8, 13, DOI:10.1038/s41524-022-00696-9.
- B. Mortazavi, F. Shojaei, M. Shahrokhi, T. Rabczuk, A. V. Shapeev and X. Zhuang, Electronic, Optical, Mechanical and Li-Ion Storage Properties of Novel Benzotrithiophene-Based Graphdiyne Monolayers Explored by First Principles and Machine Learning, Batteries, 2022, 8(10), 194, DOI:10.3390/batteries8100194.
- H. Yao, L. Ouyang and W.-Y. Ching, Ab Initio Calculation of Elastic Constants of Ceramic Crystals, J. Am. Ceram. Soc., 2007, 90, 3194–3204, DOI:10.1111/j.1551-2916.2007.01931.x.
- M. Marlo and V. Milman, Density-functional study of bulk and surface properties of titanium nitride using different exchange-correlation functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 2899–2907, DOI:10.1103/PhysRevB.62.2899.
- J. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- G. I. Csonka, J. P. Perdew, A. Ruzsinszky, P. H. T. Philipsen, S. Lebègue, J. Paier, O. A. Vydrov and J. G. Ángyán, Assessing the performance of recent density functionals for bulk solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 155107, DOI:10.1103/PhysRevB.79.155107.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Improved adsorption energetics within density-functional theory using revised Perdew–Burke–Ernzerhof functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421, DOI:10.1103/PhysRevB.59.7413.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470, DOI:10.1103/PhysRevB.52.R5467.
- E. R. Ylvisaker, W. E. Pickett and K. Koepernik, Anisotropy and magnetism in the LSDA+U method, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 35103, DOI:10.1103/PhysRevB.79.035103.
- B. Himmetoglu, A. Floris, S. de Gironcoli and M. Cococcioni, Hubbard-corrected DFT energy functionals: the LDA+U description of correlated systems, Int. J. Quantum Chem., 2014, 114, 14–49, DOI:10.1002/qua.24521.
- B. Mortazavi and G. Cuniberti, Atomistic modeling of mechanical properties of polycrystalline graphene, Nanotechnology, 2014, 25, 215704, DOI:10.1088/0957-4484/25/21/215704.
- A. Laio and F. L. Gervasio, Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science, Rep. Prog. Phys., 2008, 71, 126601, DOI:10.1088/0034-4885/71/12/126601.
- A. Kushima, X. Lin, J. Li, J. Eapen, J. C. Mauro, X. Qian, P. Diep and S. Yip, Computing the viscosity of supercooled liquids, J. Chem. Phys., 2009, 130, 224504, DOI:10.1063/1.3139006.
| This journal is © The Royal Society of Chemistry 2023 |
