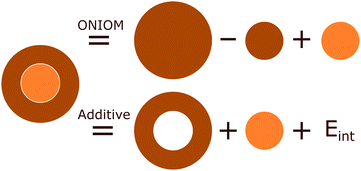Simulating excited states in metal organic frameworks: from light-absorption to photochemical CO₂ reduction

Abstract

Metal–organic frameworks (MOFs) have a wide range of optoelectronic and photochemical applications, many of which are directly dependent on their excited states. Computational modelling of excited state processes could aid the rational design of effective catalysts, but simulating MOFs in their excited state is challenging. This is due to the inherent molecule/crystal duality of MOFs, their large and diverse unit cells, and the unfavourable scalability of quantum chemical methods. However, periodic and cluster models have been developed and applied to characterise the excited states of MOFs and their properties, such as charge transfer, luminescence, and photocatalytic mechanisms. Additionally, embedding techniques provide a means of explicitly incorporating the crystal environment in such models. Although many high-quality reviews have assessed computational modelling in MOFs, most have focused on the study of ground-state electronic properties. In this perspective, we focus on the computational methods available to describe the excited states of MOFs from the molecular, periodic, and embedding perspectives. To illustrate the performance of cluster and periodic models, we compare the results obtained using both approaches at different levels of theory for an exemplary MOF. We also analyse examples from modelling relevant photochemical and photophysical including charge transfer, exciton effects, chemosensing, host–guest mechanisms, thermally activated delayed fluorescence and room temperature phosphorescence. Additionally, we show how such methods can be applied to predict MOF-based photocatalytic CO₂ reduction to value-added chemicals. We emphasise the advantages and limitations of current methodologies, as well as the potential for utilising databases and machine learning models in this context.

---

1 Introduction

The versatile electronic structure of metal–organic frameworks (MOFs) engenders a rich excited-state chemistry. As such, MOFs find varied optoelectronic and photochemical applications including photovoltaic cells,¹ single-molecule magnets (SMMs),² chemosensors,³ and heterogeneous photocatalysts.⁴ MOFs are composed of modular secondary building units (SBUs): polydentate organic ligands, known as linkers, and transition metal clusters (TMCs), known as nodes. These SBUs combine to form a mesoporous crystal with a well-defined network topology. The remarkable excited-state chemistry of MOFs arises from the fact MOFs often retain the photochemical and optical properties of their constituent SBUs.⁵ Consequently, optimal light-harvesting (LH) units and photoactive catalytic sites can be selected to create desirable photophysics in semiconducting solids.⁶ Additionally, pre- and post-synthetic functionalisation,⁷ extensive defect chemistry,⁸ guest–host interactions,⁹ and formation of MOF composites with other functional materials may further install bespoke photophysical effects.

The excited electronic structure of a material dictates its photochemical processes such as light absorption, luminescence, charge transfer, energy transfer, and conductivity.¹⁰ Excited states therefore control the applications of a MOF, whether it be in chemosensors, where a target analyte binding to a MOF can selectively quench or promote luminescence;³ conduction, where excitonic effects control charge carrier dynamics;¹¹ or in a photocatalyst, where photoinduced charge transfer may be used to split the C=O bond of carbon dioxide (CO₂) using sunlight (C=O bond energy is 804.4 kJ mol⁻¹ at 298 K¹²).¹³ Upon photoexcitation, a MOF may undergo a number of competing pathways. Some of these are emissive, such as room temperature phosphorescence (RTP)^14,15 or thermally activate delayed fluorescence (TADF),^16,17 and some radiationless, such as internal conversion (IC), singlet fission (SF) or intersystem crossing (ISC).¹⁸ These processes are governed by their excited-state potential energy surface (PES), which can be characterised to better control the light-activated mechanisms. Electronic structure calculations can provide a detailed atomistic description of MOFs, aiding in the design of successful materials for a broad range of applications.

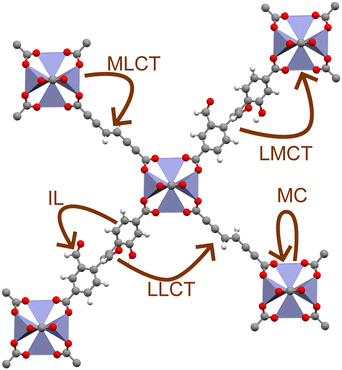
MOFs are unique materials in that each constituent node and linker are joined at an organic–inorganic interface, resulting in a highly localised excited-state structure.¹⁹ As a result, whilst MOFs are often discussed in terms of their electronic band structure, their excitation behaviour is often best understood in terms of coordination chemistry.^6,20 For instance, light-irradiation causes electrons to undergo a variety of excitations processes pertinent to photocatalysis (Fig. 1), such as ligand-centred (LC), metal-centred (MC), metal-to-ligand charge transfer (MLCT), ligand-to-metal charge transfer (LMCT), and ligand-to-ligand charge transfer (LLCT). Those that cross the organic–inorganic interface, such as LMCT or MLCT, present a unique capacity for spatially separating charge carriers. The ability to extend exciton lifetimes and engineer band structure is advantageous to redox applications. Equally, the porous structure of MOFs with exceptional sorption properties facilitates efficient CO₂ sequestration.²¹ Consequently, MOFs are an auspicious candidate for one-pot CO₂ capture and conversion.^22–24 The ability to sequester CO₂ in a photocatalytic network is a strong framework for high-efficiency conversion of CO₂ to high-value chemical feedstocks.²⁴ Many experimental reviews^5,25–29 have documented this progress in this respect, however computational investigations are essential for elucidating excited-state chemistry.

Fig. 1 Different types of charge transfer available in MOFs: ligand-to-metal charge transfer (LMCT); metal-to-ligand charge transfer (MLCT); ligand-to-ligand charge transfer (LLCT); intra-ligand charge transfer (IL); and metal-centred charge transfer (MC).

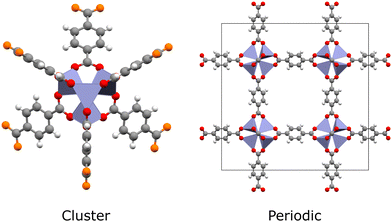
Quantum chemical methods such as time-dependent density functional theory (TDDFT) and multiconfigurational techniques are the microscope through which we see excited states.¹⁰ They can now describe ground- and excited-state electron densities to a high degree of accuracy, enabling quantitative estimation of photochemical properties such as excited-state energies, excitation energies, oscillator strengths and charge transfer behaviour. Furthermore, key photoreaction quantities can be calculated, such as band gaps, excitation energies, charge mobility, and energy barriers.^30,31 This gives computational studies a unique capacity to elucidate spectroscopic results. However, simulating excited states in MOFs remains a significant challenge. In the hierarchy of quantum chemical methods available, those with quantitative accuracy come at the greatest computational cost. Generally speaking, methods such as complete active space self-consistent field (CASSCF), complete active space second-order perturbation theory (CASPT2), or coupled cluster (CC) are limited to small molecules due to unfavourable scaling with the number of electrons. In this respect, MOFs are very demanding to simulate, even in the case of hybrid Kohn–Sham density functional theory (KS-DFT), due to their large and chemically diverse unit cells. Often, simulations must cater for multiple metal-centres, a variety of spin-states, chromophoric linkers, excitonic effects, and complicated charge transfer processes. As such, a largely software-driven paradigm has emerged in which MOFs are treated as either extended periodic crystals or as individual molecules (Fig. 2).³² In reality, the localised electronic structure is modulated by the crystal environment. This places MOFs somewhere on a spectrum between molecule and solid, meaning that MOFs cannot be fully understood from either perspective alone. In conjunction with the improved availability of high performance computing (HPC) and massively-parallel processing, significant research attention has been dedicated to improving the tractability of quantum chemical methods through the use of embedding schemes.^33–37

Fig. 2 Cluster and unit cell representations of MOF-5 (Zn: blue, C: grey, O: red, H: white). Periodic codes perform calculations on the repeating unit cell in a PW basis set, whereas molecular codes perform calculations on clusters, in a GTO basis set. The outer oxygen atoms (orange) of the cluster are one half of a bond cut; these dangling bonds must be saturated using a capping scheme.

Many high-quality reviews have assessed the validity of both cluster and periodic models in MOFs,^19,30,32 but none are directed towards the excited-state chemistry. Herein, we first provide an overview of the most popular computational chemistry methods available (Section 2). Second, we discuss the models used to simulate MOF excited states, from the periodic (Section 3), molecular (Section 4), and embedding (Section 4.4) perspectives, which we compare in our own computational study (Section 4.7). We then consider machine learning and databases in MOFs (Section 5), before seeing how excited-state methods have been used to study photophysical processes in MOFs (Section 6). Finally, we turn to the application of these methods to MOF-based photocatalytic CO₂ reduction (Section 7).

2 Periodic and molecular perspectives

There is a divide in the implementation of quantum chemical software stemming from the choice of basis set. Plane wave (PW) basis sets are a natural choice for approximating the fully periodic wavefunctions, whereas Gaussian-type orbitals (GTOs) provide a more chemically intuitive atomic orbital description. Due to the difficulties in evaluating multielectronic integrals, the use of Slater-type orbitals (STOs) is less extended, however, the Amsterdam Density Functional (ADF) code implements molecular and periodic calculations employing STOs.³⁸ The periodic nature of plane waves is advantageous in describing the repeating unit cell of a crystal. Periodic boundary conditions (PBCs) are used to approximate the system in its infinite limit. The periodic wavefunction is described in terms of Bloch functions, which are composed of a PW and a periodic function. Standard solid-state modelling techniques include KS-DFT, density of states (DOS) and projected density of states (PDOS) calculations, where cost-saving measures including pseudopotentials (to approximate the core electrons) and energy cut-offs may be used. Codes such as CPMD³⁹ and QBox⁴⁰ focus specifically on KS-DFT, however others provide excited-state functionality through methods such as post-HF, TDDFT, Møller–Plesset pertubation theory (MP), GW, and Bethe-Salpeter equation (BSE). Notable codes implementing these methods include ONETEP,⁴¹ VASP,⁴² Quantum Espresso,⁴³ CASTEP,⁴⁴ ABINIT,⁴⁵ and YAMBO.⁴⁶ The principal advantage of plane wave basis sets is their accuracy, which can be systematically improved by increasing the number of plane waves. However, plane waves are not well-suited for modelling localised features, such as local excitations, transition states, and defect chemistry. Additionally, plane wave calculations can be computationally expensive, especially when using hybrid functionals.

Molecular codes, on the other hand, perform calculations on isolated molecules, or clusters thereof, within an atom-centred basis set (GTOs in most cases), which we refer to here as cluster models. The molecular wavefunction is approximated in terms of localised basis functions, composed of linear combinations of contracted Gaussian functions, in what is considered a chemically intuitive description of the atomic orbitals. The overall wavefunction is constructed via linear combinations of GTOs, and the basis set size can be expanded using a larger zeta-basis and incorporating PE or diffuse functions; size extrapolations to an infinite basis have been developed.⁴⁷ Many popular codes, such as Dalton,⁴⁸ GAMMES,⁴⁹ Q-Chem,⁵⁰ ORCA,⁵¹ or MOLCAS,⁵² include molecular dynamics (MD), HF, post-HF, MP, DFT, TDDFT, and coupled-cluster (CC) methods within their respective implementations. The CRYSTAL,⁵³ TURBOMOLE,⁵⁴ and PySCF⁵⁵ packages allow for periodic calculations which solve for Bloch orbitals in a GTO basis. The Gaussian program,⁵⁶ while mostly considered a molecular code, also allows the use of PBCs, allowing calculations to be performed on a molecule in the presence of its periodic images. Truncating the bulk crystal into a more tractable cluster model affords higher level theories such as post-HF and post-DFT methods, but risks omitting wider effects of the crystal environment, such as band conduction, and can therefore yield spurious result if a cluster is poorly chosen. Some codes, such as NWChem,⁵⁷ have implementations in both GTOs and PW bases.

There are other less common basis sets that can be used, for instance, numerical atomic orbital (NAO) basis sets.⁵⁸ These are akin to atom-centred basis sets but are numerically optimised to individual atoms, instead of using the analytical function itself, improving efficiency and scalability. NAOs are implemented for many methods including TDDFT and GW in codes such as FHI-aims,⁵⁹ SIESTA,⁶⁰ and DMol3. The CASINO package⁶¹ has NAO, PW, and atom-centred basis set implementations for quantum Monte Carlo (QMC), a highly-scalable method albeit rarely applied to MOFs due to a costly pre-factor.^62,63 However, QMC has been applied to MOFs to investigate magnetic coupling parameters,⁶⁴ and to calculate catalytic energy barriers.⁶⁵ Finally, KS-DFT has been implemented in a wavelet basis set in the MADNESS⁶⁶ and BigDFT⁶⁷ codes, with the later providing functionality for TDDFT. Wavelet basis sets provide a high degree of localisation making them suited to studies on molecules. Wavelet studies are yet to be reported in the MOF literature.

The CP2K package uniquely bridges the two types of basis set,⁶⁸ in its implementation of the Gaussian-and-plane-wave (GPW) and Gaussian-and-augmented-plane-wave (GPAW) methods, in which an auxiliary PW basis set is used within the otherwise atom-centred basis.⁶⁸ This combines the best of both methods by maintaining a natural description of the periodic structure, whilst also facilitating a chemically intuitive description of the valence orbitals. Equally, embedding techniques, such as hybrid QM/MM and QM/QM′, seek a compromise by using multilevel schemes to extract a much larger region of the bulk crystal within an atom-centred basis set. These methods are a size-extrapolation of a high-level molecular calculation, from a small region to a significantly larger one at low computational cost. Hybrid methods will be detailed in Section 4.4. Many popular codes include QM/MM implementations including Gaussian,⁶⁹ CP2K,⁶⁸ ORCA,⁵¹ FHI-aims,⁵⁹ DFTB+,⁷⁰ COBRAMM,⁷¹ ChemShell,⁷² and, most recently, xTB.⁷³

2.1 Optical and fundamental band gaps

The investigation of electronic excitations under periodic models generally involves calculating the fundamental and optical band gaps, as well as the electronic band structure. The fundamental band gap, E_g, is defined as the difference between the ionisation potential, IP, and the electron affinity, EA (Fig. 3). This considers charged excitations between the neutral material and either its anionic or cationic equivalent.³¹ The optical gap, E_opt, is the difference between the ground state and lowest dipole-allowed excited state. Unlike E_g, E_opt comes from a neutral excitation, and is generally smaller than E_g.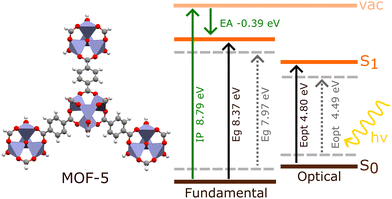

Fig. 3 Schematic comparing the optical (E_opt) and fundamental (E_g) band gaps obtained from BSE/evGW/PBE0 h-capped cluster model (bold lines) and BSE/evGW/Gau-PBE periodic model (dashed lines) calculations in MOF-5, obtained by Kshirsagar et al. (ref. 74). The ionisation potential (IP) and electron affinity (EA) obtained for the cluster model are also shown. The periodic IP of MOF-5 has been previously reported as 7.30 eV (HSE06).⁷⁵

The difference between the optical and fundamental gaps is known as the exciton binding energy, E_B, determined by the energy required to split a photogenerated electron–hole pair due to their Coulombic attraction. Following photoexcitation, a quasi-electron and quasi-hole pair are created, which mutually attract to narrow the band gap. Essentially, each quasiparticle creates an effective image charge which reduces, in the case of the quasi-hole, or enhances, in the case of the quasi-electron, the energy required to add or remove an electron from the system. This process is known as gap renormalisation, and the resulting quasiparticle gap may be as large as 6 eV smaller than the fundamental gap.^76,77 Gap renormalisation is predominantly a non-local electron correlation effect, must be accounted for to achieve accurate band energies. Fundamental gaps are classified as direct when the valence band maximum (VBM) and conduction band minimum (CBM) fall on the same k-point in the Brillouin zone, or indirect otherwise. Indirect band gaps are attractive in photocatalysis as they offer longer diffusion lengths and lower recombination rates. However, excitations of this nature require a change in momentum, through coupling to a phonon vibration. Regardless, almost all MOFs exhibit direct band gaps.³²

Predicting band gaps and excitonic effects represents a significant challenge in MOFs,⁷⁸ and is also difficult to corroborate experimentally. In conventional semiconductors, where electron mobility is high, E_g can often be adequately approximated as E_opt due to negligible electron–hole binding energy. Spectroscopic methods, such as diffuse reflectance UV-vis, can straightforwardly characterise the gap using a Tauc analysis to estimate the onset of absorption. However, this is not the case for MOFs, where electron mobility and band dispersion is low. In fact, the small DOS of MOFs has lead to some studies identifying a Gaussian peak-fitting approach as a more reliable estimation of the optical gap for all but a small subset of MOFs.⁷⁹ In fact, such studies note that deriving the fundamental gap from optical gaps in a largely insulating class of material is an increasingly poor approximation as E_b becomes large. In MOFs, computational studies have shown that the fundamental gap can be double the optical gap, casting doubt on experimental values of E_g obtained with traditional spectroscopic techniques,⁷⁴ and even defining the band gap as direct or indirect becomes ambiguous.²⁰ Instead, to experimentally measure E_g in MOFs a mixture of photoelectron spectroscopies must be used, such as X-ray photoelectron spectroscopy (XPS), ultraviolet photoelectron spectroscopy (UPS), and others.

A higher resolution analysis of excitations is often achieved by directly simulating the molecular orbitals and excited states involved via a GTO basis.¹¹ For instance, although photoconduction is possible via through-bond conductivity in the framework itself, it is generally unlikely for a MOF to have sufficient delocalisation across the organic–inorganic interface for this to occur. Instead, spatial-hopping through the framework pores is generally a more accessible mechanism for conduction, with quantum-dot-like node behaviour of the metal nodes or through-space π-stacking channels, providing alternative conduction pathways.²⁰ Conductive MOFs are, however, rare. In fact, the local coordination environment of the metal nodes readily facilitates ultra-fast electron transfer, such as MLCT, LMCT, or LLCT, between spatially-separated SBUs.⁸⁰ These kinds of local excitation are especially pertinent to photocatalysis, and are best simulated in a GTO basis.³⁰ Other excitations, such as LC and MC, remain localised on an SBU, and show higher recombination rates, and are associated with short-lived and intense emission, such as luminescence, or instead radiationless decay. Finally, excitations delocalised across multiple molecules, known as excitons, may further lengthen recombination rates. This, of course, adds additional complexity to excited-state studies.⁸¹

Overall, the dichotomy between PW and GTO basis sets is in contrast with the inherent duality of MOFs. MOFs are frequently well-represented by carefully chosen cluster models due to localisation of their electronic structure on their SBUs, however the reliability of each model must be carefully benchmarked against periodic calculations. In the following sections, we examine the excited-state methods using periodic and cluster models in MOFs.

3 Periodic models

Periodic models are the benchmark against which cluster models should be compared, as they accurately describe the crystal environment and its long-range effects. This is especially important in instances where delocalisation of electronic bands predominates. Electronic structure is highly sensitive to geometry, and MOF excited-state studies frequently perform preliminary relaxations of the crystallographic coordinates using periodic KS-DFT as the starting point for cluster calculations to obtain accurate atomic coordinates in the solid state. Although KS-DFT provides a formally exact theory for calculating ground-state electron densities, the exact exchange–correlation functional remains unknown.¹⁰ The hierarchy of approximate functionals, often referred to as Jacob's ladder, provides researchers a road map in compromising cost and accuracy in the search for the heaven of chemical accuracy,⁸² and predicted band gaps can vary considerably depending on the DFT functional and in the case of hybrid functionals, the fraction of exchange used. For instance, the generalised-gradient approximation (GGA) functional most widely used in the solid-state community, PBE, has a tendency to consistently underestimate fundamental gaps. In MOFs, it has been observed that when the gaps are above 1 eV and the systems are closed-shell, a straightforward linear equation of the form 1.09E_g,PBE + 1.04 eV can yield HSE06 band gap predictions with an R² value of 0.92 eV (see Section 5).⁸³ The linear relationship is not generalised for all systems and the results are more scattered for the open-shell systems. However, significant chemical diversity is found within MOFs, and similar trends have been observed in inorganic materials with nonzero fundamental band gaps.⁸⁴ In the absence of the universal functional, the lack of systematic improvability is a central limitation of KS-DFT. Nevertheless, hybrid functionals, such as HSE06, PBE0, or ωB97X-D, partially rectify band gap prediction by incorporating a fraction of exact Hartree–Fock (HF) exchange. However, in a plane wave basis set, hybrids may be orders of magnitude costlier than GGA or meta-GGA functionals, even with the use of cost-saving approximations such as small energy cut-offs and pseudopotentials. MOFs routinely exhibit unit cells with extremely large size, volume, and complexity, making such computational studies challenging, and often ruling out the use of supercells, for example. As a result, the convention is to perform geometry relaxations at the GGA-level, followed by a single-point calculation in the case of MOFs. The alternative to using hybrid functionals, is to add a semi-empirical Hubbard correction, known as DFT+U. In highly correlated materials such as Mott insulators, the use of local and semilocal functionals can result in excessive delocalisation of electronic states due to the self-interaction error reducing on-site Coulomb repulsion. This can result in incorrect predictions regarding conductivity.⁸⁵ An effective potential, U_eff, known as the Hubbard correction, is added to the Hamiltonian to improve the description of both correlation and on-site exchange, increasing the degree of localisation of these states. The implementation of this correction is simple computationally, and comes at a much lower cost than hybrids. The main issue is finding the optimal value of U_eff, which is not a universal parameter, and hardly depends on the material and the DFT functional. While U_eff can be obtained from first principles, most strategies involve semiempirical fitting to reproduce experimental data, including band gaps and oxidation potentials.³² Additionally, DFT+U affects band dispersion about the Fermi level, however this is not significant in MOFs, which rarely display high electron mobility.⁸⁵ In MOFs and metal complexes, the DFT+U method has been effectively used to predict correlation in the metal node of MOFs with open d or f shells where KS-DFT breaks down, and in simulating spin-crossover (SCO), where the materials reversibly changes spin-states upon exposure to an external stimuli such as magnetic field, temperature, or light.⁸⁶

3.1 Band gap screening studies in MOFs

An important advance in the study of solid-state materials and the field of photocatalysis is to characterise the band structure (Section 2.1) using KS-DFT, which has significant impact on its photocatalytic potential. To some extent, this enables ground-state densities to be used to investigate MOF excited states. In terms of their band structure, MOFs are generally wide-band gap materials with flat band structures and low electron mobility. Conductivity is therefore typically low, ranging from 10⁻⁹ to 10⁻³ S cm⁻¹.^19,87 The modularity of MOFs and their composite materials enables the band structure to be tuned, specifically the band gaps and band edges, which can lead to improved conductivity. Low conductivity is inconvenient for photocatalysis, which requires highly mobile photogenerated charge carriers. Nevertheless, this arises from a localised electronic structure, which is equally attractive for photocatalysis as it provides easy access to potentially dense populations of high-energy electrons.³² The DOS and PDOS may also be obtained from periodic KS-DFT calculations, and used to gain insight into the relative effect of different functionalisations of a MOF. Whilst the DOS describes the density of electronic states from a global perspective of the material, the PDOS projects the DOS onto specific atomic orbitals, to provide a local perspective of individual atoms. When determining the band structure of a material, the energies of the band structure are often aligned to the Fermi level. However, this alignment does not clearly indicate how a change in structure shifts the energetics. Instead, aligning the bands to either a reference electrode or, more commonly, the vacuum level provides a framework for straightforward comparison between different MOFs. Another approach is to empirically fit the CBM to an experimental value or accurate benchmark via the so-called scissor operation, which corrects the systematic energy error from the functional.⁸⁸ Many studies have used vacuum-aligned band structure calculations to compare band gaps in screening studies. The modular structure of MOFs allows SBUs to be functionalised on an atomic level, modulating the band gap. Screening studies compare various functionalisations by substituting the metal, node or linker, or by introducing defects. This might involve substitution of the transition metal in the node;⁸⁹ changing the coordination environment of the node; substitution of the linker;²² substitution of functional groups within the linker;⁹⁰ introduction of photocatalytic guests;⁹¹ or a combination of these. The relative energies and band gaps can then be compared to reveal qualitative trends. The consequence of this is a relatively cheap protocol for making catalytic predictions by comparing the HOMO and LUMO levels to redox potentials. For instance, in photocatalytic CO₂ reduction, the HOMO and LUMO levels may be compared to the relevant CO₂ redox potentials (Section 7), the competing hydrogen evolution reaction (HER, H⁺ + e⁻ → ½H₂), and water-splitting.²² This can reveal qualitative trends on how functionalisation improves, or inhibits, the Faraday efficiency towards the photochemical CO₂RR. For instance, in a screening study on a two-dimensional porphyrin-MOF (PMOF), Fe was reported to be an ideal dopant for engineering the band gap engineering towards solar-fuel and water-splitting photocatalysis (Fig. 4).⁹² The incorporation of the Fe dopant introduces occupied 3d levels above the porphyrin HOMO and empty 3d levels below the porphyrin LUMO, tailoring it towards the appropriate redox potentials. An optimal mix was found by doping PMOF with a mixture of Fe and Al at the octahedral node sites and Zn at the porphyrin site was able to fine-tune the band edges, towards photocatalytic applications. Overall, screening studies of this nature enable theoreticians to predict which MOFs are most likely to display a given material property, saving experimentalists time and money synthesising targets which are unlikely to succeed. The wider use of KS-DFT in MOFs has been reviewed in detail.³²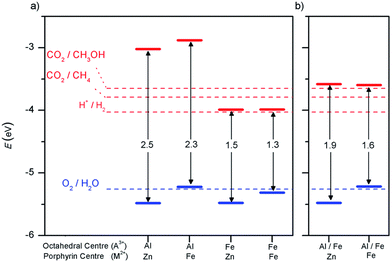

Fig. 4 KS-DFT (HSE06) band gap values for (a) PMOF with either Fe or Al at each octahedral centre and (b) a 50% mixture of Al/Fe. The metal at the porphyrin centre is also shown. Redox potentials are shown for water-splitting, HER, and CO₂RR production of methane and methanol. Reproduced from ref. 92 with permission from the Royal Society of Chemistry, copyright 2017.

3.2 Time-dependent density functional theory (TDDFT)

TDDFT generalises KS-DFT into the time-domain to explicitly calculate excited states. The primary advantage of TDDFT is a modest cost-accuracy ratio. This facilitates excited-state calculations to a reasonable degree of accuracy at a lower cost than other high-level methods. This enables calculations to be performed on larger systems (hundreds of atoms) such as MOFs, relative to multiconfigurational or perturbation theory-based techniques. For molecular systems, TDDFT is generally carried out using either the full Casida formalism⁹³ or the Tamm–Dancoff approximation (TDA). The full formalism of solving the Casida equations can calculate E_opt by finding excitations as poles of the response function including forward and backward excitations, whereas TDA provides a more computationally efficient solution by neglecting backward excitations. In addition to being computationally simpler, TDA has the advantage of improving the triplet instability issue in TDDFT.⁹⁴ The results of TDDFT calculations are determined by the employed functional. The use of a local density approximation (LDA) or GGA functional results in the well-known drawbacks of TDDFT, such as the underestimation of band gaps, prediction of spurious charge transfer states, and incorrect simulation of Rydberg states.⁹⁵ Most of these problems are associated with the incorrect asymptotic behaviour of most XC-functionals and the self-interaction error, which is partially but not completely resolved in hybrids.⁹⁶ This is further improved by using a range-corrected and/or optimally-tuned hybrid functional, however, this is computationally demanding with a PW basis, especially for systems as large and complex as MOFs. To alleviate cost, there have been attempts to improve efficiency in TDDFT, including the auxiliary density matrix method (ADMM), simplified TDDFT (sTDDFT) and the simplified Tamm–Dancoff Approximation (sTDA).⁹⁷ ADMM carries out a calculation in an auxiliary basis and provides a correction term for the basis set superposition error (BSSE), and can be additionally used in conventional KS-DFT. sTDA provides the most substantial savings in computer time, by incorporating an empirically parameterised tight-binding approximation. sTDA has been implemented in xTB⁹⁸ and recently, within the GPW method of CP2K.⁹⁹ Additionally, the Hubbard correction has also been applied to TDDFT (TDDFT+U) in the context of excited states.¹⁰⁰ Despite the associated computational cost, periodic TDDFT calculations of MOFs have been performed by Fumanal, Tavernelli, et al., who have explored the excited states of several MOFs.^{11,78,101–103}

The choice of functional directly influences the accuracy of the excited states in MOFs. Due to the substantial contribution of organic ligands to the band edges of MOFs, the common challenges encountered in predicting excited states in isolated organic molecules are also observed in MOFs. The influence of both band gap narrowing and excitonic effects were studied using TDDFT cluster and periodic models on of M-PMOF Al-PMOF, its two metalated forms, Zn–Al-PMOF and Co–Al-PMOF. Both TDA and full Casida approaches were considered under the PBE, PBE0, and CAM-B3LYP functionals.⁷⁸ The PBE functional estimated the optical gap to be larger than the fundamental gap, ignoring the excitonic effects. Despite E_opt agreeing with the experiment and correctly describing the Q bands of the porphyrin, PBE is susceptible to overstabilising LMCT interactions from the porphyrin linker to the metal node. As observed, this was corrected by CAM-B3LYP, suggesting that the use of long-range corrected functionals is likely a minimum requirement when simulating absorption spectra with TDDFT, at least in the case of porphyrins. Interestingly, the predictions of E_opt and E_g were not significantly different between cluster and periodic models, however neither were able to correctly recover gap renormalisation with or without a hybrid functional. The TDA predicted spectra contained some artificial excitations, a blue shift, and improper descriptions of the Soret band. Whilst these results support the use of cluster models in MOFs, it highlights that higher-level methods, such as GW, are required for accurate quasiparticle energies and prediction of excitonic effects in both cluster and periodic models, a current challenge in MOFs. This distinguishes studies on MOFs from conventional semiconductor studies, in which exciton binding can be small.

3.3 The GW-approximation

The GW-approximation of many-body perturbation theory (MBPT) provides the highest accuracy band gap data compared to experiment. GW determines the quasiparticle gap directly, by perturbatively correcting the self-interaction error of the KS-DFT molecular orbitals.^104,105 This is achieved by solving the Dyson equation in terms of one-particle Green functions, G, and a dynamically screened Coulomb potential, W, yielding accurate gap renormalisation, quasi-particle energies, IPs, and EAs. This is typically implemented in a eigenvalue-only self-consistent scheme (evGW) which corrects the self-energy error in the eigenstates and eigenvalues obtained within KS-DFT. Additionally, the Bethe-Salpeter equation (BSE/GW) may be solved to estimate E_opt and the excited states. The GW method is very expensive and only in a few instances has it been applied to MOF excited states. However, the application of BSE/GW to MOF-5⁷⁴ and PCN-123¹⁰⁶ has illustrated how representative fragment approaches can be highly valuable in recovering optical properties.

The determination of optical and fundamental gaps in MOF-5 has been challenging due to strong exciton binding effects.⁷⁴ KS-DFT calculations estimated fundamental gaps of 3.57 eV using a GGA functional (PBE) and 4.48 eV using a hybrid functional (Gau-PBE), agreeing well with the spectroscopic optical band gap of 4.5 eV. However, this was likely a serendipitous result for both the theoretical and experimental methods: the large E_b value of MOF-5, a probable wide-band gap insulator, is likely to cause a considerable difference between E_opt and E_g, and GGA functionals underestimate band gaps. Unlike DFT, the use of the BSE Hamiltonian provides correct asymptotic behaviour and accurate determination of quasiparticle energies. Instead, using BSE/GW an E_B value of 3.5 eV and a fundamental gap of 8 eV, almost twice as large as E_opt. The simulation was embedded in a PCM to account for the solvation effect of the ligand, and was incorporated into the screened Coulomb potential. The renormalisation of the fundamental gap of the ligand due to dielectric solvent effects is substantial, approximately 1.4 eV. However, the optical gap is only minimally affected, by approximately 0.1 eV. Additional BSE/GW calculations on two representative H-capped clusters, one small and one large, revealed a quasiparticle band gap of 8.75 eV, a small overestimation. Interestingly, embedding these fragments in a PCM improved the discrepancy between cluster and fragment calculations, meaning the cluster largely recovered the properties of the periodic solid, and reflected the low dielectric screening of the crystal environment. Interestingly, the fortuitous agreement of these results suggests that hybrid functional DFT may be a useful method for estimating optical gaps in circumstances where BSE/GW is prohibitively expensive.⁷⁹ In the wider context of molecular crystals, Refaely-Abramson et al. have demonstrated the efficacy of non-local functionals with an optimally tuned-range separated (OT-RSH) parameterisation for obtaining GW-level accuracy for quasiparticle gaps using traditional KS-DFT.^107,108 This approach yielded quasi-particle gaps with results comparable to experimental and theoretical benchmarks. The use of such functionals remains an unexplored avenue in MOFs.

The similarities between the molecular excitations in periodic MOFs and the molecular models where investigated in PCN-123, which is obtained by functionalising MOF-5 with azobenzene.^106,109 Clusters of various sizes were constructed, ranging from a lone azobenzene linker to a cluster containing four metal nodes. In the simulated BSE/GW absorption spectra (Fig. 5), it was shown that even in the smallest model the spectral properties were largely recovered relative to the fully periodic f-PCN-123 benchmark. A conductor-like screening model (COSMO) was used to handle polarisation of the fragments, and a QM/MM model to account for screening by the environment. The most significant artefact in the BSE/GW cluster method was introduced to by the truncation procedure. The spectrum of the smallest model showed a much less prominent S₁ band relative to the fully periodic cis azobenzene isomer of PCN-123. More generally, the results were indicative of a fast photoisomerisation of the azobenzene functionality within PCN-123, and provides strong evidence that a well-designed cluster model can reproduce optical properties of the fully periodic system.

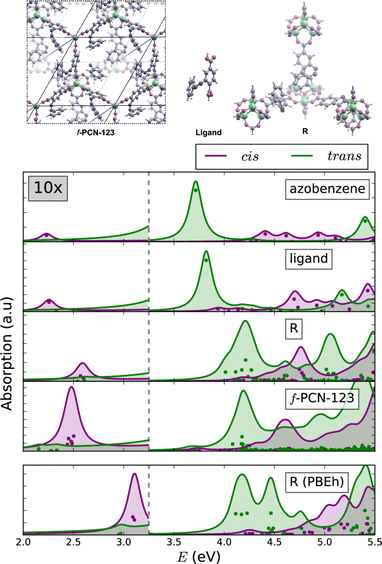Fig. 5 Comparison of the BSE/evGW/PBE spectra of azobenzene, a single ligand, a cluster of SBUs, and a fully periodic model. The lowest panel was performed at the BSE/evGW/PBEh level (including 40% HF exchange). These results show the capacity of cluster models to recover key features of the optical absorption spectrum of the fully periodic wavefunction. Adapted with permission from ref. 109. Copyright 2020 American Chemical Society.

4 Cluster models

Cluster models are often a judicious method for simulating MOF excited states, as MOFs often preserve the photochemical and optical properties of their constituent metal nodes and organic linkers. Despite their crystallinity, the flat band structure of MOFs means they are particularly suited to modelling from the molecular perspective.¹⁰⁶ In photocatalytic applications, MOF band edges are often engineered to increase dispersion and improve charge carrier mobility (Fig. 6),²⁰ however band conduction is rare in MOFs⁶ and conductivity follows a spatial hopping scheme. Additionally, the explicit treatment of local electronic structure through an atom-centred basis allows an intuitive treatment of local phenomena, such as excitations, transition states, charge transfer effects (LMCT, MLCT, LC, MC), and defect chemistry. Truncating a region of the periodic crystal into a cluster, or fragment, reduces the system size and alleviates computational cost. This affords higher-levels of theory and, in principle, more accurate calculations such as correlated wavefunction methods (CASSCF, CC2, or MRCI), as well as time dependent methods such as TDDFT or BSE/evGW.¹⁰³ Additionally, large diffuse and polarisable basis sets are often afforded. For the transition metal centres, the zero-order regular approximation (ZORA) to the Dirac equation is sometimes used to incorporate relativistic effects and spin–orbit coupling (SOC). Basis sets, such as LANL2DZ, are often used for transition metal centres, which include an effective core potential (ECP) to reduce the computational cost by approximating electrons in the core, with standard basis sets used for non-heavy atoms.¹¹⁰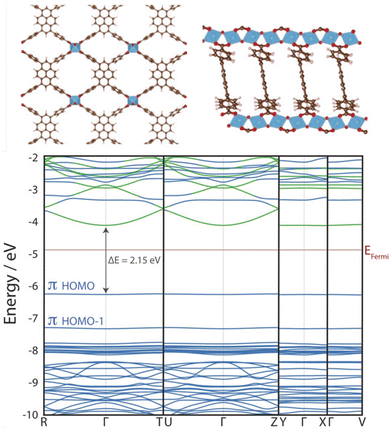

Fig. 6 KS-DFT (HSE06) electronic band structure of ACM-1 across four k-paths. The almost entirely flat valence band maximum (VBM) indicates highly localised electronic structure. This photocatalytic MOF has been engineered to include improved band dispersion in the conduction band along the R–Γ–T and U–Γ–Z paths, facilitated by 1D Ti-oxo chains that improve photoexcited charge carrier mobility. Adapted with permission from ref. 111, copyright 2020 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.

4.1 Cluster extraction

The method with which a cluster is extracted from the bulk crystal directly influences the calculated properties. Excited-state chemistry is controlled by geometry and local electronic structure, meaning care is required to avoid artificially losing information from the cluster extraction procedure. A poor truncation choice can easily change the overall charge, symmetry, or spin of the system, or the oxidation states of the ligands or metal centres.¹¹² Such systems may be difficult to converge and product spurious results. For instance, covalent (C–C bond in linker) or dative (M–L bond between node and linker) bonds must be necessarily cut due to the extended coordination structure of MOFs. To prevent the cluster being charged and in its open-shell state, extrinsic capping groups must be applied to dangling bonds; for every σ-bond cleaved, a new capping σ-bond must be created. Capping schemes vary in complexity, the most simple and common being to cap the cluster with a hydrogen ‘link’ atom. Equally, molecular orbitals, tuned-fluorine atoms, or even multi-atom groups such as methyl or ammonia groups¹¹³ may be used to best recover the electronic structure of the periodic crystal. When link atoms are used during optimisations, they contribute non-negligible artificial gradients to the system, which are treated analytically using a Jacobian when implemented in multilevel embedding schemes (see Section 4.4).^69,73 In vibrational analysis, this is an important procedure to prevent imaginary modes occurring due system not being at a true local minimum.¹¹⁴ Overall, during cluster extraction, it is favourable to cut the most neutral bonds possible, such as covalent bonds in alkyl chains.

In MOFs, the localised electronic structure means even very small clusters (an isolated linker) can perform exceptionally well,¹⁰⁶ however caution is required to select relevant chemical moieties to ensure the wider electronic structure is reflected. As such, Mancuso et al. suggest two main approaches for cluster extraction: (1) include complete metal nodes, with some approximation to the coordinating linkers (for instance, formate in the place of benzene dicarboxylate (BDC); or (2) use complete linkers and approximate the metal node in some way (for instance, use of a geometrically similar metal centre, such as Mg²⁺ for Fe²⁺).³² In our own calculations (Section 4.7), we found keeping the linkers largely intact, but cutting at the nearest C–C bond to the M–L bond to be an effective alternative to (2). A suitable choice of cluster depends on the desired level of theory, the region(s) of chemical interest, and the effect of the crystal environment. For example, if the mechanisms involves the population of exciton and charge transfer states, the model should incorporate all relevant fragments for the process. Equally, the model must not be biased by only including select moieties towards a specific result. As a result, the subjective nature of cluster extraction makes benchmark calculations critical. These might include periodic models or large clusters with embedding.

4.2 Combining periodic and cluster models

Periodic and cluster models are routinely combined to provide a more complete and accurate description of a system than either model type can provide alone. Periodic calculations are used to recover geometric properties of the crystal structure, and TDDFT transition metal cluster models for a detailed understanding of excited-state electronic structure. A recent work by Fumanal et al. considers this strategy to analyse the structure, fundamental gaps, optical gaps, and excited states of MUV-11, NTU-9 and CAT-5.¹⁰³ Periodic calculations with ADMM-accelerated KS-DFT (PBE-D3BJ) were used to relax the crystallographic structure, followed by PBE0 calculations. All metals (M = Ti, Zr, Zn, Cd, Fe, Ru) were simulated in the closed shell singlet state, except for Fe(II) which was also simulated in the quintuplet high-spin state. They found significant differences between the M–O lengths in the periodic and clusters with unrestricted KS-DFT for the high spin state, which has a strong effect on the optical properties. The KS-DFT fundamental gaps obtained (ranging from 1.2 eV to 4.2 eV across all topologies) exclude excitonic effects and gap renormalisation corresponding to an overestimate. The optical gaps obtained using LR-TDDFT calculations (ωB97X-D/def2-SVP) for the clusters illustrate the strong correlation and systematic shift of 0.44 eV due to E_B in the optical and fundamental gaps of the periodic KS-DFT system (Fig. 7a). Fig. 7b directly compares gap values for periodic and cluster calculations (PBE0). While variations exist between the molecular fundamental gap and the solid-state band gap, the majority of values exhibit a linear trend. Most notably in CAT-5, ascribed to a loss of symmetry in the LUMO of the CAT-5 ligand due to truncation at the M–L boundary. This is notably not observed in Ti(IV) and Zr(IV) where the d-orbitals are empty. This work also highlights the need for long-range corrected functionals for the characterisation of the nature of excited states (Fig. 7c/d). While for Zn/Cd-MUV-11, Ti-MUV-11 and Zr-MUV-11, both PBE0 and ωB97X-D provide similar classifications. The lowest excitations in Fe-MUV-11, Fe-NTU-9 and Ru-CAT-5 are assigned as MLCT transitions with PBE0, and as MC with ωB97X-D.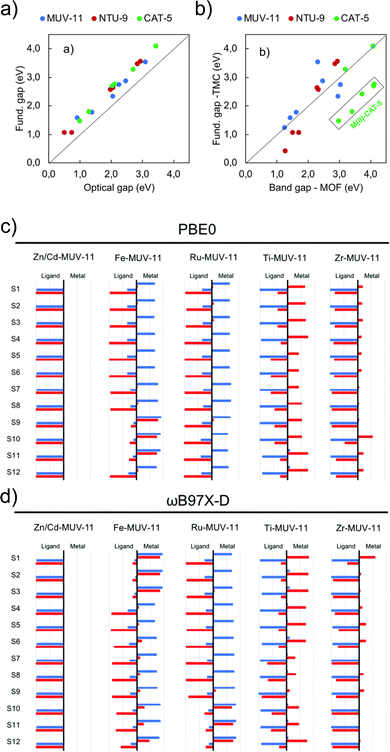

Fig. 7 Correlation plots for (a) DFT (PBE0/def2-SVP) cluster model fundamental and optical gaps, and (b) the DFT (PBE0) band gap values in the periodic and cluster models. Analysis of electron and hole localisation on either ligand or metal using the (c) TD-PBE0/def2-SVP and (d) TD-ωB97X-D/def2-SVP functions. These characterise excitations as MLCT, LMCT, IL, or MC. Modified from ref. 103 with permission from the Royal Society of Chemistry, copyright 2020.

4.3 Multiconfigurational approaches

Cluster models offer a remarkable advantage by providing access to higher levels of theory. Multiconfigurational wavefunction methods are required for circumstances in which a single Slater determinant is an inadequate description of the electronic structure. For instance, MOF nodes contain transition metals such as Fe(II) which can exist in both high- and low-spin states,¹⁰³ which influences properties such as magnetism. Although different spin-states may be modelled using spin-polarised DFT, multiconfigurational methods such as CASSCF, CASPT2, or DMRG provide a more complete description. For instance, GGA functionals are known to overestimate the stability of the low-spin states, and hybrid functionals that of the high-spin state. Furthermore, the accessibility of spin states is controlled by the crystal environment. SOCs are particularly important in the context of photochemistry because it enables ISC processes and influences spectroscopic selection rules, excited-state lifetimes, emission, and absorption. SOCs have an important influence on magnetic properties of a material, and MOFs have drawn attention as SMMs.¹¹⁵ In quantum computing, SMM-materials are of interest as their doublet ground state can be used as a quantum bit (qubit).¹¹⁶ Multireference methods can be used to characterise the materials in these spin states, and quantify effects such as SOC. For instance, CASSCF calculations rationalised the node nanomagnet behaviour of Co(NCS)₂)₃(κ3-TPT)₄]·a(H₂O)·b(MeOH) under an applied static field.² Using a cluster model with an activate space of seven electrons (7,5), including all quadruplet and doublet states, CASSCF helped characterise the significant changes in magnetic behaviour resulting from a change in coordination sphere of Co(II). In this model, dynamic correlation effects were incorporated through n-electron valence state perturbation theory (NEVPT2) and SOC via quasi-degenerate perturbation theory (QDPT). This method allowed for straightforward extraction of the excitation energies. A cheap DFT calculation can be used to qualitatively identify important the metal d-orbitals, that can be ambiguous to identify with CASSCF alone. Similar methods have also been used to investigate low-T SMM behaviour in Co(II)-based 3-aminoisonicotinate MOF, corroborating experimental findings of field-induced SMM behaviour at low temperature.¹¹⁷ CASSCF-NEVPT2 attributed this effect to easy-plane magnetic anisotropy and significant SOC.

The difficulty in coupling porosity and strong magnetic coupling makes high-T magnetism uncommon in MOFs.¹¹⁶ However, transition metal sites with partially full d-shells (such as Fe) can exhibit orbital splitting dependent on ligand geometry, creating high- and low-spin states. This adds additional complexity in simulating these systems and necessitates the use of spin-polarised quantum chemical methods, such as spin-polarised DFT. Unpaired spins may either be ordered parallel (ferromagnetic, FM), or antiparallel (antiferromagnetic, AFM), dictated by magnetic coupling. However, knowing which model to select requires prior experimental probes, such as EPR, to fully characterise oxidation state and spin-polarisation in the MOF. While all MOFs can be straightforwardly modelled as FM (spin-aligned), to construct an AFM model may require the use of prohibitively costly supercells in periodic models (Fig. 8).³² Cluster models are unlikely to be of sufficient size to capture long-range magnetic interactions. This demonstrates the inherent added difficulty in modelling open-shell systems. Finally, off-axis spin-alignment arising from SOC may strongly influence photomechanisms such as ISC and therefore RTP.¹¹⁸ However, although it may be difficult to construct a reliable cluster model, once found, the high-level multiconfigurational methods will always be advantageous to the accuracy of subsequent study.

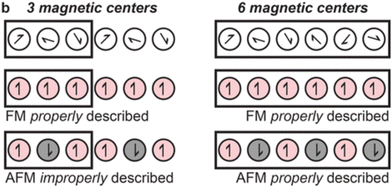Fig. 8 If the magnetic interactions in a MOF are over a greater distance than a given unit cell, caution is required when describing antiferromagnetic (AFM) states and more costly supercells may be necessary. Adapted with permission from ref. 32. Copyright 2020 American Chemical Society.

4.4 Embedding techniques

The inherent duality of MOFs means they cannot be described from solely a periodic or molecular perspective as the whole can be much greater than the sum of its parts. One compromising approach is to use hybrid quantum mechanic in molecular mechanics (QM/MM) and quantum mechanics in quantum mechanics (QM/QM′) methods, with the use of embedding techniques. These methods treat a subsystem of chemical interest, the model region, in the presence of a much larger cluster environment of surrounding atoms, the env region. These combine to form a complete cluster, the real system, which is partitioned both by size and level of theory. Consequently, hybrid methods are a size-extrapolation of the model region, seeking to approximate the accuracy of the high-level method of the model region to the entire cluster at a considerably lower computational cost. Excellent examples of this are in biomolecular systems such as proteins, in which only a very small portion (such as an enzymatic active site) need be treated at the quantum mechanical level.¹¹⁹ In recent years, embedding techniques have increasingly drawn interest in the solid-state community,^35,36 as they facilitate convenient simulation of local behaviour, but also incorporate the long-range effects of the wider bulk crystal.

The formal mathematical framework for partitioning the total electron density of a system into interacting subsystems is found in frozen density embedding theory (FDET),^120,121 which uses electron density, a quantum mechanical observable, to couple wavefunction and DFT approaches.¹⁰ The coupling of the model and env subsystems results in an interaction energy. As shown in as shown in Fig. 9, the treatment of the interaction energy can be incorporated through either an explicit term in the Hamiltonian, E_int, as in the additive schemes,

E_high/low = E_high,model + E_low,env + E_int (1)

or is accounted for implicitly through subtraction, known as our own N-layer integrated molecular orbital (ONIOM),³⁷

E_ONIOM = E_high,model + E_low,real − E_low,model (2)

By subtracting a low-level model region calculation from the real-region, the double-counted low-level contributions to the energy are removed. The ONIOM scheme is conceptually simpler than constructing an additive Hamiltonian, however both methods have drawn success. ONIOM is an N-layer scheme, referring to the fact that an arbitrary number of layers can be used, for example ONIOM(QM:QM:MM).³⁷ However, two-layer schemes are by far the most common, and it is very rare to include more than three-layers, unless specific divide-and-conquer type schemes are desired.³⁴ Of course, for an embedding model to be considered, it is important to question how strongly the crystal environment controls the local electronic structure. Is an embedding model truly required? As we have seen throughout, many examples in the MOF literature where standard cluster models are an excellent approximation to the periodic MOF, however this is not always the case. We investigate this in our own calculations, in Section 4.7. One such example is guest@MOF materials (Section 6.5), where interactions of the guest and MOF pore generally play a crucial role in the observed photomechanisms. Hybrid methods using both additive and ONIOM schemes have been employed in the MOF literature, to study photochromism,¹¹³ aggregate-caused quenching (ACQ),¹²² and TADF.¹²³

Fig. 9 Two-layer hybrid model methods extrapolate a high-level of theory (orange) of a model region to the complete real system, which is simulated at a low-level of theory (brown). The ONIOM scheme accounts for interactions between these subsystems implicitly via subtraction in the total Hamiltonian, whereas the additive scheme treats the model and env systems separately, with an explicit energetic coupling term, E_int.

Like in isolated cluster models, hybrid methods allow the model region to be treated at the correlated wavefunction or TDDFT level, enabling accurate treatment of localised excitation processes, whilst a much larger environment region is treated at the low-level, for instance using molecular mechanics force field methods (QM/MM) or a relatively cheap quantum mechanical method (QM/QM′). One significant advantage of utilising embedding techniques is the ability to combine not only TDDFT but also multiconfigurational techniques, thereby enabling the investigation of excited states with a multiconfigurational nature (Section 4.3) and nonradiative decay processes. This is advantageous, as correlated wavefunction methods and to a lesser extent TDDFT are limited to simulating small molecules. In hybrid methods, often only the central region atoms are optimised within a fixed environment extracted from the relaxed crystal structure.³⁷ Originally motivated by simulation of proteins, the environment described by the real region can be thousands of atoms large, and therefore provide a much more faithful description of the periodic lattice.

From the QM/MM perspective, popular generic force fields, such as Amber¹²⁴ or CHARMM,¹²⁵ OPLS, or the universal force field (UFF) may be used, however they are often parameterised for biomolecular systems, making them less transferable to MOFs. Whilst these FFs provide a good description of the organic SBUs, modelling the organic–inorganic interface becomes challenging, especially across a range of metal centres.¹²⁶ Many studies have been devoted to developing new ab initio force fields specifically for MOFs, such as MOF-FF,¹²⁷ BTW-FF,¹²⁸ QuickFF, or have extended more generic fields to the solid-state, such as UFF,¹²⁹ or MM3.¹³⁰ Of these, polarisable force fields are used to ensure that the region of interest is able to respond to polarising effects, for instance photoexcitation. MOF are inherently flexible materials, albeit to varying degrees, and electronic structure is very sensitive to changes in nuclear geometry.¹³¹ Polarisation effects can be included through additional induced dipole and higher-order multipole terms in the force field potential energy function. Polarisable force fields can be developed using energy paramaters obtained from QM calculations, which can in turn be optimised to accurately recover the PES. The accuracy of the force field is therefore dependent on the accuracy of the underlying quantum chemical method. For instance, a polarisable force field has been used to describe challenging interactions between open metal sites and guest molecules in M-MOF-74, for simulation of CH₄ adsorption,¹²⁶ and CO₂¹³² and using Lennard-Jones parameters derived from KS-DFT.

Equally, from the QM/QM′ perspective, density functional tight-binding (DFTB), as implemented in DFTB+⁷⁰ and xTB, incorporates a portion of empirical parameterisation and a localised atomic orbital basis in KS-DFT to approximate quantum chemical accuracy on large-scale systems. Using two or more layers of quantum chemical method can offer an improved description of the electron density in the real region and therefore the crystal environment, however may also limit the system size relative to the use of force fields. A periodic KS-DFT calculation may be used to full description of the periodic lattice, known as periodic embedding.³⁵ Three-layer ONIOM(QM:QM:MM) schemes can enable a compromise where the atoms in the two QM layers are variable, for instance allowing the middle region to respond to a photoexcitation event whilst still being constrained within the outer MM environment. Notably, in these schemes, a second layer of bond cutting, and link atom capping is required at the QM/QM′ boundary, in addition to the model region. Each level of theory used corresponds to another layer of bond cuts.

The central challenge in embedding methods is to avoid overpolarisation, an effect that arises from the purely Coulombic treatment of the electrostatic interaction in the Hamiltonian. At small interatomic distances, the potential becomes infinitely attractive, resulting in unphysical electron densities when, for instance, point charges lie too close to the QM/QM′ boundary.^133,134 Excited states are particularly susceptible to overpolarisation by the choice of point charge embedding in the environment, however this is particularly challenging in MOFs due to the polarity of the M–L bonds at the organic–inorganic interface.¹¹² In hybrid methods, a hierarchy of embedding schemes have been developed: mechanical embedding (ME), where point charge embedding is omitted entirely in a purely classical treatment of interactions, where no polarisation is account for; electrostatic embedding (EE), where QM wavefunction is embedded in point charges and can therefore be polarised by the environment; and PE embedding (PE), where both model and real region may mutually polarise each other in a self-consistent fashion.¹⁰

4.5 Point-charge embedding

The importance of accurate point charges in embedding calculations cannot be overstated, as the quality of the embedding dictates the polarisation of the model region wavefunction. Poorly constructed electronic embedding is by no means better than mechanical embedding. Point charges generally aim to accurately represent the electrostatic potential (ESP). However, charge is not a formally defined observable in quantum mechanics, providing a degree of arbitrariness in the choice of method. In an atom-centred basis, simple models such as Mulliken or Löwdin can be used, but more robust models such as the restrained electrostatic potential (RESP), Hirshfeld and CHELPG better represent the ESP. Beyond partial charges, rapidly-convergent summation schemes, such as the Ewald,¹³⁵ Evjan,¹³⁶ or Wolf,¹³⁷ may be used to generate arrays of point charges that approximate the exact Madelung potential of the crystal. Charge assignment is less well-defined in a PW basis.¹³⁸ The most widely used periodic scheme is the atoms-in-molecules (AIM) of Bader,^139,140 which partitions electron density into basins, and provides a formally precise definition of atoms. However, Bader charges are frequently overestimated, and can fail to capture anisotropic charge distribution. Alternatively, density derived electrostatic and chemical charges (DDEC), charge Model 5 (CM5) and repeating electrostatic potential extracted atomic (REPEAT) charges directly reproduce the ESP within periodic systems, and have been applied to MOFs.⁸³ Conveniently, combining PW and atom-centred bases, the GPW method in CP2K enables periodic calculations to utilise conventional population analyses, such as RESP, Hirshfeld, Mulliken or Löwdin. Of course, in some systems it may be possible to neglect the crystal entirely and obtain gas-phase charges from cluster models.¹³⁸ Finally, solvation effects may be incorporated via point charge models obtained from the apparent surface charge (ASC) distribution, such as the PE continuum model (PCM), or the Conductor-like Screening Model (COSMO), which approximate the dielectric medium.¹⁴¹ To further refine these charges schemes, self-consistent algorithms have also been developed, for instance self-consistent Ewald in molecular crystals in the fromage program.^35,36 One self-consistent charge scheme uses link atom charges as a constraint in RESP fits to provide better charge distributions in extended covalent systems.¹⁴² Equally, charges can be on-the-fly within the ONIOM SCF calculation. For instance, one scheme self-consistently tunes the nuclear potential of the link atoms at the QM/MM boundary to reproduce ESP of the model-high calculation, without artificially creating or destroying charge, known as ONIOM-CT.^143,144 Moreover, embedding techniques must be carefully selected to minimise overpolarisation and must be considered carefully when an embedding is favoured over an isolated cluster. As a result, embedding techniques tailored to MOFs have been developed. Wu et al. extended the tuned F* link atom approach¹⁴⁵ to allow more than one type of bond to be cut at the QM/MM boundary. In MOFs, this is required, for instance, when boundary cuts are required at both M–O and O–M (where A–B is the QM/MM cut, in that order) bonds.¹⁴⁶ The original F* method was developed for cleaving highly polar covalent bonds found in enzymatic systems, where the linear organic backbone only required one type of bond cut. Here, the fluorine link atoms with an effective core potential (ECP) are tuned with a pseudopotential such that the sum of partial charges on the capped QM system is equal to the sum of partial charges on the equivalent region in the full QM calculation. Performing the F* tuning of each parameter for multiple bond cuts simultaneously would otherwise yield infinite unphysical, solutions. The new method was generalised to multiple types of bond cut, by finding the tuning parameter for each type of bond cut individually, which are then further tuned using an additional overarching multilink tuning parameter, C_ML. This method yields F* link atoms which preserve the polarity of the cleaved bond and was validated by studying the dimerization reaction of ethylene to 1-butene in the Zr-based MOF, NU-1000, where the F* multilink method was compared to a fully QM benchmark.

4.6 Periodic embedding

Some subsystem schemes embed the model region in a fully periodic calculation.^147–149 Periodic wavefunction-in-DFT methods also arise from FDET, and enable local electron structure effects, such as a defect or adsorbate on a metallic surface, to be simulated at the post-HF level, in the presence of a periodic embedding potential simulated at with KS-DFT under PBCs.^150,151 Accurate excited-state calculations can be performed when the periodic env electron density is calculated from an ONIOM-like scheme, subtracting the model subsystem density from the total density.^152,153 Whilst local geometry and electronic structure are updated in this scheme, the geometry of the periodic images remains unchanged meaning periodic embedding schemes can model local phenomena. Standard PW models can be expensive when modelling local effects due to the use of large supercells, necessary to avoid artificially high defect concentrations and finite-size effects under PBCs. Periodic embedding schemes, like molecular FDET, are in principle an exact, however in practice the nonadditive kinetic energy (NAKE) functional is unknown and must be approximated.¹⁰ The advantage of embedding a cluster within a PW calculation is that the environment system is inherently periodic, allowing an intuitive description of the periodic crystal. However, efficient implementation of the PW calculation can be demanding computationally, meaning periodic embedding schemes do not always offer the same efficiency improvements as analogous molecular embedding codes.¹⁵⁴ Periodic embedding schemes have been implemented in various codes such as CP2K,⁶⁸ ABINIT,⁴⁵ Quantum Espresso,⁴³ and CASTEP.⁴⁴ These methods have not been extensively used in MOF, due to their computational cost.

Zheng and Sakaki implemented a cluster-method-in-periodic-method (CM/PM) and a quantum-method-in-periodic-molecular-mechanics (QM/periodic-MM) ONIOM schemes for study of gas absorption and emission in soft materials such as MOFs and molecular crystals.¹⁵⁵ In these schemes, the high-level region is treated at a post-HF or DFT level. In CM/PM, KS-DFT is used to calculate the periodic electron density, and a post-HF method is used to simulate local excitations. On the other hand, QM/periodic-MM treats the environment with a periodic MM calculation under PBCs. In this study, only the CM/PM model was applied to MOFs and was used to characterise gas adsorption rather than photochemistry. Specifically, it was used to determine the dispersion interaction using multireference methods, where positive results were obtained for binding energies and adsorption energies for a flexible MOF, PCP-N. Electrostatic embedding was not used, and a link atoms were used for QM/MM boundary cuts. As such, this framework can be rapidly extended to the study of MOF excited-states. The QM/periodic-MM calculation used Ewald embedding for the QM wavefunction. However, a major limitation of this methodology is that the excited-molecule must be surrounded by many ground-state molecules due to its small relative population. In turn, this requires large supercells which can be prohibitively expensive due to the large unit cells of MOFs. Although, the QM/periodic-MM method performed better for simulating transition metal molecular crystals, both methods were found to be unsatisfactory for excited-state studies. However, they did enable determination of an accurate ground state geometry, from which additional excited-state cluster analysis can be performed.

4.7 Case study: cluster and periodic models

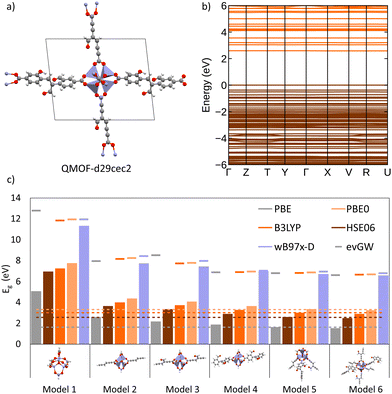
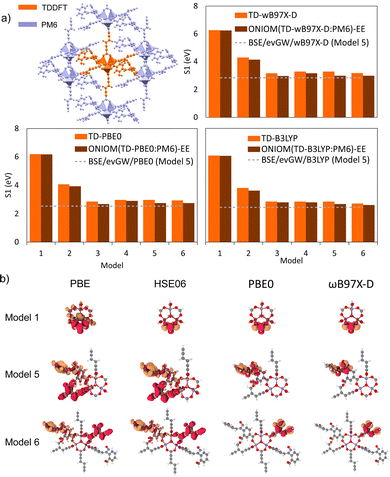
To investigate the interplay between periodic and cluster models in modelling excited states of MOFs and to validate some of the suggested protocols in this study, we have conducted our own excited-state calculations. Our candidate for this study is a theoretical MOF, QMOF-d29cec2, from the QMOF database (Fig. 10a). QMOF-d29cec2 was generated using ToBasCCO as part of the Boyd and Woo database, a theoretical screening study for finding optimal MOFs for wet flue gas capture, and is not yet synthesised.²¹ We chose QMOF-d29cec2 for three reasons. Firstly, its relative modest unit cell size (70 atoms) reduces the computational overhead for our periodic benchmarks. Secondly, it has Zn-metal nodes (d¹⁰), meaning all calculations can be performed within their restricted formalism. Lastly, QMOF-d29cec2 has a well-defined pore structure with three distinct linkers in a local octahedral coordination environment. As a result, we are able to systematically investigate how the local coordination environment of the Zn node influences the MOF excited states, using six cluster models of increasing size. Here, we combine periodic KS-DFT calculations and cluster model TDDFT, ONIOM(TDDFT:PM6), evGW, and BSE calculations into a single excited-state study. The specific computational details for these calculations can be found in the ESI† (Section S1).

Fig. 10 (a) Unit cell of QMOF-d29cec2 (Zn: blue, C: grey, O: red, H: white). (b) Electronic band structure calculated using periodic KS-DFT/HSE06. (c) Comparison of the KS-DFT/TZVP fundamental band gap across five functionals (PBE, HSE06, B3LYP, PBE0, ωB97X-D) on six cluster models (bars). The dashed-lines correspond to the fundamental gap obtained from the periodic KS-DFT calculation for each functional. Finally, the evGW quasiparticle-corrected fundamental gap is shown as a dash above each bar.

4.7.1 Results. From our periodic studies, we find the PBE fundamental gap to be 1.64 eV, approximately half that of the hybrid PBE0, HSE06, and B3LYP functionals (3.02 to 3.38 eV). Similar to many previous studies on MOFs, we observed an extremely flat band structure HSE06 level (Fig. 10b). Band curvature dictates the effective mass of charge carriers. The flat bands therefore indicate that electron and hole mobility is extremely low in QMOF-d29cec2, suggesting that a cluster model is valid if sufficiently large to cater for all electronic effects. By systematically increasing our model sizes, we are able to test the significance of cluster size on the excited states. From the ground-state KS-DFT densities, the fundamental gaps was determined for each model. As shown in Fig. 10c, E_g is massively overestimated in Model 1 which improves with inclusion of just two linkers. When one of each linker type is included, as in Model 5, the fundamental gap converges within 0.02 eV of the periodic benchmark. Notably, the value of E_g is strongly dependent on the type of functional used extending beyond just the inclusion of exact exchange, with ωB97X-D having values almost double that of the other hybrid functionals (6.59 eV in Model 6). This suggests exciton binding is significant in QMOF-d29cec2, and that it is likely insulating in nature, a qualitative difference in conduction behaviour. This claim is supported by RI-evGW calculations which gave quasiparticle gaps of 6.62 to 6.79 eV in Model 6. This was the case for PBE/RI-evGW, suggesting GGA orbitals can be corrected using GW. We were unable to perform a periodic GW calculation due to computational expense.

In the excited-state calculations, we see a similar trend with respect to model size. Turning our attention to the first three excited states (Table 1), we see better agreement between the hybrid functional, with ωB97X-D still the largest. The oscillator strengths associated with each excitation can be found in the ESI† (Section S3). Many of the excitations considered herein have very low oscillator strengths; for example, in the case of Model 1, all excitations have oscillator strengths below 0.0011. Due to the symmetry and high degeneracy of the excited states, in some cases, it is necessary to compute more than 30 excited states to find the first bright excitation and obtain the optical gap.⁹⁰ For the larger cluster models (models 4–6), the first non-dark excitation for most levels of theory is S₁ or S₂. Our focus here is to analyze the first excitations and their character. PBE once again underestimates the S₁–S₀ gap. Interestingly, the PBE oscillator strengths obtained for all models are very small. Except for one S₃ excitation in Model 4 (f = 0.0953), all the other values are below 0.0004.

Table 1 TDDFT/TZVP excited states (eV) for our cluster models 1 to 6. Excited states with oscillator strengths higher than 0.1 are highlighted in bold letters. See ESI, Section S31

Model	ES	PBE	PBE0	HSE06	B3LYP	ωB97X-D
1	S1	5.10	6.19	6.18	6.08	6.27
	S2	5.13	6.25	6.23	6.14	6.32
	S3	5.18	6.28	6.27	6.17	6.36
2	S1	2.61	4.07	3.65	3.81	4.31
	S2	3.42	4.08	4.01	3.94	4.41
	S3	3.44	4.13	4.04	3.97	4.42
3	S1	2.27	2.92	2.90	2.86	3.17
	S2	2.28	3.13	3.11	3.08	3.34
	S3	2.32	3.86	3.35	3.54	4.07
4	S1	1.89	2.97	2.89	2.85	3.29
	S2	2.18	3.04	2.90	2.95	3.31
	S3	2.22	3.20	3.00	3.08	3.67
5	S1	1.65	2.97	2.62	2.79	3.29
	S2	1.94	3.09	2.89	2.85	3.34
	S3	2.18	3.13	3.05	3.08	3.67
6	S1	1.54	2.93	2.50	2.71	3.18
	S2	1.68	2.98	2.65	2.82	3.29
	S3	1.82	3.01	2.82	2.86	3.30

---

In the absence of experimental data for QMOF-d29cec2, we use GW and BSE/GW calculations as reference for optical and fundamental band gaps respectively. This is a common approach when experimental data is not available.¹⁵⁶ The errors in the fundamental and GW band gaps are on the order of 0.2 eV, which is consistent with experimental uncertainty.¹⁵⁷ Similarly, the errors in excitation energies with BSE/GW are on the order of those obtained with wavefunction methods, such as CASPT2 or EOM-CCSD.¹⁵⁸ We were unable to perform a periodic BSE/evGW calculation due to its computational expense. Models 3 to 5 are in good agreement (Fig. 11a), suggesting these SBUs are likely most important during photoexcitation. The poor agreement of Model 2 suggests this linker, the simplest with a smaller degree of conjugation, is the least important during photoexcitation. Interestingly, although we have demonstrated the efficacy of the isolated cluster model in MOFs, we observe that the accuracy is further refined by incorporating an ONIOM-EE embedding scheme. In particular, in Model 3 the ONIOM result is in excellent agreement with the BSE benchmark in PBE0 and ωB97X-D, and yet not in B3LYP. Model 1 is hardly improved by the use of electronic embedding, however it is highly constrained in terms of its electronic structure by its small size. This is rationalised by visualising the density difference between the ground and first-excited states (Fig. 11b), where PBE, HSE06, and B3LYP predict LLCT charge transfer in the larger models, whereas the more accurate functionals, PBE0 and ωB97X-D predict LC. This is once again, a key qualitative difference that is directly dependent on choice of functional.

Fig. 11 (a) S₁ for TDDFT/TZVP and ONIOM(TDDFT/TZVP:PM6)-EE. The grey dashed-line corresponds to the value of S₁ obtained from the BSE/evGW/KS-DFT calculation of Model 5 for each functional, which we treat as a benchmark, in the absence of periodic BSE/GW calculations. (b) Transition densities between first excited-state, S₁, and the ground-state, S₀, using TDDFT/TZVP for the four PBE-based functionals (PBE, HSE06, PBE0, and ωB97X-D).

Overall, in this case study of QMOF-d29cec2, we corroborate many findings of the methods used in this perspective. Firstly, that cluster models are highly effective if sufficiently large to cater for excited-state chemistry. Secondly, the DFT and TDDFT calculations are highly sensitive to the choice of functional, and in particular that hybrid functionals must be used for reliable excited-state studies. Thirdly, we note the excellent performance of ωB97X-D (and TD-ωB97X-D) relative to our most accurate evGW and BSE/evGW/DFT calculations. These results support previous GW-studies on the band gap of MOF-5, in which qualitative differences were found by choice of method.⁷⁴ Furthermore, this suggests that range-separation could provide an excellent cost-effective protocol for estimating binding energies and fundamental gaps in MOFs with exceptionally large unit cells. Therefore, this has large implications in screening studies estimating excited-state properties from single-point hybrid calculations. This would be pertinent in database generation, where the unfavourable scaling of RI-GW (N⁴) and GW (N⁶) are limiting. In future work, we seek to gauge how optimal tuning can further refine DFT calculations. Progress is therefore required in either (a) the development of range-separation functionals in periodic DFT, or (b) the automated generation of cluster models in MOFs. The ostensible high accuracy afforded by just modest cluster sizes (namely, the first coordination sphere), suggests that the development of automated tools for cluster model generation from unit cells can in time provide a more tractable approach to the generation of databases with reliable excited-state data. In turn, this would be indispensable for training ML-models and streamlining HT screening in MOFs, a key objective of the field. Finally, it is, of course, imperative to test the limit at which the cluster model approximation breaks down. This will also be the foundation of our future work.

5 Databases, high-throughput and machine learning models

5.1 Excited-state machine learning potentials

In this perspective, we have explored the exceptional capacity of quantum chemical methods for investigating excited states in MOFs, however such studies are always inherently limited by the computational resources available. Machine learning (ML) techniques offer an alternative pathway that bypasses costly ab initio calculations, providing high-quality excited-state data at a fraction of the cost (see ref. 159 for detailed review).¹⁵⁹ This holds promise for increasing the spatial and time scales of dynamics simulations, accelerating excited-state property predictions, and automating complex procedures of methods in high-throughput applications. Developing ML potentials for the excited-state is demanding because, at a minimum, the problem must be solved for multiple states (ground and excited), often with varying multiplicities, to obtain multiple properties. Although a model might find the complete electronic wavefunction, from which all other properties can be derived, specific excited-state properties, including excited-state energies, oscillator strengths, or nonadiabatic couplings, are usually targeted. The type of ML model is also important. Neural-network (NN) models have been most extensively applied to the excited states in organic molecules, for instance in performing photodynamics simulations on the nanosecond scale¹⁶⁰ or efficiently predicting optical spectra.^161,162 Kernel ridge regression (KRR) models have been used to interpolate diabatic potentials.¹⁶³ Decision tree models have automated active space selection in CASSCF studies, a notoriously difficult task.^163,164 However, the majority of ML studies on excited states use molecule-wise descriptors, making them specific to the molecule being studies. Models which use atom-wise descriptors will improve transferability of ML force fields in the future.¹⁶⁵ In the next sections we cover: (a) high-throughput/database-driven ML methods, the most commonly employed strategy in MOFs, although a ground state DFT electron density is used to estimate HOMO–LUMO gaps with ML, this is inherently an excited-state property, and (b) diagonistic techniques for multiconfigurational states, which critically influence excited-state properties; diagnostic techniques will be valuable in the development of MOF excited-state ML potentials.

5.2 MOF databases and high-throughput study

Machine learning methods have been used in MOFs to exploit the wealth of experimental data available, for instance in structural property prediction. Extensive crystallographic and material data for experimentally synthesised and computer-generated MOFs can be found in various structural databases. This has lead to significant interest in the development of ML potentials and high-throughput studies. For instance, the Cambridge Structural Database (CSD) contains over 100 000 MOF-based entries.¹⁶⁶ Boyd and Woo developed a database containing over 300 000 MOFs generated with the Topology Based Crystal Constructor (ToBasCCO) program.²¹ Here, data-mining methods identified optimal targets for CO₂ capture in wet flue gas. Some database are designed specifically towards high-throughput computational investigations, containing cleaned data for quantum chemical calculations. One example is the Computation-Ready, Experimental Metal–Organic Framework (CoRE MOF) database,¹⁶⁷ This streamlines intensive preliminary data-cleaning processes in large-scale computational studies. Rosen et al. developed the Quantum MOF (QMOF) database, a subset of the CSD, that contains over 20 000 experimental MOF structures optimised towards the study of quantum chemical properties.¹⁶⁸ The structures contained within the database are relaxed using periodic KS-DFT, and contain important quantum mechanical quantities, such as band gaps, partial charges, spin densities, geometric features, and band gaps. So far, databases and ML models in MOFs focus entirely on ground state densities obtained with KS-DFT. There is a shortage of databases containing MOF excited-state data derived entirely from time-dependent, multiconfigurational or perturbation theory-based methods due to the associated computational cost. However, such a database would be a valuable tool in screening MOFs for photochemical properties.

Multireference (MR) diagnostics seeks to determine the multireference character of a material, prior to carrying out expensive calculations. One recent HT study used KS-DFT to distinguish between MOFs that will require multiconfigurational methods and those that will be described adequately by a single-reference method such as TDDFT.¹⁶⁹ This study used a traditional metric, r_ND, that represents the ratio of the nondynamic correlation to the total correlation, which was compared to a new metric r_FOD which accounts for the ratio to fractional occupied density number and r_ND. Crucially, r_ND and r_FOD can be estimated from densities obtained using KS-DFT. A subset of 274 MOFs was extracted from the CoRE database to alleviate computational overhead by only selecting MOFs containing Sc, Zn, Y, and Cd. These metals are always in the singlet ground state and have only one oxidation state. Additionally, only MOFs with unit cells containing less than 200 atoms were used. From these periodic structures, cluster models containing a single metal node and its coordinating ligands, where automatically extracted from the relaxed periodic structure, and saturated with hydrogens using the CCDC Python-API. Calculations were performed on both this cluster, and the constituent SBUs, and the fully periodic MOF with KS-DFT. Overall, a strong correlation between r₂ and both band gap and r_FOD was found (Fig. 12). This suggests a general trend in in which wide-band gap materials are likely have low multireference character, a useful diagnostic found from ground-state densities.

Fig. 12 Correlation between r_ND and band gap, and r_ND and r_FOD used as MR diagnostics, obtained from semi-local DFT (PBE/LACVP*) calculations. Reprinted with permission from ref. 169. Copyright 2023 American Chemical Society.

It is imperative not to compromise accuracy for convenience when developing ML-models. For instance, the modest cost of GGA functionals might appear attractive to those developing quantum chemical databases, however, GGA functionals will be insufficiently accurate to generate a model for certain photochemical predictions. Rosen et al. have shown this within the QMOF database (Fig. 13a), where the distributions of band gaps shifts higher in energy when increasing the level of DFT functional, using GGA (PBE), meta-GGA (HLE17), and hybrid functionals (HSE06 and HSE06*, *indicates a lower portion, 10%, of HF exchange).⁸³ This results in gaps more in line the generally insulating nature of most MOFs. Additionally, in PBE, HLE17, and HSE06*, the band gaps are seen to be bimodally distributed. This can be rationalised by splitting the dataset into its closed- and open-shell MOFs (Fig. 13b). Interestingly, here HLE17 performs surprisingly well, relative to HSE06*, without including exact exchange. However, only HSE06 provides the level of accuracy required to reliably screen MOFs. Training a model with underestimated GGA band gaps makes the model susceptible to spurious property predictions, such as band conduction in an insulating MOF.¹⁹ In studies seeking to identify purely metallic MOFs using quantum chemical methods,⁸⁷ caution is required. Of course, thermal conductivity may alternatively be studied using molecular dynamics.¹⁷⁰

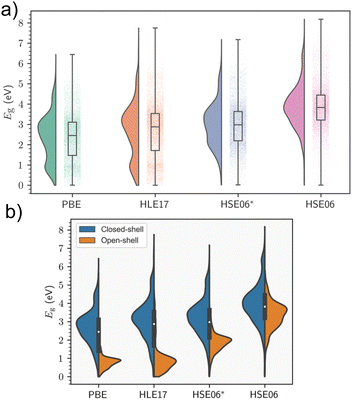Fig. 13 (a) Distribution of band gaps, E_g, for the 10 720 structures found within the QMOF database, determined using periodic DFT using GGA (PBE), meta-GGA (HLE17), and hybrid (HSE06, HSE06*) functionals, and (b) decomposed into the closed- and open-shell contributions. Adapted with permission figure from ref. 83. IOP Publishing. Reproduced with permission. All rights reserved.

6 Photochemical and photophysical processes

A detailed understanding of the excited states of a material is required when studying photomechanisms within a material. Many MOFs display remarkable luminescence properties, with many potential applications in lighting, single-molecule detection, biosensing, and optoelectronics. When a material absorbs light, a multitude of competing radiative and nonradiative processes occur, depending on the excited-state potential energy surface and interactions between excited states.¹⁸ An ability to characterise charge transfer processes, such as LMCT, is crucial for understanding charge separation and recombination in photocatalysts. In MOFs, photomechanisms can be as extensive as photoisomerisations of linkers in the framework, as seen in PCN-123.¹⁰⁶ The coordination environment of the organic linker to the metal node in MOFs can often increase the efficiency of intersystem crossing (ISC), a nonradiative change in spin state arising from strong SOC. Kasha's rule states that for given multiplicity, only the lowest energy excited-state will facilitate fluorescence or phosphorescence behaviour. While non-Kasha behaviour is known in some materials, these cases have rarely been reported in MOFs.¹⁷¹ Consequently, excited-state geometry optimisations in the excited state potential energy surfaces offers a means of investigating radiative emission.¹⁷² In this section, we look at how the models discussed previously can elucidate photochemical and photophysical processes by calculating the excited states of MOFs.

6.1 Prediction of UV-Vis spectra

The use of cluster models affords time-dependent and multiconfigurational techniques for predicting absorption spectra.¹⁰³ Simulated spectra are often directly comparable to emission and absorption experiments, providing detailed insight into MOF excited states. Of these methods, TDDFT provides a favourable cost-accuracy trade-off for computing UV-Vis absorption spectra to a reasonable degree of accuracy, which can be expensive due to the large number of excited states that need to be calculated. KS-DFT has been investigated as a method for generating reasonable spectra in MOFs.¹⁷³ Initially, excited-state calculations produce line spectra, which are made visually comparable to experimental spectra by using broadening techniques such as Gaussian or Lorentzian functions.¹⁷⁴ Equally, nuclear motion can be incorporated by using simulations in the time-domain, such as MD, ab initio molecular dynamics (AIMD),¹⁷⁵ or through phonon calculations. Simulated TDDFT absorption spectra have been used to probe MOF excited states for some time. For instance, this was performed for Zr-UiO-66 functionalised with three different linkers.¹⁷⁶ In comparing the simulated spectrum with experiment (Fig. 14), TDDFT/PBE calculations on the H-capped clusters confirmed that the observed absorption peaks corresponded to the nature of the bond connecting each functional group and the adjacent aromatic carbon, which modulates the band gap. In the same MOFs, KS-DFT was later used to investigate charge carrier mobility, another important property in photocatalysis.¹⁷⁷

Fig. 14 Comparison of experimental and TD-PBE simulated spectra of Zr-UiO-66 with three different functionalisations. Modified from ref. 176 with permission from Royal Society of Chemistry, copyright 2014.

In fact, UV/vis spectra may be used to study the colour of the MOF itself. For instance, the various chromophoric units included in a MOFs can give rise to a range of colours. The Cu(II)-based HKUST-1 is typically associated with a green/turquoise hue attributed to strongly coloured d–d excitations, however, in a high-quality pristine thin-film form it is observed to be colourless.¹⁷⁴ To investigate the role defect chemistry might play, cluster models were constructed for both the DFT-relaxed pristine and defective HKUST-1 structures. CASSCF calculations were then used to predict the absorption spectrum. The defective structures were formed by introducing a Cu⁺ ion, by removing a linker, and by distorting the Cu–O bond to change the symmetry. The predicted spectra revealed that the intensity of the d–d excitations in the pristine structure were two orders of magnitude smaller than that of each defective species. This agrees with the experimental absorption spectra and the qualitative finding that the defective species was turquoise whereas the pristine HKUST-1 films is colourless. This was likely due to a loss of symmetry due to the defect relaxing spectroscopic selection rules.

6.2 Charge transfer

When modelling charge transfer processes in MOFs, the level of theory must be carefully selected, because hybrid functionals, such as B3LYP, overstabilise CT states. The use of long-range corrected functionals might be needed. These methods are becoming popular in the molecular modelling community. Recent work by Ortega-Guerrero et al. showcases the potential of excited-state modelling in unravelling CT processes and challenging experimental interpretations.¹⁰¹ Periodic TDDFT (PBE-D3/PBE0-D3) and cluster model TDDFT (CAM-B3LYP) calculations have been used in tandem on the study of charge transfer in porphyrinic Ru-TBP-Zn. The experimental crystal structure of this system was incomplete and the Ru atom has an incorrect coordination environment. Consequently, the authors designed two models including Cl (RuTBPZn-Cl) and OH (RuTBPZn-OH) ligands. The first absorption band was modelled using a periodic model with 35 excited states and PBE0-TC-LRC. Despite the larger contribution of the states of Ru to the conduction band than those from porphyrin, the first absorption band for both models are ligand centred π → π* transitions, as described by the Gouterman four-orbital model of porphyrins.¹⁷⁸ This is in line with the significant role excitonic effects play in these materials. However, in contrast with RuTBPZn-OH, RuTBPZn-Cl displays low-lying charge transfer states LMCT (porphyrin → Ru) after the Q band. The TDDFT cluster calculations computed the entire optical spectrum, enabling characterisation of the key excitation as LMCT. To further explore the feasibility for charge separation (E_int = E_e–h − (E_e⁻ − E_h⁺)), the authors calculated the interaction energy between the LMCT (relaxation energy: E_e–h) and the separated polarons (with relaxation energies of E_e⁻ and E_h⁺). The interacting LMCT was optimised using constrained DFT (C-DFT) using both periodic and cluster models (Table 2). By constraining the electron densities on specific molecular units, C-DFT allows for describing diabatic charge transfer states.^179,180 Although the magnitude of the interaction energies differ between the periodic and cluster models, both indicate that RuTBPZn–Cl is a better photocatalyst than RuTBPZn–OH for HER, as the Cl group contributed to a repulsive electron–hole interaction. This promoted charge separation, lowering recombination probability, via LMCT. This work demonstrates the effectiveness of combining periodic and cluster TDDFT methods for characterising excited states in MOFs.¹⁰²

Table 2 TDDFT exciton energetics obtained calculated using for both periodic and cluster models obtained by Ortega-Guerrero et al. (ref. 101). Adapted with permission from ref. 101. Copyright 2020 American Chemical Society

Energy (eV)	MOF RuTBPZn		Cluster RuTBPZn
	Cl	OH	Cl	OH
E h^+	−0.190	−0.407	−0.960	−0.097
E e^−	−0.217	−0.471	−1.188	−0.735
E e–h	−0.247	−1.130	−0.441	−0.946
E int	0.16	−0.252	1.707	−0.114

---

A desirable design objective of MOFs is to tune luminescence properties via structural modifications. This has been observed in pyrazole-based M[H₂DMPMB] (M = Zn, Cd), a pair of isoreticular MOFs differing in identity of the metal centre.¹⁸¹ Within the same network topology, the Zn-based MOF emits at 441 nm whereas Cd-based MOF emits at 335 nm, corresponding to a blue-shift of 0.88 eV. In this study, M[DMPMB] cluster models were extracted from the periodic DFT-relaxed (PBE0-D2) structure. TDDFT calculations were used to determine vertical excitations and oscillator strengths, and to predict the absorption spectra. The singlet excitations associated with Zn[BMPMB] have insufficient oscillator strength to be associated with intense photoluminescence emission, and emission from the triplet state has been observed previously in d¹⁰ complexes.¹⁸² Overall, theoretical calculations indicated that the difference in emission behaviour arises from the fact that the high-energy emission in the Cd structure likely originates from an LC singlet π–π* transition, whereas it more likely comes from a LC triplet π–π* excited-state in the Zn example.

Cluster models are an effective tool in the challenging task of distinguishing between the array of charge transfer processes accessible to MOFs. For instance, the luminescent MOF, [Zn(NH₂ bdc)(bix)]_n, experiences quenching through an internal conversion (IC) decay processes in the presence of formaldehyde, making it a candidate for single-molecule chemosensing.¹⁸³ The S₁ state critically depends on hydrogen bond behaviour, with increased hydrogen bonding corresponding to a decrease in emission intensity. Previously, luminescence emission was associated with a LMCT transition, however TDDFT cluster calculations (CAMB3LYP/BVP86/LANL2DZ/6-311++G(d,p)) with and without the formaldehyde guest indicated luminescence was most likely an LLCT process. The presence of the formaldehyde guest increased the strength of the hydrogen bonding, quenching luminescence by improving access to the IC decay pathway. Similar results have been obtained for dichloromethane-detection using Cu₂(5-(4-pyridyl)tetrazole)₂, where cluster calculations indicated an LMCT-driven luminescence processes depending on excited-state hydrogen bonding could be quenched by introduction of a guest-species.¹⁸⁴ Strengthening of hydrogen bonding in the exited-state narrowed the energy gap between the ground- and excited states, increasing the rate of IC. Here, TDDFT cluster models were valuable in distinguished between MLCT and LMCT processes.

Similarly, in Zr- and La-based UiO-66, luminescence behaviour has been attributed primarily to linker-localised excitations using TDDFT cluster models.^175,185 In this study, the well-known flexibility of the framework was introduced via AIMD simulations in include nuclear motion. A PE continuum model (PCM) to simulate the DMF solvent environment.¹⁷⁵ The TDDFT calculations for each configuration yielded the dynamic average, which showed good agreement with the experimental data, except for an unsystematic shift in the dynamic values compared to the static relaxed geometry. Additionally, they performed periodic KS-DFT with a hybrid functional to benchmark the findings. The TDDFT cluster calculations indicates that the π → π* excitations have much larger oscillator strength than the competing LMCT excitation, indicating photoexcitation largely takes place from linker-localised excitations. In later work,¹⁸⁵ LR-TDDFT spectra was predicted for the UiO-66 (M = Ce, Hf, Ti) for both the pristine and lanthanide-doped species using static cluster models, with Gaussian broadening being preferred to AIMD. La-cations are difficult to model using KS-DFT, however the results were compared to band structure calculations using the HSE06 functional. This work, and another,¹⁸⁶ indicated that introducing Ce⁴⁺ into the UiO-66 architecture can promote LMCT mechanisms in favour of the linker-localised excitations. In this circumstance, screening of the linker functionalisation indicated that band gap engineering towards redox applications, such as CO₂ reduction was possible, whilst retaining LMCT character of the underlying transition. TDDFT cluster and PDOS calculations indicated this arises due to the introduction of low-lying Ce(IV) f-orbitals into the band gap, which makes LMCT state far more accessible. Overall, cluster calculations and spectroscopic studies working in tandem revealed a design principle (transmetalation with Ce(IV)) for engineering LMCT behaviour, and therefore charge separation, into a target MOF. Charge recombination and migration can be investigated using electron transport theories such as Marcus theory. Nonadiabatic simulations have the potential to be valuable tools for studying these processes.¹⁸⁷ However, conducting such calculations for MOFs can be computationally demanding. A recent study by Syzgantseva et al. introduces an algorithm that efficiently computes nonadiabatic couplings, which are sometimes the limiting factor in nonadiabatic dynamic simulations for MOFs. This algorithm utilises a grid representation of the wave functions.¹⁸⁸ An effective choice could be the combination of approximate electronic structure approaches⁹⁹ and estimation of couplings based on energy and gradients such as described in ref. 189 and 190.

Beyond transmetalation, Hendrickx et al.^175,185 and Wu et al.^186,191 demonstrated how linker functionalisation can control the photoexcitation process in UiO-66. The ability to engineer light absorption into the vis-region is important for photocatalytic applications which rely on solar energy (Section 7). Here, light harvesting was optimised through functionalisation of the BDF linker. First, in Zr-UiO-66, the BDC linker was mono- and di-functionalised with OH, NH₂, and SH groups, reducing the band gap of 4.0 eV (with the unmodified BDC linker) to 2.2 eV (in SH di-functionalised BDC).¹⁷⁵ These extended previous experimental findings in UiO-66, where amino-functionalisation was seen to shift absorption to wavelengths above 300 nm, without influencing the underlying photochemistry.¹⁹² Wu et al. screened twelve mono-substituted functionalisations (NH₂, NO₂, F, Cl, Br, I, OH, SH, COOH, CH₃, CF₃,and SO₃H) of the BDC linker in Ce-UiO-66.¹⁸⁶ Each functionalisation reduced the band gap relative to the pristine species, with SH once again providing the largest reduction (1.55 eV). Using isolated cluster models for linkers was a good strategy for screening linkers for optimal light harvesting. Most crucially, functionalisation of the linker with electron-withdrawing groups enabled the LMCT energy, E_LMCT, to be raised to values where both efficient LMCT and absorption of visible light take place. This effect was enhanced by the number of functionalisation groups, indicating linker functionalisation provides a promising strategy for photocatalytic redox applications. Using these principles, Wu et al. extended these findings to optimise photocatalysis through doping with Zr or Ti into the UiO-66 framework.¹⁹¹ In this respect, for optimal compromise between E_LMCT and visible light absorption, Ce-UiO-66(Ti₄)-I was proposed as a promising candidate for water-splitting. Although the relationship between band gaps and linker functionalisation has been studied for common MOFs such as UiO-66, MIL-125,¹⁹³ and MOF-5,¹⁹⁴ the effect of linker functionalisation on excited states has not yet been explored.

6.3 Excitonic effects

In the context of Kasha's exciton model, excitonic effects arise from the electrostatic interactions between independent molecular units, thereby lifting the degeneracy of excited states of the independent chromophores. More sophisticated models include contributions from electron exchange and also consider charge transfer states.^18,195 However, traditional H and J dimers are still useful and very popular for the interpretation of experimental and computational results. An interesting discussion about the interpretation of experimental results based on exciton models can be found in ref. 196–198. It is important to distinguish the term exciton from the general notion of electron–hole pairs. Excitons are lower in energy than uncorrelated pairs and possess a pseudo-spin configuration due to strong coupling between the spins of the photogenerated electrons and holes.¹⁹⁹ This gives rise to effects such as band gap narrowing, trapping-states, and subsequent photomechanisms. The exciton effect is especially pertinent to MOF photocatalysis, as it plays a critical role in the formation of reactive species via charge and energy transfer mechanisms.⁸¹

When simulating MOFs using cluster models, it is important to consider and inter-chromophoric interactions which give rise to excitonic effects, depending on network topology. TDDFT cluster models reasonably described inter-chromophoric interactions in MOFs.^200,201 Here, TD-CAM-B3LYP/LANL2DZ calculations characterised the inter-chromophoric interaction between the S₀ and S₁ emissive and absorption states in H₄ TBAPy-based ROD-7, NU-901,and NU-1000, using pyrene-pyrene and pyrene–phenyl dimeric models of the clusters. This revealed long-lived emissive excimer states that were observed in time-resolved emission spectroscopy (TRES). Additionally, a trend in emissive state lifetimes, ROD-7 > NU-901 > NU-1000, consistent with band gap measurements was seen. The strength of the inter-chromophoric reaction was sensitive to linker positioning, a property which can be tuned in MOFs. Similarly, this has been observed in a comparative study between the anthracene dibenzoic acid (ADB) in the solution phases and as a linker within Zn-based SURMOF-2.¹¹⁰ In the latter, optical spectra did not exhibit the blue-shifted absorption maximum expected when excitonic coupling arises from H-type aggregation of the interacting chromophores. Instead, a red-shift arose due to dominating π-conjugation between linkers, most clearly observed in the simulated and experimental emission spectrum. TDDFT cluster calculations predicted accessible red-shifted excitations with low, but non-zero, oscillator strength. TDDFT indicated that the fixed network topology constrains the ADB chromophores, which change considerably within the MOF and create a red-shift for each excited-state, outweighing the expected blue-shift; the framework flexibility facilitates a significant change in conformation following photoexcitation. In H₄ TBAPy-based Zr-NU-901 and NU-1000 transition density matrix (TDM) calculations and additional transient absorption spectroscopy (TAS), cluster calculations revealed optically allowed S₁ and S₂ states are delocalised over multiple linkers with excitons as large as 1.7 nm, covering two chromophores.²⁰² A topological dependence of the excited states was illustrated, as in NU-1000 these CT states were allowed, whereas in NU-901 they were forbidden. Moreover, TDDFT cluster models can help to untangle the web of interactions, such as inter-chromophore coupling and packing-induced effects, on which the photochemical properties depend.

6.4 Chemosensing

A combination of multiconfigurational and TDDFT-based approaches can be used to reveal entire photophysical mechanisms from cluster models. For instance, Eu-MOF has shown selective luminescence quenching is observed in the presence of aniline, for applications in single-molecule chemosensing.²⁰³ Here, absorption is localised on the linker and emission from the Eu-centre. Cluster models using both CASSCF/NEVPT2 and sTDDFT revealed the entire sensitisation pathway, and particularly the interaction between the aniline guest and the framework. The calculations revealed that initially, the ligand S₁ state was converted to the T₁ state via ISC. Energy transfer was then transferred to the ⁵D₀ state of the Eu node, before final emission from the Eu-centre to ⁷F_J state. The photoluminescence pathway is strongly dependent on the guest–host interactions between the framework and the analyte. A dimer cluster model was used, where KS-DFT geometry optimisations (BP86/STO-TZ2P) of both the Eu-MOF and Eu-MOF-analyte systems were performed, and an S₁ optimisation of the antenna fragment at the DFT level (B3LYP/STO-TZ2P). TDDFT was used to simulate the emission spectrum, and molecular sTDDFT (CAM-B3LYP) to simulate the UV/Vis absorption spectrum. In later work, this was applied to other chemosensing systems for azobenzene derivatives, such as [Cd₂(H₂L)₂(H₂O)₅]·5H₂O (L = 5,5′-((thiophene-2,5-dicarbonyl)bis(azanediyl))diisophthalic acid).²⁰⁴ Here, a photoinduced electron transfer (PET) from Cd-MOF to the aniline guest was responsible for quenching, as demonstrated by S₀ and S₁ TDDFT geometry optimisations. Additionally, AIMD indicated intermolecular hydrogen bonding was consistent throughout the simulation, indicating pNA is confined inside Cd-MOF. The optical results agreed well with the experiment, validating the truncated structure (<115 atoms). The Morokuma–Ziegler energy decomposition scheme with the NOVC approach was used to verify the specific contribution of hydrogen bonding. Finally, this protocol was replicated to simulate the excited-state dynamics of a Tb-MOF chemosensor.³ In these example, multireference and TDDFT calculations have been used to detail entire chemosensing pathways including nonradiative processes such as ISC and IC, as well as the key emissive steps (Fig. 15). The combination of these techniques is therefore a powerful tool for the study of MOF excited states.

Fig. 15 Energy level diagram of the most likely sensitisation and emission pathway obtained by Híldago-Rosa et al. using a multireference CAS(8,7)SCF/NEVPT2 and TD-B3LYP/def2-TZVPP/CPCM protocol. Reprinted with permission from ref. 3. Copyright 2022 American Chemical Society.

6.5 Guest–host photomechanisms

Luminescence arising from guest–host interactions is a well-established photomechanism in MOFs.⁹ Guests can be introduced to enable specific charge transfer behaviour, giving rise to special properties. In particular, the excited states of π-conjugated linkers and a guest species may interact to form an emissive exciplex. For instance, by introducing Buckyball (C₆₀) molecules into the porphyrinic MOFs, PCN-222, DA-MOF, and F-MOF, was shown to induce luminescence. Periodic GPW/DFT (PBEsol-D3/DZVP-MOLOPT-SR-GTH/GTH) and TDDFT cluster model (M06-L/6-31G(d)-SDD) calculations were combined to suggest luminescence arises from PET from the porphyrin linker to the electron-deficient Buckyball guests.^205,206 Additionally, photochromic guests can be encapsulated into the mesoporous structure of MOFs, to induce photochromic properties.¹¹³ Photochromism is a process in which a material changes colour upon light irradiation, with applications such as photoswitching and super-resolution fluorescence imaging, and can arise from LMCT. Here, ONIOM(QM:MM) was used to study laser-induced photochromic fluorescence in a fluorophore-MOF material. Guest@MOF species are suited to study using hybrid models, as the guest and MOF are not typically covalently bonded, making partitioning the high- and low-level subsystems straightforward. Of course, the outer MOF layer must still be extracted from the bulk crystal and capped with link atoms. This method initially relaxed the outer MOF cluster using a self-consistent charge density-functional tight binding (SCC-DFTB), with fixed positions for the metal nodes. Subsequently, an ONIOM(B3LYP:UFF) simulation was performed, in which the high-level TDDFT region was the fluorophore (DMASP) guest. The truncated MM framework was capped using methyl and ammonia groups. Overall, the calculations revealed that the UV photoexcitation caused the DMASP to relocate within the PORE from polar to nonpolar sites, changing the fluorescence properties and resulting in photochromism.

Some emissive dyes experience quenching of luminescence in the solid-state material, known as ACQ. For instance, this occurs in flavin dyes, which display intense emission in solution, but not in the molecular crystal. However, dyes can be introduced into a guest@MOF material, where the MOF pore creates a pseudo-solution environment where luminescence is not quenched. Retaining luminescence in the solid-state is useful for device manufacture. The flavin-derivative, 10-methyl-isoalloxazine (MIA) showed a significant reduction in ACQ when introduced to MOF-5 and MIL-53.¹²² This was investigated with both periodic DFT and QM/MM embedded calculations. Using embedding techniques, the photoactive MIA dye molecule was simulated using costly multireference calculations, with the surrounding MOF pore modelled using the AMBER16 force field. As a reference, QM/MM calculations were also performed for the MIA molecular crystal, with mono-, di-, and trimers being used as the model regions. The clusters were relaxed using a QM/MM geometry optimisation with fixed metal centres. Spectral properties were predicted using the DFT/MRCI (multireference configuration interaction) method at the BHLYP/TZVP level.²⁰⁷ The additive R2016 Hamiltonian, as implemented in Turbomole was used to account for interactions between the model region and the MOF environment. The calculations revealed that ACQ arises in the MIA crystal due to π-stacking interactions in the aggregated phase, creating charge transfer states with low-oscillator strength. When the dye is instead incorporated into the MOF, the pore structure provides a single-molecule environment dispersed throughout the crystal pores. Consequently, π-conjugation and corresponding quenching behaviour does not occur, resulting in fluorescence behaviour weaker than solution, but much stronger than the MIA crystal phase (Fig. 16). The emission wavelength calculated from the S₁ state was an order of magnitude larger for the MOF phases than the MIA crystal, and matched that of the vacuum, illustrating the efficacy of MOFs in isolating the flavin die from its aggregation behaviour. In this respect, both MOFs displayed similar emission properties, however the greater flexibility of the MIL-53 framework facilitated a stronger van der Waals interaction with the dye and the pore-wall, resulting in increased order across the one-dimensional channel. Guest–host interactions in MOFs have also been exploited to improve conductivity in MOFs.^205,206

Fig. 16 DFT/MRCI absorption spectra (BHLYP/TZVP) using the R2016 Hamiltonian of MIA fluorophore in vacuum, crystal, and MOF (MIL-53 and MOF-5) environments. The clusters were obtained using a hybrid QM/MM (PBE0/AMBER16) geometry optimisation, where the model region was the fluorphore dye. The phenyl linkers in MOF-5 in the MOF can point in the inward (left) and outward cage configurations. Modified from ref. 122, with permission.

6.6 Thermally activated delayed fluorescence (TADF)

In TADF, an efficient reverse intersystem crossing (rISC) pathway, driven by thermal energy, facilitates the population of emissive singlet excited states from an initially populated triplet excited state. This mechanism delays the emission process and has been exploited for the creation of efficient OLEDs with significant photoluminescence quantum yield (PLQY).²⁰⁸ As seen previously, ACQ in the solid-phase interferes with emissive pathways in otherwise fluorescent molecules. TADF has been observed in a diphenylamine-tetraphenylethylene (DPA-TPE) dye when incorporated into the thin-film surface supported MOF (SURMOF), SURMOF-2 (Fig. 17).²⁰⁹ DPA-TPE is not emissive in solution, but displays TDAF in the dye@SURMOF material. Here, an electrostatically embedded ONIOM(QM:MM) model treated the DPA-TEP linker at the TDA-TDDFT (BMK-D3/def2-SVP) level. TDA-TDDFT was chosen to avoid the triple instability problem. The larger region was modelled at the UFF level, using a cluster extracted from the relaxed (KS-DFT/optB86-vdW) structure containing 27 DPA-TPE linkers was modelled at the UFF level. The BMK²¹⁰ functional (42% HF exchange) was selected as it had been used in previous studies to accurately simulate TADF.^16,17 By calculating the S₁ and T₂ excited states, an adiabatic energy gap was reduced from 0.354 eV in the isolated molecule, to 0.23 eV in the MOF cage. This is indicative of the hot exciton mechanism that drives the rISC process. Similarly, TADF with modular PLQY was introduced into a MOF by incorporating triphenylene (Tpl) into a cage-based NKU-111 host (Tpl@NKU-111).¹²³ The resulting through-space charge transfer mechanism enabled a double-channel T₁ and T₂ rISC to an emissive S₁ state to achieve TADF. An ONIOM(QM:MM)-EE containing an A1-D-A2 Tpl-based fragment treated at the DFT and TDA-TDDFT (M06-2X) levels, with the wider truncated cluster treated with the AMBER force field. The ONIOM(TDDFT:AMBER)-EE model was used to optimise both the S₁ and T₁ states to give an adiabatic gap of 0.05 eV, consistent with emission spectroscopy. Specifically, this elucidated a mechanism where excitations originated in the degenerate HOMO−1 and HOMO levels of the guest donor, to the acceptor LUMO+1, via the double-channel ISC process. The PLQY intensity was able to be controlled using the guest loading ratio when forming the composite.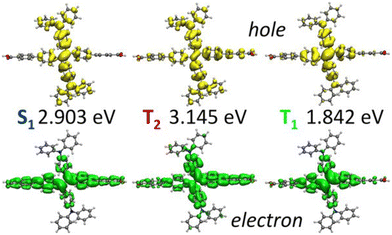

Fig. 17 Visualisation of electron and holes in the S₁, T₁, and T₂ states, obtained using ONIOM(TDA-BMK-D3/def2-SVP:UFF). Reprinted from ref. 209 with permission.

6.7 Room temperature phosphorescence (RTP)

Unlike fluorescence, phosphorescence is a long-lived emission process, where light is re-emitted from a state of different multiplicity than the state from which it was absorbed. The change in multiplicity is driven by a nonradiative ISC between isoenergetic singlet and triplet states. Phosphorescence is typically performed at low-T due to weak SOC and nonradiative recombination pathways, such as triplet–triplet annihilation (TTA), that compete with phosphorescence. On the other hand, RTP materials display phosphorescence under ambient conditions. RTP is a desirable property for applications such as fingerprinting, photovoltaics and anti-counterfeiting technology.¹¹⁸ To achieve an appreciable PLQY at room temperature, a material must efficiently populate triplet excitons via an ISC process, which in turn must be stabilised to avoid undesirable quenching pathways. Purely inorganic materials suffer from high cost and difficult machinability, whereas purely inorganic materials suffer from weak SOC and high recombination rates.¹⁴ MOFs offer a compromise in which guest–host interactions are exploited in the inorganic–organic framework to induce RTP. The transition metal centres incorporate greater SOC.¹⁵ Excited-state methods provide a means of disaggregating the competing pathways, and identifying favourable ISC conditions. For instance, the MOF, [NH₃Me]·[Zn₂(HEDP)(TPA)_0.5(H₂O)₂]·2H₂O (TMA), has been shown to exhibit highly-efficient blue RTP.¹¹⁸ TDDFT cluster model calculations on TMA in the singlet and triplet states indicated the energy gap between states were small (0.004 eV) providing facile ISC that drives the subsequent emission process. Crucially, steric constraints by both the framework, and the interaction with its chromophoric guest inhibit the accessibility of nonradiative annihilation pathways, resulting in efficient RTP. Guest–host interactions have also been used to provide RTP in [Zn₂(4,5-ImDC)₂]M₂ (NKU-132, M = (CH₃)₂NH₂ or (CH₂CH₃)₂NH₂).¹⁴ TDDFT cluster model calculations were once again used to show similar energy of the S₁ and T₁ states, with each photogenerated charge carrier (hole and electron) are transferred to spatially separated ligands. Finally, two MOF glasses, M-DCl-glass (M = Zn and Cd), have been shown to exhibit ultra-long blue and green RTP, respectively.¹⁵ TDDFT cluster calculations indicate photoexcitation and emission largely stem from a ligand-to-ligand charge transfer (LLCT) process from the frontier orbitals centred on the cyano and imidazole ligands. This was corroborated by TAS, and a notable lack of election population was found on either metal centre, making MLCT or LMCT processes unlikely. Finally, triplet–triplet gaps were shown to be small in both species, facilitating efficient ISC, especially compared to the pristine MOF.

7 MOF photocatalysis and CO₂ reduction

The combination of metal centers and ligands gives MOFs the ability to serve as photocatalysts for various chemical reactions. Given its significance, our focus here lies on the simulations of the processes involved in CO₂ reduction. Anthopogenic CO₂ is the major contributor to global warming,²¹¹ making it desirable and economical to produce multicarbon chemical feedstocks, such as ethanol (C₂H₆OH), ethylene (C₂H₄), or propanol (C₃H₈OH), from its emissions. This is in line with the Net Zero targets set by governments. In recent years, significant research attention has been directed toward materials that facilitate reduction using solar energy in recent years.^{13,24,212–215} The difficulty in achieving appreciable catalysis is due to the stability of the C=O bond, which typically requires energy-intensive conditions to break.¹⁷² Photocatalysis, or artificial photosynthesis, provides a pathway which can be carried out under ambient reaction conditions via the carbon dioxide reduction reaction (CO₂RR)s.²¹⁶ The permanent porosity of MOFs facilitates efficient carbon capture and absorption,^217–219 and the use of light-harvesting SBUs enable efficient catalysis.^5,19,216,220 The result is that the entire CO₂RR mechanism may be performed in a single heterogeneous catalyst using MOFs.

Chen et al. report four main pathways for converting CO₂ into value-added chemicals: photocatalytic reduction; electrocatalytic reduction; catalytic hydrogenation with H₂; and cycloaddition with epoxides to cyclic carbonates.²²¹ Here, we focus on photocatalysis, where excited-state studies are uniquely advantageous. In semiconductors, the mechanism for CO₂RR is as follows: (1) sunlight excites a photosensitised chromophore unit typically reduced by a sacrificial agent, creating charge separation; (2) CO₂ adsorbed on the catalyst surface, in its bent configuration, is reduced to CO₂⁻ at the conduction band;

CO₂ + e⁻ → CO₂⁻ E° = 1.85 V (3)

(3) CO₂⁻ accepts protons generated from oxidation of water to form a reduction product, the relevant reduction potentials of one-carbon (C₁) products against the standard hydrogen electrode are given;²¹⁶

CO₂ + 2H⁺ + 2e⁻ → HCOOH E° = −0.61 V (4)

CO₂ + 2H⁺ + 2e⁻ → CO + H₂O E° = −0.53 V (5)

CO₂ + 4H⁺ + 4e⁻ → CH₂O + H₂O E° = −0.48 V (6)

CO₂ + 6H⁺ + 6e⁻ → CH₃OH + H₂O E° = −0.38 V (7)

CO₂ + 8H⁺ + 8e⁻ → CH4 + 2H₂O E° = −0.24 V (8)

(4) the reduction product can undergo subsequent reductions, for instance C–C coupling to generate multi-carbon (C₂₊) products (5) the final product desorbs from the catalytic site (Fig. 18).^5,216

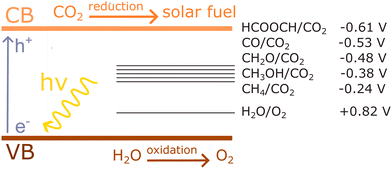Fig. 18 The general scheme for the photochemical carbon dioxide reduction reaction (CO₂RR). The reduction potentials are from ref. 216.

A suitable photocatalyst must therefore satisfy a formidable set of criteria: it must efficiently adsorb CO₂;²²² it must be semiconducting with a band gap below 3.2 eV to maximise the absorption of sunlight;²²³ photoexcited electrons must have sufficient energy to reduce CO₂ adsorbates as per the reduction potentials listed above;²³ photoexcited holes must have sufficient energy to oxidise water, a typical low-cost source of protons; and recombination rates must be low. This is without considering practical requirements such as low-cost, non-toxicity, synthetic feasibility, and stability in aqueous, often acidic, solutions. Although effective photocatalysts have been generated towards C₁ products, it is difficult to optimise selectivity towards C₂₊ products.²²³ The carbon atom in CO₂ is in its highest oxidation state and therefore a mixture of products including CO, CH₄, CH₃ OH, HCHO, or HCOOH are all on competing reaction paths.²⁴ Producing a mixture of products results in smaller yields and costly product separation processes. An additional inefficiency arises from the competing hydrogen evolution reaction (HER) which has a similar thermodynamic potential (−0.414 V²²⁴) to that of CO₂RR. Inorganic photocatalysts, such as Pt nanoparticles or TiO₂ have shown high efficiency in light absorption during CO₂RR photocatalysis, but are not sufficiently selective.³⁰ The unique structure of MOFs provides a promising alternative. Pre- and post-synthetic functionalisation can be used to modulate MOF band gaps, the frontier orbital energies, the shape of the pore, and charge separation processes, to match the required redox potentials and optical properties of the CO₂RR and water-splitting reactions. A carefully engineered pore-structure can stabilise the C₂₊ radical, enabling selective two-carbon solar fuel production.⁵ Moreover, the oxidation state of the metal centres can influence the faradaic efficiency towards the CO₂RR.^225,226 The ability to modulate pore size and composition in MOFs allows careful control of the local electronic structure and therefore CO₂ adsorption and optical properties. In MOFs, depending on the SBUs, either the linker or node may be responsible for light absorption.⁵ Beyond MOFs, excited-state techniques have been applied to CO₂RR photocatalysis in the study of non-MOF materials, for instance carbon nitride (CN),^227,228 COFs with a metal guests,²¹⁵ and microporous polymer ladders.²²⁹

7.1 Photoexcitation

In this section, we focus on the application of excited state methods to MOF studies in the context of CO₂ reduction mechanisms detailed in Section 7. Ground-state DFT calculations have been a valuable investigative method for studying CO₂RR in MOFs, as has been recently reviewed, including the use of embedding schemes.¹³ Equally, TDDFT has elucidated photoreduction mechanisms, for instance, to show how different structural functionalisation influences CT character, for instance in porphyrinic 2D, M-TCPP.⁹⁰ Here, various structural modifications were tested: substituting the metal centre in the paddlewheel metal node (Co(II), Ni(II), Cu(II), or Zn(II)) or in the porphyrin macrocycle centre (Zn(II) or Co(II)); reducing the porphyrin linker to chlorine; substituting the molecular unit which joins the porphyrin linker and the metal node. The band gap was estimated using single-point KS-DFT (HSE06) on structures optimised with both PBE+U and the much more computationally demanding HSE06 functionals, which did not yield a significantly different result. It was necessary to have a good understanding of LMCT interactions to determine how light absorption could be improved in the visible region of the spectrum. TD-HSE06/6-311G(d,p) cluster calculations evaluated the first 75 excited states, revealing that although the T₁ state exhibits LMCT transitions, many of these are inaccessible dark states with negligible oscillator strength. By reducing the pophyrin linker to chlorin, the first bright state, T₄₄, was shifted into the vis-region, T₁₆, with improved light absorption (Fig. 19). Finally, cluster calculations were used to characterise absorption as LMCT. A simple Marcus model was developed, which related LMCT behaviour to the length of the conjugated bridge joining the porphyrin and the node. In another example, TDDFT cluster calculations have been used to study PCN-601(MTPP) (M = Fe, Co, or Cu) in the context of CO₂-to-CH₄ conversion.²³⁰ Here, photoexcitation was mainly attributed to LC excitations on the porphyrin LH-unit, rather than LMCT processes. However, cluster model TDDFT calculations indicated that the unoccupied Ni(II) porphyrin orbitals could be made more accessible by introducing unoccupied orbitals from a different metal species (Fe, Co, or Cu), improving visible light absorption. The photogenerated electrons trapped on the metal node may then participate in CO₂ photoreduction. Finally, IRMOF-1-derived MOFs have been functionalised with coumarin groups and frustrated Lewis pairs to improve their visible light absorption and enable CO₂ photoreduction.²²² TDDFT cluster calculations supported this improvement. Moreover, light-harvesting is the initial step in the photocatalytic cycle, meaning a detailed understanding is necessary in the design of optimal photocatalysts that fully utilise solar energy. Excited-state methods provide a means of gaining this understanding.

Fig. 19 Simulated TD-HSE06/6-311G(d,p) spectra for porphyrin- and clorin-based M-TCPP. Chlorin has a similar structure to porphyrin, however one pyrrole group hydrogenated (highlighted in red) in chlorin. Modified figure from ref. 90.

7.2 C₁ Production formation

A techno-economic evaluation of low-temperature CO₂ electrolysis found that C₁ products such as formic acid (HCOOH), carbon monoxide (CO), methane (CH₄), and methanol (CH₃ OH) can be produced at costs competitive with conventional processes, while C₂₊ products are substantially more expensive.²³¹ This suggests that CO₂RR to C₁ products could achieve a sustainable carbon-neutral energy cycle. For example, the CO generated from the two-electron, two-proton eCO₂RR (CO₂ + 2H⁺ + 2e⁻ → CO + H₂O) could be subsequently used as a feedstock for the synthesis of alkanes through the classic Fischer–Tropsch process,²³² often together with CO₂ still present in the CO + H₂ system. Selectively producing carbon monoxide (CO) alone is advantageous because it avoids costly separation procedures. Previous computational investigations of the electrochemical CO₂RR have shown that theoretical methods can be used to screen the composition of metal alloys that are selective towards the catalytic CO₂-to-CO conversion.^233,234 Similarly, in photoelectrochemical CO₂RR, band gap engineering using defect chemistry is a promising approach for obtaining selective CO₂-to-CO photocatalysis. For instance, high selectivity (100%) was achieved in Zr-Ui0-66 by functionalisation with aminobenzoic acids in place of formic acid in the pristine species.²³⁵ In terms of photoexcitation, diffuse reflectance UV-vis spectroscopy indicated strong absorbance in the vis region, and interestingly, as defect concentration was increased and the band gap narrowed, stability of the framework decreased. Crucially, DFT (PBE/DZVP-MOLOPT-SR-GTH/GTH-PBE) cluster calculations indicated that a new pair of degenerate HOMO orbitals are introduced at the location of the defect (Fig. 20), narrowing the band gap. The LUMO was not perturbed by the functionalisation, remaining delocalised over the framework. The cluster calculations used the PBE functional, as the hybrid PBE0 functional was found to be too computationally intensive. The cluster calculation was verified by a fully periodic DFT benchmark. The use of a GGA functional systematically underestimates the band gap in every instance, predicting the same overall qualitative trend (Table 3). TDDFT cluster model calculations have been used to study electrocatalytic CO₂RR applications, for instance, in DPNDI-based csiMOF-6 in a CO₂-to-CO reduction with a [Re(bipy-tBu)(CO)₃Cl] electrocatalyst.²³⁶ In this example, DPNDI ligand dimers can be cofacially stacked to exhibit photocathode behaviour. The TDDFT cluster model was used to directly characterise the dimer-to-pyridyl charge transfer process, the generates the photoexcited radical state, and therefore its photoelectrochemical potential.

Fig. 20 Defect functionalisation of UiO-66 introduces a new HOMO localised on the site of the aminobenzene defect, improving selectivity in photocatalytic CO₂-to-CO conversion. Visualisations obtained using TD-PBE/DZP-MOLPLOT-SR-GTH/GTH-PBE cluster calculations using the GPW method. Reproduced from ref. 235 with permission from Royal Society of Chemistry, copyright 2019.

Table 3 Comparison of experimental and TDDFT (PBE/DZVP-MOLOPT-SR-GTH/GTH-PBE) computed band gap values. Reproduced from ref. 235 with permission from Royal Society of Chemistry. copyright 2019

Sample	Exp. band gap (eV)	Calc. HOMO–LUMO gap (eV)
Defect-free UiO-66	4.10^237	3.2
FA_mod	4.10	3.2
FA_mod-4ABA	3.80	2.2
FA_mod-3ABA	3.50	1.9
FA_mod-2ABA	3.30	1.8
FA_mod-35DABA	3.30	1.6

---

Recombination of photogenerated charge carriers is a key parameter in the efficiency of photocatalysts and depends on the charge separation achieved during photoexcitation. MOFs such as pyrazolyl porphyrinic Ni-based PCN-601 have been studied for selective CO₂-to-CH₄ conversion, with higher efficiencies than analogous architectures.⁸⁰ Photoexcitation and charge separation takes place at the porphyrin ligand which acts as LH units, where they may be transferred to the Ni Node. Interestingly, whilst photogenerated electrons can migrate to the node via N–Ni bridges to participate in CO₂, the holes cannot remain local to the porphyrin where water-splitting takes place (Fig. 21). Charge separation was demonstrated using both periodic and cluster models, where the former was used DFT (PBEsol) to characterise the PDOS and characterise electron paramagnetic (EPR) spectroscopy, whereas the latter used LR-TD-HSE06/def2-TZVP to directly characterise the two possible excitations. This confirmed that in terms of oscillator strength, linker-localised excitations outweighed LMCT contributions when absorbing visible light. This indicates that photoexcitation followed by electron migration is more likely than direct photoexcitation to the node.

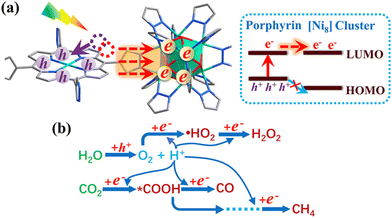Fig. 21 Proposed mechanism for CO₂-to-CH₄ photocatalysis. Reprinted with permission from ref. 80. Copyright 2020 American Chemical Society.

Another possible photoreduction product is formate (HCOO⁻), which can be easily post-processed to other value-added chemicals such as methanol or formic acid. In the CO₂-to-formate scheme, Zr-based AUBM-4, for instance, can be functionalised via introduction of a one-dimensional Ru(cptpy)₂ strut to improve selectivity.⁹¹ TDDFT (B3LYP-6-311G(d,p)) cluster models were used to characterise the excited states and elucidate the visible-light catalysed photoreduction mechanism. The calculations predicted low oscillator strengths for metal-centred excitations, indicating that a Ru-to-cptpy MLCT takes place, suggesting that the photoreduction likely takes place at the cptpy portion of the strut. This charge transfer enables an efficient reduction mechanism in AUBM-4 in which adsorbed CO₂ is reduced at either at the cpcpt centre or in proximal Zr metals following LMCT. In another example, the porphyrinic MOF, TNP-MOF, has drawn interest in near-infrared (NIR) CO₂-to-formate photocatalysis, where TD-B3LYP/def2-SVP/PCM cluster models indicated systematically extending π-conjugation of the porphyrin unit within the same topology shifted light absorption from vis to NIR regions.²³⁸ Upon photoexcitation, charge separation is achieved via LMCT from the large π-conjugated organic semiconductor linkers to the metal node, where the adsorbed CO₂ can be reduced. In contrast, another CO₂-to-formate photocatalyst, Zr-based MOF-545(M) (M = Mn(III), Fe(III), Co(II), Cu(II), Zn(II)), (6000 μmol g⁻¹) exhibits LC photoexcitation on the porphyrin linker orbitals. TDDFT cluster models indicated that the porphyrin LUMO and empty d-orbitals of the Zr₆ node are substantially different in energy (≥1.5 eV), rendering it inaccessible to a LMCT mechanism. This ruled out the possibility of Zr(III) being involved in the photomechanism. The lack of LMCT behaviour was consistent with time-resolved spectroscopic measurement, and is akin to light-absorption seen previously in pristine UiO-66(Zr).^8,175 In the mechanism, a sacrificial donor, triethanolamine (TEOA), is oxidised at the porphyrin centre before acting as a hydride-donor in the Zr₆-catalysed reduction of CO₂.

7.3 CO₂ epoxidation and C₂-product formation

Another popular strategy to valorise C₂ emissions is via epoxidation to a five-membered cyclic carbonates (CCs), which can be rapidly processed into other value-added solvents, battery electrolytes, and polymers.¹³ For instance, a Mg-centred porphyrinic MOF, PCN-224(Mg), has been investigated using cluster models for visible-light catalysed CO₂-to-CC conversion.²³⁹ TD-PBE/LANL2DZ/6-31G* studies simulated the first 300 states to reveal a LMCT mechanism from the Mg-porphyrin to the Zr₆-oxo group, lowering the reaction activation energy to the cycloaddition to adsorbed CO₂. The calculations indicated that the electron-donating nature of the epoxide enhances the LMCT behaviour, and changes the energy of the HOMO and LUMO levels. A study of the free energy profile during each step of the cycloaddition was used to reveal the complete photocatalytic mechanism (Fig. 22). Crucially, an LMCT photoexcitation drives the catalytic cycle.

Fig. 22 Mechanism proposed for the PCN-224(Mg-photocatalysed cycloaddition of epoxide to CO₂. Reprinted with permission from ref. 239. Copyright 2022 American Chemical Society.

By far the most valuable photocatalytic process is conversion to C₂₊ products. Whilst there are examples of this,²⁴ efficient and selective coupling of C–C bonds during the catalytic cycle remains challenging. The C₂ product, acetic acid (CH₃COOH) has been investigated using UiO-66-bpydc with an additional [Ru(bpy)₂Cl₂] LH unit (Ce-MOF).²⁴⁰ This has been shown to demonstrate efficient (1133 μmol g⁻¹) and selective (>99.5%) CO₂-to-acetate production. Theoretical and experimental studies had previously indicated efficient LMCT in the vis-region could be engineered into UiO-66(Ce) through metal and linker functionilisation,^185,186,191 making Ce-MOF an attractive candidate photocatalyst. In light of this, a [Ru(bpy)₂Cl₂] photosensiter was introduced post-synthetically to improve visible light absorption. TDDFT cluster model calculations (B3LYP/6-31G(d)/LANL2DZ) embedded in a PCM to simulate the solvent environment, indicated that Ce-MOF presents linker-defect sites that can accommodate two adsorbed CO₂ molecules in proximity, facilitating rapid electron transfer kinetics. TAS spectroscopy indicated the presence of MLCT Ru-to-bpy at the same positions indicated by TDDFT. Subsequent LMCT from the bpy linker to the low-lying Ce 4f states, facilitated rapid C–C coupling with a high selectivity towards acetic acid, a C₂ product. There was a notable selection against C₁ products, but a small amount of H₂ was produced. Studies such as this indicate the future of CO₂ capture and conversion is bright.

8 Conclusions

The utilisation of cluster and periodic models in the application of quantum chemical methods to MOFs is pivotal in gaining deeper insights into their excited-state chemistry. Currently, the field of modelling excited states of MOFs is still relatively unexplored, however, computational investigations have already played an important role in corroborating experimental findings and in the interpretation of spectroscopic results. As MOFs transcend traditional definitions of molecule and solid, the choice of computational model becomes central in unravelling their photochemical properties, from light-absorption to photocatalytic CO₂ reduction. This is reflected in quantum chemistry codes, in which implementations are divided by the choice of localised or plane wave basis set.

It is essential to benchmark computational investigations using periodic models which fully incorporate long-range effects in the MOF crystal. In this respect, it is advisable to obtain relaxed geometric coordinates, for both periodic and cluster studies, from optimisations at the GGA-with-dispersion-level. KS-DFT is still the most commonly used tool to estimate band gap values in MOFs. The low-cost of GGA functionals has lead to their use in high-throughput studies, however ML models based off of GGA data must be cautious of their objectives and the limitations of such functionals. Here, we emphasise that hybrid functionals must be used for reliable DFT gap predictions, in spite of the associated computational overhead in their PW implementations. The QMOF database, which contains many entries at the hybrid-level, should be utilised to this end. The large and chemically diverse unit cells of MOFs makes high-level periodic studies challenging, and generally rules out demanding calculations such as GW. Of course, we also emphasise KS-DFT cannot reliably capture gap renormalisation. The most notable example is MOF-5, an insulator, in which DFT studies massively underestimate the exciton binding energy, erroneously predicting MOF-5 to be semiconducting. Subsequent GW calculations were necessary to obtain the true quasiparticle gap, illustrating that exact methods that go beyond ground-state electron densities can be required for even qualitatively correct conclusions to be drawn. Advances are therefore required in both periodic GW methods. In our cluster calculations, we found that range-separated hybrid functionals may be fruitful for finding better renormalised gaps; PW implementations should also be explored. Periodic TDDFT been pioneered in MOFs by some groups, and with the continued development of cost-saving approximations, such as sTDA and ADMM, may provide an exciting avenue for excited-state MOF studies going forward. Finally, from this perspective, multiconfigurational periodic methods will also be of interest.

Despite lacking environmental effects, cluster models afford high-level methods such as hybrid TDDFT, multiconfigurational methods, and BSE/GW calculations, and have been routinely exploited to yield remarkable insight into MOF excited states. While choice of cluster size is inherently subjective, excellent results have been obtained for even modestly-sized clusters. Automation of this process will be interesting with respect to high-throughput studies and the generation of excited-state MOF databases. The use of GTO basis sets enables a chemically intuitive molecular orbital description of MOFs, and the coordination chemistry processes that often dominate their excited-state character. In our own calculations, we have seen embedding techniques, such as ONIOM, can refine the values obtained for isolated cluster models by embedding them in lower-level method, and will be developed going forward. Such schemes are a natural choice in guest@MOF materials when studying photoluminescence, such as TADF and RTP. Cluster models also facilitate excited-state dynamics simulations, an area of MOF excited-states that must be explored.

Excited-state methods have been valuable in CO₂RR, through simulating light absorption, the first step in photocatalytic cycles, and in developing complex reaction pathways. In particular, they have been used to characterise LMCT, MLCT, and LLCT excitations that facilitate significant spatial charge separation and reduce recombination rates. Current MOF photocatalysts have not yet been used as industrial catalysts, however their potential as a one-pot system for both the capture and photocatalytic conversion of CO₂ makes this class of material highly appealing for the future of carbon capture and utilisation. There are abundant opportunities in the field of MOF excited states, spanning from leveraging artificial intelligence techniques to enhance predictions, to implementing more suitable models that combine cluster and periodic approaches. These techniques should be capable of capturing excitonic effects and accurately predicting band renormalisation in the crystal environment, which are both current challenges with the existing approaches.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

R. C. O and D. D. T. acknowledge the UK's Royal Society International Exchanges Cost Share (IEC92R392193106). D. D. T. acknowledges the ACT program (Accelerating CCS Technologies, Horizon2020 Project No. 294766), which funded the FUNMIN project. This research has been supported by the Leverhulme Trust (RPG-2019-122) and EPSRC (EP/T518086/1). We are grateful to the UK Materials and Molecular Model-ling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1). Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER2 U.K. National Supercomputing Service (https://www.archer.ac.uk). This research utilised Queen Mary's Apocrita HPC facility, supported by QMUL Research-IT.

Notes and references

1. C.-C. Chueh, C.-I. Chen, Y.-A. Su, H. Konnerth, Y.-J. Gu, C.-W. Kung and K. C.-W. Wu, J. Mater. Chem. A, 2019, 7, 17079–17095.
2. G. Brunet, D. A. Safin, J. Jover, E. Ruiz and M. Murugesu, J. Mater. Chem. C, 2017, 5, 835–841.
3. Y. Hidalgo-Rosa, K. Mena-Ulecia, M. A. Treto-Suárez, E. Schott, D. Páez-Hernández and X. Zarate, J. Phys. Chem. A, 2022, 126, 7040–7050.
4. Y. Benseghir, A. Solé-Daura, D. R. Cairnie, A. L. Robinson, M. Duguet, P. Mialane, P. Gairola, M. Gomez-Mingot, M. Fontecave, D. Iovan, B. Bonnett, A. J. Morris, A. Dolbecq and C. Mellot-Draznieks, J. Mater. Chem. A, 2022, 10, 18103–18115.
5. A. Alshammari, Z. Jiang and K. E. Cordova, in Semiconductor Photocatalysis – Materials, Mechanisms and Applications, ed. W. Cao, InTech, 2016, pp. 301–341.
6. C. H. Hendon, A. J. Rieth, M. D. Korzynski and M. Dinca, ACS Cent. Sci., 2017, 3, 554–563.
7. G. D. Degaga, R. Pandey, C. Gupta and L. Bharadwaj, RSC Adv., 2019, 9, 14260–14267.
8. A. De Vos, K. Hendrickx, P. Van Der Voort, V. Van Speybroeck and K. Lejaeghere, Chem. Mater., 2017, 29, 3006–3019.
9. M. D. Allendorf, C. A. Bauer, R. K. Bhakta and R. J. T. Houk, Chem. Soc. Rev., 2009, 38, 1330–1352.
10. A. S. P. Gomes and C. R. Jacob, ‘’Annu. Rep., Sect. C: Phys. Chem., 2012, 108, 222–277.
11. M. Fumanal, A. Ortega-Guerrero, K. M. Jablonka, B. Smit and I. Tavernelli, Adv. Funct. Mater., 2020, 30, 2003792.
12. C. Wang, Z. Sun, Y. Zheng and Y. H. Hu, J. Mater. Chem. A, 2019, 7, 865–887.
13. H. Chen, Front. Energy Res., 2022, 10, 1–8.
14. R. Feng, Z.-Y. Li, Z.-Q. Yao, Z.-A. Guo, Y.-N. Zhang, H.-X. Sun, W. Li and X.-H. Bu, Sci. China: Chem., 2022, 65, 128–134.
15. B. Zhou, Z. Qi and D. Yan, Angew. Chem., Int. Ed., 2022, 61, e202208735.
16. J. Fan, L. Lin and C.-K. Wang, J. Mater. Chem. C, 2017, 5, 8390–8399.
17. X.-K. Chen, S.-F. Zhang, J.-X. Fan and A.-M. Ren, J. Phys. Chem. C, 2015, 119, 9728–9733.
18. F. J. Hernández and R. Crespo-Otero, Annu. Rev. Phys. Chem., 2023, 74, 547–571.
19. X.-P. Wu, I. Choudhuri and D. G. Truhlar, Energy Environ. Mater., 2019, 2, 251–263.
20. N. Kolobov, M. G. Goesten and J. Gascon, Angew. Chem., Int. Ed., 2021, 60, 26038–26052.
21. P. G. Boyd, A. Chidambaram, E. García-Díez, C. P. Ireland, T. D. Daff, R. Bounds, A. Gladysiak, P. Schouwink, S. M. Moosavi, M. M. Maroto-Valer, J. A. Reimer, J. A. R. Navarro, T. K. Woo, S. Garcia, K. C. Stylianou and B. Smit, Nature, 2019, 576, 253–256.
22. R. Grau-Crespo, A. Aziz, A. W. Collins, R. Crespo-Otero, N. C. Hernández, L. M. Rodriguez-Albelo, A. R. Ruiz-Salvador, S. Calero and S. Hamad, Angew. Chem., Int. Ed., 2016, 55, 16012–16016.
23. M. Ramyashree, S. Shanmuga Priya, N. C. Freudenberg, K. Sudhakar and M. Tahir, J. CO₂ Util., 2021, 43, 101374.
24. J. Wang, Y. Zhang, Y. Ma, J. Yin, Y. Wang and Z. Fan, ACS Mater. Lett., 2022, 2058–2079.
25. B. Bie, Z. Jiang, J. Zhang, H. Deng and C. Yang, Chem. Eng. J., 2022, 431, 133897.
26. G. Scandura, S. Eid, A. A. Alnajjar, T. Paul, G. N. Karanikolos, D. Shetty, K. Omer, R. Alqerem, A. Juma, H. Wang, H. A. Arafat and L. F. Dumée, Mater. Adv., 2023, 4, 1258–1285.
27. J. Hao, X. Xu, H. Fei, L. Li and B. Yan, Adv. Mater., 2018, 30, 1705634.
28. A. M. Rice, C. R. Martin, V. A. Galitskiy, A. A. Berseneva, G. A. Leith and N. B. Shustova, Chem. Rev., 2020, 120, 8790–8813.
29. E. Dolgopolova, A. Rice, C. Martin and N. Shustova, Chem. Soc. Rev., 2018, 47, 4710–4728.
30. J. Chen, J. Kato, J. B. Harper, Y. Shao and J. Ho, J. Phys. Chem. B, 2021, 125, 9304–9316.
31. L. Kronik and J. B. Neaton, Annu. Rev. Phys. Chem., 2016, 67, 587–616.
32. J. L. Mancuso, A. M. Mroz, K. N. Le and C. H. Hendon, Chem. Rev., 2020, 120, 8641–8715.
33. N. Reuter, A. Dejaegere, B. Maigret and M. Karplus, J. Phys. Chem. A, 2000, 104, 1720–1735.
34. P. Seeber, S. Seidenath, J. Steinmetzer and S. Gräfe, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, e1644.
35. M. Rivera, M. Dommett and R. Crespo-Otero, J. Chem. Theory Comput., 2019, 15, 2504–2516.
36. M. Rivera, M. Dommett, A. Sidat, W. Rahim and R. Crespo-Otero, J. Comput. Chem., 2020, 41, 1045–1058.
37. L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796.
38. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
39. J. Hutter and M. Iannuzzi, Z. Kristallogr. – Cryst. Mater., 2005, 220, 549–551.
40. F. Gygi, IBM J. Res. Dev., 2008, 52, 137–144.
41. J. C. A. Prentice, J. Aarons, J. C. Womack, A. E. A. Allen, L. Andrinopoulos, L. Anton, R. A. Bell, A. Bhandari, G. A. Bramley, R. J. Charlton, R. J. Clements, D. J. Cole, G. Constantinescu, F. Corsetti, S. M.-M. Dubois, K. K. B. Duff, J. M. Escartín, A. Greco, Q. Hill, L. P. Lee, E. Linscott, D. D. ORegan, M. J. S. Phipps, L. E. Ratcliff, L. R. Serrano, E. W. Tait, G. Teobaldi, V. Vitale, N. Yeung, T. J. Zuehlsdorff, J. Dziedzic, P. D. Haynes, N. D. M. Hine, A. A. Mostofi, M. C. Payne and C.-K. Skylaris, J. Chem. Phys., 2020, 152, 174111.
42. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
43. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. D. Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
44. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. – Cryst. Mater., 2005, 220, 567–570.
45. X. Gonze, B. Amadon, P. M. Anglade, J. M. Beuken, F. Bottin, P. Boulanger, F. Bruneval, D. Caliste, R. Caracas, M. Côté, T. Deutsch, L. Genovese, P. Ghosez, M. Giantomassi, S. Goedecker, D. R. Hamann, P. Hermet, F. Jollet, G. Jomard, S. Leroux, M. Mancini, S. Mazevet, M. J. T. Oliveira, G. Onida, Y. Pouillon, T. Rangel, G. M. Rignanese, D. Sangalli, R. Shaltaf, M. Torrent, M. J. Verstraete, G. Zerah and J. W. Zwanziger, Comput. Phys. Commun., 2009, 180, 2582–2615.
46. A. Marini, C. Hogan, M. Grüning and D. Varsano, Comput. Phys. Commun., 2009, 180, 1392–1403.
47. A. J. C. Varandas, Phys. Chem. Chem. Phys., 2019, 21, 8022–8034.
48. K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Salek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284.
49. Y. Alexeev, M. P. Mazanetz, O. Ichihara and D. G. Fedorov, Curr. Top. Med. Chem., 2012, 12, 2013–2033.
50. A. I. Krylov and P. M. Gill, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 317–326.
51. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
52. F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. Fdez. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. K. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117.
53. R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D’Arco, Y. Noël, M. Causà, M. Rérat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317.
54. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodynski and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
55. Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340.
56. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16, Revision A.03, 2016.
57. E. Aprà, E. J. Bylaska, W. A. de Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Martin Del Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. Van Voorhis, Á. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Wolinski, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102.
58. J. Junquera, s Paz, D. Sánchez-Portal and E. Artacho, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 235111.
59. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
60. A. García, N. Papior, A. Akhtar, E. Artacho, V. Blum, E. Bosoni, P. Brandimarte, M. Brandbyge, J. I. Cerdá, F. Corsetti, R. Cuadrado, V. Dikan, J. Ferrer, J. Gale, P. García-Fernández, V. M. García-Suárez, S. García, G. Huhs, S. Illera, R. Korytár, P. Koval, I. Lebedeva, L. Lin, P. López-Tarifa, S. G. Mayo, S. Mohr, P. Ordejón, A. Postnikov, Y. Pouillon, M. Pruneda, R. Robles, D. Sánchez-Portal, J. M. Soler, R. Ullah, V. W.-Z. Yu and J. Junquera, J. Chem. Phys., 2020, 152, 204108.
61. P. Hovington, D. Drouin and R. Gauvin, Scanning, 1997, 19, 1–14.
62. M. D. Allendorf, A. Schwartzberg, V. Stavila and A. A. Talin, Chem. – Eur. J., 2011, 17, 11372–11388.
63. H. Rathnayake, S. Saha, S. Dawood, S. Loeffler and J. Starobin, J. Phys. Chem. Lett., 2021, 12, 884–891.
64. W.-X. Chen, L. Tan, Q.-P. Liu, G.-R. Qiang and G.-L. Zhuang, Dalton Trans., 2014, 43, 16515–16521.
65. A. Benali, Y. Luo, H. Shin, D. Pahls and O. Heinonen, J. Phys. Chem. C, 2018, 122, 16683–16691.
66. R. J. Harrison, G. Beylkin, F. A. Bischoff, J. A. Calvin, G. I. Fann, J. Fosso-Tande, D. Galindo, J. R. Hammond, R. Hartman-Baker, J. C. Hill, J. Jia, J. S. Kottmann, M.-J. Yvonne Ou, J. Pei, L. E. Ratcliff, M. G. Reuter, A. C. Richie-Halford, N. A. Romero, H. Sekino, W. A. Shelton, B. E. Sundahl, W. S. Thornton, E. F. Valeev, L. Vázquez-Mayagoitia, N. Vence, T. Yanai and Y. Yokoi, SIAM J. Sci. Comput., 2016, 38, S123–S142.
67. B. Natarajan, L. Genovese, M. E. Casida, T. Deutsch, O. N. Burchak, C. Philouze and M. Y. Balakirev, Chem. Phys., 2012, 402, 29–40.
68. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöß, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103.
69. S. Dapprich, I. Komáromi, K. S. Byun, K. Morokuma and M. J. Frisch, THEOCHEM, 1999, 1–21.
70. B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrica, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubar, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Rezác, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W.-Z. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101.
71. O. Weingart, A. Nenov, P. Altoè, I. Rivalta, J. Segarra-Martí, I. Dokukina and M. Garavelli, J. Mol. Model., 2018, 24, 271.
72. Y. Lu, K. Sen, C. Yong, D. S. D. Gunn, J. A. Purton, J. Guan, A. Desmoutier, J. Abdul Nasir, X. Zhang, L. Zhu, Q. Hou, J. Jackson-Masters, S. Watts, R. Hanson, H. N. Thomas, O. Jayawardena, A. J. Logsdail, S. M. Woodley, H. M. Senn, P. Sherwood, C. R. A. Catlow, A. A. Sokol and T. W. Keal, Phys. Chem. Chem. Phys., 2023, 25, 21816–21835.
73. C. Plett, A. Katbashev, S. Ehlert, S. Grimme and M. Bursch, Phys. Chem. Chem. Phys., 2023, 25, 17860–17868.
74. A. R. Kshirsagar, X. Blase, C. Attaccalite and R. Poloni, J. Phys. Chem. Lett., 2021, 12, 4045–4051.
75. K. T. Butler, C. H. Hendon and A. Walsh, J. Am. Chem. Soc., 2014, 136, 2703–2706.
76. N. Sato, K. Seki and H. Inokuchi, J. Chem. Soc., Faraday Trans. 2, 1981, 77, 1621–1633.
77. L. Kronik and S. Kümmel, Adv. Mater., 2018, 30, 1706560.
78. A. Ortega-Guerrero, M. Fumanal, G. Capano and B. Smit, J. Phys. Chem. C, 2020, 124, 21751–21760.
79. K. Fabrizio, K. N. Le, A. B. Andreeva, C. H. Hendon and C. K. Brozek, ACS Mater. Lett., 2022, 4, 457–463.
80. Z.-B. Fang, T.-T. Liu, J. Liu, S. Jin, X.-P. Wu, X.-Q. Gong, K. Wang, Q. Yin, T.-F. Liu, R. Cao and H.-C. Zhou, J. Am. Chem. Soc., 2020, 142, 12515–12523.
81. W. Zhang, W. Huang, B. Wu, J. Yang, J. Jin and S. Zhang, Coord. Chem. Rev., 2023, 491, 215235.
82. J. P. Perdew, A. Ruzsinszky, L. A. Constantin, J. Sun and G. I. Csonka, J. Chem. Theory Comput., 2009, 5, 902–908.
83. A. S. Rosen, V. Fung, P. Huck, C. T. ODonnell, M. K. Horton, D. G. Truhlar, K. A. Persson, J. M. Notestein and R. Q. Snurr, npj Comput. Mater., 2022, 8, 1–10.
84. T. Wang, X. Tan, Y. Wei and H. Jin, Mater. Today Commun., 2021, 29, 102932.
85. S. A. Tolba, K. M. Gameel, B. A. Ali, H. A. Almossalami, N. K. Allam, S. A. Tolba, K. M. Gameel, B. A. Ali, H. A. Almossalami and N. K. Allam, Density Functional Calculations – Recent Progresses of Theory and Application, IntechOpen, 2018, pp. 1–30.
86. T. Saha-Dasgupta and P. M. Oppeneer, MRS Bull., 2014, 39, 614–620.
87. F. Zanca, L. T. Glasby, S. Chong, S. Chen, J. Kim, D. Fairen-Jimenez, B. Monserrat and P. Z. Moghadam, J. Mater. Chem. C, 2021, 9, 13584–13599.
88. Z. H. Levine and D. C. Allan, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 4187–4207.
89. S. Hamad, N. C. Hernandez, A. Aziz, A. R. Ruiz-Salvador, S. Calero and R. Grau-Crespo, J. Mater. Chem. A, 2015, 3, 23458–23465.
90. V. Posligua, D. Pandya, A. Aziz, M. Rivera, R. Crespo-Otero, S. Hamad and R. Grau-Crespo, J. Phys.: Energy, 2021, 3, 034005.
91. M. Elcheikh Mahmoud, H. Audi, A. Assoud, T. H. Ghaddar and M. Hmadeh, J. Am. Chem. Soc., 2019, 141, 7115–7121.
92. A. Aziz, A. R. Ruiz-Salvador, N. C. Hernández, S. Calero, S. Hamad and R. Grau-Crespo, J. Mater. Chem. A, 2017, 5, 11894–11904.
93. M. E. Casida, Recent Advances in Density Functional Methods, World Scientific, 1995, vol. 1, pp. 155–192.
94. S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299.
95. R. J. Magyar and S. Tretiak, J. Chem. Theory Comput., 2007, 3, 976–987.
96. S. O. Odoh, C. J. Cramer, D. G. Truhlar and L. Gagliardi, Chem. Rev., 2015, 115, 6051–6111.
97. S. Grimme and C. Bannwarth, J. Chem. Phys., 2016, 145, 054103.
98. C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493.
99. A.-S. Hehn, B. Sertcan, F. Belleflamme, S. K. Chulkov, M. B. Watkins and J. Hutter, J. Chem. Theory Comput., 2022, 18, 4186–4202.
100. O. K. Orhan and D. D. O’Regan, Phys. Rev. B, 2019, 99, 165120.
101. A. Ortega-Guerrero, M. Fumanal, G. Capano, I. Tavernelli and B. Smit, Chem. Mater., 2020, 32, 4194–4204.
102. M. Fumanal, G. Capano, S. Barthel, B. Smit and I. Tavernelli, J. Mater. Chem. A, 2020, 8, 4473–4482.
103. M. Fumanal, C. Corminboeuf, B. Smit and I. Tavernelli, Phys. Chem. Chem. Phys., 2020, 22, 19512–19521.
104. L. Hedin, Phys. Rev., 1965, 139, A796–A823.
105. S. Ghosh, P. Verma, C. J. Cramer, L. Gagliardi and D. G. Truhlar, Chem. Rev., 2018, 118, 7249–7292.
106. A. R. Kshirsagar, G. DAvino, X. Blase, J. Li and R. Poloni, J. Chem. Theory Comput., 2020, 16, 2021–2027.
107. S. Refaely-Abramson, S. Sharifzadeh, M. Jain, R. Baer, J. B. Neaton and L. Kronik, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 081204.
108. S. Refaely-Abramson, M. Jain, S. Sharifzadeh, J. B. Neaton and L. Kronik, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 081204.
109. A. R. Kshirsagar, C. Attaccalite, X. Blase, J. Li and R. Poloni, J. Phys. Chem. C, 2021, 125, 7401–7412.
110. A. Windischbacher, L. Steiner, R. Haldar, C. Wöll, E. Zojer and A.-M. Kelterer, Molecules, 2020, 25, 4230.
111. A. Cadiau, N. Kolobov, S. Srinivasan, M. G. Goesten, H. Haspel, A. V. Bavykina, M. R. Tchalala, P. Maity, A. Goryachev, A. S. Poryvaev, M. Eddaoudi, M. V. Fedin, O. F. Mohammed and J. Gascon, Angew. Chem., Int. Ed., 2020, 59, 13468–13472.
112. K. Cui and J. R. Schmidt, J. Phys. Chem. C, 2020, 124, 10550–10560.
113. K. Hirai, T. Kitagawa, H. Fujiwara, J. Pirillo, Y. Hijikata, T. Inose and H. Uji-i, Chem. Commun., 2020, 56, 9651–9654.
114. I. Pallikara, P. Kayastha, J. M. Skelton and L. D. Whalley, Electron. Struct., 2022, 4, 033002.
115. D. Shao and X.-Y. Wang, Chin. J. Chem., 2020, 38, 1005–1018.
116. G. M. Espallargas and E. Coronado, Chem. Soc. Rev., 2018, 47, 533–557.
117. O. Pajuelo-Corral, S. Pérez-Yáñez, I. J. Vitorica-Yrezabal, G. Beobide, A. Zabala-Lekuona, A. Rodríguez-Diéguez, J. M. Seco and J. Cepeda, Mater. Today Chem., 2022, 24, 100794.
118. H. Liu, W. Ye, Y. Mu, H. Ma, A. Lv, S. Han, H. Shi, J. Li, Z. An, G. Wang and W. Huang, Adv. Mater., 2022, 34, 2107612.
119. A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249.
120. T. A. Wesolowski and A. Warshel, J. Phys. Chem., 1993, 97, 8050–8053.
121. T. A. Wesolowski, S. Shedge and X. Zhou, Chem. Rev., 2015, 115, 5891–5928.
122. D. Püschel, S. Hédé, I. Maisuls, S.-P. Höfert, D. Woschko, R. Kühnemuth, S. Felekyan, C. A. M. Seidel, C. Czekelius, O. Weingart, C. A. Strassert and C. Janiak, Molecules, 2023, 28, 2877.
123. X.-T. Liu, W. Hua, H.-X. Nie, M. Chen, Z. Chang and X.-H. Bu, Natl. Sci. Rev., 2022, 9, nwab222.
124. D. A. Case, T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688.
125. B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614.
126. T. M. Becker, J. Heinen, D. Dubbeldam, L.-C. Lin and T. J. H. Vlugt, J. Phys. Chem. C, 2017, 121, 4659–4673.
127. S. Bureekaew, S. Amirjalayer, M. Tafipolsky, C. Spickermann, T. K. Roy and R. Schmid, Phys. Status Solidi B, 2013, 250, 1128–1141.
128. J. K. Bristow, D. Tiana and A. Walsh, J. Chem. Theory Comput., 2014, 10, 4644–4652.
129. M. A. Addicoat, N. Vankova, I. F. Akter and T. Heine, J. Chem. Theory Comput., 2014, 10, 880–891.
130. M. Tafipolsky, S. Amirjalayer and R. Schmid, J. Phys. Chem. C, 2010, 114, 14402–14409.
131. J. Heinen and D. Dubbeldam, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1363.
132. T. M. Becker, L.-C. Lin, D. Dubbeldam and T. J. H. Vlugt, J. Phys. Chem. C, 2018, 122, 24488–24498.
133. K. Senthilkumar, J. I. Mujika, K. E. Ranaghan, F. R. Manby, A. J. Mulholland and J. N. Harvey, J. R. Soc., Interface, 2008, 5, 207–216.
134. J. Neugebauer, Phys. Rep., 2010, 489, 1–87.
135. M. Klintenberg, S. E. Derenzo and M. J. Weber, Comput. Phys. Commun., 2000, 131, 120–128.
136. H. M. Evjen, Phys. Rev., 1932, 39, 675–687.
137. D. Wolf, P. Keblinski, S. R. Phillpot and J. Eggebrecht, J. Chem. Phys., 1999, 110, 8254–8282.
138. D.-L. Chen, A. C. Stern, B. Space and J. K. Johnson, J. Phys. Chem. A, 2010, 114, 10225–10233.
139. R. F. W. Bader, J. Phys. Chem. A, 2010, 114, 7431–7444.
140. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
141. M. Nottoli, L. Cupellini, F. Lipparini, G. Granucci and B. Mennucci, Annu. Rev. Phys. Chem., 2021, 72, 489–513.
142. A. Biancardi, J. Barnes and M. Caricato, J. Chem. Phys., 2016, 145, 224109.
143. N. J. Mayhall and K. Raghavachari, J. Chem. Theory Comput., 2010, 6, 3131–3136.
144. L. W. Chung, H. Hirao, X. Li and K. Morokuma, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 327–350.
145. B. Wang and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 359–369.
146. X.-P. Wu, L. Gagliardi and D. G. Truhlar, J. Chem. Theory Comput., 2019, 15, 4208–4217.
147. R. Bjornsson and M. Bühl, J. Chem. Theory Comput., 2012, 8, 498–508.
148. K. Götz, F. Meier, C. Gatti, A. M. Burow, M. Sierka, J. Sauer and M. Kaupp, J. Comput. Chem., 2010, 31, 2568–2576.
149. K. Iwano and Y. Shimoi, Phys. Rev. Lett., 2013, 110, 116401.
150. N. Govind, Y. Wang, A. Da Silva and E. Carter, Chem. Phys. Lett., 1998, 295, 129–134.
151. N. Govind, Y. A. Wang and E. A. Carter, J. Chem. Phys., 1999, 110, 7677–7688.
152. P. Huang and E. A. Carter, J. Chem. Phys., 2006, 125, 084102.
153. D. K. Kanan, S. Sharifzadeh and E. A. Carter, Chem. Phys. Lett., 2012, 519–520, 18–24.
154. A. Krishtal, D. Sinha, A. Genova and M. Pavanello, J. Phys.: Condens. Matter, 2015, 27, 183202.
155. J.-J. Zheng and S. Sakaki, J. Photochem. Photobiol., C, 2022, 51, 100482.
156. J. M. Crowley, J. Tahir-Kheli and W. A. I. Goddard, J. Phys. Chem. Lett., 2016, 7, 1198–1203.
157. A. Rasmussen, T. Deilmann and K. S. Thygesen, npj Comput. Mater., 2021, 7, 1–9.
158. D. Jacquemin, I. Duchemin and X. Blase, J. Phys. Chem. Lett., 2017, 8, 1524–1529.
159. J. Westermayr and P. Marquetand, Chem. Rev., 2021, 121, 9873–9926.
160. J. Westermayr, M. Gastegger, M. F. S. J. Menger, S. Mai, L. González and P. Marquetand, Chem. Sci., 2019, 10, 8100–8107.
161. S. Ye, W. Hu, X. Li, J. Zhang, K. Zhong, G. Zhang, Y. Luo, S. Mukamel and J. Jiang, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 11612–11617.
162. M. S. Chen, T. J. Zuehlsdorff, T. Morawietz, C. M. Isborn and T. E. Markland, J. Phys. Chem. Lett., 2020, 11, 7559–7568.
163. G. W. Richings and S. Habershon, J. Chem. Phys., 2020, 152, 154108.
164. W. Jeong, S. J. Stoneburner, D. King, R. Li, A. Walker, R. Lindh and L. Gagliardi, J. Chem. Theory Comput., 2020, 16, 2389–2399.
165. J. Westermayr, M. Gastegger and P. Marquetand, J. Phys. Chem. Lett., 2020, 11, 3828–3834.
166. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
167. Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling, J. S. Camp, B. Slater, J. I. Siepmann, D. S. Sholl and R. Q. Snurr, J. Chem. Eng. Data, 2019, 64, 5985–5998.
168. A. S. Rosen, S. M. Iyer, D. Ray, Z. Yao, A. Aspuru-Guzik, L. Gagliardi, J. M. Notestein and R. Q. Snurr, Matter, 2021, 4, 1578–1597.
169. Y. Cho, A. Nandy, C. Duan and H. J. Kulik, J. Chem. Theory Comput., 2023, 19, 190–197.
170. M. Islamov, H. Babaei, R. Anderson, K. B. Sezginel, J. R. Long, A. J. H. McGaughey, D. A. Gomez-Gualdron and C. E. Wilmer, npj Comput. Mater., 2023, 9, 1–12.
171. Y. Xie, L. Liu, Z. Huang, H. Miao, W. Zhaxi, F. Duan, W. Huang and D. Wu, Inorg. Chem., 2023, 62, 3170–3177.
172. Ž. Kovacic, B. Likozar and M. Huš, ACS Catal., 2020, 10, 14984–15007.
173. B. Chan and K. Hirao, J. Phys. Chem. Lett., 2020, 11, 7882–7885.
174. K. Müller, K. Fink, L. Schöttner, M. Koenig, L. Heinke and C. Wöll, ACS Appl. Mater. Interfaces, 2017, 9, 37463–37467.
175. K. Hendrickx, D. E. P. Vanpoucke, K. Leus, K. Lejaeghere, A. Van Yperen-De Deyne, V. Van Speybroeck, P. Van Der Voort and K. Hemelsoet, Inorg. Chem., 2015, 54, 10701–10710.
176. T. Musho, J. Li and N. Wu, Phys. Chem. Chem. Phys., 2014, 16, 23646–23653.
177. T. Musho and N. Wu, Phys. Chem. Chem. Phys., 2015, 17, 26160–26165.
178. M. Gouterman, G. H. Wagnière and L. C. Snyder, J. Mol. Spectrosc., 1963, 11, 108–127.
179. B. Kaduk, T. Kowalczyk and T. Van Voorhis, Chem. Rev., 2012, 112, 321–370.
180. P. Ramos and M. Pavanello, Phys. Chem. Chem. Phys., 2016, 18, 21172–21178.
181. L. Wilbraham, F.-X. Coudert and I. Ciofini, Phys. Chem. Chem. Phys., 2016, 18, 25176–25182.
182. W.-Y. Wong, L. Liu and J.-X. Shi, Angew. Chem., Int. Ed., 2003, 42, 4064–4068.
183. Y. Yao, X. Song, J. Qiu and C. Hao, J. Phys. Chem. A, 2014, 118, 6191–6196.
184. X. Sui, W. Mi, M. Ji, C. Hao and J. Qiu, J. Lumin., 2013, 142, 110–115.
185. K. Hendrickx, J. J. Joos, A. De Vos, D. Poelman, P. F. Smet, V. Van Speybroeck, P. Van Der Voort and K. Lejaeghere, Inorg. Chem., 2018, 57, 5463–5474.
186. X.-P. Wu, L. Gagliardi and D. G. Truhlar, J. Am. Chem. Soc., 2018, 140, 7904–7912.
187. R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026–7068.
188. M. A. Syzgantseva and O. A. Syzgantseva, J. Phys. Chem. A, 2021, 125, 9700–9706.
189. K. K. Baeck and H. An, J. Chem. Phys., 2017, 146, 064107.
190. M. T. do Casal, J. M. Toldo, M. Pinheiro and M. Barbatti, Open Res. Eur., 2022, 1, 49.
191. X.-P. Wu, L. Gagliardi and D. G. Truhlar, J. Chem. Phys., 2019, 150, 041701.
192. C. Gomes Silva, I. Luz, F. X. Llabrés i Xamena, A. Corma and H. García, Chem. – Eur. J., 2010, 16, 11133–11138.
193. C. H. Hendon, D. Tiana, M. Fontecave, C. Sanchez, L. Darras, C. Sassoye, L. Rozes, C. Mellot-Draznieks and A. Walsh, J. Am. Chem. Soc., 2013, 135, 10942–10945.
194. A. Kuc, A. Enyashin and G. Seifert, J. Phys. Chem. B, 2007, 111, 8179–8186.
195. N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163.
196. V. A. Milichko, S. V. Makarov, A. V. Yulin, A. V. Vinogradov, A. A. Krasilin, E. Ushakova, V. P. Dzyuba, E. Hey-Hawkins, E. A. Pidko and P. A. Belov, Adv. Mater., 2017, 29, 1606034.
197. R. G. Polozkov, N. Y. Senkevich, I. I. Vrubel and I. A. Shelykh, Adv. Mater., 2017, 29, 1702463.
198. V. A. Milichko, E. V. Khramenkova, V. P. Dzyuba and E. A. Pidko, Adv. Mater., 2017, 29, 1705261.
199. H. Wang, W. Liu, X. He, P. Zhang, X. Zhang and Y. Xie, J. Am. Chem. Soc., 2020, 142, 14007–14022.
200. P. Deria, J. Yu, T. Smith and R. P. Balaraman, J. Am. Chem. Soc., 2017, 139, 5973–5983.
201. P. Deria, J. Yu, R. P. Balaraman, J. Mashni and S. N. White, Chem. Commun., 2016, 52, 13031–13034.
202. J. Yu, J. Park, A. Van Wyk, G. Rumbles and P. Deria, J. Am. Chem. Soc., 2018, 140, 10488–10496.
203. Y. Hidalgo-Rosa, M. A. Treto-Suárez, E. Schott, X. Zarate and D. Páez-Hernández, J. Comput. Chem., 2020, 41, 1956–1964.
204. Y. Hidalgo-Rosa, K. Mena-Ulecia, M. A. Treto-Suárez, E. Schott, D. Páez-Hernández and X. Zarate, J. Mater. Sci., 2021, 56, 13684–13704.
205. S. M. Pratik, L. Gagliardi and C. J. Cramer, J. Phys. Chem. C, 2020, 124, 1878–1887.
206. S. M. Pratik, L. Gagliardi and C. J. Cramer, Chem. Mater., 2020, 32, 6137–6149.
207. S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645–5655.
208. H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238.
209. R. Haldar, M. Jakoby, M. Kozlowska, M. Rahman Khan, H. Chen, Y. Pramudya, B. S. Richards, L. Heinke, W. Wenzel, F. Odobel, S. Diring, I. A. Howard, U. Lemmer and C. Wöll, Chem. – Eur. J., 2020, 26, 17016–17020.
210. A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405–3416.
211. S. Fankhauser, S. M. Smith, M. Allen, K. Axelsson, T. Hale, C. Hepburn, J. M. Kendall, R. Khosla, J. Lezaun, E. Mitchell-Larson, M. Obersteiner, L. Rajamani, R. Rickaby, N. Seddon and T. Wetzer, Nat. Clim. Change, 2022, 12, 15–21.
212. H.-Q. Liang, T. Beweries, R. Francke and M. Beller, Angew. Chem., Int. Ed., 2022, 61, e202200723.
213. A. Behera, A. Kumar Kar and R. Srivastava, Mater. Horiz., 2022, 9, 607–639.
214. Y. A. Alli, P. O. Oladoye, A. T. Onawole, H. Anuar, S. Adewuyi, O. D. Ogunbiyi and K. Philippot, Fuel, 2023, 344, 128101.
215. F. A. Rahimi, S. Dey, P. Verma and T. K. Maji, ACS Catal., 2023, 5969–5978.
216. A. Ejsmont, A. Jankowska and J. Goscianska, Catalysts, 2022, 12, 110.
217. M. Ding, R. W. Flaig, H.-L. Jiang and O. M. Yaghi, Chem. Soc. Rev., 2019, 48, 2783–2828.
218. G. Avci, I. Erucar and S. Keskin, ACS Appl. Mater. Interfaces, 2020, 12, 41567–41579.
219. W. Gao, S. Liang, R. Wang, Q. Jiang, Y. Zhang, Q. Zheng, B. Xie, C. Y. Toe, X. Zhu, J. Wang, L. Huang, Y. Gao, Z. Wang, C. Jo, Q. Wang, L. Wang, Y. Liu, B. Louis, J. Scott, A.-C. Roger, R. Amal, H. He and S.-E. Park, Chem. Soc. Rev., 2020, 49, 8584–8686.
220. A. Dhakshinamoorthy, A. M. Asiri and H. García, Angew. Chem., Int. Ed., 2016, 55, 5414–5445.
221. J. Chen, R. Abazari, K. A. Adegoke, N. W. Maxakato, O. S. Bello, M. Tahir, S. Tasleem, S. Sanati, A. M. Kirillov and Y. Zhou, Coord. Chem. Rev., 2022, 469, 214664.
222. P. Chacón, J. G. Hernández-Lima, A. Bazán-Jiménez and M. A. García-Revilla, Molecules, 2021, 26, 3060.
223. W. Zhan, H. Gao, Y. Yang, X. Li and Q.-L. Zhu, Adv. Energy Sustainability Res., 2022, 3, 2200004.
224. J.-W. Yoon, J.-H. Kim, C. Kim, H. W. Jang and J.-H. Lee, Adv. Energy Mater., 2021, 11, 2003052.
225. H. Cove, D. Toroz and D. Di Tommaso, Mol. Catal., 2020, 498, 111248.
226. M. Yamamoto, K. Takahashi, M. Ohwada, Y. Wu, K. Iwase, Y. Hayasaka, H. Konaka, H. Cove, D. Di Tommaso, K. Kamiya, J. Maruyama, F. Tani and H. Nishihara, Catal. Today, 2021, 364, 164–171.
227. A. Hayat, J. Khan, M. U. Rahman, S. B. Mane, W. U. Khan, M. Sohail, N. U. Rahman, N. Shaishta, Z. Chi and M. Wu, J. Colloid Interface Sci., 2019, 548, 197–205.
228. A. Hayat, M. Sohail, T. A. Taha, A. M. Alenad, A. Irfan, N. Shaishta, A. Hayat, S. K. B. Mane and W. U. Khan, CrystEngComm, 2021, 23, 4963–4974.
229. S. Izumi, K. Inoue, Y. Nitta, T. Enjou, T. Ami, K. Oka, N. Tohnai, S. Minakata, T. Fukushima, F. Ishiwari and Y. Takeda, Chem. – Eur. J., 2023, 29, e202202702.
230. T.-T. Liu, X.-P. Wu and X.-Q. Gong, J. Phys.: Energy, 2021, 3, 034016.
231. H. Shin, K. U. Hansen and F. Jiao, Nat. Sustainability, 2021, 4, 911–919.
232. T. Riedel, M. Claeys, H. Schulz, G. Schaub, S.-S. Nam, K.-W. Jun, M.-J. Choi, G. Kishan and K.-W. Lee, Appl. Catal., A, 1999, 186, 201–213.
233. C. Costentin and J.-M. Savéant, Curr. Opin. Electrochem., 2019, 15, 58–65.
234. A. Muthuperiyanayagam, A. G. Nabi, Q. Zhao, A. ur Rehman and D. D. Tommaso, Phys. Chem. Chem. Phys., 2023, 25, 13429–13441.
235. M. Taddei, G. M. Schukraft, M. E. A. Warwick, D. Tiana, M. J. McPherson, D. R. Jones and C. Petit, J. Mater. Chem. A, 2019, 7, 23781–23786.
236. B. Ding, B. Chan, N. Proschogo, M. B. Solomon, C. J. Kepert and D. M. D’Alessandro, Chem. Sci., 2021, 12, 3608–3614.
237. E. Flage-Larsen, A. Røyset, J. H. Cavka and K. Thorshaug, J. Phys. Chem. C, 2013, 117, 20610–20616.
238. J.-Y. Zeng, X.-S. Wang, B.-R. Xie, Q.-R. Li and X.-Z. Zhang, J. Am. Chem. Soc., 2022, 144, 1218–1231.
239. R. Das, S. S. Manna, B. Pathak and C. M. Nagaraja, ACS Appl. Mater. Interfaces, 2022, 14, 33285–33296.
240. S. Karmakar, S. Barman, F. Ahamed Rahimi, S. Biswas, S. Nath and T. Kumar Maji, Energy Environ. Sci., 2023, 2187–2198.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00518f

---