Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Transient absorption spectroscopy reveals that slow bimolecular recombination in SrTiO3 underpins its efficient photocatalytic performance†
Anna A.
Wilson
 a,
Lucy
Hart
a,
Lucy
Hart
 a,
Thomas
Shalvey
b,
Michael
Sachs
a,
Thomas
Shalvey
b,
Michael
Sachs
 a,
Weidong
Xu
a,
Benjamin
Moss
a,
Eva
Mazzolini
a,
Asim
Mumtaz
c and
James R.
Durrant
a,
Weidong
Xu
a,
Benjamin
Moss
a,
Eva
Mazzolini
a,
Asim
Mumtaz
c and
James R.
Durrant
 *ad
*ad
aDepartment of Chemistry and Centre for Processable Electronics, Imperial College London, London, W12 0BZ, UK. E-mail: j.durrant@imperial.ac.uk
bStephenson Institute for Renewable Energy, Department of Physics, University of Liverpool, Liverpool, L69 7ZF, UK
cSchool of Physics, Electronics & Technology, University of York, Heslington, York YO10 5DD, UK
dSpecific IKC, Faculty of Science and Engineering, Swansea University, Swansea, SA2 7AX, UK
First published on 25th October 2023
Abstract
The charge carrier dynamics of SrTiO3 are measured by ultrafast transient absorption spectroscopy, revealing bimolecular recombination kinetics that are at least two magnitudes slower than alternative metal oxides. This slow recombination is associated with its high dielectric constant, and suggested to be central to SrTiO3's high performance in photocatalytic systems.
SrTiO3 is a central component of several state-of-the-art particulate systems for unassisted photocatalytic water splitting, offering impressive activity alongside scalability and stability when modified by doping or co-catalyst addition.1–4 Recently, Domen and co-workers fabricated photocatalysts comprised of Al3+ doped SrTiO3 particles modified with a RhCrOx co-catalyst, to safely and stably split water for over 1000 hours.3,4 With the selective photodeposition of metal oxide based co-catalysts, to catalyse the hydrogen/oxygen evolution reactions and enhance stability,4,5 an apparent quantum yield (AQY) of 93% was achieved at 365 nm.2 This near-unity AQY is indicative of remarkably efficient preservation and utilisation of photogenerated charges to drive the desired catalytic reactions.
Charge carrier dynamics are a key determinant of efficiency in most photocatalysts, with bulk recombination often being the dominant loss pathway. Considering the imbalance between the timescales of fast recombination processes (ps–μs) that result in significant losses to photogenerated charge carriers,6–9 and slow interfacial water splitting reactions (μs–s), materials that suppress fast recombination are essential to achieve high water splitting activity. The near-unity AQY achieved by SrTiO3-based photocatalysts, without applied bias or scavengers, suggests that the intrinsic properties of SrTiO3 suppress recombination losses and enable the lifetime gain required. Several studies have focused on SrTiO3 recombination kinetics on slower (μs–s) timescales, or on the tracking of water oxidation reaction intermediates.10–13 Previous ultrafast studies of SrTiO3 have reported charge lifetimes on ns timescales,14–16 with Yamada et al.18 highlighting the dominance of Auger, and absence of bimolecular, recombination in SrTiO3 single crystals under high intensity laser excitation. However, apart from a study by Kato et al. comparing single crystal and powder SrTiO3 (highlighting the role of defect states in slowing recombination),16 they lack a comprehensive investigation of the wavelength and intensity dependence of the decay kinetics.14,15 More importantly for understanding the success of SrTiO3 as a photocatalyst, there have been no direct comparisons of the charge carrier recombination kinetics between SrTiO3 and alternative photocatalytic materials.
Herein, we employ transient absorption spectroscopy (TAS), to investigate the ultrafast charge carrier dynamics of thin SrTiO3 films on ps–ns timescales (see ESI† for details of fabrication and characterisation). Through spectral deconvolution and kinetic analysis, the wavelength dependent decay kinetics and the temporal spectral evolution is investigated, with the relaxation of charges and recombination of the resulting localised states assigned to distinct spectral components. Most notably, intensity dependent bimolecular decays are measured and compared to other metal oxides for the first time, to reveal significantly slower bimolecular recombination in SrTiO3 and aid explanation of its state-of-the-art performance.
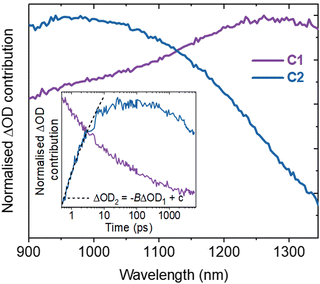
The ultrafast TAS spectrum is comprised of features in the visible and NIR regions (Fig. 1), assigned to hole and electron species respectively.11,12,16–19 Two features are present in the NIR, where one grows over the first 10 ps as the other decays. The decay kinetics are highly wavelength dependent and decelerate with decreasing probe wavelengths (Fig. S5, ESI†). Consequently, the spectrum blue shifts on ps timescales following photoexcitation. This is in agreement with previous observations for SrTiO3,14 but its origins have not been explored previously. At ≤1100 nm probe wavelengths, a slow rise is observed over the first ∼10 ps. In contrast, the signal decays immediately after photoexcitation at higher probe wavelengths. To understand the contributions of this decay and the slow rise to the spectra, and the relationship between them, we performed spectral deconvolution and a subsequent kinetic analysis on the TAS data.
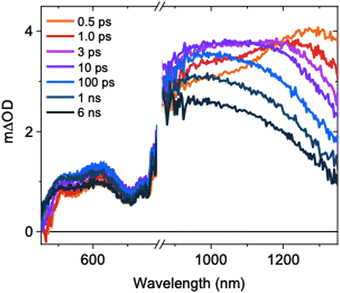 | ||
| Fig. 1 Ultrafast TAS spectrum of SrTiO3 measured across the visible and NIR, measured in Ar using a laser excitation intensity of 0.40 mJ cm−2. | ||
Spectral deconvolution in the NIR (900–1350 nm) extracts two components (C1 and C2 hereafter, Fig. 2). C1 and C2 are dominant above and below ∼1100 nm respectively and their spectral contributions are consistent across the range of excitation intensities used (Fig. S6a, ESI†). C1 exhibits an immediate decay following excitation (Fig. 2 inset), with intensity independent kinetics that are indicative of a monomolecular first-order process (Fig. S6b, ESI†)18 and in agreement with the intensity independence of the as-measured kinetics >1100 nm (Fig. S7, ESI†). Using a simple kinetic model (details in ESI†), the rise kinetics of C2 are found to be directly proportional to the decay kinetics of C1 (Fig. 2, inset), across all the excitation intensities analysed (Fig. S8, ESI†). This indicates that the decay of C1 results in the formation of C2, as discussed below.
The initial decay of C1 is assigned to charge localisation,17,20,21 most likely associated with shallow charge trapping.17,20,21 This is consistent with its monomolecular kinetics, and with the concomitant rise of C2, which we assigned to the resultant localised charges. Charge trapping of free carriers into defects has been reported to occur in 20 ps in SrTiO3,16 and into shallow trap states in 10 ps in TiO2,22,23 which is consistent with our assignment. Meanwhile, polaron formation in metal oxides is expected to occur on faster timescales (0.1–1 ps),17,24 thus polaron formation is the less likely origin of the slow rise herein. Both C1 and C2 are dominant in the NIR, associated with electrons in metal oxides.11,12,17–19 Thus, the charges undergoing this trapping process are assigned primarily to electrons.
Following the slow rise of C2, decay kinetics accelerate with increasing excitation intensities exceeding ∼0.22 mJ cm−2 (Fig. S6c, ESI†). An analogous intensity dependence is observed for the as-measured kinetics probed from 500–1100 nm (Fig. S7, ESI†). This is characteristic of bimolecular recombination being the dominant decay process,21,25 noting that at the excitation densities employed herein, Auger recombination is unlikely to be significant loss pathway.14 The intensity independence observed at excitation intensities below ∼0.22 mJ cm−2 is assigned to pseudo-first order recombination, due to the photogenerated charge density being below the dark intrinsic doping density, as explored further below.18 The intensity dependent kinetics exhibit power law decays (Fig. S9, ESI†) that continue to ms timescales (Fig. S10, ESI†). The C2 power law exponent of ∼0.17 (Fig. S9, ESI†) is indicative of trapping–detrapping limited bimolecular recombination, due to a degree of disorder in the material that is common in metal oxides.23,26–28 This further supports the assignment of the rise of C2 (and decay of C1) to shallow charge trapping. Fig. 3 illustrates the charge localisation into shallow trap states over the first ∼10 ps and their subsequent recombination on ns timescales.
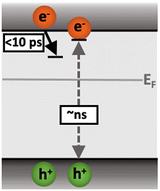 | ||
| Fig. 3 Illustration of the charge localisation (C1) and bimolecular recombination (C2) processes observed in SrTiO3. | ||
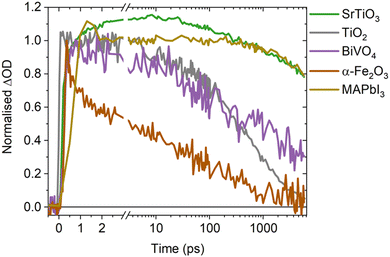
A direct comparison of the SrTiO3 bimolecular recombination kinetics observed herein to metal oxides commonly employed in photocatalytic applications (TiO2, BiVO4 and α-Fe2O3) is shown in Fig. 4. This reveals significantly slower kinetics in SrTiO3 that are similar to that of MAPbI3 (as explored later in the discussion), with the slow recombination kinetics observed herein supported by the observation of even longer lifetimes in single crystal SrTiO3 morphologies.14 The slower recombination of SrTiO3 was quantified by calculating approximate bimolecular rate constants (Table 1), using the charge lifetimes (t50%) and photogenerated charge densities at a given excitation intensity (Fig. S11 and Table S1, ESI†). The bimolecular rate constant of SrTiO3 estimated from C2 and the as-measured decays are notably slow (10−11 cm3 s−1), being two magnitudes slower than that calculated for TiO2 and BiVO4 (10−9 cm3 s−1) and three magnitudes slower than α-Fe2O3 (10−8 cm3 s−1) (we note that potential contributions from Auger recombination would be unlikely to significantly alter this order of magnitude comparison). Although we are only comparing a single morphology of each metal oxide in this case, the bimolecular recombination rate has been shown to be largely independent of morphology.18 The slower bimolecular recombination in SrTiO3 indicates a lower loss of photogenerated charges on fast timescales and therefore, a greater yield of charges available to participate in the interfacial water splitting reactions on slower timescales.
In addition to the bimolecular rate constant, the intrinsic doping density was estimated from the intensity dependent decays of C2 (Fig. S6c (ESI†) and Table 1), with the parameters used included in Table S2 (ESI†). At photogenerated charge densities lower than the intrinsic doping density, photogenerated charges predominantly recombine with the intrinsic charge carriers, leading to intensity independent pseudo-first order recombination. When the photogenerated charge density exceeds the intrinsic doping density, photogenerated charges predominantly recombine with each other via non-linear processes such as bimolecular recombination. Therefore, the photogenerated charge density from which clear intensity dependence is observed is taken as an approximate indicator of the intrinsic doping density, with contributions from the electronic doping density (i.e. the majority carrier density) and shallow chemical dopants that can mediate bimolecular recombination. The intrinsic doping densities thus estimated for all four metal oxides are of equivalent magnitude (∼1018 cm−3, Table 1), and in the range of doping densities reported previously for anatase TiO2 and BiVO4 (1016–1019 cm−3),29,30 and α-Fe2O3 (1017–1020 cm−3).31,32 The similar order of magnitude doping density of SrTiO3 compared to other metal oxides, indicates that its notably slow recombination does not result from a unique doping density. A possible explanation for the remarkably low bimolecular rate constant of SrTiO3, is its high dielectric constant. As the dielectric constant increases, Coulomb interactions are screened and the probability of photogenerated charges recombining is decreased.33 Consequently, an increase in dielectric constant can decrease bimolecular recombination rates and increase lifetimes, as has been observed in perovskite and organic photovoltaics.33–35 With the dielectric constant of SrTiO3 (∼300)36–39 being significantly higher than that of anatase TiO2 (13–45),40 BiVO4 (32–86)41–43 and α-Fe2O3 (18–26),44 increased dielectric screening effects in SrTiO3 may play a key role in suppressing recombination and enhancing charge lifetimes, thus explaining the slower rate of bimolecular recombination. Alternatively, defects in SrTiO3 have also been shown to have a critical role in enabling long lifetimes on ns–ms timescales.12,16 However, as defects are prevalent in metal oxides and not unique to SrTiO3,20 their presence alone is insufficient explanation of the notably slower recombination kinetics.
Intriguingly, MAPbI3 (a high performance photovoltaic material that shares the perovskite crystal structure of SrTiO3)45–47 exhibits similar bimolecular decay kinetics to SrTiO3 (Fig. 4), with a reported bimolecular rate constant in the range of 10−11–10−10 cm3 s−1 that is similar to that calculated for SrTiO3.9,48–50 With both SrTiO3 and MAPbI3 employed in state-of-the-art devices for their respective applications, it is interesting to note that compared to their counterparts they both exhibit notably higher dielectric constants and thus charge screening effects.45 These effects are recognised as an influential factor in perovskite photovoltaics,33,45 but are often overlooked in photocatalysts despite the important role they could play.
In summary, we have measured the charge carrier dynamics of SrTiO3 on fast (ps–ns) timescales, to reveal significantly slower bimolecular decay kinetics than other metal oxides commonly employed in photocatalytic applications. This is quantified by estimating a bimolecular rate constant for SrTiO3, which is at least two magnitudes lower than the other metal oxides studied. As significant losses to the yield of useful photogenerated charges occurs via fast recombination processes, the slow bimolecular recombination of SrTiO3 maximises the yield of photogenerated charges available to catalyse slow interfacial water splitting reactions. Due to the recognised effects of dielectric screening, the high dielectric constant of SrTiO3 is proposed as an explanation for its low bimolecular rate constant. It is evident herein that the intrinsic properties of SrTiO3 enable suppressed recombination and enhanced lifetimes, without applied bias or scavengers. This is an integral feature of overall photocatalytic water splitting materials, and together with the chemical flexibility and tunability of its perovskite structure, aids explanation of the prevalence of SrTiO3 in state-of-the-art systems.
For this work A. W. thanks the EPSRC for DTP funding and J. R. D. thanks the EPSRC ATIP project (EP/TO28513/1).
Conflicts of interest
There are no conflicts of interest to declare.Notes and references
- Q. Wang, T. Hisatomi, Q. Jia, H. Tokudome, M. Zhong, C. Wang, Z. Pan, T. Takata, M. Nakabayashi, N. Shibata, Y. Li, I. D. Sharp, A. Kudo, T. Yamada and K. Domen, Nat. Mater., 2016, 15, 611–615 CrossRef CAS PubMed.
- T. Takata, J. Jiang, Y. Sakata, M. Nakabayashi, N. Shibata, V. Nandal, K. Seki, T. Hisatomi and K. Domen, Nature, 2020, 581, 411–414 CrossRef CAS PubMed.
- Y. Goto, T. Hisatomi, Q. Wang, T. Higashi, K. Ishikiriyama, T. Maeda, Y. Sakata, S. Okunaka, H. Tokudome, M. Katayama, S. Akiyama, H. Nishiyama, Y. Inoue, T. Takewaki, T. Setoyama, T. Minegishi, T. Takata, T. Yamada and K. Domen, Joule, 2018, 2, 509–520 CrossRef CAS.
- T. Minegishi, H. Nishiyama, T. Hisatomi, M. Yoshida, H. Lyu, M. Katayama, K. Domen, Y. Goto, K. Asakura, Y. Sakata, T. Yamada, T. Higashi and T. Takata, Chem. Sci., 2019, 10, 3196–3201 RSC.
- K. Maeda, K. Teramura, D. Lu, N. Saito, Y. Inoue and K. Domen, J. Phys. Chem. C, 2007, 111, 7554–7560 CrossRef CAS.
- R. Godin and J. R. Durrant, Chem. Soc. Rev., 2021, 50, 13372–13409 RSC.
- R. Godin, A. Kafizas and J. R. Durrant, Curr. Opin. Electrochem., 2017, 2, 136–143 CrossRef CAS.
- E. V. Peán, S. Dimitrov, C. S. De Castro and M. L. Davies, Phys. Chem. Chem. Phys., 2020, 22, 28345–28358 RSC.
- C. L. Davies, M. R. Filip, J. B. Patel, T. W. Crothers, C. Verdi, A. D. Wright, R. L. Milot, F. Giustino, M. B. Johnston and L. M. Herz, Nat. Commun., 2018, 9, 1–9 CrossRef CAS PubMed.
- J. J. M. Vequizo, S. Nishioka, J. Hyodo, Y. Yamazaki, K. Maeda and A. Yamakata, J. Mater. Chem. A, 2019, 7, 26139–26146 RSC.
- R. Chen, D. Zhang, Z. Wang, D. Li, L. Zhang, X. Wang, F. Fan and C. Li, J. Am. Chem. Soc., 2023, 145, 4667–4674 CrossRef CAS PubMed.
- A. Yamakata, J. J. M. Vequizo and M. Kawaguchi, J. Phys. Chem. C, 2015, 119, 1880–1885 CrossRef CAS.
- D. M. Herlihy, M. M. Waegele, X. Chen, C. D. Pemmaraju, D. Prendergast and T. Cuk, Nat. Chem., 2016, 8, 549–555 CrossRef CAS PubMed.
- Y. Yamada, H. Yasuda, T. Tayagaki and Y. Kanemitsu, Appl. Phys. Lett., 2009, 95, 121112 CrossRef.
- D. H. K. Murthy, H. Matsuzaki, Q. Wang, Y. Suzuki, K. Seki, T. Hisatomi, T. Yamada, A. Kudo, K. Domen and A. Furube, Sustainable Energy Fuels, 2018, 3, 1–10 Search PubMed.
- K. Kato and A. Yamakata, J. Phys. Chem. C, 2020, 124, 11057–11063 CrossRef CAS.
- E. Pastor, J. S. Park, L. Steier, S. Kim, M. Grätzel, J. R. Durrant, A. Walsh and A. A. Bakulin, Nat. Commun., 2019, 10, 1–7 CrossRef CAS PubMed.
- M. Sachs, E. Pastor, A. Kafizas and J. R. Durrant, J. Phys. Chem. Lett., 2016, 7, 3742–3746 CrossRef CAS PubMed.
- M. Sachs, J. S. Park, E. Pastor, A. Kafizas, A. A. Wilson, L. Francàs, S. Gul, M. Ling, C. Blackman, J. Yano, A. Walsh and J. R. Durrant, Chem. Sci., 2019, 10, 5667–5677 RSC.
- S. Corby, R. R. Rao, L. Steier and J. R. Durrant, Nat. Rev. Mater., 2021, 6, 1136–1155 CrossRef CAS.
- J. Nelson and R. E. Chandler, Coord. Chem. Rev., 2004, 248, 1181–1194 CrossRef CAS.
- Y. Tamaki, A. Furube, R. Katoh, M. Murai, K. Hara, H. Arakawa and M. Tachiya, C. R. Chim., 2006, 9, 268–274 CrossRef CAS.
- J. Tang, J. R. Durrant and D. R. Klug, J. Am. Chem. Soc., 2008, 130, 13885–13891 CrossRef CAS PubMed.
- J. S. Pelli Cresi, L. Di Mario, D. Catone, F. Martelli, A. Paladini, S. Turchini, S. D’Addato, P. Luches and P. O’Keeffe, J. Phys. Chem. Lett., 2020, 11, 5686–5691 CrossRef CAS PubMed.
- T. M. Clarke, F. C. Jamieson and J. R. Durrant, J. Phys. Chem. C, 2009, 113, 20934–20941 CrossRef CAS.
- M. Barroso, S. R. Pendlebury, A. J. Cowan and J. R. Durrant, Chem. Sci., 2013, 4, 2724–2734 RSC.
- S. R. Pendlebury, X. Wang, F. Le Formal, M. Cornuz, A. Kafizas, S. D. Tilley, M. Grätzel, J. R. Durrant and F. Formal, J. Am. Chem. Soc., 2014, 136, 9854–9857 CrossRef CAS PubMed.
- A. J. Cowan, W. Leng, P. R. F. Barnes, D. R. Klug and J. R. Durrant, Phys. Chem. Chem. Phys., 2013, 15, 8772–8778 RSC.
- A. Kafizas, X. Wang, S. R. Pendlebury, P. Barnes, M. Ling, C. Sotelo-Vazquez, R. Quesada-Cabrera, C. Li, I. P. Parkin and J. R. Durrant, J. Phys. Chem. A, 2016, 120, 715–723 CrossRef CAS PubMed.
- Y. Ma, S. R. Pendlebury, A. Reynal, F. Le Formal and J. R. Durrant, Chem. Sci., 2014, 5, 2964–2973 RSC.
- Z. Luo, C. Li, S. Liu, T. Wang and J. Gong, Chem. Sci., 2016, 8, 91–100 RSC.
- Y. Liang, C. S. Enache and R. Van De Krol, Int. J. Photoenergy, 2008, 2008, 739864 CrossRef.
- R. Su, Z. Xu, J. Wu, D. Luo, Q. Hu, W. Yang, X. Yang, R. Zhang, H. Yu, T. P. Russell, Q. Gong, W. Zhang and R. Zhu, Nat. Commun., 2021, 12, 2479 CrossRef CAS PubMed.
- Z. Fu, X. Zhang, H. Zhang, Y. Li, H. Zhou and Y. Zhang, Chin. J. Chem., 2021, 39, 381–390 CrossRef CAS.
- G. Zhang, T. M. Clarke and A. J. Mozer, J. Phys. Chem. C, 2016, 120, 7033–7043 CrossRef CAS.
- N. F. Muhamad, R. A. Maulat Osman, M. S. Idris and M. N. Mohd Yasin, EPJ Web Conf., 2017, 162, 2–5 Search PubMed.
- B. Pongthippitak, P. Wongtha, P. Reabroy, P. Kunsuwan and S. Thountom, J. Phys.: Conf. Ser., 2018, 1144, 012162 CrossRef.
- M. Marques, L. K. Teles, V. Anjos, L. M. R. Scolfaro, J. R. Leite, V. N. Freire, G. A. Farias and E. F. Da Silva, Appl. Phys. Lett., 2003, 82, 3074–3076 CrossRef CAS.
- R. M. Doughty, B. Hodges, J. Dominguez, R. Han, Z. Zhao, S. Assavachin and F. E. Osterloh, J. Phys. Chem. C, 2020, 124, 18426–18435 CrossRef CAS.
- M. Dou and C. Persson, J. Appl. Phys., 2013, 113, 083703 CrossRef.
- S. Sarkar and K. K. Chattopadhyay, Phys. E, 2012, 44, 1742–1746 CrossRef CAS.
- K. H. Ye, X. Yu, Z. Qiu, Y. Zhu, X. Lu and Y. Zhang, RSC Adv., 2015, 5, 34152–34156 RSC.
- D. K. Zhong, S. Choi and D. R. Gamelin, J. Am. Chem. Soc., 2011, 133, 18370–18377 CrossRef CAS PubMed.
- R. A. Lunt, A. J. Jackson and A. Walsh, Chem. Phys. Lett., 2013, 586, 67–69 CrossRef CAS.
- J. Y. Kim, J. W. Lee, H. S. Jung, H. Shin and N. G. Park, Chem. Rev., 2020, 120, 7867–7918 CrossRef CAS PubMed.
- N. J. Jeon, H. Na, E. H. Jung, T. Y. Yang, Y. G. Lee, G. Kim, H. W. Shin, S. Il Seok, J. Lee and J. Seo, Nat. Energy, 2018, 3, 682–689 CrossRef CAS.
- X. Zheng, B. Chen, J. Dai, Y. Fang, Y. Bai, Y. Lin, H. Wei, X. C. Zeng and J. Huang, Nat. Energy, 2017, 2, 1–9 Search PubMed.
- L. M. Pazos-Outón, T. P. Xiao and E. Yablonovitch, J. Phys. Chem. Lett., 2018, 9, 1703–1711 CrossRef PubMed.
- J. G. Labram and M. L. Chabinyc, J. Appl. Phys., 2017, 122, 065501 CrossRef.
- C. Wehrenfennig, G. E. Eperon, M. B. Johnston, H. J. Snaith and L. M. Herz, Adv. Mater., 2014, 26, 1584–1589 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cc04616h |
| This journal is © The Royal Society of Chemistry 2023 |