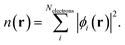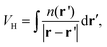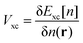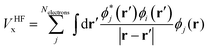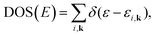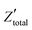Open Access Article
Open Access ArticleThe electrochemical double layer at the graphene/aqueous electrolyte interface: what we can learn from simulations, experiments, and theory
Joshua D.
Elliott
 a,
Athanasios A.
Papaderakis
a,
Athanasios A.
Papaderakis
 b,
Robert A. W.
Dryfe
b and
Paola
Carbone
b,
Robert A. W.
Dryfe
b and
Paola
Carbone
 *a
*a
aDepartment of Chemical Engineering, University of Manchester, Oxford Road, Manchester M13 9PL, UK. E-mail: joshua.elliott@manchester.ac.uk; joshua.elliott@diamond.ac.uk; paola.carbone@manchester.ac.uk
bDepartment of Chemistry and Henry Royce Institute, University of Manchester, Manchester M13 9PL, UK. E-mail: athanasios.papaderakis@manchester.ac.uk; robert.dryfe@manchester.ac.uk
First published on 3rd October 2022
Abstract
The physical-chemistry of the graphene/aqueous–electrolyte interface underpins the operational conditions of a wide range of devices. Despite its importance, this interface is poorly understood due to the challenges faced in its experimental characterization and the difficulty of developing models that encompass its full physics. In this review we first summarize the classical theory of the electrochemical double layer, with the aim of defining a universal nomenclature to link experiments and simulations within a single unified framework. We then present the most recent experimental, theoretical and computational data and discuss how they compare with standard theory. The review ends with some remarks about how to compare simulations and experimental data and how this technology might evolve in the future.
1. Introduction
Nanotechnology has promised a revolution in many industrial sectors that is slowly becoming reality, but full realisation of its potential requires deeper understanding of the physics at the nanoscale. Carbon-based nanomaterials and related technologies are at the forefront of this revolution. In fact, the unique variety of thermodynamically stable configurations that carbon shows at the nanoscale (e.g. carbon-nanotubes, graphene and fullerene) allow for tailored manipulation of its mechanical, optical and electronic properties. As a consequence, carbon materials are nowadays employed in a broad range of applications including in medicine as diagnostic as well as therapeutic tools,1 in energy storage and conversion,2 in electronics3 and in environmental science as sorbents, filters or sensors.4 In the majority of these applications, the carbonaceous material is in contact with a water-based electrolyte and the functionality of the devices is dictated by physico-chemical phenomena taking place at this interface. Despite its vital importance in many areas of science, this solid/liquid interface is however not fully understood at the atomic level and in particular, the mechanism of ion adsorption/desorption onto the surface is still unclear and highly debated in the scientific community.5–7 This lack of knowledge hinders the development of a wide range of technologies that rely on this physical phenomenon such as supercapacitors but also electrochemical sensors, rechargeable batteries and many optical devices. Consequently, a surprisingly large number of fundamental questions about this interface remain unanswered including: (i) what is the atomic-level structure of the electrical double layer? (ii) what are the competing interactions that drive the ions’ adsorption? (iii) how does the application of an external potential affect the ions distribution and dynamics at the interface? (iv) how does confinement of an electrolyte affect the ions’ dynamics and the solution electrochemical properties? The answers to these questions lead directly more technological question such as: what is the role of the ion/surface interaction on the performance of electrical double layer devices?The emergence of graphene as a new material had created the golden opportunity to answer many of the questions posed above, since its theoretical atomic scale smoothness and single atom 2D geometrical nature make it not only the perfect substrate to perform highly controlled experiments, but also the perfect material to carry out molecular simulations to compare with experimental results. However, the lack of complexity of the experimental system is only an apparent one. Graphene often contains impurities (not only affecting its surface chemistry, but also compromising its presumed atomistic smoothness) and/or structural defects (with consequences for its electronic structure). Moreover, simulations are plagued by well-known problems associated with an uncertainty of the model (i.e. force field), limitations of fully classical simulations to model charge redistribution or charge transfer and the spatial and temporal limitations associated with the scale of quantum mechanical simulations.
The literature on graphene/electrolyte interface is vast especially concerning simulations (classical and quantum mechanical) with some valuable other review papers published fairly recently on the topic (see for example ref. 8). Here we focus solely on the work done to characterize the interface from an electrochemical point of view and the efforts that have been made to compare simulation and experimental data. We only report on water-based electrolytes with specific reference to electrolytes containing alkali metals; these have been used as model systems in experimental and theoretical studies due to the well-established fundamental theory of the thermodynamics of the electrochemical double layer.
The review starts with a summary of the classical theory of the electrochemical double layer (EDL). Despite this being textbook knowledge, we use this initial introduction to define a universal nomenclature and to link experiments and simulations within a single unified framework to make clear and unequivocal the link between the two throughout the whole review. The subsequent sections review the computational methods developed to model the interface (neutral and electrified) and the experimental electrochemical techniques for the study of the EDL, followed by a summary of the available capacitance data (experimental or calculated) and proposed ion adsorption mechanisms. We then move on to consider the effect of confinement on the EDL structure and ions’ dynamics. The review ends with some remarks about how to compare simulations and experimental data and the next challenges in the field.
2. Theory, experiments and computational methods that describe the electrochemistry of the interface
2.1 Classical theories of the electrochemical double layer
The term interface is used to describe the imaginary plane that separates two immiscible physical phases being in contact with each other. The thickness of such a physical interface is strictly defined to be no more than that of a complete atomic monolayer (usually on the order of a few Å) and hence the interface is treated as a two-dimensional object. If the interface extends deeper into the tangential individual phases (i.e., from at least two monolayers up to the μm scale), the term interfacial region is used instead. In both cases, the properties of the new phase formed in the vicinity of the geometrical boundary of the individual phases, are different (often significantly) compared to those of the homogeneous phases. When the individual phases are electrical conductors and at least one of them is also an ionic conductor, the interface/interfacial region is defined as an electrochemical interface/interfacial region. Interfaces of this type are formed when a metal, semiconductor, or other types of (semi)conductive materials such as graphite, conductive polymers, and various ceramics, are in contact with an ionic conductor, e.g., an electrolytic solution, solid electrolytes, ionic melts, membranes, etc.The formation of an electrochemical interface is known to be accompanied by a spatial separation of charge, which leads to a local potential difference between the electrode surface and the electrolyte solution and perturbs the activities of the various components in the vicinity of the interface. Considering the extremely small thickness of the interface, the potential gradient arising exceeds 107 V cm−1.9 The substantial strength of this electric field is not attributed to the amount of accumulated charge at the interface (most often being on the order of a few μC cm−2), but to its distribution and consequently the unique structure of the electrochemical interface or, as frequently reported in the literature, the EDL.
Several phenomenological models of the EDL have been developed since the middle of the nineteenth century. The fundamental basis of these models was established from macroscopic measurements under equilibrium conditions, involving mainly the interfacial tension (electrocapillary curves; see below) and double layer capacitance.10 The change of these parameters with the applied potential and the activities of various species in the electrolyte was monitored. The suggested theories developed to describe the system were based on a thermodynamic treatment. The general approach relies on the concept of the ideally polarizable electrode, i.e., an electrode where no charge transfer processes occur, introduced by Koenig.11 In this case the system obeys Gibbs’ equation of electrocapillarity in the form:10,12
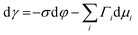 | (1) |
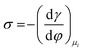 | (2) |
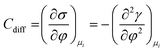 | (3) |
As mentioned previously, the dependence of γ on potential has been studied in parallel to that of C towards the investigation of the structural characteristics of EDL. This was made possible by the fact that the earliest quantitative experimental studies of the electrode/electrolyte interface were primarily focused on mercury, due to the feasibility of producing a contaminant-free and reproducible surface as well as its relatively expanded, compared to other metals, potential window of stability in aqueous solvents.12 From eqn (2) and (3) it can be inferred that for σ = 0, and because C cannot be negative, the second derivative of γ with respect to φ is negative. This means that the change of γ with φ exhibits a maximum. Such plots are referred to as electrocapillary curves and their maximum value corresponds to the potential of zero charge (PZC) at the interface. The latter represents the potential at which the net surface charge at the EDL is zero and is a key parameter of the electrochemical interface as it is a property of both the electrode (through its electron work function) and the detailed composition of the solution phase.13,14 At potentials more negative or more positive than PZC, γ decreases as a result of the increased presence of cations and anions, respectively. By definition, at the PZC, C will attain its minimum value.
Based on the above thermodynamic analysis, the first and simplest model introducing the concept of the formation of a double layer at the electrochemical interface and thus describing the structure of the EDL, was formulated by Helmholtz.9,10,12 It was assumed that no neutral species other than solvent dipoles are present and adsorption of electrolyte ions occurs solely due to electrostatic interactions, i.e., non-specific adsorption. Helmholtz envisaged that the total charge on the electrode is balanced by a monolayer of ions of opposite charge located adjacent to the surface, referred to as the Helmholtz layer. In this respect, the potential gradient is linear and steep over the thickness of the monolayer. For the region extended outside the Helmholtz layer, the model states that both its potential and composition equal those of the bulk solution, with equal concentrations of anions and cations moving randomly in the solution. In this sense, the EDL represents a nano-condenser in which the two charged planes containing the excess electrons (or holes) and the counterions are separated by a solvent layer of thickness, dH. The ratio of the electronic charge density at the electrode and the potential difference at the interface (i.e., the total potential difference required to place this charge at the interface), Δφi, gives the integral Helmholtz double layer capacitance per unit area (also known as simply integral capacitance):10,15
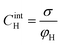 | (4) |
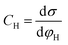 | (5) |
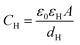 | (6) |
The Helmholtz model, described by eqn (4)–(6), has been found to qualitatively follow the experimental data for relatively concentrated solutions (usually higher than 0.1 M) in the absence of ion-specific adsorption, i.e., surface inactive electrolytes, however it exhibits two fundamental drawbacks: (i) the apparent independence of CH on the applied potential, which has been disproved experimentally for various systems and (ii) its inability to explain the dependence of CH (or the electrode charge) on the electrolyte concentration, which is observed experimentally in sufficiently dilute solutions.17,18
In more detail, despite the fact that the Helmholtz model has been a cornerstone towards the foundation of the EDL theory, it does not consider three important physical factors, which are the applied potential, the interplay between the randomized thermal motion of the ions and that imposed by the polarity of the electrode (being more pronounced at low electrolyte concentrations) as well as the interaction between solvent molecules’ dipole moments and the electrode. Gouy and Chapman postulated that even though the charge at the electrode is strictly located at the surface, this might not be the case for the solution side. In dilute electrolytes, one must consider the low density of charge carriers in the solution phase. Under such conditions, the excess charge required to counterbalance that confined to the surface of the electrode will be distributed within a larger region in the solution. This newly introduced layer will have a composition different from the bulk and it will exhibit characteristics of a diffuse layer. The potential within the diffuse layer is expected to drop smoothly from the surface of the electrode (where electrostatic forces overcome thermal processes and therefore the greatest excess charge density in the solution phase is observed) to the bulk, with a decreasing gradient across the layer. In this respect, they developed a model of the electrochemical interface adopting the following assumptions:19,20 (i) the electrode is a perfect conductor with an evenly distributed charge on its surface, (ii) the solvent is treated as a uniform dielectric continuum characterized by εr and (iii) the ions are considered as point particles whose distribution is determined by the Poisson–Boltzmann equation. Adopting this approach for the case of a symmetrical electrolyte, the expression for the Gouy–Chapman differential capacitance per unit area is derived to be,
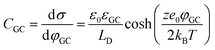 | (7) |
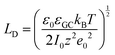 | (8) |
Despite addressing a major weakness (constant double layer capacitance with changes in potential) of the Helmholtz model, the Gouy–Chapman model, also exhibits weak points. Firstly, it only adequately follows the experimental data in dilute electrolyte solutions and is applicable for a narrow region near the PZC. Additionally, the model considers the ions as point charges, which leads to an anomalous rise in capacitance at high polarization (since the ions as point charges can approach the surface without any restriction due to physical barriers), while ion–ion interactions, which become particularly important at higher concentrations, are neglected. The last point is the assumption of a constant electrolyte permittivity in the whole region between the electrode and the bulk solution. This assumption is inaccurate since the relative permittivity of the electrolyte decreases when moving from the bulk solution to the diffuse layer,16 and is in fact dramatically decreased inside the compact layer at the immediate vicinity of the electrode surface12,16,21–23 as a consequence of the decrease in the rotational freedom of water dipoles near surfaces.12,16,21–23 The next step towards the establishment of a solid theory for the structure of the EDL, was made by Stern.9,10,12,15 His suggestion was to combine the approaches of Helmholtz and Gouy–Chapman and thus consider the electrochemical interface as consisting of two layers. In the first compact layer, the charge on the solution side is located close to the electrode surface, i.e., the Helmholtz layer, and the rest of it is distributed in the solution within the limits defined by the compact layer and the bulk solution, i.e., the Gouy–Chapman diffuse layer. In this layer, the point charge approximation is now eliminated, and the ion–ion interactions are considered by taking the ion centres as not able to approach the electrode surface closer than a specified distance. This results in a linear potential drop adjacent to the electrode surface, following the Helmholtz model, and an approximately exponential decay in the region from the compact layer to the bulk, based on the Gouy–Chapman theory. A direct consequence of the above model (referred in the literature as the Gouy–Chapman–Stern model) is the separation of differential capacitance across the interface in two components, that of the compact layer, CH, and the one from the diffuse layer, CGC. Hence, in the same way as would be expected for two electrical capacitors connected in series, we can write the reciprocal of the total capacitance of the EDL as:10,12,15
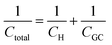 | (9) |
An attempt for a refinement of the Stern model, was done by Grahame in a series of seminal works, the results of which are summarized in ref. 17. As described in an authoritative review article by the pioneers in interfacial physical electrochemistry, Damaskin and Petrii,24 Grahame stated that the potential difference at the interface, Δφm,s (the indices m and s refer to the metal electrode and the solution respectively), can be expressed using the Galvani potentials approach as,
| Δφm,s = Δφion + Δφdip + Δφmet | (10) |
| Δφm,s = ΔφH + [Δφdip − (Δφdip)pzc] + [Δφmet − (Δφmet)pzc] + ΔφGC | (11) |
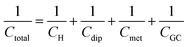 | (12) |
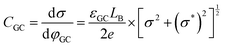 | (13) |
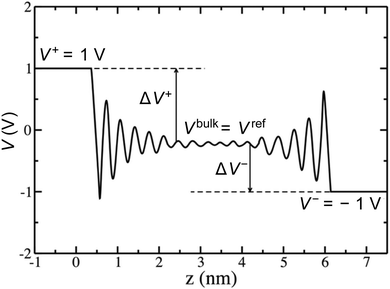
Rather than the smooth exponential decay described by Gouy–Champan–Stern model, a theoretical description of the electrode–electrolyte interface at the atomistic level necessarily includes the fine structure and local arrangement of the atoms and molecules in the EDL (Fig. 1). This gives rise to a more complex electrostatic potential profile, V, which can be obtained from the charge density distribution ρ by solving the Poisson's equation along the surface normal,
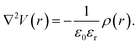 | (14) |
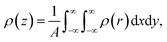 | (15) |
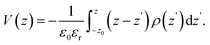 | (16) |
From the electrostatic potential profile we can extract electrostatic potential difference across the interface, setting the bulk electrostatic potential as the electrostatic potential of a reference electrode (Fig. 1).25 In doing so, this lets us extract both the theoretical electrochemical double layer Integral capacitance, similar to eqn (4)
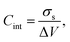 | (17) |
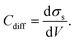 | (18) |
2.2 The EDL theory for carbon–electrolyte interfaces
The fundamental EDL theories, described in the previous section, were established considering a highly conductive solid phase. This is attributed to the fact that the early experimental studies of the EDL were restricted to metals with an initial strong emphasis on mercury and a gradual expansion of the research to various metals (including both single crystals and polycrystalline materials), following the developments and applications of ultra-high vacuum techniques of surface science. In the case of an electrode with a lower carrier density in the vicinity of the Fermi level compared to metals, e.g., a semiconductor or a semimetal, the above models need to be revised to include the appropriate charge contributions arising from the distribution of charge in the semiconducting solid side. The latter is known in the literature as the space-charge region and is a solid-state analogue of the diffuse layer developed within the solution phase.The potential and charge distribution within the space charge region can be described quantitatively by the Poisson–Boltzmann equation, in a similar way to the classical model for the diffuse layer of the EDL. This is reasonable since the space-charge layer can be considered as a diffuse layer with electrons instead of ions as mobile carriers. In this respect, the differential capacitance of the space charge layer, CSC, is defined by:
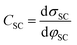 | (19) |
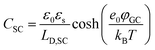 | (20) |
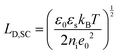 | (21) |
It is noteworthy that as follows from eqn (20) the minimum of the space charge capacitance, located at φSC = 0, corresponds to a finite value for CSC (since cosh(0) = 1). This is because CSC is a differential capacitance defined by eqn (19) which is not zero at φSC = 0.26
In a similar way to what has been described earlier, the overall capacitance of the semiconductor–electrolyte interface, Ctotal,SC, in the absence of surface states, is given by the sum of the individual contributions of the capacitances of the space charge, the Helmholtz and the diffuse layers, following the rules for capacitors connected in series:26–28
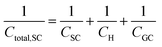 | (22) |
In the context of carbon electrodes, Randin and Yeager29,30 were the first to experimentally investigate the capacitance of the basal plane of stress-annealed pyrolytic graphite adopting the theory for the structure of the EDL at the semiconductor–electrolyte interface. In complete analogy with the semiconductors, the semi-metallic character of graphite gives rise to a space charge layer capacitance in the solid. The authors used eqn (22) to describe the overall capacitance of the graphite – aqueous NaF solutions in the electrolyte concentration range between 10−5 and 0.9 M. According to the potential dependence of CSC as that described in eqn (20), they calculated the contribution of the space charge capacitance in graphite, CGR, by using the following relation,29,30
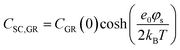 | (23) |
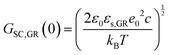 | (24) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31) and φs the potential at the surface of the electrode. The theoretical and experimental values for CSC,GR(0) reported by Randin and Yeager are 4.5 and 3 μF cm−2, respectively.29 The authors ascribe the observed difference to the uncertainty as to the exact values of c and εs,GR. It is worth noting that CSC,GR(0) values are ca. one order of magnitude smaller compared to e.g., those usually recorded at PZC for various metals.9,10,12 Gerischer attributed this finding to the low density of states (DOS) in the neighbourhood of the Fermi level on graphite.32 The same author, determined the dependence of the minimum of CSC,GR2 on the DOS at the Fermi level, N0 (cm−3 eV−1), by integration of the Poisson–Boltzmann equation in the direction across the interface using the boundaries φ = φs at x = 0 and φ = 0 at x → ∞,:28,32
31) and φs the potential at the surface of the electrode. The theoretical and experimental values for CSC,GR(0) reported by Randin and Yeager are 4.5 and 3 μF cm−2, respectively.29 The authors ascribe the observed difference to the uncertainty as to the exact values of c and εs,GR. It is worth noting that CSC,GR(0) values are ca. one order of magnitude smaller compared to e.g., those usually recorded at PZC for various metals.9,10,12 Gerischer attributed this finding to the low density of states (DOS) in the neighbourhood of the Fermi level on graphite.32 The same author, determined the dependence of the minimum of CSC,GR2 on the DOS at the Fermi level, N0 (cm−3 eV−1), by integration of the Poisson–Boltzmann equation in the direction across the interface using the boundaries φ = φs at x = 0 and φ = 0 at x → ∞,:28,32| CSC,GR2 = ε0εs,GRe0N0 | (25) |
Finally, in the presence of surface states, i.e., additional energy levels close to the Fermi level emerging due to the intrinsic properties of the material (such as disruptions in the crystal lattice) or as a consequence of the interaction with species at the external ambient (e.g., in the presence of adsorption), extra charge is stored in the solid phase. This accumulation of charge gives rise to an additional capacitance contribution in the solid and eqn (22) becomes,26,27
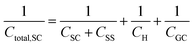 | (26) |
In the classical theory of capacitors, the relationship between the charge and the voltage is expressed as,
| Q = CV. | (27) |
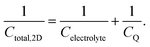 | (28) |
Ji et al. used a band theory picture, which does not account for any of the contributions of the electrolyte, to assess the contribution of the CQ to the total capacitance,
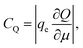 | (29) |
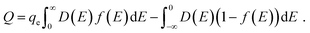 | (30) |
As opposed to models of the graphene band structure, electronic structure theory simulations based on DFT can instead provide access to the graphene DOS.34,35,37 For instance Zhan et al. employed DFT simulations in vacuum and using an implicit solvent model to describe the electrolyte, to perform an analogous study to Ji et al.33,37 The DFT-computed CQ was also found to increase with the number of graphene layers included in the model (without converging), however, at variance with experimental measurements, the relative change in the capacitance with electrode charge is less steep for systems with fewer graphene layers.
An additional advantage of computing the CQ from the graphene DOS is the ability of this approach to capture the asymmetry between the positive and negative charging branches. Zhan et al. find that the CQ increases more rapidly on the positive charging branch, while Bhushan et al. observe the opposite trend for the differential of an integrated CQ. Our approach, based on DFTB-QMMD can also be employed to extract the CQ from the graphene DOS – factoring in changes due to the electrostatic potential of the electrolyte environment, we found only a minor asymmetry between the two branches of the differential capacitance with the negative branch increasing more rapidly.40 This leads to the conclusion that strong asymmetries in the total capacitance arise from the CEDL component and the preferential adsorption and structuring of either cations or anions on the surface.
The direct relation of CQ to the graphene DOS, has raised additional interest towards the impact of lattice imperfections, such as topological defects, on CQ. Topological defects in graphene arise by the local rearrangement of atomic bonds that break the hexagonal symmetry of the 2D lattice, i.e., forming non-hexagonal carbon rings.41,42 The simplest topological defects include disclinations (individual pentagons and heptagons) and dislocations (pairs of pentagon and heptagon).41,42 Wood et al.43 used DFT calculations to investigate the effect of various types of native graphene point defects on CQ, including Stone–Wales defects, and mono- and divacancies. Their calculations show that the introduction of topological defects in sufficient concentrations, significantly increases CQ. Further DFT calculations carried out by Pak et al.,44 probed the impact of individual point-like topological defects on CQ. Their model consisted of Stone–Wales, divacancies and diinterstitials at a defect density of ca. 0.8 at%. Assuming a marginal effect of these point-like defects on CH (which however might not be valid for higher concentrations and larger-scale defects), they demonstrated that the defective graphene layers tend to enhance CQ compared to pristine graphene. They attributed this finding to the introduction of quasi-localized states of varying degrees near the Fermi level, arising due to the disruption of graphene's extended π system. An additional noteworthy outcome of both studies is that the type of defects determines the potential range within which CQ increases; the charging behaviour of the electrode becomes asymmetric with respect to PZC. For example, Stone–Wales imperfections exhibit a much larger effect at higher voltage magnitudes and hence could be potentially more effective as positive electrodes in energy storage applications. In another very interesting work, Chen et al.45 have studied the influence of Stone–Wales point-like defects of varying concentration on the total capacitance of the monolayer graphene/aqueous electrolyte interface, by combining electrochemical experiments with DFT calculations using the approaches described above. In line with the previous studies, they concluded that the presence of Stone–Wales defects can significantly improve the DOS of graphene near the Fermi level and therefore influence CQ. This was manifested in experimentally determined integral capacitance, which is profoundly increased for the defective graphene monolayer/4 M KCl(aq) interface when compared to the pristine graphene layer (note though that CH was assumed to be unaffected by the presence of topological defects and hence its contribution to the total capacitance of the interface was taken as constant). In addition, the rate of increase in Cdiff with E was found to rise significantly as a function of the defect concentration and the capacitance minimum in the Cdiff–E plots was increased up to 70% (1.7 μF cm−2), relative to the pristine value, for the graphene layer with the highest defect concentration.
A newly discovered type of topological defects in graphene that give rise to remarkable physical properties, is the twisted bilayer.46 These defects arise from the weak interlayer interactions between bilayer graphene, which allow independent control of arbitrary azimuthal orientations between the 2D lattices. The most extraordinary example of the effect of such structural modifications on the electronic properties of graphene is the twist of a graphene bilayer from a Bernal (AB) stacking configuration to a ‘magic angle’ of ca. 1.1°, which leads to the formation of electronic bands with very weak dispersion in momentum space, so-called ‘flat’ bands.47 In a recent seminal work, Yu et al.48 established the fundamental baseline for the understanding of the heterogeneous kinetics at the twisted bilayer graphene/aqueous electrolyte interface, by probing the dependence of the heterogeneous electron transfer rate on the twist angle using both electrochemical methods and theoretical calculations. This was achieved by investigating the effect of the twist angle on graphene DOS in the vicinity of the Fermi level. To evaluate CQ in the twisted bilayer graphene, they computed the electronic band structures over a range of twist angles. The results show that CQ is notably enhanced near the neutrality point, for twist angles ranging between 1° and 2°. This is attributed to the increased population of the DOS near the Fermi level calculated in this range. Interestingly, within the same twist angle range, the fraction of the applied potential found to be confined in the EDL was increased (i.e., lower voltage drop in the twisted graphene bilayer compared to the electrolyte side), which in combination with the increase in CQ highlights the fact that the introduction of flat bands can promote a bulk metal-like behaviour in low-dimensional electrodes. Furthermore, examination of the real space distribution of the electronic states reveals that in the ‘magic angle’ of 1.1° the local DOS near charge neutrality is strongly localized at AA sites, whereas much lower values are calculated at AB/BA or SP stacking configuration sites. This finding was strongly observed in the significantly increased CQ values (by an average factor of ca. 4) over AA sites compared to those determined for the corresponding AB/BA sites.
Following the above discussion on CQ and its calculation using electronic structure theory, it becomes evident that an unambiguous and direct relation between theory and experiment is yet to be established. From the experimental point of view, the uncertainty associated with the accurate independent determination of CH (even at high electrolyte concentrations) renders its deconvolution (see eqn (28)) from the experimentally recorded total capacitance of the interface (see Section 2.4) at best highly approximate, if not unreliable. Commonly used assumptions considering the invariance of CH on electrode material (e.g., using CH values determined at arbitrarily chosen metal electrodes, such as Pt and Au) and/or electrolyte are far from realistic and need to be revisited. Consequently, obtaining CQ directly from experimental electrochemical data becomes a rather challenging task. On the other hand, the lack of a universally accepted computational approach for the theoretical calculation of CQ, free from approximations such as the frozen bands approximation, and from idealized (often non-realistic) models, as well as from the inherent limitations in commonly adopted assumptions regarding the complete description of CH where its variation with applied potential and electrolyte identity is considered, hinders the correlation of theoretical findings with experimental data. In this respect, a complete understanding of the EDL at the graphene/aqueous electrolyte interface would require the development of new methods where theoreticians and experimentalists work in parallel.
2.3 Computational methods to model carbon/electrolyte interface
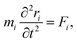 | (31) |
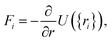 | (32) |
| U({ri}) = Ubond({ri}) + Uelec({ri}) + ULJ({ri}). | (33) |
All non-bonded interactions that are not considered to be electrostatic are treated as a van der Waals interaction in the classical FF. These essentially approximate the many-body electron exchange and correlation interactions that give rise to the dispersive, repulsive, and inductive forces. In many popular MD force-fields, van der Waals interactions are modelled by the Lennard-Jones (LJ) 12–6 potential,
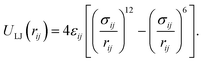 | (34) |
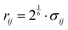 between the two atoms.
between the two atoms.
In the simulations of solid/electrolyte interfaces, one of the key interactions that governs the behaviour of ions and molecules at the interface is the attractive interaction induced by the redistribution of the electronic density within the surface and that gives rise to the double layer in the solution side mentioned in the Introductory part. The nature and strength of this interaction is determined by the surface polarizability and is a purely quantum mechanical effect. Over the years, methods to include this polarization mediated surface stabilization implicitly or explicitly into classical models have been developed. In the first case, the procedure involves the reparameterization of the Lennard-Jones non-bonded parameters σij and εij using the free energy of adsorption obtained from quantum chemical calculations.51
Beyond an implicit description of the induced polarization captured in the pairwise non-bonded Lennard-Jones potential, several methods exist which account for the atomic polarization explicitly. Perhaps foremost of such methods are polarizable force fields (PFF), of which there are three leading flavours: (i) induced point dipoles, (ii) fluctuating charges and (iii) Drude oscillators.52–55 Of these, in the modelling of graphitic surfaces the Drude oscillator model has found use in the computation of the induced polarization in the surface carbon atoms.56–59
In the Drude oscillator approach, each atomic polarizability, α, is modelled by tethering a Drude particle to the nuclear coordinate. The Drude particle is massless and carries a fraction of the atomic partial charge qD; in this way, the partial charge of the atom is given by q − qD. The Drude particle is bound to the atom via a harmonic potential with a force constant kD. This is a universal force constant for all atoms, which is selected such that the distance between any atom and its Drude particle is always less than any interatomic distances. In the absence of any external electric field the Drude particle oscillates around the position of the atomic coordinate. However, in the presence of a field, E, for instance the one that arises from the electrostatic potential of other atoms, the Drude particle instead oscillates around position r+d, where r is the atomic coordinate and 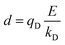 is a small displacement. On this basis, it is possible to define the induced atomic dipole
is a small displacement. On this basis, it is possible to define the induced atomic dipole 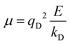 and atomic polarizability
and atomic polarizability 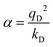 .
.
The addition of the set of Drude particles to the atoms gives rise to a FF of the form,
| U({ri},{d}) = Uself({d}) + Ubond({ri}) + Uelec({ri},{d}) + ULJ({ri}), | (35) |
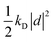 otherwise known as the self polarization, Ubond is the standard intramolecular potential arising from the bonds, angles and dihedrals, Uelec describes the Coulomb potential between atom pairs, atom-Drude particle pairs and Drude particle pairs and ULJ is the Lennard-Jones non-bonded potential. At each time step, each of the Drude particles should be first shifted to their local potential energy minima, which then allows for the self-consistent field computation of the forces acting on the atoms in the Born–Oppenheimer approximation. The computational feasibility of optimizing the positions of each Drude particle at each time step is often questionable. Instead, a viable alternative, which approximates the potential energy surface, is to afford each of the Drude particles a fraction of the atomic mass and kinetic energy through extended Lagrangian mechanics. This allows for the treatment of the motion of the Drude particles on an equal footing to the atomic nuclei via an additional thermostat with temperature set to T* and the condition that T* ≪ T. In this regime the Drude particles only carry a small kinetic energy that updates their positions in accordance with the thermalisation of the nuclei.
otherwise known as the self polarization, Ubond is the standard intramolecular potential arising from the bonds, angles and dihedrals, Uelec describes the Coulomb potential between atom pairs, atom-Drude particle pairs and Drude particle pairs and ULJ is the Lennard-Jones non-bonded potential. At each time step, each of the Drude particles should be first shifted to their local potential energy minima, which then allows for the self-consistent field computation of the forces acting on the atoms in the Born–Oppenheimer approximation. The computational feasibility of optimizing the positions of each Drude particle at each time step is often questionable. Instead, a viable alternative, which approximates the potential energy surface, is to afford each of the Drude particles a fraction of the atomic mass and kinetic energy through extended Lagrangian mechanics. This allows for the treatment of the motion of the Drude particles on an equal footing to the atomic nuclei via an additional thermostat with temperature set to T* and the condition that T* ≪ T. In this regime the Drude particles only carry a small kinetic energy that updates their positions in accordance with the thermalisation of the nuclei.
Also within a fully classical setup, the electrostatic response of an electrode surface to variations in the electrolyte configuration can be approximated using the constant potential method (CPM) as introduced by Siepmann and Sprik60 and further developed by Reed et al.61 The CPM leverages the fact that, as we discussed at length in Section 2, for perfect conductors the internal electric field is zero and the relative permittivity is infinite, thus the electrostatic potential experienced inside the electrode should be constant. To this end, in a CPM simulation the partial charges of the electrode surface atoms are variable and determined self-consistently at each time step to maintain an overall constant electrostatic potential throughout the electrode.
In practice, in the CPM the electrode charge density is typically described by a set of overlapping atom-centred Gaussian functions,
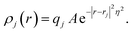 | (36) |
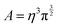 . The charge density arising from the electrolyte atoms is described by a set of point charges ρi(r) = qiδ(r − ri), yielding a functional form for the Coulomb energy based on the system total charge density (electrode + electrolyte),
. The charge density arising from the electrolyte atoms is described by a set of point charges ρi(r) = qiδ(r − ri), yielding a functional form for the Coulomb energy based on the system total charge density (electrode + electrolyte),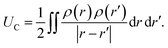 | (37) |
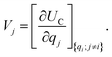 | (38) |
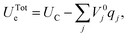 | (39) |
This minimization step has an associated computational cost reducing the scope of MD simulations with respect to the constant surface charge methods described above. Yet, the self-consistent determination of the set of qj, in direct response to the specific configuration of the electrolyte atoms at the interface facilitates simulations on the nm and ns length and time scales that include the effects of long-ranged redistribution of metallic electrode partial charges. The importance of these effects on the structural and dynamical properties of the system at hand can be used to determine computational accuracy-viability trade-offs.62 In addition, in contrast to each of the other methods discussed here, which are all performed at constant surface charge, the CPM lets the user set the electrode potential analogous to the situation in a potentiostatically-controlled electrochemical experiment.
Recently, hybrid quantum mechanical-classical molecular dynamics (QM/MD) methods have also emerged as an alternative to PFFs and the CPM as a way to incorporate the fluctuations of the electrode surface charge density in classical FFs.63 Unlike quantum mechanics-molecular mechanics (QMMM) approaches that target the properties of a quantum mechanical region embedded inside a classical electrostatic potential, these QM/MD schemes seek to describe the evolution of the classical system subject to the evolving quantum mechanical polarization of the surface.
QM/MD approaches directly couple electronic structure theory calculations of the electrode surfaces to the classical evolution of the electrolyte. As shown in Fig. 2, this is achieved by means of an iterative procedure that makes calls to QM and MD calculators. Firstly, for a given electrode–electrolyte configuration, the electrolyte coordinates are transformed to a set of point charges {qi}, these form the background electrostatic potential for the QM calculation. The QM calculation is performed considering only the electrode atoms explicitly, with the surface electron density distribution optimized according to the background electrostatic potential. In the second step, through post-processing and decomposition of the electron density, a set of atomic charges are computed that constitute the updated partial charges in the classical FF. This means that the polarization mediated interactions are captured inside the Coulomb potential of the MD steps, other non-bonded interactions such as van der Waals and London dispersion interactions remain treated in a pairwise manner via a Lennard-Jones type potential as described by eqn (34). It should be noted that this carries the implication that classical force-fields that parameterize the polarization mediated interactions, such as Williams et al., cannot be combined with the QMMD approach due to a double counting of this interaction. Evolving the entire system in time, subject to the QM partial charges, via MD establishes a new configuration for the step one.
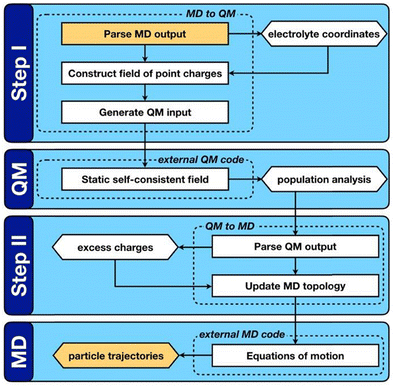 | ||
| Fig. 2 Reprinted (adapted) with permission from ref. 63. Copyright 2020 American Chemical Society. Schematic representation of the QM/MD workflow. Key computable quantities are represented by hexagonal boxes and square boxes represent computational processes. The two boxes coloured gold link sequential iterations. | ||
QM/MD approaches benefit from several advantages, the in situ calculation of the electronic structure provides access to the electrode band structure, density of states and electron density distribution in the presence of electrostatic potential arising from electrolyte configuration. While there is no formal quantum mechanical operator for defining the atomic electronic occupations, the distribution of the atomic charges can be grounded in charge partitioning schemes within electronic structure theory. Therefore, this method does not require the electrode to be metallic, i.e. the QM/MD approach (unlike the CPM) can equally treat semi-metallic or semiconducting electrodes such as those made of bulk carbon materials and graphene. The procedure is however more computationally intensive than standard MD simulations due to the frequent need for QM calculations to update the surface charges. The increase in computational demand can be mitigated by adopting an analytical description of the surface polarization in the form of a so-called “machine learning model”. To this end, our group has recently developed a procedure to train a multi-input multi-output neural network that treats the surface polarization as a discrete classification problem. The procedure is generic and introduces the electronic polarization into classical Molecular Dynamics (MD) force fields using a hybrid pairwise-machine learning force field. Assuming a good training set of data is available, the Neural Network Molecular Dynamics (NNMD) simulations can be deployed to obtain results comparable to those obtained by the QM/MD simulations but at computational complexity of a standard MD simulation.
DFT is underpinned by the fact that for any given system of interacting electrons which exist in an external potential arising from the coordinates of the atomic nuclei, the ground-state total energy has a functional form expressed in terms of the ground-state electronic density. This dependency of the energy on the electronic density, rather than the many-body electronic wavefunction, is advantageous because it drastically reduces the complexity of the problem to be solved. Formally, DFT is an exact formulation for the ground state energy, however, in practice solutions of the Kohn–Sham equations require the introduction of approximations since the total energy functional remains unknown.67,68
The formulation of Kohn–Sham DFT relies on the two Hohenberg and Kohn theorems (1964),69 the first of which legitimises the use of the electronic density as a variable by proving there is a one-to-one correspondence between the external potential and the electronic density. The second theorem provides a variational principle for the ground state energy. Thus, together these two theorems rewrite quantum mechanics not as a Schrödinger equation, but instead as an exact variational principle of the electronic density. The issue is that the functional is not defined. Kohn and Sham introduced a practical approach to solve the energy functional introducing a set of auxiliary non-interacting electrons, these exactly reproduce the ground state electronic density of the fully interacting system. This leads to the definition of a set of self-consistent single particle equations, known as the Kohn–Sham equations,70
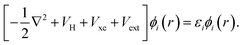 | (40) |
The Hartree potential which accounts for coulombic electron–electron interactions takes the form,
while the quantum mechanical electron–electron interactions are grouped into the exchange correlation potential, whose functional form is not known, but may be expressed as the variation of the exchange–correlation functional, Exc[n], with respect to the density,
As a result, to perform practical simulations within DFT, approximations to Vxc must be introduced. In fact, many approximations to the Vxc have been introduced over time; a popular library of exchange–correlation potentials adopted by many of the leading DFT software packages boasts ∼400 different functionals as of 2018.71,72 Approximations to the Vxc can be classified into families, and these families increase in complexity. The simplest form for Vxc is the Local Density Approximation (LDA), whereby the value of the Exc at a given point in space depends on the value of the density ELDAxc = ELDAxc[n]. The description is improved by introducing a dependence of Exc on the gradient of the density, in the so-called Generalized Gradient Approximation (GGA) EGGAxc = EGGAxc[n,∇n]. Meta GGAs (mGGAs) extend this trend, incorporating a dependence of Exc on further derivatives of the density and on the kinetic energy density EmGGAxc = EmGGAxc[n,∇n,∇2n,τ] and are increasing in popularity.
A different approach to approximating Vxc is to mix a fraction of Hartree–Fock (HF) exchange into the energy functional. This can be advantageous because HF theory treats the exchange interaction exactly,
Within various approximations of the Vxc, solution of the Kohn–Sham equations yields the self-consistent electron-density. Decomposition of the electron density, via charge partitioning schemes,73–77 can provide information on the polarization of the electrode surfaces and charge-transfer between the ions, molecules and the surface. Furthermore, the electronic density of states (DOS) and band structure are typically readily available from the ϕi(r) and εi. Of particular importance for the calculation of graphene electrodes is the computation of the DOS from DFT,
While DFT based simulations provide insight not obtainable from classical simulations, they are significantly more computationally demanding than any of the other MD methods described above. This is due to the fact that formally DFT scales as the third power O(N3) of the size of the system. In routine application, these are limited to systems containing several hundreds of atoms and therefore miss length and time scales appropriate for a wide range of thermodynamic and kinetic properties of the electrode interface.
2.4 Electrochemical techniques for the study of the EDL
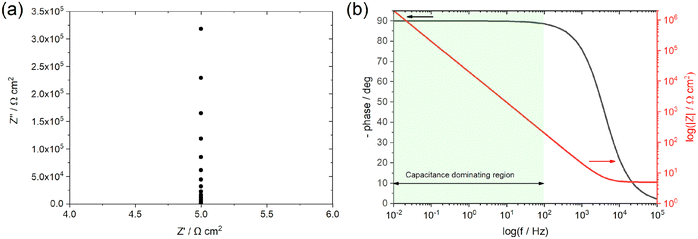
The electrochemical study of the EDL at the interface between solid electrodes and various electrolyte media, has primarily relied on the investigation of the total capacitance of the interface with respect to the applied bias. Such studies are performed under equilibrium within a potential window where no faradaic reactions occur, that is the interface is considered as ideally polarizable. The individual capacitive contributions of the phases are deconvoluted and subsequently used for the determination of various thermodynamic and electronic parameters, based on the phenomenological models described earlier (see Section 2.1). The main techniques implemented for the experimental determination of the capacitance of the interface are electrochemical impedance spectroscopy (EIS), cyclic voltammetry (CV) and galvanostatic charge/discharge method (GCD).EIS measures the total impedance of an electrochemical system by applying a periodic perturbation signal of small amplitude, superimposed on a constant DC potential pulse (input signal) and recording the current through the cell (output signal). Both signals are periodic functions of time and are presented in the frequency domain by means of a Fourier transform. This is in contrast to the classical electrochemical techniques where the measured parameters such as current, charge and potential are presented as functions of time.
In the simplest case of a purely capacitive interface (also known in the literature as a blocking electrode), the AC response of the system can be represented by the electrical analog of an Rs,e − Ctotal connection in series, where Rs,e is an ohmic resistor related to the combined contributions of the electrolyte resistance and the electronic resistance of the cell components (i.e., electrical connections, electrode resistance, etc.) and Ctotal a capacitor resembling the total capacitance of the interface. The total impedance of such a system in the frequency domain and in rectangular form is given by,78
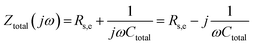 | (41) |
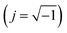 . It is obvious that the total reactance of the system is solely attributed to the capacitive element and thus Ctotal can be easily determined at each applied frequency by the experimental values of the imaginary component of the total impedance,
. It is obvious that the total reactance of the system is solely attributed to the capacitive element and thus Ctotal can be easily determined at each applied frequency by the experimental values of the imaginary component of the total impedance,  , through the relation,
, through the relation,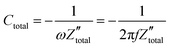 | (42) |
In most practical cases, the capacitance of the system does not display an ideal behavior and hence cannot be represented by the simple model described above. The origin of this deviation arises from the presence of frequency dispersion effects. Typical phenomena leading to frequency dispersion are (i) the dispersion of time constants and (ii) kinetic dispersion effects.79 The former is attributed to distributions of time constants along either the area of the electrode (2D) or along the axis normal to the electrode surface (3D), both resulting due to a non-uniformly active electrode area. In the second case, the dispersion arises because of the slow adsorption processes of ions and/or impurities (most often neutral molecules) on the surface of the electrode. In systems displaying frequency dispersion, the classical capacitor is replaced by the constant phase element (CPE) whose impedance is given by the formula,79
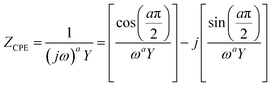 | (43) |
Orazem and co-workers have developed a graphical approach to calculate the total capacitance of the interface for systems exhibiting frequency dispersion effects.80 Based on this approach, the value of the constant phase exponent, a, is determined by the slope of the 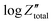 vs. log
vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f plot and the effective capacitance, Ceff, is then calculated at each frequency using the following equation:
f plot and the effective capacitance, Ceff, is then calculated at each frequency using the following equation:
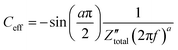 | (44) |
CV is a non-steady state potentiodynamic electrochemical technique, which is a powerful method of studying the various physicochemical processes occurring at the electrochemical interface. It involves the application of a continuous triangular DC potential pulse versus time. During the experiment, the potential is swept linearly within a range where electrode reactions occur and subsequently the direction of the scan is reversed. In this way, the charge transfer reactions occurring at the electrode are probed during the first potential ramping, while the stability and nature of the electroactive species formed at the immediate vicinity of the electrode are also investigated upon changing the direction of the scan. In general, the response is presented as a plot of current (or current density, jg, i.e., current normalized per the nominal surface area of the electrode) versus the applied potential. The controlled parameters during a CV measurement are the potential limits, the direction of the scan, the potential scan rate and the number of potential cycles.
Complementary to the study of charge transfer processes, CV can be also used for the determination of the capacitance of the interface. The approach is based on the linear dependence of the capacitive current density, jc, on the potential scan rate, ν, according to the formula,63–65
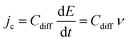 | (45) |
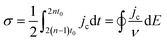 | (46) |
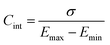 | (47) |
Finally, for applications in energy storage systems, the GCD method is most often used to calculate Cint. The latter can be directly related to the overall performance of the device and hence is preferred over Cdiff. The method measures the potential of the electrode under the application of a constant current pulse for multiple consecutive cycles. Cint is determined from the charging and discharging currents using the following formula,91
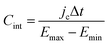 | (48) |
3. Review of the existing capacitive data obtained from experimental and computational studies
3.1 Experimental data on the graphene–electrolyte capacitance
Above we have outlined the classical and computational approaches to the electrical double layer, and the experimental methods used to interrogate the double layer, we now consider some of the experimental studies relating to the capacitance of the graphene/electrolyte interface, in particular. This interface has attracted considerable attention over the past decade or so, for a number of reasons. Graphene is the thinnest possible electrode material, thus from a “device” perspective, it should offer a route to maximise the gravimetric energy density (energy per unit mass) stored in a capacitor based on carbon electrodes. It should be noted that virtually all commercial supercapacitor devices are currently based on high surface area carbon materials, usually derived from activated carbon. The two-dimensional nature of graphene also raises interesting questions of a more fundamental nature, for example how does the capacitance of the material evolve with thickness? What effect, if any, does the adsorption of different ions have on the capacitance of graphene? Given that in any real device, graphene would be supported on a substrate, what effect does substrate identity or roughness have on the capacitance of the graphene-based structure? From a computational perspective, the smaller number of atoms in a “slab” of graphene also make it an attractive target. These factors, coupled with the general interest in graphene as a material, and in electrochemical energy storage as an approach to increase the uptake of renewable energy, have led to an avalanche of papers on the use of graphene in capacitive energy storage (the search term “graphene and supercap-” finds more than 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 papers on the Web of Science database). Clearly it is impossible to produce any kind of sensible review of this enormous body of literature, but a few salient points should be noted.
000 papers on the Web of Science database). Clearly it is impossible to produce any kind of sensible review of this enormous body of literature, but a few salient points should be noted.
The majority of these works use graphene derived from solution-based chemical methods (such as the Hummers' method92), meaning that the carbon material is more properly termed graphene oxide, or at least reduced graphene oxide, in most cases. Moreover, it is difficult to realise a practical device consisting solely of graphene sheets, therefore it is also very common for the graphene to be used as a composite material with (for example) conducting polymers such as polypyrrole93 or metal oxides such as manganese oxide.94 Of course, ternary structures can also be produced by simultaneously combining graphene with a metal oxide and an appropriate polymer.95 Most of the aforementioned studies are “top-down”, i.e. a relatively complex electrode material is formed, its (apparent) capacitance is measured, and some ex situ structural studies are performed in an attempt to justify the high gravimetric capacitance that is generally reported. How these capacitances relate to microscopic process at the electrode/electrolyte interface, given the complex physical and chemical structure of the material, is usually unclear. One recurring difficulty is the assessment of the electrochemical surface area of the porous electrode structure that is normally required for supercapacitor applications. Gas sorption measurements can give a guide, but are likely to overestimate the area exposed to the electrolyte, hence capacitance values are commonly quoted gravimetrically (i.e. per unit of electrode mass); where areal values are quoted, it is not always clear how the area has been determined. Some more discerning works have recognised this problem, and have offered routes to resolve it, further recognising that potential-dependent ingress of ions to smaller pores is likely to occur, i.e. the effective surface area is likely to be potential-dependent in many cases.96 A much more promising approach, therefore, is to employ well-defined graphene structures, such as those formed by chemical vapour deposition methods, where a defined geometric area (and thickness) of the sample can be exposed to an electrolyte solution and the capacitance of the electrode (or electrodes in the case of a “device”) is measured. Unfortunately, there is a relative paucity of such studies in the literature, however the key points from some of the more important studies of this type will be summarised here.
The most prominent early paper on the capacitance of monolayer graphene was the report from the laboratory of the late N. J. Tao,97 who measured the capacitance of the graphene/aqueous electrolyte (NaF) and graphene/ionic liquid (1-butyl-3-methylimidazolium hexafluorophosphate) interfaces. The authors isolated the quantum capacitance term, which can be equated with CSC in the bulk material (see eqn (22)), by assuming that the solution components of the capacitance (CH at high ionic strengths) would be identical to those at the Pt/aq and Pt/ionic liquid interfaces. This is a questionable assumption, since it assumes that the organisation of the solvent molecules and ions are identical in both cases. Notwithstanding this assumption, the authors obtained experimental values for the quantum capacitance of graphene, which were of the order of 7–10 μF cm−2, and could only be fitted to theory with the introduction of an effective charge carrier term due to charged impurities imparted by the substrate (oxide-covered Si).
An interesting follow-up to the work of Tao, came from the group of Ruoff, who reported the capacitance of monolayer CVD graphene where either both sides, or only one side, of the sample were exposed to an aqueous electrolyte (H2SO4).98 The results were interpreted within the same framework as developed by Tao et al.,97 although capacitance could be interpreted without recourse to the “charged impurities” invoked by Tao. Whether this is because of the difference in substrate, or because of a difference in sample preparation, is not clear at present. In fact, the article is more notable for what it omits: the two-sided configuration developed could provide extremely interesting insights on the screening of electrolyte by different thicknesses of graphene, or the effects of ion size on interactions “across” the graphene but the authors did not extend their study to these areas. The difficulties in obtaining consistent results for nominally the same CVD graphene configuration is illustrated by a report using CVD graphene with a polymer gel electrolyte, where an areal capacitance of 80 μF cm−2 is quoted.99 The relatively low areal capacitance of individual graphene sheets, and the propensity of multiple graphene sheets to re-aggregate led to the development of more complex growth strategies where, for example, vertically-oriented graphene sheets were grown from conducting substrates.100 These approaches, while interesting from the perspective of practical devices, led once again to difficulties in understanding the origin of the higher capacitance observed, since the geometries of the electrode structures are irregular, and the presence of graphene “edges” will substantially increase the capacitance.101 The subsequent trajectory of the literature has been to focus on the preparation of increasingly complex structures (both physically and chemically), although a few papers have retained a focus on the capacitance of well-defined samples. For example, Chen et al. explored the effect of nitrogen-doping on the capacitance of (predominantly monolayer) CVD graphene in an aq. KCl solution. The doping imparted by the introduction of N atoms was found to increase the capacitance of the sample, particularly at potentials negative of the PZC and yielded a positive shift of the PZC.45
More recently, however, there has been a renewed interest in more “fundamental” studies of the capacitance of graphene electrodes, with a focus on the effects of ion and substrate identity. For example, electrochemical impedance spectroscopy and quartz crystal microbalance methods have been confined to interrogate the double-layer formed with ionic liquids (either neat, or dissolved in acetonitrile) at monolayer graphene electrodes, prepared via CVD.102 Specific adsorption of the imidazolium cation is the notable finding of this work, attributed to π–π interactions between the graphene and the cation. The “substrate effect” has also been explored in recent literature: Kwon et al. deposited CVD graphene on substrates with a range of hydrophobicity/hydrophilicity and found a trend of decreasing capacitance with increasing water-in-air contact angle.103 This was attributed to change in the local water structure, as expressed through the local relative permittivity, due to the interaction of the interfacial water. Unfortunately, these experimental findings are completely at odds with an earlier molecular dynamics study, which had suggested that the capacitance of monolayer graphene would be largely invariant with substrate hydrophobicity.104 The computational work did recognise that the differences in interfacial water ordering would be anticipated but predicted that these effects would be offset by changes in the ion distributions within the Helmholtz layer.
In summary, the complexities in the preparation and structure of many solution-processed graphene materials, including composite materials, makes it very hard to compare capacitance data between works. Factors such as sample thickness and porosity for these “macroscopic” electrodes are often not discussed, and even where they are, it is not straightforward to correct for these effects to allow for comparison between samples. Greater insight can be obtained by focussing on well-defined samples (prepared using either CVD or mechanical exfoliation) where the surface area exposed to the electrolyte and graphene thickness is accurately known.
As we have seen above, there is still some further work required to give convergence between experimental works on the capacitance of graphene and atomistic simulations. One important point, which is not always appreciated in the computational literature, is that any electrode/electrolyte interface has a finite range of stability, i.e. a so-called “potential window”. Excursions above and below this potential window will lead to oxidation and reduction processes, respectively, which are often irreversible. These processes change the composition of the cell, which is undesirable for a device meant to be functioning solely as a capacitor. Furthermore, such processes could lead to catastrophic breakdown of the device because a conducting material can be irreversibly oxidised, resulting in material loss due to electrodissolution,105–109 formation of a poorly conducting film in the case of a metal electrode,110,111 or the evolution of gaseous products, e.g. CO2, in the case of a carbon electrode.112,113 The potential window of each interface is governed by the electrochemical stability of the least stable component, from the electrodes, solvent and electrolytic salt. Water has a particularly limited range of stability, both oxidative and reductive: the thermodynamic limit of water's stability gives a potential window of 1.23 V,9,114 although this is extended by kinetic factors due to the slow electrolytic breakdown of water on carbon electrodes in particular.105,112,115 For this reason, organic-based electrolytes are used in commercial supercapacitors, with acetonitrile combined with tetraalkylammonium salts of anions such as tetrafluoroborate, being a common choice. This solvent/salt combination, coupled with activated carbon electrodes, gives an operational voltage of 2.7 V for commercial supercapacitors,116 although research is based on improving the stability of the components to increase this voltage and thus enhance the energy density of the devices.117
The voltages quoted above should be borne in mind for computational studies. Occasionally, substantially higher voltages are mentioned in the literature,118 but these will lead to cell breakdown, at least for currently known electrode/electrolyte combinations and are therefore simply “unphysical”. One interesting, but unresolved, area of research is how the electrochemical stability of graphene compares with that of the activated carbons used in current commercial devices. In principle, this factor should be easier to determine than it is with activated carbons, due to the heterogeneity of the latter.
3.2 Computational studies on the double layer structure and ions adsorption mechanisms
The graphene/electrolyte interface is also more amenable to accurate simulation, than the physically and chemically complex activated carbon materials. Simulations provide the bulk of the understanding we have currently about the atomic scale properties of the graphene/electrolyte interface. The graphene–water interface has been intensively investigated119 in the context of both MD56,120–126 and ab initio simulations.127–139 Here we focus on the electrochemistry of the interface, which necessarily involves the physisorption and chemisorption of ions from the aqueous solutions onto the electrode surface. The addition of ions, and the inclusion of surface charge, changes and increases the complexity of the problem at hand; in MD simulations the additional ion–water and ion–surface interactions are a delicate balance, whereas in DFT simulations, the trade-off between chemical accuracy and computational viability becomes ever more important.Chialvo and Cummings employed constant-pressure constant-temperature (NPT) MDs to characterize the graphene–electrolyte interface for cations of different ionic charge and radius and subject to confinement.140 In their work they considered finite, free standing graphene sheets immersed in both pure SPC/E water (simple point charge model with rigid bonds) and aqueous 2 M LiCl, BaCl2 and YCl3 solutions. The C atoms within graphene were treated as non-polarizable Lennard-Jones spheres using Steele's parameters,141 with C–O and C–ion interaction potentials determined via Lorentz–Berthelot combining rules.
Plots of the atom-resolved density distribution along the direction of the surface normal reveals that for each LiCl there is preferential adsorption of the cation closer to the surface than the Cl− anion. This gives rise to the characteristic double layer structure. In addition, an important feature that arises from Chialvo and Cummings’ simulations is the retention of the ion hydration shell in the adsorbed configuration. Their density plots show that oxygen atoms belonging to the SPC/E water molecules always adsorb closer to the graphene surface than the Li cations. The adsorption of the various cations in their fully hydrated configurations leads to so-called “specific ion effects”, where the smaller Li + ion has a strong adsorption peak 0.4 nm from the surface, while larger Ba2+ and Y3+ ions behave differently. The intermediate Ba2+ ion has a similar, but significantly less intense, adsorption peak at 0.55 nm from the surface and a strong adsorption at 0.8 nm. Finally, Y3+ being the largest ion investigated has a first adsorption peak at 1.5 nm, thereby inverting the charge density distribution of the double layer by residing further away from the graphene than the Cl− counterion.
Recognizing the importance of surface polarization effects, and in particular the effect of cation–π orbital stabilization on the renormalization of the graphene–ion interaction potential Williams et al. employed DFT simulations in order to parameterize a set of Lennard-Jones parameters suitable for Li+, Na+, K+, Mg2+ and Ca2+ chloride salts adsorbed on a graphene layer.51
To model the interactions between ions and graphene Williams et al. used a hexagonal graphene flake, terminated with hydrogen atoms at the edges and a single cation adsorbed directly in the centre of the flake. To account for the role of the water molecules, they employed an implicit solvent model based on the conductor-like polarizable continuum model (CPCM), with modified cavity radii optimized to match experimental hydration free energies. Inspection of the DFT adsorption free energies suggests that in the aqueous phase, all cations considered, and the chloride anion, prefer to adsorb on the surface rather than remaining in the bulk phase. In the gas phase, Williams observed a clear trend with the ion adsorption energy becoming increasingly negative with smaller ionic radii, which suggests more favourable adsorption. In the aqueous phase adsorption energies are significantly damped, with no identifiable trends in ionic radius. The divalent ions Mg2+ and Ca2+ have stronger adsorption energies than Li+, Na+ and K+, and Cl− has a significantly less negative adsorption energy than each of the cations.
Based on the DFT adsorption profiles, Williams et al. derived a set of Lennard-Jones parameters for MD simulations by matching adsorption free energies computed from MD potential of mean force142 calculations to the optimized DFT adsorption energy. As such, the DFT adsorption energy for each specific ion was rigorously computed by employing an implicit solvent model143 which was modified to match the experimental free energy of hydration for each ion.51
Subsequent MD simulations of an electroneutral infinite graphene sheets in contact with 1 M electrolytes for each of the cation chloride salts permitted inspection of the interfacial structuring of the ions. Williams et al.'s force field predicts that monovalent cations always adsorb closer to the surface than the Cl− ions and that in the adsorbed configuration, Na+ and K+ are partially dehydrated suggesting direct adsorption of the ion on the surface. In contrast to the monovalent ions, the divalent Mg2+ and Ca2+ are found to reside further from the surface than the Cl−, which contributes to them retaining the full hydration shell.
Several groups have adopted this parameter set to investigate different facets of the aqueous ion–graphene interface.144–146 For instance, Dočkal et al. have examined the water and ion structural and diffusive properties within the interfacial layers. They found strong, densely packed layered structure up to 1 nm from the surface, and that the cations act as structure makers. These structure makers are found to slow the diffusion coefficients of water molecules with increasing salt concentration.145 Within the interfacial layers where the ion concentration is highest, water molecules are most greatly slowed. Very recently Dočkal et al. also considered the cation behaviour on charged graphene sheets,146 in summary, while the long-ranged structuring of the water layers are largely unaffected by the charged state of the electrode, locally the hydration shells of the Na+ and K+ ions are found to be disrupted. Through the calculation of the screening factor, counterintuitively it was found that the concentration of Cl− ions at the negative electrode increases due to the increase in concentration of positive ions (and vice versa) creating a surplus of ions. This surplus of ions can lead to a situation where water dipoles are oriented with the dipole pointing (in the conceptually opposite direction) at the surface. Finally, Finney et al. employed the NaCl parameters to investigate both surface charging and ion concentration effects on the computed electrode capacitance.144 In particular, they also found that the Cl− ion, has an increased concertation close to the negative electrode, forming a charge compensation layer. Finney et al. were able to uncover a switch in this EDL charge screening behaviour that occurs as the concentration exceeds 0.6 M. Above 0.6 M alternating layers of positive and negative ions form in decreasing concentration until the surface charge is completely screened. Finally, they subtracted the computed double layer differential capacitance, obtained through eqn (18), from the measured specific electrode differential capacitance to gain insight on the role of the quantum capacitance. Finney et al. conclude that for graphitic electrodes close to the potential of zero charge, the relative magnitudes of the CEDL and CQ are the same; as such they point out that even at moderate concentrations the capacitance does not report directly on the electrode density of states.
Prior to their work on the behaviour of ions at the graphene–electrolyte interface, Misra and Blankschtein developed a polarizable force field capable of capturing the self-consistent polarization of the surface C atoms based on the Drude oscillator approach.56 In the design of their force field, Misra and Blankschtein began by considering the adsorption of monomeric water molecules onto polyaromatic hydrocarbons of increasing sizes (C6H6, C54H18 & C96H24) via ab initio simulation methods. By benchmarking against Coupled Cluster Singles Doubles and perturbative Triples (CCSD(T)) and quantum Monte Carlo approaches, they determine that the water molecule binding energy obtained at the symmetry adapted perturbation theory (SAPT0/jun-cc-pVDZ) level could be reliably extrapolated to the case of infinitely periodic graphene. Decomposing the SAPT0 total energy into its constituent contributions, Misra and Blankschtein parameterized a classical water–graphene LJ potential according to the quantum mechanical charge penetration (charge transfer), electron exchange and dispersion interactions. It is worthwhile to highlight that they removed the contributions due to the charge–multipole interactions in polyaromatic hydrocarbons, that are known to lead to under- and over-binding in periodic graphene.63 They surveyed several different adsorption orientations for the H2O molecule, in spite of the fact that the SAPT0 predicted a larger binding energy for water molecules with 1 or 2 hydrogen atoms pointing towards the surface, ensuing MD simulations (both with nonpolarizable and polarizable carbon atoms) instead indicated that the stabilization brought about by maximizing the interfacial hydrogen bonding network leads to water molecules that lie parallel to the surface. This finding is consistent with the latest experimental surface sensitive-spectroscopic measurements.147 Consequently, the LJ potential was parameterized according to the adsorption profile for the parallel (tangential in their work) configuration.
The contribution to the water molecule binding energy due to polarization effects can be separated into two components: (i) the polarization of the carbon atoms in the graphene layer in response to the water molecule electric field and (ii) the induced polarization of the water molecules, Misra and Blankschtein employ the Drude oscillator model.56 They identify two parameters, αC; the static dipole polarizability of the C atoms and aC; the damping parameter for electrostatic interactions between the Drude particles and the nuclei introduced by Thole. These parameters can be used to build the dipole field tensor, T, associated with two interacting dipoles, μp and μq,
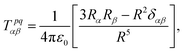 | (49) |
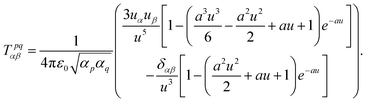 | (50) |
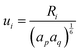 , while
, while 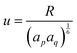 and αi is the dipole polarizability of the ith atom. The parameter a is the Thole damping parameter. By computing the induced polarization in a graphene cell, via the induced dipole moments of the C atoms and leveraging reported computed Berry's phase values for the out-of-plane polarizability α⊥ = 0.837 Å3 of a single graphene sheet and anisotropy ratio
and αi is the dipole polarizability of the ith atom. The parameter a is the Thole damping parameter. By computing the induced polarization in a graphene cell, via the induced dipole moments of the C atoms and leveraging reported computed Berry's phase values for the out-of-plane polarizability α⊥ = 0.837 Å3 of a single graphene sheet and anisotropy ratio 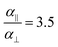 , Misra and Blankschtein derive αC = 1.139 Å3 and aC = 1.507 parameters for the Drude oscillators that exactly reproduce the polarizability tensor for a periodic graphene sheet.
, Misra and Blankschtein derive αC = 1.139 Å3 and aC = 1.507 parameters for the Drude oscillators that exactly reproduce the polarizability tensor for a periodic graphene sheet.
Comparison of the developed PFF with SAPT0 results revealed an underestimation in the computed induction energy of water molecules on the surface, but not with a Na+ or Cl− ion. The underestimation arises in the case of water due to quantum mechanical charge penetration (transfer) effects at close distances that cannot be captured classically. Instead, a refitting of the parameters αC = 1.80 Å3 and aC = 0.50 according to the SAPT0 induction energy yields a polarizable force field in excellent agreement with the ab initio results.
Turning to the polarization of the graphene by ions, Misra and Blankschtein applied their approach to the behaviour of SCN− ions at the graphene/electrolyte interface (Fig. 4).58 SAPT0 calculations carried out in vacuum indicate a strong adsorption of the ion due to local polarization of the carbon atoms. Parameterization of the (Drude oscillator model) and ensuing simulations of the SCN− electrolyte/graphene interface reveals that the strong polarization of the graphene by the SCN− is significantly dampened in the presence of water. The fields generated by the ions and the water molecules are found to destructively interfere, which leads to a water-mediated screening of the ion. Interestingly, analogous calculations using a static polarization model, with a specifically parameterized LJ potential, and surface charge distributions that do not change over time, fail to capture this water screening leading to an overbinding of the ion, a clear limitation of this static polarization. This ultimately leads to polarization results being equivalent to no-polarizations results, however, in the event that the screening by the solvent is reduced (i.e. in nanochannels, ion intercalation, nanotubes, etc.) these results will diverge and a dynamical polarizability will likely be required.
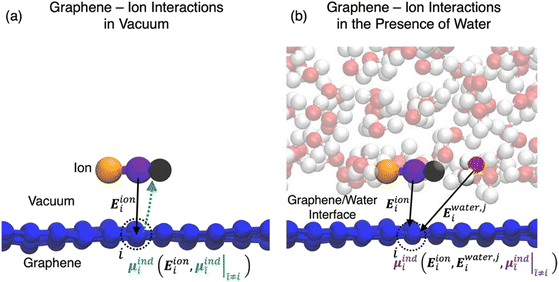 | ||
| Fig. 4 Reprinted (adapted) with permission from ref. 58. Copyright 2020 American Chemical Society. Schematics comparing the interactions of a SCN− ion with graphene in vacuum (shown in (a)) to the interactions in the presence of water molecules at the graphene/water interface (shown in (b)). As shown in (a), the electric field exerted by the SCN− ion in vacuum polarizes the carbon atoms in graphene (shown by the black solid arrow), which in turn exert back electric fields onto the SCN− ion (shown by the green dashed arrow). The induced dipole moment of carbon atom i in graphene, μindi, is a function of the electric field exerted by the SCN− ion and the electric fields from all of the other induced dipoles in graphene. On the other hand, at the graphene/water interface shown in (b), both the SCN− ion and water molecules exert electric fields, which polarize the carbon atoms in graphene. As an example, we show the electric fields exerted by the SCN− ion and a highlighted water molecule, j, on carbon atom i in graphene (shown by black solid arrows). The polarized carbon atom i, in turn, exerts back electric fields onto the SCN− ion and the water molecule (shown by the purple dashed arrows). Because μindi depends on both the electric field exerted by the SCN− ion and the electric fields exerted by all of the water molecules in the system, the graphene–ion and graphene–water interactions are therefore coupled. Color code: sulfur in SCN−: orange; carbon in SCN−: violet; nitrogen in SCN−: black; carbon in graphene: blue; oxygen in water: red; and hydrogen in water: white. The directions of the electric field vectors are for representation purposes; we adopt a sign convention which assumes the electric field vectors to emanate from a positive charge distribution. | ||
Most recently, Misra and Blankstein have extended their optimized Drude Oscillator approach to survey the properties of several different anions:59 SCN−, NO3−, Cl−, F− and SO42− that make up the Hofmeister series.148,149 These are ions that increase in hydration free energy moving from SCN− to SO42−, which leads to a decrease in protein solubility in solutions of those ions. As with their previous work, the focus is on the ion and water-dipole induced polarization effects on the carbon atoms in the graphene surface, and the ensuing feedback which governs the ion adsorption behaviour.
In the first instance, they consider the extremes of the Hofmeister series, the highly kosmotropic anion SO42− and the highly chaotropic anion SCN−. Static QM simulations, based on the SAPT0 approach, of a single ion adsorbed on the graphene surface in vacuum (note that graphene is modelled as a polycyclic aromatic hydrocarbon), indicate that both ions adsorb with a favourable negative change in the Helmholtz energy. Decomposition of the SAPT0 total energy suggests that the induced-polarization energy dominates the interaction between the ion and graphene. In addition, in line with the expected trend that the polarization energy varies with the square of the ion charge, the SO42− ion is found to adsorb with approximately 4× the energy of the SCN−.
Misra and Blankstein verified that their optimized Drude oscillator model can reproduce the results of the QM simulations in vacuum, and used this as a platform to investigate the effects of all of the ions in solution interacting with a periodic graphene layer. We note that these simulations are still carried out using a single ion, with the center of mass kept at fixed height above the graphene, but allowed to evolve in the in-plane directions. In solution only the chaotropic ions SCN− and NO3− are found to favourably adsorb on the surface, at approximately 0.35 nm; Cl−, F− and SO42− are instead all repelled from the graphene layer. Examination of the electric fields generated by the ions and water molecules moving in the vicinity of the surface suggests the formation of so-called molecular waves. These are formed from the ions and water molecules as they move over the graphene surface. The molecular waves interfere destructively to significantly reduce the polarization mediated stabilization (observed in vacuum). Consequently, Misra and Blankstein find that in solution the adsorption behaviour of the ions is instead dominated by the ion–water and water–water interactions, which explain the trends observed for adsorption of the Hofmeister series of ions. The interaction of the water molecules with the graphite and graphene dominates for small ionic concentrations, driving the wetting of the surface and thus potentially affecting the ions adsorption. Interestingly the investigations of the wetting phenomenon highlighted one of the major differences between graphene (i.e. one or few layers of one atom thick material) and graphite interfacial properties. While graphite, as any bulk material, has a well-defined water contact angle (WCA) in air, the graphene WCA changes depending on the nature of the supporting substrate and the number of graphene layers.126 Assuming there are no airborne contaminants affecting the surface wettability,150 experiments and simulations have indicated that the wetting of graphene depends on the wettability of the supporting substrate as the contact angle is affected by both the liquid–graphene and, due to the graphene angstrom-scale thickness, the liquid-substrate interactions.151–153 In some cases, this solvent-substrate correlation across the graphene layer not only affects the WCA154 but also the ions’ adsorption.
Pykal et al. employed a polarizable Drude oscillator model to inspect different graphene/electrolyte interfaces.155 In particular, they compared differently structured interfaces where graphene was in contact with (i) electrolyte on both sides (EGE), (ii) electrolyte and pure water (EGW) on different sides, and (iii) electrolyte and vacuum (air) (EGA) on different sides (see Fig. 5).
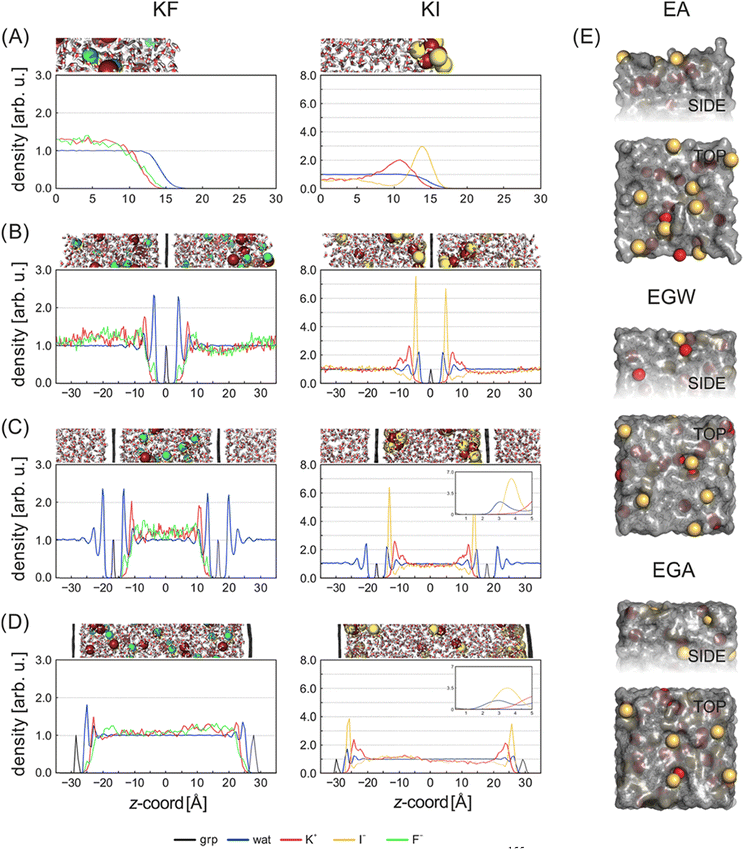 | ||
| Fig. 5 Reprinted (adapted) with permission from ref. 155 Copyright 2019 American Chemical Society. Axial density profiles for KF and KI solutions at (A) a simple EA interface and at (B) EGE (rigid graphene), (C) EGW (two thermal graphenes), and (D) EGA (left: rigid graphene; right: thermal graphene) interfaces (insets show nearest 5 region at the EGW/EGA interface). (E) Side and top views of ion arrangement in the interfacial region of an EA, EGW, and EGA interface in KI (in the latter cases, graphene is omitted for clarity). Coloring scheme: blue, water; black, graphene; red, potassium; green, fluorine; and yellow, iodine. | ||
The Drude Oscillator model they employ is adapted from the work of Ho and Striolo,120 with isotropically polarizable graphene. Furthermore, the Drude Oscillators are fine-tuned by means of the Thole parameter. In their work, Pykal et al. avoided salt precipitation by tuning the Thole parameter of the SWM4-NDP water156,157 to match the experimental osmotic pressures of the KF and KI solutions.
For the electrolyte, Pykal et al. investigated the behaviour of KF and KI solutions at the three differently structured interfaces (EGE, EGW and EGA). The concentration of these solutions was selected to be approximately 1.2 M; simulations carried out at 0.6 M were used to verify that there are no effects of the concentration on the ion properties at the interface. The KF and KI were chosen since the dissolved F− and I− ions exhibit qualitatively different behaviour at other interfaces (such as the electrolyte/air interface) due to the interplay between the adsorption and hydration free energies.
Across the different interfaces, the simulations of Pykal et al. suggest similar adsorption behaviour for H2O, K+ and the two different anions. As depicted in the bulk-normalized density plots of Fig. 5, the water adsorbs with characteristic two-layer structure, while I− always resides preferentially in the interfacial region and F− in the bulk. The different behaviour of the F− and I− can be understood from the fact that the hydration free energy of the F− ion is significantly more negative than the I− and that taking a F− from the bulk phase to the interface, thence removing water molecules from its solvation shells, is a net gain in energy.58 Both anions are found to have an adsorption peak closer to the graphene than cation K+, a result which is at odds with many of the other investigations carried out for neutral graphene–electrolyte interfaces.51,63,158 This could stem directly from the different (and modified) water model155,156 and specific ion parametrization157 or more generally from the use of Drude Oscillators to model the polarization.
The fine structure of the first few layers, closest to the graphene, is found to vary between models. On the one hand, the EGE and EGW models yield similar results, with a denser packing of the water molecules at the surface. On the other hand, the EGA model, has less dense packing on top of the surface. This difference is attributed to attractive dispersion interactions between the water molecules through the graphene sheet in the case of the EGE and EGW models. Interestingly, Pykal et al. highlight that the hydrophobicity of the graphene contributes to an effective shielding of ions from the surface. Ultimately this leads them to conclude that ion–ion interactions through the graphene layer do not take place, and an independent ordering of the ions is observed for all the systems.
We developed our QMMD approach and used it to investigate the behaviour of 1 M NaCl solutions in contact with (i) hexagonal graphene flakes whose edges are hydrogenated, and (ii) free-standing infinite graphene sheets. First, we quantified the magnitude of the polarization of the graphene flake in the presence of an ion by computing the surface Mulliken charges in response to a point charge fixed at different heights above the graphene layer. We carried out this analysis in vacuum at the DFT level (6-31G/B3LYP)159–161 and at the DFTB level (mio-1-1),162 leveraging the symmetry of the graphene flake to measure the redistribution of charge amongst the rings of atoms as depicted in Fig. 6.
 | ||
| Fig. 6 Reprinted (adapted) with permission from ref. 63 Copyright 2020 American Chemical Society (a) Geometry of the hexagonal C96 graphene flake; dashed red circles illustrate radially equivalent atoms at increasing distances r from the location of the point charge (black dot). (b) Plot comparing the DFTB (solid) and DFT (dashed) integrated Mulliken charges as a function of radius r and point-charge adsorption height d⊥ (q = −1.0 e). Vertical dashed lines mark the radii of the C atoms in the C96 flake. | ||
From this we observed a long-ranged redistribution of the Mulliken charges, which becomes stronger with the proximity of the charge to the surface. We were able to identify radial trends in the polarization state of the surface: (i) an accumulation region in the carbon rings closest to the adsorbing atom where there is an excess of charge density, (ii) a buffer region which is invariant to the presence of the ion and (iii) a depletion region defined by the rings furthest away from the adsorption site (and closest to the flake edges), which registers a loss of charge density. It is worth noting that the charge accumulation region can be as far reaching as three carbon bonds, which demonstrates the non-locality of the overall polarization gradient.
For dynamical investigation of the graphene-ion systems it is important that there is a smooth handshake between the QM and Classical parts of the simulations, in particular that the electrostatic forces acting on point charges due to the Mulliken charges are conserved when treating the electrostatic forces between the ions and the surface partial charges in the classical system. We verified from the derivative of the DFTB total energy,
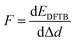 | (51) |
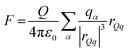 | (52) |
The method was applied to the case of 0.5 M and 1 M NaCl solutions in contact with the graphene flake, with a view to understanding the structuring of the cation and anion at the interface. Na+ cations were found to reside within the water layers closest to the surface, while Cl− tends to be in the bulk water. Decomposition of the non-bonding interactions in the classical force-field shows that for Na+ the attractive Coulomb interaction overlaps with the attractive part of the Lennard-Jones interaction profile, whereas for Cl− the two components always cancel out. These results suggest that cations may adsorb more favourably on graphene surfaces as has already been discussed in this section of the review. Concerning the local structure of the Na+ ion at the interface, the QMMD simulations revealed that the Na+ ions preferentially adsorb indirectly on the surface, that is with the full first solvation shell of surrounding water molecules. It is thought that this arises from the relatively strong hydration free energy of the Na+ ion, the non-bonded interactions between the ion and the surface are not strong enough to overcome the interactions between the water molecule and the ion and thus it remains hydrated.
Finally, we considered the effect of charging the graphene surface to see how this affects the ion adsorption properties; to this end, we considered an infinite graphene sheet. Negative charging of the surface was found to increase the density of Na+ ions in the water layers close to the interface, but not to induce dehydration of the ion. On the positively charged surface, the density of Cl− ions in the EDL is also found to increase, with the position of the main peak in the density profile relative to the graphene found to occur in the same place.
We further extended this work to consider different water models and a host of different ions pairs,40 namely the TIP4P-2005 water model163 that is known to best describe the interactions between graphene and water126 and the Madrid-2019 ions Li+, Na+, K+, Mg2+ and Ca2+.164 We considered the local adsorption properties for each of these ions on the infinite graphene sheet under neutral and biased (charged) conditions, the density profiles are reported in Fig. 7.
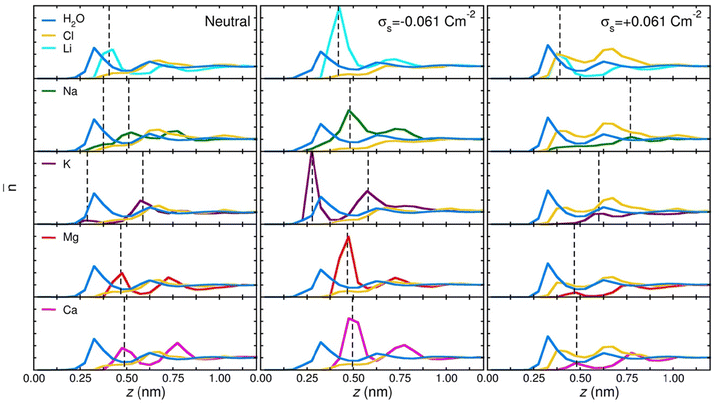 | ||
| Fig. 7 Plot of the bulk normalized densities along the surface normal for each of the different electrolytes considered for a neutral (left) and negative (centre) and positively (right) charged electrode. Vertical dashed lines denote the positions of the first cation adsorption peaks. Reproduced from ref. 40. | ||
Following on from our earlier work, we found similar properties for each of the ions when the surface is electroneutral, i.e. that cations preferentially adsorb closer to the surface than Cl− anions and that they retain their solvation shells adsorbing indirectly. However, owing to its comparatively low hydration free energy, upon negative charging of the graphene, the K+ cation is observed to lose one water molecule and directly adsorb to the surface approximately 0.5 nm closer than the neutral case. Investigation of the dynamical properties of the various ions revealed that the direct adsorption of K+ leads to a decrease in the in-plane diffusivity when the surface is charged,40 while for the other ions the diffusivity is relatively unaffected by the surface and the charged state.
Intuitively, it is reasonable to expect that the fundamentally different adsorption mechanism and dynamical behaviour of the K+ ion could lead to differences, sometimes referred to as specific ion effects, in the measured capacitance. Yasuda et al.165 have recently identified experimentally such phenomena on monolayer graphene on atomically flat Au(111) substrates. By using electrochemical techniques, in situ Raman spectroscopy and crystal truncation rod surface diffraction measurements, they show that K+ adsorption on graphene triggers electron doping with lattice expansion. The latter leads to a significant increase of the interfacial capacitance within the potential window where the adsorption process occurs. Our simulations however, revealed that the EDL contribution to the electrode integral capacitance is constant across the monovalent ions Li+, Na+ and K+, a feature we attribute to the fact that the potential drop, obtained from eqn (16), involves integration over the entire double layer and so long as the concentration of ions in the EDL is constant, then the Δφ could reasonably be expected to be constant also.
Colherinhas et al. made use of DFT simulations in order to understand how the adsorption of cations on the surface impacts on the electronic structure of graphene.166 They modelled graphene, in open boundary conditions which necessitates H-termination of the graphene edges, with circumcoronene and used the BLYP GGA exchange correlation potential167 and LANL2DZ Gaussian function basis set. Within this setup the so-called graphene exhibits molecular properties such as a finite energy gap between the Highest Occupied (HOMO) and Lowest Unoccupied (LUMO) Molecular Orbitals. Colherinhas et al. looked at the adsorption behaviours of single Li+, Na+ and Mg2+ cations in the absence of any solvent effects. They track the relative energetic alignment of the empty metal orbitals with respect to those of the graphene as a function of the ion adsorption height. An interesting outcome of their work is that at particularly short distances (<0.3 nm) the LUMO associated with the Li+ and Na+ ions drops below the LUMO of the circumcoronene, thereby in effect tuning the size of the electronic gap. It is posited that this effect could therefore be brought about by applying external pressure on the system. Instead, Mg2+ does not replicate this behaviour due to a much stronger interaction with the graphene than the monovalent ions. In this case, hybridisation of the Mg2+ and graphene molecular orbitals leads to charge transfer interactions and a 4 times stronger adsorption energy.
A similar investigation was carried out by Sangavi and co workers, who investigated the adsorption of Li+, Na+ and K+ cations on graphene and defective graphene structures.168 Again, due to complications associated with charged systems, Sangavi et al. modelled their graphene in open boundary conditions, with terminating H atoms and in the absence of solvent effects. They considered a 6 × 6 rhombohedral arrangement of the C atoms and constructed models of di- and tetravacancies as well as the well-known Stone–Wales (SW) defect. Sangavi et al. compared the results of the M06-2X hybrid metafunctional169 with the PBE GGA,170 using the 6-311G(d,p) and 6-31G(d) basis sets respectively.171,172 The introduction of defects in the structure leads to the formation of Ångstrom scale pores in the hexagonal lattice, which increase in size from the SW to divalent and finally tetravalent defects; in fact defect-induced strain leads to the rippling of the tetravalent graphene sheet. It is not clear whether such ripples would be present in larger or infinite graphene models. The simulations of Sangavi et al. suggest that while the optimised adsorption distances do not vary across the graphene models, the monovalent ions, and in particular Li+, adsorb more favourably onto the di- and tetravalent defects. Li+ is adsorbed most favourably due to a strong electrostatic attraction between the Li ion and defect site brought about by the purely ionic bond formed.
On the other hand, similar investigations of anions adsorbed on graphene have been carried out by Xiaozhen et al.;173 they carried out DFT simulations on several different classes of anion spanning the Hofmeiester series. Structures were optimised with the B3LYP hybrid exchange correlation functional,174 while the adsorption energies for each of the ions on top of graphene were computed using the ωB79X-D range separated hybrid functional,175 empirically corrected for dispersion interactions and 6-31G+(d,p) Gaussian basis set.171,172 To model the graphene, Xiaozhen et al. considered a rectangular polyaromatic hydrocarbon with H-termination at the boundaries. A key takeaway from the work of Xiaozhen et al. is that anions with a higher ionic charge adsorb more strongly to the graphene surface due to increased mixing of the graphene and ion orbitals. Specifically, of the ions tested HPO42− and SO42− were found to have the most negative adsorption energy. Xiaozhen et al. have attempted to account for the role of ion hydration on the properties of the adsorbed ionic species by including one hydrating water molecule in their simulations. While, the effect of the water was to lower the adsorption energies, the trend in adsorbing ions with a higher charge more strongly was preserved. This result is in stark contrast to the classical molecular dynamics models outlined above, where higher charged ions do not adsorb strongly on the surface due to high energy barriers preventing their dehydration and exposure to the graphene surface.
In two separate works Olsson et al.176,177 instead considered the adsorption and mobility of (atomic) Li, Na, and K, and Mg, Ca and Zn on graphene in periodic boundary conditions and using a plane waves basis set. Olsson et al. treated their graphene models with the PBE170 exchange correlation potential, including Grimme's D3 empirical dispersion correction scheme.178 Simulating the adsorption of atomic metals on the graphene sheet overcomes complications associated with charged simulation cells, but describes a chemical situation somewhat different to those described above. For example, in the case of the monovalent metals,176 Olsson et al. report that Li and K exhibit preferential adsorption on the graphene surface compared with Na. This is linked to the ability of the metal to transfer charge to the graphene: For Li, Na and K the energy of the valence s-orbital relative to the system Fermi levels are 1.11, 0.27 and 0.57 eV respectively. Consequently, the Na ion that forms can most easily revert to its atomic state and is least bound to the surface. In the case of the divalent metals, Olsson et al. observe that Ca adsorption is favoured in comparison to Mg and Zn metals.177 The adsorption of Ca is so favoured that its migration across the surface, measured by means of Nudged Elastic Band calculations, is hindered.
Leveraging the insight from electronic structure theory simulations, Zhan et al. have also explored the role of specific ion effects in the structuring and properties of the graphene/electrolyte interface.179 As discussed in Section 1.3.2 while ab initio simulations based on DFT have a limited scope in terms of the number of atoms simulated, they explicitly account for electronic polarization effects that govern the ion adsorption behaviour, and model charge transfer that can occur between the surface and the ions.
To overcome limitations on the number of particles in their simulations, Zhan et al. made use of an implicit solvent model, which replaces the water molecules with a background dielectric continuum.143 Specifically, they use the reference interaction site model (RISM) that is capable of describing the electrolyte molarity using an effective screening approach;180 this permits them to model the properties of the interface between graphene and a 1 M electrolyte solution using just a single adsorbed ion. Zhan et al. considered the different adsorption behaviour of Li+, Na+, K+ and Cs+ at a charge-neutral and negatively charged graphene electrodes. They found generally weaker interactions between the surface and the ions than Williams et al.,51 which was attributed to the electrolyte concentration in the RISM approach, compared with the pure water CPCM method, However an additional factor could be the inclusion of the point charge-quadrupole moment interactions that arise from the use of a hexagonal graphene flake in Williams et al.'s approach.181
Zhan's work suggests that of the ions considered, only the K+ and Cs+ ions adsorb favourably on the surface, i.e. within the Helmholtz plane. Instead, they find that, from a thermodynamic perspective, the Li+ and Na+ ions prefer to remain in solvated in bulk, which is in keeping with our QMMD results.40 However, it is observed that the minimum in the potential energy surface increases in distance from the graphene surface with the increase in ionic radius. Zhan et al. indicate that the negative adsorption energies of the larger ions, further away from the surface are not just due to the hydration free energy difference between the ions as asserted from classical simulations, but also due to a charge transfer mediated stabilization mechanism. They performed Bader charge density analysis74 on the optimized electron density distribution in order to infer the fraction of charge transferred from the graphene to the adsorbed ion. This analysis revealed that even at the closest adsorption distances, there is negligible charge transfer between the smaller ions (Li+ and Na+) and the surface. However, the larger ions, with considerably more diffuse valence states that can strongly overlap with the π-electron cloud of the graphene, exhibit a significant amount of back electron transfer in the direction from the graphene to the cation. For example, the Cs+ ion 3 Å (optimal computed adsorption height 3.5 Å) from the surface exhibits a computed partial charge of around 0.9 e, indicating a 10% fraction of electron transfer. This large fraction of charge transfer is thought to contribute to the energetic stabilization of the ion on the surface. These results underline the value of electronic structure theory and the necessity of multiscale simulations in the determination of interfacial properties.
A clear limitation of electronic structure theory based approaches is the computational cost associated with explicit solvation of the ions. Much of the available work describes ions which bind very strongly to the graphene electrode surface, both in the case that graphene is modelled as an infinite sheet or by a finite structure. Yet contrasting these results with Classical molecular dynamics, it is hard to ignore the fact that few classical models predict adsorption of the ions on the surface due the presence of explicit water. Ab initio molecular dynamics simulation of the graphene–electrolyte interface would address this issue, however obtaining sufficient time scales and ionic concentrations represents a severe challenge to this approach. With improved software algorithms, one avenue of exploration is to apply static DFT simulations directly on top of snapshots from Classical MD trajectories,182 this has recently been applied to the graphene–ionic liquid interface by Da Silva et al.183 and could form the basis for future investigations of the graphene–electrolyte interface.
Finally, based on models outlined in Section 1 and on our QMMD results40 we have seen that the different adsorption behaviour of ions at the interface can underpin the EDL capacitance and device performance. Other MD simulations of the EDL capacitance have been conducted, aiming to reveal the role of specific ion effects and in particular the role those different cations have on the measured value, with somewhat conflicting results. Jiang et al. examined the EDL integral of capacitance Na-, K-, Cs- and RbCl salts by means of MD simulations with no polarization of the surface.118 Contrary to our finding that the integral capacitance is constant, Jiang et al. report a decreasing CEDL with increasing ionic radius. Dočkal et al. also very recently computed the integral capacitance of the Chloride salts parameterized by Williams et al.51,146 Their results again contradict previous simulations suggesting that the CEDL increases with ionic radius. Yang et al. also performed MD simulations of the same chloride salts, as well as mixtures of the different cations and were unable to detect any change in the computed capacitance.184 One key difference between our work40 and the work of Yang,184 and the work of Jiang118 and Dočkal146 is the treatment of the truncation of the dipole field in the dielectric constant. While Jiang and Dočkal do not introduce any dependence of the dielectric constant on the distance from the surface, Yang et al. use a lower value of the dielectric constant in the Helmholtz plane, and we adopt the approach of Finney et al.,144 fitting the dielectric constant to a computed function.185 This change to the dielectric constant close to the graphene has a direct impact on the computed potential drop and therefore can lead to the different trends observed in the simulations. In order to dispute or validate the results of these simulations, further characterization of the interface i.e. by techniques such as in-operando X-Ray absorption spectroscopy (XANES/EXAFS) or X-Ray reflectivity which provide information on the local structuring of the ions are required.
3.3 Effect of confinement on the electrolyte properties and its dynamics
Understanding the thermodynamics and dynamical properties of electrolytes under confinement is paramount for the design of carbon-based devices such as capacitors or membranes for water treatment. Graphene has been increasingly used as model material to build nanopores with controlled geometry and size to unravel the complex interplay between surface effects and bulk properties occurring at the nanoscale and how this affects important physical properties such relative permittivity, friction, surface tension and diffusion.186–190 Carbon nanotubes (CNT) are probably the first example of carbon-based nanopores with well-defined sizes. The highly tuneable diameter of the tubes allowed controlled experiments to be performed that (in conjunction with simulations) indicated that narrow pores are characterized by extraordinary transport properties in terms of efficiencies and selectivities.191–193 More recently a new technique pioneered by Radha et al.194 opened up the possibility to fabricate atomically smooth two-dimensional graphite channels by removing selectively individual graphene sheets from graphite bulk crystals. The ability to build such highly size-controlled 2D capillaries has allowed direct measurements of the relative permittivity of water under confinement195 and to characterize the water and electrolyte flow properties.196 A direct comparison between the flow data obtained for the graphite capillaries and the CNTs is difficult as many of the interfacial properties of the latter seems to be highly dependent on the tube diameter (i.e. be curvature dependent).197 Below we focus only on data obtained on the former.Permeation experiments using both external electric fields or concentration gradients have shed light on the dynamics of the ions within 2D capillaries and contributed to develop better material-specific continuum theories. Since the early work198 the permeation data showed a certain degree of ion specificity indicating that the ions’ dynamics are not only driven by their bulk properties (i.e. hydration radius) but also by surface effects. Esfandiar et al.198 measured the ionic conductivity of KCl solutions of different concentrations (between 1 and 10−6 M) in graphene capillaries as small as 0.67 nm in height. They found that at high salt concentrations the ionic conductance was proportional to the electrolyte concentration and matched the KCl bulk conductivity, but for lower concentrations, 10−4 M ca., the linear proportionality ceased to exist. Their graphene capillaries show a very low surface charge (ρ ≤ 20 μC m−2, order of magnitudes smaller compared to carbon nanotubes) and the dependence of the conductivity with the salt concentration was then attributed to OH− adsorption on the capillary walls. The authors also found that exchanging the K+ ion with cations with larger hydration radius (larger than the capillary size) the electrolyte conductivity would reduce but would not be zero. They concluded that either the cations solvation shell would deform, or the ions would partially dehydrate. Finally performing drift-diffusion experiments at constant electrolyte concentration, they also noticed that, unlike K+ ions, the Cl− ions have lower mobility under confinement than in bulk and also lower mobility than several of the cations investigated, despite having similar or smaller hydration radius. They explained this effect again in terms of the presence of OH− groups on the capillary walls that, interacting with the water in the Cl− solvation shell, would slow down the ions. The same group199 manufactured graphene-slits of height of 0.34 nm and show that with such capillaries size only the proton could permeate.
Jung et al.200 investigated the ionic conductivity of deionised water and NaCl solutions of 0.02 and 0.2 M concentrations in graphene and SiO2 capillaries of sizes 3.6, 10 and 50 nm.200 They found that graphene nanochannels show significantly higher ionic conductance than SiO2 ones at all conditions investigated but the enhanced conductivity was more dramatic in the smaller channels and decreased with the salt concentration (see Fig. 8). The adsorption of hydroxide ions onto the surface of the graphene capillaries (in this case to explain the higher permeation of the ions in the graphene channels) and a change in slip length, are proposed to explain the difference in ionic mobility data between graphene and SiO2 channels. The effect of the ionic concentration was explained in terms of Debye length which, decreasing with increasing concentration, was assumed to become smaller than the channel height for the smallest capillaries, thus increasing the electroosmotic ion transport and plug flow. The overall ion mobility increased with the channel sizes but the difference between the ionic conductivity measured in the graphene and silica nanochannels reduced with the channel size.
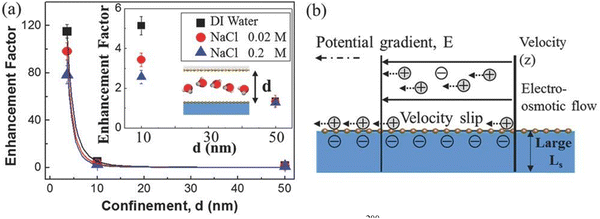 | ||
| Fig. 8 Reproduced with permission from ref. 200 copyright 2017 Wiley. (a) Flow enhancement factors of graphene-based nanochannels compared with SiO2/Si-based nanochannels. Inset figure of (a) shows the enlargement of the enhancement factors of 10 and 50 nm channels. (b) Concept illustrations of the enhanced electroosmotic flow in graphene-based 3.6 nm channels having a high hydrophobicity, large slip length, and nanoconfined properties. | ||
The experiments from Cheng et al.201 clearly showed that conventional continuum theory cannot be used to predict the ion mobility for electrolytes under extreme confinement due to modification in the electrical double layer (EDL) structure. The authors fabricated graphene capillaries with interlayer distances between 0.8 nm and 5.4 nm and measured the ions permeation of KCl and K2SO4 solutions of different concentrations as a function of the EDL thickness. The latter was tuned by changing the surface potential either by varying the externally applied potential or the degree of nanoconfinement. They found that both the potential sign and the degree of confinement affect the ion permeability which is ion-specific: applying a small negative voltage enhanced the ionic flux by up to 4 times compared to just a minor increase if a positive voltage of the same magnitude was used. Their experiments also showed that the ion permeation rates could be spontaneously changed, depending on the potential applied. The enhanced permeation was evident at strong confinement (capillaries smaller than 2 nm) and low electrolyte concentrations, but it was smaller for the larger channels (5.4 nm). The authors interpreted the results in terms of EDL atomic structure and the water arrangement in the first solvation shell of the ions. The fact that the potential sign affected the permeation indicated, the authors claimed, that the EDL structure differs depending on the nature of the counterions. This was confirmed by comparing the results across different cations and anions, which indicated a significant role in the permeation data of specific noncovalent interactions between the hydrated cations and anions in the EDL structure modulation. The authors then modified the Poisson–Nernst–Planck model to take into account that within small channels oscillating counter- and co-ion peaks in the ions’ density profile should replace the ideal, exponential decay of the ion concentrations in the EDL predicted by the theory in bulk (see section 2.1). The authors showed that using a new analytical model that includes the ions’ correlation effect, the trend of the calculated flux data with electrolyte concentrations and degree of confinement agree with their experiments.
This ions-dependence and flux enhancement, when a small external voltage is applied, as observed by Chen et al. has been confirmed by Mouterde et al.202 who fabricated slit-like channels of both graphite and hexagonal boron nitride (hBN) of height 0.68 nm. The authors found again that Cl− anions have lower mobility than K+ cations and that, in the graphitic channels, even with no external potential applied, the streaming mobility (i.e. the pressure driven component of the ionic current normalized by the channel length, pressure gradient and channel cross sectional channel) of potassium is higher than that reported for SiO2 channels. When a small positive voltage was applied (75 mV), the potassium mobility was increased by 20 times. This gating effect was observed in both graphite and hexagonal boron nitride channels, but it was remarkably larger in the former. The authors attributed this high ionic mobility mainly to the fast transport of water (and hence hydrated ions, at molecular distances from the channel surfaces) observed in these types of channels and to the existence of an effective water–wall friction that depends on ion concentrations rather than to a change in the wall (graphite or hBN) capacitance. They then developed an ‘Extended Poisson–Nernst–Planck’ model that qualitatively reproduced most of their experimental observations including the large increase in streaming mobility under applied bias.
Due to the difficulty associated in building such nanoscopic channels and the possible contamination of the capillaries, most of the literature deals with molecular simulations work where it is much simpler to build perfectly aligned, rigid, graphene sheets sandwiched to form 2D symmetric channels of different heights, with the aim of disentangling the various competing effects affecting the permeability data. Molecular simulations have helped in clarifying important aspects of the ions mobility under confinement, for example that the ions rejection in small capillaries is dictated by the ion's hydration free energy rather than its van der Waals size,203,204 that the preferential adsorption of some ions onto the graphite wall reduces the free energy of permeation into the capillaries205 (see also Section 3.2), that water molecules when intercalated within the graphitic capillaries form discrete layers with lower dielectric constant206 and that both Coulomb and Lennard-Jones interactions play a role on the ions’ adsorption on the capillary walls depending on the channel size.207 Molecular simulations have also been used to investigate the reduction in the dielectric constant of the liquid trapped inside nanocapillaries as its value affects the capacitance (see eqn (7)), EDL structure and ultimately flux data.16,206,207 Experimentally Fumagalli et al.23 measured the εr of water trapped in 1 nm graphite capillaries and found it to be as low as 2 (compared to 80 in bulk). However due to the challenges in carrying out the measurements and in the difficulty of ensuring no hydrocarbon contaminants are present in the channels, experimental values are scarce. Simulations have tried to shed light on the physical origin behind this reduction which happens also in more “soft confinement” than carbon slits.22,208 Most of the literature has focused on water and generally ascribes the low εr calculated in the simulations to the molecular ordering and related reduced mobility of the confined water molecules (“ice-like”) particularly in the direction orthogonal to the channel walls,16,22,207–209 although a recent work by Olivieri et al.185 proposed a new interpretation of the data and argued that the low dielectric constant value arises from the anisotropy of the long-ranged dipole correlation combined with an excluded-volume effect of the low- dielectric confining material.
Computer modelling allows also to design specific geometrical arrangements of the graphene sheets which might be difficult to achieve experimentally but nevertheless can provide guidelines for device design to maximize for example desalination processes or energy storage.210,211
Of course, the availability of reliable molecular model parameters to simulate water and electrolytes under confinement is vital to obtain useful results. For example it has been shown that different water models have different phase diagram,122,212,213 friction coefficient214 and viscosity215 within sub-nanometer carbon slits. The importance of reaching a consensus within the community on the most accurate model to be used for water under confinement and for the graphene/electrolyte interactions (hampered so far also by the scarce number of experimental data) is proved by the plethora of (sometimes contradictory) results published in the literature including on the structure of the water. Moreover, as the model parameters employed in the simulations are different, it is difficult to paint a single picture of the behaviour of confined electrolyte. In general, molecular simulations indicated that for some degree of confinement and for some electrolytes, the ions mobility can be increased by confining the liquid. One of the early molecular dynamics study of NaCl electrolyte confined in infinite carbon slits216 found that the diffusion coefficient of the ions increased by up to 20% in the largest slit (4 nm) while it was the same as bulk or slightly reduced for smaller interlayer distances (down to 1 nm). The same authors went on to investigate several other electrolytes of monovalent ions217 (LiCl, NaCl, KCl, RbCl, CsCl, NaF, NaCl, NaBr, NaI) in the 4 nm slit and found that ion pairing either increased or decreased with confinement depending on the counterions and the anions without following a specific trend. Regarding the ions mobility the authors found that the chloride diffusion coefficient did not change substantially irrespectively to alkali ions but that potassium had significant rise in diffusivity relative to the other cations studied. They attributed this result to the lowering of water–water hydrogen bonds relative to the sodium chloride solution in the slit.
Chialvo and Cummings140 simulated electrolytes of metal chloride (Li+, Ba2+, Y3+, Cl−) in free-standing graphene slits with interlayer distances up to 3 nm. This set-up (i.e. open capillaries in equilibrium with a reservoir) had the advantage, compared to the infinite channel set-up, of removing any bias in terms of electroneutrality or density. The authors found that letting the ions move freely from the channel to the reservoir and vice versa show that as the graphene plate separation became smaller than the size of the ions first solvation shell, the ion would leave the capillary and move into the surrounding bulk electrolyte effectively charging the capillary. They also found that the slit-pore would de-wet as the interplate separation is reduced below 0.9 nm ca.
Sala et al.218 focused on aqueous solutions of sodium halide (NaF, NaCl and NaI) of different molalities (1, 2, 4 mol kg−1) confined inside a graphene channel of size 3.1 nm. Unlike the previous studies the authors employed a polarizable model for both water and ions but not for the graphene. From a structural point of view, the effect of using a polarizable force field made a difference only for the position of anions (which are fully hydrated in the channel or closer to the capillary walls when modelled with non-polarizable or polarizable force field respectively). Both force fields predicted higher permittivity at the interface compared to the bulk value (in contrast with the standard theoretical and simulation results144,219) and similar diffusion coefficients. In terms of ions relative diffusion, the effect of confinement was found to be minor for all the ions except for fluoride whose dynamics slow down.
Kong et al.220 investigated the effect that temperature (283, 298, 313 and 333 K) and surface charge have on the ions dynamics simulating a NaCl solution confined in a graphene slit with heights of 0.7, 1.2, 1.7 nm, respectively, in contact with two 2 M electrolyte reservoirs. In this case the constituent atoms of the graphene have a small partial charge associated (the same for all carbons) in order to reproduce a surface charge of |5| μC cm−2. As in the set-up of Chialvo,140 the capillaries are in contact with a solution reservoir and therefore their electrolyte concentration may vary. The results show that ions confined in neutral nanochannels diffused faster than in charged ones (this was attributed to the interaction between the charged wall and the counterions) and the electrolyte conductivity in charged channels decreased with decreasing channel height. As expected, an increase in temperature led to enhanced thermal motion of ions, but the overall effect of the temperature of the diffusion was negligible.
Having the capillaries in contact with the electrolyte reservoirs allowed Kalluri et al.221 to investigate the charging of graphitic slit pores of different sizes as a function of electrolyte concentration and surface charge. The pores of size 0.9, 1.2, and 1.6 nm and charge densities ranging from 0 (neutral pore), 20, 30, and 40 μC cm−2 were soaked in aqueous solutions of NaCl at 1.5 and 1.6 M. The authors found that the pores were fully wetted by the electrolyte solutions only when they were charged and that at the maximum graphene surface charge density considered, the ionic concentration within the pores could become ∼10 times as high as that outside the pores. Such high surface charge led to ions condensation on the slit walls sometimes in multiple layers. Within this set up and FF choice, capillaries of width 1.2 nm seem to be those with the highest charge accumulation.
The effect on the channel electrification on the capacitance and EDL structure has been investigated by Feng et al.222 who modelled graphene slits with widths ranging from 0.94 to 1.47 nm and surface charge of −5.5 μC cm−2. Only potassium cations were dissolved into water to neutralize the simulation box and no counterions were included. The MD simulation results showed that the cations concentration profile followed the classical EDL theory (i.e. adsorbed at the wall) only for the smallest slit width (0.94 nm) while for larger channels the ions tended to accumulate in the middle of the capillary. In the smallest channels however, they found that the adsorption of the cations to the capillary walls led to a depletion of ions in the middle of the channel. The authors attributed this result to both effects accounted for in the original EDL theory and others arising from the discrete nature of the electrolyte and therefore not included in the EDL. The former include the long-range electrostatic ion–ion repulsion (driving ions toward the two slit walls) and entropic effects (driving ions and water away from the wall); the latter are the van der Waals ion-slit wall attractions, the hydration free energy of the ions (driving ions into the middle of the channels to be fully hydrated) and the interactions between an ion's hydration water molecules and their surrounding water molecules. The ions/wall attraction due to surface polarization was excluded in this analysis as the molecular model employed did not include this effect which however exists (see Section 3.2 above). The authors then proposed to calculate the capacitance of nanopores approximating the slit capacitor as two plate capacitors in parallel and calculated the differential Helmholtz double layer capacitance of each wall using eqn (5) (rather than using the ions distribution profile obtained via the MD simulations and eqn (18)). Despite this approximation assuming a specific geometry of the pore, they then showed that the parallel plate capacitor approximation fitted the experimental data well for the capacitance of activated carbon.
More speculative work, which is harder to compare or validate with the experiments due to the greater mismatch between the idealized model and the actual device includes the calculations of the graphene edge's capacitance. MD simulations have been performed on aqueous electrolytes in contact with vertically-oriented graphene flakes.223,224 The results of these simulations need to be taken with caution though, as the H atoms of the graphene edges are much more reactive than the carbon atoms of the basal plane and therefore the assumption made in the model that the edges are not functionalized makes the comparison with the experimental data difficult. Anyhow, the MD results indicated that the specific capacitance, Cdiff, of the edges can achieve a 2-fold increase compared to the basal one when the interlayer spacing is ∼0.5 nm. An analysis of the EDL structure showed that the calculated capacitance arises from the presence of the water in the EDL rather than the adsorption of the ions. Experimentally the edge capacitance is also larger than the basal one but the increase is much higher than the simulation results indicated, probably due to the functionalization of the graphene edges which is not taken into account in the model.92,225
4. Conclusions and outlook
Despite the intense research done on the topic, a molecular-level understanding of the electrochemical properties of graphene (including few layer graphene) and aqueous electrolyte is still elusive. The possibility of using experimental methods in conjunction with simulations, represents a powerful tool that can be exploited further as long as experiments and simulations look at the same system. On the simulation side, considerations of the electrochemical stability of the electrolyte solutions at high applied voltage should be given particular attention and therefore simulations with high surface charge should be avoided. If electron transfer is accurately included, however, then simulations could offer valuable insight into the range of electrochemical stability of graphene vs. graphite in different electrolyte solutions. Simulations have also quite clearly indicated now that including polarization in models of the electrolyte solution has a minor effect on the structure of the interface but including the surface polarizability is important to simulate the ion's adsorption and wetting. The routine use of defect-free pristine graphene in the simulation should also be reconsidered or at least tested as even the most controlled experimental set-ups present surface defects and, most probably, contaminations including the presence of various functional groups. The latter observation is even more pertinent when simulations are carried out on graphene edges whose capping hydrogen atoms are particularly reactive. The surface defects, in particular for graphene, could also have particular relevance in the quantum capacitance calculations as the latter is intimately related to the DOS of the material. As discussed earlier in the review, a range of possible structural defects can exist, and the experimental complication is the difficulty in ensuring that only one class of defect is introduced into the graphene structure. This is, again, where interplay between experiment and simulation becomes particularly useful, because the latter can indicate which defects would be most likely to produce the largest perturbation of the sample's DOS and hence capacitance. A further effect which has seen relatively little exploration from the experimental side, is the extent to which the underlying substrate influences the properties (e.g. capacitance) of the graphene/electrolyte interface. Monolayer graphene samples are required to maximise the strength of this phenomenon.Furthermore, for a quantitative comparison between simulation and electrochemical experimental data, several points need still to be clarified. For instance, it is still unclear what value of the local permittivity should be used for the capacitance calculation (eqn (7), (16) and (17)) considering both the higher ionic concentration in the EDL compared to bulk and the effect of the proximity of the surface185or if interfacial crystallization occurs in the EDL layer144 opening up the possibility of a completely different interpretation of the experimental results. Simulations are particularly important for shedding light on the effect that confinement has on the electrochemical properties. As said, much of the work has been focused on clarifying the atomistic structure of the confined EDL but information about the electrolyte physical properties beyond the EDL are also vital. These parameters are important because they inform continuum equations to predict ion and water diffusivity and channels flux properties. Among them wetting phenomena (relevant also in the bulk) occurring in nano-confined systems189 although likely to be relevant, have not been heavily explored.
Finally, this review has focused at low-medium concentrated electrolytes, but a new type of highly concentrated electrolyte (known as water-in-salt)226 has been emerging as environmentally-friendly, water-based electrolyte for use in energy storage devices. These seem to represent a new frontier in the field and much of their electrochemical properties are still to be explored in detail. For example, the general trend observed is that these highly soluble salts greatly extend the stable potential window at the graphite (carbon)/aqueous electrolyte interface, to values way in excess the thermodynamic 1.23 V discussed in section 1.5 above. The factors underlying this stabilisation are not entirely clear, with a reduced thermodynamic activity of water (associated with the loss of “free” water molecules) being an obvious explanation, however some works claim that at least part of the stabilisation is due to the decomposition of some of the ionic species to form a solid-electrolyte interface layer, which insulates the water from the electrode and thus suppresses the hydrogen evolution process.226,227 Understanding how graphene interacts with such highly concentrated electrolytes will be extremely interesting, both from the fundamental and “technological” perspectives.
List of symbols and abbreviations
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the European Union's Horizon 2020 research and innovation programme project VIMMP under grant number 760907 and the Leverhulme Trust (grant RPG-2019-250) for funding.References
- C. Cha, S. R. Shin, N. Annabi, M. R. Dokmeci and A. Khademhosseini, Carbon-Based Nanomaterials: Multifunctional Materials for Biomedical Engineering, ACS Nano, 2013, 7(4), 2891–2897, DOI:10.1021/nn401196a.
- L. Dai, D. W. Chang, J.-B. Baek and W. Lu, Carbon Nanomaterials for Advanced Energy Conversion and Storage, Small, 2012, 8(8), 1130–1166, DOI:10.1002/smll.201101594.
- P. Avouris, Z. Chen and V. Perebeinos, Carbon-Based Electronics, Nat. Nanotechnol., 2007, 2, 605 CrossRef CAS PubMed.
- M. S. Mauter and M. Elimelech, Environmental Applications of Carbon-Based Nanomaterials, Environ. Sci. Technol., 2008, 42(16), 5843–5859, DOI:10.1021/es8006904.
- F. Zaera, Probing Liquid/Solid Interfaces at the Molecular Level, Chem. Rev., 2012, 112(5), 2920–2986, DOI:10.1021/cr2002068.
- D. L. McCaffrey, S. C. Nguyen, S. J. Cox, H. Weller, A. P. Alivisatos, P. L. Geissler and R. J. Saykally, Mechanism of Ion Adsorption to Aqueous Interfaces: Graphene/Water vs. Air/Water, Proc. Natl. Acad. Sci. U. S. A., 2017, 201702760, DOI:10.1073/pnas.1702760114.
- P. Jungwirth and P. S. Cremer, Beyond Hofmeister, Nat. Chem., 2014, 6(4), 261–263, DOI:10.1038/nchem.1899.
- Z. E. Hughes and T. R. Walsh, Computational Chemistry for Graphene-Based Energy Applications: Progress and Challenges, Nanoscale, 2015, 7(16), 6883–6908, 10.1039/C5NR00690B.
- D. Pletcher, A First Course in Electrode Processes, 2009 Search PubMed.
- L. R. Faulkner and A. J. Bard, Double-Layer Structure and Adsorption, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, NY, 2001 Search PubMed.
- F. O. Koenig, The Thermodynamics of the Electrocapillary Curve. II. The Variation of the Electrocapillary Curve with Composition, J. Phys. Chem., 1934, 38(3), 339–363, DOI:10.1021/j150354a007.
- J. O. Bockris and A. K. N. Reddy, The Electrified Interface, Modern Electrochemistry, Kluwer Academic/Plenum Publishers, New York, NY, 2002, vol. 2 Search PubMed.
- S. D. Argade and E. Gileadi, The Potential of Zero Charge. in Electrosorption, ed. E. Gileadi, Springer US, Boston, MA, 1967, pp. 87–115 DOI:10.1007/978-1-4684-1731-9_5.
- O. A. Petrii, Zero Charge Potentials of Platinum Metals and Electron Work Functions (Review), Russ. J. Electrochem., 2013, 49(5), 401–422, DOI:10.1134/S1023193513050145.
- A. A. Kornyshev; E. Spohr and M. A. Vorotyntsev, Electrochemical Interfaces: At the Border Line, Encyclopedia of Electrochemistry – Thermodynamics and Electrified Interfaces, Wiley-VCH, 2007 Search PubMed.
- B. E. Conway, J. O. Bockris and I. A. Ammar, The Dielectric Constant of the Solution in the Diffuse and Helmholtz Double Layers at a Charged Interface in Aqueous Solution, Trans. Faraday Soc., 1951, 47(0), 756–766, 10.1039/TF9514700756.
- D. C. Grahame, The Electrical Double Layer and the Theory of Electrocapillarity, Chem. Rev., 1947, 41(3), 441–501, DOI:10.1021/cr60130a002.
- R. Payne, The Electrical Double Layer: Problems and Recent Progress, J. Electroanal. Chem. Interfacial Electrochem., 1973, 41(2), 277–309, DOI:10.1016/S0022-0728(73)80444-9.
- S. Wolfgang, Electrochemical Double Layers, Encyclopedia of Electrochemistry – Thermodynamics and Electrified Interfaces, Wiley-VCH, 2007 Search PubMed.
- H. H. Girault, Electrified Interfaces, Analytical and Physical Electrochemistry, EPFL Press, New York, 2004 Search PubMed.
- H. Wang and L. Pilon, Accurate Simulations of Electric Double Layer Capacitance of Ultramicroelectrodes, J. Phys. Chem. C, 2011, 115(33), 16711–16719, DOI:10.1021/jp204498e.
- A. Sugahara, Y. Ando, S. Kajiyama, K. Yazawa, K. Gotoh, M. Otani, M. Okubo and A. Yamada, Negative Dielectric Constant of Water Confined in Nanosheets, Nat. Commun., 2019, 10(1), 850, DOI:10.1038/s41467-019-08789-8.
- L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. S. Novoselov and A. K. Geim, Anomalously Low Dielectric Constant of Confined Water, Science, 2018, 360(6395), 1339–1342, DOI:10.1126/science.aat4191.
- B. B. Damaskin and O. A. Petrii, Historical Development of Theories of the Electrochemical Double Layer, J. Solid State Electrochem., 2011, 15(7), 1317–1334, DOI:10.1007/s10008-011-1294-y.
- C. Pean, B. Daffos, C. Merlet, B. Rotenberg, P.-L. Taberna, P. Simon and M. Salanne, Single Electrode Capacitances of Porous Carbons in Neat Ionic Liquid Electrolyte at 100 °C: A Combined Experimental and Modeling Approach, J. Electrochem. Soc., 2015, 162(5), A5091–A5095, DOI:10.1149/2.0151505jes.
- R. Memming, Solid–Liquid Interface, Semiconductor Electrochemistry, John Wiley & Sons, Ltd, 2015, pp. 89–125 DOI:10.1002/9783527688685.ch5.
- N. Sato, Chapter 5 – Electric Double Layer At Electrode Interfaces, in Electrochemistry at Metal and Semiconductor Electrodes, ed. N. Sato, Elsevier Science, Amsterdam, 1998, pp. 119–199 DOI:10.1016/B978-044482806-4/50005-2.
- H. Gerischer, An Interpretation of the Double Layer Capacity of Graphite Electrodes in Relation to the Density of States at the Fermi Level, J. Phys. Chem., 1985, 89(20), 4249–4251, DOI:10.1021/j100266a020.
- J.-P. Randin and E. Yeager, Differential Capacitance Study of Stress-Annealed Pyrolytic Graphite Electrodes, J. Electrochem. Soc., 1971, 118(5), 711, DOI:10.1149/1.2408151.
- J.-P. Randin and E. Yeager, Differential Capacitance Study on the Basal Plane of Stress-Annealed Pyrolytic Graphite, J. Electroanal. Chem. Interfacial Electrochem., 1972, 36(2), 257–276, DOI:10.1016/S0022-0728(72)80249-3.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, S. V. Dubonos, Y. Zhang and D. Jiang Room-Temperature Electric Field Effect and Carrier-Type Inversion in Graphene Films, 2004, ArXivcond-Mat0410631.
- H. Gerischer, R. McIntyre, D. Scherson and W. Storck, Density of the Electronic States of Graphite: Derivation from Differential Capacitance Measurements, J. Phys. Chem., 1987, 91(7), 1930–1935, DOI:10.1021/j100291a049.
- H. Ji, X. Zhao, Z. Qiao, J. Jung, Y. Zhu, Y. Lu, L. L. Zhang, A. H. MacDonald and R. S. Ruoff, Capacitance of Carbon-Based Electrical Double-Layer Capacitors, Nat. Commun., 2014, 5(1), 3317, DOI:10.1038/ncomms4317.
- B. S. Bhushan and A. SrivastavaIntegrated and Differential Quantum Capacitance of Graphene, A DFT Study, Bikaner, India, 2018, p. 140125 DOI:10.1063/1.5033300.
- F. Parhizgar, A. Qaiumzadeh and R. Asgari, Quantum Capacitance of Double-Layer Graphene, Phys. Rev. B, 2017, 96(7), 075447, DOI:10.1103/PhysRevB.96.075447.
- J. Xia, F. Chen, J. Li and N. Tao, Measurement of the Quantum Capacitance of Graphene, Nat. Nanotechnol., 2009, 4(8), 505–509, DOI:10.1038/nnano.2009.177.
- C. Zhan, J. Neal, J. Wu and D. Jiang, Quantum Effects on the Capacitance of Graphene-Based Electrodes, J. Phys. Chem. C, 2015, 119(39), 22297–22303, DOI:10.1021/acs.jpcc.5b05930.
- N. Ma and D. Jena, Carrier Statistics and Quantum Capacitance Effects on Mobility Extraction in Two-Dimensional Crystal Semiconductor Field-Effect Transistors, 2D Mater., 2015, 2(1), 015003, DOI:10.1088/2053-1583/2/1/015003.
- A. H. Biby, B. A. Ali and N. K. Allam, Interplay of Quantum Capacitance with van der Waals Forces, Intercalation, Co-Intercalation, and the Number of MoS2 Layers, Mater. Today Energy, 2021, 20, 100677, DOI:10.1016/j.mtener.2021.100677.
- J. D. Elliott, M. Chiricotto, A. Troisi and P. Carbone, Do Specific Ion Effects Determine Performance of Aqueous Graphene-Based Supercapacitors?Perspectives from Multiscale QMMD Simulations, 2022, ArXiv220302469 Cond-Mat.
- B. Ni; T. Zhang; J. Li; X. Li and H. Gao, Topological Design of Graphene, Handbook of Graphene Set, John Wiley & Sons, Ltd, 2019, pp. 1–44 DOI:10.1002/9781119468455.ch19.
- J. Lu, Y. Bao, C. L. Su and K. P. Loh, Properties of Strained Structures and Topological Defects in Graphene, ACS Nano, 2013, 7(10), 8350–8357, DOI:10.1021/nn4051248.
- B. C. Wood, T. Ogitsu, M. Otani and J. Biener, First-Principles-Inspired Design Strategies for Graphene-Based Supercapacitor Electrodes, J. Phys. Chem. C, 2014, 118(1), 4–15, DOI:10.1021/jp4044013.
- A. J. Pak, E. Paek and G. S. Hwang, Tailoring the Performance of Graphene-Based Supercapacitors Using Topological Defects: A Theoretical Assessment, Carbon, 2014, 68, 734–741, DOI:10.1016/j.carbon.2013.11.057.
- J. Chen, Y. Han, X. Kong, X. Deng, H. J. Park, Y. Guo, S. Jin, Z. Qi, Z. Lee, Z. Qiao, R. S. Ruoff and H. Ji, The Origin of Improved Electrical Double-Layer Capacitance by Inclusion of Topological Defects and Dopants in Graphene for Supercapacitors, Angew. Chem., Int. Ed., 2016, 55(44), 13822–13827, DOI:10.1002/anie.201605926.
- E. Y. Andrei and A. H. MacDonald, Graphene Bilayers with a Twist, Nat. Mater., 2020, 19(12), 1265–1275, DOI:10.1038/s41563-020-00840-0.
- M. I. B. Utama, R. J. Koch, K. Lee, N. Leconte, H. Li, S. Zhao, L. Jiang, J. Zhu, K. Watanabe, T. Taniguchi, P. D. Ashby, A. Weber-Bargioni, A. Zettl, C. Jozwiak, J. Jung, E. Rotenberg, A. Bostwick and F. Wang, Visualization of the Flat Electronic Band in Twisted Bilayer Graphene near the Magic Angle Twist, Nat. Phys., 2021, 17(2), 184–188, DOI:10.1038/s41567-020-0974-x.
- Y. Yu, K. Zhang, H. Parks, M. Babar, S. Carr, I. M. Craig, M. Van Winkle, A. Lyssenko, T. Taniguchi, K. Watanabe, V. Viswanathan and D. K. Bediako, Tunable Angle-Dependent Electrochemistry at Twisted Bilayer Graphene with Moiré Flat Bands, Nat. Chem., 2022, 14(3), 267–273, DOI:10.1038/s41557-021-00865-1.
- T. Mark Statistical Mechanics: Theory and Molecular Simulation, Illustrated, OUP Oxford, Oxford United Kingdom, 2010 Search PubMed.
- F. Daan and S. Berend, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, Oxford United Kingdom, 2nd edn, 2001 Search PubMed.
- C. D. Williams, J. Dix, A. Troisi and P. Carbone, Effective Polarization in Pairwise Potentials at the Graphene–Electrolyte Interface, J. Phys. Chem. Lett., 2017, 8(3), 703–708, DOI:10.1021/acs.jpclett.6b02783.
- G. Lamoureux and B. Roux, Modeling Induced Polarization with Classical Drude Oscillators: Theory and Molecular Dynamics Simulation Algorithm, J. Chem. Phys., 2003, 119(6), 3025–3039, DOI:10.1063/1.1589749.
- V. M. Anisimov, G. Lamoureux, I. V. Vorobyov, N. Huang, B. Roux and A. D. MacKerell, Determination of Electrostatic Parameters for a Polarizable Force Field Based on the Classical Drude Oscillator, J. Chem. Theory Comput., 2005, 1(1), 153–168, DOI:10.1021/ct049930p.
- W. Jiang, D. J. Hardy, J. C. Phillips, A. D. MacKerell, K. Schulten and B. Roux, High-Performance Scalable Molecular Dynamics Simulations of a Polarizable Force Field Based on Classical Drude Oscillators in NAMD, J. Phys. Chem. Lett., 2011, 2(2), 87–92, DOI:10.1021/jz101461d.
- J. A. Lemkul, J. Huang, B. Roux and A. D. MacKerell, An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications, Chem. Rev., 2016, 116(9), 4983–5013, DOI:10.1021/acs.chemrev.5b00505.
- R. P. Misra and D. Blankschtein, Insights on the Role of Many-Body Polarization Effects in the Wetting of Graphitic Surfaces by Water, J. Phys. Chem. C, 2017, 14 Search PubMed.
- R. P. Misra, J. P. de Souza, D. Blankschtein and M. Z. Bazant, Theory of Surface Forces in Multivalent Electrolytes, Langmuir, 2019, 35(35), 11550–11565, DOI:10.1021/acs.langmuir.9b01110.
- R. P. Misra and D. Blankschtein, Ion Adsorption at Solid/Water Interfaces: Establishing the Coupled Nature of Ion–Solid and Water–Solid Interactions, J. Phys. Chem. C, 2021, 125(4), 2666–2679, DOI:10.1021/acs.jpcc.0c09855.
- R. P. Misra and D. Blankschtein, Uncovering a Universal Molecular Mechanism of Salt Ion Adsorption at Solid/Water Interfaces, Langmuir, 2021, 37(2), 722–733, DOI:10.1021/acs.langmuir.0c02829.
- J. I. Siepmann and M. Sprik, Influence of Surface Topology and Electrostatic Potential on Water/Electrode Systems, J. Chem. Phys., 1995, 102(1), 511–524, DOI:10.1063/1.469429.
- S. K. Reed, O. J. Lanning and P. A. Madden, Electrochemical Interface between an Ionic Liquid and a Model Metallic Electrode, J. Chem. Phys., 2007, 126(8), 084704, DOI:10.1063/1.2464084.
- C. Merlet, C. Péan, B. Rotenberg, P. A. Madden, P. Simon and M. Salanne, Simulating Supercapacitors: Can We Model Electrodes As Constant Charge Surfaces?, J. Phys. Chem. Lett., 2013, 4(2), 264–268, DOI:10.1021/jz3019226.
- J. D. Elliott, A. Troisi and P. Carbone, A QM/MD Coupling Method to Model the Ion-Induced Polarization of Graphene, J. Chem. Theory Comput., 2020, 16(8), 5253–5263, DOI:10.1021/acs.jctc.0c00239.
- M. Ferri, J. D. Elliott, M. F. Camellone, S. Fabris and S. Piccinin, CuFeO 2 –Water Interface under Illumination: Structural, Electronic, and Catalytic Implications for the Hydrogen Evolution Reaction, ACS Catal., 2021, 11(4), 1897–1910, DOI:10.1021/acscatal.0c05066.
- E. Poli, J. D. Elliott, L. E. Ratcliff, L. Andrinopoulos, J. Dziedzic, N. D. M. Hine, A. A. Mostofi, C.-K. Skylaris, P. D. Haynes and G. Teobaldi, The Potential of Imogolite Nanotubes as (Co-)Photocatalysts: A Linear-Scaling Density Functional Theory Study, J. Phys. Condens. Matter, 2016, 28(7), 074003, DOI:10.1088/0953-8984/28/7/074003.
- E. Poli, K. H. Jong and A. Hassanali, Charge Transfer as a Ubiquitous Mechanism in Determining the Negative Charge at Hydrophobic Interfaces, Nat. Commun., 2020, 11(1), 901, DOI:10.1038/s41467-020-14659-5.
- R. G. Parr and Y. Weitao, Density-Functional Theory of Atoms and Molecules, OUP Oxford, Oxford United Kingdom, 1989 Search PubMed.
- R. M. Martin, Electronic Structure: Basic Theory and Practical Methods, Cambridge University Press, Cambridge United Kingdom, 2004 Search PubMed.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136(3B), B864–B871, DOI:10.1103/PhysRev.136.B864.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140(4A), A1133–A1138, DOI:10.1103/PhysRev.140.A1133.
- M. A. L. Marques, M. J. T. Oliveira and T. Burnus, Libxc: A Library of Exchange and Correlation Functionals for Density Functional Theory, Comput. Phys. Commun., 2012, 183(10), 2272–2281, DOI:10.1016/j.cpc.2012.05.007.
- S. Lehtola, C. Steigemann, M. J. T. Oliveira and M. A. L. Marques, Recent Developments in Libxc—A Comprehensive Library of Functionals for Density Functional Theory, SoftwareX, 2018, 7, 1–5, DOI:10.1016/j.softx.2017.11.002.
- R. S. Mulliken, Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I, J. Chem. Phys., 1955, 23(10), 1833–1840, DOI:10.1063/1.1740588.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A Fast and Robust Algorithm for Bader Decomposition of Charge Density, Comput. Mater. Sci., 2006, 36(3), 354–360, DOI:10.1016/j.commatsci.2005.04.010.
- T. A. Manz and N. G. Limas, Introducing DDEC6 Atomic Population Analysis: Part 1. Charge Partitioning Theory and Methodology, RSC Adv., 2016, 6(53), 47771–47801, 10.1039/C6RA04656H.
- N. G. Limas and T. A. Manz, Introducing DDEC6 Atomic Population Analysis: Part 2. Computed Results for a Wide Range of Periodic and Nonperiodic Materials, RSC Adv, 2016, 6(51), 45727–45747, 10.1039/C6RA05507A.
- T. A. Manz, Introducing DDEC6 Atomic Population Analysis: Part 3. Comprehensive Method to Compute Bond Orders, RSC Adv., 2017, 7(72), 45552–45581, 10.1039/C7RA07400J.
- A. Lasia, Definition of Impedance and Impedance of Electrical Circuits, in Electrochemical Impedance Spectroscopy and its Applications, ed. A. Lasia, Springer, New York, NY, 2014, pp. 7–66 DOI:10.1007/978-1-4614-8933-7_2.
- A. Lasia, Dispersion of Impedances at Solid Electrodes, in Electrochemical Impedance Spectroscopy and its Applications, ed. A. Lasia, Springer, New York, NY, 2014, pp. 177–201 DOI:10.1007/978-1-4614-8933-7_8.
- M. E. Orazem, N. Pébère and B. Tribollet, Enhanced Graphical Representation of Electrochemical Impedance Data, J. Electrochem. Soc., 2006, 153(4), B129, DOI:10.1149/1.2168377.
- J. Kubisztal, A. Budniok and A. Lasia, Study of the Hydrogen Evolution Reaction on Nickel-Based Composite Coatings Containing Molybdenum Powder, Int. J. Hydrog. Energy, 2007, 32(9), 1211–1218, DOI:10.1016/j.ijhydene.2006.11.020.
- M. C. Lefebvre, R. B. Martin and P. G. Pickup, Characterization of Ionic Conductivity Profiles within Proton Exchange Membrane Fuel Cell Gas Diffusion Electrodes by Impedance Spectroscopy, Electrochem. Solid-State Lett., 1999, 2(6), 259, DOI:10.1149/1.1390804.
- E. B. Easton and P. G. Pickup, An Electrochemical Impedance Spectroscopy Study of Fuel Cell Electrodes, Electrochimica Acta, 2005, 50(12), 2469–2474, DOI:10.1016/j.electacta.2004.10.074.
- O. Reid, F. S. Saleh and E. B. Easton, Determining Electrochemically Active Surface Area in PEM Fuel Cell Electrodes with Electrochemical Impedance Spectroscopy and Its Application to Catalyst Durability, Electrochimica Acta, 2013, 114, 278–284, DOI:10.1016/j.electacta.2013.10.050.
- P. Córdoba-Torres, N. T. C. Oliveira, C. Bolfarini, V. Roche and R. P. Nogueira, Electrochemical Impedance Analysis of TiO2 Nanotube Porous Layers Based on an Alternative Representation of Impedance Data, J. Electroanal. Chem., 2015, 737, 54–64, DOI:10.1016/j.jelechem.2014.06.034.
- M. de Pauli, A. M. C. Gomes, R. L. Cavalcante, R. B. Serpa, C. P. S. Reis, F. T. Reis and M. L. Sartorelli, Capacitance Spectra Extracted from EIS by a Model-Free Generalized Phase Element Analysis, Electrochimica Acta, 2019, 320, 134366, DOI:10.1016/j.electacta.2019.06.059.
- B. E. Conway, Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications, Springer US, 1999 DOI:10.1007/978-1-4757-3058-6.
- L. M. Da Silva, L. A. De Faria and J. F. C. Boodts, Determination of the Morphology Factor of Oxide Layers, Electrochimica Acta, 2001, 47(3), 395–403, DOI:10.1016/S0013-4686(01)00738-1.
- H. Wang and L. Pilon, Physical Interpretation of Cyclic Voltammetry for Measuring Electric Double Layer Capacitances, Electrochimica Acta, 2012, 64, 130–139, DOI:10.1016/j.electacta.2011.12.118.
- M. Arulepp, L. Permann, J. Leis, A. Perkson, K. Rumma, A. Jänes and E. Lust, Influence of the Solvent Properties on the Characteristics of a Double Layer Capacitor, J. Power Sources, 2004, 133(2), 320–328, DOI:10.1016/j.jpowsour.2004.03.026.
- H. Wang and L. Pilon, Reply to Comments on “Intrinsic Limitations of Impedance Measurements in Determining Electric Double Layer Capacitances” by H. Wang, L. Pilon [Electrochimica Acta 63 (2012) 55], Electrochimica Acta, 2012, 76, 529–531, DOI:10.1016/j.electacta.2012.05.039.
- P. P. Brisebois and M. Siaj, Harvesting Graphene Oxide – Years 1859 to 2019: A Review of Its Structure, Synthesis, Properties and Exfoliation, J. Mater. Chem. C, 2020, 8(5), 1517–1547, 10.1039/C9TC03251G.
- L. Lai, L. Wang, H. Yang, N. G. Sahoo, Q. X. Tam, J. Liu, C. K. Poh, S. H. Lim, Z. Shen and J. Lin, Tuning Graphene Surface Chemistry to Prepare Graphene/Polypyrrole Supercapacitors with Improved Performance, Nano Energy, 2012, 1(5), 723–731, DOI:10.1016/j.nanoen.2012.05.012.
- Q. Chen, Y. Meng, C. Hu, Y. Zhao, H. Shao, N. Chen and L. Qu, MnO2-Modified Hierarchical Graphene Fiber Electrochemical Supercapacitor, J. Power Sources, 2014, 247, 32–39, DOI:10.1016/j.jpowsour.2013.08.045.
- Y. S. Lim, Y. P. Tan, H. N. Lim, N. M. Huang, W. T. Tan, M. A. Yarmo and C.-Y. Yin, Potentiostatically Deposited Polypyrrole/Graphene Decorated Nano-Manganese Oxide Ternary Film for Supercapacitors, Ceram. Int., 2014, 40(3), 3855–3864, DOI:10.1016/j.ceramint.2013.08.026.
- B. Lobato, L. Suárez, L. Guardia and T. A. Centeno, Capacitance and Surface of Carbons in Supercapacitors, Carbon, 2017, 122, 434–445, DOI:10.1016/j.carbon.2017.06.083.
- J. Xia, F. Chen, J. Li and N. Tao, Measurement of the Quantum Capacitance of Graphene, Nat. Nanotechnol., 2009, 4(8), 505–509, DOI:10.1038/nnano.2009.177.
- M. D. Stoller, C. W. Magnuson, Y. Zhu, S. Murali, J. W. Suk, R. Piner and R. S. Ruoff, Interfacial Capacitance of Single Layer Graphene, Energy Environ. Sci., 2011, 4(11), 4685–4689, 10.1039/C1EE02322E.
- J. J. Yoo, K. Balakrishnan, J. Huang, V. Meunier, B. G. Sumpter, A. Srivastava, M. Conway, A. L. Mohana Reddy, J. Yu, R. Vajtai and P. M. Ajayan, Ultrathin Planar Graphene Supercapacitors, Nano Lett., 2011, 11(4), 1423–1427, DOI:10.1021/nl200225j.
- Y. Zhang, Q. Zou, H. S. Hsu, S. Raina, Y. Xu, J. B. Kang, J. Chen, S. Deng, N. Xu and W. P. Kang, Morphology Effect of Vertical Graphene on the High Performance of Supercapacitor Electrode, ACS Appl. Mater. Interfaces, 2016, 8(11), 7363–7369, DOI:10.1021/acsami.5b12652.
- J. R. Miller, R. A. Outlaw and B. C. Holloway, Graphene Electric Double Layer Capacitor with Ultra-High-Power Performance, Electrochimica Acta, 2011, 56(28), 10443–10449, DOI:10.1016/j.electacta.2011.05.122.
- Y.-C. Wu, J. Ye, G. Jiang, K. Ni, N. Shu, P.-L. Taberna, Y. Zhu and P. Simon, Electrochemical Characterization of Single Layer Graphene/Electrolyte Interface: Effect of Solvent on the Interfacial Capacitance, Angew. Chem., Int. Ed., 2021, 60(24), 13317–13322, DOI:10.1002/anie.202017057.
- S. S. Kwon, J. Choi, M. Heiranian, Y. Kim, W. J. Chang, P. M. Knapp, M. C. Wang, J. M. Kim, N. R. Aluru, W. I. Park and S. Nam, Electrical Double Layer of Supported Atomically Thin Materials, Nano Lett., 2019, 19(7), 4588–4593, DOI:10.1021/acs.nanolett.9b01563.
- H. Yang, Z. Bo, J. Yang, J. Kong, X. Chen, J. Yan and K. Cen, Substrate Effects in Graphene-Based Electric Double-Layer Capacitors: The Pivotal Interplays between Ions and Solvents, ChemElectroChem, 2017, 4(11), 2966–2974, DOI:10.1002/celc.201700733.
- Y. Yi, G. Weinberg, M. Prenzel, M. Greiner, S. Heumann, S. Becker and R. Schlögl, Electrochemical Corrosion of a Glassy Carbon Electrode, Catal. Today, 2017, 295, 32–40, DOI:10.1016/j.cattod.2017.07.013.
- S. Cherevko, S. Geiger, O. Kasian, N. Kulyk, J.-P. Grote, A. Savan, B. R. Shrestha, S. Merzlikin, B. Breitbach, A. Ludwig and K. J. J. Mayrhofer, Oxygen and Hydrogen Evolution Reactions on Ru, RuO2, Ir, and IrO2 Thin Film Electrodes in Acidic and Alkaline Electrolytes: A Comparative Study on Activity and Stability, Catal. Today, 2016, 262, 170–180, DOI:10.1016/j.cattod.2015.08.014.
- C. Roy, R. R. Rao, K. A. Stoerzinger, J. Hwang, J. Rossmeisl, I. Chorkendorff, Y. Shao-Horn and I. E. L. Stephens, Trends in Activity and Dissolution on RuO2 under Oxygen Evolution Conditions: Particles versus Well-Defined Extended Surfaces, ACS Energy Lett., 2018, 3(9), 2045–2051, DOI:10.1021/acsenergylett.8b01178.
- H.-S. Oh, H. N. Nong, T. Reier, A. Bergmann and M. Gliech, Ferreira de Araújo, J.; Willinger, E.; Schlögl, R.; Teschner, D.; Strasser, P. Electrochemical Catalyst–Support Effects and Their Stabilizing Role for IrOx Nanoparticle Catalysts during the Oxygen Evolution Reaction, J. Am. Chem. Soc., 2016, 138(38), 12552–12563, DOI:10.1021/jacs.6b07199.
- I. S. Filimonenkov, C. Bouillet, G. Kéranguéven, P. A. Simonov, G. A. Tsirlina and E. R. Savinova, Carbon Materials as Additives to the OER Catalysts: RRDE Study of Carbon Corrosion at High Anodic Potentials, Electrochimica Acta, 2019, 321, 134657, DOI:10.1016/j.electacta.2019.134657.
- Y. Matsumoto and E. Sato, Electrocatalytic Properties of Transition Metal Oxides for Oxygen Evolution Reaction, Mater. Chem. Phys., 1986, 14(5), 397–426, DOI:10.1016/0254-0584(86)90045-3.
- P. J. Boddy, Oxygen Evolution on Semiconducting TiO2, J. Electrochem. Soc., 1968, 115(2), 199, DOI:10.1149/1.2411080.
- C. A. Goss, J. C. Brumfield, E. A. Irene and R. W. Murray, Imaging the Incipient Electrochemical Oxidation of Highly Oriented Pyrolytic Graphite, Anal. Chem., 1993, 65(10), 1378–1389, DOI:10.1021/ac00058a014.
- R. E. Panzer and P. J. Elving, Nature of the Surface Compounds and Reactions Observed on Graphite Electrodes, Electrochimica Acta, 1975, 20(9), 635–647, DOI:10.1016/0013-4686(75)90061-4.
- L. R. Faulkner and A. J. Bard, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, NY, 2nd edn, 2001 Search PubMed.
- F. Zoller, S. Häringer, D. Böhm, J. Luxa, Z. Sofer and D. Fattakhova-Rohlfing, Carbonaceous Oxygen Evolution Reaction Catalysts: From Defect and Doping-Induced Activity over Hybrid Compounds to Ordered Framework Structures, Small, 2021, 17(48), 2007484, DOI:10.1002/smll.202007484.
- C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, A Review of Electrolyte Materials and Compositions for Electrochemical Supercapacitors, Chem. Soc. Rev., 2015, 44(21), 7484–7539, 10.1039/C5CS00303B.
- E. Redondo, L. W. L. Fevre, R. Fields, R. Todd, A. J. Forsyth and R. A. W. Dryfe, Enhancing Supercapacitor Energy Density by Mass-Balancing of Graphene Composite Electrodes, Electrochimica Acta, 2020, 360, 136957, DOI:10.1016/j.electacta.2020.136957.
- G. Jiang, C. Cheng, D. Li and J. Z. Liu, Molecular Dynamics Simulations of the Electric Double Layer Capacitance of Graphene Electrodes in Mono-Valent Aqueous Electrolytes, Nano Res., 2016, 9(1), 174–186, DOI:10.1007/s12274-015-0978-5.
- C. Melios, C. E. Giusca, V. Panchal and O. Kazakova, Water on Graphene: Review of Recent Progress, 2D Mater., 2018, 5(2), 022001, DOI:10.1088/2053-1583/aa9ea9.
- T. A. Ho and A. Striolo, Polarizability Effects in Molecular Dynamics Simulations of the Graphene-Water Interface, J. Chem. Phys., 2013, 138(5), 054117, DOI:10.1063/1.4789583.
- X. Li, L. Li, Y. Wang, H. Li and X. Bian, Wetting and Interfacial Properties of Water on the Defective Graphene, J. Phys. Chem. C, 2013, 117(27), 14106–14112, DOI:10.1021/jp4045258.
- T. A. Ho and A. Striolo, Molecular Dynamics Simulation of the Graphene–Water Interface: Comparing Water Models, Mol. Simul., 2014, 40(14), 1190–1200, DOI:10.1080/08927022.2013.854893.
- G. Tocci, L. Joly and A. Michaelides, Friction of Water on Graphene and Hexagonal Boron Nitride from Ab Initio Methods: Very Different Slippage Despite Very Similar Interface Structures, Nano Lett., 2014, 14(12), 6872–6877, DOI:10.1021/nl502837d.
- M. Ma, G. Tocci, A. Michaelides and G. Aeppli, Fast Diffusion of Water Nanodroplets on Graphene, Nat. Mater., 2016, 15(1), 66–71, DOI:10.1038/nmat4449.
- T. Dreher, C. Lemarchand, N. Pineau, E. Bourasseau, A. Ghoufi and P. Malfreyt, Calculation of the Interfacial Tension of the Graphene-Water Interaction by Molecular Simulations, J. Chem. Phys., 2019, 150(1), 014703, DOI:10.1063/1.5048576.
- M. Chiricotto, F. Martelli, G. Giunta and P. Carbone, Role of Long-Range Electrostatic Interactions and Local Topology of the Hydrogen Bond Network in the Wettability of Fully and Partially Wetted Single and Multilayer Graphene, J. Phys. Chem. C, 2021, 125(11), 6367–6377, DOI:10.1021/acs.jpcc.0c11455.
- G. Cicero, J. C. Grossman, E. Schwegler, F. Gygi and G. Galli, Water Confined in Nanotubes and between Graphene Sheets: A First Principle Study, J. Am. Chem. Soc., 2008, 130, 1871–1878 CrossRef CAS PubMed.
- T. O. Wehling, A. I. Lichtenstein and M. I. Katsnelson, First-Principles Studies of Water Adsorption on Graphene: The Role of the Substrate, Appl. Phys. Lett., 2008, 93(20), 202110, DOI:10.1063/1.3033202.
- O. Leenaerts, B. Partoens and F. M. Peeters, Adsorption of H 2 O, N H 3, CO, N O 2, and NO on Graphene: A First-Principles Study, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(12), 125416, DOI:10.1103/PhysRevB.77.125416.
- G. R. Jenness, O. Karalti and K. D. Jordan, Benchmark Calculations of Water–Acene Interaction Energies: Extrapolation to the Water–Graphene Limit and Assessment of Dispersion–Corrected DFT Methods, Phys. Chem. Chem. Phys., 2010, 12, 6375–6381 RSC.
- R. R. Q. Freitas, R. Rivelino, F. Mota, B. de and C. M. C. de Castilho, DFT Studies of the Interactions of a Graphene Layer with Small Water Aggregates, J. Phys. Chem. A, 2011, 115(44), 12348–12356, DOI:10.1021/jp208279a.
- J. Ma, A. Michaelides, D. Alfè, L. Schimka, G. Kresse and E. Wang, Adsorption and Diffusion of Water on Graphene from First Principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(3), 033402, DOI:10.1103/PhysRevB.84.033402.
- E. Voloshina, D. Usvyat, M. Schütz, Y. Dedkov and B. Paulus, On the Physisorption of Water on Graphene: A CCSD(T) Study, Phys. Chem. Chem. Phys., 2011, 13(25), 12041, 10.1039/c1cp20609e.
- L. D’Urso, C. Satriano, G. Forte, G. Compagnini and O. Puglisi, Water Structure and Charge Transfer Phenomena at the Liquid–Graphene Interface, Phys. Chem. Chem. Phys., 2012, 14(42), 14605, 10.1039/c2cp42249b.
- I. Hamada, Adsorption of Water on Graphene: A van der Waals Density Functional Study, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(19), 195436, DOI:10.1103/PhysRevB.86.195436.
- X. Li, J. Feng, E. Wang, S. Meng, J. Klimeš and A. Michaelides, Influence of Water on the Electronic Structure of Metal-Supported Graphene: Insights from van der Waals Density Functional Theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(8), 085425, DOI:10.1103/PhysRevB.85.085425.
- G. Levita, P. Restuccia and M. C. Righi, Graphene and MoS2 Interacting with Water: A Comparison by Ab Initio Calculations, Carbon, 2016, 107, 878–884, DOI:10.1016/j.carbon.2016.06.072.
- J. G. Brandenburg, A. Zen, M. Fitzner, B. Ramberger, G. Kresse, T. Tsatsoulis, A. Grüneis, A. Michaelides and D. Alfè, Physisorption of Water on Graphene: Subchemical Accuracy from Many-Body Electronic Structure Methods, J. Phys. Chem. Lett., 2019, 10(3), 358–368, DOI:10.1021/acs.jpclett.8b03679.
- M. Hernández, A. Cabo Montes de Oca, M. Oliva-Leyva and G. Naumis, How Water Makes Graphene Metallic, Phys. Lett. A, 2019, 383(29), 125904, DOI:10.1016/j.physleta.2019.125904.
- A. A. Chialvo and P. T. Cummings, Aqua Ions–Graphene Interfacial and Confinement Behavior: Insights from Isobaric–Isothermal Molecular Dynamics, J. Phys. Chem. A, 2011, 115(23), 5918–5927, DOI:10.1021/jp110318n.
- W. A. Steele, The Physical Interaction of Gases with Crystalline Solids, Surf. Sci., 1973, 36, 316 CrossRef.
- B. Roux, The Calculation of the Potential of Mean Force Using Computer Simulations, Comput. Phys. Commun., 1995, 91(1–3), 275–282, DOI:10.1016/0010-4655(95)00053-I.
- J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105(8), 2999–3094, DOI:10.1021/cr9904009.
- A. R. Finney, I. J. McPherson, P. R. Unwin and M. Salvalaglio, Electrochemistry, Ion Adsorption and Dynamics in the Double Layer: A Study of NaCl(Aq) on Graphite, Chem. Sci., 2021, 12(33), 11166–11180, 10.1039/D1SC02289J.
- J. Dočkal, F. Moučka and M. Lísal, Molecular Dynamics of Graphene–Electrolyte Interface: Interfacial Solution Structure and Molecular Diffusion, J. Phys. Chem. C, 2019, 123(43), 26379–26396, DOI:10.1021/acs.jpcc.9b07487.
- J. Dočkal, M. Lísal and F. Moučka, Molecular Dynamics of the Interfacial Solution Structure of Alkali-Halide Electrolytes at Graphene Electrodes, J. Mol. Liq., 2022, 118776, DOI:10.1016/j.molliq.2022.118776.
- S. Singla, E. Anim-Danso, A. E. Islam, Y. Ngo, S. S. Kim, R. R. Naik and A. Dhinojwala, Insight on Structure of Water and Ice Next to Graphene Using Surface-Sensitive Spectroscopy, ACS Nano, 2017, 11(5), 4899–4906, DOI:10.1021/acsnano.7b01499.
- Y. Zhang, S. Furyk, D. E. Bergbreiter and P. S. Cremer, Specific Ion Effects on the Water Solubility of Macromolecules: PNIPAM and the Hofmeister Series, J. Am. Chem. Soc., 2005, 127(41), 14505–14510, DOI:10.1021/ja0546424.
- Y. Zhang and P. Cremer, Interactions between Macromolecules and Ions: The Hofmeister Series, Curr. Opin. Chem. Biol., 2006, 10(6), 658–663, DOI:10.1016/j.cbpa.2006.09.020.
- Z. Li, Y. Wang, A. Kozbial, G. Shenoy, F. Zhou, R. McGinley, P. Ireland, B. Morganstein, A. Kunkel, S. P. Surwade, L. Li and H. Liu, Effect of Airborne Contaminants on the Wettability of Supported Graphene and Graphite, Nat. Mater., 2013, 12(10), 925–931, DOI:10.1038/nmat3709.
- C.-J. Shih, Q. H. Wang, S. Lin, K.-C. Park, Z. Jin, M. S. Strano and D. Blankschtein, Breakdown in the Wetting Transparency of Graphene, Phys. Rev. Lett., 2012, 109(17), 176101, DOI:10.1103/PhysRevLett.109.176101.
- C.-J. Shih, M. S. Strano and D. Blankschtein, Wetting Translucency of Graphene, Nat. Mater., 2013, 12(10), 866–869, DOI:10.1038/nmat3760.
- A. Kozbial, C. Trouba, H. Liu and L. Li, Characterization of the Intrinsic Water Wettability of Graphite Using Contact Angle Measurements: Effect of Defects on Static and Dynamic Contact Angles, Langmuir, 2017, 33(4), 959–967, DOI:10.1021/acs.langmuir.6b04193.
- N. Ojaghlou, D. Bratko, M. Salanne, M. Shafiei and A. Luzar, Solvent–Solvent Correlations across Graphene: The Effect of Image Charges, ACS Nano, 2020, 14(7), 7987–7998, DOI:10.1021/acsnano.9b09321.
- M. Pykal, M. Langer, B. Blahová Prudilová, P. Banáš and M. Otyepka, Ion Interactions across Graphene in Electrolyte Aqueous Solutions, J. Phys. Chem. C, 2019, 123(15), 9799–9806, DOI:10.1021/acs.jpcc.8b12055.
- G. Lamoureux, E. Harder, I. V. Vorobyov, B. Roux and A. D. MacKerell, A Polarizable Model of Water for Molecular Dynamics Simulations of Biomolecules, Chem. Phys. Lett., 2006, 418(1–3), 245–249, DOI:10.1016/j.cplett.2005.10.135.
- H. Yu, T. W. Whitfield, E. Harder, G. Lamoureux, I. Vorobyov, V. M. Anisimov, A. D. MacKerell and B. Roux, Simulating Monovalent and Divalent Ions in Aqueous Solution Using a Drude Polarizable Force Field, J. Chem. Theory Comput., 2010, 6(3), 774–786, DOI:10.1021/ct900576a.
- N. Di Pasquale, J. D. Elliott, P. Hadjidoukas and P. Carbone, Dynamically Polarizable Force Fields for Surface Simulations via Multi-Output Classification Neural Networks, J. Chem. Theory Comput., 2021, 17(7), 4477–4485, DOI:10.1021/acs.jctc.1c00360.
- J. S. Binkley, J. A. Pople and W. J. Hehre, Self-Consistent Molecular Orbital Methods. 21. Small Split-Valence Basis Sets for First-Row Elements, J. Am. Chem. Soc., 1980, 102(3), 939–947, DOI:10.1021/ja00523a008.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, Self-consistent Molecular Orbital Methods. XXIII. A Polarization-type Basis Set for Second-row Elements, J. Chem. Phys., 1982, 77(7), 3654–3665, DOI:10.1063/1.444267.
- J.-D. Chai and M. Head-Gordon, Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections, Phys. Chem. Chem. Phys., 2008, 10(44), 6615, 10.1039/b810189b.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, Th Frauenheim, S. Suhai and G. Seifert, Self-Consistent-Charge Density-Functional Tight-Binding Method for Simulations of Complex Materials Properties, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(11), 7260–7268, DOI:10.1103/PhysRevB.58.7260.
- J. L. F. Abascal and C. Vega, A General Purpose Model for the Condensed Phases of Water: TIP4P/2005, J. Chem. Phys., 2005, 123(23), 234505, DOI:10.1063/1.2121687.
- I. M. Zeron, J. L. F. Abascal and C. Vega, A Force Field of Li+, Na+, K+, Mg2+, Ca2+, Cl−, and SO42− in Aqueous Solution Based on the TIP4P/2005 Water Model and Scaled Charges for the Ions, J. Chem. Phys., 2019, 151(13), 134504, DOI:10.1063/1.5121392.
- S. Yasuda, K. Tamura, M. Kato, H. Asaoka and I. Yagi, Electrochemically Driven Specific Alkaline Metal Cation Adsorption on a Graphene Interface, J. Phys. Chem. C, 2021, 125(40), 22154–22162, DOI:10.1021/acs.jpcc.1c03322.
- G. Colherinhas, E. E. Fileti and V. V. Chaban, The Band Gap of Graphene Is Efficiently Tuned by Monovalent Ions, J. Phys. Chem. Lett., 2015, 6(2), 302–307, DOI:10.1021/jz502601z.
- A. D. Becke and M. R. Roussel, Exchange Holes in Inhomogeneous Systems: A Coordinate-Space Model, Phys. Rev. A, 1989, 39(8), 3761–3767, DOI:10.1103/PhysRevA.39.3761.
- S. Sangavi, N. Santhanamoorthi and S. Vijayakumar, Density Functional Theory Study on the Adsorption of Alkali Metal Ions with Pristine and Defected Graphene Sheet, Mol. Phys., 2019, 117(4), 462–473, DOI:10.1080/00268976.2018.1523480.
- Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals, Theor. Chem. Acc., 2008, 120(1), 215–241, DOI:10.1007/s00214-007-0310-x.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions, J. Chem. Phys., 1980, 72(1), 650–654, DOI:10.1063/1.438955.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules, J. Chem. Phys., 1971, 54(2), 724–728, DOI:10.1063/1.1674902.
- F. Xiaozhen, L. Xing, H. Zhenglin, Z. Kaiyuan and S. Guosheng, DFT Study of Common Anions Adsorption at Graphene Surface Due to Anion-π Interaction, J. Mol. Model., 2022, 28(8), 225, DOI:10.1007/s00894-022-05218-4.
- A. D. Becke, Density-functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98(7), 5648–5652, DOI:10.1063/1.464913.
- J.-D. Chai and M. Head-Gordon, Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections, Phys. Chem. Chem. Phys., 2008, 10(44), 6615–6620, 10.1039/B810189B.
- E. Olsson, G. Chai, M. Dove and Q. Cai, Adsorption and Migration of Alkali Metals (Li, Na, and K) on Pristine and Defective Graphene Surfaces, Nanoscale, 2019, 11(12), 5274–5284, 10.1039/C8NR10383F.
- E. Olsson, T. Hussain, A. Karton and Q. Cai, The Adsorption and Migration Behavior of Divalent Metals (Mg, Ca, and Zn) on Pristine and Defective Graphene, Carbon, 2020, 163, 276–287, DOI:10.1016/j.carbon.2020.03.028.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465, DOI:10.1002/jcc.21759.
- C. Zhan, M. R. Cerón, S. A. Hawks, M. Otani, B. C. Wood, T. A. Pham, M. Stadermann and P. G. Campbell, Specific Ion Effects at Graphitic Interfaces, Nat. Commun., 2019, 10(1), 4858, DOI:10.1038/s41467-019-12854-7.
- S. Nishihara and M. Otani, Hybrid Solvation Models for Bulk, Interface, and Membrane: Reference Interaction Site Methods Coupled with Density Functional Theory, Phys. Rev. B, 2017, 96(11), 115429, DOI:10.1103/PhysRevB.96.115429.
- M. Kocman, M. Pykal and P. Jurečka, Electric Quadrupole Moment of Graphene and Its Effect on Intermolecular Interactions, Phys. Chem. Chem. Phys., 2014, 16(7), 3144, 10.1039/c3cp54701a.
- E. Poli, K. H. Jong and A. Hassanali, Charge Transfer as a Ubiquitous Mechanism in Determining the Negative Charge at Hydrophobic Interfaces, Nat. Commun., 2020, 11(1), 901, DOI:10.1038/s41467-020-14659-5.
- D. A. C. Silva, A. J. P. da; Neto, A. M. Pascon, E. E. Fileti, L. R. C. Fonseca and H. G. Zanin, Exploring Doped or Vacancy-Modified Graphene-Based Electrodes for Applications in Asymmetric Supercapacitors, Phys. Chem. Chem. Phys., 2020, 22(7), 3906–3913, 10.1039/C9CP06495H.
- H. Yang, J. Yang, Z. Bo, X. Chen, X. Shuai, J. Kong, J. Yan and K. Cen, Kinetic-Dominated Charging Mechanism within Representative Aqueous Electrolyte-Based Electric Double-Layer Capacitors, J. Phys. Chem. Lett., 2017, 8(15), 3703–3710, DOI:10.1021/acs.jpclett.7b01525.
- J.-F. Olivieri, J. T. Hynes and D. Laage, Confined Water's Dielectric Constant Reduction Is Due to the Surrounding Low Dielectric Media and Not to Interfacial Molecular Ordering. J. Phys, Chem. Lett., 2021, 12(17), 4319–4326, DOI:10.1021/acs.jpclett.1c00447.
- J. Maier, Nanoionics: Ion Transport and Electrochemical Storage in Confined Systems, Materials for Sustainable Energy, Co-Published with Macmillan Publishers Ltd, UK, 2010, pp. 160–170. DOI:10.1142/9789814317665_0023.
- J. Gao, Y. Feng, W. Guo and L. Jiang, Nanofluidics in Two-Dimensional Layered Materials: Inspirations from Nature, Chem. Soc. Rev., 2017, 46(17), 5400–5424, 10.1039/C7CS00369B.
- A. R. Koltonow and J. Huang, Two-Dimensional Nanofluidics, Science, 2016, 351, 1395–1396, DOI:10.1126/science.aaf5289.
- Z. Wei, M. Chiricotto, J. D. Elliott, F. Martelli and P. Carbone, Wettability of Graphite under 2D Confinement, Carbon, 2022, 198, 132–141, DOI:10.1016/j.carbon.2022.07.019.
- C. D. Williams, Z. Wei, M. R. Shaharudin and P. bin; Carbone, A Molecular Simulation Study into the Stability of Hydrated Graphene Nanochannels Used in Nanofluidics Devices, Nanoscale, 2022, 14(9), 3467–3479, 10.1039/D1NR08275B.
- S. Faucher, N. Aluru, M. Z. Bazant, D. Blankschtein, A. H. Brozena, J. Cumings, J. Pedro de Souza, M. Elimelech, R. Epsztein, J. T. Fourkas, A. G. Rajan, H. J. Kulik, A. Levy, A. Majumdar, C. Martin, M. McEldrew, R. P. Misra, A. Noy, T. A. Pham, M. Reed, E. Schwegler, Z. Siwy, Y. Wang and M. Strano, Critical Knowledge Gaps in Mass Transport through Single-Digit Nanopores: A Review and Perspective, J. Phys. Chem. C, 2019, 123(35), 21309–21326, DOI:10.1021/acs.jpcc.9b02178.
- R. H. Tunuguntla, R. Y. Henley, Y.-C. Yao, T. A. Pham, M. Wanunu and A. Noy, Enhanced Water Permeability and Tunable Ion Selectivity in Subnanometer Carbon Nanotube Porins, Science, 2017, 357(6353), 792–796, DOI:10.1126/science.aan2438.
- S. Faucher, M. Kuehne, V. B. Koman, N. Northrup, D. Kozawa, Z. Yuan, S. X. Li, Y. Zeng, T. Ichihara, R. P. Misra, N. Aluru, D. Blankschtein and M. S. Strano, Diameter Dependence of Water Filling in Lithographically Segmented Isolated Carbon Nanotubes, ACS Nano, 2021, 15(2), 2778–2790, DOI:10.1021/acsnano.0c08634.
- B. Radha, A. Esfandiar, F. C. Wang, A. P. Rooney, K. Gopinadhan, A. Keerthi, A. Mishchenko, A. Janardanan, P. Blake, L. Fumagalli, M. Lozada-Hidalgo, S. Garaj, S. J. Haigh, I. V. Grigorieva, H. A. Wu and A. K. Geim, Molecular Transport through Capillaries Made with Atomic-Scale Precision, Nature, 2016, 538(7624), 222–225, DOI:10.1038/nature19363.
- L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. S. Novoselov and A. K. Geim, Anomalously Low Dielectric Constant of Confined Water, Science, 2018, 360, 1339–1342, DOI:10.1126/science.aat4191.
- A. Keerthi, S. Goutham, Y. You, P. Iamprasertkun, R. A. W. Dryfe, A. K. Geim and B. Radha, Water Friction in Nanofluidic Channels Made from Two-Dimensional Crystals, Nat. Commun., 2021, 12(1), 3092, DOI:10.1038/s41467-021-23325-3.
- E. Secchi, S. Marbach, A. Niguès, D. Stein, A. Siria and L. Bocquet, Massive Radius-Dependent Flow Slippage in Carbon Nanotubes, Nature, 2016, 537(7619), 210–213, DOI:10.1038/nature19315.
- A. Esfandiar, B. Radha, F. C. Wang, Q. Yang, S. Hu, S. Garaj, R. R. Nair, A. K. Geim and K. Gopinadhan, Size Effect in Ion Transport through Angstrom-Scale Slits, Science, 2017, 358, 511–513, DOI:10.1126/science.aan5275.
- K. Gopinadhan, S. Hu, A. Esfandiar, M. Lozada-Hidalgo, F. C. Wang, Q. Yang, A. V. Tyurnina, A. Keerthi, B. Radha and A. K. Geim, Complete Steric Exclusion of Ions and Proton Transport through Confined Monolayer Water, Science, 2019, 363, 145–148, DOI:10.1126/science.aau6771.
- W. Jung, J. Kim, S. Kim, H. G. Park, Y. Jung and C.-S. Han, A Novel Fabrication of 3.6 Nm High Graphene Nanochannels for Ultrafast Ion Transport, Adv. Mater., 2017, 29(17), 1605854, DOI:10.1002/adma.201605854.
- C. Cheng, G. Jiang, G. P. Simon, J. Z. Liu and D. Li, Low-Voltage Electrostatic Modulation of Ion Diffusion through Layered Graphene-Based Nanoporous Membranes, Nat. Nanotechnol., 2018, 13(8), 685–690, DOI:10.1038/s41565-018-0181-4.
- T. Mouterde, A. Keerthi, A. R. Poggioli, S. A. Dar, A. Siria, A. K. Geim, L. Bocquet and B. Radha, Molecular Streaming and Its Voltage Control in Ångström-Scale Channels, Nature, 2019, 567(7746), 87–90, DOI:10.1038/s41586-019-0961-5.
- L. A. Richards, A. I. Schäfer, B. S. Richards and B. Corry, The Importance of Dehydration in Determining Ion Transport in Narrow Pores, Small, 2012, 8(11), 1701–1709, DOI:10.1002/smll.201102056.
- J. Abraham, K. S. Vasu, C. D. Williams, K. Gopinadhan, Y. Su, C. T. Cherian, J. Dix, E. Prestat, S. J. Haigh, I. V. Grigorieva, P. Carbone, A. K. Geim and R. R. Nair, Tunable Sieving of Ions Using Graphene Oxide Membranes, Nat. Nanotechnol., 2017, 12(6), 546–550, DOI:10.1038/nnano.2017.21.
- C. D. Williams and P. Carbone, Selective Removal of Technetium from Water Using Graphene Oxide Membranes, Environ. Sci. Technol., 2016, 50(7), 3875–3881, DOI:10.1021/acs.est.5b06032.
- D. Muñoz-Santiburcio and D. Marx, Confinement-Controlled Aqueous Chemistry within Nanometric Slit Pores, Chem. Rev., 2021, 121(11), 6293–6320, DOI:10.1021/acs.chemrev.0c01292.
- P. Loche, C. Ayaz, A. Schlaich, D. J. Bonthuis and R. R. Netz, Breakdown of Linear Dielectric Theory for the Interaction between Hydrated Ions and Graphene, J. Phys. Chem. Lett., 2018, 9(22), 6463–6468, DOI:10.1021/acs.jpclett.8b02473.
- A. Schlaich, E. W. Knapp and R. R. Netz, Water Dielectric Effects in Planar Confinement, Phys. Rev. Lett., 2016, 117(4), 048001, DOI:10.1103/PhysRevLett.117.048001.
- M. H. Motevaselian and N. R. Aluru, Universal Reduction in Dielectric Response of Confined Fluids, ACS Nano, 2020, 14(10), 12761–12770, DOI:10.1021/acsnano.0c03173.
- T. A. Ho and A. Striolo, Promising Performance Indicators for Water Desalination and Aqueous Capacitors Obtained by Engineering the Electric Double Layer in Nano-Structured Carbon Electrodes, J. Phys. Chem. C, 2015, 119(6), 3331–3337, DOI:10.1021/jp5084899.
- J. Muscatello, F. Jaeger, O. K. Matar and E. A. Müller, Optimizing Water Transport through Graphene-Based Membranes: Insights from Nonequilibrium Molecular Dynamics, ACS Appl. Mater. Interfaces, 2016, 8(19), 12330–12336, DOI:10.1021/acsami.5b12112.
- J. Dix, L. Lue and P. Carbone, Why Different Water Models Predict Different Structures under 2D Confinement, J. Comput. Chem., 2018, 39(25), 2051–2059, DOI:10.1002/jcc.25369.
- V. Satarifard, M. Mousaei, F. Hadadi, J. Dix, M. Sobrino Fernandez, P. Carbone, J. Beheshtian, F. M. Peeters and M. Neek-Amal, Reversible Structural Transition in Nanoconfined Ice, Phys. Rev. B, 2017, 95(6), 064105, DOI:10.1103/PhysRevB.95.064105.
- K. Falk, F. Sedlmeier, L. Joly, R. R. Netz and L. Bocquet, Molecular Origin of Fast Water Transport in Carbon Nanotube Membranes: Superlubricity versus Curvature Dependent Friction, Nano Lett., 2010, 10(10), 4067–4073, DOI:10.1021/nl1021046.
- A. P. Markesteijn, R. Hartkamp, S. Luding and J. Westerweel, A Comparison of the Value of Viscosity for Several Water Models Using Poiseuille Flow in a Nano-Channel, J. Chem. Phys., 2012, 136(13), 134104, DOI:10.1063/1.3697977.
- M. C. F. Wander and K. L. Shuford, Molecular Dynamics Study of Interfacial Confinement Effects of Aqueous NaCl Brines in Nanoporous Carbon, J. Phys. Chem. C, 2010, 114(48), 20539–20546, DOI:10.1021/jp104972e.
- M. C. F. Wander and K. L. Shuford, Electrolyte Effects in a Model System for Mesoporous Carbon Electrodes, J. Phys. Chem. C, 2011, 115(11), 4904–4908, DOI:10.1021/jp1089068.
- J. Sala, E. Guàrdia and J. Martí, Specific Ion Effects in Aqueous Eletrolyte Solutions Confined within Graphene Sheets at the Nanometric Scale, Phys. Chem. Chem. Phys., 2012, 14(30), 10799–10808, 10.1039/C2CP40537G.
- B. E. Conway, J. O. Bockris and I. A. Ammar, The Dielectric Constant of the Solution in the Diffuse and Helmholtz Double Layers at a Charged Interface in Aqueous Solution, Trans. Faraday Soc., 1951, 47, 756, 10.1039/tf9514700756.
- J. Kong, Z. Bo, H. Yang, J. Yang, X. Shuai, J. Yan and K. Cen, Temperature Dependence of Ion Diffusion Coefficients in NaCl Electrolyte Confined within Graphene Nanochannels, Phys. Chem. Chem. Phys., 2017, 19(11), 7678–7688, 10.1039/C6CP08752C.
- R. K. Kalluri, D. Konatham and A. Striolo, Aqueous NaCl Solutions within Charged Carbon-Slit Pores: Partition Coefficients and Density Distributions from Molecular Dynamics Simulations, J. Phys. Chem. C, 2011, 115(28), 13786–13795, DOI:10.1021/jp203086x.
- G. Feng, R. Qiao, J. Huang, B. G. Sumpter and V. Meunier, Ion Distribution in Electrified Micropores and Its Role in the Anomalous Enhancement of Capacitance, ACS Nano, 2010, 4(4), 2382–2390, DOI:10.1021/nn100126w.
- Z. Bo, H. Yang, S. Zhang, J. Yang, J. Yan and K. Cen, Molecular Insights into Aqueous NaCl Electrolytes Confined within Vertically-Oriented Graphenes, Sci. Rep., 2015, 5(1), 14652, DOI:10.1038/srep14652.
- H. Yang, X. Zhang, J. Yang, Z. Bo, M. Hu, J. Yan and K. Cen, Molecular Origin of Electric Double-Layer Capacitance at Multilayer Graphene Edges, J. Phys. Chem. Lett., 2017, 8(1), 153–160, DOI:10.1021/acs.jpclett.6b02659.
- P. Iamprasertkun, W. Hirunpinyopas, A. Keerthi, B. Wang, B. Radha, M. A. Bissett and R. A. W. Dryfe, Capacitance of Basal Plane and Edge-Oriented Highly Ordered Pyrolytic Graphite: Specific Ion Effects, J. Phys. Chem. Lett., 2019, 10(3), 617–623, DOI:10.1021/acs.jpclett.8b03523.
- L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, “Water-in-Salt” Electrolyte Enables High-Voltage Aqueous Lithium-Ion Chemistries, Science, 2015, 350(6263), 938–943, DOI:10.1126/science.aab1595.
- N. Dubouis, P. Lemaire, B. Mirvaux, E. Salager, M. Deschamps and A. Grimaud, The Role of the Hydrogen Evolution Reaction in the Solid–Electrolyte Interphase Formation Mechanism for “Water-in-Salt” Electrolytes, Energy Environ. Sci., 2018, 11(12), 3491–3499, 10.1039/C8EE02456A.
| This journal is © The Royal Society of Chemistry 2022 |