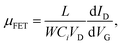Magnetoresistance of high mobility HgTe quantum dot films with controlled charging†
Menglu
Chen
 *a,
Xinzheng
Lan
b,
Margaret H.
Hudson
b,
Guohua
Shen
b,
Peter B.
Littlewood
c,
Dmitri V.
Talapin
b and
Philippe
Guyot-Sionnest
*bc
*a,
Xinzheng
Lan
b,
Margaret H.
Hudson
b,
Guohua
Shen
b,
Peter B.
Littlewood
c,
Dmitri V.
Talapin
b and
Philippe
Guyot-Sionnest
*bc
aSchool of Optics and Photonics, Beijing Institute of Technology, No. 5, Zhongguancun South Street, Beijing, China. E-mail: menglu@bit.edu.cn
bDepartment of Chemistry, The University of Chicago, 929 East 57th Street, Chicago, Illinois 60637, USA. E-mail: pgs@uchicago.edu
cDepartment of Physics, The University of Chicago, 929 East 57th Street, Chicago, Illinois 60637, USA
First published on 20th January 2022
Abstract
The magnetoresistance of HgTe quantum dot films, exhibiting a well-defined 1Se state charging and a relatively high mobility (1–10 cm2 V−1 s−1), is measured as a function of temperature down to 10 K and controlled occupation of the first electronic state. There is a positive-quadratic magnetoresistance which can be several 100% at low temperature and scales like x(1 − x) where x is the filling fraction of the lowest quantum dot state in the conduction band, 1Se. This positive magnetoresistance is orders of magnitude larger than the effect estimated from mobile carriers and it is attributed to the increased confinement induced by the magnetic field. There is also a negative magnetoresistance of 1–20% from 300 K to 10 K which is rather independent of the fractional occupation, and which follows a negative exponential dependence with the magnetic field. It can be empirically fit with an effective g-factor of ∼55 and it is tentatively attributed to the reduction of barrier heights by the Zeeman splitting of the 1Se state.
Introduction
Electronic transport of colloidal quantum dot (CQD) solids is a topic of basic interest1 of relevance to devices such as photodetectors,2 solar cells,3 and light emitting diodes.4 It has been widely studied using common methods like field-effect transistors (FET),5 the time-of-flight (TOF)6 technique and electrochemistry,7 giving useful information on mobility, carrier lifetime and doping. Magnetoresistance (MR) measurements open another window into the dispersion, dynamics and spins of charge carriers in mesoscopic structures. There is also much interest in magnetic doping of CQDs where the coupling between the magnetic moments and the CQD excitons provides giant effective g-factor,8 allows for magnetic polarons9,10 and produces strong magneto-optical effects.11 Therefore, CQDs present an opportunity for enhanced or novel magneto-optical and magneto-electronic properties by tailoring the energy levels and the strength of the Zeeman effect.12 Over the past decades, the use of charge stabilized CQDs has allowed to decrease the interparticle distance in CQD films resulting in much improved mobility and bandlike transport.13–16 In particular, simply dried HgTe CQD films have shown n and p-type mobility in the 1–10 cm2 V−1 s−1.17,18 They showed a strong modulation of the conductivity by the quantum dot state occupation, and bandlike transport, defined as an increasing mobility with reduced temperature, down to 70 K. In a hopping model, the high mobility implies hopping times in the 1–10 ps range which are orders of magnitude faster than in prior studies of CQD solid that showed state resolved transport. In addition, the Hall and drift mobility were similar in this high mobility solid, and this suggested the possibility of ballistic electronic motion at least in some extended domains.18 In the prior MR studies of CQD films, hoping times were in the >1 ns range, such that no electron coherence was expected,19 and all the MR effects were effectively local.20–22 A broad quadratic positive MR was attributed to the reduction of the interparticle coupling by the additional magnetic field confinement. A sharp positive MR was attributed to spin-blockade mediated by spin relaxation through the hyperfine interaction, similar to observations with weakly conductive organic films.23 This description was satisfactory in the low doping regime, ≤1 electron per dot, and with low enough electric field that would not promote tunnelling to different quantum dot states. The HgTe CQD films studied here may be in a quite different regime, with high mobility, bandlike transport, and well-resolved conductance modulation by the state charge occupation,18,24 such that the MR measurement might exhibit new effects and possible signs of delocalization and ballistic charge motion.Magnetoresistance: general features
The HgTe CQD films and substrates are made following a method previously reported.17,18 The HgTe quantum dots are synthesized using the long chain oleylamine as a surfactant for steric stabilization.25,26 Average sizes from 8 nm to 15 nm diameter are studied (TEM shown in ESI,† Fig. S1). The HgTe CQDs are spin-coated on a 300 nm SiO2/Si FET substrate that has been patterned with Au interdigitated electrodes for source and drain. Applying a gate to the Si substrate allows to tune the doping by up to several electrons for the CQD layer closest to the gate. The film thickness is kept to a few monolayers in order to have a significant effect of gating but complete device coverage, and the films are simply dried at room temperature. The device properties are stable in air such that the samples can then be loaded in a physical property measurement system (PPMS) for electrical characterization.
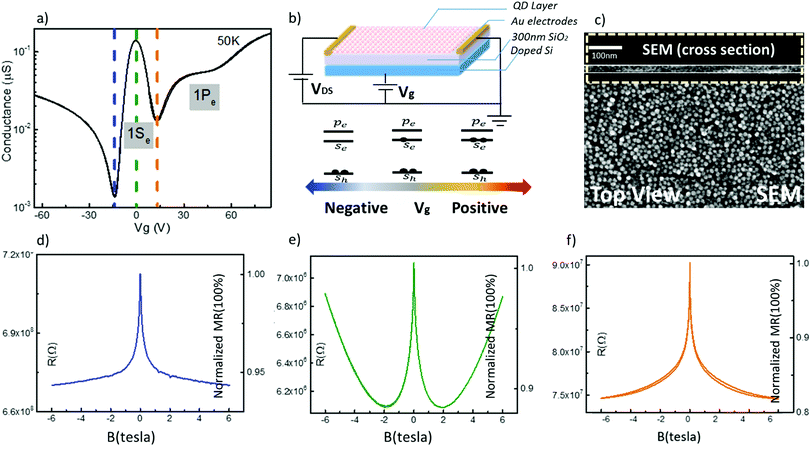
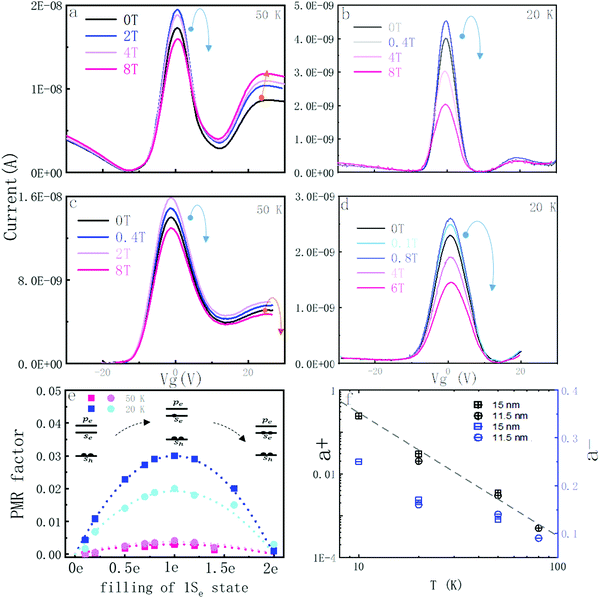
Fig. 1a shows a typical source–drain transfer curve as a function of the gate voltage at 50 K with high linear mobility 2.8 ± 0.5 cm2 V−1 s−1 at 1Se state.18 The modulation of the source–drain conductance with gate voltage is due to the filling of the quantum dot states 1Se and 1Pe which are the first two confined conduction band states in the quantum dots. As previously reported, the 1Se state shows a well-defined peak in the conductance.18 The next shoulder on the n-side is attributed to the 1Pe electrons state. Fig. 1b shows the FET device diagram and energy band structure while tuning gate potential. The estimate of the doping from the capacitance and size of the CQDs agrees quantitatively with the filling of the 1Se state, consistent with its two-fold degeneracy.18 The Hg2+ amount used during the solvent transfer is also used to control the doping.17 We could thus verify that the application of the gate does not introduce artificial MR by comparing samples that start with different doping. By measuring the MR with no gate or different gate voltage but for the same charging, the measurement results show no obvious difference between these samples (ESI,† 2). Fig. 1a corresponds to a doping of one electron in the 1Se state at zero gate bias. The 50 K MR at Vg = 0 V is shown in Fig. 1e. The normalized MR is defined as 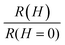 where H is the applied magnetic field. The MR initially goes quickly negative by ∼12% and then grows positive in a parabolic fashion. Fig. 1d and f show the MR at Vg = −15 V for a filled 1Se state and at Vg = +14 V for an empty 1Se state. In both cases, the MR varies little at high magnetic field. Exploring a range of charging is conveniently done by varying the gate potential at fixed magnetic field and temperature. The source–drain current curves at different magnetic fields for 15 nm and 11.5 nm diameter HgTe CQDs at 20 K and 50 K are shown in Fig. 2. These curves show a well resolved 1Se source–drain current peak with clear MR response. However, when the solids are gated at 1Pe state, there is no systematic MR behavior. As previously reported,18 the conductivity in the 1Pe state is strikingly lower than in the 1Se state at the temperatures shown in Fig. 2. This can be assigned to the splitting of the Pe states26 which effectively lowers the density of states, as well as the directional frustrations for transport along P-orbitals. The discussion will therefore focus on the charging of the 1Se but will not discuss MR in the 1Pe state.
where H is the applied magnetic field. The MR initially goes quickly negative by ∼12% and then grows positive in a parabolic fashion. Fig. 1d and f show the MR at Vg = −15 V for a filled 1Se state and at Vg = +14 V for an empty 1Se state. In both cases, the MR varies little at high magnetic field. Exploring a range of charging is conveniently done by varying the gate potential at fixed magnetic field and temperature. The source–drain current curves at different magnetic fields for 15 nm and 11.5 nm diameter HgTe CQDs at 20 K and 50 K are shown in Fig. 2. These curves show a well resolved 1Se source–drain current peak with clear MR response. However, when the solids are gated at 1Pe state, there is no systematic MR behavior. As previously reported,18 the conductivity in the 1Pe state is strikingly lower than in the 1Se state at the temperatures shown in Fig. 2. This can be assigned to the splitting of the Pe states26 which effectively lowers the density of states, as well as the directional frustrations for transport along P-orbitals. The discussion will therefore focus on the charging of the 1Se but will not discuss MR in the 1Pe state.
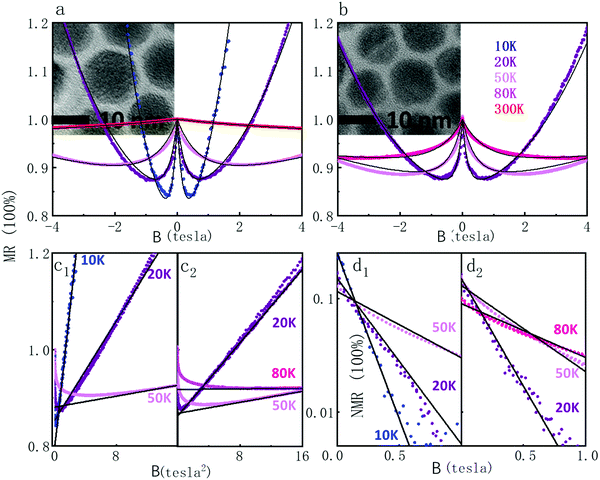
In the following, we define the filling factor x of the 1Se state between 0 (for zero electron in 1Se) and 1 (for 2 electrons) and explore the MR as a function of x. We first describe the MR at a fixed occupation fraction of x = 1/2, for different temperatures and two diameters (15 nm and 11.5 nm) of HgTe QDs as shown in Fig. 3.
To analyze the MR, we separate the MR into a negative MR (NMR) ρ(H)− and a positive MR (PMR) ρ(H)+, such that the normalized MR is expressed as
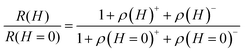 | (1) |
We made several tests to verify that the MR was not an artifact of the device shape or material (ESI,† 4). For the same CQD film preparation, we observed similar MR on a glass substrate and on the Si/SiO2 substrate at zero gate. We verified that the MR was not affected by the choice of gold or platinum for the electrodes and also not by the size of the device. Since this study was motivated by the high mobility achieved, we measured the MR of the same HgTe CQDs cross-linked with ethanedithiol. Such films are more resistive with a two orders of magnitude lower mobility, however they showed similar PMR and NMR (ESI,† 5).
While the similarity of the MR with films of low mobility suggests that the MR arises from local effects acting on individual CQDs or pairs of CQDs rather than from extended interactions, we analyze possible mechanisms for the positive and negative MR.
Discussion
Positive magnetoresistance
A quadratic PMR naturally arises within the classical picture of a ballistic carrier with a single Drude relaxation time. As the Lorentz force causes the electron to deviate from the linear travel direction along the electric field, it travels a shorter distance in the direction of the electric field, and the resistance increase is quadratic for small H. The generalization of this effect is called Kohler's rule27 and leads to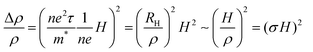 | (2) |
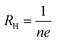 is the Hall parameter, n is the carrier density, τ is the relaxation time, e is the elementary electron charge, m* is the effective mass, and
is the Hall parameter, n is the carrier density, τ is the relaxation time, e is the elementary electron charge, m* is the effective mass, and 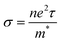 is the conductivity (all equations are in SI units).
is the conductivity (all equations are in SI units).
In a system with a single mobile carrier, the Hall effect compensates for the deviation such that the MR disappears. Extending Kohler's rule to two carriers, there is still a net positive magnetoresistance that is quadratic for low enough field.
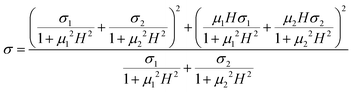 | (3) |
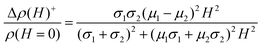 | (4) |
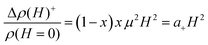 over the range of magnetic field accessible in the experiment. This expression captures the experimental quadratic MR and the x-dependence. However, it predicts a strong effect of the mobility which is not supported by the experiments. Furthermore, the observed magnitude is much larger than the prediction. Indeed, for the measured mobility of ∼1 cm2 V−1 s−1, the model predicts a+ ∼ 10−8 m4 V−2 s−2 at half filling compared to the observed value of 10−1m4 V−2 s−2 at 10 K. We also note that the model of a miniband with partial filling predicts that the mobility should switch sign on either side of the 1Se conductance peak, but this is inconsistent with the measured Hall mobility which is rather independent of the fractional occupation. The absence of a ballistic effect is consistent with a mean free path shorter than the dot spacing, and therefore a hopping conduction in these glassy structure CQD films. On the other hand, as the estimate above shows, the ballistic effect is weak and can be masked by stronger effects.
over the range of magnetic field accessible in the experiment. This expression captures the experimental quadratic MR and the x-dependence. However, it predicts a strong effect of the mobility which is not supported by the experiments. Furthermore, the observed magnitude is much larger than the prediction. Indeed, for the measured mobility of ∼1 cm2 V−1 s−1, the model predicts a+ ∼ 10−8 m4 V−2 s−2 at half filling compared to the observed value of 10−1m4 V−2 s−2 at 10 K. We also note that the model of a miniband with partial filling predicts that the mobility should switch sign on either side of the 1Se conductance peak, but this is inconsistent with the measured Hall mobility which is rather independent of the fractional occupation. The absence of a ballistic effect is consistent with a mean free path shorter than the dot spacing, and therefore a hopping conduction in these glassy structure CQD films. On the other hand, as the estimate above shows, the ballistic effect is weak and can be masked by stronger effects.
Magnetic confinement could be another explanation. In the CQD films at cryogenic temperatures, the mobility decreases with decreasing temperature with an activated behavior. A possible source of the PMR is therefore an increase of the hopping activation energy that could come from the magnetic confinement. This magnetic freeze-out was observed in narrow gap bulk semiconductors with light effective mass.28,29 For these narrow gap materials, the electrons hop in the impurity band and the increased impurity binding energy with magnetic field can lead to dramatic increase of the resistance. The magnetic confinement arises from the squared potential vector term in the Hamiltonian such that 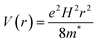 and is quadratic in the magnetic field. Therefore, for small MR, we propose
and is quadratic in the magnetic field. Therefore, for small MR, we propose 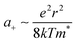 . For a 15 nm diameter CQD, the effective mass at the 1Se state energy is 0.025me, as estimated by a K·P model of the energy dispersion (ESI,† 6), and the confinement potential is then
. For a 15 nm diameter CQD, the effective mass at the 1Se state energy is 0.025me, as estimated by a K·P model of the energy dispersion (ESI,† 6), and the confinement potential is then 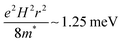 at 5 T. Such local mechanism would explain why similar PMR is observed for low and high mobility films. The magnitude is about right since
at 5 T. Such local mechanism would explain why similar PMR is observed for low and high mobility films. The magnitude is about right since 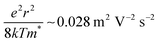 for r = 7.5 nm and T = 20 K compared to a value of 0.03 in Fig. 2e. However, this magnetic confinement model predicts a T−1 temperature dependence of a+ compared to the observed T−3. A different temperature dependence can be obtained within the Efros-Shklovskii variable range hopping model as the electron path adjusts to the temperature, and this gives
for r = 7.5 nm and T = 20 K compared to a value of 0.03 in Fig. 2e. However, this magnetic confinement model predicts a T−1 temperature dependence of a+ compared to the observed T−3. A different temperature dependence can be obtained within the Efros-Shklovskii variable range hopping model as the electron path adjusts to the temperature, and this gives 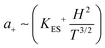 ,30 where
,30 where 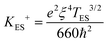 . Using a localization length ξ = 15–40 nm with hoping temperature TES ∼ 350 K,18 gives values of the PMR parameter 0.015–0.75 at 20 K which are also rather consistent with the experiment. The magnitude estimate roughly supports the attribution of the PMR to the magnetic field confinement at the single dot level, but the temperature dependence and the scaling with (1 − x)x remain to be satisfactorily explained.
. Using a localization length ξ = 15–40 nm with hoping temperature TES ∼ 350 K,18 gives values of the PMR parameter 0.015–0.75 at 20 K which are also rather consistent with the experiment. The magnitude estimate roughly supports the attribution of the PMR to the magnetic field confinement at the single dot level, but the temperature dependence and the scaling with (1 − x)x remain to be satisfactorily explained.
Negative magnetoresistance
The NMR is rather independent of the doping level as shown in Fig. 1b–d. It appears to be associated with a rather large effective g-factor, and it depends at most weakly on the mobility. The weak effect of the mobility allows to rule out a negative MR that involves coherent back scattering that leads to weak localization.31 We also rule out spin blockade effect. The MR attributed to spin blockade was observed in weakly conductive organic films23 and weakly coupled CdSe CQD films, it was also in the 10% range but even narrower and positive, with a fixed and very small magnetic field range of ∼50 mT that was independent of temperature. That effect is assigned to electron spins needing to precess around the random hyperfine field, reaching the favorable spin orientation before tunneling. When the magnetic field overcomes the hyperfine field, the electron spin orientations become defined, up or down, blocking tunneling depending on the relative spin orientations. The spin-blockade effect is possible when the exchange interaction is smaller than the hyperfine interaction and this requires a very weak coupling. This was used to explain why the CdSe CQD films show the spin-blockade at low bias, and low temperature when nearest neighbor hopping is unfavorable. Such explanation for the absence of spin blockade apply here in the higher mobility HgTe CQD films as well as the EDT treated films because nearest neighbor hopping is the dominant situation at the investigated temperatures.In another model, applying a magnetic field may partially order the spins and reduce the scattering of conduction electrons. Such effect is predicted for transition metals, where the conduction electrons can be affected by scattering due to the random spin orientation of d-shell electrons. Fisher and Langer32 predicted, with only short-range spin fluctuation, that the decrease in the resistance would be proportional to the square of the magnetization M. The magnetic field dependence of the magnetization of the 1Se state electrons of g-factor g, is given by the Brillouin function 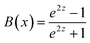 where Z = JgμBH/kBT and J = 1/2. Then
where Z = JgμBH/kBT and J = 1/2. Then 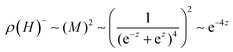 and
and 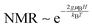 . The model does not provide an estimate for the prefactor a− as this would depend on the interaction between 1Se electrons with some other electron spins. It should also depend on the number of spins as they are the source of scattering. The mechanism should also disappear for full or empty 1Se states and give a strong dependence of x, which is not seen. It is also not likely to be applicable to a hopping conduction regime, where the scattering is already strong enough to localize the carriers on single sites.
. The model does not provide an estimate for the prefactor a− as this would depend on the interaction between 1Se electrons with some other electron spins. It should also depend on the number of spins as they are the source of scattering. The mechanism should also disappear for full or empty 1Se states and give a strong dependence of x, which is not seen. It is also not likely to be applicable to a hopping conduction regime, where the scattering is already strong enough to localize the carriers on single sites.
A third possible explanation in the hopping regime is that the Zeeman effect on the 1Se state under a magnetic can reduce the energy barriers. Indeed, if two neighboring dots have an energy difference E, the Zeeman effect can increase the lower state energy by gμBH and decrease the higher state energy by the same amount. Assuming that spin is not conserved upon tunneling, the barrier becomes smaller by 2gμBH. The thermal activation is reduced by the Zeeman effect and this can lead to an NMR that is simply 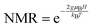 , with the coefficient a− = 1. This allows to relate the real g-factor to the fitted values by ½. However, a− = 1 is clearly larger than the experiment which indicates a− ∼ 0.1. One possible reason is the assumption of the spin being flipped while only a fraction of the hops may benefit from spin flipping. One also needs to justify the value of the g-factor. The data gives
, with the coefficient a− = 1. This allows to relate the real g-factor to the fitted values by ½. However, a− = 1 is clearly larger than the experiment which indicates a− ∼ 0.1. One possible reason is the assumption of the spin being flipped while only a fraction of the hops may benefit from spin flipping. One also needs to justify the value of the g-factor. The data gives 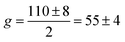 and
and 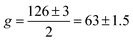 for 15 nm and 11.5 nm dot, respectively. The value is close to tight binding values for InSb dots of similar gap33 (up to a sign) These values are also consistent with the K·P formula,34
for 15 nm and 11.5 nm dot, respectively. The value is close to tight binding values for InSb dots of similar gap33 (up to a sign) These values are also consistent with the K·P formula,34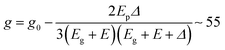 with g0 free electron g factor, Δ spin–orbit splitting, Eg bulk gap, and E electron energy relative to its zone-center. However, the value is ∼3 times larger than the predicted electron g-factor in HgTe quantum dots of the investigated size range.35 This explanation implies a saturation of the NMR at high field since 1 tesla magnetic field would shift the energies by ∼5 meV while the typical site barrier is closer to 10 meV,17 but this is likely masked by the stronger PMR in that field range. In preliminary infrared transmission measurements, we also did not see (ESI,† 7) the Zeeman effect and a stronger magnetic field will be needed.
with g0 free electron g factor, Δ spin–orbit splitting, Eg bulk gap, and E electron energy relative to its zone-center. However, the value is ∼3 times larger than the predicted electron g-factor in HgTe quantum dots of the investigated size range.35 This explanation implies a saturation of the NMR at high field since 1 tesla magnetic field would shift the energies by ∼5 meV while the typical site barrier is closer to 10 meV,17 but this is likely masked by the stronger PMR in that field range. In preliminary infrared transmission measurements, we also did not see (ESI,† 7) the Zeeman effect and a stronger magnetic field will be needed.
Conclusion
In this work, we studied a system consisting of a glassy disordered film of rather monodisperse HgTe quantum dots with high mobility (1–10 cm2 V−1 s−1), and we observed a strong modulation of the conductance with charging and magnetic field. With an FET structure, we measured the MR down to 10 K, as a function of the occupation of the lowest energy 1Se electron state. We observed a positive-quadratic magnetoresistance which can be several 100% at low temperature and scales like x(1 − x) where x is the fractional occupation of the 1Se state. This positive magnetoresistance is many orders of magnitude larger than the effect that could arise from ballistic carriers within the relaxation time approximation. Instead, it is tentatively attributed to the increased confinement induced by the magnetic field and the increased hopping activation energy. There is also a negative magnetoresistance of 1–20% from 300 K to 10 K which is rather independent of the fractional occupation, and which follows a negative exponential dependence with the magnetic field. It can be empirically fit with an effective g-factor of ∼60 and it is tentatively attributed to the reduction of barrier heights by the Zeeman splitting of the 1Se state. Although these results are not fully understood, they suggest that most of the magnetic effects are rather local in nature despite the rather high mobility and bandlike transport in these films. These local effects may be masking more subtle MR response expected for delocalized charge carriers. These studies could be extended to magnetically doped quantum dots which may have further interesting properties.Experiment methods
Monodisperse HgTe CQDs were prepared following ref. 25 and 26. A two-phase ligand exchange process was applied to transfer the HgTe QDs from hexane to polar dimethylformamide (DMF) where HgCl2, 2-mercaptoethanol, butylamine, and butylammonium chloride co-serve as the hybrid ligands.18 Several different sizes HgTe dots were investigated.Film preparation
The HgTe QD films were prepared by spin-coating on patterned Au electrode on 300 nm SiO2/Si substrate. Area between the electrodes was 1 mm × 3 mm. The absorption spectra were measured for films made with the same procedure on ZnSe windows (SI).FET measurement
The CQD film is a drop cast on 4 pairs of interdigitated evaporated gold fingers of width 20 microns, gap 20 microns, and length 300 microns that have been made by lithography on a SiO2/Si wafer. The voltage is applied by the National Instrument USB-6218 Multifunction I/O device with a voltage gain. The source–drain current is pre-amplified by the Stanford research system model SR570 then collected by a LabVIEW program. For normal FET measurement, mobility (μFET), extracted in the linear regime, was calculated by fitting the experimental data to the following equation:where L, W, Ci, VD, ID, and VG are the channel length, channel width, capacitance per unit area, drain voltage, drain current, and gate voltage, respectively.
MR measurement
The CQD solids were inserted into a Physical Property Measurement System (PPMS-9, Quantum Design) under a helium inert atmosphere. The applied magnetic field was perpendicular to the films. The resistance was measured by a Keithley 2636A Dual Channel Source meter with the Four-point sensing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Christopher Melnychuk for very useful discussions. This work was supported by the National Natural Science Foundation of China under grant number 62105022, the University of Chicago Materials Research Science and Engineering Center, which was funded by the National Science Foundation under award number DMR1420709, and by the Department of Defense (DOD) Air Force Office of Scientific Research under grant number FA9550-18-1-0099.References
- C. R. Kagan, E. Lifshitz, E. H. Sargent and D. V. Talapin, Science, 2016, 353, 5523 CrossRef PubMed
.
- G. Konstantatos, I. Howard, A. Fischer, S. Hoogland, J. Clifford, E. Klem, L. Levina and E. H. Sargent, Nature, 2006, 442, 180–183 CrossRef CAS PubMed
.
- E. M. Sanehira, A. R. Marshall, J. A. Christians, S. P. Harvey, P. N. Ciesielski, L. M. Wheeler, P. Schulz, L. Y. Lin, M. C. Beard and J. M. Luther, Sci. Adv., 2017, 3, 4204 CrossRef PubMed
.
- V. Wood and V. Bulović, Nano Rev., 2010, 1, 5202 CrossRef PubMed
.
- Y. Liu, M. Gibbs, J. Puthussery, S. Gaik, R. Ihly, H. W. Hillhouse and M. Law, Nano Lett., 2010, 10, 1960–1969 CrossRef CAS PubMed
.
- N. Yazdani, D. Bozyigit, O. Yarema, M. Yarema and V. Wood, J. Phys. Chem. Lett., 2014, 5, 3522–3527 CrossRef CAS PubMed
.
- D. Yu, C. Wang and P. Guyot-Sionnest, Science, 2003, 300, 1277–1280 CrossRef CAS PubMed
.
- D. J. Norris, N. Yao, F. T. Charnock and T. A. Kennedy, Nano Lett., 2001, 1, 3–7 CrossRef CAS
.
- R. Beaulac, P. I. Archer, S. T. Ochsenbein and D. R. Gamelin, Adv. Funct. Mater., 2008, 18, 3873–3891 CrossRef CAS
.
- V. Pinchetti, Q. Di, M. Lorenzon, A. Camellini, M. Fasoli, M. Zavelani-Rossi, F. Meinardi, J. Zhang, S. A. Crooker and S. Brovelli, Nat. Nanotechnol., 2018, 13, 145–151 CrossRef CAS PubMed
.
- V. A. Vlaskin, R. Beaulac and D. R. Gamelin, Nano Lett., 2009, 9, 4376–4382 CrossRef CAS PubMed
.
- R. Rinaldi, P. v. Giugno, R. Cingolani, H. Lipsanen, M. Sopanen, J. Tulkki and J. Ahopelto, Phys. Rev. Lett., 1996, 77, 342 CrossRef CAS PubMed
.
- J.-S. Lee, M. v. Kovalenko, J. Huang, D. S. Chung and D. V. Talapin, Nat. Nanotechnol., 2011, 6, 348–352 CrossRef CAS PubMed
.
- J.-H. Choi, A. T. Fafarman, S. J. Oh, D.-K. Ko, D. K. Kim, B. T. Diroll, S. Muramoto, J. G. Gillen, C. B. Murray and C. R. Kagan, Nano Lett., 2012, 12, 2631–2638 CrossRef CAS PubMed
.
- M. Scheele, Z. Phys. Chem., 2015, 229, 167–178, DOI:10.1515/zpch-2014-0587
.
- M. V. Kovalenko, M. Scheele and D. V. Talapin, Science, 2009, 324, 1417–1420 CrossRef CAS PubMed
.
- M. Chen, X. Lan, X. Tang, Y. Wang, M. H. Hudson, D. V. Talapin and P. Guyot-Sionnest, ACS Photonics, 2019, 6, 2358–2365 CrossRef
.
- X. Lan, M. Chen, M. H. Hudson, V. Kamysbayev, Y. Wang, P. Guyot-Sionnest and D. V. Talapin, Nat. Mater., 2020, 19, 323–329 CrossRef CAS PubMed
.
- P. Guyot-Sionnest, J. Phys. Chem. Lett., 2012, 3, 1169–1175 CrossRef CAS PubMed
.
- H. Liu and P. Guyot-Sionnest, J. Phys. Chem. C, 2015, 119, 14797–14804 CrossRef CAS
.
- A. Pourret, A. Ramirez and P. Guyot-Sionnest, Appl. Phys. Lett., 2009, 95, 142105 CrossRef
.
- P. Guyot-Sionnest, D. Yu, P. H. Jiang and W. Kang, J. Chem. Phys., 2007, 127, 014702 CrossRef PubMed
.
- Y. Sheng, T. D. Nguyen, G. Veeraraghavan, Ö. Mermer, M. Wohlgenannt, S. Qiu and U. Scherf, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 045213 CrossRef
.
- M. Chen, G. Shen and P. Guyot-Sionnest, J. Phys. Chem. Lett., 2020, 11, 2303–2307 CrossRef CAS PubMed
.
- G. Shen, M. Chen and P. Guyot-Sionnest, J. Phys. Chem. Lett., 2017, 8, 2224–2228 CrossRef CAS PubMed
.
- M. H. Hudson, M. Chen, V. Kamysbayev, E. M. Janke, X. Lan, G. Allan, C. Delerue, B. Lee, P. Guyot-Sionnest and D. V. Talapin, ACS Nano, 2018, 12, 9397–9404 CrossRef CAS PubMed
.
-
J. M. Ziman, Electrons and Phonons: The Theory of Transport Phenomena in Solids, Oxford University Press, 1960, p. 490 Search PubMed
.
- R. Mansfield and L. Kusztelan, J. Phys. C-Solid State Phys., 2001, 11, 4157, DOI:10.1088/0022-3719/11/20/012
.
- S. B. Rafol, X. Chu and J. P. Faurie, J. Appl. Phys., 1993, 74, 1151, DOI:10.1063/1.354915
.
-
B. I. Shklovskiĭ and A. L. Efros, Electroniroperties of Doped Semiconductors, Springer, Berlin, 1984 Search PubMed
.
- G. Bergmann, Phys. Rep., 1984, 107, 1–58, DOI:10.1016/0370-1573(84)90103-0
.
- M. E. Fisher and J. S. Langer, Resistive Anomalies at Magnetic Critical Points, Phys. Rev. Lett., 1968, 20, 665–668 CrossRef CAS
.
- A. Tadjine, Y.-M. Niquet and C. Delerue, Phys. Rev. B, 2017, 95, 235437, DOI:10.1103/PhysRevB.95.235437
.
- A. A. Kiselev, E. L. Ivchenko and U. Rössler, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 16353, DOI:10.1103/PhysRevB.58.16353
.
- X. W. Zhang and J. B. Xia, J. Phys. D: Appl. Phys., 2006, 39, 1815–1820, DOI:10.1088/0022-3727/39/9/017
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc05202k |
| This journal is © The Royal Society of Chemistry 2022 |