Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A microfluidic approach for synthesis and kinetic profiling of branched gold nanostructures†
Qi
Cai‡§
 a,
Valentina
Castagnola‡¶
a,
Valentina
Castagnola‡¶
 a,
Luca
Boselli‡||
a,
Luca
Boselli‡||
 *a,
Alirio
Moura
b,
Hender
Lopez
*a,
Alirio
Moura
b,
Hender
Lopez
 c,
Wei
Zhang
a,
João M.
de Araújo
b and
Kenneth A.
Dawson
c,
Wei
Zhang
a,
João M.
de Araújo
b and
Kenneth A.
Dawson
 *a
*a
aCentre for BioNano Interactions, School of Chemistry, University College Dublin, Belfield, Dublin 4, Ireland. E-mail: luca.boselli@cbni.ucd.ie; luca.boselli@iit.it; kenneth.a.dawson@cbni.ucd.ie
bDepartamento de Física Teórica e Experimental, Universidade Federal do Rio Grande do Norte, 59078-970, Natal, RN, Brazil
cSchool of Physics and Optometric & Clinical Sciences, Technological University Dublin, Grangegorman, D07 XT95, Ireland
First published on 4th February 2022
Abstract
Automatized approaches for nanoparticle synthesis and characterization represent a great asset to their applicability in the biomedical field by improving reproducibility and standardization, which help to meet the selection criteria of regulatory authorities. The scaled-up production of nanoparticles with carefully defined characteristics, including intrinsic morphological features, and minimal intra-batch, batch-to-batch, and operator variability, is an urgent requirement to elevate nanotechnology towards more trustable biological and technological applications. In this work, microfluidic approaches were employed to achieve fast mixing and good reproducibility in synthesizing a variety of gold nanostructures. The microfluidic setup allowed exploiting spatial resolution to investigate the growth evolution of the complex nanoarchitectures. By physically isolating intermediate reaction fractions, we performed an advanced characterization of the shape properties during their growth, not possible with routine characterization methods. Employing an in-house developed method to assign a specific identity to shapes, we followed the particle growth/deformation process and identified key reaction parameters for more precise control of the generated morphologies. Besides, this investigation led to the optimization of a one-pot multi-size and multi-shape synthesis of a variety of gold nanoparticles. In summary, we describe an optimized platform for highly controlled synthesis and a novel approach for the mechanistic study of shape-evolving nanomaterials.
New conceptsPrecise control of synthetic nanoshapes is especially relevant not only to correlate outcomes in biology, sensing, and catalysis with intrinsic nanoparticles morphological features but also to precisely tuning such features based on the targeted application. The present work shows how a spatially resolved microfluidic shape-control setup can be used to reproducibly and rapidly synthesize gold nanoshapes. We report a novel microfluidic synthesis for complex nano geometries, introducing a novel in-flow approach to isolate and characterize reaction intermediates from continuous flow synthesis, which provides the unique chance to describe the nanoparticles’ growth while happening. The reaction intermediates are captured and digitized using electron microscopy, allowing us to understand the reaction coordinate of shape growth and providing a novel approach to study and comprehend nanoscale shape reactions systematically. This methodology also allowed synthesizing and isolating multiple nanoparticles shapes batches within the same reaction. With the support of computational tools that define nanoscale shape and shape ensemble identity, we developed a novel workflow for nanoshape generation, widely relevant for the nano-community. The synthetic insights combined with the computational approach provide a reliable starting point for the systematic biological investigation of nanoscale shapes, which has recently opened up to interesting questions. |
Introduction
In the last decade, a wide variety of synthetic strategies have been developed to synthesize nanoparticles (NP) with different geometries.1–10 Gold nanoparticles (GNP) with complex irregular shapes (i.e., branched) present fascinating physicochemical properties, such as a localized surface plasmon resonance peak (LSPR) in the visible-near-infrared (Vis-NIR) spectra and surface-enhanced Raman spectroscopy (SERS) activity, which makes them very attractive for several applications in biology (i.e., imaging, photothermal therapy), sensing and catalysis.11–16 Of particular interest is the recently observed shape-dependent biological activity, which could be exploited to design sophisticated tools for interaction with the cellular machinery (including the immune system), promoting an exchange of stimuli-response signals.13–15Several challenges are associated with the production of branched GNP, including the quality of the scaled-up products and the reproducibility (intra-batch and inter-batches shape variability), as an intrinsic consequence of the synthetic process. These factors can profoundly affect the interpretation of biological outcomes/readouts, as well as the clinical and technological transfer of such GNP (including difficulties in patenting specific nanoformulations).17 The quality of GNP batches and the final physical features of the particles are strongly affected by the growth route underlying their formation. The study of NP nucleation and growth as complex and stochastic processes has been tackled for many years using complementary approaches. A widely used method to directly capture each step in the nucleation pathway of single particles is in situ transmission electron microscopy (TEM) that allowed following the interactions of the building blocks as they crystallize.18–21
Microfluidics approaches for NP synthesis and time-resolved in situ analysis have recently attracted increasing interest.22–30 With these methods, the NP synthesis can be carried out in continuous flow using small volumes in an operator-free fashion, and some recent technical advancements, mainly promoted by sensing applications,31,32 also allow for in situ microfluidic measurements of physical properties.33–35
Here, we developed an in-flow microfluidic synthetic platform to prepare several different high-quality GNP with branched shapes. In addition, by exploiting the spatial resolution of the fluidic system to achieve temporal resolution, we investigated reaction pathways for the produced nanoshapes. This novel methodology allowed to precisely isolate reaction intermediates, even at very early times, in a semi-automated fashion and complement the characterization of physicochemical features with morphological analysis. Our approach allowed us to study fast kinetics and provided a complete picture of the intermediate steps that cannot be achieved merely by looking at optical properties. In our recent work, we presented an electron microscopy-based computational method to identify shape signature features and fingerprint the variability of both regular and complex geometrical 3D nano-objects, laying down the first brick for a more ordered understanding of shape-dependent interactions at the nanoscale.36,37 Here, the shape metrology method is greatly improved, allowing for the extraction of multiple geometrical parameters, including size, concavity depth (related to core and tip size), and surface curvature which is proportional to the surface potential. These are important aspects that can allow to control the physicochemical and biological properties of complex nanostructure, as discussed in this work, and potentially impact our future understanding on the surface organization of synthetic functional groups as well as NP-protein interactions and protein corona organization. Furthermore, in the future, this platform might be employed to investigate nanostructure concavities ability to trap small molecules, for example, to build a new generation of highly sensitive biosensors based on plasmon coupling and SERS or to understand key shape parameters to predict and control light to heat conversion properties of plasmonic GNPs. Here, by applying the enhanced computational shape analysis method to time-resolved reaction intermediates, we were able to directly analyze/parametrize the evolving structures of the different GNP shapes, building trajectories in the geometrical hyperspace and exploring the growth mechanism, demonstrating how in some cases, this process deviates from a mere size expansion.
Understanding the growth process is essential to produce high-quality NP shapes and move towards controlled engineering of NP morphological properties. This workflow, combining the isolation of the NP at different kinetic stages with the computational method used to classify their shape, and map their surface potential, is intended as a first example to identify some of the critical parameters that can be used to predict the course of the reactions and potentially anticipate the final shape outcomes.
Results and discussion
A novel workflow for synthesis and geometrical characterization of branched gold nanoparticles
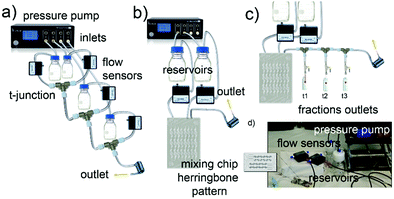
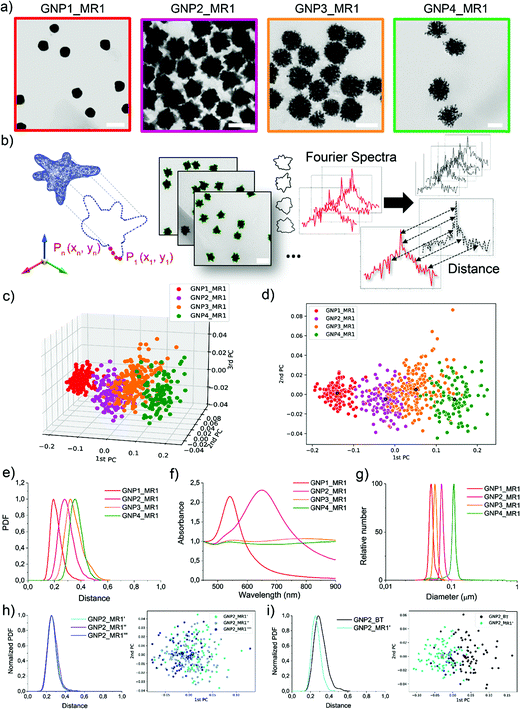
The synthesis of a family of branched GNPs was optimized using different fluidic setups (microreactors – MR, see Fig. 1, Methods and Fig. S1, ESI†).All the synthetic processes were seed-mediated, starting from the same 15 nm seeds, and were optimized as detailed in Methods and Fig. S2–S5 (ESI†). In Fig. 2, the complete characterization of a series of GNP (including branched GNP2-4 and spherical GNP1 control) produced with the microfluidic reactor 1 (MR1) is reported.
GNP1-2_MR1, GNP3_MR1, and GNP4_MR1 were prepared using hydroquinone (HQ), 2,6-dihydroxynaphtalene (DHN), and resorcinol (RES) as reducing agents, respectively. The concentration of the reductive hydroxy phenols, the position of their hydroxylate groups (ortho, meta, para), and the number of aromatic rings influence the redox potential and the charge transport capability, affecting the growth mechanism and, therefore, the final shape of the GNP.38
Fig. 2a depicts a representative TEM micrograph for each GNP produced. In a single TEM image, where the NP contours shape represents the projection of a 3D NP on the grid, dozens of NPs can be analyzed simultaneously. Several different TEM images of the batches (as schematized in Fig. 2b) were acquired, and the coordinates of the contours were extracted and analyzed to obtain the shape descriptors (Fourier coefficients obtained by a discrete Fourier transform – DFT – see Experimental methods).36 Considering a NP batch as a collection of nano-objects resulting from a specific synthetic process and containing a variety of nanostructures supposed to have a high similarity among them, we can express the degree of similarity as the “distance” between the shape of each particle and any other particle in the batch (see Experimental and Methods for more details, ESI†). The concept of “distance” between the shape fingerprints (Fourier Spectra) was used to build a cluster analysis based on principal components (PCs) reported in Fig. 2c and d. This concept was also used to define shape variance reported in Fig. 2e. Finally, the characterization of the optical properties and size distribution was performed using UV-Vis-NIR spectroscopy and differential centrifugal sedimentation (DCS) (Fig. 2f and g).
The shape analysis gives us information on the particle shape identity and the intra-batch variability or “shape distribution” (Fig. 2c–e). The localization of different clusters in the PC analysis and the shape distribution (or shape variance) as a function of the distances reflect an excellent quality and a precise identity for all the branched GNP produced. In the shape distribution (Fig. 2e), the intra-batch particle distances increase with the intrinsic shape complexity. However, all samples exhibited one single population at relatively short intra-particle distances (below 0.5), suggesting that a relatively good shape homogeneity can be achieved despite the irregular geometrical features. As expected, GNP1_MR1, presenting spherical geometry, exhibited sharper shape distribution with low intra-particle distances, while GNP4_MR1 presented the highest shape complexity resulting in more considerable intra-particle distances. Increasing shape complexity/irregularity (i.e., when making multi-branched NP) often leads to an increased shape variance that can generally originate from faster growth rates, which are more “sensitive” to the presence of local inhomogeneities in the reactor (temperature, reagent concentrations, mixing). This also leads to higher batch-to-batch variability. Therefore, the microfluidic approach, by reducing the volume of reactions, and providing an operator-free continuous flow, clearly limits the local inhomogeneities resulting in more reproducible outcomes. In Fig. 2h, an example of shape distribution reproducibility is reported where all the synthesis has been carried out using MR and starting from the same seeds (further examples also involving two independent users are reported in Fig. S6 and S7, ESI†). The shape variability observed for branched NP is also improved with this method compared to the traditional bench-top approach (Fig. 2i).
DCS analysis confirmed monodisperse size distribution for all GNP. The UV-Vis-NIR absorption spectroscopy analysis revealed the characteristic LSPR bands for spherical and branched GNP, the latter typically exhibiting LSPR in the NIR region.39,40 However, both GNP3_MR1 and GNP4_MR1 present peculiar LSPR profiles, covering all the Vis-NIR regions without a clear, well-defined peak. It is interesting to note that while these two shapes cannot easily be distinguished by visual TEM observation nor absorption spectroscopy, they form two distinct clusters in the shape analysis.
Isolation of reaction intermediates to study the growth kinetics profile
A simple configuration as MR1 is a fast and cost-effective method to produce high-quality GNP on a large scale (about 150 mL in 15 min). The mixing of the reagents in these conditions, relatively quick due to the small volumes involved, occurs by diffusion (see Methods, ESI†) and probably advection generated by secondary flows due to tubing bending and coiling.In order to achieve a faster mixing of the reagents (in the milliseconds time scale), and being able to separate the mixing and the reaction area, particularly relevant when aiming to study the kinetics of fast reactions, a micromixer chip was then introduced in the configuration (see MR2 configuration in Methods and Fig. 1 and Fig. S1, ESI†). This modification was essential for studying the early time points, which revealed critical mechanistic features of the reaction.
Following the fast mixing of the gold precursor solution (including the seeds) with the reducing agent solution in the mixing area, the reaction takes place along the outlet tubing in the reaction area, the length of which determines the residence time. The flow rate was optimized to guarantee adequate mixing and proper spatial resolution in the reaction area and achieve good reproducibility (see Fig. S6–S8, ESI†). Using this setup, we followed the growth of four different GNP in-flow reactions, here called DHN1, DHN2, HQ1, HQ2. The nomenclature refers to the type and amount of reducing agent employed (see synthetic details in Methods and Table S1, ESI†).
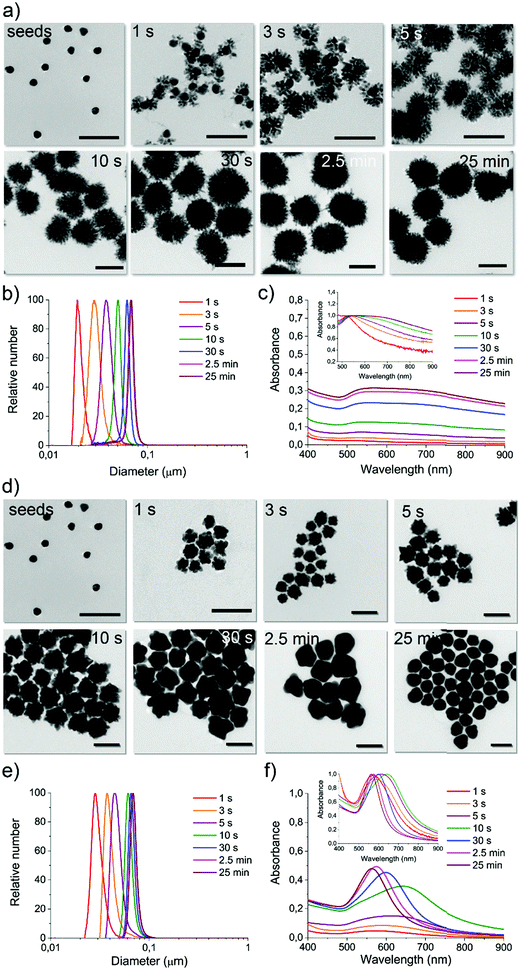
For a constant flow rate (2 or 3 mL min−1, ensured by the flow sensors feedback loop, see Fig. S8, ESI†), we could collect reaction intermediates corresponding to specific time points (see Table S2, ESI†) of the reaction by placing flow switches at different outlet tubing lengths. By “freezing” the product of each time point, we could perform a kinetic study with direct in-line isolation of the in-flow evolving sample at different residence times, meaning different stages of the very same starting reaction. To “freeze” the reaction process and isolate the kinetic intermediates, a large excess of an appropriate thiol-based blocking ligand (see Methods, reaction intermediate isolation) that did not affect the isolated GNP morphologies was selected for each synthesis (see Fig. S9–S11, ESI†). All the collected fractions were fully characterized by absorption spectroscopy, DCS, TEM, and shape analysis (see Fig. 3 and Fig. S13–S19, ESI†).
For reaction DHN1 (Fig. 3a–c and Fig. S13, ESI†), it was possible to isolate very early time points, and the spatial resolution allowed for the precise growth pathway reconstruction. The particle evolution revealed a fast kinetic, where after 1 to 3 seconds of reaction, besides a slight growth of the seeds, a rapid formation of dendritic structures decorating the spherical core (seeds) can be observed. The seeds' structure appears to support the formation of the branches while maintaining their spherical features, linking the growing extensions through just a few points of contact. The kinetic profile suggests a diffusion-limited reaction, in which fast coalescence of new nuclei formed in the proximity of the NP results in fractal structures. Over time, the branches increase in number and density, leading to a more homogenous final structure and masking the internal spherical core. The TEM images in Fig. 3a show complex three-dimensional crystalline hierarchical structures in which the branching sites seem, at least in the first phase, to engage with the seeds almost as individual entities. The complex dendritic structure can be obtained through the oriented attachment of NP over the crystallographic directions (Fig. S12a, ESI†).41 The traditional Ostwald ripening mechanism also probably acts to smooth the dendritic morphology over time during the reaction.
We can now have a better interpretation of the peculiar UV-Vis-NIR spectra. The LSPR peak centered at about 540 nm is continuously present in the spectra over time, presenting a slight red-shift due to the little growth of the core during the first few seconds of reaction. The absorption spectra in the NIR region increase with increasing branches' length and density and, in parallel, with the particles' size. The extended profile of the spectrum, presenting a pretty broad cross-section even over 900 nm, is characteristic of fractal NP conformation in which multiple longitudinal LSPR and intra-particle plasmon coupling occur.42–44 By increasing the fractal order, plasmon oscillations related to the different length scales inside the fractal structure increase, including degeneracies. Therefore, fractals can exhibit broad and multi-peaked spectra from plasmons with large degeneracy, which leads to spectrum-spanning.
Both DCS (Fig. 3b) and TEM statistical analysis (not reported) show a monomodal size and shape distribution for all the isolated reaction intermediates. Therefore, this strategy can be considered a pioneering approach to preparing multiple GNP batches with different sizes and shapes in a single “one-pot” reaction procedure, avoiding the gold precursor/reducing agent tuning process commonly performed when aiming to synthesize a series of sizes and shapes.45
When using the same configuration, starting from the same reagents but replacing the reducing agent DHN with HQ, the resulting kinetic profile changed utterly. For the reaction called HQ1 (see synthetic details in Experimental methods), a significant excess of the reducing agent on the gold precursor led to a final product which presents a spiky structure as the one previously observed in GNP2_MR1 and also similar to others obtained by using chemically similar methods (although not inflow).45,46
From the kinetic profiling (see the characterization of isolated fractions in Fig. S14 and S15, ESI†), it is possible to observe that at early time points (first few seconds), the tips are already clearly visible on the growing seeds, and this morphological change is reflected in the clear red-shift of LSPR compared to the one characteristic of spherical GNP of similar sizes. This evidence suggests a direct tip growth over the seeds faces, as confirmed by HR-TEM analysis (see Fig. S12b, ESI†) and other studies reported in the literature.45,47,48
A gradual significant overall size growth can be observed from increasing time points, which, however, does not significantly affect the shape defined at a very early growth stage (no further LSPR red-shift is observed after the first 3 seconds of reaction). The mechanism involved appears different from the one observed for DHN1. Here the seeds do not merely act as a template, but they grow in larger structures, meaning that the reduction of the gold is most favored on the surface of the seed and that coalescence can be avoided. This process was previously investigated with traditional approaches, but due to the fast kinetic, a precise analysis of the reaction intermediate (including the LSPR evolution) was not performed, as the isolation of homogenous reaction intermediates is particularly challenging.45
A more interesting kinetic profile was observed when using a lower concentration of the reducing agents, as in reactions DHN2 (Fig. S16 and S17, ESI†) and HQ2 (Fig. 3d–f and Fig. S18, S19, ESI†). Both of these synthetic approaches lead to the formation of spherical particles, and in both cases, by capturing the evolution of the shape (TEM imaging) and physical parameters (LSPR), we observed multiple shape transition from spherical seeds to branched/spiky NP and back to a final spherical shape.
Coupling microfluidics synthetic approach and shape analysis platform to study reaction pathways
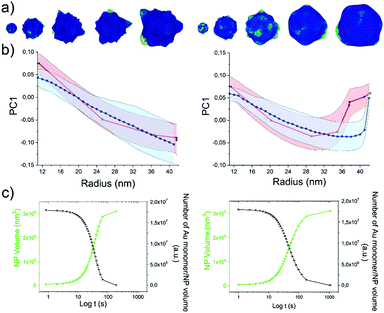
As the HQ1 and HQ2 reactions directly involve the growth on the surface and the shape modifications of the seeds, we selected them as suitable models to illustrate the use of our platform for the study of NP growth along the reaction pathway (Fig. 4). Some of the chemistry involved in these processes has been previously described elsewhere,49 allowing for more robust process reconstruction. Our platform, coupling the microfluidic in-flow isolation of reaction intermediates and the 2D computational shape analysis illustrated before, allows extraction of a series of physical and geometrical parameters in a statistically relevant fashion, which are not accessible using routinely employed characterization techniques (see Methods for more details, ESI†). The intra-batch particle distances and the variance for each reaction time point describe the reaction based on characteristic growth patterns (or reaction fingerprint). In the case of HQ2 (Fig. 4a), this pattern presents a maximum for distances, while for HQ1 (Fig. S20, ESI†), the reaction moves directly towards the final shape.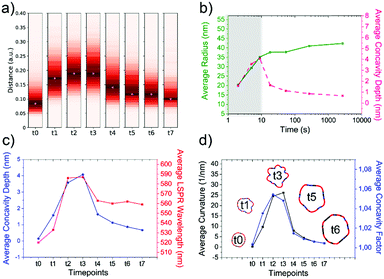 | ||
| Fig. 4 Computational analysis of reaction intermediates for the HQ2 synthesis. (a) GNP distribution of distances between the Fourier spectras of the GNP contours at each time point (see Table S2 for time points values, ESI†) for HQ2; (b) Average values of radius (green curve) and concavities depth (pink curve) calculated starting from the coordinates of the contour for each time point of HQ2. The trends define two separate regions: firstly, the total radius and the concavities depth increase together and the GNP shape is defined (gray area), secondly, the radius stabilizes to its final value and the concavities are filled (white area). (c) Average concavity depth and average LSPR wavelengths for the different time points of HQ2. (d) Average surface curvature (proportional to the average surface potential) for each time point of HQ2 calculated as the difference between the curvature of the circumscribed sphere (thermodynamically favorable configuration) and the actual GNP shape. The trend for the surface curvature is compared to the concavity factor. The concavity factor is calculated as the surface area of the GNP over the surface of the convex polygon hull. Representative GNP micrographs for different time points and the related surface curvature (color code: black = 0, red = positive, blue = negative) are also shown. | ||
As mentioned before, when following the reactions of HQ1 and HQ2, it is possible to isolate a series of GNP batches with increasing size and changing shape (which is a non-trivial task when dealing with non-geometrical nanostructures). As shown in Fig. 4 (and Fig. S20, ESI†), this platform allows extracting particle-by-particle statistical parameters directly connected to the GNP branches. In this way, it is relatively easy to follow the evolution of the total size and the branches and, for example, stop the reaction at the desired geometry. In this regard, LSPR is a handy shape-dependent physical parameter strictly related to the branches' development. However, this parameter alone does not allow distinguishing the contribution of size and shape, as similar LSPR maxima can be observed for different shapes (see Fig. 2f and Fig. S21, ESI†). In this case, additional parameters such as the depth and the angle of the inter-tips concavities allow achieving a more detailed picture in the view of linking NP features to their application.
Finally, exploiting the assumption detailed in Methods (ESI†), the surface curvature, which is proportional to the surface chemical potential, can be calculated and plotted for HQ2, as shown in Fig. 4d (and Fig. S20 for HQ1, ESI†). This parameter plays a critical role during the growth process of the nanoparticles and, being associated with morphological features, correlates very well with the level of “spikiness” of the shape (here called “concavity factor” and intended as the difference between the surface area of the shape and the circumscriptive convex polygon hull, as shown in Fig. S22, ESI†).
From our experimental observations and previous reports results, it can be hypothesized that in the first stage of the HQ reactions, a large number of gold atoms (with zero-valence) are forming onto the surface of the seeds (nanocrystals), which are acting as surface-catalyzed canters of nucleation (avoiding secondary nucleation in bulk).49–51
Here the reaction rate is very high, and most of the gold precursor is consumed during this step. The high concentration of gold atoms instantaneously available allows for preferential growth on specific high-energy facets (presenting larger surface area) of the seed crystals, therefore, leading to anisotropic tips formation. This step occurs far from the equilibrium condition. The early time points of HQ1 and HQ2 (<30 s) indeed clearly show branched nanostructures, but then a different kinetic pathway takes place in the two cases.
Considering this is a diffusion-limited reaction, the decreasing amount of gold concentration over time will also result in a slow-down of the process. Therefore, the gold binding probability decreases over time, leading to the expected slower growth at longer time points. For HQ2, there is a crucial turning point in the NP growth in which a critical gold atom concentration (reaction rate) and critical differences in the intra-particle surface potential are reached. From this point, the growth becomes a thermodynamically driven process. In this regime, the most stable structures that try to minimize the total interfacial free energy are produced in a more substantial amount, and we observe a smoothening of the edges, gold filling of concavities, and final spherical shape. The preference of atomic addition to the concave surface can be understood considering the concept of chemical potential, which is defined as the Gibbs free energy per atom.52–54 This is comparable to the process described in inert gas or vacuum by the Wulff theorem, where a single crystal assumes the equilibrium shape of the so-called Wulff polyhedron.52,55 Similarly, in our case, the concavity formed during the first stage now presents lower chemical potential than the tips (Fig. 4c), and this aspect, combined with the surface mobility (dependent on the capping agent amount and efficacy which is lower for the formed quinone than for starting hydroquinone), plays the principal role in the shape changes and final rearrangement.
In contrast, for the case of HQ1, a large excess of HQ reducing/capping agent is employed, and the reaction occurs far from equilibrium until the total consumption of the regent. This process happens with a faster reaction rate and negligible surface atom mobility, which translates to very few rearrangements of the gold atoms, leading to a relatively stable spiky final shape.
Based on these mechanistic hypotheses, it was possible to introduce a mesoscopic kinetic model of the GNP growth based on a deformation algorithm for solids, presented in Fig. 5a and Fig. S23 (ESI†), and described in detail in Methods (ESI†). This model employs a series of initial conditions from experimental data (such as gold precursor/seeds ratio, reducing agent/capping agent amount), reasonable assumptions (such as the increasing probability that reduced gold attaches on larger facets) and one free parameter here defined as “surface rearrangement”, which is influenced by multiple factors (such as gold atoms mobility, surface stress, and strain, capping agent, temperature, chemical environment).52,56–61 2D particle projections were extracted from the in silico grown 3D structures (see Fig. 5a) for each time point along with the reaction coordinates and compared with the experimental results (Fig. 5b and Fig. S24, ESI†). The free parameter of the model (the surface rearrangement) is tuned to obtain the final shape of each reaction (HQ1 or HQ2), providing a good match between the extrapolated and the experimental time points.
From the model, it is possible to extract advanced statistical information such as the volume growth and the reaction rate (Fig. 5c and Fig. S24, ESI†), avoiding extremely time-consuming processes such as the 3D-tomography reconstruction of hundreds of particles which, given the complexity of the structures would lead to approximate results.
Therefore, our model might help to predict some intermediate growth shapes and could be used as an exploratory tool to assist the synthesis and design of new nanostructure. We believe that in the future it could help to predict optical, catalytic, and, with a series of reiterative processes, even biological properties (i.e., adjuvancy).
Experimental
Synthesis of GNP1-4 using MR1
Four glass bottle reservoirs containing 50 mL of reagents were used. All the glassware and stir bars were previously cleaned with aqua regia and thoroughly rinsed with fresh Milli-Q water.The reaction took place in PTFE tubing and T-junctions. Four flow sensors were placed between reservoirs and T-junctions to monitor the flow rate. The tubing length between the reservoir and the flow sensor was 30 cm. The flow sensors were connected to a T-junction with 10 cm tubing while the outlet tubing was 15 m long. The total flow rate used in the synthesis was 10 mL min−1, and the ratio of the flow rate of the four inlets is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
All the syntheses were seed-mediated, and the 15 nm seeds described above were used. The amount of HAuCl4 and trisodium citrate (Na3Ct) was kept constant for all the GNP, specifically:
• Reservoir 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mL of an aqueous solution of HAuCl4 (5 × 10−5 mol, 1 × 10−3 M);
50 mL of an aqueous solution of HAuCl4 (5 × 10−5 mol, 1 × 10−3 M);
• Reservoir 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mL of an aqueous solution of Na3Ct (1.5 × 10−5 mol, 3 × 10−4 M);
50 mL of an aqueous solution of Na3Ct (1.5 × 10−5 mol, 3 × 10−4 M);
The amount of reducing agent and seeds was varied, as detailed below.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 mL of seeds from the stock (8 × 10−12 mol) was added to 42 mL of H2O for a final concentration of 1.6 × 10−10 M;
8 mL of seeds from the stock (8 × 10−12 mol) was added to 42 mL of H2O for a final concentration of 1.6 × 10−10 M;
• Reservoir 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mL of an aqueous solution of HQ (6 × 10−5 mol, 1.2 × 10−3 M).
50 mL of an aqueous solution of HQ (6 × 10−5 mol, 1.2 × 10−3 M).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mL of seeds from the stock (1 × 10−12 mol) was added to 49 mL of H2O for a final concentration of 2 × 10−11 M;
1 mL of seeds from the stock (1 × 10−12 mol) was added to 49 mL of H2O for a final concentration of 2 × 10−11 M;
• Reservoir 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mL of an aqueous solution of HQ (6 × 10−4 mol, 1.2 × 10−2 M).
50 mL of an aqueous solution of HQ (6 × 10−4 mol, 1.2 × 10−2 M).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mL of seeds from the stock (3 × 10−12 mol) was added to 47 mL of H2O for a final concentration of 6 × 10−11 M;
3 mL of seeds from the stock (3 × 10−12 mol) was added to 47 mL of H2O for a final concentration of 6 × 10−11 M;
• Reservoir 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mL of an aqueous solution of DHN (6 × 10−4 mol, 1.2 × 10−2 M).
50 mL of an aqueous solution of DHN (6 × 10−4 mol, 1.2 × 10−2 M).
• Reservoir 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mL of seeds from the stock (2 × 10−12 mol) was added to 48 mL of H2O for a final concentration of 4 × 10−11 M;
2 mL of seeds from the stock (2 × 10−12 mol) was added to 48 mL of H2O for a final concentration of 4 × 10−11 M;
• Reservoir 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mL of aqueous RES solution (6 × 10−4 mol, 1.2 × 10−2 M).
50 mL of aqueous RES solution (6 × 10−4 mol, 1.2 × 10−2 M).
Synthesis of HQ1, HQ2, DHN1, and DHN2
The NPs were synthesized using MR2 via seed-mediated growth methods starting from the 15 nm gold seeds, as described before. All the glassware and stir bars were previously cleaned with aqua regia and thoroughly rinsed with fresh Milli-Q water. The concentrations of the reagent solutions used are summarized in Table S1 (ESI†).Milli-Q water used was degassed under vacuum for 30 min and stored at 4 °C prior to use for all reagent solutions. Glycerol was added into water (about 250 μL of glycerol in 100 mL of water) to prevent the formation of ice crystals during the experiment. Two glass bottle reservoirs with a total volume of 20 mL each were placed in an ice bath to slow down possible reactions inside the reservoirs. A micromixer chip was used as described before and showed in Fig. 1 and Fig. S1 (ESI†). Two flow sensors were placed between the reservoirs and the mixing chip. The mixing chip was placed on the TCU set to 1 °C and left to stabilize for 15 min before starting the experiment. The tubing length between the reservoir and the flow sensor was 30 cm, and it was 10 cm between the flow sensors and the mixing chip. The flow rate ratio between inlet 1 and inlet 2 was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and the total flow rate was 3 mL min−1 for HQ1, HQ2 and DHN1, and it was 2 mL min−1 for DHN2.
1, and the total flow rate was 3 mL min−1 for HQ1, HQ2 and DHN1, and it was 2 mL min−1 for DHN2.
Reaction intermediates isolation
Luer-lock T-junction and microfluidic sample injection shut-off valves were placed at established distances on the outlet tube (as shown in Fig. S1.c, ESI†). The distances between the valves and the starting point of the outlet tube determined different time points based on the actual flow rate recorded. The flow rate ratio between inlet 1 and inlet 2 was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and the total flow rate was 3 mL min−1 for HQ1, HQ2, and DHN1, and 2 mL min−1 for DHN2. About 1 mL for each fraction was collected in glass vials containing 200 μL of 0.01 M of carboxyl-terminated thiol ligand solution under vigorous stirring. Specifically, PEG ligand (HS-C11-EG6-OCH2-COOH) was used for HQ1 and HQ2, and 3-mercaptopropionic acid (3-MPA, HS-CH2CH2-COOH) for DHN1 and DHN2 reactions. An aliquot of the final fraction was left without the thiol ligand solution for 15 min to verify reaction completion.
1, and the total flow rate was 3 mL min−1 for HQ1, HQ2, and DHN1, and 2 mL min−1 for DHN2. About 1 mL for each fraction was collected in glass vials containing 200 μL of 0.01 M of carboxyl-terminated thiol ligand solution under vigorous stirring. Specifically, PEG ligand (HS-C11-EG6-OCH2-COOH) was used for HQ1 and HQ2, and 3-mercaptopropionic acid (3-MPA, HS-CH2CH2-COOH) for DHN1 and DHN2 reactions. An aliquot of the final fraction was left without the thiol ligand solution for 15 min to verify reaction completion.
After collection, all the fractions were washed multiple times with ultrapure water (CHROMASOLV® Plus, for HPLC) by using centrifugal filters (Sartorius, 10 kDa, 1000 rcf for 10 min) to remove unreacted reagents before preparing TEM samples.
Nanoparticles contour extraction from TEM imaging
According to a protocol described elsewhere,36 most of the samples used for the shape analysis were deposited onto the TEM grids, which allows for nanoparticles spreading and avoids aggregation due to drying effects. Briefly, the samples were diluted to the concentration of 1–3 × 1011 NP mL−1 and incubated at R.T. in 0.2% methylcellulose overnight. Ultrathin carbon on holey 400 mesh Cu grids (Ted Pella Inc.) was previously treated with a glow discharger were used. Images were taken on a FEI Tecnai G2 20 Twin operating at 120 kV, at magnifications between 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000× and 62
000× and 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×.
000×.
For few TEM images deposited by drop-casting without methylcellulose pre-incubation, some pre-treatment was necessary to extract the contours. Therefore, some TEM micrographs were slightly modified using the free software GIMP 2.10.12.
Shape analysis of the 2D NP contours
TEM micrographs were used to analyze the shape of different batches of GNP, following a procedure described elsewhere.36 Briefly, the GNP contours were obtained from the TEM images using the Open Source Computer Vision Library (OpenCV). The extracted contours consist of closed 2D curves, which coordinates define the GNP contours. The coordinates were then used to perform a Discrete Fourier Transform (DFT) of each contour. In order to define shape clusters, we employed either the Fourier coefficients (FCs) or the Principal Components (PC) extracted from a principal component analysis (PCA) of the FCs. The probability distribution function (PDF) of the shapes was obtained from the L1 norm distances between all the FCs in a batch. For further details on the contour extraction and the shape analysis, see our previous publication.36Conclusions
With the present work, we demonstrate a novel in-flow approach to isolate and characterize reaction intermediates from continuous flow synthesis of inorganic NPs with complex geometries. Our platform introduces the possibility of investigating morphological and optical evolution of NP growth, even in the case of complex shapes and fast kinetics reactions. The microfluidic “spatial resolution” strategy gives access to new kinds of information that complements existing approaches and will support modelling and prediction of NP shape evolution.This platform provides the unique chance to describe the NP growth while happening, producing a variety of branched GNP (some have never been reported before or never been prepared using this method) that present distinguishable features. Exploiting the spatial resolution allowed by the fluidic reactor and the fast mixing, it was possible to capture multiple intermediates of the reaction for a given synthetic process, including early time points. This methodology also allowed to synthesize GNP batches with different sizes and shapes simultaneously in a single-step “one-pot” reaction. The GNP and their reaction intermediates were analyzed by a recently developed method based on extrapolation of key physical and geometrical features (size, branches geometry, surface potential) from the 2D projection of the particles obtained by TEM imaging. The data obtained by this treatment allowed for more precise identification of nanoshapes and reaction pathways but also helped to develop a 3D model of the NP growth process. The proposed mesoscopic model of the growth kinetic can be used to predict the final shape of the NP depending on the time of the reaction, which can potentially be used to isolate selected shapes intermediates during the reaction and predict products for unexplored chemical combinations, but further improvements are needed to achieve more precise predictions. In this regard, the microfluidic approach opens up to intriguing opportunities to monitor and isolate specific morphologies. With the combination of microfluidics and computational tools here reported, we aim to pave the way for a novel paradigm of shape generation, including enhanced control over the quality, reproducibility, and final geometry, still lacking nowadays for most of the synthetic approaches. Precise control of the produced nanoshapes is especially relevant in order to correlate outcomes in biology, sensing, and catalysis with intrinsic NP morphological features and achieve a precise tuning of such features based on the targeted application.
Author contributions
Q. C, V. C, L. B. performed all the experiments. A. M., H. L. J. M. A. performed the computer simulations and the numerical calculations. W. Z. reproduced the syntheses. V. C., L. B., K. A. D. conceived the work. Q. C., V. C., L. B., H. L., A. M. and K. A. D. wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
K. A. D. acknowledges that this publication has emanated from research supported in part by grants from Science Foundation Ireland (17/NSFC/4898 and 17/ERCD/4962). L. B. acknowledges financial support from the EU H2020 Nanofacturing project (grant agreement no. 646364). L. B. and V. C. acknowledge financial support from CALIN. H. L., V. C., and Q. C. acknowledge financial support from the Irish Research Council (H. L., EPSPD/2015/5; V. C., GOIPD/2016/128; Q. C., GOIPG/2014/874). Q. C. and W. Z acknowledge the Chinese Scholarship Council (agreement no. 201408300003 and 201706220062). J. M. A. acknowledges CNPq for support through Bolsa de Produtividade em Pesquisa No. 313431/2018-3. Access to and use of the UCD Conway Electron Microscopy Facility is gratefully acknowledged. The authors acknowledge Dr. Sean O’Brien and Dr. Camila Pedroso Silveira.References
- M. Grzelczak, J. Pérez-Juste, P. Mulvaney and L. M. Liz-Marzán, Chem. Soc. Rev., 2008, 37, 1783–1791 RSC
.
- E. Hao, G. C. Schatz and J. T. Hupp, J. Fluoresc., 2004, 14, 331–341 CrossRef CAS PubMed
.
- T. K. Sau and C. J. Murphy, J. Am. Chem. Soc., 2004, 126, 8648–8649 CrossRef CAS PubMed
.
- H. Yuan, C. G. Khoury, H. Hwang, C. M. Wilson, G. A. Grant and T. Vo-Dinh, Nanotechnology, 2012, 23, 075102 CrossRef PubMed
.
- X. Ye, L. Jin, H. Caglayan, J. Chen, G. Xing, C. Zheng, V. Doan-Nguyen, Y. Kang, N. Engheta and C. R. Kagan, ACS Nano, 2012, 6, 2804–2817 CrossRef CAS PubMed
.
- L. Manna, E. C. Scher and A. P. Alivisatos, J. Am. Chem. Soc., 2000, 122, 12700–12706 CrossRef CAS
.
- Y. Sun and Y. Xia, Science, 2002, 298, 2176–2179 CrossRef CAS PubMed
.
- T. S. Ahmadi, Z. L. Wang, T. C. Green, A. Henglein and M. A. El-Sayed, Science, 1996, 272, 1924 CrossRef CAS PubMed
.
- N. R. Jana, L. Gearheart and C. J. Murphy, Adv. Mater., 2001, 13, 1389 CrossRef CAS
.
- G. Maiorano, L. Rizzello, M. A. Malvindi, S. S. Shankar, L. Martiradonna, A. Falqui, R. Cingolani and P. P. Pompa, Nanoscale, 2011, 3, 2227–2232 RSC
.
- G. H. Jeong, Y. W. Lee, M. Kim and S. W. Han, J. Colloid Interface Sci., 2009, 329, 97–102 CrossRef CAS PubMed
.
- J. Xie, Q. Zhang, J. Y. Lee and D. I. Wang, ACS Nano, 2008, 2, 2473–2480 CrossRef CAS PubMed
.
- L. Talamini, M. B. Violatto, Q. Cai, M. P. Monopoli, K. Kantner, Z. Krpetic, A. Perez-Potti, J. Cookman, D. Garry and C. P. Silveira, ACS Nano, 2017, 5519–5529 CrossRef CAS PubMed
.
- A. Albanese, E. A. Sykes and W. C. Chan, ACS Nano, 2010, 4, 2490–2493 CrossRef CAS PubMed
.
- J. Wang, H. J. Chen, T. Hang, Y. Yu, G. Liu, G. He, S. Xiao, B. R. Yang, C. Yang, F. Liu, J. Tao, M. X. Wu and X. Xie, Nat. Nanotechnol., 2018, 13, 1078–1086 CrossRef CAS PubMed
.
- P. Donati, T. Pomili, L. Boselli and P. P. Pompa, Front. Bioeng. Biotechnol., 2020, 8, 1404 Search PubMed
.
- M. Faria, M. Björnmalm, K. J. Thurecht, S. J. Kent, R. G. Parton, M. Kavallaris, A. P. Johnston, J. J. Gooding, S. R. Corrie and B. J. Boyd, Nat. Nanotechnol., 2018, 13, 777–785 CrossRef CAS PubMed
.
- M. L. Tang, N. Liu, J. A. Dionne and A. P. Alivisatos, J. Am. Chem. Soc., 2011, 133, 13220–13223 CrossRef CAS PubMed
.
- H. Zheng, R. K. Smith, Y.-W. Jun, C. Kisielowski, U. Dahmen and A. P. Alivisatos, Science, 2009, 324, 1309–1312 CrossRef CAS PubMed
.
- T. J. Woehl, J. E. Evans, I. Arslan, W. D. Ristenpart and N. D. Browning, ACS Nano, 2012, 6, 8599–8610 CrossRef CAS PubMed
.
- Z. Ou, Z. Wang, B. Luo, E. Luijten and Q. Chen, Nat. Mater., 2020, 19, 450–455 CrossRef CAS PubMed
.
- J. B. Edel and R. Fortt, Chem. Commun., 2002, 1136–1137 RSC
.
- E. M. Chan, R. A. Mathies and A. P. Alivisatos, Nano Lett., 2003, 3, 199–201 CrossRef CAS
.
- H. Huang, H. du Toit, S. Ben-Jaber, G. W. Wu, L. Panariello, N. T. K. Thanh, I. P. Parkin and A. Gavriilidis, Reaction Chem. Eng., 2019, 4, 884–890 RSC
.
- S. Abalde-Cela, P. Taladriz-Blanco, M. G. de Oliveira and C. Abell, Sci. Rep., 2018, 8, 2440 CrossRef PubMed
.
- K. Abdel-Latif, R. W. Epps, C. B. Kerr, C. M. Papa, F. N. Castellano and M. Abolhasani, Adv. Funct. Mater., 2019, 1900712 CrossRef
.
- D. Alloyeau, W. Dachraoui, Y. Javed, H. Belkahla, G. Wang, H. L. N. Lecoq, S. Ammar, O. Ersen, A. Wisnet and F. Gazeau, Nano Lett., 2015, 15, 2574–2581 CrossRef CAS PubMed
.
- M. Rubio-Martinez, I. Imaz, N. Domingo, A. Abrishamkar, T. S. Mayor, R. M. Rossi, C. Carbonell, A. J. deMello, D. B. Amabilino and D. Maspoch, Adv. Mater., 2016, 28, 8150–8155 CrossRef CAS PubMed
.
- S. Sevim, A. Sorrenti, C. Franco, S. Furukawa, S. Pané, A. Demello and J. Puigmartí-Luis, Chem. Soc. Rev., 2018, 47, 3788–3803 RSC
.
- J. Nette, P. D. Howes and A. J. deMello, Adv. Mater. Technologies, 2020, 5, 2000060 CrossRef CAS
.
- J. Parisi, Q. Dong and Y. Lei, RSC Adv., 2015, 5, 14081–14089 RSC
.
- J. Parisi, L. Su and Y. Lei, Lab on a Chip, 2013, 13, 1501–1508 RSC
.
- S. Seibt, P. Mulvaney and S. Förster, Colloids Surf., A, 2019, 562, 263–269 CrossRef CAS
.
- M. Herbst, E. Hofmann and S. Förster, Langmuir, 2019, 35, 11702–11709 CrossRef CAS PubMed
.
- S. Merkens, M. Vakili, A. Sánchez-Iglesias, L. Litti, Y. Gao, P. V. Gwozdz, L. Sharpnack, R. H. Blick, L. M. Liz-Marzán and M. Grzelczak, ACS Nano, 2019, 13, 6596–6604 CrossRef CAS PubMed
.
- L. Boselli, H. Lopez, W. Zhang, Q. Cai, V. A. Giannone, J. Li, A. Moura, J. M. de Araujo, J. Cookman and V. Castagnola, Commun. Mater., 2020, 1, 1–12 CrossRef
.
- M. Calvaresi, Nat. Nanotechnol., 2020, 15, 512–513 CrossRef CAS PubMed
.
- Y. Lee and T. G. Park, Langmuir, 2011, 27, 2965–2971 CrossRef CAS PubMed
.
- S. Trigari, A. Rindi, G. Margheri, S. Sottini, G. Dellepiane and E. Giorgetti, J. Mater. Chem., 2011, 21, 6531–6540 RSC
.
- K. L. Kelly, E. Coronado, L. L. Zhao and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 668677 CrossRef
.
- Y. Cheng, Y. Wang, D. Chen and F. Bao, J. Phys. Chem. B, 2005, 109, 794–798 CrossRef CAS PubMed
.
- J. Kim, G. L. Liu, Y. Lu and L. P. Lee, Opt. Express, 2005, 13, 8332–8338 CrossRef PubMed
.
- S. Gottheim, H. Zhang, A. O. Govorov and N. J. Halas, ACS Nano, 2015, 9, 3284–3292 CrossRef CAS PubMed
.
- S. Kim, K. L. Shuford, H.-M. Bok, S. K. Kim and S. Park, Nano Lett., 2008, 8, 800–804 CrossRef CAS PubMed
.
- J. Li, J. Wu, X. Zhang, Y. Liu, D. Zhou, H. Sun, H. Zhang and B. Yang, J. Phys. Chem. C, 2011, 115, 3630–3637 CrossRef CAS
.
- M. Potenza, Ž. Krpetić, T. Sanvito, Q. Cai, M. Monopoli, J. de Araújo, C. Cella, L. Boselli, V. Castagnola and P. Milani, Nanoscale, 2017, 9, 2778–2784 RSC
.
- W. Lv, C. Gu, S. Zeng, J. Han, T. Jiang and J. Zhou, Biosensors, 2018, 8, 113 CrossRef CAS PubMed
.
- S. Saverot, X. Geng, W. Leng, P. Vikesland, T. Grove and L. Bickford, RSC Adv., 2016, 6, 29669–29673 RSC
.
- S. D. Perrault and W. C. Chan, J. Am. Chem. Soc., 2009, 131, 17042–17043 CrossRef CAS PubMed
.
- M. Mostafavi, J. Marignier, J. Amblard and J. Belloni, Int. J. Radiat. Appl. Instrum., Part C, 1989, 34, 605–617 Search PubMed
.
- T. Linnert, P. Mulvaney, A. Henglein and H. Weller, J. Am. Chem. Soc., 1990, 112, 4657–4664 CrossRef CAS
.
- Y. Xia, Y. Xiong, B. Lim and S. E. Skrabalak, Angew. Chem., Int. Ed., 2009, 48, 60–103 CrossRef CAS PubMed
.
- A. S. Keys, C. R. Iacovella and S. C. Glotzer, J. Comput. Phys., 2011, 230, 6438–6463 CrossRef CAS
.
- G. Ouyang, C. Wang and G. Yang, Chem. Rev., 2009, 109, 4221–4247 CrossRef CAS PubMed
.
- G. Wulff, Z. Kristallogr., 1901, 34, 449 CAS
.
- J. Kim, S. Manna, S. Dietze, A. Ulvestad, R. Harder, E. Fohtung, E. Fullerton and O. Shpyrko, Appl. Phys. Lett., 2014, 105, 173108 CrossRef
.
- A. E. Baber, S. C. Jensen, E. V. Iski and E. C. H. Sykes, J. Am. Chem. Soc., 2006, 128, 15384–15385 CrossRef CAS PubMed
.
- L. Zhao, X. Ji, X. Sun, J. Li, W. Yang and X. Peng, J. Phys. Chem. C, 2009, 113, 16645–16651 CrossRef CAS
.
- H.-Y. Wu, M. Liu and M. H. Huang, J. Phys. Chem. B, 2006, 110, 19291–19294 CrossRef CAS PubMed
.
- G. Xiong, J. N. Clark, C. Nicklin, J. Rawle and I. K. Robinson, Sci. Rep., 2014, 4, 6765 CrossRef PubMed
.
- L. Marks and L. Peng, J. Phys.: Condens. Matter, 2016, 28, 053001 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nh00540e |
| ‡ Equal contribution. |
| § Current address: Department of Mechanical Engineering, The University of Texas at Dallas, Richardson, TX, 75080, USA. |
| ¶ Current address: Center for Synaptic Neuroscience and Technology, Istituto Italiano di Tecnologia, Largo Rosanna Benzi 10, 16132, Genova, Italy; IRCCS Ospedale Policlinico San Martino, Largo Rosanna Benzi 10, 16132, Genova, Italy. |
| || Current address: Nanobiointeractions and Nanodiagnostics, Istituto Italiano di Tecnologia, Via Morego 30, 16163 Genova, Italy. |
| This journal is © The Royal Society of Chemistry 2022 |