Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Significance of atomic-scale defects in flexible surfaces on local solvent and ion behaviour†
Veselina
Marinova
*,
Colin L.
Freeman
 and
John H.
Harding
and
John H.
Harding

Department of Materials Science and Engineering, The University of Sheffield, Sheffield, S1 3JD, UK. E-mail: v.marinova@sheffield.ac.uk
First published on 5th April 2022
Abstract
Many factors can affect the course of heterogeneous nucleation, such as surface chemistry, flexibility and topology, substrate concentration and solubility. Atomic-scale defects are rarely investigated in detail and are often considered to be unimportant surface features. In this work, we set out to investigate the significance of atomic-scale defects in a flexible self-assembled monolayer surface for the behaviour of clusters of Ca2+ and CO32− ions in water. To this end, we use molecular dynamics simulations to estimate the diffusion coefficients of ion clusters at different topological surface features and obtain ionic radial distribution functions around features of interest. Well-tempered metadynamics is used to gain insight into the free energy of ions around selected surface defects. We find that certain defects, which we refer to as active defects, can impair ionic surface diffusion, as well as affect the diffusion of ions in close proximity to the surface feature in question. Our findings suggest that this effect can result in an ability of such topological features to promote ion clustering and increase local ionic concentration at specific surface sites. The work reported here shows how the presence of small atomic-scale defects can affect the role of a surface in the process of heterogeneous nucleation and contributes towards a rational definition of surfaces as effective nucleating agents.
1 Introduction
Crystallisation is a process of fundamental importance in both nature and industry. Examples include the formation of exoskeletons in marine species at ambient temperature and pressure,1–3 the synthesis of active pharmaceutical ingredients with high purity4,5 and the prevention of the formation of scale in industrial environments.6–8 An in-depth understanding of the mechanisms which promote crystallisation is necessary to synthesise specific polymorphs, prevent the formation of crystals where it is unwanted, and tailor crystalline materials for a vast range of applications.In an uncontrolled environment, crystallisation might be expected to occur on any available surface. However, although classical nucleation theory (CNT) suggests that many surfaces should promote nucleation and crystal formation, in fact surfaces with effective nucleating properties are often hard to identify.9 It is generally acknowledged that a nucleant can operate in several ways. Some surfaces promote nucleation through the strength of the binding affinity of crystallising species to them, giving the convention that “good binders are good nucleators”.10,11 A particular example is epitaxial matching,12–15 where a close lattice match between the growing crystal and substrate is believed to indicate strong binding between them. The presence of a surface may increase local supersaturation at the substrate (particularly if the surface is charged), decreasing nucleation times.16 Nucleants may also exhibit surface features in the form of defects, pits or cracks, which can increase localised ion concentrations and so promote the formation of a nucleus.14,17,18 Understanding the surface characteristics which promote and direct nucleation is key to controlling surface-aided crystallisation.
Self-assembled monolayers (SAMs) provide a diverse platform for studying surface effects on substrate behaviour, as their surface chemistry, charge and flexibility are easily varied, both in a computational and in an experimental setting. Nucleation of CaCO3 on alkanethiol SAMs has been extensively studied as a model system for biomineralisation processes in living organisms.19 Head-group charge,16,20 changing functional groups,10 epitaxial matching,20 flexibility and disorder21,22 have all been demonstrated to play a role in the crystal formation of CaCO3 at the SAM surface. While little is known about the role of nanoscale surface defects on the local solution and ionic behaviour, previous work has revealed that the non-uniform surface chemistry of SAMs can affect the strength of the interactions and behaviour of certain biomolecular systems.23,24 Specific studies on SAM surface defects suggest that these confined environments can affect the growth of nanoparticles.25 We therefore believe that there is more to be discovered about the role of imperfections on flexible surfaces in crystal growth.
In this paper, we investigate the effect of relatively small (atomic-scale) defects in the surface of a self-assembled monolayer of 16-mercaptohexadecanoic acid (16-MHDA) on the behaviour of ionic clusters of Ca2+ and CO32− ions using molecular dynamics (MD) simulations. We generate several surface topographies, for which we calculate the diffusion coefficient associated with the movement of ions out of the surface defect. In the most compelling case, we also obtain the free energy associated with the movement of a single Ca2+ and a single CO32− ion in and out of the defect to understand more about the observed cluster behaviour. For the latter, we perform additional simulations at high ionic concentrations in solution. Our work shows how a better understanding of the way surface features affect surface-aided crystallisation can help us design and tailor effective nucleating agents.
2 Methods
In this work, we investigate the ion cluster behaviour of Ca2+ and CO32− ions in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
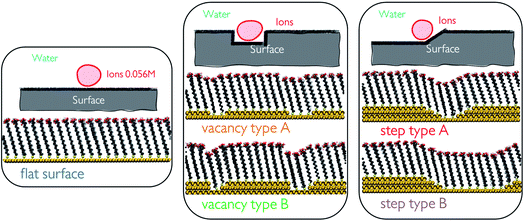
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ratio at 5 different SAM surface defects in water. Generating surface defects in the monolayers was achieved through the removal of one or several surface atoms from the underlying Au(111) surface. This procedure creates nm-scale steps and vacancies which promote interactions between the functional groups of neighbouring chains through the offset produced. We generate a total of 5 configurations, which we refer to as flat surface, vacancy type A, vacancy type B, step type A and step type B, as displayed in Fig. 1.
50 ratio at 5 different SAM surface defects in water. Generating surface defects in the monolayers was achieved through the removal of one or several surface atoms from the underlying Au(111) surface. This procedure creates nm-scale steps and vacancies which promote interactions between the functional groups of neighbouring chains through the offset produced. We generate a total of 5 configurations, which we refer to as flat surface, vacancy type A, vacancy type B, step type A and step type B, as displayed in Fig. 1.
We calculate the mean squared displacement (MSD) for each ion within the clusters to obtain average cluster diffusion coefficients. Solvent behaviour at the SAM surface was investigated using residence time analysis. A combination of MD and well-tempered metadynamics (WTmetaD) was used to obtain a profile of the single ion movement towards and away from the surface labelled vacancy type B for each ion type. We also perform large-scale simulations at much higher ionic concentrations to obtain an RDF profile between the surface and the solute.
2.1 Simulation setup
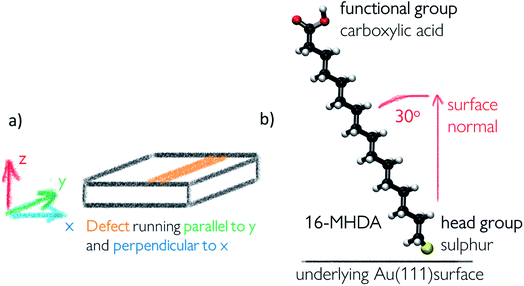
Self-assembled monolayer surfaces were generated using 16-MHDA as a building block on an 80 × 80 Å grid of an Au(111) surface using a total of 340 alkanethiol molecules. In this system, the 30° angle of the chains with respect to the normal to the surface plane (marked as the z-axis on Fig. 2a) was maintained throughout.25,26 A spacing of 4.98 Å between the sulphur atoms in the xy-plane was maintained in all configurations with the exception of the surface labelled vacancy type B, where distances between the sulphurs within the defect had to be adjusted marginally to avoid overlap between the chains and to maintain consistency in the angle of the 16-MHDA molecules with respect to the underlying surface. More details on the spacing between building blocks can be found in the ESI.†Surface defects were generated by removing layers of underlying Au atoms. The cross-section of the defect in the xz-plane is displayed in Fig. 1, while the defect itself runs parallel to the y-axis, a schematic of which can be seen in Fig. 2a.
2.1.2.1 SAM–water simulations. Simulations of each of the 5 surface configurations in water were carried out. Production run lengths for these were 2 ns, with an additional initial 200–300 ps of system relaxation and water density equilibration.
2.1.2.2 Ion clusters at SAM defects in water. MD simulations of CaCO3 ionic clusters at the SAM surface and within defects (where present) were carried out. The ionic clusters were generated using Packmol 20.010.39 They contained 10 Ca2+ and 10 CO32− ions, making up a total system concentration of 0.056 M. Clusters were positioned close to the surface defect and the cluster structure alone was relaxed with a short simulation of 100 ps. Three different cluster configurations per surface topography type were generated, which we will refer to as set 1, set 2 and set 3. Set 1 and set 3 were equilibrated by relaxing the ions onto the surface for 50 ps, followed by water relaxation for another 100 ps. On the other hand, set 2 was set up by relaxing the water onto the surface, followed by relaxation of the ions onto the surface. This variation in the setup enables us to evaluate whether the presence of water on the surface before relaxing the ions affects cluster behaviour on the surface. Each of the 3 setups for each surface type was run for a total of 56 ns.
2.1.2.3 Single ion at vacancy type B in water. In the case of surface vacancy type B, we perform further analysis by setting up simulations of a single ion at the surface in water. We perform a simulation for each ion type: Ca2+ and CO32−. These simulations were configured by removing the extra ions from the starting configuration for set 1 of vacancy type B.
2.1.2.4 Large-scale simulations at vacancy type B in water. We perform additional simulations in the presence of a SAM surface which has a vacancy of type B. We refer to them as large-scale as the underlying surface grid is in this case 170 × 80 Å. Two different simulation sets were carried out, where Ca2+ and CO32− ions are dispersed in solution, away from the surface, at the beginning of the simulation at concentrations of 0.41 M and 0.69 M. Starting configurations were generated using Packmol 20.010.
The biasing potential was applied every 500 steps in the form of Gaussian functions of width 0.2 Å in the x-axis and 0.4 Å in the z-axis and a height of 12 kJ mol−1. The bias factor for implementing WTmetaD was set to 10. Metadynamics was implemented by using the open source community-developed PLUMED library, version 2.6.42,43
Free energy surfaces were recovered using the sum_hills functionality in PLUMED. Simulations were run until the average positional error in the resulting free energy profile was within 1.5 kBT units. More detail on our convergence analysis can be found in the ESI.†
2.2 Water analysis
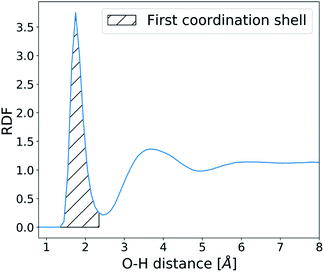
The structure and dynamics of water were analysed in the absence of CaCO3 ions in order to understand the effects of surface defects on local solvent behaviour. Water residence times at the SAM surface were calculated by counting the number of frames an O-atom of a water molecule spends within 2.45 Å of the H-atom on the –COOH SAM functional group (based on the RDF calculated between the two atom types as shown in Fig. 4). At each frame where a water molecule goes beyond that distance, the counting is stopped and only restarted when the molecule is back within the given distance range.This procedure allows us to calculate an array of individual uninterrupted residence times of a water molecule on each SAM functional group, from which we obtain the average. These values are further averaged across the y-axis, as shown in Fig. 2, and residence times of water at the SAM functional groups along the x-axis of the surface are reported.
2.3 Functional group flexibility analysis
The degree of movement in the SAM –COOH functional groups was recorded as a mean squared displacement of the carboxylic C-atom with respect only to the initial surface configuration, taken after equilibration at the start of the SAM-water production run. Similarly to the residence time analysis, we average the time-averaged functional group MSD across the y-axis of the surface and report the values along the cross-section of the defect in the surface x-direction.2.4 Diffusion coefficient calculations
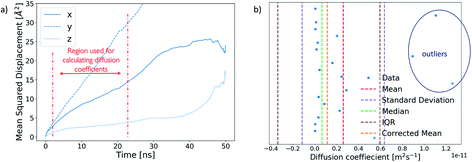
A diffusion coefficient for each ion cluster was obtained by calculating a mean squared displacement (MSD) for each ion within a cluster. The diffusion coefficient was extracted from the slope of a corresponding MSD plot for the time step fragment between 2 ns and 20 ns in each production run, as shown in Fig. 5a.To obtain an average cluster diffusion coefficient which is consistent with the overall cluster behaviour, we perform an interquartile range (IQR) analysis on the 3D MSD values across the cluster and exclude any outliers. An example of this analysis is shown in Fig. 5b. The plot shows all individual ion diffusion data points (in blue) and the mean value of the cluster diffusion coefficient (in red). The mean cluster diffusion is skewed by the diffusion of several ions which are orders of magnitude higher than the median of the dataset (shown in green). These points correspond to individual ions which have detached from the cluster and therefore need to be excluded from the diffusion coefficient calculation of the ionic cluster. We use the IQR (in brown) to determine which points are to be excluded and report the corrected mean (in orange) in our results. All interquartile statistical analysis carried out when determining the mean cluster diffusion is reported in the ESI.†
All simulation images in this paper have been produced using VMD.44 Trajectory analysis was carried out using Python 3.45
3 Results
The results reported in this section are split into four main parts. We first take a look at the water behaviour in the presence of the different surface defect types on the SAM. In the second part, we discuss ionic cluster behaviour at the surface and how that varies at and around the different defect sites. Next, we report our work on the free energy calculations associated with an ion moving in and out of the surface defect of type vacancy type B. Finally, we discuss large-scale simulations where we start with CaCO3 ions dispersed in solution and examine how the presence of a defect affects their behaviour using RDF analysis.3.1 Water behaviour at the SAM surface
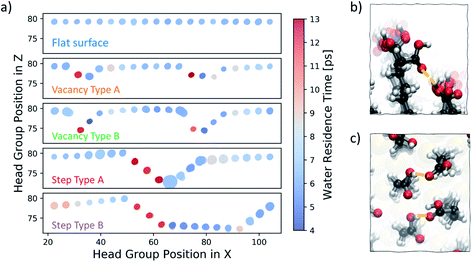
We start our investigation into the surface defects of a self-assembled monolayer of 16-MHDA by performing molecular dynamics simulations of each of the surface configurations, as described in Fig. 1, in pure water. Our analysis is focused on evaluating the degree of flexibility in the SAM functional groups, as well as recording the residence time of a water molecule at each individual chain, noting any particular features associated with the presence of a defect. A summary of this is reported in Fig. 6a. The figure shows the five different surface types we consider, where the x-axis of the plot corresponds to the functional group position along the x-axis of the SAM and the y-axis of the plot corresponds to the position in the z-direction of the box. As discussed in the Methods section, metrics on flexibility and residence times have been averaged across the y-axis of the surface, to which the defects run parallel, as shown in Fig. 2.In Fig. 6a, each functional group is displayed as a circle, the colour of which represents the residence time of a water molecule at that particular chain using the colour bar on the right. The degree of movement in the –COOH group, on the other hand, is represented by the size of the circle; larger circles correspond to greater movement. For more information on the calculation of the residence times and flexibility of the SAM functional groups, the reader should refer to the Water analysis section in the Methods section.
Our analysis shows that, on a perfectly ordered defect-free region within a surface of a SAM which we refer to as a flat surface, the residence time of a water molecule at an individual chain is consistently around 6 ps. Equally, the variability in the degree of movement in the surface is minimal, as shown by the consistent size of the circles across the surface.
Moving to vacancy type A and B, we observe some variation in water residence times compared to that of a non-defective surface. At the first offset –COOH group, which is immediately next to the aliphatic chain of the previous, non-offset chain, the water residence time is 13 ps, which is more than double the average residence time we observe for the flat surface case. Additionally, we also note a slightly higher residence time of around 8–9 ps immediately next to the defect on the right. These results demonstrate that, due to the presence of a vacancy in the underlying Au layer, regions of higher water residence time emerge as a direct consequence of the disrupted surface pattern. The degree of movement in the –COOH functional group around vacancy type A is of a similar magnitude to that of the flat surface case, while for the chains immediately next to vacancy type B the flexibility is greater. Because of the large offset of approximately 5 Å, the part of the chain exposed to the solution has enough room to move more freely. In fact, as shown in Fig. 6b, the space is sufficient for the carboxylic acid group to twist and interact with the neighbouring offset chains through hydrogen bonding.
Step type A has three stepped chains of one offset Au-atom each, followed by three steps bringing the surface to its original level, forming a bowl-shaped defect. Step type B is similar, with the exception of having a larger separation in-between the two step defects, as shown in Fig. 1. An important feature of these stepped defects is the –COOH group spacing. The left-hand step defect has carboxylic acid groups which are marginally further apart, whereas at the right-hand going up the step the functional groups are a little closer together. This effect naturally emerges after equilibration and is a consequence of the characteristic 30° angle of the 16-MHDA aliphatic chain with respect to the normal to the plane (see Fig. 2b), in combination with the presence of steps in the underlying Au(111) surface. As a result, water residence times at the left-hand side steps are twice to three times larger that those observed on a defect-free SAM. Conversely, on the right-hand side of the steps, lower water residence times are observed, combined with a slightly higher degree of surface mobility. Looking at the trajectories, we find that in the latter regions we encounter coordination between the functional groups via hydrogen bonding, as shown in Fig. 6c.
In this section, we show that the presence of the defects affects both the residence times of water at the SAM functional groups and the flexibility of the SAM functional groups. The altered solvent behaviour at such defects can have important consequences for the solute. Longer water residence times will reduce solvent–solute exchange rates at the surface, increasing solute binding strengths and lowering surface diffusion rates. These effects, whether individually or combined, affect the kinetics of solute cluster formation, and therefore nucleation at surfaces.
3.2 Behaviour of the ionic clusters at the SAM surface
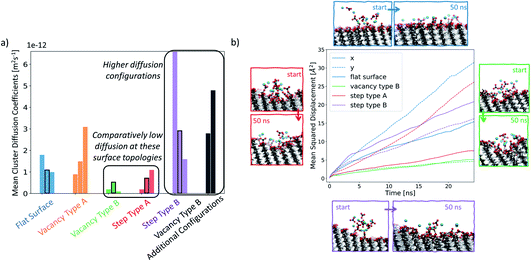
In order to understand how defects can affect ionic cluster behaviour at the SAM/water interface, we first set up simulations with each of the given SAM surface configurations and an ion cluster of 10 Ca2+ and 10 CO32−, placed at a defect. A reference case using the defect-free surface was also included. In our system, this number of ions is equivalent to an overall concentration of 0.056 M. However, in this setup we are starting from a non-equilibrium system configuration, where all ions are placed in one particular place on the surface. We are interested in the rate of system evolution (i.e. ion surface diffusion) towards reaching equilibrium, which will give us insight into the role of defects on ionic behaviour. The setup procedure is performed 3 times, each with a different ion cluster configuration, for each surface type, producing three data points in the form of simulations when studying the ionic cluster behaviour. We refer to these simulations as set 1, set 2 and set 3 where applicable. For more information on the setup, the reader is referred to the section Simulation setup in the Methods section.In Fig. 7a, we report the mean diffusion coefficient for the cluster, calculated as per the procedure outlined in the Diffusion coefficient calculations section in the Methods section. Additionally, we report all mean diffusion values, along with the lower and upper half averages of the diffusion values within each cluster, in Table 1. The latter numbers indicate whether both slow and fast diffusing ions are present within the cluster (and hence the likelihood that the cluster will fragment).
| LH | Set 1 | UH | LH | Set 2 | UH | LH | Set 3 | UH | |
|---|---|---|---|---|---|---|---|---|---|
| Flat surface | 0.2 | 1.8 | 3.3 | 0.5 | 1.1 | 1.7 | 0.2 | 1.0 | 1.8 |
| Vacancy type A | 0.4 | 3.1 | 5.9 | 0.4 | 1.5 | 2.6 | 0.2 | 0.9 | 1.5 |
| Vacancy type B | 0.06 | 0.2 | 0.3 | 0.1 | 0.5 | 0.8 | 0.06 | 0.1 | 0.2 |
| Step type A | 0.09 | 0.7 | 1.5 | 0.1 | 1.1 | 2.2 | 0.06 | 0.2 | 0.4 |
| Step type B | 1.5 | 6.6 | 12.7 | 0.9 | 2.9 | 5.3 | 0.3 | 1.6 | 3.2 |
| Vacancy type B shifted cluster | 1.2 | 4.2 | 8.0 | 0.7 | 2.8 | 4.9 | — | — | — |
The mean diffusion coefficient of an ion cluster on a defect-free flat surface ranges between 1 and 2 × 10−12 m2 s−1. In this case, there are no topographical surface features and so we take this range as the benchmark for ionic surface diffusion when discussing the rest of the surface configurations.
In the case of vacancy type A (shown in orange), we can see that in two of the cases, the mean ionic diffusion is comparable to that in the flat surface case, indicating that the presence of one Au offset vacancy defect does not affect the cluster behaviour much. An exception can be seen in set 1 of this group, where much higher average cluster diffusion is observed. In this case, the spread of diffusion coefficients is also large, showing that the cluster has fragmented.
Significantly smaller values of the mean cluster diffusion coefficients are found when ions are placed at vacancy type B (green) or step type A (red). In several of these cases, this is accompanied by an extremely compact cluster behaviour. These defect types create an environment where the ionic clusters are restrained and diffuse very little during our simulations. This implies that even relatively small surface features of the order of magnitude of tens of Å can substantially affect ionic cluster diffusion by providing a barrier to their natural surface mobility. Reducing cluster mobility, on the other hand, can produce more rapid growth of clusters around this defect as passing ions become trapped in its vicinity.
Ionic clusters placed at step type B (in purple) generally display quite dynamic cluster behaviour with mean diffusion coefficients between 2 × 10−12 m2 s−1 and 6 × 10−12 m2 s−1, which are an order of magnitude higher than what we see in the flat surface case. We selected several of the configurations, highlighted by a black rectangular border in Fig. 7a, for more detailed analysis. Fig. 7b displays a visual representation of the starting and the ending configurations for each of the selected cases, together with a corresponding mean squared displacement plot along the x- and y-surface axes. Visual analysis of the ions on the flat surface SAM shows how the cluster has transformed to resemble an ionic layer across the surface. The corresponding MSD analysis shows that this spread occurs across both the x- and y-axes of the surface, being more substantial for the latter. This phenomenon is due to the packing arrangement of the underlying Au(111) surface, resulting in larger spacing between –COOH groups in the y-direction of the surface than in the x-direction. In the case of step type B, shown in purple, the slopes of the x- and y-component of the MSD are comparable to each other, indicating that the ions are diffusing both across and along the surface. Additionally, as shown in Fig. 7b in purple, the diffusion along the x-axis occurs preferentially away from the stepped region. This observation is consistent across all three simulations of this group, suggesting that the equilibration process of the ionic cluster is more favourable across a defect-free environment, rather than “climbing” the steps, and indicates a presence of a barrier associated with diffusion across the defect.
For the cases where a more compact cluster behaviour is observed, namely vacancy type B and step type A, a corresponding shift in the MSD, shown respectively in green and red in Fig. 7b, can be seen. In the case of step type A in set 2, the movement associated with spread across the y-axis (along the defect) is much larger than that observed in the x-axis (perpendicular to the defect), correlating with the general argument that has emerged from our simulations that defected surface features present a barrier to ionic surface diffusion.
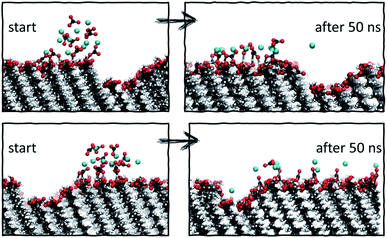 | ||
| Fig. 8 Starting and final configurations of simulations of ion clusters placed next to vacancy type B, showing the preferential diffusion of ions across the defect-free surface side. | ||
Analysis of the ionic cluster behaviour indicates that some surface defects will impair ion mobility across a surface, while others will not. We will refer to the former as active defects. Moreover, we see a general trend that in the process of equilibration, ion clusters diffuse much less readily across the active defect than across a defect-free feature, suggesting that topographical defects create a barrier to diffusion, reducing the available surface space. In our simulations, when starting with a local enhanced concentration, this effect results in higher diffusion rates away from a defect compared to the flat surface reference case, as shown in Fig. 7a (purple and black cases). However, as discussed, these simulations have artificially placed ion clusters as starting configurations and so the higher diffusion is due to the non-equilibrium starting conditions and the relaxations away from this state.
3.3 Free energy calculations on single ion movements with respect to vacancy type B
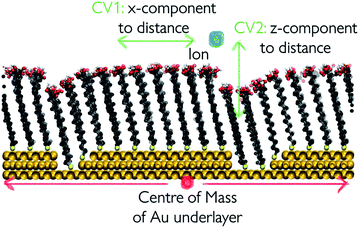
We take a closer look at the free energy associated with the movement of Ca2+ and CO32− ions in and out of vacancy type B to gain insight into the solute–surface interactions promoting the observed ion cluster behaviour. Simulations were performed in combination with WTmetaD and the full details of the setup are outlined in the Well-tempered metadynamics setup section in the Methods section. Each simulation was carried out until the average positional standard error was within 1.5 kBT units. All convergence analysis is reported in the ESI.†Fig. 9 displays the free energy profiles recovered from the metadynamics runs. The free energy reported is projected onto the 2-dimensional space of the x- and z-distance components between the ion of interest and the centre of mass of the underlying Au surface. In this representation, we are making the assumption that, since the defect runs parallel with the y-axis of the box, ionic movements along that axis are degenerate. The free energy profile of the movement associated with a Ca2+ ion, reported on the left of Fig. 9, shows small variations across the system as a consequence of the presence of surface defects. In particular, we see a more stable state within the right-hand defect, which is the slightly wider of the two (refer to Fig. 1). This effect is relatively long-ranged, stretching as far as 10 Å away from the well of the defect. On either side of the defect, we see higher energy states of the Ca2+ ion. Despite the fact that the free energy difference is not large, energetically varied ionic states at and a few Å away from the surface can be clearly identified.
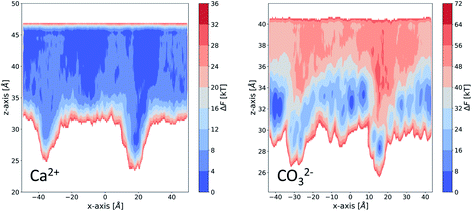 | ||
| Fig. 9 Free energy profiles obtained from enhanced sampling metadynamics simulations of a single Ca2+ (left) and a single CO32− (right) in water in the presence for surface vacancy type B. | ||
Looking at the right-hand side free energy surface of the counter CO32− ion, we see a substantial shift in the energetics of the system, where the solution is now much less favourable than the surface states. This trend is closely related to the fact that the functional groups at the SAM surface are uncharged and CO32− ions are associating strongly with the surface through hydrogen bonding. We can speculate that if the chains were charged and had a –COO− functionality instead, the Ca2+ ions would be the ones with the stronger surface–solute interaction. Nonetheless, we believe that in the context of surface topography effects, our observations are valid and give insight into general mechanisms by which small surface defects can operate on nucleating species. The free energy surface (FES), corresponding to the movement of CO32−, also shows a high energy region in the solution right above the defect, particularly for the wider defect on the right-hand side. This observation explains why we see little diffusion of ions out of and into this defect in our simulations – there is a barrier associated with the movement of ions. The effect can be seen stretching as far as 10 Å away from the surface.
By combining metadynamics with MD simulations, we have been able to gain further insight into the ion–surface interactions which dictate the observed ion cluster behaviour. We find that, in response to the altered surface topography, high and low energy regions emerge which stretch over a relatively large distance into the solution. These regions will control ionic diffusion at and close to the surface.
3.4 Large-scale MD simulations at vacancy type B
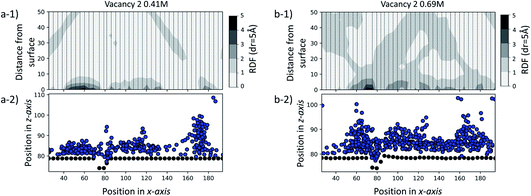
To further test our hypothesis, we performed two additional sets of simulations at a SAM surface of size 170 × 80 Å with a vacancy type B surface feature. Unlike the set of simulations previously discussed, in this case the initial configurations contain ions of Ca2+ and CO32− randomly dispersed in solution at two concentrations: 0.41 M and 0.69 M. Our objective is to probe whether the surface feature will have a noticeable effect on the ionic system behaviour using an equilibrium starting configuration rather than the non-equilibrium configurations with clusters placed close to defects as discussed above. The simulations were performed for 35 ns for the 0.41 M system and for 70 ns for the 0.69 M system.In Fig. 10, we report the radial distribution function (RDF) between each unique –COOH functional group position along the x-axis and Ca2+ and CO32− ions for the last 5 ns of each simulation. Individual 1-dimensional RDFs, calculated as a function of the distance from the –COOH group to the ions, follow a dashed line. The RDFs have been plotted side by side, creating an overall 2-dimensional representation of the ionic distribution across and away from the surface. For clarity, we also provide a schematic of the corresponding system configuration by representing C-atoms on the functional group as black dots and ions as blue.
From the visual representation of the ions, we can see that there is clustering of ions close to and within the defect, running parallel to the y-axis and around 70–80 Å along the x-axis. Our RDF analysis reveals that for both cases, the surface generally attracts ions, as we see 2–3 times higher probability of ionic concentration in most surface areas compared to a random distribution. However, we can see a further distinct increase in and around the defect site of 3–5 times higher ionic distribution. More details on the calculation of the RDF distributions, and details of how the RDF evolves in time for the duration of each simulation, are provided in the ESI.†
The observations made here indicate that, even in a simulation environment where ions are initially distributed randomly, the presence of an active surface defect can affect the behaviour of ion clustering at the surface, which in turn can affect the rate at which ionic clusters form and grow.
4 Conclusions
This work investigates the effect of atomic-scale defects in a flexible SAM on the behaviour of the solvent, as well as on that of ionic CaCO3 clusters. Our analysis shows that the presence of features in the surface topography alters the local behaviour of the solvent by providing sites where the adsorbed state of a solvent molecule is longer lived in comparison to a defect-free surface. Furthermore, the presence of surface defects affects the ion cluster behaviour at the SAM surfaces. Certain surface features in our investigation are clearly able to reduce the mobility of ions across the surface. When placed immediately next door to steps or vacancies, ions preferentially diffuse away from these features, showing that there is a barrier associated with diffusion across them. This is further supported by the WTmetaD simulations on the ion mobility across vacancy type B, where we see long-ranged disruption in the free energy. In simulations with significantly higher ionic concentrations, where ions are randomly dispersed in solution to start with, we see the same effects, where ions notably cluster around defect sites.Our findings have important consequences for understanding heterogeneous nucleation. Firstly, only certain defect sites will act as active nucleation sites and therefore we can expect that not all surface features will aid nucleation, as indicated in Fig. 11 by the label inactive defects.
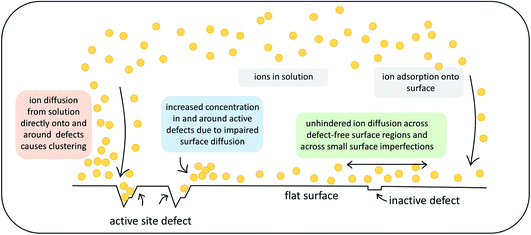 | ||
| Fig. 11 Schematic summary of the observed effects that atomic-scale surface defects can exert on ionic substrates. | ||
Secondly, the presence of active defects affects the solvent and solute behaviour, limiting the mobility of ions around the defect. We speculate that there are two mechanisms involved. Ions will cluster either when descending close to an active site from solution or when diffusing around on the surface before reaching an active site (as indicated in Fig. 11). Both mechanisms will result in higher concentration of ions in the solution around the defect. We recall that classical nucleation theory (like many rare event theories) involves an assumption of quasi-equilibrium between species in the initial state. It is nevertheless a theory about kinetics, not thermodynamics. The system passes along a single coordinate (traditionally defined as cluster size but modern computational methods have greatly widened this choice).46 The enhanced local concentrations are consistent with an assumption of quasi-equilibrium at the surface but, as the local initial state for the nucleation process, it will also increase the probability of forming a critical nucleus at these sites.
In the context of heterogeneous nucleation, the implications of our observations perhaps help explain why and how few surfaces operate as effective nucleating agents. Surfaces are generally understood to stabilise a nucleus by lowering its interfacial energy and hence, aid nucleation (as would be predicted by the Joule–Thompson relation), but these interfacial energies are always assumed to be those of the bulk interface, ignoring local effects caused by defects. Reliable nucleating agents are in reality hard to find. If only certain surface topological features stimulate a significant increase in local supersaturation, as indicated by our work, then a defect-free region, which would be the majority of the surface area, will not be particularly good at inducing clustering in itself. Nuclei that form in the absence of surface active sites may be stabilised by the surface, however the probability of their formation will not be enhanced. In the presence of an active defect, the increase in local supersaturation, under the mechanisms we propose, will enhance the probability of nuclei formation. The concentration of active defects, however, will always be limited and only mildly dependent on the surface chemistry. This means that the number of nuclei that can form at active sites at any one time will also be limited. In the context of thermodynamics, these nuclei will therefore be stabilised by the fact that their number is self-limited and system solute concentration is not depleted upon their formation, until they reach critical size and crystal formation is underway.
The results presented in this work demonstrate that even small features in flexible surfaces can affect solvent and solute behaviour at and a few Ångstroms away from the surface. The presence and density of these atomic-scale defects can alter the course of nucleation in a heterogeneous environment. Understanding the role of these active sites is essential for the design of effective nucleating agents.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support of the Engineering and Physical Sciences Research Council (EPSRC), grant no. EP/R018820/1 which funds the Crystallization in the Real World consortium. Via our membership of the UK’s HEC Materials Chemistry Consortium, which is funded by the EPSRC (EP/R029431), this work used the UK Materials and Molecular Modelling Hub for computational resources, MMM Hub, which is partially funded by the EPSRC (EP/T022213) and the ARCHER2 UK National Supercomputing Service (http://www.archer2.ac.uk).Notes and references
- L. Addadi and S. Weiner, Angew. Chem., Int. Ed. Engl., 1992, 31, 153–169 CrossRef.
- S. Weiner and P. M. Dove, Rev. Mineral. Geochem., 2003, 54, 1–29 CrossRef CAS.
- S. Weiner and L. Addadi, Annu. Rev. Mater. Res., 2011, 41, 21–40 CrossRef CAS.
- S. Kim, C. Wei and S. Kiang, Org. Process Res. Dev., 2003, 7, 997–1001 CrossRef CAS.
- N. Variankaval, A. S. Cote and M. F. Doherty, AIChE J., 2008, 54, 1682–1688 CrossRef CAS.
- S. J. Dyer and G. M. Graham, J. Pet. Sci. Eng., 2002, 35, 95–107 CrossRef CAS.
- J. MacAdam and S. A. Parsons, Rev. Environ. Sci. Bio/Technol., 2004, 3, 159–169 CrossRef CAS.
- A. Antony, J. H. Low, S. Gray, A. E. Childress, P. Le-Clech and G. Leslie, J. Membr. Sci., 2011, 383, 1–16 CrossRef CAS.
- M. A. Levenstein, C. Anduix-Canto, Y.-Y. Kim, M. A. Holden, C. G. Niño, D. C. Green, S. E. Foster, A. N. Kulak, L. Govada, N. E. Chayen, S. J. Day, C. C. Tang, B. Weinhausen, M. Burghammer, N. Kapur and F. C. Meldrum, Adv. Funct. Mater., 2019, 29, 1808172 CrossRef.
- L. M. Hamm, A. J. Giuffre, N. Han, J. Tao, D. Wang, J. J. D. Yoreo and P. M. Dove, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1304–1309 CrossRef CAS PubMed.
- M. L. Whittaker, P. M. Dove and D. Joester, MRS Bull., 2016, 41, 388–392 CrossRef CAS.
- A. Mcpherson and P. Shlichta, Science, 1988, 239, 385–387 CrossRef CAS PubMed.
- A. Markus Travaille, L. Kaptijn, V. Paul, B. Hulsken, J. A. A. W. Elemans, R. J. M. Nolte and H. van Kempen, J. Am. Chem. Soc., 2003, 125, 11571–11577 CrossRef PubMed.
- E. Saridakis and N. E. Chayen, Trends Biotechnol., 2009, 27, 99–106 CrossRef CAS PubMed.
- J. P. Mithen and R. P. Sear, J. Chem. Phys., 2014, 140, 084504 CrossRef CAS PubMed.
- D. M. Duffy and J. H. Harding, Surf. Sci., 2005, 595, 151–156 CrossRef CAS.
- T. F. Whale, M. A. Holden, A. N. Kulak, Y.-Y. Kim, F. C. Meldrum, H. K. Christenson and B. J. Murray, Phys. Chem. Chem. Phys., 2017, 19, 31186–31193 RSC.
- M. A. Holden, T. F. Whale, M. D. Tarn, D. O’Sullivan, R. D. Walshaw, B. J. Murray, F. C. Meldrum and H. K. Christenson, Sci. Adv., 2019, 5, eaav4316 CrossRef PubMed.
- J. Aizenberg, A. J. Black and G. M. Whitesides, J. Am. Chem. Soc., 1999, 121, 4500–4509 CrossRef CAS.
- C. L. Freeman, J. H. Harding and D. M. Duffy, Langmuir, 2008, 24, 9607–9615 CrossRef CAS PubMed.
- J. Aizenberg, A. J. Black and G. M. Whitesides, Nature, 1998, 394, 868–871 CrossRef CAS.
- C. L. Freeman, Q. Hu, M. H. Nielsen, J. Tao, J. J. De Yoreo and J. H. Harding, J. Phys. Chem. C, 2013, 117, 5154–5163 CrossRef CAS.
- K. Sprenger, Y. He and J. Pfaendtner, Probing How Defects in Self-assembled Monolayers Affect Peptide Adsorption with Molecular Simulation, in Foundations of Molecular Modeling and Simulation, ed. R. Snurr, C. Adjiman and D. Kofke, Springer, Singapore, 2016, pp. 21–35 Search PubMed.
- G. Chong, I. U. Foreman-Ortiz, M. Wu, A. Bautista, C. J. Murphy, J. A. Pedersen and R. Hernandez, J. Phys. Chem. C, 2019, 123, 27951–27958 CrossRef CAS.
- C. Vericat, M. E. Vela and R. C. Salvarezza, Phys. Chem. Chem. Phys., 2005, 7, 3258–3268 RSC.
- A. Ulman, Chem. Rev., 1996, 96, 1533–1554 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- P. Raiteri and J. D. Gale, J. Am. Chem. Soc., 2010, 132, 17623–17634 CrossRef CAS PubMed.
- P. K. Ghorai and S. C. Glotzer, J. Phys. Chem. C, 2007, 111, 15857–15862 CrossRef CAS.
- H. A. Lorentz, Ann. Phys. Chem., 1881, 248, 127–136 CrossRef.
- D. Berthelot, C. R. Hebd. Seances Acad. Sci., 1898, 1703–1855 Search PubMed.
- C. L. Freeman, J. H. Harding, D. J. Cooke, J. A. Elliott, J. S. Lardge and D. M. Duffy, J. Phys. Chem. C, 2007, 111, 11943–11951 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, Hilger, Bristol, 1988 Search PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef PubMed.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- A. Barducci, M. Bonomi and M. Parrinello, WIREs Computational Molecular Science, 2011, 1, 826–843 CrossRef CAS.
- M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972 CrossRef CAS.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- G. Van Rossum and F. L. Drake, Python 3 Reference Manual, CreateSpace, Scotts Valley, CA, 2009, p. 242 Search PubMed.
- B. Peters, J. Phys. Chem. B, 2015, 119, 6349–6356 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1fd00082a |
| This journal is © The Royal Society of Chemistry 2022 |