Open Access Article
Open Access ArticleBenchmark of a functional-group database for distributed polarizability and dipole moment in biomolecules†
Raphael F.
Ligorio
a,
Jose L.
Rodrigues
b,
Anatoly
Zuev
a,
Leonardo H. R.
Dos Santos
 b and
Anna
Krawczuk
b and
Anna
Krawczuk
 *a
*a
aInstitut für Anorganische Chemie, Universität Göttingen, Tammannstrasse 4, D-37077 Göttingen, Germany. E-mail: anna.krawczuk@uni-goettingen.de
bDepartamento de Química, Universidade Federal de Minas Gerais, Av. Pres. Antônio Carlos 6627, 31270-901 Belo Horizonte, MG, Brazil
First published on 22nd November 2022
Abstract
The extraction of functional-group properties in condensed phases is very useful for predicting material behaviors, including those of biomaterials. For this reason, computational approaches based on partitioning schemes have been developed aiming at rapidly and accurately estimating properties from chemically meaningful building blocks. A comprehensive database of group polarizabilities and dipole moments is useful not only to predict the optical properties of biomacromolecules but also to improve molecular force fields focused on simulating biochemical processes. In this work we benchmark a database of distributed polarizabilities and dipole moments for functional groups extracted from a series of polypeptides. This allows reconstruction of a variety of relevant chemical environments. The accuracy of our database was tested to predict the electro-optical properties of larger peptides and also simpler amino acids for which density functional theory calculations at the M06-HF/aug-cc-pVDZ level of theory was chosen as the reference. This approach is reasonably accurate for the diagonal components of the polarizability tensor, with errors not larger than 15–20%. The anisotropy of the polarizability is predicted with smaller efficacy though. Solvent effects were included explicitly by surrounding the database entries by a box of water molecules whose distribution was optimized using the CHARMM force field.
1 Introduction
Biomaterials are either artificial substances incorporated in living systems, or natural bioproducts with broader applications in materials science and nanotechnology.1,2 From an optical point of view, biomaterials are evaluated based on refractive indices and transparency, whereas mechanical, chemical and biological properties may strongly depend on the specific application. Despite their satisfactory performance, current biomaterials are mainly developed based on a trial-and-error optimization, rather than being properly engineered.3 For optimizing the materials efficiency, it is vital to develop accurate methodologies aiming at rapid screening of the best candidates for a given functionality.4 The long-term goal of our work is to develop algorithms for optimizing the optical efficiency of functional biomaterials, based on their breakdown into smaller building blocks which could be amino acids, peptides, lipids, nucleic acids, etc. This implies additive schemes for the rapid prediction of bulk properties.A variety of schemes has been proposed to calculate the dipole moments and distributed functional-group polarizabilities.5–12 Bader chose the topological partitioning of the charge density based on Quantum Theory of Atoms In Molecules (QTAIM).13 Keith generalized the Bader approach within the “atomic response theory”,14 which was later implemented in the PolaBer program.15 One of the advantages is the removal of origin-dependent terms that are particularly troublesome for the transferability of the functional groups. Indeed, QTAIM offers advantages because it leads to an exact partitioning of the charge density in real space. This contrasts with schemes such as the one proposed by Stone in the framework of the distributed multipole analysis16 and with the method proposed by Angyan, in which atomic polarizabilities are obtained by differentiating the energy, rather than dipole moments.17–20
The modelling of biomolecules through charge-density based parameters has become an important research field. Databases of functional groups have been created aiming at having a more realistic reconstruction of the electro-optical and electrostatic properties of molecules.21,22 The hypothesis of transferability in biomolecules is strongly supported.23 More recently, generalized databases which include polarizability tensors of various relevant functional groups have been proposed.24 In that work, the polarizability of a transferable functional group is reconstructed from a set of previously selected molecular entries rotated to a common coordinate system and then clustered appropriately using a genetic algorithm. A combination of the building blocks thus allows prediction of the electro-optical properties with high accuracy. Methods based on artificial intelligence can also be used to precisely estimate atomic polarizabilities from a very large molecular training set.25
We note that the inclusion of polarizabilities as parameters to describe part of the molecular energy in classical force-field simulations could significantly improve the accuracy, in particular if one is interested in taking into account effects due to long-range interactions such as intermolecular contacts. Traditionally, additive force fields have been developed including point atomic charges to compute the electrostatic contribution of intermolecular interactions, thus neglecting details of the charge density distribution. This results in an incomplete inclusion of polarization effects due to the vicinity. New developments in molecular mechanics have started to correct for such perturbations by considering distributed polarizabilities within a set of parameters.26 Therefore, an accurate database of polarizability tensors would also be desirable from this perspective.
While building blocks can be extracted from very accurate gas-phase calculations, their properties are only representative of the actual biomaterial when the chemical environment is taken into account. For biomolecules, this necessarily implies careful consideration of intermolecular interactions. Because these contacts are typically weaker than covalent bonds, semi-empirical approaches based on classical electrostatics have long been used to estimate the opto-electronic properties of the biomaterial from gas-phase calculations.27–31 In such methods, the electric field experienced by a particular molecule in the condensed phase has additive contributions from an externally applied field and from the field produced by all vicinal dipoles. Most of these implementations reduce entire molecules to point dipoles, thus do not explicitly treat functional groups. One of these implementations is known as the dipole interaction model (DIM), and uses a dipole field tensor whose components depend on each interacting pair.32 We have built a modified version of DIM which employs a distributed functional-group algorithm.33,34 Here, we propose a systematic building-block database for estimating electro-optical properties of biomolecules, particularly proteins, in both gas and condensed phase. Given the importance of aqueous medium in biochemistry, the database entries are suitable for biomolecules solvated with water. We used the database to estimate the properties of a series of amino acids and polypeptides, and benchmarked the results against quantum-mechanical calculations.
2 Computational methods
We have used a protein of the melanoma-antigen gene family, MAGE-1,35 as a reference to create entries for our database. A fragment consisting of nine amino acid fragments, namely H-Glu-Ala-Asp-Pro-Thr-Gly-His-Ser-Tyr-OH, was selected. Then, the residues were randomly combined to create seven peptides, each one consisting of five amino acid residues: H-Asp-Ala-Glu-Gly-Ser-OH, H-Thr-Gly-Pro-Tyr-Ser-OH, H-His-Ala-Glu-Pro-Tyr-OH, H-Thr-Asp-His-Pro-Ala-OH, H-Tyr-Ser-Glu-Asp-His-OH, H-Ala-Thr-Ser-Gly-His-OH and H-Glu-Pro-Asp-Tyr-Thr-OH. Zwitterions were always chosen. The molecular geometries for these peptides were optimized in the gas phase using the CHARMM additive force field.36 Building blocks were extracted after calculating the dipole moment and polarizability for each atom. Database entries were generated by averaging those quantities for each functional group.To assess the quality of the database, a testing set containing twenty four different molecules was chosen. It includes eight amino acids, namely Ala, Gly, Glu, Asp, His, Ser, Tyr, and Thr, and some of their corresponding di- and tri-peptides. Geometries were again optimized in the gas phase and zwitterionic form, using the CHARMM force field.
2.1 Quantum-mechanical calculations
Although the gold standard for wave-function calculations in small organic molecules is coupled-cluster, inclusion of an electronic-correlation level higher than CCSD typically improves the polarizabilities only slightly.37 Hybrid and meta-hybrid DFT functionals proved to be very efficient at reproducing CCSD polarizabilities38 for organic molecules, including amino acids and peptides.31,33 In particular, functionals of the M06 class39 give very consistent quantities when compared to the CCSD results. Thus, in this work, M06-HF is used.We have also benchmarked some correlation-consistent basis functions for small organic molecules, ranging from cc-pVDZ to cc-pVQZ and include many of their augmented versions.33 The combination of basis-set polarization and diffusion was shown to be extremely important for obtaining good-quality polarizabilities. The inclusion of diffuse functions is usually more important than the valence splitting. For this reason, aug-cc-pVDZ returns similar values to cc-pVQZ, a much larger basis, and to aug-cc-pVQZ, the largest basis tested. Inclusion of more functions, as in the case of d-aug-cc-pVDZ, did not show any significant improvement. Quantum calculations in this work were performed at the aug-cc-pVDZ level of theory. Gaussian 1640 was used for DFT calculations. AIMAll41 software was employed to partition the charge density according to QTAIM.
2.2 Dipole-moment and polarizability calculations
PolaBer15 was used to compute origin-independent dipole moments and distributed atomic polarizabilities. The dipole moment of an atomic basin Ω is the sum of a polarization component μp(Ω) and a charge-translation contribution μc(Ω):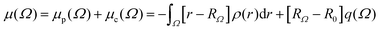 | (1) |
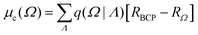 | (2) |
Calculations were performed using a static field with a magnitude of 0.001 a.u. applied along each one of the positive and negative Cartesian directions. The polarizability tensor components of a given basin are calculated by numerically differentiating the dipole moment with respect to the applied field. This procedure is exact provided that the perturbation is small enough to guarantee a linear response. The αij(Ω) component of the tensor is given by:
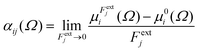 | (3) |
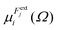 is the dipole component in the i direction calculated with the uniform field Fext applied along the j direction.
is the dipole component in the i direction calculated with the uniform field Fext applied along the j direction.
Atomic polarizability tensors can be visualised in the same space as the molecule assuming 1 Å3 ≡ 1 Å. A scaling factor, usually of 0.2 Å−2, may be necessary to reduce the size of ellipsoids for visualization purposes. The isotropic polarizability is computed as the arithmetical average of the main diagonal components and the anisotropy of the tensor is estimated as:
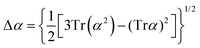 | (4) |
2.3 Database
After calculation and functional-group extraction, dipole-moment vectors and polarizability tensors are oriented according to a specific framework defined by the geometry of each functional group. Because they are orientation dependent, the first step in order to generate an exportable building block is to rotate equivalent groups to a common framework. This can be achieved by employing a rotation matrix obtained from diagonalization of the charge tensor Q, analogous to the inertia tensor where masses are replaced by atomic numbers Z:24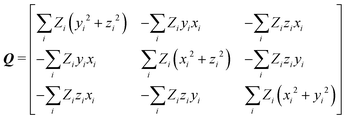 | (5) |
The charge-density distribution of a building block, hence its associated dipole moment and polarizability, depends on the charge distribution of the surroundings. For example, the properties of a –CH2– group extracted from a highly symmetrical molecule such as methane would be different from those extracted from a less symmetrical molecule such as glycine. In the former, the charge density of the group possesses the same symmetry as the idealized –CH2– group which is C2v. In the latter, although the idealized functional group should still have C2v symmetry, the presence of different atoms directly attached to it (C and N atom) lowers its effective symmetry to Cs. For a C2v charge density distribution, the polarizability tensor must have all off-diagonal terms equal to zero but for the Cs symmetry, the values for off-diagonal tensor components can be either positive or negative. In order to ensure consistent off-diagonal components after group rotation, we have explicitly included neighboring atoms to compute the transferable functional group. This implies that our –CH2– building block is actually a R1–CH2–R2 group, where R1 and R2 are dummies (Fig. 1).
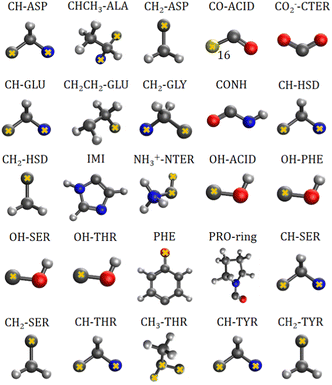 | ||
| Fig. 1 Twenty five transferable building blocks extracted from the prototypical peptides and their correspondent dummy atoms (marked with yellow crosses). | ||
2.4 Classical molecular dynamics
Fifty eight water molecules were added surrounding a central glycine molecule, using the CHARMM-GUI42 feature. The geometry of the aggregate was optimized using the Adopted Basis Newton Raphson Method, implemented on the CHARMM36 additive force field, free version 46b1. Further equilibration was performed and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps were computed using the NVT ensemble, with an interval of 1 fs. A Nose–Hoover thermostat43,44 was used for temperature control, at 303.15 K. Afterwards, molecular dynamics were performed using the NPT ensemble. Berendsen's45 thermostat was used to control the temperature and pressure at 303.15 K and 1 atm. 200
000 steps were computed using the NVT ensemble, with an interval of 1 fs. A Nose–Hoover thermostat43,44 was used for temperature control, at 303.15 K. Afterwards, molecular dynamics were performed using the NPT ensemble. Berendsen's45 thermostat was used to control the temperature and pressure at 303.15 K and 1 atm. 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecular frames were calculated with a 2 fs interval, giving an overall time of 400 ps. The geometries were extracted every 20 ps and further used for estimation of group polarizabilities with the database approach.
000 molecular frames were calculated with a 2 fs interval, giving an overall time of 400 ps. The geometries were extracted every 20 ps and further used for estimation of group polarizabilities with the database approach.
3 Results and discussion
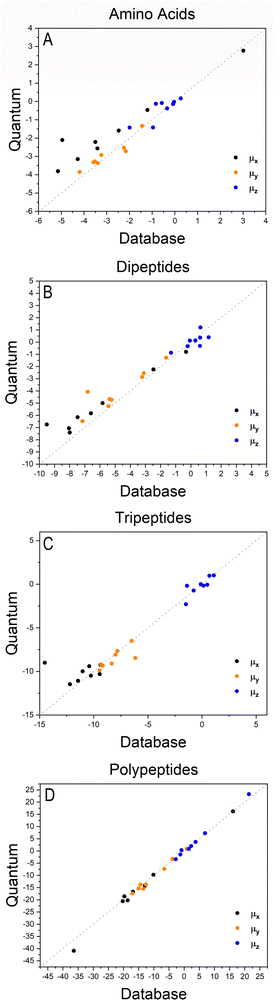
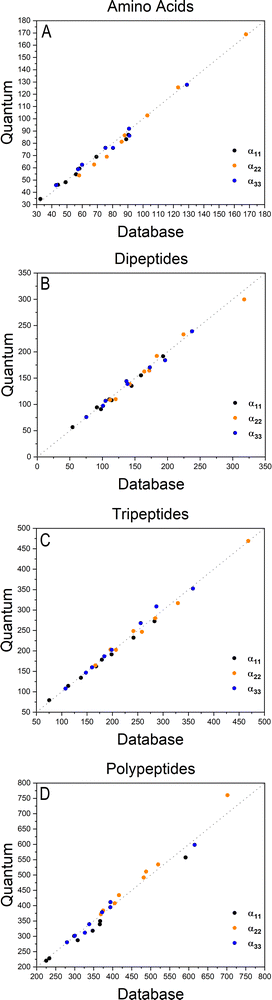
The importance of taking into account both inter- and intramolecular chemical environments of a building block when estimating the opto-electronic properties of molecular biomaterials from transferable functional groups was discussed in our previous works.33,34 Covalent bonds are certainly the most relevant interactions to be considered in case highly accurate polarizability tensors are desired. Intermolecular contacts, on the other hand, such as hydrogen bonds or other non-covalent contacts, play a smaller role and therefore can be efficiently taken into account by means of semi-empirical approaches such as a DIM. When transferable building blocks were extracted from simple amino acids or amino acid residues, we needed to properly correct for intramolecular environment effects. In this work we propose an alternative that is to extract building blocks from larger systems, namely, polypeptides containing five amino acid residues. In this case, the most relevant intramolecular polarization effects are already properly considered at the electronic-structure calculation stage without the need for further corrections. As we show in the next paragraphs, the functional groups are capable of reconstructing dipole moments and polarizabilities of other biomolecules with acceptable quality. As for the effect of intermolecular interactions, our database is expanded to explicitly consider water molecules solvating the functional groups.Fig. 2 shows how the Cartesian components of dipole moments for thirty two molecules reconstructed using our database compare with the quantum-mechanical results. Deviations from the quantum reference are more pronounced in the cases where no peptide bonds are present, as for the amino acids. The correlation coefficient (R2) is just 0.87. Because the dipole moments directly depend on charges of the atomic basins, they are very sensitive to the chemical environment, either intra- or intermolecular. The proximity between the carboxylate and the ammonium groups in the zwitterionic forms of the amino acids induces some charge-density redistribution when compared to the same terminal groups in larger peptides, where they are more distant apart. Upon adding one or two peptide bonds, thus generating di- and tri-peptides, the accuracy of the database reconstruction improves, with correlation coefficients of R2 = 0.96 and R2 = 0.92, respectively. This is justified by the fact that the terminal charges are more distant to each other, as occurs for the pentapeptides used to calculate the transferable building blocks. Just as a consistency check, we have verified how the database reconstruction replicates the dipole moments of these polypeptides as well. The correlation coefficient is of course almost perfect, R2 = 0.99. Since the database entries were generated by averaging data, each functional group possesses a certain level of molecular flexibility that depends on the similarity of the chemical environments among the set of prototypical molecules used in the definition of the building block, as shown in Table 1. Molecular polarizabilities estimated with the database are very accurate, as shown in Fig. 3. Each component of the diagonalized tensor is accurately reproduced as well (numerical data can be found in the ESI†).
 . The functional groups terminology follows Fig. 1; CTER and NTER refer to the terminal groups of the peptide chain
. The functional groups terminology follows Fig. 1; CTER and NTER refer to the terminal groups of the peptide chain
| μ x | μ y | μ z | α xx | α yy | α zz | α xy | α xz | α yz | |
|---|---|---|---|---|---|---|---|---|---|
| CH-ASP | −1.5655 | 0.1040 | −0.0917 | 10.620 | 5.995 | 7.889 | 1.615 | 1.345 | 1.479 |
| SD | 0.2944 | 0.2009 | 0.1943 | 1.5984 | 0.723 | 0.556 | 0.675 | 0.691 | 0.560 |
| CHCH3-ALA | −0.2090 | −1.4430 | 0.1223 | 25.238 | 22.684 | 18.067 | −0.339 | 1.531 | 0.811 |
| SD | 0.1998 | 0.2016 | 0.0436 | 1.3220 | 1.153 | 0.993 | 1.715 | 0.547 | 0.728 |
| CH2-ASP | −0.2088 | 0.0164 | −0.2216 | 12.198 | 9.135 | 11.303 | −0.276 | 0.445 | 1.446 |
| SD | 0.2584 | 0.0260 | 0.1996 | 1.0385 | 0.420 | 0.606 | 0.700 | 0.516 | 0.713 |
| CO-ACID | −1.2924 | 0.9607 | −0.0470 | 14.503 | 16.399 | 8.159 | −4.667 | −0.702 | 0.479 |
| SD | 0.4615 | 0.3995 | 0.1601 | 2.6708 | 1.356 | 0.385 | 0.923 | 1.552 | 1.314 |
| COO−-CTER | −0.3515 | 2.5330 | 0.1233 | 27.600 | 29.122 | 16.258 | −2.463 | 0.223 | 0.233 |
| SD | 0.5143 | 0.4160 | 0.2218 | 2.1888 | 2.686 | 1.589 | 2.029 | 2.627 | 1.114 |
| CH-GLU | −1.5930 | 0.2158 | 0.1305 | 10.323 | 6.928 | 9.562 | 0.783 | 0.746 | 1.803 |
| SD | 0.3344 | 0.1405 | 0.1565 | 1.5714 | 1.083 | 0.951 | 1.314 | 0.669 | 0.693 |
| CH2CH2-GLU | 0.0421 | 0.2309 | 0.1488 | 27.357 | 23.330 | 18.707 | −0.483 | 0.164 | 3.406 |
| SD | 0.4350 | 0.2592 | 0.1294 | 1.4756 | 1.143 | 0.599 | 1.104 | 1.247 | 1.152 |
| CH2-GLY | −1.8027 | 0.1847 | −0.0246 | 12.766 | 9.243 | 8.219 | 1.312 | 0.720 | 0.393 |
| SD | 0.1652 | 0.0759 | 0.0396 | 1.5685 | 1.170 | 0.728 | 1.342 | 0.579 | 0.615 |
| CONH | −0.1341 | 3.7732 | −0.0563 | 30.210 | 34.645 | 12.955 | −9.197 | 0.859 | 0.442 |
| SD | 0.4193 | 0.5946 | 0.1156 | 2.1619 | 2.626 | 1.156 | 2.962 | 2.177 | 1.988 |
| CH-HSD | −1.4580 | 0.2301 | 0.1644 | 10.228 | 6.897 | 9.030 | 0.923 | 0.301 | 1.877 |
| SD | 0.3587 | 0.0959 | 0.1612 | 1.6542 | 0.773 | 0.612 | 1.001 | 0.842 | 0.259 |
| CH2-HSD | 0.0369 | −0.0406 | 0.0420 | 12.121 | 8.658 | 13.974 | 0.104 | 0.815 | −0.420 |
| SD | 0.2009 | 0.0244 | 0.1004 | 0.4177 | 0.605 | 1.165 | 0.843 | 0.449 | 0.751 |
| IMI | −1.2614 | 1.1101 | −0.0789 | 48.111 | 58.992 | 31.601 | −0.254 | 2.149 | −0.319 |
| SD | 0.2862 | 0.5789 | 0.2798 | 6.1780 | 1.119 | 1.245 | 2.549 | 3.349 | 1.519 |
| NH3+-NTER | 1.3408 | 0.2149 | −0.0512 | 13.455 | 8.353 | 8.412 | 2.494 | 0.598 | 0.132 |
| SD | 0.2141 | 0.1208 | 0.2050 | 0.8095 | 0.530 | 0.864 | 0.335 | 0.482 | 0.356 |
| OH-ACID | −0.4716 | 0.8199 | 0.0162 | 11.910 | 6.428 | 6.472 | 1.172 | −0.146 | −0.110 |
| SD | 0.1968 | 0.1430 | 0.0709 | 1.5458 | 0.356 | 1.444 | 0.823 | 0.670 | 0.717 |
| OH-PHE | −0.8353 | 0.4923 | 0.0347 | 16.206 | 7.757 | 5.301 | −0.220 | −0.264 | −0.434 |
| SD | 0.2606 | 0.2314 | 0.0501 | 1.4456 | 2.393 | 0.605 | 1.420 | 0.471 | 0.744 |
| OH-SER | −0.8759 | 0.5959 | −0.0045 | 13.490 | 8.420 | 6.000 | 0.401 | −0.070 | −0.183 |
| SD | 0.3459 | 0.2484 | 0.0492 | 1.0083 | 0.947 | 0.619 | 1.743 | 0.894 | 1.209 |
| OH-THR | −0.4889 | 0.8809 | −0.0242 | 12.488 | 8.162 | 5.411 | 0.690 | 0.111 | 0.019 |
| SD | 0.1739 | 0.2544 | 0.0325 | 0.3543 | 1.719 | 0.676 | 1.147 | 0.675 | 0.767 |
| PHE | −0.8746 | 0.0284 | −0.3525 | 82.087 | 67.753 | 39.262 | 1.487 | 5.254 | 0.906 |
| SD | 0.5222 | 0.0903 | 0.2786 | 7.0060 | 1.932 | 3.821 | 2.518 | 3.156 | 1.627 |
| PRO-ring | 1.0803 | −4.8003 | 1.1733 | 81.985 | 70.247 | 49.983 | −7.335 | −2.320 | −5.746 |
| SD | 0.5198 | 0.4051 | 0.3166 | 4.0049 | 3.267 | 2.515 | 4.250 | 2.373 | 1.666 |
| CH-SER | −1.0798 | −0.0184 | −0.1136 | 9.496 | 6.870 | 8.256 | 1.603 | 1.217 | 1.060 |
| SD | 0.2107 | 0.1878 | 0.1927 | 0.6564 | 0.313 | 0.527 | 0.670 | 0.546 | 0.711 |
| CH2-SER | −0.2809 | 0.0089 | 0.0546 | 12.324 | 9.314 | 7.800 | −0.253 | −0.604 | 0.492 |
| SD | 0.1998 | 0.0487 | 0.1454 | 0.6112 | 0.331 | 0.353 | 0.355 | 0.253 | 0.721 |
| CH-THR | −1.2957 | 0.2127 | 0.1282 | 8.716 | 7.077 | 7.794 | 0.673 | 0.618 | 1.258 |
| SD | 0.2277 | 0.1119 | 0.1374 | 0.6678 | 0.491 | 0.307 | 1.042 | 0.318 | 0.686 |
| CH3-THR | 0.0817 | 0.1038 | 0.4302 | 26.699 | 19.869 | 20.134 | 0.530 | 0.024 | −0.365 |
| SD | 0.1841 | 0.2011 | 0.2361 | 3.0589 | 0.782 | 1.801 | 1.086 | 0.844 | 1.510 |
| CH-TYR | −1.4295 | 0.0024 | −0.1510 | 10.949 | 7.953 | 9.053 | 2.089 | 1.324 | 2.357 |
| SD | 0.2783 | 0.1611 | 0.1704 | 1.4963 | 1.027 | 0.886 | 0.611 | 1.383 | 1.073 |
| CH2-TYR | −0.2982 | −0.0052 | −0.1210 | 13.720 | 8.411 | 15.348 | −0.521 | 1.923 | 0.807 |
| SD | 0.1636 | 0.0831 | 0.1877 | 0.8230 | 0.706 | 0.897 | 0.606 | 1.608 | 0.269 |
Fig. 4 compares the magnitude and the direction of the molecular dipole moment vectors obtained using the database with those calculated from quantum mechanics. Our database is efficient to estimate not only the magnitude of the dipoles, with a mean percentual deviation of 14%, but also their directions, with an average difference of around 6°. Fig. 5 stresses the quality of the building blocks to reproduce the overall isotropic polarizability αiso and its anisotropy Δα. The latter quantity is, as one would expect, more variable, emphasizing the importance of intramolecular environment effects on determining the shape and orientation of the polarizability ellipsoids.
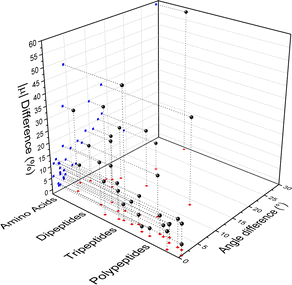 | ||
| Fig. 4 Dipole moment deviation (percent), and angle differences (degrees) between quantum quantities and those obtained using the database. | ||
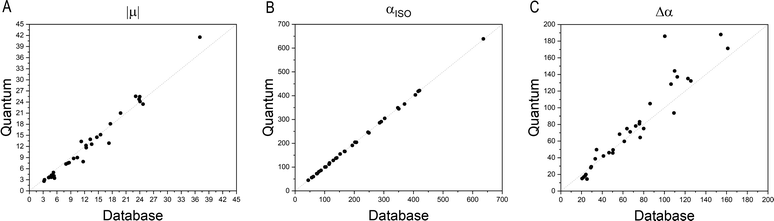 | ||
| Fig. 5 Comparison between quantum and database properties for the module of dipole moments (left), the polarizabilities isotropy, (middle) and anisotropy (right). All values are in atomic units. | ||
3.1 Electrostatic potential maps
Aiming to test the efficiency of our database to estimate other properties in biomolecules, we have used the transferable functional groups to reconstruct the dipolar electric potential for the MAGE-1 fragment (Fig. 6), which is a good approximation to the total electric potential.46 The dipolar potential of an atomic group defining a basin Ω at a position r was therefore calculated from the ground-state dipole moment of the functional group: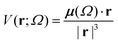 | (6) |
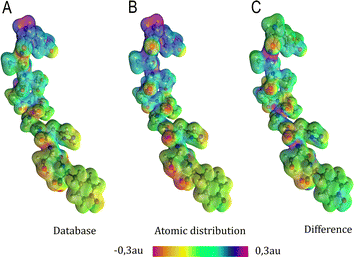 | ||
| Fig. 6 Electrostatic potential map in atomic units of the MAGE-1 fragment plotted over a 0.01 a.u. isodensity surface calculated from eqn (6) using a functional group (database) and an atomic distribution approach. | ||
Electrostatic potential maps estimated using the dipole moments coming from the building-block database do not superimpose perfectly with the ones calculated using an atomic distribution of dipoles. Nevertheless, our database provides a satisfactory panorama, being particularly useful when a quick assessment is desired. The difference map shown in Fig. 6 indicates that the largest deviations occur in regions associated to the peptide bonds and the carboxyl terminal group. It does not necessarily imply that the dipole moments of such groups are ill defined. The inaccuracy may be a deficiency of the dipolar simplification itself, which reduces entire functional groups to point dipoles. The map constructed using the database presents a largely negative region around the –COO− group that is concentrated between the oxygen atoms. This almost coincides with the direction of the dipole moment vector for the group. An alternative to improve the description of the electrostatic potentials could be to split the group dipole vector into bond contributions.
3.2 Condensed-phase properties
Among several approaches to compute the influence of the intermolecular chemical environment in the electro-optical properties, calculations under periodic boundary conditions are certainly considered the most powerful ones. However, besides being restricted to crystalline systems, the amount of electronic correlation one can introduce is still quite limited. As an alternative, finite molecular aggregates can be used to estimate the properties of condensed phases, either crystalline or non-crystalline. In some cases, this can be done by means of an electrostatic dipole interaction model (DIM),47 in others, by quantum-mechanically calculating the charge density of the entire cluster.48Consideration of a condensed medium has a profound impact on the properties derived from the charge density distribution. The presence of strong hydrogen bonds may induce severe changes in both the orientation and size of polarizability tensors and dipole moments.33,48 Here, we explicitly considered interactions between the peptides used to build the database and a solvent, represented by water molecules.
The semi-empirical DIM method is very fast, yet capable of returning accurate results compared to quantum-mechanical calculations. The idea is to correct gas-phase properties for effects of the medium a posteriori. It is based on electrostatic interactions between pairs of dipole moments that simulate the effective electric field felt by a molecule, an atom or a building block. In our previous work, we demonstrated that replacing atoms or functional groups, instead of entire molecules, by point dipoles is more accurate.33 According to our implementation, the i component of the local (applied plus induced) field on the basin Ω due to all neighboring basins Λ can be written as:
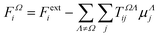 | (7) |
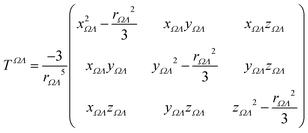 | (8) |
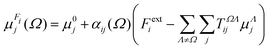 | (9) |
We used glycine as a model. To ensure that the intermolecular-interaction sphere around a given central molecule is complete and that all relevant interactions are included, we explicitly added fifty eight water molecules around a glycine. This aggregate was subjected to geometry optimization using the CHARMM force field. A representation of the aggregate together with polarizability ellipsoids is given in Fig. 7. To complement our analysis, we also performed a quantum-mechanical calculation using an implicit polarizable continuum medium (PCM). The results can be found in Table 2.
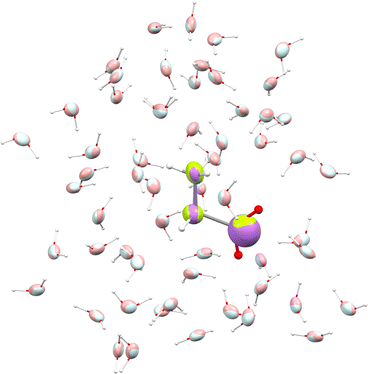 | ||
| Fig. 7 Glycine molecule surrounded by water. Ellipsoids compare functional-group polarizabilities in the gas-phase (green/light blue) and in the condensed phase after using the DIM (purple/pink). | ||
| μ x | μ y | μ z | |μ| | α 11 | α 22 | α 33 | α ISO | |
|---|---|---|---|---|---|---|---|---|
| a 25 °C, 1 M, pH 6.7 using Kirkwoods dielectric mixture theory.52 b From molar refraction measured in aqueous solution at λ = 589 nm and 25 °C using the Clausius–Mossotti equation.53 | ||||||||
| Isolated | 2.78 | −1.42 | −3.85 | 4.96 | 34.5 | 45.8 | 53.9 | 44.7 |
| DIM | 3.55 | −1.91 | −5.05 | 6.47 | 35.7 | 44.9 | 53.1 | 44.6 |
| PCM | 3.36 | −1.74 | −4.70 | 6.02 | 43.3 | 56.7 | 64.1 | 54.7 |
| MD | 6.28 ± 0.31 | 34.4 ± 1.4 | 47.6 ± 1.4 | 53.1 ± 2.0 | 44.9 ± 0.4 | |||
| EXP | 6.2 ± 0.1a | 44.3 ± 0.6b | ||||||
It is known that including an isotropic polarization due to the environment by means of implicit solvents may provide unreliable properties, in particular for those that depend most on the anisotropic polarization of the charge density.49,50 Nevertheless, both DIM and PCM showed an increment in the dipole moment with respect to the glycine molecule in isolation, about 10–30% when focusing on individual vector components. The magnitude of the dipole changes from 4.96 a.u. in the isolated situation to 6.5 a.u. when using DIM, and to 6.0 a.u. when employing PCM. The former method gives a dipole moment which deviates 0.9° from the vector direction obtained in the gas phase, whereas the latter provides a smaller deviation of 0.3°. This small reorientation is expected from PCM because it lacks directional intermolecular interactions.
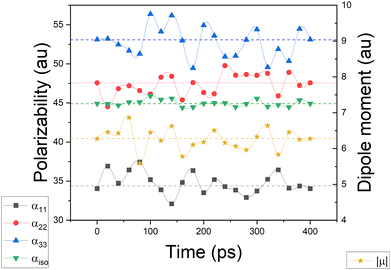
Simulating the chemical environment of a molecule increases the electric field felt by it, which increases the charge-density polarization. However, it is not uncommon to observe a decrement in the molecular polarizability when moving from gas to condensed phases. This is justified by a volume restriction imposed on the central molecule when it is explicitly surrounded by solvent molecules.31 Since PCM does not include any kind of volume restriction, we observed an increment of about 20–25% in each component of the diagonalized polarizability tensor whereas, for DIM, the components changed only slightly with respect to glycine in the gas phase. For the sake of clarity and to make sure that the obtained values of polarizabilities are representative for possible conformers of glycine, we performed additional molecular dynamic simulations to consider more than one geometry (for Cartesian coordinates and molecular geometries, the reader is referred to the ESI† pdb file). Once those geometries were obtained, we calculated molecular dipole moments and polarizabilities and compared them to other models used in this work. Graphical representation of the time evolution of dipole moments and polarizabilities is given in Fig. 8. To evaluate how reasonable the database-derived electric properties are, we used polarizabilities estimated via the Clausius–Mossotti equation as benchmark values, which shows the relationship between the experimentally derived dielectric constant and atomic polarizabilities. One must be however aware that the above-mentioned relationship works best for gases and is only approximately true for liquids or solids, particularly if the dielectric constant is large. In fact, to the best to our knowledge, there is no experimental polarizability data available, in particular for amino-acid systems which would allow us to accurately compare the full anisotropy of the polarizability tensor. Thus our goal here is rather to make sure that the database delivers values of the same order of magnitude, rather than benchmark against exact numbers. The results are summarized in Table 2. The values referring to MD simulation agree well with both experimental values and the frozen local-minima geometry obtained by DIM, proving that for small systems such as glycine, the conformational changes are not significantly affecting the discussed electric properties.
4 Conclusions
In this work, we proposed a database to quickly and accurately estimate dipole moments and distributed polarizabilities of polypeptides. The database entries consist of twenty five unique building blocks. We discussed two applications. The first one is related to the reconstruction of electrostatic potential maps for biomolecules. The second is associated with the determination of properties for the condensed phase which includes water molecules within a region around an amino acid. A dipole interaction model was employed to take into account the polarization effects due to solvent molecules. Although we have used medium-size peptides as precursors for generating the database, it was proved to be useful to quickly obtain dipole moments and polarizabilities for smaller molecules, having a slightly different chemical nature, and larger peptides (up to nine amino acid residues). The next step of our work is to increase the variety of database entries allowing estimation of the properties of larger peptides and proteins. Certainly that will require inclusion of dynamic solvation medium, to better describe the influence of the solvent on the electric properties of the studied system. Furthermore, since our approach delivers currently only static polarizability tensors, neglecting the effects from oscillating electric fields, our intention is to eventually introduce frequency dependent polarizabilities, following for example the procedure already present in the literature.51 This approach will for sure be more beneficial for benchmarking database-derived polarizabilities against experimentally available parameters.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by the Brazilian agency FAPEMIG (project APQ-01465-21) and by the Polish PLGrid Infrastructure. AK dedicates this manuscript to Ryszard Jachimek.Notes and references
- S. Shabahang, S. Kim and S.-H. Yun, Adv. Funct. Mater., 2018, 28, 1706635 CrossRef PubMed.
- D. Shan, E. Gerhard, C. Zhang, J. W. Tierney, D. Xie, Z. Liu and J. Yang, Bioact. Mater., 2018, 3, 434–445 CrossRef PubMed.
- B. D. Ratner, J. Biomed. Mater. Res., 1993, 27, 837–850 CrossRef CAS PubMed.
- A. D. Costache, J. Ghosh, D. D. Knight and J. Kohn, Adv. Eng. Mater., 2010, 12, B17 CrossRef.
- J. Applequist, Acc. Chem. Res., 1977, 10, 79–85 CrossRef CAS.
- K. J. Miller, J. Am. Chem. Soc., 1990, 112, 8533–8542 CrossRef CAS.
- T. Zhou and C. E. Dykstra, J. Phys. Chem. A, 2000, 104, 2204–2210 CrossRef CAS.
- C. S. Ewig, M. Waldman and J. R. Maple, J. Phys. Chem. A, 2002, 106, 326–334 CrossRef CAS.
- M. in het Panhuis, R. W. Munn and P. L. A. Popelier, J. Chem. Phys., 2004, 120, 11479–11486 CrossRef CAS PubMed.
- D. Geldof, A. Krishtal, P. Geerlings and C. V. Alsenoy, J. Phys. Chem. A, 2011, 115, 13096–13103 CrossRef CAS PubMed.
- N. Otero, C. V. Alsenoy, C. Pouchan and P. Karamanis, J. Comput. Chem., 2015, 36, 1831–1843 CrossRef CAS PubMed.
- Y. Mei, A. C. Simmonett, F. C. Pickard, R. A. DiStasio, B. R. Brooks and Y. Shao, J. Phys. Chem. A, 2015, 119, 5865–5882 CrossRef CAS PubMed.
- K. E. Laidig and R. F. W. Bader, J. Chem. Phys., 1990, 93, 7213–7224 CrossRef CAS.
- T. A. Keith, in The Quantum Theory of Atoms in Molecules, ed. C. F. Matta and R. J. Boyd, Wiley-VCH, Weinheim, 2007, ch. 3, pp. 61–94 Search PubMed.
- A. Krawczuk, D. Perez and P. Macchi, J. Appl. Crystallogr., 2014, 47, 1452–1458 CrossRef CAS.
- A. J. Stone and M. Alderton, Mol. Phys., 2002, 100, 221–233 CrossRef.
- J. G. Angyan, G. Jansen, M. Loos, C. Hättig and B. A. Heß, Chem. Phys. Lett., 1994, 219, 267–273 CrossRef CAS.
- J. G. Angyan, C. Chipot, F. Dehey, C. Hättig and C. Millot, J. Comput. Chem., 2003, 24, 997–1008 CrossRef CAS PubMed.
- G. Jansen, C. Hättig, B. A. Heß and J. G. Angyan, Mol. Phys., 1996, 88, 69–92 CrossRef CAS.
- C. Hättig, G. Jansen, B. A. Heß and J. G. Angyan, Mol. Phys., 1997, 91, 145–160 CrossRef.
- P. M. Dominiak, A. Volkov, A. P. Dominiak, K. N. Jarzembska and P. Coppens, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 485–499 CrossRef CAS PubMed.
- B. Dittrich, T. Koritsanszky and P. Luger, Angew. Chem., Int. Ed., 2004, 43, 2718–2721 CrossRef CAS PubMed.
- C. F. Matta and R. W. F. Bader, Proteins: Struct., Funct., Genet., 2000, 40, 310–329 CrossRef CAS.
- M. Ernst, L. H. R. Dos Santos, A. Krawczuk and P. Macchi, in Understanding Intermolecular Interactions in the Solid State: Approaches and Techniques, ed. D. Chopra, The Royal Society of Chemistry, London, 2019, ch. 7, pp. 211–242 Search PubMed.
- A. Kumar, P. Pandey, P. Chatterjee and A. D. MacKerell Jr., J. Chem. Theory Comput., 2022, 18, 1711–1725 CrossRef PubMed.
- C. M. Baker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 241–254 CAS.
- D. A. Dunmur, Mol. Phys., 1972, 23, 109–115 CrossRef CAS.
- H. Reis, S. Raptis, M. G. Papadopoulos, R. H. C. Jansen, D. N. Theodorou and R. W. Munn, Theor. Chem. Acc., 1998, 99, 384–390 Search PubMed.
- M. A. Spackman, P. Munshi and D. Jayatilaka, Chem. Phys. Lett., 2007, 443, 87–91 CrossRef CAS.
- A. M. Mkadmh, A. Hinchliffe and F. M. Abu-Awwad, THEOCHEM, 2009, 901, 9–17 CrossRef CAS.
- L. H. R. Dos Santos, A. Krawczuk and P. Macchi, J. Phys. Chem. A, 2015, 119, 3285–3298 CrossRef CAS PubMed.
- M. Guillaume and B. Champagne, Phys. Chem. Chem. Phys., 2005, 7, 3284–3289 RSC.
- R. F. Ligorio, A. Krawczuk and L. H. R. Santos, J. Phys. Chem. A, 2020, 124, 10008–10018 CrossRef CAS PubMed.
- R. F. Ligorio, A. Krawczuk and L. H. R. Santos, J. Phys. Chem. A, 2021, 125, 4152–4159 CrossRef CAS PubMed.
- J. C. Cheville and P. C. Roche, Mod. Pathol., 1999, 12, 974–978 CAS.
- B. R. Brooks, C. L. B. III, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30(10), 1545–1614 CrossRef CAS PubMed.
- J. R. Hammond, N. Govind, K. Kowalski, J. Autschbach and S. S. Xantheas, J. Chem. Phys., 2009, 131, 214103 CrossRef PubMed.
- D. Hait and M. Head-Gordon, Phys. Chem. Chem. Phys., 2018, 20, 19800 RSC.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- T. A. Keith, AIMAll (Version 19.10.12), TK Gristmill Software, Overland Park KS, USA, 2019, http://aim.tkgristmill.com Search PubMed.
- S. Jo, T. Kim, V. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef CAS PubMed.
- S. Nose, Mol. Phys., 1986, 57, 187–191 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1965–1967 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS.
- A. Jabluszewska, A. Krawczuk, L. H. R. Dos Santos and P. Macchi, ChemPhysChem, 2020, 21, 2155–2165 CrossRef CAS PubMed.
- L. Silberstein, Philos. Mag., 1917, 33, 92–128 CAS.
- L. H. R. Dos Santos and P. Macchi, Crystals, 2016, 6, 43 CrossRef.
- J. Zhang, H. Zhang, T. Wu, Q. Wang and D. van der Spoel, J. Chem. Theory Comput., 2017, 13, 1034–1043 CrossRef CAS PubMed.
- J. R. Spaeth, I. G. Kevrekidis and A. Z. Panagiotopoulos, J. Chem. Phys., 2011, 134, 164902 CrossRef PubMed.
- T. Seidler, A. Krawczuk, B. Champagne and K. Stadnicka, J. Phys. Chem. C, 2016, 120, 4481–4494 CrossRef CAS.
- M. W. Aaron and E. H. Grant, Trans. Faraday Soc., 1963, 59, 85–89 RSC.
- T. L. McMeekin, M. L. Groves and N. J. Hipp, Refractive indices of amino acids, proteins, and related substances, in Amino Acids and Serum Proteins, ed. J. Stekol, American Chemical Society, Washington DC, 1964, pp. 54–66 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Atomic coordinates, dipole moments and distributed polarizabilities of amino acids, peptides and molecular aggregates. Dipole moments and polarizabilities for the database entries. See DOI: https://doi.org/10.1039/d2cp04052b |
| This journal is © the Owner Societies 2022 |