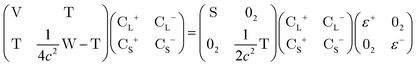Relativistic nonorthogonal configuration interaction: application to L2,3-edge X-ray spectroscopy†
Adam
Grofe
 and
Xiaosong
Li
and
Xiaosong
Li
 *
*
Department of Chemistry, University of Washington, Seattle, Washington 98195, USA. E-mail: xsli@uw.edu
First published on 22nd April 2022
Abstract
In this article, we develop a relativistic exact-two-component nonorthogonal configuration interaction (X2C-NOCI) for computing L-edge X-ray spectra. This article to our knowledge is the first time NOCI has been used for relativistic wave functions. A set of molecular complexes, including SF6, SiCl4 and [FeCl6]3−, are used to demonstrate the accuracy and computational scaling of the X2C-NOCI method. Our results suggest that X2C-NOCI is able to satisfactorily capture the main features of the L2,3-edge X-ray absorption spectra. Excitations from the core require a large amount of orbital relaxation to yield reasonable energies and X2C-NOCI allows us to treat orbital optimization explicitly. However, the cost of computing the nonorthogonal coupling is higher than in conventional CI. Here, we propose an improved integral screening using overlap-scaled density combined with a continuous measure of the generalized Slater–Condon rules that allows us to estimate if an element is zero before attempting a two-electron integral contraction.
1 Introduction
In electronic structure theory, the power of a method is determined by the ability to simultaneously treat static correlation, dynamic correlation, orbital optimization, and relativistic effects in an efficient manner. Hartree–Fock (HF) theory efficiently treats orbital optimization but neglects both forms of correlation (under the definition of correlation by Löwdin).1 Then multiconfigurational self-consistent field (MCSCF) combines both static correlation and orbital optimization. Finally, multireference configuration interaction (MRCI) and full CI incorporates orbital optimization and both forms of electron correlation, but are significantly more expensive than the other two methods. All of these methods use orthogonal orbitals and orthogonal configurations which through meticulous book keeping is able to represent all of the degrees of freedom exactly once (i.e., no double counting). In orthogonal CI, the excitation operators are able to treat static correlation, dynamic correlation, and orbital optimization simultaneously (given a sufficient level of excitation). While these expansions are complete, they are inefficient in representing the wave function. The CI Hamiltonians are often sparse with many unimportant degrees of freedom. Thus, selected CI techniques seek to compress the CI wave function by only including the most important degrees of freedom.2–5Nonorthogonal configuration interaction (NOCI) takes a different approach where the constraint on orthogonality of configurations is lifted.6–14 This allows the orbitals of each configuration to be optimized individually so that the configurations are at their lowest energy before mixing. This results in the NOCI Hamiltonian to become more dense compared to the conventional orthogonal CI but with the advantage of being able to recover static correlations with a smaller set of nonorthogonal determinants.11 This makes NOCI particularly useful for studies of photochemical processes,15–23 where there exists a dense manifold of excited states. Additionally, several groups have developed post-NOCI methods to account of additional dynamic correlations.24–31
In relativistic multi-configurational electronic structure methods, the scalar-relativistic effects are usually included variationally at the molecular orbital level. The spin–orbit coupling can be treated perturbatively32–35 or variationally,36–47 with the latter becoming more accurate for elements further down the periodic table. The inclusion of relativistic effects (scalar relativity and spin–orbit coupling) in NOCI is nontrivial, which, to the best of our knowledge, has never been developed. Relativistic orbital space is generally more dense due to their underlying spinor or bi-spinor electronic structure. As a result, obtaining optimized excited nonorthogonal determinants becomes more challenging. Recently, we proposed an effective algorithm to optimize excited determinants with desired electronic structure characteristics using the generalized block localized wave function (gBLW) method within the exact-two-component47–66 framework.67,68 With a carefully designed optimization space, the X2C-gBLW method is able to produce excited determinants including relativistic effects variationally. In this work, we extend the X2C-gBLW optimized nonorthogonal determinants to the NOCI regime. We introduce a set of integral screening approaches to reduce the computational cost of NOCI.
X-ray absorption spectroscopy is a good application of X2C-NOCI where excitations from the core introduce large perturbations to the electronic structure. Thus, explicit optimization of orbitals significantly lowers the energy of the determinant. Additionally, since both scalar relativity and spin–orbit couplings are significant in X-ray L-edge spectroscopy (excitations from the 2p core orbitals), variational treatment of relativistic effects are essential in accurate prediction of electronic excited states. There have been many advancements in modelling X-ray spectroscopy with orthogonal configuration interaction techniques that we will not review here, but will point the reader toward comprehensive reviews on the subject.69,70 In this article, we compute the L2,3-edge spectra, which requires relatively large NOCI expansions in order to represent the whole spectrum.
2 Theoretical methods
Throughout this article we use the following notations to keep track of the nature of the index with respect to the basis.• The Greek letters (μ, ν, λ, σ) index atomic spinor orbitals (AO's)
• Lowercase Latin letters (i, j, k) index occupied molecular orbitals (MO's)
• Uppercase Latin letters (I, J, K, L) index determinants
• Matrices in the sans Serif font 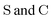 are in the atomic spinor basis
are in the atomic spinor basis
• Matrices in the bold font (S and C) are in the nonorthogonal molecular orbital basis
• Matrices in the blackboard font (![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) and
and ![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) ) are in the nonorthogonal determinant basis
) are in the nonorthogonal determinant basis
• Quantities in the calligraphic font (![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) and
and ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ) are in the NOCI state basis
) are in the NOCI state basis
The X2C-NOCI wave function is expressed as a linear combination of nonorthogonal spinor configurations, which need to be obtained based on the chemical problem of interest. In this work, we use the X2C-gBLW67,68 approach to generate a set of nonorthogonal spinor configurations for X2C-NOCI. Because both the X2C transformation and gBLW approach are well established in the authors' previous work, brief reviews of the methods are presented in the Appendix.
2.1 Nonorthogonal configuration interaction
The X2C-gBLW procedure produces a series of determinants,68 |ψI〉, each with a unique set of molecular orbitals that can be nonorthogonal between different configurations. A wave function expanded in nonorthogonal X2C configurations gives rise to the X2C-NOCI framework. The elements of CI Hamiltonian can be computed using density matrices71 or corresponding orbitals,16,17,72–74 with the latter being more computational efficient.To compute the corresponding orbitals, we begin by computing the overlap matrix of occupied molecular orbitals between any two determinants,
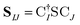 | (1) |
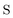 is the spinor atomic orbital (AO) overlap matrix.
is the spinor atomic orbital (AO) overlap matrix. 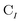 and
and 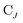 are the occupied orbital coefficient matrices for determinant I and J. It should be noted that the molecular orbitals within each determinant are orthonormal, but the orbitals between determinants may not be orthogonal to each other. Then performing a singular value decomposition of the overlap matrix in the nonorthogonal molecular orbital basis
are the occupied orbital coefficient matrices for determinant I and J. It should be noted that the molecular orbitals within each determinant are orthonormal, but the orbitals between determinants may not be orthogonal to each other. Then performing a singular value decomposition of the overlap matrix in the nonorthogonal molecular orbital basis| SIJ = UIJsIJV†IJ | (2) |
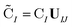 | (3) |
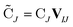 | (4) |
![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) IJ IJ ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) det(SIJ) = det(UIJ)det(VIJ)det(sIJ) det(SIJ) = det(UIJ)det(VIJ)det(sIJ) | (5) |
The nonorthongonal one-electron transition density matrix71 in the AO basis can be defined as
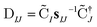 | (6) |
The NOCI Hamiltonian in determinant basis, formulated in the AO-direct algorithm, can then be constructed using17,74
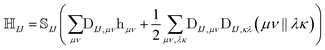 | (7) |
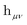 is the one-electron Hamiltonian matrix, and (μν‖λσ) are the antisymmetrized two-electron integrals in Mulliken (chemical) notation. The one-electron Hamiltonian is the X2C Hamiltonian (see Appendix 1) that includes the scalar relativistic correction and one-electron spin–orbit coupling. The two-electron spin–orbit terms have been approximated using the empirical scaling terms due to Boetteger.76
is the one-electron Hamiltonian matrix, and (μν‖λσ) are the antisymmetrized two-electron integrals in Mulliken (chemical) notation. The one-electron Hamiltonian is the X2C Hamiltonian (see Appendix 1) that includes the scalar relativistic correction and one-electron spin–orbit coupling. The two-electron spin–orbit terms have been approximated using the empirical scaling terms due to Boetteger.76
The NOCI coefficients can then be determined by solving the generalized eigenvalue problem
![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) ![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) n = n = ![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) ![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) n n![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) n n | (8) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) n and
n and ![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) n are the NOCI energy eigenvalues and eigenvectors. In the limit that the orbitals become orthogonal, the sIJ−1 scaling of the transition density matrix elements in eqn (6) cancels with the determinant overlap
n are the NOCI energy eigenvalues and eigenvectors. In the limit that the orbitals become orthogonal, the sIJ−1 scaling of the transition density matrix elements in eqn (6) cancels with the determinant overlap ![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) IJ in eqn (7) to yield the Slater–Condon rules.
IJ in eqn (7) to yield the Slater–Condon rules.
2.2 Improved integral screening
The computational cost of eqn (7) formally scales as M2N4, where M is the number of determinants and N is the number of basis functions. Usually M is much smaller than N in NOCI calculations, making the computation of the AO two-electron integrals and contraction the dominant cost. Kathir et al. reduced this cost through a reduced orbital basis set which decreased the number of integrals that need to be contracted.77,78 In an AO direct NOCI implementation, we choose to do the first contraction of the two-electron integrals with AO transition densities (i.e., over indices λ, κ) by taking advantage of the integral and contraction screening developed for the AO Fock build,79,80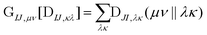 | (9) |
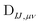 can be contracted with
can be contracted with 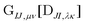 and multiplied by the overlap to yield the two-electron NOCI energy. This contraction scheme will be referred to as the unscaled algorithm.
and multiplied by the overlap to yield the two-electron NOCI energy. This contraction scheme will be referred to as the unscaled algorithm.
The elements of the transition density matrix can be quite large due to the dependence on the inverse of the corresponding orbital overlap in eqn (6), which may prevent the direct algorithms from effectively screening unnecessary integrals. We propose to reformulate the two-electron part of the NOCI Hamiltonian by distributing the square-root of the determinantal overlap ![[Doublestruck S]](https://www.rsc.org/images/entities/char_e176.gif) 1/2IJ to the transition density matrix,
1/2IJ to the transition density matrix,
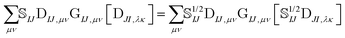 | (10) |
Eqn (10) includes the generalized Slater–Condon rules, which suggest that an element is zero if there are more than two orbital differences between the two determinants. These differences are readily seen in the singular values of the corresponding orbitals. If there are two or less singular values that are zero then the two electron operator is nonzero (assuming the element is not zero by some other mechanism such as symmetry). Likewise, if there are three or more zeroes, then we know that the element will be zero. Here, we define a continuous measure based on the generalized Slater–Condon rules to predict whether a determinant coupling is likely to be zero.
For cases with small but not nonzero singular values we can compute
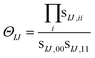 | (11) |
2.3 NOCI oscillator strength
The NOCI oscillator strength can be computed by treating the dipole moment integrals as a one-electron operator using the generalized Slater–Condon rules. Thus, the dipole vector in the NOCI determinant basis is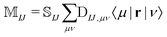 | (12) |
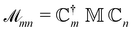 | (13) |
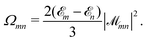 | (14) |
3 Results and discussion
The X2C-NOCI method introduced here is implemented in the development version of Chronus Quantum.81,82 All benchmark timings were performed on an Intel Xeon W 2.5 GHz CPU using the Clang compiler version 12.0.5. The calculations were performed in parallel using 28 threads using Chronus Quantum. Additionally, screening of the two-electron terms was performed using the Schwarz inequality.80L2,3-edge X-ray absorption spectroscopy features excitations from 2p core electrons into the frontier orbitals. Due to spin–orbit coupling, the 2p orbitals are split into p3/2 and p1/2 manifolds. The L-edge spectra of three molecular systems were computed: (1) SF6, (2) [FeCl6]−3, (3) SiCl4. The geometries for SiCl4 and [FeCl6]−3 were taken from ref. 83. For SF6, the geometry was optimized using M06-2X84 with the aug-cc-pVDZ basis set.85 Throughout this article, we compute vertical excitations from these geometries.
To determine the optimal number of states to include in our NOCI, we performed an iterative search by steadily increasing the number of optimized determinants until the energy range of each spectra was satisified. During this search, we include reference virtual orbitals in the set of target orbitals (see appendix) manifold by manifold to ensure that all spin microstates are well represented. We observed little benefit in including further determinants once the energy range was satisfied (see Section 3.3).
The spectra were computed by first convoluting the eigenvalues and oscillator strengths with a Lorentzian broadening function followed by a convolution with a Gaussian function. For SiCl4, the full width at half max (FWHM) for the Lorentzian function was 0.15 eV and the standard deviation of the Gaussian was also 0.15 eV. For [FeCl6]3−, the FWHM was 0.40 eV and the standard deviation was 0.20 eV. For SF6, the FWHM was 0.30 eV and the standard deviation was 0.30 eV.
While the scalar relativistic effects of SF6 and SiCl4 are not large, the spin–orbit coupling is significant enough to lead to splitting of the peaks (see ESI†). While this effect can be well captured using perturbative techniques, this presents a unique challenge for excited state determinant optimizations. In two-component methods, such as X2C, spin symmetry is no longer maintained, which makes the excited state manifold more dense. Additionally, in X2C-NOCI it is necessary to perform an adequate scan over all of the states in a manifold to ensure that X2C-NOCI space is spin-complete. Previously, we demonstrated that the gBLW optimization scheme can be used to scan over excited state manifolds in an efficient manner while maintaining all of the microstates for a given spin manifold. Here, we apply this same scheme to the computation of hundreds of individually optimized determinants.
3.1 SF6 L2,3-edge
In this section, we test the effect that optimization of the orbitals has on the overall spectrum, specifically looking at SF6. For SF6, we excited the 2p electrons into the first 88 reference virtual orbitals and then optimized the determinants, resulting in a total of 529 nonorthogonal determinants in the X2C-NOCI calculations. The set of reference orbitals are the ground state molecular orbitals (see Appendix 2). All of the determinants were optimized with X2C-gBLW and the Sapporo double zeta basis set with diffuse functions.86–89Here, we tested four levels of constraint in X2C-gBLW optimizations of excited determinants for X2C-NOCI calculations. Using 2p → t2g, eg excitations as an example, these constraints can be described as:
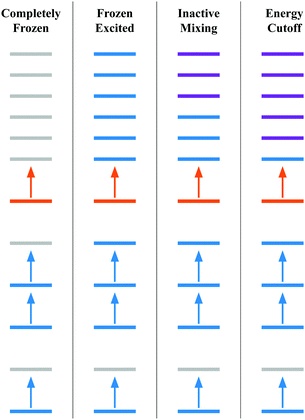
• Completely frozen – the core (the unexcited electrons e.g., 1s, 2s, etc.) and excited orbitals (e.g., t2g, eg) are frozen. This scheme does not need any gBLW optimizations and is equivalent to the conventional orthogonal CI method within an active space.
• Frozen excited – the excited electron is kept frozen to the target orbital (e.g., one of the t2g orbitals). In this scheme, only the core subspace is subject to the gBLW optimization by mixing with virtual orbitals.
• Inactive mixing – The excited electron is only allowed to mix with virtuals outside the ligand-field orbitals, i.e., virtual orbitals higher in energy than t2g and eg manifolds are included in the excited subspace. In this scheme, both the core and excited subspaces are subject to the gBLW optimization.
• Energy cutoff – including all higher energy orbitals outside an energy cut-off of 0.1 Hartree in the excited subspace. The purpose of this scheme is to allow the excited electron to mix with all virtual orbitals that are not degenerate with the target orbital. For instance, if an eg orbital is selected as the target orbital, all higher energy virtuals except those in the eg manifold are included in the excited subspace. Note that including nearby virtuals could lead to a large orbital rotation away from the target orbital, undesired population inversion, and potential redundancy in the NOCI determinant basis. For SF6, we only observed significant rotations away from the target orbital for a small number of determinants.
Fig. 1 presents the approximation schemes based on orbital diagrams. Colors are used to represent the subspaces that each reference molecular orbital is a member of. The reference molecular orbitals are the ground state molecular orbitals, but it is possible to use any reasonable set of reference molecular orbitals.68 The electron configuration in Fig. 1 resemble those of a core excited state where a low energy orbital is removed from the space that acts as the hole. Then this electron is occupied in a higher energy target orbital (orange). This target orbital is allowed to mix with the higher energy orbitals (purple) to optimize the energy.
The computed spectra for SF6 are presented in Fig. 2. All peaks are uniformly shifted by −8.55 eV, −2.75 eV, −2.45 eV and −2.40 eV for the completely frozen, frozen excited, inactive mixing, and energy cutoff constraints, respectively. This series suggests that as the optimization space is increased, the shift to experiment decreases, indicating the variational nature of this method. Additionally, relaxation of the core electrons has the largest effect on the absolute position of the spectra. The difference in shift between completely frozen and energy cutoff constraints suggests that the orbital optimization accounts for at least 6.15 eV of the correlation energy in this system. The singular values, which represent the orbital overlaps with the ground state, suggest that nearly all core orbitals are rotated to optimize the energy.
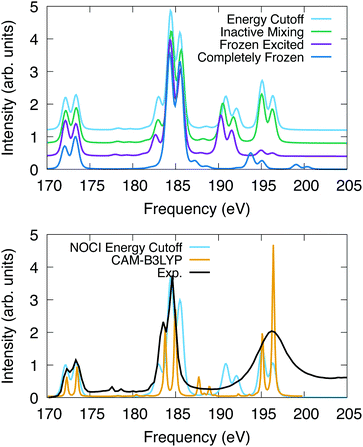 | ||
| Fig. 2 L2,3 edge X-ray absorption spectroscopy for SF6. The spectra were shifted and normalized to coincide with the peak at 173 eV. X2C-NOCI was performed using the Sapporo double zeta basis. The bottom plot also has the experimental spectrum,90 and one computed using response theory with CAM-B3LYP.91. | ||
For the computed spectra, we observe the largest changes of the features going from the completely frozen to the frozen excited constraint. For instance, the shoulder on the low frequency side of the peak at 185 eV becomes more apparent. Additionally, the set of peaks between 193–202 eV decrease in energy by roughly 4 eV and the oscillator strengths increase. The spectral features at 195–196 eV display a significant increase in intensity going from the frozen excited to the inactive mixing and energy cutoff constraints, due to the optimization of the excited electron. Furthermore, there are a set of weakly absorbing Rydberg peaks between 176 eV and 180 eV that are observed using constraints that feature orbital optimization but are not observed in the completely frozen scheme. Overall, these results suggest that the inactive mixing scheme is the most efficient for two reasons. First, the SCF is generally easier to converge using this constraint compared to the energy cutoff scheme. Second, the spectrum is largely indistinguishable from the energy cutoff scheme, which indicates that accuracy is largely unaffected.
In Fig. 2, we also compare the L2,3-edge spectrum computed using X2C-NOCI to both experiment90 and the computed spectrum in ref. 91 that used response theory (complex polarization propagator92,93) with density functional theory (CAM-B3LYP). This system features a small spin–orbit splitting of 1.2 eV according to experiment. NOCI agrees well with a value of 1.3 eV. Overall, the X2C-NOCI computed spectrum agrees fairly well with both experiment and response theory. Notable differences include the peak at 185 features a shoulder on the high energy side that is not observed in the other two. Additionally, X2C-NOCI underestimates the intensity of the shoulder on the low frequency side of the 185 eV peak. However, the absolute NOCI frequencies are more accurate than the response theory results, which needed to be shifted by 7.01 eV. Both X2C-NOCI and response theory observe a set of peaks between 186 and 194 eV that are not specifically observed in experiment. Mulliken population analysis combined with the singular values of the corresponding orbitals suggest these are single-electron transitions into high energy sulfur d-orbitals (≈70 orbitals above the occupied set). This spectral feature is present in all schemes for orbital optimization that we tested, which suggests it is not an artifact of orbital optimization. These same features are seen in the completely frozen approximation, but they are at higher energy due to the neglect of orbital optimization. The significance of these peaks is not clear.
3.2 SiCl4 L2,3-edge
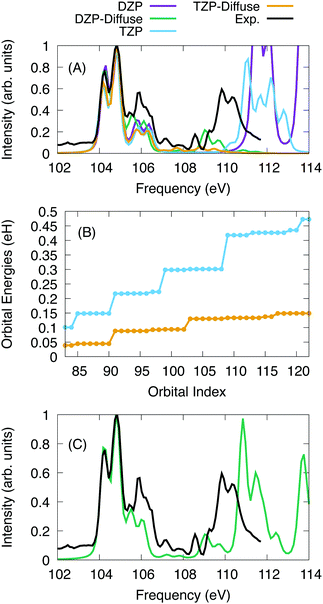
For SiCl4, the calculations were performed with a series of basis sets to test the scaling of the X2C-NOCI algorithm and the effect that the screening algorithm presented in Section 2.1. The Sapporo basis set family86–89 was used. For the algorithmic scaling tests, all six 2p electrons were excited into first 40 reference virtual orbitals, resulting in a total of 241 determinants. Subsequently, all excited determinants were optimized using the inactive mixing scheme. For calculations using the Sapporo-dzp basis with diffuse functions, we computed the additional excitations into the next 28 virtual orbitals (a total of 409 nonorthogonal determinants in X2C-NOCI).The computed and experimental spectra are displayed in Fig. 3. The spectra were shifted by −3.85 eV, −3.40 eV, −2.00 eV, and −2.00 eV for the DZP, DZP-all, TZP and TZP-all bases, respectively. Overall, we see similar results between the basis sets for the low energy peaks around 104–107 eV. However for the higher energy peaks, the effects of basis set quickly become apparent. The basis sets that include diffuse functions feature small peaks in the range of 108–110 eV. These peaks represent Rydberg excitations.91 In Fig. 3A, the spectra using basis sets that include diffuse functions go to zero at roughly 109 eV due to not including enough excitations to represent the higher energy features. Meanwhile for the basis sets without diffuse functions, none of the Rydberg peaks appear and the peaks around 110 eV are at higher energy by about 2 eV. Overall, the basis sets without diffuse functions are able to qualitatively describe the main features in the L2,3-edge spectra of SiCl4 but are missing the Rydberg states. The splitting of the two peaks between 104 and 105 eV is 0.59 eV, 0.60 eV, 0.63 eV and 0.63 eV for DZP, DZP-Diffuse, TZP and TZP-Diffuse, respectively. This compares well with the experimentally determined value of 0.61 eV. Additionally, for the full DZP-Diffuse spectrum (Fig. 3C) the strongly absorbing peak around 111 eV is higher than experiment by 1 eV.
To understand the origin of the large difference due to diffuse functions, the energies for the target excited orbitals are given in Fig. 3B. It is clear that including diffuse functions leads to a much slower increase in the orbital energy, which means that the number of states needed to optimize for higher energies are greatly increased. Additionally, the excited state manifolds become more dense with many states providing little contribution to the final spectrum. For Sapporo-dzp with diffuse functions, we computed an additional 168 determinants (see Fig. 3C). This yields a better representation of the experimental peak at 109–110 eV, but it is higher in energy by about 1 eV. Overall, as one increases the size of the one-particle basis set, the NOCI becomes more accurate. However, the number of states required to represent the same energy range may increase also.
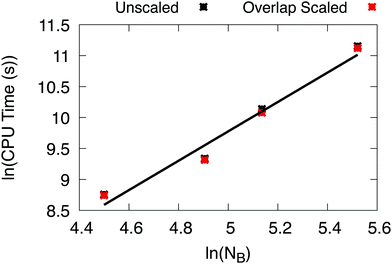
We tested the effective scaling of X2C-NOCI when using the AO direct algorithm (eqn (7)) with the improved integral screening using overlap-scaled density. Since the dominant computational cost in X2C-NOCI is the AO direct Fock build, the effective scaling can be computed using80
ln(t) ∝ α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(NB) ln(NB) | (15) |
3.3 [FeCl6]3− L2,3-edge
For [FeCl6]3−, we excited the 2p electrons into first 43 reference virtual orbitals, resulting in a total of 259 nonorthogonal determinants. The X2C-HF determinants were optimized using the Sapporo double zeta basis set with diffuse functions.86–89 The X2C-NOCI L2,3-edge spectrum has been shifted and renormalized to have the largest peak coincide with the experiment.Overall, we observe good agreement between the X2C-NOCI computed spectrum and the experimental spectrum (Fig. 5). The experimental peaks at ∼713 eV involve both single and double excitations in the form of shake-up peaks. There are several papers already in the literature that perform peak assignment for this system.94,95 Thus, our goal here is to evaluate the performance and accuracy of X2C-NOCI for computing L-edge spectra. Even though the X2C-NOCI method is capable of computing double excitations,67 we will leave the optimization of doubly excited determinants to a future study. The X2C-NOCI spectrum displays shoulders on the higher energy side of L2 edge. Orbital analysis suggests that these are transitions from the p3/2 to orbitals dominated by the iron d-orbitals with some mixing with the chlorine s and d orbitals. The agreement on the higher energy L3 peaks between 720 and 725 eV for both the relative energy and relative oscillator strength is excellent. However, for the L2 edge, we observe a shoulder on the high frequency side of the largest peak which is not observed in experiment. Examining the largest contributions to these states suggest that these are single excitation states (i.e., only one orbital difference in the singular values of the corresponding orbitals to the ground state). Furthermore, we computed an additional 156 optimized determinants and did not observe a significant change in the spectrum. The energies of the most significant peaks featured small changes on the order of 10−5 eV, and no additional features arise in the extended calculation. It is possible that the intensity and positions of these peaks require higher order correlations and vibronic couplings. This effect warrants further development and investigation. The X2C-NOCI computed spectrum was shifted down by 9.9 eV. We suspect this large shift is due to lack of dynamic correlation. There are published methods for including dynamic correlation in NOCI through perturbation theory,96–99 configuration interaction,11,31 and density functional theory.17,21,23
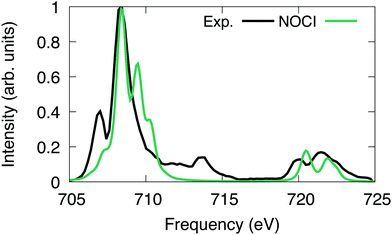 | ||
| Fig. 5 [FeCl6]3− L-edge spectrum computed using NOCI compared to experiment.100 The computed NOCI spectrum has been shifted down by 9.9 eV to align with the first peak in the experiment. | ||
The [FeCl6]3− molecule provides an interesting test for the screening of the two electron terms in the NOCI Hamiltonian. Here, there are a number of low lying reference orbitals that readily mix during the optimization of the excited states. Thus, there are many states where the corresponding orbitals between the excited and ground state determinants have multiple (more than two) singular values that are less than 0.1. Therefore, the screening techniques presented in Section 2.1 are more likely to be effective.
In Table 1, we display the speed-ups (ratios of CPU times) in forming the X2C-NOCI Hamiltonian using overlap-scaled density (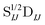 in eqn (10)), and overlap-scaled density with Slater–Condon estimation (eqn (11)), respectively, compared to using the unscaled density (
in eqn (10)), and overlap-scaled density with Slater–Condon estimation (eqn (11)), respectively, compared to using the unscaled density (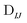 in eqn (9)). The density-contracted Cauchy–Schwarz integral screening scheme with a threshold of 10−12 is used. Overall, we observed significantly faster computation of the Hamiltonian using both the overlap-scaled density and also with Slater–Condon screening. With the latter we observe a speed-up of roughly 1.6 times compared to the conventional algorithm using unscaled density. To make sure we are not introducing too large of an approximation, we computed the error in the energy eigenvalues compared to the conventional algorithm. We observe a very small error with the maximum error being less than 10−4 eV and the mean unsigned error being less than 10−6 eV. Overall, the improved screening techniques show significant reduction in computational cost compared to the conventional algorithm when computing systems where there are large rotations among the core electrons.
in eqn (9)). The density-contracted Cauchy–Schwarz integral screening scheme with a threshold of 10−12 is used. Overall, we observed significantly faster computation of the Hamiltonian using both the overlap-scaled density and also with Slater–Condon screening. With the latter we observe a speed-up of roughly 1.6 times compared to the conventional algorithm using unscaled density. To make sure we are not introducing too large of an approximation, we computed the error in the energy eigenvalues compared to the conventional algorithm. We observe a very small error with the maximum error being less than 10−4 eV and the mean unsigned error being less than 10−6 eV. Overall, the improved screening techniques show significant reduction in computational cost compared to the conventional algorithm when computing systems where there are large rotations among the core electrons.
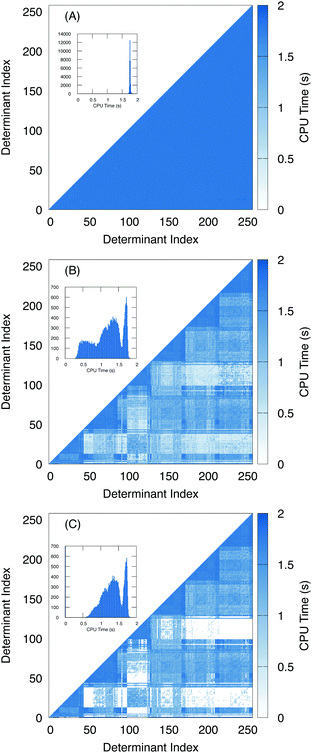
To further examine the effects of the screening, we plotted the amount of time it takes to compute the two electron terms as a heat map with respect to the determinant index (Fig. 6). For the algorithm using unscaled density (Fig. 6A), we see that the amount of time it takes to compute the two-electron terms is roughly constant regardless of the nature of the two determinants. A histogram of the number of Hamiltonian elements with respect to time is given in the inset, and shows that the two electron coupling takes roughly 1.8 seconds to compute with little variance.
In contrast, with the overlap-scaled density (Fig. 6B) we observe a large variance in the timing ranging from less than half a second to roughly 1.8 seconds. Furthermore, in the heat map we see that most of the time-saved is in computing the off-diagonal elements. Here, the determinants are ordered by the origin of the excitation. Thus, the first group are all of the excitations from the lowest energy electron. Then all of the excitations from the next lowest electron. Since we are interested in the L2,3-edge X-ray spectrum, we are exciting the 2p electrons, which means there are six groups of excitations. This is observed in the heat map where the two electron terms that take the longest time to compute are associated with determinants from the same group. Meanwhile, the blocks between excitation groups are the ones that exhibit the most screening. This is to be expected because the determinants have a difference of roughly two or more electrons depending on how much mixing the core electrons have with the frontier orbitals. Meanwhile, since the Slater–Condon screening is able to estimate that Hamiltonian terms are close to zero and can skip the computation entirely, addition speed-up is observed (Fig. 6C).
4 Conclusions
In this work, we introduced a variational relativistic non-orthogonal configuration interaction method using the exact-two-component transformation (X2C-NOCI). The generalized block localized wave function (gBLW) technique was used to optimize determinants of interest where relativistic effects (scalar relativity and spin–orbit) are variationally included for describing the X2C-NOCI wave function.We used nonorthogonal configuration interaction to compute the L2,3-edge spectra for several molecular systems including SF6, SiCl4 and [FeCl6]3−. Overall, X2C-NOCI is able to recover the main features of the L2,3-edge spectra.
We tested the effects that orbital relaxation has on the final spectrum using SF6. Overall, relaxation of the core electrons leads to the largest change in both the absolute energy and relative changes in the spectral features. Furthermore, we suggest that the inactive mixing approximation is the most efficient both in terms of SCF convergence and scanning the excited state manifold.
We proposed a screening technique using the overlap-scaled density matrix and a measure defined based on the generalized Slater–Condon rules for estimating which NOCI elements are zero before computing the two-electron term. This improved screening significantly increases the efficiency of the NOCI especially for a system where large rotations away from the reference orbitals are common such as in [FeCl6]3−. This lead to 1.6 times faster evaluation of the X2C-NOCI Hamiltonian compared to the conventional method. Meanwhile, these screening techniques introduced almost no error into the X2C-NOCI energy eigenvalues showing a mean unsigned error of 2.0 × 10−7 eV.
The X2C-NOCI method developed in this work has several unique advantages for the computation of X-ray spectroscopy. First, in the X2C-NOCI scheme, we are optimizing all of the determinants in the two-component framework so that each spin–orbit micro-state is at a variational minimum and all micro-states are treated on an equal-footing. Second, since spin–orbit couplings are included variationally at the orbital level, there is no need to use perturbative techniques.101 Although the tests carried out in this work can be readily done with perturbative techniques, it remains to be seen when variational X2C-NOCI is necessary when the subject matter contains heavier elements. A systematic benchmark is needed and will be a future work. Third, the resulting CI reference wave function is more compact than the conventional orthogonal CI method for a given chemical problem (see ref. 102 for the size of CI space needed for [FeCl6]3−), making it an attractive method for multireference CI (MRCI) or second-order perturbation (MRPT) treatment of dynamic correlation. However, challenges abound. Constrained optimizations to generate nonorthogonal determinants may not converge when orbitals in different subspaces have significant overlap. The nonorthogonal MRCI and MRPT treatments are nontrivial because the external space in MRCI/MRPT can be redundant with respect to the NOCI orbital rotation. The authors envision that variational relativistic NOCI will become a unique tool for resolving certain challenging chemical problems (e.g., L- and M-edge spectra). Of course, further developments and extensive benchmarks are needed to characterize this new variational relativistic NOCI framework.
Author contributions
A. G. performed the software implementation, data acquisition and data analysis. Both A. G. and X. L. contributed to conception/design of the study along with writing/revision of the article.Conflicts of interest
There are no conflicts to declare.Appendix A
A.1 Exact-two-component transformation
In this appendix, we briefly outline the exact-two-component transformation.The restricted kinetically-balanced (RKB) Dirac equation in matrix representation is:103,104
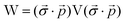 | (16) |
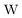 term gives rise to relativistic corrections and spin couplings in an atomic/molecular system. c is the speed of light.
term gives rise to relativistic corrections and spin couplings in an atomic/molecular system. c is the speed of light. 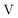 ,
, 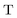 , and
, and 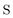 are the two-component non-relativistic potential energy, kinetic energy, and overlap matrices, respectively.
are the two-component non-relativistic potential energy, kinetic energy, and overlap matrices, respectively. ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) is the linear momentum operator and
is the linear momentum operator and ![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) is the vector of Pauli matrices. The solutions of eqn (16) include sets of positive/negative eigenvalues ({ε+}, {ε−}) with corresponding molecular orbital coefficients
is the vector of Pauli matrices. The solutions of eqn (16) include sets of positive/negative eigenvalues ({ε+}, {ε−}) with corresponding molecular orbital coefficients 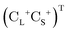 and
and 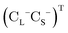 .105 Usually, only the positive energy solutions, {ε+}, are important for chemical systems.
.105 Usually, only the positive energy solutions, {ε+}, are important for chemical systems.
The exact-two-component (X2C)47–66 method seeks to “fold” the small component coefficients into the large component by a one-step unitary transformation 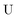 ,
,
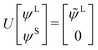 | (17) |
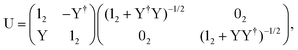 | (18) |
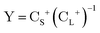 | (19) |
In this work, we employ the one-electron X2C approach which is a one-step procedure to construct the transformation matrix through the diagonalization of the one-electron four-component core Hamiltonian. However, since the two-electron spin–orbit terms contribute with an opposite sign to the spin–orbit terms, we used the Boetteger factors to scale the one-electron spin–orbit effect to semi-empirically treat the two-electron spin–orbit terms.76
A.2 Generalized block localized wave function
Here, we only present a brief review on the X2C-gBLW method and how it can be used to compute nonorthogonal excited determinants.67,68We use the following notations to keep track of the nature of the index with respect to the basis.
• The Greek letters (μ, ν, λ, σ) index atomic spin orbitals (AO's)
• The primed Greek letters (μ′, ν′, λ′, σ′) index transformed bases that span wave functions in a subspace
• The lowercase Latin letters (i, j, k) index occupied molecular orbitals (MO's)
• (A) indexes subspaces in generalized block-localized wave function (gBLW)
The gBLW method optimizes a set of molecular orbitals for a given determinant subject to constraints which are often based on chemical intuitions (e.g., π → π* transition). The constraints are encoded in a transformation from the original space of N basis functions to a set of subspaces. Molecular orbitals of each subspace (ψA,i) are linear combinations of transformed bases that are defined by the gBLW transformation matrix (ψA,νν)
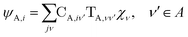 | (20) |
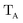 is a rectangular transformation matrix of dimension N × NA where N is the total number of atomic basis functions and NA is the number of selected transformed bases that span subspace A.
is a rectangular transformation matrix of dimension N × NA where N is the total number of atomic basis functions and NA is the number of selected transformed bases that span subspace A.
The SCF is performed by solving independent Roothaan–Hall equations for each subspace.
| FACA = SACAeA | (21) |
| FA = T†AP†AFPATA | (22) |
| SA = T†ASPATA | (23) |
| PA = 1 − DS + DAS | (24) |
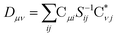 | (25) |
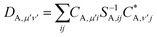 | (26) |
To compute an excited state determinant,68 we first define a reference state from which to get a set of molecular orbitals that well represent the problem. Subsets of the reference molecular orbitals comprise the gBLW transformation matrix. Orbitals that are excluded from a subspace are absent in the transformation matrix, which eliminates their contribution to the subspace.
For a given gBLW determinant, we separate the electrons into two subspaces: (1) a subspace to represent the core electrons that remain in roughly the ground state configuration, (2) a subspace to represent the excited electron. Different constraints are employed on the two spaces to yield the best representation of the excited state. For the core electrons, the occupied orbitals of the reference state are usually allowed to mix with all orbitals except hole orbital from which the excited electron is excited, which prevents variational collapse. Additionally, we exclude the orbital we wish to occupy by the excited electron (the target orbital) to avoid redundancies that prevent convergence of the SCF procedure.
Meanwhile, the excited electron subspace includes the target orbital along with all virtual orbitals of the reference that are higher in energy. These higher energy orbitals mix with the target orbital to lower the energy of the determinant. Additional reference orbitals can be excluded from the excited electron space to aid in convergence of the self-consistent field, to guarantee that target states are represented in the determinant expansion, or to provide further understanding of the determinant optimization.68 For nonorthogonal configuration interaction (NOCI), a set of determinants that span the excited manifold of interest are optimized. Thus, excluding orbitals from the excited electron space could be used to prevent large rotations away from the target orbital. While these rotations away from the target orbital are useful for obtaining a variational minimum, it makes it more difficult to ensure the proper scanning of an excited state manifold. Thus, it may prevent the optimization of a spin-complete set of determinants. The effect of these constraints is tested in Section 3.1.
After all subspace MOs are fully optimized, all occupied orbitals from all subspaces are orthogonalized using Löwdin orthongonalization to yield a set of orthonormal molecular orbitals.
The procedure illustrated above is carried out for each desired gBLW determinant to be used in the NOCI calculation. Note that occupied MOs in each gBLW determinant are orthogonal but can be nonorthogonal to MOs that belong to a different gBLW configuration.
Acknowledgements
A. G. thanks Ruxin Qu for help in creating the figures. X. L. acknowledges support from the US Department of Energy, Office of Science, Basic Energy Sciences, in the Heavy-Element Chemistry program (Grant No. DE-SC0021100) for the development of relativistic electronic structure methods. The study of L-edge XAS is supported by the Ultrafast Initiative of the US Department of Energy, Office of Science, Office of Basic Energy Sciences, through Argonne National Laboratory under Contract No. DE-AC02-06CH11357.Notes and references
- P. O. Löwdin, Phys. Rev., 1955, 97, 1509–1520 CrossRef.
- R. J. Harrison, J. Chem. Phys., 1991, 94, 5021–5031 CrossRef CAS.
- A. A. Holmes, N. M. Tubman and C. J. Umrigar, J. Chem. Theory Comput., 2016, 12, 3674–3680 CrossRef CAS PubMed.
- N. M. Tubman, C. D. Freeman, D. S. Levine, D. Hait, M. Head-Gordon and K. B. Whaley, J. Chem. Theory Comput., 2020, 16, 2139–2159 CrossRef CAS PubMed.
- J. B. Schriber and F. A. Evangelista, J. Chem. Theory Comput., 2017, 13, 5354–5366 CrossRef CAS PubMed.
- S. Shaik and P. C. Hiberty, A Chemist's Guide to Valence Bond Theory, John Wiley & Sons, Ltd, 2007 Search PubMed.
- W. Wu, P. Su, S. Shaik and P. C. Hiberty, Chem. Rev., 2011, 111, 7557–7593 CrossRef CAS PubMed.
- Z. Chen and W. Wu, J. Chem. Phys., 2020, 153, 090902 CrossRef CAS PubMed.
- P. C. Hiberty and S. Shaik, Theor. Chem. Acc., 2002, 108, 255–272 Search PubMed.
- D. L. Cooper and J. Gerratt, Chem. Soc. Rev., 1997, 26, 87–100 RSC.
- S. Ten-no, Theor. Chem. Acc., 1998, 98, 182–191 Search PubMed.
- M. Head-Gordon, P. E. Maslen and C. A. White, J. Chem. Phys., 1998, 108, 616–625 CrossRef CAS.
- Q. Wu, C. L. Cheng and T. Van Voorhis, J. Chem. Phys., 2007, 127, 164119 CrossRef PubMed.
- B. Kaduk, T. Kowalczyk and T. Van Voorhis, Chem. Rev., 2012, 112, 321–370 CrossRef CAS PubMed.
- A. J. W. Thom and M. Head-Gordon, Phys. Rev. Lett., 2008, 101, 193001 CrossRef PubMed.
- A. J. Thom and M. Head-Gordon, J. Chem. Phys., 2009, 131, 124113 CrossRef PubMed.
- A. Cembran, L. Song, Y. Mo and J. Gao, J. Chem. Theory Comput., 2009, 5, 2702–2716 CrossRef CAS PubMed.
- Y. Mo, P. Bao and J. Gao, Phys. Chem. Chem. Phys., 2011, 13, 6760–6775 RSC.
- H. Ren, M. R. Provorse, P. Bao, Z. Qu and J. Gao, J. Phys. Chem. Lett., 2016, 7, 2286–2293 CrossRef CAS PubMed.
- J. Gao, A. Grofe, H. Ren and P. Bao, J. Phys. Chem. Lett., 2016, 7, 5143–5149 CrossRef CAS PubMed.
- A. Grofe, X. Chen, W. Liu and J. Gao, J. Phys. Chem. Lett., 2017, 8, 4838–4845 CrossRef CAS PubMed.
- L. Yang, A. Grofe, J. Reimers and J. Gao, Chem. Phys. Lett., 2019, 736, 136803 CrossRef.
- R. Zhao, A. Grofe, Z. Wang, P. Bao, X. Chen, W. Liu and J. Gao, J. Phys. Chem. Lett., 2021, 7409–7417 CrossRef CAS PubMed.
- Z. Chen, X. Chen and W. Wu, J. Chem. Phys., 2013, 138, 164119 CrossRef PubMed.
- Z. Chen, X. Chen and W. Wu, J. Chem. Phys., 2013, 138, 164120 CrossRef.
- Z. Chen, X. Chen, F. Ying, J. Gu, H. Zhang and W. Wu, J. Chem. Phys., 2014, 141, 134118 CrossRef PubMed.
- X. Chen, Z. Chen and W. Wu, J. Chem. Phys., 2014, 141, 194113 CrossRef PubMed.
- J. Olsen, J. Chem. Phys., 2015, 143, 114102 CrossRef PubMed.
- S. Kähler and J. Olsen, J. Chem. Phys., 2017, 147, 174106 CrossRef PubMed.
- S. Kähler and J. Olsen, J. Chem. Phys., 2018, 149, 144104 CrossRef.
- T. Tsuchimochi and S. Ten-No, J. Chem. Theory Comput., 2016, 12, 1741–1759 CrossRef CAS PubMed.
- P. Å. Malmqvist, Int. J. Quantum Chem., 1986, 30, 479–494 CrossRef CAS.
- P. Å. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
- P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- F. Lipparini and J. Gauss, J. Chem. Theory Comput., 2016, 12, 4284–4295 CrossRef CAS PubMed.
- H. J. A. Jensen, K. G. Dyall, T. Saue and K. Fægri, J. Chem. Phys., 1996, 104, 4083–4097 CrossRef CAS.
- J. Thyssen, T. Fleig and H. J. A. Jensen, J. Chem. Phys., 2008, 129, 034109 CrossRef PubMed.
- A. Almoukhalalati, S. Knecht, H. J. A. Jensen, K. G. Dyall and T. Saue, J. Chem. Phys., 2016, 145, 074104 CrossRef PubMed.
- S. Knecht, H. J. A. Jensen and T. Saue, Nat. Chem., 2019, 11, 40–44 CrossRef CAS PubMed.
- J. E. Bates and T. Shiozaki, J. Chem. Phys., 2015, 142, 044112 CrossRef PubMed.
- R. D. Reynolds, T. Yanai and T. Shiozaki, J. Chem. Phys., 2018, 149, 014106 CrossRef PubMed.
- T. Shiozaki and W. Mizukami, J. Chem. Theory Comput., 2015, 11, 4733–4739 CrossRef CAS PubMed.
- B. Vlaisavljevich and T. Shiozaki, J. Chem. Theory Comput., 2016, 12, 3781–3787 CrossRef CAS PubMed.
- S. Knecht, O. Legeza and M. Reiher, J. Chem. Phys., 2014, 140, 041101 CrossRef PubMed.
- S. Battaglia, S. Keller and S. Knecht, J. Chem. Theory Comput., 2018, 14, 2353–2369 CrossRef CAS.
- A. J. Jenkins, H. Liu, J. M. Kasper, M. J. Frisch and X. Li, J. Chem. Theory Comput., 2019, 15, 2974–2982 CrossRef CAS PubMed.
- H. Hu, A. J. Jenkins, H. Liu, J. M. Kasper, M. J. Frisch and X. Li, J. Chem. Theory Comput., 2020, 16, 2975–2984 CrossRef CAS PubMed.
- W. Kutzlenigg and W. Liu, J. Chem. Phys., 2005, 123, 241102 CrossRef.
- W. Liu and D. Peng, J. Chem. Phys., 2006, 125, 044102 CrossRef PubMed.
- D. Peng, W. Liu, Y. Xiao and L. Cheng, J. Chem. Phys., 2007, 127, 104106 CrossRef PubMed.
- M. Ilias and T. Saue, J. Chem. Phys., 2007, 126, 064102 CrossRef.
- W. Liu and D. Peng, J. Chem. Phys., 2009, 131, 031104 CrossRef.
- W. Liu, Mol. Phys., 2010, 108, 1679–1706 CrossRef CAS.
- T. Saue, ChemPhysChem, 2011, 12, 3077–3094 CrossRef CAS PubMed.
- Z. Li, Y. Xiao and W. Liu, J. Chem. Phys., 2012, 137, 154114 CrossRef PubMed.
- D. Peng, N. Middendorf, F. Weigend and M. Reiher, J. Chem. Phys., 2013, 138, 184105 CrossRef PubMed.
- F. Egidi, J. J. Goings, M. J. Frisch and X. Li, J. Chem. Theory Comput., 2016, 12, 3711–3718 CrossRef CAS.
- J. J. Goings, J. M. Kasper, F. Egidi, S. Sun and X. Li, J. Chem. Phys., 2016, 145, 104107 CrossRef PubMed.
- L. Konecny, M. Kadek, S. Komorovsky, O. L. Malkina, K. Ruud and M. Repisky, J. Chem. Theory Comput., 2016, 12, 5823–5833 CrossRef CAS PubMed.
- F. Egidi, S. Sun, J. J. Goings, G. Scalmani, M. J. Frisch and X. Li, J. Chem. Theory Comput., 2017, 13, 2591–2603 CrossRef CAS PubMed.
- A. Petrone, D. B. Williams-Young, S. Sun, T. F. Stetina and X. Li, Eur. Phys. J. B, 2018, 91, 169 CrossRef.
- W. Liu and Y. Xiao, Chem. Soc. Rev., 2018, 47, 4481–4509 RSC.
- C. E. Hoyer, D. B. Williams-Young, C. Huang and X. Li, J. Chem. Phys., 2019, 150, 174114 CrossRef PubMed.
- T. F. Stetina, J. M. Kasper and X. Li, J. Chem. Phys., 2019, 150, 234103 CrossRef PubMed.
- T. Zhang, J. M. Kasper and X. Li, Chapter two – Localized relativistic two-component methods for ground and excited state calculations, in Annual Reports in Computational Chemistry, ed. D. A. Dixon, Elsevier, 2020, vol. 16, pp. 17–37 Search PubMed.
- C. E. Hoyer and X. Li, J. Chem. Phys., 2020, 153, 094113 CrossRef CAS PubMed.
- A. Grofe, R. Zhao, A. Wildman, T. F. Stetina, X. Li, P. Bao and J. Gao, J. Chem. Theory Comput., 2021, 17, 277–289 CrossRef CAS PubMed.
- A. Grofe, J. Gao and X. Li, J. Chem. Phys., 2021, 155, 014103 CrossRef CAS PubMed.
- J. M. Kasper, T. F. Stetina, A. J. Jenkins and X. Li, Chem. Phys. Rev., 2020, 1, 011304 CrossRef.
- P. Norman and A. Dreuw, Chem. Rev., 2018, 118, 7208–7248 CrossRef CAS PubMed.
- P. O. Löwdin, Phys. Rev., 1955, 97, 1474–1489 CrossRef.
- A. T. Amos and G. G. Hall, Proc. R. Soc. Lond., 1961, 263, 483–493 Search PubMed.
- H. F. King, R. E. Stanton, H. Kim, R. E. Wyatt and R. G. Parr, J. Chem. Phys., 1967, 47, 1936–1941 CrossRef CAS.
- L. Song, J. Song, Y. Mo and W. Wu, J. Comput. Chem., 2009, 30, 399–406 CrossRef CAS PubMed.
- A. Szabo and N. S. Ostlund, Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, Dover Publications Inc, Mineola, New York, 1996 Search PubMed.
- J. C. Boettger, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 7809–7815 CrossRef CAS.
- R. K. Kathir, C. De Graaf, R. Broer and R. W. A. Havenith, J. Chem. Theory Comput., 2020, 16, 2941–2951 CrossRef CAS PubMed.
- T. P. Straatsma, R. Broer, S. Faraji, R. W. A. Havenith, L. E. A. Suarez, R. K. Kathir, M. Wibowo and C. De Graaf, J. Chem. Phys., 2020, 152, 064111 CrossRef CAS PubMed.
- M. Häser and R. Ahlrichs, J. Comput. Chem., 1989, 10, 104–111 CrossRef.
- D. L. Strout and G. E. Scuseria, J. Chem. Phys., 1995, 102, 8448–8452 CrossRef CAS.
- X. Li, E. F. Valeev, D. Williams-Young, F. Ding, H. Liu, J. Goings, A. Petrone and P. Lestrange, Chronus Quantum, Beta Version, 2016, https://www.chronusquantum.org.
- D. B. Williams-Young, A. Petrone, S. Sun, T. F. Stetina, P. Lestrange, C. E. Hoyer, D. R. Nascimento, L. Koulias, A. Wildman, J. Kasper, J. J. Goings, F. Ding, A. E. DePrince III, E. F. Valeev and X. Li, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1436 CAS.
- J. M. Kasper, P. J. Lestrange, T. F. Stetina and X. Li, J. Chem. Theory Comput., 2018, 14, 1998–2006 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- T. Koga, H. Tatewaki, H. Matsuyama and Y. Satoh, Theor. Chem. Acc., 1999, 102, 105–111 Search PubMed.
- M. Sekiya, T. Noro, T. Koga and H. Matsuyama, J. Mol. Struct., 1998, 451, 51–60 CrossRef CAS.
- T. Noro, M. Sekiya, T. Koga and H. Matsuyama, Theor. Chem. Acc., 2000, 104, 146–152 Search PubMed.
- H. Tatewaki, T. Koga and H. Takashima, Theor. Chem. Acc., 1997, 96, 243–247 Search PubMed.
- E. Hudson, D. A. Shirley, M. Domke, G. Remmers, A. Puschmann, T. Mandel, C. Xue and G. Kaindl, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 361–373 CrossRef CAS PubMed.
- T. Fransson, D. Burdakova and P. Norman, Phys. Chem. Chem. Phys., 2016, 18, 13591–13603 RSC.
- P. Norman, D. M. Bishop, H. Jorgen, A. Jensen and J. Oddershede, J. Chem. Phys., 2001, 115, 10323–10334 CrossRef CAS.
- P. Norman, D. M. Bishop, H. J. A. Jensen and J. Oddershede, J. Chem. Phys., 2005, 123, 194103 CrossRef PubMed.
- R. V. Pinjari, M. G. Delcey, M. Guo, M. Odelius and M. Lundberg, J. Chem. Phys., 2014, 141, 124116 CrossRef PubMed.
- R. V. Pinjari, M. G. Delcey, M. Guo, M. Odelius and M. Lundberg, J. Comput. Chem., 2016, 37, 477–486 CrossRef CAS PubMed.
- H. G. A. Burton and A. J. W. Thom, J. Chem. Theory Comput., 2020, 16, 5586–5600 CrossRef CAS PubMed.
- S. R. Yost, T. Kowalczyk and T. Van Voorhis, J. Chem. Phys., 2013, 139, 174104 CrossRef PubMed.
- S. R. Yost and M. Head-Gordon, J. Chem. Phys., 2016, 145, 054105 CrossRef PubMed.
- S. R. Yost and M. Head-Gordon, J. Chem. Theory Comput., 2018, 14, 4791–4805 CrossRef CAS PubMed.
- E. C. Wasinger, F. M. F. de Groot, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 2003, 125, 12894–12906 CrossRef CAS PubMed.
- M. L. Vidal, P. Pokhilko, A. I. Krylov and S. Coriani, J. Phys. Chem. Lett., 2020, 11, 8314–8321 CrossRef CAS PubMed.
- A. J. Jenkins, H. Hu, L. Lu, M. J. Frisch and X. Li, J. Chem. Theory Comput., 2022, 18, 141–150 CrossRef CAS PubMed.
- K. G. Dyall and K. Fægri, Jr., Introduction to Relativistic Quantum Chemistry, Oxford University Press, 2007 Search PubMed.
- M. Reiher and A. Wolf, Relativistic Quantum Chemistry, Wiley-VCH, 2nd edn, 2015 Search PubMed.
- S. Sun, T. F. Stetina, T. Zhang, H. Hu, E. F. Valeev, Q. Sun and X. Li, J. Chem. Theory Comput., 2021, 17, 3388–3402 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01127a |
| This journal is © the Owner Societies 2022 |