Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electrochemical gating enhances nearfield trapping of single metalloprotein junctions†
Albert C.
Aragonès
 * and
Katrin F.
Domke
*
* and
Katrin F.
Domke
*
Max Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: albert.cortijos@mpip-mainz.mpg.de; domke@mpip-mainz.mpg.de
First published on 27th May 2021
Abstract
Metalloprotein based junctions are widely used as model systems in the field of molecular bioelectronics to miniaturise electronic circuitry with help of biomolecular device components. To further progress in the field, new approaches are sought to form junctions with longer lifetimes than the current limit of hundreds of milliseconds, ideally approaching timescales sufficient for detailed junction characterization or even relevant for device operation. Here, we present an electrochemically gated plasmon-supported break-junction (EC-PBJ) platform that prolongs the lifetime of single-molecule junctions of Azurin (Azu) under strict electrochemical control and physiological conditions. EC-PBJ efficiently combines nearfield and electrochemical gating effects that stabilise the formed metalloprotein junction while maintaining the native structure of the biomolecule. For moderate far-field power densities of ca. 9.49 mW μm−2, the lifetime of individual oxidised Azu junctions is increased by a factor of 40 compared to laser-OFF conditions, which equals a nearfield trapping efficiency increase close to three orders of magnitude compared with reduced Azu junctions at the lowest used power density. We ascribe the lifetime tuning through EC-PBJ to two synergistic parameters: (i) the control of the redox state of trapped Azu that affects its resonant state and polarisability, and (ii) the steering of the localised surface plasmon resonance (LSPR) of the junction nanogap through electrode potential control. At the used laser mid-power range, the Azu redox state and polarisability have a more significant effect on the nearfield trapping efficiency than the LSPR shift. Non-invasively increased junction lifetimes pave the way for the development of improved biomolecular sensing and recognition platforms.
Introduction
Single metalloprotein charge-transport (CT) junctions serve as ideal model systems for the sophisticated bio-molecular machinery Nature has developed to achieve outstanding CT underlying a vast number of fundamental life processes such as enzymatic catalysis, photosynthesis or respiration.1,2 The field of biomolecular electronics (BioME) aims at constructing a detailed knowledge base of the physico-chemical properties of biosystem-based junctions and the mechanistics behind biological CT.2 Such knowledge is the key to designing the next generation of hybrid (bio)electronic high-performance devices for a wide variety of applications in organic electronics, sensing, optoelectronics and bio-manufacturing.1As (metallo)proteins possess a broad range of electric properties, such as photoconductivity,3 rectification,4 transistor-like response,5 switching behaviour6 and electrocatalysis7 among others,2,8 they have been proposed as suitable candidates to develop electronic (nano)biomaterials.8 The macroscale (electronic) properties of such novel kind of materials are controlled by the functionalities of the building-block target molecules. Metalloprotein-based biomaterials offer the potential to process and/or transfer an electric signal (charge) and are therefore prime candidates to engineer hybrid devices with bioelectronic interfaces.9Pseudomonas aeruginosa Azurin (Azu), the molecule employed in the study at hand, is a globular metalloprotein containing a coordinated redox Cu centre (see ESI S1,† for structural details). Azu is a widely used test-bench molecule in the field of biomolecular electronics.2,9,10 Because of its unique electrical properties, it has been predicted to be the cornerstone molecule for the development of functional biomaterials with tailored electronic properties,10 standing out from other potential candidates by providing a particularly high electrode coverage capacity,11 robust surface immobilisation via strong thiol–Au bond,12 highly efficient intra- and intermolecular CT,13 high current densities at low bias potentials as well as temperature-independent CT over long distances.12–14 To date, Azu has been employed as functional bio(nano)material to functionalise electrodes and assemble molecule-based device architectures such as bio-memories,6 transistors,5 solid-state rectifiers,4 and optoelectronic devices.15 Despite the broad use of Azu as target test species, various aspects of the Azu|electrode interface have remained elusive,2 such as the CT mechanism(s) and the relationship between electronic function and molecular geometry, i.e., orientation and conformation.13,16 A consensus on how structural parameters affect the CT, and vice versa, has not yet been reached in the scientific community, but is strongly desirable because of the imminent potential of Azu as the prototype building block for functional biomaterials and biomolecular electronic devices.2,9
Robust tools are being developed for high-precision electrical characterization of biomolecules from molecular ensembles (monolayers)12,16–18 to single-molecule contacts.19–24 Single-molecule approaches open the gate to access the characteristic molecular length scales of the contacted molecules, allowing to explore individual molecule properties that are inaccessible in ensemble experiments. Part of these approaches rely on the detection of individual biomolecular binding events in an inter-electrode nanogap of a fixed size as a function of time.19,20,23,24 The main aim is to resolve variations in the detected current behaviour during the junction lifetime and to correlate these variations, for example, with conformational changes or other physical and chemical molecular properties or processes.19,20,22
Despite the large amount of information that single-molecule approaches offer, the detected junction lifetimes are often only in the order of tens to hundreds of milliseconds.19,20,22–24 Such short lifetimes are one of the major bottlenecks for the characterization of individual metalloprotein junctions since they hinder the extended capturing of the variations in junction states. Short junction lifetimes are mainly due to the rather weak electrostatic or hydrophobic interactions that underlie the metalloprotein|electrode contacts.1 Undoubtedly, longer interrogation times for the contacted biomolecules, i.e., achieving increased junction lifetimes, is one of the main challenges BioME research is facing.
In molecular electronics, different strategies have been tested to obtain durable and mechanically robust molecular junctions, including the use of different electrode materials and the inclusion or modification of anchoring groups to promote specific molecule–electrode interaction.25–27 Unfortunately, these alternatives are difficult to implement in biosystems because of the implications that structural modification of biomolecules entail for their CT properties. Additionally, chemical alterations of the molecule|electrode directed at immobilising the biomolecule at the electrode may render CT-inactive molecular conformations.1 Thus, the field of BioME requests the development of different techniques to capture biomolecule junctions with increased lifetimes in a non-invasive and widely applicable way.
Nanophotonics have emerged as a valuable alternative to efficiently capture molecules in a specific location with help of plasmonic trapping.28 In a plasmonic trap, a metallic nanogap acts as a nanoantenna that confines and enhances the electromagnetic farfield (laser beam) well below the Abbe limit of diffraction when the localised surface plasmon resonance (LSPR) of the gap is in resonance with the laser excitation line.29 The resulting nearfield is typically up to three orders of magnitude stronger than the farfield, rendering feasible even the trapping of molecules.30,31
Recently, we have reported a plasmon-supported break-junction (PBJ) platform that increases the lifetime of single-molecule junctions by one order of magnitude without the need for chemical modification of molecule and/or electrode.32 The PBJ platform is based on the blinking approach33 of the scanning tunnelling microscope break-junction technique (STM-BJ),34 using stable and fixed-distance nanogaps between common Au STM electrodes to form single-molecule junctions.35 Under laser illumination, the nanogap serves as nanoantenna, and the nearfield gradient established upon gap illumination is exploited to reinforce the stochastically formed molecular junctions.36 PBJ is a non-invasive tool suitable for biomolecular junction measurements because it is a motionless electrode approach, thus mechanically stable, where the native structure of a contacted molecule is preserved,37,38 and because only moderate farfield power densities in the order of a few mW μm−2 are used.
Electronic resonance is an optical property that can be exploited to enhance the nearfield trapping since it provides an increased molecular polarisability.39,40 Various studies have reported resonant optical manipulation of nanosized objects such as dye-doped polystyrene nanospheres41 as well as CuCl,42 Au,43 and Ag nanoparticles.44 Inspiring works have exploited the resonance enhancement to achieve improved optical manipulation at the molecular level employing farfield radiation for the trapping of antibodies labelled with fluorophores45 or small heme-proteins.46 Shoji et al. made use of a nearfield to trap polymeric nanospheres.47 Interestingly, the oxidized Azu Cu(II) form exhibits an intense absorption band in the visible at 625 nm due to a ligand-to-metal charge-transfer electronic transition48,49 that is in good resonance with the excitation line at 632.8 nm (cf. Methods). In contrast, the reduced Cu(I) Azu form shows an electronic absorption state only in the UV region at around 280 nm.50 The Cu redox centre can be switched between the reduced Cu(I) and the oxidized Cu(II) state with electrochemical (EC) control of the substrate electrode.5,19,21 Therefore, by switching between the Cu(I) and Cu(II) redox states, we tune the optical-resonance property of the contacted Azu molecule. The resonant TER excitation and the tuneable redox state, in addition to the aforementioned electrical capabilities, render Azu an excellent showcase molecule to study resonance effects in nearfield trapping.
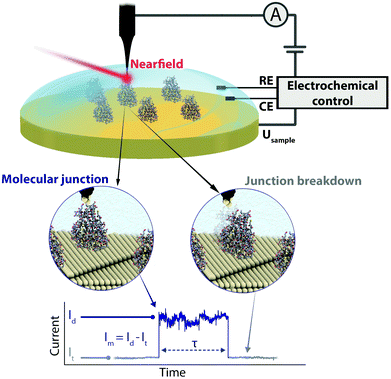
We present an EC gating variant of PBJ that relies on a commercial EC-STM microscope interfaced with an EC tip-enhanced Raman spectrometer (EC-TERS) (Fig. 1 top).51 The metalloprotein junction in a physiological environment (buffer solution) is characterised by its current (Im) that is maintained for the lifetime (τ) of the molecular junction (Fig. 1 bottom). With EC-PBJ, we can tune the nearfield trapping efficiency (proportional to τ) of Azu junctions resulting in a τ increase by a factor 40 with a combination of moderate farfield laser power densities of up to ca. 9.49 mW μm−2 and EC gating. We demonstrate that the Azu junction lifetime increase is a synergistic result of tuning (i) the Azu oxidation state and thus its electronic resonance character, and (ii) the LSPR of the nanogap through electrode potential control. The EC-PBJ approach provides a versatile route to enhance biomolecular junction lifetimes in a non-invasive way.
Methods
EC-PBJ single-molecule experiments were performed with a home-built setup based on a commercial EC-STM (Keysight Technologies – former Agilent – 5420). The current signal from the EC-STM was captured using a NI-DAQmx/BNC-2110 interface acquisition system (National Instruments), analyzed without any pre-selection with home-written LabVIEW and Python codes and plotted with Matplotlib.52 EC-TERS measurements were performed with a coupled HeNe laser (632.8 nm; REO LSRP-3501, 35 mW maximum output power, linearly polarised) and a Horiba iHR 550 spectrograph with an N2 cooled CCD camera (Symphony II, Horiba). The set-up is based on a side-illumination configuration with an angle of 55° between the focusing/collection objective and the substrate surface. The EC-TER backscattering was recollected along the same path. For a more detailed description about the experimental set-up as well as data capture and treatment, see ESI S1.†Pseudomonas aeruginosa Azurin was purchased from Sigma-Aldrich. All chemicals were used as received. A Au(111) single crystal (10 mm × 4 mm, MaTecK) of 5 N purity, an orientation accuracy of <0.1° and a roughness of <0.01 μm was employed as substrate electrode. Before each experiment, the Au(111) crystal was electropolished to eliminate possible residual contamination, rinsed with Milli-Q water, annealed in a butane flame for 10 minutes and then cooled down in an Ar atmosphere (6 N, Westfalen). The crystal was then immediately immersed in an Ar-purged 10 μM Azu 50 mM NH4Ac buffer solution (pH 4.55) for 3 h to form an Azu sub-monolayer. Azu molecules covalently bind to the Au substrate through two strong thiol–Au bonds with the Cys3 and Cys26 residues (Fig. S1, ESI†) without the need for an additional linker.5,53 The Azu-functionalized Au(111) surface was washed thoroughly with de-aerated buffer solution and Milli-Q water, dried under a stream of Ar and assembled in the EC-STM cell. A volume of 80 μL of Ar-purged buffer solution water was added to the cell. The EC-STM tips were cut from a 0.25 mm diameter Au wire (Alfa Aesar, Premion, 99.9985% metal basis) to be of ca. 1.5 cm length, electrochemically etched and coated with Zapon lack (CLOU). As counter electrode, a 0.25 mm diameter Au wire (Alfa Aesar, Premion, 99.9985% metal basis) was used. A hydrogen-loaded Pd wire (Pd–H; 0.5 mm diameter, MaTecK, 99.95% metal basis) was employed as reference electrode. All potentials are quoted versus Pd–H, which roughly equals the reversible hydrogen electrode potential. For a detailed description about the experimental procedures, see ESI S1.†
Results
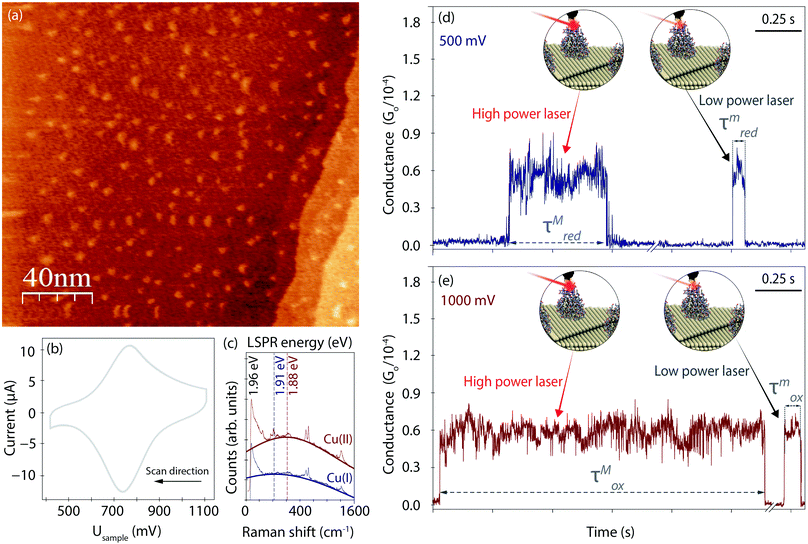
Fig. 2a displays an EC-STM image recorded prior to the EC-PBJ experiments. The dots of ca. 1 nm apparent height and 3–5 nm diameter depict individual Azu molecules adsorbed at the Au(111) surface at intermediate surface coverage, in accordance with previously reported images.37 Cyclic voltammetry (CV) is carried out in the same sample cell to characterise the EC behaviour of the Azu|Au substrate interface.19,37 Under our experimental conditions, the Azu redox potential occurs at ca. 750 mV, in agreement with values reported in earlier work (Fig. 2b).53 Under the given conditions, buffer surface reactions can be ruled out.53EC-TER spectra (experimental details in ESI S2,† and full-range spectra in Fig. S2, ESI†) are recorded to further characterize the oxidation state of the Azu molecules in the inter-electrode nanogap as well as the LSPR of the gap (Fig. 2c). As is known from earlier works, oxidized Cu(II) Azu (red spectrum) provides an electronic resonance at 625 nm (1.98 eV) close to the employed laser energy of 632.8 nm (1.96 eV).48 The Cu(II) Azu spectrum exhibits three enhanced characteristic modes at ca. 369, 408 and 424 cm−1 associated with the Cu(II) active site.49 Upon reduction of Azu to Cu(I), the electronic resonance and as such the enhanced modes of the active center disappear. From the TER spectral background maximum, the energy of the LSPR of the junction can be extracted with help of Lorentzian fitting.51 The gap LSPR (blue)shifts from ca. 1.88 eV at Usample = 1000 mV to ca. 1.91 eV at Usample = 500 mV, as can be expected for the given changes in electrode potential.54,55
Fig. 2d and e displays examples for the lifetime variation of Azu junctions recorded at minimum (τm) and maximum (τM) laser power densities of 9.49 mW μm−2 and 6.72 × 10−1 mW μm−2, respectively, for Usample = 500 mV and Usample = 1000 mV. With increasing laser power, we observe an increase in lifetime for both electrode potentials. Interestingly, the magnitude of the τ increase differs for the different Usample, with τMox (τmox) > τMred(τmred).
Azurin junction lifetime
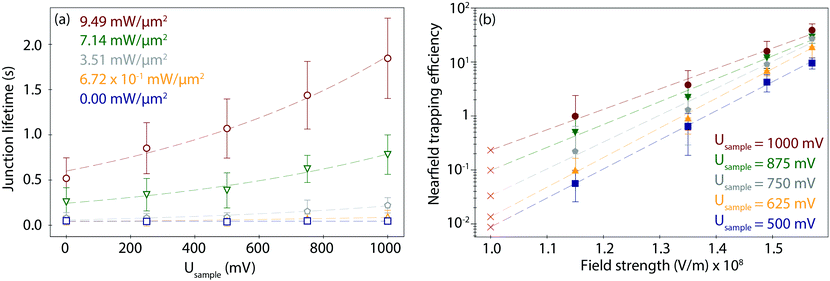
To study the combined effect of laser power density and applied electrode potential, we have systematically varied both parameters and captured and evaluated the corresponding PBJ current traces (see CT details and current characterisation in ESI S3 and Fig. S3–S5, ESI†). Fig. 3a shows the mean detected lifetimes (see details in ESI S4,† and histograms in Fig. S6, ESI†) as a function of Usample ranging between 0 and 1000 mV and of employed laser power density between 0 and 9.49 mW μm−2 (detailed information about the estimation of the laser power densities and photothermal effects in ESI S5†).At 0 mW (laser-OFF control experiments), i.e., without nearfield excitation, the detected Azu junction mean τ is 4.63 × 10−2 ± 0.40 × 10−2 s, independently of the employed Usample (Fig. 3a, blue trace, squares). In other words, in the absence of the nearfield, we do not observe an electrochemical gating effect on the junction lifetime. Under laser illumination, τ increases with increasing laser power density and electrode potential. A maximum value of τ = 1.85 ± 0.44 s is achieved for Usample = 1000 mV and the highest employed laser power density of 9.49 mW μm−2 (Fig. 3a, red trace, circles). This change in τ equals to a factor of 40 lifetime increase compared to the laser-OFF conditions at the same Usample. The dependence of τ on Usample follows an exponential behaviour for all employed laser power densities (ESI,† Table S1 for an overview of all lifetime detected values). The exponential increase becomes more evident with increasing power, as evident from the correlated increasing slope values ranging from 1.27 × 103 at 6.72 × 101 mW μm−2 to 2.47 × 103 at 9.49 mW μm−2 (Table S2, ESI†).
In addition, Fig. 3a shows an increase in τ as a function of laser power density for any given Usample that also follows an exponential behaviour (Fig. S7, ESI†), in line with what has been previously reported.32 This behaviour is explained by the fact that the trapping time probability is given by a Boltzmann factor45 related to the increase in the created nearfield gradient that exerts an increased trapping force on the trapped molecule.56 Consequently, the nearfield gradient – tuned by the applied laser power density – is used to overcome the native stochastic disconnection of the junction.36 Therefore, the nearfield enhances the stability of the metalloprotein junction, promoting the lifetime enlargement.
Furthermore, the combination of nearfield and EC gating also tunes the lifetime dispersion of the lifetime values. The lifetime dispersion can be displayed by means of the standard deviation (Table S1, ESI†) and is visualized by the error bars in Fig. 3a. The correlation between lifetime values and their dispersion has been reported for metallic57 and for single-molecule junctions.32 The dispersion increase has been attributed to the growth of the dissociation activation energy barrier,58 due to multiple factors such as the change of the pulling rate in a junction57 or the varying force exerted by the nearfield gradient.32
Nearfield trapping efficiency
To evaluate a net nearfield trapping efficiency as resulting from the interrelated laser power density and EC gating effects, we first need to exclude other parameters that may potentially affect the junction lifetime, like the lifetime variance between sets of experiments under equivalent conditions. Thus, we calculate a normalized nearfield trapping efficiency,32η, for each junction, where η = (τP − τOFF)/τOFF, where τP is the lifetime at a specific incident laser power density, P, and τOFF is the lifetime measured under identical conditions with the laser beam blocked (0 mW).32In Fig. 3b, η is plotted versus the nearfield strength (V m−1) in the junction (details in Table S3, ESI†). The field strength magnitude has been estimated considering the contribution of the nearfield corresponding to each laser power density in addition to the field gradient associated with the applied bias voltage Ubias of 300 mV at an inter-electrode distance of 3 nm (details in ESI S5†). The obtained field gradients are in the order of 108 V m−1, in line with the ones calculated for a similar inter-electrode nanogap for a set-up based on a gated (mechanically controlled) break-junction platform under laser illumination.59 The data shows a positive correlation of η with Usample. The nearfield trapping efficiency increases exponentially as a function of the field strength, with a maximum difference, i.e., an effective enlargement, close to 3 orders of magnitude between η = 5.65 × 10−2 (at 1.15 × 108 V m−1 and Usample = 500 mV) and η = 3.89 × 101 (at 1.57 × 108 V m−1, Usample = 1000 mV).
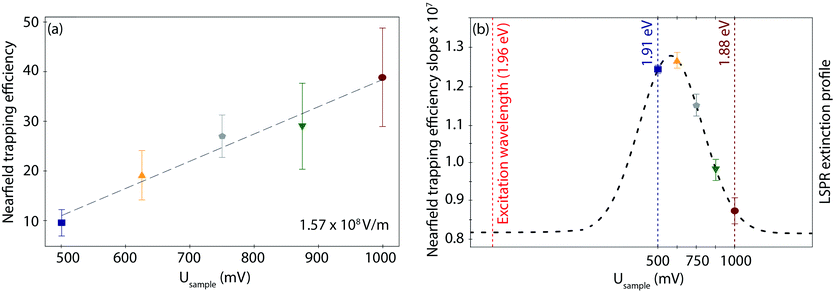
Interestingly, the behaviour of η as a function of field strength exhibits differences according to the applied Usample, both in the slope, i.e., the trapping susceptibility with respect to the field strength, and in the observed increase in magnitude at each given Usample. As displayed in Fig. 4a for the highest field strength example (other data sets in Fig. S8, ESI†), the initial (minimum) η value for the fully reduced Azu Cu(I) junction progressively increases toward the fully oxidized Azu Cu(II) state in a linear way. On the other hand, the extracted slopes do not show any obvious (linear or exponential) correlation with respect to the applied potential (Table S4, ESI†). However, they can be overlayed on a Gaussian curve (dashed line as a guide to the eye in Fig. 4b), with the (local) maximum located at 625 mV and the (local) minimum located at 1000 mV.
Discussion
How can we understand the two different types of behaviour of the nearfield trapping efficiency slope and magnitude observed in the Au|Azu|Au EC-PBJ experiment? There are two plausible physical origins that support the trends of magnitude increase and slope as a consequence of the EC gating of the nearfield trap. The first one is related to the resonant character of the Azu Cu(II) state stabilised at high applied potentials,48,49 or, more precisely, to the Cys → Cu(II) charge-transfer transition (as also indicated by the TER spectral intensities at Usample = 1000 mV in Fig. 2c). The second one is the EC gating effect on the LSPR of the nanogap as a result of tuning Usample and thus the electrode surface charge density, as previous works have reported.54,60Molecular resonance tuning
It has been predicted that the optical trapping efficiency should be greatly enhanced when the (farfield) incident light is tuned to the electronic (or excitonic) resonance energy of the trapped particle, i.e., when working under resonant excitation conditions.39,40 The basic principle behind such resonance-enhanced trapping lies in the induced polarisation that is enhanced when the trapping field is energetically resonant with an electronic transition of the trapped particle. In a plasmonic trap, the emerging gradient force of the nearfield acting on the particle is proportional to the polarisability of the particle or molecule.61 Thus, the exerted force is enlarged when the molecule exhibits electronic resonances.For Azu, as discussed above, the electronic resonance can be tuned by tuning the oxidation state of the Cu center, from the UV in the reduced Cu(I) state into the visible (red) in the oxidized Cu(II) state. The farfield laser line is located at 1.96 eV and the gap resonance responsible for the electromagnetic field enhancement is located close by at ca. 1.88 eV. As such, applying more positive potentials to the substrate, the metalloprotein in the junction is oxidized and an electronic resonance state with the red excitation is created. Accordingly, the polarisability enhancement mechanism amplifies the nearfield exerted force over Azu molecules under resonant conditions, i.e., in the oxidized Cu(II) state.
The observed linear increase in the magnitude of η with Usample (Fig. 4a) is in line with a linear resonance-induced polarisation of the trapped metalloprotein.62 The gradual increase of η with potential can be understood by the fact that the transition redox character of individual Azu molecules is characterised by a progressive redox transition,63i.e., by a progressive shifting of orbitals toward an electronic resonance in the visible and related increase in polarisability, and not by a step-function (binary) redox behaviour. Similar progressive redox processes have been reported also in previous Azu EC single-molecule studies.5,19 While being beyond the scope of the work at hand, analogous EC-PBJ experiments with redox-inactive Azu variants, such as its Zn analogue or its apo (metal-free) form, would provide a deeper insight into the resonance contribution to the EC gating effect on the junction lifetime.
LSPR tuning
The LSPR energy of the nanogap depends on the applied electrode potential because of the resulting charge density tuning, as the Drude model explains.64 This model predicts a blue-shift (red-shift) toward higher (lower) LSPR energies when the surface electrode charge density is increased (decreased). In our case, the charge density of the Au electrodes is determined by the Fermi level displacement as controlled by the EC gate, i.e., the applied reductive (oxidative) potential. The origin of the EC gated LSPR shift has been studied with spectro-electrochemistry, such as surface-enhanced Raman55 and darkfield spectroscopies.54 Similar to the EC gated LSPR shifts reported, our TER spectra reveal an LSPR blue-shift from 1.88 eV to 1.91 eV upon lowering the applied potential from oxidation (Usample = 1000 mV) to reduction (Usample = 500 mV) potential (Fig. 2c), indicating that the range of EC gating in our measurements is efficiently tuning the LSPR. The magnitude of LSPR shift of ca. 0.05 eV V−1 is perfectly consistent with previously reported shifts (more details in ESI S2†).54,60,65Interestingly, inside the LSPR energy window, η versus Usample can be overlayed with a Gaussian distribution (Fig. 4b). The fact that a typical LSPR extinction spectrum is known to exhibit a Gaussian behaviour within its characteristic energetic range66 leads us to suggest a direct proportionality between η and the LSPR energy profile of the nanogap. The LSPR extinction is correlated with the wavelength-dependent electric field enhancement (E2),66,67 that, in turn, controls the nearfield exerted force,56,61 and thus η. As such, we speculate that the irregular trend of the η slope within the studied potential range, visualizes the LSPR and resulting nearfield strength profiles in the junction. Directly measuring the gap LSPR extinction spectra during the corresponding EC-PBJ experiments would provide more precise information on the relationship between gap resonance and η but lies currently outside the capabilities of our setup.
As Fig. 4b shows, the LSPR modes of the junction are moderately red-detuned from the excitation wavelength (632.8 nm, 1.96 eV), which may diminish the nearfield trapping efficiency.68 Despite these imperfect LSPR resonance conditions, the calculated optical potential of the junction is in the order of 10 to 17kBT for the 3 nm nanogap (details in Table S5, ESI†). This value is of the same order of magnitude as optical potentials characteristic for conventional optical traps,45 and comparable to values previously reported resulting from tens of mW μm−2 excitation power.32,69
A tunable laser source could potentially enlarge the nearfield trapping efficiency of the EC-PBJ platform even further. Improving the LSPR mode matching could enhance the gradient trapping force.29 Furthermore, laser line tuning would open the route to optomechanical tweaking of EC-PBJ, for example, through achieving self-induced back action to additionally improve the efficiency of nearfield molecular traps.32,70,71
Combined electrochemically gated nearfield effects
In our experiments, the observed maximum difference in net nearfield trapping efficiency reaches ca. 3 orders of magnitude. This number is approaching theoretical predictions that show an increase of optical trapping efficiency of particles smaller than 10 nm radius by up to 5 orders of magnitude compared to the nonresonant case.40 In our case, the net increase is the result of the synergistic combination of the two EC gating effects discussed above: the molecular polarisability and the LSPR shift. In the following, we explore in more detail how the two effects interplay and affect η. While the molecular resonance effect is intuitively displayed also in the enhancement of the lifetimes at higher Usample, η gives more precise insight into the interaction between both factors.As evident from the η graphs in Fig. 4, the molecular resonance and LSPR shift show an additive effect for a reductive Usample between 500 and 625 mV. For an oxidative Usample between 625 and 1000 mV for a given field strength, we find an opposing effect. Hence, let us consider the three representative scenarios of Usample = 1000 mV, Usample = 500 mV and Usample = 625 mV.
At Usample = 1000 mV, the molecular resonance and polarisability are large while the LSPR-extinction related E2 is small (red trace in Fig. 4b). For this reason, at this Usample, the observed nearfield trapping efficiency values are the highest ones at all employed field strengths (Fig. 3b, red traces). On the other hand, the η increase factor between the lowest and highest field strengths is the lowest, namely ca. a factor 39, as the nearfield trapping susceptibility is the smallest, i.e., exhibiting the smallest η slope.
At Usample = 500 mV, the resonant polarisability contribution of Azu is lowest (blue trace in Fig. 4a), and the nearfield trapping efficiency values (Fig. 3b, blue traces) decrease by up to one order of magnitude below the ones observed at Usample = 1000 mV at equivalent power densities. However, E2 is notably high (blue trace in Fig. 4b) and results in a significant nearfield trapping susceptibility observed as an increase factor of ca. 170 in η between the employed laser power density extremes.
At Usample = 625 mV, the resonance contribution is higher than the one at Usample = 500 mV (yellow trace in Fig. 4a), resulting in a larger η (see Fig. 3b, yellow traces). Additionally, E2 reaches its maximum (yellow trace in Fig. 4b). Therefore the difference in increase in η between used laser power density extremes (trapping susceptibility) is the highest one achieved, ca. a factor 192, due to the synergy of molecular resonance and LSPR electrochemical gating effects. In other words, for our experimental conditions, Usample = 625 mV represents a unique scenario where both parameters contribute equally to η. Interestingly, despite this synergistic effect, the net nearfield trapping efficiency, and thus the observed lifetime, is not the highest one observed. This result can be attributed to the fact that within the employed field-strength range, the resonance effect constitutes the more relevant factor affecting the junction stability. According to our data, it is expected that at field strengths larger than 1.72 × 108 V m−1, the substrate potential of Usample = 625 mV results in the highest nearfield trapping efficiency (calculation in Fig. S9, ESI†) compared to the other employed Usample values. Again, control experiments in non-resonance conditions with Zn-based or apo Azu structures would help to further differentiate between the contributions of molecular resonance and LSPR shift, but are beyond the scope of this work.
Conclusions
In summary, we have demonstrated how electrochemical gating greatly improves nearfield trapping in PBJ experiments. While conventional optical tweezers exert barely sufficient radiation force for the manipulation of small metalloproteins such as Azu, EC-PBJ enables trapping of single Azu molecules in a non-invasive way. We have achieved an efficient nearfield trapping at low to mid-power (farfield) densities (0.67 to 9.49 mW μm−2) that manifests itself in an exponential increase in junction lifetime to up to 1.85 s, or a maximum factor 40 compared to laser-OFF conditions. EC gating allows to tune two synergistic effects that affect the overall nearfield trapping efficiency by varying Usample: the resonant character and thus the polarisability of trapped Azu and the LSPR mode of the cavity. The employed excitation wavelength is in resonance with both the LSPR of the nanogap and the contacted target oxidized Azu. With this combined effect, we have achieved an increase in net nearfield trapping efficiency of about three orders of magnitude.Our results have revealed that Au|Azu|Au based junctions exhibit longer lifetimes when switched to the Cu(II) oxidized Azu state than in non-resonant, reduced Cu(I) conditions. Furthermore, the EC gated LSPR mode shifting of the nanogap modulates the nearfield trapping susceptibility that appears to follow the electric field strength as a result of the changes attributed to the electric field enhancement due to the LSPR shift. In the used farfield laser power range, the molecular resonance effect has been observed to dominate over the LSPR mode effect. EC-PBJ constitutes a versatile new trapping tool for BioME because the molecular electronic resonance and the LSPR mode both depend on the properties of the electronic states of the molecule|electrode interface and can thus be controlled in situ. Furthermore, the EC-PBJ approach requires only low laser power to exert a sufficient stabilizing force for the trapping of single metalloprotein molecules for >1.8 s junction lifetime.
The electrochemically gated single-molecule nearfield trapping platform we present opens new pathways for the development of improved molecular sensing and recognition platforms. On the one hand side, EC-PBJ enables bio-molecular junction lifetimes that allow junction characterization on the time scale of seconds. The approach provides a pathway to the capture of molecular processes with slow kinetics, such as, for example, junction conformational changes or variation in molecular orientation. Likewise, longer junction lifetimes permit to efficiently combine electrical and spectroscopic detection, in this way enhancing sensing capabilities. Spectral acquisitions timescales, as required in TERS or similar spectroscopies, often lie in the second time range and are thus significantly higher than the ones in the milliseconds time range offered by current-based molecular platforms. Conveniently, EC-PBJ covers both timescales. To summarize, the longer the interrogation times of the junction that can be achieved, the larger is essentially the amount information that can be gathered on the junction properties. As such, reaching a lifetime of 1.8 s with an Azu junction constitutes a crucial step toward resolving fundamental questions about Azu as functional biomaterial and advancing the rational design of Azu-based biomolecular electronic devices. Furthermore, EC-PBJ can be applied to other biomolecular junctions to characterise the desired target species during second-long timescales, in this way helping to develop future molecular building blocks to be incorporated in bio-mimicking electronic devices.
On the other hand side, EC-PBJ enables molecular recognition based on nearfield trapping and exploiting the electronic resonance character of target molecules. The excitation wavelength may be tuned to electronic absorption transitions of the target species in the nanogap to prolong the single-molecule junction lifetime. The (EC-)PBJ approach provides a versatile route to capture specific (resonant) molecules in heterogeneous media or even specific molecular forms such as redox states or isomers in dynamic systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. C. A. thanks the European Union for a H2020-MSCA-IF-2018 Fellowship (TECh-MoDE, 844668). K. F. D. is grateful for generous funding through the Plus 3 program of the Boehringer Ingelheim Foundation. Open Access funding provided by the Max Planck Society.Notes and references
- C. D. Bostick, S. Mukhopadhyay, I. Pecht, M. Sheves, D. Cahen and D. Lederman, Rep. Prog. Phys., 2018, 81, 026601 Search PubMed.
- T. Q. Ha, I. J. Planje, J. R. White, A. C. Aragonès and I. Díez-Pérez, Curr. Opin. Electrochem., 2021, 28, 100734 Search PubMed.
- S. Nakamaru, F. Scholz, W. E. Ford, Y. Goto and F. Wrochem, Adv. Mater., 2017, 29, 1605924 Search PubMed.
- R. Rinaldi, A. Biasco, G. Maruccio, R. Cingolani, D. Alliata, L. Andolfi, P. Facci, F. D. Rienzo, R. D. Felice and E. Molinari, Adv. Mater., 2002, 14, 1453–1457 Search PubMed.
- J. M. Artés, I. Díez-Pérez and P. Gorostiza, Nano Lett., 2012, 12, 2679–2684 Search PubMed.
- C. Baldacchini, V. Kumar, A. R. Bizzarri and S. Cannistraro, Appl. Phys. Lett., 2015, 106, 183701 Search PubMed.
- V. Climent, Y. Fu, S. Chumillas, B. Maestro, J.-F. Li, A. Kuzume, S. Keller and T. Wandlowski, J. Phys. Chem. C, 2014, 118, 15754–15765 Search PubMed.
- R. C. G. Creasey, A. B. Mostert, T. A. H. Nguyen, B. Virdis, S. Freguia and B. Laycock, Acta Biomater., 2018, 69, 1–30 Search PubMed.
- P. Facci, Biomolecular Electronics: Bioelectronics and the Electrical Control of Biological Systems and Reactions. Chapter 1: Biomolecular Electronics, William Andrew Publishing, Oxford, 2014, pp. 1–17 Search PubMed.
- S. S. Panda, H. E. Katz and J. D. Tovar, Chem. Soc. Rev., 2018, 47, 3640–3658 Search PubMed.
- J. M. Artés, I. Díez-Pérez, F. Sanz, P. Gorostiza, J. M. Artes and I. Diez-Perez, ACS Nano, 2011, 5, 2060–2066 Search PubMed.
- N. Amdursky, L. Sepunaru, S. Raichlin, I. Pecht, M. Sheves and D. Cahen, Adv. Sci., 2015, 2, 1400026 Search PubMed.
- S. Valianti, J.-C. Cuevas and S. S. Skourtis, J. Phys. Chem. C, 2019, 123, 5907–5922 Search PubMed.
- L. Sepunaru, I. Pecht, M. Sheves and D. Cahen, J. Am. Chem. Soc., 2011, 133, 2421–2423 Search PubMed.
- C. Baldacchini, A. R. Bizzarri and S. Cannistraro, Appl. Phys. Lett., 2014, 104, 093702 Search PubMed.
- J. A. Fereiro, G. Porat, T. Bendikov, I. Pecht, M. Sheves and D. Cahen, J. Am. Chem. Soc., 2018, 140, 13317–13326 Search PubMed.
- K. S. Kumar, R. R. Pasula, S. Lim and C. A. Nijhuis, Adv. Mater., 2016, 28, 1824–1830 Search PubMed.
- S. Mukhopadhyay, S. K. Karuppannan, C. Guo, J. A. Fereiro, A. Bergren, V. Mukundan, X. Qiu, O. E. C. Ocampo, X. Chen, R. C. Chiechi, R. McCreery, I. Pecht, M. Sheves, R. R. Pasula, S. Lim, C. A. Nijhuis, A. Vilan and D. Cahen, iScience, 2020, 23(5), 101099 Search PubMed.
- J. M. Artés, M. López-Martínez, I. Díez-Pérez, F. Sanz and P. Gorostiza, Small, 2014, 10, 2537–2541 Search PubMed.
- P. T. Bui, T. Nishino, H. Shiigi and T. Nagaoka, Chem. Commun., 2015, 51, 1666–1669 Search PubMed.
- H. Wu, X. Feng, B. D. Kieviet, K. Zhang, H. J. Zandvliet, G. W. Canters, P. M. Schön and G. J. Vancso, Eur. Polym. J., 2016, 83, 529–537 Search PubMed.
- G. He, J. Li, H. Ci, C. Qi and X. Guo, Angew. Chem., Int. Ed., 2016, 55, 9036–9040 Search PubMed.
- B. Zhang, W. Song, P. Pang, Y. Zhao, P. Zhang, I. Csabai, G. Vattay and S. Lindsay, Nano Futures, 2017, 1, 035002 Search PubMed.
- L. Tang, B. P. Nadappuram, P. Cadinu, Z. Zhao, L. Xue, L. Yi, R. Ren, J. Wang, A. P. Ivanov and J. B. Edel, Nat. Commun., 2021, 12, 913 Search PubMed.
- W. Hong, H. Li, S. X. Liu, Y. Fu, J. Li, V. Kaliginedi, S. Decurtins and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 19425–19431 Search PubMed.
- A. C. Aragonès, N. Darwish, S. Ciampi, F. Sanz, J. J. Gooding and I. Díez-Pérez, Nat. Commun., 2017, 8, 15056 Search PubMed.
- C. R. Peiris, Y. B. Vogel, A. P. Le Brun, A. C. Aragonès, M. L. Coote, I. Díez-Pérez, S. Ciampi and N. Darwish, J. Am. Chem. Soc., 2019, 141, 14788–14797 Search PubMed.
- M. L. Juan, M. Righini and R. Quidant, Nat. Photonics, 2011, 5, 349–356 Search PubMed.
- T. D. Bouloumis and S. Nic Chormaic, Appl. Sci., 2020, 10, 1375 Search PubMed.
- J.-A. Huang, M. Z. Mousavi, Y. Zhao, A. Hubarevich, F. Omeis, G. Giovannini, M. Schütte, D. Garoli and F. De Angelis, Nat. Commun., 2019, 10, 5321 Search PubMed.
- Y. Kitahama, M. Funaoka and Y. Ozaki, J. Phys. Chem. C, 2019, 123, 18001–18006 Search PubMed.
- A. C. Aragonès and K. F. Domke, Cell Rep. Phys. Sci., 2021, 100389 Search PubMed.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91 Search PubMed.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 Search PubMed.
- W. Haiss, R. J. Nichols, H. van Zalinge, S. J. Higgins, D. Bethell and D. J. Schiffrin, Phys. Chem. Chem. Phys., 2004, 6, 4330–4337 Search PubMed.
- J. A. Asar, M. M. Mariscal and E. P. Leiva, Electrochim. Acta, 2009, 54, 2977–2982 Search PubMed.
- M. P. Ruiz, A. C. Aragonès, N. Camarero, J. G. Vilhena, M. Ortega, L. A. Zotti, R. Pérez, J. C. Cuevas, P. Gorostiza and I. Díez-Pérez, J. Am. Chem. Soc., 2017, 139, 15337–15346 Search PubMed.
- C. Romero-Muñiz, M. Ortega, J. G. Vilhena, I. Díez-Pérez, R. Pérez, J. C. Cuevas and L. A. Zotti, J. Phys. Chem. C, 2021, 125, 1693–1702 Search PubMed.
- R. R. Agayan, F. Gittes, R. Kopelman and C. F. Schmidt, Appl. Opt., 2002, 41, 2318–2327 Search PubMed.
- T. Iida and H. Ishihara, Phys. Rev. Lett., 2003, 90, 4 Search PubMed.
- M. A. Osborne, S. Balasubramanian, W. S. Furey and D. Klenerman, J. Phys. Chem. B, 1998, 102, 3160–3167 Search PubMed.
- K. Inaba, K. Imaizumi, K. Katayama, M. Ichimiya, M. Ashida, T. Iida, H. Ishihara and T. Itoh, Phys. Status Solidi B, 2006, 243, 3829–3833 Search PubMed.
- K. C. Toussaint, M. Liu, M. Pelton, J. Pesic, M. J. Guffey, P. Guyot-Sionnest and N. F. Scherer, Opt. Express, 2007, 15, 12017–12029 Search PubMed.
- A. Ohlinger, S. Nedev, A. A. Lutich and J. Feldmann, Nano Lett., 2011, 11, 1770–1774 Search PubMed.
- H. Li, D. Zhou, H. Browne and D. Klenerman, J. Am. Chem. Soc., 2006, 128, 5711–5717 Search PubMed.
- T. Shoji, N. Kitamura and Y. Tsuboi, J. Phys. Chem. C, 2013, 117, 10691–10697 Search PubMed.
- T. Shoji, Y. Mizumoto, H. Ishihara, N. Kitamura, M. Takase, K. Murakoshi and Y. Tsuboi, Jpn. J. Appl. Phys., 2012, 51, 092001 Search PubMed.
- T. J. Thamann, P. Frank, L. J. Willis and T. M. Loehr, Proc. Natl. Acad. Sci. U. S. A., 1982, 79, 6396–6400 Search PubMed.
- S. Kradolfer, E. Lipiec, C. Baldacchini, A. R. Bizzarri, S. Cannistraro and R. Zenobi, ACS Nano, 2017, 11, 12824–12831 Search PubMed.
- A. Szabo, T. Stepanik, D. Wayner and N. Young, Biophys. J., 1983, 41, 233–244 Search PubMed.
- N. Martín Sabanés, L. M. A. Driessen and K. F. Domke, Anal. Chem., 2016, 88, 7108–7114 Search PubMed.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- Q. Chi, J. Zhang, J. U. Nielsen, E. P. Friis, I. Chorkendorff, G. W. Canters, J. E. T. Andersen and J. Ulstrup, J. Am. Chem. Soc., 2000, 122, 4047–4055 Search PubMed.
- C. Novo, A. M. Funston, A. K. Gooding and P. Mulvaney, J. Am. Chem. Soc., 2009, 131, 14664–14666 Search PubMed.
- G. D. Martino, V. A. Turek, C. Tserkezis, A. Lombardi, A. Kuhn and J. J. Baumberg, Faraday Discuss., 2017, 205, 537–545 Search PubMed.
- L. Long, J. Chen, H. Yu and Z.-Y. Li, Photonics Res., 2020, 8, 1573 Search PubMed.
- M. Tsutsui, K. Shoji, M. Taniguchi and T. Kawai, Nano Lett., 2008, 8, 345–349 Search PubMed.
- E. Evans, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 105–128 Search PubMed.
- C. Guo, X. Chen, S.-Y. Ding, D. Mayer, Q. Wang, Z. Zhao, L. Ni, H. Liu, T. Lee, B. Xu and D. Xiang, ACS Nano, 2018, 12, 11229–11235 Search PubMed.
- C. P. Byers, B. S. Hoener, W.-S. Chang, M. Yorulmaz, S. Link and C. F. Landes, J. Phys. Chem. B, 2014, 118, 14047–14055 Search PubMed.
- L. Novotny, R. X. Bian and X. S. Xie, Phys. Rev. Lett., 1997, 79, 645–648 Search PubMed.
- T. Iida and H. Ishihara, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 245319 Search PubMed.
- J. Zhang, Q. Chi, A. M. Kuznetsov, A. G. Hansen, H. Wackerbarth, H. E. M. Christensen, J. E. T. Andersen and J. Ulstrup, J. Phys. Chem. B, 2002, 106, 1131–1152 Search PubMed.
- X. Fan, W. Zheng and D. J. Singh, Light: Sci. Appl., 2014, 3, 179 Search PubMed.
- S. S. E. Collins, X. Wei, T. G. McKenzie, A. M. Funston and P. Mulvaney, Nano Lett., 2016, 16, 6863–6869 Search PubMed.
- A. D. McFarland, M. A. Young, J. A. Dieringer and R. P. Van Duyne, J. Phys. Chem. B, 2005, 109, 11279–11285 Search PubMed.
- G. C. Schatz and R. P. V. Duyne, Handbook of Vibrational Spectroscopy, John Wiley & Sons, Ltd, New York, 2002, pp. 759–774 Search PubMed.
- P. Mestres, J. Berthelot, S. S. Acimovic and R. Quidant, Light: Sci. Appl., 2016, 5, 16092 Search PubMed.
- H. Xu and M. Käll, Phys. Rev. Lett., 2002, 89, 246802 Search PubMed.
- M. L. Juan, R. Gordon, Y. Pang, F. Eftekhari and R. Quidant, Nat. Phys., 2009, 5, 915–919 Search PubMed.
- C. Zhan, G. Wang, J. Yi, J.-Y. Wei, Z.-H. Li, Z.-B. Chen, J. Shi, Y. Yang, W. Hong and Z.-Q. Tian, Matter, 2020, 3, 1350–1360 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc01535d |
| This journal is © The Royal Society of Chemistry 2021 |