Open Access Article
Open Access ArticlePitfalls on evaluating pair exchange interactions for modelling molecule-based magnetism
Maria
Fumanal
 a,
Joaquim
Jornet-Somoza
a,
Joaquim
Jornet-Somoza
 abc,
Sergi
Vela
abc,
Sergi
Vela
 a,
Juan J.
Novoa
a,
Jordi
Ribas-Arino
a,
Juan J.
Novoa
a,
Jordi
Ribas-Arino
 *a and
Mercè
Deumal
*a and
Mercè
Deumal
 *a
*a
aDept Ciència de Materials i Química Física and IQTCUB, Facultat de Química, Universitat de Barcelona, Martí i Franquès 1, E-08028 Barcelona, Spain. E-mail: j.ribas@ub.edu; merce.deumal@ub.edu
bIZO-SGI SGiker, Euskal Herriko Unibertsitatea (UPV/EHU), Joxe Mari Korta Center, Av. Tolosa 72, 20018 Donostia, Euskadi, Spain
cThe Max Planck Institute for the Structure and Dynamics of Matter (MPSD), Bldg. 99 (CFEL) Luruper Chaussee 149, 22761 Hamburg, Germany
First published on 5th July 2021
Abstract
Molecule-based magnetism is a solid-state property that results from the microscopic interaction between magnetic centres or radicals. The observed magnetic response is due to unpaired electrons whose coupling leads to a particular magnetic topology. Therefore, to understand the magnetic response of a given molecule-based magnet and reproduce the available experimental magnetic properties by means of statistical mechanics, one has to be able to determine the value of the JAB magnetic exchange coupling between radicals. The calculation of JAB is thus a key point for modelling molecule-based magnetism. In this Perspectives article, we will build upon our experience in modelling molecular magnetism to point out some pitfalls on evaluating JAB couplings. Special attention must be paid to the cluster models used to evaluate JAB, which should account for cooperative effects among JAB interactions and also consider the environment (counterions, hydrogen bonding) of the two radicals whose interaction has to be evaluated. It will be also necessary to assess whether a DFT-based or a wavefunction-based method is best to study a given radical. Finally, in addition to model and method, the JAB couplings have to be able to adapt to changes in the magnetic topology due to thermal fluctuations. Therefore, it is most important to appraise in which systems molecular dynamics simulations would be required. Given the large number of issues one must tackle when choosing the correct model and method to evaluate JAB interactions for modelling magnetic properties in molecule-based materials, the “human factor” is a must to cross-examine and challenge computations before trusting any result.
1. Introduction
In molecule-based magnetic materials, the microscopic interactions between magnetic centres or radicals, whose unpaired electrons couple leading to a specific magnetic topology, play a key role in defining their macroscopic magnetic properties.1 There are two main strategies to reproduce experimental magnetic properties (e.g. magnetic susceptibility, heat capacity, magnetization) by means of statistical mechanics2 depending on whether the electronic structure is explicitly considered or not. The latter approach aims at providing a numerical magnetic response for a given molecular material. A very successful approach,3a which does not explicitly account for the crystal geometry (except in a parametric form3), is based on the use of a generalized spin Hamiltonian. Alternatively, the electronic structure-based strategy targets on capturing the microscopic complexity of the molecular material to understand, as well as reproduce, the experimental magnetic data.4 As computational chemists, we seek modelling molecule-based materials as a tool to rationalize their physical properties. Accordingly, within the framework of molecular magnetism, one has to be able to evaluate the magnitude of the JAB magnetic exchange coupling between radicals. The calculation of the JAB radical⋯radical interaction is thus one of the key points for modelling magnetism, and can be a demanding task if the number of JAB couplings is large. At this point, anyone working in the field of molecular magnetism has wished there was a fully automated procedure to determine the magnetic response of a given molecule-based compound in a black-box fashion. Such automated code would most probably resort to the simplest model (dimer) and the least expensive method (DFT broken symmetry level)5 to evaluate all JAB coupling interactions.5b,c,6 Also the magnetic unit cell would perforce have to be found in an automated way. Model, method and magnetic unit cell would have a difficult validation since, by definition, there is no diagnosis to check whether the results obtained from a “black-box procedure” are correct or not. We must acknowledge that the selection of the right model and method to compute the JAB magnetic coupling is sometimes very challenging. Therefore, due to the large number of issues one must tackle, the automatized selection of the model and method can be an extremely difficult task. The take-home message of this paper is not that its design is not feasible, but that there must be some careful thought behind it. This Perspective paper aims at reflecting on how molecule-based magnetism is modelled, which pitfalls could be encountered, and how to detect and prevent them.Usually, the working strategy that we follow to calculate macroscopic magnetic properties from microscopic magnetic interactions among radicals uses only the knowledge of X-ray crystallographic data. A four-step procedure7 can be followed. First, the crystal packing is analysed to select pairs of A, B radicals that might be magnetically important, in terms of radical⋯radical distances. Secondly, once all those A⋯B dimers that are univocally defined within the crystal have been identified, the microscopic JAB radical⋯radical magnetic interactions are computed using quantum chemistry methods. Depending on the system, one can resort to a variety of either Density Functional Theory DFT5 or wavefunction-based (e.g. CASSCF, RASSCF, DDCI)8 methods. Also depending on the system, one can resort to a variety of different schemes to obtain the numerical value of JAB magnetic coupling: localized vs. delocalized, projected vs. unprojected, etc.5,6 Due to the molecular nature of the magnetic materials we are interested to study, the JAB magnetic coupling between radicals is of short-range, which allows evaluating the JAB interactions using truncated cluster models. The simplest dimer model works in most of the cases. For a pair of S = 1/2 radicals, the JAB microscopic exchange interaction is calculated as the energy difference between open-shell singlet and triplet states.5 However, a dimer model is not always the best option to compute JAB. The enlargement of the size of the cluster model (e.g. using tetramer, decamer models) is sometimes a must to account for cooperative effects among JAB interactions not included in a radical–radical pair calculation (i.e. dimer model).9 The selection of the correct model must also consider the environment of the two radicals whose interaction has to be evaluated, namely counterions,10 hydrogen bonding,11etc. To sum up, irrespective of the model, within this approach, the JAB interactions are evaluated at the fixed relative positions (an X-ray resolved structure or, alternatively, an optimized structure12) of the selected pairs of radicals within the crystal. Since the thermal oscillations of the spin carrying units around their equilibrium positions are ignored in this type of analysis, it can be stated that the standard approach is based on a static perspective. However, for materials with dominant exchange interactions propagating through π–π labile networks,13 one might have to resort to a dynamic perspective, in which thermal vibrations are explicitly considered.14 Therefore, in order to get a physically correct interpretation of the magnetic response of a given molecular material one has to be able to determine whether the static perspective will suffice or, on the contrary, molecular dynamics simulations would be required.
Let us now digress to comment on the possibility of using a periodic approach rather than a cluster model to evaluate the JAB magnetic coupling between radicals. This alternative might appeal as being an easier option since unit cells with different spin settings could be used to calculate the JAB magnetic coupling interactions between different spin centres without having to worry about the representation of the environment. Yet performing periodic computations on the crystal structure is comparatively more difficult for two main reasons. First, the number of radicals in the unit cell (Z) can be large, which would require the evaluation of a large number of spin states that, in most cases, will become intractable (e.g. a fairly small Z = 4 in ref. 9b generates over 14 potential JAB magnetic interactions that need to be assessed). Moreover, in most cases those spin states are not the ground state for a given spin multiplicity and, thus, the definition and – especially – the preservation of the desired spin configuration represents a challenge for solid state codes. Second, evaluation of JAB interactions with accurate methods in solid state has an extremely large computational cost and, in many cases, both non-hybrid and hybrid DFT functionals accessible for periodic computations may have difficulties in capturing the true electronic nature of the radicals within the crystal. For these reasons, cluster models offer great advantages to calculate JAB magnetic interactions in molecular materials at high level accurate methods. Still, the choice of the actual cluster model (dimer, tetramer, etc.) needs to be validated to ensure the reliability of the JAB values.
Once all JAB's have been evaluated, the magnetic topology can be next defined in terms of all computed non-negligible JAB magnetic coupling interactions. From the magnetic topology, we select a representative magnetic model, which will enable us to consider the unpaired electrons being completely coupled antiferromagnetically (AFM), completely coupled ferromagnetically (FM), or in any other of the many states obtained as a result of solving the secular equation problem together with the energy spectra and corresponding spin quantum numbers. It is important to stress that the definition of the magnetic model is crucial since the full diagonalisation15 will be done in the space expanded by this model. One could think that the selection of the magnetic model is a question of computer power and should not be difficult to automatically build a model Hamiltonian based on the hierarchy of the JAB magnetic couplings. However, the choice of the most appropriate magnetic model is inherently difficult in molecule-based magnets as they are usually characterised by many JAB magnetic couplings. As a consequence, convergence with respect to the model Hamiltonians size is required, which complicates its automatic selection.
Finally, the resulting energy spectra and spin quantum numbers are used in the appropriate statistical mechanics expressions to simulate the macroscopic magnetic properties.2 Here we must highlight that all simulations are always compared to the available experimental data for validation purposes. Therefore, one can calculate magnetic susceptibility, heat capacity, or magnetization, depending on the available experimental data.
In summary, the working strategy above outlined is first-principles (FP) because the JAB magnetic interactions are computed using DFT or other wavefunction-based techniques from crystallographic data, and is bottom-up (BU) because we use microscopic data to calculate macroscopic properties. This First-Principles Bottom-Up FPBU7 working strategy has been applied successfully to compute the magnetic response of a variety of prototypical molecule-based magnets of different magnetic dimensionality. However, it is not just the magnetic response that is targeted, since we have been able to understand and rationalize the magnetic behaviour depending on a range of different situations such as influence of temperature,16 effect of the Madelung field,10 effect of the crystal defects,17 effect of the ligands,11,18 magnetic dimensionality,19 bistability20…. At this point, one has to realize that a too simple automated procedure would imply applying too many unsurveyed restrictions: dimer model and unrestricted DFT to compute energies and, in turn, JAB; estimation of the magnetic unit cell upon quantitative criteria; etc. In fact, the only attempt we have come across which automatically handle all these issues is applied to neutral organic-based 1D magnets.4d The choice of these materials greatly simplifies calculations. Yet it would most probably face serious challenges when applied to more complex materials (as the examples we discuss below). Therefore, however appraising, black-box and modelling magnetism do not necessarily hold hands. Basically, a black-box procedure based on the static evaluation of JAB's using a dimer model with unrestricted DFT limits predictability and might only be useful for description purposes. Description purposes are obviously important. However, as computational chemists, we usually have more questions than answers, and the questions usually come out unexpectedly. Therefore using a too simple automated code is thoughtless. In fact, we will next proceed to discuss issues we must consider in terms of models and in terms of methods in order to evaluate the radical⋯radical magnetic interactions and, in the long run, simulate magnetism.
First, we will show that the dimer model cannot be taken for granted to evaluate the magnetic JAB interaction between two radicals. In fact, the size of the cluster model to calculate JAB must be assessed in order to be certain about it. Note that a wrong value of JAB coupling will lead to the wrong magnetic topology which, in turn will give rise to the wrong minimal magnetic model whose eigenvalues have to be used to simulate the relevant magnetic data. This is precisely the case of Cu2(1,4-diazacycloheptane)2Cl4 (CuHpCl in Fig. 1a):9b,21 the use of the wrong model to evaluate JAB results in a spin-ladder magnetic topology instead of a 3D network of interconnected squared-plaquettes. Secondly, we will address the choice of the right method to calculate JAB. The calculation of a given JAB involves the evaluation of the energy of, at least, two states. This energy evaluation can be done by means of either DFT-based or wavefunction-based methods. Since DFT calculations are less demanding, in terms of resources and computational time, it is considered as the default method to be used to calculate the energy of the states involved. Although DFT is known to provide acceptable values for JAB coupling in many systems,9–11,14,16–20 we will exemplify which are the effects of choosing the wrong method with the phenylsemiquinone-bridged bisdithiazolyl (PhBBO in Fig. 1b) compound.22,23 Finally, we will address the use of molecular dynamics simulations when studying bistable compounds whose radicals pack forming π-stacks along a given crystallographic direction and, thus, thermal fluctuations might have an impact on the magnetic topology. We have encountered that JAB couplings have to be able to adapt to changes due to intermolecular vibrations as in the case of 1,3,5-trithia-2,4,6-triazapentalenyl (TTTA in Fig. 1c),14a,24 which undergoes phase transition between a low temperature LT and a high temperature HT phases.
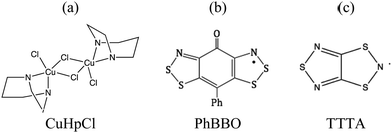 | ||
| Fig. 1 Chemical formula for (a) Cu2(1,4-diazacycloheptane)2Cl4, CuHpCl, (b) phenylsemiquinone-bridged bisdithiazolyl, PhBBO, and (c) 1,3,5-trithia-2,4,6-triazapentalenyl, TTTA. | ||
2. Methodology
The standard static First-Principles Bottom-Up (FPBU) procedure is applied to study the alleged magnetically isolated cuprate spin-ladder CuHpCl system, and to rationalize the magnetism of the purely organic PhBBO semiquinone-bridged bisdithiazolyl compound. Yet it is found that the study of the LT and HT phases of TTTA requires a dynamic perspective. Hereafter both working strategies will be described.The first-principles bottom-up FPBU7 procedure implies four steps, as summarized herein. First, after inspection of the crystal structure, the symmetry-unique radical pairs that are likely to be magnetically relevant are identified (using a radical⋯radical distance cutoff value between spin-carrying moieties). Second, their magnetic exchange interactions, JAB, are computed and the magnetic topology of the crystal (i.e., the network of connectivity defined by all relevant JAB values) is defined. When necessary, wavefunction-based multireference CASSCF/PT2 and RASSCF/PT2 energies (ELS, EHS)8,25 using a DZV basis set26 are obtained from Molcas 7.6.27 Otherwise energies at UB3LYP28 or range-corrected CAM-B3LYP29 level using 6-31+G(d) or 6-311++G(d,p) basis sets30 are computed using Gaussian0931 for the dimer model and Orca 3.032 package for the tetramer model. From the general Heisenberg Hamiltonian for a pair of S = 1/2 spin centres,
| Ĥ = −2JABŜAŜB, | (1) |
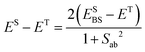 | (2) |
| JAB = ESBS − ET. | (3) |
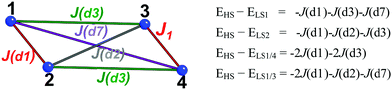 | ||
| Fig. 2 Tetramer model and set of equations used to calculate J(di) magnetic interactions between CuHpCl radicals (numbered 1 to 4). HS/LS stands for high spin and low spin, respectively. | ||
Third, the Heisenberg Hamiltonian is applied to a model space (i.e. a subset of the magnetic topology), which is designed in such a way that, ideally, the resulting set of eigenvalues reproduces those that result from the application of the Heisenberg Hamiltonian to the full infinite crystal. Finally, the resulting energies and total spin numbers are introduced into the proper statistical mechanics expressions to calculate the macroscopic properties of the system, such as the magnetic susceptibility χT(T), heat capacity Cp(T) and magnetization M(H).2
The computational scheme adopted for the study of the interplay between thermal fluctuations and magnetism in TTTA consists of three steps: (i) ab initio molecular dynamics (AIMD) simulations33 for both LT and HT phases of TTTA; (ii) computation of JAB values between pairs of radicals for a large number of frames along the AIMD trajectories; and lastly, (iii) calculation of the vibrationally-averaged magnetic susceptibility ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) vib on the basis of full diagonalizations of the Heisenberg Hamiltonian built from the previously evaluated JAB values. Accordingly, first of all, AIMD simulations33 are performed at 300 K for both the LT and HT phases of TTTA (ca. 10 ps, time step 4 a.u.) as implemented in the CPMD package.34 Note the temperature is chosen to be 300 K because TTTA is bistable at that temperature and there is crystallographic data available for both LT and HT phases. Supercells include 32 TTTA molecules (8 stacks of 4 radicals each). DFT calculations are carried out at PBE level35 within the spin unrestricted formalism (broken symmetry singlet MS = 0 state) using plane wave pseudopotentials36 expanded at a kinetic energy cutoff of 25 Ry, together with Vanderbilt ultrasoft pseudopotentials,37 a fictitious mass for the orbitals of 400 a.u., and Γ-point sampling of the Brillouin zone. The semiempirical dispersion potential introduced by Grimme,38 in its DFT-D2 parameterization is also considered. In addition, the AIMD simulations are performed in the canonical (or NVT) ensemble using Nosé–Hoover chain thermostats.39 Periodic boundary conditions in all three directions are imposed in all AIMD simulations. Pairs of radicals are then excised from the supercell of 32 radicals after AIMD simulations every 0.97 fs. Calculations of JAB at UB3LYP/6-31+G(d)28,30 level are conducted using dimer models: approximately 20
vib on the basis of full diagonalizations of the Heisenberg Hamiltonian built from the previously evaluated JAB values. Accordingly, first of all, AIMD simulations33 are performed at 300 K for both the LT and HT phases of TTTA (ca. 10 ps, time step 4 a.u.) as implemented in the CPMD package.34 Note the temperature is chosen to be 300 K because TTTA is bistable at that temperature and there is crystallographic data available for both LT and HT phases. Supercells include 32 TTTA molecules (8 stacks of 4 radicals each). DFT calculations are carried out at PBE level35 within the spin unrestricted formalism (broken symmetry singlet MS = 0 state) using plane wave pseudopotentials36 expanded at a kinetic energy cutoff of 25 Ry, together with Vanderbilt ultrasoft pseudopotentials,37 a fictitious mass for the orbitals of 400 a.u., and Γ-point sampling of the Brillouin zone. The semiempirical dispersion potential introduced by Grimme,38 in its DFT-D2 parameterization is also considered. In addition, the AIMD simulations are performed in the canonical (or NVT) ensemble using Nosé–Hoover chain thermostats.39 Periodic boundary conditions in all three directions are imposed in all AIMD simulations. Pairs of radicals are then excised from the supercell of 32 radicals after AIMD simulations every 0.97 fs. Calculations of JAB at UB3LYP/6-31+G(d)28,30 level are conducted using dimer models: approximately 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 60
000 and 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 JAB evaluations are carried out for the LT and HT polymorphs, respectively. Finally, the vibrationally-averaged magnetic susceptibility
000 JAB evaluations are carried out for the LT and HT polymorphs, respectively. Finally, the vibrationally-averaged magnetic susceptibility ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) vib for the HT phase at 300 K is computed by averaging the χ value over the whole set of configurations that are used to determine the time-evolution of the JAB values between adjacent radicals within a stack. That is to say, the χ value is computed for an overall of ca. 10
vib for the HT phase at 300 K is computed by averaging the χ value over the whole set of configurations that are used to determine the time-evolution of the JAB values between adjacent radicals within a stack. That is to say, the χ value is computed for an overall of ca. 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 different molecular configurations (each configuration was collected every 0.97 fs throughout the AIMD simulations) and, then, averaged. The resulting
000 different molecular configurations (each configuration was collected every 0.97 fs throughout the AIMD simulations) and, then, averaged. The resulting ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) vib at 300 K14a is last compared to the χ value obtained from a static analysis20 and from experiment.24
vib at 300 K14a is last compared to the χ value obtained from a static analysis20 and from experiment.24
3. Results and discussion
In order to stress the importance of the models and methods used to evaluate the JAB magnetic coupling between radicals, three examples will be reported in which a too simple black-box study (based on static DFT calculations performed on dimers) would have prevented us from capturing the true nature of the magnetism of those three different molecule-based magnets.3.1. On the size of the cluster model to evaluate JAB magnetic coupling between radicals
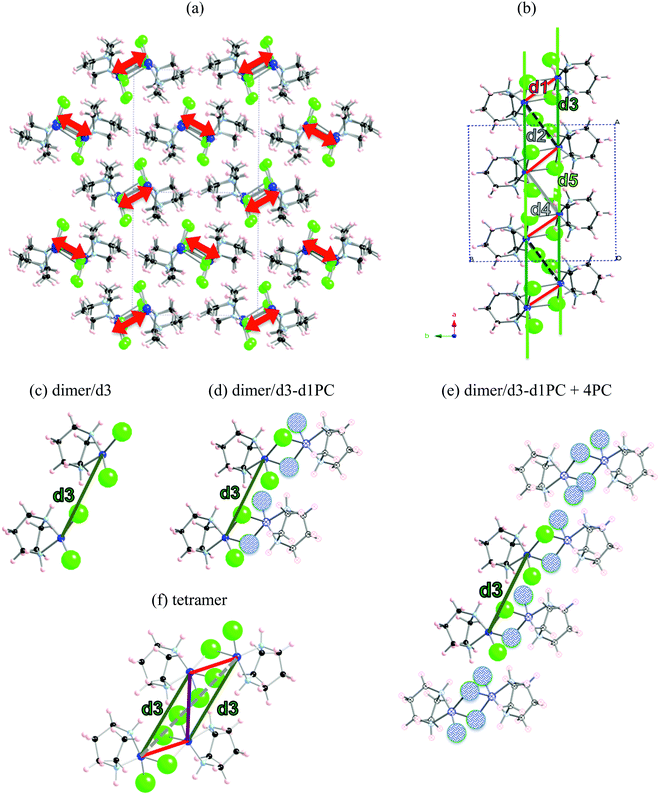
The first example is the Cu2(1,4-diazacycloheptane)2Cl4 molecular transition metal AFM complex (in short CuHpCl, see Fig. 1a). Since it was synthetized in 1997,21 CuHpCl has been the prototypical compound to quote when a magnetically isolated spin-ladder system was required due to its crystal packing consisting in well-separated ladder arrangements of copper atoms (see Fig. 3a). Therefore, from direct crystal observation, the magnetic topology consists of (apparently) non-connected spin-ladders with uniform rails (see Fig. 3b). Interestingly there is a large variety of experimental data, and therefore its study is very appealing. The overall AFM behaviour of CuHpCl has been characterized by measures of magnetic susceptibility, heat capacity, magnetisation, spin gap, inelastic neutron scattering, etc. Although the magnetic topology appears to be clear, according to literature, the fittings of experimental magnetic susceptibility data to different ladder models were not conclusive.40 It thus follows that this copper derivative is more challenging than anticipated, as it must have many competing microscopic magnetic JAB interactions. The alleged spin ladder magnetic topology of CuHpCl has been a long lasting issue.For CuHpCl, all possible intra-ladder nearest-neighbour pairs of radicals were selected, namely d1, d2, d4 as rungs and d3, d5 as rails (see Fig. 3b). Once selected, all five corresponding JAB magnetic couplings were evaluated using a dimer model. The only magnetically significant radical pairs were d1 (rung), and d3, d5 (rails) (see Table 1). Accordingly, the magnetic topology could be ascribed to consist of spin-ladders. Strikingly, the JAB magnetic interaction for d3 and d5 (the rail interactions) has opposite sign. This magnetic behaviour is apparently at odds with their geometry, which would suggest that the spin-ladder should have uniform rails. Therefore, to be certain about the numerical value of JAB for d3 and d5 pairs of radicals, the importance of the surrounding radicals was assessed by using different size cluster models with or without point charges (PC)41 representing the environment of the radicals whose magnetic strength was evaluated. For instance, regarding d3, we evaluated J(d3) using a dimer with its first nearest-neighbour replaced by point charges (namely dimer/d3-d1PC), using the previous model embedded in the point charges of its second nearest neighbour radicals (namely, [dimer/d3-d1PC]-4PC), and using a tetramer model (see Fig. 3c–f). The results show that with a tetramer model both rail interactions are AFM but not uniform at all (see Table 1). It is thus exceedingly important to stress that if the environment is not well described the coupling interactions are meaningless. For CuHpCl, it is also fundamental to realize that for a good description of each Cu monomer one has to account explicitly for the d1 pair, which becomes the magnetic building block of this compound and corresponds to a ferromagnetic FM interaction (see Fig. 4a in red, and Table 2). Each two of these dinuclear FM building blocks are then connected antiferromagnetically by d5 pairs of radicals (see Fig. 4a in green). It thus follows that the final 3D magnetic topology results from weaker AFM interactions (see Fig. 4a in orange; Fig. 4b shows a global view). Notice that the remaining non-negligible J(di) interactions are one order of magnitude smaller than d1, d5, d12 and d14 (see Table 2). Therefore, these magnetic couplings will not be important for simulation purposes. The resulting magnetic topology can be pictured as a 3D network of interacting squared plaquette magnetic building blocks. The simulation of the χ(T) magnetic susceptibility using JAB magnetic interactions extracted from dimer and tetramer models further supports the failure of the dimer model since the numerical error involved in χ(T) when using the JAB calculated at dimer level is larger than 200% compared to experiment, irrespective of the magnetic model used being an isolated spin-ladder or a 3D model of interacting spin-ladders (see full symbols in Fig. 4c). Yet the simulation using a 3D magnetic model of interacting plaquettes parameterized with JAB's obtained from a 4-radical tetramer cluster model certainly agrees with the experimental data (see empty symbols in Fig. 4c). We can thus safely conclude that for CuHpCl the dimer model fails to evaluate JAB magnetic couplings. Further we can also come to the conclusion that the resulting 3D magnetic topology is by far more complex than the alleged spin-ladder hinted from direct observation of the crystal packing (compare Fig. 3b and 4b).9b
| Model | J(d1) | J(d3) | J(d5) |
|---|---|---|---|
| Dimer | +3.13 | +2.11 | −3.12 |
| [dimer/di-d1PC] | +3.13 | +0.08 | −4.31 |
| [dimer/di-d1PC] – 4PC | +2.02 | +0.28 | −3.68 |
| Tetramer | +2.30 | −0.37 | −3.88 |
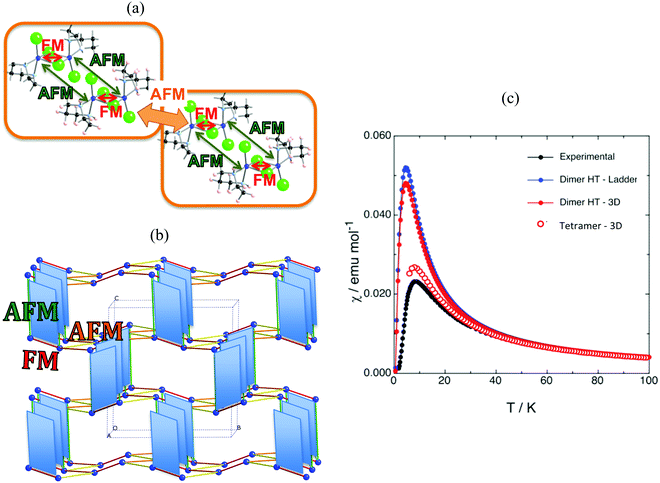 | ||
| Fig. 4 (a) Schematic representation of two interacting squared-plaquette magnetic motifs. (b) Magnetic topology of CuHpCl, where only copper atoms are represented. Colour code: intra-plaquette AFM J(d5) green, and FM J(d1) red; inter-plaquettes AFM J(d12) orange and AFM J(d14) yellow. (c) Magnetic susceptibility curves for (i) JAB values obtained with the dimer approach using one isolated spin-ladder magnetic model (full blue circles) and a 3D magnetic model consisting of three interacting ladder models (full red circles), and (ii) JAB values obtained by the tetramer approach using a 3D magnetic model that includes four interacting plaquette-based magnetic building blocks (empty red circles). Note that experimental data is given for comparison purposes (full black circles).21 | ||
| J(di)/“intra” | J(d1) | J(d3) | J(d5) |
| +2.30 | −0.37 | −3.88 |
| J(di)/“inter” | J(d6) | J(d7) | J(d10) | J(d11) | J(d12) | J(d14) |
| −0.29 | −0.12 | +0.22 | −0.31 | −1.05 | −1.38 |
3.2. Assessing the adequacy of the method to evaluate JAB magnetic coupling between radicals
The main objection in the CuHpCl case laid on the size of the dimer model, i.e. the dimer model was too small to evaluate correctly the JAB microscopic interaction between two radicals. Changing gear, we will focus on the methods rather than on the models to evaluate JAB magnetic coupling between radicals. The choice of the right method is also crucial and has to be assessed while studying the molecule-based material of interest. We would like to mention that CuHpCl was studied at UB3LYP/6-31+G(d) level,28,30 which our experience grants as appropriate for a large variety of systems.9–11,14,16–20 We will now resort to the PhBBO magnet22 that belongs to the purely organic semiquinone-bridged bisdithiazolyl family of compounds (see Fig. 1b). In short, it has a 1D electronic structure due to the presence of π-stack motifs and paucity of close inter-column radical⋯radical contacts (see Fig. 5a). The experimental magnetic susceptibility χT(T) data suggests paramagnetic behaviour, with strong local FM interactions (see black line in Fig. 5c). This data was fitted to the Baker model for Heisenberg 1D FM chain of S = 1/2 centers resulting in J = +29.5 cm−1 and a mean field parameter zJ′ = −2.5 cm−1. PhBBO was also found to exhibit a phase transition at 4.5 K.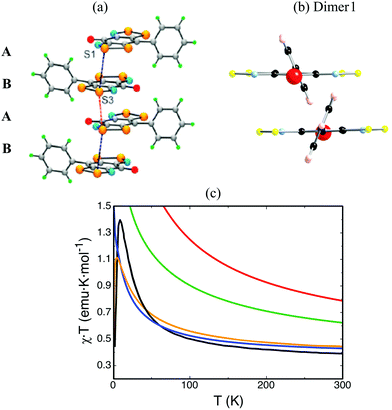 | ||
| Fig. 5 (a) ab-View of the alternating ABAB π-stacks of PhBBO with intrastacks S3⋯S1 contacts d1 = 3.68 Å (in black) and d2 = 3.81 Å (in red) along the a-axis (π-stacking axis). (b) ac-View of Dimer1 along the a-axis (π-stacking axis). (c) Magnetic susceptibility as a function of temperature using JAB calculated at unrestricted B3LYP (in red), CAM-B3LYP (in green), CASSCF(14,14) (in blue) and RASSCF(38,2,2;16,6,4) (in orange). Note that the line in black corresponds to experimental data.22 | ||
In this case, DFT-based methods (such as unrestricted B3LYP28 or range-corrected CAM-B3LYP29) provide a good description of the spin density of an isolated radical (see monomer in Table 3). However, using a dimer model to evaluate the magnetic interaction between two radicals, DFT-based methods are able to correctly describe the spin density for the triplet state but fail to describe the open-shell singlet state (see Dimer1 in Fig. 5b and Table 3 for spin density). As a result, the FM interaction that we want to evaluate is overestimated at DFT level (+343.5 cm−1 at UB3LYP, and +193.3 cm−1 at CAM-B3LYP, see Table 4). We must then resort to wavefunction-based methods (such as CASSCF and RASSCF) in order to correctly describe the radicals spin density and, in turn, compute adequately the JAB coupling interaction between them (see Tables 3 and 4). The JAB magnetic interaction results to be +34.6 cm−1 at CASSCF(14,14) and 49.7 cm−1 at RASSCF(38,2,2;16,6,4) levels. Calculations at CASPT2 level are helpful to assess that dynamic correlation does not necessarily need to be considered to adequately evaluate JAB magnetic interactions (see Table 4). The magnetic susceptibility is then calculated at all levels of theory. Clearly, unrestricted both B3LYP and CAM-B3LYP overestimate the value of χT at any given temperature (red and green lines in Fig. 5c). Contrarily, at CASSCF(14,14) level, χT is underestimated (blue line in Fig. 5c). One has to resort to RASSCF(38,2,2;16,6,4) to reproduce correctly the experimental data (orange line in Fig. 5c). For PhBBO, it can thus be concluded that DFT methodology dramatically fails.23 Instead wavefunction-based methods are here required. The reason for the DFT failure turns out to be simple. It is because semiquinone-bridged bisdithiazolyl compounds are multireference systems due to the presence of low-lying open-shell states (what is called multi-orbital effect by experimentalists). This is thus the second example in which a black-box study based on standard DFT methods would have led to an incorrect interpretation, and to quantitatively-wrong values for the JAB pair interactions of PhBBO.
| Method | System | Spin state | Spin density | |
|---|---|---|---|---|
| N1 | N2 | |||
| B3LYP | Monomer | Doublet | +0.27 | +0.14 |
| Dimer1 | Triplet | +0.27 (+0.27) | +0.13 (+0.13) | |
| J(Dimer1) = +343.5 cm−1 | Singlet BS | +0.27 (−0.26) | +0.06 (−0.05) | |
| CAM-B3LYP | Monomer | Doublet | +0.32 | +0.21 |
| Dimer1 | Triplet | +0.30 (+0.30) | +0.21 (+0.21) | |
| J(Dimer1) = +193.3 cm−1 | Singlet BS | +0.25 (−0.24) | +0.16 (−0.16) | |
| Basis | Method | J AB/cm−1 | Spin density | |
|---|---|---|---|---|
| N1 | N2 | |||
| 6-311++g(d,p) | B3LYP | 343.5 | +0.27 | +0.13 |
| CAM-B3LYP | 193.3 | +0.30 | +0.21 | |
| DZV | CASSCF(14,14) | 34.6 | +0.30 | +0.15 |
| RASSCF(38,2,2;16,6,4) | 49.7 | +0.29 | +0.15 | |
| RASPT2 | 48.7 | |||
3.3. Addressing thermal fluctuations to evaluate JAB magnetic coupling between radicals
Finally, in addition to model and method, the JAB couplings have to be able to adapt to changes in the magnetic topology due to thermal fluctuations. We have encountered that molecular dynamics simulations are necessary when studying bistable compounds whose radicals pack forming π-stacks along a given crystallographic direction, as in the case of 1,3,5-trithia-2,4,6-triazapentalenyl (TTTA, see Fig. 1c).14 Note that bistability is the ability of a material to present two stable phases that can both exist within a given range of temperatures but above and below that range only one or the other phase exists. TTTA was chosen because the neutral radical TTTA is the most studied molecule among dithiazolyl DTA radicals. Therefore, TTTA has become a prototypical molecule-based bistable material whose low temperature (LT, see Fig. 6a) phase is diamagnetic and high temperature (HT, see Fig. 6b) phase is paramagnetic.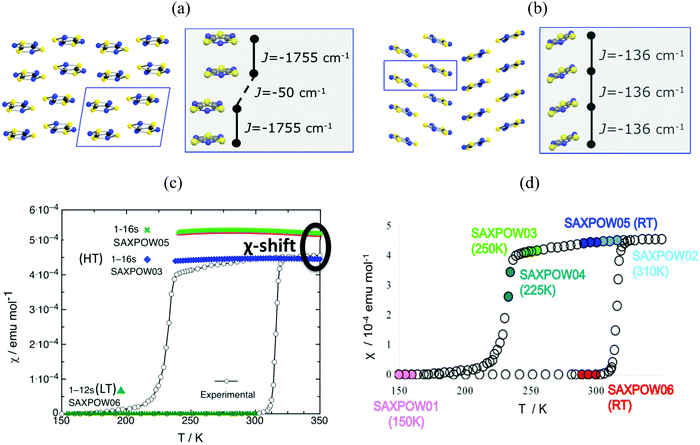 | ||
Fig. 6 Packing of the monoclinic HT (SAXPOW05) and triclinic LT (SAXPOW06) crystal structures recorded at room temperature (RT): π stacks in the (a) LT (viewed along c) and (b) HT (viewed along b) phases. See inset values of JAB magnetic couplings for (a) eclipsed and slipped pairs and (b) regular π-stacking pair. (c) Magnetic susceptibility χ(T) for LT and HT phases using structures determined at RT SAXPOW06 ( ) and 250 K SAXPOW03 ( ) and 250 K SAXPOW03 ( )/RT SAXPOW05 ( )/RT SAXPOW05 ( ) employing a 16-radical magnetic model. The experimental curve showing the thermal hysteresis present in the range 210–320 K, where HT and LT structures can both exist, is also given in black. All calculations were done at UB3LYP/Aug-cc-pVTZ level. (d) χ(T) plot with the approximate positions on hysteresis loop of each of the six published X-ray data sets of TTTA crystal (LT: recorded at 150 K and RT, SAXPOW01 and 06; HT: recorded at 225 K, 250 K, RT, and 310 K, SAXPOW04, -03, -05 and -02).24 Refcodes SAXPOW01-06 given by the Cambridge Crystallographic Data Base CCDC.42 ) employing a 16-radical magnetic model. The experimental curve showing the thermal hysteresis present in the range 210–320 K, where HT and LT structures can both exist, is also given in black. All calculations were done at UB3LYP/Aug-cc-pVTZ level. (d) χ(T) plot with the approximate positions on hysteresis loop of each of the six published X-ray data sets of TTTA crystal (LT: recorded at 150 K and RT, SAXPOW01 and 06; HT: recorded at 225 K, 250 K, RT, and 310 K, SAXPOW04, -03, -05 and -02).24 Refcodes SAXPOW01-06 given by the Cambridge Crystallographic Data Base CCDC.42 | ||
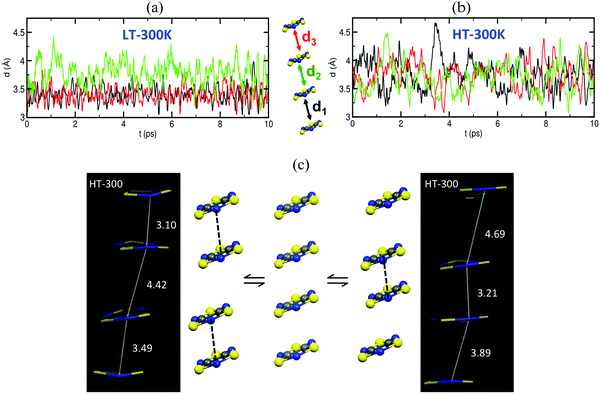
Analysis of the crystallographic data at room temperature shows that the radicals pack forming π-stacks of eclipsed and slipped dimers in the LT phase (Fig. 6a) and regular π-stacks in the HT phase (Fig. 6b). The evaluation of JAB magnetic coupling between radicals indicates that at LT the magnetic topology consists in AFM chains of strongly AFM dimers (−1755 cm−1, see Table 5). In fact, it is because dimers have such strong AFM coupling that the LT phase is magnetically silent (see SAXPOW06 data in Fig. 6c). Contrarily, the HT phase shows a regular AFM chain topology (−135.6 cm−1, see Table 5), which results in a paramagnetic response (see SAXPOW05 data in Fig. 6c). Since there are X-ray data at 4 different temperatures for the HT phase and at 2 different temperatures for the LT phase (see Fig. 6d), we wondered which would be the effect (if any) of the temperature in the evaluation of JAB. New calculations showed that the magnetic topology was preserved as AFM π-stacks of TTTA radicals (see Table 5), irrespective of the temperature at which the crystal data was characterized. Note that basis set was also tested, and corroborated to not influence in the final JAB calculated. The LT phase always behaves as magnetically silent due to the very large AFM interaction between radicals (see bottom simulation in Fig. 6c). In contrast, for HT, depending on the temperature, a shift in the value of the magnetic susceptibility was observed (see upper simulation in green and blue in Fig. 6c). That is, the dependence of JAB magnetic coupling on the interplanar distance between radicals, which decreases as temperature lowers, causes the magnetic response to also be temperature-dependent. At this point, it is clear that the importance of thermal fluctuations must be quantified. Therefore, molecular dynamics simulations were carried out to be able to account for them in order to properly study TTTA.
| LT pair | Basis set | J AB/cm−1 | HT pair | Basis set | J AB/cm−1 |
|---|---|---|---|---|---|
| 150 K SAXPOW01 | 6-31+G(d) | −2020.1 | 225 K SAXPOW04 | 6-31+G(d) | −175.0 |
| aug-cc-pVTZ | −2261.1 | aug-cc-pVTZ | −199.9 | ||
| T room SAXPOW06 | 6-31+G(d) | −1755.0 | 250 K SAXPOW04 | 6-31+G(d) | −160.6 |
| aug-cc-pVTZ | −1967.3 | aug-cc-pVTZ | −183.8 | ||
| T room SAXPOW05 | 6-31+G(d) | −135.6 | |||
| aug-cc-pVTZ | −155.6 | ||||
| 310 K SAXPOW02 | 6-31+G(d) | −134.2 | |||
| aug-cc-pVTZ | −154.1 | ||||
The time resolved evolution of the distance between centroids of adjacent TTTA radicals in one π-stack of the LT phase at 300 K shows that the arrangement of eclipsed dimers and slipped dimers is retained throughout the dynamics (see Fig. 7a). In contrast, the dynamics of the HT polymorph at 300 K shows that a given TTTA radical continually exchanges adjacent neighbour (upper or lower) with which it forms an eclipsed dimer (see Fig. 7b). In other words, our results indicate that each regular π-stacking of radicals in the HT phase is the resulting average of a fast pair exchange dynamics, characterized by a rapid interconversion between two degenerate distorted stacks (see Fig. 7c), which we have named pair exchange dynamics. This dynamic picture at the structural level leads to wondering whether it makes sense to use the common static approach to interpret the magnetism of TTTA, since each geometrical arrangement along the dynamics must involve a different magnetic coupling. Using selected geometries directly extracted from the molecular dynamics trajectories, the corresponding JAB values of both polymorphs were evaluated (see Fig. 8a and b). Clearly the values of JAB magnetic couplings feature remarkable large-amplitude fluctuations because the structure of the material undergoes large fluctuations over time. For LT, all evaluated JAB are very large and negative along the entire trajectory (Fig. 8a), and lead to the overall diamagnetic behaviour of this polymorph. For HT, the effect of the thermal fluctuations is more important since the values of JAB range from FM to highly AFM (see Fig. 8b and c for JAB values in two random snapshots at 2.5 and 4.5 ps). Note that 1 ps involves the evaluation of 1000 JAB interactions between pairs of radicals, i.e. the calculation of 1000 triplet and 1000 open-shell singlet states. In fact, if each set of these JAB fluctuations is used to calculate their corresponding value of the magnetic susceptibility at 300 K and, then, the vibrationally-averaged magnetic susceptibility14a is calculated, a substantial improvement is observed compared to the static data (see Fig. 8d). Specifically, one must compare an experimental χ(T) value of 4.5 × 10−4 emu mol−1 to the computed magnetic susceptibility value using the static FPBU approach of 6.7 × 10−4 emu mol−1 and the corresponding computed vibrationally average value of 5.2 × 10−4 emu mol−1. As mentioned, the improvement obtained using a dynamical perspective is evident. Yet a diagnostic criterion is still missing and, thus, it is most important to assess in which systems molecular dynamics simulations are required.
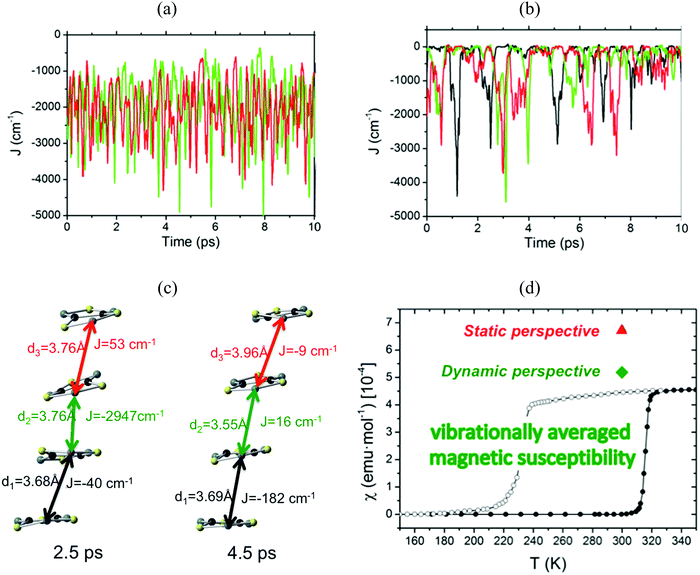 | ||
| Fig. 8 Time-resolved fluctuations of (a) J(d1) and J(d3) for the LT polymorph, and (b) J(d1), J(d2) and J(d3) for the HT polymorph. Each of these J(dn) values corresponds to the pair of radicals marked with dn in Fig. 7. (c) JAB values and corresponding distances in two random snapshots at 2.5 and 4.5 ps. (d) Comparison between the values of the magnetic susceptibility calculated using the static FPBU approach (red) and its vibrationally averaged counterpart (green) at 300 K. Notice that the experimental temperature dependence of the magnetic susceptibility for TTTA on cooling (empty symbols) and on heating (full symbols) is given as a reference. | ||
Overall, insight into the JAB coupling between magnetic sites is crucial to understand the properties of magnetic molecule-based materials. Quantum chemical calculations are thus essential to shed light on the nature and mechanism of the magnetic coupling, namely whether it is through space/through ligand, direct exchange/kinetic exchange, spin polarization/spin delocalization, etc. Understanding and determining the nature and magnitude of the microscopic interactions and their dependence on electronic and structural factors is thus exceedingly important to make real advances in the fields of experimental characterization and modelling.
4. Conclusions
Albeit highly pursued, the total automatization of the modelling of the magnetism of molecular materials using their crystallographic data as only input faces significant challenges. A sufficiently complex automated black-box procedure should be able to address (i) whether the size of the cluster models to calculate the JAB magnetic coupling is the most adequate, (ii) which is the most correct method to be used in the JAB calculation (DFT vs. wavefunction-based, static vs. dynamic approach) and, finally, (iii) (although not discussed here) whether the chosen magnetic models that will be used for full diagonalisation purposes are the most suitable. Three examples have been carefully chosen to emphasize the importance of controlling the evaluation of the JAB magnetic coupling to model and rationalize magnetism in molecule-based materials.In the first case, a dimer-based automated procedure would have prevented uncovering the 3D nature of the magnetic topology of CuHpCl. Let us stress that this 3D magnetic topology is not hinted by JAB values extracted from a dimer model nor could be inferred from direct observation of the crystal. In the second case, an overestimation of the FM interaction between radicals would have been obtained for PhBBO at the default unrestricted DFT level. Instead, wavefunction-based methods are required to adequately describe the presence of low-lying open-shell states in these PhBBO semiquinone-bridged bisdithiazolyl compounds. Finally, it has been shown that for compounds with π–π radical labile packing, such as TTTA, thermal fluctuations entail large amplitude variations in the value of JAB's, which have significant effects in the magnetic response of the material. Effects that would have gone undetected under a total automatization of the modelling of the magnetism of TTTA using a static approach.
To sum up, in order to evaluate correctly JAB exchange interactions, we need to control the size of the cluster models, and the correct method to be used. In addition to model and method, the JAB couplings have to be able to adapt to changes in the magnetic topology due to thermal fluctuations. Therefore, building upon experience, in the field of modelling molecule-based magnetic systems, the “human know-how” cannot yet be replaced by a simple automated black-box procedure. Our take-home message is not that the design of an automated strategy is not attainable, but that needs to be incorporated in a sufficiently complex workflow. Considering the recent advances in Chemo-Informatics and Machine-Learning tools at complementing automatized workflows relevant to the task (e.g. oxidation state recognition,43 active-space selection44), we anticipate that these techniques will soon be able to ease part of the current working strategy.
Conflicts of interest
There are no conflicts to declare.Note added after first publication
This article replaces the version published on 5th July 2021, which contained errors in Tables 3 and 5.Acknowledgements
MD, JRA, and JJN acknowledge financial support from MINECO (CTQ2017-87773-P/AEI/FEDER, UE), Spanish Structures Excellence María de Maeztu program (MDM-2017-0767), and Catalan DURSI (2017SGR348).References
- (a) E. Coronado, Nat. Rev. Mater., 2020, 5, 87 CrossRef; (b) A. E. Thorarinsdottir and T. D. Harris, Chem. Rev., 2020, 16, 8716 CrossRef PubMed; (c) Molecular Magnetic Materials: Concepts and Applications, ed. B. Sieklucka and D. Pinkowicz, Wiley-VCH, 2017 Search PubMed; (d) S. M. Winter, S. Hill and R. T. Oakley, J. Am. Chem. Soc., 2015, 137, 3720 CrossRef PubMed; (e) J. S. Miller, Mater. Today, 2014, 16, 224 CrossRef; (f) I. Ratera and J. Veciana, Chem. Soc. Rev., 2012, 41, 303 RSC; (g) Molecular Materials, ed. D. W. Bruce, D. O’Hare and R. I. Walton, Wiley, 2011 Search PubMed; (h) P. M. Lahti, Adv. Phys. Org. Chem., 2011, 45, 93 CrossRef; (i) Stable Radicals: Fundamentals and Applied Aspects of Odd-Electron Compounds, ed. R. Hicks, Wiley, New York, 2010 Search PubMed.
- (a) R. L. Carlin, Magnetochemistry, Springer-Verlag, Berlin Heidelberg, 1986 CrossRef; (b) O. Kahn, Molecular Magnetism, VCH Publishers, New York, 1993 Search PubMed; (c) R. Boca, Theoretical Foundations of Molecular Magnetism, Current Methods in Inorganic Chemistry, Elsevier Science, Amsterdam, 1999, vol. 1 Search PubMed.
- (a) J. J. Borras-Almenar, J. M. Clemente-Juan, E. Coronado and B. S. Tsukerblat, J. Comput. Chem., 2001, 22, 985 CrossRef; (b) W. Duffy and K. P. Barr, Phys. Rev., 1968, 165, 647 CrossRef; (c) K. M. Diederix, H. W. J. Blote, J. P. Groen, T. O. Klaassen and N. J. Poulis, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 420 CrossRef; (d) J. W. Hall, W. E. Marsh, R. R. Weller and W. E. Hatfield, Inorg. Chem., 1981, 20, 1033 CrossRef; (e) W. E. Hatfield, J. Appl. Phys., 1981, 52, 1985 CrossRef; (f) E. Coronado, M. Drillon, A. Fuertes, D. Beltran, A. Mosset and J. Galy, J. Am. Chem. Soc., 1986, 108, 900 CrossRef; (g) T. Barnes, E. Dagotto, J. Riera and E. S. Swanson, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 3196 CrossRef PubMed; (h) J. J. Borras-Almenar, E. Coronado, J. Curely, R. Georges and J. C. Gianduzzo, Inorg. Chem., 1994, 33, 5171 CrossRef.
- (a) J. J. Novoa, M. Deumal and J. Jornet-Somoza, Chem. Soc. Rev., 2011, 40, 3182 RSC; (b) N. A. G. Bandeira, D. Maynau, V. Robert and B. Le Guennic, Inorg. Chem., 2013, 52, 7980 CrossRef; (c) J. P. Malrieu, R. Caballol, C. J. Calzado, C. de Graaf and N. Guihery, Chem. Rev., 2014, 114, 429 CrossRef PubMed; (d) T. Dresselhaus, S. Eusterwiemann, D. R. Matuschek, C. G. Daniliuc, O. Janka, R. Pottgen, A. Studera and J. Neugebauer, Phys. Chem. Chem. Phys., 2016, 18, 28262 RSC; (e) C. de Graaf and R. Broer, Magnetic Interactions in Molecules and Solids, Springer, 2016 CrossRef; (f) G. David, F. Wennmohs, F. Neese and N. Ferre, Inorg. Chem., 2018, 57, 12769 CrossRef.
- (a) R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989 Search PubMed; (b) L. Noodleman, J. Chem. Phys., 1981, 74, 5737 CrossRef; (c) L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131 CrossRef.
- For a discussion on unrestricted DFT with broken symmetry, see: (a) L. Noodlemann and D. A. Case, Adv. Inorg. Chem., 1992, 38, 423 CrossRef; (b) L. Noodlemann, C. Y. Peng, D. A. Case and J. M. Mouesca, Coord. Chem. Rev., 1995, 144, 199 CrossRef; (c) E. Ruiz, P. Alemany, S. Alvarez and J. Cano, J. Am. Chem. Soc., 1997, 119, 1297 CrossRef CAS; (d) R. Caballol, O. Castell, F. Illas, I. D. R. Moreira and J. P. Malrieu, J. Chem. Phys. A, 1997, 101, 7860 CrossRef CAS; (e) E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391 CrossRef CAS; (f) H. Nagao, M. Nishino, Y. Shigeta, T. Soda, Y. Kitagawa, T. Onishi, Y. Yoshioka and K. Yamaguchi, Coord. Chem. Rev., 2000, 198, 265 CrossRef CAS; (g) J.-M. Mouesca, J. Chem. Phys., 2000, 113, 10505 CrossRef CAS; (h) F. Illas, I. D. R. Moreira, C. de Graaf and V. Barone, Theor. Chem. Acc., 2000, 104, 265 Search PubMed; (i) F. Neese, Coord. Chem. Rev., 2009, 253, 526 CrossRef CAS.
- M. Deumal, M. J. Bearpark, J. J. Novoa and M. A. Robb, J. Phys. Chem. A, 2002, 106, 1299 CrossRef CAS.
- (a) T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic-structure Theory, Wiley, Chichester, 2000 Search PubMed; (b) C. de Graaf and R. Broer, Magnetic Interactions in Molecules and Solids, Springer, 2016 CrossRef.
- (a) S. Vela, A. Sopena, J. Ribas-Arino, J. J. Novoa and M. Deumal, Chem. – Eur. J., 2014, 20, 7083 CrossRef CAS; (b) J. Jornet-Somoza, F. Cosi, M. Fumanal and M. Deumal, Dalton Trans., 2021, 50, 1754 RSC.
- (a) M. Deumal, G. Giorgi, M. A. Robb, M. M. Turnbull, C. P. Landee and J. J. Novoa, Eur. J. Inorg. Chem., 2005, 4697 CrossRef CAS; (b) A. Shapiro, C. P. Landee, M. M. Turnbull, J. Jornet, M. Deumal, J. J. Novoa, M. A. Robb and W. Lewis, J. Am. Chem. Soc., 2007, 129, 952 CrossRef CAS PubMed.
- (a) S. Vela, J. Jornet-Somoza, M. M. Turnbull, R. Feyerherm, J. J. Novoa and M. Deumal, Inorg. Chem., 2013, 52, 12923 CrossRef CAS PubMed; (b) J. C. Monroe, M. A. Carvajal, M. Deumal, C. P. Landee, M. Rademeyer and M. M. Turnbull, Inorg. Chem., 2020, 59, 6319 CrossRef CAS PubMed.
- (a) M. Fumanal, S. Vela, J. J. Novoa and J. Ribas-Arino, Chem. Commun., 2015, 51, 15776 RSC; (b) M. Fumanal, F. Mota, J. J. Novoa and J. Ribas-Arino, J. Am. Chem. Soc., 2015, 137, 12843 CrossRef CAS.
- (a) J. L. Brusso, O. P. Clements, R. C. Haddon, M. E. Itkis, A. A. Leitch, R. T. Oakley, R. W. Reed and J. F. Richardson, J. Am. Chem. Soc., 2004, 126, 8256 CrossRef CAS; (b) J. L. Brusso, O. P. Clements, R. C. Haddon, M. E. Itkis, A. A. Leitch, R. T. Oakley, R. W. Reed and J. F. Richardson, J. Am. Chem. Soc., 2004, 126, 14692 CrossRef CAS; (c) A. Alberola, D. J. Eisler, L. Harvey and J. M. Rawson, CrystEngComm, 2011, 13, 1794 RSC; (d) W. Fujita, K. Kikuchi and K. Awaga, Angew. Chem., Int. Ed., 2008, 47, 9480 CrossRef CAS PubMed; (e) M. Nakano, R. Kishi, K. Yoneda, Y. Inoue, T. Inui, Y. Shigeta, T. Kubo and B. Champaigne, J. Phys. Chem. A, 2011, 115, 8767 CrossRef CAS; (f) R. C. Haddon, A. Sarkar, S. K. Pal, X. Chi, M. E. Itkis and F. S. Tham, J. Am. Chem. Soc., 2008, 130, 13683 CrossRef CAS PubMed; (g) K. Lekin, H. Phan, S. M. Winter, J. W. L. Wong, A. A. Leitch, D. Laniel, W. Yong, R. A. Secco, J. S. Tse, S. Desgreniers, P. A. Dube, M. Shatruk and R. T. Oakley, J. Am. Chem. Soc., 2014, 136, 8050 CrossRef CAS.
- (a) S. Vela, M. Deumal, M. Shiga, J. J. Novoa and J. Ribas-Arino, Chem. Sci., 2015, 6, 2371 RSC; (b) M. Fumanal, S. Vela, J. Ribas-Ariño and J. J. Novoa, Chem. – Asian J., 2014, 9, 3612 CrossRef CAS.
- All energy levels are essential in the computation of magnetic susceptibility data. Unsuccessful attempts to calculate magnetic susceptibility data: (i) used a finite-size cluster approach to compute the energy levels of only the four lowest-lying spin states for binuclear complexes ( K. Fink, C. Wang and V. Staemmler, Inorg. Chem., 1999, 38, 3847 CrossRef CAS ), and (ii) solved the Heisenberg Hamiltonian using Lanczos techniques on large (20–32 spins) clusters to obtain the lowest/highest energy levels and then assumed an analytical density of states for the middle eigenvalues ( C. S. Hellberg, W. E. Pickett, L. L. Boyer, H. T. Stokes and M. J. Mehl, J. Phys. Soc. Jpn., 1999, 68, 3489 CrossRef ).
- (a) M. Deumal, M. J. Bearpark, M. A. Robb, Y. Pontillon and J. J. Novoa, Chem. – Eur. J., 2004, 10, 6422 CrossRef CAS PubMed; (b) J. Jornet-Somoza, M. Deumal, M. M. Turnbull and J. J. Novoa, Polyhedron, 2009, 28, 1965 CrossRef CAS; (c) M. Deumal, J. M. Rawson, A. E. Goeta, J. A. K. Howard, R. C. B. Copley, M. A. Robb and J. J. Novoa, Chem. – Eur. J., 2010, 16, 2741 CrossRef CAS PubMed.
- J. Jornet-Somoza, M. Deumal, M. A. Robb, C. P. Landee, M. M. Turnbull, R. Feyerhem and J. J. Novoa, Inorg. Chem., 2010, 49, 1750 CrossRef CAS.
- (a) J. Jornet-Somoza, N. Codina-Castillo, M. Deumal, F. Mota and J. J. Novoa, Inorg. Chem., 2012, 51, 6315 CrossRef CAS; (b) Ref. 11a.
- S. Vela, M. Deumal, M. M. Turnbull and J. J. Novoa, Polyhedron, 2013, 52, 699 CrossRef CAS.
- C. S. Clarke, J. Jornet-Somoza, F. Mota, J. J. Novoa and M. Deumal, J. Am. Chem. Soc., 2010, 132, 17817 CrossRef CAS PubMed.
- (a) B. Chiari, O. Piovesana, T. Tarantelli and P. F. Zanazzi, Inorg. Chem., 1990, 29, 1172 CrossRef CAS; (b) M. B. Stone, Y. Chen, J. Rittner, H. Yardimci, D. H. Reich, C. Broholm, D. V. Ferraris and T. Lectka, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65 Search PubMed.
- X. Yu, A. Mailman, P. A. Dube, A. Assouda and R. T. Oakley, Chem. Commun., 2011, 47, 4655 RSC.
- M. Fumanal and M. Deumal, Phys. Chem. Chem. Phys., 2016, 18, 20738 RSC.
- (a) W. Fujita and K. Awaga, Science, 1999, 286, 261 CrossRef CAS; (b) G. D. McManus, J. M. Rawson, N. Feeder, J. van Dujin, E. J. L. McInnes, J. J. Novoa, R. Burriel, F. Palacio and P. Oliete, J. Mater. Chem., 2001, 11, 1992 RSC; (c) W. Fujita, K. Awaga, H. Matsuzaki and H. Okamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 064434 CrossRef.
- P.-A. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477 CrossRef CAS.
- DZV contraction of the ANO-RCC basis set using (3s2p1d) for N, O and C atoms, (2s) for H, and (4s3p1d) for S atoms: (a) P.-O. Widmark, P.-A. Malmqvist and B. O. Roos, Theor. Chim. Acta, 1990, 77, 291 CrossRef CAS; (b) B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851 CrossRef CAS.
- F. Aquilante, L. De Vico, N. Ferre, G. Ghigo, P.-A. Malmqvist, P. Neogrady, T. B. Pedersen, M. Pitonak, M. Reiher, B. O. Roos, L. Serrano-Andres, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224 CrossRef CAS PubMed.
- (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (c) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS.
- (a) P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213 CrossRef CAS; (b) M. M. Francl, W. J. Petro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 365 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- F. Neese, ORCA-An ab initio, Density Functional and Semi-empirical Program Package, Version 3.0, Max Planck Institute for Bioinorganic Chamistry, Mullheim, 2012 Search PubMed.
- (a) D. Marx and J. Hutter, Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods, Cambridge University Press, 2009 CrossRef; (b) R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471 CrossRef CAS PubMed.
- CPMD, Version 3.13.2; copyright IBM Corp., 1990–2009, copyright MPI fur Festkorperforschung Stuttgart, 1997–2001; http://www.cpmd.org.
- (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- E. G. Parr and W. Yang, Density Functional Theory, Oxford University Press, New York, 1989 Search PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635 CrossRef.
- (a) G. Chaboussant, M.-H. Julien, Y. Fagot-Revurat, M. Hanson, L. P. Lévy, C. Berthier, M. Horvatic and O. Piovesana, Eur. Phys. J. B, 1998, 6, 167 CrossRef CAS; (b) G. Chaboussant, M.-H. Julien, Y. Fagot-Revurat, L. P. Levy, C. Berthier, M. Horvatic and O. Piovesana, Phys. Rev. Lett., 1997, 79, 925 CrossRef CAS; (c) G. Chaboussant, Y. Fagot-Revurat, M.-H. Julien, M. E. Hanson, C. Berthier, M. Horvatic, L. P. Levy and O. Piovesana, Phys. Rev. Lett., 1998, 80, 2713 CrossRef CAS; (d) G. Chaboussant, M.-H. Julien, Y. Fagot-Revurat, H. Mayaffre, M. Horvatic, L. P. Levy, C. Berthier and O. Piovesana, Phys. B, 2000, 280, 315 CrossRef CAS; (e) P. R. Hammar and D. Reich, J. Appl. Phys., 1996, 79, 5392 CrossRef CAS; (f) P. R. Hammar, D. H. Reich, C. Broholm and F. Trouw, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 7846 CrossRef CAS; (g) X. Wang and L. Yu, Phys. Rev. Lett., 2000, 84, 5399 CrossRef CAS; (h) W. Zheng, R. R. P. Singh and J. Oitmaa, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 8052 CrossRef.
- Point charges (PC) used are fitted to reproduce the electrostatic potential of the isolated cations according to Merz–Singht–Kollman scheme: (a) B. H. Besler, K. M. Merz Jr. and P. A. Kollman, J. Comput. Chem., 1990, 11, 431 CrossRef CAS; (b) U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129 CrossRef CAS.
- CCDC: (a) F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, B58, 380 CrossRef CAS; (b) F. H. Allen and W. D. S. Motherwell, Acta Crystallogr., Sect. B: Struct. Sci., 2002, B58, 407 CrossRef CAS.
- K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, 2020. https://chemrxiv.org/articles/preprint/Using_Collective_Knowledge_to_Assign_Oxidation_States/11604129/1.
- (a) C. J. Stein and M. Reiher, J. Chem. Theory Comput., 2016, 12, 1760–1771 CrossRef CAS; (b) C. J. Stein and M. Reiher, J. Comput. Chem., 2019, 40, 2216 CAS.
| This journal is © The Royal Society of Chemistry 2021 |