Open Access Article
Open Access ArticleUncovering an oxide ion substitution for the OH− + CH3F reaction†
Domonkos A.
Tasi
 * and
Gábor
Czakó
* and
Gábor
Czakó
 *
*
MTA-SZTE Lendület Computational Reaction Dynamics Research Group, Interdisciplinary Excellence Centre, Department of Physical Chemistry and Materials Science, Institute of Chemistry, University of Szeged, Rerrich Béla tér 1, Szeged H-6720, Hungary. E-mail: dtasi@chem.u-szeged.hu; gczako@chem.u-szeged.hu
First published on 14th October 2021
Abstract
Theoretical investigations on chemical reactions allow us to understand the dynamics of the possible pathways and identify new unexpected routes. Here, we develop a global analytical potential energy surface (PES) for the OH− + CH3F reaction in order to perform high-level dynamics simulations. Besides bimolecular nucleophilic substitution (SN2) and proton abstraction, our quasi-classical trajectory computations reveal a novel oxide ion substitution leading to the HF + CH3O− products. This exothermic reaction pathway occurs via the CH3OH⋯F− deep potential well of the SN2 product channel as a result of a proton abstraction from the hydroxyl group by the fluoride ion. The present detailed dynamics study of the OH− + CH3F reaction focusing on the surprising oxide ion substitution demonstrates how incomplete our knowledge is of fundamental chemical reactions.
Introduction
In chemistry, one of the most important reactions is the bimolecular nucleophilic substitution (SN2). The traditional picture of the SN2 reactions was described by Ingold and co-workers more than 80 years ago,1,2 and since then these reactions have always been in the focus of scientific interest.3–16 In a schematic X− + CH3Y → CH3X + Y− SN2 reaction, the widely-known Walden inversion usually occurs as follows: in the entrance channel the reactants form an ion-dipole X−⋯CH3Y complex, and then a [X⋯CH3⋯Y]− transition state can be found, which finally leads to a XCH3⋯Y− complex in the product channel. The above presented mechanism inverts the configuration of the CH3Y reactant, due to the umbrella motion of the CH3 group. Besides inversion, at higher collision energies (Ecoll), retention can also be eventuated, and thus the configuration of the CH3X product remains the same as that of the CH3Y reactant. There are two mechanisms that result in retention: front-side attack and the recently discovered double-inversion pathway.17 In the case of the front-side attack, the reaction pathway goes through a high-energy [XYCH3]− transition state. The double-inversion mechanism is defined by a proton-abstraction induced inversion followed by a traditional Walden inversion.17 However, if one considers the reaction conditions and differentiate several direct (rebound and stripping) and indirect (ion-dipole, hydrogen-bond and frontside complex formations, roundabout, barrier recrossing) pathways, the description of the SN2 reactions becomes more complex.14 Regarding our previous studies,17–19 we consider the above mechanisms as variants of the back-side attack Walden-inversion. It should also be noted that competing with SN2, in most cases, proton abstraction can occur leading to the HX + CH2Y− products.SN2 reactions are mostly studied between halide ions and methyl halides, however, over the past 30 years the variety of the analysed reactions has widened. On one hand, halide ions can be replaced with several other nucleophiles, such as OH−, SH−, CN−, NH2−, PH2−, etc.,19–25 on the other hand, methyl halides can be substituted with relevant alkyl halides.26–30 For the OH− + CH3Y [Y = F, Cl, Br, I] gas-phase SN2 reactions, previous studies showed that in the product channel, instead of the traditional HOCH3⋯Y− ion-dipole complex, a hydrogen-bonded CH3OH⋯Y− global minimum can be found.21,22,31 In 2002, Hase and co-workers investigated the impact of the CH3OH⋯F− deep well on the OH− + CH3F SN2 reaction by using direct dynamics simulations.6 64 trajectories were initiated from the top of the [HO⋯CH3⋯F]− barrier towards the CH3OH + F− products, and each trajectory was propagated until the distance of the products reached 17 Å or the lifetime of the trajectory exceeded 3 ps. Among these trajectories, 33 reversed to the entrance channel by forming the OH−⋯CH3F complex and 27 followed a direct reaction path, where the leaving F− avoids the deep minimum along the O–C⋯F− axis. Only 4 trajectories went through an indirect reaction path and were trapped in the region of the CH3OH⋯F− well, of which only one trajectory formed the CH3OH + F− products in the 3 ps propagation time. Concerning the role of the deep potential well in the dynamics of the title reaction, similar findings were revealed in the studies of Tsutsumi et al.32,33 and Hare et al.34
In the present work, nearly 20 years after the studies of Hase and co-workers,6 we investigate the OH− + CH3F reaction performing high-level dynamics simulations. Our main goal is to take into account the effect of the deep post-reaction well on the title SN2 reaction by computing nearly 1 million full-length quasi-classical trajectories (QCT) and considering a wide range of Ecoll. To perform these QCT computations, relying on our previous study,35 we construct a global full-dimensional ab initio potential energy surface (PES) for the OH− + CH3F reaction utilizing the ROBOSURFER program package recently developed in our group.36 Our dynamics simulations reveal a novel reaction route, observed at lower Ecoll, where a fluoride ion is substituted by an oxide ion leading to the HF + CH3O− products. How does this oxide ion substitution proceed and how competitive is it with the traditional reaction paths? In the following we answer these questions by providing a detailed dynamical characterization of the title reaction.
Results and discussion
Description of the SN2 potential energy surface
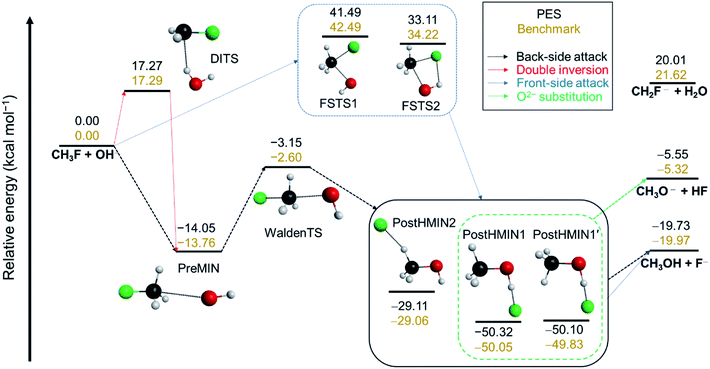
In order to describe the possible reaction pathways of any given reaction, first a benchmark characterization of the stationary points on its PES (minima and transition states) must be performed. The schematic PES of the OH− + CH3F SN2 reaction is shown in Fig. 1. A detailed description of the applied computations for the stationary-point characterization can be found in the ESI.† While proton abstraction is endothermic (21.62 kcal mol−1), SN2 turns out to be an exothermic reaction with an energy of −19.97 kcal mol−1 relative to the reactants (Fig. 1). As expected, in the entrance channel of the back-side attack, a traditional ion-dipole complex (PreMIN) is situated with a central transition state (WaldenTS). The global minimum of the OH− + CH3F reaction is in the product channel, where two different types of H-bonded complexes are obtained (PostHMIN1 and PostHMIN2). Note that, as a result of the CH3 group rotation, PostHMIN1 and PostHMIN1′ are conformational isomers, and PostHMIN1 is below the latter by 0.22 kcal mol−1. The back-side attack goes through a submerged WaldenTS with a relative energy of −2.60 kcal mol−1, whilst the transition states of the front-side attack have barrier heights of 42.49 (FSTS1) and 34.22 (FSTS2) kcal mol−1. Concerning the double-inversion mechanism, DITS is found to be energetically lower than FSTS2 by ∼17 kcal mol−1. Besides SN2, proton abstraction is investigated as well, and the resulting two minima are presented together with all benchmark Cartesian coordinates and energies of the stationary points in the ESI.† Based on the defined stationary points, our next step is to build a global, analytical PES for the OH− + CH3F reaction using the ROBOSURFER program system.36 The computational details of the PES development are summarised in the ESI.† To underline the accuracy of the PES, the obtained relative energies of the stationary points must be compared with the benchmark values. As Fig. 1 shows, in most cases the PES reproduces the all-electron CCSDT(Q)/complete-basis-set-quality benchmark energies within chemical accuracy (1 kcal mol−1), with a slightly higher difference of ∼1.6 kcal mol−1 for the H2O + CH2F− products.Reaction dynamics simulations: the novel oxide ion substitution
Building upon an accurate global analytical PES, high-level dynamics simulations can be performed to study the chemical reaction of interest at an atomic level. For the OH− + CH3F reaction QCT computations are carried out at several Ecoll. Details of the QCT simulations are provided in the ESI.† Besides the usual products of SN2 and proton abstraction, the simulation trajectories resulted in the HF and CH3O− compounds in certain cases, revealing the existence of a new reaction path. We further call this pathway as an oxide ion substitution indicating that the F− of the CH3F reactant is exchanged by an O2−. As seen in Fig. 1, for the title reaction, oxide ion substitution happens to be exothermic and the reaction energy obtained on the PES (−5.55 kcal mol−1) is in excellent agreement with the benchmark value (−5.32 kcal mol−1). The snapshots of a representative trajectory are shown in Fig. 2 depicting the oxide ion substitution at a Ecoll of 10 kcal mol−1. Using time step intervals of 0.0726 fs, dynamics simulations allow us to follow the motion of the atoms step by step. Within the entrance channel of the reaction, the two reactants approach each other for ∼0.35 ps. Afterwards, within a timeframe of only ∼0.6 ps, Walden inversion occurs via the above-described pathway (PreMIN → WaldenTS → PostHMIN), and the system gets trapped in the post-reaction deep well complex for ∼2.4 ps. Subsequently, the F− removes the proton from the hydroxyl group leading to generation of the products, HF + CH3O− in ∼0.07 ps. The average lifetime of the PostHMIN1 complex, 1–5 ps depending on Ecoll, is given in Table S1.† Thus, the typical trajectory of oxide ion substitution spends long time in the PostHMIN1 region, however, PreMIN complex formation and fast proton abstraction in the product well can also be found. To confirm the certainty of this novel oxide ion substitution, ab initio computations are performed along representative trajectories. As also seen in Fig. 2, the direct ab initio energies and the PES values are in good agreement indicating that the given path does exist for the title reaction. In the ESI,† the interested reader can find an actual QCT simulation of the oxide ion substitution in motion along with the other (SN2, proton abstraction, proton exchange, etc.) pathways.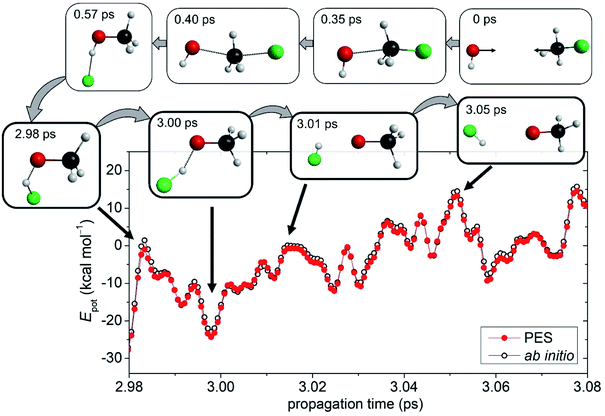 | ||
| Fig. 2 The novel reaction pathway: snapshots of a dynamics simulation representing the oxide ion substitution for the OH− + CH3F reaction at a collision energy of 10 kcal mol−1 (b = 0). In the course of the exceptional proton abstraction by the fluoride ion, the direct ab initio potential energies are compared with the fitted PES values, relative to OH−(eq.) + CH3F(eq.), as a function of time. The ab initio energies are obtained at the CCSD-F12b/aug-cc-pVTZ + BCCD(T)/aug-cc-pVDZ − BCCD/aug-cc-pVDZ composite level of theory and the PES values correspond to the present analytical fitted composite PES. The time evolution of the potential energies for the complete reaction pathway from reactants to products is shown in Fig. S4.† | ||
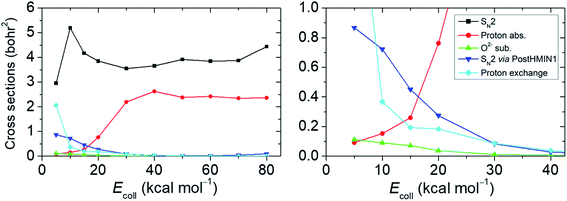
Following the approach of Hase and co-workers,6 our next goal is to identify the SN2 reactions taking place via the deep PostHMIN1 and to define the probability relation of these pathways with regard to the oxide ion substitution. For this purpose, we follow the relevant atomic distances from the end of the trajectories (see the ESI† for details). The integral cross sections (ICSs) and their ratios as a function of the Ecoll for the examined reaction routes are shown in Fig. 3 and Table S2,† respectively. Cross sections, which are proportional with the measureable reactivity at a given Ecoll, are obtained by integrating initial orientation- and vibrational-phase-averaged b-weighted reaction probabilities over b impact parameters. Provided that the back-side attack substitution is a submerged exothermic path, SN2 has the largest ICS at each Ecoll with a maximum of ∼5.2 bohr2 at Ecoll = 10 kcal mol−1. The ICS of the proton abstraction suffers a significant increase starting from Ecoll of 20 kcal mol−1 and plateaus around 2.2–2.6 bohr2 at higher energies. (It is important to note that proton abstraction still occurs at Ecoll below the reaction endothermicity due to the zero-point energy (ZPE) violation of the products, which has not been considered for Fig. 3.) The highest possibility of SN2 occurring via PostHMIN1 is at Ecoll = 5 kcal mol−1 with an ICS of ∼0.9 bohr2. Dynamics simulations also show PreMIN complex formation, but the trajectories usually spend more time in the post-reaction well. As can be expected for a barrierless (WaldenTS is below the reactants) exothermic reaction, the direct path of SN2 becomes more and more dominant with the gradual increase of Ecoll avoiding the H-bonded global minimum in the product channel. The finding that the trajectories avoid the H-bonded minimum at high Ecoll can be explained by the fact that the PostHMIN1 complex is not along the O–C–F reaction coordinate and at higher translational energies F− directly departs along the nearly collinear O–C–F arrangement without roaming around the CH3OH fragment to form an OH-bonded complex. The above tendency is also reflected by the internal and the translational energy distributions of the SN2 and the proton-abstraction products (see Fig. S1 and S2 in the ESI†). Upon increasing Ecoll, translational energies of the products are clearly higher in contrast to the less impacted internal energies. This indicates that the direct reaction path is favoured in both, SN2 and proton abstraction as well. Analogously to the SN2 via PostHMIN1, the ICS of the oxide ion substitution also peaks at an Ecoll of 5 kcal mol−1 with a maximum value of ∼0.1 bohr2, and the reaction practically vanishes at higher Ecoll. Oxide ion substitution is highly indirect, as indicated by the cold product relative translational energy distributions shown in Fig. S3.† The differential labelling of the four H atoms enables us to distinguish between all protons in the course of a dynamics simulation. Hence, it is also possible to detect proton exchange reactions of OH− and CH3F, although the products are seemingly identical to the reactants. This proton exchange pathway begins with a proton abstraction by OH′− from CH3F, followed by a rotation of the HOH′ fragment and a transfer of H′+ to form CH2H′F. When the reaction path is more indirect, proton exchange turns out to be a viable possibility as its ICS at Ecoll = 5 kcal mol−1 is lower by only ∼0.9 bohr2 than the corresponding value of SN2. Note that in a few cases we find that proton exchange can be followed by oxide ion substitution leading to the HF + CH2H′O− products. Besides the Walden-inversion SN2 pathway, we also find trajectories with retention of the initial CH3F configuration (see Table S2†). At low collision energies retention proceeds with double inversion, whereas at high Ecoll front-side attack becomes the dominant retention pathway with about 3% probability of the total reactivity at Ecoll = 80 kcal mol−1.
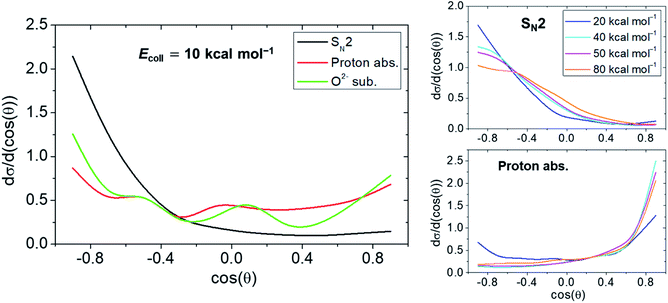
Scattering angular distributions of selected OH− + CH3F reaction pathways determined at various Ecoll are displayed in Fig. 4. Details of the calculations are provided in the ESI.† Owing to the structure of the WaldenTS, SN2 results in backward scattered products with the highest proportion being at Ecoll = 10 kcal mol−1. As for the proton abstraction, the increasing Ecoll supresses backward scattering, and at sufficiently high values, forward scattered products become prominent signifying a direct stripping mechanism. On the other hand, at an Ecoll of 10 kcal mol−1, the oxide ion substitution displays a largely isotropic angular distribution. Thus, the mechanism is proven indirect, as the reaction can be easily trapped in the deep minimum of the PostHMIN1 complex.
Conclusions
The present work reveals a high-level dynamics investigation of the OH− + CH3F reaction consisting of nearly 1 million full-length QCT simulations at several Ecoll on a global ab initio full-dimensional PES developed using the in-house ROBOSURFER program package.36 At lower Ecoll, dynamics simulations reveal the existence of a novel exothermic reaction pathway forming the unexpected product pair of HF and CH3O−. This indirect oxide ion substitution is enabled by an energetically trapped region, the deep well of the PostHMIN1 complex, where the proton from the hydroxyl group of CH3OH can be removed by the fluoride ion. Identified SN2 reactions from the direction of PostHMIN1 indicate that the relevance of the deep potential well has been previously underestimated by Hase and co-workers.6 This study is aimed to emphasise the importance of theoretical investigations on fundamental reactions exploring new possible pathways, and calls for a further experimental verification of the obtained results. As the masses of the product anions, considering the most abundant isotopes, F− (19 u), CH2F− (33 u), and CH3O− (31 u), are different, the experimental detection of the oxide ion substitution channel is possible. Note that a recent crossed-beam study could measure reaction channels with branching ratios less than 2%,37 which further supports the future experimental observation of the low-probability oxide ion substitution. Furthermore, similar post-reaction proton-transfer processes revealed in the present work may occur in other chemical reactions as well, providing novel product channels. On the one hand, one may consider different leaving groups for the OH− + CH3Y reaction such as Y = Cl, Br, I, NH2, CN, etc. In the case of Y = Cl, Br, and I, the HY + CH3O− formation is less possible due to the higher and higher thermodynamic preference of the SN2 channel as the atomic number of Y increases, although, for Y = NH2 and CN oxide ion substitution may occur due to the high proton affinity of NH2− and CN−. On the other hand, various nucleophiles such as SH−, PH2−, NH2−, CCH−, AsH2−, CH3−, SiH3−, GeH3−, SeH−, etc.15,26 may favour post-reaction proton transfer. One of the most promising candidates is the SH− + CH3F system, where the exothermic HF + CH3S− path is thermodynamically more favoured than the endothermic F− + CH3SH SN2 channel. Obviously, future reaction dynamics investigations will be necessary to determine the probability of post-reaction hydrogen-bonded complex formation which facilitates novel proton-abstraction induced product formation.Methods
Benchmark ab initio thermochemistry
The stationary points of the OH− + CH3F reaction are searched using the second-order Møller–Plesset perturbation theory (MP2) with the aug-cc-pVDZ basis set. Then the explicitly-correlated coupled-cluster singles, doubles, and perturbative triples (CCSD(T)-F12b) method was employed with the aug-cc-pVDZ and aug-cc-pVTZ basis sets in order to improve the accuracy of the structures, energies and frequencies of the stationary points. The benchmark classical energies are computed at the CCSD(T)-F12b/aug-cc-pVTZ geometries using the CCSD(T)-F12b method with the aug-cc-pVQZ basis set, as well as considering post-CCSD(T) correlation effects up to CCSDT(Q) and core correlation effects. The benchmark relative energies of the stationary points are adapted from ref. 31, and FSTS2, PostHMIN1′ and PostHMIN2 are newly characterized in this work.Development of the potential energy surface
For the development of the global analytical ab initio PES of the OH− + CH3F reaction the same procedure is utilized as in the case of the OH− + CH3I reaction described in ref. 35. The PES development is performed with the ROBOSURFER program package at the MP2/aug-cc-pVDZ level of theory. The first step is to generate an initial dataset by modifying the geometries of the stationary points randomly. Then, this dataset is used to start the ROBOSURFER program, which adds the remaining points by iterative selection of the energies of the new geometries derived from QCT simulations. Performing 655 iterations overall at 1, 5, 10, 20, 30, 40, 50, 60, 70 and 80 kcal mol−1Ecoll, the dataset contains 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 434 energy points. The permutationally invariant polynomial approach is used for fitting the PES applying a fifth-order polynomial expansion of Morse-like variables, exp(–rij/a), where rij represents the inter-atomic distances and a = 3 bohr. The 4693 polynomial coefficients of the fit are determined by a weighted linear least-squares fit applying the weight function of E0/(E + E0) × E1/(E + E1), where E0 = 94 kcal mol−1, E1 = 314 kcal mol−1, and E is the energy relative to the global minimum. Similar to the OH− + CH3I reaction, at certain geometries the gold-standard CCSD(T) breaks down providing too negative energies, therefore to solve this problem, the energy points are recalculated at the CCSD-F12b/aug-cc-pVTZ + BCCD(T)/aug-cc-pVDZ − BCCD/aug-cc-pVDZ composite level of theory. Moreover, we add about 1000 composite ab initio energy points to improve the HF + CH3O− product region of the PES. The final PES contains 51
434 energy points. The permutationally invariant polynomial approach is used for fitting the PES applying a fifth-order polynomial expansion of Morse-like variables, exp(–rij/a), where rij represents the inter-atomic distances and a = 3 bohr. The 4693 polynomial coefficients of the fit are determined by a weighted linear least-squares fit applying the weight function of E0/(E + E0) × E1/(E + E1), where E0 = 94 kcal mol−1, E1 = 314 kcal mol−1, and E is the energy relative to the global minimum. Similar to the OH− + CH3I reaction, at certain geometries the gold-standard CCSD(T) breaks down providing too negative energies, therefore to solve this problem, the energy points are recalculated at the CCSD-F12b/aug-cc-pVTZ + BCCD(T)/aug-cc-pVDZ − BCCD/aug-cc-pVDZ composite level of theory. Moreover, we add about 1000 composite ab initio energy points to improve the HF + CH3O− product region of the PES. The final PES contains 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431 energy points and the root-mean-squared fitting errors are: 0.83 kcal mol−1, 1.69 kcal mol−1, and 2.54 kcal mol−1 for the energy ranges 0–94 kcal mol−1, 94–188 kcal mol−1 and 188–471 kcal mol−1, respectively.
431 energy points and the root-mean-squared fitting errors are: 0.83 kcal mol−1, 1.69 kcal mol−1, and 2.54 kcal mol−1 for the energy ranges 0–94 kcal mol−1, 94–188 kcal mol−1 and 188–471 kcal mol−1, respectively.
Quasiclassical trajectory calculations
QCT computations are carried out for the OH− + CH3F reaction at ten Ecoll: 5, 10, 15, 20, 30, 40, 50, 60, 70 and 80 kcal mol−1 using a time step of 0.0726 fs. The ground vibrational states of OH− and CH3F are prepared by standard normal-mode sampling and the rotational angular momenta are set to 0. The initial distance of the reactants is 25 bohr with a given impact parameter, b, and the initial spatial orientation of the reactants is randomly sampled. At each b, 5000 trajectories are run and b is scanned with the step size of 0.5 bohr from 0 to bmax, where the probability of the reaction becomes 0. Each trajectory is propagated until the largest interatomic separation becomes larger by 1 bohr than the largest initial one. The identification of the SN2 reaction, which does not avoid the CH3OH⋯F− deep well (PostHMIN1), is based on a similar method used for the numerical separation of the front-side attack and double-inversion mechanisms.38A more detailed description of the computations is given in the ESI.†
Data availability
The datasets generated and analysed during the current study are not publicly available due to their large size but are available from the authors on reasonable request.Author contributions
G. C. designed the research, D. A. T. carried out the computations and analysed the data, D. A. T. and G. C. discussed the results, and D. A. T. wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support of the National Research, Development and Innovation Office – NKFIH (K-125317), the Ministry of Human Capacities, Hungary (20391-3/2018/FEKUSTRAT), and the Momentum (Lendület) Program of the Hungarian Academy of Sciences.References
- W. A. Cowdrey, E. D. Hughes, C. K. Ingold, S. Masterman and A. D. Scott, J. Chem. Soc., 1937, 1252 RSC.
- C. K. Ingold, Structure and Mechanism in Organic Chemistry, Cornell Univ. Press, Ithaca, NY, 1953 Search PubMed.
- S. S. Shaik and A. Pross, J. Am. Chem. Soc., 1982, 104, 2708 CrossRef CAS.
- S. S. Shaik, H. B. Schlegel and S. Wolfe, Theoretical Aspects of Physical Organic Chemistry: The SN2 Mechanism, Wiley, New York, 1992 Search PubMed.
- W. L. Hase, Science, 1994, 266, 998 CrossRef CAS PubMed.
- L. Sun, K. Song and W. L. Hase, Science, 2002, 296, 875 CrossRef CAS PubMed.
- J. I. Brauman, Science, 2008, 319, 168 CrossRef CAS PubMed.
- J. Mikosch, S. Trippel, C. Eichhorn, R. Otto, U. Lourderaj, J. X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, Science, 2008, 319, 183 CrossRef CAS PubMed.
- A. P. Bento and F. M. Bickelhaupt, J. Org. Chem., 2008, 73, 7290 CrossRef CAS.
- R. Otto, J. Brox, S. Trippel, M. Stei, T. Best and R. Wester, Nat. Chem., 2012, 4, 534 CrossRef CAS PubMed.
- P. Manikandan, J. Zhang and W. L. Hase, J. Phys. Chem. A, 2012, 116, 3061 CrossRef CAS PubMed.
- I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953 RSC.
- M. Stei, E. Carrascosa, M. A. Kainz, A. H. Kelkar, J. Meyer, I. Szabó, G. Czakó and R. Wester, Nat. Chem., 2016, 8, 151 CrossRef CAS PubMed.
- J. Xie and W. L. Hase, Science, 2016, 352, 32 CrossRef CAS PubMed.
- T. A. Hamlin, M. Swart and F. M. Bickelhaupt, ChemPhysChem, 2018, 19, 1315 CrossRef CAS.
- R. Wester, Mass Spectrom. Rev., 2021 DOI:10.1002/mas.21705.
- I. Szabó and G. Czakó, Nat. Commun., 2015, 6, 5972 CrossRef PubMed.
- I. Szabó and G. Czakó, J. Phys. Chem. A, 2017, 121, 9005 CrossRef PubMed.
- D. A. Tasi, Z. Fábián and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 7924 RSC.
- J. M. Gonzales, R. S. Cox, S. T. Brown, W. D. Allen and H. F. Schaefer, J. Phys. Chem. A, 2001, 105, 11327 CrossRef CAS.
- L. Sun, K. Song, W. L. Hase, M. Sena and J. M. Riveros, Int. J. Mass Spectrom., 2003, 227, 315 CrossRef CAS.
- J. Xie, S. C. Kohale, W. L. Hase, S. G. Ard, J. J. Melko, N. S. Shuman and A. A. Viggiano, J. Phys. Chem. A, 2013, 117, 14019 CrossRef CAS PubMed.
- J. Xie, R. Sun, M. R. Siebert, R. Otto, R. Wester and W. L. Hase, J. Phys. Chem. A, 2013, 117, 7162 CrossRef CAS PubMed.
- E. Carrascosa, M. Bawart, M. Stei, F. Linden, F. Carelli, J. Meyer, W. D. Geppert, F. A. Gianturco and R. Wester, J. Chem. Phys., 2015, 143, 184309 CrossRef CAS PubMed.
- J. Xie, J. Zhang and W. L. Hase, Int. J. Mass Spectrom., 2015, 378, 14 CrossRef CAS.
- X.-P. Wu, X.-M. Sun, X.-G. Wei, Y. Ren, N.-B. Wong and W.-K. Li, J. Chem. Theory Comput., 2009, 5, 1597 CrossRef CAS PubMed.
- E. Carrascosa, J. Meyer, J. Zhang, M. Stei, T. Michaelsen, W. L. Hase, L. Yang and R. Wester, Nat. Commun., 2017, 8, 25 CrossRef PubMed.
- C. Vallance, Nature, 2017, 546, 608 CrossRef CAS PubMed.
- L. Satpathy, P. K. Sahu, P. K. Behera and B. K. Mishra, J. Phys. Chem. A, 2018, 122, 5861 CrossRef CAS PubMed.
- X. Liu, J. Zhang, L. Yang and W. L. Hase, J. Am. Chem. Soc., 2018, 140, 10995 CrossRef CAS PubMed.
- D. A. Tasi, Z. Fábián and G. Czakó, J. Phys. Chem. A, 2018, 122, 5773 CrossRef CAS PubMed.
- T. Tsutsumi, Y. Ono, Z. Arai and T. Taketsugu, J. Chem. Theory Comput., 2018, 14, 4263 CrossRef CAS PubMed.
- T. Tsutsumi, Y. Ono, Z. Arai and T. Taketsugu, J. Chem. Theory Comput., 2020, 16, 4029 CrossRef CAS PubMed.
- S. R. Hare, L. A. Bratholm, D. R. Glowacki and B. K. Carpenter, Chem. Sci., 2019, 10, 9954 RSC.
- D. A. Tasi, T. Győri and G. Czakó, Phys. Chem. Chem. Phys., 2020, 22, 3775 RSC.
- T. Győri and G. Czakó, J. Chem. Theory Comput., 2020, 16, 51 CrossRef PubMed.
- J. Meyer, V. Tajti, E. Carrascosa, T. Győri, M. Stei, T. Michaelsen, B. Bastian, G. Czakó and R. Wester, Nat. Chem., 2021, 13, 977 CrossRef CAS PubMed.
- P. Papp, V. Tajti and G. Czakó, Chem. Phys. Lett., 2020, 755, 137780 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed computational methods, relative translational energy and internal energy distributions of the products, ratio (%) of the integral cross sections of each pathway [SN2 (via PostHMIN1, retention and inversion), proton abstraction, oxide anion substitution (with ZPE-constraints) and proton exchange], lifetime of PostHMIN1 in the deep well of the oxide anion substitution at several collision energies and impact parameters, benchmark Cartesian coordinates (Å) and energies (Eh) of the stationary points, and representative trajectories of each reaction pathway. See DOI: 10.1039/d1sc03834f |
| This journal is © The Royal Society of Chemistry 2021 |