Crystal growth of the core and rotated epitaxial shell of a heterometallic metal–organic framework revealed with atomic force microscopy

Abstract

Atomic force microscopy has been used to determine the surface crystal growth of two isostructural metal–organic frameworks, [Zn₂(ndc)₂(dabco)] (ndc = 1,4-naphthalenedicarboxylate, dabco = 4-diazabicyclo[2.2.2]octane) (1) and [Cu₂(ndc)₂(dabco)] (2), from a core crystal of 1 for the former and a core–shell 1@2 crystal for the latter. AFM studies show that the surface terrace morphology expressed is a function of supersaturation, with steps parallel to both the <100> and <110> directions being expressed at higher supersaturations for 1, and steps parallel to the <110> direction being expressed solely at low supersaturation for 1 and 2. The crystal growth mechanisms for both 1 and 2 are essentially identical and involve 2D nucleation and spreading of 0.5 nm high metastable sub-layers of the stable extended 1.0 nm high growth terrace. Surface growth features of 2 indicate that there is an in-plane rotational epitaxy between 2 and 1 of 5.9(7)° that may be directed by the synthesis conditions and that intimate mixtures of different domains of ±5.9(7)° rotational epitaxy are not observed to coexist on the several micron scale on the shell surface. The results provide potential routes and understanding to fabricate MOFs of different crystal forms and defect structures, which are necessary for future advanced function of these versatile materials.

---

Introduction

Crystalline metal–organic frameworks (MOFs) form the largest family of nanoporous materials in numerical terms and still sustain great interest due to their underlying chemistry and potential applications.^1–3 One important subset of interest of the MOF family are MOF-on-MOF compounds that consist of a shell of one MOF grown on a core of another different MOF to form a core–shell product.^4–8 These core–shell compounds possess unique properties and diverse structures. The variety of the latter is enhanced by the ability of MOFs to form core–shell MOFs from lattice-matched and lattice-mismatched pairs of MOFs.^9–16 The synthesis of core–shell MOF-on-MOF compounds of particular form and function will be aided by greater understanding of the growth of such compounds and the influence of the core on the growth of the shell through the interface between the different MOFs.¹⁷ However, there is a paucity of information regarding the formation of such compounds at the nanoscopic level of detail that is required to gain significant understanding of such processes.

Ex and in situ atomic force microscopy (AFM) provides a unique technique to probe the crystal growth processes at the nanoscale which is further complemented by aspects of the MOFs themselves, for example the presence of the pore space in the framework, the relatively large chemical components of the MOF and the ability to grow MOFs under ambient conditions.^18–20 Combination of these aspects has enabled nanoscopic information on the formation of different types of core–shell MOF-on-MOF compounds to be determined, including lattice-matched and lattice-mismatched pairs of MOFs.^21–23

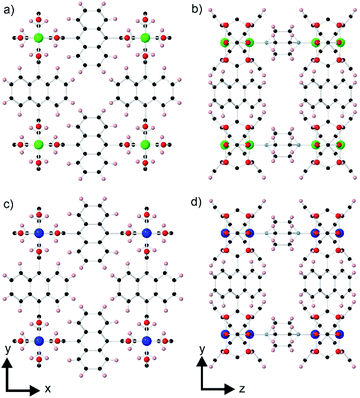
A rare type of core–shell MOF-on-MOF compound that has been reported is one in which there is a slight lattice-mismatch of the core and the shell that is compensated for in the core–shell product through inclusion of an in-plane rotational epitaxy between the shell and the core.²⁴ The only reported example of such a compound consists of a [Zn₂(ndc)₂(dabco)] (ndc = 1,4-naphthalenedicarboxylate, dabco = 4-diazabicyclo[2.2.2]octane) core crystal (1)²⁵ and a [Cu₂(ndc)₂(dabco)] shell (2).²⁶ The structure of 1 contains Zn₂(ndc)₂ layers containing metal paddle wheel dimers that are connected together by the ditopic dabco ligands as shown in Fig. 1a and b. The ndc ligands are rotationally disordered over four positions in the structure. 2 is isostructural to 1 as shown in Fig. 1c and d. 1 and 2 are both tetragonal (space group P4/mmm) and possess slightly different lattice parameters (a = 10.921(1), c = 9.611(1) Å for 1 and a = 10.8190(3), c = 9.6348(6) Å for 2).²⁴ The slight mismatch in the a-lattice parameters of the MOFs gives an approximate mismatch [{a(1) − a(2)}/a(1)] of 0.93% which is compensated for in the core–shell product by an in-plane rotational epitaxy between 1 and 2 on the {001} facets. This behaviour contrasts with the growth of [Zn₂(ndc)₂(dpndi)] (dpndi = N,N′-di(4-pyridyl)-1,4,5,8-naphthalenetetracarboxydiimide) as the shell on 1, where the negligible difference in the a-lattice parameters leads to epitaxial growth on the {001} facets without any in-plane rotational component.²⁷

Fig. 1 Crystal structures of 1 (a, b) and 2 (c, d) viewed perpendicular to the ab-plane (a, c) and the bc-plane (b, d). Zn, Cu, C, O, N, and H are coloured green, blue, black, red, light blue, and pink, respectively.

Currently little is known about the crystal growth of 1, 2 or core–shell 1@2 at the nanoscopic level. A lattice resolution in situ AFM study of the {001} facets of 1 has been reported, which observed modifications in the surface terraces or terrace dissolution upon interaction with different organic molecules.²⁸ Growth of coordinatively immobilized monolayers of monocarboxylic acid has also been demonstrated on the {100} facets of 1.²⁹ Nanoparticles, nanocubes and nanorods of 2 have also been synthesised through a process of coordination modulation to direct the resultant crystal morphology to favour growth in the <001> direction.³⁰

In this work, we use a combination of ex and in situ AFM to investigate the crystal growth of 1 solely, and 2 as part of core–shell 1@2 to provide information at the nanoscale concerning the formation of these compounds and the influence of the slight mismatch in the a-lattice parameters on the growth of 2via the interface with 1. Such information will aid future synthetic efforts to produce such core–shell MOF-on-MOF compounds.

Experimental

Materials

The chemicals 1,4-naphthalenedicarboxylic acid (1,4-ndc) (98%, Alfa Aesar), Zn(NO₃)₂·6H₂O (98%, Sigma Aldrich), 4-diazabicyclo[2.2.2]octane (dabco) (99%, Sigma Aldrich), N,N-dimethylformamide (DMF) (99.8%, Sigma Aldrich) and CuSO₄·5H₂O (98.5%, BDH Chemical) were used as received.

Synthesis of 1

A mixture of 1,4-ndc (0.05 mmol, 11 mg) and Zn(NO₃)₂·6H₂O (0.1 mmol, 30 mg) was placed in a 20 mL scintillation vial. The mixture was then dissolved in 1.5 mL of DMF and sonicated for at least 30 min until the solid reagents were completely dissolved. Dabco (0.05 mmol, 6 mg) was added to the reaction mixture which was then sonicated for 60 min, resulting in a turbid solution. The solution was centrifuged at 3000 rpm to obtain a colourless filtrate that was then transferred to a new scintillation vial. A round glass cover slide (diameter of 13 mm, thickness no. 1.5, VWR) was inserted into the vial. The mixture was capped and heated in a pre-heated oven at 120 °C. The reaction was heated for different time periods of 24, 48, 72, 96 and 120 h to yield brick-shaped crystals attached to the round glass cover slide.²⁵

Powder X-ray diffraction (PXRD) was used to determine the phase purity of the samples of 1. Diffraction data were collected from ground samples contained in a cut silicon sample holder using a Philips X’Pert diffractometer (Cu-Kα radiation) under ambient conditions in the 2θ range of 3.5–50°. Scanning electron microscopy (SEM) was used to determine the crystal habit of 1. SEM images were collected from gold coated crystals of 1 using a Quanta environmental scanning electron microscope (20 kV, 90–110 μA).

Atomic force microscopy

All AFM experiments were conducted on a NanoWizard II (JPK instruments AG) in contact mode using rectangular-shaped silicon cantilevers (MikroMasch) with a nominal tip radius curvature of 10 nm, a force constant of 0.18 N m⁻¹ and a scan rate of 3.0 Hz. Scanning of crystal faces approximately parallel to the glass cover slide was performed to avoid artefacts created by the non-linear displacement of the piezoelectric scanner along the z-axis. Image analyses were conducted using the JPK image processing software provided by JPK Instruments AG. AFM height images were used to determine the height of surface nuclei and terrace layers. The height images were flattened through a line-by-line fitting routine, followed by a plane fit to further correct for any residual tilt prior to height measurements. The height of the nuclei and layers was measured using cross-section analyses with a single scan line passing through the highest point of the nuclei or terrace layers.

Measurement of the rotational angles of the crystals in the optical micrographs and the crystal surface features in the AFM deflection micrographs relative to the edges of the micrographs was carried out using standard geometric measurement software (CorelDRAW 2018).

Ex situ AFM of 1. The round glass cover slide with crystals of 1 attached was dipped several times in fresh DMF, air-dried at room temperature and attached to the AFM instrument. The dried crystal samples were imaged in air.

In situ AFM of 1. Crystals of 1 were prepared as described above with a 48 h reaction time. The round glass cover slide with crystals of 1 attached was initially washed with fresh DMF to wash away any remaining growth solution from the crystal surfaces. In situ growth experiments were performed by fixing the round glass cover slide with crystals of 1 onto a homemade AFM fluid-cell that was then attached to the AFM. Only flat crystals firmly affixed to the glass cover slide on the large {001} facets were scanned, as firmly fixed crystals with the {100} facets attached to the glass cover slide were not formed.

Growth solution 1 used in the in situ AFM experiments was the remaining supernatant from a 48 h synthesis of 1 from which the solid products had been separated.

In situ AFM of core–shell 1@2. In situ AFM experiments were performed on crystals of 1 which had been prepared through the 48 h synthesis of 1. A round glass cover slide with affixed crystals of 1 was washed with fresh DMF and then attached to the homemade AFM fluid-cell before being positioned on the AFM.

Growth solution 2 was prepared by mixing CuSO₄·5H₂O (0.084 mmol, 0.021 g), 1,4-ndc (0.084 mmol, 0.0182 g), and dabco (0.041 mmol, 0.0046 g) in a 20 mL scintillation vial. The mixture was dissolved in 5 mL of DMF and sonicated for 60 min to yield a turbid green solution that was centrifuged at 3000 rpm to obtain a colourless filtrate. The colourless solution was heated for 48 h at 120 °C. The supernatant was decanted to separate it from the solid product and then loaded into a 3 mL syringe prior to the in situ AFM experiment.

Initially, the AFM fluid-cell containing crystals of 1 was filled with 0.7 mL of DMF, and AFM scanning was performed on the {001} facets of selected crystals. 0.2 mL of growth solution 2 was injected into the fluid cell using an automatic syringe pump at a low flow rate of 0.05 mL min⁻¹ to minimise the disturbance to the system during scanning. The crystal was scanned continuously during the introduction of growth solution 2 to fully capture the growth processes.

Results and discussion

The synthesis of 1 resulted in tetragonal prism-shaped crystals terminated by the (100), (1̄00), (010), (01̄0), (001), and (001̄) crystal faces as shown in the SEM images in Fig. S1.†^24,28 The PXRD pattern of the as-synthesised sample is shown in Fig. S2† and indicates the formation of 1 in addition to another unidentified crystalline phase.²⁴ The latter is also observable in the SEM images (Fig. S1†).

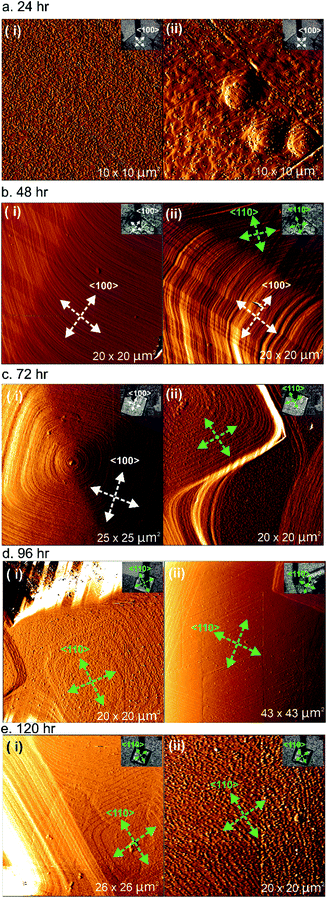
A series of ex situ AFM experiments was conducted on the {001} facets for all five different samples prepared after 24, 48, 72, 96 and 120 h of reaction time, and the resulting micrographs are shown in Fig. 2. The ex situ AFM images of 1 after 24 h of reaction time (see Fig. 2a) indicate a crystal surface with a rough appearance due to the presence of many two-dimensional (2D) nuclei on the surface. Crystal terraces are observable beneath these nuclei. In addition, there are also several observable hillocks of growth islands in Fig. 2a(ii) of somewhat isotropic shape that are covered by 2D nuclei. Both these features suggest that the supersaturation of the crystal growth solution after 24 h is still relatively high.

Fig. 2 Ex situ AFM deflection images of 1 formed after different reaction times. Optical images of the respective crystals of 1 are provided in the inset of each image. The white and green arrows indicate the <100> and <110> directions, respectively.

The AFM deflection images of 1 after 48 h of reaction time shown in Fig. 2b reveal crystal surfaces with few 2D nuclei present compared to the sample after 24 h of reaction time. Surface crystal terraces emanating from dominant growth mounds cover the observed crystal surfaces and these terraces display a more pronounced shape with steps parallel to both the <100> and <110> directions expressed, as indicated by the white and green arrows in the AFM images, compared to the orientation of the scanned crystals given in the respective optical images. These observations suggest that the supersaturation of the crystal growth solution after 48 h was much lower than that after 24 h of reaction time, but that the supersaturation level is still high enough for step growth in a specific direction not to dominate. Similar phenomena were also detected for the sample of 1 after heating for 72 h of reaction time, as shown in Fig. 2c. However, examples of approximately square growth mounds with steps expressed parallel to either the <100> directions or the <110> directions solely were observed in different areas of the crystal surface as shown in Fig. 2c(i) and (ii), respectively. At this lower supersaturation, there is some indication that the rate of growth in the <100> directions is becoming dominant, as evidenced by the nature of the growth mound in Fig. 2c(ii) and also the terraces at the top of the growth mound in Fig. 2c(i) that are beginning to significantly express steps parallel to the <110> directions.

After 96 h and 120 h of reaction time, the AFM deflection images of 1 exhibit a much more pronounced terrace orientation, with birth and spread growth producing terraces with steps parallel to the <110> directions as shown in Fig. 2d and e(i). This indicates that the supersaturation level has dropped to the point where step growth in a specific direction dominates. Some crystal surfaces in the sample of 1 heated for 120 h also appear much rougher, as shown in Fig. 2e(ii), suggesting that after this heating time the supersaturation level may be close to its equilibrium value and surface dissolution and redeposition is occurring. The formation of terraces with steps parallel to the <110> directions has also been reported in prior studies of 1.²⁸

The ex situ AFM results of 1 isolated at different reaction times indicate that at a high supersaturation level, approximately isotropic terraces are formed that begin to express steps parallel to both the <100> and <110> directions as the supersaturation drops further. The tendency to express steps parallel to the <100> directions is greater at higher supersaturation levels, as is also reflected by the overall crystal morphology. As the supersaturation drops further, the rate of growth in the <100> directions becomes dominant and terraces with steps parallel to the <110> directions form solely. This suggests that the overall crystal morphology of 1 can be modified by extended treatment of the crystals in low supersaturation solutions to produce crystals expressing the {110} facets.²⁰ Such crystals may have different surface adsorption and diffusion properties. A change in the overall crystal morphology is known to occur for molecular crystals grown at different supersaturations,^31–33 and for MOF crystal morphologies as the supersaturation level in the growth medium drops.³⁴ However, this represents the first observation of the variation of terrace growth in distinct crystallographic directions on the surface of a MOF as a function of supersaturation only.

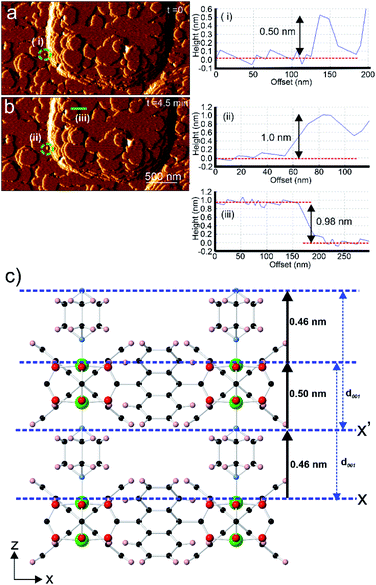
Analyses of AFM height images of numerous surface terraces show that most have step heights of 0.98 ± 0.1 nm (see Fig. 3b and S3†) which corresponds to the d₀₀₁ lattice spacing of 1. This is similar to the value reported by Hosono et al. from their study of 1.²⁸ The growth mechanism from nucleation to completion of the 0.98 nm high extended terraces was revealed by the in situ AFM study and images as shown in Fig. 3. A 0.98 nm high growth island is observed to grow via a 2D nucleus with a height of 0.50 ± 0.1 nm (see Fig. 3a(i)) prior to forming a 1.00 ± 0.1 nm (see Fig. 3b(ii)) growth island as the stable extended terrace height. The latter is further confirmed by the cross-section analysis of another completed stable terrace with the step height of 0.98 ± 0.1 nm (see Fig. 3b(iii)). This series of heights provides some information on the surface crystallographic plane that terminates the extended growth terraces. Comparison of the crystal structure of 1 and the observed heights suggests that the surface plane is formed by the uppermost Zn²⁺ ions and the H atoms of the C₆H₄ rings of the ndc linkers in the [Zn₂(ndc)₂] layers, or by the nitrogen atoms of the dabco ligands exposed on the {001} facets, as indicated by X and X′ in Fig. 3c, respectively. Plane X in Fig. 3c is shown passing through the most rigid part of this surface plane, which consists of the uppermost Zn²⁺ ions of the [Zn₂(ndc)₂] layers, however the actual averaged surface may be approximately 0.07 nm higher when the orientations of the ndc ligands defined within the crystal structure are considered. Additional uncertainty in the orientation of the ndc ligands also arises as the surface orientation of the ndc ligands may not be the same as that in the bulk, and rotation of the ndc groups may occur through surface tip interactions during collection of the AFM images in contact mode. The possibility of these two different surface terminations arises because the vertical distance of a dabco ligand and the associated Zn–N bond is indistinguishable from the vertical distance of a Zn₂(ndc)₄ dimer unit and the associated Zn–N bond in the crystal structure of 1 when the error of AFM height measurements (±0.1 nm) is considered. Both terminating planes will yield the same d₀₀₁ lattice spacing distance after growth of a new growth terrace as indicated by the blue arrows in Fig. 3c.

Fig. 3 In situ AFM deflection images of 1 with cross-section analyses showing the developing 2D nuclei (encircled by dotted green circles in (a and b)). Crystal structure of 1 (c) displaying the various vertical heights of certain structural components above the possible surface terminating planes X and X′. AFM image size is 3.0 × 1.5 μm².

Comparison of the observed step heights and the interatomic distances in the crystal structure of 1 provides information regarding the crystal growth mechanism of 1. If it is assumed that the unsaturated Zn²⁺ ions terminate the crystal surface, as has been previously reported for in situ AFM studies on other MOFs,^{18–20,22,35,36} then the first observed 0.50 ± 0.1 nm high metastable nucleus corresponds to the attachment of a dabco ligand at an under-coordinated Zn²⁺ ion in the [Zn₂(ndc)₂] layer at the terminating plane X (corresponding calculated height from crystal structure = 0.46 nm as shown in Fig. 3c or 0.40 nm if the averaged surface 0.07 nm above X is used).²⁵ Completion of the 1.0 ± 0.1 nm high growth island from the metastable nucleus is achieved by addition of the Zn₂(ndc)₄ dimers and subsequent formation of the [Zn₂(ndc)₂] layer (corresponding calculated height from crystal structure = 0.96 nm as shown in Fig. 3c). The formation of the 1.0 nm high growth island will also involve additional species, presumably solvent molecules, in the formation of the meta-stable nucleus and sub-layer involving the dabco ligands to enable the correlated growth observed for these growth islands. The same type of mechanism would also be observed if the surface termination plane was X′, as shown in Fig. 3c, with attachment of Zn₂(ndc)₄ dimers and subsequent formation of the [Zn₂(ndc)₂] layer on the nitrogen atoms of the dabco molecules followed by the addition of dabco ligands.

Furukawa et al. report that formation of single crystal domains of 2 could only be achieved by forming core–shell 1@2.²⁴In situ AFM was used to study the formation of core–shell 1@2 to investigate the crystal growth of 2 and the effect of the in-plane rotational epitaxy between 2 and 1 on crystal growth.

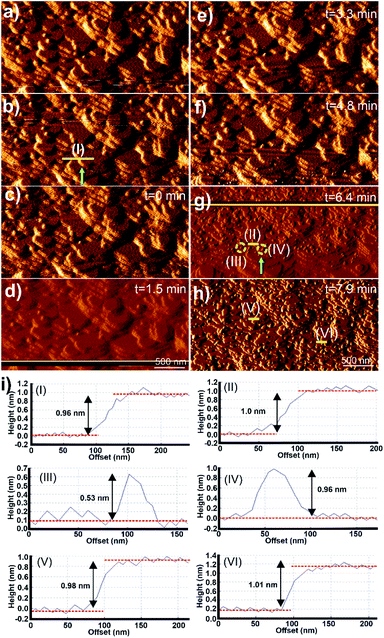
Micrographs of the surface of 1 under DMF and after injection of a growth solution of 2 are shown in Fig. 4. The surface of 1 imaged under DMF is shown in Fig. 4a and b. The images display terraces and small growth islands of 1 with the expected step height of 0.96 ± 0.1 nm as shown in Fig. 4i(I). A growth solution of 2 was injected using an automatic syringe pump and the resulting AFM images captured under this growth solution are shown in Fig. 4c–h. Few apparent changes occur at the crystal surface of 1 under the growth solution of 2 for 6.4 min after injection as shown in Fig. 4c–f. However, the AFM image obtained after 6.4 min after injection of the growth solution of 2 shows the presence of many 2D nuclei and small growth islands of 2 spread across the surface of 1 as shown, and exemplified by the yellow circles, in Fig. 4g. The number density and size of the nuclei of 2 increase from the bottom to the top of the image as this is the scanning direction of the AFM tip during data collection for this image. Direct comparison of Fig. 4b and g as a whole and at points such as that indicated by the green arrow in these figures demonstrates that the new 2D nuclei of 2 grew on the apparently intact terraces of 1 present from the start of the experiment (a direct comparison of these two images is provided in Fig. S4†). The cross-section analyses of the step marked by the yellow line in approximately the same position in Fig. 4b and g are shown in Fig. 4i(I) and (II), which again indicates that the terraces of 1 remain intact during this in situ experiment with a height of 1.0 ± 0.1 nm. Rapid birth and spread growth of 2 on the terraces of 1 continues as indicated by the presence of the large growth islands and multiple terraces of 2 shown in Fig. 4h, the subsequent image collected at time 7.9 min. Cross-section analyses of numerous surface terraces in Fig. 4h show that most have step heights of 1.00 ± 0.1 nm, as exemplified in Fig. 4h and i(V) and (VI), which agrees with the expected d₀₀₁ lattice spacing of 2 (0.96 nm).²⁴

Fig. 4 A series of in situ AFM deflection images of 1 in the presence of DMF (a, b) and after the injection of the growth solution of 2 (c–h), and the corresponding cross-section analyses of selected terraces and 2D nuclei as indicated by yellow lines and circles respectively (i). AFM image sizes are 3.0 × 1.5 μm².

The growth mechanism from nucleation to completion of the 0.96 nm high extended terraces of 2 was also revealed by the in situ AFM study and images as shown in Fig. 4. Cross-section analyses were performed on selected nuclei in Fig. 4g and it was found that these nuclei had two distinct heights, as exemplified by the 2D nuclei (III) and (IV) marked in Fig. 4g, whose heights are 0.53 and 0.96 ± 0.1 nm, respectively, as is shown in the cross-section analyses in Fig. 4i(III) and (IV) respectively. Comparison of these observed heights and the interatomic distances in the crystal structure of 2 indicates that the growth islands and terraces of 2 formed on the crystal surface of 1 follow an identical growth mechanism to that observed for 1. This is expected due to the isostructural nature, and the similarity in unit cell parameters and chemical components of 1 and 2. The rapid terrace formation and spreading in lateral directions also indicate that the in-plane rotational epitaxy between 2 and 1 and the presence of the resultant defects at the interface between 1 and 2 produce little impediment to terrace spreading and growth.

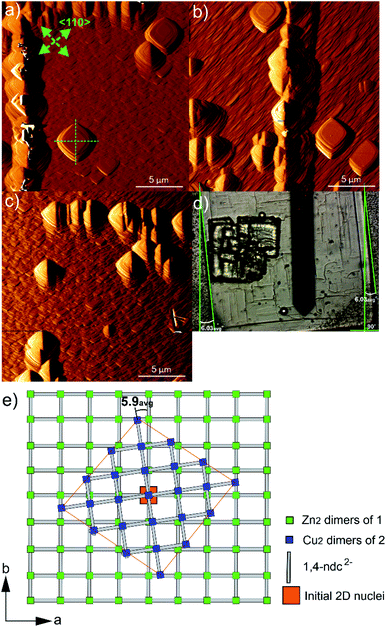
The potential effects of the in-plane rotational epitaxy between 2 and 1²⁴ on the crystal growth of core–shell 1@2 were investigated further by considering the crystal surface of 2 on crystals of 1@2 that had been grown for numerous minutes after introduction of a growth solution of 2 above the core crystals of 1. AFM images of some regions of 2 that had been grown on 1 for approximately 106–119 min are shown in Fig. 5a–c. The entire crystal surface in all the images consists of terraces, growth mounds and growth spirals. The growth mounds and spirals are square with steps expressed parallel to the <110> directions of 2. Consideration of the ex situ AFM studies of 1 suggests that the crystal growth is occurring from a growth solution of 2 with low supersaturation in which the rate of growth in the <100> directions is dominant. It is unsurprising that the relative growth kinetics in particular directions of 1 and 2 appear comparable due to the close similarities of many aspects of 1 and 2.

Fig. 5 AFM deflection images of 1 105.6 min (a), 109.7 min (b) and 118.5 min (c) after injection of growth solution 2, showing the orientation of several growth layers, mounds and spirals relative to the bulk crystal of 1 in optical micrograph (d). Schematic of the in-plane rotational epitaxy between 2 and 1 in core–shell 1@2 (e). The green arrows indicate the <110> directions, and the green dashed and solid lines act as guides to indicate the relative orientations of the surface features and crystals respectively. The AFM image sizes are 20 × 20 μm².

Closer inspection of the square growth mounds and spirals in Fig. 5a–c indicate that their diagonals are not parallel to the edge of the actual core–shell 1@2 crystal as seen in the optical image shown in Fig. 5d. This demonstrates that there is an in-plane rotational epitaxy between 2 and 1 as reported by Furukawa et al. that can be identified through use of AFM. Measurement of the angles between the diagonals of several square growth layers, mounds and spirals and the edges of the core–shell 1@2 crystals (as listed in Table S1†) indicates that this in-plane rotational epitaxy between 2 and 1 is 5.9(7)° where the number in parentheses denotes the standard deviation of the last digit of the mean value. This in-plane rotational epitaxy between 2 and 1 is shown schematically in Fig. 5e. Interestingly this value is approximately half the in-plane rotational epitaxy angle of 11.7° reported by Furukawa et al. that was determined by surface synchrotron X-ray diffraction analysis of a core–shell 1@2 crystal.²⁴ The difference in in-plane rotation angles may be due to the different preparative routes of 2. In this work, 2 was grown from a growth solution using DMF as the solvent at 298 K, whilst Furukawa et al. used a toluene/methanol solvent mixture and the mixture was heated at 393 K for 48 h.²⁴ The lower in-plane rotational epitaxy angle reported here will result in the interface between 1 and 2 being directly connected by fewer dabco ligands per unit area in their normal coordination mode than in the compound reported by Furukawa et al., using the same model as that proposed by those authors in this assignment. This implies the presence of a more highly defective interface in the compound reported here. The formation of such a highly defective interface with a paucity of dabco linkers connecting 1 and 2 is plausible as 2D MOFs constructed from [Cu₂(ndc)₂] layers with water or methanol molecules occupying the final coordination site of the Cu coordination environment have been reported, for instance [Cu(ndc)(MeOH)]·MeOH and [Cu(ndc)(H₂O)]·1.8H₂O.³⁷ The [Cu₂(ndc)₂] layers in these compounds are held together by a combination of sufficiently strong interactions to allow crystal formation, thus supporting the suggested presence of a highly defective interface in 1@2. Such a defective interface would introduce a highly probable cleavage plane in the resulting core–shell 1@2 crystal. The formation of different in-plane rotational epitaxy angles between 1 and 2 demonstrates the structural versatility of MOFs to accommodate different defect structures of differing degrees of defectiveness.

Furukawa et al. also reported that domains of 2 could grow on 1 with an in-plane rotational epitaxy between 2 and 1 of ±11.7°.²⁴ This would suggest that growth features of 2 with two possible relative orientations to each other could be present in close proximity on the crystal surface. Inspection of the features in the AFM images captured for the surface of 2 in 1@2, such as the square growth layers, mounds and spirals shown in Fig. 5a–c, suggests that this is not the case and that these features all have approximately the same orientation within the imaged 400 μm² regions of the surface. The bulk crystal structures of 1 and 2 do not provide an apparent reason as to why one in-plane rotational epitaxy direction between 2 and 1 should be favoured over another, so presumably the reason lies within the crystal growth processes occurring. One potential reason could involve a process where after initial nucleation and development of small growth islands with either in-plane rotational epitaxy angle, random faster growth and merging of growth islands of one in-plane rotational epitaxy angle could isolate growth islands of the other in-plane rotational epitaxy angle. This will create numerous growth islands that cannot simply merge to form a continuous layer as there will be extended structure incoherency at the interface of the island edges. However, these isolated growth islands may undergo a process of dissolution and assimilation into adjacent growth islands as all the necessary components of 2 are in the local vicinity for such a process and bond formation in a MOF is a rapidly reversible process.³⁸ After the first layer of 2 is formed over the crystal surface, further crystal growth of 2 can occur easily as the underlying structure is now 2, although there will be defects present where larger domains of 2 with either in-plane rotational epitaxy angle merge.

Conclusions

AFM has been applied successfully for the first time to identify in-plane rotational epitaxy in a core–shell MOF and indicates that the rotational epitaxy within core–shell MOFs can be different for the same pair of MOF frameworks, so demonstrating the structural versatility of MOFs to accommodate different interfacial defect structures. Intimate mixtures of different domains of growth features of different in-plane rotational epitaxy angle also do not appear to be apparent on the several micron scale. Use of this approach has also determined the influence of supersaturation on the surface crystal growth of two isostructural MOFs and an essentially identical crystal growth mechanism for both MOFs that involves 2D nucleation and spreading of metastable sublayers of the stable extended growth terrace. The latter mechanism appears to be common amongst MOFs grown under low supersaturation conditions. These results provide potential routes and understanding to fabricate MOFs of different crystal forms and defect structures, which are necessary for future advanced function of these versatile materials that may integrate attributes from the component MOFs and their interfacial connection.

Author contributions

FIP conducted all the experimental work and analysed the data, MPA and MWA conceived and supervised the work and all authors contributed to the production of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the Indonesia Endowment Fund for Education (LPDP) under the Ministry of Finance, Indonesia.

Notes and references

1. H. Furukawa, K. E. Cordova, M. O’Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444.
2. J. R. Long and O. M. Yaghi, Chem. Soc. Rev., 2009, 38, 1213–1214.
3. N. Stock and S. Biswas, Chem. Rev., 2012, 112, 933–969.
4. A. D. Burrows, CrystEngComm, 2011, 13, 3623–3642.
5. M. L. Foo, R. Matsuda and S. Kitagawa, Chem. Mater., 2014, 26, 310–322.
6. L. Feng, K.-Y. Wang, J. Willman and H.-C. Zhou, ACS Cent. Sci., 2020, 6, 359–367.
7. L. Feng, K.-Y. Wang, G. S. Day and H.-C. Zhou, Chem. Soc. Rev., 2019, 48, 4823–4853.
8. A. Legrand, Z. Wang, J. Troyano and S. Furukawa, Chem. Sci., 2021, 12, 18–33.
9. K. Koh, A. G. Wong-Foy and A. J. Matzger, Chem. Commun., 2009, 6162–6164.
10. J. Tang, R. R. Salunkhe, J. Liu, N. L. Torad, M. Imura, S. Furukawa and Y. Yamauchi, J. Am. Chem. Soc., 2015, 137, 1572–1580.
11. T.-Y. Luo, C. Liu, X. Y. Gan, P. F. Muldoon, N. A. Diemler, J. E. Millstone and N. L. Rosi, J. Am. Chem. Soc., 2019, 141, 2161–2168.
12. S. Choi, T. Kim, H. Ji, H. Jung Lee and M. Oh, J. Am. Chem. Soc., 2016, 138, 14434–14440.
13. X. Yang, S. Yuan, L. Zou, H. Drake, Y. Zhang, J. Qin, A. Alsalme and H. Zhou, Angew. Chem., 2018, 130, 3991–3996.
14. K. Ikigaki, K. Okada, Y. Tokudome, T. Toyao, P. Falcaro, C. J. Doonan and M. Takahashi, Angew. Chem., Int. Ed., 2019, 58, 6886–6890.
15. Z. Wang, J. Liu, B. Lukose, Z. Gu, P. G. Weidler, H. Gliemann, T. Heine and C. Woll, Nano Lett., 2014, 14, 1526–1529.
16. D. Kim, G. Lee, S. Oh and M. Oh, Chem. Commun., 2019, 55, 43–46.
17. J. Ha and H. R. Moon, CrystEngComm, 2021, 23, 2337–2354.
18. P. Y. Moh, P. Cubillas, M. W. Anderson and M. P. Attfield, J. Am. Chem. Soc., 2011, 133, 13304–13307.
19. R. Wagia, I. Strashnov, M. W. Anderson and M. P. Attfield, Angew. Chem., Int. Ed., 2016, 55, 9075–9079.
20. P. Cubillas, M. W. Anderson and M. P. Attfield, Chem. – Eur. J., 2012, 18, 15406–15415.
21. P. Cubillas, M. W. Anderson and M. P. Attfield, Cryst. Growth Des., 2013, 13, 4526–4532.
22. R. Wagia, I. Strashnov, M. W. Anderson and M. P. Attfield, Cryst. Growth Des., 2018, 18, 695–700.
23. F. I. Pambudi, M. W. Anderson and M. P. Attfield, Chem. Sci., 2019, 10, 9571–9575.
24. S. Furukawa, K. Hirai, K. Nakagawa, Y. Takashima, R. Matsuda, T. Tsuruoka, M. Kondo, R. Haruki, D. Tanaka, H. Sakamoto, S. Shimomura, O. Sakata and S. Kitagawa, Angew. Chem., Int. Ed., 2009, 48, 1766–1770.
25. H. Chun, D. N. Dybtsev, H. Kim and K. Kim, Chem. – Eur. J., 2005, 11, 3521–3529.
26. T. Uemura, Y. Ono, K. Kitagawa and S. Kitagawa, Macromolecules, 2008, 41, 87–94.
27. S. Furukawa, K. Hirai, Y. Takashima, K. Nakagawa, M. Kondo, T. Tsuruoka, O. Sakata and S. Kitagawa, Chem. Commun., 2009, 5097–5099.
28. N. Hosono, A. Tearashima, S. Kusaka, R. Matsuda and S. Kitagawa, Nat. Chem., 2019, 11, 109–116.
29. M. Kondo, S. Furukawa, K. Hirai and S. Kitagawa, Angew. Chem., Int. Ed., 2010, 49, 5327–5330.
30. T. Tsuruoka, S. Furukawa, Y. Takashima, K. Yoshida, S. Isoda and S. Kitagawa, Angew. Chem., Int. Ed., 2009, 48, 4739–4743.
31. Z. Liang, M. Zhang, F. Wu, J. Chen, C. Xue and H. Zhao, Comput. Chem. Eng., 2017, 99, 296–303.
32. T. T. H. Nguyen, R. B. Hammond, K. J. Roberts, I. Marziano and G. Nichols, CrystEngComm, 2014, 16, 4568–4586.
33. W. Tan, X. Yang, X. Duan, X. Zhang, G. Qian and X. Zhou, Cryst. Res. Technol., 2016, 51, 23–29.
34. S. R. Venna, J. B. Jasinski and M. A. Carreon, J. Am. Chem. Soc., 2010, 132, 18030–18033.
35. P. Cubillas, K. Etherington, M. W. Anderson and M. P. Attfield, CrystEngComm, 2014, 16, 9834–9841.
36. P. Cubillas, M. W. Anderson and M. P. Attfield, Chem. – Eur. J., 2013, 19, 8236–8240.
37. P. Kanoo, K. L. Gurunatha and T. K. Maji, J. Mater. Chem., 2010, 20, 1322–1331.
38. S. L. James, Chem. Soc. Rev., 2003, 32, 276–288.

---

Footnote

† Electronic supplementary information (ESI) available: Preliminary characterisation results, additional AFM micrographs and geometric measurement data. See DOI: 10.1039/d1fd00033k

---