Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of temperature and adsorbate on negative gas adsorption transitions of the mesoporous metal–organic framework DUT-49†
Simon
Krause
 *ab,
Jack D.
Evans
*ab,
Jack D.
Evans
 *a,
Volodymyr
Bon
*a,
Volodymyr
Bon
 a,
Irena
Senkovska
a,
François-Xavier
Coudert
a,
Irena
Senkovska
a,
François-Xavier
Coudert
 c,
Daniel M.
Többens
c,
Daniel M.
Többens
 d,
Dirk
Wallacher
d,
Dirk
Wallacher
 d,
Nico
Grimm
d and
Stefan
Kaskel
d,
Nico
Grimm
d and
Stefan
Kaskel
 *a
*a
aChair of Inorganic Chemistry, Technische Universität Dresden, Bergstrasse 66, 01062 Dresden, Germany. E-mail: jack.evans@tu-dresden.de; stefan.kaskel@tu-dresden.de
bCentre for Systems Chemistry, Stratingh Institute for Chemistry, University of Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands. E-mail: simon.krause@rug.nl
cChimie ParisTech, PSL University, CNRS, Institut de Recherche de Chimie, Paris, 75005, Paris, France
dHelmholtz-Zentrum Berlin für Materialien und Energie, Hahn-Meitner-Platz 1, 14109, Berlin, Germany
First published on 30th April 2020
Abstract
Unusual adsorption phenomena, such as breathing and negative gas adsorption (NGA), are rare and challenge our thermodynamic understanding of adsorption in deformable porous solids. In particular, NGA appears to break the rules of thermodynamics in these materials by exhibiting a spontaneous release of gas accompanying an increase in pressure. This anomaly relies on long-lived metastable states. A fundamental understanding of this process is desperately required for the discovery of new materials with this exotic property. Interestingly, NGA was initially observed upon adsorption of methane at relatively low temperature, close to the respective standard boiling point of the adsorptive, and no NGA was observed at elevated temperatures. In this contribution, we present an extensive investigation of adsorption of an array of gases at various temperatures on DUT-49, a material which features an NGA transition. Experiments, featuring a wide range of gases and vapors at temperatures ranging from 21–308 K, were used to identify for each guest a critical temperature range in which NGA can be detected. The experimental results were complemented by molecular simulations that help to rationalize the absence of NGA at elevated temperatures, and the non-monotonic behavior present upon temperature decrease. Furthermore, this in-depth analysis highlights the crucial thermodynamic and kinetic conditions for NGA, which are unique to each guest and potentially other solids with similar effects. We expect this exploration to provide detailed guidelines for experimentally discovering NGA and related “rule breaking” phenomena in novel and already known materials, and provide the conditions required for the application of this effect, for example as pressure amplifying materials.
Introduction
Structural flexibility and softness in porous crystals has generated new adsorption phenomena beyond the classified types of isotherms known for rigid adsorbents.1 While gradual swelling of soft porous solids upon adsorption of fluids is well known,2 cooperative defined structural transformations in soft porous crystals have led to predefined adsorption behavior governed by crystal to crystal structural transformations.3 Especially in the field of metal–organic frameworks (MOFs) adsorption-induced flexibility has recently been frequently observed giving rise to stepwise isotherms governed by single or multiple steps, and wide hysteresis dictated by expansion or contraction of the pores.4 Due to their uncommon adsorption behavior these materials are being discussed as alternative adsorbents in the area of gas sensing,5,6 storage7 or separation.8–11 In early examples of adsorption-induced transitions in MOFs it was shown that the pores in a condensed framework can be expanded upon application of gas pressure. In this phenomenon called gate-opening the adsorbate stabilizes the presence of the open pores (op) which subsequently collapses upon reduction in gas pressure and subsequent desorption of the gas molecules from the pores.12 However, attractive solid–fluid and fluid–fluid interactions can also result in large-scale contraction of the pores upon adsorption. This was first demonstrated in the MIL-53(Al) in which the open pore (op) channels are found to undergo contraction upon adsorption of gases at intermediate pressure.13 With increase in gas pressure the contracted pores (cp) are reopened to the initial op structure via structural expansion, and the overall observed transitions in MIL-53 were thus referred to as breathing.14 In both gate-opening and breathing materials, the experimentally observable isotherms represent a mixture of the single component isotherm of each structural phase with transition regions which represent a mixture present in the corresponding pressure range. The step-wise isotherms and switching of the solid is caused by highly inelastic transformations and an anharmonic potential energy function (Helmholtz free energy).15 In recent years, computational analysis especially, has demonstrated that adsorption-induced structural transitions are a complex interplay between the structural flexibility of the MOF, as well as the solid–fluid and fluid–fluid interactions.16–18 Beyond the nature of the solid and fluid, temperature effects were found to have a large impact on the presence of breathing in systems like MIL-53 (ref. 19 and 20) and ZIF-8,21 however little experimental and computational work has been performed beyond these systems.In 2016, we discovered the phenomenon of negative gas adsorption (NGA), initially observed in the MOF DUT-49 (Dresden University of Technology No. 49, general formula [Cu2(C40H20N2O8)], first reported in ref. 22), which is characterized by a negative step in the adsorption isotherm originating from adsorption-induced structural contraction of the pores.23 This adsorption behavior is unique for both rigid and flexible adsorbents, although large-scale adsorption induced structural contraction is known to occur in other solids such as MIL-53. Computational analysis revealed that the formation of a metastable adsorption state is a prerequisite for NGA.24 The op–cp transition is energetically driven by an increase in adsorption interactions in the reduced pore volume, well reflected by an increase in adsorption enthalpy upon contraction, which was investigated both experimentally and computationally.25 The excess amount of adsorbate present in the pores of the op state before contraction (nop) in excess of the amount of adsorbate present in the cp phase after contraction (ncp), defines the amount of gas released upon NGA, further termed ΔnNGA.
| ΔnNGA = nop − ncp | (1) |
The structural contraction strongly depends on the softness of the framework, and we recently found that shortening of the ligand backbone increases stability and consequently prevents NGA while elongation increases softness and resulted in the second known NGA material, DUT-50.26 Although this study demonstrated design principles towards other materials capable of NGA, the initial discovery and experimental adsorption conditions used in previous studies, such as methane adsorption at 111 K are very much serendipitous and were chosen for instrumental reasons to be able to record the full relative pressure range below ambient pressure and avoid the application of high pressure. Interestingly, observation of NGA upon adsorption of other gases such as n-butane (298 K),23 nitrogen (77 K),27 and xenon (200 K)28,29 was observed at temperatures close to the respective standard boiling point of the respective adsorptive, while no structural contraction and NGA was found to be present at elevated temperatures and pressures (methane 298 K, xenon 273 K). In addition, structural contraction without the presence of NGA similar to adsorption behavior found for MIL-53 (ref. 19 and 20) is observed upon adsorption at reduced temperatures for some gases (n-butane at 273 K, xenon at 195 K). Consequently, three distinct adsorption trajectories have been identified for DUT-49: structural contraction without NGA, structural contraction with NGA, and no adsorption-induced structural contraction (Fig. 1).
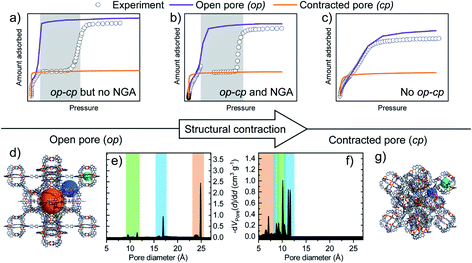 | ||
| Fig. 1 Adsorption isotherms of DUT-49 upon (a) structural contraction without NGA, (b) structural contraction with NGA, and (c) no structural transition (grey area indicates presence of cp phase), (d) crystal structure of DUT-49op and (e) corresponding pore size distribution (d and e both taken from ref. 26, 2019), (f) corresponding pore size distribution and (g) crystal structure of DUT-49cp. Cuboctahedral pore green, tetrahedral pore blue, octahedral pore orange. | ||
For the adsorption of methane, NGA was observed over an extended temperature range of 91–121 K.23 However, within this temperature window the values for ΔnNGA were found to vary non-monotonically and a similar behavior was observed upon adsorption of n-butane (273–303 K) and xenon (195–273 K). Guest-free DUT-49op was found to exhibit no temperature-induced structural contraction in the range of 77–600 K and only minor elastic negative thermal expansion was found using variable temperature PXRD.23 Computational analysis of the structural transition supports this finding and showed that entropic and temperature effects in the solid phase have negligible contributions to the structural contraction and NGA.24 Structural contraction upon adsorption of methane, investigated by in situ PXRD, was found to yield identical cp phases in the temperature range of 91–120 K demonstrating that ΔnNGA is not a function of variation in structural contraction.23 Consequently, the origin of variation in NGA-behavior is expected to originate from the temperature-dependent solid–fluid and fluid–fluid interactions. Hence, we raise the question: which adsorption conditions beyond structural contraction are required to obtain NGA and maximize ΔnNGA in DUT-49?
In this contribution we analyze the presence of NGA in DUT-49 experimentally by adsorption experiments with 14 different gases and vapors covering a temperature range of 21–303 K. From these experiments we derive an empirical correlation between the critical temperature of the fluid, the presence of NGA, and its magnitude defined by ΔnNGA. Furthermore, we rationalize the observed high and low temperature limits of NGA by making use of molecular simulations and define the criteria which might lead to the discovery of NGA in other flexible, and previously thought non-flexible, porous solids.
Results and discussion
Adsorption experiments
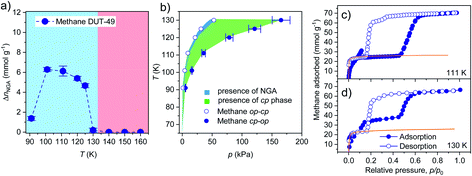
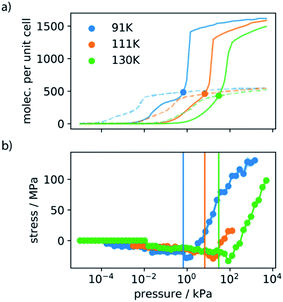
To ensure that the adsorption behavior is free of sample effects such as particle size and defects, which were found to impact NGA in DUT-49,27 a large batch of DUT-49 was synthesized and activated according to the previously published procedure.23 All experiments described in this work were conducted on samples from this particular batch. Using a home built high pressure adsorption cell connected to a helium closed-cycle cryostat system and commercial adsorption instrumentation, we are able to record adsorption/desorption isotherms with high accuracy in the temperature and pressure range of 7–310 K and 0.001–6 MPa (see ESI Section 2 for details†). Starting from the initial dataset of methane in the range of 91–121 K (ref. 23) we repeated and extended the temperature range by recording isotherms in the range of 91–190 K in steps of 10 K. Attempts to record methane adsorption isotherms at temperatures lower than 91 K were experimentally unfeasible due to condensation of the fluid in the sample cell. Interestingly, structural contraction evident by hysteresis at intermediate pressures and NGA are only observed in the temperature range of 91–130 K. From this adsorption data a phase diagram for the presence of the op and cp phase of DUT-49 upon adsorption of methane can be established (Fig. 2b). When compared to the phase diagram of methane adsorption in MIL-53,20 one of the few flexible MOFs known to undergo breathing transitions, the T–p range in which the cp phase is present is strongly reduced for DUT-49. This can be explained by the smaller pore size of the channels in MIL-53 that are expected to exhibit strong confinement-induced solid–fluid interactions even at elevated adsorption temperatures.20 Nevertheless, the shape and p–T range in which structural contraction occurs are similar for both materials, with the exception that a small range at the lower edge of the phase diagram shows the presence of NGA in DUT-49, experimentally not observed for MIL-53 so far.As previously observed, ΔnNGA values extracted from the isotherms in the range of 91–130 K show as a function of temperature, a non-monotonic evolution with a maximum of 6.15 mmol g−1 at 100 K. With increasing temperature, the hysteresis width at intermediate pressure which corresponds to the cp to op transition was found to shrink (Fig. 2c, d, and ESI Fig. 3†), and the plateau corresponding to adsorption in the cp phase was found to exhibit a higher uptake than expected for DUT-49cp (Fig. 2c and d). This behavior can either be assigned to the formation of intermediate phases (ip) or incomplete contraction of the bulk op phase. Both scenarios were previously observed upon adsorption of nitrogen at 77 K in DUT-49 samples with reduced crystal size.27 Upon desorption, isotherms in the range of 91–135 K exhibit an inverse hysteresis around the NGA step in which the desorption branch undercuts the adsorption branch (Fig. 2c and d). This indicates the structural contraction upon isothermal desorption from the pores. In the temperature range of 140–190 K no hysteresis was observed indicating the absence of structural transitions (ESI Fig. 3†). Consequently, recovery of guest free DUT-49op after NGA could be achieved by increasing the adsorption temperature at a pressure beyond 300 kPa, increasing the temperature beyond 160 K, and subsequently removing the methane in vacuum. This allows to cycle NGA by subsequently performing adsorption at reduced temperatures in the range of 91–130 K.
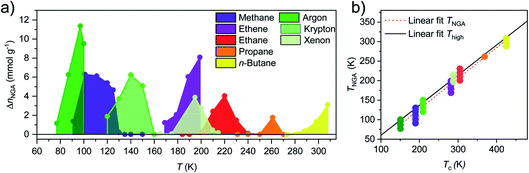
To investigate whether the non-monotonic evolution of ΔnNGA as a function of temperature is universal, the study on adsorption of methane was extended by first analysing a series of hydrocarbons and hydrogen at their respective standard boiling points or below (ESI Fig. 1†). Among these tested adsorptive/temperature combinations, hydrogen is the only adsorptive to show neither contraction or NGA. Methane (111 K) and ethene (169 K) exhibit NGA while the rest of the series exhibit contraction and hysteresis without the presence of NGA. As previously observed for n-butane,23 NGA was found to occur with increasing adsorption temperature. Thus, isotherms at temperatures above the boiling point were recorded for ethene, ethane, propane, and n-butane. With the increase in temperature from 169 to 199 K, ΔnNGA increases from 1.23 to 8.08 mmol g−1 upon adsorption of ethene (ESI Fig. 4†). The ΔnNGA value recorded at 199 K is the highest observed for all hydrocarbons investigated in this study. Upon adsorption of ethane, NGA is observable in the range of 200 to 240 K and ΔnNGA reaches a maximum of 4.03 mmol g−1 at 220 K. Above 220 K no NGA, and in the range of 184 to 220 K structural contraction without NGA, is observed (ESI Fig. 5†). NGA observed at 230 and 240 K occurs at 132 and 216 kPa, pressure amplification well above ambient pressure is required for air bag-type or pneumatic applications. The series of experiments was further extended with adsorption of propane in the temperature range of 231 to 298 K (ESI Fig. 6†). At the investigated temperatures, NGA is only observed at 261 K with a respective ΔnNGA value of 1.77 mmol g−1 and no contraction is observed at 298 K. The shape of the adsorption branch indicates that structural contraction occurs at all temperatures except at 298 K, without NGA however. To further characterize the nature of the structural transition we investigated DUT-49 further with in situ PXRD upon adsorption of propane at 231 K (ESI Fig. 17†) and ethane at 185 K (ESI Fig. 18†). In comparison to the structural contraction upon adsorption of methane at 111 K and n-butane at 298 K which was previously analysed,23 a similar cp formation is observed upon adsorption of ethane and propane (ESI Fig. 19†). However, severe peak broadening and the presence of an additional peak at lower diffraction angles in the case of cp formation upon adsorption of propane, indicate the formation of a more disordered state which might explain the difference in adsorption behaviour compared to other hydrocarbons. Nevertheless, in all cases DUT-49 responds in a comparable fashion which allows the direct comparison of the isotherms and NGA transitions. When including the previously published adsorption data of n-butane in the arrange of 273–308 K (ref. 23), an interesting trend can be observed: for each gas a non-monotonic evolution of ΔnNGA with temperature is observed (Fig. 3).
As described above, for each gas a low temperature limit is observed for which DUT-49 is found to contract with an absence of NGA, referred to as Tlow (the minimal T for which ΔnNGA > 0). With increasing temperature ΔnNGA is found to increase, reaching a maximum at a given temperature, TNGA. Following a further increase in temperature, a decrease in ΔnNGA is observed and an increase in uptake in the plateau after structural contraction is observed, which was previously assigned to incomplete structural contraction of the bulk sample demonstrated by in situ PXRD.27 At a certain upper temperature limit, referred to as Thigh (the maximum T for which ΔnNGA > 0), no structural contraction and reversible adsorption/desorption behaviour is observed. In the following, we thus define the temperature T = TNGA at which ΔnNGA reaches a maximum for a given adsorbate, T = Tlow for the low temperature limit of NGA, T = Thigh for the high temperature limit of NGA, and Thigh–Tlow thus defines the range where NGA is observed for a respective adsorptive.
Although all gases are hydrocarbon-based, their increase in chain length suggests that the observed behaviour is of a more general nature and not a factor of chemical composition. In fact, the same evolution of ΔnNGA was previously found upon adsorption of xenon used as a probe molecule for in situ NMR experiments.28,29 To test whether this observation is supported for other noble gases a series of adsorption experiments was conducted using argon and krypton in the temperature range of 77–110 K and 120–160 K, respectively. A comparable temperature dependent evolution of ΔnNGA is obtained for both gases with argon reaching a maximum of 10.5 mmol g−1 at 95 K, and krypton 6.3 mmol g−1 at 140 K. Interestingly, no NGA and structural contraction were observed upon adsorption of argon at 105 K, however structural contraction and inversed hysteresis were observed upon desorption in the low-pressure range. This indicates that the activation barrier for adsorption-induced contraction is lower upon desorption compared to the adsorption process, and might provide further insight to the irreversible contraction upon desorption of other adsorbates.
Most importantly, the experiments conducted demonstrate that NGA in DUT-49 can be obtained over a wide temperature range of 77–310 K by selecting the appropriate adsorbate. This is an important fundamental observation but might be also relevant for considering the utilization of NGA for pneumatic or other applications. However, the experiments raise two fundamental questions: first, is there a generalizable correlation for a family of adsorbates that enables prediction of the temperature range where there is presence of ΔnNGA; and secondly, what properties govern this observed temperature dependence of NGA?
Empirical correlation of Tc with TNGA
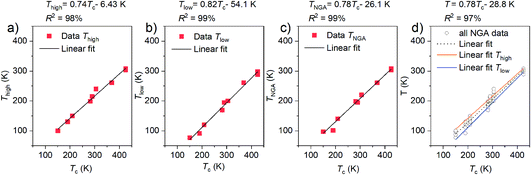
In cylindrical mesoporous solids, semi-empirical correlation of the pore critical temperature and the melting point depression with the critical temperature of the fluid are found for a variety of different pore sizes.30–32 Shrinkage and disappearance of the hysteresis loop at the hysteresis critical temperature reflects the temperature dependence of capillary condensation33 known to be related to NGA in DUT-49.26To probe the presence of a correlation we plotted the Thigh, Tlow, TNGA, and the whole temperature ranges against the physical properties of the applied gases such as the standard boiling point the critical temperature and their ratio (ESI Fig. 15†). In fact, the temperature range in which NGA is observed for each adsorptive shows a linear correlation with the critical temperature, Tc, of the fluid and is expressed in eqn (2)
| TNGA = iΔTc + j | (2) |
Parameters i and j were determined to be i = 0.74 and j = −6.43 K for Thigh, and i = 0.82 and j = −54.1 K for Tlow, thus setting the limits for TNGA which is fitted with parameters of 0.78 and −26.1 K, respectively. The similarity of the slopes i demonstrate that the temperature range of NGA for these gases is governed by a universal correlation. The difference in the j parameters obtained for both fits shows the average deviation of around 20 K between Thigh, Tlow, and TNGA. This variation is found to be well within the temperature steps of 10 K applied in the performed adsorption experiments and shows that the resolution of the experiments is high enough to detect NGA for other gases not applied in this study. The correlation of Tc with TNGA is particularly useful as it allows us to predict the temperature range in which NGA can be expected to occur and peak for other adsorptives. Because structural contraction with the absence of NGA did occur at or below the standard boiling point for long chain hydrocarbons, we can use eqn (2) and the derived parameters to estimate TNGA for other adsorptives. n-Pentane with a critical temperature of 469.6 K is expected to show NGA at 340 K, n-hexane (Tc = 507.6 K) at 369 K and n-heptane (Tc = 540.6 K) at 394 K. Hydrogen with a critical temperature of 33.1 K is expected to show NGA at 8.5 K, a temperature which is 13 K below the investigated temperature at which no structural contraction was observed. As demonstrated, ΔnNGA is found to first increase with increasing temperature. Thus, eqn (2) should not only allow us to estimate the temperature region in which NGA occurs, but also the temperature range in which ΔnNGA reaches its maximum, found to be close to max TNGA. This is demonstrated in the example of the adsorption of C4 hydrocarbons n-butane, 1,3-butadiene, and 2-methylpropane with Tc of 425.2 K, 425.1 K, and 407.7 K, respectively where ΔnNGA for the adsorption of n-butane and 1,3-butadiene at 298 K is comparable at around 1.3 mmol g−1 but over double this for the adsorption of 2-methylpropane. Although it was found that ΔnNGA decreases with increasing molar volume of the condensed fluid at the given adsorption temperature and saturation pressure (p/p0 = 1), which correlates in part with Tc, no direct correlation was found to allow estimation of the magnitude of ΔnNGA as a function of temperature based on the performed experiments. Even though the total uptake of condensed fluid in the pores of DUT-49op and cp can be estimated at saturation using the pore volume of the structures and the molar volume of the fluid, the magnitude of ΔnNGA is primarily dictated by how much the op phase can be overloaded beyond the intersection of the op/cp isotherms. This point of structural transition not only correlates to a specific loading of fluid, but also to a specific pNGA, the absolute pressure at which NGA occurs. Because adsorption isotherms as a function of absolute pressure are strongly impacted by the adsorption temperature, comparison of the relative pressure obtained from division with the vapour pressure, p0, at a given temperature allows us to compare isotherms at different temperatures at the same relative pressure range. In all experiments performed, structural contraction and NGA were found to be in the relative pressure region of 0.09 to 0.19 which correlates to the pressure range in which mesopore filling occurs, previously analysed by in situ neutron diffraction.26 With increasing T and ΔnNGA not only the absolute pressure of transition at which NGA occurs, pNGA, but also the relative transition pressure, pNGA/p0, was found to be shifted to higher pressures. Similar to the correlation between Tc and TNGA, the relative transition pressure pNGA/p0 was found to linearly grow with the critical pressure pc of the fluid (ESI Fig. 16†). To estimate an empirical correlation similar to the study on the temperature dependence, values of pNGA/p0 were taken at TNGA for the series of gases previously discussed. For some gases, the upper temperature limit of NGA has not been reached because ΔnNGA as a function of T was analysed in 10 K steps. This is expected to impact the accuracy of the pressure more drastically than for the previous correlation with temperature. Thus, an error for pNGA/p0 was estimated based on the resolution of the pressure range obtained from the conducted experiments. Using eqn (3), pNGA can be estimated for different gases using the vapor pressure p0 as a function of TNGA.
| pNGA = (lΔpc)Δp0 | (3) |
Due to the relatively low number of adsorption experiments around the upper temperature limit, the empirically estimated factor l of 0.032 is expected to underestimate pNGA. However, it does provide an estimation of the transition pressure at which contraction and NGA are to be expected, and thus presents another tool for narrowing the conditions in which NGA transitions are to be expected for a given adsorptive in DUT-49.
Canonical ensemble for determination of high temperature limit (Thigh)
Although the described empirical correlations provide guidelines for the discovery of NGA transitions in DUT-49 in the defined temperature and pressure ranges, the current study lacks an analysis of the fundamental thermodynamic and kinetic aspects responsible for the non-linear evolution of ΔnNGA with temperature. As described in eqn (1) NGA is merely an interplay between the adsorption properties of the op and cp phase in DUT-49. As the metastable region in the isotherm that represents the NGA transition is difficult to capture using existing experimental and computational techniques, as a first approximation we consider the presence of adsorption-induced structural contraction as a prerequisite for NGA to occur. Coudert et al. were previously successful in simulating the p,T phase-diagram of methane adsorption in MIL-53 using the osmotic ensemble, ΔΩOS(T,p), as a function of adsorption temperature, T, and pressure, p, the free energy difference between the open and contracted state, Fop–cp, and change in volume, Vop–cp, the adsorbed amount, nads, as well as the molar fluid volume Vm, described in eqn (4).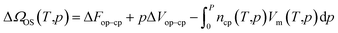 | (4) |
While detailed analysis about the guest-free structural transition and Fop–cp of DUT-49 has been performed24 in detail, the temperature dependent adsorption energetics are less well characterized. To analyze the energetics for adsorption-induced structural transition upon adsorption of methane in DUT-49 we thus simulated a series of isotherms for the op and cp phase in the temperature range of 91–190 K with 10 K steps using grand canonical Monte Carlo (GCMC) simulations. These simulations complement the previously discussed experimentally recorded isotherms. In general, we find good agreement between the simulated and experimental adsorption isotherms and capture the intersection of the isotherms of both phases with high accuracy validating the computational analysis and derived adsorption energetics. As a primary condition for NGA, we define structural contraction of the op phase beyond the crossing point of the isotherms of op and cp phase defined by the adsorbed amount nop–cp and pressure pop–cp. From the simulated isotherms these values can easily be defined and Δfi can now be expressed as a function of ΔnNGA using eqn (5).
| Δfi = ΔΩOS − ΔFop−cp | (5) |
The difference in osmotic potential not only allows us to characterize the energetic conditions for temperature dependent adsorption-induced contraction in DUT-49, it also allows the characterization of the free energy difference upon contraction as a function of ΔnNGA allowing us to define the limits of structural contraction. The p,n region in which Δf exceeds the energy required for structural contraction (ca. 900 kJ mol−1)24 matches well with the experimentally observed presence of structural contraction upon adsorption of methane (91–130 K). Please note we make a constant approximation for the free energy of structure contraction, ΔFop–cp, as entropy was previously reported to have a negligible contribution to the guest-free framework transition.24 This obtained thermodynamic analysis of the evolution of ΔnNGA, in particular the increase with decreasing temperature, is in contrast to the experimental observations. In fact, from an equilibrium thermodynamic standpoint it is impossible to predict the temperature dependence. One could argue that ΔnNGA is expected to decrease with decreasing temperature because |Δf|, the driving force accelerating the transition, increases with decreasing temperature. In this case ΔnNGA could exhibit negative values which would indicate a sudden jump towards a higher adsorbed amount in the isotherm (Fig. 5). However, this analysis is complicated by two important aspects intrinsically connected to NGA, the metastability of the transition and the desorption of gas upon structural contraction. Both features are not captured by the above methodology and thus do not allow us to draw any conclusion in the evolution of ΔnNGA with temperature. The conducted thermodynamic characterisation, however, does capture and rationalize the upper temperature limit, Thigh, for structural contraction very accurately and supports the empirical correlation of Tc and TNGA. In the next section, we rationalise the non-monotonic NGA behaviour and estimate ΔnNGA based on a different theoretical model – a mechanical model based on adsorption-induced stress.
Adsorption stress model for determination of the low temperature limit (Tlow)
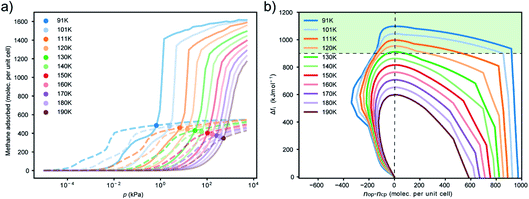
Analyzing the adsorption mechanism via in situ neutron diffraction and GCMC simulations we derived that the adsorption-induced stress occurring upon filling of the larger pores in the DUT-framework precedes the structural contraction. In fact, several studies on ordered mesoporous silicates show that the adsorption induced stress reaches a maximum value before capillary condensation occurs in the mesopores.2,34 This phase transition in the fluid phase is found to be metastable and is characterized by a hysteresis depending on the diameter of the pore. With decreasing adsorption temperature, the activation barrier for capillary condensation is found to increase and a widening of the hysteresis is observed.31,35,36 Recent computational analysis of the adsorption kinetics in carbonaceous materials demonstrated this metastable phenomena.37 However, these molecular simulations in a complex pore system, such as DUT-49, are computationally very challenging. Instead, we recently demonstrated that thermodynamic and kinetic conditions for NGA can be modeled in a simple slit-pore toy model.15Instead of simulating this complex full energy landscape we here consider NGA as a result of structural contraction induced by adsorption-induced stress. Characterization of the mechanical properties of the DUT-49 framework has estimated that the critical stress for structural contraction is in the range of 35 MPa, supported by experimental hydrostatic compression of DUT-49 crystals and molecular simulations.25 Rather than analyzing the metastability of NGA we decided to probe the region in which the adsorption-induced stress reaches a critical level for structural contraction. Adsorption stress isotherms were established for methane adsorption in DUT-49 using a series of classical molecular dynamics simulations in the NVT ensemble. We employed these simulations for methane adsorption at three temperatures at which NGA was experimentally observed, namely 91, 111 and 130 K (Fig. 6).
This adsorption-induced stress follows the non-monotonic behavior of many mesoporous materials.2,38 Although structural contraction and the presence of a metastable state beyond the crossing point of the isotherm (nop = ncp) are required for NGA and are strongly influenced by the mechanical properties of the framework, prior to this the mechanical role of the adsorbate has not been investigated. We observe that the process of methane adsorption can produce considerable adsorption-induced stress. Notably the minimum between −30 and −40 MPa compares well to the experimental transition pressures previously reported for hydrostatic compression.25 Since the structural contraction is found to be independent of temperature effects, especially in such a small temperature range, the critical stress for contraction might be assumed to be the same for all investigated temperatures. Similar to our previous analysis of the free energy change as a function of nop–ncp the adsorption stress isotherms can be transferred as a function of nop–ncp (Fig. 7).
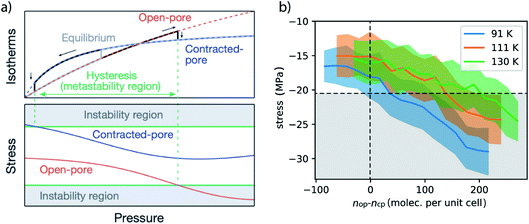 | ||
| Fig. 7 (a) A representation of a stress-based model for adsorption-induced structural transformations in DUT-49 reprinted from ref. 23, 2016. (b) Adsorption-induced stress in the range of the crossing point of the op and cp isotherms computed from 100 unique NVT simulations where the mean is plotted with standard deviations depicted by opacity. (a) is a partial reprint from ref. 23 and is reprinted with permission from Nature Publishing Group. | ||
Although the slope of the stress isotherms as a function of nop–ncp are comparable, they exhibit an offset towards increased ΔnNGA values with increasing temperature. To reproduce the ΔnNGA observed experimentally, ΔnNGA at 91 K is estimated at 50 CH4 per unit cell (calculated 2.6 mmol g−1, experimental 1.36 mmol g−1), 150 CH4 per unit cell (calculated 7.9 mmol g−1, experimental 6.1 mmol g−1) at 111 K and 200 CH4 per unit cell (calculated 10.5 mmol g−1, experimental 0.2 mmol g−1, estimated for complete op–cp transition 8.3 mmol g−1) at 130 K, the corresponding critical stress is in the range of −25 MPa to −20 MPa. This critical stress is in the same numerical range of the transition pressure of DUT-49 (35 MPa) measured by mercury intrusion, thus supporting the validity of this adsorption-stress model, which was initially tested on a very different material, namely the breathing of MIL-53.39,40 Changes in adsorption temperature will influence the adsorption in both phases and as a result the crossing point is shifted towards decreasing relative pressure with a decrease in temperature. Consequently, at lower temperature the critical adsorption stress appears to occur at a pressure where structural contraction is thermodynamically possible but at a pressure closer to the crossing point of the op–cp isotherms which in consequence leads to inferior ΔnNGA. With increasing temperature, the transition region is shifted to higher pressure as well as higher nop beyond the intersection of the isotherms, and thus results in enhancement of ΔnNGA.
Conclusion
In conclusion, we have demonstrated the presence of negative gas adsorption transitions upon adsorption of a series of hydrocarbons and noble gases in DUT-49 in defined temperature and pressure ranges. For each adsorptive, NGA was observed in a limited temperature range Thigh − Tlow, which linearly correlates with the critical temperature of the adsorptive. The empirical correlation was found to be universal for hydrocarbons as well as noble gases and allows us to predict the temperature range in which NGA is expected to occur for fluids not investigated in this study. From the experimental isotherms a non-monotonic evolution of ΔnNGA with temperature was observed with a high temperature and low temperature limit. The thermodynamic interactions responsible for these limits were further characterised by computational methods using methane adsorption as an example. First, the high temperature limit of adsorption-induced structural contraction was analysed using the osmotic ensemble on a series of GMCM modelled isotherms. It was found that beyond a certain temperature limit the change in adsorption energetics between the op and cp state no longer allows for compensation of the energy required for structural contraction. Although the computationally predicted upper temperature limit correlates well with experimental observations and thus provides a novel tool to predict structural contraction in the DUT-49 system ab initio, it provides no information on the experimentally observed lower temperature window and the evolution of ΔnNGA with temperature. Because kinetic analysis of adsorption in a large system like DUT-49 is so far not accessible, we instead decided to characterise the temperature dependence of the adsorption-induced stress responsible for structural contraction. With decreasing temperature, the magnitude of adsorption-induced stress increases at a given relative pressure. The stress minimum is found to be shifted with decreasing temperature to lower adsorption relative pressures, closer to the intersection of the isotherms of DUT-49op and cp. Consequently, ΔnNGA is found to decrease with decreasing temperature. The predicted transition pressures from the stress-based analysis correlate well with the experimental observations and allow us to replicate the evolution, and to some extent the magnitude, of ΔnNGA consequently providing an explanation for the observed non-monotonic NGA behaviour.The presented study on the role of temperature on NGA transitions addresses important questions. It mainly demonstrates that NGA is a physical phenomenon dictated by the solid–fluid and fluid–fluid interactions found to be general for a series of different gases in different temperature regimes. However, this study raises two questions: first, is the empirically derived correlation between TNGA and Tc valid for other adsorptives that exhibit enhanced solid–fluid and fluid–fluid interactions such as CO2 or other very polar gases? Secondly, is the analysis valid for other materials known to exhibit NGA such as DUT-50 with a very different pore size distribution, and can a more general correlation be found that links these parameters to the ones identified in the present study? Ideally, such correlations can be identified purely ab initio by the use of computational analysis. However, so far we are not able to compute the full energy landscape of gas adsorption in DUT-49 at different temperatures involving entropic and enthalpic factors occurring by the release of gas upon NGA, as well as the evolution of kinetic barriers known to be responsible for NGA to occur. Such computations might not only be helpful to characterize the system of DUT-49 in more detail but also help to identify novel NGA-capable porous solids. For now, rather simplistic thermodynamic and stress-based models, as well as empirical correlations derived from experimental analysis provide a conceptual guideline for the temperature range in which NGA is to be expected, potentially in systems other than DUT-49. For example, generally lower adsorption temperatures benefit structural contraction by enhanced adsorption-induced stress and thus present one of the prerequisites for NGA to occur.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 742743). The authors thank the BMBF (No. 05K19OD2) and ANR/DFG Programme FUN for financial support, and Helmholtz-Zentrum Berlin für Materialien und Energie for allocated 1 beam time at KMC-2 and travel funding. S. Krause thanks the Alexander von Humboldt Foundation for financial support. The authors would like to thank P. Iacomi, G. Maurin and P. Llewellyn for helpful discussions. J. D. E. acknowledges the support of the Alexander von Humboldt Foundation and HPC platforms provided by a GENCI grant (A0070807069) and the Center for Information Services and High Performance Computing (ZIH) at TU Dresden.References
- G. Ferey, Dalton Trans., 2016, 45, 4073–4089 RSC.
- G. Y. Gor, P. Huber and N. Bernstein, Appl. Phys. Rev., 2017, 4, 011303 Search PubMed.
- S. Horike, S. Shimomura and S. Kitagawa, Nat. Chem., 2009, 1, 695 CrossRef CAS.
- A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096 RSC.
- P. Freund, I. Senkovska and S. Kaskel, ACS Appl. Mater. Interfaces, 2017, 9, 43782–43789 CrossRef CAS.
- S. Wannapaiboon, A. Schneemann, I. Hante, M. Tu, K. Epp, A. L. Semrau, C. Sternemann, M. Paulus, S. J. Baxter, G. Kieslich and R. A. Fischer, Nat. Commun., 2019, 10, 346 CrossRef CAS.
- J. A. Mason, J. Oktawiec, M. K. Taylor, M. R. Hudson, J. Rodriguez, J. E. Bachman, M. I. Gonzalez, A. Cervellino, A. Guagliardi, C. M. Brown, P. L. Llewellyn, N. Masciocchi and J. R. Long, Nature, 2015, 527, 357–361 CrossRef CAS.
- M. K. Taylor, T. e. Runčevski, J. Oktawiec, J. E. Bachman, R. L. Siegelman, H. Jiang, J. A. Mason, J. D. Tarver and J. R. Long, J. Am. Chem. Soc., 2018, 140, 10324–10331 CrossRef CAS.
- L. Li, R.-B. Lin, R. Krishna, X. Wang, B. Li, H. Wu, J. Li, W. Zhou and B. Chen, J. Am. Chem. Soc., 2017, 139, 7733–7736 CrossRef CAS.
- L. Li, R. Krishna, Y. Wang, J. Yang, X. Wang and J. Li, J. Mater. Chem. A, 2016, 4, 751–755 RSC.
- H. Sato, W. Kosaka, R. Matsuda, A. Hori, Y. Hijikata, R. V. Belosludov, S. Sakaki, M. Takata and S. Kitagawa, Science, 2014, 343, 167–170 CrossRef CAS.
- D. Li and K. Kaneko, Chem. Phys. Lett., 2001, 335, 50–56 CrossRef CAS.
- T. Loiseau, C. Serre, C. Huguenard, G. Fink, F. Taulelle, M. Henry, T. Bataille and G. Férey, Chem.–Eur. J., 2004, 10, 1373–1382 CrossRef CAS.
- G. Férey and C. Serre, Chem. Soc. Rev., 2009, 38, 1380–1399 RSC.
- J. D. Evans, S. Krause, S. Kaskel, M. B. Sweatman and L. Sarkisov, Chem. Sci., 2019, 10, 5011–5017 RSC.
- F.-X. Coudert and A. H. Fuchs, Coord. Chem. Rev., 2016, 307, 211–236 CrossRef CAS.
- F.-X. Coudert, Chem. Mater., 2015, 27, 1905–1916 CrossRef CAS.
- S. M. J. Rogge, M. Waroquier and V. Van Speybroeck, Acc. Chem. Res., 2018, 51, 138–148 CrossRef CAS.
- A. Boutin, M.-A. Springuel-Huet, A. Nossov, A. Gédéon, T. Loiseau, C. Volkringer, G. Férey, F.-X. Coudert and A. H. Fuchs, Angew. Chem., Int. Ed., 2009, 48, 8314–8317 CrossRef CAS.
- A. Boutin, F. X. Coudert, M. A. Springuel-Huet, A. V. Neimark, G. Férey and A. H. Fuchs, J. Phys. Chem. C, 2010, 114, 22237 CrossRef CAS.
- H. Tanaka, S. Ohsaki, S. Hiraide, D. Yamamoto, S. Watanabe and M. T. Miyahara, J. Phys. Chem. C, 2014, 118, 8445–8454 CrossRef CAS.
- U. Stoeck, S. Krause, V. Bon, I. Senkovska and S. Kaskel, Chem. Commun., 2012, 48, 10841–10843 RSC.
- S. Krause, V. Bon, I. Senkovska, U. Stoeck, D. Wallacher, D. M. Többens, S. Zander, R. S. Pillai, G. Maurin, F.-X. Coudert and S. Kaskel, Nature, 2016, 532, 348–352 CrossRef CAS.
- J. D. Evans, L. Bocquet and F.-X. Coudert, Chem, 2016, 1, 873–886 CAS.
- S. Krause, J. D. Evans, V. Bon, I. Senkovska, S. Ehrling, U. Stoeck, P. G. Yot, P. Iacomi, P. Llewellyn, G. Maurin, F.-X. Coudert and S. Kaskel, J. Phys. Chem. C, 2018, 33, 19171–19179 CrossRef.
- S. Krause, J. D. Evans, V. Bon, I. Senkovska, P. Iacomi, F. Kolbe, S. Ehrling, E. Troschke, J. Getzschmann, D. M. Többens, A. Franz, D. Wallacher, P. G. Yot, G. Maurin, E. Brunner, P. L. Llewellyn, F.-X. Coudert and S. Kaskel, Nat. Commun., 2019, 10, 3632 CrossRef.
- S. Krause, V. Bon, I. Senkovska, D. M. Többens, D. Wallacher, R. S. Pillai, G. Maurin and S. Kaskel, Nat. Commun., 2018, 9, 1573 CrossRef.
- J. Schaber, S. Krause, S. Paasch, I. Senkovska, V. Bon, D. M. Többens, D. Wallacher, S. Kaskel and E. Brunner, J. Phys. Chem. C, 2017, 121, 5195–5200 CrossRef CAS.
- F. Kolbe, S. Krause, V. Bon, I. Senkovska, S. Kaskel and E. Brunner, Chem. Mater., 2019, 31, 6193–6201 CrossRef CAS.
- K. Morishige and M. Ito, J. Chem. Phys., 2002, 117, 8036–8041 CrossRef CAS.
- K. Morishige, N. Tateishi and S. Fukuma, J. Phys. Chem. B, 2003, 107, 5177–5181 CrossRef CAS.
- K. Morishige, H. Yasunaga and Y. Matsutani, J. Phys. Chem. C, 2010, 114, 4028–4035 CrossRef CAS.
- K. Morishige and M. Shikimi, J. Chem. Phys., 1998, 108, 7821–7824 CrossRef CAS.
- B. Kuchta, E. Dundar, F. Formalik, P. L. Llewellyn and L. Firlej, Angew. Chem., Int. Ed., 2017, 56, 16243–16246 CrossRef CAS.
- A. Wongkoblap, D. D. Do, G. Birkett and D. Nicholson, J. Colloid Interface Sci., 2011, 356, 672–680 CrossRef CAS.
- T. Hiratsuka, H. Tanaka and M. T. Miyahara, J. Phys. Chem. C, 2017, 121, 26877–26886 CrossRef CAS.
- S. Dantas, K. C. Struckhoff, M. Thommes and A. V. Neimark, Langmuir, 2019, 35, 11291–11298 CrossRef CAS.
- G. Y. Gor and A. V. Neimark, Langmuir, 2010, 26, 13021–13027 CrossRef CAS.
- A. V. Neimark, F.-X. Coudert, A. Boutin and A. H. Fuchs, J. Phys. Chem. Lett., 2010, 1, 445–449 CrossRef CAS.
- A. V. Neimark, F.-X. Coudert, C. Triguero, A. Boutin, A. H. Fuchs, I. Beurroies and R. Denoyel, Langmuir, 2011, 27, 4734–4741 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional experimental details, synthesis procedures as well as adsorption isotherms and in situ PXRD data. See DOI: 10.1039/d0fd00013b |
| This journal is © The Royal Society of Chemistry 2021 |