Active learning a coarse-grained neural network model for bulk water from sparse training data

Abstract

Neural network (NN) based potentials represent flexible alternatives to pre-defined functional forms. Well-trained NN potentials are transferable and provide a high level of accuracy on-par with the reference model used for training. Despite their tremendous potential and interest in them, there are at least two challenges that need to be addressed – (1) NN models are interpolative, and hence trained by generating large quantities (∼10⁴ or greater) of structural data in hopes that the model has adequately sampled the energy landscape both near and far-from-equilibrium. It is desirable to minimize the number of training data, especially if the underlying reference model is expensive. (2) NN atomistic potentials (like any other classical atomistic model) are limited in the time scales they can access. Coarse-grained NN potentials have emerged as a viable alternative. Here, we address these challenges by introducing an active learning scheme that trains a CG model with a minimal amount of training data. Our active learning workflow starts with a sparse training data set (∼1 to 5 data points), which is continually updated via a nested ensemble Monte Carlo scheme that iteratively queries the energy landscape in regions of failure and improves the network performance. We demonstrate that with ∼300 reference data, our AL-NN is able to accurately predict both the energies and the molecular forces of water, within 2 meV per molecule and 40 meV Å⁻¹ of the reference (coarse-grained bond-order potential) model. The AL-NN water model provides good prediction of several structural, thermodynamic, and temperature dependent properties of liquid water, with values close to those obtained from the reference model. The AL-NN also captures the well-known density anomaly of liquid water observed in experiments. Although the AL procedure has been demonstrated for training CG models with sparse reference data, it can be easily extended to develop atomistic NN models against a minimal amount of high-fidelity first-principles data.

---

Design, System, Application

Artificial neural networks (ANNs) for molecular simulations are currently trained by generating large quantities (on the order of 10⁴ or greater) of structural data in hopes that the ANN has adequately sampled the energy landscape both near and far-from-equilibrium. This can, however, be a bit prohibitive when it comes to more accurate levels of quantum theory. As such, it is desirable to train a model using the absolute minimal data set possible, especially when costs of high-fidelity calculations such as CCSD and QMC are high. Here, we present an active learning approach that starts with a minimal number of training data points, iteratively samples the energy landscape using nested ensemble Monte Carlo to identify regions of failure and retrains the neural network on-the-fly to improve its performance. We find that this approach is able to train a neural network to reproduce thermodynamic, structural and transport properties of bulk liquid water by sampling less than 300 configurations and their energies. This study reports a new active learning scheme with a promising sampling and training strategy to develop accurate force-fields for molecular simulations using extremely sparse training data sets. The approach is quite generic and can be easily extended to other classes or materials.

Introduction

Molecular dynamics (MD) is a popular simulation technique that is widely used to understand the evolution of structure and dynamics of materials. There are various flavors of MD ranging from the highly accurate ab initio molecular dynamics to the highly efficient coarse-grained molecular dynamics. The former is limited in system sizes (typically a few nanometers) and time scales (typically picoseconds) that can be accessed, whereas the latter is efficient (sizes up to micron and timescales in microseconds) but involves several approximations that reduce its predictive power. Molecular simulations employing classical force-fields rely strongly on the quality of the inter-atomic potential used to describe the interactions between the atoms or coarse-grained beads. Additionally, classical MD involves pre-defined functional forms to describe these interactions. Pre-defined functional forms are primarily motivated by physics and remain extremely popular owing to their high computational efficiency. Also, these functional forms have fewer parameters to train and as such, require less amount of training data to parameterize these functional forms. The use of pre-defined functional forms, however, can also limit the chemistry and physics that can be captured. Despite recent advances in data driven approaches that employ extensive training data sets and advanced optimization,^1–3 pre-defined functional forms impose serious limitations on the flexibility and transferability of force-fields (e.g. metals to oxides).

In this context, it should be noted that neural network based potential models^4–7 provide flexibility and can simultaneously be efficient if appropriately trained. NN models are emerging as a popular technique owing to the rapid advancement in the computational resources as well as a myriad of electronic structure codes that allow for efficient generation of training data. Bulk of the work on NN models is on representing atomistic interactions, with an underlying aim to retain first-principles accuracy at a comparatively lower computational cost. Nonetheless, NN potentials remain expensive compared to pre-defined functional forms and improving the efficiency remains a challenge. The other challenge with NN models is the need for large amounts of training data – NN models are interpolative, and as such the traditional approach for training NNs has relied on generating as large training data as possible. Often, large-scale generation of high-fidelity training data can become challenging.

To address the time scale challenge of the DNN models, one can circumvent their high computational cost via coarse-graining. CG models tend to sacrifice accuracy to gain efficiency. Zhang and co-workers have recently introduced a deep-learning coarse-grained potential (DeePCG) that constructs a coarse-grained neural network trained with full atomistic data that preserves the natural symmetries of the system.⁸ These models sample configurations of the coarse-grained variables accurately albeit at a much lower computational cost than the original atomistic model. Our previous work on the development of a CG-DNN model showed that one can accurately predict both the energies and the molecular forces of water, within 0.9 meV per molecule and 54 meV Å⁻¹ of a reference (bond-order potential) model.⁶ While this CG-DNN water model provides good prediction of several structural, thermodynamic, and temperature dependent properties of liquid water, it did require elaborate training data, i.e. energies of ∼30 000 bulk water configurations. Generating such extensive training data is difficult, especially if one is interested in high-fidelity calculations such as quantum Monte Carlo (QMC).

There have been several recent efforts on the use of active learning strategies to address the challenge of generation and efficient sampling of training data for NN models. Smith et al. have employed active learning (AL) via Query by Committee (QBC) to develop a machine learning model.⁹ QBC uses the disagreement between ensembles of ML potentials to infer the reliability of the ensemble's prediction. QBC automatically samples regions of chemical space where the potential energy is not accurately represented by the ML potential. They validated their AL approach on a COMP6 benchmark containing a diverse set of organic molecules. They demonstrated that one requires only 10% to 25% of the data to accurately represent the chemical space of these molecules. Likewise, Zhang et al. have developed an active learning scheme (deep potential generator (DP-GEN)) that can be used to construct machine learning models for molecular simulations of materials.^10,11 Their procedure involves exploration, generation of accurate reference data, and training. Using Al and Al–Mg as examples, they demonstrate that ML models can be developed with a minimum number of reference data. On the other hand, Vandermause et al. have recently introduced an adaptive Bayesian inference method to automate the training of low-dimensional multiple element interatomic force fields using structures sampled on the fly from AIMD.¹² Their active learning framework uses internal uncertainty of a Gaussian process regression model to decide the acceptance of model prediction or the need to augment training data. The aim in these studies is to minimize the ab initio training data required to develop interatomic potential.

Here, we introduce an active learning (AL) strategy that starts with minimal training data (∼1 to 5 data points) and is continually updated via a nested ensemble Monte Carlo scheme that iteratively queries the energy landscape in regions of failure and improves the network performance. We choose water as a representative system given its various thermodynamic anomalies, which have proven to be a challenge for modeling.¹ Liquid water exhibits its density maximum at 277K.⁶ Several existing water models fail to capture the density anomaly accurately.⁷ One of the main barriers to the development of accurate CG-DNN models is the lack of large amount of high-quality data that are essential for understanding neural network topology, basis functions and parameterizations for capturing a wide range of water properties across different thermodynamic conditions. Given these challenges, water represents an excellent test system for testing the efficacy of our AL learning procedure. Note that our focus is not on developing a new coarse-graining procedure, but instead is on the ability to train a CG-DNN using sparse training data. We show that our AL-NN is able to adequately represent the CG energy landscape and the thermodynamic and structural properties of water by sampling minimal amount of reference data (∼300 total reference data).

Methods

Our AL strategy is shown schematically in Fig. 1 and involves the following major steps: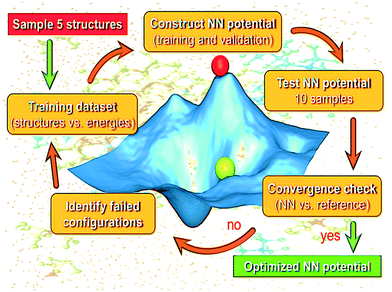

Fig. 1 Schematic showing the active learning workflow employed for the generation of the NN potential model for bulk liquid water.

1. Training of the NN using the current structure pool (of bulk water configurations).

2. Running a series of stochastic algorithms to test the trained network's current predictions.

3. Identification of configurational space where the NN is currently struggling.

4. An update of the structure pool with failed configurations.

5. Retraining of the NN with the updated pool and back to step 2.

To test our AL scheme, we train a neural network to a reference Tersoff based coarse grained water model (BOP water), which contains two and three body terms in its functional form.¹ The neural networks used in this study were constructed and trained using the Atomic Energy Network (AENet) software package,¹³ which was modified to implement the active learning scheme outlined above. Simulations using these networks were carried out using AENet interfaces with the Classy Monte Carlo simulation software to perform the AL iterations. The main steps in our active learning iteration include the following:

NN architecture

Our NN consists of four layers of neurons; all the neurons/nodes of a layer are connected to every node in the next layer by weights in the manner of an acyclic graph. The two intermediate layers (hidden layers) consist of 10 nodes each. The input layer has 50 nodes, which hold 50 symmetry functions that represent coordinates of the water's potential energy surface (PES). The network parameters used here were taken from previous work (ref. 6) in order to maintain an accurate comparison between this network and networks trained using more traditional approaches. The output layer consists of one node that represents the potential energy of a water molecule in a given configuration. Besides, the input layer and the hidden layers contain a bias node that provides a constant signal to all the nodes of its next layer. The choice of this network topology is based on a large number of trials for capturing temperature dependent properties. Within this network topology, the three-dimensional Cartesian coordinate of the centroid of a water molecule i in its liquid state is mapped into rotational and translational invariant coordinates as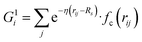 and 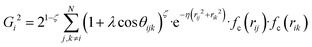, where 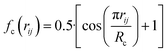for r_ij < R_c and f_c(r_ij) = 0.0 otherwise. The indices j and k run over all the neighboring particles within a cut-off distance of R_c = 3.5 Å. We have used 25 radial symmetry functions G¹ each with a distinct value of η, which are tabulated in Table 1. Similarly, 25 angular symmetry functions G² are used, each with a distinct set of values. The parameters of these 25 angular symmetry functions are reported in Table 2. The functional forms of these symmetry functions (Behler–Parrinello type symmetry functions, which include many body interactions) have been used successfully to construct a PES of different molecular systems including water.^14–16

Table 1 Parameters of the 25 radial symmetry functions, G¹, that describe a local physiochemical environment within a cut-off distance of R_c = 3.5 Å. We chose the shift parameter R_s to be 0.0

G ^1	η (Å^−2)	G ^1	η (Å^−2)	G ^1	η (Å^−2)	G ^1	η (Å^−2)	G ^1	η (Å^−2)
1	0.00417	6	0.01551	11	0.0576	16	0.21386	21	0.79406
2	0.00543	7	0.02016	12	0.07488	17	0.27802	22	1.03229
3	0.00706	8	0.02621	13	0.09734	18	0.36143	23	1.34197
4	0.00917	9	0.03408	14	0.12654	19	0.46986	24	1.74456
5	0.01193	10	0.04430	15	0.16451	20	0.61082	25	2.26790

---

Table 2 Parameters of the 25 angular symmetry functions, G², that describe a local chemical environment within a cut-off distance of R_c = 3.5 Å

G ^2	η (Å^−2)	λ	ζ	G ^2	η (Å^−2)	λ	ζ
1	0.0004	1	2	14	0.0654	1	4
2	0.0054	1	2	15	0.0704	1	4
3	0.0104	1	2	16	0.0754	−1	4
4	0.0154	−1	2	17	0.0804	−1	4
5	0.0204	−1	2	18	0.0854	−1	4
6	0.0254	−1	2	19	0.0904	1	5
7	0.0304	1	3	20	0.0954	1	5
8	0.0354	1	3	21	0.1004	1	5
9	0.0404	1	3	22	0.1054	−1	5
10	0.0454	−1	3	23	0.1104	−1	5
11	0.0504	−1	3	24	0.1154	−1	5
12	0.0554	-1	3	25	0.1204	1	6
13	0.0604	1	4

---

Here, we employ the generalized representation of NNs for constructing the PES.¹⁵ Within this representation, each molecule of a given configuration is represented by a NN. The total energy of a configuration is thus obtained as a sum of the molecular energies, defined as 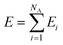, where E_i is the output of the i^th NN and N_A is the total number of molecules in a given configuration. We note that the architecture and weight parameters of all the molecular NNs are identical. During the training, the symmetry functions of each molecule of a configuration are fed to the corresponding NN via its input layer. In every NN, all the compute nodes in the hidden layers receive the weighted signals from all the nodes of its previous layer and feed them forward to all the nodes of the next layer via an activation function 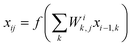. Here, f(x) = tanh(x) is used as the activation function for all the compute nodes. As mentioned earlier, the sum of all the outputs from all the NNs serves as the predicted energy of the system. The error in the NNs, which is the difference between the predicted and reference energies of a given configuration, is propagated backward via the standard backpropagation algorithm.¹⁷ All the weights that connect any two nodes are optimized using the Levenberg–Marquardt method¹⁸ in order to minimize the error, as implemented within the framework of AENet¹³ open-source code (see the next sub-section for details).

NN training and optimization

The Levenberg–Marquardt approach was used to optimize the neural network weights for each AL generation. This was carried out with a batch size of 32 structures and a learn rate of 0.1 once the structure pool was large enough to accommodate these settings. Initially, the batch size was set to 1, given the small initial training data set. For each network generation, the neural network is trained for a total of 2000 epochs, where each epoch represents one complete training cycle. The AENet makes use of a k-fold cross validation scheme, where a given fraction (k) of the training set is not used for the objective minimization. Thus, the data are partitioned into k equal-sized subsets, where k = 10, i.e. its a ten-fold validation. Then, the model is trained k times, each time with one of the k partitions left out, which is used for validation and the rest (k − 1) for training. The NN with the lowest CV error is then picked during each complete training cycle or epoch (see the ESI† for a typical plot). Note that the next AL epoch is initiated with this NN. For each AL iteration, therefore, the network which had the lowest error from the cross validation was chosen as the best network for this AL iteration and is carried forward.

Configuration sampling

Once the best network has been chosen, a series of simulations are run to actively sample the configurational space predicted by the current NN. It was found that MD is not suitable for sampling within this scheme due to the fact that when the network is still in its infancy, large spikes in the forces can lead to unphysical acceleration of particles within the simulation box. In addition, even in a reasonably well-trained network, MD can be trapped in a local energy well that prevents it from searching the phase space outside of this well. This can often create models that work well within the trained local minima, but can have catastrophically bad predictions when the models are applied to environments found outside of the training set. Monte Carlo and other similar sampling methods, in contrast, are much less sensitive to spikes on the energy surface, which make them more suitable methods for sampling poorly trained energy landscapes.

In addition, a wide collection of non-physical moves or non-thermal sampling approaches can be used. For the purposes of this work, the Boltzmann based Metropolis sampling and a nested ensemble based approach¹⁹ were used to generate the structures for each AL iteration. This was performed to gather information on both thermally relevant structures predicted by the neural network as well as higher energy structures, which may still be important for creating an accurate model. The Metropolis simulation was run for 5000 MC cycles at 300 K with the initial structure being randomly picked from the current neural network training pool. The nested ensemble simulations were run for another 5000 cycles. Here, a Monte Carlo cycle is defined as the number of moves such that on average each particle has a chance to move at least once. This is traditionally performed to facilitate a comparison to molecular dynamics, where every particle moves on the same time step. Thus, if there are N molecules in the system, a cycle is defined as N attempted moves.

Note that the nested sampling works by a halving approach with respect to the density of states. Initially, when the nested-MC simulation is performed, the atoms are allowed to move around freely with no rejection. During this stage, the probability as a function of system's potential energy is collected. After a specified number of cycles, the median energy value of the population is estimated from the probability distribution. This value now becomes the new maximum limit for the system. During the next run, if a given move will cause the system energy to go above the median value from the previous run, the move is rejected and returned to the previous state in a manner analogous to the Metropolis sampling. After the same amount of time, the median energy of this run is computed and used as the maximum limit of the next run. This is continuously applied until the system is stuck (implying a local minima has been found) or the maximum number of cycles is achieved.

The primary purpose of a nested sampling approach is that it is able to identify not only situations where a potential energy surface is under-predicted, but also situations where it is grossly over-predicted and will be naturally blocked from access under thermal sampling. It ensures a nice spread from very high energies (∼+0.01 eV per atom) down to the most stable configurations (≃0.42 eV per atom). This combats the entropic problems in sampling, where there are far more high energy structures than low energy ones and also combats problems associated with thermal sampling in that it can access high energy regions to look for configurations that are over-predicted by the neural network.

Testing of the NN

After the stochastic sampling step is completed, a set of 10 structures are gathered from the trajectory files of the Metropolis and nested sampling files. The real energy of these structures is computed and compared. For each structure, if the neural network prediction and the exact energy do not agree within a given tolerance, the structure is then added to the training pool to be used for the next AL iteration. This entire process is continued until the exit criteria is hit. For this work, we specified that if no new structures were added in 5 consecutive AL iterations, the potential has converged. For the addition tolerance, we specified that any structure with a difference greater than 1 meV between the real energy and predicted energy should be added to the training pool.

Initialization of the AL-NN

The initial neural network cannot be trained on zero data; therefore, a single structure is used to seed the initial neural network in order to kick off the training process. A reasonably minimized structure was chosen in order to ensure at least one low energy configuration was contained in the training set. Theoretically, one could begin with any number of seed structures, but for the purposes of evaluating the efficiency of this approach, the absolute minimal seed data were used. It is worth noting that one would require much more than one structure to train a NN, which has many weights or parameters that need to be optimized. During the early stages of configuration sampling using the (poorly trained) NN as the energy landscape, it is natural that the NN will generate wild high-energy configurations. The primary reason to start with just 1 configuration was to minimize the amount of user input and allow the algorithm to figure out what is needed on its own. A single seed structure was used as it is the bare minimum required to train the initial network since it's not possible to train a network on zero data. The initial network is of course very poor in quality because it lacks a lot of information. So, usually in the first several iterations, every structure is accepted into the training pool with a 100% acceptance rate. As the algorithm moves on, the network predictions improve incrementally as it continues to identify new structures. However, this is by design, since we are looking for the smallest training data that has the minimal human bias introduced into the training set. Seeding with too much data can cause problems associated with biasing or over-sampling of certain regions in the configurational space.

In order to rigorously validate the neural network models, we created a test set that consists of roughly ∼150 000 bulk configurations of liquid water. Each bulk configuration for training and testing has 108 water molecules. The test set was generated using a combination of nested, random, and thermal sampling employing the reference (Tersoff) potential to derive as diverse a set of system configurations as possible.

Results and discussion

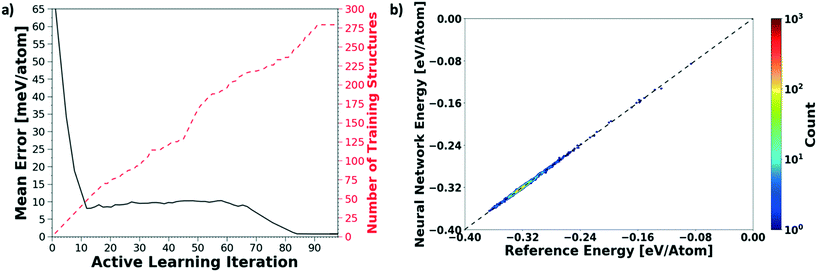
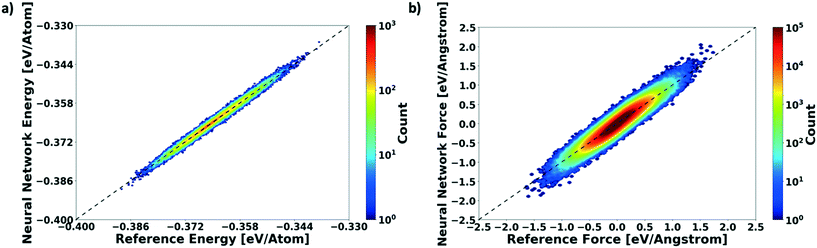
We evaluate the performance of our active learning (AL) scheme outlined in the Methods section. The mean absolute error (MAE) in meV per atom as a function of the AL iterations is depicted in Fig. 2(a). Note that each AL iteration corresponds to an epoch or complete training cycle. The RHS ordinate in Fig. 2(a) corresponds to the number of structures added for each AL iteration. The NN training begins with the minimal number of training configurations. As a consequence, the NN has high errors, ∼65 meV per atom. As the NN learns and samples configurations in regions of failure, the errors drop progressively from ∼65 meV per atom at iteration 1 to less than 2 meV per atom at iteration ∼90, as more distinct (failed) structures are added to the pool. Initial training errors are nearly on the same magnitude as the total system energy of ∼100 meV per atom. The MAE drops sharply and plateaus around 5 meV per atom at AL iteration ∼10, which may suggest that the NN search has reached the local minimum. Eventually, we see that the MAE drops to ∼1.2 meV per molecule. After about a total of 100 AL iterations, our system finally reaches the stopping criteria, i.e. no new structures are added during 15 consecutive test cycles. At this point, the final structure count reaches a total of 275 unique training structures. Fig. 2(b) shows the correlation plot showing the performance of the final optimized network on the 280 structure training set. The predictions of the AL-NN are compared against the energies for the reference model. The mean absolute error for the training set was found to be less than 2 meV per molecule.

Fig. 2 Active learning of a NN potential for bulk liquid water. (a) We plot the mean absolute error of the AL-NN tested on the 150 000 bulk water test set given as a function of active learning iteration or generation (solid black curve). The scale on the RHS of the plot shows the size of the training data (dashed red curve) for the same training generation. (b) A correlation plot showing the performance of the final optimized network on the 280 structure training set. The predictions of the actively learnt NN are compared against the energies for the reference model. The mean absolute error for the training set was found to be <2 meV per atom.

To measure the network performance as a function of the number of AL iterations, we choose the best network from each AL iteration and use it to predict the energy on a test set that comprises 150 000 configurations and their energies. The correlation between the energy predicted by the AL-NN and the reference energy (BOP energy) for the training data sets generated over the course of the active learning is shown in Fig. 3a. As expected, we find that the final optimized network is able to reliably predict the cluster energies for the test data set generated not only in the near equilibrium, but also in the highly non-equilibrium region that extends far beyond. In addition to evaluating the performance of the energy predictions of the AL-NN, we also evaluate its performance for forces. Note that the forces were not included as a part of the training during the AL iterations. The correlation plot comparing the predicted and reference forces is shown in Fig. 3(b). Each point in the correlation plot represents the reference and predicted values of one of the force components, Fx, Fy and Fz, acting on a particle. The overall MAE between the reference and AL-NN predicted forces was found to be ∼40 meV Å⁻¹. Considering that the network had not been trained on the forces, the agreement was found to be of excellent quality. Overall, the AL-NN optimized network performs satisfactorily over the extensively sampled configurations in the test data set.

Fig. 3 Performance of the actively learned NN model on an extensively sampled test data set. (a) Energy correlations comparing actively learnt NN-prediction with the reference BOP energy for a test set that comprises 150 000 configurations. The dotted line represents the zero MAE. (b) Force correlations comparing actual force derived from reference analytical model versus that derived from the actively learnt NN over the same test set. The color bar indicates the number of molecular configurations at a specific value of energy (a) or force (b).

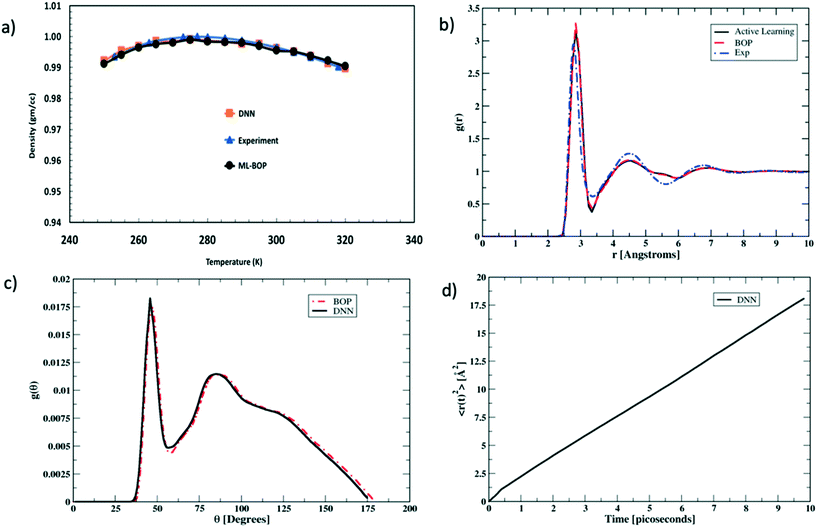
We next rigorously assess the performance of the actively learnt NN water model by computing the various temperature dependent properties of liquid water as obtained from our MC simulations. The MC simulations are all performed under an isothermal isobaric (NPT) ensemble at P = 1 bar and the temperatures are varied in the range of 250–320 K to extract the bulk water properties. Each simulation consisted of a system of bulk water with 1024 water molecules. The systems are equilibrated for 10⁵ MC cycles in a periodic simulation box. The equilibration run is then followed by another 10⁵ MC cycles to perform the production run. At each temperature, the values of the properties are averaged over four independent production runs. Fig. 4 compares one such temperature dependent property computed using our actively learnt NN model vs. the predictions of our reference BOP coarse-grained model as well as experimental²⁰ values. The reference properties for the BOP model are computed from MD simulations performed using LAMMPS.²¹Fig. 4a shows the performance of the models in capturing the most famous density anomaly of liquid water. The actively learnt NN predicts the temperature of maximum density (TMD) to be T = ∼278 K, which is close to both the target BOP model (TMD = ∼280 K) and the experimental values (TMD = 277 K). Overall, we find that the actively learnt NN predicts temperature dependent density values that are well within 0.01 gm cc⁻¹ of the reference model and experiments. For instance, our AL-NN predicts a liquid water density of 1.001 gm cc⁻¹ at T = 300 K, which is in excellent agreement with the BOP predicted value of 0.9997 gm cc⁻¹. Overall, our actively learnt NN model captures the correct temperature–density correlation in liquid water (including capturing the notoriously difficult density anomaly of liquid water).

Fig. 4 Evaluating the performance of the actively learned NN model using properties of liquid water computed via molecular simulations. (a) The water density as a function of temperature is shown for the actively learned NN and the reference BOP model used for training. The experimental data are also shown for comparison. (b) The radial distribution functions calculated based on the actively learned NN and BOP potentials are compared along with the experimental data for temperature T = 300 K. (c) Angle distribution function P(θ) for the actively learned NN and BOP models at T = 300 K. (d) Transport properties evaluated at T = 300 K. Mean square displacement of a molecule (〈r²(t)〉) in liquid water at T = 300 K is computed via MD simulations using the actively learned NN model.

We next assess the structural predictions by evaluating structural correlation functions such as the radial distribution function (RDF) and angular distribution function (ADF) of liquid water at a representative temperature of T = 300 K. Fig. 4b and c compare the RDF and ADF between the actively learnt NN and the BOP model, respectively. The RDF in our AL-NN water model displays 1st, 2nd and 3rd peak (corresponding to the first, second and third coordination shells, respectively) at r = 2.8 Å, 4.5 Å, and 6.8 Å. Likewise, the ADF for our AL-NN shows the 1st and 2nd peaks at θ = ∼ 47° and θ = ∼ 95°, respectively. Both the RDF and ADF peak positions are in excellent agreement with those of the reference BOP model. Moreover, there is an excellent quantitative agreement, i.e. the peak intensities and width of both models for the RDF and ADF are also in excellent agreement. As shown in Fig. 4b, we observe that the predicted RDF minimum for the AL-NN at ∼3.4 Å is deeper than the experimental RDF.²² This might indicate the over-structuring of liquid water, where the exchange of molecules between the first and second coordination shells is underestimated. The over-structuring feature is also evident in the reference model. However, the average coordination number of water molecules, i.e., number of water neighbors in the first solvation shell, integrated out to the experimentally determined temperature independent isosbestic point (r = 3.25 Å), is 4.7. This is in excellent agreement with the typical range of 4.3–4.7 observed in experiments.^22,23 Overall, the AL-NN model reasonably captures the molecular structure of liquid water. We further assess the dynamical properties of the AL-NN by performing MD simulations in an NPT ensemble using the ASE open source package.²⁴Fig. 4d shows the block averages of the mean square displacement (MSD) of a water molecule at T = 300 K obtained over the first 10 ps of an MD simulation. The calculated water diffusivity from the slope of the MSD curve is ∼3.05 × 10⁻⁵ cm² s⁻¹, which is close to the value of 3.04 × 10⁻⁵ cm² s⁻¹ predicted by the BOP model and the experimental value of 2.3 × 10⁻⁵ cm² s⁻¹.²⁵

We find that the quality of the output network is more highly correlated to data quality than data quantity, meaning that simply flooding the training process with data can actually produce worse results compared with the most commonly used loss functions. The primary problem of a lot of current approaches is oversampling, i.e. an excess of training in one area and a lack of training data in another. We note that the AL training is able to adequately sample the configurational space while minimizing the number of training configuration. In some of our initial tests of the AL workflow, we observed that over representation of a given region can bias the data and influence the neural network's weight fitting procedure. If a given area of the phase space has several samples of the structures, i.e. over-sampled compared to another region, the fitting process is able to achieve a low loss function value by simply fitting the over-represented region well. Unfortunately, this occurs at the expense of the less represented regions. An over-abundance of one type of data is actually a problem for training a neural network, which we address in this work. Hence, we do not include all the expensive ground-truth calculations primarily to avoid degeneracy, which helps improve the predictive power of the trained network.

Conclusions

We introduce an automated AL workflow for training NN force-fields from sparse training data. We choose bulk liquid water as a representative system given its various thermodynamic anomalies, which have proven to be a challenge for molecular models. Our AL scheme starts with minimal reference data and uses a nested ensemble Monte Carlo to perform on-the-fly sampling of the configurational and potential energy surfaces. We iteratively sample configurations in regions of failure and improve the network performance. Our AL scheme produces an optimal high-quality neural network with a sparse data set, i.e. total sampled bulk configurations included were only 280 unique bulk water structures. We test the network performance in terms of energies and forces of bulk configurations (over an extensively sampled test set of ∼150 000 samples) that were not included in training. We further rigorously assess the performance of the optimized NN in predicting the thermodynamic and structural properties of liquid water. The AL-NN trained network captures the temperature dependent variation of the density of liquid water, which is in excellent agreement with those of the reference model and experiments. More importantly, it captures the density anomaly with a TMD of ∼ 278 K. The structural predictions and transport properties also agree well with both experiments and the reference model. Overall, the AL-NN model is able to capture several properties of bulk liquid water while training with the minimal number of reference data. In training NN models against high-fidelity reference data from quantum Monte Carlo (QMC) and coupled clusters (CCSD), one can only generate a limited number of training data. In this context, our AL scheme demonstrates the power of on-the-fly nested ensemble MC sampling of configurations from regions of failure to improve network performance with a minimal amount of training data.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Use of the Center for Nanoscale Materials and the resources from the Argonne Leadership Computing Facility was also supported by the U. S. Department of Energy (DOE), Office of Science, Office of Basic Science, under contract no. DE-AC02-06CH11357. This research used resources from the National Energy Research Scientific Computing Center, a DOE office of science user facility supported by the Office of Science of the US Department of Energy under contract no. DE-AC02-05CH11231. SKRS acknowledges faculty start-up grant from UIC.

References

1. H. Chan, M. J. Cherukara, B. Narayanan, T. D. Loeffler, C. Benmore, S. K. Gray and S. K. R. S. Sankaranarayanan, Machine Learning Coarse Grained Models for Water, Nat. Commun., 2019, 10(1), 379,  DOI:10.1038/s41467-018-08222-6.
2. H. Chan, B. Narayanan, M. J. Cherukara, F. G. Sen, K. Sasikumar, S. K. Gray, M. K. Y. Chan and S. K. R. S. Sankaranarayanan, Machine Learning Classical Interatomic Potentials for Molecular Dynamics from First-Principles Training Data, J. Phys. Chem. C, 2019, 123(12), 6941–6957,  DOI:10.1021/acs.jpcc.8b09917.
3. V. Botu, R. Batra, J. Chapman and R. Ramprasad, Machine Learning Force Fields: Construction, Validation, and Outlook, J. Phys. Chem. C, 2017, 121(1), 511–522,  DOI:10.1021/acs.jpcc.6b10908.
4. J. Behler, Constructing High-Dimensional Neural Network Potentials: A Tutorial Review, Int. J. Quantum Chem., 2015, 115(16), 1032–1050,  DOI:10.1002/qua.24890.
5. J. Behler, Perspective: Machine Learning Potentials for Atomistic Simulations, J. Chem. Phys., 2016, 145(17), 170901,  DOI:10.1063/1.4966192.
6. T. K. Patra, T. D. Loeffler, H. Chan, M. J. Cherukara, B. Narayanan and S. K. R. S. Sankaranarayanan, A Coarse-Grained Deep Neural Network Model for Liquid Water, Appl. Phys. Lett., 2019, 115(19), 193101,  DOI:10.1063/1.5116591.
7. T. Morawietz, V. Sharma and J. Behler, A Neural Network Potential-Energy Surface for the Water Dimer Based on Environment-Dependent Atomic Energies and Charges, J. Chem. Phys., 2012, 136(6), 064103,  DOI:10.1063/1.3682557.
8. L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, DeePCG: Constructing Coarse-Grained Models via Deep Neural Networks, J. Chem. Phys., 2018, 149(3), 034101,  DOI:10.1063/1.5027645.
9. J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, Less Is More: Sampling Chemical Space with Active Learning, J. Chem. Phys., 2018, 148(24), 241733,  DOI:10.1063/1.5023802.
10. Y. Zhang, H. Wang, W. Chen, J. Zeng, L. Zhang, H. Wang and E. Weinan, DP-GEN: A Concurrent Learning Platform for the Generation of Reliable Deep Learning Based Potential Energy Models. ArXiv191012690 Phys. 2019.
11. L. Zhang, D.-Y. Lin, H. Wang, R. Car and E. Weinan, Active Learning of Uniformly Accurate Interatomic Potentials for Materials Simulation, Phys. Rev. Mater., 2019, 3(2), 023804,  DOI:10.1103/PhysRevMaterials.3.023804.
12. J. Vandermause, S. B. Torrisi, S. Batzner, Y. Xie, L. Sun, A. M. Kolpak and B. Kozinsky, On-the-Fly Active Learning of Interpretable Bayesian Force Fields for Atomistic Rare Events, 2019, ArXiv:190402042 Cond-Mat Physicsphysics.
13. N. Artrith and A. Urban, An Implementation of Artificial Neural-Network Potentials for Atomistic Materials Simulations: Performance for TiO2, Comput. Mater. Sci., 2016, 114, 135–150,  DOI:10.1016/j.commatsci.2015.11.047.
14. J. Behler, Atom-Centered Symmetry Functions for Constructing High-Dimensional Neural Network Potentials, J. Chem. Phys., 2011, 134(7), 074106,  DOI:10.1063/1.3553717.
15. J. Behler and M. Parrinello, Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces, Phys. Rev. Lett., 2007, 98(14), 146401,  DOI:10.1103/PhysRevLett.98.146401.
16. T. Morawietz and J. Behler, A Density-Functional Theory-Based Neural Network Potential for Water Clusters Including van Der Waals Corrections, J. Phys. Chem. A, 2013, 117(32), 7356–7366,  DOI:10.1021/jp401225b.
17. Y. LeCun, L. Bottou, G. B. Orr and K.-R. Müller, Efficient BackProp, in Neural Networks: Tricks of the Trade, ed. G. B. Orr and K.-R. Müller, Lecture Notes in Computer Sciencem, Springer, Berlin Heidelberg, 1998, pp. 9–50,  DOI:10.1007/3-540-49430-8_2.
18. K. Levenberg, A Method for the Solution of certain non-linear problems in least squares, Q. Appl. Math., 1944, 2(2), 164–168.
19. S. O. Nielsen, Nested Sampling in the Canonical Ensemble: Direct Calculation of the Partition Function from NVT Trajectories, J. Chem. Phys., 2013, 139(12), 124104,  DOI:10.1063/1.4821761.
20. D. R. Lide, CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data, CRC Press, 1995.
21. S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117(1), 1–19,  DOI:10.1006/jcph.1995.1039.
22. L. B. Skinner, C. J. Benmore, J. C. Neuefeind and J. B. Parise, The Structure of Water around the Compressibility Minimum, J. Chem. Phys., 2014, 141(21), 214507,  DOI:10.1063/1.4902412.
23. A. K. Soper, The Radial Distribution Functions of Water as Derived from Radiation Total Scattering Experiments: Is There Anything We Can Say for Sure?, ISRN Phys. Chem., 2013, 1–67.
24. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dulak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al. The Atomic Simulation Environment—a Python Library for Working with Atoms, J. Phys.: Condens. Matter, 2017, 29(27), 273002,  DOI:10.1088/1361-648X/aa680e.
25. M. Holz, S. R. Heil and A. Sacco, Temperature-Dependent Self-Diffusion Coefficients of Water and Six Selected Molecular Liquids for Calibration in Accurate 1H NMR PFG Measurements, Phys. Chem. Chem. Phys., 2000, 2(20), 4740–4742,  10.1039/B005319H.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9me00184k

---