Molecules in confinement in liquid solvents: general discussion

Jeremy Richardson opened a general discussion of the paper by Petr Slavicek: Is there a simple one-dimensional model system we can use to test your approach against exact quantum mechanics?

Petr Slavicek responded: Linear potential is probably the most convenient test case as one can perform all of the calculations analytically (see also the answer to the next question). The use of the delta function constraint can also be justified within a more general semiclassical treatment of an excitation process with arbitrary laser pulse as outlined in ref. 1 (see also older related work in ref. 2 where the problem is discussed for a Gaussian shaped pulse). Here, an excitation Wigner function is introduced which is shown to be a Wigner function of the pulse envelope A(t), multiplied by the unfiltered Wigner function. For a constant envelope, we end up with the delta function.

1 A. Martínez-Mesa and P. Saalfrank, J. Chem. Phys., 2015, 142, 194107.

2 C. Meier and V. Engel, Phys. Chem. Chem. Phys., 2002, 4, 5014.

Jeremy Richardson added: Can you use this to rigorously justify using a delta-function constraint when the wave function of the excited state has the form of an Airy function?

Petr Slavicek replied: We ask the following question: what is the stationary state of the system prepared via a CW laser field which could be described within the spirit of classical mechanics? The linear potential is a good example as we know the exact solution: the wavefunction is represented by the Airy function, with the maximum slightly off the classical turning point. One can then show¹ that replacing the Airy function with a delta function centered at the classical turning point provides a Franck–Condon factor that is correct through the order a⁽⁻²⁾, where a = [2μE’(χ₀)/ℏ² ]^1/3.

1 E. A. Gislason, J. Chem. Phys., 1973, 58, 3702–3707.

Majdi Hochlaf asked: What is the influence of the S2 close lying electronic states in the further dynamics outcomes?

Petr Slavicek responded: The higher electronic states have very limited impact on the dynamics, especially when we model the system with the constraint on the excitation wavelength. Here, we restrict the excitation process into a region which is well separated from the higher electronic states.

Adam Kirrander remarked: The non-Condon excitation scheme proposed in your paper is intriguing. In first-order perturbation theory and in the long-pulse limit, the intensity of the transition is proportional to the dipole transition moment matrix element, which includes an integral over the nuclear coordinates and the coordinate-dependent vertical electronic transition moment. Such effects can be very important in symmetric molecules where otherwise forbidden transitions gain intensity (e.g. the Renner–Teller effect). In a quantum mechanical calculation, I would have calculated the initial state and the final state separately, and then gotten the strength of the transition from the first-order perturbation theory. Therefore, in my mind, there is a certain separation between the dynamics on the excited state and the transition itself. However, in your semiclassical treatment, the initial conditions bear a strong imprint of the excitation process. I would be curious to hear your comments on this.

Petr Slavicek responded: In our semiclassical approach, we weight the initial conditions by the oscillatory strength at each geometry. This can be disturbing at first view: in the long-pulse limit, we should generate a single stationary state and we should describe that state in semiclassical terms. The transition dipole moments should be important only for comparing the outcome of the simulations at different wavelengths. However, we cope with degeneracies in the manifold of the final states (especially in the context of multidimensional systems) and the weighting with the local oscillatory strengths seems to be a proper way of dealing with the situation.

Joel Bowman noted: Thanks for the thought provoking talk. In a semiclassical time dependent approach Heller argued that the initial conditions for propagation on the excited state should be in the initial wavepacket on the lower surface times the electronic transition moment.

Gilberte Chambaud asked: In Fig. 5 (DOI: 10.1039/c8fd00088c), you show the role of the correlation energy correction (CEC) of the potential energy surface (PES) on the shape of the distribution of the kinetic energy on the fragment Cl. Can you explain how you proceed to evaluate this correction and what part of the potential energy surface is more specifically concerned by this correction?

Petr Slavicek answered: The correction is based on the assumption that the missing part is the dynamical correlation related to the increasing distance between electrons within the dissociation process. We therefore decided to take the C–Cl distance as the only parameter for the correlation correction potential and adjust the potential in such a way that the dissociation energy reproduces high level ab initio methods. The assumption seems to be valid when we test this strategy for a dissociation of two chlorine atoms.

Jens Petersen commented: When using harmonic Wigner distributions for sampling initial conditions, in some cases of organic molecules very elongated C–H bonds can be observed, leading to artificially large bond oscillations and even bond breaking in the course of the molecular dynamics simulations. Did you experience similar behaviour with initial conditions generated via the quantum thermostat approach?

Petr Slavicek responded: We observe spurious effects when using Wigner sampling within harmonic approximation in weakly bound molecular systems. The reason is related to the coupling between the stiff and floppy modes (see also the next comment from Anne B. McCoy). While the stiff modes are essentially harmonic, the frequency is modulated by the instantaneous intermolecular arrangement. Previously, we have coped with the problem in a pragmatic way, discarding all of the frequencies below 500 cm⁻¹, see e.g. ref. 1. We do not encounter this type of problem with the quantum thermostat as the modes are coupled, even if only in an approximate fashion.

1 O. Svoboda, M. Ončák and P. Slavicek, J. Chem. Phys., 2011, 135, 154301.

Anne B. McCoy commented: I suspect that the problem with the Wigner distributions providing displacements of CH stretches that are unphysically large comes from the contributions of these stretches to the soft modes. When normal modes are constructed as linear combinations of cartesian displacements, large amplitude bend or hindered rotor motions have normal mode displacement vectors that lie perpendicular to the bond axis. As a result, large amplitude displacements of these coordinates can lead to significant changes in the corresponding bond length. This is illustrated in the cartoon, below, which has been reproduced from ref. 1. The length of the dashed line is the same in both images, but while the line connects to the arrow when the bend displacement is made in internal coordinates, there is a gap when the bend displacement is executed in Cartesian coordinates. The extension of an XH bond length through displacement of low-frequency modes can also lead to unphysical results when the harmonic Franck–Condon factors are calculated using these normal modes as was illustrated for CDCl₂⁻.² The above problem can be minimized by constructing the normal modes as linear combinations of displacements of internal coordinates as described by Wilson, Decius and Cross,³ and outlined in our contribution to this volume (DOI: 10.1039/c8fd00120k).

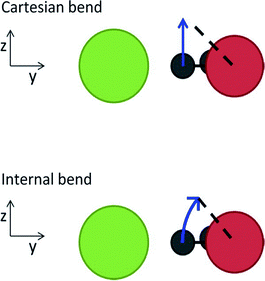Fig. 1 Illustrations of the out-of-plane bend in the Cl–·H₂O complex when the displacement is made in the normal mode based on Cartesian and internal coordinates. [reproduced from ref. 1]

1 A. B. McCoy, J. Phys. B, 2014, 118, 8286–8294.

2 K. M. Vogelhuber, S. W. Wren, A. B. McCoy, K. M. Ervin and W. C. Lineberger, J. Chem. Phys., 2011, 134, 184306.

3 E. B. Wilson, J. C. Decius and P. C. Cross, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, Dover, New York, 1955.

Petr Slavicek responded: Thank you for the comment, see also my answer to the question from Jens Petersen above.

Adam Kirrander commented: This enjoyable and interesting paper brought to mind work by Moshe Shapiro and Paul Brumer on the excitation process in first-order perturbation theory. They showed that one could, at least mathematically, gain insight into the excitation process by calculating something called the complex excitation function.¹ This function has many interesting properties that appear physically intuitive. For instance, the bandwidth initially perceived by the molecule is greater than the actual bandwidth, causing virtual states to be transiently excited, until the molecule has “experienced” the entire excitation pulse and the bandwidth is thus fully defined. At some point, we derived quite a bit of pleasure from calculating and visualising such complex excitation functions for various combinations of excitation pulses, including frequency combs^2,3 and phase-shaped pulses.^4,5

1 Moshe Shapiro and Paul Brumer, Principles of the Quantum Control of Molecular Processes, Wiley, 2003.

2 A. Kirrander, H. H. Fielding and Ch. Jungen, J. Chem. Phys., 2007, 127, 164301.

3 A. Kirrander, Ch. Jungen and H. H. Phys. Chem. Chem. Phys., 2010, 12, 8948.

4 A. Kirrander, Ch. Jungen and H. H. Fielding, J. Phys. B, 2008, 41, 074022.

5 A. Kirrander and H. H. Fielding and Ch. Jungen, J. Chem. Phys., 2010, 132, 024313.

Petr Slavicek communicated in reply: Thank you for bringing our attention to these works.

Jeremy Richardson opened a general discussion of the paper by Martin Dracinsky: You show that you can get good agreement with experiment by employing PIMD simulations. What would have been the error if you had used classical MD?

Martin Dracinsky answered: The isotope effects are consequences of nuclear quantum effects and so cannot be calculated by classical molecular dynamics; this makes them good tests of predictions of NQEs In addition, we demonstrated in our previous work (e.g. ref. 1) that PIMD simulations improve the agreement with experiment significantly when compared with classical MD even in cases with no isotope exchange. PIMD simulations provide substantially broader probability distributions of bond distances, which are closely related to nuclear shielding.

1 M. Dracinsky and P. Hodgkinson, Chem.–Eur. J., 2014, 20, 2201–2207.

Ingo Fischer asked: Many years ago the groups of Matthanja de Vries, Kleinermanns and others conducted IR/UV experiments on G/C base pairs and related dimers in the gas phase and as far as I remember they looked for proton transfer in the base pairs. How do your computations compare to these gas phase results and what is the influence of the solvation?

Martin Dracinsky answered: IR/UV spectra of nucleobase base pairs have indeed been recorded.^1,2 Microhydration of base pairs has also been studied by this technique.³ However, no conclusive result confirming or disproving proton transfer in the ground state has been obtained. On the other hand, excited-state proton transfer has been confirmed in several studies, for a review see ref. 4 and 5.

1 A. Abo-Riziq, L. Grace, E. Nir, M. Kabelac, P. Hobza and M. S. de Vries, Proc. Nat. Acad. Sci. USA, 2005, 102, 20–23.

2 J. M. Bakker, I. Compagnon, G. Meijer, G. von Helden, M. Kabeláč, P. Hobza and M. S. de Vries, Phys. Chem. Chem. Phys., 2004, 6, 2810–2815.

3 A. Abo-Riziq, B. Crews, L. Grace and M. S. de Vries, J. Am. Chem. Soc., 2005, 127, 2374–2375.

4 J. Wierzchowski, Nucleosides, Nucleotides and Nucleic Acids, 2014, 33, 626–644.

5 K. Kleinermanns, D. Nachtigallova and M. S. de Vries, Int. Rev. Phys. Chem., 2013, 32, 308–342.

Ingo Fischer asked: The proton transfer in the electronic ground state of GC base pairs could be experimentally addressed by IR/UV spectroscopy. In the first step you excite the base pair by an IR photon to induce proton transfer, in the second step you probe the structural changes by UV photoionisation. One could also microsolvate GC with water and investigate small solvent clusters. This kind of experiment would give you information on whether proton transfer does take place and how much energy is needed.

Martin Dracinsky responded: These experiments have been performed. See the answer to the question above for more information.

Krzysztof Szalewicz opened a general discussion of the paper by Mikolaj Janicki: What was the relation between your DFT and ADC(2) calculations? Was it ADC(2) based on Kohn–Sham orbitals?

Mikolaj Janicki replied: The KS-DFT-D3 method was only used to locate the equilibrium ground-state geometry and to compute harmonic vibrational frequencies. The excited-state calculations were performed using the ADC(2) Hamiltonian with the HF orbitals.

Krzysztof Szalewicz continued: What exactly was the method that you used for the non-adiabatic dynamics?

Mikolaj Janicki responded: The non-adiabatic ab initio molecular dynamics simulations were performed using the fewest-switches surface hopping (FSSH) method at the ADC(2) level with the aug-cc-pVDZ basis set.

Anne Zehnacker-Rentien commented: You have shown that adding 5 molecules to the chromophore is enough to capture the electron-driven proton transfer mechanism and that the seven lower-energy transitions all have a pi–sigma^* character. Still, I am surprised that you do not calculate any bright states lower in energy than the pi–sigma^* state. I wonder whether you wouldn’t modify the relative energy of the excited states if you put more water molecules, not on the NH₂ and NH group as you did but on a different side of the molecule, for example in interaction with the other nitrogen of the ring. This might mimic what happens in water better.

Mikolaj Janicki responded: Naturally a different structure of the water cluster, in particular the one suggested in your question, would alter the spectrum of electronic states in the Franck–Condon region to some extent.

However, the studied complex was a model system for photoinduced electron-driven proton transfer. This determines to some extent construction of the water cluster, which has to be large enough to accommodate the solvated electron. It should be noted that all the low-lying dark states denoted as pi–sigma^* have significant charge-transfer-to-solvent component, thus we do not believe that the introduction of additional water molecules would change the spectra qualitatively. In the future, we are planning to extend our study and enclose the chromophore in a small water droplet which would allow us to more realistically simulate the aqueous surrounding.

Anne Zehnacker-Rentien added: We have studied the same sort of photoinduced electron-driven proton transfer process in protonated quinine derivatives isolated in the gas phase.¹ I thought the proton was moving first and was followed by the electron. You showed the opposite during your talk, thank you for these results that enlightened me as to what exactly is involved in this process.

1 Kumar et al., Phys. Chem. Chem. Phys., 2016, 18, 22668–22677.

Mikolaj Janicki responded: Thank you for that comment. In fact, the photoinduced electron-driven proton transfer (EDPT) mechanism discussed in our paper (DOI: 10.1039/c8fd00086g) and in our previous works^1–3 is very similar to the EDPT process characterized previously by Sobolewski and Domcke in Watson-Crick base pairs.⁴ In all these systems the nonradiative deactivation is enabled after conversion to a dark charge-transfer state and subsequent proton transfer induced by the change in electronic distribution.

1 R. Szabla et al., Phys. Chem. Chem. Phys., 2014, 16, 17617–17626.

2 R. Szabla et al., J. Phys. Chem. Lett., 2015, 6, 1467–1471.

3 R. Szabla et al., Faraday Discuss., 2016, 195, 237–251.

4 A. L. Sobolewski and W. Domcke, Europhys. News, 2006, 37, 20–23.

Stephen Bradforth asked: The πσ^* states are normally pushed up in energy due to the Pauli repulsion of the diffuse Rydberg character in the electronic wave function. So you would expect the magnitude of that energy shift to be dependent on the number of solvent molecules added to the cluster and how well encapsulated by solvent the system is. Therefore the probability of electrons detaching to the water cluster should be extremely sensitive to the solvation. Do you see this in your calculations?

Mikolaj Janicki responded: Actually, in our calculations consecutive introduction of water molecules to the chromophore in the vicinity of σ^* orbitals led to increasing delocalization of such an orbital on the cluster and its consequent stabilization. In fact, our model system is marked by several such low-lying πσ^* states, in which σ^* orbitals are delocalized on the water cluster, indicating their charge-transfer-to-solvent (CTTS) character. These CTTS states appear even below the corresponding πσ^* states of the isolated chromophore owing to stabilization of solvated electrons by explicit water molecules forming the cluster. Although our conclusions are based on calculations for a relatively small model system, we believe that the importance of CTTS states in our nonadiabatic simulations may indicate that EDPT is an important photorelaxation channel for 2-aminoimidazole in aqueous solution.

Stephen Bradforth continued: In my previous question, I’ve made an assumption that there is a high degree of Rydberg character in the Franck–Condon region of the πσ^* state of your system. Is that true in your calculations?

Mikolaj Janicki responded: Indeed, all the low-lying πσ^* states have quasi-Rydberg character with a large spatial extent.

Robert Góra commented: Comment on the last question, asking about the influence of water molecules on πσ^* states. This confusion is due to the nomenclature of the excited states that we assumed in the paper (DOI: 10.1039/c8fd00086g). In fact, Mr. Janicki was discussing charge-transfer-to-solvent (CTTS) states. These, however, do correspond to the particular πσ^* states of isolated chromophore. In fact, the cluster studied in our paper was built by consecutive attachment of water molecules to the chromophore in the region where the σ^* orbital was localized. Our nonadiabatic dynamics simulations indicate that after internal conversion to the πσ^* state, its character is gradually changed and the solvated electron is formed. On the other hand, our calculations rely on the cluster model which has its limitations. Still, based on our results we believe that even though the πσ^* states in bulk would be destabilized in the Franck–Condon region, they should still be accessible in this system and, consequently, the described deactivation mechanism should be qualitatively correct.

Stephen Bradforth asked: What are the observables predicted in your calculation that could be probed experimentally?

Mikolaj Janicki replied: Naturally, the simulated UV absorption spectrum of our model system could be experimentally verified. Although we did not attempt to simulate the transient absorption spectra in our work, we estimated the excited state lifetime at about 1 ps. Moreover, we believe that experimental observation of the spectral signatures of solvated electrons in time-resolved spectroscopy could support our conclusion that electron-driven proton transfer is the main nonradiative deactivation channel in this system.

Anne B. McCoy remarked: If some of these states involve charge transfer to solvent transitions, one of the known challenges with DFT approaches is that they tend to place these transitions at frequencies that are too low. Have you thought about this or tried other approaches to assess the accuracy of DFT in calculating these transition frequencies?

Mikolaj Janicki replied: All the excited-state calculations were, in fact, performed using the ADC(2)/aug-cc-pVDZ method. DFT was used only for ground state geometry optimizations.

Gilberte Chambaud queried: Is it correct that you include the dispersion effects via the D3 usual term in your DFT calculation of the structure of the hydrated 2-aminoimidazole?

Mikolaj Janicki answered: Actually, we used D3 correction with the Becke–Johnson (BJ) damping which should be sufficiently accurate for the studied system. In fact, the structure of the complex optimized at the DFT-D3(BJ) level was virtually identical to the one obtained at the MP2 level.

Majdi Hochlaf commented: For nitrogen containing heterocycles, we found several types of bonding between these molecules and CO₂. These include sigma-type hydrogen bonding, pi-stacking complexes and solvated molecules. They are described in ref. 1–8. I suggest that you may try to find the other isomers of your clusters based on these findings.

1 K. Boussouf, R. Boulmene, M. Prakash, N. Komiha, M. Taleb, M. Mogren Al-Mogren and M. Hochlaf, Phys. Chem. Chem. Phys., 2015, 17, 14417.

2 K. Mahjoubi, D. M. Benoit, N.-E. Jaidane, M. Mogren Al-Mogren and M. Hochlaf, Phys. Chem. Chem. Phys., 2015, 17, 17159.

3 K. Boussouf, T. Khairat, M. Prakash, N. Komiha, G. Chambaud and M. Hochlaf, J. Phys. Chem. A, 2015, 119, 11928.

4 R. Boulmene, K. Boussouf, M. Prakash, N. Komiha, M. Mogren Al-Mogren and M. Hochlaf, ChemPhysChem, 2016, 17, 994.

5 R. Boulmène, M. Prakash and M. Hochlaf, Phys. Chem. Chem. Phys., 2016, 18, 29709.

6 V. Timon, M. L. Senent and M. Hochlaf, Microporous and Mesoporous Materials, 2015, 218, 33.

7 Y. Makina, K. Mahjoubi, D. M. Benoit, N.-E. Jaidane, M. Mogren Al-Mogren and M. Hochlaf, J. Phys. Chem. A, 2017, 121, 4093.

8 R. Dahmani, S. Ben Yaghlane, S. Boughdiri, M. Mogren Al-Mogren, M. Prakash and M. Hochlaf, Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2018, 193, 373.

Mikolaj Janicki replied: I would like to thank you for these suggestions which could be helpful in our future studies. Naturally, the particular choice of a water cluster in our work was to study nonradiative deactivation via an electron-driven proton transfer mechanism in a model system, which according to our nonadiabatic dynamics simulations, could be the major deactivation channel in hydrated 2-aminoimidazole.

Robert Góra addressed Mikolaj Janicki and Majdi Hochlaf: Regarding the structure of the studied microhydrated 2-aminoimidazole cluster, our calculations are in a way biased, since we were focusing on nonradiative deactivation channels via electron-driven proton transfer. In this process, a photoexcited chromophore undergoes ultrafast deactivation to the ground state due to internal conversion to a charge-transfer-to-solvent state and subsequent multiple proton transfers following the solvated electron. We characterized this process previously in a few model systems, including microhydrated 2-aminooxazole, imidazole, adenine and 4-aminoimidazole-5-carbonitrile (cf. ref. 2, 3, 5, and 21 in the paper, DOI: 10.1039/c8fd00086g). In order to characterize such a process, a particular arrangement of water molecules in the solvation shell is required which enables the formation of solvated electrons. However, our non-adiabatic dynamics simulations indicate that the timescale of such a process is in a sub-picosecond regime, which is much faster than equilibration of the solvation shell after photoexcitation. Our simulations indicate that in microhydrated imidazole and 2-aminoimidazole most of the trajectories follow this channel. Of course, our results were obtained for a model molecular cluster but we believe that there is already experimental evidence of such a process in other systems, like for instance formation of phenoxyl radicals and solvated electrons observed in the transient absorption spectra of phenol (cf. ref. 38 in the paper, DOI: 10.1039/c8fd00086g).

Jens Petersen asked: How did you construct the structure of the microsolvated model system? Specifically, how did you decide where to place the water molecules relative to the 2-aminoimidazole?

Mikolaj Janicki replied: The structure of the microsolvated model system was prepared based on our previous studies (cf. for instance ref. 1 and 2) in which we also investigated the EDPT mechanism and tested different sizes and shapes of the hydration cluster to properly describe electron-driven proton transfer mechanism. Our studies showed that the solvated electron and the subsequent electron-driven proton transfers require at least five water molecules. Our preliminary investigations of 2-aminoimidazole indicated that a proton transfer might be observed from either the –NH or –NH² group. Therefore, the water cluster was attached to the chromophore in order to create hydrogen bonds between the water cluster and the –NH or –NH² group of the chromophore. It enabled us to observe proton transfer from 2-aminoimidazole towards water molecules and the formation of the solvated electron.

1 R. Szabla, J. Šponer and R. W. Góra, J. Phys. Chem. Lett. 2015, 6, 1467–1471.

2 R. Szabla, J. E. Šponer, J. Šponer , A. L. Sobolewski and R. W. Góra, Phys. Chem. Chem. Phys., 2014, 16, 17617–17626.

Jens Petersen added: We performed similar calculations on tyrosine in water, employing the field-induced surface hopping (FISH) method combined with the QM/MM approach.¹ The quantum mechanical subsystem consisted of tyrosine and the three water molecules situated nearest to its protonated amino group, while the rest of the surrounding solvent (∼1200 water molecules) was described using a classical force field. We found that initial photoexcitation to the bright L_a state is followed by internal conversion to an nπ^* state, on which proton transfer to a close-lying water molecule takes place, similar to the observations found by Janicki et al. However, in the case of tyrosine, a second proton transfer from water to the phenyl ring occurs before the final transition to the electronic ground state proceeds via a conical intersection involving out of plane motion of a ring carbon.

1 G. Tomasello, M. Wohlgemuth, J. Petersen and R. Mitric, J. Phys. Chem. B, 2012, 116, 8762–8770.

Gilberte Chambaud commented: It is generally observed that the solvation of molecules containing nitrogen or oxygen atoms with explicit water molecules corresponds to stable structures where relatively simple 5- or 6-membered rings are involved. In your study you present the solvation by a group of 5 water molecules where most of them are not in the close vicinity of the nitrogen atoms of the molecule. Are all these water molecules necessary to describe the solvation or could it be enough to involve 2 or 3 of them?

Mikolaj Janicki answered: Indeed, adopting a different number of water molecules (around the chromophore) will have an influence mainly on the position of the absorption band in the simulated UV-vis spectrum; 2–4 water molecules forming hydrogen bonds with a chromophore could suffice. However, the primary objective of our work was to characterize the nonradiative deactivation of the hydrated 2-aminoimidazole via electron-driven proton transfer (EDPT). In this process, a state crossing with the ground state is formed after internal conversion to a charge-transfer-to-solvent state, resulting in the formation of a solvated electron and subsequent single or multiple proton transfers from a chromophore via a Grotthuss-like mechanism. In our previous studies (cf. for instance ref. 1 and 2) we have shown that such a process could be an important nonradiative deactivation channel. However, the formation of the corresponding EDPT state crossing requires a sufficiently large solvation shell. In our previous studies, we tested different sizes and shapes of the hydration cluster for a selection of heteroaromatic chromophores and concluded that at least five water molecules are needed to accommodate the solvated electron and allow for the subsequent electron-driven proton transfers. Although, in the case of microhydrated 2-aminoimidazole we observed for the first time formation of the EDPT state crossing after a single proton transfer, still a sufficiently large cluster was required to allow formation of a solvated electron.

1 R. Szabla, J. Šponer and R. W. Góra, J. Phys. Chem. Lett. 2015, 6, 1467–1471.

2 R. Szabla, J. E. Šponer, J. Šponer , A. L. Sobolewski and R. W. Góra, Phys. Chem. Chem. Phys., 2014, 16, 17617–17626.

Petr Slavicek asked: The simulations aim to model molecules in the liquid state. The choice of initial conditions is then potentially important. There are two issues to worry about: (i) Using gas phase clusters is not always a good approximation for a liquid state. The cluster structures are not necessarily representative of the liquid phase structure. (ii) Sampling of the initial conditions within a harmonic approximation requires special care due to the presence of highly anharmonic modes.

In our experience, one needs to ignore soft modes below approximately 500 cm⁻¹ otherwise we encounter structures with unphysically high energies, see e.g. ref. 1. The problem is solved by generating the initial conditions within molecular dynamics simulations including zero point energy, see e.g. ref. 2. Such an approach is easy to use for liquid state as well.

1 O. Svoboda et al., J. Chem. Phys., 2011, 135, 154302.

2 D. Hollas et al., J. Chem. Theory Comput., 2016, 12, 5009–5017.

Mikolaj Janicki responded: We are aware of the possible caveats with using Wigner distribution to generate initial conditions for weakly bound systems. However, in the system studied here and in our previous works we did not observe any such problems. This may be due to the fact that our model systems are made of a chromophore and a few explicit water molecules which form a compact and relatively strong hydrogen bonding network.

Still, we thank you for that comment. We shall definitely attempt the mentioned approach to generate initial conditions in our future work.

Loren Ban opened a general discussion of the paper by Stephen Bradforth: I would like to follow up on this interesting paper by Prof. Bradforth and co-workers. The authors determined vertical ionization energies of aqueous indole and tryptophan from liquid-jet photoelectron spectroscopy. Additionally, they use a correction for electron inelastic scattering effects based on a recent paper by Luckhaus et al.¹ At the electron kinetic energies concerned in this work, inelastic scattering can have a significant effect on the photoelectron kinetic energy spectra and one would ideally want to analyse the measurements with a detailed scattering model.^1–3 This is because the loss of electron kinetic energy due to inelastic scattering is a non-trivial function of the laser photon energy (Fig. 3 and S6 in ref. 1). While the approach presented by the authors accounts well for the shifts in the vertical ionization energies, one would need to perform a complete scattering simulation to understand the peak shapes and, even more importantly, photoelectron anisotropies.

1 D. Luckhaus, Y.-i. Yamamoto, T. Suzuki and R. Signorell, Sci. Adv., 2017, 3, e1603224.

2 R. Signorell, M. Goldmann, B. L. Yoder, A. Bodi, E. Chasovskikh, L. Lang and D. Luckhaus, Chem. Phys. Lett., 2016, 658, 1.

3 M. Michaud, A. Wen and L. Sanche, Radiat. Res., 2003, 159, 3.

Stephen Bradforth replied: I completely agree with the issue raised in this comment. As pointed out, as the inelastic scattering varies strongly with the outgoing kinetic energy of the electron, the shape of each photoelectron band can become distorted from the expected energy distribution as electrons depart the indole molecule. Computing the effects of scattering on the peak shape is an important next step in exploiting photoelectron spectroscopy from liquids. Currently, because of the magnetic bottle design of our spectrometer, we do not record photoelectron angular distributions. However, collaborative work with Seidel and Winter have shown at higher electron kinetic energies, angular distributions are largely preserved from the gas phase.¹ Therefore, future experiments are likely to capture and attempt to interpret the photoelectron anisotropy, and thus simulations that capture the effect of both elastic and inelastic scattering will become increasingly important.

1 S. Thürmer, R. Seidel, M. Faubel, W. Eberhardt, J. C. Hemminger, S. E. Bradforth and B. Winter, Phys. Rev. Lett., 2013, 111, 173005.

Ingo Fischer asked: In liquid jet experiments electrons can be ejected from molecules either at the surface or in the bulk. Both can show very different behaviour. Which indole molecules do you probe in your experiments?

Stephen Bradforth replied: You are correct that we might expect the dynamics to be different at an aqueous interface compared to the bulk. The photoelectron technique in principle can be used to look at both interfacial and bulk regions by tuning the outgoing kinetic energy of the photoelectrons (via selection of the photon energy). As the inelastic scattering cross sections change dramatically with kinetic energy for electron scattering from water molecules in the liquid, the electron attenuation (or probing) length varies considerably employing laser photons¹ in the UV/VUV and extreme UV from either high harmonic sources or synchrotrons.^2–4 The current experiments are carried out with 4–5 eV photons liberating electrons with kinetics energies with 0.8–2.5 eV; in this range the expected probing lengths are ∼5 nm,¹ effectively probing the bulk region as far as a small solute like indole is concerned.

1 D. Luckhaus, Y.-I Yamamoto, T. Suzuki and R. Signorell, Sci. Adv. , 2017, 3, e1603224.

2 N. Ottosson, M. Faubel, S. E. Bradforth, P. Jungwirth and B. Winter, J. Elec. Spec Related Phenom., 2010, 177, 60–70.

3 S. Thürmer, R. Seidel, M. Faubel, W. Eberhardt, J. C. Hemminger, S. E. Bradforth and B. Winter, Phys. Rev. Lett., 2013, 111, 173005.

4 Y.-I Suzuki, K. Nishizawa, N. Kurahashi and T. Suzuki, Phys. Rev. E, 2014, 90, 010302.

Petr Slavicek remarked: Looking at the reported values of the ionization energies, the solvent shift seems to be a bit too small according to my experience. In similar systems, the solvent shift is typically 0.75–1 eV, see e.g. ref. 1. I also found larger values in my calculations using the non-equilibrium dielectric continuum model, using both the MP2 and DFT methods. The IE was calculated to be 7.72 eV in the gas phase and 7.01 eV in aqueous environment (at the BMK/6-31+g* level of theory). The calculations also indicate a smaller difference between the 1^st and 2^nd ionization that the reported one (0.5 eV using BMK/6-31+g* estimate). The smaller energy difference seems also consistent with the reported photoemission spectra in the gas phase.

How much can one rely on the estimates of the VIE within the R2PI PES technique? I can imagine two possible sources of problems: (i) fast dynamics on the intermediate states, and (ii) non-Condon effects.

1 E. Pluharova et al., Acc. Chem. Res. 2015, 48, 1209–1217.

Stephen Bradforth answered: The value of 0.5 eV for the gas-liquid shift is in the same range as for similar aromatic systems previously measured by water jet photoelectron spectroscopy. For example, 0.5–0.6 eV decreases in vertical ionization energies are reported for aniline, veratrole alcohol, imidazole and thymidine in ref. 1 and even lower values are reported for cytidine.² However, we agree that care needs to be taken in interpreting the R2PI peak positions. As described in some detail, the peak shape depends on dynamics (both intramolecular and solvation) on the intermediate state in relation to the pulse width and the ionization rate on absorbing the second photon.³ As far as we aware, no one has considered non-Condon effects on aqueous phase photoionization to date and such a study would be of considerable merit.

1 P. R. Tentscher, R. Seidel, B. Winter, J. J. Guerard and J. S. Arey, J. Phys. Chem. B, 2015, 119, 238–256.

2 P. Slavicek, B. Winter, M. Faubel, S. E. Bradforth and P. Jungwirth, J. Am. Chem. Soc., 2009, 131, 6460–6467.

3 A. Roy, R. Seidel, G. Kumar and S. E. Bradforth, J. Phys. Chem. B, 2018, 122, 3723–3733.

Loren Ban asked: You mentioned that the decrease in the vertical ionization energy corresponding to the D₀–S₀ transition upon hydration is 0.5 eV for indole, while 0.8 eV was determined for phenol in the work of Riley et al.¹ Although corrections for the inelastic scattering effects are not included in the case of phenol, could one still relate this difference to the solvation effects? Or even naively to the H-bonding strength of indole and phenol?

1 J. W. Riley, B. Wang, J. L. Woodhouse, M. Assmann, G. A. Worth and H. H. Fielding, J. Phys. Chem. Lett., 2018, 9, 678.

Stephen Bradforth answered: In earlier work we have determined a decrease for the vertical ionization energy of aqueous phenol from gas phase as 0.75 eV using non-resonant XPS measurements in a thorough study that included detailed theory on the origin of the solvation shift and hydrogen bonding of water with the neutral molecule.¹ Because R2PI experiments are likely more sensitive to inelastic scattering, and pulse-length dependent intermediate state dynamics, we believe the XPS liquid jet results are to be preferred when available. Considering the cumulative error bars in play, we hesitate to draw too much attention to gas-liquid shifts ∼0.2 eV.

1 D. Ghosh, A. Roy, R. Seidel, B. Winter, S. E. Bradforth and A. I. Krylov, J. Phys. Chem. B, 2012, 116, 7269–7280.

Ingo Fischer commented: Many experiments on indole have been conducted before. Are there experiments looking at H-atom loss from isolated indole as a probe of πσ^* states and what were the results?

Stephen Bradforth replied: There have been a wide range of gas phase experiments designed to explore and understand the H-atom dissociation pathway on photoexcitation of indole. These have been thoroughly reviewed in the literature, see for example ref. 1 from Lin and coworkers, using photofragment translation spectroscopy, found evidence of fast (attributed to direct dissociation) as well as slow dissociation (on the ground state surface). 80% of the dissociation takes place on the excited state surface at 248 nm.² Using H-atom Rydberg time-of-flight spectroscopy at multiple longer pump wavelengths,³ Ashfold’s group found a threshold for fast H-atom fragmentation 4.7 eV (at 263 nm) and considered the dynamics revealed in their experiment to be consistent with molecules on the excited ππ^* state having sufficient energy to access a conical intersection with the dissociative πσ^* surface. Townsend’s group have applied time-resolved photoelectron spectroscopy of indole in a molecular beam to establish the electronic signature of the πσ^* in the excited state photoelectron spectrum and its photoelectron angular distribution. Their work suggests the involvement of the πσ^* state at photolysis wavelengths longer that 263 nm and only a slight slowing of the passage time of the system over a small barrier along the H-atom dissociation coordinate on the πσ^* surface as the wavelength is increased to 273 nm.^4,5 This is not consistent with the ultrafast electron diffraction results of Zewail and coworkers.⁶ Ullrich and her coworkers, combining femtosecond resolution of the H-atom kinetic energy release and time-resolved photoelectron spectroscopy, and the time-resolved ion yield measurements of Longarte and coworkers,⁷ come up with a picture more consistent with the Ashfold work where direct dissociation via the πσ^* channel is not operative below 4.7 eV excitation energy.¹ We note that the vertical excitation energies in solution are red-shifted and we cannot simply determine the equivalent threshold for reaching the πσ^* in aqueous solution. However, the detailed picture in the gas phase provides an excellent platform to attempt to connect dissociation in the isolated molecule with radiationless decay pathways for aqueous indole that involve the πσ^* state.

1 T. J. Godfrey, H. Yu, M. S. Biddle and S. Ullrich, Phys. Chem. Chem. Phys., 2015, 17, 25197–25209.

2 M. F. Lin, C.-M. Tseng, Y. T. Lee and C.-K. Ni, J. Chem. Phys., 2005, 123, 124303.

3 M. G. D. Nix, A. L. Devine, B. Cronin and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2006, 8, 2610–2618.

4 M. M. Zawadzki, J. O. F. Thompson, E. A. Burgess, M. J. Paterson and D. Townsend, Phys. Chem. Chem. Phys., 2015, 17, 26659–26669.

5 R. Livingstone, O. Schalk, A. E. Boguslavskiy, G. Wu, L. Therese Bergendahl, A. Stolow, M. J. Paterson and D. Townsend, J. Chem. Phys., 2011, 135, 194307–13.

6 S. T. Park, A. Gahlmann, Y. He, J. S. Feenstra and A. H. Zewail, Angew. Chem. Int. Ed., 2008, 47, 9496–9499.

7 R. Montero, Á. P. Conde, V. Ovejas, F. Castaño and A. Longarte, J. Phys. Chem. A, 2012, 116, 2698–2703.

Ingo Fischer asked: Can you also summarise the results of earlier transient absorption experiments of indole in water solutions?

Stephen Bradforth replied: Because of the importance to the photophysics of tryptophan, there have been several transient absorption experiments, going back to early flash photolysis measurements from Bent and Hayon.¹ These include single probe color and broadband probe experiments.^2–5 Our group has recently been re-examining the broadband spectroscopy at several pump wavelengths employing both a visible and near-UV continua as well as various excited state scavengers, and we will be reporting results and a thorough comparison to previous work in an upcoming paper.⁶ In general, the difficulty has been in assigning the transient absorption spectra, as absorption bands attributed to indole radical cations, solvated electrons, radicals, triplets, and the parent excited state absorption all overlap.

1 D. V. Bent and E. Hayon, J. Am. Chem. Soc., 1975, 97, 2612–2619.

2 T. Bizjak, P. B. Bisht, S. Lochbrunner E. and Riedle, Femtochemistry and Femtobiology, 2018, 229–232.

3 J. Peon, J. D. Hoerner and B. Kohler, Liquid Dynamics: Experiment, Simulation, and Theory, 2002, 820, 122–135.

4 J. Peon, G. C. Hess, J.-M. L. Pecourt, T. Yuzawa and B. Kohler, J. Phys. Chem. A, 1999, 103, 2460–2466.

5 J. C. Mialocq, E. Amouyal, A. Bernas and D. Grand, J. Phys. Chem., 1982, 86, 3173–3177.

6 G. Kumar, T. A. A. Oliver and S. E. Bradforth, Phys. Chem. Chem. Phys., in preparation.

Jens Petersen communicated: There have been theoretical investigations on the photodynamics of indole both in the gas phase as well as in a water environment some time ago, conducted by Wohlgemuth, Bonacic-Koutecky and Mitric.¹ The authors performed trajectory surface-hopping simulations, which for the solvated indole were combined with the QM/MM approach, describing indole and three water molecules quantum mechanically while the remaining solvent was represented by a sphere of ∼2000 water molecules described by a classical force field. It was shown that in the gas phase, after excitation to the bright π–π^* states the system quickly switches to the lowest excited state and mostly remains there for the simulation time of 300 fs. In the course of the dynamics, the lowest excited state may assume π–σ^* character, but within the simulation time, only for 1% of the trajectories. This leads to a return to the ground state via an N–H bond stretching motion. This is consistent with results of Townsend et al.² who found evidence for a picosecond lifetime of indole in the π–σ^* state. In an aqueous environment, indole behaves differently in that a significant part (about 30%) of the trajectories return to the ground state within 300 fs due to the formation of a charge-transfer-to-solvent state, which represents a precursor of a solvated electron. This is clearly consistent with the spectral evidence for ultrafast solvated electron formation as reported by Bradforth et al. in the present discussion (DOI: 10.1039/c8fd00123e). Besides that, the simulations also showed occurrences (less than 10%) of proton transfer from indole to a close-lying water molecule, confirming the assumption of Bradforth et al. that this might be an alternative relaxation pathway.

1 Y. Pu, L. T. Watson and Y. Cao, J. Chem. Phys., 2011, 135, 054105.

2 R. Livingstone, O. Schalk, A. E. Boguslavskiy, G. Wu, L. T. Bergendahl, A. Stolow, M. J. Paterson and D. Townsend, J. Chem. Phys. 2011, 135, 194307.

Conflicts of interest

There are no conflicts to declare.

---