Open Access Article
Open Access ArticleTuning Pt and Cu sites population inside functionalized UiO-67 MOF by controlling activation conditions
L.
Braglia
ab,
E.
Borfecchia
 a,
K. A.
Lomachenko
bc,
A. L.
Bugaev
ab,
A. A.
Guda
b,
A. V.
Soldatov
b,
B. T. L.
Bleken
d,
S.
Øien-Ødegaard
d,
U.
Olsbye
d,
K. P.
Lillerud
d,
S.
Bordiga
a,
K. A.
Lomachenko
bc,
A. L.
Bugaev
ab,
A. A.
Guda
b,
A. V.
Soldatov
b,
B. T. L.
Bleken
d,
S.
Øien-Ødegaard
d,
U.
Olsbye
d,
K. P.
Lillerud
d,
S.
Bordiga
 ad,
G.
Agostini
ce,
M.
Manzoli
ad,
G.
Agostini
ce,
M.
Manzoli
 f and
C.
Lamberti
f and
C.
Lamberti
 *bg
*bg
aDepartment of Chemistry, NIS Interdepartmental Centre and INSRM Reference Centre, University of Turin, via Quarello 15A, I-10135 Turin, Italy
bIRC “Smart Materials”, Southern Federal University, Zorge Street 5, 344090 Rostov-on-Don, Russia
cEuropean Synchrotron Radiation Facility, 71 avenue des Martyrs, CS 40220, 38043 Grenoble Cedex 9, France
dinGAP Centre for Research Based Innovation, Department of Chemistry, University of Oslo, Oslo, Norway
eLeibniz Institute for Catalysis at the University of Rostock (LIKAT), Albert-Einstein-Str. 29A, D-18059 Rostock, Germany
fDepartment of Drug Science and Technology, NIS Interdepartmental Centre, University of Torino, Via P. Giuria 9, 10125 Torino, Italy
gDepartment of Chemistry, CrisDi Interdepartmental Centre and INSRM Reference, University of Turin, via Pietro Giuria 7, 10125 Turin, Italy. E-mail: carlo.lamberti@unito.it
First published on 6th February 2017
Abstract
The exceptional thermal and chemical stability of the UiO-66, -67 and -68 classes of isostructural MOFs [J. Am. Chem. Soc., 2008, 130, 13850] makes them ideal materials for functionalization purposes aimed at introducing active centres for potential application in heterogeneous catalysis. We previously demonstrated that a small fraction (up to 10%) of the linkers in the UiO-67 MOF can be replaced by bipyridine-dicarboxylate (bpydc) moieties exhibiting metal-chelating ability and enabling the grafting of Pt(II) and Pt(IV) ions in the MOF framework [Chem. Mater., 2015, 27, 1042] upon interaction with PtCl2 or PtCl4 precursors. Herein we extend this functionalization approach in two directions. First, we show that by controlling the activation of the UiO-67-Pt we can move from a material hosting isolated Pt(II) sites anchored to the MOF framework with Pt(II) exhibiting two coordination vacancies (potentially interesting for C–H bond activation) to the formation of very small Pt nanoparticles hosted inside the MOF cavities (potentially interesting for hydrogenation reactions). The second direction consists of the extension of the approach to the insertion of Cu(II), obtained via interaction with CuCl2, and exhibiting interesting redox properties. All materials have been characterized by in situ X-ray absorption spectroscopy at the Pt L3- and Cu K-edges.
1. Introduction
Metal–organic frameworks (MOFs) are crystalline, porous solids consisting of metal ions or clusters, coordinated with organic molecules. The large number of combinations for inorganic and organic building units offers an almost infinite variety of structural solutions with a wide range of properties.1–7 An additional degree of freedom is the functionalization of the MOFs that further extends the range of possibly obtainable structures.8–14 For about one decade, MOFs have been considered as potential candidates for shape-selective heterogeneous catalysis for reactions running at mild conditions.15–24As the metal sites in the cornerstones of most of the MOF structures show a maximum of one coordination vacancy (see e.g. the HKUST-1 (ref. 25–27) and the CPO-27, or MOF-74,28–31 cases), non-functionalized MOFs have limited application in catalysis, where at least two coordination vacancies are required in the active site. Consequently, functionalization represents an attractive way to introduce active sites in MOF structures.
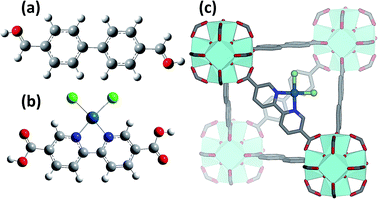
The recently discovered UiO-66, -67 and -68 classes of iso-structural MOFs are obtained by connecting Zr6O4(OH)4 inorganic cornerstones with 1,4-benzene-dicarboxylate (bdc), 4,4′-biphenyl-dicarboxylate (bpdc) or 4,4′-terphenyl-dicarboxylate (tpdc) linkers, for the UiO-66, UiO-67 and UiO-68 MOFs, respectively.32–34 Due to their outstanding stability at high temperatures, high pressures and in the presence of different solvents, these materials are among the few MOFs already commercialized for potential applications in the fields of catalysis, gas storage, and gas purification. For the same reasons the UiO-66, -67 and -68 family has already been subjected to several functionalization procedures, involving both the Zr6O4(OH)4 inorganic cornerstone and the organic linkers, as well as intentionally toned defect insertion.35–38 As far as the inorganic cornerstone functionalization is concerned, Zr atoms have been partially or totally substituted with Hf39,40 or Ce41–44 atoms. Substitution with cerium allows alteration of the Ce(IV) ↔ Ce(III) redox chemistry, providing some reactivity to the cornerstone. Coming to the linker functionalization, several routes have been undertaken, including: (i) grafting of –NH2, –NO2, –Br groups σ-bonded to the bdc ring;45–49 grafting of Cr(CO)3 complexes π-bonded to the bdc ring;50 (iii) encapsulation of Pt,51,52 Pd,53,54 Au,55 AuPd,56 Ru,57 Ag,58 or metal nanoparticles (NPs) inside the tetrahedral and octahedral MOF cavities. Moreover, for UiO-67, the substitution of a small fraction of bpdc linkers by bipyridine-dicarboxylate (bpydc) moieties, exhibiting metal-chelating ability, enables the path for post-synthetic grafting of metal ions in the MOF framework upon interaction with metal precursors.51,59,60
Herein we extend this functionalization approach into two directions. First, by tuning the H2 flow during the activation procedure of the UiO-67-Pt we can move from a material hosting isolated framework Pt(II) exhibiting two coordination vacancies (potentially interesting for C–H bond activation) to the formation of very small Pt NPs hosted inside the MOF cavities (potentially interesting for hydrogenation reactions). The second direction consists of the extension of the approach to the insertion of Cu(II), obtained via interaction with CuCl2, leading to interesting redox properties already evidenced in other Cu-containing MOFs.61–63
The fact that MOFs are mainly constituted by low Z elements (C, O, N, H) implies that they are almost transparent to hard X-rays;64,65 this allows the collection of high quality transmission X-ray absorption spectra at the metal K- or L-edges, characterized by an optimized edge jump Δμx as high as 1.0–1.5, resulting in accurate data, analyzable up to 15–20 Å−1 (vide infraFig. 3a). This makes X-ray absorption techniques both in the extended X-ray absorption fine structure (EXAFS) and X-ray absorption near edge structure (XANES) regions a technique of choice in characterizing the electronic and structural configuration of metal centers hosted in MOF structures, as testified by many previous studies.28,29,32–34,40,48,59,64,66–90 In this study we have characterized Pt- and Cu-functionalized UiO-67 MOFs via in situ X-ray absorption spectroscopy at the Pt L3- and Cu K-edges, respectively.
2. Experimental and methods
2.1. Materials
All chemicals were used as received. ZrCl4 (Sigma) must be dry and of high purity for successful synthesis.Crystals of H2bpydc suitable for single crystal XRD were obtained directly from the autoclave. A complete data set was acquired on a Bruker D8 Venture equipped with a Photon 100 detector, using Mo Kα radiation (λ = 0.71073 Å). Data reduction was performed with the Bruker Apex3 Suite, the structure was solved with ShelxT91 and refined with ShelxL.92 Olex2 was used as the user interface.93 The H2bpydc molecules form 1D H-bonded chains analogous to the previously reported structure,94 but the packing mode is slightly different.
The material, 1000 mg, was submerged in a solution of 112 mg K2PtCl4 in 20 mL DMF and kept at 373 K for 24 hours while stirring. A bright yellow powder was isolated by filtration, washed twice with 50 mL portions of hot DMF (373 K), 2 times with 50 mL portions of dry acetone, and then dried in air at 423 K.
2.2. Pt L3- and Cu K-edge XAS data collections, EXAFS data analysis
Pt L3-edge (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 560 eV) and Cu K-edge (8980 eV) XAS data were collected at the I811 beamline of the Max Lab II source (Lund, Sweden).96 Max Lab II was operated at 1.5 GeV with a uniform current between 250 and 100 mA. The white beam produced by a liquid He-cooled superconducting wiggler was monochromatized by a horizontally sagittally focused double-crystal Si(111) monochromator. At the Cu K-edge the monochromator was detuned to 20% to minimize the third harmonic, while this procedure is not needed at the Pt L3-edge. Spectra were collected in transmission mode using 30 cm ionization chambers for I0 and I1; the intensity I2 transmitted by a Pt (or Cu) reference foil located after the sample was measured using a photodiode, and the resulting spectrum was employed for energy alignment purposes.
560 eV) and Cu K-edge (8980 eV) XAS data were collected at the I811 beamline of the Max Lab II source (Lund, Sweden).96 Max Lab II was operated at 1.5 GeV with a uniform current between 250 and 100 mA. The white beam produced by a liquid He-cooled superconducting wiggler was monochromatized by a horizontally sagittally focused double-crystal Si(111) monochromator. At the Cu K-edge the monochromator was detuned to 20% to minimize the third harmonic, while this procedure is not needed at the Pt L3-edge. Spectra were collected in transmission mode using 30 cm ionization chambers for I0 and I1; the intensity I2 transmitted by a Pt (or Cu) reference foil located after the sample was measured using a photodiode, and the resulting spectrum was employed for energy alignment purposes.
All XAS spectra were measured employing a home-made cell allowing sample activation in temperature and gas dosage under in situ or operando conditions,97 monitoring the evolution of the XAS features while controlling the temperature and gas feed. The XAS data reduction and EXAFS extraction procedure was performed using the Athena codes.98 The parametric EXAFS data analysis was performed with IFEFFIT99 code that employs phases and amplitudes computed by FEFF6 code,100,101 as detailed elsewhere.59
2.3. Pt L3-edge XANES simulations
For all clusters simulating the local environments of Pt atoms hosted inside the UiO-67-Pt MOF and successive modification by chemical reactivity with H2, Br2 and toluene-3,4-dithiol (H2tdt), the ground-state electronic structures and atomic geometries were calculated using the hybrid DFT B3LYP level of theory102 using the ADF-2015 program package.103,104 The QZ4P basis set was used in all calculations. Thus, each atomic orbital was represented as a combination of four Slater type orbitals with different exponential powers and four polarization functions. We first obtain eigenvalues and corresponding wave functions. The matrix elements are then evaluated for transitions between the 2p core level and unoccupied MOs using dipole transition operators. In order to compare with experimental XANES spectra, a convolution of calculated matrix elements was performed with a Lorentzian profile using the energy-dependent line width. In the pre-edge region, the width of the Lorentzian profile corresponds to a core hole lifetime broadening for Pt. This value is then increased in higher energy intervals with a smooth arctangent function. The parameters of the matrix element calculations (grid step, size number of unoccupied MOs) and energy convolution are fixed once for all complexes. The calculated spectra were subsequently aligned according to the energy value of the Pt 2p orbital, thus reproducing the chemical shift for different species. A rigid shift with the identical value was applied for all spectra in order to align the energy scale between experimental data and theoretical calculations.3. Results and discussion
3.1. Pt-functionalization of UiO-67 MOF: state of the art
Introducing a chemically active Pt site as part of the UiO-67 framework is of great interest as platinum has rich redox chemistry, showing 0, II and IV stable oxidation states. Moreover, certain square planar Pt(II) coordination complexes are known to be active in C–H bond activation,105 for example see the scheme reported in Fig. 1b and c. In particular, dichlorobipyrimidyl platinum(II), PtCl2(BPYM), performs the catalytic oxidation in fuming or concentrated sulfuric acid, achieving high yields of methanol with selectivity higher than 90%.106,107 It is consequently of potential interest to investigate the possibility to heterogenize such a process anchoring the active Pt(II) complex on some high surface area material such as that recently shown by the group of Schüth, for polymers first108,109 and for N-doped carbons110 successively, or as done more recently by Øien et al.59 who have succeeded in functionalizing UiO-67 with (H2bpydc)PtCl2 or (H2bpydc)PtCl4 units, substituting 10% of the standard bpdc linkers. The authors used EXAFS, XANES and valence-to-core resonant inelastic X-ray scattering techniques to prove the insertion of Pt atoms in the expected framework position of UiO-67 (see Fig. 1c).Using EXAFS and XANES, the local coordination environment and the oxidation state of Pt can be monitored under in situ conditions. The elimination of chloride ligands from Pt in a continuous gas flow of diluted H2 (3% H2 in He) have been monitored by EXAFS during temperature ramping (Fig. 2a). The spectrum collected at room temperature (black curve) exhibits both the first shell Pt–N and the Pt–Cl contributions centred around 1.5 and 1.9 Å in the phase uncorrected Fourier transform (FT), highlighted by vertical blue and green dashed lines, respectively. Upon increasing the temperature, both contributions decrease in intensity because of the increased Debye–Waller factors (σN2 and σCl2). Starting from about 600 K the Pt–Cl contribution shows a much more relevant decrease in temperature than the Pt–N contribution, suggesting that the system starts losing chlorine ligands. A standard EXAFS analysis failed because of the high correlation between the coordination numbers (NPt–N; NPt–Cl) and the thermal parameters (σN2; σCl2).59 The problem was solved by applying an advanced data analysis approach briefly summarized hereafter.
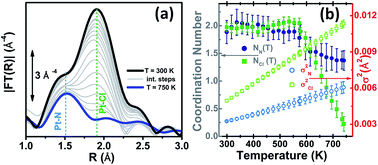 | ||
| Fig. 2 Part (a): k3-weighted, phase uncorrected FT of Pt L3-edge EXAFS spectra collected during the in situ H2-TPR experiments on the PtCl2(H2bpydc) functionalized UiO-67-Pt(II) MOF in the 300 K (black spectrum)–750 K (blue spectrum) range performed with diluted H2 flow (3% H2 in He). Part (b): quantitative data analysis of the set of spectra shown in part (a) by modelling the temperature dependence of the Debye–Waller factors (σN2 and σCl2) based on the Einstein model. Previously unpublished figure replotting data published in ref. 59. | ||
First, we worked only on the sub-set of data in the interval between RT and 473 K. In this temperature range no bond breaking occurs, so it was possible to fix NN = NCl = 2. On that sub-set of in situ EXAFS data a parametric refinement was performed, commonly employed in XRPD Rietveld refinements,111,112 adopting the Einstein model to describe the temperature dependence of both σN2 and σCl2 factors. The Einstein model approximates the vibrational density of states as a Dirac delta function spiked at a single frequency named the Einstein frequency (ωE). The model assumes that the Pt–N pairs (or Pt–Cl) behave as a quantum harmonic oscillator of mass equal to the reduced mass of the atomic pair (M = 13.070 and 30.004 amu for the Pt–N and Pt–Cl pairs, respectively). Under such assumptions, the σ2(T) behaviour is straightforwardly determined by the only ωE parameter according to eqn (1):59,113
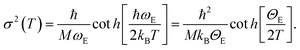 | (1) |
Θ E is the Einstein temperature of the Pt–N (or Pt–Cl) bond, related to the Einstein frequency by the relationship: ħωE = kBΘE, where ħ = 1.055 × 10−34 J s is the reduced Planck constant and kB = 1.38 × 10−23 J K−1 is the Boltzmann constant.
This approach allowed us to reduce the number of parameters used to optimize the thermal factors of the series from ∼40 to only two, ΘE(Pt–N) and ΘE(Pt–Cl), with a consequent reduction of the correlation among the optimized parameters and thus a reduction of the relative error bars. Once the Einstein temperatures ΘE(Pt–N) = (709 ± 63) K and ΘE(Pt–Cl) = (333 ± 9) K were obtained, the dependence of both σN2 and σCl2vs. T was straightforwardly obtained viaeqn (1) and extrapolated on the whole set of data (i.e. also above 473 K). This strategy allowed stable fits in the whole temperature range while optimizing both NN and NCl, as shown in Fig. 2b. From this data analysis, it is evident that both NN and NCl are stable to the stoichiometric values of 2.0 up to 575 K, when they start to decrease together. However, while NCl decreases almost linearly to 0.4 at 750 K, NN undergoes a fast decrease to 1.6 at 610 K and then remains almost stable, with a value at 750 K of 1.4. This means that a prolonged activation in diluted H2 of the UiO-67-Pt(II) MOF in the 610–640 K interval will result in a minimal loss of Pt-sites, which will lose the Pt–N connection with the framework, but break of an important fraction of the Pt–Cl bonds. The experiment reported in Fig. 2 proved that this activation temperature interval is ideal to obtain a material where most of the Pt species are still linked to the MOF framework, exhibiting the coordination vacancies needed to make the UiO-67-Pt(II) material a potential heterogeneous catalyst.59 The presence of coordination vacancies at platinum sites was also directly testified by IR spectroscopy of adsorbed CO. No evidence of a Pt–Pt signal of an aggregated platinum phase was observed in the experiment reported in Fig. 2.
EXAFS was also used to prove the high reactivity of the Pt(II) species hosted in the UiO-67 MOF. We followed the liquid-phase ligand exchange with toluene-3,4-dithiol (H2tdt) and the liquid-phase oxidative addition of Br2 to Pt (see Fig. 3). All the observed reactions take place without any degradation of the framework, as testified by parallel XRPD experiments.
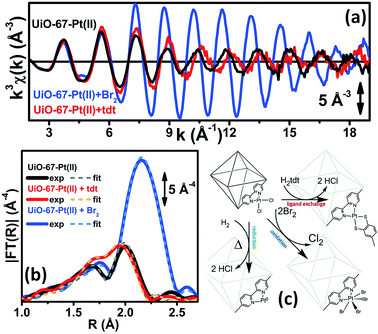 | ||
| Fig. 3 Part (a): experimental Pt L3-edge k3χ(k) spectra of UiO-67-Pt(II) before (black line) and after interaction with H2tdt (red line) and Br2 (blue line). Part (b): modulus of the k3-weighted, phase uncorrected FT of the experimental EXAFS spectra reported in part (a), solid lines, same color code as in part (a). The corresponding best fits are also reported, as dashed lines of similar colour. Part (c): schematic representation of the reactivity of Pt(II) species in functionalized UiO-67-Pt MOFs that has been highlighted in the EXAFS study reported in Fig. 2 and in parts (a and b) of this figure. The sketched square bi-pyramid represents the octahedral large cavity of UiO-67, measuring about 16 Å in diagonal.32,34 Previously unpublished figure replotting data published in ref. 59. | ||
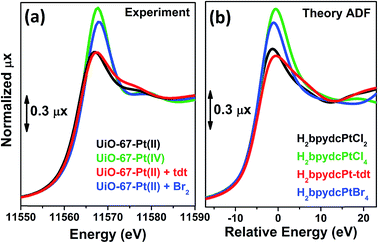
Also the XANES part of the XAS spectrum is sensitive to the changes undergone by the local environment of Pt(II) along the chemical reactions reported in Fig. 3. Upon a change in the Pt oxidation state, the Pt L3-edge XANES will show a very small edge shift while it will exhibit a noticeable variation of the intensity of the “white-line” peak.59,114–116 Indeed, the XANES part of the Pt L3-edge mainly derives from the promotion of core 2p3/2 electrons into empty 5d3/2, 5d5/2 and 6s valence states, so mainly probing the unoccupied density of 5d-states and partially 6s-states. The XANES spectra reported in Fig. 4a for the UiO-67-Pt(II) MOF before (red line) and after interaction with H2tdt (blue line) and Br2 (green line) clearly follow this phenomenological trend. In particular, interaction with H2tdt (blue spectrum in Fig. 4a) does not affect the white line intensity, affecting only the post edge and EXAFS region of the spectrum; on this basis it was concluded that a ligand exchange reaction occurs where two Cl ligands are exchanged with the two S atoms of the bulky H2tdt unit. Conversely, interaction with Br2 (green spectrum in Fig. 4a) results in a significant increase in the white line intensity, testifying an oxidation process from Pt(II) to Pt(IV).59,116
On a more quantitative ground, simulation of the XANES spectra, on the H2bpydcPtCl4, H2bpydcPtCl2, H2bpydcPt-tdt and H2bpydcPtBr4 molecular fragments (Fig. 4b), was able to reproduce correctly the variation of the white line intensity, and post edge features.116 The data reported in Fig. 4 testifies the potentialities of the XANES simulations.117
3.2. Tuning the Pt site population inside UiO-67-Pt MOF by controlled H2-TPR
The interesting results obtained by us in the Pt-functionalisation of UiO-67 (here summarized in Section 3.1), together with the relevance of hosting reactive metal NPs inside the MOF cavities,51–58 encouraged us to investigate different activation conditions in order to be able to tune the population of Pt phases inside functionalised UiO-67, from isolated Pt sites anchored to the MOF framework with Pt exhibiting two coordination vacancies (potentially interesting for C–H bond activation) to small Pt NPs (potentially interesting for hydrogenation reactions).In the following two subsections, we report the XANES and EXAFS results, and the corresponding data analysis, obtained by thermal activation of the functionalised UiO-67-Pt MOF under an inert flow (He, 3.2.1) and under a concentrated H2 flow (10% H2 in He, 3.2.2). In both cases the EXAFS data have been analysed using a parametric refinement allowing us to obtain, along the activation procedure, the first shell Pt coordination numbers (NPt–N, NPt–Cl and, when present, NPt–Pt) with the minimal correlation possible with the corresponding Debye–Waller parameters. From such data, the fractions of the different platinum phases present in the sample have been obtained, as outlined hereafter. The following nomenclature has been adopted for the different relative fractions of Pt species formed in the experiments: fbpyCl2 corresponds to Pt atoms coordinated to the bpydc linker in the MOF framework, still containing the Cl ligands; fbpy stands for Pt atoms coordinated to the bpydc linker in the MOF framework after the loss of two Cl ligands; fextra represents non-aggregated extra-framework Pt atoms; and fNPs stands for extra-framework Pt atoms aggregated in NPs. While the fbpyCl2, fbpy and fNPs fractions correspond to well defined Pt species, fextra does not. Although it is fully reasonable to infer that, once the Pt–N bonds within the framework are broken, Pt atoms will behave as isolated species for a while before being incorporated into a pre-existing NP (or before interacting with other isolated Pt atoms to produce a new NP), the local environment of such Pt species is very difficult to predict. Most probably such Pt atoms will experience a large variety of different local environments resulting in an average contribution to the measured EXAFS spectrum that is very low because of heterogeneity. This fact has been very well documented by EXAFS studies on Fe-substituted zeolites showing that the amplitude of the experimental EXAFS signal is strongly dimmed once Fe atoms migrate from the framework into extra-framework sites,118–120 contributing only in the very short k-range (typically up to 6 Å−1).
| fNPs = 0; fbpyCl2 = NCl/2; fextra = (2 − NN)/2; fbpy = 1 − fbpyCl2 − fextra | (2) |
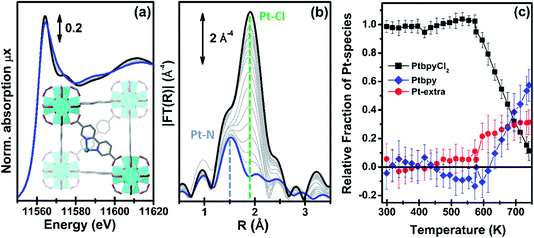 | ||
| Fig. 5 Part (a): evolution of the Pt L3-edge XANES spectra during in situ thermal activation of the functionalized UiO-67-Pt MOF under an inert He flow in the 300–750 K range. The inset shows a cartoon description of the dominant final phase (framework-coordinated Pt atom that has lost the two Cl ligands). Part (b): as part (a) for the k3-weighted, phase uncorrected FT of the corresponding EXAFS data. Also highlighted with blue and green dashed lines are the typical positions of the Pt–N and Pt–Cl contributions, respectively. Part (c): fraction of the different Pt phases present in the sample, estimated from the NPt–N and NPt–Cl coordination numbers obtained from the parametric refinement of the whole set of EXAFS data, according to the assumptions reported in eqn (2). | ||
The analysis of the evolution during the activation experiment of the relative fractions of the different Pt phases performed according to eqn (2) is reported in Fig. 5c. Up to 550 K, within the experimental errors, fbpyCl2 = 1 and fextra = fbpy = 0. Then, fbpyCl2 starts to rapidly decrease down to 0.1 in an almost linear fashion with the increasing temperature; an opposite trend is observed for fbpy, reaching 0.6 at 750 K, while fextra exhibits an abrupt increase at ca. 570 K, and subsequently stabilizes at around 0.3.
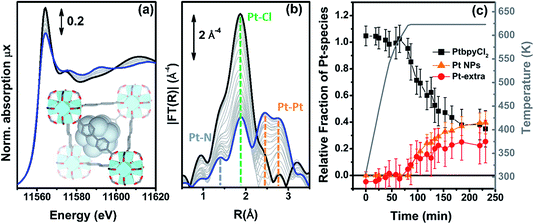 | ||
| Fig. 6 Part (a): evolution of the Pt L3-edge XANES spectra during the in situ H2-TPR experiment of the PtCl2(H2bpydc) functionalized UiO-67-Pt(II) MOF performed in a concentrated H2 flow (10% H2 in He). The inset shows a cartoon description of the dominant final phase (metal NPs). Part (b): as part (a) for the k3-weighted, phase uncorrected FT of the corresponding EXAFS data. Also highlighted with blue, green and orange dashed lines are the typical positions of the Pt–N, Pt–Cl and Pt–Pt contributions, respectively. Part (c), full black, red and orange symbols, left ordinate axis: fraction of the different Pt phases present in the sample, estimated from the NPt–N, NPt–Cl and NPt–Pt coordination numbers obtained from the parametric refinement in the whole set of EXAFS data, according to the assumptions reported in eqn (5). Part (c), open grey triangles, right ordinate axis: evolution of the sample temperature with time, highlighting the linear increase up to 625 K in 65 min followed by 2 h 55 min in isotherm. | ||
Different to what was observed in the previous cases, where NPt–Cl started to decrease significantly before NPt–N, in the present case both NPt–N and NPt–Cl remain, within the associated error bars, equal to 2 during the whole heating ramp up to 625 K (indicating fbpyCl2 = 1) and start to decrease in the same way during the isotherm (data not reported for brevity). This indicates that, under a concentrated H2 flow, when framework Pt(II) species lose the Pt–Cl bond they almost simultaneously also lose the Pt–N bond and thus the connectivity with the MOF framework, thus becoming extra-framework species. Based on this evidence, we can assume fbpy = 0, while fbpyCl2 can be determined by averaging the contribution of both Pt–Cl and Pt–N bonds: fbpyCl2 = (NCl/2 + NN/2)/2.
A second important difference, very evident in Fig. 6b, is the structured signal in the 2.5–3.5 Å range, typical of the single and multiple scattering Pt–Pt contributions of the fcc metal phase, testifying the formation of Pt NPs. Hence, the EXAFS data analysis also provides a first shell NPt–Pt coordination number. Unfortunately the fraction of Pt atoms in the NPs phase cannot be straightforwardly deduced from the NPt–Pt number obtained from the EXAFS data analysis, because the average coordination number of a fcc NP increases with the particle size, asymptotically reaching the value of 12 of the bulk in the first shell.121–125 Consequently, the NPt–Pt ↔ fNPs relationship can be established only if the particle size distribution has been determined by an independent SAXS126–133 or TEM74,124,133–135 study.
Indeed, at the end of the H2-TPR experiment reported in Fig. 6, the sample was cooled down to 300 K under He flow, recovered and subjected to a TEM study (see Fig. 7b and c for two selected micrographs taken at different magnifications), giving the particle size distribution wP(di) reported in Fig. 7a (orange bars) and obtained by selecting the NPs in 12 classes of amplitude 1 nm. wP(di) reports the fraction of NPs that have a diameter d falling in the class centred in di and results in an average NP diameter of 〈d〉P = 3.5 nm with a standard deviation of 1.2 nm. The orange NP distribution wP(di) is the standard output from a TEM analysis, but is however not the correct one to be used to extrapolate the average coordination number measured in the EXAFS study. Indeed, the measured EXAFS signal is the average signal coming from all the Pt atoms in the sample. This means that a large particle contributes more to the EXAFS signal than a small one, because it contains more atoms. The orange wP(di) distribution, weighted by particles, has to be corrected by weighting for the corresponding volume fraction into wV(di), defined as follows:
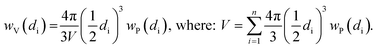 | (3) |
 | ||
| Fig. 7 Part (a): Pt NP distributions (weighted by number of particles (orange) or by volume (blue): wP(di) and wV(di), respectively, see eqn (3)) obtained from the TEM analysis of the PtCl2(H2bpydc) functionalized UiO-67-Pt(II) MOF measured after the H2-TPR XAS experiment reported in Fig. 6. Parts (b) and (c) report two micrographs at different magnifications. | ||
The volume-weighted NP distribution, obtained from wP(di) viaeqn (3), is reported in Fig. 7a (orange bars) and results in a (volume-weighted) average NP diameter of 〈d〉V = 5.5 nm with a standard deviation of 1.5 nm. Comparing wP(di) and wV(di), the more important role played by the high-d region is evident. Knowing the average coordination number of an fcc NP with a given diameter, N(di), the volume-weighted NP distribution allows us to obtain the average coordination number of the whole particle distribution estimated from the TEM analysis (NTEM) as:
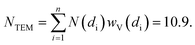 | (4) |
Once NTEM has been determined, the fraction of Pt atoms occurring as NPs is obtained as fNPs = NPt/NTEM, while the fraction of Pt atoms in non-aggregated extra-framework positions is obtained by the difference between the unit and the sum of the other two fractions. Summarizing:
| fbpy = 0; fbpyCl2 = (NCl/2 + NN/2)/2; fNPs = NPt/NTEM; fextra = 1 − fbpyCl2 − fNPs. | (5) |
The evolution of the relative fractions of the different Pt phases during the in situ H2-TPR experiment in a concentrated H2 flow is summarized in Fig. 6c. The weakness of this approach is the fact that we assume the same NP size distribution along the whole H2-TPR experiment. Nonetheless, this approach provides a correct evaluation of fNPs for the last points of the treatment, which is the required information in the view of potential application in catalysis.
Within the experimental error, along the whole heating ramp up to 625 K, Pt atoms maintain the same square planar coordination with two nitrogen and two chlorine ligands in their first coordination shell. During the isotherm, they break simultaneously the bonds with both the Cl ligands and the MOF framework, becoming extra-framework species, that progressively aggregate into NPs. After 3 h of isotherm at 625 K the distribution among the different Pt phases reaches an asymptotic equilibrium.
3.3. Structure and redox properties of isolated Cu sites in UiO-67-Cu MOF
The interesting results obtained on the Pt-functionalised UiO-67 MOF encouraged us to extend the study using other metals. Because of its interesting redox chemistry, our first choice was on copper. We consequently prepared a Cu-functionalized UiO-67 MOF by contacting the bpydc-containing UiO-67-bpy MOF with a CuCl2 dihydrate precursor.60 The synthesis method succeeded in grafting isolated Cu(II) ions on the functionalised bpydc linkers of the UiO-67 framework but, contrary to what was expected, the local environment of copper was not composed of two nitrogen and two chlorine atoms as it was the case for the Pt-functionalised MOF (see Fig. 1b and c).Indeed, just from a first simple comparison of the XANES (Fig. 8a) and EXAFS (Fig. 8b) data collected on as-prepared UiO-67-Cu (black) and on the tBbpyCuCl2 model compound (green, where Cu(II) is in a square planar geometry coordinating 2 N and 2 Cl atoms, see Fig. 8c) clearly testifies that the local environment of Cu atoms in the two materials is significantly different. The EXAFS data clearly shows a lack of an EXAFS signal in the (1.5–2.1) Å region in the MOF, suggesting the presence of only one Cl atom in the first coordination shell of the Cu(II).
 | ||
| Fig. 8 Part (a): Cu K-edge XANES spectra of the tBbpyCuCl2 model compound (green) and of the UiO-67-Cu MOF before and after the in situ thermal activation in an N2 flow (black and blue spectra, respectively). Part (b): as part (a) for the k3-weighted, phase uncorrected FT of the corresponding EXAFS data. Also highlighted with blue and green dashed lines are the typical positions of the (Cu–N or Cu–OH) and Cu–Cl contributions, respectively. Part (c): structure of the tBbpyCuCl2 model compound as obtained from the single-crystal XRD refinement (data collected at 100 K). Parts (d) and (e): DFT-optimized structures of the Cu(II)ClOH(H2bpydc) and Cu(I)Cl(H2bpydc) complexes used as a starting point for the EXAFS fits of the UiO-67-Cu MOF before and after the in situ thermal activation. Atom colour code: Cu: orange; O: red; N: blue; Cl: green, C: gray; H: white. Previously unpublished figure reporting spectra and structures from ref. 60. | ||
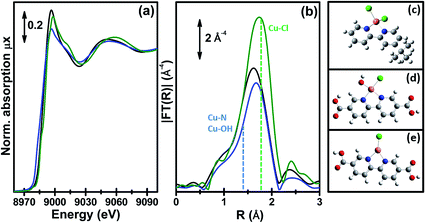
Fig. 9 reports the XANES spectra (part a) and the k3-weighted, phase uncorrected (part b) FT EXAFS spectra for the exemplificative case of UiO-67-Cu during the thermal treatment in an inert gas flow, from RT (as-prepared state, black) to 523 K (blue). Spectra collected at intermediate temperatures are also reported, as thin gray lines.
 | ||
| Fig. 9 Part (a): evolution of the Cu K-edge XANES spectra during the in situ thermal activation in an N2 flow of the CuClOH(H2bpydc) functionalized UiO-67-Cu(II) MOF in the 300–523 K range. The inset shows a cartoon description of the dominant final phase (framework-coordinated Cu(I) species with a Cl ligand). Part (b): as part (a) for the k3-weighted, phase uncorrected FT of the corresponding EXAFS data. Also highlighted with blue and green dashed lines are the typical positions of the (Cu–N or Cu–OH) and Cu–Cl contributions, respectively. Part (c), full black and blue symbols, left ordinate axis: fraction of the different Cu phases present in the sample estimated according to a linear combination of the XANES spectra of the starting and final phases. Part (c), open grey triangles, right ordinate axis: evolution of the sample temperature with time, highlighting the linear increase up to 523 K in 23 min followed by 13 min in isotherm. Previously unpublished figure reporting spectra from ref. 60. | ||
The XANES spectrum for the as-prepared material is characterized by the absence of any defined pre-edge/edge peaks, and by a rather intense white line feature at ∼8996.6 eV, typical of Cu(II) centres coordinated to water molecules and, eventually, OH groups.136–141 As also supported by the comparison with the tBbpyCuCl2 model compound, the overall shape and the edge energy position in the XANES spectrum of the as-prepared material are consistent with a 2+ oxidation state of copper. The spectral changes observed during thermal activation involve a clear decrease of the white line feature, accompanied by a significant shift of the absorption edge towards lower energies (ca. 3.6 eV), as evaluated by monitoring the energy position of the first main maximum of the first derivative spectra.142,143 At the end of the heating ramp, a shoulder starts to be distinguishable in the XANES edge-rising region at ca. 8983 eV, falling in an energy range typical of two- or three-coordinated Cu(I) sites.144,145 These evidences suggest a ligand loss process associated with the reduction of the starting Cu(II) sites into Cu(I), as thermal treatment proceeds. Such spectral modifications are also accompanied by the sample color change from green to light-green/white as the temperature increases, supporting the formation of coordinatively unsaturated Cu(I) sites after mild thermal treatment in an inert atmosphere.
We succeeded in reproducing the EXAFS and XANES spectra of the as prepared UiO-67-Cu MOF using as a starting model that obtained from the optimization of the [Cu(II)(bpydc)(OH)Cl] complex (see Fig. 8d) at the DFT level of theory with VASP 5.3 code,146,147 using a kinetic energy cut-off for the plane-wave basis set of 400 eV. The EXAFS-optimized distances were: RCu–OH = 1.91 ± 0.01 Å, RCu–N = 2.026 ± 0.006 Å and RCu–Cl = 2.265 ± 0.006 Å, in reasonable agreement with the DFT-optimized distances.60 The same holds for the DFT-optimized [Cu(I)(bpydc)Cl] complex (see Fig. 8e), that was able to correctly reproduce the EXAFS spectrum of the N2-activated UiO-67-Cu MOF, resulting in RCu–N = 1.989 ± 0.008 Å and RCu–Cl = 2.249 ± 0.007 Å. The progressive evolution from the [Cu(II)(bpydc)(OH)Cl] complex into the [Cu(I)(bpydc)Cl] complex upon thermal activation in an inert atmosphere has been quantified by linear combination of the XANES spectra and is reported in Fig. 9c.
Further insights into the nature and reactivity of these [Cu(I)(bpydc)Cl] complexes, representing an interesting platform for future experiments on Cu(I)-catalyzed reactions, were achieved by monitoring with XAS and FTIR the interaction of the thermally-treated material with the CO probe molecule. Both techniques pointed out the efficient and reversible formation of Cu(I)-mono-carbonyl adducts with CO, compatible with [Cu(I)(bpydc)(CO)Cl] species as highlighted by EXAFS fitting.
The overall picture is confirmed by XANES simulations performed with the FDMNES code117 for the key experimental conditions investigated, including as-prepared MOFs in air, after thermal treatment in N2-flux and upon interaction with CO.60
4. Conclusions
A post-synthesis functionalisation approach has been successfully employed to graft Pt(II) and Cu(II) atoms on the UiO-67 MOF functionalized with 10% of bpydc ligands. The in situ EXAFS analysis, for all the series of samples at RT, demonstrates that the Pt atoms are grafted to the bpydc-linkers in a square planar coordination with two Cl and two N atomic neighbors. XAS spectroscopy was used in operando conditions to study the activation of UiO-67-Pt functionalized MOFs, demonstrating that, by tuning the activation conditions, two types of catalytically active sites can be formed in the cavities of the MOF: (i) isolated, highly uncoordinated framework![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) Pt species bound to the two N atoms of the functionalising bpydc linkers of the MOF and (ii) Pt NPs. XAS was used for monitoring the temperature-dependent behavior of UiO-67-Pt during the thermal activation process, in different gas feeds (pure He, 3% H2/He and 10% H2/He). EXAFS analysis of the data collected during operando H2-TPR was performed using the Einstein model to predict the temperature dependence of the Debye–Waller factors and to reduce the correlation among the optimized parameters. In a 10% H2/He flow, EXAFS clearly shows the loss of both Cl and N scattering contributions, while the rising of an intense signal at around 2.7 Å, associated with the Pt–Pt contributions, unambiguously indicates Pt NPs formation. Conversely, in a pure He flow, the only significant change observed during TPR is the progressive decrease of the Pt–Cl single scattering contribution, leading to the conclusion that the Pt grafted to the bpydc-linkers remains naked. In general, Pt sites in UiO-67-Pt MOFs tend to form Pt NPs in the presence of H2 and remain naked, but still grafted to the bpydc-linkers, in an inert gas flow. This study demonstrates that two families of different catalytically active Pt sites can be generated in UiO-67-Pt MOFs by properly tuning the activation conditions. In situ IR, ex situ TEM and catalytic tests support the operando XAS study.
Pt species bound to the two N atoms of the functionalising bpydc linkers of the MOF and (ii) Pt NPs. XAS was used for monitoring the temperature-dependent behavior of UiO-67-Pt during the thermal activation process, in different gas feeds (pure He, 3% H2/He and 10% H2/He). EXAFS analysis of the data collected during operando H2-TPR was performed using the Einstein model to predict the temperature dependence of the Debye–Waller factors and to reduce the correlation among the optimized parameters. In a 10% H2/He flow, EXAFS clearly shows the loss of both Cl and N scattering contributions, while the rising of an intense signal at around 2.7 Å, associated with the Pt–Pt contributions, unambiguously indicates Pt NPs formation. Conversely, in a pure He flow, the only significant change observed during TPR is the progressive decrease of the Pt–Cl single scattering contribution, leading to the conclusion that the Pt grafted to the bpydc-linkers remains naked. In general, Pt sites in UiO-67-Pt MOFs tend to form Pt NPs in the presence of H2 and remain naked, but still grafted to the bpydc-linkers, in an inert gas flow. This study demonstrates that two families of different catalytically active Pt sites can be generated in UiO-67-Pt MOFs by properly tuning the activation conditions. In situ IR, ex situ TEM and catalytic tests support the operando XAS study.
By combining in situ and operando XAS and FTIR spectroscopy, we also assessed the successful incorporation of well-defined Cu complexes in the UiO-67 framework in the form of the [Cu(II)ClOH(H2bpydc)] complex, that evolves into [Cu(I)Cl(H2bpydc)] upon thermal activation in an inert atmosphere. We explored the local coordination geometry, redox properties and reactivity of the dominant Cu species formed in different conditions relevant to potential future applications in catalysis. EXAFS fits and XANES simulations, based on DFT-optimized geometries, yielded detailed structural and electronic information on the major Cu-species formed.
The methodology of the post-synthesis functionalisation of the UiO-67 MOF, here described for PtCl2 and CuCl2, has been recently successfully extended using RhCl3 and IrCl3 precursors, while a first attempt to insert gold via HAuCl4 as the precursor failed.148 The same strategy has been followed by the group of Long, who succeeded in preparing UiO-67-M grafting NiBr2,149 CuCl2,150 CoCl2,150 FeBr2,150 and Cr(CO)4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 on functionalized H2bpydc linkers in UiO-67. In this regard, very interesting are also the works of the Lin group who synthesized UiO-66-like class of MOFs using long [Ir(ppy)2(bpy)]+-derived dicarboxylate ligands; successive photoreduction of K2PtCl4 resulted in Pt nanoparticles hosted inside the large MOFs cavities.51 Successively, the same group used Re(CO)3Cl grafted to 4,4′-(2,2′-bipyridine-5,5′-diyl)dibenzoate151 and FeBr2 grafted to 4,4′-(1,10-phenanthroline-3,8-diyl)dibenzoic acid152 linkers to obtain metal functionalized MOFs with UiO-66-like structure with interesting catalytic activities. Of interest is also the post-synthesis functionalization strategy used to insert the β-diketiminate functionality in a MOF of UiO-topology. Metalation of the β-diketiminate-MOF with iron, copper, and cobalt metal salts afforded the desired MOF-supported β-diketiminate-M complexes (M = Fe, Cu, and Co).88
150 on functionalized H2bpydc linkers in UiO-67. In this regard, very interesting are also the works of the Lin group who synthesized UiO-66-like class of MOFs using long [Ir(ppy)2(bpy)]+-derived dicarboxylate ligands; successive photoreduction of K2PtCl4 resulted in Pt nanoparticles hosted inside the large MOFs cavities.51 Successively, the same group used Re(CO)3Cl grafted to 4,4′-(2,2′-bipyridine-5,5′-diyl)dibenzoate151 and FeBr2 grafted to 4,4′-(1,10-phenanthroline-3,8-diyl)dibenzoic acid152 linkers to obtain metal functionalized MOFs with UiO-66-like structure with interesting catalytic activities. Of interest is also the post-synthesis functionalization strategy used to insert the β-diketiminate functionality in a MOF of UiO-topology. Metalation of the β-diketiminate-MOF with iron, copper, and cobalt metal salts afforded the desired MOF-supported β-diketiminate-M complexes (M = Fe, Cu, and Co).88
Acknowledgements
LB, ALB, AAG, AVS and CL acknowledge the Megagrant of the Russian Federation Government to support scientific research at the Southern Federal University, no. 14.Y26.31.0001. KAL acknowledges the support from the Russian Foundation for Basic Research, Project no. 16-32-00572 mol_a. The authors are grateful to MAX-lab for the allocation of the beam time (proposal 20140449) and to Dr Stefan Carlson for the technical support during the experiments at the I811 beamline.Notes and references
- S. L. James, Chem. Soc. Rev., 2003, 32, 276–288 RSC.
- J. L. C. Rowsell and O. M. Yaghi, Microporous Mesoporous Mater., 2004, 73, 3–14 CrossRef CAS.
- G. Ferey, Chem. Soc. Rev., 2008, 37, 191–214 RSC.
- N. Stock and S. Biswas, Chem. Rev., 2012, 112, 933–969 CrossRef CAS PubMed.
- T. R. Cook, Y. R. Zheng and P. J. Stang, Chem. Rev., 2013, 113, 734–777 CrossRef CAS PubMed.
- H. Furukawa, K. E. Cordova, M. O’Keeffe and O. M. Yaghi, Science, 2013, 341, 974–987 CrossRef CAS PubMed.
- V. V. Butova, M. A. Soldatov, A. A. Guda, K. A. Lomachenko and C. Lamberti, Russ. Chem. Rev., 2016, 85, 280–307 CrossRef CAS.
- Z. Q. Wang and S. M. Cohen, Chem. Soc. Rev., 2009, 38, 1315–1329 RSC.
- K. K. Tanabe and S. M. Cohen, Chem. Soc. Rev., 2011, 40, 498–519 RSC.
- D. Zhao, D. J. Timmons, D. Q. Yuan and H. C. Zhou, Acc. Chem. Res., 2011, 44, 123–133 CrossRef CAS PubMed.
- S. M. Cohen, Chem. Rev., 2012, 112, 970–1000 CrossRef CAS PubMed.
- F. A. A. Paz, J. Klinowski, S. M. F. Vilela, J. P. C. Tome, J. A. S. Cavaleiro and J. Rocha, Chem. Soc. Rev., 2012, 41, 1088–1110 RSC.
- W. G. Lu, Z. W. Wei, Z. Y. Gu, T. F. Liu, J. Park, J. Park, J. Tian, M. W. Zhang, Q. Zhang, T. Gentle, M. Bosch and H. C. Zhou, Chem. Soc. Rev., 2014, 43, 5561–5593 RSC.
- J. D. Evans, C. J. Sumby and C. J. Doonan, Chem. Soc. Rev., 2014, 43, 5933–5951 RSC.
- D. Farrusseng, S. Aguado and C. Pinel, Angew. Chem., Int. Ed., 2009, 48, 7502–7513 CrossRef CAS PubMed.
- J. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. T. Hupp, Chem. Soc. Rev., 2009, 38, 1450–1459 RSC.
- L. Q. Ma, C. Abney and W. B. Lin, Chem. Soc. Rev., 2009, 38, 1248–1256 RSC.
- A. Corma, H. Garcia and F. Xamena, Chem. Rev., 2010, 110, 4606–4655 CrossRef CAS PubMed.
- M. Ranocchiari and J. A. van Bokhoven, Phys. Chem. Chem. Phys., 2011, 13, 6388–6396 RSC.
- A. Dhakshinamoorthy and H. Garcia, Chem. Soc. Rev., 2012, 41, 5262–5284 RSC.
- M. Yoon, R. Srirambalaji and K. Kim, Chem. Rev., 2012, 112, 1196–1231 CrossRef CAS PubMed.
- Metal Organic Frameworks as Heterogeneous Catalysts, ed. F. Xamena and J. Gascon, Royal Society of Chemistry, Cambridge, 2013 Search PubMed.
- J. W. Liu, L. F. Chen, H. Cui, J. Y. Zhang, L. Zhang and C. Y. Su, Chem. Soc. Rev., 2014, 43, 6011–6061 RSC.
- A. H. Chughtai, N. Ahmad, H. A. Younus, A. Laypkov and F. Verpoort, Chem. Soc. Rev., 2015, 44, 6804–6849 RSC.
- S. S. Y. Chui, S. M. F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150 CrossRef CAS PubMed.
- C. Prestipino, L. Regli, J. G. Vitillo, F. Bonino, A. Damin, C. Lamberti, A. Zecchina, P. L. Solari, K. O. Kongshaug and S. Bordiga, Chem. Mater., 2006, 18, 1337–1346 CrossRef CAS.
- S. Bordiga, L. Regli, F. Bonino, E. Groppo, C. Lamberti, B. Xiao, P. S. Wheatley, R. E. Morris and A. Zecchina, Phys. Chem. Chem. Phys., 2007, 9, 2676–2685 RSC.
- F. Bonino, S. Chavan, J. G. Vitillo, E. Groppo, G. Agostini, C. Lamberti, P. D. C. Dietzel, C. Prestipino and S. Bordiga, Chem. Mater., 2008, 20, 4957–4968 CrossRef CAS.
- S. Chavan, J. G. Vitillo, E. Groppo, F. Bonino, C. Lamberti, P. D. C. Dietzel and S. Bordiga, J. Phys. Chem. C, 2009, 113, 3292–3299 CAS.
- P. D. C. Dietzel, P. A. Georgiev, J. Eckert, R. Blom, T. Strassle and T. Unruh, Chem. Commun., 2010, 46, 4962–4964 RSC.
- E. D. Bloch, L. J. Murray, W. L. Queen, S. Chavan, S. N. Maximoff, J. P. Bigi, R. Krishna, V. K. Peterson, F. Grandjean, G. J. Long, B. Smit, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14814–14822 CrossRef CAS PubMed.
- J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850–13851 CrossRef PubMed.
- L. Valenzano, B. Civalleri, S. Chavan, S. Bordiga, M. H. Nilsen, S. Jakobsen, K. P. Lillerud and C. Lamberti, Chem. Mater., 2011, 23, 1700–1718 CrossRef CAS.
- S. Chavan, J. G. Vitillo, D. Gianolio, O. Zavorotynska, B. Civalleri, S. Jakobsen, M. H. Nilsen, L. Valenzano, C. Lamberti, K. P. Lillerud and S. Bordiga, Phys. Chem. Chem. Phys., 2012, 14, 1614–1626 RSC.
- S. Øien, D. Wragg, H. Reinsch, S. Svelle, S. Bordiga, C. Lamberti and K. P. Lillerud, Cryst. Growth Des., 2014, 14, 5370–5372 Search PubMed.
- G. C. Shearer, S. Chavan, J. Ethiraj, J. G. Vitillo, S. Svelle, U. Olsbye, C. Lamberti, S. Bordiga and K. P. Lillerud, Chem. Mater., 2014, 26, 4068–4071 CrossRef CAS.
- G. C. Shearer, S. Chavan, S. Bordiga, S. Svelle, U. Olsbye and K. P. Lillerud, Chem. Mater., 2016, 28, 3749–3761 CrossRef CAS.
- G. C. Shearer, J. G. Vitillo, S. Bordiga, S. Svelle, U. Olsbye and K. P. Lillerud, Chem. Mater., 2016, 28, 7190–7193 CrossRef CAS.
- K. E. deKrafft, W. S. Boyle, L. M. Burk, O. Z. Zhou and W. B. Lin, J. Mater. Chem., 2012, 22, 18139–18144 RSC.
- S. Jakobsen, D. Gianolio, D. S. Wragg, M. H. Nilsen, H. Emerich, S. Bordiga, C. Lamberti, U. Olsbye, M. Tilset and K. P. Lillerud, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 125429 CrossRef.
- A. M. Ebrahim and T. J. Bandosz, ACS Appl. Mater. Interfaces, 2013, 5, 10565–10573 CAS.
- M. Lammert, M. T. Wharmby, S. Smolders, B. Bueken, A. Lieb, K. A. Lomachenko, D. De Vos and N. Stock, Chem. Commun., 2015, 51, 12578–12581 RSC.
- F. Nouar, M. I. Breeze, B. C. Campo, A. Vimont, G. Clet, M. Daturi, T. Devic, R. I. Walton and C. Serre, Chem. Commun., 2015, 51, 14458–14461 RSC.
- R. Dalapati, B. Sakthivel, A. Dhakshinamoorthy, A. Buragohain, A. Bhunia, C. Janiak and S. Biswas, CrystEngComm, 2016, 18, 7855–7864 RSC.
- S. J. Garibay and S. M. Cohen, Chem. Commun., 2010, 46, 7700–7702 RSC.
- M. Kandiah, S. Usseglio, S. Svelle, U. Olsbye, K. P. Lillerud and M. Tilset, J. Mater. Chem., 2010, 20, 9848–9851 RSC.
- M. Kandiah, M. H. Nilsen, S. Usseglio, S. Jakobsen, U. Olsbye, M. Tilset, C. Larabi, E. A. Quadrelli, F. Bonino and K. P. Lillerud, Chem. Mater., 2010, 22, 6632–6640 CrossRef CAS.
- S. M. Chavan, G. C. Shearer, S. Svelle, U. Olsbye, F. Bonino, J. Ethiraj, K. P. Lillerud and S. Bordiga, Inorg. Chem., 2014, 53, 9509–9515 CrossRef CAS PubMed.
- J. Ethiraj, E. Albanese, B. Civalleri, J. G. Vitillo, F. Bonino, S. Chavan, G. C. Shearer, K. P. Lillerud and S. Bordiga, ChemSusChem, 2014, 7, 3382–3388 CrossRef CAS PubMed.
- S. Chavan, J. G. Vitillo, M. J. Uddin, F. Bonino, C. Lamberti, E. Groppo, K. P. Lillerud and S. Bordiga, Chem. Mater., 2010, 22, 4602–4611 CrossRef CAS.
- C. Wang, K. E. deKrafft and W. B. Lin, J. Am. Chem. Soc., 2012, 134, 7211–7214 CrossRef CAS PubMed.
- P. H. Ling, J. P. Lei, L. Jia and H. X. Ju, Chem. Commun., 2016, 52, 1226–1229 RSC.
- R. Kardanpour, S. Tangestaninejad, V. Mirkhani, M. Moghadam, I. Mohammadpoor-Baltork, A. R. Khosropour and F. Zadehahmadi, J. Organomet. Chem., 2014, 761, 127–133 CrossRef CAS.
- W. H. Dong, C. Feng, L. Zhang, N. Z. Shang, S. T. Gao, C. Wang and Z. Wang, Catal. Lett., 2016, 146, 117–125 CrossRef CAS.
- K. Tulig and K. S. Walton, RSC Adv., 2014, 4, 51080–51083 RSC.
- J. Yang, L. T. Yang, H. L. Ye, F. Q. Zhao and B. Z. Zeng, Electrochim. Acta, 2016, 219, 647–654 CrossRef CAS.
- Q. Q. Yuan, D. M. Zhang, L. van Haandel, F. Y. Ye, T. Xue, E. J. M. Hensen and Y. J. Guan, J. Mol. Catal. A: Chem., 2015, 406, 58–64 CrossRef CAS.
- E. Plessers, D. E. De Vos and M. B. J. Roeffaers, J. Catal., 2016, 340, 136–143 CrossRef CAS.
- S. Øien, G. Agostini, S. Svelle, E. Borfecchia, K. A. Lomachenko, L. Mino, E. Gallo, S. Bordiga, U. Olsbye, K. P. Lillerud and C. Lamberti, Chem. Mater., 2015, 27, 1042–1056 CrossRef.
- L. Braglia, E. Borfecchia, L. Maddalena, S. Øien, K. A. Lomachenko, A. L. Bugaev, S. Bordiga, A. V. Soldatov, K. P. Lillerud and C. Lamberti, Catal. Today, 2017, 283, 89–103 CrossRef CAS.
- F. Xamena, O. Casanova, R. G. Tailleur, H. Garcia and A. Corma, J. Catal., 2008, 255, 220–227 CrossRef.
- A. Corma, M. Iglesias, F. Xamena and F. Sanchez, Chem.–Eur. J., 2010, 16, 9789–9795 CrossRef CAS PubMed.
- I. Luz, F. Xamena and A. Corma, J. Catal., 2010, 276, 134–140 CrossRef CAS.
- E. Borfecchia, D. Gianolio, G. Agostini, S. Bordiga and C. Lamberti, in Metal Organic Frameworks as Heterogeneous Catalysts, ed. F. Xamena and J. Gascon, Royal Society of Chemistry, Cambridge, 2013, pp. 143–208 Search PubMed.
- S. Bordiga, E. Groppo, G. Agostini, J. A. van Bokhoven and C. Lamberti, Chem. Rev., 2013, 113, 1736–1850 CrossRef CAS PubMed.
- K. C. Szeto, K. P. Lillerud, M. Tilset, M. Bjorgen, C. Prestipino, A. Zecchina, C. Lamberti and S. Bordiga, J. Phys. Chem. B, 2006, 110, 21509–21520 CrossRef CAS PubMed.
- K. C. Szeto, C. Prestipino, C. Lamberti, A. Zecchina, S. Bordiga, M. Bjorgen, M. Tilset and K. P. Lillerud, Chem. Mater., 2007, 19, 211–220 CrossRef CAS.
- J. Hafizovic, M. Bjorgen, U. Olsbye, P. D. C. Dietzel, S. Bordiga, C. Prestipino, C. Lamberti and K. P. Lillerud, J. Am. Chem. Soc., 2007, 129, 3612–3620 CrossRef CAS PubMed.
- S. Chavan, F. Bonino, J. G. Vitillo, E. Groppo, C. Lamberti, P. D. C. Dietzel, A. Zecchina and S. Bordiga, Phys. Chem. Chem. Phys., 2009, 11, 9811–9822 RSC.
- S. Bordiga, F. Bonino, K. P. Lillerud and C. Lamberti, Chem. Soc. Rev., 2010, 39, 4885–4927 RSC.
- E. Borfecchia, S. Maurelli, D. Gianolio, E. Groppo, M. Chiesa, F. Bonino and C. Lamberti, J. Phys. Chem. C, 2012, 116, 19839–19850 CAS.
- L. Valenzano, J. G. Vitillo, S. Chavan, B. Civalleri, F. Bonino, S. Bordiga and C. Lamberti, Catal. Today, 2012, 182, 67–79 CrossRef CAS.
- E. Borfecchia, L. Braglia, F. Bonino, S. Bordiga, S. Øien, U. Olsbye, K. P. Lillerud, J. A. van Bokhoven, K. A. Lomachenko, A. A. Guda, A. V. Soldatov and C. Lamberti, in XAFS Techniques for Catalysts, Nanomaterials, and Surfaces, ed. Y. Iwasawa, K. Asakura and M. Tada, Springer, Berlin, 2017, pp. 397–430 Search PubMed.
- M. Muller, S. Hermes, K. Kaehler, M. W. E. van den Berg, M. Muhler and R. A. Fischer, Chem. Mater., 2008, 20, 4576–4587 CrossRef.
- E. D. Bloch, D. Britt, C. Lee, C. J. Doonan, F. J. Uribe-Romo, H. Furukawa, J. R. Long and O. M. Yaghi, J. Am. Chem. Soc., 2010, 132, 14382–14384 CrossRef CAS PubMed.
- S. Gross and M. Bauer, Adv. Funct. Mater., 2010, 20, 4026–4047 CrossRef CAS.
- T. B. Celic, M. Rangus, K. Lazar, V. Kaucic and N. Z. Logar, Angew. Chem., Int. Ed., 2012, 51, 12490–12494 CrossRef PubMed.
- T. H. Zhou, Y. H. Du, A. Borgna, J. D. Hong, Y. B. Wang, J. Y. Han, W. Zhang and R. Xu, Energy Environ. Sci., 2013, 6, 3229–3234 CAS.
- M. Carboni, Z. K. Lin, C. W. Abney, T. Zhang and W. B. Lin, Chem.–Eur. J., 2014, 20, 14965–14970 CrossRef CAS PubMed.
- X. L. Li, Z. Y. Guo, C. X. Xiao, T. W. Goh, D. Tesfagaber and W. Y. Huang, ACS Catal., 2014, 4, 3490–3497 CrossRef CAS.
- C. X. Xiao, T. W. Goh, K. Brashler, Y. C. Pei, Z. Y. Guo and W. Y. Huang, J. Phys. Chem. B, 2014, 118, 14168–14176 CrossRef CAS PubMed.
- Z. Y. Zhang, H. Yoshikawa and K. Awaga, J. Am. Chem. Soc., 2014, 136, 16112–16115 CrossRef CAS PubMed.
- D. R. Sun, F. X. Sun, X. Y. Deng and Z. H. Li, Inorg. Chem., 2015, 54, 8639–8643 CrossRef CAS PubMed.
- M. Du, L. Li, M. X. Li and R. Si, RSC Adv., 2016, 6, 62705–62716 RSC.
- J. Ethiraj, F. Bonino, J. G. Vitillo, K. A. Lomachenko, C. Lamberti, H. Reinsch, K. P. Lillerud and S. Bordiga, ChemSusChem, 2016, 9, 713–719 CrossRef CAS PubMed.
- Z. G. Hu, J. J. Lin, N. Ogiwara, A. Rodriguez, Y. W. Peng, Y. X. Wang, S. Horike and D. Zhao, CrystEngComm, 2016, 18, 2803–2807 RSC.
- A. S. Munn, F. Millange, M. Frigoli, N. Guillou, C. Falaise, V. Stevenson, C. Volkringer, T. Loiseau, G. Cibin and R. I. Walton, CrystEngComm, 2016, 18, 8108–8114 RSC.
- N. C. Thacker, Z. K. Lin, T. Zhang, J. C. Gilhula, C. W. Abney and W. B. Lin, J. Am. Chem. Soc., 2016, 138, 3501–3509 CrossRef CAS PubMed.
- G. Wang, K. Leus, S. Couck, P. Tack, H. Depauw, Y. Y. Liu, L. Vincze, J. F. M. Denayer and P. Van der Voort, Dalton Trans., 2016, 45, 9485–9491 RSC.
- D. Yang, S. O. Odoh, J. Borycz, T. C. Wang, O. K. Farha, J. T. Hupp, C. J. Cramer, L. Gagliardi and B. C. Gates, ACS Catal., 2016, 6, 235–247 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 CrossRef PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- C. C. Wang, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, o2081 CAS.
- A. Schaate, P. Roy, A. Godt, J. Lippke, F. Waltz, M. Wiebcke and P. Behrens, Chem.–Eur. J., 2011, 17, 6643–6651 CrossRef CAS PubMed.
- S. Carlson, M. Clausen, L. Gridneva, B. Sommarin and C. Svensson, J. Synchrotron Radiat., 2006, 13, 359–364 CrossRef CAS PubMed.
- C. Lamberti, C. Prestipino, S. Bordiga, G. Berlier, G. Spoto, A. Zecchina, A. Laloni, F. La Manna, F. D’Anca, R. Felici, F. D’Acapito and P. Roy, Nucl. Instrum. Methods Phys. Res., Sect. B, 2003, 200, 196–201 CrossRef CAS.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- M. Newville, J. Synchrotron Radiat., 2001, 8, 322–324 CrossRef CAS PubMed.
- S. I. Zabinsky, J. J. Rehr, A. Ankudinov, R. C. Albers and M. J. Eller, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 2995–3009 CrossRef CAS.
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef CAS.
- M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55 CrossRef CAS.
- C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- M. Lersch and M. Tilset, Chem. Rev., 2005, 105, 2471–2526 CrossRef CAS PubMed.
- R. A. Periana, D. J. Taube, S. Gamble, H. Taube, T. Satoh and H. Fujii, Science, 1998, 280, 560–564 CrossRef CAS PubMed.
- D. Wolf, Angew. Chem., Int. Ed., 1998, 37, 3351–3353 CrossRef CAS.
- R. Palkovits, M. Antonietti, P. Kuhn, A. Thomas and F. Schüth, Angew. Chem., Int. Ed., 2009, 48, 6909–6912 CrossRef CAS PubMed.
- R. Palkovits, C. von Malotki, M. Baumgarten, K. Mullen, C. Baltes, M. Antonietti, P. Kuhn, J. Weber, A. Thomas and F. Schüth, ChemSusChem, 2010, 3, 277–282 CrossRef CAS PubMed.
- M. Soorholtz, R. J. White, T. Zimmermann, M. M. Titirici, M. Antonietti, R. Palkovits and F. Schüth, Chem. Commun., 2013, 49, 240–242 RSC.
- G. W. Stinton and J. S. O. Evans, J. Appl. Crystallogr., 2007, 40, 87–95 CAS.
- G. Agostini, C. Lamberti, L. Palin, M. Milanesio, N. Danilina, B. Xu, M. Janousch and J. A. van Bokhoven, J. Am. Chem. Soc., 2010, 132, 667–678 CrossRef CAS PubMed.
- G. Bunker, Introduction to XAFS A Practical Guide to X-ray Absorption Fine Structure Spectroscopy, Cambridge University Press, Cambridge, 2010 Search PubMed.
- M. D. Hall, G. J. Foran, M. Zhang, P. J. Beale and T. W. Hambley, J. Am. Chem. Soc., 2003, 125, 7524–7525 CrossRef CAS PubMed.
- H. Yoshida, S. Nonoyama, Y. Yazawa and T. Hattori, Phys. Scr., 2005, 115, 813–815 CrossRef.
- E. Borfecchia, S. Oien, S. Svelle, L. Mino, L. Braglia, G. Agostini, E. Gallo, K. A. Lomachenko, S. Bordiga, A. A. Guda, M. A. Soldatov, A. V. Soldatov, U. Olsbye, K. P. Lillerud and C. Lamberti, J. Phys. Conf. Ser., 2016, 712, 012125 CrossRef.
- S. A. Guda, A. A. Guda, M. A. Soldatov, K. A. Lomachenko, A. L. Bugaev, C. Lamberti, W. Gawelda, C. Bressler, G. Smolentsev, A. V. Soldatov and Y. Joly, J. Chem. Theory Comput., 2015, 11, 4512–4521 CrossRef CAS PubMed.
- G. Berlier, G. Spoto, S. Bordiga, G. Ricchiardi, P. Fisicaro, A. Zecchina, I. Rossetti, E. Selli, L. Forni, E. Giamello and C. Lamberti, J. Catal., 2002, 208, 64–82 CrossRef CAS.
- G. Berlier, G. Spoto, P. Fisicaro, S. Bordiga, A. Zecchina, E. Giamello and C. Lamberti, Microchem. J., 2002, 71, 101–116 CrossRef CAS.
- A. Zecchina, M. Rivallan, G. Berlier, C. Lamberti and G. Ricchiardi, Phys. Chem. Chem. Phys., 2007, 9, 3483–3499 RSC.
- A. I. Frenkel, J. Synchrotron Radiat., 1999, 6, 293–295 CrossRef CAS PubMed.
- A. I. Frenkel, C. W. Hills and R. G. Nuzzo, J. Phys. Chem. B, 2001, 105, 12689–12703 CrossRef CAS.
- D. Glasner and A. I. Frenkel, in X-Ray Absorption Fine Structure-XAFS13, ed. B. Hedman and P. Painetta, American Institute of Physics, Melville, 2007, vol. 882, pp. 746–748 Search PubMed.
- G. Agostini, R. Pellegrini, G. Leofanti, L. Bertinetti, S. Bertarione, E. Groppo, A. Zecchina and C. Lamberti, J. Phys. Chem. C, 2009, 113, 10485–10492 CAS.
- G. Agostini, A. Piovano, L. Bertinetti, R. Pellegrini, G. Leofanti, E. Groppo and C. Lamberti, J. Phys. Chem. C, 2014, 118, 4085–4094 CAS.
- B. Abecassis, F. Testard, O. Spalla and P. Barboux, Nano Lett., 2007, 7, 1723–1727 CrossRef CAS PubMed.
- J. Polte, T. T. Ahner, F. Delissen, S. Sokolov, F. Emmerling, A. F. Thunemann and R. Kraehnert, J. Am. Chem. Soc., 2010, 132, 1296–1301 CrossRef CAS PubMed.
- E. Groppo, G. Agostini, A. Piovano, N. B. Muddada, G. Leofanti, R. Pellegrini, G. Portale, A. Longo and C. Lamberti, J. Catal., 2012, 287, 44–54 CrossRef CAS.
- G. Agostini, C. Lamberti, R. Pellegrini, G. Leofanti, F. Giannici, A. Longo and E. Groppo, ACS Catal., 2014, 4, 187–194 CrossRef CAS.
- E. Groppo, G. Agostini, E. Borfecchia, L. Wei, F. Giannici, G. Portale, A. Longo and C. Lamberti, J. Phys. Chem. C, 2014, 118, 8406–8415 CAS.
- N. T. K. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610–7630 CrossRef CAS PubMed.
- E. Groppo, G. Agostini, E. Borfecchia, A. Lazzarini, W. Liu, C. Lamberti, F. Giannici, G. Portale and A. Longo, ChemCatChem, 2015, 7, 2188–2195 CrossRef CAS.
- P. Kluth, B. Johannessen, G. J. Foran, D. J. Cookson, S. M. Kluth and M. C. Ridgway, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 9 CrossRef.
- L. Guczi, A. Beck, A. Horvath, Z. Koppany, G. Stefler, K. Frey, I. Sajo, O. Geszti, D. Bazin and J. Lynch, J. Mol. Catal. A: Chem., 2003, 204, 545–552 CrossRef.
- A. Witkowska, A. Di Cicco and E. Principi, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 12 CrossRef.
- G. Turnes Palomino, P. Fisicaro, S. Bordiga, A. Zecchina, E. Giamello and C. Lamberti, J. Phys. Chem. B, 2000, 104, 4064–4073 CrossRef.
- F. X. Llabrés i Xamena, P. Fisicaro, G. Berlier, A. Zecchina, G. Turnes Palomino, C. Prestipino, S. Bordiga, E. Giamello and C. Lamberti, J. Phys. Chem. B, 2003, 107, 7036–7044 CrossRef.
- M. Benfatto, P. D’Angelo, S. Della Longa and N. V. Pavel, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 174205 CrossRef.
- E. M. Alayon, M. Nachtegaal, M. Ranocchiari and J. A. van Bokhoven, Chem. Commun., 2012, 48, 404–406 RSC.
- F. Giordanino, E. Borfecchia, K. A. Lomachenko, A. Lazzarini, G. Agostini, E. Gallo, A. V. Soldatov, P. Beato, S. Bordiga and C. Lamberti, J. Phys. Chem. Lett., 2014, 5, 1552–1559 CrossRef CAS PubMed.
- E. Borfecchia, K. A. Lomachenko, F. Giordanino, H. Falsig, P. Beato, A. V. Soldatov, S. Bordiga and C. Lamberti, Chem. Sci., 2015, 6, 548–563 RSC.
- C. Lamberti, C. Prestipino, F. Bonino, L. Capello, S. Bordiga, G. Spoto, A. Zecchina, S. D. Moreno, B. Cremaschi, M. Garilli, A. Marsella, D. Carmello, S. Vidotto and G. Leofanti, Angew. Chem., Int. Ed., 2002, 41, 2341–2344 CrossRef CAS PubMed.
- N. B. Muddada, U. Olsbye, L. Caccialupi, F. Cavani, G. Leofanti, D. Gianolio, S. Bordiga and C. Lamberti, Phys. Chem. Chem. Phys., 2010, 12, 5605–5618 RSC.
- L. S. Kau, D. J. Spirasolomon, J. E. Pennerhahn, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1987, 109, 6433–6442 CrossRef CAS.
- M. H. Groothaert, J. A. van Bokhoven, A. A. Battiston, B. M. Weckhuysen and R. A. Schoonheydt, J. Am. Chem. Soc., 2003, 125, 7629–7640 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- L. Braglia, E. Borfecchia, K. A. Lomachenko, S. Oien, K. P. Lillerud and C. Lamberti, J. Phys. Conf. Ser., 2016, 712, 012053 CrossRef.
- M. Gonzalez, J. Oktawiec and J. R. Long, Faraday Discuss., 2017 10.1039/c7fd00061h.
- M. I. Gonzalez, E. D. Bloch, J. A. Mason, S. J. Teat and J. R. Long, Inorg. Chem., 2015, 54, 2995–3005 CrossRef CAS PubMed.
- R. Y. Huang, Y. Peng, C. Wang, Z. Shi and W. B. Lin, Eur. J. Inorg. Chem., 2016, 4358–4362 CrossRef CAS.
- N. C. Thacker, P. Ji, Z. Lin, A. Urban and W. Lin, Faraday Discuss., 2017 10.1039/c7fd00030h.
| This journal is © The Royal Society of Chemistry 2017 |