Isotopomeric polymorphism in a “doubly-polymorphic” multi-component molecular crystal

Abstract

The deuterated molecular complexes of isonicotinamide with oxalic acid crystallise in two polymorphs, which are found to be distinct from the two polymorphs of the hydrogenous complexes previously reported. This phenomenon is known as isotopomeric polymorphism, is rarely observed in molecular materials and in particular the presence of multiple polymorphic forms of each isotopic material observed here appears to be unprecedented. The four polymorphic forms are found to exhibit different degrees of hydron transfer. Unlike the hydrogenous forms, the deuterated polymorphs do not show short, strong hydrogen bonding between the acid and the pyridine base. Periodic electronic structure calculations establish an energy scale for the polymorphism in these isotopomeric polymorphs.

---

Introduction

In the assembly of molecular materials into the solid state, including the formation of polymorphic solid forms and the use of the techniques of crystal engineering, the hydrogen bond is the most important intermolecular interaction. It is widely present, not only in small molecule chemical systems and complexes, but also in a wider range of materials from inorganic minerals to biologically active macromolecules. Hydrogen bonds largely govern the structure of extended materials in which they are present, contributing to their physical properties and (bio)chemical reactivity. Short, strong hydrogen bonds (SSHBs) are of particular interest because they show some unique physical and chemical properties. They are characterised by a large redshift of the donor-hydrogen stretching frequency until, for very strong hydrogen bonds, they are replaced by a broad absorption region in the low frequency range (absorption continuum)^1,2 and a far downfield shift of the ¹H NMR signal. As the SSHB becomes shorter, the H atom position shifts towards the centre of the hydrogen bond until it is no longer possible to differentiate between H acceptor and donor, accompanied by an increasing degree of covalency in the hydrogen bond,^3,4 and the electrostatic and covalent hydrogen bond models have been unified in an “electrostatic-covalent H-bond model” (ECHBM).⁵

SSHBs are found when donor and acceptor atoms compete for the H atom, often the situation when the system is on the verge of exhibiting H transfer. SSHBs in the solid state may thus be regarded as model systems for H transfer processes, effectively emulating the transition states of, for example, enzymatic reactions,⁶ and mediating conversion between neutral and ionic molecular complexes that can be relevant in the structure and properties of such systems.

The SSHB has been used as a design aim in crystal engineering studies of molecular complexes,⁷ with clear possibilities in the control of physical properties,⁸ and variable temperature diffraction studies on model solid state systems have been used to examine proton transfer in SSHB systems.^9,10 In its most simple formulation, the strength of a hydrogen bond can be measured by the donor–acceptor distance in the nearly linear geometries found in most SSHBs; for O⋯H⋯N bonds such as those discussed here, the minimum O⋯N distance is around 2.50 Å, at which point the H generally occupies a centered position, bonding with equal strength to O and N.⁹

The SSHB of interest here is formed between carboxylic O and pyridyl N atoms by co-crystallisation of isonicotinamide (IN) with oxalic acid (OA) in the ratio 2 : 1. The original structure of the resulting molecular complex IN₂/OA was obtained from a 1 : 1 ethanol–water solution, crystallising with block or plate shaped morphology (form I, space group C2/c),¹¹ with a second polymorphic form subsequently obtained from the same solution, crystallising in rod shaped crystals (form II, space group P1̄). X-ray crystal structures of both polymorphs and a variable temperature neutron diffraction experiment for form I have been reported,¹² and are shown in Fig. 1 and 2.

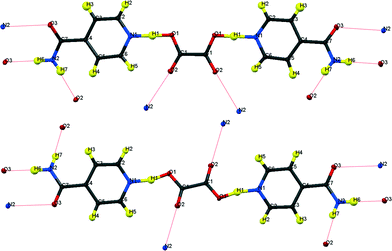Fig. 1 Formula units of hydrogenous IN₂–OA (ref. 12) including the hydrogen bonding schemes indicated by dotted lines; (top) “cis”-form, form I; (bottom) “trans”-form, form II.

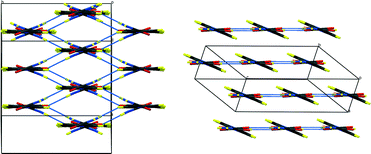Fig. 2 Packing schemes of hydrogenous IN₂–OA (ref. 12), viewed along the –IN–OA–IN– chains; (left) form I, (right) form II. Hydrogen bonds are shown in blue dotted lines.

The key difference between the two reported polymorphs is a “cis/trans” isomerism of the oxalic acid hydroxyl groups; form I displays the cis-configuration and form II the trans. Both polymorphs share a repeating ⋯IN–OA–IN⋯ hydrogen-bonded chain motif in which O1⋯H1⋯N1 SSHBs link IN and OA molecules, while moderate amide–amide (N–H⋯O) hydrogen bonds link IN molecules. The chains are cross-linked by further moderate strength (N–H⋯O) hydrogen bonds, forming a three-dimensional network in form I and a two-dimensional layered structure in form II (Fig. 2). The OA unit lies on a symmetry element in both polymorphs: a 2-fold axis in form I, and an inversion centre in form II. The two SSHBs formed by OA are thus equivalent; the difference in symmetry of the OA dictates the cis/trans isomerism of the OH group. O1⋯N1 distances of 2.549(1) and 2.529(1) Å for form I and II, respectively, place these SSHBs amongst the shortest O⋯H⋯N type bonds observed to date.

The investigation of the effect of isotopic substitution of H for D in the molecular complex IN₂–OA presented here, was motivated by the possibility of obtaining additional, valuable information about the nature of the SSHB found in the polymorphs of this complex. However, the effects of deuteration on structure are not always predictable. There are known examples in molecular systems of a different polymorph being adopted on deuteration; the phenomenon of isotopic polymorphism,^13,14 Although this is relatively rarely reported, in contrast, the related phenomenon of H/D isotope effects on phase transitions, particularly in inorganic materials, has been well studied by both experimental and theoretical methods and shown to offer profound insights into transition mechanisms and both structure and dynamics of such systems. These effects can be manifest in both dramatic effects on phase transition temperature¹⁵ and in completely different phase transition sequences between H and D containing materials.¹⁶ More subtle isotope-dependent effects have also been observed in hydrogen-bonded molecular systems.¹⁷

Any observation of H/D isotope effects, both the intrinsic structural influence and the equilibrium H/D isotope effect,¹⁸ should help in determining the “true” potential energy surface for H transfer in this material. Aside from the structural information obtained by diffraction experiments on deuterated polymorphs, the hydron motion in hydrogen bonds would in this case become observable by solid state NMR experiments for D atoms.

Experimental

All materials were purchased from Sigma Aldrich and used without further purification.

Deuteration in this system was easily achieved by co-crystallising IN and OA from D₂O instead of H₂O. In addition to the acidic oxalic acid H atoms, the amide H atoms were also almost completely exchanged¹⁹ (demonstrated by the absence of the N–H stretch in the IR spectrum, ESI†). As for the hydrogenous complexes, IN₂–d-OA crystallises in two polymorphic forms, crystals of which could be isolated and their structures determined by X-ray diffraction on a Bruker AXS Apex-II diffractometer at 100 K (Table 1). Structures were solved by direct methods using SHELXS-97 (ref. 20) and refined on F² using SHELXL-97 ²⁰ within the WinGX program suite.²¹

Table 1 Crystallographic data for both polymorphs of hydrogenous¹² and deuterated structures

	[IN2–OA] form I (ref. 12)	[IN2–OA] form II (ref. 12)	[IN2–d-OA] form I	[IN2–d-OA] form II supercell
Formula	C14H14N4O6	C14H14N4O6	C14H8D6N4O6	C14H8D6N4O6
M r	334.3	334.3	340.3	340.3
T/K	100	100	100	100
Crystal system	Monoclinic	Triclinic	Triclinic	Triclinic
Space group	C2/c	P1̄	P1̄	P1̄
a/Å	11.6911(12)	3.6811(7)	3.7233(3)	6.9765(7)
b/Å	9.9945(10)	7.5912(14)	7.4294(5)	8.1978(8)
c/Å	12.1366(12)	12.455(2)	12.3158(10)	13.1421(10)
α/°	90	85.638(9)	98.262(4)	106.725(5)
β/°	102.743(5)	87.856(10)	90.019(4)	92.458(5)
γ/°	90	84.221(10)	91.709(5)	105.171(6)
V/Å^3	1383.2(2)	345.11(11)	336.99(4)	689.04(11)
Z	4	1	1	2
ρ (calcd)/Mg m^−3	1.605	1.608	1.677	1.640
μ/mm^−1	0.128	0.128	0.131	0.129
F(000)	696	174
θ range for data collection/°	2.71–33.97	1.64–33.92	1.67–33.99	1.63–34.11
Reflections collected	10 080	8 148	10 173	14 726
No. of unique data [R(int)]	2782 [0.0299]	2759 [0.0223]	2744 0.0216	5595 0.0320
No. of data with I > 2σ(I)	2541	2340	2505	3329
Final R1 (I > 2σ(I))	0.0356	0.0405	0.0344	0.0462
Final R1 (all data)	0.0383	0.0474	0.0373	0.0860

---

Both forms of IN₂–d-OA co-crystallise from the same solution, form I with rod shaped morphology and form II with plate shaped, and both in the space group P1̄. Form I is by far the dominant species in the deuterated system, in which only a few crystals of form II could be obtained from the chosen crystallisation conditions. A second crystallisation from a mixture of D₂O and EtOD had no effect on this finding. The crystals of form II furthermore dissolve on a timescale of a few days if they are not isolated from the solution. It is thus reasonable to assume that form I is both the energetically and kinetically favoured polymorph under the present experimental conditions. Interestingly, when IN and OA are co-crystallised from a mixture of H₂O and D₂O, crystals of both IN₂–OA and IN₂–d-OA (form I in each case) are obtained, with the deuterated complex forming prior to the non-deuterated crystals.

The crystal structure of IN₂–d-OA form I was refined to a resolution of sin θ/λ = 0.78 Å⁻¹, where all positional parameters and ADPs including those for the H and D atoms were refined. The crystal structure of IN₂–d-OA form II displays a superstructure. It can be solved and refined in two different unit cell settings, referred to here as “supercell” and “small cell”, of which the correct structure is determined in the supercell.‡ As for form I, all positional and displacement parameters have been fully refined, to a resolution of sin θ/λ = 0.78 Å⁻¹. In the supercell, for the first time in this system, one complete formula unit is independent, while in the small cell, half an IN₂–d-OA formula unit is independent with the OA unit lying on an inversion symmetry element, as found in the previous structures.^11,12

Ab initio calculations studies have been carried out in the periodic environment in an analogous way to those previously reported for the non deuterated forms.¹² The ground state energies were determined by means of geometry optimisations in the full periodic environment with the atomic orbital (AO) approach using the CRYSTAL03 code.²² The starting geometries for the optimisation runs were taken from the X-ray diffraction experiments, in the case of form II from the refinement in the supercell. For both forms crystallographic symmetry was employed. The AO (CRYSTAL) calculations were carried out at the B3PW/6-31g** level of theory. Becke's 3 parameter exchange functional with 20% Hartree–Fock exchange was combined with Perdew–Wang correlation, yielding the B3PW functional.²³ For the description of the AOs, Gaussian basis sets of 6-31g** type were used, including polarisation functions on all atoms (p basis function for H, and d for C, N, and O). For the calculation on atoms or molecules in the gas phase this basis set might be considered incomplete, but for solid state calculations it provides a sufficiently complete description of the wave function, because the close packing of AOs makes the use of diffuse functions unnecessary. On the contrary, introducing more diffuse functions can lead to overcompleteness and numerical instability. The shrinking factors of the Monkhorst–Pack reciprocal space sampling mesh were set to 5 × 3 × 2 and 4 × 3 × 2 for forms I and II, respectively.

Results

Surprisingly none of the deuterated structures proved to be isostructural to any of the hydrogenous forms, exhibiting “doubly” isotopomeric polymorphism on deuteration.¹⁴

The two deuterated structures are formulated as:

IN₂–d‐OA form I ≡ 2[C₆H₄D₃N₂O]⁺[C₂O₄]²⁻

IN₂–d‐OA form II ≡ C₆H₄D₃N₂O[C₆H₄D₃N₂O]⁺[C₂O₄D]⁻

Fig. 3 shows the formula units of the two IN₂–d-OA polymorphs. They share the (–IN–OA–IN–)_n chain motif familiar from the hydrogenous analogues.^11,12 The main structural difference manifests in the way in which OA is hydrogen bonded to the IN molecules. The OA units in both forms are rotated about 90° in the IN–OA–IN plane with respect to OA in the hydrogenous forms, and as a consequence now, rather unexpectedly, forms bifurcated hydrogen bonds to IN. The “secondary” hydrogen bonded motif, on the other hand, is similar to that in the non deuterated system. This includes the amide–amide hydrogen bonds as well as the interchain amide–carbonyl hydrogen bonds, of which the latter are responsible for the formation of the hydrogen bonded extended networks (Fig. 4). Both forms I and II of the deuterated complexes show two-dimensional layered structures and are in this respect comparable to the hydrogenous form II. In fact, the crystal packing schemes of IN₂–d-OA form I and IN₂–OA form II are very similar; this is also reflected by very similar lattice parameters (Table 1). The main structural difference between the two deuterated forms arises from the stacking of the tape-like –IN–OA–IN– chains. In form I, both the OA and the IN units are stacked upon each other in a parallel fashion (as found in IN₂–OA form II), whereas in form II the OA units are situated directly above the centres of the amide–amide hydrogen bonds.

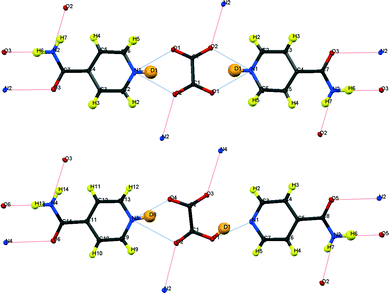Fig. 3 Formula units of IN₂–d-OA including the hydrogen bond schemes, (top) form I, (bottom) form II; although labelled as H, the amide H are largely exchanged by D.¹⁹

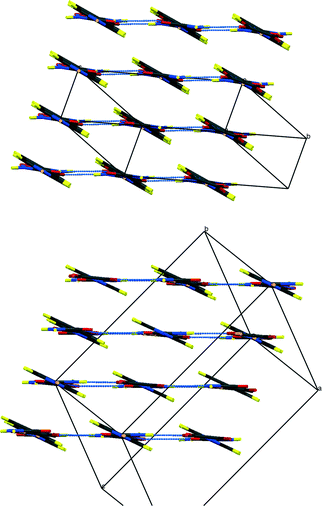Fig. 4 Packing schemes of IN₂–d-OA, viewed along the –IN–OA–IN– chains; (left) form I, (right) form II. Hydrogen bonds are shown in blue dotted lines.

Form I

As in the hydrogenous forms, OA is situated on a symmetry element (an inversion centre in this case), and consequently only one bifurcated hydrogen bond formed by OA is independent. The hydrogen bond can no longer be considered a SSHB, with heteroatom distances of N1⋯O1 = 2.708(1) and N1⋯O2a = 2.773(1) Å. Each component of the bifurcated hydrogen bond is of medium length and hence can be regarded as of only moderate strength. The hydrogen bond parameters for both forms of IN₂–d-OA are summarised in Table 2. It is evident from difference Fourier maps (ESI†) that the D atoms have been completely transferred from d-OA towards the IN molecules. This is also reflected by the C–O bond lengths of 1.247(1) and 1.263(1) Å which are characteristic of carboxylate anions, and the CNC bond angle of 122.40(6)° which agrees very well with those found for fully protonated IN cations²⁴ (the C–O and CNC parameters are listed in the ESI†).

Table 2 Hydrogen bond parameters for IN₂–d-OA

	Hydrogen bond	D–H/Å	H⋯A/Å	D⋯A/Å	∠DHA/°
a Atoms generated by symmetry.
Form I	N1–D1⋯O1	0.98(2)	1.94(2)	2.7077(8)	133.1(15)
	N1–D1⋯O2^a	0.98(2)	1.970(19)	2.7727(8)	137.5(15)
	N2–H6⋯O3^a	0.954(14)	1.947(14)	2.8999(8)	176.9(12)
	N2–H7⋯O2^a	0.899(13)	1.963(13)	2.8252(8)	160.1(12)
Form II	O1–D1⋯N1	0.95(2)	1.74(2)	2.6231(14)	152.1(18)
	N3–D8⋯O4	1.08(2)	1.61(2)	2.6137(14)	150.7(17)
	N3–D8⋯O2	1.08(2)	2.30(2)	3.0307(13)	123.3(14)
	N2–H6⋯O5^a	1.02(2)	1.87(2)	2.8847(14)	175.3(16)
	N2–H7⋯O2^a	0.875(17)	2.161(16)	3.0041(13)	161.6(15)
	N4–H13⋯O6^a	0.978(18)	1.914(18)	2.8868(13)	172.6(14)
	N4–H14⋯O3^a	0.954(17)	1.954(16)	2.8767(12)	162.0(14)

---

Form II

The ellipsoid plots (Fig. 5) and difference Fourier maps (ESI†) reveal the reason for the occurrence of the superstructure: only one D atom is transferred from d-OA to IN. Refining the structure in the small cell results in an “artificial” D disorder with a 50 : 50 ratio (and also affects the appearance of the heavy atom ellipsoids; Fig. 5 bottom), because here only one of the two O⋯D⋯N hydrogen bonds is crystallographically independent. The “disorder” is resolved by refinement in the supercell, which also leads to improved ADPs on the heavy atoms (Fig. 5 top). The hydrogen bond configurations with respect to d-OA can be denoted as N–D⋯OOC–COO–D⋯N, where the orientation of the covalent X–D bonds alternate in the –IN–OA–IN– chains within each IN₂–OA unit from right to left. This can be visualised by means of the inversion centres occurring at the midpoint of the diamide hydrogen bonds common to all co-crystals of IN with OA. The hydrogen bonds between OA and IN have separation distances of O1⋯N1 = 2.623(1) Å and O4⋯N3 = 2.614(1) Å (see Table 2) and are hence borderline cases regarding a classification as strong or moderate, being significantly stronger than the hydrogen bonds in form I. The high quality difference Fourier maps in this case (ESI†) are indicative of the presence of partial covalent character in the short hydrogen bonds, as observed for the SSHBs in the hydrogenous structures.¹² The occurrence of the superstructure with the possibility of modelling with incorrect disorder in this polymorphic form of the IN₂–d-OA system provides insight into the interpretation of results in other systems potentially showing H atom disorder in short hydrogen bonds.

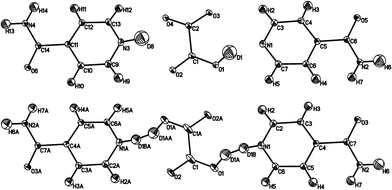Fig. 5 Ellipsoid plots of IN2–d-OA form II at the 50% probability level as refined in the supercell (top) and the small cell (bottom). The poor shape of the ellipsoids in the latter provides further evidence of the refinement model, with disordered D atoms, in this smaller cell being incorrect. The slightly larger U_iso values for D1 and D8 (average value 0.057 Ų) reflects the slight delocalisation of this D atom density due to the normally elongated shape of the SSHB potential well. Although labelled as H, the amide H are largely exchanged by D.¹⁹

Hydron transfer and polymorphism

In the hydrogenous forms, IN₂–OA,^11,12 no formal H transfer is observed. However, the covalent O–H bonds are considerably elongated, as is known to be common for SSHBs, to the extent that the H atom in form II occupies a near central position in the SSHB. It can thus be argued that in form II partial H transfer has taken place, in agreement with the chemical pK_a values. Both IN₂–OA polymorphs can be seen as incipient H transfer complexes. The deuterated forms, IN₂–d-OA, reported here, remarkably do clearly show D transfer. In the case of form I, both D atoms of d-OA are transferred to IN resulting in an ionic complex, while in case of form II, only one D is transferred. In the end, all levels of hydron transfer are observed, 0%, 50% and 100%, in this isotopomeric polymorphic system upon co-crystal formation.

Computational studies of the isotopomeric polymorphic forms; the energy scale for polymorphism

The previously reported determination of the energies involved in the formation of the polymorphic forms in IN₂–OA (ref. 12) has been extended to the deuterated forms, IN₂–d-OA. The isotopic substitution in this case has no effect on the ground state energy calculations because the electronic configuration is the same for H and D, and the atomic masses do not contribute to the static energetics of optimised structures, in contrast to the situation for molecular dynamics studies. For this reason, the calculated total energies of the sets of isotopomeric polymorphs are directly comparable. The computed parameters for the hydrogen bonds between OA and IN are shown in Table 3. The experimental hydrogen bond configurations are fairly well reproduced by the AO CRYSTAL calculations. In the absence of accurate neutron H parameters, the computed hydrogen bond geometries can only be compared with the experimental by means of the O⋯N heteroatom distances. The overall intermolecular hydrogen bond lengths are reasonably well reproduced by the calculations; the slight inconsistencies result from small rotations of the OA unit in the IN–OA–IN plane during the optimisation runs.

Table 3 Computed hydrogen bond parameters for IN₂–d-OA; the experimental D⋯A distances are given in parentheses for easier comparison

		Hydrogen bond	D–H/Å	H⋯A/Å	D⋯A/Å
CRYSTAL	Form I	N1–D1⋯O1	1.067	1.641	2.590 (2.708)
		N1–D1⋯O2	1.067	2.151	2.902 (2.773)
	Form II	O1–D1⋯N1	1.030	1.641	2.589 (2.623)
		N3–D8⋯O4	1.068	1.617	2.591 (2.614)
		N3–D8⋯O2	1.068	2.322	3.075 (3.031)

---

One important parameter that can be extracted from these solid-state computations is that of the energies involved in the formation of various polymorphs, and an assessment of the energy scale for polymorphism in this isotopomeric polymorphic system.¹² The energies involved in the formation of both forms of the hydrogenous IN₂–OA complexes and both, isotopomeric, deuterated polymorphic forms of IN₂–d-OA reported here are given in Table 4. The CRYSTAL calculations show the deuterated forms as energetically unfavoured by ~5 kJ mol⁻¹ when compared to the hydrogenous, with the lower energy within the deuterated forms assigned to IN₂–d-OA form II. This appears to contradict the experimental observations that the crystals of form II not only precipitate in much lower quantities, but also redissolve after time to leave only crystals of form I. As noted above, the calculated ground state energies of deuterated and non deuterated materials are directly comparable.

Table 4 Energy scale for polymorphism in the isotopomeric polymorphic systems IN₂–OA and IN₂–d-OA

			Optimal OA geometry	ΔE/kJ mol^−1
CRYSTAL	IN2–OA	Form I	HOOC–COOH	0
		Form II	HOOC–COO	+3.14
	IN2–d-OA	Form I	OOC–COO	+6.05
		Form II	DOOC–COO	+4.49

---

The reason the deuterated complexes adopt structures that appear to be less energetically favoured should therefore be attributed to kinetic effects which play an important role during crystallisation processes. It should be noted, however, that the energy differences between the pairs of polymorphs (H forms I & II, D forms I & II) are small (maximum ~3 kJ mol⁻¹), at the level of accuracy that might be expected for such calculations that omit vibrational contributions. The energy scale for polymorphism, however, typically estimated to be of order a few kJ mol⁻¹, is again confirmed, and shown also to be consistent between the pairs of isotopomeric polymorphs discussed here. With respect to the experimental isolation of favoured polymorphic forms, of course, other parameters must be taken into account that will affect the solid form produced in such polymorphic systems including relative solubilities, dissolution and precipitation rates, and other solution state factors affecting the crystallisation process.

Conclusions

Isotopomeric polymorphism is found to be present in the isonicotinamide–oxalic acid complexes studied; indeed each of the hydrogenous and deuterated isomeric complexes are themselves polymorphs, a rare example of a “doubly” polymorphic system. The immediate target of obtaining further information on the SSHBs through direct comparison of isotope effects in the deuterated complexes was thus not accessible; any potential H/D isotope effect in the SSHB could in this case be caused by a change in the crystalline environment. More profoundly, the dramatic change of the hydrogen bonds between OA and IN also frustrates this original aim; these hydrogen bonds are bifurcated in the deuterated forms and have thus changed from strong interactions in IN₂–OA to rather moderate hydrogen bonds in IN₂–d-OA. The isotopic substitution has thus not allowed the direct comparison of structure and dynamics across similar hydrogen bond geometries, but the deuterated system is of interest in its own right, and opens up opportunities for investigating the driving forces behind the “structural” H/D isotope effect, i.e. the isotopomeric polymorphism.

The occurrence of isotopomeric polymorphism in itself is rarely observed in molecular materials¹⁴ and the formation of more than one isotopomeric polymorph in this case appears to be unprecedented. The IN₂–OA/d-OA system should thus be of wider interest, to the crystal structure prediction community for example, as an investigation of kinetic effects would seem to be essential to explain the observed H/D isotope effects. Furthermore, the fact that all four forms in this system show a variable degree of hydron transfer, accompanied in the various cases by a significant change in the nature of the hydrogen bond, also renders this material an ideal model system to study the influence of crystal field effects upon the hydron transfer behaviour.

Acknowledgements

We acknowledge funding from EPSRC under awards EP/E050859 and GR/T21615.

Notes and references

1. Z. Malarski, M. Rospenk, L. Sobczyk and E. Grech, J. Phys. Chem., 1982, 86, 401.
2. G. Zundel, Adv. Chem. Phys., 2000, 111, 1.
3. C. Flensburg, S. Larsen and R. F. Stewart, J. Phys. Chem., 1995, 99, 10130.
4. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170.
5. G. Gilli and P. Gilli, J. Mol. Struct., 2000, 552, 1.
6. W. Cleland, Biochemistry, 1992, 31, 317; W. W. Bachovchin, Magn. Reson. Chem., 2001, 39, S199 and references therein.
7. A. O. F. Jones, C. K. Leech, G. J. McIntyre, C. C. Wilson and L. H. Thomas, CrystEngComm, 2014, 16, 8177.
8. D. M. S. Martins, D. S. Middlemiss, C. R. Pulham, C. C. Wilson, M. T. Weller, P. F. Henry, N. Shankland, K. Shankland, W. G. Marshall, R. M. Ibberson, K. Knight, S. Moggach, M. Brunelli and C. A. Morrison, J. Am. Chem. Soc., 2009, 131, 3884.
9. T. Steiner, I. Majerz and C. C. Wilson, Angew. Chem., Int. Ed., 2001, 40, 2651.
10. J. C. Cowan, J. A. K. Howard, G. J. McIntyre, S. M.-F. Lo and I. D. Williams, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 794; P. Gilli, V. Bertolasi, L. Pretto, A. Lycka and G. Gilli, J. Am. Chem. Soc., 2002, 124, 13554; A. Parkin, S. M. Harte, A. E. Goeta and C. C. Wilson, New J. Chem., 2004, 28, 718; J. A. Cowan, J. A. K. Howard, G. J. McIntyre, S. M.-F. Lo and I. D. Williams, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 724.
11. P. Vishweshwar, A. Nangia and V. Lynch, Cryst. Growth Des., 2003, 3, 783.
12. M. Schmidtmann, M. J. Gutmann, D. S. Middlemiss and C. C. Wilson, CrystEngComm, 2007, 9, 743; M. Schmidtmann, L. J. Farrugia, D. S. Middlemiss, M. J. Gutmann, G. J. McIntyre and C. C. Wilson, J. Phys. Chem. A, 2009, 113, 13985.
13. I. Majerz, Z. Malarski and T. Lis, J. Mol. Struct., 1990, 240, 47.
14. J. Zhou, Y.-S. Kye and G. S. Harbison, J. Am. Chem. Soc., 2004, 126, 8392.
15. W. Bantle, Helv. Phys. Acta, 1942, 15, 373; R. Blinc, J. Phys. Chem. Solids, 1960, 13, 204; R. J. Nelmes, Ferroelectrics, 1987, 71, 87; M. I. McMahon, R. J. Nelmes, W. F. Kuhs, R. Dorwarth, R. O. Piltz and Z. Tun, Nature, 1990, 348, 317; V. Srinivasan and D. Sebastiani, J. Phys. Chem. C, 2015, 115, 12631; C. C. Wilson, Mineral. Mag., 1994, 58, 629.
16. Y. Kume, Y. Miyazaki, T. Matsuo, H. Suga, W. I. F. David and R. M. Ibberson, Phys. B, 1992, 180–181, 594; B. Pasquier, N. Le Calvé, N. Leygue, M. H. Limage, F. Romain and G. Sagon, Chem. Phys. Lett., 1997, 278, 360.
17. G. K. H. Madsen, G. J. McIntyre, B. Schiøtt and F. K. Larsen, Chem. – Eur. J., 2007, 13, 5539.
18. J. M. Robertson and A. R. Ubbelohde, Proc. R. Soc. A, 1939, 170, 222.
19. M. Schmidtmann, P. Coster, P. F. Henry, V. P. Ting, M. T. Weller and C. C. Wilson, CrystEngComm, 2014, 16, 1232.
20. G. M. Sheldrick, Acta Crystallogr., 2007, 64, 112.
21. L. J. Farrugia, J. Appl. Crystallogr., 1999, 32, 837.
22. V. R. Saunders, R. Dovesi, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, N. M. Harrison, K. Doll, B. Civalleri, I. J. Bush, P. H. D'Arco and M. Llunell, CRYSTAL 2003: CRYSTAL User's Manual, University of Torino, Torino.
23. A. D. Becke, J. Chem. Phys., 1993, 98, 5648; J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244.
24. A. Angeloni and A. G. Orpen, Chem. Commun., 2001, 343; C. J. Adams, P. C. Crawford, A. G. Orpen and T. J. Podesta, Dalton Trans., 2006, 4078.

---

Footnotes

† Electronic supplementary information (ESI) available: Fourier difference maps, bond length information, cifs CCDC 1043942–1043943, IR spectrum of IN₂–d-OA form I. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5ce00123d

‡ The supercell can be transformed into the small cell by applying the transformation matrix (1 0 0, 0.5 0 0.5, 0 −1 0). The small cell can be visualised as the primitive setting of a B centred supercell, with consequently half the volume of the supercell. The intensities of reflections contributing to the supercell (h + l = odd) are on average lower by a factor ~25. In the supercell, for the first time in this system, one complete formula unit is independent. In the small cell, half a formula unit IN₂–d-OA is independent with the OA unit lying on an inversion symmetry element as known from the previous structures. Individual datasets have been integrated for the two unit cell settings from the same experiment, with the resolution was set in both cases to sin θ/λ = 0.78 Å⁻¹. All positional and displacement parameters were fully refined; in the small cell to R₁ = 3.99 and 5.12%, and in the supercell to R₁ = 4.62 and 8.60% for the observed (Fobs > 4σ(Fobs)) and all data, respectively. The higher residuals after the supercell refinement are naturally caused by the inclusion of the low intensity supercell reflections.

---