Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
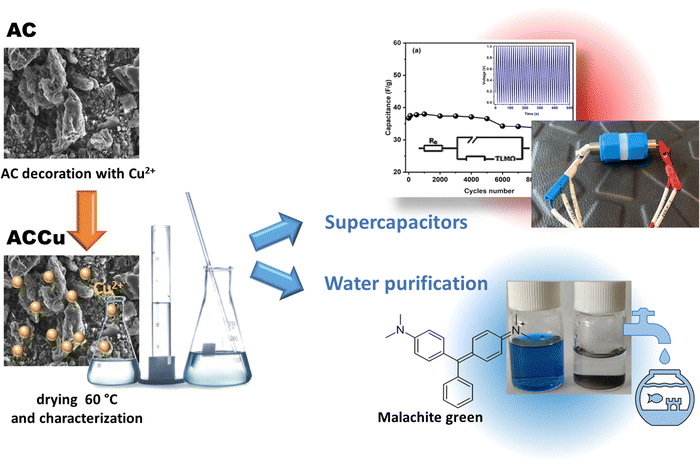
Carbon framework modification; an interesting strategy to improve the energy storage and dye adsorption†
Monika
Michalska
 a,
Paulina
Pietrzyk-Thel
b,
Kamil
Sobczak
c,
Mathijs
Janssen
a,
Paulina
Pietrzyk-Thel
b,
Kamil
Sobczak
c,
Mathijs
Janssen
 d and
Amrita
Jain
d and
Amrita
Jain
 *b
*b
aDepartment of Chemistry and Physico-Chemical Processes, Faculty of Materials Science and Technology, VSB-Technical University of Ostrava, 17. listopadu 2172/15, 708-00 Ostrava-Poruba, Czech Republic
bInstitute of Fundamental Technological Research, Polish Academy of Sciences, Pawińskiego 5B, 02-106 Warsaw, Poland. E-mail: ajain@ippt.pan.pl
cFaculty of Chemistry, Biological and Chemical Research Centre, University of Warsaw, Żwirki i Wigury 101, 02-089 Warsaw, Poland
dNorwegian University of Life Sciences, Faculty of Science and Technology, Ås, Norway
First published on 14th May 2024
Abstract
Porous carbons find various applications, including as adsorbents for clean water production and as electrode materials in energy storage devices such as supercapacitors. While supercapacitors reach higher power densities than batteries, they are less widely used, as their energy density is lower. We present a low-temperature wet ultrasonochemical synthesis technique to modify the surface of activated carbon with 1 wt% Cu nanoparticles. We analyzed the modified carbon using X-ray diffraction, Raman spectroscopy, scanning electron microscopy, and transmission electron microscopy and confirmed the composite formation by N2 adsorption–desorption isotherms at 77 K. For comparison, we did the same tests on pristine carbon. We used the modified carbon as an electrode material in a home-built supercapacitor filled with gel polymer electrolyte and as an absorbent of Malachite green dye. In both applications, the modified carbon performed substantially better than its pristine counterpart. The modified-carbon supercapacitor exhibited a single electrode-specific capacitance of approximately 68.9 F g−1. It also demonstrated an energy density of 9.8 W h kg−1 and a power density of 1.4 kW kg−1. These values represent improvements over the pristine-carbon supercapacitor, with increases of 25.7 F g−1 in capacitance, 3.8 W h kg−1 in energy density, and 0.5 kW kg−1 in power density. After 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 charging–discharging cycles, the capacitance of the modified-carbon supercapacitor decreased by approximately 10%, indicating good durability of the material. We found that the modified carbon's absorbance capacity for Malachite dye is more than that of the pristine carbon; the adsorption capacity value was ∼153.16 mg g−1 for modified carbon with pseudo-second kinetic order, in accordance with the Redlich–Peterson adsorption model.
000 charging–discharging cycles, the capacitance of the modified-carbon supercapacitor decreased by approximately 10%, indicating good durability of the material. We found that the modified carbon's absorbance capacity for Malachite dye is more than that of the pristine carbon; the adsorption capacity value was ∼153.16 mg g−1 for modified carbon with pseudo-second kinetic order, in accordance with the Redlich–Peterson adsorption model.
Introduction
Ever-increasing demands for clean energy and portable water challenge materials scientists and electrochemists alike. Green energy and clean water production are two key challenges the world faces this century. Energy plays a crucial role in a country's economic growth; energy demands will increase at a higher pace, from 50% to 75%, between 2025 and 2075.1,2 The main source of energy comes from non-renewable fossil fuel sources like coal, oil, and natural gas, generating greenhouse gases and causing climate change and global warming.3,4 Renewable sources like solar and wind are intermittent in nature, so balancing supply and demand requires energy storage devices like batteries and supercapacitors. Better materials must be developed for these devices that, besides maximizing performance, are sustainable, durable, and non-toxic. Such new materials may find applications beyond energy storage devices; the electrode materials of supercapacitors, for example, may help desalinate seawater or absorb toxic contents from polluted streams.Supercapacitors have attracted much attention recently because of their high power density, fast charging and discharging, and high capacitance.5,6 These devices store energy through electric double layer-formation in electrolyte-filled porous electrodes. Both the electrolyte and electrode materials crucially affect supercapacitor performance. The liquids that fill some supercapacitors are flammable, have small potential windows, and could leak out. A safe alternative is gel polymer electrolytes (GPEs), which entrap a liquid electrolyte in a polymer matrix. In particular, the amorphous polymer poly(vinylidene fluoride-co-hexafluoropropylene) (PVdF-HFP) has attracted much interest due to its high dielectric constant, thermal stability, and ability to entrap much electrolyte.
Supercapacitor electrodes are usually made from activated carbon because carbon is widely available, cheap, and has a high electrical conductivity; the high specific surface areas of activated carbons lead to high-capacitance supercapacitors.7,8 Activated carbons are especially appealing as they can have a controlled and organised pore size distribution with high specific surface area, which makes them suitable electrode candidates.9,10 The surface chemistry of carbon materials can be changed by post-treating them with reactive heteroatom sources. Composites of carbon with conductive polymers, metallic or metal oxide particles, or other carbon species have also been developed.11–13 Such surface modifications can boost supercapacitor performance.14–17
The activated carbons of supercapacitor electrodes can also be utilised to produce clean water. Carbons can remove toxic contents from water by physical adsorption, which is more suitable and efficient than, for instance, photodegradation, photothermal conversion, and membrane technology. Physical adsorption yields fewer by-products and can be fast and highly efficient.18 The high surface area of activated carbon gives it good adsorbing capacity for dyes.19 Though it can adsorb most of the dyes, its adsorbing ability can still be improved, and one possible option is to make a composite with metal nanoparticles.20 Such modification can improve the material mechanically and thermally and help develop the surface structure and morphology of the material.
The purpose of this study was to investigate the impact of surface modification with Cu nanoparticles (Cu NPs) on the surface of activated carbon (AC) and to assess its utility for energy storage and dye adsorption applications. A new low-temperature ultrasonication approach was applied for decorating AC material with Cu NPs without the use of a reducing agent. This proposed approach is simple, straightforward and cost-effective. The altered material was used to fabricate electrodes for a symmetric supercapacitor. The supercapacitor was filled with a GPE using PVdF-HFP as the host polymer, propylene carbonate (PC) as a plasticiser, and magnesium perchlorate (Mg(ClO4)2) as a salt. The electrode and electrolyte described above were employed to prepare supercapacitor cells, which were subsequently electrochemically characterised. Furthermore, the modified carbon material was evaluated as an adsorbent for dyes, specifically Malachite green in this article. This study aimed to demonstrate the effect of using only 1 wt% of copper metal nanoparticles on improving the carbon framework.
Experimental details
Preparation of activated carbon–copper composites
The activated carbon material was surface-modified using Cu nanoparticles via the following procedure. First, copper(II) nitrate trihydrate (Cu(NO3)2·3H2O, pure p.a., Sigma-Aldrich) was dissolved in 50 mL of ethanol (96%, Merck). Second, activated carbon (AC) (activated charcoal pure p.a., CHEMPUR) was added to the prepared nitrate–ethanol solution of Cu. The whole synthesis was done in an ultrasonic bath cleaner for 1 h (10 min of sonication separated by 20 min intervals). Third, the black composite was air-dried at ∼60 °C and then later at ∼150 °C for a few hours. Last, the activated carbon material with 1 wt% of copper was ground in an agate mortar to produce a fine composite powder. The as-prepared sample was labelled ACCu1, and a control sample without Cu nanoparticles was labelled AC. Fig. 1 schematically shows the synthesis and application.Instrumental details
Morphological studies of ACCu1 were performed with an FEI Talos F200X scanning/transmission electron microscope (S/TEM) at 200 kV. TEM and STEM-mode measurements were recorded using a high-angle annular dark-field detector. Energy-dispersive X-ray spectroscopy (EDX) on a Brucker BD4 instrument was used to map the elements' distribution. Sample preparation for the TEM observations was done by dropping the colloidal particle dispersion on a carbon film which was supported on a 300-mesh copper grid. Scanning electron microscopy (SEM) was carried out using an SEM/FIB-Zeiss Crossbeam 350, Germany; EDX was carried out using an Ametek EDAX, Octane Elite with accelerating voltage of 7 kV to minimise the penetrating depth. X-ray powder diffraction (XRD) analysis was performed with an X-ray diffractometer of MiniFlex 600 (Rigaku, Japan) equipped with a Co tube, operated at 40 kV and 15 mA, and a DteX Ultra 250 detector. The XRD patterns of the prepared materials were collected in the 10–60° 2θ range with a step of 0.01° and a scanning rate of 10° min−1. The results were evaluated using the PDXL software (Rigaku, Japan) and the PDF 2 database, which was released in 2019. The N2 adsorption–desorption studies of the ACCu1 and AC samples were performed using an AutoSorb IQ, Quantachrome, USA, with nitrogen adsorption at 77 K. The pore size distribution curves were obtained using the built-in density functional theory (DFT) model using the adsorption branch of the isotherms. The dye adsorption experiment was carried out using a PerkinElmer (UV/VIS/NIR) Lambda 1050+ spectrophotometer. Measurements were performed in a quartz cuvette from 250 to 800 nm. Malachite green was purchased from Warchem Poland Sp. z o.o. (purity 99%), and NaCl from Sigma-Aldrich, Germany (purity > 99.9%). MilliQ-water to prepare the solutions was supplied by the Hydrolab watering system – Gliwice, Poland.Assembly and characterization of EDLC cells
We constructed electric double-layer capacitor (EDLC) cells using magnesium ion-based GPE, which also acted as a separator, and electrodes made from the Cu-modified activated carbon. The electrodes were prepared by mixing the active materials (ACCu1 and AC) with polymeric binder (PVdF) in the ratio of 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (wt%
10 (wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wt%) using an agate pestle and mortar. Drop by drop acetone was added to obtain slurries of the mixtures, which were coated on carbon cloth (AVCarb, USA), which was used as the current collector. The electrodes dried at ∼100 °C for 8 h before they were used to prepare the EDLCs. The electrolyte was prepared using the host polymer poly(vinylidene fluoride-co-hexafluoropropylene) (PVdF-HFP), mixed with propylene carbonate (PC) as a plasticizer, magnesium perchlorate Mg(ClO4)2 was used as a salt, and tetrahydrofuran (THF) as a solvent. All materials were purchased from Merck and were used as received. Details of the electrolyte preparation and characterization are discussed elsewhere.21
wt%) using an agate pestle and mortar. Drop by drop acetone was added to obtain slurries of the mixtures, which were coated on carbon cloth (AVCarb, USA), which was used as the current collector. The electrodes dried at ∼100 °C for 8 h before they were used to prepare the EDLCs. The electrolyte was prepared using the host polymer poly(vinylidene fluoride-co-hexafluoropropylene) (PVdF-HFP), mixed with propylene carbonate (PC) as a plasticizer, magnesium perchlorate Mg(ClO4)2 was used as a salt, and tetrahydrofuran (THF) as a solvent. All materials were purchased from Merck and were used as received. Details of the electrolyte preparation and characterization are discussed elsewhere.21
EDLC cells were prepared by sandwiching the GPE between the prepared electrodes as shown below:
| Cell A: ACCu1|GPE film|ACCu1 |
| Cell B: AC|GPE film|AC |
Adsorption studies
Next, we explored the potential of the ACCu1 material for adsorption applications, for instance, to remove toxic chemicals from a solution. Measurements were performed using 20 mL of fresh Malachite green (MG) dye solutions with a concentration of 20 mg L−1 (54.8 μmol). As adsorption depends on multiple parameters, we measured different contact times, mass, pH, and ionic strength to determine the optimal conditions. Furthermore, to understand the adsorption mechanism, kinetic studies were performed, and isotherms were estimated. The surveys were recorded by varying the mass from 2.5 mg to 10 mg, contact time from 1 min to 30 min, and interrupt effects like pH from 2–10 and ionic strength from 0.04 to 0.20 mol L−1 concentration of NaCl solution. The amount of adsorbed dye (Q) on the carbon surface was calculated using eqn (S5) and (S6) of the ESI.†Results and discussion
Characteristics of the prepared carbon composites
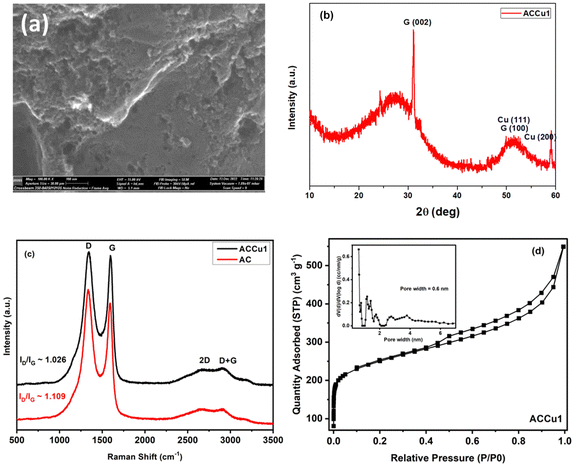
Fig. 2a shows a TEM image of the ACCu1 material, with a zoomed-in view in the right panel. The figure shows a typical amorphous carbon structure. We investigated the distribution of copper in the porous carbon matrix by EDX. Fig. 2b shows the high-angle annular dark-field (HAADF) imaging results, with the corresponding EDX map of the Cu and C elements in Fig. 2c (with EDX spectrum in the Cu energy window). These data show the presence of Cu atoms, or at most Cu atomic clusters. No particles larger than a nanometer can be observed.Fig. 3a shows the morphology of the activated carbon modified with copper nanoparticles. As can be seen from the image, the material is dense and amorphous. This kind of morphology is suitable for the electrode material for supercapacitor applications. The EDX spectra of the ACCu1 sample are provided in the ESI† (Fig. S1); from that analysis, the presence of copper particles is confirmed. Fig. 3b shows the XRD pattern of the ACCu1 sample. This pattern has diffraction peaks around 2θ values of 31 and 51°, matching the crystal planes of (002) and (100) of the graphite (PDF card: 03-065-6212) phase, respectively. The peak around 51° is caused by overlapping phases of graphite (100) and Cu (111). The diffraction line around 59° corresponds to the crystal plane of (200) of the copper phase. The XRD pattern of the pristine AC material was presented in our previous work.22
Fig. 3c shows Raman spectra for the ACCu1 and AC samples. The spectra have bands at ∼1334, ∼1587, ∼2688, and ∼2920 cm−1, which matches the D, G, 2D, and D + G bands of the typical graphitic materials, respectively. The bands (D, G, 2D, D + G) are in almost the same position as in previous works, and their attribution is similar. To support the structural results, the Raman spectroscopy measurements were investigated. Fig. 3c shows Raman spectra for the ACCu1 and AC samples. Due to the prevalence of sp3 hybridization in the carbon structure and the E2g phonon vibrations of the sp2 carbon atoms, the D and G bands are associated with the A1g vibrational mode of the disordered carbon structure. The scattering of phonons near the zone boundary (K-point) forms the second-order vibration of the G-mode, referred to as the 2D-mode. The presence of defects in the graphitic structure is indicated by the D + G band linking the D and G bands.22,23 Considering the degree of graphitization, which suggests the crystallinity level of carbon materials in the present case, the ratio of the intensity lines (ID/IG) for ACCu1 and AC was found to be 1.026 and 1.109, respectively. Furthermore, the ID/IG ratio decreases most probably due to the reason for our novel low-temperature chemical method that has been proposed to surface modify the activated carbon material with copper metallic nanoparticles. Similar observations regarding the decrease in ID/IG ratio have been noticed in our previous works.22,23
Fig. 3d and Fig. S2 (ESI†) show N2 adsorption–desorption isotherms of ACCu1 and AC, respectively, with corresponding pore-size distribution curves as insets (calculated using the DFT method). The isotherm of commercial carbon follows a type I curve, confirming its microporous structure. Meanwhile, the isotherm of ACCu1 follows a type IV pattern, wherein we have observed a small hysteresis loop in the relative pressure range in between 0.4–1.0, which confirms the mesoporous characteristics of the material with a capillary condensation phenomenon. Hence, the mesoporous nature of carbon increases after adding copper. However, the ACCu1 isotherms rise in the low-pressure region (P/P0 < 0.03), showing that the ACCu1 composite also contains micropores. Hence, ACCu1 has a mixture of micropores and mesopores, which is beneficial for energy storage and dye adsorption applications. Table 1 lists the values of specific surface area, micro, meso, and macro pore volumes, and pore sizes of the ACCu1 and AC materials resulting from the adsorption–desorption spectra. Both materials are composed of a mixture of micropores and mesopores. However, the volume of the micropores in ACCu1 is lower than that of the mesopores, which is preferable in the present case. The high surface area and mesoporous structure probably relieve slight changes in the material's volume during the charge–discharge process, providing better pathways for electrolyte transport.24 This phenomenon may also be the reason for our novel low-temperature chemical method involving an ultrasonication process that has been proposed to surface modify the activated carbon material with copper metallic nanoparticles. Our method enables the deposition of metal nanoparticles on the grains of the material to be modified, rather than becoming embedded in the pores of the material like other chemical methods used to modify the surface of materials with metallic coatings/layers/nanoparticles. Similar observations regarding the increase in BET surface area were found in our previous works.22,23 The pore size distribution curves further confirm the co-existence of micropores, mesopores, and macropores. As per the literature, micropores enhance the electrochemical double-layer capacitance, mesopores can decrease the ion-transport resistance, and macropores minimize the diffusion distances.25–27 In the present case, ACCu1 has a good balance of pores and a pore structure beneficial for electrolyte transfer. Moreover, the copper in the carbon structure provides abundant active sites, giving superior electrochemical and dye adsorption properties; hence, it is chosen as an electrode and adsorbate material.
| Samples | S BET (m2 g−1) | V micro (cm3 g−1) | V meso (cm3 g−1) | V total (cm3 g−1) | D 0 (nm) |
|---|---|---|---|---|---|
| Note: SBET, specific surface area; Vmicro, micropore volume; Vmeso, mesopore volume; Vtotal, total volume and D0, average pore width. | |||||
| ACCu1 | 893.6 | 0.16 | 0.69 | 0.85 | 3.1 |
| AC | 657.6 | 0.12 | 0.5 | 0.62 | 3.8 |
Electrochemical characterization of EDLC cells
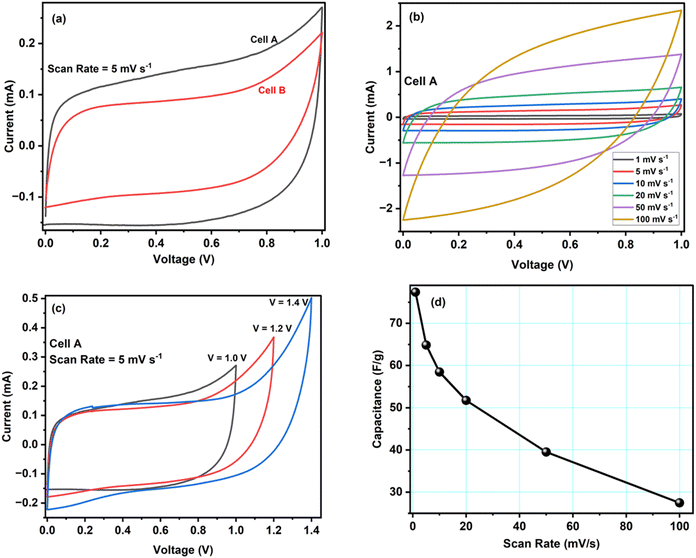
The electrochemical evaluation of ACCu1 and AC was investigated using CV, EIS, and GCD tests in a two-electrode configuration. Fig. 4a shows cell A and B's CV curves at a scan rate of 5 mV s−1 at room temperature. Box-type or rectangular-type shapes have been observed for both cells with varying covering areas. The CV curve of cell A spans a larger area than that of cell B, which confirms the superior performance of cell A over B, and the capacitance of cell A (C = 64.8 F g−1) is higher than that of cell B (C = 46.8 F g−1), accordingly. The higher capacitance value shows that the modification of carbon with copper has increased the material's overall conductivity and mesoporosity, which enhanced its electrochemical performance. An optimum meso-to-microporosity ratio provides porous pathways to electrolyte ions, i.e., facile insertion/de-insertion of electrolyte ions (Mg2+ and ClO4− in the existing system) for double-layer formation. Fig. 4b shows CV curves of cell A for scan rates from 1 mV s−1 to 100 mV s−1 in between 0 to 1 V. Cell A has box-like or rectangular-like CV curves up to 50 mV s−1, confirming the fast and easy switching of the ions (Mg2+ and ClO4−). Beyond 100 mV s−1, the CV curves become less rectangular, showing less capacitance of ∼27.5 F g−1. To evaluate the optimal potential stability range of cell A, the CV of cell A has been recorded with voltage limits of 1.0 V to 1.4 V, see Fig. 4c. The CV curves have symmetrical box-type shapes until 1.2 V. Later, their shapes cease to be rectangular, indicating that the cell is electrochemically stable up to 1.2 V. Hence, the rest of the electrochemical studies were conducted in the range from 0 to 1.0 V for safety operation of the device. The working voltage range is also confirmed by GCD studies discussed below.Fig. 4d shows how the specific capacitance of cell A varies with the scan rate between 1 mV s−1 to 100 mV s−1. The capacitance decreases fast at first and more gradually later. An increased ion adsorption and mass transfer may cause the capacitance to decrease at high scan rates, and the electric double layer may have been gathered over a relatively shorter distance. As a result, ions do not properly settle inside or within the pores of the electrode material, and the capacitance decreases. On the contrary, at lower values of scan rate, the mass transport of ions is relatively slower at the electrode–electrolyte interface.28 Therefore, all the ions can easily diffuse inside the pores, enhancing charge storage and specific capacitance.
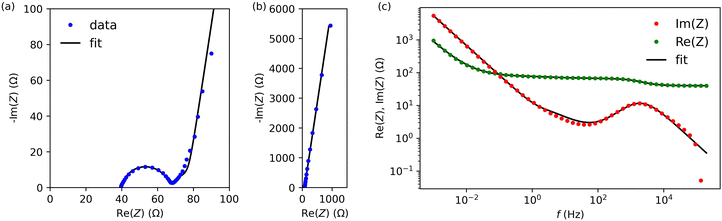
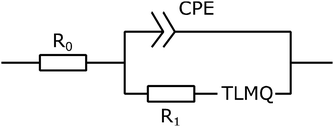
Next, we characterised cells A and B by electrochemical impedance spectroscopy in the frequency range from 1 mHz to 200 kHz. Fig. 5 and Fig. S3 (ESI†) present results for cells A and B, respectively (we used the lin-KK method of the impedance.py package29 to check the validity of these data). Both figures contain a complex-plane impedance plot (a), a zoomed-in view of the high frequencies regime (b), and the frequency dependence of Re(Z) and Im(Z) (c). The complex plane plots of both cells show the following features: (1) at low frequencies, the cells have a phase angle of about 80 degrees; that is, they deviate substantially from a pure capacitance. (2) At intermediate frequencies, the Nyquist plots have phase angles around (but larger than) that of the Warburg impedance (45 degrees). (3) There is a high-frequency arc. This arc is slightly depressed; its apex lies lower than half its base width.
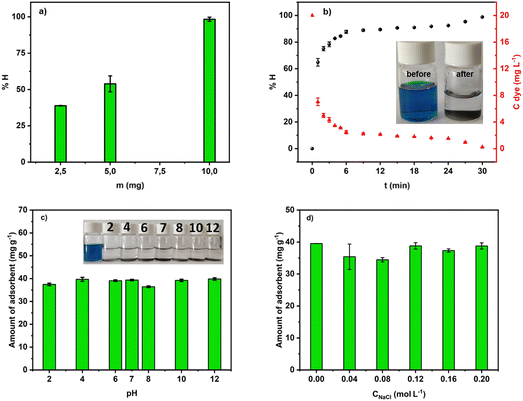
To create an equivalent circuit model for both cells, we note that observations (1) and (2) suggest using a finite-length Warburg open impedance, modified with a CPE-like parameter to fit the low frequencies, 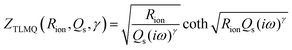 . Here, we note that using a finite-length Warburg element is natural in the case of a porous electrode with finite-length pores. Correcting the low-frequency phase angle of the Warburg open impedance by a CPE parameter was done previously by ref. 30 and 31. Next, the high-frequency depressed arc can be modelled by a CPE,
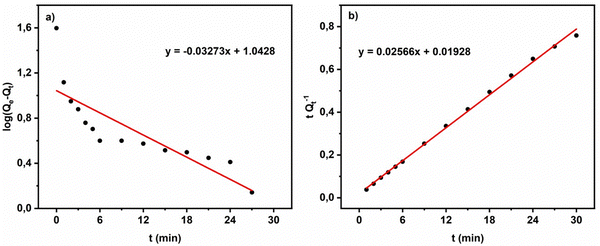
. Here, we note that using a finite-length Warburg element is natural in the case of a porous electrode with finite-length pores. Correcting the low-frequency phase angle of the Warburg open impedance by a CPE parameter was done previously by ref. 30 and 31. Next, the high-frequency depressed arc can be modelled by a CPE, 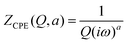 , in parallel with resistor R1. Interfacial redox reactions of impurities or surface functionalities at the carbon surface may have caused this arc.28 However, the high-frequency arcs do not need to be caused by a charge transfer. If a pore has a narrow entrance, narrower than the rest of the pore, this may also lead to an impedance curve of a similar shape.32 Finally, at the highest frequencies, we measure the electrolyte resistance R0 of the bulk electrolyte between the two electrodes. We connect the above circuit elements into the following Randles-like circuit:
, in parallel with resistor R1. Interfacial redox reactions of impurities or surface functionalities at the carbon surface may have caused this arc.28 However, the high-frequency arcs do not need to be caused by a charge transfer. If a pore has a narrow entrance, narrower than the rest of the pore, this may also lead to an impedance curve of a similar shape.32 Finally, at the highest frequencies, we measure the electrolyte resistance R0 of the bulk electrolyte between the two electrodes. We connect the above circuit elements into the following Randles-like circuit:
Table 2 reports the fit parameters and their standard variation. We see that the bulk resistance is roughly the same in both cells, which makes sense as we used the same electrolyte and cell layout in both cases. Next, cell A has lower R1 and Rion resistances than cell B, which reinforces our earlier observation that the ACCu1 electrode of cell A has a lower internal electrolyte resistance. The capacitance-like Qs parameter is also higher for this cell, further suggesting that the modification of carbon with copper improved the electrochemical properties of the material.
| Cell A | Cell B | |
|---|---|---|
| R 0 | 4.00 × 101 (±4.40 × 100) [Ω] | 4.44 × 101 (±3.93 × 100) [Ω] |
| Q | 6.37 × 10−6 (±1.66 × 10−5) [Ω−1sa] | 8.94 × 10−6 (±4.79 × 10−6) [Ω−1sa] |
| a | 9.25 × 10−1 (±2.90 × 10−1) [—] | 7.78 × 10−1 (±6.30 × 10−2) [—] |
| R 1 | 2.56 × 101 (±6.37 × 100) [Ω] | 1.10 × 102 (±6.13 × 100) [Ω] |
| R ion | 3.24 × 101 (±1.57 × 101) [Ω] | 1.10 × 102 (±1.53 × 101) [Ω] |
| Q s | 1.80 × 10−2 (±9.69 × 10−5) [F sγ−1] | 1.05 × 10−2 (±2.90 × 10−5) [F sγ−1] |
| γ | 9.05 × 10−1 (±1.06 × 10−3) [—] | 9.09 × 10−1 (±5.99 × 10−4) [—] |
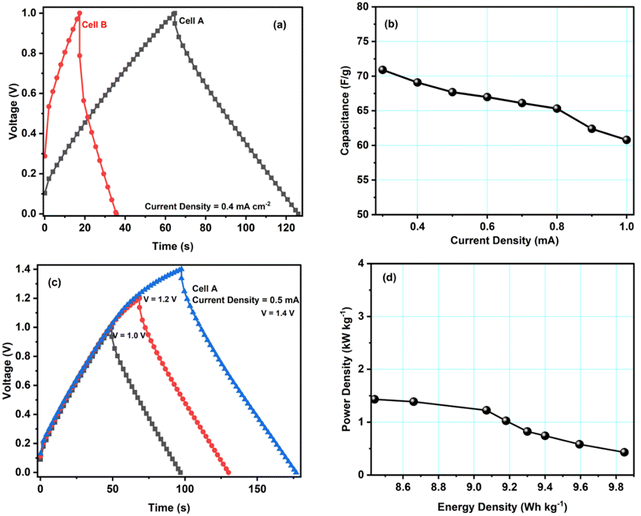
Galvanostatic charge–discharge (GCD) tests have also been carried out for cells A–B to calculate their specific capacitance, energy and power density values. Fig. 6a shows GCD curves for cells A and B, recorded at a current density of 0.4 mA cm−2. The figure shows an almost triangular-shaped GCD pattern for cell A, which confirms that the charge storage is purely due to electrical double-layer formation and not because of the pseudocapacitance. We determined the equivalent series resistance ESR = ΔV/2I by applying the sudden voltage drop (ΔV) in the discharge curve, leading to the constant current I. Table 3 lists the ESR and specific capacitances of cells A and B. These data show that cell A has a lower ESR and a higher capacitance, in accordance with the results obtained with other techniques like CV and EIS. Hence, the GCD study further confirms that the modification of carbon with copper enhances the electrochemical performance of the material.
| Cell | Discharge capacitance values (Cd) [F g−1] | ESR Ω cm2 | Energy density (E) [W h kg−1] | Power density (P) [kW kg−1] |
|---|---|---|---|---|
| A | 66.9 | 297.5 | 9.8 | 1.4 |
| B | 43.2 | 871.8 | 6.0 | 0.9 |
Fig. 6b shows the specific discharge capacitance for different current densities. The figure shows that cell A's specific capacitance decreases with increasing current density, possibly due to the ion adsorption and mass transfer, which reduced the mobility of ions at the electrode–electrolyte interfaces due to high current values. GCD studies for voltages from 1.0 V to 1.4 V also revealed the maximum operating voltage range to agree with the CV studies. As can be seen, up to 1.4 V, the triangular pattern of the curves is maintained (Fig. 6c). Hence, the safer limit of the prepared cell is up to 1.4 V. This agrees with the CV measurements discussed above.
Fig. 6d presents cell A's Ragone plot (specific energy density values versus specific power density values). The plot clearly shows that the energy density of cell A depreciates with the increment in the power density values. Here, the energy density varies from 9.8 W h kg−1 to 8.4 W h kg−1, and the power density varies from 1.4 to 0.4 kW kg−1. These values are similar to other EDLC/supercapacitor cells reported in the literature.33–37
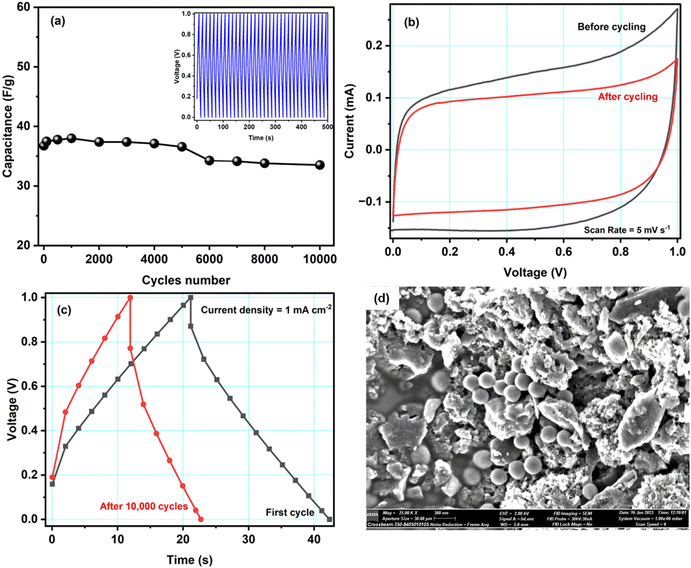
Fig. 7a shows the specific capacitance of cell A during ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 charge–discharge cycles recorded at a current density of 1.6 mA cm−2 at 1.0 V. During the first 100 cycles, the capacitance was unstable, possibly due to irreversible electrochemical reactions at the electrode–electrolyte interface. Later, the cell was stable. Overall, cell A had excellent cyclability as it retained ∼91% of its capacitance after 10
000 charge–discharge cycles recorded at a current density of 1.6 mA cm−2 at 1.0 V. During the first 100 cycles, the capacitance was unstable, possibly due to irreversible electrochemical reactions at the electrode–electrolyte interface. Later, the cell was stable. Overall, cell A had excellent cyclability as it retained ∼91% of its capacitance after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. We did not observe substantial structural changes in the active material, so the slight decrease in the capacitance may have been caused by micropores being blocked by ions, which is supported by scanning electron microscopy performed on the electrode after cycling (discussed below). The inset of Fig. 7a shows the first fifty GCD cycles of cell A. The GCD curves kept their triangular shape with good repeatability.
000 cycles. We did not observe substantial structural changes in the active material, so the slight decrease in the capacitance may have been caused by micropores being blocked by ions, which is supported by scanning electron microscopy performed on the electrode after cycling (discussed below). The inset of Fig. 7a shows the first fifty GCD cycles of cell A. The GCD curves kept their triangular shape with good repeatability.
Fig. 7b and c show CV curves at the scan rate of 5 mV s−1 and GCD curves at a current density of 1 mA cm−2 before and after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GCD cycles. Both figures show slight differences in the respective curves. As mentioned above, the capacitance decreased by about 10%. However, even after 10
000 GCD cycles. Both figures show slight differences in the respective curves. As mentioned above, the capacitance decreased by about 10%. However, even after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, the cell is working properly. Hence, the Cu-modified carbon material shows great promise as an electrode material. To get further insight into cell A's cyclability, SEM images with EDX spectra of the cycled electrode were obtained, see Fig. 7d. The SEM images before and after cycling show no significant difference. Some small spheres were observed, which might appear from magnesium salt or polymer from the electrolyte material. From the EDX studies, shown in Fig. S4 in the ESI,† it is also clear that, after cycling, the traces of Mg, F, Cl, O, etc. have been found in the electrode sample, which is clearly because of the interaction of the electrode and electrolyte during electrochemical testing of the cell. Some ions might get stuck in the electrode's pores, which would explain the observed decrease in capacitance. The literature comparison of other carbon-based materials for symmetric supercapacitors is presented in Table 4. It is important to underline that in our work we proposed an easy, straightforward and cost-effective method for depositing Cu NPs on activated carbon surface without the use of reducing agent. Furthermore, in this study we have also fabricated a symmetrical supercapacitor cell comprising ACCu1, in which the gel polymer electrolyte is immersed. This is the first time that this particular cell configuration has been examined.
000 cycles, the cell is working properly. Hence, the Cu-modified carbon material shows great promise as an electrode material. To get further insight into cell A's cyclability, SEM images with EDX spectra of the cycled electrode were obtained, see Fig. 7d. The SEM images before and after cycling show no significant difference. Some small spheres were observed, which might appear from magnesium salt or polymer from the electrolyte material. From the EDX studies, shown in Fig. S4 in the ESI,† it is also clear that, after cycling, the traces of Mg, F, Cl, O, etc. have been found in the electrode sample, which is clearly because of the interaction of the electrode and electrolyte during electrochemical testing of the cell. Some ions might get stuck in the electrode's pores, which would explain the observed decrease in capacitance. The literature comparison of other carbon-based materials for symmetric supercapacitors is presented in Table 4. It is important to underline that in our work we proposed an easy, straightforward and cost-effective method for depositing Cu NPs on activated carbon surface without the use of reducing agent. Furthermore, in this study we have also fabricated a symmetrical supercapacitor cell comprising ACCu1, in which the gel polymer electrolyte is immersed. This is the first time that this particular cell configuration has been examined.
| Electrode material | Capacitance (F g−1) | Power density (kW kg−1) | Energy density (W h kg−1) | Cycle stabilisation | Ref. |
|---|---|---|---|---|---|
| Pinecone | 43 | 0.454 | 16.1 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
38 |
| Rotten potato | 54 | 0.524 | 20.8 | 5000 | 39 |
| AC@Co | 66 | 15 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
40 | |
| Carbon aerogels | 21 | 1.9 | 11.5 | 3000 | 41 |
| Rotted cucurbita pepo-derived activated carbon | 55 | 0.176 | 14.98 | 8000 | 42 |
| Mango seeds | 28.17 | 0.375 | 35.21 | 6000 | 43 |
| Activated carbon + Fe3O4 | 54.4 | 1.2 | 4.7 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
44 |
| ACCu1 | 68.9 | 1.4 | 9.8 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
This work |
Dye adsorption studies
 | ||
| Fig. 8 (a) Mass effect in the removal of MG into aqueous solution at pH 7; (b) efficiency of the adsorption process at pH 7; (c) and (d) effect of pH and ionic strength. | ||
Fig. 8b depicts the efficiency of MG removal versus time. In about 4 min, more than 80% of the dye was adsorbed. Within 30 min, ACCu1 eliminated 98.68% (9.77 ppm) of the dye. Hence, ACCu1 has excellent potential to remove this toxic dye. The inset of Fig. 8b shows the solution before and after the adsorption process.
 | ||
| Fig. 9 Kinetic orders for the adsorption process of MG by ACCu1: (a) pseudo-first order, (b) pseudo-second-order. | ||
| Material | k 1 (min−1) × 10−3 | Q ecal. (mg g−1) | R 2 | k 2 (g mg−1 min−1) | Q ecal. (mg g−1) | Q exp. (mg g−1) | R 2 |
|---|---|---|---|---|---|---|---|
| AC Cu | 14.212 | 11.036 | 0.6692 | 78.774 | 38.971 | 38.162 | 0.9977 |
Comparing the R2 values of the kinetic model fits, the process of MG adsorption by ACCu1 follows pseudo-second-order kinetics. The value of the experimental adsorption capacity is close to the calculated capacity, which confirms the equilibrium. The pseudo-second-order constant has a higher value, showing that MG adsorption on the ACCu1 surface is very fast, consistent with the obtained experimental data.
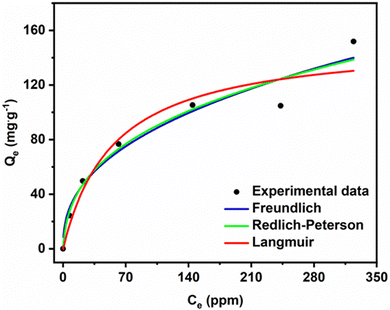
Fig. 10 shows that Qe increases with increasing MG concentration. The figure also shows the fits of the non-linear isotherm models to our experimental data; Table 5 presents the corresponding fit parameters. We see there that the Redlich–Peterson model has a higher R2 coefficient (R2 = 0.9453) than the Langmuir and Freundlich (having almost identical values, R2 = 0.9298 and R2 = 0.9248). Hence, the Redlich–Peterson model provides a slightly better fit.
We found an adsorption capacity of 153.16 mg g−1 using the Langmuir eqn (S10) (ESI†). The value of the heterogeneity factor (n > 1) confirms that the adsorption process is favourable in the present case.
The dimensionless g factor of the Redlich–Peterson model lies between 0 and 1. In our case, it is equal to 0.6487 (Table 6), which shows that the Redlich–Peterson model describes the adsorption process of MG dye on the ACCu1 sample well. In Table S1 (ESI†), a comparison of the adsorption capacity with different adsorbents has been summarised by using MG dye.
| Langmuir | Freundlich | Redlich-Peterson | |||
|---|---|---|---|---|---|
| Q max (mg g−1) | 153.16 | K F (mg g−1 (mg L−1)−1/nF) | 13.327 | g (L g−1) | 0.6487 |
| K L (L mg−1) | 0.0177 | n | 2.4576 | K RP | 13.824 |
| R 2 | 0.9298 | R 2 | 0.9248 | a RP (mg L−1)−g | 0.7363 |
| R 2 | 0.9453 | ||||
Conclusion
By a low-temperature wet ultrasonochemical method that was both simple, economical and environmentally friendly, we modified the surface of activated carbon with Cu nanoparticles. We used this material, ACCu1, as an electrode material in a home-built supercapacitor and as an adsorbent of Malachite green dye. In both these applications, ACCu1 performed substantially better than its pristine carbon counterpart. The supercapacitor with ACCu1 electrodes had a specific capacitance of ∼68.9 F g−1, an energy density of 9.8 W h kg−1, and a power density of 1.4 kW kg−1; this was 43.2 F g−1, 6.0 W h kg−1, and 0.9 kW kg−1, respectively, for the pristine-carbon counterpart. After 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 consecutive charge–discharge cycles, the capacitance had dropped by only 10% proving the durability of ACCu1 as an electrode material. The adsorption studies performed with ACCu1 showed that, within 6 minutes, more than 80% of the Malachite dye was removed; after 30 minutes, the system was close to equilibrium. The adsorption process was of pseudo-second kinetic order. The Redlich–Peterson model fitted well to the obtained experimental data. The adsorption capacitance for MG was 153.16 mg g−1, which is higher than reported in the literature for other materials. ACCu1 is thus a multifunctional composite material with great potential in supercapacitor development and water-purification applications.
000 consecutive charge–discharge cycles, the capacitance had dropped by only 10% proving the durability of ACCu1 as an electrode material. The adsorption studies performed with ACCu1 showed that, within 6 minutes, more than 80% of the Malachite dye was removed; after 30 minutes, the system was close to equilibrium. The adsorption process was of pseudo-second kinetic order. The Redlich–Peterson model fitted well to the obtained experimental data. The adsorption capacitance for MG was 153.16 mg g−1, which is higher than reported in the literature for other materials. ACCu1 is thus a multifunctional composite material with great potential in supercapacitor development and water-purification applications.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
Monika Michalska: conceptualization, methodology, formal analysis, investigation, writing – original draft, writing – review and editing, visualization, supervision, funding acquisition. Paulina Pietrzyk-Thel: conceptualization, methodology, formal analysis, investigation, writing – original draft, writing – review and editing, visualization. Kamil Sobczak: formal analysis, investigation, writing – original draft. Mathijs Janssen: formal analysis, investigation, writing – original draft, writing – review and editing, resources. Amrita Jain: conceptualization, methodology, formal analysis, investigation, writing – original draft, writing – review and editing, resources, visualization, funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
We thank Dr Magdalena Osial (IPPT PAN) for UV-Vis spectroscopic measurements, Dr Kamil Bochenek (IPPT PAN) for SEM measurements and Dr Vlastimil Matejka (VSB-TUO) for XRD measurements of the ACCu1 sample. This work was financially supported by the National Centre for Research and Development (NCBR, Poland); Project number: V4-Japan/2/17/AtomDeC/2022 and the Ministry of Education, Youth and Sports, Czech Republic (contract no. 8F21007) under the Visegrad Group-Japan 2021 Joint Call on Advanced Materials in cooperation with the International Visegrad Fund. M. J. was supported by a FRIPRO grant from The Research Council of Norway (Project No. 345079).References
- V. Thavasi, G. Singh and S. Ramakrishna, Energy Environ. Sci., 2008, 1, 205 RSC.
- M. M. Mekonnen and A. Y. Hoekstra, Sci. Adv., 2016, 2(2) DOI:10.1126/sciadv.1500323.
- M. Ge, C. Cao, J. Huang, S. Li, Z. Chen, K.-Q. Zhang, S. S. Al-Deyab and Y. Lai, J. Mater. Chem. A, 2016, 4, 6772–6801 RSC.
- K. Aruchamy, K. Dharmalingam, C. W. Lee, D. Mondal and N. Sanna Kotrappanavar, Chem. Eng. J., 2022, 427, 131477 CrossRef CAS.
- K. Samdhyan, P. Chand, H. Anand and S. Saini, J. Energy Storage, 2022, 46, 103886 CrossRef.
- J. Sun, C. Liu, X. Song, J. Zhang, Y. Liu, L. Liang, R. Jiang and C. Yuan, Appl. Phys. Rev., 2022, 9, 031301 CAS.
- D. Wang, J. Nai, H. Li, L. Xu and Y. Wang, Carbon, 2019, 141, 40–49 CrossRef CAS.
- D. Wang, S. Liu, L. Jiao and G. Fang, Electrochim. Acta, 2017, 252, 109–118 CrossRef CAS.
- A. Shokry, M. Karim, M. Khalil, S. Ebrahim and J. El Nady, Sci. Rep., 2022, 12, 11278 CrossRef CAS PubMed.
- Z. Zhai, L. Zhang, T. Du, B. Ren, Y. Xu, S. Wang, J. Miao and Z. Liu, Mater. Des., 2022, 221, 111017 CrossRef CAS.
- S. Wang, Z. Hu, Z. Pan and D. Wang, J. Alloys Compd., 2021, 876, 160203 CrossRef CAS.
- R. Yuksel, O. Buyukcakir, P. K. Panda, S. H. Lee, Y. Jiang, D. Singh, S. Hansen, R. Adelung, Y. K. Mishra, R. Ahuja and R. S. Ruoff, Adv. Funct. Mater., 2020, 30(10), 1909725 CrossRef CAS.
- F. Schütt, S. Signetti, H. Krüger, S. Röder, D. Smazna, S. Kaps, S. N. Gorb, Y. K. Mishra, N. M. Pugno and R. Adelung, Nat. Commun., 2017, 8, 1215 CrossRef PubMed.
- S. Kour, S. Tanwar and A. L. Sharma, J. Alloys Compd., 2022, 910, 164834 CrossRef CAS.
- A. Kumar, H. K. Rathore, D. Sarkar and A. Shukla, Electrochem. Sci. Adv., 2021, 2(6), e2100187 CrossRef.
- Y. Teng, K. Liu, R. Liu, Z. Yang, L. Wang, H. Jiang, R. Ding and E. Liu, Mater. Res. Bull., 2017, 89, 33–41 CrossRef CAS.
- L. Zhang, S. L. Candelaria, J. Tian, Y. Li, Y. Huang and G. Cao, J. Power Sources, 2013, 236, 215–223 CrossRef CAS.
- Z. Liu, X. Huang, Y. Miao, B. Gao, Y. Shi, J. Zhao and S. H. Tan, Ind. Crops Prod., 2022, 187, 115510 CrossRef CAS.
- Z. Sun, K. Qu, J. Li, S. Yang, B. Yuan, Z. Huang and Z. Guo, Adv. Compos. Hybrid Mater., 2021, 4, 1413–1424 CrossRef CAS.
- A. Q. Alorabi, M. Shamshi Hassan and M. Azizi, Arabian J. Chem., 2020, 13, 8080–8091 CrossRef CAS.
- S. K. Tripathi, A. Jain, A. Gupta and M. Mishra, J. Solid State Electrochem., 2012, 16, 1799–1806 CrossRef CAS.
- A. Jain, M. Michalska, A. Zaszczyńska and P. Denis, J. Energy Storage, 2022, 54, 105367 CrossRef.
- A. Jain, M. Ghosh, M. Krajewski, S. Kurungot and M. Michalska, J. Energy Storage, 2021, 34, 102178 CrossRef.
- G. Wang, M. Zhang, L. Lu, H. Xu, Z. Xiao, S. Liu, S. Gao and Z. Yu, ChemNanoMat, 2018, 4, 964–971 CrossRef CAS.
- Y. Li, Z. Fu and B. Su, Adv. Funct. Mater., 2012, 22, 4634–4667 CrossRef CAS.
- Q. Zhao, X. Wang, C. Wu, J. Liu, H. Wang, J. Gao, Y. Zhang and H. Shu, J. Power Sources, 2014, 254, 10–17 CrossRef CAS.
- Y. Lv, L. Gan, M. Liu, W. Xiong, Z. Xu, D. Zhu and D. S. Wright, J. Power Sources, 2012, 209, 152–157 CrossRef CAS.
- Mohit, N. Yadav and S. A. Hashmi, J. Energy Storage, 2022, 55, 105421 CrossRef.
- M. Murbach, B. Gerwe, N. Dawson-Elli and L. Tsui, J. Open Source Software, 2020, 5, 2349 CrossRef.
- J. Landesfeind, J. Hattendorff, A. Ehrl, W. A. Wall and H. A. Gasteiger, J. Electrochem. Soc., 2016, 163, A1373–A1387 CrossRef CAS.
- A. Lasia, Electrochemical Impedance Spectroscopy and its Applications, Springer New York, New York, NY, 2014, pp. 85–125 Search PubMed.
- H. Keiser, K. D. Beccu and M. A. Gutjahr, Electrochim. Acta, 1976, 21, 539–543 CrossRef CAS.
- N. M. Santhosh, K. K. Upadhyay, G. Filipič, J. Zavašnik, M. de Fátima Montemor and U. Cvelbar, Carbon, 2023, 203, 686–694 CrossRef.
- R. Rohith, A. T. Prasannakumar, R. R. Mohan, V. Manju and S. J. Varma, ChemistrySelect, 2022, 7(41), e202203068 CrossRef.
- M. F. Koudahi and E. Frąckowiak, Energy Storage Mater., 2022, 49, 255–267 CrossRef.
- K. Subhani, N. Hameed, A. Al-Qatatsheh, J. Ince, P. J. Mahon, A. Lau and N. V. Salim, J. Energy Storage, 2022, 56, 105936 CrossRef.
- A. Jain, S. R. Manippady, R. Tang, H. Nishihara, K. Sobczak, V. Matejka and M. Michalska, Sci. Rep., 2022, 12, 21024 CrossRef CAS.
- M. Rajesh, R. Manikandan, S. Park, B. C. Kim, W. Cho, K. H. Yu and C. J. Raj, Int. J. Energy Res., 2020, 44, 8591–8605 CrossRef CAS.
- A. Wang, K. Sun, R. Xu, Y. Sun and J. Jiang, J. Clean Prod., 2021, 283, 125385 CrossRef CAS.
- K. A. Abdullin, M. T. Gabdullin, Z. K. Kalkozova, S. T. Nurbolat and M. Mirzaeian, Energies, 2023, 16, 4287 CrossRef CAS.
- H. D. Asfaw, A. Kucernak, E. S. Greenhalgh and M. S. P. Shaffer, Compos. Sci. Technol., 2023, 238, 110042 CrossRef CAS.
- S. Peng, Y. Wu, S. Lu, R. Zhao, L. Dai, B. Chen, Q. Xie and Y. Ruan, Diam. Relat. Mater., 2024, 141, 110646 CrossRef CAS.
- S. Lu, W. Yang, M. Zhou, L. Qiu, B. Tao, Q. Zhao, X. Wang, L. Zhang, Q. Xie and Y. Ruan, J. Colloid Interface Sci., 2022, 610, 1088–1099 CrossRef CAS PubMed.
- A. Witecka, P. Pietrzyk-Thel, M. Krajewski, K. Sobczak, A. Wolska and A. Jain, J. Alloys Compd., 2024, 985, 174040 CrossRef CAS.
- L. B. Carvalho, P. M. B. Chagas, T. R. Marques, A. Razafitianamaharavo, M. Pelletier, P. Nolis, C. Jaime, S. S. Thomasi and L. D. M. A. Pinto, J. Environ. Chem. Eng., 2019, 7, 103492 CrossRef CAS.
- M. Marković, M. Gorgievski, N. Štrbac, V. Grekulović, K. Božinović, M. Zdravković and M. Vuković, Metals, 2023, 13, 206 CrossRef.
- Y. S. Ho and G. McKay, Process Biochem., 1999, 34, 451–465 CrossRef CAS.
- M. J. Ahmed and S. K. Dhedan, Fluid Phase Equilib., 2012, 317, 9–14 CrossRef CAS.
- M. Yadav and N. K. Singh, Appl. Water Sci., 2017, 7, 4793–4800 CrossRef CAS.
- K. Y. Foo and B. H. Hameed, Chem. Eng. J., 2010, 156, 2–10 CrossRef CAS.
- K. Vasanth Kumar, M. M. de Castro, M. Martinez-Escandell, M. Molina-Sabio, J. Silvestre-Albero and F. Rodriguez-Reinoso, Chem. Phys. Lett., 2010, 492, 187–192 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00159a |
| This journal is © The Royal Society of Chemistry 2024 |