Microscopic mechanism of thermal amorphization of ZIF-4 and melting of ZIF-zni revealed via molecular dynamics and machine learning techniques†
Emilio
Méndez
 and
Rocio
Semino
and
Rocio
Semino
 *
*
Sorbonne Université, CNRS, Physico-chimie des Electrolytes et Nanosystèmes Interfaciaux, PHENIX, F-75005 Paris, France. E-mail: rocio.semino@sorbonne-universite.fr
First published on 24th January 2024
Abstract
We investigate the microscopic mechanism of the thermally induced ambient pressure ordered–disordered phase transitions of two zeolitic imidazolate frameworks of formula Zn(C3H3N2)2: a porous (ZIF-4) and a dense, non-porous (ZIF-zni) polymorph via a combination of data science and computer simulation approaches. Molecular dynamics simulations are carried out at the atomistic level through the nb-ZIF-FF force field that incorporates ligand–metal reactivity and relies on dummy atoms to reproduce the correct tetrahedral topology around Zn2+ centres. The force field is capable of reproducing the structure of ZIF-4, ZIF-zni and the amorphous (ZIF_a) and liquid (ZIF_liq) phases that respectively result when these crystalline materials are heated. Symmetry functions computed over a database of structures of the four phases are used as inputs to train a neural network that predicts the probabilities of belonging to each of the four phases at the local Zn2+ level with 90% accuracy. We apply this methodology to follow the time-evolution of the amorphization of ZIF-4 and the melting of ZIF-zni along a series of molecular dynamics trajectories. We first computed the transition temperature and determined the associated thermodynamic state functions. Subsequently, we studied the mechanisms. Both processes consist of two steps: (i) for ZIF-4, a low-density amorphous phase is first formed, followed by the final ZIF_a phase while (ii) for ZIF-zni, a ZIF_a-like phase precedes the formation of the liquid phase. These processes involve connectivity changes in the first neighbour ligands around the central Zn2+ cations. We find that the amorphization of ZIF-4 is a non-isotropic process, and we trace back the origins of this anisotropic behaviour to the density and lability of coordination bonds.
1 Introduction
Amorphous metal–organic frameworks (MOFs) have been long known, but only very recently they have attracted attention from the research community.1 Indeed, since amorphous MOFs may conserve building blocks and practically all connectivity from their crystalline counterparts, they combine attractive properties such as intrinsic porosity and high surface areas2 of crystalline phases with mechanical robustness and the presence of multiple defects that can act as catalytic centres typical of amorphous phases.3 Amorphous MOFs can be synthesised as such, but they are mostly obtained from their parent crystalline structures by exerting an external stimulus on them.4 Since these ordered–disordered transitions are reversible, guests within the pores of the crystalline phases can become trapped when the structure becomes amorphous to be later released by forcing the MOF to return to its crystalline state. This principle makes these materials attractive for important industrial and environmental applications including water purification,5 drug delivery,6,7 capture of radioactive species8,9 and catalysis,10,11 among others. Moreover, it is easier to adequately shape amorphous materials for applications (for example as pellets, extrudates or sprays) without compromising their porosity or chemical properties.12Zeolitic imidazolate frameworks (ZIFs) constitute an exceptionally stable family of MOFs with potential applications in many societal challenging processes. These MOFs have the particularity that their distribution of metal–ligand–metal angles is analogous to that of Si–O–Si angles in zeolites, but since their bonds are longer, their porosities are larger. This offers some advantages in terms of potential guest–host-based applications, but it also gives ZIFs more flexibility (i.e. their elastic moduli are at least one order of magnitude lower than those of zeolites),13 as coordination bonds are weaker than covalent bonds. In addition, amorphization of ZIFs occurs under milder conditions (for example, lower temperatures) than for their zeolite analogues,14,15 as deforming the metal–ligand4 tetrahedron involves reorganising much weaker bonds than it does for the SiO4 case.
Many ZIFs exhibit ordered–disordered phase transitions. These may be induced by changes in temperature16,17 and pressure,18 mechanical grinding,19 interaction with X-rays,20 or even eliminating water from their structures.21 Heat-induced amorphization was observed in a number of MOFs;3,22–24 in this work we will concentrate our efforts on ZIF-4. This MOF is well-known for its applications in separating alkenes from alkanes among other gas mixtures,25 and its synthesis has been scaled-up.26 It is one of the many existing polymorphs of chemical formula Zn(C3H3N2) and it exhibits a cag topology with connected cages with a diameter of 4.9 Å.27 ZIF-4 has a complex phase diagram, consisting of a series of amorphous and crystalline phases.28 At ambient pressure, the following phase transitions have been experimentally detected:
Transition 1 is an amorphization phase transition from the crystalline porous ZIF-4 to ZIF_a, an amorphous phase that has a continuous random network structure similar to that of amorphous silica.16 This transition occurs at T1 = 589 K.29 Further heating leads to transition 2: a recrystallization of ZIF_a into a crystalline dense ZIF-zni solid, which occurs at T2 = 773 K. It is interesting to note that other Zn(C3H3N2) polymorphs, including ZIF-1 (crb topology), ZIF-3 (dft topology) and ZIF-6 (gis topology) also yield the same amorphous phase upon heating that subsequently crystallises into ZIF-zni.17 Finally, transition 3 involves the melting of ZIF-zni at T3 = 863 K to give a liquid MOF (ZIF_liq).30 Bennett and coworkers showed that heating ZIF-4 first leads to the formation of a low density phase before reaching the high density amorphous phase that transforms into ZIF-zni upon further increasing the temperature.31
Neutron total diffraction data revealed that the Zn-centred tetrahedron remains quite rigid during the amorphization, although an out-of-plane ligand motion can act slightly reducing the total connectivity of the amorphous phase with respect to the full connectivity of ZIF-4.30 High field 13C and 15N NMR measurements can help differentiate ZIF-4 from ZIF-zni and show that there is an important structural similarity between ZIF_a and both crystalline phases, despite signal broadening for the amorphous material. This confirms that the amorphous phases obtained by thermal annealing starting from ZIF-4 or ZIF-zni are identical.32In situ far infra-red spectroscopy proved that the ligand does not significantly strain during the amorphization process and that collective modes involving the deformation of the ZnN4 tetrahedron are the main contributors to the amorphization.33 From a computational standpoint, Gaillac and coworkers studied the melting mechanism of ZIF-4 via ab initio molecular dynamics simulations.34,35 In these studies, ZIF-4 is considered as a starting point, since treating representative sections of ZIF_a and ZIF-zni would yield systems that are too large to be subjected to ab initio molecular dynamics while spanning reasonable timescales to get correct simulation averages. Very high temperatures, of the order of 1000 K or more, are explored in order to get enough statistics, so the intermediate states between ZIF-4 and ZIF_liq are ignored. The authors reach a good agreement between the structural characteristics of their model and the experimental PDFs; they find that under-coordinated Zn centres act as “seeds” for the melting process to occur and they propose a molecular mechanism for the melting involving first-neighbour exchanges. Despite this wealth of information, many questions remain unanswered, including what is the mechanism of the amorphization of ZIF-4? What is the mechanism of the melting of ZIF-zni? What happens beyond first-neighbour distances in these transformations? In order to answer these questions we need larger simulation cells; thus, it is necessary to rely on a computational model where electronic degrees of freedom are averaged following the Born–Oppenheimer approximation. However, including reactivity, in particular, metal–ligand reactivity, is essential to model these kinds of ordered–disordered phase transitions. A popular reactive force field, ReaxFF, has been tested for this task, but the modelling community has not yet reached a consensus on whether this force field is adequate to model amorphous ZIFs.36,37
In this contribution, we rely on nb-ZIF-FF (non-bonded ZIF-FF)38 to study the ordered–disordered transitions 1 and 3 cited above. This force field, originally developed by Balestra and Semino38 with the purpose of modelling the self-assembly of ZIFs, features metal–ligand reactivity by means of Morse potentials to treat coordination bonds. We found that it captures structural, mechanical and thermodynamic properties of the amorphous and liquid phases as well as of the crystalline ones. We circumvent the inherent difficulty of differentiating multiple ordered and disordered phases through the training of a neural network sorting algorithm that identifies the correct phase at the local, atomic level with high accuracy. This data science augmented molecular dynamics approach allows us to obtain molecular details in the study of the mechanisms of these ordered–disordered transformations and to answer the questions raised above. We observe the formation of a phase recognised as liquid-like prior to the formation of ZIF_a upon heating ZIF-4 at a temperature T > T1, which can be associated with experimental observations.31 For ZIF-zni, we found the opposite: the density decreases monotonically, going from an amorphous-classified state to a liquid. Both processes occur in an anisotropic fashion, which can be correlated with the local density and labilities of coordination bonds within the materials.
This work is structured as follows. Sec. 2 details the systems of study, the algorithm applied to generate disordered structures, the development of our neural network sorting algorithm and the molecular dynamics simulations details. We then present and discuss our results in Sec. 3 and summarise them in Sec. 4.
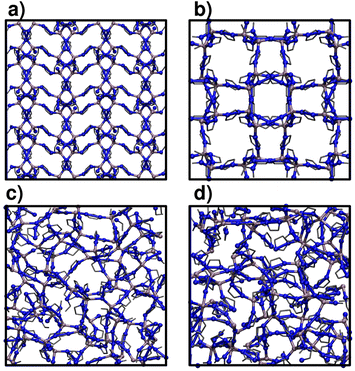
2 Methods
2.1 Systems of study
We focus on two crystalline MOFs within the Zn(C3H3N2)2 series of polymorphs:27 ZIF-4 and ZIF-zni, a porous and a dense phase respectively. We analyse the phase transitions that transform ZIF-4 into ZIF_a and ZIF-zni into a melt: ZIF_liq (transition 1 and transition 3, see Sec. 1).28 These two are ordered–disordered transitions, so we can adequately sample them by just increasing the temperature (to increase the kinetic energy) of the materials. Studying transition 2 is a much more complicated problem, since it would involve using more sophisticated enhanced sampling simulation methods to correctly sample the collection of rare events that lead from a disordered to an ordered phase.Fig. 1 illustrates the structure of the four studied systems. ZIF-4 and ZIF-zni initial structures were obtained from the Cambridge Structural Database.39 ZIF_a configurations were generated by simulated annealing of these two crystalline phases via the procedure that we detail below, in Sec. 2.2. ZIF_liq is obtained by heating ZIF-zni or ZIF-4 to T = 700 K. All materials were modelled at the atomistic level through the nb-ZIF-FF force field.38 This force field partially includes reactivity, by allowing the metal–ligand bond to break and form throughout classical molecular dynamics simulations. This is the only kind of reactivity needed to model amorphization of ZIF-4, since the integrity of the ligands along the process was confirmed experimentally.33 The metal–ligand bond is modelled through a Morse potential, which yields zero pairwise forces at long metal–ligand distances. The correct tetrahedral local symmetry around Zn2+ cations is enforced by distributing part of the cation's charge into the four vertices of a flexible tetrahedron that holds it in its centre (cationic dummy atom model). This force field has been carefully validated for reproducing structural and mechanical properties of a series of ZIFs, including ZIF-4 and ZIF-zni. For more details concerning the nb-ZIF-FF force field, the reader is referred to ref. 38.
2.2 Generation of the amorphous structures
To generate ZIF_a, we started either from ZIF-4 or from ZIF-zni. The crystalline structures were subjected to a temperature ramp through which the material is heated from 300 to 900 K, then a short constant T = 900 K run is performed and finally a second temperature ramp brings the system back to 300 K. We tested ramps of 1 K ps−1 and 4.8 K ps−1, which comply with the less-than-5 K ps−1 rule proposed by Castel and Coudert to avoid damaging the full coordination of the Zn2+ centres in the crystalline form.37 We note that these ramps are orders of magnitude higher than those experimentally achievable (on the order of 5–100 K min−1).31 We compared radial distribution functions (RDFs) of the amorphous materials generated with these two temperature ramp values and found no significant differences. Constraints were added on the 900 K constant temperature simulation so that the final materials have an approximately cubic shape.To sample the diversity of glass configurations, we generated three independent runs starting from ZIF-4 and three starting from ZIF-zni, that differ in the total time span of the 900 K constant temperature section: 250, 500 or 750 ps. The calculated properties of the glass correspond to an average of the six independent structures obtained after annealing. During the heating ramp, the volume of the system suffers from an abrupt change that can be distinguished from the expected fluctuations, signalling the phase transition. Even though at the end of the simulation experiment the temperature is brought back to its initial value of 300 K, the final volume differs from the initial one, thus demonstrating that the phase transition has taken place and has not reverted.
ZIF_a configurations generated from ZIF-4 or from ZIF-zni are indistinguishable, and they describe the experimentally characterised amorphous material quite well in terms of density, typical neighbour distances and angles and its bulk modulus, as shown in Table 1.
The bulk modulus K was calculated from the volume fluctuations in the NPT ensemble:
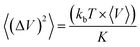 | (1) |
Besides correctly capturing average distance and angle values, nb-ZIF-FF also passes an even more difficult test: it yields correct distributions for these properties. To the best of our knowledge, the angle distributions have to date only been correctly predicted by ab initio molecular dynamics; this is the first time that an atomistic force field incorporating reactivity has accomplished this challenging task, particularly for the N–Zn–N angle distribution that is known to slightly widen in the amorphous phase.30 Indeed, as pointed out by Castel and Coudert,40 the most widely used reactive force field, ReaX-FF,36 fails to reproduce the N–Zn–N angle distribution. Fig. S1 in the ESI† shows that nb-ZIF-FF is capable of predicting the subtle widening of the angle distribution that is due to the presence of a small proportion of tri-coordinated Zn cations in ZIF_a.
The subtle under coordination of the Zn2+ centres in the amorphous material can be appreciated in Fig. 2. The left panel shows the Zn–N radial distribution function for the four phases studied. Even though all structures are quite similar and difficult to distinguish experimentally,32 we can already see some subtle differences in their RDFs. Indeed, the peaks for the liquid are broader than those from the amorphous solid and those are, in turn, broader than those for the crystals. In the inset of the left panel, we can see that the RDF does not go to zero between the first two peaks for ZIF_a nor forZIF_liq, which indicates nitrogen exchanges in the first coordination sphere of the zinc cations and is in agreement with previous findings.35 The right panel of Fig. 2 shows the integral of the Zn–N RDF for the four phases, which gives us information on the number of N that can be found on average around a Zn2+ centre as a function of the distance. The curves for ZIF-4 and ZIF-zni reach a value of four at 2.3 Å, indicating the expected perfect tetrahedral coordination in their first neighbour sphere. On the other hand, the curve corresponding to ZIF_a shows a loss in the average Zn–N coordination for the same distance, which is even more pronounced in the case of ZIF_liq. This indicates that both disordered phases typically contain a small proportion of tri-coordinated Zn2+ centres, as a result of the increased flexibility of ligand motions, as found experimentally.33
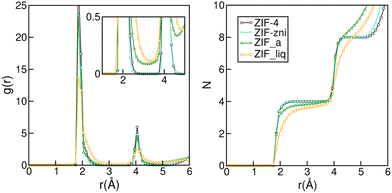 | ||
| Fig. 2 Zn–N radial distribution (left panel) and its integral (right panel) for ZIF-4, ZIF-zni, ZIF_a and ZIF_liq obtained by molecular dynamics simulations employing nb-ZIF-FF as a force field. | ||
The excellent performance of the combination of nb-ZIF-FF with our simulated annealing method in yielding ZIF_a configurations in good agreement with several experimentally measured properties make us confident in our model for this glassy material.
2.3 Machine learning methods
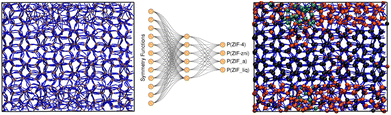
To succeed in our goal of studying the mechanism of the ZIF-4 and ZIF-zni ordered–disordered phase transitions, we first need to define a metric that allows us to distinguish between these crystalline phases and their disordered counterparts at the local, atomic environment level. Such a local metric would allow us to track the evolution of the amorphization and melting processes throughout a simulation, to observe their progression from the deformation of the local structure around a single Zn2+ centre (i.e. distortions in the tetrahedral spatial arrangement of the first ligand neighbours) to the generation of larger disordered domains within the crystal, and how these domains propagate or merge until they take over and the phase transformation reaches its end.Amorphous materials have traditionally been characterised via an extensive exploration of structural properties including RDFs, structure factors and pore size distribution.41 These ways of describing amorphous materials, albeit useful, rely on preconceived ideas of the underlying chemistry of these materials. Machine learning methods based on agnostic descriptors have been developed to automatically identify, differentiate and classify long-range ordered materials in an unbiased way, free of preconceptions. The task becomes more daunting when the collection of objects to be classified includes amorphous materials, due to their inherent lack of translational symmetry which makes both the choice of appropriate descriptors as well as the sampling of structural diversity, harder. A number of methods have been proposed to deal with this difficult task.42–47 Here, we test the performance of Behler–Parrinello symmetry functions (BPSF)48 as unbiased generic descriptors that act at the atomic environment level, to inform the degree of ZIF_a-ness, ZIF-4-ness, ZIF-zni-ness and ZIF_liq-ness of a given Zn2+-centred environment. These functions fulfill the basic criteria for being well-behaved chemical descriptors, that is, they yield the same value for two configurations that are related in that one of them is the result of a translation, rotation or same-element-atom permutation operation applied over the other. These atom-centred many-body functions can be classified into two types: radial and angular. The former ones are given by the sum over two-body terms and are related to the connectivity of the central atom, while in the latter ones, three-body terms are considered. We tested twelve symmetry functions of the type:
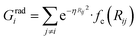 | (2) |
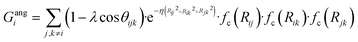 | (3) |
Before analysing our trajectories through the lens of our chosen descriptors, we sought to verify their aptitude in recognising the four systems studied. To this end, we built a database comprising 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations in total, out of which 3000, 3000, 12
000 configurations in total, out of which 3000, 3000, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 12
000 and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 correspond to ZIF-4, ZIF-zni, ZIF_a and ZIF_liq, respectively, each of them comprising 64 atomic Zn2+-centred environments. The amount of non-crystalline structures is higher to improve the classification, since the differentiation between these two groups will be the most challenging task for the algorithm. The configurations correspond to microstates obtained from MD simulations at temperatures spanning the whole stability range in the case of crystalline structures, while for ZIF_a the sampling was made at temperatures between 300 K and 500 K. As mentioned above, liquid state configurations were sampled at 700 K. We justify this criterion by the change in the slope at ∼600 K observed in the curve of mean potential energy vs. temperature (see Fig. S3†) associated with the jump in Cp that occurs at the glass transition temperature (ZIF_a → ZIF_liq).
000 correspond to ZIF-4, ZIF-zni, ZIF_a and ZIF_liq, respectively, each of them comprising 64 atomic Zn2+-centred environments. The amount of non-crystalline structures is higher to improve the classification, since the differentiation between these two groups will be the most challenging task for the algorithm. The configurations correspond to microstates obtained from MD simulations at temperatures spanning the whole stability range in the case of crystalline structures, while for ZIF_a the sampling was made at temperatures between 300 K and 500 K. As mentioned above, liquid state configurations were sampled at 700 K. We justify this criterion by the change in the slope at ∼600 K observed in the curve of mean potential energy vs. temperature (see Fig. S3†) associated with the jump in Cp that occurs at the glass transition temperature (ZIF_a → ZIF_liq).
We then computed the symmetry functions described by using eqn (2) and (3) for each of their Zn2+-centred environments via the RuNNer code49 and plotted their value distributions for all structures together as box plots in R.50 The resulting graph is shown in Fig. S4.† We can see from the plot that none of the symmetry functions alone suffices to distinguish between the four phases. We thus used them as features to be fed into a neural network that was trained to output the probabilities that the Zn2+-centred environment belongs to a ZIF-4, ZIF_a, ZIF_liq or ZIF-zni phase (four output values).
In order to train the neural network, we divided our database, composed of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920
920![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Zn2+-centred environments (64 × 30
000 Zn2+-centred environments (64 × 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures) into train and test sets in a 80
000 structures) into train and test sets in a 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 proportion. The neural network architecture was composed of an input layer of 12 nodes, corresponding to the symmetry functions, a single hidden layer comprising 6 nodes, and an output layer of 4 nodes, each one representing the probability of an environment to be classified as one of the reference structures (see Fig. 3). Further details can be found in the ESI.† If we assign the environment to the class that has the highest associated probability to obtain a clear-cut sorting, our neural network yields 90.3% accuracy in the classification exercise for the test set.
20 proportion. The neural network architecture was composed of an input layer of 12 nodes, corresponding to the symmetry functions, a single hidden layer comprising 6 nodes, and an output layer of 4 nodes, each one representing the probability of an environment to be classified as one of the reference structures (see Fig. 3). Further details can be found in the ESI.† If we assign the environment to the class that has the highest associated probability to obtain a clear-cut sorting, our neural network yields 90.3% accuracy in the classification exercise for the test set.
In Table 2 we show the confusion matrix obtained for the test set (which is composed of structures that were not used in the training process). This table indicates the fractions of environments of each type (rows) classified as each of the possible structures (columns). The diagonal elements correspond to the fraction of correct classifications. As expected, the highest source of error (∼10%) was obtained from the miss-classification of ZIF_a and ZIF_liq structures,51 while the classification of crystalline structures was satisfactory in 95% of cases. Indeed, by simple visual inspection both disordered phases seem to be indistinguishable (see Fig. 1). A hint that the classification was possible was given by the fact that the Zn–N radial distribution functions for ZIF_a and ZIF_liq differ, as shown above in Fig. 2a. It is, however, quite remarkable that the neural network manages to distinguish them with such low error despite their important structural similarity. The accuracy of the classification is even more impressive if we take into account that it was made based on structural information only, as it is well-known that the main difference between glasses and their parent crystalline structures lies in their dynamics rather than in their structures. Incorporating dynamics information into the features for a neural network distinguishing amorphous materials would most likely further improve the accuracy.
| ZIF-4 | ZIF-zni | ZIF_a | ZIF_liq | |
|---|---|---|---|---|
| ZIF-4 | 0.951 | 0.000 | 0.004 | 0.045 |
| ZIF-zni | 0.000 | 0.946 | 0.044 | 0.010 |
| ZIF_a | 0.000 | 0.019 | 0.895 | 0.086 |
| ZIF_liq | 0.012 | 0.002 | 0.098 | 0.888 |
Fig. 3 shows an example of how our neural network can be applied to follow the time evolution of an amorphization process. In the left part, we can see a material that exhibits coexisting ordered and disordered domains. By applying our neural network, we can distinguish between ZIF-4-, ZIF-zni-, ZIF_a- and ZIF_liq-like environments. Finally, to check that the classification of the amorphous phases is meaningful, we plotted the fraction of disordered-like centres that are classified as being ZIF_liq-like instead of ZIF_a-like as a function of temperature (see Fig. S5†). We can see from this plot that there is a clear temperature dependence on the labelling, which is consistent with what is expected for the thermodynamic stability of these two distinct disordered states (see Fig. S3†).
2.4 Molecular dynamics simulations
Classical molecular dynamics simulations were carried out through the LAMMPS open source simulation package52 with nb-ZIF-FF as a force field.38 The integration of equations of motion was performed in the NPT ensemble, with Nose–Hoover thermostats and barostats. The damping parameters were set to 100 time steps for the thermostat and 1000 time steps for the barostat. Unless the contrary is specified, the barostat alters the box sizes in an isotropic way. In all cases the pressure was set to 1 bar. The time step was set to 0.5 fs except for simulations with a temperature over 700 K, in which a time step of 0.25 fs was used. For generating configurations for the neural network training set, systems of 64 Zn atoms were used, which correspond to a 2 × 2 × 1 supercell of ZIF-4 or a ZIF-zni unit cell (1600 particles in total, including both crystallographic and dummy atoms), while for production runs, the number of Zn2+ cations was 1024 and the total number of atoms was 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600, which correspond to a 4 × 4 × 4 and a 2 × 2 × 4 supercell for ZIF-4 and ZIF-zni, respectively, and initial box sizes of 61.58 × 61.23 × 73.70 Å3 and 46.66 × 46.66 × 101.51 Å3. These sizes are chosen to be significantly larger than the correlation length of the glass, ∼8 Å, obtained from the convergence of the Zn–Zn radial distribution function (see Fig. S2†), in order to avoid finite size effects.
600, which correspond to a 4 × 4 × 4 and a 2 × 2 × 4 supercell for ZIF-4 and ZIF-zni, respectively, and initial box sizes of 61.58 × 61.23 × 73.70 Å3 and 46.66 × 46.66 × 101.51 Å3. These sizes are chosen to be significantly larger than the correlation length of the glass, ∼8 Å, obtained from the convergence of the Zn–Zn radial distribution function (see Fig. S2†), in order to avoid finite size effects.
3 Results and discussion
3.1 Thermodynamic analyses
We start our study of ZIF-4 → ZIF_a (amorphization, transition 1) and ZIF-zni → ZIF_liq (melting, transition 3) by determining their equilibrium temperatures. We could be tempted to extract the transition temperature from the simulations that we performed to generate the amorphous structures (see Sec. 2.2) as the temperature that matches the drastic volume change of the system, which signals that the amorphization process has taken place. However, this would be misleading: the temperature ramp is so fast that the system cannot reach thermal equilibrium at each temperature. The false transition temperature we see when we apply a temperature ramp to heat the system has to be higher than the thermodynamic transition temperature. In order to find the equilibrium temperature for transitions 1 and 3, we need to find conditions under which both phases are equally stable.53 We first generated a simulation box where ZIF_a and ZIF-4 coexist and occupy approximately the same volume each by running a short simulation at the temperature at which we observed the phase transition in the simulated annealing (T = 550 K). Subsequently, we started a series of molecular dynamics simulations in the NPT ensemble, each with a different target constant temperature. We let the system evolve, and then we assessed whether the number of amorphous sites had increased, decreased or remained stable. The temperature at which the two phases coexist without one of them gaining terrain over the other is the equilibrium temperature. We followed the same procedure to determine the ZIF-zni melting temperature. Fig. S6† shows the time evolution of the number of liquid-like Zn2+ centres for ZIF-zni at different temperatures. We can see that the number of liquid-like centres fluctuates around a constant value at T = 625 K. Through this procedure we found T_amorphization = T1 = 420 K and T_melting = T3 = 625 K. The experimental counterparts are at around 520 K and 860 K, respectively.28In order to evaluate the possibility of finite size effects influencing our results, we repeated the previous analysis for a smaller ZIF-4 system that contained 3 × 3 × 3 unit cells, and we obtained a result for an amorphization temperature of 425 K, which is within ∼1% of the value found in the 4 × 4 × 4 case. This supports our choice of system size.
We can also obtain the amorphization and melting entropies (ΔS1 and ΔS3) from these simulations. At the temperature at which the phases coexist, their chemical potentials are equal and ΔG = 0, so the entropy can be readily obtained from the enthalpy by diving it by T. The enthalpy is given by the internal energy coming from the force field plus the pressure–volume term. In addition, we can obtain free energy differences at temperature T by integration of the Gibbs–Helmholtz equation:
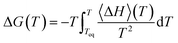 | (4) |
Our computed enthalpies are in good agreement with the reference experimental and ab initio values. From the free energy difference we obtain the correct thermodynamic stability trend: ZIF-4 is in fact metastable at ambient temperature and pressure. Entropies can be rationalized in terms of structural properties. Indeed, the disordered phases have higher entropies than the ordered ones, and if we compare the entropies associated with the crystalline phases, we can see that it is higher for ZIF-4 than for ZIF-zni. This is a consequence of the lower density (higher porosity) of ZIF-4, which provides it with the possibility of adopting many more equivalent microstates than its high density counterpart can. We note that our equilibrium temperatures are deviated from the experimental values. Even though we cannot predict the right values, the tendencies are reproduced. Experimental values should also be carefully considered, since it has been proven that the amorphization temperature is very sensible to the temperature ramp used to trigger it.31
3.2 Mechanisms of the phase transitions
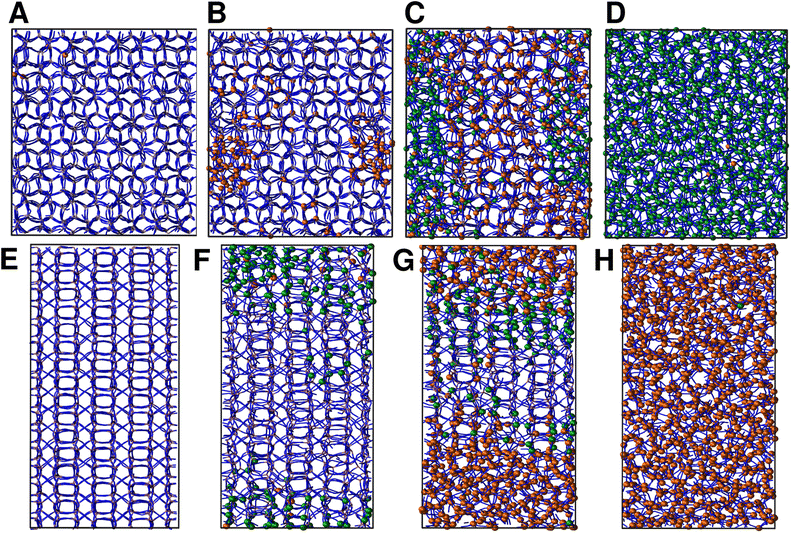
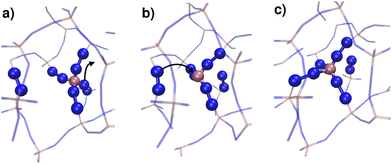
We continue our study by simulating the amorphization and melting processes in an NPT ensemble at P = 1 bar and T = 550 K for ZIF-4 and T = 700 K for ZIF-zni. These temperatures are higher than the respective transition temperatures, to guarantee thermodynamic feasibility and reasonably fast kinetics. At the end of these simulations, we reach the corresponding disordered phase (glass from ZIF-4 and liquid from ZIF-zni). We run four independent systems for each transition in order to take into consideration their stochastic character; the results presented below come from an average of these four independent simulation experiments. We also run the same simulations for ZIF-4 and ZIF-zni but with a box consisting of 3 × 3 × 3 unit cells to verify whether the size of the simulation box was large enough to avoid unphysical finite size effects that could occur if the process was favoured by an early artificial percolation of the new phase in a small simulation box. The rates of formation of the final phases are within a difference of less than 3% in the smaller systems with respect to those obtained for the larger ones, while also preserving all the qualitative features mentioned in our analysis. We can thus confirm that our analyses are robust with respect to box size.A series of snapshots of the system throughout the simulation is shown in Fig. 4. Panel A shows the initial configuration, which corresponds to a ZIF-4 crystal. As expected, and confirming the validity of our neural network, the amount of environments classified as ZIF-zni-like remains negligible during the whole simulation. We first observe the generation of a liquid-like phase (coloured in orange, panel B). Subsequently, the amorphous ZIF_a phase is formed within this lower density phase (coloured in green, panel C) and gradually expands until it takes over the whole system (panel D, final configuration). The amorphization process thus consists of two steps: a first step in which the Zn–N connectivity slightly drops to yield a more disordered, low density state, followed by a second stage that gives rise to ZIF_a. The intermediate liquid-like phase that is first formed could be associated with the experimentally identified low density non-crystalline phase.31 Indeed, this phase is less dense than ZIF_a by about ∼10% which is comparable to the experimentally obtained density difference between the low density and high density amorphous phases.31 The liquid phase, in turn, is more dense than the porous ZIF-4 crystal. Note that we did not explicitly include the experimentally found low density phase in the training of the neural network, but the algorithm identified it as a liquid-like phase probably due to the correlation between local density and the symmetry function values. Furthermore, since the classification is performed only by using structural information, the fact that the intermediate phase is assigned as a liquid does not imply that the dynamics are faster than those associated with the amorphous final phase.
For ZIF-zni (Fig. 4, panels E–H), the situation is reversed: from the crystal (panel E), the connectivity starts gradually diminishing to yield an amorphous-like phase in the first stage (panel F), whose density then continues to decrease to reach the final ZIF_liq state (panel G). The liquid phase grows inside the amorphous phase until it takes over the whole simulation box. This suggests that both transitions are thus two-step processes, and what they have in common is that the intermediate phase that is formed in the first step has an intermediate density between that of the initial and the final phases (ρZIF-4 < ρZIF_liq < ρZIF_a < ρZIF-zni).
In all simulation experiments, we observed that the disordered phases grow as a single cluster that expands and reorganises in terms of the Zn–N connectivity, instead of forming a series of disordered micro-domains that subsequently aggregate. The formation of the higher density amorphous phase does not seem to occur at the interface between crystalline and liquid environments: in contrast, it is generated in the bulk liquid and propagates until practically all environments are ZIF_a-like. For the melting of ZIF-zni, we also observe that the final phase is formed within the bulk of the intermediate disordered phase.
The time-evolution of the fraction of Zn2+ centres XZn that correspond to ZIF-4-, amorphous- and liquid-like states is plotted in Fig. 5 and in Fig. S7† for transitions 1 and 3 respectively. From these plots we can first confirm the two above mentioned stages for both processes. We can also see in Fig. 5 that once the amorphous cluster is formed, it grows until it takes over the whole simulation box.
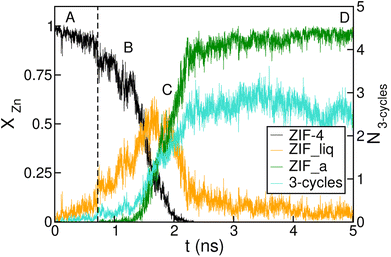 | ||
| Fig. 5 Time evolution of the fraction of disordered (amorphous-, green, and liquid-like, orange) and crystalline (ZIF-4-like, black) Zn2+ centres for an amorphization simulation starting from a ZIF-4 crystal (ZIF-4 → ZIF_a). A, B, C and D mark the points of the trajectory from which we obtained the snapshots in Fig. 4. The vertical dotted line indicates the occurrence of a change in connectivity of the type shown in Fig. 6. The number of 3 membered rings formed by neighbour Zn2+ centres per unit cell is shown in cyan, and the scale is given on the right side y axis. | ||
To unveil the microscopic processes that trigger the initial steps of amorphization, we performed a simulation starting from ZIF-4 at a slightly lower temperature than the above described (T = 540 K) at which no amorphization is observed during the whole simulation time span, due to the fact that this is a slow activated process. Indeed, the classification algorithm only identifies a small fraction (∼2%) of non-crystalline Zn2+ centres, which corresponds to low-lifetime random fluctuations of the network. The presence of tricoordinated Zn2+ is observed in both cases, and these represent ∼2% of the metallic cations. These unstable defects are generated by breaking of Zn–N bonds, and have an average lifetime of ∼3 ps, meaning that the process is reversible. This indicates that bond breaking events leading to undercoordinated Zn2+ centres are not sufficient to trigger the amorphization process.
By monitoring the connectivity of the Zn–N network over time we can observe all possible pathways to restore the tetrahedric coordination of a defect site. Three different mechanisms can be identified: (i) the broken Zn–N bond is restored, leading to exactly the same connectivity as that before defect formation; (ii) the tricoordinated Zn2+ binds to the other nitrogen that belongs to the same ligand moiety, i.e. a rotation of the imidazolate restores the original connectivity; or (iii) a new bond is formed between the Zn2+ and a different ligand molecule, leading to a change in the connectivity of the system. This latter mechanism is illustrated in Fig. 6. The first two mechanisms were observed in both T = 540 K and T = 550 K simulations, but the last one only took place in significant amounts in the high temperature system, which exhibits amorphization. In the 540 K simulation, just a few (13) events of this kind were registered along the simulation, and every one of them finally reverted to the original connectivity after a short period of time. These may be considered as failed initial attempts of the new phase to nucleate. This scenario suggests that the first steps of amorphization are related to the formation of Zn–N bonds that change the original connectivity of the network. This kind of event is much more infrequent than simple bond breaks or the formation of tricoordinated sites. Processes of type (iii) typically occur for the first time in a simulation at about t = 100 ps, while type (ii) process rotations take place every 1.5 ps on average, and simple bond breaking is observed every 0.1 ps. These results are averages over four independent runs at T = 550 K. In Fig. 5 we include a dotted line indicating the time of occurrence of a type (iii) event. We can see that the process is accompanied by a sudden jump in the number of liquid-like environments recognised by the neural network, thus triggering the amorphization transition.
The same analysis was performed for the melting of ZIF-zni, by comparing simulations performed at T = 700 K and T = 670 K, in which no melting was observed, leading to a similar classification of timescales. In this case, since we are at a higher temperature, the characteristic times are reduced to ∼50 ps for the first type (iii) event to occur, while type (ii) rotations take place every 0.5 ps on average and bond breakings occurs every 0.02 ps.
We complement the microscopic description of the amorphization process by studying the evolution of the number of 3 membered rings formed by neighbour Zn2+ centres (here we count only Zn2+, in fact the rings are formed by alternating metals and ligands, such as the (Si–O)n rings in zeolites). These kinds of structures are known to be present in the glass state but not in the crystal state, which exhibits rings of 4, 6 and 8 members.37 We can see in Fig. 5 that the number of 3 membered rings in the early stage correlates with the growth of the intermediate low density phase, thus suggesting that the formation of this kind of structure could be an important step in the amorphization process. The correlation seems to be amplified in the stage of formation of the final glass structure. This indicates that the final configurations are richer in 3 membered ring patterns, while the intermediate phase preserves more of the topological features of ZIF-4.
To gain further microscopic insight into the propagation of the disordered phases during these ordered–disordered transitions and taking into account the anisotropy of the crystal structures, we plotted the average disordered (amorphous- and liquid-like) cluster size projected onto the three Cartesian axes as a function of the number of disordered Zn2+ centres NZn in Fig. 7, to check if there is a preferential growth direction. To calculate the cluster size, we first computed the contact matrix of Zn atoms. This matrix of size NZn × NZn is defined such that the element ij is equal to 1 if atoms i and j are at a distance lower than 6.5 Å, and 0 otherwise. This cutoff length is chosen to include the first neighbor shell of Zn atoms. Then, we implemented a search clustering algorithm to calculate all cluster sizes in the system. A cluster is defined as a set of atoms in which any pair of them can be connected through a path of neighbors. The size of the cluster in a specific direction is computed as the maximum difference in the position between atoms that belong to the cluster on the corresponding axis. A similar plot for transition 3 can be found in Fig. S8.† We can see from the curves in Fig. 7 that the growth of the disordered phase is anisotropic: it occurs faster in the x direction than in the other two. This behaviour is reproduced in all the independent simulations we ran and can be observed both for the first disordered liquid-like low density phase as well as for the final ZIF_a amorphous phase. In the case of transition 3, ZIF-zni melting, no preferential direction can be clearly distinguished during the whole interval of cluster sizes.
Anisotropy in the formation of amorphous domains has also been experimentally hypothesised for ZIF-4 systems.20Fig. 7b depicts local density histograms for ZIF-4 projected onto the three Cartesian axes. We can see that the local density stays more or less constant when projected onto the x axis, thus facilitating the connectivity exchange events that drive amorphization, as discussed above. Indeed, the porosity along this direction is more connected than in the other two, which show jumps in the local density that are associated with cage changes. We complement this analysis by adding information about the lower temperature simulations carried out at T = 540 K and T = 670 K which exhibit bond breaking and formation while preserving the original crystalline structures of ZIF-4 and ZIF-zni respectively. We associated each bond breaking event with a ligand position in the unit cell, in order to check if there are ligand sites that are more labile than others. We found that in the case of ZIF-4, the 32 ligand sites of the unit cell are divided as follows: 8 of them present a high stability, breaking at a rate of approximately once every 4 ps; 8 of them present the highest tendency to break (once every 2.5 ps), while the others exhibit an intermediate reactivity. In the inset of the top panel of Fig. 7 we show a plot of the xy plane of the unit cell where the ligands have been coloured according to their rate of bond breaking. We can observe that bonds oriented in the x direction are the most labile, while the ones pointing in the y or z directions are more stable, in agreement with our previous results. The origin of the difference in stability may be found in the participation of each ligand in different rings. The most stable bonds are those that are part of a four Zn membered ring, while the most labile are only part of six membered rings.
In the case of ZIF-zni at T = 670 K, the classification of the 128 ligand positions results in 32 members that are more stable than the others, each breaking their coordination bonds every 4.5 ps on average. The others present mean breaking times spanning an interval between 1.9 and 2.7 ps. In this case, members of four Zn membered rings present an intermediate stability. It is found that the most and least labile bonds have important projections in the z direction; this can be observed in the colouring in the inset of Fig. S8.†
4 Conclusions
We have studied the molecular mechanisms and thermodynamic properties of a series of phase transformations that link two crystalline polymorph ZIFs (ZIF-4 and ZIF-zni), with two disordered phases, a lower density, liquid-like one (ZIF_liq) and a higher density, amorphous solid (ZIF_a). To this end, we have modelled these states via a force field that incorporates reactivity in the coordination bonds. We validate our model by successfully comparing structural and mechanical properties computed from it with reference experimental and ab initio data. We have augmented our molecular dynamics method with a phase sorting algorithm based on a neural network that can assign Zn2+ centred environments to their parent state with high accuracy. The accuracy is quite astounding taking into account that the algorithm has only been fed structural features as inputs and that it can even distinguish between disordered phases.Our molecular dynamics simulations allowed us to determine thermodynamic state functions of the ZIF-4 → ZIF_a and ZIF-zni → ZIF_liq transitions as well as for ZIF_a → ZIF_liq via thermodynamic integration. Specially relevant are those state functions related to the transition between the two crystalline polymorphs that are difficult to measure experimentally. Our results are in good agreement with reference values, and those that were not previously measured can be rationalized in terms of the disorder and porosity of the different phases.
We have furthermore followed the amorphization of ZIF-4 and the melting of ZIF-zni processes and obtained mechanistic details at the microscopic level. We identified two stages in both processes. Density changes monotonically in both cases, as does the connectivity. These processes occur via changes in the identity of the first neighbour ligand moieties that are coordinatively bonded to the Zn2+ centres. Kinetics of the amorphization of ZIF-4 are faster in a preferential direction. We have rationalised this through the analysis of local densities projected onto the three Cartesian axes and the study of the lability of the coordination bonds.
This work sheds light on the mechanism of important phase transformations for materials that are excellent candidates for solving pressing environmental and industrial issues. More specifically, our results help better understand the process of generation of amorphous MOFs, which have been suggested to be key in bridging the gap between the research laboratory and real-world applications of these promising and versatile porous materials. We also hope that the methods that we developed and deployed are useful to other researchers in this and other fields to study the amorphization of other families of materials, or even more broadly to study other kinds of reactive processes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the European Union ERC Starting grant MAGNIFY, grant number 101042514. This work was granted access to the HPC resources of CINES under the allocation A0130911989 made by GENCI and to the HPC resources of the MeSU platform at Sorbonne-Université.References
- S. Horike, S. S. Nagarkar, T. Ogawa and S. Kitagawa, Angew. Chem., Int. Ed., 2020, 59, 6652–6664 CrossRef CAS PubMed.
- A. W. Thornton, K. E. Jelfs, K. Konstas, C. M. Doherty, A. J. Hill, A. K. Cheetham and T. D. Bennett, Chem. Commun., 2016, 52, 3750–3753 RSC.
- N. Ma and S. Horike, Chem. Rev., 2022, 122, 4163–4203 CrossRef CAS PubMed.
- J. Fonseca, T. Gong, L. Jiao and H.-L. Jiang, J. Mater. Chem. A, 2021, 9, 10562–10611 RSC.
- T. Zhang, J. Wang, W. Zhang, C. Yang, L. Zhang, W. Zhu, J. Sun, G. Li, T. Li and J. Wang, J. Mater. Chem. A, 2019, 7, 2845–2854 RSC.
- C. Orellana-Tavra, R. J. Marshall, E. F. Baxter, I. A. Lázaro, A. Tao, A. K. Cheetham, R. S. Forgan and D. Fairen-Jimenez, J. Mater. Chem. B, 2016, 4, 7697–7707 RSC.
- C. Orellana-Tavra, M. Köppen, A. Li, N. Stock and D. Fairen-Jimenez, ACS Appl. Mater. Interfaces, 2020, 12, 5633–5641 CrossRef CAS PubMed.
- D. F. Sava, M. A. Rodriguez, K. W. Chapman, P. J. Chupas, J. A. Greathouse, P. S. Crozier and T. M. Nenoff, J. Am. Chem. Soc., 2011, 133, 12398–12401 CrossRef CAS PubMed.
- K. W. Chapman, D. F. Sava, G. J. Halder, P. J. Chupas and T. M. Nenoff, J. Am. Chem. Soc., 2011, 133, 18583–18585 CrossRef CAS PubMed.
- B. Yu, J. Hou and J. Gong, Catal. Sci. Technol., 2017, 7, 5004–5010 RSC.
- Y. Duan, Z.-Y. Yu, S.-J. Hu, X.-S. Zheng, C.-T. Zhang, H.-H. Ding, B.-C. Hu, Q.-Q. Fu, Z.-L. Yu, X. Zheng, J.-F. Zhu, M.-R. Gao and S.-H. Yu, Angew. Chem., Int. Ed., 2019, 58, 15772–15777 CrossRef CAS PubMed.
- D. Bazer-Bachi, L. Assié, V. Lecocq, B. Harbuzaru and V. Falk, Powder Technol., 2014, 255, 52–59 CrossRef CAS.
- J. C. Tan, T. D. Bennett and A. K. Cheetham, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9938–9943 CrossRef CAS.
- G. N. Greaves, F. Meneau, A. Sapelkin, L. M. Colyer, I. ap Gwynn, S. Wade and G. Sankar, Nat. Mater., 2003, 2, 622–629 CrossRef CAS PubMed.
- I. Peral and J. Íñiguez, Phys. Rev. Lett., 2006, 97, 225502 CrossRef PubMed.
- T. D. Bennett, A. L. Goodwin, M. T. Dove, D. A. Keen, M. G. Tucker, E. R. Barney, A. K. Soper, E. G. Bithell, J.-C. Tan and A. K. Cheetham, Phys. Rev. Lett., 2010, 104, 115503 CrossRef PubMed.
- T. D. Bennett, D. A. Keen, J.-C. Tan, E. R. Barney, A. L. Goodwin and A. K. Cheetham, Angew. Chem., Int. Ed., 2011, 50, 3067–3071 CrossRef CAS PubMed.
- T. D. Bennett, P. Simoncic, S. A. Moggach, F. Gozzo, P. Macchi, D. A. Keen, J.-C. Tan and A. K. Cheetham, Chem. Commun., 2011, 47, 7983 RSC.
- T. D. Bennett, S. Cao, J. C. Tan, D. A. Keen, E. G. Bithell, P. J. Beldon, T. Friscic and A. K. Cheetham, J. Am. Chem. Soc., 2011, 133, 14546–14549 CrossRef CAS PubMed.
- R. N. Widmer, G. I. Lampronti, N. Casati, S. Farsang, T. D. Bennett and S. A. T. Redfern, Phys. Chem. Chem. Phys., 2019, 21, 12389–12395 RSC.
- J.-B. Weiß and S. Henke, Nat. Synth., 2023 DOI:10.1038/s44160-023-00425-0.
- N. Masciocchi, S. Bruni, E. Cariati, F. Cariati, S. Galli and A. Sironi, Inorg. Chem., 2001, 40, 5897–5905 CrossRef CAS PubMed.
- K. Ohara, J. Martí-Rujas, T. Haneda, M. Kawano, D. Hashizume, F. Izumi and M. Fujita, J. Am. Chem. Soc., 2009, 131, 3860–3861 CrossRef CAS PubMed.
- L. León-Alcaide, R. S. Christensen, D. A. Keen, J. L. Jordá, I. Brotons-Alcázar, A. Forment-Aliaga and G. M. Espallargas, J. Am. Chem. Soc., 2023, 145, 11258–11264 CrossRef PubMed.
- M. Hartmann, U. Böhme, M. Hovestadt and C. Paula, Langmuir, 2015, 31, 12382–12389 CrossRef CAS PubMed.
- M. Hovestadt, J. V. Schmitz, T. Weissenberger, F. Reif, M. Kaspereit, W. Schwieger and M. Hartmann, Chem. Ing. Tech., 2017, 89, 1374–1378 CrossRef CAS.
- K. S. Park, Z. Ni, A. P. Côté, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191 CrossRef CAS PubMed.
- R. N. Widmer, G. I. Lampronti, S. Chibani, C. W. Wilson, S. Anzellini, S. Farsang, A. K. Kleppe, N. P. M. Casati, S. G. MacLeod, S. A. T. Redfern, F.-X. Coudert and T. D. Bennett, J. Am. Chem. Soc., 2019, 141, 9330–9337 CrossRef CAS PubMed.
- T. D. Bennett, Y. Yue, P. Li, A. Qiao, H. Tao, N. G. Greaves, T. Richards, G. I. Lampronti, S. A. T. Redfern, F. Blanc, O. K. Farha, J. T. Hupp, A. K. Cheetham and D. A. Keen, J. Am. Chem. Soc., 2016, 138, 3484–3492 CrossRef CAS PubMed.
- E. O. R. Beake, M. T. Dove, A. E. Phillips, D. A. Keen, M. G. Tucker, A. L. Goodwin, T. D. Bennett and A. K. Cheetham, J. Phys.: Condens. Matter, 2013, 25, 395403 CrossRef CAS PubMed.
- T. D. Bennett, J.-C. Tan, Y. Yue, E. Baxter, C. Ducati, N. J. Terrill, H. H. M. Yeung, Z. Zhou, W. Chen, S. Henke, A. K. Cheetham and G. N. Greaves, Nat. Commun., 2015, 6, 8079 CrossRef CAS.
- E. F. Baxter, T. D. Bennett, C. Mellot-Draznieks, C. Gervais, F. Blanc and A. K. Cheetham, Phys. Chem. Chem. Phys., 2015, 17, 25191–25196 RSC.
- M. R. Ryder, T. D. Bennett, C. S. Kelley, M. D. Frogley, G. Cinque and J.-C. Tan, Chem. Commun., 2017, 53, 7041–7044 RSC.
- R. Gaillac, P. Pullumbi, K. A. Beyer, K. W. Chapman, D. A. Keen, T. D. Bennett and F.-X. Coudert, Nat. Mater., 2017, 16, 1149–1154 CrossRef CAS PubMed.
- R. Gaillac, P. Pullumbi and F.-X. Coudert, J. Phys. Chem. C, 2018, 122, 6730–6736 CrossRef CAS.
- Y. Yang, Y. K. Shin, S. Li, T. D. Bennett, A. C. T. van Duin and J. C. Mauro, J. Phys. Chem. B, 2018, 122, 9616–9624 CrossRef CAS PubMed.
- N. Castel and F.-X. Coudert, J. Phys. Chem. C, 2022, 126, 19532–19541 CrossRef CAS.
- S. R. G. Balestra and R. Semino, J. Chem. Phys., 2022, 157, 184502 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- N. Castel and F.-X. Coudert, Chem. Mater., 2023, 35, 4038–4047 CrossRef CAS.
- A. F. Sapnik, C. Sun, J. E. M. Laulainen, D. N. Johnstone, R. Brydson, T. Johnson, P. A. Midgley, T. D. Bennett and S. M. Collins, Commun. Chem., 2023, 6, 92 CrossRef CAS PubMed.
- N. C. Karayiannis, K. Foteinopoulou and M. Laso, J. Chem. Phys., 2009, 130, 074704 CrossRef PubMed.
- F. Pietrucci and R. Martoňák, J. Chem. Phys., 2015, 142, 104704 CrossRef PubMed.
- M. A. Caro, A. Aarva, V. L. Deringer, G. Csányi and T. Laurila, Chem. Mater., 2018, 30, 7446–7455 CrossRef CAS PubMed.
- K. Swanson, S. Trivedi, J. Lequieu, K. Swanson and R. Kondor, Soft Matter, 2020, 16, 435–446 RSC.
- S. Banik, D. Dhabal, H. Chan, S. Manna, M. Cherukara, V. Molinero and S. K. R. S. Sankaranarayanan, npj Comput. Mater., 2023, 9, 23 CrossRef.
- J. Rogal, E. Schneider and M. E. Tuckerman, Phys. Rev. Lett., 2019, 123, 245701 CrossRef CAS.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef CAS.
- R Core Team, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, 2022 Search PubMed.
- S. S. Schoenholz, E. D. Cubuk, D. M. Sussman, E. Kaxiras and A. J. Liu, Nat. Phys., 2016, 12, 469–471 Search PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- K. Govers, S. Lemehov, M. Hou and M. Verwerft, J. Nucl. Mater., 2008, 376, 66–77 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta07361k |
| This journal is © The Royal Society of Chemistry 2024 |