Open Access Article
Open Access ArticleReview and assessment of models for predicting biocrude yields from hydrothermal liquefaction of biomass†
Peter M.
Guirguis
 ,
Mahadevan Subramanya
Seshasayee
,
Bita
Motavaf
and
Phillip E.
Savage
,
Mahadevan Subramanya
Seshasayee
,
Bita
Motavaf
and
Phillip E.
Savage
 *
*
Chemical Engineering Department, Pennsylvania State University, 121D CBEB Building, University Park, PA 16802, USA. E-mail: psavage@psu.edu
First published on 6th March 2024
Abstract
Hydrothermal liquefaction (HTL) is a thermochemical process that converts biomass into a renewable, heavy oil that can be upgraded and refined to make liquid fuels. Quantitative models for correlating and then predicting yields of crude bio-oil from HTL of biomass date back to 2011. The literature provides 18 variations of component additivity models and another 24 different lumped kinetic models. Herein, we review the progress, development, and implementation of both types of models and assess their abilities to predict the biocrude yields from an extensive set of experimental data published for HTL of a range of different biomass feedstocks. We identify two component additivity models that provided the lowest mean absolute residuals and the kinetics model that best predicted the published biocrude yields. There is no single model that predicts well the biocrude yields for HTL of all the different types of biomass feedstocks. We offer guidance regarding which model to choose for any specific feedstock. This review and assessment also identifies opportunities for improving the quantitative modeling of HTL outcomes.
Sustainability spotlightThis article focuses on hydrothermal liquefaction, a proven method for converting biomass to biocrude oil. This comprehensive review and assessment of models for biocrude production critically examines the pathways and ability to predict biocrude yields. By spotlighting the strengths and limitations of existing models, this review paves the way for development of even better models for describing this promising technology for producing renewable liquid fuels. This research aligns with the ethos of RSC Sustainability, providing a roadmap for assessing and optimizing biomass-to-biocrude models. |
1 Introduction
Hydrothermal liquefaction (HTL) uses hot, compressed water (≈250–450 °C) in the liquid or supercritical state to convert biomass into a crude bio-oil. The many prior reviews1–15 of HTL and hydrothermal chemistry show that water provides a favorable environment11 (low dielectric constant, high ion product) for organic chemical reactions12 that concentrate the chemical energy resident in the original biomass into the molecules in the oil phase. However, as is typical of complex chemical reaction networks, competing reactions also produce molecules that appear in gas, solid, and aqueous phases after reaction. Gasification and cracking reactions lead to gas formation. Hydration and amination reactions increase the polarity of molecules, which along with the initial depolymerization of heteroatom-rich biopolymers, leads to formation of aqueous-phase products.1,7 Addition reactions among the organic molecules form heavier molecules in the oil fraction and eventually solid char.2Kinetic models based on a set of governing reaction pathways facilitate investigation of the rates of competing pathways in HTL and identification of optimal feedstock characteristics16 and reaction conditions17 for specific desired outcomes. Kinetic models have been developed for HTL and used to first correlate and then predict yields of different product fractions for different feedstocks at different conditions. Simpler algebraic models have also been developed to correlate and predict HTL outcomes. These typically calculate yields of biocrude from HTL at a single specific set of reaction conditions for feedstocks with different biochemical compositions (e.g., different relative amounts of lipids, protein, polysaccharide). Such models have been termed component additivity models as they sum together expected contributions from HTL of each of the different biochemical components individually to estimate oil production from HTL of a more complex biomass feedstock.
This review and assessment highlights the state of the art in HTL modeling and chronicles the progress made to this end. We assess the abilities of both component additivity models and kinetic models to predict experimental biocrude yields compiled from literature for HTL of biomass such as microalgae, food waste, sewage sludge, and lignocellulosic materials. We note that machine learning models have recently emerged for HTL,18–22 but these are far fewer and less developed than the kinetics and component additivity modes, so we do not include them in the present review and assessment. Additionally, we confine the review to the very large number of HTL experiments that used dichloromethane to recover the crude bio-oil. A few experimental studies used other solvents, and these are omitted unless noteworthy in some way (e.g., historical context).
Though there have been many previous reviews1–15 on HTL of biomass, none focus on the mathematical models that predict product yields from HTL. Only Yang et al.8 and Kumar9 include these topics in their reviews and they offer just brief discussions of the various models. They provide no comparisons or assessments of the different models. There are also no published comparisons of the effectiveness of component additivity models vs. reaction engineering models for predicting HTL outcomes. This article, which includes an assessment of how well different component additivity models and different kinetics models predict the published data, fills these gaps. Additionally, we identify research topics that would provide opportunities for advancing the field by developing improved models.
2 Assessment methods
We used published models with the parameters as provided to predict published experimental biocrude yields from HTL of different biomass feedstocks at the reaction conditions and with the feedstock composition used in each study. A spreadsheet with these experimental data is available online in the ESI.† These model predictions and comparisons with literature data were automated using python code. The ESI† provides more details.We calculate several measures of how well a given model predicts the data set based on the set of individual residuals (difference between model prediction and experimental result). The ESI elaborates on these metrics in eqn (S1)–(S4),† and they include the median residual (error), Med[ε], the mean absolute residual, 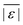 , the median absolute error, Med[|ε|], and the mean absolute percent error, MAPE. We also report the fraction of the experimental biocrude yields that each model predicts to within 5 wt% and 10 wt% of the published yields. Finally, we report the percentage of predictions with greater than 100% relative error.
, the median absolute error, Med[|ε|], and the mean absolute percent error, MAPE. We also report the fraction of the experimental biocrude yields that each model predicts to within 5 wt% and 10 wt% of the published yields. Finally, we report the percentage of predictions with greater than 100% relative error.
3 Component additivity models
We define a component additivity model as an algebraic equation that provides an outcome for HTL of some feedstock based on the relative amounts of the different components (e.g., cellulose, protein) in the feedstock. The outcome of interest in this review is the yield of biocrude. Some component additivity models include process variables (time, temperature) along with the component mass fractions. An algebraic equation that incorporates process variables but has no dependence on feedstock composition would not qualify as a component additivity model. Such equations are excluded from this review. In Section 3.1, we provide an overview of all the component additivity models including chosen parameters and conditions used to collect the data for parameter estimation. In Section 3.2, we assess predictions from the models for biocrude yields in the literature.3.1 Review of component additivity models for HTL of biomass
Component additivity models typically provide the yield of biocrude expected from HTL of a biomass feedstock with a known biochemical composition (e.g., lipid, protein, polysaccharide, lignin content) at a specific set of HTL conditions (time, temperature). The model is often a simple linear equation that estimates the biocrude yield expected from HTL of whole biomass or a mixture of components based on the yields associated with HTL of each biochemical component alone at the specified conditions. Component additivity models can also include second-order terms that account for synergistic or antagonistic interactions between two different biochemical components, as well as more complicated expressions. Table S1† shows the published component additivity models for calculating biocrude yield from HTL of biomass.| Biocrude yield (wt%) = a1Xcarb + a2Xprot + a3Xlip | (1) |
The oil yields from HTL experiments with model biochemical components were used to determine the ai coefficients. The model was then used to predict the experimental oil yields reported in the same publication from HTL of microalgae. The model predicts well the oil yields from HTL (350 °C and 60 min) of microalgae that had low (<10 wt%) carbohydrate content, but more poorly for microalgae with high (>20 wt%) carbohydrate content. Since this model did not account for any potential interactions between biochemical components, it missed the effect of Maillard reactions between proteins and carbohydrates that can increase bio-oil yields by providing a new pathway to oil-phase molecules.24 Omitting this feature likely contributed to the inaccuracies in predicting biocrude yields from HTL of protein-containing algae with high carbohydrate content.
Leow et al.25 and Shakya et al.16 adopted the approach of Biller and Ross23 Leow et al.25 obtained the model parameters by using biocrude yields from HTL (300 °C, 30 min) of different batches of the same strain of microalgae with known biochemical content (rather than model compounds). A single microalga, Nannochloropsis, was cultivated under different conditions to obtain biomass feedstocks with protein, carbohydrate, and lipid contents that varied from 17–58 wt%, 11–22 wt%, and 23–59 wt% respectively. Leow et al.25 used nine different algae strains with a wider range of protein (7–62 wt%), carbohydrate (8–54 wt%), and lipid (13–55 wt%) and conducted HTL at 280 °C and 320 °C for 30 min.
Wagner et al.26 used the component additivity model in eqn (1) with data from HTL or model compounds (oil, soy protein, and corn flour) to correlate biocrude yields from HTL at 300, 320, 340 and 360 °C. The model coefficients are closer to those determined by Biller and Ross,23 who also used individual model biochemical components, than those of Leow et al.,25 who used whole microalgal biomass exclusively to determine model parameters.
Li et al.27 advanced the field by expanding the number and types of HTL outcomes that could be correlated and then predicted using a linear component additivity model. They developed correlations for solid, aqueous, and gas phase yields, biocrude higher heating value (HHV), elemental composition, energy recovery, and aqueous phase total organic carbon and total nitrogen. The authors used data from HTL of 24 batches of microalgae with varied biochemical compositions to regress the parameters in the component additivity models. Their model indicates that HTL of lipids at 300 °C for 30 min would produce biocrude alone, HTL of proteins alone would produce no solids, and HTL of carbohydrates alone would produce no aqueous-phase products. These model outcomes are not consistent with literature reports of significant aqueous-phase yields from HTL of carbohydrates such as starch and cellulose,28 of HTL of lipids contributing to gas and aqueous-phase products29 and of HTL of protein contributing to biochar.30
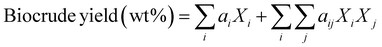 | (2) |
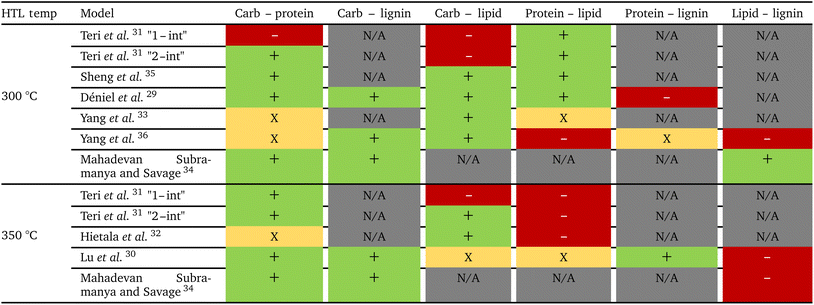
Hietala et al.,32Yang et al.,33 Lu et al.,30 and Déniel et al.29 subsequently published models with second-order interactions. Hietala et al.32 developed a model using data from HTL of 1-, 2-, 4-, and 6-species cultures of different microalgae, which provided an expanded range of carbohydrate, lipid, and protein contents. The authors also divided the lipid fraction into saturated, monounsaturated, and polyunsaturated fatty acids in the model. Interactions among the types of fatty acids had an influence on the oil yield. A 5 wt% increase in monounsaturated fatty acids with a corresponding decrease in polyunsaturated fatty acids decreases the oil yield by 8 wt%. Models were also parameterized to predict the H/C ratio, N content, O content, and heating value of the bio-oil. Déniel et al.29 were the first to include lignin in a component additivity model, and they also included interactions of lignin with other biochemical components.
Lu et al.30 and Yang et al.33 were the first to include hemicellulose in a component additivity model, which broadened the applicability of such models to a wider range of feedstocks. Lu et al.30 were the first to report the synergistic interactions (i.e., increased oil yield) between lignin and cellulose or hemicellulose and antagonistic interactions (i.e., decreased oil yield) between lignin and lipids for HTL at 350 °C. Yang et al.33 reported that celluloses and hemicelluloses (xylose) have synergistic interactions with lipids during HTL at 300 °C.
Table 1 summarizes the interactions reported in component additivity models for HTL of different pairs of biochemical components of biomass. When there are measurable interactions, they are synergistic for carbohydrate with protein and, except for Teri et al.,31 for carbohydrate with lipid. Protein–lipid interactions, when present, are synergistic for HTL at 300 °C and antagonistic at 350 °C. Gasification of long-chain fatty amides (products from interactions between lipid-derived and protein-derived molecules) at high temperatures would cause this shift from synergy at milder temperatures to antagonism at higher temperatures. When present, interactions between carbohydrates and proteins with lignin are synergistic at both temperatures. Lipids typically show antagonistic interactions with lignin except for the model of Mahadevan Subramanya and Savage34 at 300 °C.
Sheng et al.35 modified the way binary interactions had been modeled by dividing the second-order term (aijXiXj) by the absolute difference in mass fraction for the two components as shown in eqn (3). They argued that the denominator term arose naturally from the governing reaction engineering equations, but their derivation was incorrect. The ESI† provides more details. This modified form for the interaction terms does not have any physical meaning.
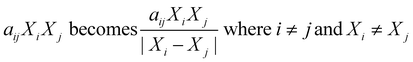 | (3) |
Yang et al.36 were the first to include temperature, time, and biomass loading as variables in a component additivity model. Three different temperatures, time, and biomass loading combinations were used in the experiments. An ANOVA model was then used to determine the algebraic equation that best described the data. This approach proved successful in predicting biocrude yields to within 10 wt%, but one can ask whether it is meaningful to include temperature, time, or biomass loading as terms in a component additivity model. Doing so destroys the physical underpinnings of such a model and leads to an expression that is not connected to any fundamental chemical principles. An alternate approach would be to make the ai and aij parameters in a component additivity model functions of temperature, time, or biomass loading. These variables are known to influence biocrude yields from HTL of individual biochemical components, so allowing them to influence the values of the ai and aij parameters would be a natural way of incorporating that influence.
In 2021, Mahadevan Subramanya and Savage34 published experimental results from HTL of multiple model polysaccharides, which allowed inclusion of separate terms for distinct polysaccharides (e.g., starch and cellulose) in a component additivity model. The experiments showed that HTL of cellulose produces less bio-oil than starch under all temperatures examined. This study was the first to extend component additivity models for biomass to supercritical temperatures (up to 425 °C). A final novel feature from this study was finding the second-order interaction coefficient (aij in eqn (2)) for cellulose and proteins for HTL at 300 °C and 30 min was a function of feedstock composition. The authors introduced the expression for acell,P shown in eqn (4) to account for this composition dependence.
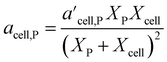 | (4) |
Yan et al.,37 in pioneering work, used ReaxFF molecular dynamics (MD) to simulate HTL of biopolymers and advance molecular-level understanding of the same. The researchers examined “cellulose” (modeled as a long unbranched chain of glucose), “hemicellulose” (modeled as long branched chain of glucose (even though hemicellulose contains C5 sugars)), lipids (triglycerides and fatty acids), and “lignin” (structure specified from Adler38) and did work at different HTL temperatures. The model is limited to lignocellulosic biomass by its exclusion of protein. Following earlier work,39 they correlated the very high simulation temperatures to more physically reasonable temperatures that would be used for HTL in practice. The simulations included binary, ternary, and quaternary combinations of the biopolymers. They identified bonds most likely to break in the biomolecules, interactions that can occur, and products from HTL. C4 molecules with oxygen and C5–C31 molecules with fewer than three oxygen atoms were taken to be biocrude. The authors used the simulation results to posit a component additivity model that included component interactions and temperature.
3.2 Assessment of component additivity models for HTL of biomass
In this section, we assess the model predictions for biocrude yields from HTL of two different classes of biomass feedstocks at different temperatures and times. To avoid over-extrapolating any of the models, we tested their predictive ability only near the temperatures and times used in the HTL experiments that led to the model parameters. For example, Biller and Ross23 did experiments at 350 °C for 60 min to get their model parameters. We would then test this model over a range of times around 60 min and temperatures around 350 °C. Teri et al.31 and Mahadevan Subramanya and Savage34 show there is a region of HTL reaction severity surrounding a specific time and temperature wherein the component additivity models are able to give reliable predictions. We limit the assessment to HTL experimental data taken with this region. Details are provided in the ESI.†We begin assessing the component additivity models in Section 3.2.1 by first using them to predict published biocrude yields from HTL of biomass feedstocks that contained all the same biochemical components used to parameterize the model. For example, the model from Biller and Ross23 applies to biomass with carbohydrates, protein, and lipids. When assessing that model, we use biocrude yields solely from HTL studies of biomass that contained carbohydrates, protein, and lipids (all three components), and no other biochemical components.
In Section 3.2.2, we test the ability of the component additivity models to predict biocrude yields from HTL of biomass feedstocks that contain any of the components used to develop the model. We relax the requirement above that all components must be in the biomass feedstock. One can reasonably expect the predictive abilities of the models to be poorer in this assessment than in the previous section, as that assessment used biomass that was used to develop the models. Even so, the present assessment is instructive as it provides information about the robustness and generalizability of each of the component additivity models. For example, in the prior assessment, if a model was developed using biomass that contained protein, lipids, and polysaccharides, it was tested only on literature data from HTL of biomass that contained all three components. In the present assessment, we also include literature data from HTL of biomass that contain a subset of the components (e.g., HTL of a model polysaccharide alone).
Some of the component additivity models separated the contributions to biocrude yield from hemicellulose, cellulose, and/or starch. However, in many cases the experimental data used in this assessment are from HTL of biomass with only the total polysaccharide content given. No breakdown between cellulose, hemicellulose, and/or starch is available. Since we do not know the relative amounts of the different polysaccharides for these feedstocks, we assign the total polysaccharide content, which is known, to one of the polysaccharide components in the model, with the other polysaccharide component(s) being zero. We then repeat this assessment with another polysaccharide component(s) being assigned the total polysaccharide content in the biomass. The results from these assessments then provide boundaries for the predicted biocrude yields. Results from models with multiple polysaccharides are shown herein for the case wherein all polysaccharides are treated as hemicellulose, or as starch, if hemicellulose is not part of the model. The ESI† provides a summary of statistics for other cases.
Another detail related to this section of the assessment is that the model of Hietala et al.32 distinguishes between saturated, monounsaturated, and polyunsaturated fatty acids (PUFA). The ratio of the three classes of fatty acids influences model predictions. When assessing this model with literature data for HTL of biomass that did not provide this fatty acid breakdown, we assumed a split of 39.4%, 15.8%, and 44.8% for SAFA, MUFA, and PUFA, respectively, based on the averages from Hietala et al.32
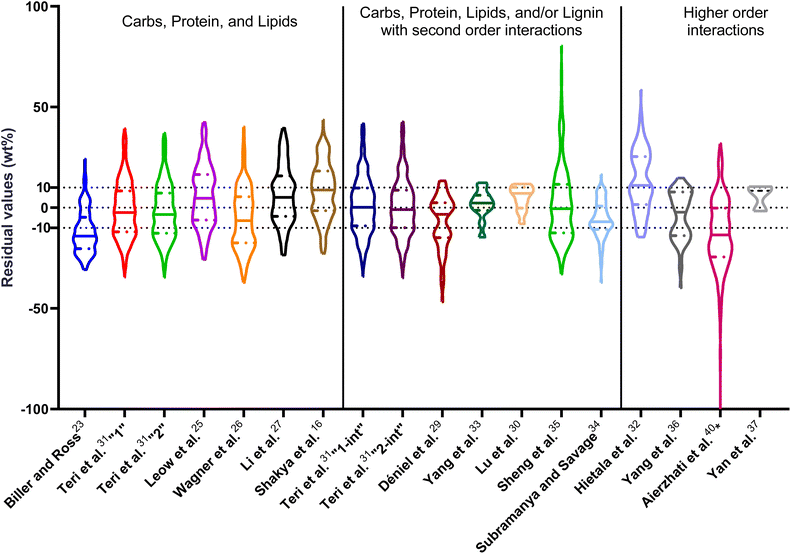 | ||
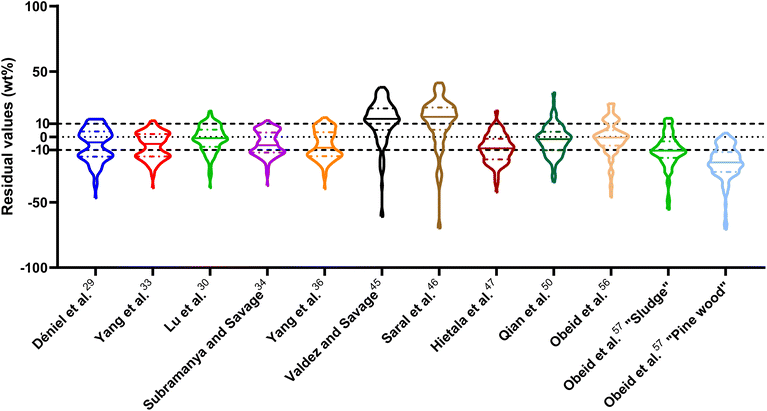
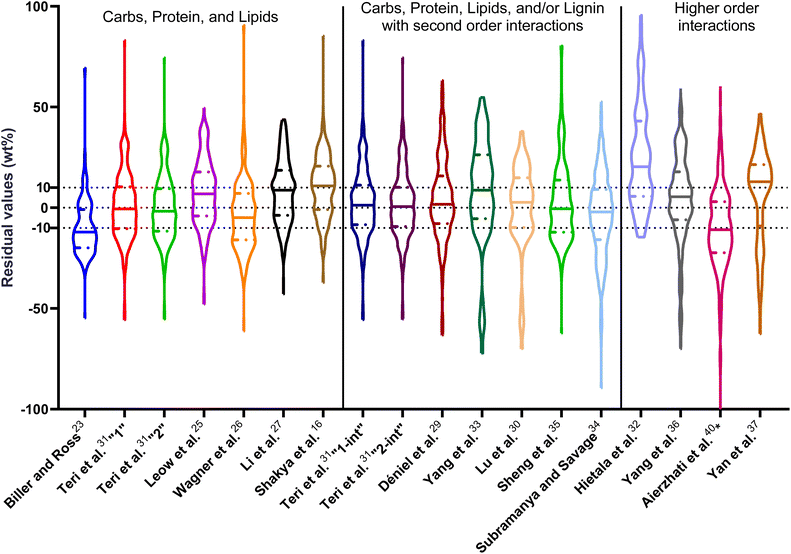
| Fig. 1 Distribution of residuals with median (solid line) and quartiles (dashed line) for biocrude yields predicted by component additivity models for HTL of the intended biomass feedstock near the intended HTL conditions. *Residuals from Aierzhati et al.40 reached −274 wt%. | ||
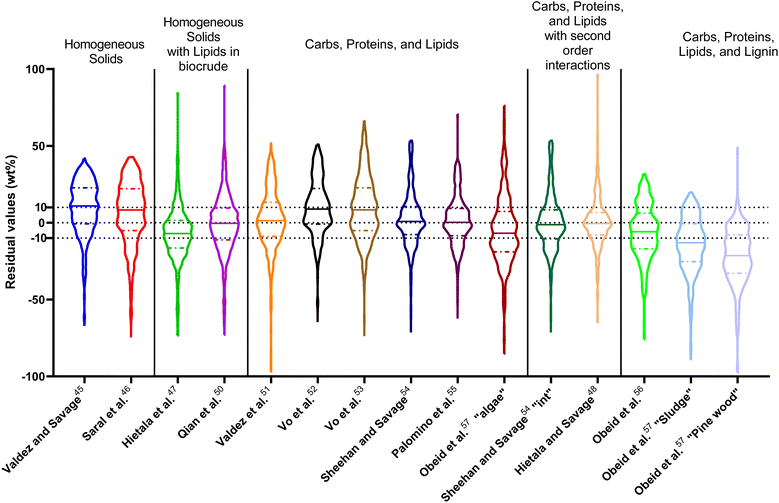
The first set of models farthest to the left in Fig. 1 is the set entitled, “Carbs, Proteins, and Lipids”. These models have in view HTL of biomass such as microalgae or food waste, which have only polysaccharides, proteins, and lipids, and they use a simple linear combination of first-order effects (eqn (1)). These models tend to be biased as the median values (−14.1, −2.4, −3.4, 4.7, −6.4, 5.1, and 8.8 wt%, in the order presented in the graph) are not zero. The mean and median of the absolute values of the residuals, 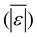 and Med[|ε|], range from 11.4–14.1 wt% and 10.0–14.3 wt%, respectively (Table S2†). The model by Li et al.27 appears to give the best predictions based on lowest Med[|ε|] and highest percent of predictions within 5 wt% and 10 wt% for this class of models and these types of feedstocks.
and Med[|ε|], range from 11.4–14.1 wt% and 10.0–14.3 wt%, respectively (Table S2†). The model by Li et al.27 appears to give the best predictions based on lowest Med[|ε|] and highest percent of predictions within 5 wt% and 10 wt% for this class of models and these types of feedstocks.
The next set of models in Fig. 1 form a group entitled, “carbs, proteins, lipids, and/or lignin, with second-order interactions”. These models allow for second-order interactions between different components (i.e., 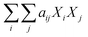 in eqn (2)). This group includes the least biased models, as the median residuals were 0.2, −0.9, −3.3, 2.3, 7.1, −0.5, and −6.9 wt%, in the order presented in Fig. 1. This group also has lower mean absolute residuals and median absolute residuals than did the previous group.
in eqn (2)). This group includes the least biased models, as the median residuals were 0.2, −0.9, −3.3, 2.3, 7.1, −0.5, and −6.9 wt%, in the order presented in Fig. 1. This group also has lower mean absolute residuals and median absolute residuals than did the previous group.
The final and right-most set of models in Fig. 1 is entitled “higher order interactions”, which can include self-interactions (terms with X2). Predictions of biocrude yields from these models are worse than those from the previous set of models that had second-order interactions. The mean absolute residuals ranged from 6.9 to 17.9 wt%. The median absolute residuals ranged from 8.4 to 16.3 wt%. The residuals from the model of Aierzhati et al.40 exceeded 100 wt% at times. This outcome is physically impossible, but it arises because the model terms including time and temperature allow prediction of biocrude yields exceeding 100 wt%. This mathematical feature of the model likely limits its utility to conditions near those where the parameters were determined.
The lowest mean absolute residuals from the models in Fig. 1 are 5.7 wt% from Yang et al.33 followed by 6.9 wt% from both Lu et al.30 and Yan et al.37 However, the assessment of all three models was limited to only a small dataset (12 published biocrude yields for Yang et al.33 and Lu et al.30 and 3 published biocrude yields for Yan et al.37). For Yang et al.,33 the low HTL temperature (290 °C) and short time (10 min) employed limited the model assessment to fewer published biocrude yields. For Lu et al.,30 the small number of published HTL studies that including all the components, polysaccharides, lipids, proteins, and lignin, is limiting. The model from Yan et al.37 can be used to predict only three published biocrude yields in the present assessment, as it can handle biomass that contained carbohydrates, lipids, and lignin but nothing else. These three predictions are for HTL of mixtures of model compounds and not whole biomass.
For models assessed against more than 100 published biocrude yields, the two by Teri et al.31 labeled “1-int” and “2-int” have the lowest 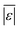 (11.2 wt%). The model from Teri et al.31 labeled “1-int” also has the highest percentage (27.5%) of biocrude yields predicted within 5 wt% while the model labeled “2-int” has the highest percentage (53.8%) of biocrude yields predicted within 10 wt% of the experimental value. Of all the models, the one proposed by Aierzhati et al.40 could be assessed against the largest number (519) of published biocrude yields. The model uses time and temperature as variables in the model, and it can be assessed for HTL from 280 to 360 °C and from 10 to 60 min. The models provided by Teri et al.31 could be assessed over the second-largest number of biocrude yields (465), followed by the model from Wagner et al.26 at 314. These latter two studies provide models for two and four distinct time–temperature combinations, respectively, thereby allowing assessment over a larger number of published studies. Considering the models in chronological order of publication does not show any trend of increasing accuracy over time.
(11.2 wt%). The model from Teri et al.31 labeled “1-int” also has the highest percentage (27.5%) of biocrude yields predicted within 5 wt% while the model labeled “2-int” has the highest percentage (53.8%) of biocrude yields predicted within 10 wt% of the experimental value. Of all the models, the one proposed by Aierzhati et al.40 could be assessed against the largest number (519) of published biocrude yields. The model uses time and temperature as variables in the model, and it can be assessed for HTL from 280 to 360 °C and from 10 to 60 min. The models provided by Teri et al.31 could be assessed over the second-largest number of biocrude yields (465), followed by the model from Wagner et al.26 at 314. These latter two studies provide models for two and four distinct time–temperature combinations, respectively, thereby allowing assessment over a larger number of published studies. Considering the models in chronological order of publication does not show any trend of increasing accuracy over time.
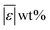 , and a greater percentage of biocrude yields predicted to within ±5 wt% and ±10 wt% than do the models without interactions and the models that include “higher order interactions”. The two models from Teri et al.31 labeled “1-int” and “2-int” have the lowest mean (12.6 and 12.5 wt%) and median (9.6 and 9.7 wt%) absolute residuals. Moreover, ≈26% of their residuals are within 5 wt% of the experimental biocrude yields and ≈52% are within 10 wt% (see Table S3†). These percentages of predictions within 5 wt% and 10 wt% are the highest of all the component additivity models assessed herein. Based upon the metrics noted above, the two models from Teri et al.31 that include interactions give the best predictions of experimental biocrude yields. It is worth noting that models from Teri et al.31 including interaction terms (labeled 1-int and 2-int) outperform the models excluding interaction terms (labeled 1 and 2). The authors had drawn the opposite conclusion in their work, perhaps because they considered only a small number of biomass feedstocks and did not have the advantage of the large data set that now exists for HTL of diverse biomass materials.
, and a greater percentage of biocrude yields predicted to within ±5 wt% and ±10 wt% than do the models without interactions and the models that include “higher order interactions”. The two models from Teri et al.31 labeled “1-int” and “2-int” have the lowest mean (12.6 and 12.5 wt%) and median (9.6 and 9.7 wt%) absolute residuals. Moreover, ≈26% of their residuals are within 5 wt% of the experimental biocrude yields and ≈52% are within 10 wt% (see Table S3†). These percentages of predictions within 5 wt% and 10 wt% are the highest of all the component additivity models assessed herein. Based upon the metrics noted above, the two models from Teri et al.31 that include interactions give the best predictions of experimental biocrude yields. It is worth noting that models from Teri et al.31 including interaction terms (labeled 1-int and 2-int) outperform the models excluding interaction terms (labeled 1 and 2). The authors had drawn the opposite conclusion in their work, perhaps because they considered only a small number of biomass feedstocks and did not have the advantage of the large data set that now exists for HTL of diverse biomass materials.
 | ||
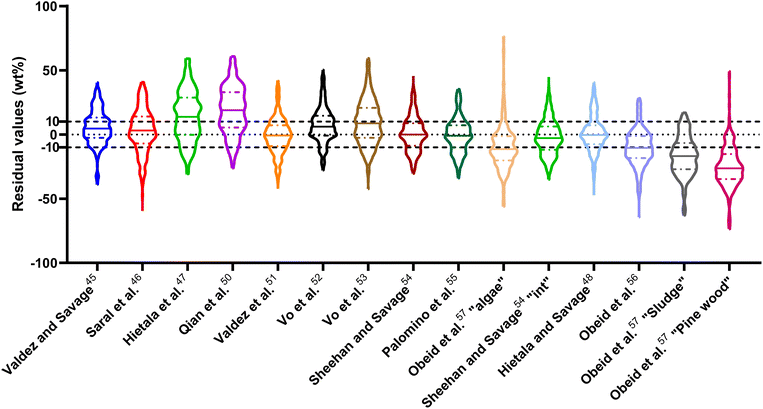
| Fig. 2 Distribution of residuals with median (solid line) and quartiles (dashed line) for biocrude yields predicted by component additivity models for HTL of all relevant biomass feedstocks and HTL conditions. *Residuals for Aierzhati et al.40 extend to −274 wt%. | ||
The ESI† provides results from a final assessment of these models for predicting biocrude yields from HTL of microalgae. This biomass feedstock has been used frequently in HTL experiments and the data set had 530 experimental biocrude yields. The trends noted earlier in this section for HTL of the intended biomass appear again when examining the microalgal dataset, but with less variation and fewer outliers. The model from Li et al.,27 which was parameterized using data from HTL of microalgae, makes the best predictions in this section. The results appear in Fig. S1 and Table S4.†
4 Kinetic models
Kinetic models are built upon the reaction pathways that occur during the chemical conversion being modeled. The major features of these pathways are generally known for HTL of most types of biomass.7,41 Initially, the biomass (typically a solid) undergoes hydrolysis and thermolysis and the proteins, lipids, carbohydrates, and lignin break down into polypeptides, oligosaccharides, fatty acids, and phenol derivatives. These intermediates further hydrolyze to their respective monomeric units (e.g., sugars, amino acids). The monomers then undergo rearrangements, coupling reactions, dehydration, deamination, and decarboxylation to form small molecules that are distributed among the aqueous, oil, and gas phases. Saccharides dehydrate to form furans, furfurals, cyclopentanones, and furanones, and then undergo aldol condensation to form single-ring aromatics. Single-ring aromatics and fatty acids can oligomerize to form solids. Peptides can undergo hydrolysis to form amines in the biocrude phase and deamination to form water-soluble organic acids. Fatty acids decarboxylate to form alkanes and alkenes. Denitrogenation and decarboxylation of protein and carbohydrates cause the formation of gases such as NH3 and CO2. Maillard reactions form N-containing heterocyclic compounds, aldols, and high molecular weight compounds.HTL chemistry is complex and there can be more than 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 individual molecules in the biocrude alone.42 This complexity, along with the chemical diversity in the biochemical components of biomass, makes it difficult to model the reactions at the level of elementary reaction steps (e.g., a microkinetic model). Rather, researchers have developed kinetic models where the numerous reaction products are lumped into a small number of different classes based on their solubilities. For instance, models would account for transformations between oil-phase, aqueous-phase, gas-phase, and solid-phase product fractions. See Table S5† for a summary of the reaction networks10 that have been proposed for HTL of biomass. Lumped kinetic models have long been used by the petroleum and chemical processing industry to describe complex reacting systems with many different molecular species and many different reactions connecting them.43
000 individual molecules in the biocrude alone.42 This complexity, along with the chemical diversity in the biochemical components of biomass, makes it difficult to model the reactions at the level of elementary reaction steps (e.g., a microkinetic model). Rather, researchers have developed kinetic models where the numerous reaction products are lumped into a small number of different classes based on their solubilities. For instance, models would account for transformations between oil-phase, aqueous-phase, gas-phase, and solid-phase product fractions. See Table S5† for a summary of the reaction networks10 that have been proposed for HTL of biomass. Lumped kinetic models have long been used by the petroleum and chemical processing industry to describe complex reacting systems with many different molecular species and many different reactions connecting them.43
This section reviews the kinetics models that have been developed for HTL of biomass and then assesses how well each predicts many published biocrude yields from HTL experiments. This review and assessment provide guidance regarding the development of better kinetics models for HTL as well as guidance for understanding the level of confidence to have in predictions from a given model.
4.1 Review of kinetic models for HTL of biomass
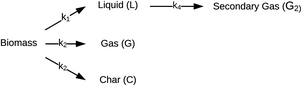 | ||
| Fig. 3 Reaction network for HTL proposed by Zhang et al.44 | ||
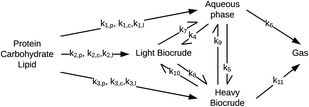
Valdez and Savage45 presented the first kinetic model for HTL of biomass that defined biocrude in the conventional manner (as the dichloromethane-soluble material recovered after the reaction). The authors subsequently used hexane extraction to divide the biocrude into heavy (hexane-insoluble) and light (hexane-soluble) fractions. Rather than presuming what reaction paths were active during HTL, these investigators did HTL experiments with the original algal biomass and then also with each of the product fractions recovered from HTL of the algae. These experiments revealed which product fractions were formed from algae and which could be formed from each of the product fractions via subsequent reactions. Fig. 4 shows the network they deduced.
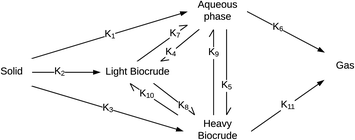 | ||
| Fig. 4 Reaction network for HTL of microalgae developed by Valdez and Savage.45 | ||
The algal solids decompose to give light oil, heavy oil, and aqueous phase products. These three primary product fractions all have reversible interconversion pathways amongst themselves. The latter two also have a gasification pathway. Experimental data for the yields of different production fractions from HTL of algae over a range of temperatures and times were used to determine the Arrhenius parameters for each rate constant in the model. All reactions were taken to be pseudo-first order. Saral et al.46 use the reaction network from Fig. 4 for HTL of Spirulina platensis but combine the light and heavy fractions into a single biocrude product fraction.
Fig. 5 shows the relative rates within the network at two different times. At shorter times (≈5 min), the fastest reactions involve algal biomass solids degrading into aqueous-phase products and heavy biocrude and molecules in the heavy biocrude moving into the aqueous-phase products. After 20 min, the biomass has been decomposed so those primary reactions are much slower. The fastest reactions involve repartitioning of molecules within the light and heavy biocrudes and the aqueous-phase products.
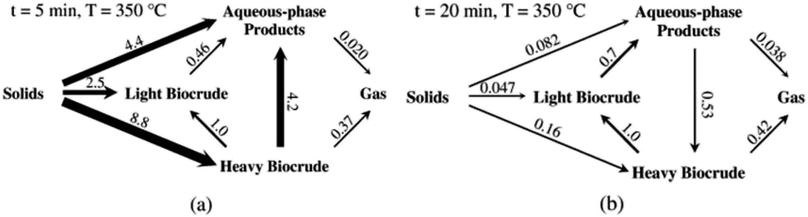 | ||
| Fig. 5 The relative rates for the reaction paths at (a) short and (b) long times during HTL of microalgae. Reproduced from Valdez and Savage45 with permission from Algal Research Journal, copyright 2013. | ||
Hietala et al.47 were the first to provide a kinetic model and reaction network (Fig. 6) that faithfully described outcomes from both isothermal and fast HTL. The latter technique uses rapid heating and non-isothermal processing, and it converts microalgae into biocrude in just tens of seconds.42
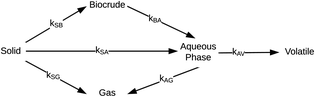 | ||
| Fig. 6 Reaction network for HTL of microalgae developed by Hietala et al.47 | ||
The authors modified reaction pathways in earlier studies to better represent the experimental product fraction yields, especially at shorter HTL times. Their network included a direct pathway from biomass solids to gas-phase products and a pathway to “volatiles” from the aqueous-phase products. Hietala et al.47 were the first to distinguish between permanent gas products and “volatiles”, which were low-boiling aqueous-phase products lost to evaporation as this product fraction was dried to remove the water. The model was developed for HTL of Nannochloropsis sp., and a key contribution was modeling reaction times as short as 10 s along with longer times up to 45 min. Fig. 7 shows the model calculations faithfully reproduced the main trends in the experimental product yields (note the log scale on the x-axis).
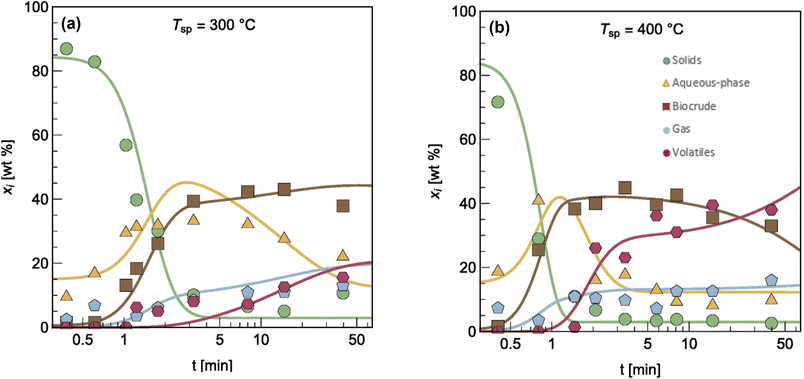 | ||
| Fig. 7 Model calculations and experimental product yields for HTL of microalgae. Reprinted in part from Hietala et al.47 with permission from Bioresource Technology Journal, copyright 2016. | ||
Hietala et al.47 were also the first to use initial conditions that did not require all the algal biomass to be in the “solids” phase at t = 0. Instead, the authors set the initial condition for the “solids” as 100 wt% minus the lipids wt% in the biomass. The initial condition for the biocrude phase was the lipids wt% in the biomass. Though not all algal lipids are extractable at room temperature and t = 0,48 the lipids would be released within seconds, as cell lysis occurred.49 Handling the initial conditions in this way allowed the model to better correlate yields of product fractions from HTL at short reaction times. Qian et al.50 later used the same model, reaction network, and initial condition concept for modeling fast and isothermal HTL of sewage sludge.
Note that the fast HTL experiments (t < 5 min in Fig. 7) were essential for obtaining data in regions where the yields of the product fractions were undergoing the greatest changes with time. These data are critical for determining meaningful values of the kinetics parameters. All the previous modeling work, and most that has been done since, did not consider this lower-severity HTL region and the parameter estimation suffered as a result. If the modeler had data only from isothermal HTL (say t = 5 min and longer), Fig. 7 shows that there would be very little variation in the product yields with time, which would make it difficult to determine precise values of the kinetics parameters.
All the models in this subsection treat whole biomass as a single pseudo-component. They can do a good job of correlating experimental HTL results for that particular biomass. Whether a set of model parameters determined for HTL of one biomass feedstock can be applied to HTL of a different feedstock remains to be determined. Recognizing this potential limitation of these single-pseudo-component models led to development of the more generalizable models discussed in the next section.
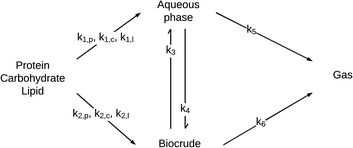 | ||
| Fig. 8 Generalized reaction network for HTL of microalgae from Valdez et al.51 | ||
The reaction network is the same as that in Fig. 4, but with the light and heavy biocrude fractions combined into a single lumped product fraction and the initial biomass solids being apportioned into protein, lipids, or carbohydrates. The primary pathways allow for conversion, at different rates, of protein, lipid, and carbohydrate components in microalgae into products that partition into the aqueous-phase or biocrude product fractions. There can be interconversion between these product fractions as well as gas formation.
HTL experiments were done at 250, 300, 350, and 400 °C from 10–60 min with three different microalgae (Chlorella protothecoides, Scenedesmus sp., and Nannochloropsis sp.) that had different biochemical contents. The set of differential equations implied by the reaction pathways for HTL in a batch reactor was then solved simultaneously along with parameter estimation to determine the best-fit rate constants for each path. A good fit (χ2 = 1.5) of the model to the experimental yields of product fractions was observed. The rate constants obtained indicated faster production of biocrude from the HTL of algae that are richer in lipids or proteins than in polysaccharides.
Vo et al.52 used the reaction network in Fig. 8 to model the product yields from HTL of Aurantiochytrium sp. KRS101. Like Valdez et al.,51 they conducted experiments at 250–400 °C for 10–60 min and used the product yields to determine the rate constants by minimizing the least square errors. The model successfully correlated the data for HTL of that specific microalga and thereby demonstrated the general applicability of the Valdez et al.51 reaction network.
Vo et al.53 further developed a kinetic model for HTL of Tetraselmis sp. by combining the concepts of deconstructing the biomass feed into protein, lipid, and carbohydrate components and partitioning the biocrude into light (hexane-soluble) and heavy (DCM-soluble) fractions as shown in Fig. 9. They were able to correlate all product fraction yields (solid, aqueous, biocrude) to within ±5 wt%.
Sheehan and Savage54 introduced a reaction engineering model for HTL where second order reactions can occur between carbohydrates, proteins, and lipids. For example, the model would account for a reaction between carbohydrates and proteins in a batch system as shown in eqn (5). They combined the experimental data from Valdez et al.51 and Vo et al.52 to determine values for the model parameters in the reaction network in Fig. 8. The predictive ability of the model was then tested on 133 other published biocrude yields from HTL of microalgae. The model predicted 70 biocrude yields to within 5 wt% error. The authors found that including second-order interactions in the model led to poorer predictions of the published biocrude yields. We believe this may be due to the equations inability to provide mass balance closure. Therefore, we included this model both with and without interactions as part of the present assessment, which uses a much larger set of published biocrude yields. More information is given in the ESI.†
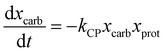 | (5) |
Palomino et al.55 published a simplified reaction network (Fig. 10) and corresponding model that focused on biocrude exclusively (no aqueous-phase products, no char, no gas). The biocrude, once formed, does not react further. The authors prevented the model from reaching 100% yields of biocrude by incorporating additional fitted parameters (Xi) that give the maximum biocrude yield available from each of the biochemical components.
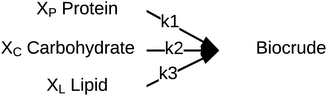 | ||
| Fig. 10 Reaction network proposed by Palomino et al.55 | ||
Obeid et al.56 were the first to introduce a HTL reaction engineering model that includes lignin as an explicit biochemical component (Fig. 11). The network also introduces a “solids” product fraction that is different from the initial solid feedstock components (e.g., carbs, proteins, lignin). These solids represent material formed during the hydrothermal reaction process. The authors determined values for the kinetics parameters by using experimental data from HTL of a four-component mixture of sunflower oil, microcrystalline cellulose, bovine serum albumin, and alkaline lignin. Their experiments considered only nominally isothermal HTL and reaction times exceeding five minutes. Consistent with the results in Fig. 7, there was little variation in the yields of the product fractions over the range of times examined. Unlike previous reaction networks, the reaction paths in Fig. 11 do not allow for direct conversion of lignin, protein, or carbohydrates to biocrude. Rather, these biochemical components first form aqueous-phase products, which can then react further to produce DCM-soluble biocrude.
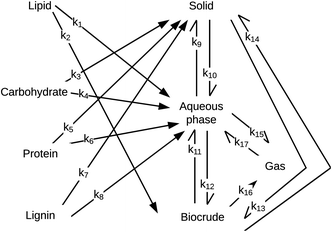 | ||
| Fig. 11 HTL reaction network from Obeid et al.56 | ||
Obeid et al.57 later used this same network and associated differential equations to correlate data from HTL of different whole biomass feedstocks (i.e., a microalga, sewage sludge, and pine wood sawdust). The models correlated the results for HTL of these different feedstocks, but the rate constants determined for the various reaction paths were different for each feedstock. For example, the rate constant for conversion of protein to aqueous-phase products (k6 in Fig. 11) at 300 °C was 3 s−1 for pine wood, 21 s−1 for a mixture of model,56 24 s−1 for algae, and 42 s−1 for sludge. The activation energy for conversion of protein to aqueous-phase products was 0.3 kJ mol−1 for algae, 8.3 kJ mol−1 for sludge, 28 kJ mol−1 for the mixture of biopolymers,56 and 78 kJ mol−1 for pinewood. This feedstock-dependence of the kinetics for each step in the network likely confines the utility of the networks to the specific feedstocks for which the parameters were determined. It also defeats one of the purposes of developing such models, which is to decompose conceptually and mathematically the biomass into a small number of biochemical components that can be taken to react at the same rate for all whole biomass feedstocks. In the assessment in the next section, we label each model with the biomass feedstock used to produce the HTL data that led to its parameters.
Hietala and Savage48 advanced kinetics models for HTL by using molecularly explicit reaction pathways for each biochemical component as the foundation. Fig. 12 shows the reaction network. Each molecular product was apportioned into the biocrude, gas, solid, or aqueous-phase product fractions, to enable comparison with experimental results. This work also advanced HTL kinetic modeling by being the first to account for the biomass concentration (loading) in the reactor, which is known to influence HTL outcomes.13,32,42,58 The polynomial used to correlate the density of water as a function of temperature gives faithful estimates only up to 450 °C. Using the model at higher temperatures could give inaccurate results. The model comprised 16 pathways (each is numbered in Fig. 12) that include reactions such as hydrolysis, addition, cyclodehydration, retro-aldol condensation, deamination, and decarboxylation. The model also included polysaccharide–protein interactions via explicit inclusion of the chemical reactions themselves. This work was the first to include Maillard reactions in a reaction engineering model for HTL of whole biomass.
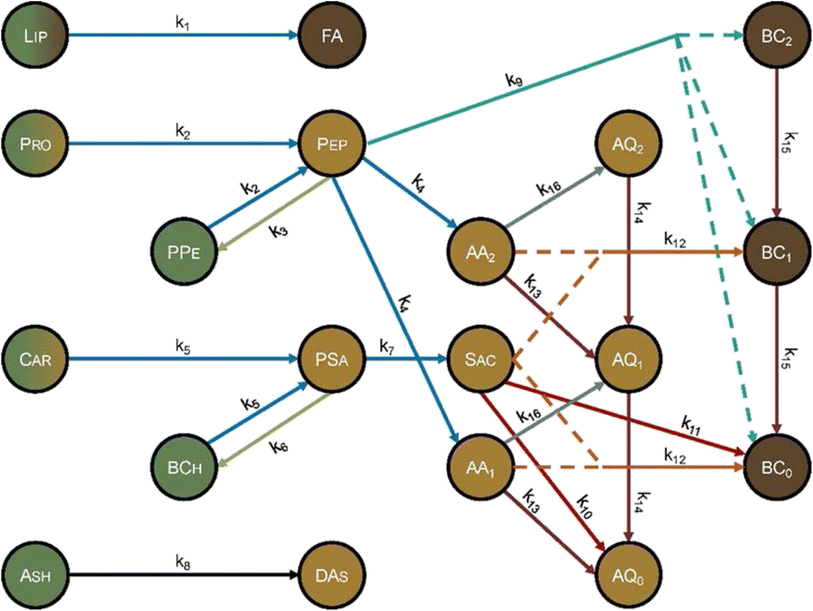 | ||
| Fig. 12 Molecular reaction pathways for HTL of microalgae adapted from Hietala and Savage.48 The colors represent the solubility of each component. Dark brown is DCM soluble, light brown is water soluble, and green is insoluble. A gradient represents partial solubility. AA = amino acid, AQ = aqueous-phase product, BC = biocrude, BCh = biochar, Car = carbohydrates, DAs = dissolved ash, FA = fatty acids, Lip = lipid, Pep = peptide, PPe = polypeptide, Pro = protein, PSa = polysaccharide, Sac = saccharide. The subscripts on AA, AQ, and BC refer to the number of amine groups in the molecule. Reproduced from Hietala and Savage48 with permission from Chemical Engineering Journal, copyright 2021. | ||
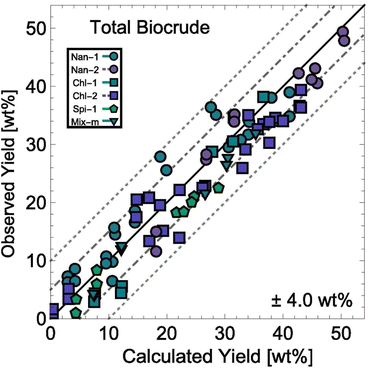
HTL experiments with different mono- and polycultures of whole algal biomass provided the data used to determine the model parameters. Experiments were conducted from 150–350 °C and for 1–100 min, and the data set included both isothermal and non-isothermal (fast) HTL conditions. The rate constants were determined by using 1070 different product yields obtained from experiments with 103 unique sets of process variables. Fig. 13 shows the biocrude yields calculated from the model were within 4 wt% root-mean-square deviation of the experimental biocrude yields.
Obeid et al.61 provided experimental data for HTL of four different biochemical components alone (cellulose, alkaline lignin, bovine serum albumin, and sunflower oil). They used reduced versions of the Valdez et al.51 reaction network in Fig. 8 to correlate the data. Chloroform was used to recover the biocrude. This solvent gave a 5 wt% higher yield of biocrude than did DCM for HTL of a Nannochloropsis microalga.62 Following Hietala et al.,47 Obeid et al.61 took the initial (t = 0) yield of biocrude to be equal to the lipid content in the biomass. They also measured the portion of the feedstock that was water-soluble even prior to HTL and used this value as the initial condition in the model. The model is the first to introduce a different initial fraction for carbohydrates and lignin into initial conditions for products.
These authors subsequently developed lumped kinetics models for hydrothermal conversion of glucose, guaiacol, L-alanine, and oleic acid.56 These small molecules (monomers) were intended to mimic carbohydrates, lignin, protein, and lipids, respectively. The authors used a modified version of the reaction network in Fig. 8 wherein the pathways involving solids were reversible. Though the reaction networks are identical to those used in the earlier work,61 the rate constants were quite different. For example, the rate constant for the pathway from cellulose to aqueous-phase products was 3.3 s−1 for HTL at 350 °C. For D-glucose it was 22.7 s−1 at the same temperature. The rate constants for conversion of proteins and lignin were also much lower than those for disappearance of alanine and guaiacol. This comparison of the reactivity of biopolymers and their corresponding monomers showed that the initial depolymerization of the macromolecule is much slower than the subsequent reactions of monomers.
4.2 Assessment of kinetic models for HTL of biomass
Similar to Section 3.2.1, in Section 4.2.1 we first assess the kinetics models using literature data from HTL of biomass feedstocks that contain all the biochemical components included as reactants in the models. For example, the Valdez et al.51 model correlated biocrude yields from HTL of microalgae that contained proteins, lipids, and carbohydrates. There are 659 entries in the database that are from HTL of biomass with all three of these components and only those components. These were used to assess the model. If the biomass contained lignin or lacked carbohydrates, proteins, or lipids, those data were not used to assess the Valdez et al. model (or others that considered all three components and only those three components).In Section 4.2.2 we repeat for the kinetics models the assessment that was done with the component additivity models in Section 3.2.2. We assess the kinetics models for biocrude yields with a broader dataset by including HTL experiments with biomass feedstocks containing only some of the biochemical components the model can handle. The model from Obeid et al.,61 for example, can handle biomass feedstocks with carbohydrates, proteins, lipids, and lignin. In this section, the model will be assessed using data from HTL of biomass with all four components as well as biomass feedstocks with three or fewer of the components.
We assessed the kinetics models at all temperatures and times in the database for biocrude yields. This approach sometimes led to extrapolation outside the ranges used to determine model parameters.
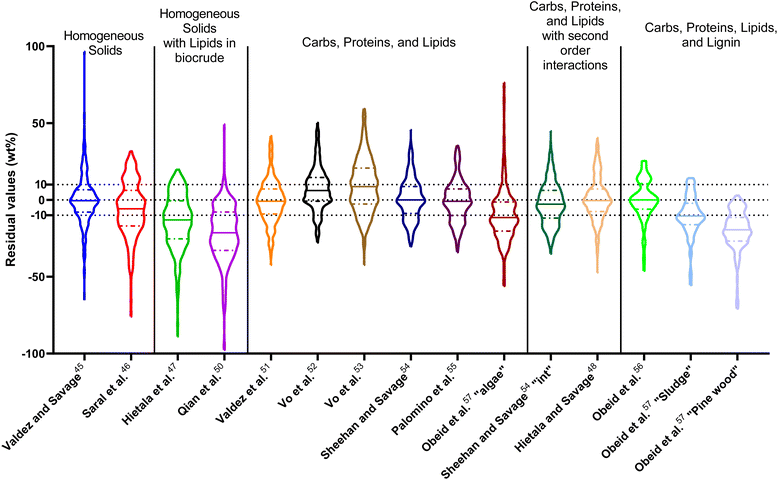 | ||
| Fig. 14 Distribution of residuals with median (solid line) and quartiles (dashed line) for predicting biocrude yields from HTL of intended biomass with lumped kinetic models. | ||
The first group of models in Fig. 14 treats the biomass feedstock as a uniform, homogeneous solid at t = 0. Table S6† shows that both models in this category have higher biases, higher mean and median absolute residuals, and fewer yields predicted within 5 wt% and 10 wt% than models that allow for different reactivities for proteins, lipids, and polysaccharides. The second group of models in Fig. 14 partition the biomass into a uniform, homogeneous solid portion, and a separate lipid portion, all of which starts in the biocrude product fraction at t = 0. The models in this group give better predictions, on average, than those that treat the entire biomass feedstock as “homogeneous solids”.
The third group of models allows polysaccharides, proteins, and lipids to have different reactivities during HTL. These models all provide better predictions than those that treat the biomass feedstock as a single homogeneous solid. This outcome is not surprising, as these models better incorporate the physical realities and include additional parameters. Based on the 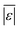 and Med[|ε|] statistics, the models with the best predictions in this group are from Valdez,51 Sheehan,54 and Palomino.55 The fourth group of models includes biomass interactions. The predictive ability of the models is similar to that of the models without interactions. Based on the average absolute residuals, median residual, MAPE, median absolute relative error, and percent of residuals within 10 wt%, the best performing model for HTL of biomass with proteins, lipids, and polysaccharides is that of Hietala and Savage.48
and Med[|ε|] statistics, the models with the best predictions in this group are from Valdez,51 Sheehan,54 and Palomino.55 The fourth group of models includes biomass interactions. The predictive ability of the models is similar to that of the models without interactions. Based on the average absolute residuals, median residual, MAPE, median absolute relative error, and percent of residuals within 10 wt%, the best performing model for HTL of biomass with proteins, lipids, and polysaccharides is that of Hietala and Savage.48
The last group of models in Fig. 14 can handle biomass feedstocks that include lignin. The number of published biocrude yields available for assessment of these models is smaller (138) than those available for assessing the models that exclude lignin (659). Of the models in this group, the one from Obeid et al.63 that is based on biopolymer model compounds makes the best predictions. Table S10† shows it has the lowest 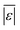 , Med[|ε|], and Med[APE] and the highest percent of residuals within ±5 wt% and ±10 wt%.
, Med[|ε|], and Med[APE] and the highest percent of residuals within ±5 wt% and ±10 wt%.
As was the case with the assessment for HTL of the intended biomass, the model from Hietala and Savage48 shows the lowest 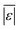 , Med[|ε|], and MAPE, while having the highest percentage of residuals within 5 and 10 wt%. This model appears to be the best for predicting biocrude yields from HTL of biomass containing protein, lipids, and polysaccharides.
, Med[|ε|], and MAPE, while having the highest percentage of residuals within 5 and 10 wt%. This model appears to be the best for predicting biocrude yields from HTL of biomass containing protein, lipids, and polysaccharides.
The 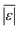 and Med[|ε|] statistics are significantly higher for the models that included lignin than the models that did not. Lignin can have strong positive or negative interactions with other biochemical components (see Table 1 and S1†). Since the models with lignin do not include interaction terms, the interactions are confounded into the existing reactions and their rate constants, which likely makes the models less robust in predicting outcomes from HTL of feedstocks with widely varying compositions.
and Med[|ε|] statistics are significantly higher for the models that included lignin than the models that did not. Lignin can have strong positive or negative interactions with other biochemical components (see Table 1 and S1†). Since the models with lignin do not include interaction terms, the interactions are confounded into the existing reactions and their rate constants, which likely makes the models less robust in predicting outcomes from HTL of feedstocks with widely varying compositions.
We examined the published biocrude yields that were predicted with greater than 100% relative error to see whether the feedstocks or HTL conditions shared any common features. The systems for which biocrude yields were predicted poorly are HTL of isolated carbohydrates alone, isolated proteins alone, biomass with high carbohydrate and low protein content, and biomass with high protein and low carbohydrate content.
We additionally assess the models over a subset of the data for algal biomass. Fig. S2 and Table S8† show the results. The models from Valdez and Savage45 and Valdez et al.51 perform very well and move closer to being the best models. Both models were parameterized using biocrude yields from HTL of microalgae. There is an overall decrease in variability over all the models, with more improvement for models parameterized using data from HTL of microalgae, but no change in the overall trends. The model of Hietala and Savage48 has the lowest 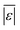 , Med[|ε|], and MAPE and the highest percentage of predictions within 5 wt% and 10 wt%. Hence, the best lumped kinetic model to predict biocrude yields from HTL of microalgal biomass is the model from Hietala and Savage48
, Med[|ε|], and MAPE and the highest percentage of predictions within 5 wt% and 10 wt%. Hence, the best lumped kinetic model to predict biocrude yields from HTL of microalgal biomass is the model from Hietala and Savage48
5 Assessment of all models for different biomass feedstocks
The assessments conducted thus far have used different sets of data for assessing the different models. This is due to each model having different intended and possible biomass feedstocks at different conditions that the model can be tested on. A different way to assess the models, and also directly compare component additivity and kinetics models, is to use each model to make predictions for precisely the same set of published biocrude yields for HTL of the same biomass feedstocks at the same conditions. This section makes these assessments for seven different types of biomass. These types are biomass composed entirely of carbohydrates, proteins, lipids, and lignin (all four components and no others), biomass composed entirely of carbohydrates, proteins, and lipids (all three and no others), biomass that contains both and only carbohydrates and lignin, and biomass that contains only carbohydrates, only proteins, only lipids, and only lignin.To identify the models best suited for predicting biocrude yields from HTL of the different types of biomass, we examined all of the statistical metrics for each case. For each metric, one of the models was best for predicting biocrude yields for a given type of feedstock. The “recommended models” in Table 2 are the ones that were best for the most metrics.| Components in biomass feedstock | Best model | Number of biocrude yields | Statistics that are best |
|---|---|---|---|
| Carbohydrates, proteins, lipids, and lignin | Obeid et al.56 | 138 | Med[ε], Med[|ε|], Med[APE], % <5 wt% |
| Carbohydrates, proteins, and lipids | Hietala and Savage48 | 659 |
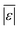 , Med[|ε|], % <5 wt%, % <10 wt% , Med[|ε|], % <5 wt%, % <10 wt% |
| Carbohydrates and lignin | Hietala et al.47 | 25 |
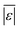 , MAPE, % <5 wt%, % <10 wt%, % > 100% relative error , MAPE, % <5 wt%, % <10 wt%, % > 100% relative error |
| Carbohydrates | Sheehan and Savage54 | 112 | Med[ε], 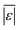 , Med[APE], % <10 wt% , Med[APE], % <10 wt% |
| Proteins | Sheehan and Savage59 | 75 | Med[ε], 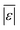 , Med[APE], % <10 wt% , Med[APE], % <10 wt% |
| Lipids | Mahadevan Subramanya and Savage34 | 28 |
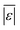 , Med[|ε|], MAPE, % >100% relative error , Med[|ε|], MAPE, % >100% relative error |
| Lignin | Hietala et al.47 | 38 | Med[ε], Med[|ε|], Med[APE], % >5 wt%, % <10 wt% |
Fig. 16 and Table S9† show the kinetics model from Obeid et al.56 was best for predicting biocrude yields from HTL of biomass consisting entirely of carbohydrates, proteins, lipids, and lignin. Fig. 17 and Table S10† show the kinetics model of Hietala and Savage48 was best for predicting biocrude yields from HTL of biomass consisting entirely and only of protein, lipid, and carbohydrate. The model was parameterized using data from HTL of microalgae, and its success here indicates it can also give good predictions for HTL of food waste, sludges, and other microbial biomass. Violin plots and tables that summarize the statistics for the different models for additional types of biomass are in the ESI (Tables S11–S15 and Fig. S3–S11).†
The kinetics model of Hietala et al.,47 though parameterized with data from HTL of a single microalga, was the best at predicting biocrude yields from HTL of lignin and biomass with solely carbohydrates and lignin. This model treated the biomass as a uniform, homogeneous solid material. It seems such a model can be extrapolated to other types of biomasses with some success.
For HTL of isolated biochemical components alone, biocrude yields from lipids are best predicted by the component additivity model from Mahadevan Subramanya and Savage.34 The model from Sheehan and Savage,59 which was parameterized using data from HTL of a protein, made the best predictions of literature biocrude yields from HTL of protein. In closing this section, we note that only one of 7 entries for recommended models in Table 2 is a component additivity model. Kinetics models generally performed better in this test, as, unlike component additivity models, they are designed to handle a broad range of reaction times and temperatures.
6 Toward improved predictive models
Having reviewed and assessed both component additivity and kinetics models for HTL of biomass, we now offer suggestions for developing more advanced models. One pathway to more advanced models is to include the initial biomass loading (wt% biomass in reactor) in the model. This process variable affects biocrude yields. For example, biocrude yields from HTL of polysaccharides can vary by a factor of 2.5 simply by changing the biomass loading from 2 wt% to 15 wt%.64 To date, only one reaction engineering model has incorporated the biomass loading, but this needs to become standard in the field.With a few exceptions, existing models make the implicit assumption that the reactivity of all types of proteins, all types of carbohydrates (structural and non-structural), and all types of lipids can be represented by the reactivity of a single representative biomolecule from each class. The literature shows this simplification is not strictly valid.28 For example, at 400 °C and 5 min, HTL of bovine serum albumin gives a biocrude yield of 4 wt% whereas the yield is 28 wt% from soy protein isolate.65 The apparent first-order rate constants for hydrothermal conversion of different amino acids ranges from 0.03 to 0.48 s−1 at 300 °C.66 Structural (cellulose) and non-structural (starch/hemicellulose) carbohydrates follow different pathways and react at different rates during HTL.13,29,30,33,34,37,67 Carbohydrates that are less structural (less branching) decompose more readily. Saturated, mono-unsaturated, and poly-unsaturated fatty acids show different hydrothermal reactivities.32 The lipid fraction can also contain phospholipids, glycolipids, sterols, and other compounds with a variety of functional groups. The limited information available,68 shows different hydrothermal reactivities for these compounds. Finally, the lignin that is isolated from biomass and used in HTL experiments is extracted using different processes (e.g., Kraft, Lignosulphonate, Organosolv) that influence the pH during HTL as well as the degree of polymerization, metal/sulfur content, and amount of the lignin extract.69 All these factors have an effect on the HTL process.70,71 We posit that more accurate and robust models could be developed by including more than one representative from each biochemical class. Of course, presuming such a model fit experimental data better, one would need to assess whether the additional goodness of fit justifies the inclusion of the additional rate constants.
Published HTL studies have used reactor heating rates ranging from 10 °C min−1 (e.g., large autoclave reactor) to 350 °C min−1 (e.g., 1 mL reactor). In most kinetic models, the heating regime (and reactor cool down) is ignored and focus is placed on the time the reaction is occurring isothermally. For studies with rapid heating and cooling and an isothermal period that is much longer than either, this simplification is reasonable. For other systems and for non-isothermal (e.g., fast) HTL, it is not. The prior modeling studies that did include the reactor heat up used a polynomial equation to fit the experimental temperature profile.47,50,59,65 We suggest that all modeling studies incorporate the non-isothermal periods experienced by the HTL reactor when estimating model parameters. Of course, doing so would require all experimental studies to measure and report the reactor temperature profiles during heating and cooling. We also propose using the error function (eqn (6)) or the Morse potential (eqn (S6)†), which we used in this assessment, to describe the heating and cooling profiles. These functions match the general shape of a reactor heating curve and have just a few adjustable parameters.
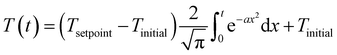 | (6) |
For kinetics models, the initial conditions affect the product yields calculated at different reaction times. In most HTL studies, the initial condition is taken as 100% of the biomass feedstock being in the solid phase and none in the gas, aqueous, or oil phases. Control experiments have shown, however, that portions of different biomass feedstocks are soluble in water (aqueous phase) or in DCM (oil phase).48,50,52,53,56,59,63,65,72,73 These portions need to be determined experimentally for each feedstock and then used as the appropriate initial conditions in a kinetics model. Some studies have taken this approach48,56,59,63,65 and it needs to become standard in the field.
The present assessment of HTL models considered only the biocrude yield. This yield is typically the most important outcome from HTL, but other outcomes are also important. There is merit in conducting a thorough assessment of how well different models predict the yields of aqueous-phase, solid, and gaseous products. Typically, more than half of the initial mass of the biomass feedstock appears in these other phases. Being able to model their yields (and compositions) would enable a more general HTL process optimization along with technoeconomic analysis and life-cycle assessment.
Some of the errors in predicting biocrude yields from different models are likely due to differences in the experimental procedures used to conduct HTL and to recover the product fractions. For example, the amounts of water and DCM used to recover reaction products can influence the partitioning of molecules between these two phases. Such details need to be provided in experimental studies and their influence on yields of biocrude and aqueous-phase products needs to be determined.
The present assessment focused on work wherein biocrude was defined as the DCM-soluble material from HTL of biomass. Other solvents such as acetone,39,74–90 chloroform,61,91,92 ethanol,93 hexane,90,94,95 toluene,90,94,96 ethyl acetate,97–99 and mixtures of these solvents100–106 have been used instead of DCM to recover HTL bio-oil. There is a need for models that can correlate and predict biocrude yields recovered with different solvents.
The present assessment of HTL models implicitly assumed that the experimental error was the same for every published biocrude yield. This approach was taken because not all published studies reported uncertainties in their biocrude yields. We recommend that experimentalists measure the uncertainty and run-to-run variability in their product yields and report the same in published studies. These uncertainties can then be used to weigh individual data points when assessing and fitting models for HTL.
The internal structure and size of biomass particles could have an impact on HTL outcomes. For example, one would expect different bio-oil production rates from HTL of a given woody biomass as wood chips, saw dust, and wood flour at a given set of conditions. The larger particles would be expected to react more slowly, and the rates would be influenced by transport rates both to the surface of the particle and possibly within the particle. Likewise, one might expect different rates for HTL of whole microalgal biomass vs. food waste. Even though the two feedstocks might contain the same proportions of protein, lipid, and polysaccharide, they have different internal physical structures that would affect reaction rates. There are some models for HTL of biomass that incorporate physical and transport effects. Iryani et al.107 used a shrinking core model for HTL of sugarcane bagasse. This type of model could also be used to account for cell lysis, which would be important for microalgae.108 Jayathilake et al.108 developed a multistage shrinking core model for the decomposition of lignin particles during HTL. None of these models were applied to a general multicomponent biomass feedstock for predicting yields of product fractions from HTL. This gap in literature is an area of opportunity.
In this assessment, models that include second-order interactions between biomass components made better predictions. Sheehan and Savage59 included interactions between all binary combinations of carbohydrates, proteins, and lipids. There is a need to quantify the interactions of lignin with the other biochemical components.
The present reaction engineering models deal with a small number of lumped product fractions. Hietala and Savage48 developed the model that is the most molecular, in that it tracks concentrations of specific groups of molecules – not solely solubility-based product fractions. More advanced models can be developed by expanding on this molecular framework. Literature provides much information that can be used to this end. The hydrothermal reactions of glucose, fructose, disaccharides, polysaccharides,109–115 peptides, polypeptides, amino acids,66,116–119 hesperidin,120 fatty acids,121–123 triglycerides,124 phospholipids,68 cholesterol,125 lignin,108,126–129 and some of their interactions such as the Maillard reaction130,131 and cellulose–lignin interactions132 have been studied on a molecular level. This information can be used to develop models for HTL that are increasingly molecular. Product fraction yields can be recovered by determining the solubility of the different products in water and DCM (or other solvents). The molecular information, however, could add value by enabling identification of high-value chemicals that one would want to separate, purify, and sell to increase the profitability of the process.
This review and assessment focused on HTL of biomass, but HTL and hydrolysis of post-consumer plastics133–140 for waste valorization and chemical recycling is an emerging field. Modeling needs to be done for HTL of plastics and for mixtures of plastics and biomass, as this would extend the applicability of HTL to any mixture of biopolymers and synthetic polymers. Seshasayee et al.134 developed the first and, to date, only model (component additivity) that predicts the crude oil yield from HTL of mixtures of biomass and plastics.
Author contributions
Peter M Guirguis: conceptualization, data curation, formal analysis, validation, visualization, writing – original draft, writing – review & editing, Seshasayee Mahadevan Subramanya: conceptualization, writing – original draft, Bita Motavaf: conceptualization, formal analysis and Phillip E. Savage: conceptualization, funding acquisition, methodology, project administration, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported with funds from the Walter L. Robb Family Chair in Chemical Engineering at Penn State.Notes and references
- S. S. Toor, L. Rosendahl and A. Rudolf, Energy, 2011, 36, 2328–2342 CrossRef CAS.
- Y. Guo, T. Yeh, W. Song, D. Xu and S. Wang, Renewable Sustainable Energy Rev., 2015, 48, 776–790 CrossRef CAS.
- A. Kruse, A. Funke and M.-M. Titirici, Curr. Opin. Chem. Biol., 2013, 17, 515–521 CrossRef CAS PubMed.
- D. C. Elliott, P. Biller, A. B. Ross, A. J. Schmidt and S. B. Jones, Bioresour. Technol., 2015, 178, 147–156 CrossRef CAS PubMed.
- T. M. Yeh, J. G. Dickinson, A. Franck, S. Linic, L. T. Thompson and P. E. Savage, J. Chem. Technol. Biotechnol., 2013, 88, 13–24 CrossRef CAS.
- Y. Chen, Y. Wu, D. Hua, C. Li, M. P. Harold, J. Wang and M. Yang, RSC Adv., 2015, 5, 18673–18701 RSC.
- S. M. Changi, J. L. Faeth, N. Mo and P. E. Savage, Ind. Eng. Chem. Res., 2015, 54, 11733–11758 CrossRef CAS.
- J. Yang, Q. S. He and L. Yang, Appl. Energy, 2019, 250, 926–945 CrossRef CAS.
- R. Kumar, Energy Nexus, 2022, 5, 100042 CrossRef CAS.
- D. López Barreiro, W. Prins, F. Ronsse and W. Brilman, Biomass Bioenergy, 2013, 53, 113–127 CrossRef.
- A. A. Peterson, F. Vogel, R. P. Lachance, M. Fröling, M. J. Antal Jr and J. W. Tester, Energy Environ. Sci., 2008, 1, 32 RSC.
- N. Akiya and P. E. Savage, Chem. Rev., 2002, 102, 2725–2750 CrossRef CAS PubMed.
- A. Gollakota, N. Kishore and S. Gu, Renewable Sustainable Energy Rev., 2018, 81, 1378–1392 CrossRef.
- J. Akhtar and N. A. S. Amin, Renewable Sustainable Energy Rev., 2011, 15, 1615–1624 CrossRef CAS.
- Y. Xue, H. Chen, W. Zhao, C. Yang, P. Ma and S. Han, Int. J. Energy Res., 2016, 40, 865–877 CrossRef CAS.
- R. Shakya, S. Adhikari, R. Mahadevan, S. R. Shanmugam, H. Nam, E. B. Hassan and T. A. Dempster, Bioresour. Technol., 2017, 243, 1112–1120 CrossRef CAS PubMed.
- S. Rezazi, S. Abdelmalek and S. Hanini, Energy Procedia, 2017, 139, 98–104 CrossRef CAS.
- A. Shafizadeh, H. Shahbeig, M. H. Nadian, H. Mobli, M. Dowlati, V. K. Gupta, W. Peng, S. S. Lam, M. Tabatabaei and M. Aghbashlo, Chem. Eng. J., 2022, 445, 136579 CrossRef CAS.
- J. Li, W. Zhang, T. Liu, L. Yang, H. Li, H. Peng, S. Jiang, X. Wang and L. Leng, Chem. Eng. J., 2021, 425, 130649 CrossRef CAS.
- W. Zhang, J. Li, T. Liu, S. Leng, L. Yang, H. Peng, S. Jiang, W. Zhou, L. Leng and H. Li, Bioresour. Technol., 2021, 342, 126011 CrossRef CAS PubMed.
- T. Katongtung, T. Onsree and N. Tippayawong, Bioresour. Technol., 2022, 344, 126278 CrossRef CAS PubMed.
- F. Cheng, E. R. Belden, W. Li, M. Shahabuddin, R. C. Paffenroth and M. T. Timko, Chem. Eng. J., 2022, 442, 136013 CrossRef CAS.
- P. Biller and A. B. Ross, Bioresour. Technol., 2011, 102, 215–225 CrossRef CAS PubMed.
- A. A. Peterson, R. P. Lachance and J. W. Tester, Ind. Eng. Chem. Res., 2010, 49, 2107–2117 CrossRef CAS.
- S. Leow, J. R. Witter, D. R. Vardon, B. K. Sharma, J. S. Guest and T. J. Strathmann, Green Chem., 2015, 17, 3584–3599 RSC.
- J. Wagner, R. Bransgrove, T. A. Beacham, M. J. Allen, K. Meixner, B. Drosg, V. P. Ting and C. J. Chuck, Bioresour. Technol., 2016, 207, 166–174 CrossRef CAS PubMed.
- Y. Li, S. Leow, A. C. Fedders, B. K. Sharma, J. S. Guest and T. J. Strathmann, Green Chem., 2017, 19, 1163–1174 RSC.
- A. Gollakota and P. E. Savage, ACS Sustainable Chem. Eng., 2020, 8, 3762–3772 CrossRef CAS.
- M. Déniel, G. Haarlemmer, A. Roubaud, E. Weiss-Hortala and J. Fages, Sustainable Energy Fuels, 2017, 1, 555–582 RSC.
- J. Lu, Z. Liu, Y. Zhang and P. E. Savage, ACS Sustainable Chem. Eng., 2018, 6, 14501–14509 CrossRef CAS.
- G. Teri, L. Luo and P. E. Savage, Energy Fuels, 2014, 28, 7501–7509 CrossRef CAS.
- D. C. Hietala, C. K. Koss, A. Narwani, A. R. Lashaway, C. M. Godwin, B. J. Cardinale and P. E. Savage, Algal Res., 2017, 26, 203–214 CrossRef.
- J. Yang, Q. S. He, H. Niu, K. Corscadden and T. Astatkie, Appl. Energy, 2018, 228, 1618–1628 CrossRef CAS.
- S. Mahadevan Subramanya and P. E. Savage, ACS Sustainable Chem. Eng., 2021, 9, 13874–13882 CrossRef CAS.
- L. Sheng, X. Wang and X. Yang, Bioresour. Technol., 2018, 247, 14–20 CrossRef CAS PubMed.
- J. Yang, Q. S. He, K. Corscadden, H. Niu, J. Lin and T. Astatkie, Appl. Energy, 2019, 233–234, 906–915 CrossRef CAS.
- S. Yan, D. Xia, X. Zhang and X. Liu, Energy, 2022, 255, 124561 CrossRef CAS.
- E. Adler, Ind. Eng. Chem., 1957, 49, 1377–1383 CrossRef CAS.
- Z. Zhu, L. Rosendahl, S. S. Toor, D. Yu and G. Chen, Appl. Energy, 2015, 137, 183–192 CrossRef CAS.
- A. Aierzhati, M. J. Stablein, N. E. Wu, C.-T. Kuo, B. Si, X. Kang and Y. Zhang, Bioresour. Technol., 2019, 284, 139–147 CrossRef CAS PubMed.
- L. Zhang, X. Dou, Z. Yang, X. Yang and X. Guo, Biomass, 2021, 1, 74–93 CrossRef.
- J. L. Faeth, P. E. Savage, J. M. Jarvis, A. M. McKenna and P. E. Savage, AIChE J., 2016, 62, 815–828 CrossRef CAS.
- X. Kang, X. Guo and H. You, Energy Sources, Part A, 2013, 35, 1921–1928 CrossRef CAS.
- B. Zhang, H.-J. Huang and S. Ramaswamy, Energy Sources, Part A, 2012, 34, 1676–1687 CrossRef CAS.
- P. J. Valdez and P. E. Savage, Algal Res., 2013, 2, 416–425 CrossRef.
- J. S. Saral, D. G. C. V. Reddy and P. Ranganathan, Biomass Convers. Biorefin., 2022, 1, 1–9 Search PubMed.
- D. C. Hietala, J. L. Faeth and P. E. Savage, Bioresour. Technol., 2016, 214, 102–111 CrossRef CAS PubMed.
- D. C. Hietala and P. E. Savage, Chem. Eng. J., 2021, 407, 127007 CrossRef CAS.
- M. Packard, E. Wheeler, E. Alocilja and M. Shusteff, Diagnostics, 2013, 3, 105–116 CrossRef PubMed.
- L. Qian, S. Wang and P. E. Savage, Appl. Energy, 2020, 260, 114312 CrossRef CAS.
- P. J. Valdez, V. J. Tocco and P. E. Savage, Bioresour. Technol., 2014, 163, 123–127 CrossRef CAS PubMed.
- T. K. Vo, O. K. Lee, E. Y. Lee, C. H. Kim, J.-W. Seo, J. Kim and S.-S. Kim, Chem. Eng. J., 2016, 306, 763–771 CrossRef CAS.
- T. K. Vo, S.-S. Kim, H. V. Ly, E. Y. Lee, C.-G. Lee and J. Kim, Bioresour. Technol., 2017, 241, 610–619 CrossRef CAS PubMed.
- J. D. Sheehan and P. E. Savage, Bioresour. Technol., 2017, 239, 144–150 CrossRef CAS PubMed.
- A. Palomino, L. C. Montenegro-Ruíz and R. D. Godoy-Silva, Algal Res., 2019, 44, 101669 CrossRef.
- R. Obeid, D. M. Lewis, N. Smith, T. Hall and P. van Eyk, Energy Fuels, 2020, 34, 419–429 CrossRef CAS.
- R. Obeid, N. Smith, D. M. Lewis, T. Hall and P. van Eyk, Chem. Eng. J., 2022, 428, 131228 CrossRef CAS.
- D. C. Hietala, C. M. Godwin, B. J. Cardinale and P. E. Savage, Algal Res., 2019, 42, 101568 CrossRef.
- J. D. Sheehan and P. E. Savage, ACS Sustainable Chem. Eng., 2016, 4, 6931–6939 CrossRef CAS.
- L. Luo, J. D. Sheehan, L. Dai and P. E. Savage, ACS Sustainable Chem. Eng., 2016, 4, 2725–2733 CrossRef CAS.
- R. Obeid, D. Lewis, N. Smith and P. van Eyk, Chem. Eng. J., 2019, 370, 637–645 CrossRef CAS.
- P. J. Valdez, J. G. Dickinson and P. E. Savage, Energy Fuels, 2011, 25, 3235–3243 CrossRef CAS.
- R. Obeid, D. M. Lewis, N. Smith, T. Hall and P. van Eyk, Chem. Eng. J., 2020, 389, 124397 CrossRef CAS.
- A. Gollakota and P. E. Savage, ACS Sustainable Chem. Eng., 2018, 6, 9018–9027 CrossRef CAS.
- J. D. Sheehan and P. E. Savage, ACS Sustainable Chem. Eng., 2017, 5, 10967–10975 CrossRef CAS.
- N. Sato, A. T. Quitain, K. Kang, H. Daimon and K. Fujie, Ind. Eng. Chem. Res., 2004, 43, 3217–3222 CrossRef CAS.
- C. Gai, Y. Zhang, W.-T. Chen, P. Zhang and Y. Dong, Energy Convers. Manage., 2015, 96, 330–339 CrossRef CAS.
- S. Changi, A. J. Matzger and P. E. Savage, Green Chem., 2012, 14, 2856 RSC.
- N. Mandlekar, A. Cayla, F. Rault, S. Giraud, F. Salaün, G. Malucelli and J.-P. Guan, Lignin – Trends and Applications, InTech, 2018 Search PubMed.
- X. Ding, S. M. Subramanya, Y. Wang and P. E. Savage, Ind. Eng. Chem. Res., 2021, 60, 8642–8648 CrossRef CAS.
- X. Ding, S. Mahadevan Subramanya, K. E. Waltz, Y. Wang and P. E. Savage, Bioresour. Technol., 2022, 352, 127100 CrossRef CAS PubMed.
- J. L. Faeth, P. J. Valdez and P. E. Savage, Energy Fuels, 2013, 27, 1391–1398 CrossRef CAS.
- P. J. Valdez, M. C. Nelson, H. Y. Wang, X. N. Lin and P. E. Savage, Biomass Bioenergy, 2012, 46, 317–331 CrossRef CAS.
- A. Demirbaş, Energy Sources, 2005, 27, 1235–1243 CrossRef.
- S. Xiu, A. Shahbazi, V. Shirley and D. Cheng, J. Anal. Appl. Pyrolysis, 2010, 88, 73–79 CrossRef CAS.
- K. Sharma, A. A. Shah, S. S. Toor, T. H. Seehar, T. H. Pedersen and L. A. Rosendahl, Energies, 2021, 14, 1708 CrossRef CAS.
- C. Xu and N. Lad, Energy Fuels, 2008, 22, 635–642 CrossRef CAS.
- L. Yang, L. Nazari, Z. Yuan, K. Corscadden, C. C. Xu and Q. S. He, Biomass Bioenergy, 2016, 86, 191–198 CrossRef CAS.
- S. Mishra and K. Mohanty, Energy Convers. Manage., 2020, 204, 112312 CrossRef CAS.
- P. de Filippis, B. de Caprariis, M. Scarsella, A. Petrullo and N. Verdone, Int. J. Sustainable Dev. Plann., 2016, 11, 700–707 CrossRef.
- F. Conti, S. S. Toor, T. H. Pedersen, A. H. Nielsen and L. A. Rosendahl, Biomass Bioenergy, 2018, 118, 24–31 CrossRef CAS.
- A. A. Shah, S. S. Toor, F. Conti, A. H. Nielsen and L. A. Rosendahl, Biomass Bioenergy, 2020, 135, 105504 CrossRef CAS.
- S. Xiu, A. Shahbazi and L. Wang, Energy Sources, Part A, 2016, 38, 459–465 CrossRef CAS.
- L. Jasiūnas, T. H. Pedersen, S. S. Toor and L. A. Rosendahl, Renewable Energy, 2017, 111, 392–398 CrossRef.
- A. Mathanker, D. Pudasainee, A. Kumar and R. Gupta, Fuel, 2020, 271, 117534 CrossRef CAS.
- S. Brand, F. Hardi, J. Kim and D. J. Suh, Energy, 2014, 68, 420–427 CrossRef CAS.
- K. Malins, Energy Convers. Manage., 2017, 144, 243–251 CrossRef CAS.
- L. Nazari, Z. Yuan, S. Souzanchi, M. B. Ray and C. C. Xu, Fuel, 2015, 162, 74–83 CrossRef CAS.
- T. Minowa, T. Kondo and S. T. Sudirjo, Biomass Bioenergy, 1998, 14, 517–524 CrossRef CAS.
- H. Jahromi, T. Rahman, P. Roy and S. Adhikari, Energy Convers. Manage., 2022, 263, 115719 CrossRef CAS.
- S. Raikova, H. Smith-Baedorf, R. Bransgrove, O. Barlow, F. Santomauro, J. L. Wagner, M. J. Allen, C. G. Bryan, D. Sapsford and C. J. Chuck, Fuel Process. Technol., 2016, 142, 219–227 CrossRef CAS.
- D. Li, L. Chen, D. Xu, X. Zhang, N. Ye, F. Chen and S. Chen, Bioresour. Technol., 2012, 104, 737–742 CrossRef CAS PubMed.
- A. Chacón-Parra, D. Lewis and P. van Eyk, Chem. Eng. J., 2021, 425, 130576 CrossRef.
- F. Cheng, Z. Cui, K. Mallick, N. Nirmalakhandan and C. E. Brewer, Bioresour. Technol., 2018, 258, 158–167 CrossRef CAS PubMed.
- F. Cheng, J. M. Jarvis, J. Yu, U. Jena, N. Nirmalakhandan, T. M. Schaub and C. E. Brewer, Bioresour. Technol., 2019, 294, 122184 CrossRef CAS PubMed.
- W. T. Chen, Y. Zhang, J. Zhang, G. Yu, L. C. Schideman, P. Zhang and M. Minarick, Bioresour. Technol., 2014, 152, 130–139 CrossRef CAS PubMed.
- L. Cao, G. Luo, S. Zhang and J. Chen, RSC Adv., 2016, 6, 15260–15270 RSC.
- X.-F. Wu, Q. Zhou, M.-F. Li, S.-X. Li, J. Bian and F. Peng, Bioresour. Technol., 2018, 270, 216–222 CrossRef CAS PubMed.
- M. Déniel, G. Haarlemmer, A. Roubaud, E. Weiss-Hortala and J. Fages, Energy Fuels, 2016, 30, 4895–4904 CrossRef.
- R. Saengsuriwong, T. Onsree, S. Phromphithak and N. Tippayawong, Bioresour. Technol., 2021, 341, 125750 CrossRef CAS PubMed.
- R. Kaur, P. Gera, M. K. Jha and T. Bhaskar, Renewable Energy, 2019, 141, 1026–1041 CrossRef CAS.
- B. Biswas, A. C. Fernandes, J. Kumar, U. D. Muraleedharan and T. Bhaskar, Fuel, 2018, 222, 394–401 CrossRef CAS.
- A. C. Fernandes, B. Biswas, J. Kumar, T. Bhaskar and U. D. Muraleedharan, Bioresour. Technol. Rep., 2021, 15, 100796 CrossRef CAS.
- J. Yu, M. Audu, M. T. Myint, F. Cheng, J. M. Jarvis, U. Jena, N. Nirmalakhandan, C. E. Brewer and H. Luo, Fuel Process. Technol., 2022, 227, 107119 CrossRef CAS.
- F. Cheng, K. Mallick, S. M. Henkanatte Gedara, J. M. Jarvis, T. Schaub, U. Jena, N. Nirmalakhandan and C. E. Brewer, Bioresour. Technol., 2019, 292, 121884 CrossRef CAS PubMed.
- B. Biswas, A. Arun Kumar, Y. Bisht, B. B. Krishna, J. Kumar and T. Bhaskar, Energy, 2021, 217, 119330 CrossRef CAS.
- D. A. Iryani, S. Kumagai, M. Nonaka, K. Sasaki and T. Hirajima, ARPN J. Eng. Appl. Sci., 2016, 11, 4833–4839 CAS.
- M. Jayathilake, S. Rudra and L. A. Rosendahl, Fuel, 2021, 305, 121498 CrossRef CAS.
- A. Chacón-Parra, D. Lewis, M. Glasius and P. van Eyk, Fuel, 2022, 311, 122499 CrossRef.
- S. H. Khajavi, S. Ota, R. Nakazawa, Y. Kimura and S. Adachi, Biotechnol. Prog., 2008, 22, 1321–1326 CrossRef PubMed.
- M. Sasaki, Z. Fang, Y. Fukushima, T. Adschiri and K. Arai, Ind. Eng. Chem. Res., 2000, 39, 2883–2890 CrossRef CAS.
- T. Oomori, S. H. Khajavi, Y. Kimura, S. Adachi and R. Matsuno, Biochem. Eng. J., 2004, 18, 143–147 CrossRef CAS.
- A. N. Alimny, M. Muharja and A. Widjaja, J. Phys.: Conf. Ser., 2019, 1373, 012006 CrossRef CAS.
- T. Rogalinski, K. Liu, T. Albrecht and G. Brunner, J. Supercrit. Fluids, 2008, 46, 335–341 CrossRef CAS.
- Z. Yan, J. Lian, Y. Feng, M. Li, F. Long, R. Cheng, S. Shi, H. Guo and J. Lu, Fuel, 2021, 289, 119969 CrossRef CAS.
- J. D. Sheehan and P. E. Savage, Chem. Eng. J., 2020, 390, 124600 CrossRef CAS.
- J. D. Sheehan, A. Abraham and P. E. Savage, React. Chem. Eng., 2019, 4, 1237–1252 RSC.
- M. Esteban, A. García, P. Ramos and M. Márquez, J. Supercrit. Fluids, 2008, 46, 137–141 CrossRef CAS.
- D. Klingler, J. Berg and H. Vogel, J. Supercrit. Fluids, 2007, 43, 112–119 CrossRef CAS.
- D. Ruen-ngam, A. T. Quitain, M. Tanaka, M. Sasaki and M. Goto, J. Supercrit. Fluids, 2012, 66, 215–220 CrossRef CAS.
- P. Khuwijitjaru, Chem. Eng. J., 2004, 99, 1–4 CrossRef CAS.
- A. L. Milliren, J. C. Wissinger, V. Gottumukala and C. A. Schall, Fuel, 2013, 108, 277–281 CrossRef CAS.
- T. Kocsisová, J. Juhasz and J. Cvengroš, Eur. J. Lipid Sci. Technol., 2006, 108, 652–658 CrossRef.
- R. Alenezi, G. Leeke, R. Santos and A. Khan, Chem. Eng. Res. Des., 2009, 87, 867–873 CrossRef CAS.
- D. C. Hietala and P. E. Savage, Chem. Eng. J., 2015, 265, 129–137 CrossRef CAS.
- N. Abad-Fernández, E. Pérez, Á. Martín and M. J. Cocero, J. Supercrit. Fluids, 2020, 165, 104940 CrossRef.
- T. L.-K. Yong and Y. Matsumura, Ind. Eng. Chem. Res., 2012, 51, 11975–11988 CrossRef CAS.
- Wahyudiono, M. Sasaki and M. Goto, J. Mater. Cycles Waste Manage., 2011, 13, 68–79 CrossRef CAS.
- Y. Cao, C. Zhang, D. C. Tsang, J. Fan, J. H. Clark and S. Zhang, Ind. Eng. Chem. Res., 2020, 59, 16957–16969 CrossRef CAS.
- A. D. Chacón-Parra, P. A. Hall, D. M. Lewis, M. Glasius and P. J. van Eyk, ACS Sustain. Chem. Eng., 2022, 10, 10989–11003 CrossRef.
- Y. Fan, U. Hornung, N. Dahmen and A. Kruse, Biomass Convers. Biorefin., 2018, 8, 909–923 CrossRef CAS.
- F. Yang, P. Zhu, H. Zheng, W. Yang, S. Wu, H. Ye and L. Che, J. Supercrit. Fluids, 2023, 199, 105943 CrossRef CAS.
- M. S. Seshasayee and P. E. Savage, Chem. Eng. J., 2021, 417, 129268 CrossRef CAS.
- M. S. Seshasayee, R. Stofanak and P. E. Savage, iScience, 2021, 24, 103498 CrossRef CAS PubMed.
- H. Jin, B. Bai, W. Wei, Y. Chen, Z. Ge and J. Shi, ACS Sustain. Chem. Eng., 2020, 8, 7039–7050 CrossRef CAS.
- Y. Liu, C. Fan, H. Zhang, J. Zou, F. Zhou and H. Jin, Int. J. Hydrogen Energy, 2019, 44, 15758–15765 CrossRef CAS.
- P. Pereira, P. E. Savage and C. W. Pester, ACS Sustain. Chem. Eng., 2023, 11, 7203–7209 CrossRef CAS.
- M. Watanabe, H. Hirakoso, S. Sawamoto, T. Adschiri and K. Arai, J. Supercrit. Fluids, 1998, 13, 247–252 CrossRef CAS.
- M. Čolnik, D. Pečar, Ž. Knez, A. Goršek and M. Škerget, Processes, 2021, 10, 24 CrossRef.
- L. Tai, S. Musivand, B. de Caprariis, M. Damizia, R. Hamidi, W. Ma and P. De Filippis, J. Cleaner Prod., 2022, 337, 130529 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Document including supplementary analysis, tables and figures and Excel sheet including all the literature data used for the analysis. See DOI: https://doi.org/10.1039/d3su00458a |
| This journal is © The Royal Society of Chemistry 2024 |