Open Access Article
Open Access ArticleCurvature induces and enhances transport of spinning colloids through narrow channels†
Eric
Cereceda-López
 ab,
Marco
De Corato
ab,
Marco
De Corato
 c,
Ignacio
Pagonabarraga
c,
Ignacio
Pagonabarraga
 ad,
Fanlong
Meng
ad,
Fanlong
Meng
 efg,
Pietro
Tierno
efg,
Pietro
Tierno
 *abd and
Antonio
Ortiz-Ambriz
*abd and
Antonio
Ortiz-Ambriz
 *h
*h
aDepartament de Física de la Matèria Condensada, Universitat de Barcelona, 08028, Spain. E-mail: ptierno@ub.edu
bInstitut de Nanociència i Nanotecnologia, Universitat de Barcelona (IN2UB), 08028, Barcelona, Spain
cAragon Institute of Engineering Research (I3A), University of Zaragoza, Zaragoza, Spain
dUniversity of Barcelona Institute of Complex Systems (UBICS), 08028, Barcelona, Spain
eChinese Academy of Sciences, CAS Key Laboratory for Theoretical Physics, Institute of Theoretical Physics, Beijing 100190, China
fUniversity of Chinese Academy of Sciences, School of Physical Sciences, Beijing 100049, China
gUniversity of Chinese Academy of Sciences, Wenzhou Institute, Wenzhou 325000, China
hTecnologico de Monterrey, School of Science and Engineering, 64849, Monterrey, Mexico. E-mail: aortiza@tec.mx
First published on 9th September 2024
Abstract
The effect of curvature and how it induces and enhances the transport of colloidal particles driven through narrow channels represent an unexplored research avenue. Here we combine experiments and simulations to investigate the dynamics of magnetically driven colloidal particles confined through a narrow, circular channel. We use an external precessing magnetic field to induce a net torque and spin the particles at a defined angular velocity. Due to the spinning, the particle propulsion emerges from the different hydrodynamic coupling with the inner and outer walls and strongly depends on the curvature. The experimental findings are combined with finite element numerical simulations that predict a positive rotation translation coupling in the mobility matrix. Further, we explore the collective transport of many particles across the curved geometry, making an experimental realization of a driven single file system. With our finding, we elucidate the effect of curvature on the transport of microscopic particles which could be important to understand the complex, yet rich, dynamics of particle systems driven through curved microfluidic channels.
1 Introduction
In viscous fluids the Reynolds (Re) number (the ratio between inertial and viscous forces) is relatively low and the Navier–Stokes equations become effectively time-reversible.1 Under such conditions, inducing the transport of microscale objects may become problematic since any reciprocal motion, namely a series of body/shape deformations that are identical when reversed in time, do not produce a net movement.2 However, many artificial prototypes are often powered by external fields, such as magnetic ones, which indeed induce periodic deformations or translations. Thus, at low Re these systems require a subtle strategy to overcome the time-reversibility and propel, such as the presence of flexibility,3–6 non linearity of the dispersing medium,7,8 or the interaction between different parts.9–11The problem of propulsion at low Re, becomes even more complex when the active object, either a microswimmer or a synthetic self-propelled particle, is confined within a narrow channel.12 The presence of confining walls can affect the microswimmer dynamics in many ways. In particular, a planar surface can attract swimming bacteria due to hydrodynamic interactions,13,14 induce circular trajectories,15,16 or curved posts can be used as reflecting barriers or traps.17 Moreover, it has been recently found that the curvature of the fallopian tubes guides the locomotion of sperm cells to promote fertilization,18 and similar situations are not limited to bacteria or sperm cells, but extend to other types of situations.19–22
On the other hand, confinement can be used to rectify the random motion of microswimmers using patterned channels and other ratcheting methods.23–31 At low Re, the close proximity of a flat wall can break the spatial symmetry of the flow field and induce propulsion in simpler artificial systems, such as rotating magnetic particles,32–35 doublets36 or elongated structures.37,38
Here we show that the geometry of the channel can be used to induce translation of a driven particle by breaking the rotational symmetry of the hydrodynamic interactions. We confine spinning magnetic colloids within narrow circular channels characterized by a width close to the particle diameter. We find that curvature can rectify the particle rotational motion inducing a net translational one. Moreover, these surface rotors are able to translate along the ring at a velocity that depends on the curvature of the channel. We explain this experimental observation using numerical simulations which elucidate the mechanism of motion based on the difference between the hydrodynamic coupling with the two confining walls, where the largest coupling is with the wall characterized by the largest curvature. Further, we investigate the collective propulsion of many driven rotors, and show that within the circular ring the magnetic particles behave as a driven single-file, with an initial diffusive regime followed by a ballistic one at a large time scale.
2. Methods
2.1. Experimental protocol
The circular microchannels are realized in polydimethylsiloxane (PDMS) with soft lithography. We first use a commercial software (AUTOCAD) to design a sequence of lithographic channels with a width w = 3 μm, see Fig. 1(a). The channels are placed concentrically so that they are always separated by a distance of 10 μm. To sample the channels in 5 μm intervals, the rings are separated in two sets, one starting at 5 μm and the other at 10 μm. The microchannels present a depth of ∼4 μm thus, larger than the particle width, such that the particles are completely surrounded by solid walls, as shown by the confocal profile in Fig. 1(b).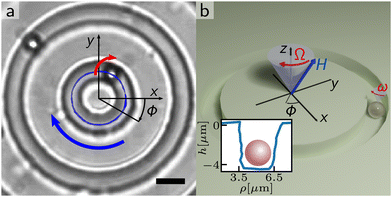 | ||
| Fig. 1 (a) Optical microscope image of two circular channels in a PDMS mold each with a spinning paramagnetic colloidal particle. The red (blue) arrow in the image indicates the direction of the particle rotation (trajectory). Scale bar is 5 μm, see also corresponding Movie S1 in the ESI.† (b) Schematic of a particle within the circular channel and of the applied precessing magnetic field H. The inset shows the transverse profile of the channel measured using confocal profilometry. | ||
We use the following procedure to realize the structures in PDMS. First, we fabricate reliefs in SU-8, an epoxy-based negative photoresist, on top of a silicon (Si) wafer. The latter was prepared by dehydrating it for 10 minutes at 200 °C on a hot plate and then plasma cleaned it for 1 minute at a pressure of 1 Torr. After that, a layer of SU-8 3005 is spin-coated on top of the Si wafer for 10 s at 500 revolution per minute (rpm), followed by spinning at 4000 rpm for 120 s, and later baked on a hot plate heated at a temperature of 95 °C for 2 minutes. The SU-8 is then polymerized via exposure to UV light through a cromium (Cr) mask for 5.6 s with a light intensity of 100 mJ cm−2 (Mask aligner, i-line configuration with wavelength λ = 365 nm). Then the exposed film is baked again for 1 min at 65 °C and for another 1 min at 95 °C, and developed for 30 s in propylene glycol methyl ether acetate. We then transfer the obtained master to PDMS by first cleaning the SU-8 structure in a plasma cleaner, operating at a pressure of 1 Torr for 1 min, and then silanizing it in a vacuum chamber with a drop of silane (SiH4) for one hour. After that, the PDMS is spin coated onto the Si wafer at 4000 rpm during 1 min and baked for 30 min above a hot plate at a temperature of 95 °C. The PDMS is then transferred to a cover glass by plasma cleaning both surfaces (1 min at 1 Torr), then joining the PDMS and the glass and finally peeling very carefully with a sharp blade the resulting PDMS film.
Once the PDMS channels are fabricated, we realize a closed fluidic cell by first painting the PDMS patterned coverglass with two strips of silicon-based vacuum grease. After that, we deposit a drop containing the colloidal particles dispersed in water on top of it, we close it with another clean coverglass and then we seal the two open sides with more grease. The colloidal suspension is prepared by dispersing 1.5 μl from the stock solution of paramagnetic colloidal particles (Dynabeads M-270, 2.8 μm in diameter) in 1 ml of ultrapure water (MilliQ system, Millipore).
The fluidic cell is placed on a custom-made inverted optical microscope equipped with optical tweezers that are controlled using two acousto-optic deflectors (AA Optoelectronics DTSXY-400-1064) driven by a radio frequency wave generator (DDSPA2X-D431b-34). The optical tweezers ensure that the channels are filled with the desired number of particles. Since it is often necessary to push the deposited particles out of the channels, the tweezers have been set up to trap from below by driving the laser radiation (Manlight ML5-CW-P/TKS-OTS) through a high numerical aperture objective (Nikon 100×, numerical aperture 1.3). The trapping objective is also used for observation and a custom-made TV lens is mounted in the microscope setup to observe a wide enough field of view, ∼100 μm2.
The external magnetic fields used to spin the particles are applied using a set of five coils, all arranged around the sample. In particular, two coils have the main axis aligned along the ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) direction, two for the ŷ direction and one for the ẑ direction which is perpendicular to the particle plane (
direction, two for the ŷ direction and one for the ẑ direction which is perpendicular to the particle plane (![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) ,ŷ). The sample is placed directly above the coil oriented along the ẑ axis. The magnetic coils are connected to three power amplifiers (KEPCO BOP 20-10) which are driven by a digital-analog card (cDAQ NI-9269) and controlled with a custom-made LabVIEW program.
,ŷ). The sample is placed directly above the coil oriented along the ẑ axis. The magnetic coils are connected to three power amplifiers (KEPCO BOP 20-10) which are driven by a digital-analog card (cDAQ NI-9269) and controlled with a custom-made LabVIEW program.
2.2. Numerical simulations
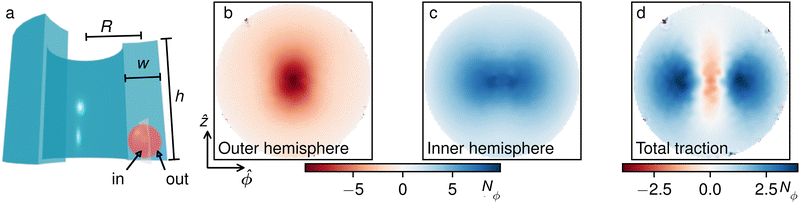
To understand the mechanism of propulsion of the rotating particle in the channel, we perform finite element simulations. We consider a sphere suspended in a Newtonian liquid with viscosity η and confined in a channel obtained from two concentric cylinders of height h, as schematically depicted in Fig. 3(a). The Reynolds number, estimated from the characteristic particle velocity in the ring, is vanishingly small and thus we neglect inertial effects. We consider a Cartesian reference frame with origin at the center of the channel (Fig. 1). We assume that the distance between the particle and the bottom wall, zp, is fixed due to the balance between gravitational forces and electrostatic repulsion. The ratio of the lateral size of the channel w and the particle radius is fixed to w/a = 2.2 which for our a = 1.4 μm particles produces a channel 3.1 μm wide, similar to that shown in the inset of Fig. 1b. To model the open channel in the experimental system, we chose h much larger than w. The particle is placed near the bottom of the domain, and horizontally at the center, as depicted in Fig. 3(a). The rotating magnetic field generates a constant torque τm along the ẑ axis, which leads to a constant angular velocity ωp along the same direction. As a result of the rotation, we expect the particle to translate along the direction that is tangential to the channel centerline,![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b5.gif) , due to the hydrodynamic coupling with the channel walls (see Fig. 1).
, due to the hydrodynamic coupling with the channel walls (see Fig. 1).
To investigate how the motion of the particle along the channel depends on the radius of curvature, we compute the mobility matrix of the particle. The mobility matrix, M, relates the translational (vp) and angular velocity (ωp) of the particle to external forces (F) and torques (t):
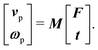 | (1) |
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b5.gif) direction.
direction.
To obtain M, we first find the resistance matrix R, and then compute M as M = R−1. To do so, we solve the Stokes equation by imposing a single component of the velocity vector and then computing the resulting force and torque acting on the particle:
| ∇2v − ∇p = 0 | (2) |
| ∇·v = 0 | (3) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = 0, being
= 0, being ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) the surface of the particle. On
the surface of the particle. On ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) we fix the velocity or the angular velocity. The total forces and torques acting on the particle are computed using:
we fix the velocity or the angular velocity. The total forces and torques acting on the particle are computed using: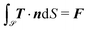 | (4) |
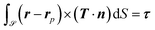 | (5) |
3. Single particle motion
We start by illustrating the dynamics of individual spinning particles dispersed within circular channels characterized by different radius R. Fig. 1(a) shows a microscope image of two channels with radii R = 5, 15 μm and filled with one paramagnetic colloidal particle each, while the corresponding schematic of the experimental system is shown in Fig. 1(b). The spinning is induced by the application of an external magnetic field that performs conical precession at a frequency ω and an angle θ around the ẑ axis:H ≡ H0[cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θẑ + sin θẑ + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(cos(ωt) θ(cos(ωt)![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) + sin(ωt)ŷ)], + sin(ωt)ŷ)], | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(cos(ωt)
θ(cos(ωt)![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) + sin(ωt)ŷ) which is used to spin the particles, and a static one perpendicular to the particle plane, Hz = H0cos
+ sin(ωt)ŷ) which is used to spin the particles, and a static one perpendicular to the particle plane, Hz = H0cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θẑ which is used to control the dipolar interactions when many particles are present. In particular, we keep constant the magnetic field values to H0 = 900 Am−1, the frequency f = 50 Hz such that ω = 2πf = 314.2 rad s−1 and the cone angle at θ = 44.5°.
θẑ which is used to control the dipolar interactions when many particles are present. In particular, we keep constant the magnetic field values to H0 = 900 Am−1, the frequency f = 50 Hz such that ω = 2πf = 314.2 rad s−1 and the cone angle at θ = 44.5°.
For the single particle case, the precessing field at relative high frequency, is able to induce an average magnetic torque, τm = 〈m × H〉, which sets the particles in rotational motion at an angular speed ωp close to the plane. This torque arises due to the finite relaxation time tr of the particle magnetization, as demonstrated in previous works.39,40 Note that here, for simplicity, we assume that the particles are characterized by a single relaxation time. For a paramagnetic colloid with radius a = 1.4 μm and magnetic volume susceptibility χ ∼ 0.4, the torque can be calculated as,41,42
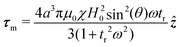 | (7) |
In the overdamped limit, the magnetic torque is balanced by the viscous torque τv arising from the rotation in water, τm + τv = 0. Close to a planar wall, τv can be written as, τv = −8πηωpa3fr(a/zp), where η = 10−3 Pa s is the viscosity of water, and fr(a/zp) is a correction term that accounts for the proximity of the bottom wall at a distance zp.43 In particular, assuming the space between the particle and the wall ∼100 nm, fr(a/h) = 1.45. In the overdamped regime, the balance between both torques allows estimating the particle mean angular velocity: 〈ωp〉 = μ0H20sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θχτrω/[6η(1 + τr2ω2)], which gives ωp = 3.27 rad s−1. Clearly, this estimate does not consider the presence of a top wall and how it reduces the particle angular rotation, as we will see later.
θχτrω/[6η(1 + τr2ω2)], which gives ωp = 3.27 rad s−1. Clearly, this estimate does not consider the presence of a top wall and how it reduces the particle angular rotation, as we will see later.
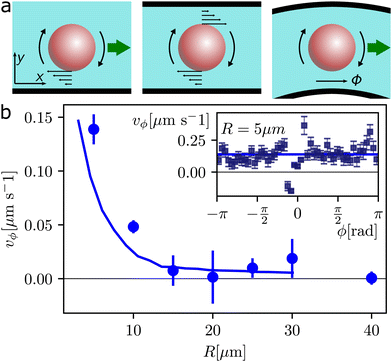
Now let's consider the general situation of a rotating free particle, far away from any surface. The rotational motion is reciprocal, and unable to induce any drift. However, if close to a solid wall, as shown in the left schematic in Fig. 2(a), the rotational motion can be rectified into a net drift velocity due to the hydrodynamic interaction with the close substrate,43 which breaks the spatial symmetry of the flow. The situation changes when the particle is squeezed between two flat channels, as in the middle of Fig. 2(a). Now the asymmetric flow close to the bottom surface is balanced by the one at the top, and the spatial symmetry is restored. As a consequence, the particle is unable to propel unless small thermal fluctuations can displace the colloid from the central position making it closer to one of the two surfaces. However, even in this case, the rectification will be balanced on average. Here we show that, in contrast to previous cases, when the particle is confined between two curved walls, the effect of curvature breaks again the spatial symmetry, and induce a net particle motion, as shown in the last schematic in Fig. 2(a).
To demonstrate this point, we perform a series of experiments by varying the channel radius R ∈ [5,40] μm and measuring the tangential velocity of the particle vϕ, Fig. 2(b). We find that while for large rings (R > 20 μm) the particle does not display any net movement, vϕ ∼ 0, below R ∼ 10 μm the effect of curvature becomes important and it can rectify the rotational motion of the particle. Indeed, for R = 5 μm the particle circulates along the channel at a non-negligible speed of vϕ = 0.146 μm s−1. The rectification process decreases by increasing R, while the sense of rotation is equal to that of the precessing field, sign that the spinning particle is more strongly coupled to the wall of high curvature of the channel.
This can be also appreciated from the Video S1 in the ESI,† where a driven particle in the small, R = 5 μm ring moves clockwise, even if the velocity is not uniform. Regarding this last point, we note that due to the resolution limit of the lithographic technique, our small channels may present imperfections such as deformations and non-uniform edges. These defects may pin a rotating particle during its movement for a longer time. This effect can be observed in the inset to Fig. 2, where we have discretized space and calculated the mean tangential velocity vϕ for each slice of the circular trajectory. Here the time spent by the particle near ϕ = 0 is larger and, at this point, the colloidal particle is trapped by a defect, taking a long time to be released by thermal motion. To avoid this problem, we have calculated the mean velocity directly from the binned series shown in the inset, giving equal weights to all the discrete slices.
We can use the equation
| vϕ = Mvϕ,τzτz | (8) |
To understand the origin of the propulsion, we have used the simulation to calculate the surface traction along a sphere rotating at a constant angular velocity. The traction is computed in each point on the particle surface from the stress tensor as T·n, where n is the unit vector normal to the surface of the sphere. In Fig. 3 we are showing only the ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b5.gif) – component of the traction vector, which points in the direction of the particle's translational motion. In Fig. 3(b) and (c), where we show the normalized traction force Nϕ calculated in the outer and inner hemispheres of the particle respectively, we find that the coupling of the particle surface to the outer wall pushes the particle back towards the negative
– component of the traction vector, which points in the direction of the particle's translational motion. In Fig. 3(b) and (c), where we show the normalized traction force Nϕ calculated in the outer and inner hemispheres of the particle respectively, we find that the coupling of the particle surface to the outer wall pushes the particle back towards the negative ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b5.gif) -direction, corresponding to a negative angular velocity. In contrast, the interaction between the inner hemisphere of the particle and the inner wall pushes the particle along the forward direction. The last panel, Fig. 3(d) shows the sum of both interactions, whose integral yields the total hydrodynamic force acting along the
-direction, corresponding to a negative angular velocity. In contrast, the interaction between the inner hemisphere of the particle and the inner wall pushes the particle along the forward direction. The last panel, Fig. 3(d) shows the sum of both interactions, whose integral yields the total hydrodynamic force acting along the ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b5.gif) direction. Even though there is a negative component in the center of the circle, which indicates a higher coupling to the outer wall, it is clear that the strongest contribution comes from the two positive lobes where the inner hemisphere coupling is stronger, and the total force along the
direction. Even though there is a negative component in the center of the circle, which indicates a higher coupling to the outer wall, it is clear that the strongest contribution comes from the two positive lobes where the inner hemisphere coupling is stronger, and the total force along the ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b5.gif) axis is positive. Thus, our finite element simulations confirm that the rectification process of a single rotating particle within a curved channel results only from the hydrodynamic interactions between the particle and the surfaces.
axis is positive. Thus, our finite element simulations confirm that the rectification process of a single rotating particle within a curved channel results only from the hydrodynamic interactions between the particle and the surfaces.
4. Driven magnetic single file
We next explore the collective dynamics of an ensemble of interacting spinning colloids that are confined along the circular channel. Since the lateral width is w ∼ 2a the colloidal particles cannot pass each other, thus effectively forming a “single file” system.44,45 While the particle dynamics in a “passive” single file, e.g. driven only by thermal fluctuations, have been a matter of much interest in the past,46–48 more scarce are realizations of “driven” single files,49,50 where the particles undergo ballistic transport due to external force and collective interactions.51–54 In our case, a typical situation is shown in Fig. 4(a), where N = 23 particles move within a channel of radius R = 35 μm (linear density ρL = Na/(2πR) = 0.15), see also Video S2 in the ESI.† The applied precessing magnetic field apart from inducing the spinning motion within the particle is also used to reduce the magnetic dipolar interaction between them. In particular, in the point dipole approximation, we can consider that the interaction potential Udd between two equal moments mi,j at relative position r = |ri − rj| is given by: Udd = μ0/4π{(mi·mj/r3) − [3(mi·r)(mj·r)/r5]}. Here the induced moment is given by, m = VχH, being V = (4πa3)/3 the particle volume. If we assume that the induced moments follow the precessing field with a cone angle θ, these interactions can be time-averaged, and become: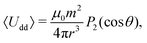 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) = (3cos2
θ) = (3cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1)/2 is the second order Legendre polynomial. For the field parameters used, the dipolar interaction is small since θ = 44.5° which is close to the “magic angle” (θ = 45.7°) where P2(cos
θ − 1)/2 is the second order Legendre polynomial. For the field parameters used, the dipolar interaction is small since θ = 44.5° which is close to the “magic angle” (θ = 45.7°) where P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) ∼ 0. From these values, we estimate that the pair repulsion is of the order of Udd = 5kBT being T = 293 K the thermodynamic temperature and kB the Boltzmann constant. Thus, the magnetic interactions are slightly repulsive to avoid the particles attracting each other at high density. Indeed, for a purely rotating magnetic field (Hz = 0, θ = 90°) the spinning particles aggregate forming compact chains that induce clogging of the channel. In contrast, to obtain a strong repulsion we would require an in-plane field component with a much lower amplitude that would induce a smaller magnetic torque.
θ) ∼ 0. From these values, we estimate that the pair repulsion is of the order of Udd = 5kBT being T = 293 K the thermodynamic temperature and kB the Boltzmann constant. Thus, the magnetic interactions are slightly repulsive to avoid the particles attracting each other at high density. Indeed, for a purely rotating magnetic field (Hz = 0, θ = 90°) the spinning particles aggregate forming compact chains that induce clogging of the channel. In contrast, to obtain a strong repulsion we would require an in-plane field component with a much lower amplitude that would induce a smaller magnetic torque.
 | ||
| Fig. 4 (a) Optical microscope image of paramagnetic colloidal particles spinning inside a circular channel with radius R = 35 μm. The scale bar is 10 μm, see also Movie S2 in the ESI.† (b) Mean squared displacement of the circumference arc 〈Δs2〉 as a function of the time intervals δt for different densities ρL. Left (right) plot shows the experimental data for a channel with radius R = 15 μm (R = 35 μm respectively). The dashed-dotted line indicates the normal diffusion (α = 1) while the dotted line shows the ballistic regime (α = 2). Colorbar, legend, and axes are common in both plots. (c) Average Kuramoto order parameter 〈r2〉 (eqn (10)) versus particle density ρL. Blue squares (red disks) are experimental data for a channel with radius R = 15 μm (R = 35 μm respectively). Inset shows the temporal evolution of 〈r2〉 for different particle densities, identified by the color bar. | ||
Thus, we perform different experiments by varying both the particle linear density within the ring, ρL, and the channel radius R, while keeping fixed the applied field parameters, which are the same as in the single-particle case. From the particle positions, we measure the mean squared displacement (MSD) along the circumference arc Δs connecting a pair of particles within the ring. Here the MSD is calculated as 〈Δs2(Δt)〉 ≡ 〈(s(t) − s(t + δt))2〉, being δt the lag time and 〈⋯〉 a time average. We use the MSD to distinguish the dynamic regimes at the steady state. Here the MSD behaves as a power law 〈Δs2(Δt)〉 ∼ τα, with an exponent α = 1 for standard diffusion and α = 2 for ballistic transport, i.e. a single file of particles with constant speed. As shown in the left plot of Fig. 4(b), for a small channel of width R = 15 μm, all MSDs behave similarly, showing an initial diffusive regime followed by a ballistic one at a longer time, and the transition between both dynamic regimes occurs at ∼10–20 s. Increasing the particle density has a small effect on the ballistic regime, where the velocity is higher at a lower density. This effect indicates that the inter-particle interactions reduce the average speed of the single file. Since magnetic dipolar interactions are minimized by spinning the field at the “magic angle”, this effect may arise from hydrodynamics. Indeed, it was recently observed that these interactions may affect the circular motion of driven systems.55,56 In contrast, the situation changes for a larger channel, R = 35 μm, see the right plot in Fig. 4(b). There, at low density ρL the particle tangential speed vanishes, vϕ = 0 (as shown in Fig. 2(b)), and thus we recover a diffusive regime also at long time until the slope fluctuates due to lack of statistics. Increasing ρL we recover the transition from the diffusive to the ballistic regime, but occurring at a relatively longer time, ∼100 s.
The emergence of a ballistic regime results from the cooperative movement of the particles which generate hydrodynamic flow fields near the surface. Indeed, while single particles display negligible translational velocity in channel of radii R = 15 μm and 35 μm (Fig. 2(a)), we observed a ballistic regime in both cases at high density. As previously observed for a linear, one-dimensional chain of rotors,42 the spinning particles generate a cooperative flow close to a bounding wall which act as a “conveyor belt effect”. Here, the situation is similar, however the larger distance between the particles due to their repulsive interactions and the presence of two walls which screen the flow reduce the average speed of the single file and increase the time required for this cooperative effect to set in.
We can estimate the transition time between both regimes for the single particle. We start by measuring the diffusion coefficient of the single particle within the channel from the MSD, D = 0.0379 ± 0.0002 μm2 s−1. Thus, the motion of an individual magnetic particle will turn from the Brownian motion with 〈Δs2〉 = 2Dt to a ballistic one with 〈Δs2〉 = (Rωpt)2 after a characteristic time τc = D/(Rωp)2. From the experimental data in Fig. 2(b) we have that ωp = 0.0073 rad s−1 for R = 15 μm which gives τc = 3.1 s, similar to the small channel in the left of Fig. 4(b).
We further analyze the relative particle displacement, and the presence of synchronized movement, by measuring a Kuramoto-like57,58 order parameter, defined as:
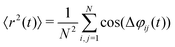 | (10) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) ) located in the particle plane. This order parameter is normalized such that 〈r2〉 ∈ [0,1], where 1 corresponds to the fully coordinated relative movement of all spinning particles. Fig. 4(c) show the average value of r2 at different density ρL. In particular, we find that r2 increases with ρL since, for high density the repulsive particles start to interact with each other and their translations become more coordinated. On the other hand, we find that 〈r2〉 decreases with the radius of curvature (data from red to blue) meaning that the curvature reduces the cooperative translation between the spinning particles. The cooperative movement revealed from the Kuramoto order parameter results from the repulsive magnetic dipolar interactions. Indeed, this parameter increases with density i.e. when the particles are closer to each other and experience stronger repulsive forces. However, the emergence of self-propulsion in our system is a pure hydrodynamic effect induced by the wall curvature. Indeed, the precessing field induces reciprocal magnetic dipolar interactions which could not give rise to any net motion of the spinning particles.
) located in the particle plane. This order parameter is normalized such that 〈r2〉 ∈ [0,1], where 1 corresponds to the fully coordinated relative movement of all spinning particles. Fig. 4(c) show the average value of r2 at different density ρL. In particular, we find that r2 increases with ρL since, for high density the repulsive particles start to interact with each other and their translations become more coordinated. On the other hand, we find that 〈r2〉 decreases with the radius of curvature (data from red to blue) meaning that the curvature reduces the cooperative translation between the spinning particles. The cooperative movement revealed from the Kuramoto order parameter results from the repulsive magnetic dipolar interactions. Indeed, this parameter increases with density i.e. when the particles are closer to each other and experience stronger repulsive forces. However, the emergence of self-propulsion in our system is a pure hydrodynamic effect induced by the wall curvature. Indeed, the precessing field induces reciprocal magnetic dipolar interactions which could not give rise to any net motion of the spinning particles.
Conclusions
We have demonstrated that a circular microfluidic channel can be used to induce and enhance the propulsion of spinning particles while the effect becomes absent for a flat one. The propulsion appears from the different hydrodynamic coupling to each of the two curved walls; even if the no-slip condition of each wall pushes the particle along an opposite direction, the two interactions are not symmetric due to the channel curvature. The dominating interaction is the one from the inner wall, which produces a rotation along the channel in the same direction as the angular velocity. We confirm this hypothesis both via experiments and finite element simulations.We note here that the realization of field-driven magnetic prototypes able to propel in viscous fluids is important for both fundamental and technological reasons. In the first case, the collection of self-propelled particles can be used as a model system to investigate fundamental aspects of non-equilibrium statistical physics.59–63 On the other hand, it is expected that these prototypes can be used as controllable inclusions in microfluidic systems,64–68 either to control or regulate the flow69–71 or to transport microscopic biological or chemical cargoes.38,72–77 The propulsion mechanism unveiled in this work could be used to move particles along a microfluidic device, either by designing it with a circular path, or by coupling many semicircles in a zig-zag way to form an elongated path.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Carolina Rodriguez-Gallo who shared the protocol for the sample preparation, and the MicroFabSpace and Microscopy Characterization Facility, Unit 7 of ICTS “NANBIOSIS” from CIBER-BBN at IBEC. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 811234). M. D. C. acknowledges funding from the Ramon y Cajal fellowship RYC2021-030948-I and the grant PID2022-139803NB-I00 funded by the MICIU/AEI/10.13039/501100011033 and by the EU under the NextGeneration EU/PRTR & FEDER programs. I. P. acknowledges support from MICINN and DURSI for financial support under Projects No. PID2021-126570NB-100 AEI/FEDER-EU and No. 2021SGR-673, respectively, and from Generalitat de Catalunya under Program Icrea Acadèmia. P. T. acknowledges support from the Ministerio de Ciencia, Innovación y Universidades (grant no. PID2022-137713NB-C21 AEI/FEDER-EU) and the Agència de Gestió d'Ajuts Universitaris i de Recerca (project 2021 SGR 00450) and the Generalitat de Catalunya (ICREA Académia).Notes and references
- J. Happel and H. Brenner, Low Reynolds number hydrodynamics: with special applications to particulate media, Springer Science and Business Media, 2012, vol. 1 Search PubMed.
- E. M. Purcell, Am. J. Phys., 1977, 45, 3–11 CrossRef.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 862–865 CrossRef CAS PubMed.
- W. Gao, S. Sattayasamitsathit, K. M. Manesh, D. Weihs and J. Wang, J. Am. Chem. Soc., 2010, 132, 14403–14405 CrossRef CAS PubMed.
- A. Cebers and K. Erglis, Adv. Funct. Mater., 2016, 26, 3783–3795 CrossRef CAS.
- T. Yang, B. Sprinkle, Y. Guo and N. Wu, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 18186–18193 CrossRef CAS PubMed.
- T. Qiu, T.-C. Lee, A. G. Mark, K. I. Morozov, R. Münster, O. Mierka, S. Turek, A. M. Leshansky and P. Fischeru, Nat. Commun., 2014, 5, 5119 CrossRef CAS PubMed.
- G. Li, E. Lauga and A. M. Ardekani, J. Non-Newtonian Fluid Mech., 2021, 297, 104655 CrossRef CAS.
- A. Snezhko and I. S. Aranson, Nat. Mater., 2016, 10, 698–703 CrossRef PubMed.
- J. García-Torres, C. Calero, F. Sagués, I. Pagonabarraga and P. Tierno, Nat. Commun., 2018, 9, 1663 CrossRef PubMed.
- G. Steinbach, M. Schreiber, D. Nissen, M. Albrecht, S. Gemming and A. Erbe, Phys. Rev. Res., 2020, 2, 023092 CrossRef CAS.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- P. D. Frymier, R. M. Ford, H. C. Berg and P. T. Cummings, Proc. Nat. Acad. Sci. U. S. A., 1995, 92, 6195–6199 CrossRef CAS PubMed.
- A. P. Berke, L. Turner, H. C. Berg and E. Lauga, Phys. Rev. Lett., 2008, 101, 038102 CrossRef PubMed.
- E. Lauga, W. R. DiLuzio, G. M. Whitesides and H. A. Stone, Biophys. J., 2006, 90, 400–412 CrossRef CAS PubMed.
- R. Di Leonardo, D. Dell'Arciprete, L. Angelani and V. Iebba, Phys. Rev. Lett., 2011, 106, 038101 CrossRef CAS PubMed.
- S. E. Spagnolie, G. R. Moreno-Flores, D. Bartolo and E. Lauga, Soft Matter, 2015, 11, 3396–3411 RSC.
- M. R. Raveshi, M. S. Abdul Halim, S. N. Agnihotri, M. K. O'Bryan, A. Neild and R. Nosrati, Nat. Commun., 2021, 12, 3446 CrossRef CAS PubMed.
- S. Bianchi, V. Carmona Sosa, G. Vizsnyiczai and R. Di Leonardo, Sci. Rep., 2020, 10, 4609 CrossRef CAS PubMed.
- M. Kuron, P. Stärk, C. Holm and J. de Graaf, Soft Matter, 2019, 15, 5908–5920 RSC.
- G. Volpe, I. Buttinoni, D. Vogt, H.-J. Kümmerer and C. Bechinger, Soft Matter, 2011, 7, 8810 RSC.
- S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105–147 CrossRef.
- P. Galajda, J. Keymer, P. Chaikin and R. Austin, J. Bacteriol., 2007, 189, 8704–8707 CrossRef CAS PubMed.
- M. B. Wan, C. J. Olson Reichhardt, Z. Nussinov and C. Reichhardt, Phys. Rev. Lett., 2008, 101, 018102 CrossRef CAS PubMed.
- B.-Q. Ai and J.-C. Wu, J. Chem. Phys., 2014, 140, 094103 CrossRef PubMed.
- E. Yariv and O. Schnitzer, Phys. Rev. E, 2014, 90, 032115 CrossRef PubMed.
- N. Koumakis, C. Maggi and R. Di Leonardo, Soft Matter, 2014, 10, 5695–5701 RSC.
- A. Pototsky, A. M. Hahn and H. Stark, Phys. Rev. E, 2013, 87, 042124 CrossRef CAS PubMed.
- B.-q Ai, Q.-y Chen, Y.-f He, F.-g Li and W.-r Zhong, Phys. Rev. E, 2013, 88, 062129 CrossRef PubMed.
- A. Guidobaldi, Y. Jeyaram, I. Berdakin, V. V. Moshchalkov, C. A. Condat, V. I. Marconi, L. Giojalas and A. V. Silhanek, Phys. Rev. E, 2014, 89, 032720 CrossRef CAS PubMed.
- V. Kantsler, J. Dunkel, M. Polin and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1187–1192 CrossRef CAS PubMed.
- P. Tierno, R. Golestanian, I. Pagonabarraga and F. Sagués, Phys. Rev. Lett., 2008, 101, 218304 CrossRef PubMed.
- M. Driscoll, B. Delmotte, M. Youssef, S. Sacanna, A. Donev and P. Chaikin, Nat. Phys., 2017, 13, 375–379 Search PubMed.
- F. Martinez-Pedrero, E. Navarro-Argemí, A. Ortiz-Ambriz, I. Pagonabarraga and P. Tierno, Sci. Adv., 2018, 4, eaap9379 Search PubMed.
- P. Tierno and A. Snezhko, ChemNanoMat, 2021, 7, 881–893 Search PubMed.
- H. Morimoto, T. Ukai, Y. Nagaoka, N. Grobert and T. Maekawa, Phys. Rev. E, 2008, 78, 021403 CrossRef PubMed.
- C. E. Sing, L. Schmid, M. F. Schneider, T. Franke and A. Alexander-Katz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 535 CrossRef CAS PubMed.
- L. Zhang, T. Petit, Y. Lu, B. E. Kratochvil, K. E. Peyer, R. Pei, J. Lou and B. J. Nelson, ACS Nano, 2010, 10, 6228–6234 CrossRef PubMed.
- P. Tierno, R. Muruganathan and T. M. Fischer, Phys. Rev. Lett., 2007, 98, 028301 CrossRef PubMed.
- X. J. A. Janssen, A. J. Schellekens, K. van Ommering, L. J. van Ijzendoorn and M. J. Prins, Biosens. Bioelectron., 2009, 24, 1937 CrossRef CAS PubMed.
- A. Cebers and H. Kalis, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 1292 Search PubMed.
- F. Martinez-Pedrero, A. Ortiz-Ambriz, I. Pagonabarraga and P. Tierno, Phys. Rev. Lett., 2015, 115, 138301 CrossRef PubMed.
- A. J. Goldman, R. G. Cox and H. Brenner, Chem. Eng. Sci., 1967, 22, 637 CrossRef CAS.
- Kärger and D. Ruthven, Diffusion in zeolites and other microporous solids, Wiley, New York, 1992 Search PubMed.
- J. Kärger, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 4173–4174 CrossRef PubMed.
- Q.-H. Wei, C. Bechinger and P. Leiderer, Science, 2000, 287, 625–627 CrossRef CAS PubMed.
- C. Lutz, M. Kollmann and C. Bechinger, Phys. Rev. Lett., 2004, 93, 026001 CrossRef PubMed.
- B. Lin, M. Meron, B. Cui, S. A. Rice and H. Diamant, Phys. Rev. Lett., 2005, 94, 216001 CrossRef PubMed.
- M. Köppl, P. Henseler, A. Erbe, P. Nielaba and P. Leiderer, Phys. Rev. Lett., 2006, 97, 208302 CrossRef PubMed.
- K. Misiunas and U. F. Keyser, Phys. Rev. Lett., 2019, 122, 214501 CrossRef CAS PubMed.
- A. Taloni and F. Marchesoni, Phys. Rev. Lett., 2006, 96, 020601 CrossRef PubMed.
- E. Barkai and R. Silbey, Phys. Rev. Lett., 2009, 102, 050602 CrossRef CAS PubMed.
- P. Illien, O. Bénichou, C. Mejía-Monasterio, G. Oshanin and R. Voituriez, Phys. Rev. Lett., 2013, 111, 038102 CrossRef CAS PubMed.
- P. Dolai, A. Das, A. Kundu, C. Dasgupta, A. Dhar and K. V. Kumar, Soft Matter, 2020, 16, 7077 RSC.
- E. Cereceda-López, D. Lips, A. Ortiz-Ambriz, A. Ryabov, P. Maass and P. Tierno, Phys. Rev. Lett., 2021, 127, 214501 CrossRef PubMed.
- D. Lips, E. Cereceda-López, A. Ortiz-Ambriz, P. Tierno, A. Ryabov and P. Maass, Soft Matter, 2022, 96, 8983–8994 RSC.
- Y. Kuramoto and I. Nishikawa, J. Stat. Phys., 1987, 49, 569–605 CrossRef.
- S. H. Strogatz, Phys. D: Nonlinear Phenom., 2000, 143, 1–20 CrossRef.
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- E. Fodor, C. Nardini, M. E. Cates, J. Tailleur, P. Visco and F. van Wijland, Phys. Rev. Lett., 2016, 117, 038103 CrossRef PubMed.
- C. Nardini, E. Fodor, E. Tjhung, F. van Wijland, J. Tailleur and M. E. Cates, Phys. Rev. X, 2017, 7, 021007 Search PubMed.
- L. S. Palacios, S. Tchoumakov, M. Guix, I. Pagonabarraga, S. Sánchez and A. G. Grushin, Nat. Commun., 2021, 12, 4691 CrossRef CAS PubMed.
- P. Tierno, R. Golestanian, I. Pagonabarraga and F. Sagués, J. Phys. Chem. B, 2008, 112, 16525 CrossRef CAS PubMed.
- J. Burdick, R. Laocharoensuk, P. M. Wheat, J. D. Posner and J. Wang, J. Am. Chem. Soc., 2008, 26, 8164–8165 CrossRef PubMed.
- S. Sundararajan, P. E. Lammert, A. W. Zudans, V. H. Crespi and A. Sen, Nano Lett., 2008, 8, 1271–1276 CrossRef CAS PubMed.
- S. Sanchez, A. Solovev, S. Harazim and O. Schmidt, J. Am. Chem. Soc., 2011, 701, 133 Search PubMed.
- P. Sharan, A. Nsamela, S. C. Lesher-Pérez and J. Simmchen, Small, 2021, 26, e2007403 CrossRef PubMed.
- A. Terray, J. Oakey and D. W. M. Marr, Science, 2002, 296, 1841 CrossRef CAS PubMed.
- T. Sawetzki, S. Rahmouni, C. Bechinger and D. W. M. Marr, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20141 CrossRef CAS PubMed.
- B. Kavcic, D. Babic, N. Osterman, B. Podobnik and I. Poberaj, Appl. Phys. Lett., 2009, 95, 023504 CrossRef.
- J. Palacci, S. Sacanna, A. Vatchinsky, P. Chaikin and D. Pine, J. Am. Chem. Soc., 2013, 135, 15978 CrossRef CAS PubMed.
- W. Gao and J. Wang, Nanoscale, 2014, 6, 10486–10494 RSC.
- F. Martinez-Pedrero and P. Tierno, Phys. Rev. Appl., 2015, 3, 051003 CrossRef.
- F. Martinez-Pedrero, H. Massana-Cid and P. Tierno, Small, 2017, 13, 1603449 CrossRef PubMed.
- G. Junot, C. Calero, J. García-Torres, I. Pagonabarraga and P. Tierno, Nano Lett., 2023, 23, 850–857 CrossRef CAS PubMed.
- X. Wang, B. Sprinkle, H. K. Bisoyi and Q. Li, Proc. Nat. Acad. Sci. U. S. A., 2023, 120, e2304685120 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Two videos illustrating the single and collective particle dynamics within the ring. See DOI: https://doi.org/10.1039/d4sm00829d |
| This journal is © The Royal Society of Chemistry 2024 |