Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Na-ion dynamics in the solid solution NaxCa1−xCr2O4 studied by muon spin rotation and neutron diffraction
Elisabetta
Nocerino
 *a,
Ola Kenji
Forslund
bm,
Hiroya
Sakurai
c,
Nami
Matsubara
a,
Anton
Zubayer
d,
Federico
Mazza
e,
Stephen
Cottrell
f,
Akihiro
Koda
g,
Isao
Watanabe
*a,
Ola Kenji
Forslund
bm,
Hiroya
Sakurai
c,
Nami
Matsubara
a,
Anton
Zubayer
d,
Federico
Mazza
e,
Stephen
Cottrell
f,
Akihiro
Koda
g,
Isao
Watanabe
 h,
Akinori
Hoshikawa
h,
Akinori
Hoshikawa
 i,
Takashi
Saito
j,
Jun
Sugiyama
i,
Takashi
Saito
j,
Jun
Sugiyama
 kl,
Yasmine
Sassa
a and
Martin
Månsson
kl,
Yasmine
Sassa
a and
Martin
Månsson
 *a
*a
aDepartment of Applied Physics, KTH Royal Institute of Technology, SE-100 44, Stockholm, Sweden. E-mail: nocerino@kth.se; condmat@kth.se
bPhysik-Institut, Universität Zürich, Winterthurerstrasse 190, Zürich, CH-8057, Switzerland
cNational Institute for Materials Science, Namiki, Tsukuba, Ibaraki 305-0044, Japan
dDepartment of Physics, Chemistry and Biology (IFM), Linköping University, SE-581 83 Linköping, Sweden
eInsitute of Solid State Physics, TU Wien, Wiedner Haupstraße 8-10, AT-1040 Wien, Austria
fISIS Facility, Rutherford Appleton Laboratory, Chilton, Didcot Oxon OX11 0QX, UK
gMuon Science Laboratory and Condensed Matter Research Center, Institute of Materials Structure Science, High Energy Accelerator Research Organization (KEK-IMSS), Tsukuba, Ibaraki 305-0801, Japan
hMuon Science Laboratory, RIKEN, 2-1 Hirosawa, Wako, Saitama 351-0198, Japan
iFrontier Research Center for Applied Atomic Sciences, Ibaraki University, IQBRC, 162-1 Shirakata, Tokai, Ibaraki 319-1106, Japan
jInstitute of Materials Structure Science, High Energy Accelerator Research Organization, 203-1 Shirakata, Tokai, Ibaraki 319-1107, Japan
kNeutron Science and Technology Center, Comprehensive Research Organization for Science and Society (CROSS), Tokai, Ibaraki 319-1106, Japan
lAdvanced Science Research Center, Japan Atomic Energy Agency, Tokai, Ibaraki 319-1195, Japan
mDepartment of Physics and Astronomy, Uppsala University, Box 516, Uppsala, SE-75120, Sweden
First published on 20th February 2024
Abstract
In this work we present a systematic set of measurements carried out by muon spin rotation/relaxation (μ+SR) and neutron powder diffraction (NPD) on the solid solution NaxCa1−xCr2O4. This study investigates Na-ion dynamics in the quasi-1D (Q1D) diffusion channels created by the honeycomb-like arrangement of CrO6 octahedra, in the presence of defects introduced by Ca substitution. With increasing Ca content, the size of the diffusion channels is enlarged; however, this effect does not enhance the Na ion mobility. Instead the overall diffusivity is hampered by the local defects and the Na hopping probability is lowered. The diffusion mechanism in NaxCa1−xCr2O4 is proposed to be interstitial and the activation energy as well as diffusion coefficient are determined for all the members of the solid solution.
1 Introduction
A growing population and rapidly developing societies are resulting in an increasing demand for clean energy supply. The harvest, transport, storage and efficient utilization of such energy are some of the grand challenges and fundamental needs for our future sustainable society. In this regard, there is a global drive to change the current energy system and move towards the abandonment of fossil sources and the adoption of renewable ones. Such striving to rebuild the energy system has led to the development of revolutionary materials science and applications, e.g., rechargeable Li-ion batteries,1,2 hydrogen storage,3–5 photovoltaics,6 and carbon capture.7 Such technologies provide some of the most efficient ways to promote a shift towards sustainable development and away from fossil fuels. There are however still many challenges that need to be addressed. For instance, in the case of Li-ion batteries, there are issues regarding scarcity and uneven geographical distribution of the resources required for the production of Li-batteries (Li, Co, Cu, Ni), as well as the high environmental impact of their extraction and the consequential high (constantly growing) manufacturing costs. As a result, such technology might soon become both environmentally as well as economically non-viable.8 This fact raises the question whether the environmental advantages of Li-batteries are canceled by the non-sustainability of their production.9 On one hand, part of the scientific community is trying to face the problem with new strategies for lithium mining and recycling,10 and on the other hand more sustainable alternatives are being investigated. For the latter, replacing Li with a similar alkali ion like Na11 or K12 is currently a very active field of research. The Na counterparts of Li-ion batteries became an object of steadily increasing interest during the past few decades, among academic and industrial researchers, due to the undeniable advantages of Na-based batteries.13 Beyond the fact that Na is one of the most abundant elements on the Earth's crust as well as in sea water, and is therefore much more accessible than Li, the main difference between the two kinds of batteries lies in the nature of the cathode material.14 While the preparation costs and procedures are comparable for both battery types, controversial elements like cobalt, required in Li-batteries, are not necessary in the production of Na-batteries. As a result, a dramatic reduction of the manufacturing costs as well as improvement of the socio-environmental impact of this technology is achieved. Researchers in this framework are encouraged to study advanced cathode (and anode) materials, in order to gain a deeper understanding of their fundamental properties. Here, one of the key aspects is to understand the link between the crystal structure and ion transport at the atomic level. The aim is to provide the know-how to systematically tailor high-capacity, reversible electrodes for Na-ion batteries.The focus of this work is the detailed study of how the crucial mechanism for Na-ion transport is linked to subtle changes in the crystal structure within the quasi-1D NaCr2O4 compound. The influence of substituted Ca ions on the Na-ion diffusive behavior in the solid solution NaxCa1−xCr2O4 is systematically investigated. This system is utilized as a model system for defects in current and future low-dimensional battery materials, e.g. the well established cathode material LiFePO4.15–17
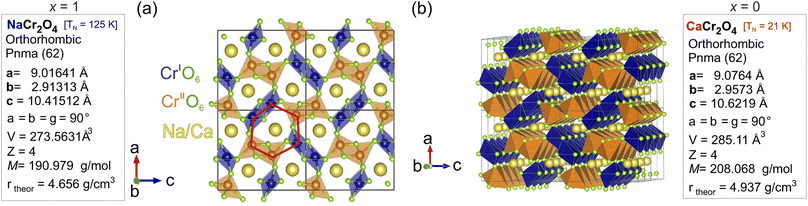
NaCr2O4 (formally NaCr3+Cr4+O4) is a spinel-ferrite18 (calcium ferrite-type), quasi-1D (Q1D) transition metal oxide19 that exhibits a Cr3+/Cr4+ mixed-valence state. Such an oxidation state for the Cr ion is very unusual, and it can only be stabilized under extreme pressure conditions (synthesis). There are very few realizations of this phenomenon in actual samples: beyond NaCr2O4, another material that exhibits the Cr3+/Cr4+ mixed-valence state is K2Cr8O18.20 This rare condition is responsible for the unconventional low temperature microscopic properties21 that make NaCr2O4 a fascinating study case also from a fundamental research perspective.22 The compound crystallizes in the orthorhombic space group 62 (Pnma), in which Cr cations occupy two distinct crystallographic positions (labelled as CrI and CrII in Fig. 1) surrounded by octahedrally coordinated oxygen atoms. The CrO6 octahedra are in turn arranged in double zig-zag chains, by sharing one edge along the b – axis. The Na+ ions are located in the hexagonal one-dimensional channels designed by the interconnections amongst the different chains [Fig. 1(a)], which are believed to be privileged directions for ion diffusion. NaxCa1−xCr2O4 is obtained as a solid solution between the iso-structural compounds β-CaCr2O4 – NaCr2O4. The evolution of the low temperature electronic and, partially, the spin structure for the NaxCa1−xCr2O4 family was studied as a function of the Na content by X-ray absorption spectroscopy (XAS),23 neutron diffraction (ND) and bulk μ+SR.24 The Na+ substitution for Ca2+ introduces holes in the electronic state of Cr ions, leading to the partial oxidation of Cr3+ to Cr4+, and induces a change in the low-temperature magnetic ordering of the Cr moment from an incommensurate anti-ferromagnetic (IC-AF) structure in CaCr2O4 to a commensurate anti-ferromagnetic (C-AF) structure in NaCr2O4. Although a material subjected to such hole doping would be expected to lend itself to charge or spin frustration,25 in NaCr2O4 an unusual coexistence of positive and negative charge transfer states is realized and lifts the frustration.23,24 Indeed, no evidence of charge frustration, charge ordering or charge/spin density wave instabilities has been reported in this material.
In this work a systematic chemical composition-dependent study on the high temperature properties of NaxCa1−xCr2O4 with [x = 0.3, 0.5, 0.7, 0.85, 0.90, 0.95, 1] is presented. Here we show how the size and the ionic content of the 1D CrO6 diffusion channels affect the kinetics of Na ions, by means of neutron powder diffraction (NPD) and muon spin rotation/relaxation (μ+SR) experimental measurements. The latter technique is widely used for the characterization of local magnetic environments in crystalline systems, and it was also shown to constitute a reliable characterization method for ion dynamics in solids, in particular, battery materials.26 Moreover, if the Ca ions are regarded as “defects”, this study provides a description of phenomena occurring in low dimensional battery materials affected by defects. The element Ca is especially suitable for this kind of investigation since it has zero nuclear magnetic moment, which makes it imperceptible to muons. This fact ensures that the dynamic behavior observed in the muon signal comes solely from Na-ions. The results obtained evidence a clear trend for the diffusion becoming more and more hampered as the Ca content increases.
2 Experimental setup
Polycrystalline samples of NaxCa1−xCr2O4 were prepared from stoichiometric mixtures of CaO, NaCrO2, Cr2O3, and CrO3 at 1300 °C under a pressure of 6 GPa, while the NaCr2O4 was prepared under a pressure of 7 GPa. Further information regarding the sample synthesis can be found in ref. 19. All the samples were synthesized at the National Institute for Materials Science (NIMS) in Tsukuba, Japan. From powder X-ray diffraction (XRD) they were proven to be single phase, with a CaFe2O4-type Pnma structure.The μ+SR spectra were acquired at the muon spectrometers EMU27 and RIKEN-RAL,28 at the ISIS Neutron and Muon source29 (United Kindom), and S1 (ref. 30) at the J-PARC research facility31 (Japan). For the muon measurements, ∼1.5 g of sample in powder form were pressed into a pellet under a pressure of about 1.9 tons. The pellet was sealed in a 23.5 mm diameter Ti cell, with Ti screws, a Ti window of 50 μm thickness and a gold O-ring for sealing. The sample was then mounted on a closed cycle refrigerator to reach temperatures from 50 K to 600 K.
The neutron powder diffraction (NPD) patterns were collected at the time-of-flight (ToF) powder diffractometers iMATERIA32 and SPICA33 at J-PARC. The neutron diffraction measurements were performed on powder samples (∼0.72 g) mounted into cylindrical vanadium cells with diameters of 6 mm (for SPICA) and 5 mm (for iMATERIA). The cell was closed with an aluminium cap, aluminium screws and indium sealing. The cell was mounted on a closed cycle refrigerator to reach temperatures between 2 K and 300 K. While the low temperature properties of the solid solution NaxCa1−xCr2O4 will be discussed elsewhere, the current work will be focused on the room temperature results.
The software VESTA34 was used for crystal structure visualization, and MATLAB35 and IGOR Pro (Wavemetrics, Lake Oswego, OR, USA)36 for parameter plotting and fitting. The software musrfit37 was used for the fit of the μ+SR data, while Fullprof38 was used for the neutron diffraction data analysis. The Bilbao Crystallographic Server has been often consulted during the preparation of this paper.39–41
3 Results and discussion
In the following section the experimental results with the related data analysis are collected.3.1 Structural evolution studied by neutron diffraction
In order to study the structural evolution of the solid solution NaxCa1−xCr2O4, room temperature neutron diffraction patterns were collected for the compositions with [x = 0.5, 0.7, 0.9] at the SPICA instrument (high angle detector bank, resolution Δd/d = 0.12%) and for [x = 1] at the iMATERIA instrument (backward detector bank, resolution Δd/d = 0.16%). As shown in Fig. 2, the observed profiles display a good agreement with the calculated models. The goodness of each model is underlined by the values of the reliability R-factors (reported in Fig. 2), none of them exceeding a few percent. The values of χ2, slightly larger than the ideal value 1, can be justified by the very high resolution of the diffractometers. It should also be noted that strain parameters are not included in this refinement.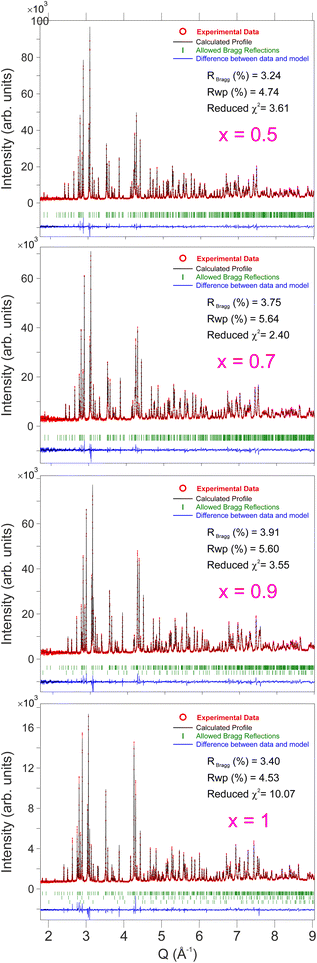 | ||
| Fig. 2 Neutron powder diffraction patterns at T = 300 K for different Na contents (x) in the solid solution NaxCa1−xCr2O4 with the respective values of the reliability factors and χ2. See also Tables 1 and 2 for detailed fitting results. | ||
The Bragg peaks were initially indexed as nuclear peaks for NaxCa1−xCr2O4, using the aforementioned Pnma space group, via the Le Bail method. Small amounts of Cr2O3 and CrO2 impurities were also present in the samples, and their Bragg peaks could be easily separated and indexed using the space groups 167 and 136 respectively. The atomic positions were extracted by Rietveld refinement. Here the positions of Ca and Na were refined together as they occupy the same crystallographic site. The data were corrected for absorption for a cylindrical sample and the chosen peak shape function is a pseudo-Voigt convoluted with a pair of back-to-back exponentials.38 The background was fitted with a linear interpolation of manually added points. The resulting cell parameters for the main phase are reported in Table 1. As expected, the size of the unit cell increases isotropically as the Ca content increases with the lattice being less and less contracted.21 The refinement of isotropic Debye–Waller factors, accounting for the thermal displacement of atoms around their ideal crystallographic positions, provided a value of ∼0.5 Å2 for the Na ions in all the members of the solid solution, indicating low mobility of the sodium at 300 K. Attempts to refine the occupation probabilities of the Na/Ca sites did not lead to any improvement of the refinement, indicating that the samples are close to their ideal stoichiometry and that no structural disorder is in place in these systems.
| Na content (x) | a (Å) | b (Å) | c (Å) |
|---|---|---|---|
| 0.5 | 9.0418(1) | 2.9297(1) | 10.5640(2) |
| 0.7 | 9.0248(9) | 2.9198(8) | 10.5199(1) |
| 0.9 | 9.0119(1) | 2.9139(1) | 10.4568(1) |
| 1 | 9.0154(1) | 2.9128(1) | 10.4138(9) |
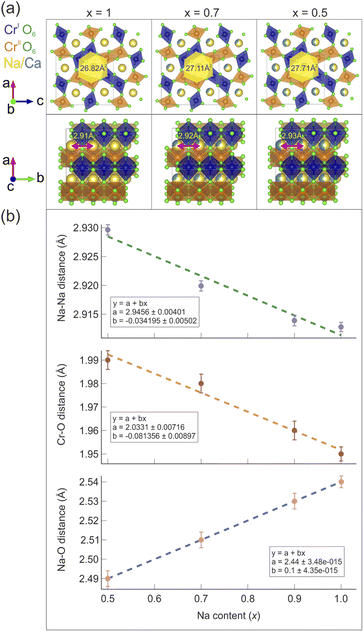
Table 2 lists the average values of the atomic distances between chromium and oxygen sites dCr1(2)–O (the two crystallographically different sites Cr1 and Cr2 have similar distances from O), with varying Na content. The distance between Na and the oxygen site O1, dNa–O1, is also reported as a marker of the composition-dependent variations of the Na–O bonds in the Na channels. As the Na concentration decreases, dCr1(2)–O increases. This is due to the gradual increase of charge separation for Cr atoms going from a mixed valence 3.5+ in the pure Na compound (x = 1) to the valence 3+ in the doped compound with x = 0.5, which results in the occurrence of a chemical pressure effect. The distance dNa–O1 instead shows an opposite trend since it decreases with lower Na content. A larger distance between Na and O implies weaker bonds between the two, which might be one of the factors that promotes Na-ion mobility.
| Na content (x) | d Cr1–O (Å) ≈ dCr2–O (Å) | d Na–O1 (Å) |
|---|---|---|
| 0.5 | 1.99 | 2.49 |
| 0.7 | 1.98 | 2.51 |
| 0.9 | 1.96 | 2.53 |
| 1 | 1.95 | 2.54 |
A model for the size of the 1D diffusion channels as a function of the Na content is displayed in Fig. 3(a). The size of the channels is estimated by geometrical considerations. It is easy to see how the channels become smaller, as an effect of the reduced unit cell volume. The atomic distances as a function of the Na content (x) are also plotted in Fig. 3(b) and the distances manifest a clear linear trend as a function of x.
A recent study by Byles and Pomerantseva on tunnel structured manganese oxides,42 carried out by galvanostatic intermittent titration and electronic conductivity measurements, reports a noteworthy relationship between the size of the structural tunnel (or 1D diffusion channel) and the diffusive behavior of the charge carrying ion. In particular, they show a comparison between the rate performances of Li-ion and Na-ion battery materials (LIB and NIB materials respectively), with channels of different sizes built by edge sharing MnO6 octahedra. The study shows that the material with the largest channels provided the best performance for the LIBs but not for the NIBs, in which smaller tunnels with more stable and well defined Na sites characterized the best performing material. A similar behavior can be recognized in NaxCa1−xCr2O4. From our current μ+SR study (see the next section), the mobility rate of Na-ions actually increases with the Na content. This means that Na-ion diffusion is enhanced with a narrower diffusion channel.
3.2 Na-ion diffusion studied by μ+SR
Beyond the well known use of the μ+SR technique for the characterization of the magnetic and electronic properties of materials in different conditions and microscopic phases,43–48 a regular and systematic use of μ+SR for studies of ion dynamics only began about a decade ago.26,49 However, since then there has been a strong and steady increase of such reports in the published literature, covering ex situ material studies for batteries15,17,50,51 which has also recently been explored with μ−SR,52 H-storage,53 and photovoltaics,54 as well as more recent in situ/operando investigations.55–57 The principle behind this rather unique method lies in the ability of the particle probe (anti-muons μ+) to detect fluctuating magnetic moments, originating from ion diffusion in solids.58 As the spin polarized muon beam is implanted into the sample, the muon spin precesses according to the local magnetic environment. In particular, considering the most general case, muons can sense the hyperfine fields due to fluctuating electronic spins, the static nuclear dipolar fields from the atoms in the lattice, and also the modulated nuclear dipolar fields due to fluctuating nuclear spins coupled with the fluctuating electronic spins.59 For the present study we will assume that the latter interaction term does not contribute to the detected muon signal. The application of an external magnetic field of weak intensity (comparable to the modulated nuclear dipolar field ≈10 G), whose flux lines are parallel to the initial direction of the polarized muon spin (so-called longitudinal field LF), allows us to partly decouple the contribution from nuclear and electronic spins.60 This protocol makes it possible to distinguish between the internal magnetic fields arising from nuclear and electronic contributions, as the muon relaxation will be different in the two cases. In this way, a robust determination of ion-diffusion related changes in the nuclear dipolar field is ensured. The μ+SR spectra of NaxCa1−xCr2O4 at T = 450 K for selected compositions are displayed in Fig. 4. Each sample was measured under the same conditions: under zero field (ZF), as well as under 5 G and 10 G decoupling LF (and also one weak transverse field calibration, not shown). As seen in Fig. 4, for the sample x = 0.5 the ZF muon spin relaxation displays the typical shape of a Kubo–Toyabe (KT) function for isotropically distributed nuclear dipolar fields. The presence of the decoupling LF causes a reduction of the signal's relaxation rate as the muon spins are ‘locked’ in their initial direction by the applied field.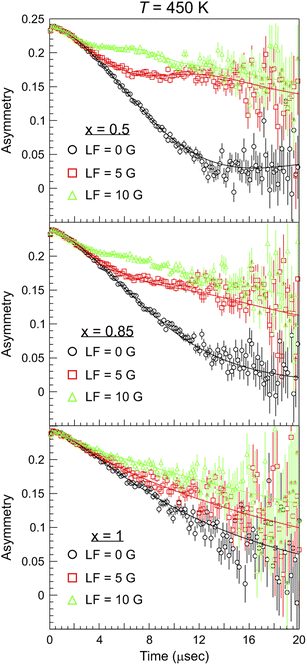 | ||
| Fig. 4 μ+SR time spectra collected at T = 450 K for different Na content (x) and values of the applied longitudinal magnetic field (LF). The solid lines are best fits to the data using eqn (1) with a global fitting protocol for each temperature. | ||
Comparing the three plots in Fig. 4 it is evident that, as the Na content increases, the muon relaxation rate is reduced (also for the ZF case) as the tail of the signal in the long time domain drifts upwards. This behavior can be explained by observing the temperature and composition dependent trends extracted from careful fitting of the μ+SR time spectra. The fit function chosen for the entire Ca1−xNaxCr2O4 family, in the full temperature range, is the following:
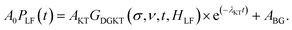 | (1) |
The function is constituted by the sum of a dynamic Gaussian Kubo–Toyabe (KT) relaxation function GDGKT, multiplied by an exponential relaxation function, plus a small background signal from the muons stopping in the sample holder ABG. Here, A0 is the initial asymmetry of the muon decay (maximum value); AKT and ABG are the asymmetries of the KT function and of the background respectively. These quantities provide an estimate of the volume fractions of the muons implanted in the sample, whose behavior is described by the related relaxation function. The dynamic Gaussian KT describes the depolarization of the muon spin in a fluctuating nuclear dipolar field, characterized by a Gaussian distribution. GDGKT is a function of several parameters: σ is related to the width of the internal field distribution Δ by the relation σ = γμΔ (here γμ is the muon gyromagnetic ratio); ν is the fluctuation rate of the field at the muon sites (which in this case translates to the Na-ion hopping rate); t is the time and HLF is the externally applied longitudinal field. The exponential decay rate λKT is due to the rapidly fluctuating electronic moments of the transition metal Cr atoms in the paramagnetic state. The exponential relaxation rate was found to be substantially independent of temperature and composition, in agreement with the trend of the magnetic susceptibility for all the members of the solid solution in this temperature range.19 Since leaving it free as a fitting parameter did not lead to significant fluctuations of its value between one temperature point and another, neither improved the calculated model, in the final fits it was kept fixed to its room temperature value λKT = (0.02 ± 0.005) μs−1. The conditions ν = 0 and HLF = 0 correspond to the static ZF case, in which the KT function describes the depolarization of the muon spin in a static nuclear dipolar field, arising from randomly oriented nuclear spins. Following upon these assumptions, the ZF and the two LF muon spectra for each temperature have been fitted simultaneously while keeping Δ and ν as common variables. This results in the reliable determination of both the static (Δ), as well as dynamic (ν), parameters. Fig. 5 displays the temperature dependence of the hopping rate for each sample in the solid solution.
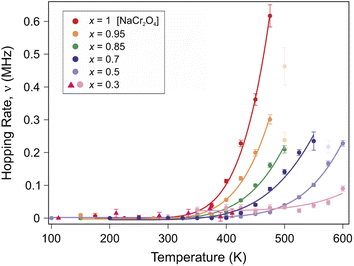 | ||
| Fig. 5 Plot of the Na-ion hopping rate ν as a function of temperature for different Na contents (x). A clear thermally activated exponential increase is observed, which is typical for a diffusion process. The solid lines are fits to the data using an Arrhenius function (eqn (3)). | ||
The systematic composition dependence of the field fluctuation rate (associated with a thermally activated diffusion process) is striking (as seen in Fig. 5). Nonetheless, a clarification is necessary here. The GDGKT relaxation function used in the fit originates from the strong collision model, according to which the dynamical behavior is described by a stochastic process. According to this model, the local field at the muon site takes a certain value for a time, given by the inverse of the hopping rate, followed by a new value uncorrelated with the previous one. Taking the example of an extreme case scenario, with a single Na ion and a single muon in the lattice, the field fluctuation rate detected by the muon will be entirely dependent on the diffusion rate of the Na ion. Considering two Na ions in the lattice, if the frequency of their diffusion is within the muon lifetime the muon will effectively detect two distinct field fluctuations, depending on its position with respect to the crystallographic sites of the diffusing specimen. Indeed, in order for a muon to detect the field fluctuation due to Na-ion diffusion within its lifetime, the amount of Na ions around the muon sites needs to be sufficient to maximize the detection probability. Based on this simple argument, since the muon sites are not changing between one sample and another (as discussed below), and by virtue of the high sensitivity of the muons to the local magnetic environment, it is reasonable to expect that a variation in the Na concentration would affect the field fluctuation rate detected by the muons, unless the Na diffusion length within the muon lifetime is longer than one formula unit along the diffusion channel (e.g. 3 formula units in the x = 0.3 case). The extent of this effect will solely rely on the presence or absence of Na ions near the identical muon sites, potentially obscuring the variations specific to the sample in the diffusion modes we aim to track using μ+SR. Therefore, assuming short Na diffusion lengths, we compute a correction factor to account for the effects of the Na concentration on the field fluctuation rate ν, for a more meaningful comparison between the Na diffusivities among the different members of the solid solution.
Intuitively, this factor will be proportional to the inverse of the Na concentration. Quantitatively, we may calculate the effect of the Na concentration on the local field in the Van Vleck limit:
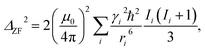 | (2) |
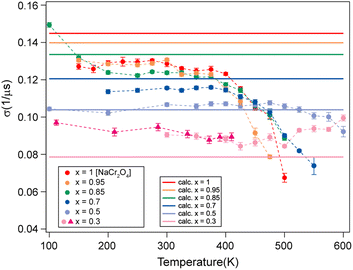 | ||
| Fig. 6 Comparison between the measured (dots) and calculated (solid lines) σ values for the different Na contents (x). | ||
| Na content (x) | Δ [G] | σ [μs−1] | Δ ratio |
|---|---|---|---|
| 0.3 | 0.922448 | 0.078557 | 1.843858 |
| 0.5 | 1.219883 | 0.103887 | 1.394284 |
| 0.7 | 1.415265 | 0.120526 | 1.201798 |
| 0.85 | 1.567904 | 0.133525 | 1.084800 |
| 0.95 | 1.641252 | 0.139848 | 1.036320 |
| 1 | 1.700863 | 0.144848 | 1 |
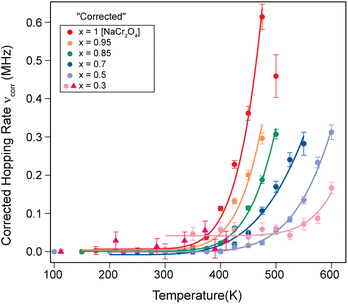 | ||
| Fig. 7 Plot of the corrected hopping rate of the Na-ion diffusion process (νcorr) as a function of temperature for several Na contents (x). The solid lines are fits to the data using the Arrhenius function (eqn (3)). | ||
We will refer to this corrected hopping rate (νcorr) for the following discussion. The exponential increase of the hopping rate νcorr with temperature is related to the onset of Na-ion diffusion. This being the case, the temperature dependence νcorr(t) displays the signature of a thermally activated (diffusion) process that can be well described by a simple model, the Arrhenius function:64
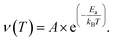 | (3) |
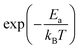 represents the fraction of atoms that possess enough kinetic energy to overcome the energy barrier between the initial (static) and final (dynamic) states. This energy barrier is the activation energy Ea in the exponential term of eqn (3), while kB is the Boltzmann constant (8.62 × 10−5 eV K−1) and T is the temperature in K. It is evident from the plot in Fig. 5 that an increase in the Na content for the solid solution causes a reduction in the temperature required to activate the process. Therefore, it might seem that the increase in the Na content induces a lowering in Ea required to start the diffusion. However, this is not really the case. In order to demonstrate this fact let us consider a different way to represent the hopping rate by plotting its logarithm as a function of the inverse temperature (see Fig. 8).
represents the fraction of atoms that possess enough kinetic energy to overcome the energy barrier between the initial (static) and final (dynamic) states. This energy barrier is the activation energy Ea in the exponential term of eqn (3), while kB is the Boltzmann constant (8.62 × 10−5 eV K−1) and T is the temperature in K. It is evident from the plot in Fig. 5 that an increase in the Na content for the solid solution causes a reduction in the temperature required to activate the process. Therefore, it might seem that the increase in the Na content induces a lowering in Ea required to start the diffusion. However, this is not really the case. In order to demonstrate this fact let us consider a different way to represent the hopping rate by plotting its logarithm as a function of the inverse temperature (see Fig. 8).
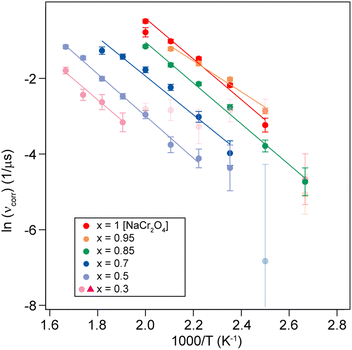 | ||
| Fig. 8 Logarithmic hopping rate [ln(νcorr)] plotted as a function of inverse temperature for different Na content (x). The solid lines are linear fits to the data, yielding the activation energy Ea. | ||
Taking the logarithm on both sides of the Arrhenius equation (eqn (3)) it is easy to see that the values of the activation energy Ea for each sample can be determined via a linear fit (Fig. 8). The results of the linear fits are plotted in Fig. 9(a), as a function of the Ca content. It is evident that Ea does not show an increasing trend as the Na content decreases, but oscillates slightly around an average value, 〈Ea〉 = (0.444 ± 0.019) eV. This value is in good agreement with the activation energy for Na diffusion in sodium-ion conductors, typically found to be in the range from 0.3 to 0.7 eV.65 The term Ea in eqn (3) was then fixed to its estimated average value 〈Ea〉 and only the pre-factor A was left free as a fitting parameter for the curves in Fig. 7. The results of these fits are displayed in Fig. 9(b).
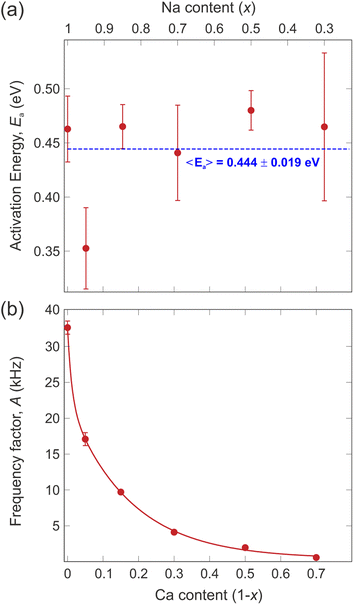 | ||
| Fig. 9 (a) Values of the activation energy (Ea) extracted from the logarithmic hopping rate (Fig. 8), the dashed line is a linear fit to the data providing the average value of the activation energy, 〈Ea〉. (b) Values of the pre-exponential factor (A) of the Arrhenius equation (eqn (3)) obtained from the fits in Fig. 7 and by using the average value of the activation energy 〈Ea〉. The continuous line is a fit to the data with an exponential decay function. | ||
The pre-exponential term A is often neglected when discussing ion diffusion since it's difficult to experimentally determine it with confidence. In the present study, however, the very systematic approach and high quality of the data allowed us to robustly extract A for each sample. The value of this parameter undergoes an exponential drop as the Na content decreases (i.e., substituted by Ca). This fact implies that in the NaxCa1−xCr2O4 system the replacement of Na with Ca has the effect of reducing the probability for a Na-ion to gain enough kinetic energy to perform a diffusive jump without modifying the potential energy landscape. As a result, the Na-ion mobility is systematically reduced and a higher temperature is required to activate the diffusion process. However, note that the activation energy (Ea) necessary for the ions to overcome the potential barrier between the static state and the dynamic state remains more or less constant. It should be noted that the exponential Ca-concentration dependence of the pre-exponential factor in Fig. 9(b) is unusual in the context of the classical over-barrier jump. Consistent with our observations, we attribute this effect to the fact that the concentration of Na ions in the solid solution can affect the diffusion by affecting the frequency of collisions between Na ions. However, further investigations involving more advanced computational modeling with molecular dynamics simulations would be needed to clarify the details of this aspect.
Finally, we would like to focus on the x = 0.95 sample that seems to display a slightly lower activation energy with respect to the other compositions [see Fig. 9(a)]. Such an effect could simply be related to fluctuations of the fitting routine. However, it should be noted that a very small amount of Ca ‘defects’ could in fact enhance the Na-ion diffusion. Such an effect has previously been shown for Na-ion battery materials, where a surprisingly strong improvement was found for tiny atomic substitutions within the lattice.50 Future detailed studies of the NaxCa1−xCr2O4 family for the range x = 1–0.9 will be necessary to conclude if this is indeed a real effect.
3.3 Na-ion diffusion path
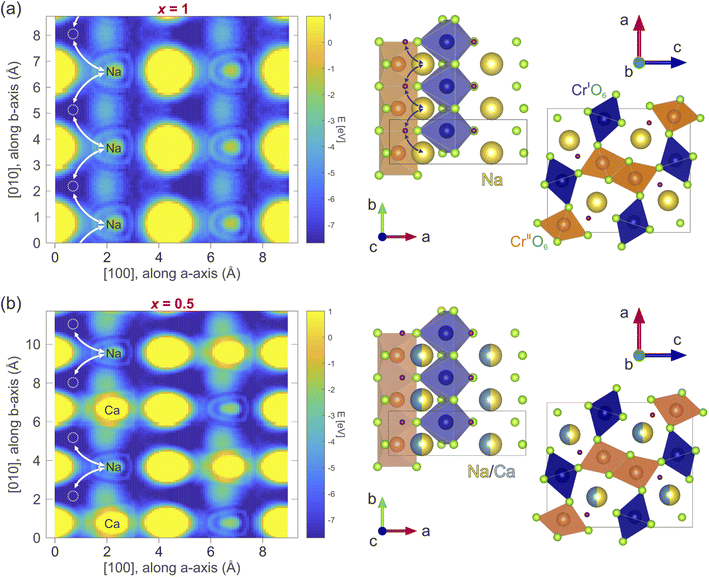
In order to determine the diffusion coefficient, the diffusion path and a possible diffusion mechanism for the considered compounds need to be determined. The most probable diffusion mechanism taking place in NaxCa1−xCr2O4 is the interstitial jumping mechanism,64 since the Na/Ca Wyckoff site 4c is fully occupied. Moreover, we will assume that the Ca is stationary and that Na is the only mobile species in this material family. Finally, only nominal → interstitial → nominal jumps are assumed to take place, while direct interstitial → interstitial jumps are not considered (see also Fig. 10).The detailed path of the interstitial mechanism is estimated based on the charge densities in the compound. This method has been utilized to estimate the diffusion path also in past studies on the interstitial mechanism.15 The charge density is calculated in the density functional theory (DFT) framework using the software package Quantum espresso.66,67 A simple self consistent calculation using the pseudo-potentials described in ref. 68 and 69 results in charge densities whose associated electrostatic potential distribution is shown in Fig. 10(a and b) for x = 1 and x = 0.5, respectively. The plots display a cut along the ab – plane and the values of the energy, expressed in eV, are reported in the corresponding color bar. The potential minima are characterized by a dark blue color in the figure. These results may be generalized for the other x contents by asserting that the interstitial sites are barely affected by the presence of Ca. This is a reasonable assumption, considering that the crystal symmetry is not affected by the Ca substitution (as clearly shown above by our NPD data). The calculated electrostatic potential distribution does not show significant differences in 3 dimensions between the x = 1 and x = 0.5 compositions. This indicates that the most probable locations of muon implantation within the crystalline lattice are the same between the extremes of the solid solution.
In order to perform the ground state calculations of the x = 0.5 system, Na and Ca ions in the crystallographic model provided by the NPD analysis have been placed in alternate sites along the b – axis, hereby doubling the unit cell. The corresponding non-doubled unit cell represented on the right side of Fig. 10(b) displays each Na/Ca site along the b – axis as having an equal probability of being occupied by either Na or Ca atoms. The crystallographic positions of the interstitial jump sites for the x = 1 and x = 0.5 samples in fractional coordinates are [0.114(6), 0.750(1), 0.287(9)] and [0.100(2), 0.750(0), 0.275(0)], respectively.
3.4 Na-ion diffusion coefficient
The diffusion coefficient is a concept based on the first and second laws of Fick. The coefficient in itself is a macroscopic parameter and describes ultimately the flow of particles. The relevant microscopic details can, however, be derived based on the random walk approach which, in many text books,64 is described as: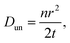 | (4) |
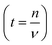 ; n is the average number of jumps. This description has in the past been shown to be accurate to describe the self diffusion of both Na and Li.15,26,70 However, a term often neglected in past studies is the correlation factor (f). In general, each hop of the diffusing species is in fact correlated to the previous jump. Given that f is simply a constant and that such values are somewhat close to 1, calculation of f is often neglected and truthfully perhaps not necessary. Nonetheless, f highly depends on the crystalline environment of the diffusing species; therefore, there will be a systematic dependence on f in this composition-dependent study. It is thus highly desirable to determine f as a function of x in order to calculate the diffusion coefficient of NaxCa1−xCr2O4. The correlation factor is given by the ratio of the real and ideal uncorrelated diffusion coefficients:
; n is the average number of jumps. This description has in the past been shown to be accurate to describe the self diffusion of both Na and Li.15,26,70 However, a term often neglected in past studies is the correlation factor (f). In general, each hop of the diffusing species is in fact correlated to the previous jump. Given that f is simply a constant and that such values are somewhat close to 1, calculation of f is often neglected and truthfully perhaps not necessary. Nonetheless, f highly depends on the crystalline environment of the diffusing species; therefore, there will be a systematic dependence on f in this composition-dependent study. It is thus highly desirable to determine f as a function of x in order to calculate the diffusion coefficient of NaxCa1−xCr2O4. The correlation factor is given by the ratio of the real and ideal uncorrelated diffusion coefficients: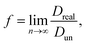 | (5) |
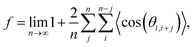 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θi,i+j)〉 = 0 for j ≠ 1, such that eqn (6) is simplified into71
cos(θi,i+j)〉 = 0 for j ≠ 1, such that eqn (6) is simplified into71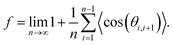 | (7) |
The above expression is valid for any diffusing species based on the interstitialcy mechanism. However, the extent of the summation changes depending on the detailed structure. From the considered diffusion path, n varies as a function of x given that the diffusion itself is hindered by the crystalline sites of the Ca. Naturally, n is infinite in the x = 1 case and eqn (7) can be analytically solved into 1 + cos(θ). For the other compositions x, n is the number of jumps in the unique path that results in a contribution to D. Given the assumption that the Ca ions are uniformly distributed, the values of n can be graphically estimated by simulating the jumping path of the Na ions between two consecutive Ca ions. Following this argument, a relation which describes the variation of n as a function of the Ca concentration ρCa can be extracted:
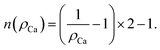 | (8) |
| Na content (x) | ρ Ca | n | θ i,i+1 | f |
|---|---|---|---|---|
| 0.3 | 3/2 | 1 | 87.217(2)° | 1 |
| 0.5 | 1/2 | 1 | 89.810(4)° | 1 |
| 0.7 | 1/3 | 3 | 92.402(8)° | 0.972(1) |
| 0.85 | 1/7 | 11 | 94.347(3)° | 0.931(8) |
| 0.95 | 1/20 | 37 | 95.643(7)° | 0.904(3) |
| 1 | 0 | ∞ | 96.292(3)° | 0.890(4) |
The value n = 1, calculated using the relation in eqn (8) for the x = 0.5 composition, is considered as a boundary value adopted also for cases x ≤ 0.5. This choice is based on the fact that a negative value for n would imply a negative number of jumps, which is un-physical. The uncorrelated diffusion coefficient for the Na ions DNa(un) for the members of the solid solution is estimated in a similar fashion as in ref. 15. Starting from the assumption that the hopping rate ν is the actual jumping rate of Na ions among neighboring sites, and treating the interstitial sites as vacancies, the general expression for DNa(un) is the following:64
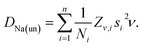 | (9) |
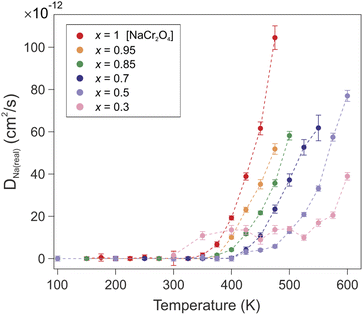 | ||
| Fig. 11 Temperature dependence of the correlated diffusion coefficient DNa(real) for all the members of the solid solution NaxCa1−xCr2O4. | ||
| Na content (x) | s[Å] | D Na(real) (T = 475 K) [cm2 s−1] |
|---|---|---|
| 0.3 | 2.122(9) | 1.4(2) × 10−12 |
| 0.5 | 2.075(1) | 5.8(7) × 10−12 |
| 0.7 | 2.027(2) | 2.3(1) × 10−11 |
| 0.85 | 1.991(4) | 3.6(2) × 10−11 |
| 0.95 | 1.967(4) | 5.2(2) × 10−11 |
| 1 | 1.955(5) | 1.04(5) × 10−10 |
The exponential temperature dependence of the diffusion coefficient denotes the thermally activated nature of the process (Fig. 11). The value of the correlated diffusion coefficient for the pure Na compound (x = 1) is one order of magnitude larger than in the other compounds (see also Table 5). This behavior should be ascribed to the concomitant contribution of several factors. The presence of Ca ions constitutes a physical impediment for the Na diffusion since it can only occur along the 1D channel. The mixed valence state Cr3.5+ induced by the presence of Na implies an enhanced Cr–O bond stability, due to the lower occupation of 3d orbitals, and a reduction of the atomic radius of Cr atoms. As a consequence, a contraction of the transition metal oxide octahedra occurs, which results in a reduced volume for the 1D diffusion channels on one hand, and a weakened Na–O bond on the other hand. The downsized 1D channels provide a more confined and advantageous diffusion path for the Na ions to move in a correlated fashion. The evolution of the electronic configuration throughout the solid solution members does not modify the energy barrier (Ea), which hinders the Na diffusion. The observed enhancement of the Na mobility is therefore a purely geometrical effect.
It should be mentioned that, since our interpretation of the μ+SR data is based on the strong collision model, the measured fluctuations in the local magnetic environment depend on the relative motion of Na ions and muons. Therefore, even though it has been shown by comparison between LF-μ+SR and other experimental techniques that the hopping rate ν effectively reflects the ion dynamics in the investigated system (as in, e.g., ref. 72), it is important to mention why such dynamics in this work are consistent with jump diffusion of Na ions rather than being due to the muons themselves. Among the possible mechanisms describing the diffusion of muons in solids as light particles, the ones that would occur in the temperature range relevant for this work are lattice-activated tunneling and over-barrier hopping.73 The onset temperature for this kind of mechanism should be expected from ∼0.2–0.3Θ and above (with Θ being the Debye temperature of the host crystal). The Debye temperature for CaCr2O4 is estimated to be ∼770 K;74 therefore, assuming a similar value for all the members of the NaxCa1−xCr2O4 solid solution, indications of muon diffusion in this system should be expected from 150 to 230 K. The onset temperature for the diffusion process observed in this work is ∼400 K at the lowest (Fig. 5). We do not observe indications of dynamical behavior between 230 K and 400 K (and higher for the other compositions) in the μ+SR spectra, but 400 K is fully consistent with the expected onset temperature for Na-ion diffusion in sodium conductors.75,76 Moreover, the activation energy experimentally estimated in this work (0.444 eV) is consistent with the activation energy for Na diffusion in sodium-ion conductors.65 This value is significantly higher than the activation energies of muon diffusion by lattice-activated tunneling and over-barrier hopping, measured in different systems to be in the range from 0.05 to 0.2 eV.77–82 Nonetheless, the difficult discernment between ion and muon self diffusion in LF-μ+SR measurements represents a major limitation for this experimental technique. Indeed, complementary methods are often needed in order to achieve a more comprehensive understanding of the probed diffusion processes. In particular, in our case, possible low temperature dynamics and subtle structural defects may be out of the sensitivity windows of the muon and neutron investigation methods adopted in this work. For this reason, high temperature neutron and X-ray diffraction, coupled with high temperature Na-NMR, would be relevant to further confirm the proposed Na diffusion mechanism, as well as to further probe the local structure deviations due to Ca substitution and associated cation defects,72 and ultimately exclude the presence of contributions from muon diffusion in this system.
As a final remark we can now calculate the upper value for the Na diffusion length LNa within the muons' mean lifetime τ = 2.2 μs for the x = 1 sample, to verify that our assumption was correct:
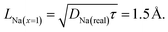 | (10) |
4 Conclusions
In this work a systematic chemical composition-dependent study on the NaxCa1−xCr2O4 family [with x = 0.3, 0.5, 0.7, 0.85, 0.90, 0.95, 1], carried out using μ+SR and NPD methods, is presented. The study shows how the Na kinetics can be tuned by the structural modifications induced by Ca substitution. In particular, we observed that a reduced volume of the 1D diffusion channel corresponds to an enhancement of the Na ion mobility, contrary to the phenomenology of Li ion 1D battery materials. Moreover, the presence of Ca has the effect of reducing the probability for a Na ion to gain enough kinetic energy to overcome the activation energy barrier between the static and the dynamic state of the system, without modifying the potential energy landscape. The ion diffusion process in NaxCa1−xCr2O4 is suggested to be an interstitial mechanism with highly correlated jumps. The diffusion coefficients for each member of the solid solution have been calculated taking into account the, usually neglected, correlation coefficient.Data availability
All the data of this work are available from the corresponding authors on request. The data are also freely available in the repositories of the related large-scale facilities.Author contributions
E. N., J. S., and M. M. conceived the experiments. E. N., O.·K.·F., N. M., F. M., A. Z., S.·C., A. K., I.·W., A. H., T. S., Y.·S., J. S. and M. M. conducted the experiments. E. N., O.·K.·F., J. S., and M. M. analyzed the results. The samples were synthesized by H.·S., who also conducted the initial sample characterizations. E. N. and M. M. made all figures. E. N. created the first draft, and all co-authors reviewed and revised the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The neutron and muon experiments at the Materials and Life Science Experimental Facility of the J-PARC were performed under a user program (Proposal No. [2019B0420], [2019A0330], [2019A0328]). We gratefully acknowledge the Science and Technology Facilities Council (STFC) for access to muon beamtimes at ISIS, and also, for the provision of sample preparation, EMU and RIKEN-RAL facilities. The authors wish to thank the technical staff of J-PARC and ISIS/RAL for the valuable support during the experiments. This research is funded by the Swedish Foundation for Strategic Research (SSF) within the Swedish national graduate school in neutron scattering (SwedNess), as well as the Swedish Research Council VR (Dnr. 2021-06157 and Dnr. 2017-05078), and the Carl Tryggers Foundation for Scientific Research (CTS-18:272). E.N is supported by the SSF-Swedness grant SNP21-0004. J. S. is supported by the Japan Society for the Promotion Science (JSPS) KAKENHI Grant No. JP18H01863, JP20K21149 and JP23H01840. O. K. F. acknowledges funding from the Swedish Research Council (VR) through the Postdoc International grant (Dnr. 2022-06217) and the Foundation Blanceflor 2023 fellow scholarship. Y. S. acknowledges funding from the Swedish Research Council (VR) through a Starting Grant (Dnr. 2017-05078) and the Knut and Alice Wallenberg Foundation through the grant 2021.0150.Notes and references
- Nobel prize in chemistry press release, 2019, https://www.nobelprize.org/prizes/chemistry/2019/press-release/ Search PubMed.
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243 RSC.
- S. Niaz, T. Manzoor and A. H. Pandith, Renewable Sustainable Energy Rev., 2015, 50, 457–469 CrossRef CAS.
- M. Koppel, R. Palm, R. Härmas, M. Russina, N. Matsubara, M. Månsson, V. Grzimek, M. Paalo, J. Aruväli, T. Romann, O. Oll and E. Lust, Carbon, 2021, 174, 190–200 CrossRef CAS.
- M. Koppel, R. Palm, R. Härmas, M. Russina, V. Grzimek, J. Jagiello, M. Paalo, H. Kurig, M. Månsson, O. Oll and E. Lust, Carbon, 2022, 197, 359–367 CrossRef CAS.
- P. K. Nayak, S. Mahesh, H. J. Snaith and D. Cahen, Nat. Rev. Mater., 2019, 4, 269–285 CrossRef CAS.
- T. Wilberforce, A. Olabi, E. T. Sayed, K. Elsaid and M. A. Abdelkareem, Sci. Total Environ., 2021, 761, 143203 CrossRef CAS PubMed.
- L. Kavanagh, J. Keohane, G. Garcia Cabellos, A. Lloyd and J. Cleary, Resources, 2018, 7, 57 CrossRef.
- G. Alexander, R. E. Allen, A. Atala, W. P. Bowen, A. A. Coley, J. B. Goodenough, M. I. Katsnelson, E. V. Koonin, M. Krenn, L. S. Madsen, M. Månsson, N. P. Mauranyapin, A. I. Melvin, E. Rasel, L. E. Reichl, R. Yampolskiy, P. B. Yasskin, A. Zeilinger and S. Lidström, Phys. Scr., 2020, 95, 062501 CrossRef CAS.
- D. B. Agusdinata, W. Liu, H. Eakin and H. Romero, Environ. Res. Lett., 2018, 13, 123001 CrossRef CAS.
- J.-Y. Hwang, S.-T. Myung and Y.-K. Sun, Chem. Soc. Rev., 2017, 46, 3529–3614 RSC.
- G. M. Kanyolo, T. Masese, N. Matsubara, C.-Y. Chen, J. Rizell, Z.-D. Huang, Y. Sassa, M. Månsson, H. Senoh and H. Matsumoto, Chem. Soc. Rev., 2021, 50, 3990–4030 RSC.
- J. F. Peters, A. Peña Cruz and M. Weil, Batteries, 2019, 5, 10 CrossRef CAS.
- C. Pillot, Information for Growth, 2017 Search PubMed.
- J. Sugiyama, H. Nozaki, M. Harada, K. Kamazawa, O. Ofer, M. Månsson, J. H. Brewer, E. J. Ansaldo, K. H. Chow, Y. Ikedo, Y. Miyake, K. Ohishi, I. Watanabe, G. Kobayashi and R. Kanno, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 054430 CrossRef.
- P. Benedek, N. Yazdani, H. Chen, N. Wenzler, F. Juranyi, M. Månsson, M. S. Islam and V. C. Wood, Sustainable Energy Fuels, 2019, 3, 508–513 RSC.
- P. Benedek, O. K. Forslund, E. Nocerino, N. Yazdani, N. Matsubara, Y. Sassa, F. Jurànyi, M. Medarde, M. Telling, M. Månsson and V. Wood, ACS Appl. Mater. Interfaces, 2020, 12, 16243–16249 CrossRef CAS PubMed.
- O. Muller and R. Roy, The Major Ternary Structural Families, Springer Verlag, 1974 Search PubMed.
- H. Sakurai, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 024416 CrossRef.
- O. K. Forslund, D. Andreica, Y. Sassa, H. Nozaki, I. Umegaki, V. Jonsson, Z. Guguchia, Z. Shermadini, R. Khasanov, M. Isobe, et al., Proceedings of the 14th International Conference on Muon Spin Rotation, Relaxation and Resonance (μSR2017), 2018, p. 011006 Search PubMed.
- T. Kolodiazhnyi and H. Sakurai, J. Appl. Phys., 2013, 113, 224109 CrossRef.
- E. Nocerino, O. K. Forslund, H. Sakurai, A. Hoshikawa, N. Matsubara, D. Andreica, A. Zubayer, F. Mazza, T. Saito and J. Sugiyama, J. Phys. Mater., 2023, 6(3), 035009 CrossRef.
- M. Taguchi, H. Yamaoka, Y. Yamamoto, H. Sakurai, N. Tsujii, M. Sawada, H. Daimon, K. Shimada and J. Mizuki, Phys. Rev. B, 2017, 96, 245113 CrossRef.
- J. Sugiyama, H. Nozaki, M. Harada, Y. Higuchi, H. Sakurai, E. J. Ansaldo, J. H. Brewer, L. Keller, V. Pomjakushin and M. Månsson, Phys. Procedia, 2015, 75, 868875 Search PubMed.
- N. Matsubara, E. Nocerino, K. Kamazawa, O. K. Forslund, Y. Sassa, L. Keller, V. Sikolenko, V. Pomjakushin, H. Sakurai and J. Sugiyama, et al. , Phys. Rev. Res., 2020, 2, 043143 CrossRef CAS.
- J. Sugiyama, K. Mukai, Y. Ikedo, H. Nozaki, M. Månsson and I. Watanabe, Phys. Rev. Lett., 2009, 103, 147601 CrossRef PubMed.
- S. Giblin, S. Cottrell, P. King, S. Tomlinson, S. Jago, L. Randall, M. Roberts, J. Norris, S. Howarth and Q. Mutamba, et al. , Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 751, 70–78 CrossRef CAS.
- K. Nagamine, T. Matsuzaki, K. Ishida, I. Watanabe, R. Kadono, G. Eaton, H. Jones, G. Thomas and W. Williams, Hyperfine Interact., 1994, 87, 1091–1098 CrossRef CAS.
- J. Houck and L. Denicola, Astronomical Data Analysis Software and Systems IX, 2000, p. 591 Search PubMed.
- K. Kojima, M. Hiraishi, A. Koda, H. Okabe, S. Takeshita, H. Li, R. Kadono, M. Tanaka, M. Shoji, T. Uchida, et al., Proceedings of the 14th International Conference on Muon Spin Rotation, Relaxation and Resonance (μSR2017), 2018, p. 011062 Search PubMed.
- S. Nagamiya, Prog. Theor. Exp. Phys., 2012, 2012(1), 02B001 Search PubMed.
- T. Ishigaki, A. Hoshikawa, M. Yonemura, T. Morishima, T. Kamiyama, R. Oishi, K. Aizawa, T. Sakuma, Y. Tomota and M. Arai, et al. , Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 600, 189–191 CrossRef CAS.
- M. Yonemura, K. Mori, T. Kamiyama, T. Fukunaga, S. Torii, M. Nagao, Y. Ishikawa, Y. Onodera, D. Adipranoto and H. Arai, et al. , J. Phys.: Conf. Ser., 2014, 012053 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- Mathworks, Matlab, https://mathworks.com Search PubMed.
- WaveMetrics, IGOR Pro, Scientific Data Analysis Software, http://www.wavemetrics.com/products/igorpro/igorpro.htm Search PubMed.
- A. Suter and B. Wojek, P. Procedia, 2012, 30, 69–73 CrossRef CAS.
- J. Rodríguez-Carvajal, CEA/Saclay, France, 2001, 1045, 132–146 Search PubMed.
- M. I. Aroyo, J. Perez-Mato, D. Orobengoa, E. Tasci, G. de la Flor and A. Kirov, Bulg. Chem. Commun., 2011, 43, 183–197 CAS.
- M. I. Aroyo, J. M. Perez-Mato, C. Capillas, E. Kroumova, S. Ivantchev, G. Madariaga, A. Kirov and H. Wondratschek, Z. fur Krist. – Cryst., 2006, 221, 15–27 CrossRef CAS.
- M. I. Aroyo, A. Kirov, C. Capillas, J. Perez-Mato and H. Wondratschek, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62, 115–128 CrossRef PubMed.
- B. W. Byles and E. Pomerantseva, Materialia, 2021, 15, 101013 CrossRef CAS.
- S. Blundell, Contemp. Phys., 1999, 40, 175–192 CrossRef CAS.
- S. J. Blundell, Chem. Rev., 2004, 104, 5717–5736 CrossRef CAS.
- J. Sugiyama, W. Higemoto, D. Andreica, O. K. Forslund, E. Nocerino, M. Månsson, Y. Sassa, R. Gupta, R. Khasanov and H. Ohta, et al. , Phys. Rev. B, 2021, 103, 104418 CrossRef CAS.
- E. Nocerino, C. Witteveen, S. Kobayashi, O. K. Forslund, N. Matsubara, A. Zubayer, F. Mazza, S. Kawaguchi, A. Hoshikawa and I. Umegaki, et al. , Sci. Rep., 2022, 12, 21657 CrossRef CAS PubMed.
- K. Papadopoulos, O. K. Forslund, E. Nocerino, F. O. Johansson, G. Simutis, N. Matsubara, G. Morris, B. Hitti, D. Arseneau and P. Svedlindh, et al. , Phys. Rev. B, 2022, 106, 214410 CrossRef CAS.
- E. Nocerino, O. K. Forslund, C. Wang, H. Sakurai, F. Elson, R. Palm, U. Miniotaite, Y. Ge, Y. Sassa and J. Sugiyama, et al. , J. Phys.: Conf. Ser., 2023, 012037 CrossRef.
- M. Månsson and J. Sugiyama, Phys. Scr., 2013, 88, 068509 CrossRef.
- L. A. Ma, R. Palm, E. Nocerino, O. K. Forslund, N. Matsubara, S. Cottrell, K. Yokoyama, A. Koda, J. Sugiyama, Y. Sassa, M. Månsson and R. Younesi, Phys. Chem. Chem. Phys., 2021, 23, 24478–24486 RSC.
- R. Palm, E. Nocerino, O. K. Forslund, N. Matsubara, S. Cottrell, K. Yokoyama, A. Koda, J. Sugiyama, Y. Sassa and M. Månsson, et al. , Phys. Chem. Chem. Phys., 2021, 23, 24478–24486 RSC.
- J. Sugiyama, I. Umegaki, S. Takeshita, H. Sakurai, S. Nishimura, O. K. Forslund, E. Nocerino, N. Matsubara, M. Månsson and T. Nakano, et al. , Phys. Rev. B, 2020, 102, 144431 CrossRef CAS.
- J. Sugiyama, Y. Ikedo, T. Noritake, O. Ofer, T. Goko, M. Månsson, K. Miwa, E. J. Ansaldo, J. H. Brewer, K. H. Chow and S. Towata, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(9), 92–103 CrossRef.
- D. W. Ferdani, S. R. Pering, D. Ghosh, P. Kubiak, A. B. Walker, S. E. Lewis, A. L. Johnson, P. J. Baker, M. S. Islam and P. J. Cameron, Energy Environ. Sci., 2019, 12, 2264–2272 RSC.
- J. Sugiyama, I. Umegaki, M. Matsumoto, K. Miwa, H. Nozaki, Y. Higuchi, T. Noritake, O. K. Forslund, M. Månsson, S. P. Cottrell, A. Koda, E. J. Ansaldo and J. H. Brewer, Sustainable Energy Fuels, 2019, 3, 956–964 RSC.
- I. McClelland, S. G. Booth, H. El-Shinawi, B. I. J. Johnston, J. Clough, W. Guo, E. J. Cussen, P. J. Baker and S. A. Corr, ACS Appl. Energy Mater., 2021, 4, 1527–1536 CrossRef CAS PubMed.
- K. Ohishi, D. Igarashi, R. Tatara, I. Umegaki, A. Koda, S. Komaba and J. Sugiyama, ACS Appl. Energy Mater., 2022, 5, 12538–12544 CrossRef CAS.
- J. Sugiyama, J. Phys. Soc. Jpn., 2013, 82, SA023 CrossRef.
- R. Hayano, Y. Uemura, J. Imazato, N. Nishida, T. Yamazaki, H. Yasuoka and Y. Ishikawa, Phys. Rev. Lett., 1978, 41, 1743 CrossRef CAS.
- T. Matsuzaki, K. Nishiyama, K. Nagamine, T. Yamazaki, M. Senba, J. Bailey and J. Brewer, Phys. Lett. A, 1987, 123, 91–94 CrossRef CAS.
- M. Månsson, I. Umegaki, H. Nozaki, Y. Higuchi, I. Kawasaki, I. Watanabe, H. Sakurai and J. Sugiyama, J. Phys.: Conf. Ser., 2014, 012035 CrossRef.
- Y. Ikedo, J. Sugiyama, O. Ofer, M. Månsson, H. Sakurai, E. Takayama-Muromachi, E. Ansaldo, J. Brewer and K. Chow, J. Phys.: Conf. Ser., 2010, 012017 CrossRef.
- I. Umegaki, H. Nozaki, M. Harada, M. Månsson, H. Sakurai, I. Kawasaki, I. Watanabe and J. Sugiyama, Proceedings of the 14th International Conference on Muon Spin Rotation, Relaxation and Resonance (μSR2017), 2018, p. 011018 Search PubMed.
- R. J. Borg and G. J. Dienes, An Introduction to Solid State Diffusion, Elsevier, 2012 Search PubMed.
- Y. Ge, X. Zhang, S. Han, B. Zhou and H. Zhang, Comput. Mater. Sci., 2023, 226, 112242 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. Dal Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. Di Marco, C. Draxl, M. Dułak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Grånäs, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iuşan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Küçükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G.-M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G.-X. Zhang and S. Cottenier, Science, 2016, 351, 6280 CrossRef PubMed.
- G. Prandini, A. Marrazzo, I. E. Castelli, N. Mounet and N. Marzari, npj Comput. Mater., 2018, 4, 72 CrossRef.
- O. K. Forslund, H. Ohta, K. Kamazawa, S. L. Stubbs, O. Ofer, M. Månsson, C. Michioka, K. Yoshimura, B. Hitti, D. Arseneau, G. D. Morris, E. J. Ansaldo, J. H. Brewer and J. Sugiyama, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 102, 184412 CrossRef CAS.
- K. Compaan and Y. Haven, Trans. Faraday Soc., 1956, 52, 786–801 RSC.
- E. Nocerino, S. Kobayashi, C. Witteveen, O. K. Forslund, N. Matsubara, C. Tang, T. Matsukawa, A. Hoshikawa, A. Koda and K. Yoshimura, et al. , Commun. Mater., 2023, 4, 81 CrossRef CAS.
- Y. Fukai, The metal-hydrogen system: basic bulk properties, Springer Science & Business Media, 2006, vol. 21 Search PubMed.
- W. Xue, K. Zhai and S. Zhai, Phys. Chem. Miner., 2021, 48, 1–7 CrossRef.
- P. G. Bruce, J. Nowiński and V. C. Gibson, Solid State Ionics, 1992, 50, 41–45 CrossRef CAS.
- I. Quinzeni, K. Fujii, M. Bini, M. Yashima and C. Tealdi, Mater. Adv., 2022, 3, 986–997 RSC.
- M. Schillaci, C. Bokema, R. Heffner, R. Hutson, M. Leon, C. Olsen, S. Dodds, D. MacLaughlin and P. Richards, Electronic Structure and Properties of Hydrogen in Metals, 1983, pp. 507–512 Search PubMed.
- R. Hempelmann, M. Soetratmo, O. Hartmann and R. Wäppling, Solid State Ionics, 1998, 107, 269–280 CrossRef CAS.
- V. Grebinnik, I. Gurevich, V. Zhukov and A. Manych, et al. , Zh. Eksp. Teor. Fiz., 1975, 68, 1548–1556 CAS.
- H. Teichler, Phys. Lett. A, 1977, 64, 78–80 CrossRef.
- H. Luetkens, J. Korecki, E. Morenzoni, T. Prokscha, N. Garif’yanov, H. Glückler, R. Khasanov, F. Litterst, T. Slezak and A. Suter, Phys. B, 2003, 326, 545–549 CrossRef CAS.
- M. Kemali, D. Ross and S. Campbell, J. Alloys Compd., 1999, 293, 292–295 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |