Tuning Rashba–Dresselhaus effect with ferroelectric polarization at asymmetric heterostructural interface†
Bangmin
Zhang
 *a,
Chunhua
Tang
b,
Ping
Yang
c and
Jingsheng
Chen
*a,
Chunhua
Tang
b,
Ping
Yang
c and
Jingsheng
Chen
 *b
*b
aGuangdong Provincial Key Laboratory of Magnetoelectric Physics and Devices, Centre for Physical Mechanics and Biophysics, School of Physics, Sun Yat-sen University, Guangzhou 510275, China. E-mail: zhangbm5@mail.sysu.edu.cn
bDepartment of Materials Science & Engineering, National University of, Singapore, 9 Engineering Drive 1, 117576, Singapore. E-mail: msecj@nus.edu.sg
cSingapore Synchrotron Light Source (SSLS), National University of Singapore, 5 Research Link, 117603, Singapore
First published on 24th October 2023
Abstract
The spin–orbit interaction (SOI) plays an essential role in materials properties, and controlling its intensity has great potential in the design of materials. In this work, asymmetric [(La0.7Sr0.3MnO3)8/(BaTiO3)t/(SrTiO3)2]8 superlattices were fabricated on (001) SrTiO3 substrate with SrO or TiO2 termination, labelled as SrO-SL and TiO2-SL, respectively. The in-plane angular magnetoresistance of the superlattices shows a combination of two- and four-fold symmetry components. The coefficient of two-fold symmetry component has opposite sign with current I along [100] and [110] directions for TiO2-SL, while it has the same sign for SrO-SL. Detailed study shows that the asymmetric cation inter-mixing and ferroelectricity-modulated electronic charge transfer induce asymmetric electronic potential for SrO-SL with dominating Rashba SOI, and symmetric electronic potential for TiO2-SL with dominating Dresselhaus SOI induced by BaTiO3. This work shows that the Rashba and Dresselhaus SOIs are sensitive to the ferroelectric polarization in the asymmetric structure.
New conceptsThe spin–orbit interaction plays an essential role in materials properties, and controlling the intensity has great potential to design materials. Most work on this topic focus on either the bulk materials or thin film with only one hetero-structural interface. In this work, the spin–orbit interaction was modulated in asymmetric hetero-structural interface, [(La0.7Sr0.3MnO3)8/(BaTiO3)t/(SrTiO3)2]8 superlattices with two different hetero-structural interfaces. It indicated that the asymmetric local structure and charge transfer probabilities works together to cause the switch from dominating Rashba SOI to dominating Dresselhaus SOI. This work shows that the Rashba and Dresselhaus SOI is sensitive to the ferroelectric polarization in asymmetric structure. Our reasons for submission of this work to Materials Horizons are given with the novelty in details as follows: (a) The asymmetric [(La0.7Sr0.3MnO3)8/(BaTiO3)t/(SrTiO3)2]8 triple-layer superlattice shows features of Rashba and Dresselhaus SOI, which is induced by the asymmetric layer structure. (b) The ferroelectric BaTiO3 layer with different self-polarization could modulate the probability of charge transfer across the LSMO/BTO interface, which induces the gradual change of Rashba and Dresselhaus SOI. (c) The strong correlation between the local structure and SOI implies the freedom to modulate materials properties with artificial structural design. |
Introduction
Current electronics utilizing the degree of charge approaching its critical boundaries for device performance and exploring the degree of spin1,2 is expected to extend the range of materials functions. Most devices employing materials’ transport properties are orbital averaging and sensitive to the spin polarization, and the spin–orbit interaction (SOI) could separate the freedom of charge and spin, which provides an opportunity to control the spin polarization3–5 of charge carriers without external magnetic fields. A moving electron in an electric field with spin polarization experiences an effective magnetic field, which causes spin precession and affects the transport properties. The Rashba SOI normally comes from the structural inversion asymmetry around a heterostructural interface, and the Dresselhaus SOI comes from the noncentrosymmertric position in bulk inversion asymmetry, which correlate with the local structure of materials. These two SOIs can coexist, and the final occurrence depends on the relative contributions.6–8 For example, a Datta–Das spin field effect4 transistor relies on coherent spin transport, which can be obtained by combination of Rashba and Dresselhaus SOIs to suppress the D’yakonov–Perel’ spin relaxation by hosting the persistent spin helix.9 Exploiting systems possessing Rashba and Dresselhaus SOIs with controllable intensity has great potential.Normally the Rashba SOI is observed at the surface/interface of heavy metals with breaking inversion symmetry,10,11 the application of which is limited by its relatively low intensity. Recently, giant Rashba SOI has been investigated by controlling the geometric environment,12,13 such as the LAO//STO/LAO system.14 The gradient of the electric potential across the STO layer in the sandwich structure induces large Rashba SOI with sensitivity to charge density. With bulk inversion asymmetry in the crystal structure, the bulk Dresselhaus SOI15–17 exists from noncentrosymmertric position, contributing to two-fold symmetry18 component of magnetoresistance in the Fe/GaAs/Au system.19 In noncentrosymmetric (FA)SnI3 with coexistence of Rashba and Dresselhaus SOIs, both could be modulated through the reverse of ferroelectric polarization.20 Although there has been a lot of work on the modulation of Rashba and Dresselhaus SOIs, the relative intensity of these SOIs with respect to the local structure requires further investigation.
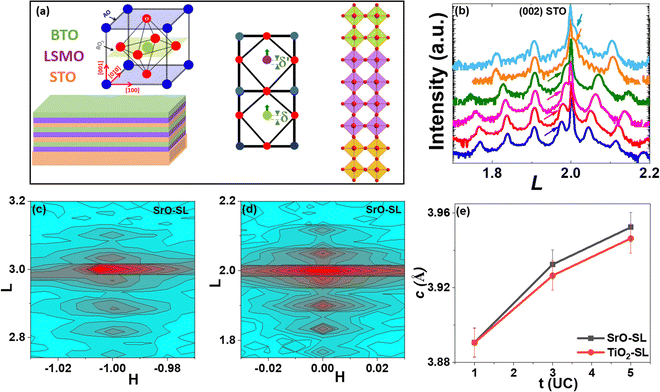
Asymmetric [(SrTiO3)2/(La0.7Sr0.3MnO3)8/(BaTiO3)t]8 superlattices (SL) on (001) SrTiO3 (STO) substrate were investigated, with triple layers in each period to introduce geometric asymmetry and ferroelectric BaTiO3 (BTO) layer to provide controllable ferroelectric state as illustrated in Fig. 1(a). t is the thickness of the BTO layer in the unit cell (UC). The SLs were fabricated on (001) STO substrate with SrO or TiO2 termination, labelled as SrO-SL and TiO2-SL, respectively. The in-plane angular magnetoresistance (AMR) of SL with t = 5 UC shows a combination of two- and four-fold symmetry components. The coefficient of two-fold symmetry component has opposite sign with current along [100] and [110] directions for TiO2-SL, while it has the same sign for SrO-SL. Further study shows that the cation intermixing and the electronic charge transfer induce asymmetric electronic potential across the La0.7Sr0.3MnO3 (LSMO) layer for SrO-SL with dominating Rashba SOI, and symmetric electronic potential across the LSMO layer for TiO2-SL with dominating Dresselhaus SOI induced by ferroelectric BTO. This work indicates that the Rashba and Dresselhaus SOIs are sensitive to the ferroelectric polarization in asymmetric structures.
Results and discussion
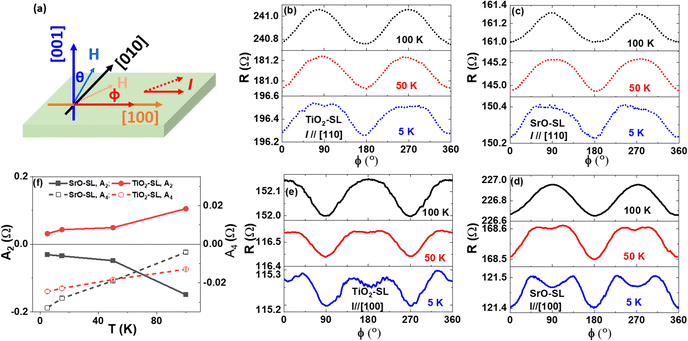
The averaged crystal structure of SL with different BTO thickness (t = 1 UC, 3 UC and 5 UC) was measured by four-circle high-resolution X-ray diffraction. From the reciprocal space mapping (RSM) and L scans in Fig. 1 and Fig. S1 in the ESI,† all SLs have epitaxial growth with 00l orientation, and the in-plane lattice constant is fully clamped by the STO substrate. The (−103) and (013) RSM show that two in-plane axes (a, b) are equivalently imprinted by the cubic (001) STO substrate. The appearance of satellites in the L scan indicates the formation of periodic superlattice structure with good heterostructural interface/surface. With the increase of BTO thickness t, the out-of-plane lattice constant c increases, which is summarized in Fig. 1(e). For the same BTO thickness, c is quite close within the measurement error range for SrO-SL and TiO2-SL. Hence, the substrate termination has limited effect on the averaged crystal structure of superlattices, and the difference in properties between them should be related to the termination-dependent local structure.Both SLs are ferromagnetic metallic below the Curie temperature as shown in Fig. S2 in the ESI.† One interesting phenomenon is that the in-plane AMR shows quite a different behavior for SrO-SL and TiO2-SL with t = 5 UC, as shown in Fig. 2. During AMR measurement, the angle ϕ is the direction of in-plane magnetic field H (9 T) with respect to the in-plane current, as shown in Fig. 2(a). With the in-plane current I//[110] direction, AMR has same angular dependence for the two SLs in Fig. 2(b) and (c): at high temperature (100 K) the resistivity shows two-fold symmetry with minimum at ϕ = 0°, and with decreasing temperature additional four-fold symmetry of resistivity appears with corresponding minimum at ϕ = 0° in addition to the two-fold symmetry. With I//[100] in Fig. 2(d) and (e), both samples show two-fold symmetry at high temperature (100 K) and a combination of two- and four-fold symmetry at low temperature (5 K). However, the AMR has minimum at ϕ = 0° for SrO-SL and at ϕ = 90° for TiO2-SL. With current along both directions, the four-fold symmetry feature becomes obvious with decreasing temperature while the two-fold symmetry feature weakens.
Further analysis provides more information by fitting the in-plane AMR according to the equation:21R = A0 + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ϕ) + A4
cos(2ϕ) + A4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(4ϕ), where A0 is a constant and A2 and A4 correspond to the coefficient of two-fold and four-fold symmetry components, respectively. The fitting details are shown in Fig. S3 in the ESI.† As shown in Fig. 2(f), with I//[100] for both TiO2-SL and SrO-SL, A4 is negative and the absolute value increases with the decrease of temperature, while A2 has different sign. The four-fold symmetry of AMR has been observed previously,22–24 resulting from the ferromagnetic phase order or the strain-induced recovery of orbital magnetic moment, involving the scattering process to the t2g band in the minority spin-down channel. With a decrease of temperature, the ferromagnetic phase order in manganite is enhanced, and the orbital magnetic moment due to the local Jahn–Teller distortion also increases due to the enhanced ferromagnetic coupling and the depressed thermal fluctuation. The film experiences mismatch strain with tetragonal distortion, and the magnetic moment of the film increases with decreasing temperature, both of which could induce the observed trend of four-fold symmetry AMR component. Current work would focus on the two-fold symmetry component A2.
cos(4ϕ), where A0 is a constant and A2 and A4 correspond to the coefficient of two-fold and four-fold symmetry components, respectively. The fitting details are shown in Fig. S3 in the ESI.† As shown in Fig. 2(f), with I//[100] for both TiO2-SL and SrO-SL, A4 is negative and the absolute value increases with the decrease of temperature, while A2 has different sign. The four-fold symmetry of AMR has been observed previously,22–24 resulting from the ferromagnetic phase order or the strain-induced recovery of orbital magnetic moment, involving the scattering process to the t2g band in the minority spin-down channel. With a decrease of temperature, the ferromagnetic phase order in manganite is enhanced, and the orbital magnetic moment due to the local Jahn–Teller distortion also increases due to the enhanced ferromagnetic coupling and the depressed thermal fluctuation. The film experiences mismatch strain with tetragonal distortion, and the magnetic moment of the film increases with decreasing temperature, both of which could induce the observed trend of four-fold symmetry AMR component. Current work would focus on the two-fold symmetry component A2.
For TiO2-SL, A2 has different sign with I//[110] (A2 < 0, Fig. 2(b)) and I//[100] (A2 > 0, Fig. 2(e)); for SrO-SL, A2 is negative with I//[100] and I//[110]. The absolute value of A2 decreases with decreasing temperature for both TiO2-SL and SrO-SL. Ferromagnetic metals exhibiting a normal AMR (A2 > 0) usually show maximum resistivity when I is parallel to the magnetization direction (ϕ = 0°), and minimum resistivity when I is perpendicular to the magnetization direction (ϕ = 90°). In magnetic materials the scattering anisotropies due to SOI25,26 were proposed to be essential in MR, and in the presence of on-site spin–orbit coupling or the Rashba type spin–orbit coupling,26 the sign of A2 flips (A2 < 0). In addition, such MR only depends on the relative direction between the current and magnetic field, which seems consistent with the results for SrO-SL. However, the sign flip of A2 with different current direction in TiO2-SL requires further study.
The two-fold symmetry of MR has been investigated previously, and the crystalline-related MR does not depend on the relative direction between current and magnetic field, such as for patterned La0.67Sr0.33MnO3 thin film27 on STO substrate. The normal Lorentz28 force could increase the carrier path length and the resistivity when the magnetic field is perpendicular to the direction of the current; the “domain drag’’ effect increases the path length due to current direction changes at domain walls, and also could affect the resistivity, which is limited in saturated film. All these considerations cannot explain the sign flip of A2 for TiO2-SL with I//[100] and I//[110]. As mentioned above, the SOC is important for MR. Both the Rashba-type29,30 and the Dresselhaus-type SOI could induce two-fold AMR (A2) as theoretically predicted,24,31 which has different dependence on the current direction and is closely related to local structure.
Then high-resolution scanning transmission electron microscopy (STEM) was employed to study the local structure of SrO-SL and TiO2-SL. The formation of SL configuration is shown in Fig. 3(a) and (e) with 8 periods, and the red dashed rectangle labels one period with 8 UC LSMO, 5 UC BTO and 2 UC STO. For TEM images, the intensity is proportional to the atomic number, and the thin black area corresponds to the STO layer in one period. Across the LSMO layer in each period of the SL, which dominates the transport properties, the electric potential would affect the charge distribution and corresponding chemical valence of ions. The different chemical valence of Mn in manganite is subtle to differentiate from Mn L3,2 electron energy loss spectroscopy (EELS) as suggested in previous work, and then layer-resolved O K edge EELS in LSMO layer is used to characterize the chemical valence of Mn due to the strong hybridization between the oxygen 2p and Mn 3d orbitals.32 As shown in Fig. 3(c) and (g), the layer-resolved O K edge EELS (orange dashed rectangle in Fig. 3(b) and (f)) shows different trend between the two SLs. For TiO2-SL, the position (maximum) of the O pre-edge is 527.9 eV and 528.1 eV at STO/LSMO and LSMO/BTO interfaces, respectively. The O K edge EELS shows uniform distribution across the LSMO layer with similar spectra at STO/LSMO and LSMO/BTO interfaces, and the energy difference of the O pre-edge is ∼0.2 eV. However, for SrO-SL the position of the O pre-edge is 527.5 eV and 528.4 eV at STO/LSMO and LSMO/BTO interfaces, respectively. The energy difference of the O pre-edge at the two interfaces is ∼0.9 eV, revealing the asymmetric electric potential across LSMO. The energy difference between pre-edge and the main peak increases monotonically from the STO/LSMO interface to the LSMO/BTO interface, which corresponds to a gradual increase of Mn chemical valence.33
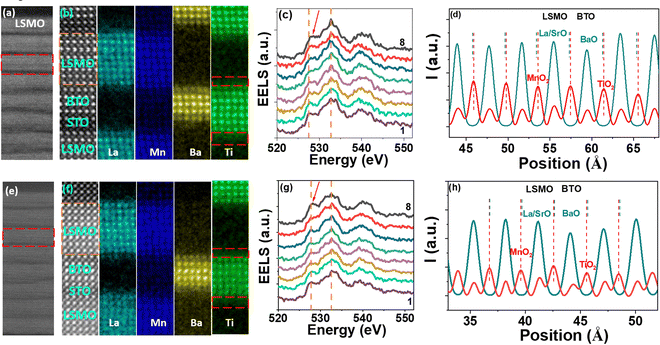 | ||
| Fig. 3 Illustration of superlattice configuration. (a) TEM image, (b) atomic-resolved EELS, (c) oxygen K-edge EELS and (d) the line scan of AO and BO lines in high-resolution STEM image around the BTO/LSMO interface for SrO-SL with t = 5 UC. (e)–(h) Corresponding information for TiO2-SL with t = 5 UC. The deviation of Mn away from the body center of LSMO unit cell is revealed as the difference between the center of La/Sr–La/Sr peak and the Mn peak. The red dashed rectangle in (a) and (e) indicates one period of the superlattice, and the orange dashed rectangle in (b) and (f) indicates LSMO layer where the EELS in (c) and (g) were obtained, respectively. The left-hand orange dashed line in (c) and (g) locates the position of O pre-edge of lowest curve 1, and red arrow indicates the position of the O pre-edge of uppermost curve 8. (d) and (h) Were obtained based on Fig. S3 and S5 (ESI†). | ||
Several factors could cause the change of Mn chemical valence, including oxygen concentration,34,35 cation diffusion,36 and electronic charge transfer.32 Combined study36 has shown previously that both the electronic charge transfer and ionic diffusion at a heterostructural interface could modify the electric potential. Oxygen vacancy37 is common in oxide which depends on the growth parameters. In the current work, both the SrO-SL and TiO2-SL were fabricated under the same conditions, and the oxygen concentration should be the same and not the origin of the different AMR behavior. Another factor is the cationic diffusion; then the cross-section of element distribution was obtained by atomic-resolved EELS mapping, as shown in Fig. 3(b) and (f). The Ti intermixing is stronger at the STO/LSMO interface, spanning longer distance in Ti EELS mapping14 marked by the red dashed square, than at the LSMO/BTO interface. With the coexistence of Mn3+ and Mn4+ in LSMO, the diffusion of Ti4+ into LSMO layer would increase the relative ratio of Mn3+ concentration in order to keep charge neutrality, and decrease the measured chemical valence of Mn. Similar atomic diffusion is observed in Fig. S4 in the ESI† for superlattice fabricated at relatively low temperature of 850 °C. Cationic intermixing would induce higher chemical valence of Mn at the LSMO/BTO interface than at the STO/LSMO interface, and asymmetric electric potential similar to the LAO//STO/LAO triple structure.14 However, the same behavior of cationic diffusion cannot explain the different trend of Mn charge valence between the two SLs.
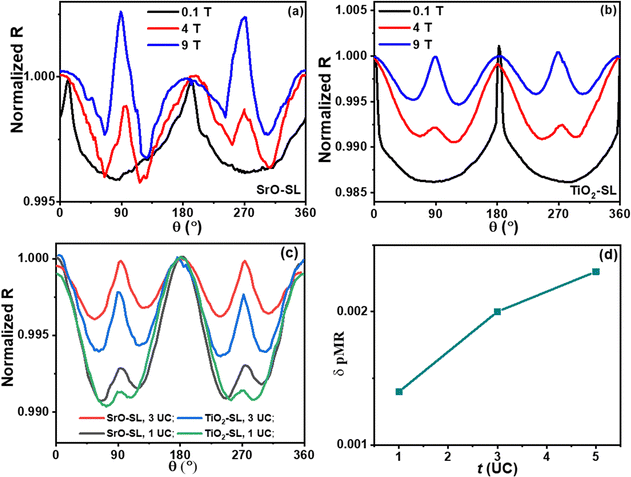
The electronic charge transfer from Mn 3d to Ti 3d orbitals has been well studied at both STO/LSMO and BTO/LSMO interfaces, which could modulate the chemical valence38 around the interface and is sensitive to the interfacial charge density. Then the effect of BTO ferroelectric polarization on the charge transfer was investigated by high-resolution STEM and perpendicular magnetoresistance (pMR). To determine the atomic position in Fig. 3(d) and (h), the averaged raw signal was obtained from Fig. S3–S5 (ESI†) to decrease the noise. After subtracting the baseline, peak fitting was employed to determine the peak position (atomic position) of B site atom in BO2 (MnO2 and TiO2) planes and the A site atom in AO (BaO and La/SrO) planes, the details of which are shown in Fig. S5 in the ESI.† It shows that the BTO polarization is pointing away from the substrate for SrO-SL (Fig. 3(d)) with hole accumulation at the LSMO/BTO interface, and pointing towards the substrate for TiO2-SL (Fig. 3(h)) with hole depletion at the LSMO/BTO interface, which is consistent with previous work.39 The hole depletion at the LSMO/BTO interface for SrO-SL would enhance the probability of electronic charge transfer from Mn to Ti ions40 and increase the Mn chemical valence. This charge transfer works together with cation intermixing to induce the monotonic change of Mn chemical valence as observed in Fig. 3(c). However, the hole accumulation at the LSMO/BTO interface for TiO2-SL has relatively low probability of electronic charge transfer with low Mn chemical valence, which would weaken the difference of Mn chemical valence induced by the cation intermixing as observed in Fig. 3(g). This BTO polarization (∼9 μC cm−2 based on STEM results) could modulate the symmetry of the electronic potential by enhancing/weakening the probability of electronic charge transfer, and then the total probability of charge transfer also changes as revealed below for pMR.
During the pMR measurement, the magnetic field (θ in Fig. 2(a)) rotates from the out-of-plane to the in-plane direction, and keeps perpendicular to the current (along [100] direction). As investigated in previous work, the electronic charge transfer between LSMO and BTO/STO would induce orbital hybridization around the interface and has strong effect on pMR at low temperature, which depends on the probability of the electronic charge transfer.38 Because all superlattices show in-plane magnetic anisotropy, as shown in Fig. S5 in the ESI,† the resistance minimum should occur with magnetic field in the film plane (θ = 90°). However, with increasing magnetic field from 0.1 T to 9 T for both SLs with t = 5 UC, an additional peak in the out-of-plane (θ = 90°) direction appears, which is related to orbital reconstruction with charge transfer. With magnetic field in the film plane, the 3d3z2−r2 band flattens at the Fermi level due to the Mn spin–orbit coupling, and results in a larger resistivity compared to that with magnetic field along the out-of-plane direction due to the decreasing electronic velocity. The stronger the orbital reconstruction with charge transfer in BTO/LSMO/STO triple layer structure, the stronger the additional peak. The stronger peak for SrO-SL suggests that BTO (t = 5 UC) enhances the probability of charge transfer compared to TiO2-SL, which is consistent with the STEM analysis. As reported,41,42 ferroelectric polarization could decrease with decreasing BTO thickness. In order to study the effect of BTO polarization, the pMR of triple-layer superlattice with different BTO thickness t was studied. With the increase of t, the intensity of the additional peak increases for both SrO-SL and TiO2-SL, which is mainly due to the increase of lattice constant.32 However, the difference of additional peak between them also increases with t, as shown in Fig. 4(d), which is caused by enhanced ferroelectric polarization of BTO.
According to the above analysis, for SrO-SL the combination of cation intermixing and electronic charge transfer enhances the potential asymmetry similar to that for the LAO//STO/LAO system, which could induce large Rashba SOI, resulting in same sign of A2 with I//[100] and I//[110] as observed. In the case of a single heterostructural interface, the interfacial Rashba SOI could exist around the interface. Normally a reversal of polarization might cause the sign change of Rashba SOI; then the sign of A2 also should flip. This could explain the sign change of A2 with I//[100] for SrO-SL and TiO2-SL; however, it cannot explain the sign change of A2 for TiO2-SL with I//[100] and I//[110]. In the current work, the asymmetric triple-layer structure with asymmetric potential distribution was proposed to be responsible for the Rashba SOI. For TiO2-SL, although the potential asymmetry across the triple layer was weakened by competing effect of charge transfer and cation intermixing, the local polar environment of the non-centrosymmetric system appears in both the BTO and the LSMO layer as shown in Fig. 3(h), which could induce bulk Dresshaus SOI. With the Dresshaus SOI dominating the electronic structure, as supported by the BTO thickness-dependent AMR in Fig. 5 discussed below, it would show opposite sign31 of A2 with I//[100] and I//[110]. As to the temperature dependence of A2, theoretical work43,44 suggests that the higher-order terms in the SOC Hamiltonian or the temperature-dependent Landé g factor might be responsible. However, further investigation is necessary to verify the mechanism.
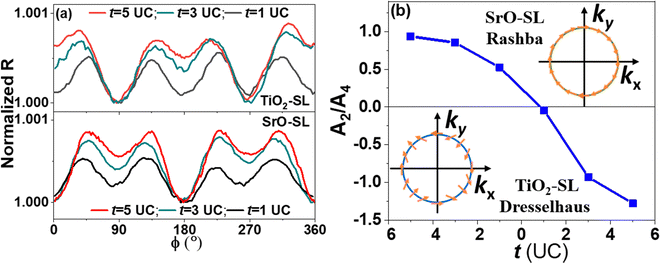 | ||
| Fig. 5 (a) The dependence of in-plane AMR on BTO thickness at 9 T, 5 K for SrO-SL and TiO2-SL. (b) Summary of A2/A4 from (a); the inset illustrates the spin texture for Rashba and Dresselhaus SOIs. | ||
The AMR of [(SrTiO3)2/(La0.7Sr0.3MnO3)8/(BaTiO3)t]8 SLs with different t was studied systematically to verify the above argument, and the results are shown in Fig. 5. At low temperature (5 K) the combination of two- and four-fold symmetry results in quite a different AMR behavior with the change of BTO thickness. The minimum of resistivity occurs at ϕ = 0° for SrO-SL and occurs at ϕ = 90° for TiO2-SL. The four-fold symmetry component becomes apparent with the decrease of BTO thickness for both SrO-SL and TiO2-SL. After fitting the AMR using eqn (1) with details shown in Fig. S7 in the ESI,† the trend of A2/A4 ratio is summarized in Fig. 5(b), which could reveal the relative intensity of the SOI.45 At 5 K, the positive A2/A4 ratio decreases to ∼0 with decreasing t for SrO-SL. The ferroelectric polarization would decrease with decreasing t, which results in the decrease of the coefficient of two-fold symmetry caused by the Rashba SOI. For TiO2-SL, with the increase of t, the ferroelectric polarization increases, resulting in enhanced symmetry breaking with Dresselhaus SOI, as observed in pMR and AMR. The dependence on the BTO thickness t reveals that the ferroelectric polarization could tune the Rashba–Dresselhaus SOI effectively.
Summary
The in-plane AMR of [(LSMO)8/(BTO)t/(STO)2]8 superlattice shows a combination of two- and four-fold symmetry components. The coefficient of the two-fold symmetry component has same sign with current along [100] and [110] directions for SrO-SL, while it has opposite sign for TiO2-SL. Further detailed study shows that cation intermixing and electronic charge transfer induce asymmetric electronic potential for SrO-SL with dominating Rashba SOI, and symmetric electronic potential for TiO2-SL with dominating Dresselhaus SOI, both of which depend on the BTO thickness. Current work shows that the Rashba and Dresselhaus SOIs could be modulated by ferroelectric polarization in asymmetric structures.Experimental methods
[(SrTiO3)2/(La0.7Sr0.3MnO3)8/(BaTiO3)t]8 superlattices were grown on (001) STO substrate at set points of 940 °C and 850 °C by pulsed laser deposition, and oxygen pressure during growth was 100 mTorr, 100 mTorr and 5 mTorr for SrTiO3, La0.7Sr0.3MnO3 and BaTiO3, respectively. The fluence of the laser is 1.5 J cm−2 for all superlattice components. After deposition, the sample was cooled down at 15 °C min−1 in a 100 mTorr oxygen atmosphere.The crystallographic property of the films at room temperature was studied using a four-circle diffractometer (Huber 4-circle system 90000-0216/0) at the Singapore Synchrotron Light Source (SSLS), with X-ray wavelength equivalent to Cu Kα1 radiation. The magnetic properties were measured by a superconducting quantum interference device (SQUID), and the transport properties were measured by a Physical Property Measurement System (PPMS) using a linear four-point probe. STEM was performed using a JEOL ARM200F operating at 200 kV and equipped with ASCOR probe corrector and Oxford XX-Max 100TLE X-ray detector.
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The research was supported by the Natural Science Foundation of Guangdong Province, China under Grant No. 2023A1515010882, the Large Scientific Facility Open Subject of Songshan Lake, Dongguan, Guangdong under Grant No. KFKT2022B06, the National Natural Science Foundation of China under Grant No. 11904415 and No. 11972382; Guangdong Provincial Key Laboratory of Magnetoelectric Physics and Devices under Grant No. 2022B1212010008; The Singapore Ministry of Education Academic Research Fund Tier 2 under the Projects No. MOE2015-T2-1-016 and MOE2018-T2-1-019, MoE T1 R-284-000-196-114, and the Singapore National Research Foundation under CRP Award No. NRF-CRP10-2012-02. PY is supported from SSLS via NUS Core Support C-380-003-003-001.References
- P. Noël, F. Trier, L. M. Vicente Arche, J. Bréhin, D. C. Vaz, V. Garcia, S. Fusil, A. Barthélémy, L. Vila and M. Bibes, et al., Non-volatile electric control of spin–charge conversion in a SrTiO3 Rashba system, Nature, 2020, 580(7804), 483 CrossRef PubMed.
- I. Marković, M. D. Watson, O. J. Clark, F. Mazzola, E. Abarca Morales, C. A. Hooley, H. Rosner, C. M. Polley, T. Balasubramanian and S. Mukherjee, et al., Electronically driven spin-reorientation transition of the correlated polar metal Ca3Ru2O7, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(27), 15524 CrossRef.
- J. Krempaský, M. Fanciulli, L. Nicolaï, J. Minár, H. Volfová, O. Caha, V. V. Volobuev, J. Sánchez-Barriga, M. Gmitra and K. Yaji, et al., Fully spin-polarized bulk states in ferroelectric GeTe, Phys. Rev. Res., 2020, 2(1), 013107 CrossRef.
- H. Lee, J. Im and H. Jin, Emergence of the giant out-of-plane Rashba effect and tunable nanoscale persistent spin helix in ferroelectric SnTe thin films, Appl. Phys. Lett., 2020, 116(2), 022411 CrossRef CAS.
- D. Di Sante, P. Barone, R. Bertacco and S. Picozzi, Electric control of the giant Rashba effect in bulk GeTe, Adv. Mater., 2013, 25(4), 509 CrossRef CAS PubMed.
- L. Meier, G. Salis, I. Shorubalko, E. Gini, S. Schön and K. Ensslin, Measurement of Rashba and Dresselhaus spin–orbit magnetic fields, Nat. Phys., 2007, 3(9), 650 Search PubMed.
- Y. Ho Park, H.-J. Kim, J. Chang, S. Hee Han, J. Eom, H.-J. Choi and H. Cheol Koo, Separation of Rashba and Dresselhaus spin-orbit interactions using crystal direction dependent transport measurements, Appl. Phys. Lett., 2013, 103(25), 252407 CrossRef.
- K. Mikael, R. Roberto, K. Claudine, S. Daniel, L. Pedesseau and J. Even, Rashba and Dresselhaus Effects in Hybrid Organic-Inorganic Perovskites: From Basics to Devices, ACS Nano, 2015, 9, 11557 CrossRef.
- J. D. Koralek, C. P. Weber, J. Orenstein, B. A. Bernevig, S. C. Zhang, S. Mack and D. D. Awschalom, Emergence of the persistent spin helix in semiconductor quantum wells, Nature, 2009, 458(7238), 610 CrossRef CAS.
- D. MacNeill, G. M. Stiehl, M. H. D. Guimaraes, R. A. Buhrman, J. Park and D. C. Ralph, Control of spin–orbit torques through crystal symmetry in WTe2/ferromagnet bilayers, Nat. Phys., 2016, 13(3), 300 Search PubMed.
- A. S. Ahmed, A. J. Lee, N. Bagues, B. A. McCullian, A. M. A. Thabt, A. Perrine, P. K. Wu, J. R. Rowland, M. Randeria and P. C. Hammel, et al., Spin-Hall Topological Hall Effect in Highly Tunable Pt/Ferrimagnetic-Insulator Bilayers, Nano Lett., 2019, 19(8), 5683 CrossRef CAS.
- Z. Zhong, L. Si, Q. Zhang, W.-G. Yin, S. Yunoki and K. Held, Giant Switchable Rashba Effect in Oxide Heterostructures, Adv. Mater. Interfaces, 2015, 2(5), 1400445 CrossRef.
- A. S. Rodin, P. Z. Hanakata, A. Carvalho, H. S. Park, D. K. Campbell and A. H. Castro Neto, Rashba-like dispersion in buckled square lattices, Phys. Rev. B, 2017, 96(11), 115450 CrossRef.
- W. Lin, L. Li, F. Dogan, C. Li, H. Rotella, X. Yu, B. Zhang, Y. Li, W. S. Lew and S. Wang, et al., Interface-based tuning of Rashba spin-orbit interaction in asymmetric oxide heterostructures with 3d electrons, Nat. Commun., 2019, 10(1), 3052 CrossRef PubMed.
- F. Dettwiler, J. Fu, S. Mack, P. J. Weigele, J. C. Egues, D. D. Awschalom and D. M. Zumbühl, Stretchable Persistent Spin Helices in GaAs Quantum Wells, Phys. Rev. X, 2017, 7(3), 031010 Search PubMed.
- L. G. D. da Silveira, P. Barone and S. Picozzi, Rashba-Dresselhaus spin-splitting in the bulk ferroelectric oxide BiAlO3, Phys. Rev. B, 2016, 93(24), 245159 CrossRef.
- P. Huang, Z. Xia, X. Gao, J. M. Rondinelli, X. Zhang, H. Zhang, K. R. Poeppelmeier and A. Zunger, Ferri-chiral compounds with potentially switchable Dresselhaus spin splitting, Phys. Rev. B, 2020, 102(23), 235127 CrossRef CAS.
- A. Sulaev, M. Zeng, S. Q. Shen, S. K. Cho, W. G. Zhu, Y. P. Feng, S. V. Eremeev, Y. Kawazoe, L. Shen and L. Wang, Electrically tunable in-plane anisotropic magnetoresistance in topological insulator BiSbTeSe2 nanodevices, Nano Lett., 2015, 15(3), 2061 CrossRef CAS.
- M. Wimmer, M. Lobenhofer, J. Moser, A. Matos-Abiague, D. Schuh, W. Wegscheider, J. Fabian, K. Richter and D. Weiss, Orbital effects on tunneling anisotropic magnetoresistance in Fe/GaAs/Au junctions, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(12), 121301(R) CrossRef.
- A. Stroppa, Di Sante, D. Barone, P. Bokdam, M. Kresse, G. Franchini, C. Whangbo, M. H. Picozzi and S. Tunable, ferroelectric polarization and its interplay with spin-orbit coupling in tin iodide perovskites, Nat. Commun., 2014, 5, 5900 CrossRef CAS.
- J. Li, S. L. Li, Z. W. Wu, S. Li, H. F. Chu, J. Wang, Y. Zhang, H. Y. Tian and D. N. Zheng, A phenomenological approach to the anisotropic magnetoresistance and planar Hall effect in tetragonal La2/3Ca1/3MnO3 thin films, J. Phys.: Condens. Matter, 2010, 22(14), 146006 CrossRef CAS.
- D. Wu, P. Wei, E. Johnston-Halperin, D. D. Awschalom and J. Shi, High-field magnetocrystalline anisotropic resistance effect in (Ga,Mn)As, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(12), 125320 CrossRef.
- J. Li, S. G. Wang, Y. Zhang, L. M. Cui, Y. R. Jin, H. Deng, D. N. Zheng, A. Zimmers, H. Aubin and P. L. Lang, Anisotropic magnetoresistance and planar Hall effect in La2/3Ca1/3MnO3 thin films with misfit strain, J. Appl. Phys., 2013, 113(5), 053901 CrossRef.
- A. Philippi-Kobs, A. Farhadi, L. Matheis, D. Lott, A. Chuvilin and H. P. Oepen, Impact of Symmetry on Anisotropic Magnetoresistance in Textured Ferromagnetic Thin Films, Phys. Rev. Lett., 2019, 123(13), 137201 CrossRef CAS.
- A. W. Rushforth, K. Vyborny, C. S. King, K. W. Edmonds, R. P. Campion, C. T. Foxon, J. Wunderlich, A. C. Irvine, P. Vasek and V. Novak, et al., Anisotropic magnetoresistance components in (Ga,Mn)As, Phys. Rev. Lett., 2007, 99(14), 147207 CrossRef CAS.
- J. Moser, A. Matos-Abiague, D. Schuh, W. Wegscheider, J. Fabian and D. Weiss, Tunneling anisotropic magnetoresistance and spin-orbit coupling in Fe/GaAs/Au tunnel junctions, Phys. Rev. Lett., 2007, 99(5), 056601 CrossRef CAS.
- A. Rajapitamahuni, L. Zhang, M. A. Koten, V. R. Singh, J. D. Burton, E. Y. Tsymbal, J. E. Shield and X. Hong, Giant Enhancement of Magnetic Anisotropy in Ultrathin Manganite Films via Nanoscale 1D Periodic Depth Modulation, Phys. Rev. Lett., 2016, 116(18), 187201 CrossRef CAS PubMed.
- Y. Z. Chen, J. R. Sun, T. Y. Zhao, J. Wang, Z. H. Wang, B. G. Shen and N. Pryds, Crossover of angular dependent magnetoresistance with the metal–insulator transition in colossal magnetoresistive manganite films, Appl. Phys. Lett., 2009, 95(13), 132506 CrossRef.
- X. Zhang, Q. Liu, J.-W. Luo, A. J. Freeman and A. Zunger, Hidden spin polarization in inversion-symmetric bulk crystals, Nat. Phys., 2014, 10(5), 387 Search PubMed.
- L. Yuan, Q. Liu, X. Zhang, J. W. Luo, S. S. Li and A. Zunger, Uncovering and tailoring hidden Rashba spin-orbit splitting in centrosymmetric crystals, Nat. Commun., 2019, 10(1), 906 Search PubMed.
- M. Trushin, K. Výborný, P. Moraczewski, A. A. Kovalev, J. Schliemann and T. Jungwirth, Anisotropic magnetoresistance of spin-orbit coupled carriers scattered from polarized magnetic impurities, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(13), 134405 CrossRef.
- B. Zhang, L. Wu, J. Zheng, P. Yang, X. Yu, J. Ding, S. M. Heald, R. A. Rosenberg, T. V. Venkatesan and J. Chen, et al., Control of magnetic anisotropy by orbital hybridization with charge transfer in (La0.67Sr0.33MnO3)n/(SrTiO3)n superlattice, NPG Asia Mater., 2018, 10(9), 931 CrossRef CAS.
- S. R. Spurgeon, P. V. Balachandran, D. M. Kepaptsoglou, A. R. Damodaran, J. Karthik, S. Nejati, L. Jones, H. Ambaye, V. Lauter and Q. M. Ramasse, et al., Polarization screening-induced magnetic phase gradients at complex oxide interfaces, Nat. Commun., 2015, 6, 6735 CrossRef CAS PubMed.
- F. Gunkel, D. V. Christensen, Y. Z. Chen and N. Pryds, Oxygen vacancies: The (in)visible friend of oxide electronics, Appl. Phys. Lett., 2020, 116(12), 120505 CrossRef CAS.
- Z.-H. Wang, Q. H. Zhang, G. Gregori, G. Cristiani, Y. Yang, X. Li, L. Gu, J. R. Sun, B. G. Shen and H. U. Habermeier, Control of charge order melting through local memristive migration of oxygen vacancies, Phys. Rev. Mater., 2018, 2(5), 054412 CrossRef CAS.
- F. Gunkel, R. Waser, A. H. H. Ramadan, R. A. De Souza, S. Hoffmann-Eifert and R. Dittmann, Space charges and defect concentration profiles at complex oxide interfaces, Phys. Rev. B, 2016, 93, 245431 CrossRef.
- J. Walter, S. Bose, M. Cabero, G. Yu, M. Greven, M. Varela and C. Leighton, Perpendicular magnetic anisotropy via strain-engineered oxygen vacancy ordering in epitaxial La1−xSrxCoO3−δ, Phys. Rev. Mater., 2018, 2, 111404(R) CrossRef.
- N. M. Nemes, M. J. Calderon, J. I. Beltran, F. Y. Bruno, J. Garcia-Barriocanal, Z. Sefrioui, C. Leon, M. Garcia-Hernandez, M. C. Munoz and L. Brey, et al., Signatures of a two-dimensional ferromagnetic electron gas at the La0.7Sr0.3MnO3/SrTiO3 interface arising from orbital reconstruction, Adv. Mater., 2014, 26(44), 7516 CrossRef CAS PubMed.
- R. Guo, L. Shen, H. Wang, Z. Lim, W. Lu, P. Yang, A. Ariando, A. Gruverman, T. Venkatesan and Y. P. Feng, et al., Tailoring Self-Polarization of BaTiO3 Thin Films by Interface Engineering and Flexoelectric Effect, Adv. Mater. Interfaces, 2016, 3(23), 1600737 CrossRef.
- B. Cui, C. Song, H. Mao, H. Wu, F. Li, J. Peng, G. Wang, F. Zeng and F. Pan, Magnetoelectric Coupling Induced by Interfacial Orbital Reconstruction, Adv. Mater., 2015, 27(42), 6651 CrossRef CAS PubMed.
- M. Trieloff, E. K. Jessberger, I. Herrwerth, J. Hopp, C. Fiéni, M. Ghélis, M. Bourot-Denise and P. Pellas, Structure and thermal history of the H-chondrite parent asteroid revealed by thermochronometry, Nature, 2003, 422(6931), 502 CrossRef CAS PubMed.
- G. De Luca, N. Strkalj, S. Manz, C. Bouillet, M. Fiebig and M. Trassin, Nanoscale design of polarization in ultrathin ferroelectric heterostructures, Nat. Commun., 2017, 8, 1419 CrossRef PubMed.
- P. S. Eldridge, W. J. H. Leyland, P. G. Lagoudakis, O. Z. Karimov, M. Henini, D. Taylor, R. T. Phillips and R. T. Harley, All-optical measurement of Rashba coefficient in quantum wells, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(12), 125344 CrossRef.
- L. Zhang, Y. B. Chen, B. Zhang, J. Zhou, S. Zhang, Z. Gu, S. Yao and Y. Chen, Sensitively Temperature-Dependent Spin–Orbit Coupling in SrIrO3 Thin Films, J. Phys. Soc. Jpn., 2014, 83(5), 054707 CrossRef.
- K. Huang, L. Wu, M. Wang, N. Swain, M. Motapothula, Y. Luo, K. Han, M. Chen, C. Ye and A. J. Yang, et al., Tailoring magnetic order via atomically stacking 3d/5d electrons to achieve high-performance spintronic devices, Appl. Phys. Rev., 2020, 7(1), 011401 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: S1: crystal structure; S2: magnetic and transport properties; S3: AMR fitting for superlattice with BTO t = 5 UC; S4: EELS for superlattice fabricated at low temperature; S5: determination of the atomic position; S6: MH loops; S7: AMR fitting for superlattice with different BTO t. See DOI: https://doi.org/10.1039/d3mh00635b |
| This journal is © The Royal Society of Chemistry 2024 |