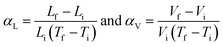Multifunctional single-component organic molecular materials: ferroelectricity, negative thermal expansion, and polymorphism

Abstract

Organic materials with multifunctional properties, such as ferroelectricity, negative thermal expansion, and the phenomenon of polymorphism, have gained enormous interest from material scientists due to their unusual characteristics and unique applications. Moreover, research on single-component systems with such unusual properties is on the rise despite the necessity of satisfying strict criteria for designing such materials. This highlight provides an overview of the evolution of research on purely organic molecular ferroelectrics and thermo-responsive materials and the importance of studying polymorphism in such materials. Starting from their basics to the role of crystallographic symmetry in designing and characterizing, the mechanisms these special classes of materials follow, and the possible use of various techniques for advancing these research areas are discussed here. This highlight is expected to advance materials science research and to motivate novice researchers to explore these key research areas.

---

Sanjay Dutta

Dr Sanjay Dutta received his PhD in Chemical Sciences from the Shiv Nadar Institution of Eminence, Delhi NCR, India, where he worked on single-component organic ferroelectric and negative thermal expansion materials under the mentorship of Prof. Parthapratim Munshi. Subsequently, he joined as a postdoctoral fellow at the Baylor University, Waco, Texas, where he worked with Prof. Caleb D Martin in boron chemistry. Currently, he is a postdoctoral researcher in the group led by Prof. Michael Stollenz, Department of Chemistry and Biochemistry at the Kennesaw State University, Georgia, USA, and working on the development of boron- and copper-based complexes as thermally activated delayed fluorescence materials and structure–property relationship.

Lalita Negi

Dr Lalita Negi is a CSIR research associate working under the supervision of Prof. Parthapratim Munshi at the Shiv Nadar Institution of Eminence, Delhi NCR, India. Before this, she was a postdoctoral fellow in the same group for over a year. Her research interest involves the study of ferroelectricity and unusual thermal expansion in single- and multi-component organic materials. She earned her BSc (Hons.) degree in Chemistry from the University of Delhi, India, and her MSc in Chemistry from the Kumaun University, Uttarakhand, India. She received her PhD from the Jawaharlal Nehru University, New Delhi, India, under the supervision of Dr. Dinabandhu Das.

Parthapratim Munshi

Dr Parthapratim Munshi is a professor of chemistry at the Shiv Nadar Institution of Eminence, Delhi NCR, India. He obtained his PhD in Chemical Crystallography from the Indian Institute of Science, Bengaluru. Subsequently, he pursued his postdoctoral research at the University of Western Australia, Nancy University (France), and Oak Ridge National Laboratory (USA). His research group focuses on multifunctional organic molecular materials. He is a recipient of the Marie-Curie International Incoming Fellowship. He was named an Emerging Investigator in Cryst. Growth & Des. He is a Fellow of the Royal Society of Chemistry, UK. Recently, he has been inducted as a member of the National Committee for the IUCr, the Commission on Quantum Crystallography of the IUCr, the University of California Berkeley's Executive Leadership Academy Alumni, and the Editorial Board of CrystEngComm and J. Mol. Struct. Currently, he is serving as a co-editor for J. Appl. Cryst.

---

1. Introduction

Solid state science has made tremendous progress towards discovering multifunctional materials, among which ferroelectrics (FEs)^1–3 have been at the forefront. Simultaneously, thermo-responsive materials with unusual negative thermal expansion (NTE) properties have gained massive interest from material scientists due to their unique characteristics.^4–7 Moreover, polymorphism⁸ has also drawn the attention of researchers as it plays a crucial role in governing material properties.

In this highlight, we aim to provide an overview of the research on purely organic molecular ferroelectrics and thermo-responsive materials and the role of polymorphism in such unusual materials. Initially, we introduce ferroelectricity and NTE properties, their applications, and the phenomenon of polymorphism. Then, we discuss the role of crystallography in designing and characterizing such materials and understanding their properties. Subsequently, we elaborate on the mechanisms these special classes of materials follow. After that, we focus on purely organic materials, especially the single-component systems. Before concluding, we discuss the possible use of various techniques for advancing these key research areas.

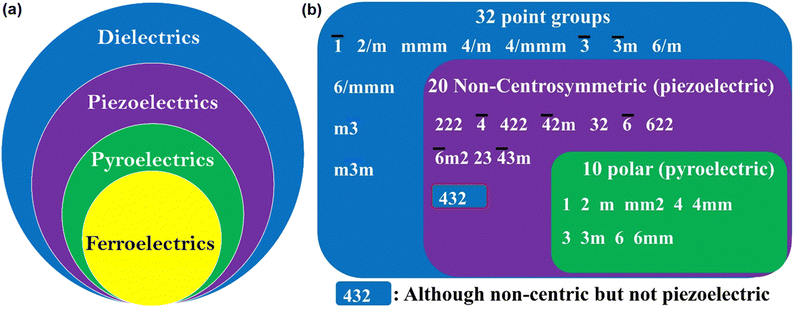
Ferroelectric is not related to the metal Fe (iron) as its name suggests, but it is analogous to ferromagnetism.⁹ Like ferromagnetic systems, FE materials consist of multiple domains comprised of electric dipoles. Domains¹⁰ are small regions within the FE crystal where a group of electric dipoles are aligned in the same direction. Under the application of a strong external electric field (E), these domains line up along its direction, resulting in net polarization (P). This leads to separation of the positive and negative poles, similar to the magnetic dipoles in iron, where the north and south poles are created under a strong magnetic field. FEs are usually accompanied by temperature-triggered structural changes to undergo a reversible ferroelectric–paraelectric phase transition, resulting in the generation and vanishing of spontaneous polarization (P_s). The net polarization in the FE materials is reversed or reoriented upon applying E. Moreover, due to their electrical bi-stability, ferroelectrics experience electrical displacement and display a hysteresis loop between P and E (Fig. 1). These characteristics are paramount for fabricating storage devices such as FeFET^2,3 and FeRAM.^2,3 Ferroelectrics can also be used as capacitors because these materials obey the Curie–Weiss law, and the dielectric constant rises rapidly during the ferroelectric to paraelectric transition, known as the Curie temperature (T_c).¹ The parameters that define the characteristics of FE materials are P_s, remnant polarization, P_r, and the coercive field, E_c (Fig. 1). The P_s value represents the maximum polarization induced in a FE material at a high E. The P_r value indicates the amount of polarization the material can retain after removing E, i.e. at E = 0 kV cm⁻¹. E_c is the electric field required to reverse the polarization direction, i.e. to bring the net polarization of the material to zero (P = 0 μC cm⁻²). The figure of merit of FE materials is assessed based on their P_s, P_r, and E_c values. Higher values of P_s and P_r and lower values of E_c signify superior characteristics of FE materials. Materials with low E_c find application in low-voltage FE devices.¹¹

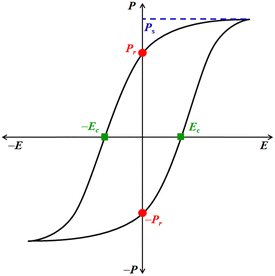Fig. 1 Typical hysteresis loop (P vs. E) of a ferroelectric material and its associated characterization parameters.

As shown in Fig. 2a, FEs are the lowest sub-group of dielectrics. They can be used in many applications due to their cross-correlation phenomena, such as piezoelectricity,¹ pyroelectricity¹ and second harmonic generation (SHG).^12,13 In piezoelectric materials, due to electro-mechanical coupling, stress changes the electric P, and conversely, E produces strain.^1,14 Thus, these materials find application in ultrasonic motion sensors, actuators, transducers, inkjet printers, and mechanical harvesters. The thermo-electric coupling leads to pyroelectric behaviour, resulting in the change in P due to uniform heating and cooling. This effect has been used in infrared detection, thermal imaging and energy harvesting.^1,15 Furthermore, the polar nature of FE materials also leads to electro-optic effects such as SHG, terahertz light emission and photovoltaic effects.

Fig. 2 (a) The dielectric spectrum showing the super- and sub-group relationship among the special class of electronic materials of various physical properties, (b) point group classification based on the symmetry.

FEs had come to the foray of research as early as 1920 when J. Valasek discovered ferroelectricity in sodium potassium tartrate salt (KNaC₄H₄O₆), also known as Rochelle salt.^16,17 However, for the next two decades, no FEs were discovered. Consequently, the research community presumed it was the biggest serendipity of nature until the discovery of potassium dihydrogen phosphate (KH₂PO₄; KDP) as a H-bonded FE in 1935.¹⁸ Subsequently, the inorganic oxide barium titanate (BaTiO₃) with perovskite structure was discovered as FE material in 1945,¹⁹ which triggered the research in this important area. Thus, in the following years, the other perovskite structures²⁰ such as lead zirconate titanate (Pb(Zr_xTi_1−x)O₃), bismuth ferrite (BiFeO₃), and lithium niobate (LiNbO₃) came to the picture. These inorganic ferroelectrics have been a subject of active research for over 50 years and are used in many industrial and technological applications.

The usual phenomenon of expansion of solids with an increase in temperature is known as positive thermal expansion (PTE), which has been exploited in solid-state chemistry. Due to change in temperature, solid materials may exhibit interesting properties leading to important applications such as heat-stimulated infrared detectors in pyroelectric materials,¹⁵ and the generation of thermo-responsive switching materials.^21,22 However, the expansion of solids upon heating hinders its applicability: for example, in large construction elements such as railway tracks, roads, bridges, and containers of liquefied natural gas and small precision devices such as fibre optic systems, organic light-emitting diodes (OLEDs), organic field-effect transistors (OFET), thin-films, catalyst supports, etc.^6,23,24 Nevertheless, the applications of multifunctional materials require not only robust physical phenomena but also controlled thermal expansion behaviour, as it enhances both lifetime and reliability. The effect of expansion upon heating can be correlated to the asymmetric shape of the Lennard-Jones potential energy well of a diatomic molecule (Fig. 3). Higher vibrational levels get populated as the molecule is heated up, and the gap between the molecules increases.⁶

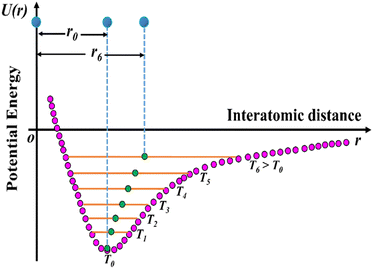Fig. 3 Schematic diagram of the potential energy well of paired atoms (adapted and modified from ref. 6).

The thermal expansion in solids is formally quantified with the coefficient of thermal expansion (CTE), α, which can be calculated using the following equation:

where α_L and α_V are linear and volumetric coefficients, L_f and V_f are the final length and final volume of the material of interest at a final temperature T_f and L_i and V_i are the initial length and initial volume at an initial temperature T_i, respectively. The CTE is generally measured in parts per million per Kelvin (K⁻¹), and its unit is K⁻¹. However, it is expressed in 10⁻⁶ K⁻¹ or M K⁻¹ for conventional use. This equation holds well for the orthogonal crystal system in which the angles are perpendicular to each other.

Thermal expansion directions are identified by considering the principal axes, the set of orthogonal axes, X1, X2 and X3, along which thermal expansion varies linearly.²⁵ Thermal expansion is a directional property and depends on the symmetry of the crystal system. For cubic systems, expansion is isotropic in all three directions. Hence α_V = 3α_L. However, for the non-orthogonal system, the expansion is anisotropic and has different magnitudes of thermal expansion along the principal axes. The volumetric expansion, α_V, can be calculated by adding α₁, α₂, and α₃, which are the CTE along each principal axis that are perpendicular to each other.

For inorganic compounds, the magnitude of α_V lies in the range of 0–20 M K⁻¹, and for molecular materials, it usually lies in the range of 100–300 M K⁻¹.²⁵ There are several techniques for monitoring thermal expansion in a solid. However, calculating the CTE using unit-cell parameters obtained via single-crystal X-ray diffraction (SCXRD) is one of the most commonly used methods. PASCal²⁶ and Win_Strain²⁷ are widely used to calculate the CTE for non-orthogonal crystal systems.

Contraction and expansion of materials upon heating and cooling, respectively, is termed NTE, a counter-intuitive phenomenon.^4–7 This special class of materials with such unusual properties can counter the PTE characteristics of the material.²⁸ However, the limited availability of NTE materials hinders the steady progress in this area of research. Thermal contraction was first documented in 1907 in quartz and silicates. Later, in 1948, NaZr₂(PO₄)₃ (NZP)²⁹ was reported to have an anisotropic NTE of α_L = −0.4 M K⁻¹ in the temperature range of 298–1273 K. The isotropic NTE effect was first discovered in 1996 by Sleight et al.³⁰ in ZrW₂O₈, which has a CTE value of −9 M K⁻¹ over a wide temperature range of 0.3 to 1050 K. This has led to the significant progress of NTE-based studies in solid-state chemistry. Ice is another popular example of NTE material which displays NTE below 75 K due to low-energy transverse vibrational modes.³¹ The emergence of the NTE phenomenon provides an excellent opportunity to control both physical and thermo-responsive properties simultaneously, especially in the case of functional materials such as dielectric, piezoelectric, pyroelectric, magnetic and optical materials. Usually, NTE characteristics are noticed in inorganic systems. Most isotropic NTEs are found in open framework structures such as AM₂O₈,³² AM₂O₇,³³ A₂M₃O₁₂,³⁴ zeolites^35–37 and ruthenium-based fluorides.^38–40 These materials experience NTE due to the transverse vibration of the bridging atom, which includes oxygen and fluorine. The other mechanisms driving the NTE phenomenon are magnetic transition,⁴¹ charge transfer,^42,43 and spontaneous volume ferro-electrostriction,^44,45 which are primarily prominent in inorganic functional materials.

NTE in FE materials is not uncommon.⁶ However, the coexistence of FE and NTE has been reported predominantly in inorganic oxides,^46–48 benzo[18]crown-6 based metal complexes,⁴⁹ and dabcoHCl·3H₂O.⁵⁰ The report on the dabco complex demonstrated that the NTE occurs due to the rotation of water molecules, and the supramolecular architecture involving linear N–H⁺⋯N bonds led to the FE behaviour. However, its anhydrous polar form divests these unusual properties. The NTE effect in FE materials generally involves multiple competing mechanisms, which are material-specific and depend on the complexity of the structural, electronic, and thermodynamic factors. NTE and FE properties are directional and are linked to temperature. While the anisotropy in a crystal structure is essential for the emergence of NTE and FE characteristics, the temperature variation can lead to a non-uniform response of the material due to the asymmetric arrangement of atoms in the crystal lattice. Moreover, under an external E, the macroscopic P reversal occurs in FE materials due to the reorientation of electric dipoles, which induces strain in the lattice with an increase or decrease in temperature, leading to lattice contraction or expansion. Furthermore, with the temperature change, the FE materials undergo structural phase transitions, which may trigger lattice softening in specific directions, leading to NTE along those directions. Further elucidation of the origin of the coexistence of these intriguing phenomena warrants more studies on versatile systems and delving into the role of microscopic interactions.

Polymorphism,⁸ the phenomenon of the existence of a compound in multiple solid forms, has been widely studied in molecular materials for tuning their properties as it can significantly influence the material properties.^51–55 Polymorphs exhibit differences in structural, thermodynamic, and other physical properties. Often, polymorphs are categorised based on their molecular conformation, packing, colour, thermodynamic stability, etc. Accordingly, polymorphism is classified as conformational polymorphism, which arises due to the existence of different conformers of the same molecule; packing polymorphism, which arises due to the difference in molecular packing of the polymorphs in their crystal lattice; colour polymorphism, which arises due to the difference in the colour of the polymorphic crystals, etc. Therefore, polymorphic materials can display distinct properties even with the slightest changes in their crystal structures.^56–58 Although polymorphs occur frequently in molecular crystals, their existence in organic materials with exotic properties is scarce.^54,59,60 Some of us have recently demonstrated that polymorphic forms exhibit distinct multifunctional properties. In the case of 2-(4-(trifluoromethyl)-phenyl)-1H-phenanthro[9,10-d]imidazole, it exhibits FE and NTE properties in its various crystal forms – trimorphs and hydrates (Fig. 4).⁶¹ One of the two polar forms exhibits FE characteristics, and the other displays a large reversible NTE below room temperature (RT). Further, the non-centrosymmetric hydrated form also experiences NTE below RT, but the centrosymmetric forms divest these properties. The other polymorphic materials with FE or NTE characteristics in organic materials have been highlighted in the following sections.

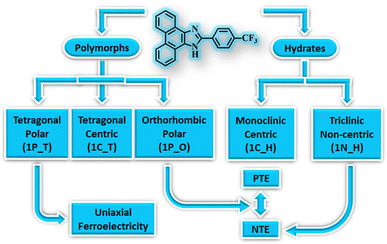Fig. 4 Multifunctional properties of polymorphic and hydrated forms of 2-(4-(trifluoromethyl)-phenyl)-1H-phenanthro[9,10-d]imidazole, a purely organic material.

2. Ferroelectricity

2.1. Crystallographic perspective

In materials science, crystallographic symmetry plays a critical role in identifying the structural phases of the solids and helps derive their structure–property relationships. The two basic symmetry operations in crystallography, rotation (n) and reflection (m) define the symmetry of a point in space. In crystallography, 32 point groups and 230 space groups defining the microscopic and macroscopic properties of the crystalline materials⁶² are distributed among the 14 Bravais lattices and seven crystal systems, from higher to lower symmetry as cubic, hexagonal, rhombohedral (trigonal), tetragonal, orthorhombic, monoclinic and triclinic. Out of 32-point groups, 11 are centrosymmetric, and the remaining 21 are non-centrosymmetric (Fig. 2b). The 21 non-centrosymmetric point groups are further classified into 10 polar point groups and the rest into non-polar point groups. The lack of centre of inversion has a paramount effect on material properties, leading to numerous important physical properties in solid state science such as SHG, piezoelectricity, pyroelectricity and most importantly, ferroelectricity.^63,64 FE materials must crystallize in one of the 10 polar point groups, and the corresponding paraelectric (PE) phase at a higher temperature must belong to one of the 32-point groups with a higher symmetry than the FE phase, as listed in Fig. 2b. However, introducing homochirality in a molecule can enhance the probability of a material crystallising in the polar space group. The chiral molecules crystallize in chiral point groups. There are 11 chiral point groups, of which five are polar, so there is an increased probability (5/11 vs. 10/32) that the molecule will crystallize in the polar point group.⁶⁵

Based on the Curie symmetry principle,⁶⁶ the symmetry of the FE phase should be a maximal subgroup of the higher symmetric PE phase along which the direction of P_s exists. In light of this group-to-subgroup relationship, Aizu has identified 88 combinations of point groups for the PE to FE phase transition.⁶⁷ If the PE phase crystallizes in the centrosymmetric point group, the FE is considered reversible, where P_s can be reversed under E. If the PE phase exists in the polar point group, then the FE is termed reorientable FE, where the direction of P_s is reoriented instead of reversing. Reorientable ferroelectrics are rare and fall into the category of relaxor-type FE. Moreover, under the guidance of the Curie symmetry-breaking principle, based on the point group symmetry of the known phase (PE), the symmetry and polarization direction of the other phase (FE) can be deduced using the Aizu relationship. Further, point group symmetry of the FE phase and its corresponding jump from the low temperature and low symmetric phase to the high temperature and high symmetry PE phase during symmetry breaking defines the number of allowed directions the P_s vector can have in FEs. These are then classified as (1) uniaxial (Rochelle salt, tri-glycine sulphate, LiNbO₃, etc.) and (2) multiaxial (BaTiO₃, PZT, etc.). In the former case, the P_s vector can reorient itself only in two polarization directions under E. For the latter case, the polarization vector can reorient itself in more than two polarization directions. As mentioned above, the point group of the FE phase is a subgroup of the PE phase. Point groups in the PE phase have various isomorphic subgroups whose polar direction corresponds to the direction of P_s, and the maximal one comprising the most symmetry elements along the polarization direction is the FE point group. Therefore, the number of polarization directions in the FE phase can be defined as n = N_PE/N_FE, where N_PE and N_FE represent the sum of symmetry elements in the PE and FE point groups, respectively. Thus, when n = 2, the FEs are uniaxial with only two opposite polarization directions, and more than two polarization directions characterize multiaxial FEs. The greater the symmetry change between the PE and FE phase, the higher the equivalent polarization directions a FE material will have. For example, in the case of LiNbO₃, both the PE space group, R3̄c (N_PE = 4), and the FE space group, R3c (N_FE = 2), belong to the trigonal crystal system. Closer lattice symmetries lead to the arousal of uniaxial nature.⁶⁸ Similarly, diisopropylammonium bromide, a molecular FE with a high T_c (426 K) and a large P_s (23 μC cm⁻²), is also uniaxial with an Aizu notation of 2/mF².⁶⁹ FE transitions from a cubic crystal system to one with much lower symmetry are generally multiaxial, and the n value can be as high as 48. For instance, in BaTiO₃, which is a multiaxial system, the successive phase transitions from cubic Pm3̄m (N_PE = 48) to tetragonal P4mm (N_FE = 8) at 393 K, to orthorhombic Amm2 (N_FE = 4) at 278 K, and then to R3m (N_FE = 6) at 183 K lead to multiaxial ferroelectric behaviour with 6, 12, and 8 equivalent polarization directions.

2.2. Ferroelectricity mechanisms

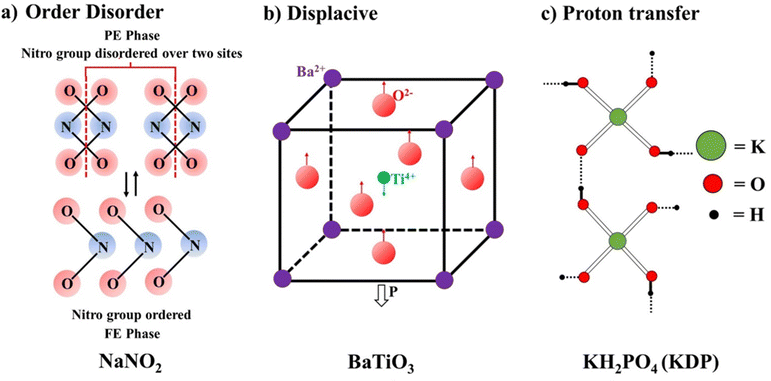
Based on the type of chemical bonding, the ferroelectrics are classified as H-bonded ferroelectrics, e.g. KH₂PO₄, Rochelle salt, tri-glycine sulphate, etc., and inorganic oxides having a perovskite structure, e.g. BaTiO₃, PZT, etc. The third classification is based on the (1) order–disorder, (2) displacive, and (3) proton transfer mechanisms.

2.2.1. Order–disorder. In this type, a thermally disordered state reorients to an ordered state. In Fig. 5a, this mechanism is represented in the case of sodium nitrite (NaNO₂),¹ where a permanent dipole of the nitrite ion (NO₂⁻) generates P_s, and reorientation of dipoles upon application of an external E gives rise to ferroelectricity. In the FE phase, the orientation of NO₂⁻ is ordered, and it becomes disordered at a higher temperature, leading to the cancellation of the dipole moment and resulting in the corresponding PE phase (Fig. 5a). Amine-based organic salts, such as diisopropylammonium bromine (C₆H₁₆NBr)⁶⁹ and chloride (C₆H₁₆NCl),⁷⁰ which are low molecular weight FEs, belong to the order–disorder type. The origin of ferroelectricity in these systems is due to the ordered arrangement of the diisopropyl ammonium cation (C₆H₁₆N) in the FE phase upon cooling down from its PE phase, where the cation exhibits rotational disorder. A similar scenario was observed in the case of DABCO-based organic salts.⁷¹

Fig. 5 Different types of mechanisms that lead to the origin of ferroelectricity polarization.

2.2.2. Displacive. If the origin of ferroelectricity is due to the relative displacement of ions or molecules, the ferroelectrics are categorized as displacive type. The classic example is BaTiO₃,¹⁹ having an ABX₃ type perovskite structure (Ba²⁺ as A, Ti⁴⁺ as B and O²⁻ as X), and its cubic structure at high temperatures undergoes three successive FE phase transitions. Each phase involves slight distortion from the high symmetry phase (Fig. 5b). The net displacement of the cations with respect to the oxygen octahedra results in P_s in the FE phases. Displacive-type FEs have also been discovered in metal–organic frameworks (MOFs). (15-crown-5)-bis(nitrato-O,O′)-Calcium(II)⁷² is an excellent example of low-temperature molecular FEs where distortion of the coordination environment of Ca²⁺ induces ferroelectricity.

2.2.3. Proton transfer. In this type, the labile protons on hydrogen bonds activate the FE ordering within the system. These are also called KDP type because the collective proton shuttling in the O–H⋯O bonds leads to the origin of ferroelectricity (Fig. 5c). Both order–disorder and displacive mechanisms are not mutually exclusive as they can exist together, and the KDP is a prime example where proton ordering triggers ferroelectricity, but the main contribution to P_s comes from the displacement of the phosphate ion (PO₄³⁻) and potassium (K⁺) ion.^18,73 A similar mechanism is proposed in the case of DABCO-based organic salt⁷¹ of [H₂dabco]·[2CB] ([H₂dabco]²⁺ = diprotonated 1,4-diazabicyclo[2.2.2]octane, 2CB⁻ = 2-chlorobenzoate), which undergoes FE to PE transition at 323 K, leading to both displacement of the proton position and simultaneously disordering of the [H₂dabco]²⁺ cation. In the PE phase, the [H₂dabco]²⁺ cation is rotationally disordered and lies at the symmetric centre of the trimer. It freezes in an ordered state upon cooling and deviates toward a 2CB⁻ anion at one end along the H-bond. This collective displacement and ordering of the cations leads to the origin of polarization in the FE phase.

Further, an optically controlled polarization switching mechanism has been explored in the domain of inorganic FEs. Various photo-excited electronic effects, such as flexoelectric and photovoltaic, have been studied to gain photocontrol in such materials. Light-driven effects, such as the flexoelectric effect due to photoexcitation of electronic effects to control optical polarization, have been seen in the case of SrTiO₃.⁷⁴ Some specific organic molecules have recently been exploited to generate polarization using light as a stimulus.⁷⁵

2.3. Organic ferroelectrics

Though the first FE material, Rochelle salt^16,17 is an organic salt, the past century has seen the dominance of inorganic ceramics, and the number of FEs that have come to the fore are mainly inorganic oxides and polymeric systems. Traditionally, inorganic ceramics have been used for many practical electronic applications due to their superior FE characteristics and robust piezoelectric behaviour. However, using inorganic compounds containing heavy elements has become a serious global concern, especially regarding health and the environment. Thus, the scientific community was forced to look for alternatives, leading to the resurgence of organic FEs in the past few decades due to their benign nature, mechanical flexibility, lightweight, environmental friendliness, cost-effective production and easy processing.^76–81 Further, organic electronics provide design flexibility to tune the properties and enhance their performance and durability. Accordingly, organic FE devices can be portable, flexible, wearable, biocompatible and usable as economical medical devices.

The order–disorder mechanism in multicomponent systems led to a significant development of molecular FEs. Sachio et al. developed several multicomponent FEs based on acid–base supramolecular co-crystals with heteronuclear hydrogen bonds, which undergo the abovementioned mechanism. Some examples are phenazine-chloranilic acid,⁸² and binary combinations of 2,5-dihalo-3,6-dihydroxy-p-benzoquinones with bases such as phenazine,⁸³ 5,5-dimethyl bipyridine,⁸⁴ and 2,3-di(2-pyridinyl)pyrazine.⁸⁵ The ferroelectricity in these systems amounts to the degree of proton transfer, which strongly depends on the acidity and basicity of the conformers. Based on the combination, there could be two types of supramolecular systems, neutral and ionic. Harada et al. used globular-shaped molecules to design molecular FEs, especially in plastic crystals.^86,87 The globular molecular structure in plastic crystals can easily undergo order–disorder transition due to the low rotational barrier, which led to the development of some multiaxial FEs such as tetramethylammonium tetrachloroferrate(III)⁸⁷ and tetramethylammonium bromotrichloroferrate(III).⁸⁷

Further, Xiong et al. developed a metal-free perovskite-based order–disorder type FE.⁸⁸ Typically, perovskites have a three-dimensional (3D) ABX₃ structure in which the A cations are located in the 3D corner-sharing framework of BX₆ octahedra (B represents the other cation, and X is an anion). Such perovskites represent one of the most pursued forms of isotropic ferroelectrics. The globular-shaped molecules based on DABCO derivatives have been used to design such molecular FEs. MDABCO-NH₄I₃ is one such derivative, which displays FEs with multiaxial characteristics above RT. In this case, the large organic cations (MDABCO), small NH⁴⁺, and halide anions (I⁻) occupy the A⁻, B⁻, and X-sites, respectively. The B-site cations are also involved in the NH⋯X hydrogen bonds with the surrounding X-site anions. The phase transition involves a cubic PE structure and a rhombohedral FE structure at 448 K, accompanied by a large off-centred displacement of the A- and B-site ions. This leads to a multiaxial nature with the Aizu notation⁶⁷ of 432F3, having eight polarization axes along [111]. The high P_s of 22 μC cm⁻² is observed due to the synergistic effect of two distinct mechanisms, ionic displacement and order–disorder orientation. The other examples are diisopropylammonium bromide,⁶⁹ diisopropylammonium chloride⁷⁰ and guanidinium perchlorate⁸⁹ with P_s of 23, 8.9 and 8.4 μC cm⁻², respectively.

Furthermore, efforts have been made to discover proton transfer mechanism-based organic FEs via database mining.⁹⁰ The study also proposed density functional theory-based prediction of E_c in such systems.

Finally, the development of isotropic molecular FEs^65,91 eased the fabrication of thin film devices. Conventional organic FEs with highly anisotropic crystal structures cannot work unless their crystal orientation leads to a uniaxial polarization in the desired direction. In contrast, the nearly isotropic characters of possible polarization vectors guarantee efficient switching, even in randomly oriented crystals such as polycrystalline thin films and compacted pellets.

2.4. Single-component organic ferroelectrics

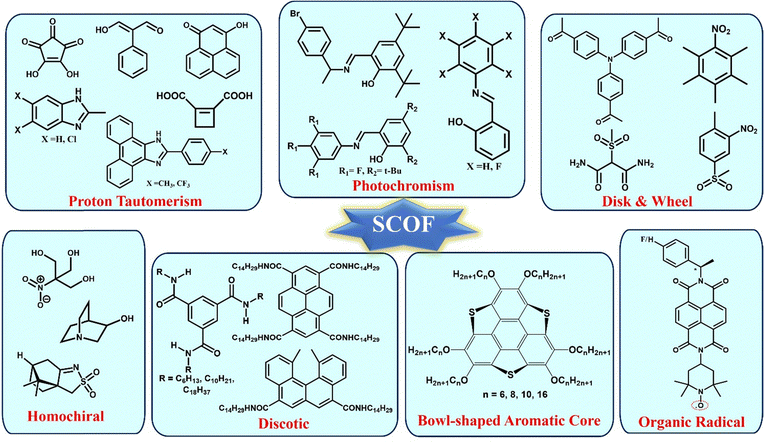
The multicomponent systems comprised of salts^66,71,92 and co-crystals^81,93 have certain disadvantages, which can be overcome through single-component organic ferroelectrics (SCOFs). The concern regarding salt systems is that they often contain metal ions, which leads to toxicity. However, the addition of metal ions may enhance P_s and T_c. Co-crystals, although benign, suffer from lower thermal stability and shelf life, hindering their applicability. These challenges have been overcome in the case of SCOFs. However, in the case of SCOFs, due to the thermal robustness of their FE phase, the T_c is usually hidden beyond its thermal stability. Various types of SCOFs reported in the literature are summarized below (Fig. 6).

Fig. 6 Examples of different types of single-component organic ferroelectrics (SCOF).

2.4.1. PTM-type ferroelectrics. Tautomeric systems, such as keto–enol and enamine–imine, which incorporates D and A in the same molecule, can be used to design SCOFs (Fig. 7a). This idea was first proposed by Haddon et al. in 1982 when H-bonded tautomeric systems could be used as model systems for memory application devices.⁹⁴ The prototype study for such systems was squaric acid^95–97 containing the β-diketone enol (enolone, HO–C=C–C=O). Squaric acid undergoes tautomerization between the keto and enol forms (Fig. 7a), exhibiting strong coupling between the proton and π-electron system. This type of prototropic system reinforces intra or intermolecular hydrogen bonds synergistically with the augmentation of the π-system delocalization, defined as the resonance-assisted H-bond (RAHB).^98–100 The FE systems developed under this principle are defined as proton tautomerization type ferroelectrics, and the corresponding mechanism is known as the proton tautomerism mechanism (PTM)⁸⁰ as illustrated in Fig. 7b.

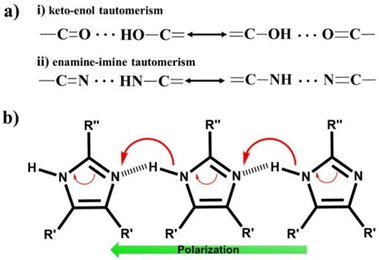Fig. 7 (a) Tautomeric system and (b) proton tautomerism mechanism in enamine-imine based single-component organic ferroelectrics.

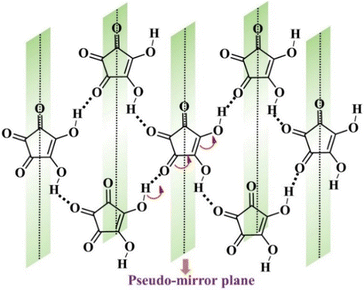
In addition to proton tautomerization, the other prime factors for designing FE systems are the presence of inherent molecular symmetry higher than C1¹⁰¹ and the ability of a polar structure to have hidden pseudosymmetry, which persists in the PE phase. The concept of pseudosymmetry in single-component systems is based on the intrinsic mechanism of ferroelectricity, where there is a subtle deviation of the polar structure in the FE state from the centrosymmetric structure, thus ensuring easier polarization switching. This principle has been utilised in the past by Zikmund et al.¹⁰² to predict the potential FE candidate. They discovered weak ferroelectricity in cyclohexane-1,1α-diacetic acid.¹⁰³ The hidden pseudosymmetry in the proton transfer type FEs can be identified by the global crystal symmetry of the proton whose position defines the crystal polarity. Local psuedosymmetries in the crystal structures can be identified using the ADDSYM option in the PLATON program.⁹⁵ Thus, based on this initial hypothesis, researchers started to explore systems consisting of tautomeric units to characterize them as FEs. The breakthrough study in this direction was achieved in 2010 when Sachio et al. discovered croconic acid (CA) as a FE material.⁷⁷ CA is a black organic dye,¹⁰⁴ a 5-member ring of oxocarbon acids (H₂C_nO_n) that is strongly acidic because its conjugate base (C₅O₅²⁻) dianion formation is favoured due to delocalization of the π-electron within the ring. This amphoteric nature of CA leads to strong RAHB^98–100 formation, thus resulting in keto–enol type of proton tautomerism and contributing to a large molecular dipole moment, which gives rise to the net polarization of 30 μC cm⁻² in its crystal form. In addition to the enhanced polarization, low E_c and robust thermal stability (∼450 K) observed in CA⁷⁷ can be correlated to the strong coupling between the proton and the π-electron cloud. The concept of hidden pseudosymmetry in the case of CA is illustrated in Fig. 8. The pseudo-mirror symmetry, which orthogonally crosses the pentagon of the CA ring, leads to the formation of the hypothetical PE phase (protons in disorder state) with space group Pcam, one of the minimal supergroups of the polar space group Pca2₁ of the FE phase. The other systems comprised of β-diketone enol O=C–C=C–OH moieties as a simpler prototype for the FE tautomerism are 2-phenylmalondialdehyde and 3-hydroxyphenalenone.⁷⁸

Fig. 8 Pseudo-mirror symmetry in croconic acid with resonance-assisted hydrogen bonds.

Ferroelectricity was also discovered in imidazole-based derivatives comprised of the enamine unit (Fig. 7b). These enamine–imine motifs in imidazole exhibit amphoteric behaviour, thus forming a proton D–A type molecular assembly based on linear N–H⋯N hydrogen bonds. Imidazole-based SCOFs were reported in the cases of two benzimidazole derivatives, namely, 2-methylbenzimidazole⁷⁹ and 5,6-dichloro-2-methylbenzimidazole.⁷⁹ Further, Fraser et al. discovered ferroelectricity in halogen-substituted imidazoles, where they confirmed the ferroelectricity based on local polarization switching using the piezo force microscopic (PFM) technique.¹⁰⁵

Recently, some of us reported SCOF in an enamine-based motif, 2-(p-tolyl)-1H-phenanthro[9,10-d]imidazole, which exists in three polymorphic forms.⁵⁴ The polar crystal form of this environmentally benign material not only displays a notable P_s of 3.0 μC cm⁻², a highly stable (98%) P_r of 3.9 μC cm⁻², and low E_c (6.2 kV cm⁻¹), it perseveres the FE phase up to a record-high temperature of ∼521 K (Fig. 9a). Subsequently, the crystal undergoes an irreversible phase transition to form non-polar (1N, P4̄2₁c) and centrosymmetric (P2₁/n) polymorphs having distinct molecular packing in their crystal lattices. These polymorphic transformations suggested that the material loses its FE characteristics beyond ∼521 K and remains non-ferroelectric. Nevertheless, this was the thermally most stable purely organic FE crystal then. Moreover, the E_c achieved in this case is much lower (6.2 kV cm⁻¹) than those reported for the well-known CA (14 kV cm⁻¹) and chloro derivative of benzimidazole (60 kV cm⁻¹) at 373 K. Our study demonstrated that the migration from benzimidazoles to phenanthroimidazoles with extended benzene rings helps maintain the FE phase at a much higher temperature. Further, the study highlighted that although the PTM triggers the generation of polarization and the polarity switching via RAHB, the low value of E_c is achieved due to the relative displacements between the two crystallographically independent molecules in its crystal lattice. This study was the first to report displacive type FE in SCOF. Otherwise, it usually occurs in inorganic oxides.

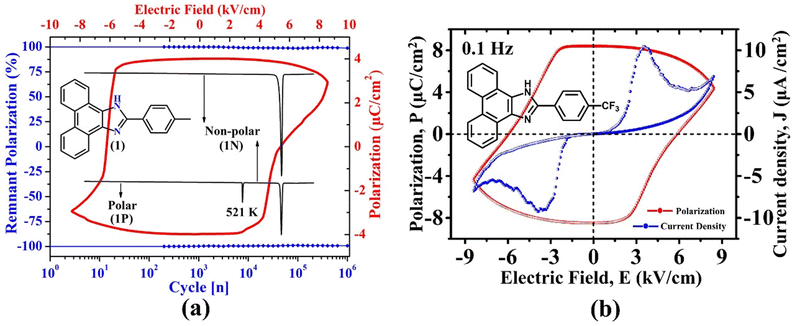Fig. 9 (a) Depiction of ferroelectricity, thermal stability and phase transition behaviour in 2-(p-tolyl)-1H-phenanthro[9,10-d]imidazole.⁵⁴ (b) Ferroelectric loop (P vs. E) and the corresponding fatigue measurements in 2-(4-(trifluoromethyl) phenyl)-1H-phenanthro[9,10-d]imidazole.⁶¹

Further, the P_s was computationally calculated using Berry phase formalism and the DFT method with the generalized gradient approximation in the Perdew–Burke–Ernzerhof (PBE) form as implemented in the Vienna ab initio simulation package (VASP). The estimated P_s of ∼3.8 μC cm⁻² compares well with that obtained from the P–E loop measurement at RT.

Furthermore, some of us discovered that the tetragonal polymorphic form (1P_T, P4₁) of 2-(4-(trifluoromethyl)phenyl)-1H-phenanthro[9,10-d]imidazole,⁶¹ a triflate-substituted phenanthro-imidazole, is a SCOF (Fig. 9b). In this case, the in-crystal polarization reversal measurement resulted in a P_s of ∼4.6 μC cm⁻², a P_r of ∼8.3 μC cm⁻² and an E_c of ∼5.8 kV cm⁻¹ with the least leakage current. Further, based on the first-principles calculations discussed above, the P_s was predicted to be 3.1 μC cm⁻², which agrees well with the experimental value. In addition to the polar FE form, this system exhibits two more polymorphs: orthorhombic polar form (1P_O, Pca2₁) and tetragonal centrosymmetric form (I4₁/a). However, the FE measurements on the pellet of 1P_O did not result in any meaningful polarization switching loop. Moreover, the P_s value estimated using VASP is also nominal (0.2 μC cm⁻²). Therefore, the in-crystal ferroelectric measurements were carried out only in the case of the 1P_T form.

2.4.2. Optically controlled ferroelectrics. Other than electric fields and temperature, structural changes can also be triggered by stimuli, such as pressure, light, mechanical stress, and magnetic fields. Among them, photoirradiation is a noncontact, noninvasive, nondestructive and remotely controlled stimulus for optical control of FE polarization. Photoinduced geometrical isomerization, such as cis–trans or keto–enol transformation, can trigger a structural phase transition leading to the photochromic effect. Despite the discovery of photochromism as early as 1867, photoswitchable FEs are rare because of the impossibility of such structural changes in inorganic systems.¹⁰⁶ Fortunately, a special class of organic materials, such as azo cis–trans, Schiff base enol–keto, etc., undergo photoisomerization in their solid state.¹⁰⁷ The recent developments on optically controlled SCOF based on salicylideneaniline derivatives and azobenzene-based crystals have shaded lights in the design of single-component photoswitchable FEs. Salicylideneaniline derivatives are a special class of organic Schiff base materials that undergo photochromism upon irradiation due to keto–enol tautomerism. This class of materials has recently been discovered as optically controlled SCOFs. Xiong et al. have reported multiple examples of salicylideneaniline derivatives to show photocontrol FE behaviour.^75,108–110 The first such example is 3,4,5-trifluoro-N-(3,5-di-tertbutyl salicylidene) aniline (TFTBSA),⁷⁵ which crystallizes in two polymorphic forms, the polar form with space group Pna2₁ (TFTBSA-1) and the centrosymmetric form with space group P2₁/n (TFTBSA-2). The polymorphs have distinct molecular conformations, i.e. they are conformational polymorphs. The polar TFTBSA-1 crystals undergo photochromism under the illumination of UV light (365 nm), resulting in changes in colour from yellow to orange (Fig. 10). In contrast, the centrosymmetric polymorph TFTBSA-2 does not change colour even after UV light is illuminated for longer. The structural switching due to photoirradiation in the case of the polar form has been confirmed through ultraviolet-visible (UV-vis) absorption, and infrared (IR) spectra are accompanied by reversible structural photoisomerization between the enol form and the trans-keto form, which is impossible to be realized in inorganic FEs. In addition, under remote-control photoirradiation, the dielectric permittivity and P_s can be switched reversibly by structural photoisomerization. In this case, the photoswitchable FE was achieved upon polarization switching through a structural phase transition triggered by photoisomerization. Furthermore, the authors also studied N-(3,5-di-tert-butylsalicylidene) aniline, another salicylideneaniline derivative that crystallizes in the polar space group Pna2₁. It was observed that despite fulfilling the structural criteria for FE, this derivative does not undergo polarization switching under the external E. This behaviour suggested that a compound must simultaneously have a polar point group and photoisomerization effect in this class of systems to achieve photo-controlled polarization switching. Moreover, in the quest for many more photocontrol FEs, they have come across multiple systems such as (R)- and (S)-N-3,5-di-tert-butylsalicylidene-1–4-bromophenylethylamine, (E)-2-((phenyl imino)methyl)phenol, (E)-2-(((perfluorophenyl) imino)methyl) phenol,¹⁰⁸ salicylidene-2,3,4,5,6-pentafluoro-aniline,¹⁰⁹ salicylidene aniline,¹¹⁰etc. Among these, (R)- and (S)-N-3,5-di-tert-butylsalicylidene-1–4-bromophenylethyl amine exhibit multichannel controlled multiferroic behaviour, where both photocontrol polarization and temperature-controlled ferroelastic domain have been observed. Further, such studies have been extended to the diarylethene,¹¹¹ fulgide,¹¹² muconic,¹¹³ and azobenzene¹⁰⁶ based family of photochromic compounds.

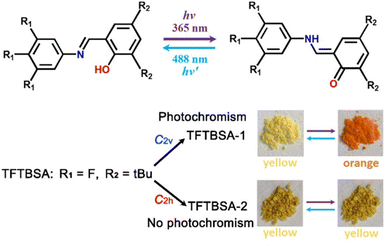Fig. 10 Conversion of the enol form to the trans-keto form and vice versa upon UV light irradiation (up) and photochromic and non-photochromic behaviour of the polymorphic forms TFTBSA-1 and TFTBSA-2, respectively. tBu = tert-butyl. Reprinted (used in part) with permission from ref. 75. Copyright 2021 American Chemical Society.

2.4.3. Disk- and wheel-like ferroelectrics. Disk- or wheel-like molecules have recently been used to develop SCOFs, where polarization switching is achieved via molecular rotation.¹¹⁴ Such FEs follow the principle of latent pseudosymmetry in their crystal structure, which leads to the achievement of the hypothetical PE phase. This allows easy polarization switching when the crystal experiences minimal deviation from a centrosymmetric structure. In such molecules, the rotational disorder can awaken the hidden symmetry of the whole crystal structure. Such FEs can be disk-type, where in-plane rotation of molecules leads to polarization switching, and wheel-type, where axial rotation can flip the molecular dipole, leading to polarization switching. Hexa-substituted benzene derivatives and 1,2,3,4,5-pentamethyl-6-nitrobenzene (PMNB)¹¹⁴ have been utilized for the development of disk-type FEs (Fig. 6). In the case of PMNB, the nitro-group is an electron-withdrawing group, and the penta-methyl group is an electron-donating group that forms a polar molecule which crystallizes in space group P1. The molecules in the crystal structure are assembled in a sheet parallel to (111̄), where each molecule is located on the pseudo-inversion symmetry. This leads to an easy P_s switching simply by the molecular disk rotation. Although the PMNB crystal exhibits a large P_r of ∼6 μC cm⁻², it experiences a very high E_c (∼100 kV cm⁻¹) at RT and a frequency of 1 Hz along the c-axis. In the case of wheel-type FEs, the axially asymmetric substituents are used as a wheel or rotary knob. The molecules are designed in tetragonal-shaped substituents –RXYZ or triangular-shaped substituents –RXY fashion to induce a large dipole moment upon introduction of an electron-donating atom or group X and electron-withdrawing atom or group Y. Recently, 2-(methylsulfonyl)-malonamide (MSMA)¹¹⁴ has been reported as a wheel-type FE (Fig. 6). MSNA experiences a net polarization of 7.3 μC cm⁻², a P_r of 3.8 μC cm⁻², and a high E_c of ∼100–160 kV cm⁻¹ at 3–30 Hz. Both PMNB and MSMA crystals exhibit a nearly temperature-independent relative permittivity at near RT, indicating the absence of a T_c.

2.4.4. Homochiral ferroelectrics. Combining quasi-spherical theory with homochiral principle dramatically improves the probability of discovering new SCOFs^65,115 (Fig. 6). The quasi-spherical principle assists in discovering materials with phase transition behaviour of order–disorder type. Further, as discussed above, the homochirality enhances the possibility of a molecule crystallizing in chiral point groups. Recently Xiong et al. exploited this concept to achieve quasi-spherical homochiral FE crystals (R)- and (S)-3-quinuclidinol by introducing the –OH group to the quinuclidinol molecule (Fig. 11).¹¹⁵ While the (R)- and (S)-forms crystallize in enantiomorphic space groups P6₁ and P6₅, respectively, (rac)-3-quinuclidinol crystallizes in the centrosymmetric space group P2₁/n. Both the polar forms undergo FE to PE phase transition at ∼400 K via an order–disorder mechanism due to the globular molecular structure with 622F6 type FE transition. They exhibit uniaxial characteristics with a P_s of ∼7 μC cm⁻² along the O–H⋯N hydrogen bond propagating along the c-axis. The uniaxial characteristics of 3-quinuclidinol limit their practical utility. Thus, the quest for FE candidates with multiaxial characteristics based on the quasi-spherical principle led to the discovery of 2-(hydroxymethyl)-2-nitro-1,3-propanediol,¹¹⁶ in which a six-fold vertex domain structure was observed for the first time. In this multiaxial FE, the transition follows the m3mF1 Aizu notation, and the change in the symmetry elements resulted in 24 equivalent FE axes and 48 crystallographic equivalent polarization directions, the highest among all ferroelectrics. Moreover, the P_s of 8.4 μC cm⁻², observed in this system, is comparatively higher than that of the well-known FE polymer PVDF. Furthermore, recently discovered homochiral SCOFs, (R)-10-camphorsulfonylimine and (S)-10-camphorsulfonylimine,¹¹⁷ under the guidance of FE chiral chemistry have been reported to exhibit the highest T_c of 429 K among the SCOFs.

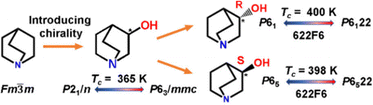Fig. 11 Scheme representing the introduction of homochirality in 3-quinuclidinol. Reprinted (used in part) with permission from ref. 118. Copyright 2020 American Chemical Society.

2.4.5. Discotic type ferroelectrics. Flexible supramolecular assemblies with directional amide-type N–H⋯O hydrogen bonds form molecular columns, leading to discotic-type materials with large macroscopic dipoles along the column axis. Based on this design principle, discotic liquid crystalline (DLC) materials with a benzene-1,3,5-tricarboxamide (BTA) core forming a hexagonal 1D columnar phase with varying lengths of alkyl chains containing C6, C10, and C18 carbons (Fig. 6), were used to study dielectric relaxation and ferroelectric/polar switching.^119,120 While the C18-based DLC yielded a significant P_r (= P_s) value of 1.3–1.8 μC cm⁻² and an E_c value of 20–30 kV cm⁻¹ in its thin film,¹²⁰ the temperature-dependent experiments in the crystals of C10- and C18-based DLC resulted in extrinsic polar switching with P_s and E_c values of 1–2 μC cm⁻² and 20–30 kV cm⁻¹, respectively. Further, Akutagawa et al. reported that the benzenecarboxamide derivatives bearing four −CONHC₁₄H₂₉ chains at the pyrene core form a π-stacked column through intermolecular N–H⋯O=C hydrogen bonds and display FE switching.¹²¹ In the case of the hexacolumnar DLC phase above 295 K, the inversion of the dipole moment due to the conformational change of the hydrogen bond along the π-stacking column under E leads to the generation of FE switching (Fig. 12). Further, the authors used non-π-planar helicene cores bearing two −CONHC₁₄H₂₉ chains (Fig. 6), forming discotic molecular assemblies with 2D intermolecular interactions to achieve superior FE properties and enhance the practical utility of such systems.¹²² They have successfully measured excellent FE properties (P_r and E_c values of 10.7 μC cm⁻² and 10.8 kV cm⁻¹, respectively) in rac-N,N′-di(tetradecyl)-1,12-dimethyl-N⁵,N⁸-ditetradecylbenzo[c]phenanthrene-5,8-dicarboxamide which forms high-density and well-oriented ferroelectric domains in a 2D hydrogen-bonding network layer.

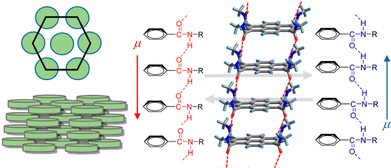Fig. 12 Schematic illustration of discotic hexacolumnar mesophase (left) and H-bonded 1D columnar structure with dipole (μ) inversion through the collective conformational change of the chain along the π-stacking direction (right). Reprinted (used in part) with permission from ref. 121. Copyright 2015 American Chemical Society.

2.4.6. Bowl-to-bowl inversion type ferroelectrics. Supramolecular assemblies based on organic molecules with a bowl-shaped π-aromatic core that undergoes bowl-to-bowl inversion and skew rotation generate ferroelectric dipole relaxation.^123,124 Organic ferroelectric materials based on hexaalkoxy trithiasumanenes (CnSS), which feature invertible bowl-shaped π-aromatic cores, constitute one such finding.¹²⁵ The study reported that the bowl-shaped aromatic cores of these CnSS molecules were stacked one-dimensionally in a columnar arrangement (Fig. 13). Such an alignment resulted in a dipole moment from the stacked bowl-shaped framework, leading to remnant polarization in the crystals. Generally, the bowl inversion barrier magnitude depends on the bowl depth of the curved π frameworks. The shallow depth of trithiasumanene (SS) led to a low bowl inversion barrier. Moreover, introducing large heteroatoms such as sulphur and selenium in curved π-molecules impacted the dynamic and electronic properties of these heterasumanenes. Six long alkoxy chains (–OC_nH_2n+1) were introduced into the SS π-core to enhance the motional freedom and facilitate bowl inversion. The above room temperature FE reversal polarizations of the CnSS series were confirmed via differential scanning calorimetry and P–E hysteresis loop measurements at 336–383 K.

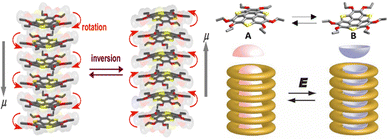Fig. 13 Schematic of the dipole inversion mechanism coupled with inversion of bowl-shaped (from A (up) to B (down)) conformation and skew rotation and a schematic model of the bowl-to-bowl structural inversion upon application of an electric field E, where molten –OC_nH_2n+1 chains surround the polar bowl column. The grey arrows indicate the dipole moment direction in each system (adapted and modified from ref. 125).

2.4.7. Organic radical and martensitic ferroelectrics. The organic radicals 2,2,6,6-tetramethylpiperidine-N-oxyl (TEMPO)¹²⁶ and [(NH₃-TEMPO) ([18]crown-6)](ReO₄)¹²⁷ are well-known single- and multi-component FE materials, respectively. However, they display either a low or no phase transition temperature (T_c). In this context, it is worth recalling that the T_c usually remains inaccessible for SCOFs. Nonetheless, the martensitic phase transition, which occurs in solids due to lattice strain,^128,129 has been reported in organic FEs, such as guanidinium nitrate¹³⁰ and diisobutylammonium bromide.¹³¹ Based on these design elements for SCOFs, Zhang et al.¹³² studied a series of asymmetric 1,4,5,8-naphthalenediimide (NDI) derivatives that form lamellar structures via π⋯π interactions, a key strategy for introducing martensitic phase transition in organic compounds. Further, to induce ferroelectricity in NDI derivatives, they attached homochiral α-methyl benzylamine on one side and NH₂-TEMPO on the other to construct organic radical ferroelectrics (Fig. 6). Subsequently, they synthesized a series of FE compounds N-[(S)- and (R)-1-phenylethyl]-N′-[1-oxyl-2,2,6,6-tetramethyl-4-piperidinyl]-1,4,5,8-naphthalenediimide (S- and R-H) and their 4-fluorophenyl analogues (S- and R-F) (Fig. 14). The study revealed that the derivatives adopt a low-symmetric polar structure and display FE properties. Further, the study demonstrated that upon H/F substitution, the fluorinated compounds experience reversible FE and martensitic transitions at 399 K, with a significant thermal hysteresis of 132 K.

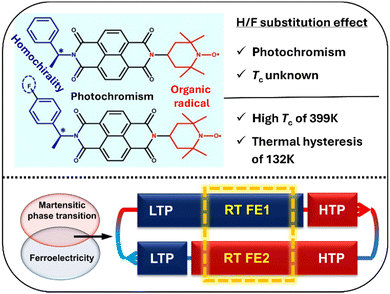Fig. 14 Effects of H/F substitution in NDI derivatives (top) and the combination of martensitic phase transition and ferroelectricity in S-/R-F NDI derivatives with two different ferroelectric phases at room temperature (bottom). LTP and HTP represent the low-temperature phase and high-temperature phase, respectively. RT FE1 and RT FE2 represent different ferroelectric phases at room temperature (adapted and modified from ref. 132).

Additionally, biodegradable ferroelectricity is reported in the molecular crystals of 2,2,3,3,4,4-hexafluoropentane-1,5-diol (HFPD), a single-component system that exhibits a large piezoelectric response.¹³³ The study demonstrated that the crystals can flexibly be made into thin, strain-sensing films. Moreover, HFPD exhibited promising biocompatibility with biological cells and desirable biodegradation and biosafety in physiological environments. Thus, it was envisaged that the material may find application in transient implantable electrochemical devices.

2.5. Advance methodologies to study H-bonded FEs

Conventionally, FE characterization techniques include X-ray diffraction for phase and structural analysis, P–E loop measurements to determine the macroscopic polarization and switching behaviour, and PFM experiment to visualize the domain structure and switching pattern based on amplitude and phase measurements to know the local FE behaviour. For H-bonded FEs, in addition to the conventional methodologies, advanced techniques such as neutron diffraction¹³⁴ and high-resolution single-crystal X-ray diffraction experiments can be employed to understand better the FE mechanisms, especially for the order–disorder and PTM-type FEs. Charge density analysis using high-resolution X-ray and neutron diffraction data allows deriving accurate topological properties of electron densities. While neutron diffraction pinpoints the position of hydrogen atoms, high-resolution X-ray diffraction provides an opportunity to measure the degree of polarization of electron densities, which are crucial for PTM-type FEs. Moreover, neutron data allow the accurate determination of the atomic displacement parameters and lead to the efficient resolution of atomic disorders. In addition, E-dependent X-ray and neutron diffraction experiments may help monitor the dynamics of the proton due to FE switching and the corresponding π-electron delocalization. Recently, Fancher et al. performed an E-dependent neutron diffraction study on KDP crystals, a H-bonded FE.¹³⁵ The study demonstrates that the macroscopic polarization reorientation is instigated by a collective change in the H-bond, leading to the reversal of the spontaneous dipole. Additionally, the decrease of secondary extinction near the E_c suggested that the inversion of macroscopic polarization is due to the nucleation and the successive growth of the new domains. Moreover, Kobayashi et al. observed electric field-induced antipolar–polar transition, along with colossal electrostriction in 2-trifluoromethyl-naphthimidazole crystals by performing an E-dependent synchrotron X-ray diffraction experiment.¹³⁶ These few studies based on advanced techniques provided crucial insights towards the improved understanding of the FE mechanisms in H-bonded FEs.

3. Negative thermal expansion

3.1. Mechanism of NTE

The NTE phenomenon is generally noticed in inorganic systems. Most isotropic NTE is reported in open framework structures such as AM₂O₈,⁸⁰ AM₂O₇,⁸¹ A₂M₃O₁₂,⁸² zeolites^83–85 and ruthenium-based fluorides.^86–88 These materials experience the NTE effect due to the transverse vibration of the bridging atom, which includes oxygen and fluorine. The other mechanisms driving the NTE phenomenon are magnetic transition,⁸⁹ charge transfer^90,91 and spontaneous volume ferro-electrostriction,^92,93 which are mostly prominent in inorganic functional materials. The possible NTE mechanisms in inorganic solids and molecular materials are summarized in the following sections.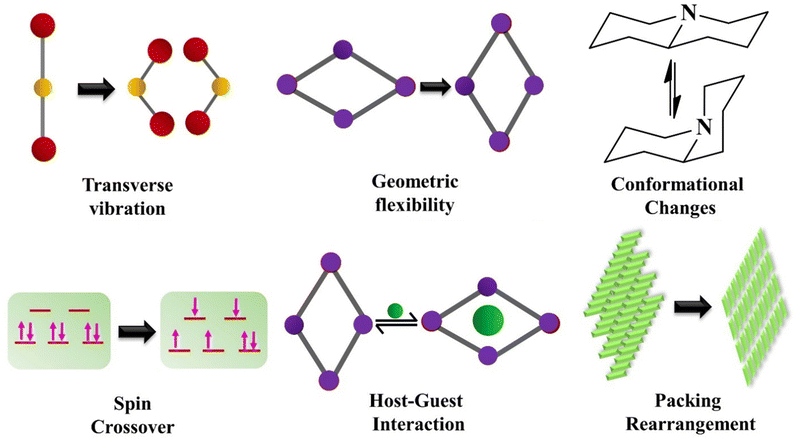

3.1.1. Transverse vibration. Transverse vibration has been one of the most common mechanisms in inorganic solids (Fig. 15). A few examples are the NZP family,²⁹ ZrW₂O₈,³⁰ AM₂O₇³³ (A = Ti, Z r, Hf, M = P, V), Sc₂(WO₄)₃,¹³⁷ zeolites,^35–37 Zr_0.4Sn_0.6Mo₂O₈,³² ScF₃,³⁸ and cyanide-containing molecular materials such as Fe[Co(CN)₆],¹³⁸ Zn(CN)₂,¹³⁹ Cd(CN)₂,¹⁴⁰ N(CH₃)₄CuZn(CN)₄,¹⁴¹ MPt(CN)₆¹⁴² (M = Mn, Fe, Co, Ni, Cu, Zn, Cd), and LnCo(CN)₆¹⁴³ (Ln = La, Pr, Sm, Ho, Lu, Y). These materials form a network of corner-shared polyhedra due to bridging atoms such as oxygen and fluorine between the metal ions. This central linking atom in the chain M1–O–M2 oscillates perpendicular to the chain upon heating, resulting in contraction of the M1⋯M2 distance (red colour atoms in Fig. 15), and the material exhibits NTE behaviour macroscopically. An alternative way to derive this mechanism is rigid unit modes (RUMs), whereby polyhedra can be treated as rigid units due to the strong bonding between M and O. The dynamic rocking motion of the rigid polyhedra causes NTE due to the temperature rise.

Fig. 15 Various mechanisms leading to negative thermal expansion (NTE) behaviour in molecular materials.

Williams et al.¹³⁹ used the cyanide molecule as the bridging agent in Zn(CN)₂ to enhance the NTE (α_L = −18 M K⁻¹) below 180 K compared to inorganic oxides such as ZrW₂O₈ with single-atom-supported RUM structures. The enhanced NTE effect in the case of diatom-supported RUMs is due to larger degrees of freedom. RUMs supported by a single atom are face-constrained, where an adjacent polyhedron influences the rotation of a polyhedron. However, for the diatom-supported RUMs, the polyhedron can rotate independently. Two neighbouring squares can rotate along the same or opposite directions, contributing to NTE.

3.1.2. Host–guest interaction and geometrical flexibility. The concept of host–guest chemistry was first established by Donald J. Cram¹⁴⁴ in 1974 to illustrate the chemistry of a multi-component system comprised of two or more molecules or ions held together by noncovalent interactions. Because the NTE effect is highly prone to crystal lattice dynamics, the introduction of guest molecules in the voids of the crystal lattice strongly influences the thermo-responsive behaviour of the molecules. Furthermore, molecular framework deformation due to geometrical flexibility under external stimuli such as temperature, pressure, guest molecule, light, and irradiation leads to outstanding stimuli-responsive behaviours. The guest molecule plays an interesting role in modulating thermal expansion properties in some host–guest complexes. In 1990, White et al. performed the first thermal expansion study on a clathrate of Dianin's compound, the host–guest system.¹⁴⁵ In this case, the high TE, particularly along the a-axis, was achieved due to an increase in the anharmonicity of the guest molecule at high temperature compared to the guest-free form. Supramolecular interactions between the host and guest compounds lead to high thermal expansion as weakly interacting atoms of the guest molecule tend to vibrate more at high temperatures. Monohydrates of dipeptide tryptophylglycine exhibit NTE due to the presence of water molecules in its crystal structure.¹⁴⁶

Geometrical flexibility is commonly observed in the case of MOFs prepared from extended ligands, resulting in a larger void within the crystal lattice and leading to a flexible structure (Fig. 15). One of the well-known examples of flexible MOFs is MIL-53,¹⁴⁷ which undergoes large pore (l_p) and narrow pore (n_p) transformation upon inclusion of the guest molecule. This effect is called the breathing effect due to chemical stimuli. Further, geometrical flexibility due to temperature as a stimulus has been observed in guest-free aluminium-based MIL-53, where n_p to l_p transformation happens above 300 K, and upon cooling, it undergoes a reversible process with a large thermal hysteresis. Furthermore, it has been observed that materials with fence-like structures undergo geometrical flexibility due to scissor-like motion.¹⁴⁸ Perdeuterated methanol monohydrate¹⁴⁹ is a simple molecular crystal which shows remarkable thermo-responsive behaviour with colossal anisotropic thermal expansion with α_b = 462(4) M K⁻¹, α_c = 93(4) M K⁻¹, and α_a = −61(4) M K⁻¹, along the b-, c-, and a-axis, respectively, at 155 K due to scissor-like motion. With the rise in temperature, the dynamic molecular motion of the scissor-jack-like structures leads to contraction in the orthogonal direction and expansion in the other direction.

Two salts of imidazole, imidazolium terephthalate (IMD-TPH) and imidazolium 4-hydroxybenzoate (IMD-HBC), were reported to have uniaxial NTE and biaxial PTE characteristics.^150,151 The unusual behavior of the salts was elucidated based on their fencing and scissor-like motion of the 2D H-bonded network, respectively. Upon changing the imidazole with 4-methylimidazole, salt 4-methylimidazolium-4-hydroxybenzoate (4-MIMD-HBC) exhibited unusual biaxial NTE owing to the scissor-like motion with the variation of temperature.¹⁵²

3.1.3. Molecular packing rearrangements and conformations. Purely organic molecular crystals with weak noncovalent interactions^153–155 facilitate the packing rearrangement and conformational change, causing anisotropic thermo-responsive effects upon thermal stimuli (Fig. 15). These materials are categorized as soft materials, as the molecules in these materials are held together via weak supramolecular interactions. The molecular packing rearrangement leading to exceptionally large reversible uniaxial PTE (156 M K⁻¹ < α_L < 515 M K⁻¹) and biaxial NTE (−32 M K⁻¹ < α_L < −85 M K⁻¹ and −48 M K⁻¹ < α_L < 204 M K⁻¹) was observed by Das and co-workers¹⁵⁶ in the case of dumbbell-shaped (S,S)-octa-3,5-diyn-2,7-diol. The colossal anisotropic PTE and NTE were confirmed based on the variable temperature (VT) SCXRD study. The study demonstrated that decreasing the temperature from 330 to 240 K results in a gradual shift in the molecular orientation, leading to contraction along the a-axis and expansion along the b- and c-axis.

In organic molecular crystals, the conformational changes and packing rearrangements lead to the structures crystallizing in polymorphic forms, which often display distinct thermo-responsive effects, as was the case for the dimorphic 4,4′-methylenebis(2,6-dimethylaniline).¹⁵⁷ The two forms crystallize in triclinic and monoclinic crystal systems and exhibit distinct thermal properties due to the striking molecular packing differences. While one polymorph experiences regular PTE, the other undergoes anisotropic NTE. Panda et al.¹⁵⁸ observed distinct thermo-responsive behaviour in two packing polymorphs of thermo-salient crystals of (phenylazophenyl) palladium hexafluoroacetylacetonate. The α-form with head-to-head molecular stacking exhibits a uniaxial NTE of −79.2 M K⁻¹ along the c-axis and a biaxial PTE of 260.4 and 39.4 M K⁻¹ along the a- and b-axis. However, the β-form with head-to-tail molecular stacking shows the usual PTE.

3.1.4. Spin crossover. Molecular materials comprised of 3d⁴–3d⁷ transition metals, due to their electronic configuration, can undergo the spin-crossover (SCO) phenomenon involving the switching process between two molecular spin states (so-called high-spin (HS) and low-spin (LS) configurations) under external stimuli^159,160 (Fig. 15). Stimuli such as temperature, pressure, light irradiation, magnetic field, and guest molecules causing the SCO effect lead to spectacular changes in numerous physical properties such as magnetic optical and dielectric properties. The change in the 3d electronic configuration due to SCO switching causes significant changes in the bond length and the corresponding molecular volume. For example, Fe(II) complexes¹⁶⁰ with octahedral geometry have been the most studied SCO systems, where 3d orbitals are split into two sub-orbitals, t_2g (triply degenerate low-energy orbital) and e_g (doubly degenerate higher energy orbital). Thus, in the LS state, six d-orbital electrons will occupy the three degenerate t_2g orbitals having the electronic configuration of (⁶t_2g, ⁰e_g), while those in the HS state adopt the (⁴t_2g, ²e_g) configuration. The electronic effect of SCO leading to electron–phonon coupling causing remarkable crystal lattice changes was exploited by Kepert et al.¹⁶¹ in designing the flexible Fe(II) complex of Fe [Au(CN)₂]₂, which undergoes SCO at 221–226 K. Further, the change in lattice deformation was controlled from abrupt to gradual by introducing Ni into the complex, which is a non-spin crossover metal. Monotonous thermomechanical motion is exhibited by the [Fe_0.84Ni_0.16] composition, which shows extreme lattice flexing. The CTE of (Fe_0.84Ni_0.16) [Au(CN)₂]₂ at 215 K are −3200, 5200, and 1500 M K⁻¹ along the three axes, respectively, which are at least one order of magnitude greater than those reported for other materials.

3.2. NTE in single-component organic materials

A recent study based on a literature survey highlighted that organic materials have received great attention in the area of NTE. The study revealed that about 30% of the molecular crystals show uniaxial NTE, whereas about 5% show biaxial NTE characteristics.¹⁶² However, NTE characteristics in the case of purely organic systems are scarce. Recently, the development of organic materials with thermo-responsive properties⁷ has been emphasized due to certain advantages such as flexibility, benign nature, and environmental friendliness. The benign nature of the organic system allows it to adapt to physiological conditions. Thus, organic NTE materials can be utilized in dental filling. Additionally, molecular materials in their condensed phase are held together via weak interactions, such as H-bonds, coordination bonds, and weak van der Waals interactions (such as π⋯π interaction, halogen bonds, etc.).^153–155 Weak interactions are highly sensitive to temperature. Therefore, a high PTE is expected for organic materials¹⁶³ in the direction of weak interactions.^164–166 Recently, the role of weak intermolecular interactions in controlling thermal expansion in molecular materials has been highlighted on a few occasions. The weak interactions provide enough flexibility due to a large degree of freedom, which results in some intriguing thermo-responsive and mechano-responsive behaviours such as NTE, breathing effect, and negative linear or area compressibility.

Switching of uniaxial PTE to NTE in two compounds, 1,4-bis(S-3-butyn-2-ol)-benzene and 2,6-bis(S-3-butyn-2-ol)-naphthalene, with similar packing, was reported in 2018.¹⁶⁶ The study claimed that the molecular packing arrangement and transverse vibration of some of the atoms led to this switching phenomenon. The report highlighted that the shortening of molecular length with the increase in temperature occurs due to the high thermal vibration of atoms. Very recently, Koshima et al. studied the switching of axial NTE to PTE in an enol form of N-3,5-di-tert-butylsalicylide-3-nitroaniline.¹⁶⁷ The material also exhibits photo actuation as it undergoes photoisomerization upon light irradiation.

3.2.1. NTE in 4-subtituted derivatives of imidazolines. In the course of the discovery of SCOFs,⁶¹ some of us have explored the thermo-responsive behaviour of imidazoline derivatives (chloro, bromo, iodo, methyl and methoxy), which comprised of an enamine unit (Fig. 7a). The bromo derivative, 2-(4-bromophenyl)-4,5-dihydro-1H-imidazole,¹⁶⁸ exhibits dimorphism at RT (highlighted in red colour) to form non-centrosymmetric (1N, space group Cc) and centrosymmetric (1C, space group P2₁/c) forms, as portrayed in Fig. 16. While polymorphic form 1N (high temperature, HT phase) exhibits colossal NTE and PTE with axial switching, polymorph 1C shows only colossal PTE. Further, both forms undergo reversible iso-symmetric single-crystal-to-single-crystal (SCSC) phase transition at low temperature (LT) to form the LT phases (highlighted in blue colour) with space groups Cc (1N′) and P2₁/n (1C′), respectively. Interestingly, all four forms belong to the monoclinic crystal system, and three experience unusual thermal expansion. Like form 1N, phase 1N′ (LT phase) exhibits colossal NTE and PTE with axial switching. While 1N shows a biaxial NTE of −175.2 and −45.76 M K⁻¹ along the principal axes X1 and X2, respectively, 1N′ shows a uniaxial NTE of −140.30 M K⁻¹ along the principal axis X1. Moreover, LT phase 1C′ experiences a moderate biaxial NTE of 37.46 and −6.09 M K⁻¹ along principal axes X1 and X2, respectively. The structure–property relationship study demonstrates that the interplay of the H-bonds and weak interactions leading to the scissor-jack-like molecular motion result in the anisotropic unusual thermal expansion over an extensive temperature range (∼40 K to ∼110 K) with record-wide thermal hysteresis. Further studies on halophenyl-substituted di-hydro imidazoles suggest that halogens play a crucial role in governing the unusual expansion in organic materials.

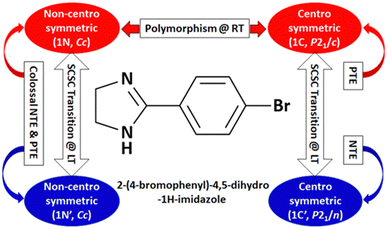Fig. 16 Polymorphism, phase transition, and unusual thermal expansion characteristics in halogen derivatives of 4-phenyl substituted imidazoline.¹⁶⁸

Further, some of us reported polymorphism and hydration-driven thermo-responsive behaviour in 2-(4-(trifluoromethyl)-phenyl)-1H-phenanthro[9,10-d]imidazole (Fig. 4).⁶¹ One of the three polymorphs, the orthorhombic form 1P_O, undergoes anisotropic reversible switching from NTE (−55 M K⁻¹) to PTE (25 M K⁻¹) along the cell edge b at below RT (∼210 K). Moreover, while the non-centrosymmetric hydrated polymorph (1N_H, space group P1) exhibits NTE in the temperature range of 100–280 K, the centrosymmetric hydrated polymorph (space group P1) shows the usual PTE behaviour. During heating, reversible biaxial NTE (−38 M K⁻¹ and −11 M K⁻¹) and PTE (187 M K⁻¹) characteristics are also noticed for 1N_H. The mechanism of NTE was investigated via molecular packing analysis in the crystal lattice as a function of temperature. In the case of 1P_O, with Z′ = 2, the A (pink) and B (red) molecules stack along [010] (Fig. 17a). The interplanar distances between the two A molecules (d_A) and that between the two B molecules (d_B) vary synchronously with the variation of temperature, leading to the contraction and the expansion of cell edge b and the decrease and increase of the interplanar distances d_A and d_B before and after the switching temperature (∼210 K), respectively (Fig. 17b). Along cell edge b, with the increase in temperature, the molecules come closer to each other (the distances d_A and d_B decrease) until ∼210 K. Therefore, cell edge b experiences NTE. After that, it switches to PTE when the molecules go apart (distances d_A and d_B increase). This synergistic decrease and increase of d_A and d_B with temperature leads to the anisotropic expansion and switching from NTE ↔ PTE along cell edge b upon heating and cooling, respectively. For 1N_H, the NTE and PTE arise due to the variation of the dihedral angles Φ and Ψ, as shown in Fig. 17c and d. The molecular planes intersect in an open bookcase-like fashion, and the opening and closing of the bookcase with temperature result in the expansion and contraction of the cell edges. While Φ controls the variation of the cell edge c, Ψ controls that of cell edges a and b. Upon heating, while the increase in Φ leads to the expansion of cell edges a and b, the corresponding decrease in Φ leads to the contraction of cell edge c.

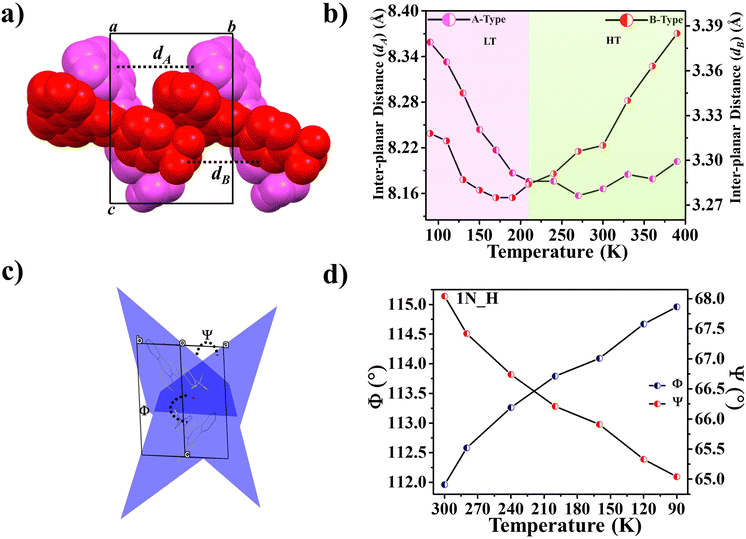Fig. 17 For 1P_O (Fig. 4), (a) stacking of molecules A (pink) and B (red) along [010] and (b) variation of inter-planar distances d_A and d_B with temperature. For 1N_H (Fig. 4), (c) dihedral angles Φ and Ψ between the molecular planes passing through the adjacent molecules A and B, forming an open bookcase-like geometry while viewing down [110] and (d) the variation of Φ and Ψ with temperature.⁶¹

3.3. NTE accompanied by order–disorder phase transformation

In the last few decades, the phase transition in molecular crystals has become an interesting topic of scientific investigation. The phase transitions are of particular interest as these studies provide the details of changes in molecular arrangements in the crystal structure and can be compared through variable temperature X-ray diffraction (VTXRD) and differential scanning calorimetry studies. Using SCXRD and PXRD techniques, the phase transition can be monitored at variable temperatures (VT). VTXRD is an ideal technique for studying disordered systems as it allows distinguishing between static and dynamic disorders. The static disorder will remain the same at VT, while the dynamic disorder may disappear. However, a limited database is available for this type of phase transition, and most of the reports belong to inorganic and multicomponent organic materials. In 2014, Shang et al. reported order–disorder-induced NTE in two ammonium Mg-formate frameworks. A few materials from the ZrW₂O₈ family are known to undergo order–disorder transition and show NTE.¹⁶⁹ Chen et al. reported H-bond driven order–disorder phase transition in an inorganic NLO material, [Ag(NH₃)₂]₂SO₄.¹⁷⁰ The order–disorder phase transition is reversible at 356 K and is associated with weak H-bonds in the crystal structure.

The role of water molecules in inducing the NTE effect has been demonstrated on a few occasions. In the crystal structure of monohydrate dipeptide, tryptophylglycine (TrpGly·H₂O), the NTE effect in the helical direction (c-axis) occurs due to the increasing order of water molecules enclosed in the helices.¹²⁴ Szafranski reported that 1,3-diazabicyclo[2.2.2]-octane hydrochloride trihydrate (dabcoHCl·3H₂O) undergoes a phase transition at 260 K and displays very strong NTE along the a- and c-axis (−529 and 33.3 M K⁻¹, respectively) at its HT phase. At 300 K, it experiences a large α_V of −386 M K⁻¹, possibly the highest value in a molecular crystal, and the NTE occurs due to the rotation of rigid water molecules (Fig. 18).^50,146

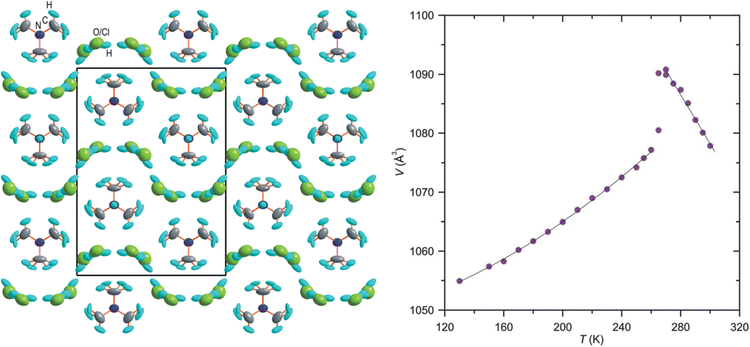Fig. 18 The crystal structure of the orthorhombic form of dabcoHCl·3H₂O at 270 K, viewed along [100], showing the H-bonded disordered H₂O molecules and Cl⁻ anions (left). Temperature dependence of the unit-cell volume of dabcoHCl·3H₂O (right). Reprinted (used in part) from ref. 50.

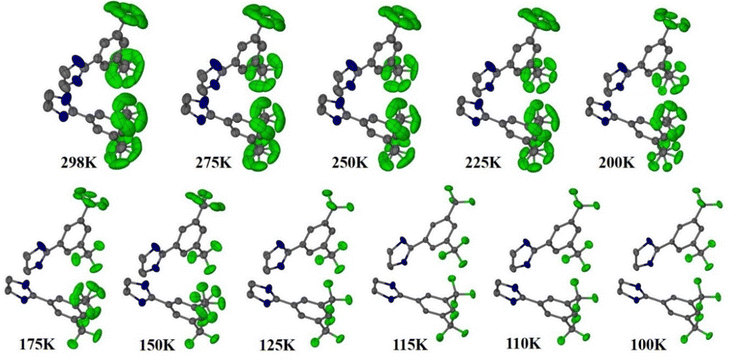
Reports of NTE induced by order–disorder phase transition in single-component organic molecular crystals are extremely rare in the literature. Takahashi et al. reported two polymorphic forms of 2,4-dinitro anisole α and β. In the case of the β polymorph, the disordered atoms in the nitro group becomes ordered at LT (261 K) and shows small biaxial NTE (−31 and −15 M K⁻¹).¹⁷¹ However, the α polymorph exhibits usual PTE behaviour. Very recently, some of us reported the thermal expansion behaviour of 2-((3,5)bis(trifluoromethyl)phenyl)-4,5-dihydro-1H-imidazole.¹⁷² This lightweight material undergoes an iso-symmetric dynamic order–disorder phase transition at LT (<150 K) (Fig. 19). Interestingly, the material exhibits PTE, near ZTE, and NTE along its respective crystallographic axes (Fig. 20) because it experiences a scissor-jack-like motion with temperature variation. The N–H⋯N hydrogen bonds in the crystal structure act as a hinge to the scissor-jack and restrict the thermal expansion along the b-axis, leading to near ZTE behaviour. The HT (298–200 K) and the LT (125–100 K) phases display uniaxial NTE with CTE of −65 and −135 M K⁻¹ along X1 and biaxial PTE along X2 and X3, respectively. The material also exhibits a rare phenomenon of negative area expansion with CTE of −18 and −61 M K⁻¹ for the HT and LT phases, respectively.

Fig. 19 Crystal structures of 2-((3,5)bis(trifluoromethyl)phenyl)-4,5-dihydro-1H-imidazole showing the transition from its disordered phase to ordered phase. H-atoms are omitted for clarity.¹⁷²

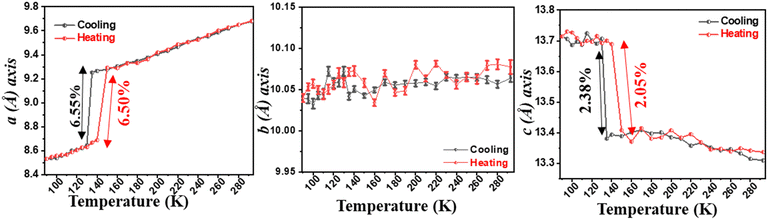Fig. 20 Variation of unit-cell lengths with temperature. The error bars highlighting the near ZTE behaviour are included for the b-axis.¹⁷²

4. Conclusions and outlook

In this highlight, we provided an overview of the evolution of research on purely organic molecular crystals with multifunctional properties, FE and NTE, and the occurrence of polymorphism in such materials.

Initially, we covered the basics of FE and NTE properties and the origin of the coexistence of these intriguing phenomena. Subsequently, we introduced the polymorphism phenomenon and its role in governing molecular properties. Further, we highlighted the crucial role of crystallographic symmetries in designing the FE materials. Furthermore, we discussed the underlying mechanisms behind the unusual FE and NTE characteristics in these special classes of materials and the importance of crystallographic techniques in characterizing FE and NTE materials. Subsequently, we focused on purely organic materials, especially the single-component organic molecular crystals, and discussed a few important cases in detail. In many cases, we discussed the existence of polymorphic forms of the FE and NTE materials and the relationship of polymorphism with the FE and NTE characteristics. We also discussed the techniques typically used for characterising FE and NTE materials and the possibility of implementing various advanced experimental techniques and theoretical approaches to advance these key research areas in materials science.

Here, we emphasized the use of organic materials and the advantage of single-component systems and summarized various principles for designing SCOFs. It was evident from the highlight that there is plenty of scope for discovering new single-component FE and NTE materials. Although the co-existence of FE and NTE properties in an organic material is yet to be discovered, we discussed that the NTE characteristic has been observed in the two polymorphic forms of a SCOF, which was a step closure to combining the FE and NTE characteristics in a single system. We expect that this highlight will guide and motivate the researchers to design such materials for practical applications in the future.

Lastly, we highlighted that due to their benign nature, flexibility, lightweight, cost-effective production, easy processing, and least toxicity, organic materials with FE and unusual thermal expansion properties are preferred over inorganic materials for application in flexible, wearable, biocompatible, reusable, economical medical devices. We envisage that this highlight will encourage scientists to explore organic materials for preparing electronic devices with precise control of thermal expansion and superior memory and energy storage capacity, e.g., sensor-based non-expansive memory devices. Further research on multifunctional organic materials is expected to yield intelligent materials for environmentally friendly applications, which may fulfil our societal needs.

Author contributions

PM has conceptualized and written the highlight. SD had written the original draft. LN contributed to the negative thermal expansion part. All the authors have contributed to editing the highlight.

Data availability

No primary research results, software, or code have been included, and no new data were generated or analyzed as part of this review.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Shiv Nadar Institution of Eminence, Delhi NCR, India, for research facilities, infrastructure, funding, and research assistantship to SD and LN. This work is supported by research grants (CRG/2018/004694 and CRG/2023/008038) from SERB, Govt. of India.

References

1. M. E. Lines and A. M. Glass, Principles and Applications of Ferroelectrics and Related Materials, Oxford University Press, Oxford, 2001.
2. J. F. Scott, Ferroelectric Memories, Springer Berlin, Heidelberg, 2000.
3. J. F. Scott, Science, 2007, 315, 954–959.
4. J. S. O. Evans, J. Chem. Soc., Dalton Trans., 1999, 0, 3317–3326.
5. K. Takenaka, Sci. Technol. Adv. Mater., 2012, 13, 013001.
6. J. Chen, L. Hu, J. Deng and X. Xing, Chem. Soc. Rev., 2015, 44, 3522–3567.
7. Z. Liu, Q. Gao, J. Chen, J. Deng, K. Lin and X. Xing, Chem. Commun., 2018, 54, 5164–5176.
8. J. Bernstein, Strength from Weakness: Structural Consequences of Weak Interactions in Molecules, Supermolecules, and Crystals, Springer Netherlands, Dordrecht, 2002, pp. 247–260.
9. T. Miyazaki and H. Jin, The Physics of Ferromagnetism, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, vol. 158.
10. A. K. Tagantsev, L. E. Cross and J. Fousek, Domains in Ferroic Crystals and Thin Films, Springer New York, New York, NY, 2010.
11. Y. Noda, T. Yamada, K. Kobayashi, R. Kumai, S. Horiuchi, F. Kagawa and T. Hasegawa, Adv. Mater., 2015, 27, 6475–6481.
12. M. Fiebig, V. V. Pavlov and R. V. Pisarev, J. Opt. Soc. Am. B, 2005, 22, 96.
13. N. E. Sherstyuk, E. D. Mishina, S. D. Lavrov, A. M. Buryakov, M. A. Marchenkova, A. S. Elshin and A. S. Sigov, Ferroelectrics, 2015, 477, 29–46.
14. K. Uchino, Ferroelectric Devices, CRC Press, 2018.
15. G. Sebald, D. Guyomar and A. Agbossou, Smart Mater. Struct., 2009, 18, 125006.
16. J. Valasek, Phys. Rev., 1920, 15, 505–564.
17. J. Valasek, Phys. Rev., 1921, 17, 475–481.
18. G. Busch and P. Scherrer, Naturwissenschaften, 1935, 23, 737.
19. G. H. Kwei, A. C. Lawson, S. J. L. Billinge and S. W. Cheong, J. Phys. Chem., 1993, 97, 2368–2377.
20. G. H. Haertling, J. Am. Ceram. Soc., 1999, 82, 797–818.
21. P. Theato, B. S. Sumerlin, R. K. O’Reilly and T. H. Epps, III, Chem. Soc. Rev., 2013, 42, 7055.
22. Y.-J. Kim and Y. T. Matsunaga, J. Mater. Chem. B, 2017, 5, 4307–4321.
23. W. Miller, C. W. Smith, D. S. Mackenzie and K. E. Evans, J. Mater. Sci., 2009, 44, 5441–5451.
24. R. H. Baughman, Science, 2002, 297, 787–792.
25. R. S. Krishnan, R. Srinivasan and S. Devanarayanan, Thermal expansion of crystals: international series in the science of the solid state, 2013.
26. M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329.
27. R. M. Hazen and L. W. Finger, Am. Sci., 1984, 72, 143–150.
28. X. Yang, X. Cheng, X. Yan, J. Yang, T. Fu and J. Qiu, Compos. Sci. Technol., 2007, 67, 1167–1171.
29. R. Roy, D. K. Agrawal and H. A. McKinstry, Annu. Rev. Mater. Sci., 1989, 19, 59–81.
30. T. A. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Science, 1996, 272, 90–92.
31. K. Röttger, A. Endriss, J. Ihringer, S. Doyle and W. F. Kuhs, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 50, 644–648.
32. S. E. Tallentire, F. Child, I. Fall, L. Vella-Zarb, I. R. Evans, M. G. Tucker, D. A. Keen, C. Wilson and J. S. O. Evans, J. Am. Chem. Soc., 2013, 135, 12849–12856.
33. V. Korthuis, N. Khosrovani, A. W. Sleight, N. Roberts, R. Dupree and W. W. J. Warren, Chem. Mater., 1995, 7, 412–417.
34. J. S. O. Evans, T. A. Mary and A. W. Sleight, J. Solid State Chem., 1997, 133, 580–583.
35. D. A. Woodcock, P. Lightfoot, L. A. Villaescusa, M.-J. Díaz-Cabañas, M. A. Camblor and D. Engberg, Chem. Mater., 1999, 11, 2508–2514.
36. D. A. Woodcock, P. Lightfoot, P. A. Wright, L. A. Villaescusa and M. A. Camblor, J. Mater. Chem., 1999, 9, 349–351.
37. P. Lightfoot, D. A. Woodcock, M. J. Maple, L. A. Villaescusa and P. A. Wright, J. Mater. Chem., 2001, 11, 212–216.
38. B. K. Greve, K. L. Martin, P. L. Lee, P. J. Chupas, K. W. Chapman and A. P. Wilkinson, J. Am. Chem. Soc., 2010, 132, 15496–15498.
39. L. Hu, J. Chen, A. Sanson, H. Wu, C. Guglieri Rodriguez, L. Olivi, Y. Ren, L. Fan, J. Deng and X. Xing, J. Am. Chem. Soc., 2016, 138, 8320–8323.
40. L. Hu, J. Chen, J. Xu, N. Wang, F. Han, Y. Ren, Z. Pan, Y. Rong, R. Huang, J. Deng, L. Li and X. Xing, J. Am. Chem. Soc., 2016, 138, 14530–14533.
41. M. van Schilfgaarde, I. A. Abrikosov and B. Johansson, Nature, 1999, 400, 46–49.
42. Y. W. Long, N. Hayashi, T. Saito, M. Azuma, S. Muranaka and Y. Shimakawa, Nature, 2009, 458, 60–63.
43. M. Azuma, W. Chen, H. Seki, M. Czapski, S. Olga, K. Oka, M. Mizumaki, T. Watanuki, N. Ishimatsu, N. Kawamura, S. Ishiwata, M. G. Tucker, Y. Shimakawa and J. P. Attfield, Nat. Commun., 2011, 2, 347.
44. J. Chen, K. Nittala, J. S. Forrester, J. L. Jones, J. Deng, R. Yu and X. Xing, J. Am. Chem. Soc., 2011, 133, 11114–11117.
45. J. Chen, F. Wang, Q. Huang, L. Hu, X. Song, J. Deng, R. Yu and X. Xing, Sci. Rep., 2013, 3, 2458.
46. Z. Pan, Y.-W. Fang, T. Nishikubo, L. Hu, S. Kawaguchi and M. Azuma, Chem. Mater., 2022, 34, 2798–2803.
47. Q. Li, K. Lin, Z. Liu, L. Hu, Y. Cao, J. Chen and X. Xing, Chem. Rev., 2022, 122, 8438–8486.
48. P. Hu, J. Chen, X. Sun, J. Deng, X. Chen, R. Yu, L. Qiao and X. Xing, J. Mater. Chem., 2009, 19, 1648.
49. S. Li, K. Takahashi, R.-K. Huang, C. Xue, K. Kokado, N. Hoshino, T. Akutagawa, S. Nishihara and T. Nakamura, Chem. Mater., 2023, 35, 2421–2428.
50. M. Szafrański, J. Mater. Chem. C, 2013, 1, 7904–7913.
51. G. H. Roche, D. Flot, J. J. E. Moreau, O. J. Dautel, J.-S. Filhol and A. van der Lee, Cryst. Growth Des., 2021, 21, 3850–3863.
52. K. K. Jha, S. Dutta and P. Munshi, Cryst. Growth Des., 2018, 18, 1126–1135.
53. A. Kumar, J. Chauhan, K. D. Dubey, S. Sen and P. Munshi, Mol. Pharmaceutics, 2022, 19, 1008–1018.
54. S. Dutta, V. Vikas, A. Yadav, R. Boomishankar, A. Bala, V. Kumar, T. Chakraborty, S. Elizabeth and P. Munshi, Chem. Commun., 2019, 55, 9610–9613.
55. G. Gupta, Y. Gupta, A. Kumar, R. Bhowal and P. Munshi, Cryst. Growth Des., 2024, 24, 646–656.
56. W. C. McCrone, Polymorphism, in Physics and Chemistry of the Organic Solid State, ed. D. Fox, M. M. Labes and A. Weissberger, Wiley-Interscience, New York, 1965, ch. 8, vol. 2, pp. 725–767.
57. K. K. Jha, S. Dutta, V. Kumar and P. Munshi, CrystEngComm, 2016, 18, 8497–8505.
58. D. Gentili, M. Gazzano, M. Melucci, D. Jones and M. Cavallini, Chem. Soc. Rev., 2019, 48, 2502–2517.
59. H. Chung and Y. Diao, J. Mater. Chem. C, 2016, 4, 3915–3933.
60. R. Bu, H. Li and C. Zhang, Cryst. Growth Des., 2020, 20, 3561–3576.
61. S. Dutta, Vikas, V. Thangavel and P. Munshi, ACS Appl. Electron. Mater., 2021, 3, 3633–3640.
62. G. B. A. M. Glazer, Space Groups for Solid State Scientists, Elsevier, 2013.
63. V. Wadhawan, Introduction to Ferroic Materials, CRC Press, 2000.
64. H. Schmid, J. Phys.: Condens. Matter, 2008, 20, 434201.
65. H.-Y. Zhang, Y.-Y. Tang, P.-P. Shi and R.-G. Xiong, Acc. Chem. Res., 2019, 52, 1928–1938.
66. P. P. Shi, Y. Y. Tang, P. F. Li, W. Q. Liao, Z. X. Wang, Q. Ye and R. G. Xiong, Chem. Soc. Rev., 2016, 45, 3811–3827.
67. K. Aizu, Phys. Rev. B: Solid State, 1970, 2, 754–772.
68. S. C. Abrahams, E. Buehler, W. C. Hamilton and S. J. Laplaca, J. Phys. Chem. Solids, 1973, 34, 521–532.
69. D.-W. Fu, H.-L. Cai, Y. Liu, Q. Ye, W. Zhang, Y. Zhang, X.-Y. Chen, G. Giovannetti, M. Capone, J. Li and R.-G. Xiong, Science, 2013, 339, 425–428.
70. D.-W. Fu, W. Zhang, H.-L. Cai, J.-Z. Ge, Y. Zhang and R.-G. Xiong, Adv. Mater., 2011, 23, 5658–5662.
71. Z. S. Yao, K. Yamamoto, H. L. Cai, K. Takahashi and O. Sato, J. Am. Chem. Soc., 2016, 138, 12005–12008.
72. H. Y. Ye, Y. Zhang, D. W. Fu and R. G. Xiong, Angew. Chem., Int. Ed., 2014, 53, 6724–6728.
73. S. Koval, J. Kohanoff, J. Lasave, G. Colizzi and R. L. Migoni, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 184102.
74. T. F. Nova, A. S. Disa, M. Fechner and A. Cavalleri, Science, 2019, 364, 1075–1079.
75. Y.-Y. Tang, J.-C. Liu, Y.-L. Zeng, H. Peng, X.-Q. Huang, M.-J. Yang and R.-G. Xiong, J. Am. Chem. Soc., 2021, 143, 13816–13823.
76. S. Horiuchi and Y. Tokura, Nat. Mater., 2008, 7, 357–366.
77. S. Horiuchi, Y. Tokunaga, G. Giovannetti, S. Picozzi, H. Itoh, R. Shimano, R. Kumai and Y. Tokura, Nature, 2010, 463, 789–792.
78. S. Horiuchi, R. Kumai and Y. Tokura, Adv. Mater., 2011, 23, 2098–2103.
79. S. Horiuchi, F. Kagawa, K. Hatahara, K. Kobayashi, R. Kumai, Y. Murakami and Y. Tokura, Nat. Commun., 2012, 3, 1306–1308.
80. S. Horiuchi, K. Kobayashi, R. Kumai and S. Ishibashi, Nat. Commun., 2017, 8, 1–9.
81. A. S. Tayi, A. Kaeser, M. Matsumoto, T. Aida and S. I. Stupp, Nat. Chem., 2015, 7, 281–294.
82. S. Horiuchi, F. Ishii, R. Kumai, Y. Okimoto, H. Tachibana, N. Nagaosa and Y. Tokura, Nat. Mater., 2005, 4, 163–166.
83. S. Horiuchi, R. Kumai and Y. Tokura, J. Mater. Chem., 2009, 19, 4421.
84. K. Kobayashi, S. Horiuchi, S. Ishibashi, F. Kagawa, Y. Murakami and R. Kumai, Chem. – Eur. J., 2014, 20, 17515–17522.
85. S. Horiuchi, R. Kumai and Y. Tokura, J. Am. Chem. Soc., 2013, 135, 4492–4500.
86. J. Harada, T. Shimojo, H. Oyamaguchi, H. Hasegawa, Y. Takahashi, K. Satomi, Y. Suzuki, J. Kawamata and T. Inabe, Nat. Chem., 2016, 8, 946–952.
87. J. Harada, N. Yoneyama, S. Yokokura, Y. Takahashi, A. Miura, N. Kitamura and T. Inabe, J. Am. Chem. Soc., 2018, 140, 346–354.
88. H.-Y. Ye, Y.-Y. Tang, P.-F. Li, W.-Q. Liao, J.-X. Gao, X.-N. Hua, H. Cai, P.-P. Shi, Y.-M. You and R.-G. Xiong, Science, 2018, 361, 151–155.
89. M. Szafranski, J. Phys. Chem. B, 2011, 115, 8755–8762.
90. S. Seyedraoufi, E. D. Sødahl, C. H. Görbitz and K. Berland, Phys. Rev. Mater., 2024, 8, 054413.
91. Y. Y. Tang, P. F. Li, W. Q. Liao, P. P. Shi, Y. M. You and R. G. Xiong, J. Am. Chem. Soc., 2018, 140, 8051–8059.
92. T. Vijayakanth, A. K. Srivastava, F. Ram, P. Kulkarni, K. Shanmuganathan, B. Praveenkumar and R. Boomishankar, Angew. Chem., Int. Ed., 2018, 57, 9054–9058.
93. R. A. Wiscons, N. R. Goud, J. T. Damron and A. J. Matzger, Angew. Chem., Int. Ed., 2018, 57, 9044–9047.
94. R. C. Haddon and A. A. Lamola, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 1874–1878.
95. D. Semmingsen and J. Feder, Solid State Commun., 1974, 15, 1369–1372.
96. G. A. Samara and D. Semmingsen, J. Chem. Phys., 1979, 71, 1401–1407.
97. Y. Moritomo, Y. Tokura, H. Takahashi and N. Mōri, Phys. Rev. Lett., 1991, 67, 2041–2044.
98. G. Gilli, F. Bellucci, V. Ferretti and V. Bertolasi, J. Am. Chem. Soc., 1989, 111, 1023–1028.
99. P. Gilli, V. Bertolasi, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 1994, 116, 909–915.
100. G. Gilli and P. Gilli, J. Mol. Struct., 2000, 552, 1–15.
101. R. R. Choudhury and R. Chitra, Cryst. Res. Technol., 2006, 41, 1045–1048.
102. Z. Zikmund, P. Vaněk, M. Havránková, B. Březina, M. Člermák and M. Vásša, Ferroelectrics, 1994, 158, 223–228.
103. J. Kroupa, P. Vaněk, R. Krupková and Z. Zikmund, Ferroelectrics, 1997, 202, 229–234.
104. D. Keil, H. Hartmann and C. Reichardt, Liebigs Ann. Chem., 1993, 935–939.
105. M. Owczarek, K. A. Hujsak, D. P. Ferris, A. Prokofjevs, I. Majerz, P. Szklarz, H. Zhang, A. A. Sarjeant, C. L. Stern, R. Jakubas, S. Hong, V. P. Dravid and J. F. Stoddart, Nat. Commun., 2016, 7, 13108.
106. H. Peng, J.-C. Qi, X.-J. Song, R.-G. Xiong and W.-Q. Liao, Chem. Sci., 2022, 13, 4936–4943.
107. M.-M. Russew and S. Hecht, Adv. Mater., 2010, 22, 3348–3360.
108. W.-Q. Liao, Y.-L. Zeng, Y.-Y. Tang, H. Peng, J.-C. Liu and R.-G. Xiong, J. Am. Chem. Soc., 2021, 143, 21685–21693.
109. W. Liao, B. Deng, Z. Wang, T. Cheng, Y. Hu, S. Cheng and R. Xiong, Adv. Sci., 2021, 8, 2102614.
110. Z. Wang, C. Huang, J. Liu, Y. Zeng and R. Xiong, Chem. – Eur. J., 2021, 27, 14831–14835.
111. Y.-Y. Tang, Y.-L. Zeng and R.-G. Xiong, J. Am. Chem. Soc., 2022, 144, 8633–8640.
112. Y. Du, C.-R. Huang, Z.-K. Xu, W. Hu, P.-F. Li, R.-G. Xiong and Z.-X. Wang, JACS Au, 2023, 3, 1464–1471.
113. H. Zhang, H. Jiang, Y. Zhang, N. Zhang and R. Xiong, Angew. Chem., Int. Ed., 2022, 61, e202200135.
114. S. Horiuchi, R. Kumai and S. Ishibashi, J. Mater. Chem. C, 2021, 9, 13739–13747.
115. P.-F. Li, W.-Q. Liao, Y.-Y. Tang, W. Qiao, D. Zhao, Y. Ai, Y.-F. Yao and R.-G. Xiong, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 5878–5885.
116. Y. Ai, Y.-L. Zeng, W.-H. He, X.-Q. Huang and Y.-Y. Tang, J. Am. Chem. Soc., 2020, 142, 13989–13995.
117. P.-F. Li, Y. Ai, Y.-L. Zeng, J.-C. Liu, Z.-K. Xu and Z.-X. Wang, Chem. Sci., 2022, 13, 657–664.
118. H.-Y. Liu, H.-Y. Zhang, X.-G. Chen and R.-G. Xiong, J. Am. Chem. Soc., 2020, 142, 15205–15218.
119. C. F. C. Fitié, W. S. C. Roelofs, M. Kemerink and R. P. Sijbesma, J. Am. Chem. Soc., 2010, 132, 6892–6893.
120. C. F. C. Fitié, W. S. C. Roelofs, P. C. M. M. Magusin, M. Wübbenhorst, M. Kemerink and R. P. Sijbesma, J. Phys. Chem. B, 2012, 116, 3928–3937.
121. H. Anetai, Y. Wada, T. Takeda, N. Hoshino, S. Yamamoto, M. Mitsuishi, T. Takenobu and T. Akutagawa, J. Phys. Chem. Lett., 2015, 6, 1813–1818.
122. H. Anetai, T. Takeda, N. Hoshino, H. Kobayashi, N. Saito, M. Shigeno, M. Yamaguchi and T. Akutagawa, J. Am. Chem. Soc., 2019, 141, 2391–2397.
123. T. Akutagawa, H. Koshinaka, D. Sato, S. Takeda, S.-I. Noro, H. Takahashi, R. Kumai, Y. Tokura and T. Nakamura, Nat. Mater., 2009, 8, 342–347.
124. D. Miyajima, F. Araoka, H. Takezoe, J. Kim, K. Kato, M. Takata and T. Aida, Science, 2012, 336, 209–213.
125. S. Furukawa, J. Wu, M. Koyama, K. Hayashi, N. Hoshino, T. Takeda, Y. Suzuki, J. Kawamata, M. Saito and T. Akutagawa, Nat. Commun., 2021, 12, 768.
126. D. Bordeaux, J. Bornarel, A. Capiomont, J. Lajzerowicz-Bonneteau, J. Lajzerowicz and J. F. Legrand, Phys. Rev. Lett., 1973, 31, 314–317.
127. C.-R. Huang, Y. Li, Y. Xie, Y. Du, H. Peng, Y.-L. Zeng, J.-C. Liu and R.-G. Xiong, Angew. Chem., Int. Ed., 2021, 60, 16668–16673.
128. S. K. Park and Y. Diao, Chem. Soc. Rev., 2020, 49, 8287–8314.
129. L. Li, P. Commins, M. B. Al-Handawi, D. P. Karothu, J. M. Halabi, S. Schramm, J. Weston, R. Rezgui and P. Naumov, Chem. Sci., 2019, 10, 7327–7332.
130. D. P. Karothu, R. Ferreira, G. Dushaq, E. Ahmed, L. Catalano, J. M. Halabi, Z. Alhaddad, I. Tahir, L. Li, S. Mohamed, M. Rasras and P. Naumov, Nat. Commun., 2022, 13, 2823.
131. A. Piecha-Bisiorek, A. Białońska, R. Jakubas, P. Zieliński, M. Wojciechowska and M. Gałązka, Adv. Mater., 2015, 27, 5023–5027.
132. N. Zhang, W. Sun, Y. Zhang, H.-H. Jiang, R.-G. Xiong, S. Dong and H.-Y. Zhang, Nat. Commun., 2023, 14, 5854.
133. H. Y. Zhang, Y. Y. Tang, Z. X. Gu, P. Wang, X. G. Chen, H. P. Lv, P. F. Li, Q. Jiang, N. Gu, S. Ren and R. G. Xiong, Science, 2024, 383, 1492–1498.
134. https://neutrons.ornl.gov/topaz .
135. C. M. Fancher, C. M. Hoffmann, X. P. Wang, L. L. Daemen and A. J. Schultz, APL Mater., 2021, 9, 021111.
136. K. Kobayashi, S. Horiuchi, S. Ishibashi, Y. Murakami and R. Kumai, J. Am. Chem. Soc., 2018, 140, 3842–3845.
137. J. S. O. Evans, T. A. Mary and A. W. Sleight, J. Solid State Chem., 1998, 137, 148–160.
138. S. Margadonna, K. Prassides and A. N. Fitch, J. Am. Chem. Soc., 2004, 126, 15390–15391.
139. D. J. Williams, D. E. Partin, F. J. Lincoln, J. Kouvetakis and M. O’Keeffe, J. Solid State Chem., 1997, 134, 164–169.
140. A. E. Phillips, A. L. Goodwin, G. J. Halder, P. D. Southon and C. J. Kepert, Angew. Chem., 2008, 120, 1418–1421.
141. A. E. Phillips, G. J. Halder, K. W. Chapman, A. L. Goodwin and C. J. Kepert, J. Am. Chem. Soc., 2010, 132, 10–11.
142. K. W. Chapman, P. J. Chupas and C. J. Kepert, J. Am. Chem. Soc., 2006, 128, 7009–7014.
143. S. G. Duyker, V. K. Peterson, G. J. Kearley, A. J. Ramirez-Cuesta and C. J. Kepert, Angew. Chem., Int. Ed., 2013, 52, 5266–5270.
144. D. J. Cram and J. M. Cram, Science, 1974, 183, 803–809.
145. M. Zakrzewski, M. A. White and W. Abriel, J. Phys. Chem., 1990, 94, 2203–2206.
146. H. Birkedal and D. Schwarzenbach, Angew. Chem., Int. Ed., 2002, 41, 754–756.
147. C. Serre, F. Millange, C. Thouvenot, M. Noguès, G. Marsolier, D. Louër and G. Férey, J. Am. Chem. Soc., 2002, 124, 13519–13526.
148. L. D. DeVries, P. M. Barron, E. P. Hurley, C. Hu and W. Choe, J. Am. Chem. Soc., 2011, 133, 14848–14851.
149. A. D. Fortes, E. Suard and K. S. Knight, Science, 2011, 331, 742–746.
150. B. Dwivedi, A. Shrivastava, L. Negi and D. Das, Cryst. Growth Des., 2019, 19, 2519–2524.
151. L. Negi, S. Kumar, B. Dwivedi and D. Das, Cryst. Growth Des., 2021, 21, 1428–1433.
152. S. Chuskit, T. Sethi, P. Harsha and D. Das, Cryst. Growth Des., 2023, 23, 1336–1342.
153. H. T. Chifotides and K. R. Dunbar, Acc. Chem. Res., 2013, 46, 894–906.
154. S.-L. Li, T. Xiao, C. Lin and L. Wang, Chem. Soc. Rev., 2012, 41, 5950.
155. J. Borges and J. F. Mano, Chem. Rev., 2014, 114, 8883–8942.
156. D. Das, T. Jacobs and L. J. Barbour, Nat. Mater., 2010, 9, 36–39.
157. S. Bhattacharya and B. K. Saha, CrystEngComm, 2014, 16, 2340.
158. M. K. Panda, T. Runčevski, S. Chandra Sahoo, A. A. Belik, N. K. Nath, R. E. Dinnebier and P. Naumov, Nat. Commun., 2014, 5, 4811.
159. A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313.
160. S. Brooker, Chem. Soc. Rev., 2015, 44, 2880–2892.
161. B. R. Mullaney, L. Goux-Capes, D. J. Price, G. Chastanet, J.-F. Létard and C. J. Kepert, Nat. Commun., 2017, 8, 1053.
162. D. Das, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2021, 77, 309–310.
163. J. F. Nye and R. B. Lindsay, Phys. Today, 1957, 10, 26.
164. A. L. Kitaigorodsky, Molecular crystals and molecules, Elsevier, 2012, vol. 29.
165. J. D. Dunitz and A. Gavezzotti, Chem. Soc. Rev., 2009, 38, 2622.
166. L. Negi, A. Shrivastava and D. Das, Chem. Commun., 2018, 54, 10675–10678.
167. S. Hasebe, Y. Hagiwara, T. Ueno, T. Asahi and H. Koshima, Chem. Sci., 2024, 15, 1088–1097.
168. S. Dutta and P. Munshi, J. Phys. Chem. C, 2020, 124, 27413–27421.
169. C. Lind, Materials, 2012, 5, 1125–1154.
170. Y.-C. Yang, X. Liu, X.-B. Deng, L.-M. Wu and L. Chen, JACS Au, 2022, 2, 2059–2067.
171. H. Takahashi and R. Tamura, CrystEngComm, 2015, 17, 8888–8896.
172. Vikas, L. Negi and P. Munshi, Cryst. Growth Des., 2024, 24, 2533–2541.

---