Open Access Article
Open Access ArticleQuantification capabilities of N2 MICAP-MS with solution nebulization and aerosol desolvation†
Monique
Kuonen
 ,
Bodo
Hattendorf
,
Bodo
Hattendorf
 and
Detlef
Günther
and
Detlef
Günther
 *
*
Department of Chemistry and Applied Biosciences, Laboratory of Inorganic Chemistry, ETH Zurich, Vladimir-Prelog-Weg 1, 8093, Zurich, Switzerland. E-mail: guenther@inorg.chem.ethz.ch
First published on 25th March 2024
Abstract
The analytical capabilities of a nitrogen-sustained high-power microwave inductively coupled atmospheric-pressure plasma mass spectrometer (N2 MICAP-MS) were investigated using solution nebulization with and without aerosol desolvation. The reduced solvent load for the desolvated aerosol and the increased aerosol transfer resulted in a signal enhancement of ten times for most elements in samples without a significant amount of dissolved solids. An exception was boron, whose signal decreased by a factor of seven when a desolvator was used. To compare the accuracy, reproducibility, and matrix susceptibility of the N2 MICAP-MS, the mass fractions of 30 elements were determined in two certified water reference materials using external calibration and standard addition. The results were generally found to agree within 10% of the certified reference values with a maximum deviation of 17% in the case of 64Zn. Comparing external calibration and standard addition provided comparable results regardless of the sample introduction method. To assess the extent of matrix effects, multi-element standard solutions were doped with amounts of up to 100 mg kg−1 calcium. This resulted in a signal suppression of up to 30% and 70% for conventional nebulization and aerosol desolvation, respectively. This substantially reduced the improvement in sensitivity observed for the desolvated aerosol. To further investigate the fundamental characteristics of the N2 MICAP-MS, the plasma gas temperature was estimated using three methods. The determined temperatures for the two most reliable methods were in the range of ∼5000–6000 K and were found to be independent of the sample introduction method and similar to those of an Ar ICP.
Introduction
In recent years, there has been a renewed interest in nitrogen-sustained microwave-induced plasmas (MIPs) for both optical emission spectroscopy (OES) and mass spectrometry (MS) due to the introduction of the microwave inductively coupled atmospheric-pressure plasma (MICAP).1 While several MIPs were investigated as an alternative ion source, early designs were limited by their low operating power.2–4 The first high-power nitrogen MIP was based on an Okamoto cavity5 and after its successful coupling to MS,6 commercial instruments were developed by Hitachi. However, these high-power N2 MIP-MS were only sold in Japan7 and have thus not been widely distributed.8 The emerging MICAP is another high-power nitrogen plasma that can be used as an alternative ion source for OES9 and MS.10 Compared to the conventional argon-based inductively coupled plasma (ICP) employed for these analytical techniques,11–13 the nitrogen microwave plasmas are more cost-effective in their operation and reduce the occurrence of argon-containing spectral interferences.6,14 In addition, the MICAP should exhibit a negligible plasma potential since the microwave coupling is purely inductive. Its plasma geometry is essentially identical to that of an Ar ICP because it is created in a conventional Fassel-type torch.1 Due to all these similarities, the MICAP can be used with all existing sample introduction methods available for ICP-MS.For conventional ICP-MS, the argon-based plasma background ions can interfere with several isotopes.15 For example, the plasma species 38Ar1H+, 40Ar+, 40Ar12C+, 40Ar16O+, and 40Ar2+ interfere with the most abundant isotopes of potassium, calcium, chromium, iron, and selenium. Other argides can be formed with abundant elements, resulting in polyatomic ions such as 40Ar35Cl+ and 40Ar23Na+, which interfere with arsenic and the major isotope of copper. Traditionally, these spectral interferences can be decreased or resolved by using reaction or collision cells16–18 or instruments with higher mass resolution.19 Replacing an argon with a nitrogen plasma is another way to reduce these interfering species. However, with a nitrogen-sustained plasma, the occurrence of nitrogen-based plasma species and nitrides of matrix elements increases. The most abundant spectral interferences are caused by 14Nx16Oy+ (x = 1–4, y = 0–2) and directly affect the detection of silicon, phosphorous, calcium, titanium, iron, and nickel, although not always their main isotope.6,10,20 In addition to oxides, the occurrence of nitride adduct ions needs to be considered due to the high abundance of nitrogen. However, since most interferences in an argon plasma occur at different m/z than those occurring in a nitrogen plasma, different elements and isotopes are affected.
Early MIPs such as the Beenakker cavity,2 the Surfatron,3 and the microwave plasma torch4 had lower matrix and mass load tolerance, which is often presumed to apply to all MIPs. However, similar to other high-power MIPs like the Okamoto5 and Hammer21 cavities, the MICAP can handle the mass load from conventional liquid sample introduction such as solution nebulization. Furthermore, the N2 MICAP has demonstrated a high solvent tolerance, as it was stable even when introducing organic solvents.9 Although there are only a few publications on the matrix tolerance of the N2 sustained MICAP, they differ in the reported severity of the matrix effects. While studies with OES detection reported significant signal suppression on ionic emission lines,9,22,23 the matrix tolerance for MS was described to be similar to that of an Ar ICP.10,24 Regardless of the employed analytical technique (OES, MS), further investigations are needed to characterize the MICAP matrix and mass load tolerance.
The solvent load of the sample introduced into the plasma can be reduced by using aerosol desolvation. This leads to a decrease in the energy required for the solvent vapor to dissociate25,26 and lowers the occurrence of solvent-based interferences.27,28 In addition to a reduced solvent load, aerosol desolvation results in a higher aerosol yield due to an increased nebulization respecively transport efficiency. While aerosol desolvation has been shown to increase the analyte signal in an Ar ICP-MS,25–28 some analytes can be lost in the desolvation unit.28–30 So far, only Schild et al.10 used a desolvation system to investigate the performance of an N2 MICAP-TOFMS and observed a five to ten-fold analyte signal increase.
Recent experiments using a nitrogen plasma,9,10,22–24,31,32 including the first successful quantification studies with ion chromatography,33 laser ablation,20 or solution nebulization34 have indicated that the MICAP can be a very promising alternative to the Ar ICP as ion source. The latter quantified heavy metals in digested soil samples with MS but was limited to only nine isotopes (51V, 53Cr, 59Co, 62Ni, 65Cu, 66Zn, 75As, 112Cd, 207Pb).34 This study is focused on the characterization of the nitrogen-sustained MICAP quadrupole MS for the multielement analysis of aqueous solutions, which is a routine application of Ar ICP-MS. Two water reference materials were used to investigate the quantification capabilities using conventional solution nebulization (SN) and aerosol desolvation (Des). The reference materials were quantified by external calibration as well as standard addition to assess the effects of signal suppression. Both sample introduction methods were employed to compare figures of merit such as trueness, precision, and limits of detection. Furthermore, to compare the N2 MICAP-MS with an Ar-based ICP-MS, the gas kinetic temperature was determined for both introduction methods using the pressure reduction in the interface region35 or the formation of singly charged monoxide rare earth elements and their known dissociation energies.36,37
Experimental
Instrumentation
The employed prototype has already been described in an earlier publication with more detail.31 In short, the nitrogen-sustained MICAP ion source (Radom Corp., USA) was coupled to an ELAN 6100 DRC quadrupole mass spectrometer (PerkinElmer/Sciex, Canada). Additionally, a pressure sensor (CMR 632, Pfeiffer, DE) was connected to the interface vacuum line to measure the interface pressure. The plasma can be ignited and controlled through the MICAP control unit and software, while the mass spectrometer is operated through the ELAN software. The liquid samples were introduced by pneumatic nebulization using a MicroMist™ glass concentric nebulizer (Glass Expansion, AUS) with a cyclonic spray chamber or inserted in an Apex-Q system (Elemental Scientific, USA) for aerosol desolvation. The sample flow rate was controlled with a peristaltic pump, adjusted to 1.37 mL min−1 for solution nebulization and 0.84 mL min−1 for desolvated sample introduction.Materials and methods
The instrument was optimized while aspirating a multi-element solution containing 1 μg kg−1 Li, Be, Na, Mg, K, Ca, Co, Zn, Ge, As, Se, Rb, Sr, Cd, In, Cs, Te, Ba, Ce, Lu, Pb, Th, U, which was prepared by diluting single-element stock solutions from Merck, Inorganic Ventures and VWR chemicals. The optimization for solution nebulization was performed by optimizing for maximum 238U+ signal intensity at a magnetron power of 1450 W and a nebulizer gas flow rate that maintained a 140Ce16O+/140Ce+ formation rate below 3%. When using aerosol desolvation, the instrument was also optimized for maximum 238U+ signal intensity while keeping the cerium oxide level below 1%. Due to the lower 140Ce16O+ abundance, aerosol desolvation allowed the use of higher nebulizer gas flow rates. An overview of the operating conditions is given in Table 1.| Parameter | Value |
|---|---|
| Cooling gas flow rate | 14 L min−1 |
| Auxiliary gas flow rate | 750 mL min−1 |
| Nebulizer gas flow rate | SN: 900 mL min−1, Des: 1000 mL min−1 |
| Magnetron power | 1450 W |
| Sampler cone | 1.1 mm Ø, Pt |
| Skimmer cone | 0.8 mm Ø, Pt |
| Quadrupole rod offset | −5 V |
| Cell rod offset | −10 V |
| Call path voltage | −50 V |
| Spray chamber temperature | SN: room temperature, Des:140 °C |
| Condenser | SN: none, Des: 2 °C |
Two water reference materials were selected for this study. The river water SLRS-6 (National Research Council Canada, NRCC), is certified for 20 elements, ranging from 0.006 μg kg−1–8800 μg kg−1, and the SRM 1643f (National Institute of Standards and Technology, NIST), which is certified for 29 elements with mass fractions between 0.96 μg kg−1–29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μg kg−1 (Fig. S1†). In both samples, Ca, Na, Mg, and K are the most abundant elements. Since NIST 1643f has higher concentrations but is otherwise similar to SLRS-6, a multi-element stock solution with similar analyte ratios as in the two (NIST 1643f and SLRS-6) reference solutions was prepared (see Table S1†). For the analysis, the river water SLRS-6 was diluted by a factor of 2 with 1% (v/v) nitric acid, while the NIST 1643f sample was diluted once by a factor of 2 and once by a factor of 10. Using the multi-element stock solution seven calibration solutions were prepared to cover the concentration range of the analytes in the reference samples for the external calibration. For the standard addition, multi-element solutions with a similar concentration to the corresponding reference sample but without the matrix elements were added to two aliquots of the reference samples. Indium was added to all solutions (samples, external calibrations, standard additions) at a concentration of 5 μg kg−1 as an internal standard. At least one isotope per element was measured with a dwell time of 500 ms using one sweep and 5 replicates.
000 μg kg−1 (Fig. S1†). In both samples, Ca, Na, Mg, and K are the most abundant elements. Since NIST 1643f has higher concentrations but is otherwise similar to SLRS-6, a multi-element stock solution with similar analyte ratios as in the two (NIST 1643f and SLRS-6) reference solutions was prepared (see Table S1†). For the analysis, the river water SLRS-6 was diluted by a factor of 2 with 1% (v/v) nitric acid, while the NIST 1643f sample was diluted once by a factor of 2 and once by a factor of 10. Using the multi-element stock solution seven calibration solutions were prepared to cover the concentration range of the analytes in the reference samples for the external calibration. For the standard addition, multi-element solutions with a similar concentration to the corresponding reference sample but without the matrix elements were added to two aliquots of the reference samples. Indium was added to all solutions (samples, external calibrations, standard additions) at a concentration of 5 μg kg−1 as an internal standard. At least one isotope per element was measured with a dwell time of 500 ms using one sweep and 5 replicates.
Previous reports have indicated that the N2 MICAP-MS has a similar matrix tolerance as a conventional Ar ICP-MS.10,24 Since Ca is the major matrix element in the investigated reference samples, the influence of an elevated calcium concentration on the analyte signal was studied. Therefore, five solutions with 1–100 mg kg−1 calcium (as nitrate) were prepared and analyzed using two different sample introduction systems (SN and Des). Each solution contained a 1000-fold dilution of the multi-element standard VI (Merck, Germany) and a total of 300 μg kg−1 boron.
Plasma gas temperatures were estimated using three different methods. The first is based on the pressure reduction in the interface when the plasma is sampled relative to the pressure at room temperature with the interface pump and the gas flows on.35 The other two methods are based on the abundance ratios of metal-oxide ions to the metal ions (MO+/M+) and their known dissociation energies. According to Longerich,36 the temperature can be estimated from the mass-bias corrected rare earth element (REE) oxide abundance ratios and their known dissociation energies with a linear regression.38 This method however appeared to overestimate the temperatures for an Ar plasma substantially when compared to other Boltzmann plot methods.39,40 Houk and Praphairaksit (abbr. as H&P)37 on the other hand suggested estimating the gas temperature from these abundance ratios via statistical thermodynamics, including partition functions and spectroscopic constants of the corresponding species.
Single element REE solutions of 100 μg kg−1 La, Ce, Pr, Eu, Tb, Ho, Tm, and Lu were prepared from stock solutions (Inorganic Ventures, USA) in 1% (v/v) nitric acid and contained 10 μg kg−1 Rh as internal standard. Each isotope was measured for 500 ms in one sweep with 5 replicates. The mass discrimination was determined from the molar sensitivities of the REE isotopes. The oxygen density in the central channel of the plasma was estimated from the solution flux (as H2O) reaching the ion source. This was determined from the difference in solution uptake and spray chamber drain. The measurements were carried out with and without aerosol desolvation using the N2 MICAP-MS and an Ar-based ICP-MS (Elan 6100 DRCII, PerkinElmer/Sciex, Canada) for comparison.
Data evaluation
Element mass fractions were determined from the blank-corrected signal intensities while taking the blank-corrected signal of the internal standard and the dilution factor into account. The uncertainties of the results were estimated from the relative standard deviation of the corresponding reference samples. Limits of quantification (LOQs) were obtained from ten times the standard deviation of the blank divided by the slope of the calibration curve. Furthermore, limits of detection (LODs) were determined from three times the standard deviation of the blank divided by the elements' blank-corrected sensitivities.The temperature in the ICP region was calculated with the pressure reduction method, which is based on the correlation of pressure and temperature:35
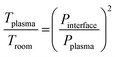 | (1) |
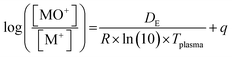 | (2) |
The third method to calculate the plasma temperature is based on the expression of the dissociation constant from statistical thermodynamics:37
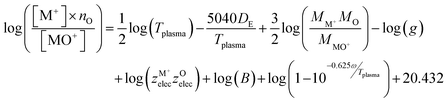 | (3) |
Results and discussion
Influence of aerosol desolvation
Experiments were performed to study if the signal enhancement observed with aerosol desolvation10 is primarily due to a reduced solvent load or an increased aerosol transfer to the ICP. To separate the two processes, the aerosol of the externally mounted spray chamber was guided through the Apex-Q system, and measurements were carried out with and without active aerosol desolvation. Ion signals were measured for a suite of selected elements while the nebulizer gas flow rate was increased from 800 mL min−1 to 1000 mL min−1. With aerosol desolvation, a five to ten times lower metal-oxide ratio was obtained.Sensitivity ratios for the measured isotopes with relative to without aerosol desolvation are given in Table S2.† Elements with ionization energies below that of NO were only moderately affected by aerosol desolvation. Interestingly, however, there was a mass-dependent effect, with lighter isotopes showing slight enhancement for the desolvated aerosol at low nebulizer gas flow rates while isotopes above m/z 133 were suppressed to a similar extent (Fig. S2†). When increasing the gas flow rate, however, the enhancement for lighter isotopes gradually ceased and eventually a similar suppression was observed for all these isotopes. Elements with a high first ionization energy (IE ≥ 9 eV) such as Be, Zn, As, Se, Cd, and Te on the other hand exhibited remarkable enhancement with the desolvated aerosol, which is assumed to be caused by the lower abundance of NO in the ion source. NO has an ionization energy of (9.264 eV),38 which is close to or below that of these elements. It is thus likely that lowering the abundance of NO in the plasma by reducing the water load (approx. 40% at 800 mL min−1) increases the ion yield of these elements and overcompensates for the suppression observed for the other elements of similar mass. In general, however, it appears that aerosol desolvation alone only leads to a substantial change in the ion yield for elements with high IE, while other elements are only moderately affected. This would indicate that the sensitivity enhancements frequently observed for aerosols produced with aerosol desolvation are primarily due to a higher transport efficiency of the elements from the nebulizer to the plasma and possibly a higher nebulization efficiency rather than by a change in plasma conditions.
Temperature determination
The plasma temperatures were determined for conventional solution nebulization and using the Apex-Q system with the nebulizer directly inserted into the heated spray chamber. The results for the three methods35–37 are summarized in Table 2 and compared to the temperatures of an Ar ICP with the same vacuum interface and MS configuration (Elan DRC II).| Method | N2 MICAP | Ar ICP | ||
|---|---|---|---|---|
| SN | Des | SN | Des | |
| Pressure reduction | 5220 K | 5270 K | 5780 K | 5680 K |
| Longerich | 12850 K | 13800 K | 13170 K | 12600 K |
| H&P LaO+/La+ | 6350 K | 6430 K | 6620 K | 6710 K |
| H&P CeO+/Ce+ | 5910 K | 5980 K | 6060 K | 6250 K |
| H&P PrO+/Pr+ | 6200 K | 6300 K | 6080 K | 6300 K |
The gas temperature estimates obtained by the pressure reduction method showed similar values with and without aerosol desolvation but differed between the N2 and Ar plasmas. The similar results for the introduction methods can be explained by the fact that they were estimated at the respective optimized conditions of the N2 MICAP-MS. The higher nebulizer gas flow rate used with aerosol desolvation leads to a cooling of the plasma similar to the water vapor present without aerosol desolvation. Reducing the nebulizer gas flow rate with aerosol desolvation from 1000 mL min−1 to 900 mL min−1 resulted in higher temperature estimates (see Table S3†). Nonetheless, the results of the pressure reduction method suggest that the gas temperature of an Ar ICP is about ∼500 K higher than that of the N2 MICAP. This difference, however, may be due to a slightly lower oxide ratio (2.6% CeO+vs. 2.9% CeO+) or the bigger pressure fluctuations that were observed when measuring the interface pressure with the plasma off. However, comparing the N2 MICAP temperature estimates with reported values for an Ar ICP, which was determined to be ∼5000 K by Fulford and Douglas35 and 5280 K by Houk and Praphairaksit,37 no substantial difference can be seen (Table 2). The temperatures obtained via the Longerich method36 are higher than the other values, however, this method has always resulted in values between 9000 K and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. Using statistical thermodynamics, temperatures of ∼5900–6700 K were obtained. These temperatures are similar for both sample introduction methods and the difference between the N2 and the Ar plasma is less than 300 K for the individual REEs. However, these differences are smaller than those between different REEs. This element dependency (TLa > TPr > TCe) and its magnitude has been previously reported by Houk and Praphairaksit37 and is possibly a result of assumptions made within this model. The substantial differences between H&P and the pressure reduction method are assumed to be due to uncertainties in the oxygen density used in our experiments. Whereas Houk and Praphairaksit37 measured the water load as trapped water vapor, the liquid sample uptake into the plasma was used in this work, which was determined from the difference in solution uptake and spray chamber drain. Based on these findings, the N2 plasma appears to have a gas temperature that is in the range of ∼5000–6000 K and is thus comparable to an Ar ICP.
000 K. Using statistical thermodynamics, temperatures of ∼5900–6700 K were obtained. These temperatures are similar for both sample introduction methods and the difference between the N2 and the Ar plasma is less than 300 K for the individual REEs. However, these differences are smaller than those between different REEs. This element dependency (TLa > TPr > TCe) and its magnitude has been previously reported by Houk and Praphairaksit37 and is possibly a result of assumptions made within this model. The substantial differences between H&P and the pressure reduction method are assumed to be due to uncertainties in the oxygen density used in our experiments. Whereas Houk and Praphairaksit37 measured the water load as trapped water vapor, the liquid sample uptake into the plasma was used in this work, which was determined from the difference in solution uptake and spray chamber drain. Based on these findings, the N2 plasma appears to have a gas temperature that is in the range of ∼5000–6000 K and is thus comparable to an Ar ICP.
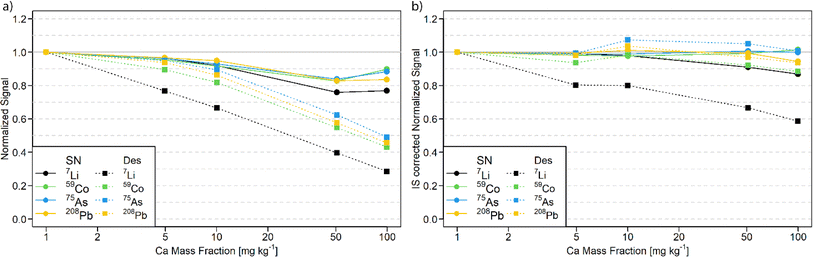
Calcium matrix tolerance
The tolerance of the N2 MICAP-MS against a calcium matrix was investigated, since Ca is a common major matrix element in environmental water samples such as the studied reference materials. Therefore, multi-element solutions with increasing amounts of Ca were measured and the signal suppression was determined with and without aerosol desolvation (Fig. 1 and Table S4†).As shown in Fig. 1a, the effect of the calcium matrix is noticeable in both cases but more pronounced for the desolvated aerosol. While the signal suppression of lighter elements is more pronounced (up to 30% and 70% for SN and Des, respectively), heavier elements and elements with higher IE exhibit the lowest signal decrease (see Table S4†). The former is most likely due to space charge effects, but the latter cannot be explained entirely. The fact that less suppression was observed for high IE elements would indicate that the ionization suppression by NO is reduced by a decreased water load in the plasma. For the remaining elements, greater suppression was observed. However, this suggests a greater loss of aerosol in the desolvation unit. The observed signal suppression without aerosol desolvation is similar to that reported for a sodium10 or iron matrix.24
The use of an internal standard of similar m/z was found to generally reduce this matrix effect. Elements of low m/z such as Li cannot be corrected using In as an internal standard. For aerosol desolvation, 7Li exhibited a signal suppression of 72% without normalization to the internal standard and a 41% suppression with internal stnadard correction at 100 mg kg−1. However, heavier isotopes deviated by less than 12% with solution nebulization (see Fig. 1b).
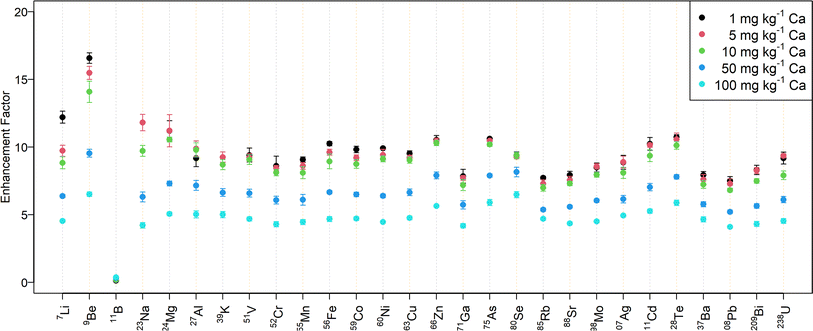
Fig. 2 shows the signal enhancement for the desolvated aerosol in samples with different amounts of calcium. While the signal intensity increased by a factor of 10–15 for a mass fraction up to 10 mg kg−1 Ca, the enhancement factor is approximately 5 for 100 mg kg−1 Ca. The abundance normalized sensitivities obtained with N2 MICAP-MS are listed in Table S5† for selected elements.
In contrast to all the other elements investigated, boron was suppressed by up to a factor of seven when aerosol desolvation was used. At the same time, the effect of the Ca matrix on B without aerosol desolvation was very similar to Be (suppression by 7% at 100 mg kg−1 Ca), while it caused an increase in B sensitivity with aerosol desolvation (increase by 165%, see Table S4†). Spectra of solutions with increasing boron concentration did not reveal the occurrence of boron-containing molecular ions and thus boron is assumed to be lost in the desolvation unit due to its high volatility.43 Jakubowski et al.28 suggested that boron in a dry aerosol is more adsorbed at the walls of the sample introduction system than in a wet aerosol. Furthermore, they observed elevated boron concentrations in the desolvation system drain.
It is important to note, that the attainable LODs for the desolvated aerosol are not only improved by the signal enhancement, because the abundance of spectral interferences is reduced as well (e.g.40Ca16O1H+vs.57Fe+ or 14N16O2+vs.46Ti+). Memory effects in the desolvation system, however, usually lead to elevated background signals for a blank sample and the LODs for a desolvated aerosol in most cases did not improve by the same factor as the sensitivity enhancement (Table S6†). While a higher signal-to-noise ratio for the desolvated aerosol results in lower detection limits for most elements, the loss of boron in the desolvation unit increased the LOD significantly.
Quantitative analyses using N2 MICAP-MS
Mass fractions for all elements were determined and, to account for possible spectral interferences, some elements were quantified using multiple isotopes, e.g.56Fe and 57Fe. Since plasma-based background ions occur predominantly at m/z 14–19, m/z 28–34, m/z 42–46, and m/z 56–58, and Ar-based molecular ions were not detected, the most abundant isotopes could be used for most elements. However, residual Ar in the nitrogen gas occurring at m/z 40 and not identified ions at m/z 80, m/z 82, m/z 108, and m/z 110,20 were found to affect the signal-to-background ratios attainable for Ca and Se in particular.Quantitative analyses using solution nebulization
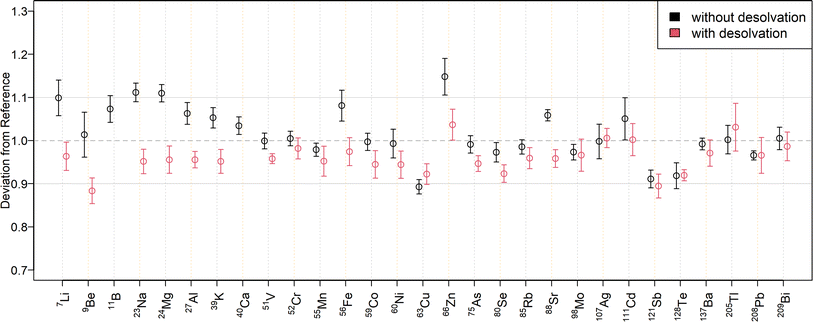
The relative deviations of the mass fractions determined in a twofold diluted NIST SRM 1643f to the reference values are shown in Fig. 3 for external calibration and in Fig. 4 when using standard additions. The corresponding mass fractions are listed in Table S7† for all measured isotopes. As can be seen in Fig. 3, most results for SN are within a range of ±10% to the reference values. Only 23Na, 24Mg, and 63Cu deviated by ±11%, while 64Zn and 66Zn deviated by +16% and +15%, respectively. Mass fractions obtained by standard addition (Fig. 4) were all within a ±10% range of the reference values. The higher deviation of the matrix elements may be because they were determined at the upper end of the calibration curve, since the determination with the tenfold dilution of NIST SRM 1643f (Table S8†) resulted in lower deviations. The mass fractions measured in the SLRS-6 reference material were found to match the certified values (Table 3 or Fig. S3 and S4†). Values were typically found within a range of ±10% of the certified values, except for 63Cu, which deviated by −12% when determined by standard addition. While the mass fraction of iron in SLRS-6 was quantified successfully on both 56Fe and 57Fe, the mass fraction in NIST SRM 1643f was overestimated when employing 57Fe regardless of the quantification method (external calibration or standard addition). This difference between the two reference standards can be explained by the approx. three times higher Ca/Fe mass fractions in NIST SRM 1643f compared to SLRS-6 (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 μg kg−1/92.51 μg kg−1vs. 8770 μg kg−1/84.5 μg kg−1). This results in a higher abundance of 40Ca16O1H+, which interferes in the determination of iron on 57Fe. In addition to the elements with a certified value, the mass fractions of Li, B, Co, Rb, and Tl were determined in SLRS-6 (Table 3) and U was quantified in NIST SRM 1643f (Tables S7 and S8†). However, the mass fractions of Be, Se, Ag, Cd, Te, and Bi were below their respective LOQ (Table S6†) in SLRS-6 and could thus not be quantified.
140 μg kg−1/92.51 μg kg−1vs. 8770 μg kg−1/84.5 μg kg−1). This results in a higher abundance of 40Ca16O1H+, which interferes in the determination of iron on 57Fe. In addition to the elements with a certified value, the mass fractions of Li, B, Co, Rb, and Tl were determined in SLRS-6 (Table 3) and U was quantified in NIST SRM 1643f (Tables S7 and S8†). However, the mass fractions of Be, Se, Ag, Cd, Te, and Bi were below their respective LOQ (Table S6†) in SLRS-6 and could thus not be quantified.
| Quantified isotope | Reference | SN ext. cal. | SN std. add. | Des ext. cal | Des std. add. | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 2SD | Mean | 2SD | Mean | 2SD | Mean | 2SD | Mean | 2SD | |
| a From GeoReM database.44 b Not certified. c Below LOQ. d Not determined. | ||||||||||
| 7Li | 0.53a | —c | —c | 0.54 | 0.06 | 0.47 | 0.05 | |||
| 11B | 7.39a | 7.8 | 0.4 | 5.69 | 0.20 | —c | —c | |||
| 23Na | 2770 | 220 | 2860 | 60 | —d | 2610 | 90 | —d | ||
| 24Mg | 2140 | 60 | 2250 | 30 | —d | 2050 | 50 | —d | ||
| 25Mg | 2140 | 60 | 2260 | 50 | —d | 2060 | 70 | —d | ||
| 27Al | 33.9 | 2.2 | 33.6 | 0.6 | 32.5 | 0.8 | 31.9 | 0.3 | 33.3 | 0.4 |
| 39K | 650 | 50 | 670 | 12 | —d | 614 | 14 | —d | ||
| 40Ca | 8770 | 200 | 8710 | 130 | —d | 8700 | 160 | —d | ||
| 41K | 650 | 50 | 648 | 10 | —d | 620 | 30 | —d | ||
| 51V | 0.352 | 0.006 | 0.351 | 0.024 | 0.362 | 0.016 | 0.361 | 0.014 | 0.351 | 0.008 |
| 52Cr | 0.252 | 0.012 | 0.255 | 0.012 | 0.234 | 0.012 | 0.249 | 0.005 | 0.236 | 0.008 |
| 53Cr | 0.252 | 0.012 | 0.24 | 0.04 | 0.24 | 0.05 | 0.251 | 0.020 | 0.227 | 0.008 |
| 55Mn | 2.12 | 0.10 | 2.13 | 0.06 | 1.972 | 0.014 | 2.10 | 0.08 | 1.93 | 0.06 |
| 56Fe | 85 | 4 | 84.1 | 1.8 | 82.5 | 1.4 | 81 | 3 | 78.1 | 2.6 |
| 57Fe | 85 | 4 | 86.0 | 1.6 | 86.7 | 1.0 | 90 | 6 | 87.5 | 2.6 |
| 59Co | 0.053b | 0.012 | 0.074 | 0.012 | 0.072 | 0.002 | 0.065 | 0.006 | 0.057 | 0.004 |
| 60Ni | 0.617 | 0.022 | 0.59 | 0.05 | 0.66 | 0.02 | 0.64 | 0.03 | 0.676 | 0.024 |
| 62Ni | 0.617 | 0.022 | 0.58 | 0.16 | 0.61 | 0.04 | 0.63 | 0.03 | 0.61 | 0.03 |
| 63Cu | 24.0 | 1.8 | 22.5 | 0.3 | 22.0 | 0.4 | 24.1 | 0.6 | 22.3 | 0.6 |
| 64Zn | 1.76 | 0.12 | 1.84 | 0.12 | 1.85 | 0.10 | 1.73 | 0.12 | 1.84 | 0.10 |
| 65Cu | 24.0 | 1.8 | 22.8 | 0.3 | 21.17 | 0.22 | 23.8 | 0.8 | 21.6 | 0.6 |
| 66Zn | 1.76 | 0.12 | 1.81 | 0.14 | 1.85 | 0.05 | 1.75 | 0.12 | 1.83 | 0.14 |
| 75As | 0.57 | 0.08 | 0.57 | 0.03 | 0.51 | 0.04 | 0.53 | 0.03 | 0.518 | 0.026 |
| 85Rb | 1.41a | 1.41 | 0.05 | 1.34 | 0.03 | 1.43 | 0.03 | 1.280 | 0.016 | |
| 88Sr | 40.7 | 0.3 | 37.2 | 0.6 | 38.8 | 0.4 | 37.5 | 1.2 | 38.7 | 0.8 |
| 95Mo | 0.215 | 0.018 | 0.296 | 0.015 | 0.208 | 0.014 | 0.201 | 0.008 | 0.196 | 0.006 |
| 98Mo | 0.215 | 0.018 | 0.198 | 0.022 | 0.194 | 0.016 | 0.198 | 0.012 | 0.192 | 0.010 |
| 121Sb | 0.338 | 0.006 | 0.357 | 0.016 | 0.314 | 0.014 | 0.354 | 0.020 | 0.308 | 0.014 |
| 137Ba | 14.3 | 0.5 | 14.4 | 0.4 | 13.4 | 0.4 | 14.5 | 0.4 | 13.2 | 0.5 |
| 138Ba | 14.3 | 0.5 | 14.9 | 0.4 | 13.8 | 0.5 | 14.2 | 0.8 | 13.4 | 0.6 |
| 205Tl | 0.0085a | 0.0093 | 0.0018 | —c | 0.0062 | 0.0005 | 0.0067 | 0.0014 | ||
| 208Pb | 0.170 | 0.026 | 0.163 | 0.014 | 0.165 | 0.006 | 0.161 | 0.014 | 0.154 | 0.005 |
| 238U | 0.070 | 0.003 | 0.0686 | 0.0024 | 0.073 | 0.004 | 0.070 | 0.003 | 0.0615 | 0.0012 |
Quantitative analyses using aerosol desolvation
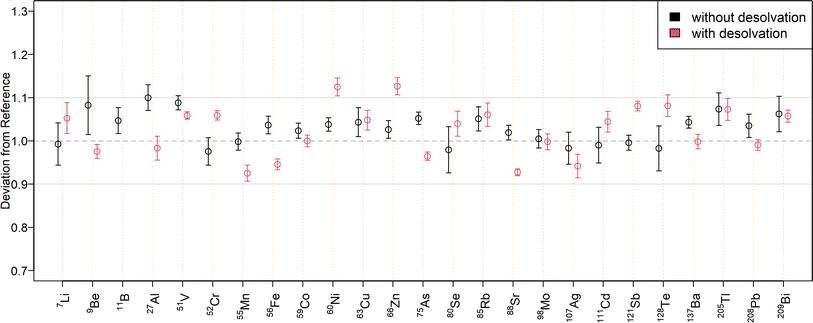
To compare the quantification capabilities of the N2 MICAP-MS when using aerosol desolvation, Fig. 3 depicts the relative deviations of the determined mass fractions in the twofold dilution of NIST SRM 1643f to the reference values for external calibration, while Fig. 4 shows the relative deviations obtained with standard addition. The determined mass fractions can be found in Table S7† for all isotopes. As can be seen in Fig. 3, all isotopes were quantified with a maximum deviation of ±10% of the certified reference values, except 11B, which was overestimated by 88%, and 9Be, and 121Sb, which were underestimated by 12% and 11%, respectively. The mass fractions obtained with aerosol desolvation and standard addition (Fig. 4) were mostly in agreement with the reference values, only 11B was underestimated by 48%, while 60Ni (12%), 64Zn (17%) and 66Zn (13%) were overestimated. The mass fraction of 40Ca could not be determined in the twofold dilution, because the ion signal exceeded the dynamic range of the detector (109 cps). However, the obtained mass fraction from the tenfold dilution could be accurately determined. As already mentioned in the matrix tolerance section, the boron sensitivity decreased with aerosol desolvation, since boron was lost in the desolvator. The determined mass fractions for SLRS-6 with aerosol desolvation were all within a ±10% range of the certified values, except for 238U, which deviated by −12% when determined by standard addition.When comparing the quantification with and without aerosol desolvation it can be seen that both trueness and precision are similar. In both SN and Des N2 MICAP-MS, the obtained mass fractions are within a range of ±12% to the reference values, with only 64Zn and 66Zn varying by +15% and +16% for SN using external calibration and by +17% and +13% for Des using standard addition with the twofold diluted NIST SRM 1643f reference material. With the tenfold dilution, these deviations decreased and were all lower than 10%, except for 64Zn with Des and standard addition, which decreased from +17% to +13%. For SLRS-6, the deviations of Zn are all within a range of ±5% to the reference values. However, as already mentioned, the determination of boron with aerosol desolvation did not yield accurate values and thus cannot be recommended. The precision of external calibration and standard addition as well as with and without aerosol desolvation was found to be similar, which is also because the errors were estimated from the standard deviations of the diluted certified reference solutions.
Conclusions
The plasma gas temperature of the nitrogen-sustained microwave inductively coupled atmospheric pressure plasma was calculated with three different methods. The values at the optimized operating conditions for conventional solution nebulization and desolvated sample introduction were found to be very similar. In addition, the values for the N2 MICAP were found to be in good agreement with gas temperatures reported for an Ar ICP, indicating that the plasma gas temperature is not substantially different. For a typical optimization, the temperature was found to be in the range of ∼5000–6000 K regardless of the plasma gas or the sample introduction method.The presence of a calcium matrix resulted in moderate suppression of the analyte sensitivities up to 30% when aspirating solutions of up to 100 mg kg−1 Ca with solution nebulization or 70% with aerosol desolvation. Indium was found to be a suitable internal standard for most elements investigated and compensated matrix effects for up to 100 mg kg−1 of Ca. The exception (Li) would require the use of an additional internal standard. Using aerosol desolvation can be beneficial due to the observed signal enhancement and lower limits of detection. However, matrix effects and possible analyte losses in the desolvator need to be considered.
The quantitative analyses of NIST 1643f and SLRS-6 have shown that using the nitrogen plasma source for inorganic mass spectrometry, the mass fractions of 30 elements could be determined. The most abundant isotopes of potassium, calcium, chromium, iron, and selenium could be used for their quantification. Since the obtained mass fractions from external calibration and standard addition are in good agreement, no substantial matrix effect was observed for the water reference materials. The trueness and precision using external calibration and standard addition as well as with and without aerosol desolvation were found to be similar. These results show that SN N2 MICAP-MS can be used as a more economic, competitive, or complementary instrument to Ar ICP-MS for routine analysis.
Author contributions
Monique Kuonen investigation, formal analysis, writing – original draft. Bodo Hattendorf supervision, writing – review & editing. Detlef Günther conceptualization, funding acquisition, supervision, writing – review & editing.Conflicts of interest
The authors have neither financial nor personal conflicts of interest to declare.Acknowledgements
The authors acknowledge the technical support from Ashok Menon and Jovan Jevtic of Radom Corporation, the assistance from the D-CHAB central and electronic workshop through Philippe Trüssel and Tiago Ferreira des Neves respectively, the help from the D-PHYS laboratory support group and the financial support from the Swiss National Science Foundation (project number 200021_197224).References
- J. Jevtic, A. Menon and V. Pikelja, US Pat., PCT/US2014/024306, 2014 Search PubMed.
- C. I. M. Beenakker, Spectrochim. Acta, Part B, 1976, 31, 483–486 CrossRef.
- J. Hubert, M. Moisan and A. Ricard, Spectrochim. Acta, Part B, 1979, 34, 1–10 CrossRef.
- Q. Jin, C. Zhu, M. W. Borer and G. M. Hieftje, Spectrochim. Acta, Part B, 1991, 46, 417–430 CrossRef.
- Y. Okamoto, M. Yasuda and S. Murayama, Jpn. J. Appl. Phys., 1990, 29, L670–L672 CrossRef CAS.
- Y. Okamoto, J. Anal. At. Spectrom., 1994, 9, 745–749 RSC.
- D. Potter, J. Anal. At. Spectrom., 2008, 23, 690–693 RSC.
- K. J. Jankowski and E. Reszke, Encyclopedia of Analytical Chemistry, 2023, pp. 1–80 Search PubMed.
- A. J. Schwartz, Y. Cheung, J. Jevtic, V. Pikelja, A. Menon, S. J. Ray and G. M. Hieftje, J. Anal. At. Spectrom., 2016, 31, 440–449 RSC.
- M. Schild, A. Gundlach-Graham, A. Menon, J. Jevtic, V. Pikelja, M. Tanner, B. Hattendorf and D. Günther, Anal. Chem., 2018, 90, 13443–13450 CrossRef CAS PubMed.
- S. Greenfield, I. L. Jones, C. T. Berry and J. M. Mermet, J. Anal. At. Spectrom., 1964, 4, 559–560 Search PubMed.
- R. H. Wendt and V. A. Fassel, Anal. Chem., 1965, 37, 920–922 CrossRef CAS.
- R. S. Houk, Anal. Chem., 1980, 52, 2283–2289 CrossRef CAS.
- W.-L. Shen, T. M. Davidson, J. T. Creed and J. A. Caruso, Appl. Spectrosc., 1990, 44, 1003–1010 CrossRef CAS.
- M. C. Lomax-Vogt, F. Liu and J. W. Olesik, Spectrochim. Acta, Part B, 2021, 179, 106098 CrossRef CAS.
- I. Feldmann, N. Jakubowski and D. Stuewer, Fresenius. J. Anal. Chem., 1999, 365, 415–421 CrossRef CAS.
- S. D. Tanner and V. I. Baranov, J. Am. Soc. Mass Spectrom., 1999, 10, 1083–1094 CrossRef CAS.
- B. Hattendorf and D. Günther, J. Anal. At. Spectrom., 2000, 15, 1125–1131 RSC.
- I. Feldmann, W. Tittes, N. Jakubowski, D. Stuewer and U. Giessmann, J. Anal. At. Spectrom., 1994, 9, 1007–1014 RSC.
- C. Neff, P. Becker, B. Hattendorf and D. Günther, J. Anal. At. Spectrom., 2021, 36, 1750–1757 RSC.
- M. R. Hammer, Spectrochim. Acta, Part B, 2008, 63, 456–464 CrossRef.
- K. M. Thaler, A. J. Schwartz, C. Haisch, R. Niessner and G. M. Hieftje, Talanta, 2018, 180, 25–31 CrossRef CAS PubMed.
- F. Hallwirth, M. Wolfgang and H. Wiltsche, J. Anal. At. Spectrom., 2023, 38, 1682–1690 RSC.
- A. Winckelmann, J. Roik, S. Recknagel, C. Abad and Z. You, J. Anal. At. Spectrom., 2023, 38, 1253–1260 RSC.
- R. C. Hutton and A. N. Eaton, J. Anal. At. Spectrom., 1987, 2, 595–598 RSC.
- S. E. Long and R. F. Browner, Spectrochim. Acta, 1988, 43, 1471 Search PubMed.
- R. Tsukahara and M. Kubota, Spectrochim. Acta, Part B, 1990, 45, 581–589 CrossRef.
- N. Jakubowski, I. Feldmann and D. Stuewer, Spectrochim. Acta, Part B, 1992, 47, 107–118 CrossRef.
- P. W. J. M. Boumans and F. J. de Boer, Spectrochim. Acta, Part B, 1976, 31, 355–375 CrossRef.
- L. Halicz and D. Günther, J. Anal. At. Spectrom., 2004, 19, 1539–1545 RSC.
- M. Kuonen, G. Niu, B. Hattendorf and D. Günther, J. Anal. At. Spectrom., 2023, 38, 758–765 RSC.
- R. Serrano, G. Grindlay, L. Gras and J. Mora, Talanta, 2024, 271, 125666 CrossRef CAS PubMed.
- S. Mukta and A. Gundlach-Graham, J. Anal. At. Spectrom., 2024, 39, 491–499 RSC.
- Z. You, A. Akkuş, W. Weisheit, T. Giray, S. Penk, S. Buttler, S. Recknagel and C. Abad, J. Anal. At. Spectrom., 2022, 37, 2556–2562 RSC.
- J. E. Fulford and D. J. Douglas, Appl. Spectrosc., 1986, 40, 971–974 CrossRef CAS.
- H. P. Longerich, J. Anal. At. Spectrom., 1989, 4, 491–497 RSC.
- R. S. Houk and N. Praphairaksit, Spectrochim. Acta, Part B, 2001, 56, 1069–1096 CrossRef.
- CRC Handbook of Chemistry and Physics, ed. J. Rumble, CRC Press, Boca Raton, FL, 104th edn, 2023 Search PubMed.
- M. Kubota, N. Fudagawa and A. Kawase, Anal. Sci., 1989, 5, 701–706 CrossRef CAS.
- N. Shibata, N. Fudagawa and M. Kubota, Spectrochim. Acta, Part B, 1993, 48, 1127–1137 CrossRef.
- H. Niu and R. S. Houk, Spectrochim. Acta, Part B, 1996, 51, 779–815 CrossRef.
- NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 20899, 2021 Search PubMed.
- M. V. Stackelberg, F. Quatram and J. Dressel, Zeitschrift für Elektrochemie und Angew. Phys. Chemie, 1937, 43, 14–28 Search PubMed.
- K. P. Jochum, U. Nohl, K. Herwig, E. Lammel, B. Stoll and A. W. Hofmann, Geostand. Geoanal. Res., 2005, 29, 333–338 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ja00058g |
| This journal is © The Royal Society of Chemistry 2024 |